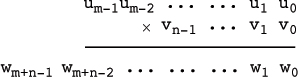
This can be done with, basically, the traditional grade-school method. But rather than develop an array of partial products, it is more efficient to add each new row, as it is being computed, into a row that will become the product.
If the multiplicand is m words, and the multiplier is n words, then the product occupies m + n words (or fewer), whether signed or unsigned.
In applying the grade-school scheme, we would like to treat each 32-bit word as a single digit. This works out well if an instruction that gives the 64-bit product of two 32-bit integers is available. Unfortunately, even if the machine has such an instruction, it is not readily accessible from most high-level languages. In fact, many modern RISC machines do not have this instruction in part because it isn’t accessible from high-level languages and thus would not be used often. (Another reason is that the instruction would be one of a very few that give a two-register result.)
Our procedure is shown in Figure 8–1. It uses halfwords as the “digits.” Parameter w gets the result, and u and v are the multiplier and multiplicand, respectively. Each is an array of halfwords,
with the first halfword (w[0], u[0], and v[0]) being the least significant digit. This is “little-endian” order. Parameters m and n are the number of halfwords in u and v, respectively.
The picture below may help in understanding. There is no relation between m and n; either may be the larger.
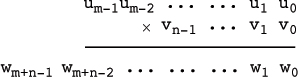
The procedure follows Algorithm M of [Knu2, 4.3.1] but is coded in C and modified
to perform signed multiplication. Observe that the assignment to t in the upper half of Figure 8–1 cannot overflow, because the maximum value that could be assigned to t is (216 – 1)2 + 2(216 – 1) = 232 – 1.
Multiword multiplication is simplest for unsigned operands. In fact, the code of Figure 8–1 performs unsigned multiplication if the “correction” steps (the lines between the three-line comment and the “return” statement) are omitted. An unsigned version can be extended to signed in three ways:
1. Take the absolute value of each input operand, perform unsigned multiplication, and then negate the result if the input operands had different signs.
2. Perform the multiplication using unsigned elementary multiplication, except when multiplying one of the high-order halfwords, in which case use signed × unsigned or signed × signed multiplication.
3. Perform unsigned multiplication and then correct the result somehow.
void mulmns(unsigned short w[], unsigned short u[],
unsigned short v[], int m, int n) {
unsigned int k, t, b;
int i, j;
for (i = 0; i < m; i++)
w[i] = 0;
for (j = 0; j < n; j++) {
k = 0;
for (i = 0; i < m; i++) {
t = u[i]*v[j] + w[i + j] + k;
w[i + j] = t; // (I.e., t & 0xFFFF).
k = t >> 16;
}
w[j + m] = k;
}
// Now w[] has the unsigned product. Correct by
// subtracting v*2**16m if u < 0, and
// subtracting u*2**16n if v < 0.
if ((short)u[m - 1] < 0) {
b = 0; // Initialize borrow.
for (j = 0; j < n; j++) {
t = w[j + m] - v[j] - b;
w[j + m] = t;
b = t >> 31;
}
}
if ((short)v[n - 1] < 0) {
b = 0;
for (i = 0; i < m; i++) {
t = w[i + n] - u[i] - b;
w[i + n] = t;
b = t >> 31;
}
}
return;
}
FIGURE 8–1. Multiword integer multiplication, signed.
The first method requires passing over as many as m + n input halfwords to compute their absolute value. Or, if one operand is positive and one is negative, the method requires passing over as many as max(m, n) + m + n halfwords to complement the negative input operand and the result. Perhaps more serious, the algorithm would alter its inputs (which we assume are passed by address), which may be unacceptable in some applications. Alternatively, it could allocate temporary space for them, or it could alter them and later change them back. All these alternatives are unappealing.
The second method requires three kinds of elementary multiplication (unsigned × unsigned, unsigned × signed, and signed × signed) and requires sign extension of partial products on the left, with 0’s or 1’s, making each partial product take longer to compute and add to the running total.
We choose the third method. To see how it works, let u and v denote the values of the two signed integers being multiplied, and let them be of lengths M and N bits, respectively. Then the steps in the upper half of Figure 8–1 erroneously interpret u as an unsigned quantity, having value u + 2MuM – 1, where uM – 1 is the sign bit of u. That is, uM – 1 = 1 if u is negative, and uM – 1 = 0 otherwise. Similarly, the program interprets v as having value v + 2NuN – 1.
The program computes the product of these unsigned numbers—that is, it computes
(u + 2MuM – 1)(v + 2NvN – 1) = uv + 2MuM – 1v + 2NvN – 1u + 2M + NuM – 1vN – 1.
To get the desired result (uv), we must subtract from the unsigned product the value 2MuM – 1v + 2NvN – 1u. There is no need to subtract the term 2M + NuM – 1vN – 1, because we know that the result can be expressed in M + N bits, so there is no need to compute any product bits more significant than bit position M + N – 1. These two subtractions are performed by the steps below the three-line comment in Figure 8–1. They require passing over a maximum of m + n halfwords.
It might be tempting to use the program of Figure 8–1 by passing it an array of fullword integers—that is, by “lying across the interface.”
Such a program will work on a little-endian machine, but not on a big-endian one.
If we had stored the arrays in the reverse order, with u[0] being the most significant halfword (and the program altered accordingly), the “lying”
program would work on a big-endian machine, but not on a little-endian one.
Here we consider the problem of computing the high-order 32 bits of the product of
two 32-bit integers. This is the function of our basic RISC instructions multiply high signed (mulhs) and multiply high unsigned (mulhu).
For unsigned multiplication, the algorithm in the upper half of Figure 8–1 works well. Rewrite it for the special case m = n = 2, with loops unrolled, obvious simplifications made, and the parameters changed to 32-bit unsigned integers.
For signed multiplication, it is not necessary to code the “correction steps” in the
lower half of Figure 8–1. These can be omitted if proper attention is paid to whether the intermediate results
are signed or unsigned (declaring them to be signed causes the right shifts to be
sign-propagating shifts). The resulting algorithm is shown in Figure 8–2. For an unsigned version, simply change all the int declarations to unsigned.
The algorithm requires 16 basic RISC instructions in either the signed or unsigned version, four of which are multiplications.
int mulhs(int u, int v) {
unsigned u0, v0, w0;
int u1, v1, w1, w2, t;
u0 = u & 0xFFFF; u1 = u >> 16;
v0 = v & 0xFFFF; v1 = v >> 16;
w0 = u0*v0;
t = u1*v0 + (w0 >> 16);
w1 = t & 0xFFFF;
w2 = t >> 16;
w1 = u0*v1 + w1;
return u1*v1 + w2 + (w1 >> 16);
}
FIGURE 8–2. Multiply high signed.
Assume that the machine can readily compute the high-order half of the 64-bit product of two unsigned 32-bit integers, but we wish to perform the corresponding operation on signed integers. We could use the procedure of Figure 8–2, but that requires four multiplications; the procedure to be given [BGN] is much more efficient than that.
The analysis is a special case of that done to convert Knuth’s Algorithm M from an unsigned to a signed multiplication routine (Figure 8–1). Let x and y denote the two 32-bit signed integers that we wish to multiply together. The machine will interpret x as an unsigned integer, having the value x + 232x31, where x31 is the most significant bit of x (that is, x31 is the integer 1 if x is negative, and 0 otherwise). Similarly, y under unsigned interpretation has the value y + 232y31.
Although the result we want is the high-order 32 bits of xy, the machine computes
(x + 232x31)(y + 232y31) = xy + 232(x31 y + y31x) + 264x31y31.
To get the desired result, we must subtract from this the quantity 232(x31y + y31x) + 264x31y31. Because we know that the result can be expressed in 64 bits, we can perform the arithmetic modulo 264. This means that we can safely ignore the last term, and compute the signed high-order product as shown below (seven basic RISC instructions).
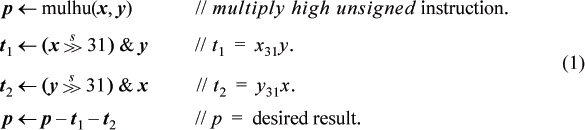
The reverse transformation follows easily. The resulting program is the same as (1), except with the first instruction changed to multiply high signed and the last operation changed to p ← p + t1 + t2.
It is nearly a triviality that one can multiply by a constant with a sequence of shift left and add instructions. For example, to multiply x by 13 (binary 1101), one can code
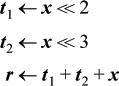
where r gets the result.
In this section, left shifts are denoted by multiplication by a power of 2, so the above plan is written r ← 8x + 4x + x, which is intended to show four instructions on the basic RISC and most machines.
What we want to convey here is that there is more to this subject than meets the eye. First of all, there are other considerations besides simply the number of shift’s and add’s required to do a multiplication by a given constant. To illustrate, below are two plans for multiplying by 45 (binary 101101).
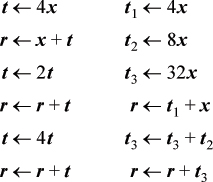
The plan on the left uses a variable t that holds x shifted left by a number of positions that corresponds to a 1-bit in the multiplier. Each shifted value is obtained from the one before it. This plan has these advantages:
• It requires only one working register other than the input x and the output r.
• Except for the first two, it uses only 2-address instructions.
• The shift amounts are relatively small.
The same properties are retained when the plan is applied to any multiplier.
The scheme on the right does all the shift’s first, with x as the operand. It has the advantage of increased parallelism. On a machine with sufficient instruction-level parallelism, the scheme on the right executes in three cycles, whereas the scheme on the left, running on a machine with unlimited parallelism, requires four.
In addition to these details, it is nontrivial to find the minimum number of operations to accomplish multiplication by a constant, where by an “operation” we mean an instruction from a typical computer’s set of add and shift instructions. In what follows, we assume this set consists of add, subtract, shift left by any constant amount, and negate. We assume the instruction format is three-address. However, the problem is no easier if one is restricted to only add (adding a number to itself, and then adding the sum to itself, and so on, accomplishes a shift left of any amount), or if one augments the set by instructions that combine a left shift and an add into one instruction (that is, such an instruction computes z ← x + (y << n)). We also assume that only the least-significant 32 bits of the product are wanted.
The first improvement to the basic binary decomposition scheme suggested above is to use subtract to shorten the sequence when the multiplier contains a group of three or more consecutive 1-bits. For example, to multiply by 28 (binary 11100), we can compute 32x – 4x (three instructions) rather than 16x + 8x + 4x (five instructions). On two’s-complement machines, the result is correct (modulo 232) even if the intermediate result of 32x overflows.
To multiply by a constant m with the basic binary decomposition scheme (using only shift’s and add’s) requires
2pop(m) – 1 – δ
instructions, where δ = 1 if m ends in a 1-bit (is odd), and δ = 0 otherwise. If subtract is also used, it requires
4g(m) + 2s(m) – 1 – δ
instructions, where g(m) is the number of groups of two or more consecutive 1-bits in m, s(m) is the number of “singleton” 1-bits in m, and δ has the same meaning as before.
For a group of size 2, it makes no difference which method is used.
The second improvement is to treat specially groups that are separated by a single 0-bit. For example, consider m = 55 (binary 110111). The group method calculates this as (64x – 16x) + (8x – x), which requires six instructions. Calculating it as 64x – 8x – x, however, requires only four. Similarly, we can multiply by binary 110111011 as illustrated by the formula 512x – 64x – 4x – x (six instructions).
The formulas above give an upper bound on the number of operations required to multiply a variable x by any given number m. Another bound can be obtained based on the size of m in bits—that is, on n = ⌊log2 m ⌋ + 1.
THEOREM. Multiplication of a variable x by an n-bit constant m, m ≥ 1, can be accomplished with at most n instructions of the type add, subtract, and shift left by any given amount.
Proof. (Induction on n.) Multiplication by 1 can be done in 0 instructions, so the theorem holds for n = 1. For n > 1, if m ends in a 0-bit, then multiplication by m can be accomplished by multiplying by the number consisting of the left n – 1 bits of m (that is, by m / 2), in n – 1 instructions, followed by a shift left of the result by one position. This uses n instructions altogether.
If m ends in binary 01, then mx can be calculated by multiplying x by the number consisting of the left n – 2 bits of m, in n – 2 instructions, followed by a left shift of the result by 2, and an add of x. This requires n instructions altogether.
If m ends in binary 11, then consider the cases in which it ends in 0011, 0111, 1011, and 1111. Let t be the result of multiplying x by the left n – 4 bits of m. If m ends in 0011, then mx = 16t + 2x + x, which requires (n – 4) + 4 = n instructions. If m ends in 0111, then mx = 16t + 8x – x, which requires n instructions. If m ends in 1111, then mx = 16t + 16x – x, which requires n instructions. The remaining case is that m ends in 1011.
It is easy to show that mx can be calculated in n instructions if m ends in 001011, 011011, or 111011. The remaining case is 101011.
This reasoning can be continued, with the “remaining case” always being of the form 101010...10101011. Eventually, the size of m will be reached, and the only remaining case is the number 101010...10101011. This n-bit number contains n / 2 + 1 1-bits. By a previous observation, it can multiply x with 2(n / 2 + 1) – 2 = n instructions.
Thus, in particular, multiplication by any 32-bit constant can be done in at most 32 instructions, by the method described above. By inspection, it is easily seen that for n even, the n-bit number 101010...101011 requires n instructions, and for n odd, the n-bit number 1010101...010110 also requires n instructions, so the bound is tight.
The methodology described so far is not difficult to work out by hand or to incorporate into an algorithm such as might be used in a compiler; but such an algorithm would not always produce the best code, because further improvement is sometimes possible. This can result from factoring the multiplier m or some intermediate quantity along the way of computing mx. For example, consider again m = 45 (binary 101101). The methods described above require six instructions. Factoring 45 as 5 · 9, however, gives a four-instruction solution:
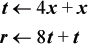
Factoring can be combined with the binary decomposition methods. For example, multiplication by 106 (binary 1101010) requires seven instructions by binary decomposition, but writing it as 7 · 15 + 1 leads to a five-instruction solution. For large constants, the smallest number of instructions that accomplish the multiplication may be substantially fewer than the number obtained by the simple binary decomposition methods described. For example, m = 0xAAAAAAAB requires 32 instructions by binary decomposition, but writing this value as 2 · 5 · 17 · 257 · 65537 + 1 gives a ten-instruction solution. (Ten instructions is probably not typical of large numbers. The factorization reflects the simple bit pattern of alternate 1’s and 0’s.)
There does not seem to be a simple formula or procedure that determines the smallest number of shift and add instructions that accomplishes multiplication by a given constant m. A practical search procedure is given in [Bern], but it does not always find the minimum. Exhaustive search methods to find the minimum can be devised, but they are quite expensive in either space or time. (See, for example, the tree structure of Figure 15 in [Knu2, 4.6.3].)
This should give an idea of the combinatorics involved in this seemingly simple problem. Knuth [Knu2, 4.6.3] discusses the closely related problem of computing am using a minimum number of multiplications. This is analogous to the problem of multiplying by m using only addition instructions.
1. Show that for a 32×32 ⇒ 64 bit multiplication, the low-order 32 bits of the product are the same whether the operands are interpreted as signed or unsigned integers.
2. Show how to modify the mulhs function (Figure 8–2) so that it calculates the low-order half of the 64-bit product, as well as the high-order
half. (Just show the calculation, not the parameter passing.)
3. Multiplication of complex numbers is defined by
(a + bi)(c + di) = ac – bd + (ad + bc)i.
This can be done with only three multiplications.1 Let
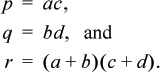
Then the product is given by
p – q + (r – p – q)i,
which the reader can easily verify.
Code a similar method to obtain the 64-bit product of two 32-bit unsigned integers using only three multiplication instructions. Assume the machine’s multiply instruction produces the 32 low-order bits of the product of two 32-bit integers (which are the same for signed and unsigned multiplication).