Chapter 18
Word Problems and Other Hot Topics
INTRODUCTION
On the SAT, word problems can present some special difficulties. The test writers love these problems because there are many ways that they can lead you into traps. This chapter presents the most effective strategies for avoiding these traps, and it covers the topics that are most likely to trip you up on hard problems.
USE BITE-SIZED PIECES
The first step in conquering word problems is to break the question into bite-sized pieces. After you Read the Full Question (RTFQ), go back to the beginning. As soon as you find something simple to do, do it! Let’s use the question below as an example.

6. In a particular bowl of candy-coated chocolates, there are twice as many red pieces as brown ones, three times as many green pieces as brown ones, and half as many yellow pieces as green ones. If there are a total of 75 candy-coated chocolates in the bowl, how many of them are not yellow?
A) 10
B) 15
C) 55
D) 60
Here’s How to Crack It
Remember to Read the Full Question (RTFQ) first, and underline what the question is asking for. Now go back to the beginning and take it one bite-sized piece at a time.
In a particular bowl of candy-coated chocolates, there are twice as many red pieces as brown ones…
You could tackle this piece of information by saying that red = 2x and brown = x. Now tackle the next bite-sized piece.
…three times as many green pieces as brown ones…
Since brown was x, green must be 3x. Move on to another bite-sized piece.
…and half as many yellow pieces as green ones.
Since green was 3x, yellow must be 
![]() (3x) = 1.5x. Move on to another bite-sized piece.
(3x) = 1.5x. Move on to another bite-sized piece.
If there are a total of 75 candy-coated chocolates in the bowl…
Since 75 is the number of red, brown, green, and yellow pieces, you can say that 2x + x + 3x + x = 75. So 7
![]() x = 75, and thus x = 10. Do not go to the answer choices yet! Very likely, 10 is there and is a wrong answer. Instead, you should finish Reading the Full Question so that you know what the question is actually asking for.
x = 75, and thus x = 10. Do not go to the answer choices yet! Very likely, 10 is there and is a wrong answer. Instead, you should finish Reading the Full Question so that you know what the question is actually asking for.
…how many of them are not yellow?
Notice that the question is not asking for x, but rather for 2x + x + 3x, which equals 6x, or 60. The correct answer is (D).

Using bite-sized pieces will help you break problems into a series of simple, manageable steps, improving both your accuracy and efficiency.
START WITH THE MOST STRAIGHTFORWARD PIECE
The example above was relatively simple because it presented the pieces in a logical order. But this won’t always happen on harder SAT questions. Two of the test writers’ favorite tricks are to make you do unnecessary work and to mix up the logical order, hiding the most useful information in the middle or near the end of the problem. Take a look at the next example.

7. Which of the following expressions is equivalent to (2a2b3c4d5)3 ?
A) 8a6b6c12d15
B) 8a6b6c7d15
C) 8a6b9c12d15
D) 8a6b9c7d15
Here’s How to Crack It
Is it helpful to calculate (2a2)3? What about (d5)3? In this case, a quick scan of the answer choices tells you that this would be a waste of time. But what happens if you calculate just (b3)3? That lets you quickly get rid of two wrong answer choices, (A) and (B). When you compare the remaining ones, you only have to calculate (c4)3 to get rid of another wrong answer choice, (D), and select the correct answer, (C). What if, instead, you started by calculating (c4)3? Again, you can quickly get rid of two wrong answer choices, (B) and (D), and then you would only have to calculate (b3)3 to get rid of another wrong answer choice, (A), and select the correct answer, (C). Always use process of elimination as you work the problem, or POE-as-you-go. Don’t waste time working all the way through it.

Let’s practice using bite-sized pieces with a word problem, eliminating after each piece.

4. Anthony is joining a tae kwon do class that charges a monthly membership fee of $19.99. A tax of 7% is applied to the monthly membership fee, and an additional graduation fee of $15 is charged each time he moves up a belt level. If Anthony moves up 2 belt levels in n months, which of the following represents his total charge, in dollars, for that period of membership?
A) 1.07(19.99n + 30)
B) 1.07(19.99n) + 30
C) 1.07n(19.99 + 2n)
D) 1.07n(19.99) + 2n
Here’s How to Crack It
The first two lines of the word problem tell you that the base fee is $19.99 plus 7% tax for each month. All four answer choices start off with exactly that information (1.07 times 19.99 times n), so starting with this initial information will waste your time. The middle part of the word problem tells you that he moves up two belt levels, which means an extra $30. You can eliminate (C) and (D) at this point, since 2n would be 4, which isn’t in the question. Since there is no mention of a tax being applied to that $30, you can also eliminate (A), and now you can select the only remaining option, (B).

To summarize: Break the problem into bite-sized pieces, and start with the most straightforward piece, which is not necessarily the first piece of the problem.
PLUG IN THE ANSWERS (PITA)
In the previous chapter, we saw how useful it can be to Plug In whenever there are variables in the answer choices. A closely related technique is Plugging In the Answers (PITA for short). When the answers contain numbers rather than variables, see if you can Plug In the Answers! Let’s look at an example.


10. A cargo ship currently holds two-thirds of its maximum capacity by weight. If seven tons of cargo were added to the ship, it would hold 75% of its maximum capacity. What is the maximum capacity, in tons, of the ship?
A) 48
B) 60
C) 84
D) 96
To Plug In the Answers, follow these simple steps:
1. Label the answer choices to avoid careless mistakes and trap answers.
2. If the question asks for the greatest or smallest value, start there. Otherwise, start with one of the answers in the middle.
3. Work the steps, using Bite-Sized Pieces.
4. Eliminate answers that are too big or small.
5. When one of the answers works—STOP.
Here’s How to Crack It
First, label the answer choices. In this case, the answers represent the maximum capacity of the ship, so write something like “max” over the answer choices. Since the question is asking for the greatest value (“maximum”!), start with (D) and work through the problem in bite-sized pieces. We need to find two-thirds of 96, which is 63. Then we need to add 7 more tons, so we have 70. Finally, we ask whether 70 is 75% of 96. That is false, so (D) is incorrect. Here’s what your work should look like so far:
A cargo ship currently holds two-thirds of its maximum capacity by weight. If seven tons of cargo were added to the ship, it would hold three-fourths of its maximum capacity. What is the maximum capacity, in tons, of the ship?
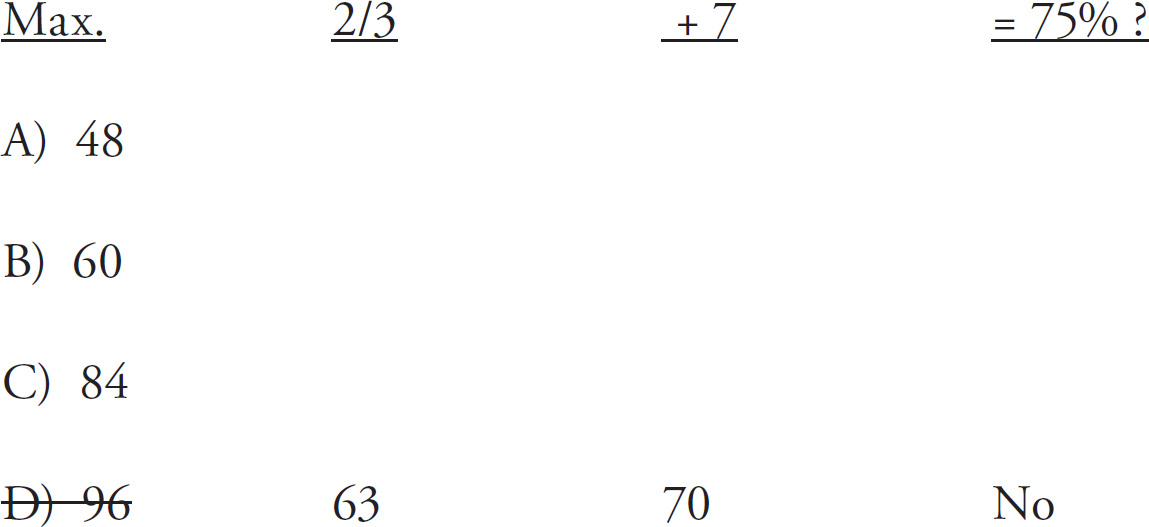
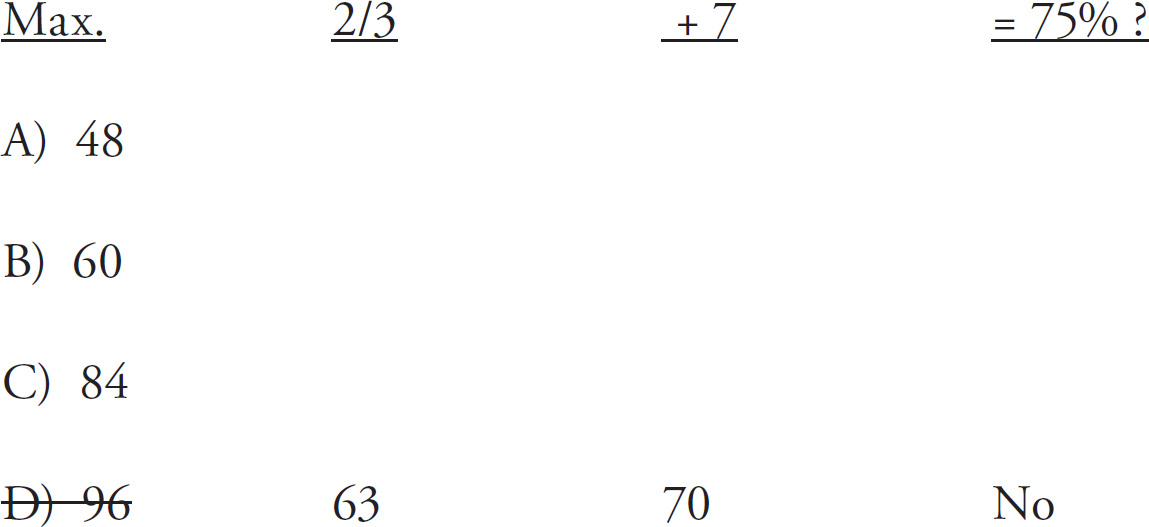
Does it matter which answer we try next? Remember that we’re looking for a maximum! So let’s try (C). Two-thirds of 84 is 56. Add 7 more tons and we have 63. Is 63 equal to 75% of 84? Yes, it is, so (C) is the correct answer. Here’s what your work should look like now:
A cargo ship currently holds two-thirds of its maximum capacity by weight. If seven tons of cargo were added to the ship, it would hold three-fourths of its maximum capacity. What is the maximum capacity, in tons, of the ship?



Remember how you have to check all the answers when you Plug In your own number? Well, when you Plug In the Answers, you don’t need to check all four answers! There is only one correct answer, so stop as soon as you find it.
Let’s try a more difficult problem.

15. During the 93 days of summer, the number of tourists at a certain resort can be modeled by the function n(d) = 
![]() d2 − 14d + c, where c is a constant and n(d) represents the number of visitors on day number d for 1 ≤ d ≤ 93. The number of visitors on day number 20 was equal to the number of visitors on what number day?
d2 − 14d + c, where c is a constant and n(d) represents the number of visitors on day number d for 1 ≤ d ≤ 93. The number of visitors on day number 20 was equal to the number of visitors on what number day?
A) 40
B) 50
C) 60
D) 70
Here’s How to Crack It
This problem is tougher than the last, but it can be beaten by the same approach. Start by labeling the answers; they represent the number of a day (for example, the 40th day, the 50th day, etc.). Now work the problem in bite-sized pieces. First, we need to know the number of visitors on the 20th day, so plug 20 into the function: n(20) = 
![]() (20)2 − 14(20) + c. This simplifies to −200 + c. What’s c? We don’t know, so we can either just leave it or else plug in our own number for c. Either way will work. Say we leave it; the total we are looking for is −200 + c.
(20)2 − 14(20) + c. This simplifies to −200 + c. What’s c? We don’t know, so we can either just leave it or else plug in our own number for c. Either way will work. Say we leave it; the total we are looking for is −200 + c.
Now tackle the answer choices, starting with one of the answers in the middle. Say we start with (B). Plug 50 into the function: n(50) = 
![]() (50)2 − 14(50) + c. This simplifies to −200 + c. Success! Choice (B) is the correct answer, and you are done working this problem! How does that feel?
(50)2 − 14(50) + c. This simplifies to −200 + c. Success! Choice (B) is the correct answer, and you are done working this problem! How does that feel?

As you can see, if the question is not asking for a greatest or least value, it pays to start with either (B) or (C). If your first choice is not the correct answer, you can usually tell which direction you should go: to the lower or to the higher number.
However, you should always remember there is an exception to this rule. As we’ve seen, when a question asks for the least value (or for the greatest value), you should start with the smallest (or the largest) answer choice. Sometimes, the fact that the test-writers are doing this can be difficult to see. Let’s try an example.

8. Linda has four children: Adam, Baron, Karin, and Darren. Each child was born exactly three years apart. In 2015, their combined ages were 34 years. What was the age in years of the youngest child in 2012?
A) 1
B) 2
C) 3
D) 4
Here’s How to Crack It
Again, start by labeling the answer choices. They represent the age of the youngest child in 2012. Since the problem asks for the age of the youngest child, you start working in bite-sized pieces with (A), the smallest number. The next column could contain the sum of the ages of the four children in 2012, which in this case is: 1 + 4 + 7 + 10 = 22. The final column should contain the sum of the ages of the four children in 2015. This is 3 years later, so you want to add 3 years for each child, or 12 years all together. In this case, that would be 22 + 12 = 34. Finally, you ask whether your calculation equals 34. Since it does, you select (A), and you are done!

As you can see, PITA is a very useful strategy: It can save you time and bail you out when you don’t know how to solve a question. Remember, when you PITA, do the following:
1. Label the answer choices.
2. If the question asks for the greatest or smallest value, start there. Otherwise, start with one of the answers in the middle.
3. Work the steps, using Bite-Sized Pieces.
4. Eliminate answers that are too big or small.
5. When one of the answer works—STOP.
To practice Plugging In the Answers, try the drill below. Then go back though the previous chapters and see if Plugging In the Answers would increase your speed on any of the questions you’ve already solved.
TRY IT EXERCISE 1
See Chapter 20 for complete answers and explanations. Only use your calculator when you are allowed to do so.

11. A physics student was conducting experiments to determine the correct equation to describe the trajectory of a ball that was thrown straight up into the air from a height of five feet above the ground with an initial velocity of 3 feet per second. If the height of the ball is given by the equation h = 5 + 3t − 2t2, where h = height in feet and t = time in seconds, at which of the following values for t will the ball have the greatest height?
A) 0.75
B) 1
C) 1.5
D) 2.5

18. Mrs. Johnson earns $60 more per week than Mr. Johnson. If three-fifths of Mrs. Johnson’s weekly salary is equal to two-thirds of Mr. Johnson’s weekly salary, how much do the Johnsons earn together in one week?
A) $540
B) $780
C) $960
D) $1,140
13. If a and c are positive integers such that 
![]() a = b and b =
a = b and b = 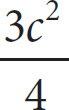
![]() , what is the least possible value of a?
, what is the least possible value of a?
A) 30
B) 36
C) 42
D) 48
For further practice, go online to your Student Tools and complete the Chapter 18 PITA Drill.
HOT TOPICS
You may not yet realize it, but the SAT is pretty predicable. The test writers like to recycle the same old topics, year after year. Below are some of the SAT’s greatest hits, with some helpful strategies to get you through these questions.
Percents
With percent questions, it’s often helpful to translate English to math. The following terms come up frequently, so make sure you know how to translate them.
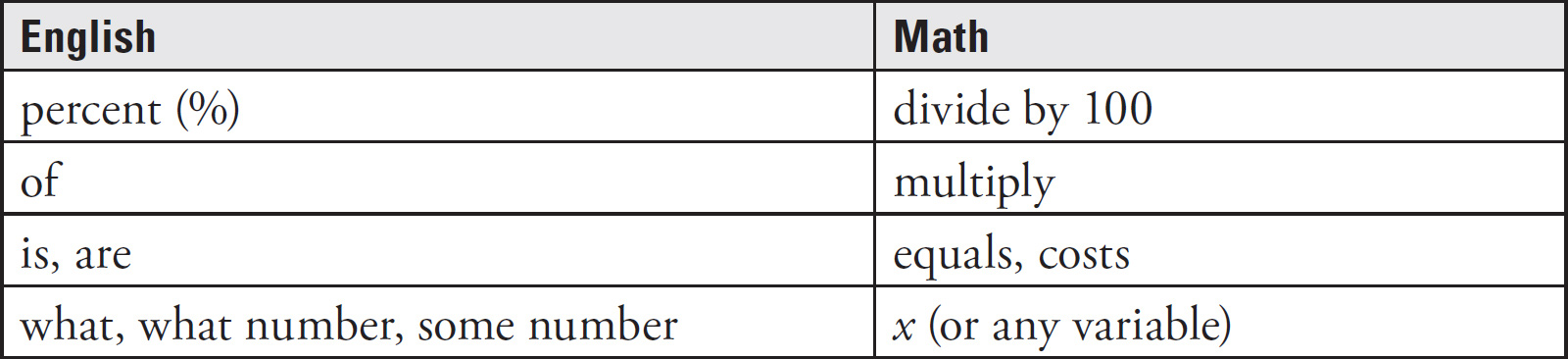

Let’s try an example.


8. A study found that 10% of Americans have a diagnosable personality disorder. If only 5% of people with personality disorders seek psychological treatment, and there are 320 million Americans, how many Americans with personality disorders (in millions) seek psychological treatment?
A) 1.6
B) 3.2
C) 6.4
D) 7.2
Here’s How to Crack It
Remember to use bite-sized pieces and translate. The phrase “10% of Americans” can be translated as 
![]() (320 million) = 32 million. The phrase “5% of people with personality disorders” can now be translated as 5% of 32 million, or
(320 million) = 32 million. The phrase “5% of people with personality disorders” can now be translated as 5% of 32 million, or 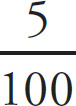
![]() (32 million) = 1.6 million. The correct answer is (A).
(32 million) = 1.6 million. The correct answer is (A).
Arithmetic concepts are often tested with charts and tables. The test writers hide the data you need in the graphic, so you have to pull the right numbers out. Let’s try an example.



5. The following bar-graph shows the densities of several pure metals, measured in grams per cubic centimeter.
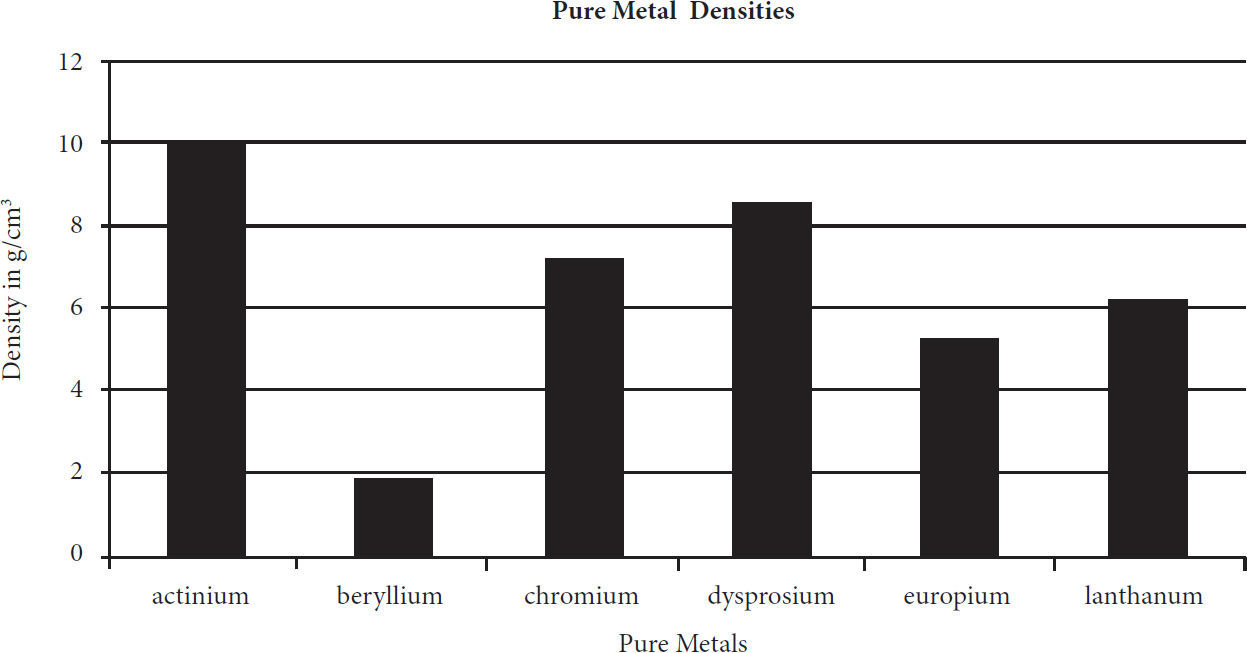

The density of beryllium is approximately what percentage of the density of actinium?
A) 5
B) 10
C) 20
D) 500
Here’s How to Crack It
Plug in the numbers from the chart: The density of beryllium is approximately 2 g/cm3, and the density of actinium is approximately 10 g/cm3. So you can read the question in this way:
2 is approximately what percentage of 10?
Now translate the English into math. 2 = 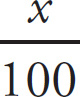
![]() • 10, which reduces to 2 =
• 10, which reduces to 2 = 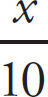
![]() , so x = 20, which is (C).
, so x = 20, which is (C).

Mean, Median, and Mode
Average (also called “arithmetic mean”) is one of the SAT’s favorite subjects. Fortunately, we’ve invented a great tool for handling average problems, called the average pie.


In any average calculation, three components are involved: the total, the number of things, and the average. What makes the average pie so useful is that it represents, in easy-to-read form, the following three versions of the calculation.
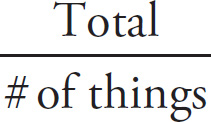
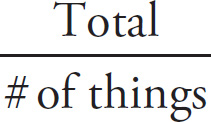 = Average
= Average 
 = #of things #of things × Average = Total
= #of things #of things × Average = Total
Any time you have two of the components, you can easily find the third by using the pie. Just think of the horizontal bar as a division symbol, and the vertical bar as a multiplication symbol. Let’s look at a sample question.


3. The average (arithmetic mean) weight of five gold bars is 9 pounds. After two more bars are added, the average weight increases to 11 pounds. What is the average weight, in pounds, of the two bars that were added?
A) 13
B) 14
C) 15
D) 16
Here’s How to Crack It
Start with the first (bite-sized) sentence. The number of things is 5 and the average is 9, so multiply to find the total and fill in the pie.


Now do the same for the next sentence. There are 7 things, and the average is 11, so the total is 77.
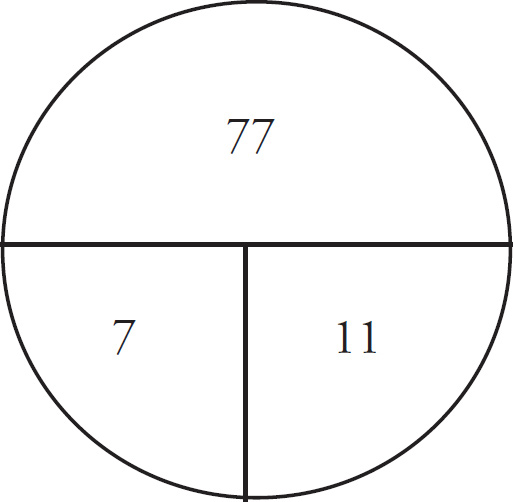

Finally, to tackle the last sentence, make a new pie. There are two things, and the total is 77 − 45 = 32, so divide to get the average, which is 16, and the correct answer is (D).



Along with average, the SAT likes to throw in the related concepts of median and mode. Just remember that median is the middle number of an ordered list, and mode is the number (or numbers) that occurs most often in an ordered list. Try a question.


24.
[1, 3, 9, 10, 17]
A list of five numbers is shown above. A new list of seven numbers is to be formed from the list above by repeating one number, using the remaining numbers once each, and adding one additional number. If the mean and median of the new list is 9, which of the following CANNOT be the mode?
A) 3
B) 9
C) 10
D) 17
Here’s How to Crack It
This is a tough question, so you need to be organized. You know that the mean (average) of the new list is 9, so make a pie and fill it in.
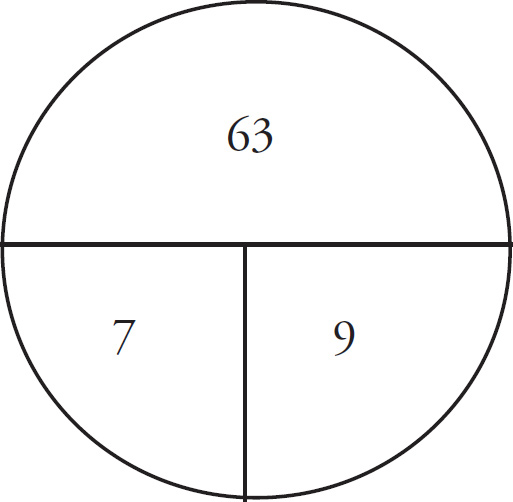

Since the original total is 1 + 3 + 9 + 10 + 17 = 40, and the new total has to be 63 in order for the mean to be 9, the repeated number plus the new number must equal 23.
You also know that the median is 9, so draw 7 spots and put 9 in the middle.
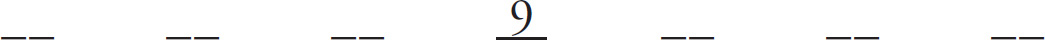
Now, PITA! Start with (B). If the mode is 9, that means the repeated number must be 9. We need to add 23, so the new number is 23 − 9 = 14. Fill in your list:
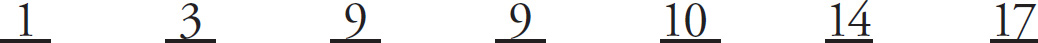
The median is still 9, so (B) checks out, which means it’s NOT the answer.
Which answer should we try next? It’s hard to tell, so if you’re not sure, pick a direction and go! Let’s try (C). If the mode is 10, that’s the number we repeat, so the new number is 23 − 10 = 13. Now fill in the list again.
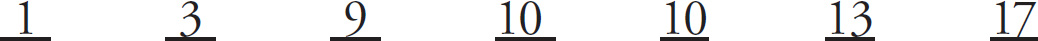
This time, the median is 10, but since the question states that the median is 9, 10 cannot be the mode, and the correct answer is (C).

One of the keys to mean, median, and mode questions is to stay organized. Using the average pie and writing everything down will help you to avoid overlooking important pieces of the puzzle.
Mean, Median, and Mode are the three big statistical concepts you can expect to see on the SAT. Since mean, median, and mode measure the middle (MMM MM!), they are called measures of central tendency. In addition to knowing about the middle of your data, sometimes you want to know about how far the data are spread, or how evenly they are spread. The next two concepts help you do just that.
Range and Standard Deviation
Range is a simple concept: the distance from the lowest to the highest number. Standard Deviation is a less simple concept, but in a nutshell, it measures the evenness of your data. Let’s illustrate both concepts with a concrete example.
Say you poll twenty people in a fast food restaurant on a given day and time. You find that the wealthiest person there makes $400,000 per year, the poorest person there makes $10,000 per year, and everybody else is somewhere in between. Based on this information alone, you can calculate the range of incomes: $400,000 − $10,000 = $390,000. This number does give you some information about the people in the restaurant that day, but not much.
To know more, you would want to know the mean, median, and/or mode. Let’s say you figure out that the mean income of your twenty people is $70,000 per year. This information answers some questions, but leaves others open. Maybe eighteen people make around $55,000 per year, and just two make much less or much more. In that case, most of the people make about the same income: That means that your data have low variability, and so you would have a small standard deviation. But maybe five people make between $10,000 and $30,000; another five make between $30,000 and $60,000; another five make between $60,000 and $70,000; another four make between $75,000 and $100,000, and just one makes $400,000. In that case, people have very different incomes: That means that your data have high variability, so you would have a higher standard deviation.
Luckily, you will never have to calculate a standard deviation for the SAT! Let’s see how the SAT might test your knowledge of range and standard deviation.


15. A billionaire visiting a fast food restaurant decides to give $20,000 to everyone in the restaurant. What effect does this gift have on the mean and standard deviation of the patrons’ incomes for that year?
A) It would increase the mean and the standard deviation.
B) It would increase the mean but have no effect on the standard deviation.
C) It would decrease the mean and the standard deviation.
D) It would decrease the mean but have no effect on the standard deviation.
Here’s How to Crack It
Since standard deviation is a measure of how spread-out or even the data is, the only things that change it are changes to individual data points. If data points are removed or added, or if some increase or decrease while others stay the same, the standard deviation will be affected. In this case, the income of all patrons in the restaurant changed, and the income changed by the same amount for everyone. The standard deviation would therefore be the same, so eliminate (A) and (C). Everyone would have more money this year, so the average or mean income would increase, making (B) the right answer.

Sampling Error and Margin of Error
Some SAT Math questions will feel more like the questions you’d find on a science test. They may give you the data from an experiment and ask questions about it. If you encounter questions that ask about the sampling error of a study, identify the variables and determine whether the conclusion is supported by the experiment or study. When considering the validity of study, check to ensure that the study was conducted on an unbiased sample that is representative of the target population, the conclusion is supported by the data, and the conclusion is based solely on the acquired data.
1. VRT is a company interested in testing out a new virtual reality device to determine whether or not the device will be popular among suburban moms. VRT decides to do product testing at four soccer tournaments around the country, requesting that all interested individuals take part in a live demonstration in each stadium’s lobby. After conducting the testing, VRT collected the data, finding that 65% of the suburban moms who participated were interested in purchasing the virtual reality device. Based on this finding, would VRT be justified in claiming that the majority of suburban moms would likely purchase the new virtual reality device?
A) Yes; the majority of suburban moms who participated in the live demonstration indicated that they would likely purchase the new virtual reality device.
B) Yes; VRT’s study used a representative sample of the target population, indicating that the conclusion is accurate.
C) No; while 65% of the suburban moms who participated in the study indicated that they would likely purchase the virtual reality device, the sample failed to accurately represent the target population.
D) No; the majority of suburban moms indicated that they would not purchase the new virtual reality device.
Here’s How to Crack It
When you encounter questions that ask about the validity of a conclusion, you want to examine the information provided, eliminating answer choices that fail to support the data. In this scenario, VRT wished to determine whether or not suburban moms would be interested in purchasing the new virtual reality device. However, the sample that VRT used was not representative of the target population. Indeed, VRT only went to four locations nationwide that were holding soccer tournaments. Not only did VRT limit the sample by only gathering data from four locations, but VRT also failed to account for the fact that not all suburban moms have children who play soccer. To make matters worse, VRT requested that individuals test the product in the lobby, meaning that only those who were interested in the product would attend the demonstration. Accordingly, VRT would not be justified in claiming that the majority of suburban moms would likely purchase the new virtual reality device as the sample was not representative of the target population; choose (C).

You may also encounter questions that ask discuss confidence intervals and margins of error, measures used to determine that a sample population is representative of the real-world population. Consider a survey with a confidence level of 95% and a margin of error of ± 5. In this scenario, the results should be repeated within 5 percentage points of the sample results 95 out of 100 times.

2. KittenFoodz Incorporated conducted a random survey of 2,500 cat owners from around the United States. 1,750 of the respondents stated that they buy grain-free cat food, while the remainder stated that they do not purchase grain-free cat food. After analyzing the results, KittenFoodz Incorporated determines that the survey results have a margin of error of 4%. Which of the following best represents the range for the percentage of the nation’s cat owners who do not purchase grain-free cat food?
A) 26−34%
B) 30−38%
C) 66−74%
D) 70−78%
Here’s How to Crack It
In order to determine the range for the percentage of the nation’s cat owners who do not purchase grain-free cat food, you must first find the percent of surveyed cat owners who do not purchase grain-free cat food. The question states that of the 2,500 cat owners surveyed, 1,750 of them purchase grain-free cat food. In turn, the number of surveyed cat owners who do not purchase grain-free cat food is 2,500 − 1,750 = 750. Next, determine the percentage of cat owners who do not purchase grain-free cat food by dividing the number of people who do not purchase grain-free cat food by the total number of individuals surveyed: 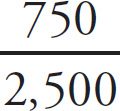
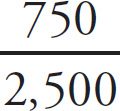 = 0.3 = 30%. Since the margin of error is 4%, the range for the percentage of the nation’s cat owners who do not purchase grain-free cat food is 30% ± 4%, or 26% − 34%. Choice (A) is the correct answer.
= 0.3 = 30%. Since the margin of error is 4%, the range for the percentage of the nation’s cat owners who do not purchase grain-free cat food is 30% ± 4%, or 26% − 34%. Choice (A) is the correct answer.

UNIT CONVERSION
The SAT can also test proportions with questions about unit conversions and scale drawings. Try this one:


33


In tabletop gaming, 28 mm scale figurines are at a 1:64 scale to their real-world equivalents. The above minotaur figurine is 43 millimeters (mm) tall. If this figurine uses 28 mm scale, then how tall would the equivalent real-world minotaur be, rounded to the nearest foot? (Note: 1 foot = 304.8 millimeters)


Here’s How to Crack It
Use proportions to convert the units to feet. First, figure out how many millimeters tall the real-world minotaur would be by setting up a proportion:
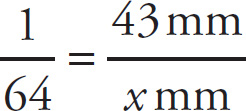
Solve for x by cross-multiplying: x = (43)(64) = 2,752 mm. Next, set up another proportion using the conversion factors. Remember to label your units and have the same units in the numerators and denominators of each fraction:

Cross-multiply to get 304.8x = 2,752. Divide both sides by 304.8 and you get x = 9.03, which rounds to 9 feet.

PROBABILITY
Here’s the basic definition of probability:
Probability = 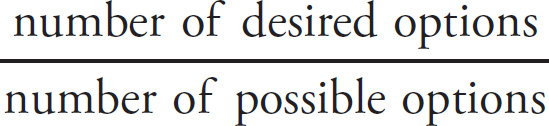
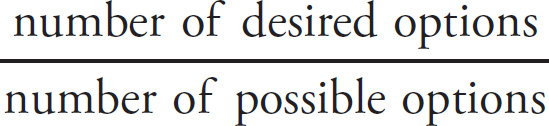
Let’s try a question.


1.
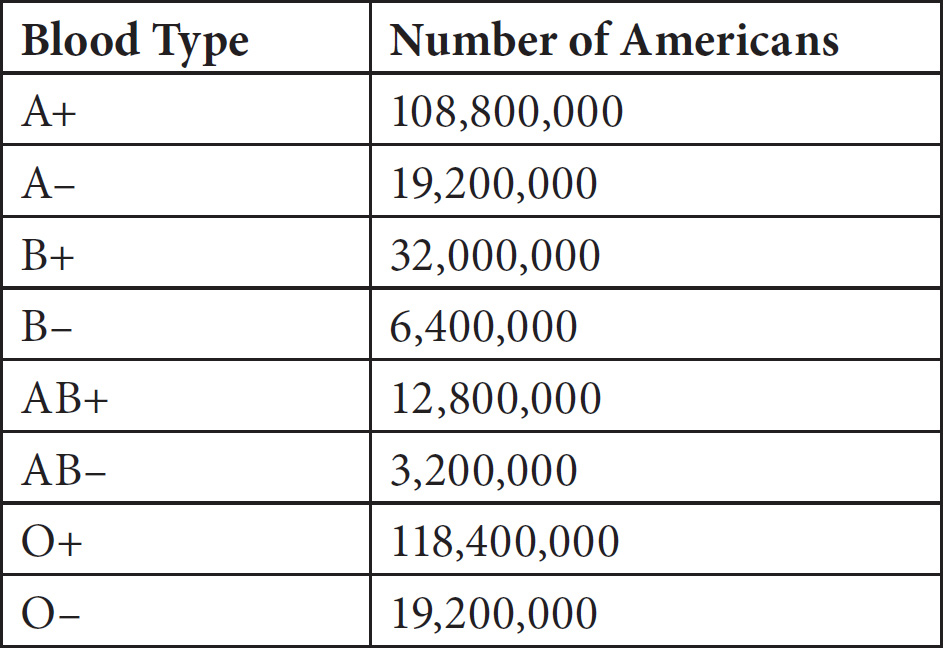

The chart above shows the number of Americans living in the United States that have a particular blood type. Based on the information provided, what is the probability that a randomly selected American in the United States will have neither an A or O blood type?
A) 5%
B) 17%
C) 57%
D) 83%
Here’s How to Crack It
In order to determine the probability that a randomly selected American in the United States will have neither an A nor O blood type you must first find the total population. Add the individual populations to find that the total population is 108,800,000 + 19,200,000 + 32,000,000 + 6,400,000 + 12,800,000 + 3,200,000 + 118,400,000 + 19,200,000 = 320,000,000. Next, you to find that the total population of Americans living in the United States that have neither A nor O blood types. Add the B+, B–, AB+, and AB– populations together to find this total to be 32,000,000 + 6,400,000 +12,800,000 + 3,200,000 = 54,400,000. Finally, you can determine the probability that a randomly selected American in the United States will have neither an A or O blood type by dividing the population that has neither A nor O blood types by the total population of Americans living in the United States; 
 = 17%. Select (B).
= 17%. Select (B).

SEQUENCES
Like several of the topics in this chapter, the most important thing to do with SAT sequences is to organize them. If a question asks you about the first six terms of a sequence, make slots for each term and label them, like this:
It also helps to look for patterns that will make the question easier to manage. Let’s try an example.

9.


In the sequence shown above, the first term is 
![]() for all values of j greater than 2. Each term after the first is equal to the preceding term multiplied by a constant. Which of the following, in terms of j, is equal to the sixth term of the sequence?
for all values of j greater than 2. Each term after the first is equal to the preceding term multiplied by a constant. Which of the following, in terms of j, is equal to the sixth term of the sequence?
A) 
![]()
B) 
![]()
C) 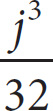
![]()
D) 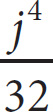
![]()
Here’s How to Crack It
Did the phrase “in terms of” ring a bell? If you thought to Plug In, that was a smart choice! Since j > 2, let’s see what happens if we plug in j = 3. Then, the first three terms are 
![]() ,
, 
![]() , and
, and 
![]() . It’s not easy to spot the relationship between these numbers. Is each term really the preceding term multiplied by a constant? It’s hard to tell, so let’s plug in another number that makes the math easier. If j = 4, then the first three terms are
. It’s not easy to spot the relationship between these numbers. Is each term really the preceding term multiplied by a constant? It’s hard to tell, so let’s plug in another number that makes the math easier. If j = 4, then the first three terms are 
![]() ,
, 
![]() , and 1. Now we can see the relationship. Each term is double the previous term! Armed with this knowledge, you should make a diagram for the first six terms:
, and 1. Now we can see the relationship. Each term is double the previous term! Armed with this knowledge, you should make a diagram for the first six terms:


The sixth term is 8, so that’s our target. Now plug j = 4 into the answers, and pick the one that equals 8; it’s (D).

GROWTH AND DECAY
Sequences reflect numbers changing in a pattern over time. If a population increases by a set factor or percent over time, it is said to be growing exponentially. Things like compound interest, the spread of viruses, or population growth of bacterium might show this sort of growth. Similarly, if it shrinks by a set factor or percent, it is showing exponential decay. The amount of radiation in an isotope or the drug concentration in a person’s body decrease in this way over time. Unlike growth at a constant rate, which involves multiplication and a linear graph, exponential growth involves exponents, hence the name.
When the growth is a percent of the total population, the formula for exponential growth or decay is
final amount = original amount (1 ± rate)number of changes
When the growth is a multiple of the total population, the formula for exponential growth or decay is
final amount = original amount (multiplier)number of changes
Use this knowledge to make the next question easier.

1. Researchers at Cat-In-A-Tube are working on technology that infuses kittens with glow cells that allow cats to glow in the dark. After much work, the researchers have created glow cells that reproduce at a rate of 32% each day. If the researchers start with two glow cells, what is the minimum number of days before the researchers have 550 glow cells?
A) 20
B) 21
C) 22
D) 23
Here’s How to Crack It
In order to determine the minimum number of days before the researchers have 550 glow cells, it is helpful to know the formula for growth: final amount = original amount × (1 + rate)n, where n = the number of changes. Here, you are told that the researchers start with two glow cells and that the population grows at a rate of 32% each day. Accordingly, the growth equation will be 550 = 2(1.32)n. Since the question provides numerical answer choices in ascending order, and asks you to find the minimum number of days to have 550 glow cells, you can use PITA to tackle this question! If you start with (B), the number of glow cells after 21 days will be 550 = 2(1.32)21; 550 = 2(340.45); 550 = 680.90. Since the question asks you to find the minimum number of days it takes to create 550 glow cells, you can now eliminate (C) and (D). Next, check (A). Here, the number of glow cells after 20 days will be 550 = 2(1.32)20; 550 = 2(257.92); 550 = 515.83. Since you have not reached the minimum number of glow cells, eliminate (A) and select (B).

EQUATIONS
Although Plugging In and PITA are extremely valuable strategies, once in a while you just have to write equations and solve. This often happens near the end of the grid-in section. When you’re faced with this situation, translate the word problem carefully, and pay close attention to what the problem is asking for. Let’s try an example.


33. Two rival cell-phone companies have different rate structures. Company X charges a flat rate of $0.15 per minute. Company Y charges $0.25 per minute for the first five minutes, and $0.10 for each minute after the first five. If a call costs the same amount with either plan, how long, in minutes, does that call last?

Here’s How to Crack It
Let’s break this down into bite-sized pieces. We’ll say that x = the number of minutes. A call with the company X costs 0.15x. A call with company Y costs—be careful here—5(0.25) + 0.1(x − 5). The two calls cost the same amount, so set them equal to each other and solve; you should get x = 15, so the correct answer is 15.

Sometimes a question will require two variables, so you’ll need to write two equations. Try the next question.

17. On Saturday, Abeke participated in a long-distance race. After the race, he learned that 11 more runners finished before him than finished after him. He also learned that the total number of runners who finished the race was four times the number of runners who finished after him. How many runners finished the race before Abeke did?


Here’s How to Crack It
When we first discussed bite-sized pieces, we said that the test writers will often hide the most useful information near the end of a problem. That’s definitely the case here. The second sentence is much easier to handle than the first, so let’s deal with it first. But even before that, draw a map or picture of the problem! The total is four times the number who finished after Abeke. Let’s say the total = t, and the number who finished after Abeke = x. Therefore, t = 4x. Now let’s translate the first sentence. If x runners finished after Abeke, then x + 11 finished before him, and the total number is x + (x + 11) + 1 (we have to count Abeke), which simplifies to 2x + 12. Now we can write a second equation: t = 2x + 12. From the first equation, substitute 4x for t in the second equation, so now you have 4x = 2x + 12. Solve this to get x = 6.
Wait! Stop! Don’t forget to RTFQ! The question asks how many runners finished before Abeke, which is x + 11, so the correct answer is 6 + 11 = 17. No matter how pleased you are when you’ve solved a question, don’t forget to READ THE FULL QUESTION.


2. The acceleration rate, a, of a panther is based on the change in velocity, ∆V, in meters per second, and the duration of the time interval at which each of the velocity measurements was taken, ∆T. If a = 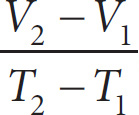
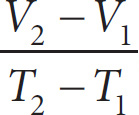 , which of the following expresses the duration of the time interval in terms of a and V ?
, which of the following expresses the duration of the time interval in terms of a and V ?
A) T = 

B) T2 − T1 = 

C) T = 

D) T2 − T1 = 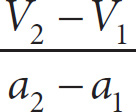
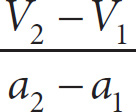
Here’s How to Crack It
While you could Plug In on this question, you are unable to use your calculator and the equation is relatively straightforward to manipulate. By crossing out the phrase “in terms of a and V,” you know that you need to find the duration of the time interval, ∆T, which is expressed as T2 – T1 in the provided equation, a = 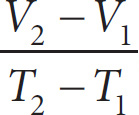
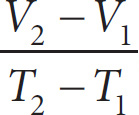 . Accordingly, you can eliminate (A) and (C) because they are simply looking at T, not ∆T expressed as T2 – T1. Next, manipulate the equation, a =
. Accordingly, you can eliminate (A) and (C) because they are simply looking at T, not ∆T expressed as T2 – T1. Next, manipulate the equation, a = 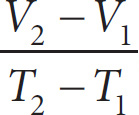
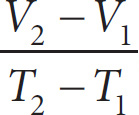 by multiplying both sides of the equation by T2 – T1 to find that a(T2 – T1) = V2 –V1. Finally, isolate T2 – T1 by dividing both sides of the equation by a to find that T2 – T1 =
by multiplying both sides of the equation by T2 – T1 to find that a(T2 – T1) = V2 –V1. Finally, isolate T2 – T1 by dividing both sides of the equation by a to find that T2 – T1 = 
 . Accordingly, eliminate (D) and select (B).
. Accordingly, eliminate (D) and select (B).
TRY IT EXERCISE 2

Questions 27 and 28 refer to the following information.


When acceleration is constant, change in displacement is directly proportional to time and proportional to the square of time. This is expressed by the Merton rule: x = x0 + v0t + 
![]() at2, where x is the final displacement, x0 is the initial displacement, v0 is the initial velocity, a is acceleration, and t is time in seconds. The graph above shows the displacement of an object under constant acceleration.
at2, where x is the final displacement, x0 is the initial displacement, v0 is the initial velocity, a is acceleration, and t is time in seconds. The graph above shows the displacement of an object under constant acceleration.

27. Which of the following expresses t in terms of x, x0, v0, and a?
A) t = 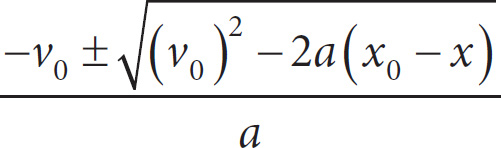
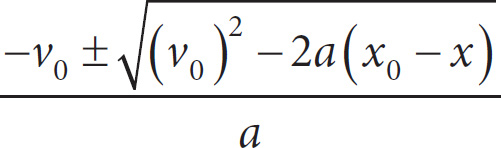
B) t = 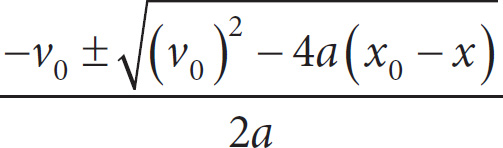
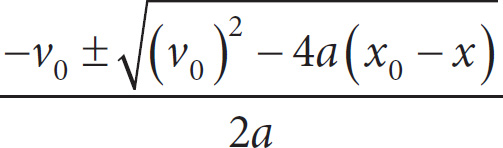
C) t = 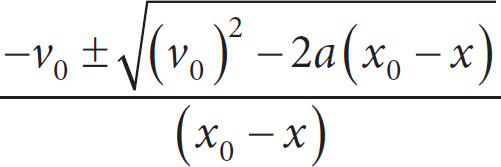
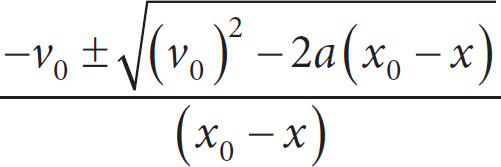
D) t = 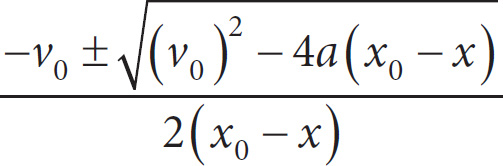
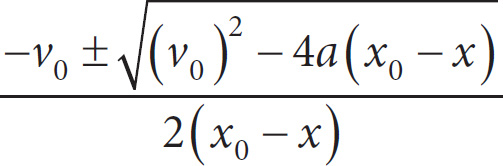
28. According to the graph and equation above, what is the value of a if the initial velocity is 0.5 m/s ?
A) 0.25
B) 0.5
C) 1.0
D) 2.0

For further practice, go online to your Student Tools and complete the Chapter 18 Arithmetic Drill.
Summary
◦ Don’t choke when you see long word problems. Instead, break down the question into manageable, bite-sized pieces and RTFQ.
◦ When you see word problems with numbers in the answer choices that are in either ascending or descending order, PITA. When you find the right answer, pick it and move on!
◦ When dealing with percent questions, translate the English words into math terms.
◦ Remember that Mean, Median, and Mode measure the middle (MMM MM).
• Mean is the average; draw an average pie to keep yourself organized.
• Median is the number in the middle of a set; make sure you put your numbers in order.
• Mode is the most frequently occurring number in a set.
◦ You won’t have to calculate a standard deviation on the SAT, but you should know that standard deviation indicates how data is distributed across a given range.
◦ When asked about sampling error, ensure that the data collection was done properly, the sample is representative of the target population, and the conclusion is based on the data.
◦ Margin of error tells you how representative a study is compared to the target population.
◦ When converting between different units, create a proportion.
◦ Probability can be thought of as 
 .
.
• If a question asks you to find the probability that one event and another event will occur, multiply the individual probabilities together.
• If a question asks you to find the probability that one event or another event occurs, add the individual probabilities together.
◦ When working with sequences, organize and label the terms in the sequence. It’ll make your life much easier.
◦ Growth and Decay
• For questions about exponential growth or decay when growth is a percent of the total population, use the formula final amount = original amount (1 ± rate)number of changes.
• For questions about exponential growth or decay when growth is a multiple of the total population, use the formula final amount = original amount (multiplier)number of changes.
◦ When working with equations, isolate the variable in question.
◦ Make sure that you only use your calculator when you are allowed to do so!