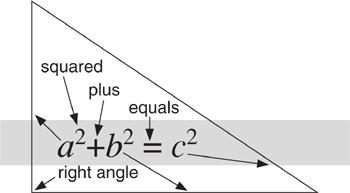
How the three sides of a right-angled triangle are related.
It provides a vital link between geometry and algebra, allowing us to calculate distances in terms of coordinates. It also inspired trigonometry.
Surveying, navigation, and more recently special and general relativity – the best current theories of space, time, and gravity.
Ask any school student to name a famous mathematician, and, assuming they can think of one, more often than not they will opt for Pythagoras. If not, Archimedes might spring to mind. Even the illustrious Isaac Newton has to play third fiddle to these two superstars of the ancient world. Archimedes was an intellectual giant, and Pythagoras probably wasn’t, but he deserves more credit than he is often given. Not for what he achieved, but for what he set in motion.
Pythagoras was born on the Greek island of Samos, in the eastern Aegean, around 570 BC. He was a philosopher and a geometer. What little we know about his life comes from much later writers and its historical accuracy is questionable, but the key events are probably correct. Around 530 BC he moved to Croton, a Greek colony in what is now Italy. There he founded a philosophico-religious cult, the Pythagoreans, who believed that the universe is based on number. Their founder’s present-day fame rests on the theorem that bears his name. It has been taught for more than 2000 years, and has entered popular culture. The 1958 movie Merry Andrew, starring Danny Kaye, includes a song whose lyrics begin:
The square on the hypotenuse
of a right triangle
is equal to
the sum of the squares
on the two adjacent sides.
The song goes on with some double entendre about not letting your participle dangle, and associates Einstein, Newton, and the Wright brothers with the famous theorem. The first two exclaim ‘Eureka!’; no, that was Archimedes. You will deduce that the lyrics are not hot on historical accuracy, but that’s Hollywood for you. However, in Chapter 13 we will see that the lyricist (Johnny Mercer) was spot on with Einstein, probably more so than he realised.
Pythagoras’s theorem appears in a well-known joke, with terrible puns about the squaw on the hippopotamus. The joke can be found all over the internet, but it’s much harder to discover where it came from.1 There are Pythagoras cartoons, T-shirts, and a Greek stamp, Figure 1.
Fig 1 Greek stamp showing Pythagoras’s theorem.
All this fuss notwithstanding, we have no idea whether Pythagoras actually proved his theorem. In fact, we don’t know whether it was his theorem at all. It could well have been discovered by one of Pythagoras’s minions, or some Babylonian or Sumerian scribe. But Pythagoras got the credit, and his name stuck. Whatever its origins, the theorem and its consequences have had a gigantic impact on human history. They literally opened up our world.
The Greeks did not express Pythagoras’s theorem as an equation in the modern symbolic sense. That came later with the development of algebra. In ancient times, the theorem was expressed verbally and geometrically. It attained its most polished form, and its first recorded proof, in the writings of Euclid of Alexandria. Around 250 BC Euclid became the first modern mathematician when he wrote his famous Elements, the most influential mathematical textbook ever. Euclid turned geometry into logic by making his basic assumptions explicit and invoking them to give systematic proofs for all of his theorems. He built a conceptual tower whose foundations were points, lines, and circles, and whose pinnacle was the existence of precisely five regular solids.
One of the jewels in Euclid’s crown was what we now call Pythagoras’s theorem: Proposition 47 of Book I of the Elements. In the famous translation by Sir Thomas Heath this proposition reads: ‘In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.’
No hippopotamus, then. No hypotenuse. Not even an explicit ‘sum’ or ‘add’. Just that funny word ‘subtend’, which basically means ‘be opposite to’. However, Pythagoras’s theorem clearly expresses an equation, because it contains that vital word: equal.
For the purposes of higher mathematics, the Greeks worked with lines and areas instead of numbers. So Pythagoras and his Greek successors would decode the theorem as an equality of areas: ‘The area of a square constructed using the longest side of a right-angled triangle is the sum of the areas of the squares formed from the other two sides.’ The longest side is the famous hypotenuse, which means ‘to stretch under’, which it does if you draw the diagram in the appropriate orientation, as in Figure 2 (left).
Within a mere 2000 years, Pythagoras’s theorem had been recast as the algebraic equation
a2 + b2 = c2
where c is the length of the hypotenuse, a and b are the lengths of the other two sides, and the small raised 2 means ‘square’. Algebraically, the square of any number is that number multiplied by itself, and we all know that the area of any square is the square of the length of its side. So Pythagoras’s equation, as I shall rename it, says the same thing that Euclid said – except for various psychological baggage to do with how the ancients thought about basic mathematical concepts like numbers and areas, which I won’t go into.
Pythagoras’s equation has many uses and implications. Most directly, it lets you calculate the length of the hypotenuse, given the other two sides. For instance, suppose that a = 3 and b = 4. Then c2 = a2 + b2 = 32 + 42 = 9 + 16 = 25. Therefore c = 5. This is the famous 3–4–5 triangle, ubiquitous in school mathematics, and the simplest example of a Pythagorean triple: a list of three whole numbers that satisfies Pythagoras’s equation. The next simplest, other than scaled versions such as 6–8–10, is the 5–12–13 triangle. There are infinitely many such triples, and the Greeks knew how to construct them all. They still retain some interest in number theory, and even in the last decade new features have been discovered.
Instead of using a and b to work out c, you can proceed indirectly, and solve the equation to obtain a provided that you know b and c. You can also answer more subtle questions, as we will shortly see.
Fig 2 Construction lines for Euclid’s proof of Pythagoras. Middle and right: Alternative proof of the theorem. The outer squares have equal areas, and the shaded triangles all have equal areas. Therefore the tilted white square has the same area as the other two white squares combined.
Why is the theorem true? Euclid’s proof is quite complicated, and it involves drawing five extra lines on the diagram, Figure 2 (left), and appealing to several previously proved theorems. Victorian schoolboys (few girls did geometry in those days) referred to it irreverently as Pythagoras’s pants. A straightforward and intuitive proof, though not the most elegant, uses four copies of the triangle to relate two solutions of the same mathematical jigsaw puzzle, Figure 2 (right). The picture is compelling, but filling in the logical details requires some thought. For instance: how do we know that the tilted white region in the middle picture is a square?
There is tantalising evidence that Pythagoras’s theorem was known long before Pythagoras. A Babylonian clay tablet2 in the British Museum contains, in cuneiform script, a mathematical problem and answer that can be paraphrased as:
4 is the length and 5 the diagonal. What is the breadth?
4 times 4 is 16.
5 times 5 is 25.
Take 16 from 25 to obtain 9.
What times what must I take to get 9?
3 times 3 is 9.
Therefore 3 is the breadth.
So the Babylonians certainly knew about the 3–4–5 triangle, a thousand years before Pythagoras.
Another tablet, YBC 7289 from the Babylonian collection of Yale University, is shown in Figure 3 (left). It shows a diagram of a square of side 30, whose diagonal is marked with two lists of numbers: 1, 24, 51, 10 and 42, 25, 35. The Babylonians employed base-60 notation for numbers, so the first list actually refers to 1 + 24/60 + 51/602 + 10/603, which in decimals is 1.4142129. The square root of 2 is 1.4142135. The second list is 30 times this. So the Babylonians knew that the diagonal of a square is its side multiplied by the square root of 2. Since 12 + 12 = 2 =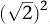 
, this too is an instance of Pythagoras’s theorem.
Fig 3 YBC 7289. Right: Plimpton 322.
Even more remarkable, though more enigmatic, is the tablet Plimpton 322 from George Arthur Plimpton’s collection at Columbia University, Figure 3 (right). It is a table of numbers, with four columns and 15 rows. The final column just lists the row number, from 1 to 15. In 1945 historians of science Otto Neugebauer and Abraham Sachs3 noticed that in each row, the square of the number (say c) in the third column, minus the square of the number (say b) in the second column, is itself a square (say a). It follows that a2 + b2 = c2, so the table appears to record Pythagorean triples. At least, this is the case provided four apparent errors are corrected. However, it is not absolutely certain that Plimpton 322 has anything to do with Pythagorean triples, and even if it does, it might just have been a convenient list of triangles whose areas were easy to calculate. These could then be assembled to yield good approximations to other triangles and other shapes, perhaps for land measurement.
Another iconic ancient civilisation is that of Egypt. There is some evidence that Pythagoras may have visited Egypt as a young man, and some have conjectured that this is where he learned his theorem. The surviving records of Egyptian mathematics offer scant support for this idea, but they are few and specialised. It is often stated, typically in the context of pyramids, that the Egyptians laid out right angles using a 3–4–5 triangle, formed from a length of string with knots at 12 equal intervals, and that archaeologists have found strings of that kind. However, neither claim makes much sense. Such a technique would not be very reliable, because strings can stretch and the knots would have to be very accurately spaced. The precision with which the pyramids at Giza are built is superior to anything that could be achieved with such a string. Far more practical tools, similar to a carpenter’s set square, have been found. Egyptologists specialising in ancient Egyptian mathematics know of no records of string being employed to form a 3–4–5 triangle, and no examples of such strings exist. So this story, charming though it may be, is almost certainly a myth.
If Pythagoras could be transplanted into today’s world he would notice many differences. In his day, medical knowledge was rudimentary, lighting came from candles and burning torches, and the fastest forms of communication were a messenger on horseback or a lighted beacon on a hilltop. The known world encompassed much of Europe, Asia, and Africa – but not the Americas, Australia, the Arctic, or the Antarctic. Many cultures considered the world to be flat: a circular disc or even a square aligned with the four cardinal points. Despite the discoveries of classical Greece this belief was still widespread in medieval times, in the form of orbis terrae maps, Figure 4.
Who first realised the world is round? According to Diogenes Laertius, a third-century Greek biographer, it was Pythagoras. In his book Lives and Opinions of Eminent Philosophers, a collection of sayings and biographical notes that is one of our main historical sources for the private lives of the philosophers of ancient Greece, he wrote: ‘Pythagoras was the first who called the Earth round, though Theophrastus attributes this to Parmenides and Zeno to Hesiod.’ The ancient Greeks often claimed that major discoveries had been made by their famous forebears, irrespective of historical fact, so we can’t take the statement at face value, but it is not in dispute that from the fifth century BC all reputable Greek philosophers and mathematicians considered the Earth to be round. The idea does seem to have originated around the time of Pythagoras, and it might have come from one of his followers. Or it might have been common currency, based on evidence such as the round shadow of the Earth on the Moon during an eclipse, or the analogy with an obviously round Moon.
Fig 4 Map of the world made around 1100 by the Moroccan cartographer al-Idrisi for King Roger of Sicily.
Even for the Greeks, though, the Earth was the centre of the universe and everything else revolved around it. Navigation was carried out by dead reckoning: looking at the stars and following the coastline. Pythagoras’s equation changed all that. It set humanity on the path to today’s understanding of the geography of our planet and its place in the Solar System. It was a vital first step towards the geometric techniques needed for mapmaking, navigation, and surveying. It also provided the key to a vitally important relation between geometry and algebra. This line of development leads from ancient times right through to general relativity and modern cosmology, see Chapter 13. Pythagoras’s equation opened up entirely new directions for human exploration, both metaphorically and literally. It revealed the shape of our world and its place in the universe.
Many of the triangles encountered in real life are not right-angled, so the equation’s direct applications may seem limited. However, any triangle can be cut into two right-angled ones as in Figure 6 (page 11), and any polygonal shape can be cut into triangles. So right-angled triangles are the key: they prove that there is a useful relation between the shape of a triangle and the lengths of its sides. The subject that developed from this insight is trigonometry: ‘triangle measurement’.
The right-angled triangle is fundamental to trigonometry, and in particular it determines the basic trigonometric functions: sine, cosine, and tangent. The names are Arabic in origin, and the history of these functions and their many predecessors shows the complicated route by which today’s version of the topic arose. I’ll cut to the chase and explain the eventual outcome. A right-angled triangle has, of course, a right angle, but its other two angles are arbitrary, apart from adding to 90°. Associated with any angle are three functions, that is, rules for calculating an associated number. For the angle marked A in Figure 5, using the traditional a, b, c for the three sides, we define the sine (sin), cosine (cos), and tangent (tan) like this:
sin A = a/c cos A = b/c tan A = a/b
These quantities depend only on the angle A, because all right-angled triangles with a given angle A are identical except for scale.
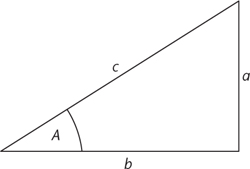
Fig 5 Trigonometry is based on a right-angle triangle.
In consequence, it is possible to draw up a table of the values of sin, cos, and tan, for a range of angles, and then use them to calculate features of right-angled triangles. A typical application, which goes back to ancient times, is to calculate the height of a tall column using only measurements made on the ground. Suppose that, from a distance of 100 metres, the angle to the top of the column is 22°. Take A = 22° in Figure 5, so that a is the height of the column. Then the definition of the tangent function tells us that
tan 22° = a/100
so that
a = 100 tan 22°.
Since tan 22° is 0.404, to three decimal places, we deduce that a = 40.4 metres.
Fig 6 Splitting a triangle into two with right angles.
Once in possession of trigonometric functions, it is straightforward to extend Pythagoras’s equation to triangles that do not have a right angle. Figure 6 shows a triangle with an angle C and sides a, b, c. Split the triangle into two right-angled ones as shown. Then two applications of Pythagoras and some algebra4 prove that
a2 + b2 − 2ab cos C = c2
which is similar to Pythagoras’s equation, except for the extra term − 2ab cos C. This ‘cosine rule’ does the same job as Pythagoras, relating c to a and b, but now we have to include information about the angle C.
The cosine rule is one of the mainstays of trigonometry. If we know two sides of a triangle and the angle between them, we can use it to calculate the third side. Other equations then tell us the remaining angles. All of these equations can ultimately be traced back to right-angled triangles.
Armed with trigonometric equations and suitable measuring apparatus, we can carry out surveys and make accurate maps. This is not a new idea. It appears in the Rhind Papyrus, a collection of ancient Egyptian mathematical techniques dating from 1650 BC. The Greek philosopher Thales used the geometry of triangles to estimate the heights of the Giza pyramids in about 600 BC. Hero of Alexandria described the same technique in 50 AD. Around 240 BC Greek mathematician, Eratosthenes, calculated the size of the Earth by observing the angle of the Sun at noon in two different places: Alexandria and Syene (now Aswan) in Egypt. A succession of Arabian scholars preserved and developed these methods, applying them in particular to astronomical measurements such as the size of the Earth.
Surveying began to take off in 1533 when the Dutch mapmaker Gemma Frisius explained how to use trigonometry to produce accurate maps, in Libellus de Locorum Describendorum Ratione (‘Booklet Concerning a Way of Describing Places’). Word of the method spread across Europe, reaching the ears of the Danish nobleman and astronomer Tycho Brahe. In 1579 Tycho used it to make an accurate map of Hven, the island where his observatory was located. By 1615 the Dutch mathematician Willebrord Snellius (Snel van Royen) had developed the method into essentially its modern form: triangulation. The area being surveyed is covered with a network of triangles. By measuring one initial length very carefully, and many angles, the locations of the corners of the triangle, and hence any interesting features within them, can be calculated. Snellius worked out the distance between two Dutch towns, Alkmaar and Bergen op Zoom, using a network of 33 triangles. He chose these towns because they lay on the same line of longitude and were exactly one degree of arc apart. Knowing the distance between them, he could work out the size of the Earth, which he published in his Eratosthenes Batavus (‘The Dutch Eratosthenes’) in 1617. His result is accurate to within 4%. He also modified the equations of trigonometry to reflect the spherical nature of the Earth’s surface, an important step towards effective navigation.
Triangulation is an indirect method for calculating distances using angles. When surveying a stretch of land, be it a building site or a country, the main practical consideration is that it is much easier to measure angles than it is to measure distances. Triangulation lets us measure a few distances and lots of angles; then everything else follows from the trigonometric equations. The method begins by setting out one line between two points, called the baseline, and measuring its length directly to very high accuracy. Then we choose a prominent point in the landscape that is visible from both ends of the baseline, and measure the angle from the baseline to that point, at both ends of the baseline. Now we have a triangle, and we know one side of it and two angles, which fix its shape and size. We can then use trigonometry to work out the other two sides.
In effect, we now have two more baselines: the newly calculated sides of the triangle. From those, we can measure angles to other, more distant points. Continue this process to create a network of triangles that covers the area being surveyed. Within each triangle, observe the angles to all noteworthy features – church towers, crossroads, and so on. The same trigonometric trick pinpoints their precise locations. As a final twist, the accuracy of the entire survey can be checked by measuring one of the final sides directly.
By the late eighteenth century, triangulation was being employed routinely in surveys. The Ordnance Survey of Great Britain began in 1783, taking 70 years to complete the task. The Great Trigonometric Survey of India, which among other things mapped the Himalayas and determined the height of Mount Everest, started in 1801. In the twenty-first century, most large-scale surveying is done using satellite photographs and GPS (the Global Positioning System). Explicit triangulation is no longer employed. But it is still there, behind the scenes, in the methods used to deduce locations from the satellite data.
Pythagoras’s theorem was also vital to the invention of coordinate geometry. This is a way to represent geometric figures in terms of numbers, using a system of lines, known as axes, labelled with numbers. The most familiar version is known as Cartesian coordinates in the plane, in honour of the French mathematician and philosopher René Descartes, who was one of the great pioneers in this area – though not the first. Draw two lines: a horizontal one labelled x and a vertical one labelled y. These lines are known as axes (plural of axis), and they cross at a point called the origin. Mark points along these two axes according to their distance from the origin, like the markings on a ruler: positive numbers to the right and up, negative to the left and down. Now we can determine any point in the plane in terms of two numbers x and y, its coordinates, by connecting the point to the two axes as in Figure 7. The pair of numbers (x, y) completely specifies the location of the point.
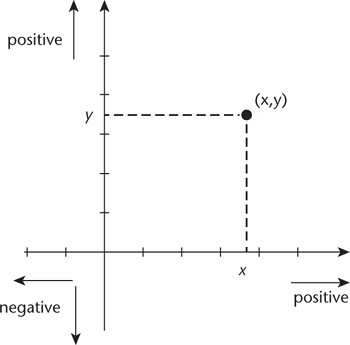
Fig 7 The two axes and the coordinates of a point.
The great mathematicians of seventeenth-century Europe realised that, in this context, a line or curve in the plane corresponds to the set of solutions (x, y) of some equation in x and y. For instance, y = x determines a diagonal line sloping from lower left to top right, because (x, y) lies on that line if and only if y = x. In general, a linear equation – of the form ax + by = c for constants a, b, c – corresponds to a straight line, and vice versa.
What equation corresponds to a circle? This is where Pythagoras’s equation comes in. It implies that the distance r from the origin to the point (x, y) satisfies
r2 = x2 + y2
and we can solve this for r to obtain
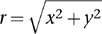
Since the set of all points that lie at distance r from the origin is a circle of radius r, whose centre is the origin, so the same equation defines a circle. More generally, the circle of radius r with centre at (a, b) corresponds to the equation
(x − a)2 + (y − b)2 = r2
and the same equation determines the distance r between the two points (a, b) and (x, y). So Pythagoras’s theorem tells us two vital things: which equations yield circles, and how to calculate distances from coordinates.
Pythagoras’s theorem, then, is important in its own right, but it exerts even more influence through its generalisations. Here I will pursue just one strand of these later developments to bring out the connection with relativity, to which we return in Chapter 13.
The proof of Pythagoras’s theorem in Euclid’s Elements places the theorem firmly within the realm of Euclidean geometry. There was a time when that phrase could have been replaced by just ‘geometry’, because it was generally assumed that Euclid’s geometry was the true geometry of physical space. It was obvious. Like most things assumed to be obvious, it turned out to be false.
Euclid derived all of his theorems from a small number of basic assumptions, which he classified as definitions, axioms, and common notions. His set-up was elegant, intuitive, and concise, with one glaring exception, his fifth axiom: ‘If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.’ It’s a bit of a mouthful: Figure 8 may help.
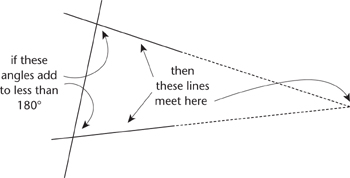
Fig 8 Euclid’s parallel axiom.
For well over a thousand years, mathematicians tried to repair what they saw as a flaw. They weren’t just looking for something simpler and more intuitive that would achieve the same end, although several of them found such things. They wanted to get rid of the awkward axiom altogether, by proving it. After several centuries, mathematicians finally realised that there were alternative ‘non-Euclidean’ geometries, implying that no such proof existed. These new geometries were just as logically consistent as Euclid’s, and they obeyed all of his axioms except the parallel axiom. They could be interpreted as the geometry of geodesics – shortest paths – on curved surfaces, Figure 9. This focused attention on the meaning of curvature.
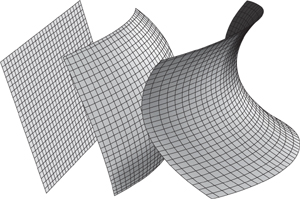
Fig 9 Curvature of a surface. zero curvature. Middle: positive curvature. negative curvature.
The plane of Euclid is flat, curvature zero. A sphere has the same curvature everywhere, and it is positive: near any point it looks like a dome. (As a technical fine point: great circles meet in two points, not one as Euclid’s axioms require, so spherical geometry is modified by identifying antipodal points on the sphere – considering them to be identical. The surface becomes a so-called projective plane and the geometry is called elliptic.) A surface of constant negative curvature also exists: near any point, it looks like a saddle. This surface is called the hyperbolic plane, and it can be represented in several entirely prosaic ways. Perhaps the simplest is to consider it as the interior of a circular disc, and to define ‘line’ as an arc of a circle meeting the edge of the disc at right angles (Figure 10).
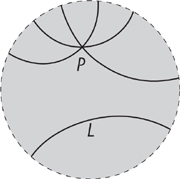
Fig 10 Disc model of the hyperbolic plane. All three lines through P fail to meet line L.
It might seem that, while plane geometry might be non-Euclidean, this must be impossible for the geometry of space. You can bend a surface by pushing it into a third dimension, but you can’t bend space because there’s no room for an extra dimension along which to push it. However, this is a rather naive view. For example, we can model three-dimensional hyperbolic space using the interior of a sphere. Lines are modelled as arcs of circles that meet the boundary at right angles, and planes are modelled as parts of spheres that meet the boundary at right angles. This geometry is three-dimensional, satisfies all of Euclid’s axioms except the Fifth, and in a sense that can be pinned down it defines a curved three-dimensional space. But it’s not curved round anything, or in any new direction.
It’s just curved.
With all these new geometries available, a new point of view began to occupy centre stage – but as physics, not mathematics. Since space doesn’t have to be Euclidean, what shape is it? Scientists realised that they didn’t actually know. In 1813, Gauss, knowing that in a curved space the angles of a triangle do not add to 180°, measured the angles of a triangle formed by three mountains – the Brocken, the Hohehagen, and the Inselberg. He obtained a sum 15 seconds of arc greater than 180°. If correct, this indicated that space (in that region, at least) was positively curved. But you’d need a far larger triangle, and far more accurate measurements, to eliminate observational errors. So Gauss’s observations were inconclusive. Space might be Euclidean, and then again, it might not be.
My remark that three-dimensional hyperbolic space is ‘just curved’ depends on a new point of view about curvature, which also goes back to Gauss. The sphere has constant positive curvature, and the hyperbolic plane has constant negative curvature. But the curvature of a surface doesn’t have to be constant. It might be sharply curved in some places, less sharply curved in others. Indeed, it might be positive in some regions but negative in others. The curvature could vary continuously from place to place. If the surface looks like a dog’s bone, then the blobs at the ends are positively curved but the part that joins them is negatively curved.
Gauss searched for a formula to characterise the curvature of a surface at any point. When he eventually found it, and published it in his Disquisitiones Generales Circa Superficies Curva (‘General Research on Curved Surfaces’) of 1828, he named it the ‘remarkable theorem’. What was so remarkable? Gauss had started from the naive view of curvature: embed the surface in three-dimensional space and calculate how bent it is. But the answer told him that this surrounding space didn’t matter. It didn’t enter into the formula. He wrote: ‘The formula … leads itself to the remarkable theorem: If a curved surface is developed upon any other surface whatever, the measure of curvature in each point remains unchanged.’ By ‘developed’ he meant ‘wrapped round’.
Take a flat sheet of paper, zero curvature. Now wrap it round a bottle. If the bottle is cylindrical the paper fits perfectly, without being folded, stretched, or torn. It is bent as far as visual appearance goes, but it’s a trivial kind of bending, because it hasn’t changed geometry on the paper in any way. It’s just changed how the paper relates to the surrounding space. Draw a right-angled triangle on the flat paper, measure its sides, check Pythagoras. Now wrap the diagram round a bottle. The lengths of sides, measured along the paper, don’t change. Pythagoras is still true.
The surface of a sphere, however, has nonzero curvature. So it is not possible to wrap a sheet of paper so that it fits snugly against a sphere, without folding it, stretching it, or tearing it. Geometry on a sphere is intrinsically different from geometry on a plane. For example, the Earth’s equator and the lines of longitude for 0° and 90° to its north determine a triangle that has three right angles and three equal sides (assuming the Earth to be a sphere). So Pythagoras’s equation is false.
Today we call curvature in its intrinsic sense ‘Gaussian curvature’. Gauss explained why it is important using a vivid analogy, still current. Imagine an ant confined to the surface. How can it work out whether the surface is curved? It can’t step outside the surface to see whether it looks bent. But it can use Gauss’s formula by making suitable measurements purely within the surface. We are in the same position as the ant when we try to figure out the true geometry of our space. We can’t step outside it. Before we can emulate the ant by taking measurements, however, we need a formula for the curvature of a space of three dimensions. Gauss didn’t have one. But one of his students, in a fit of recklessness, claimed that he did.
The student was Georg Bernhard Riemann, and he was trying to achieve what German universities call Habilitation, the next step after a PhD. In Riemann’s day this meant that you could charge students a fee for your lectures. Then and now, gaining Habilitation requires presenting your research in a public lecture that is also an examination. The candidate offers several topics, and the examiner, which in Riemann’s case was Gauss, chooses one. Riemann, a brilliant mathematical talent, listed several orthodox topics that he knew backwards, but in a rush of blood to the brain he also suggested ‘On the hypotheses which lie at the foundation of geometry’. Gauss had long been interested in just that, and he naturally selected it for Riemann’s examination.
Riemann instantly regretted offering something so challenging. He had a hearty dislike of public speaking, and he hadn’t thought the mathematics through in detail. He just had some vague, though fascinating, ideas about curved space. In any number of dimensions. What Gauss had done for two dimensions, with his remarkable theorem, Riemann wanted to do in as many dimensions as you like. Now he had to perform, and fast. The lecture was looming. The pressure nearly gave him a nervous breakdown, and his day job helping Gauss’s collaborator Wilhelm Weber with experiments in electricity didn’t help. Well, maybe it did, because while Riemann was thinking about the relation between electrical and magnetic forces in the day job, he realised that force can be related to curvature. Working backwards, he could use the mathematics of forces to define curvature, as required for his examination.
In 1854 Riemann delivered his lecture, which was warmly received, and no wonder. He began by defining what he called a ‘manifold’, in the sense of many-foldedness. Formally, a ‘manifold’, is specified by a system of many coordinates, together with a formula for the distance between nearby points, now called a Riemannian metric. Informally, a manifold is a multidimensional space in all its glory. The climax of Riemann’s lecture was a formula that generalised Gauss’s remarkable theorem: it defined the curvature of the manifold solely in terms of its metric. And it is here that the tale comes full circle like the snake Orobouros and swallows its own tail, because the metric contains visible remnants of Pythagoras.
Suppose, for example, that the manifold has three dimensions. Let the coordinates of a point be (x, y, z), and let (x + dx, y + dy, z + dz) be a nearby point, where the d means ‘a little bit of’. If the space is Euclidean, with zero curvature, the distance ds between these two points satisfies the equation
ds2 = dx2 + dy2 + dz2
and this is just Pythagoras, restricted to points that are close together. If the space is curved, with variable curvature from point to point, the analogous formula, the metric, looks like this:
ds2 = X dx2 + Y dy2 + Z dz2 + 2U dx dy + 2V dx dz + 2W dy dz
Here X, Y, Z, U, V, W can depend on x, y and z. It may seem a bit of a mouthful, but like Pythagoras’s equation it involves sums of squares (and closely related products of two quantities like dx dy) plus a few bells and whistles. The 2s occur because the formula can be packaged as a 3 × 3 table, or matrix:
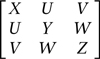
where X, Y, Z appear once, but U, V, W appear twice. The table is symmetric about its diagonal; in the language of differential geometry it is a symmetric tensor. Riemann’s generalisation of Gauss’s remarkable theorem is a formula for the curvature of the manifold, at any given point, in terms of this tensor. In the special case when Pythagoras applies, the curvature turns out to be zero. So the validity of Pythagoras’s equation is a test for the absence of curvature.
Like Gauss’s formula, Riemann’s expression for curvature depends only on the manifold’s metric. An ant confined to the manifold could observe the metric by measuring tiny triangles and computing the curvature. Curvature is an intrinsic property of a manifold, independent of any surrounding space. Indeed, the metric already determines the geometry, so no surrounding space is required. In particular, we human ants can ask what shape our vast and mysterious universe is, and hope to answer it by making observations that do not require us to step outside the universe. Which is just as well, because we can’t.
Riemann found his formula by using forces to define geometry. Fifty years later, Einstein turned Riemann’s idea on its head, using geometry to define the force of gravity in his general theory of relativity, and inspiring new ideas about the shape of the universe: see Chapter 13. It’s an astonishing progression of events. Pythagoras’s equation first came into being around 3500 years ago to measure a farmer’s land. Its extension to triangles without right angles, and triangles on a sphere, allowed us to map our continents and measure our planet. And a remarkable generalisation lets us measure the shape of the universe. Big ideas have small beginnings.
