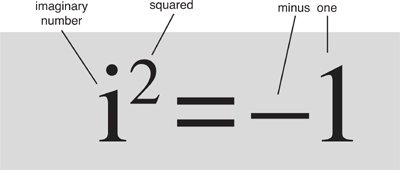
Even though it ought to be impossible, the square of the number i is minus one.
It led to the creation of complex numbers, which in turn led to complex analysis, one of the most powerful areas of mathematics.
Improved methods to calculate trigonometric tables. Generalisations of almost all mathematics to the complex realm. More powerful methods to understand waves, heat, electricity, and magnetism. The mathematical basis of quantum mechanics.
Renaissance Italy was a hotbed of politics and violence. The north of the country was controlled by a dozen warring city-states, among them Milan, Florence, Pisa, Genoa, and Venice. In the south, Guelphs and Gibellines were in conflict as Popes and Holy Roman Emperors battled for supremacy. Bands of mercenaries roamed the land, villages were laid waste, coastal cities waged naval warfare against each other. In 1454 Milan, Naples, and Florence signed the Treaty of Lodi, and peace reigned for the next four decades, but the papacy remained embroiled in corrupt politics. This was the time of the Borgias, notorious for poisoning anyone who got in the way of their quest for political and religious power, but it was also the time of Leonardo da Vinci, Brunelleschi, Piero della Francesca, Titian, and Tintoretto. Against a backdrop of intrigue and murder, long-held assumptions were coming into question. Great art and great science flourished in symbiosis, each feeding off the other.
Great mathematics flourished as well. In 1545 the gambling scholar Girolamo Cardano was writing an algebra text, and he encountered a new kind of number, one so baffling that he declared it ‘as subtle as it is useless’ and dismissed the notion. Rafael Bombelli had a solid grasp of Cardano’s algebra book, but he found the exposition confusing, and decided he could do better. By 1572 he had noticed something intriguing: although these baffling new numbers made no sense, they could be used in algebraic calculations and led to results that were demonstrably correct.
For centuries mathematicians engaged in a love–hate relationship with these ‘imaginary numbers’, as they are still called today. The name betrays an ambivalent attitude: they’re not real numbers, the usual numbers encountered in arithmetic, but in most respects they behave like them. The main difference is that when you square an imaginary number, the result is negative. But that ought not to be possible, because squares are always positive.
Only in the eighteenth century did mathematicians figure out what imaginary numbers were. Only in the nineteenth did they start to feel comfortable with them. But by the time the logical status of imaginary numbers was seen to be entirely comparable to that of the more traditional real numbers, imaginaries had become indispensable throughout mathematics and science, and the question of their meaning hardly seemed interesting any more. In the late nineteenth and early twentieth centuries, revived interest in the foundations of mathematics led to a rethink of the concept of number, and traditional ‘real’ numbers were seen to be no more real than imaginary ones. Logically, the two kinds of number were as alike as Tweedledum and Tweedledee. Both were constructs of the human mind, both represented – but were not synonymous with – aspects of nature. But they represented reality in different ways and in different contexts.
By the second half of the twentieth century, imaginary numbers were simply part and parcel of every mathematician’s and every scientist’s mental toolkit. They were built into quantum mechanics in such a fundamental way that you could no more do physics without them than you could scale the north face of the Eiger without ropes. Even so, imaginary numbers are seldom taught in schools. The sums are easy enough, but the mental sophistication needed to appreciate why imaginaries are worth studying is still too great for the vast majority of students. Very few adults, even educated ones, are aware of how deeply their society depends on numbers that do not represent quantities, lengths, areas, or amounts of money. Yet most modern technology, from electric lighting to digital cameras, could not have been invented without them.
Let me backtrack to a crucial question. Why are squares always positive?
In Renaissance times, where equations were generally rearranged to make every number in them positive, they wouldn’t have phrased the question quite this way. They would have said that if you add a number to a square then you have to get a bigger number – you can’t get zero. But even if you allow negative numbers, as we now do, squares still have to be positive. Here’s why.
Real numbers can be positive or negative. However, the square of any real number, whatever its sign, is always positive, because the product of two negative numbers is positive. So both 3 × 3 and −3 × −3 yield the same result: 9. Therefore 9 has two square roots, 3 and −3.
What about —9? What are its square roots?
It doesn’t have any.
It all seems terribly unfair: the positive numbers hog two square roots each, while the negative numbers go without. It is tempting to change the rule for multiplying two negative numbers, so that, say, −3 × −3 = −9. Then positive and negative numbers each get one square root; moreover, this has the same sign as its square, which seems neat and tidy. But this seductive line of reasoning has an unintended downside: it wrecks the usual rules of arithmetic. The problem is that —9 already occurs as 3 × −3 itself a consequence of the usual rules of arithmetic, and a fact that almost everyone is happy to accept. If we insist that −3 × −3 is also 9, then −3 × −3 = 3 × −3. There are several ways to see that this causes problems; the simplest is to divide both sides by −3, to get 3 = −3.
Of course you can change the rules of arithmetic. But now it all gets complicated and messy. A more creative solution is to retain the rules of arithmetic, and to extend the system of real numbers by permitting imaginaries. Remarkably – and no one could have anticipated this, you just have to follow the logic through – this bold step leads to a beautiful, consistent system of numbers, with a myriad uses. Now all numbers except 0 have two square roots, one being minus the other. This is true even for the new kinds of number; one enlargement of the system suffices. It took a while for this to become clear, but in retrospect it has an air of inevitability. Imaginary numbers, impossible though they were, refused to go away. They seemed to make no sense, but they kept cropping up in calculations. Sometimes the use of imaginary numbers made the calculations simpler, and the result was more comprehensive and more satisfactory. Whenever an answer that had been obtained using imaginary numbers, but did not explicitly involve them, could be verified independently, it turned out to be right. But when the answer did involve explicit imaginary numbers it seemed to be meaningless, and often logically contradictory. The enigma simmered for two hundred years, and when it finally boiled over, the results were explosive.
Cardano is known as the gambling scholar because both activities played a prominent role in his life. He was both genius and rogue. His life consists of a bewildering series of very high highs and very low lows. His mother tried to abort him, his son was beheaded for killing his (the son’s) wife, and he (Cardano) gambled away the family fortune. He was accused of heresy for casting the horoscope of Jesus. Yet in between he also became Rector of the University of Padua, was elected to the College of Physicians in Milan, gained 2000 gold crowns for curing the Archbishop of St Andrews’ asthma, and received a pension from Pope Gregory XIII. He invented the combination lock and gimbals to hold a gyroscope, and he wrote a number of books, including an extraordinary autobiography De Vita Propria (‘The Book of My Life’). The book that is relevant to our tale is the Ars Magna of 1545. The title means ‘great art’, and refers to algebra. In it, Cardano assembled the most advanced algebraic ideas of his day, including new and dramatic methods for solving equations, some invented by a student of his, some obtained from others in controversial circumstances.
Algebra, in its familiar sense from school mathematics, is a system for representing numbers symbolically. Its roots go back to the Greek Diophantus around 250 AD, whose Arithmetica employed symbols to describe ways to solve equations. Most of the work was verbal – ‘find two numbers whose sum is 10 and whose product is 24’. But Diophantus summarised the methods he used to find the solutions (here 4 and 6) symbolically. The symbols (see Table 1) were very different from those we use today, and most were abbreviations, but it was a start. Cardano mainly used words, with a few symbols for roots, and again the symbols scarcely resemble those in current use. Later authors homed in, rather haphazardly, on today’s notation, most of which was standardised by Euler in his numerous textbooks. However, Gauss still used xx instead of x2 as late as 1800.
Table 1 The development of algebraic notation.
The most important topics in the Ars Magna were new methods for solving cubic and quartic equations. These are like quadratic equations, which most of us meet in school algebra, but more complicated. A quadratic equation states a relationship involving an unknown quantity, normally symbolised by the letter x, and its square x2. ‘Quadratic’ comes from the Latin for ‘square’. A typical example is
x2 − 5x + 6 = 0
Verbally, this says: ‘Square the unknown, subtract 5 times the unknown, and add 6: the result is zero.’ Given an equation involving an unknown, our task is to solve the equation – to find the value or values of the unknown that make the equation correct.
For a randomly chosen value of x, this equation will usually be false. For example, if we try x = 1, then x2 − 5x + 6 = 1 − 5 + 6 = 2, which isn’t zero. But for rare choices of x, the equation is true. For example, when x = 2 we have x2 –5x + 6 = 4 − 10 + 6 = 0. But this is not the only solution! When x = 3 we have x2 − 5x + 6 = 9 − 15 + 6 = 0 as well. There are two solutions, x = 2 and x = 3, and it can be shown that there are no others. A quadratic equation can have two solutions, one, or none (in real numbers). For example, x2 − 2x + 1 = 0 has only the solution x = 1, and x2 + 1 = 0 has no solutions in real numbers.
Cardano’s masterwork provides methods for solving cubic equations, which along with x and x2 also involve the cube x3 of the unknown, and quartic equations, where x4 turns up as well. The algebra gets very complicated; even with modern symbolism it takes a page or two to derive the answers. Cardano did not go on to quintic equations, involving x5, because he did not know how to solve them. Much later it was proved that no solutions (of the type Cardano would have wanted) exist: although highly accurate numerical solutions can be calculated in any particular case, there is no general formula for them, unless you invent new symbols specifically for the task.
I’m going to write down a few algebraic formulas, because I think the topic makes more sense if we don’t try to avoid them. You don’t need to follow the details, but I’d like to show you what everything looks like. Using modern symbols, we can write out Cardano’s solution of the cubic equation in a special case, when x3 + ax + b = 0 for specific numbers a and b. (If x2 is present, a cunning trick gets rid of it, so this case actually deals with everything.) The answer is:
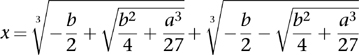
This may appear a bit of a mouthful, but it’s a lot simpler than many algebraic formulas. It tells us how to calculate the unknown x by working out the square of b and the cube of a, adding a few fractions, and taking a couple of square roots (the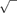 
symbol) and a couple of cube roots (the 
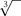symbol). The cube root of a number is whatever you have to cube to get that number.
The discovery of the solution for cubic equations involves at least three other mathematicians, one of whom complained bitterly that Cardano had promised not to reveal his secret. The story, though fascinating, is too complicated to relate here.1 The quartic was solved by Cardano’s student Lodovico Ferrari. I’ll spare you the even more complicated formula for quartic equations.
The results reported in the Ars Magna were a mathematical triumph, the culmination of a story that spanned millennia. The Babylonians knew how to solve quadratic equations around 1500 BC, perhaps earlier. The ancient Greeks and Omar Khayyam knew geometric methods for solving cubics, but algebraic solutions of cubic equations, let alone quartics, were unprecedented. At a stroke, mathematics outstripped its classical origins.
There was one tiny snag, however. Cardano noticed it, and several people tried to explain it; they all failed. Sometimes the method works brilliantly; at other times, the formula is as enigmatic as the Delphic oracle. Suppose we apply Cardano’s formula to the equation x3 − 15x − 4 = 0. The result is
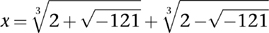
However, −121 is negative, so it has no square root. To compound the mystery, there is a perfectly good solution, x = 4. The formula doesn’t give it.
Light of a kind was shed in 1572 when Bombelli published L’Algebra. His main aim was to clarify Cardano’s book, but when he came to this particular thorny issue he spotted something Cardano had missed. If you ignore what the symbols mean, and just perform routine calculations, the standard rules of algebra show that
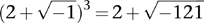
Therefore you are entitled to write
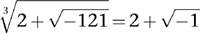
Similarly,
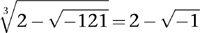
Now the formula that baffled Cardano can be rewritten as
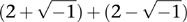
which is equal to 4 because the troublesome square roots cancel out. So Bombelli’s nonsensical formal calculations got the right answer. And that was a perfectly normal real number.
Somehow, pretending that square roots of negative numbers made sense, even though they obviously did not, could lead to sensible answers. Why?
To answer this question, mathematicians had to develop good ways to think about square roots of negative quantities, and do calculations with them. Early writers, among them Descartes and Newton, interpreted these ‘imaginary’ numbers as a sign that a problem has no solutions. If you wanted to find a number whose square was minus one, the formal solution ‘square root of minus one’ was imaginary, so no solution existed. But Bombelli’s calculation implied that there was more to imaginaries than that. They could be used to find solutions; they could arise as part of the calculation of solutions that did exist.
Leibniz had no doubt about the importance of imaginary numbers. In 1702 he wrote: ‘The Divine Spirit found a sublime outlet in that wonder of analysis, that portent of the ideal world, that amphibian between being and non-being, which we call the imaginary root of negative unity.’ But the eloquence of his statement fails to obscure a fundamental problem: he didn’t have a clue what imaginary numbers actually were.
One of the first people to come up with a sensible representation of complex numbers was Wallis. The image of real numbers lying along a line, like marked points on a ruler, was already commonplace. In 1673 Wallis suggested that a complex number x +iy should be thought of as a point in a plane. Draw a line in the plane, and identify points on this line with real numbers in the usual way. Then think of x +iy as a point lying to one side of the line, distance y away from the point x.
Wallis’s idea was largely ignored, or worse, criticised. François Daviet de Foncenex, writing about imaginaries in 1758, said that thinking of imaginaries as forming a line at right angles to the real line was pointless. But eventually the idea was revived in a slightly more explicit form. In fact, three people came up with exactly the same method for representing complex numbers, at intervals of a few years, Figure 18. One was a Norwegian surveyor, one a French mathematician, and one a German mathematician. Respectively, they were Caspar Wessel, who published in 1797, Jean-Robert Argand in 1806, and Gauss in 1811. They basically said the same as Wallis, but they added a second line to the picture, an imaginary axis at right angles to the real one. Along this second axis lived the imaginary numbers i, 2i, 3i, and so on. A general complex number, such as 3 + 2i, lived out in the plane, three units along the real axis and two along the imaginary one.
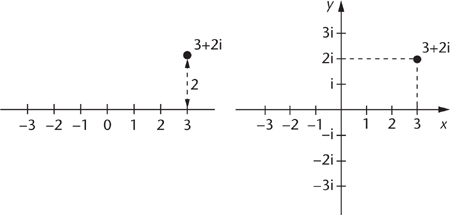
Fig 18 The complex plane. Left: according to Wallis. Right: according to Wessel, Argand, and Gauss.
This geometric representation was all very well, but it didn’t explain why complex numbers form a logically consistent system. It didn’t tell us in what sense they are numbers. It just provided a way to visualise them. This no more defined what a complex number is than a drawing of a straight line defines a real number. It did provide some sort of psychological prop, a slightly artificial link between those crazy imaginaries and the real world, but nothing more.
What convinced mathematicians that they should take imaginary numbers seriously wasn’t a logical description of what they were. It was overwhelming evidence that whatever they were, mathematics could make good use of them. You don’t ask difficult questions about the philosophical basis of an idea when you are using it every day to solve problems and you can see that it gives the right answers. Foundational questions still have some interest, of course, but they take a back seat to the pragmatic issues of using the new idea to solve old and new problems.
Imaginary numbers, and the system of complex numbers that they spawned, cemented their place in mathematics when a few pioneers turned their attention to complex analysis: calculus (Chapter 3) but with complex numbers instead of real ones. The first step was to extend all the usual functions – powers, logarithms, exponentials, trigonometric functions – to the complex realm. What is sin z when z = x + iy is complex? What is ez or log z?
Logically, these things can be whatever we wish. We are operating in a new domain where the old ideas don’t apply. It doesn’t make much sense, for instance, to think of a right-angled triangle whose sides have complex lengths, so the geometric definition of the sine function is irrelevant. We could take a deep breath, insist that sin z has its usual value when z is real, but equals 42 whenever z isn’t real: job done. But that would be a pretty silly definition: not because it’s imprecise, but because it bears no sensible relationship to the original one for real numbers. One requirement for an extended definition must be that it agrees with the old one when applied to real numbers, but that’s not enough. It’s true for my silly extension of the sine. Another requirement is that the new concept should retain as many features of the old one as we can manage; it should somehow be ‘natural’.
What properties of sine and cosine do we want to preserve? Presumably we’d like all the pretty formulas of trigonometry to remain valid, such as sin 2z = 2 sin z cos z. This imposes a constraint but doesn’t help. A more interesting property, derived using analysis (the rigorous formulation of calculus), is the existence of an infinite series:
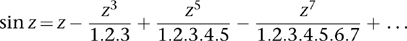
(The sum of such a series is defined to be the limit of the sum of finitely many terms as the number of terms increases indefinitely.) There is a similar series for the cosine:
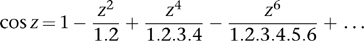
and the two are obviously related in some way to the series for the exponential:
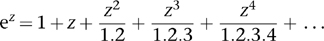
These series may seem complicated, but they have an attractive feature: we know how to make sense of them for complex numbers. All they involve is integer powers (which we obtain by repeated multiplication) and a technical issue of convergence (making sense of the infinite sum). Both of these extend naturally into the complex realm and have all of the expected properties. So we can define sines and cosines of complex numbers using the same series that work in the real case.
Since all of the usual formulas in trigonometry are consequences of these series, those formulas automatically carry over as well. So do the basic facts of calculus, such as ‘the derivative of sine is cosine’. So does ez + w = ezew. This is all so pleasant that mathematicians were happy to settle on the series definitions. And once they’d done that, a great deal else necessarily had to fit in with it. If you followed your nose, you could discover where it led.
For example, those three series look very similar. Indeed, if you replace z by iz in the series for the exponential, you can split the resulting series into two parts, and what you get are precisely the series for sine and cosine. So the series definitions imply that
eiz = cos z + i sin z:
You can also express both sine and cosine using exponentials:
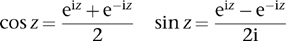
This hidden relationship is extraordinarily beautiful. But you’d never suspect anything like it could exist if you remained stuck in the realm of the reals. Curious similarities between trigonometric formulas and exponential ones (for example, their infinite series) would remain just that. Viewed through complex spectacles, everything suddenly slots into place.
One of the most beautiful, yet enigmatic, equations in the whole of mathematics emerges almost by accident. In the trigonometric series, the number z (when real) has to be measured in radians, for which a full circle of 360° becomes 2π radians. In particular, the angle 180° is π radians. Moreover, sin π = 0 and cos π = 1. Therefore
eiπ = cos π + i sin π = −1
The imaginary number i unites the two most remarkable numbers in mathematics, e and π, in a single elegant equation. If you’ve never seen this before, and have any mathematical sensitivity, the hairs on your neck raise and prickles run down your spine. This equation, attributed to Euler, regularly comes top of the list in polls for the most beautiful equation in mathematics. That doesn’t mean that it is the most beautiful equation, but it does show how much mathematicians appreciate it. Armed with complex functions and knowing their properties, the mathematicians of the nineteenth century discovered something remarkable: they could use these things to solve differential equations in mathematical physics. They could apply the method to static electricity, magnetism, and fluid flow. Not only that: it was easy.
In Chapter 3 we talked of functions – mathematical rules that assign, to any given number, a corresponding number, such as its square or sine. Complex functions are defined in the same way, but now we allow the numbers involved to be complex. The method for solving differential equations was delightfully simple. All you had to do was take some complex function, call it f(z), and split it into its real and imaginary parts:
f(z) = u(z) + iv(z)
Now you have two real-valued functions u and v, defined for any z in the complex plane. Moreover, whatever function you start with, these two component functions satisfy differential equations found in physics. In a fluid-flow interpretation, for example, u and v determine the flow-lines. In an electrostatic interpretation, the two components determine the electric field and how a small charged particle would move; in a magnetic interpretation, they determine the magnetic field and the lines of force.
I’ll give just one example: a bar magnet. Most of us remember seeing a famous experiment in which a magnet is placed beneath a sheet of paper, and iron filings are scattered over the paper. They automatically line up to show the lines of magnetic force associated with the magnet – the paths that a tiny test magnet would follow if placed in the magnetic field. The curves look like Figure 19 (left).
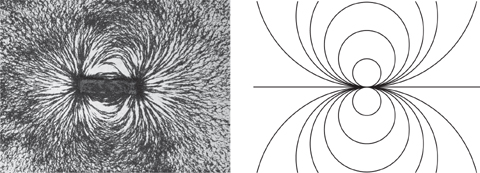
Fig 19 Left: Magnetic field of bar magnet. Right: Field derived using complex analysis.
To obtain this picture using complex functions, we just let f(z) = 1/z. The lines of force turn out to be circles, tangent to the real axis, as in Figure 19 (right). This is what the magnetic fields lines of a very tiny bar magnet would look like. A more complicated choice of function corresponds to a magnet of finite size: I chose this function to keep everything as simple as possible.
This was wonderful. There were endless functions to work with. You decided which function to look at, found its real and imaginary parts, worked out their geometry … and, lo and behold, you had solved a problem in magnetism, or electricity, or fluid flow. Experience soon told you which function to use for which problem. The logarithm was a point source, minus the logarithm was a sink through which fluid disappeared like the plughole in a kitchen sink, i times the logarithm was a point vortex where the fluid spun round and round… It was magic! Here was a method that could churn out solution after solution to problems that would otherwise be opaque. Yet it came with a guarantee of success, and if you were worried about all that complex analysis stuff, you could check directly that the results you obtained really did represent solutions.
This was just the beginning. As well as special solutions, you could prove general principles, hidden patterns in the physical laws. You could analyse waves and solve differential equations. You could transform shapes into other shapes, using complex equations, and the same equations transformed the flow-lines round them. The method was limited to systems in the plane, because that was where a complex number naturally lived, but the method was a godsend when previously even problems in the plane were out of reach. Today, every engineer is taught how to use complex analysis to solve practical problems, early in their university course. The Joukowski transformation z + 1/z turns a circle into an aerofoil shape, the cross-section of a rudimentary aeroplane wing, see Figure 20. It therefore turns the flow past a circle, easy to find if you knew the tricks of the trade, into the flow past an aerofoil. This calculation, and more realistic improvements, were important in the early days of aerodynamics and aircraft design.
This wealth of practical experience made the foundational issues moot. Why look a gift horse in the mouth? There had to be a sensible meaning for complex numbers – they wouldn’t work otherwise. Most scientists and mathematicians were much more interested in digging out the gold than they were in establishing exactly where it had come from and what distinguished it from fools’ gold. But a few persisted. Eventually, the Irish mathematician William Rowan Hamilton knocked the whole thing on the head. He took the geometric representation proposed by Wessel, Argand, and Gauss, and expressed it in coordinates. A complex number was a pair of real numbers (x, y). The real numbers were those of the form (x, 0). The imaginary i was (0, 1). There were simple formulas for adding and multiplying these pairs. If you were worried about some law of algebra, such as the commutative law ab = ba, you could routinely work out both sides as pairs, and make sure they were the same. (They were.) If you identified (x, 0) with plain x, you embedded the real numbers into the complex ones. Better still, x +iy then worked out as the pair (x, y).
Fig 20 Flow past a wing derived from the Joukowski transformation.
This wasn’t just a representation, but a definition. A complex number, said Hamilton, is nothing more nor less than a pair of ordinary real numbers. What made them so useful was an inspired choice of the rules for adding and multiplying them. What they actually were was trite; it was how you used them that produced the magic. With this simple stroke of genius, Hamilton cut through centuries of heated argument and philosophical debate. But by then, mathematicians had become so used to working with complex numbers and functions that no one cared any more. All you needed to remember was that i2 = −1.
