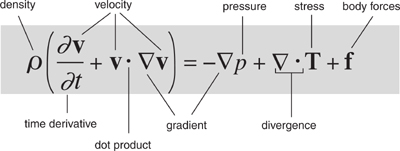

It’s Newton’s second law of motion in disguise. The left-hand side is the acceleration of a small region of fluid. The right-hand side is the forces that act on it: pressure, stress, and internal body forces.
It provides a really accurate way to calculate how fluids move. This is a key feature of innumerable scientific and technological problems.
Modern passenger jets, fast and quiet submarines, Formula 1 racing cars that stay on the track at high speeds, and medical advances on blood flow in veins and arteries. Computer methods for solving the equations, known as computational fluid dynamics (CFD), are widely used by engineers to improve technology in such areas.
Seen from space, the Earth is a beautiful glowing blue-and-white sphere with patches of green and brown, quite unlike any other planet in the Solar System – or any of the 500-plus planets now known to be circling other stars, for that matter. The very word ‘Earth’ instantly brings this image to mind. Yet a little over fifty years ago, the almost universal image for the same word would have been a handful of dirt, earth in the gardening sense. Before the twentieth century, people looked at the sky and wondered about the stars and planets, but they did so from ground level. Human flight was nothing more than a dream, the subject of myths and legends. Hardly anyone thought about travelling to another world.
A few intrepid pioneers began the slow climb into the sky. The Chinese were the first. Around 500 BC Lu Ban invented a wooden bird, which might have been a primitive glider. In 559 AD the upstart Gao Yang strapped Yuan Huangtou, the emperor’s son, to a kite – against his will – to spy on the enemy from above. Yuan survived the experience but was later executed. With the seventeeth-century discovery of hydrogen the urge to fly spread to Europe, inspiring a few brave individuals to ascend into the lower reaches of Earth’s atmosphere in balloons. Hydrogen is explosive, and in 1783 the French brothers Joseph-Michel and Jacques-Étienne Montgolfier gave a public demonstration of their new and much safer idea, the hot-air balloon – first with an unmanned test flight, then with Étienne as pilot.
The pace of progress, and the heights to which humans could ascend, began to increase rapidly. In 1903 Orville and Wilbur Wright made the first powered flight in an aeroplane. The first airline, DELAG (Deutsche Luftschiffahrts-Aktiengesellschaft), began operations in 1910, flying passengers from Frankfurt to Baden-Baden and Düsseldorf using airships made by the Zeppelin Corporation. By 1914 the St Petersburg–Tampa Airboat Line was flying passengers commercially between the two Florida cities, a journey that took 23 minutes in Tony Jannus’s flying boat. Commercial air travel quickly became commonplace, and jet aircraft arrived: the De Havilland Comet began regular flights in 1952, but metal fatigue caused several crashes, and the Boeing 707 became the market leader from its launch in 1958.
Ordinary individuals could now routinely be found at an altitude of 8 kilometres, their limit to this day, at least until Virgin Galactic starts low-orbital flights. Military flights and experimental aircraft rose to greater heights. Space flight, hitherto the dream of a few visionaries, started to become a plausible proposition. In 1961 the Soviet cosmonaut Yuri Gagarin made the first manned orbit of the Earth in Vostok 1. In 1969 NASA’s Apollo 11 mission landed two American astronauts, Neil Armstrong and Buzz Aldrin, on the Moon. The space shuttle began operational flights in 1982, and while budget constraints prevented it achieving the original aims – a reusable vehicle with a rapid turnaround – it became one of the workhorses of low-orbit spaceflight, along with Russia’s Soyuz spacecraft. Atlantis has now made the final flight of the space shuttle programme, but new vehicles are being planned, mainly by private companies. Europe, India, China, and Japan have their own space programmes and agencies.
This literal ascent of humanity has changed our view of who we are and where we live – the main reason why ‘Earth’ now means a blue–white globe. Those colours hold a clue to our newfound ability to fly. The blue is water, and the white is water vapour in the form of clouds. Earth is a water world, with oceans, seas, rivers, lakes. What water does best is to flow, often to places where it’s not wanted. The flow might be rain dripping from a roof or the mighty torrent of a waterfall. It can be gentle and smooth, or rough and turbulent – the steady flow of the Nile across what would otherwise be desert, or the frothy white water of its six cataracts.
It was the patterns formed by water, or more generally any moving fluid, that attracted the attention of mathematicians in the nineteenth century, when they derived the first equations for fluid flow. The vital fluid for flight is less visible than water, but just as ubiquitous: air. The flow of air is more complex mathematically, because air can be compressed. By modifying their equations so that they applied to a compressible fluid, mathematicians initiated the science that would eventually get the Age of Flight off the ground: aerodynamics. Early pioneers might fly by rule of thumb, but commercial airliners and the space shuttle fly because engineers have done the calculations that make them safe and reliable (barring occasional accidents). Aircraft design requires a deep understanding of the mathematics of fluid flow. And the pioneer of fluid dynamics was the renowned mathematician Leonhard Euler, who died in the year the Montgolfiers made their first balloon flight.
There are few areas of mathematics towards which the prolific Euler did not turn his attention. It has been suggested that one reason for his prodigious and versatile output was politics, or more precisely, its avoidance. He worked in Russia for many years, at the court of Catherine the Great, and an effective way to avoid being caught up in political intrigue, with potentially disastrous consequences, was to be so busy with his mathematics that no one would believe he had any time to spare for politics. If this is what he was doing, we have Catherine’s court to thank for many wonderful discoveries. But I’m inclined to think that Euler was prolific because he had that sort of mind. He created huge quantities of mathematics because he could do no other.
There were predecessors. Archimedes studied the stability of floating bodies over 2200 years ago. In 1738 the Dutch mathematician Daniel Bernoulli published Hydrodynamica (‘Hydrodynamics’), containing the principle that fluids flow faster in regions where the pressure is lower. Bernoulli’s principle is often invoked today to explain why aircraft can fly: the wing is shaped so that the air flows faster across the top surface, lowering the pressure and creating lift. This explanation is a bit too simplistic, and many other factors are involved in flight, but it does illustrate the close relationship between basic mathematical principles and practical aircraft design. Bernoulli embodied his principle in an algebraic equation relating velocity and pressure in an incompressible fluid.
In 1757 Euler turned his fertile mind to fluid flow, publishing an article ‘Principes généraux du mouvement des fluides’ (General principles of the movement of fluids) in the Memoirs of the Berlin Academy. It was the first serious attempt to model fluid flow using a partial differential equation. To keep the problem within reasonable bounds, Euler made some simplifying assumptions: in particular, he assumed the fluid was incompressible, like water rather than air, and had zero viscosity – no stickiness. These assumptions allowed him to find some solutions, but they also made his equations rather unrealistic. Euler’s equation is still in use today for some types of problem, but on the whole it is too simple to be of much practical use.
Two scientists came up with a more realistic equation. Claude-Louis Navier was a French engineer and physicist; George Gabriel Stokes was an Irish mathematician and physicist. Navier derived a system of partial differential equations for the flow of a viscous fluid in 1822; Stokes started publishing on the topic twenty years later. The resulting model of fluid flow is now called the Navier–Stokes equation (often the plural is used because the equation is stated in terms of a vector, so it has several components). This equation is so accurate that nowadays engineers often use computer solutions instead of performing physical tests in wind tunnels. This technique, known as computational fluid dynamics (CFD), is now standard in any problem involving fluid flow: the aerodynamics of the space shuttle, the design of Formula 1 racing cars and everyday road cars, and blood circulating through the human body or an artificial heart.
There are two ways to look at the geometry of a fluid. One is to follow the movements of individual tiny particles of fluid and see where they go. The other is to focus on the velocities of such particles: how fast, and in which direction, they are moving at any instant. The two are intimately related, but the relationship is difficult to disentangle except in numerical approximations. One of the great insights of Euler, Navier, and Stokes was the realisation that everything looks a lot simpler in terms of the velocities. The flow of a fluid is best understood in terms of a velocity field: a mathematical description of how the velocity varies from point to point in space and from instant to instant in time. So Euler, Navier, and Stokes wrote down equations describing the velocity field. The actual flow patterns of the fluid can then be calculated, at least to a good approximation.
The Navier–Stokes equation looks like this:
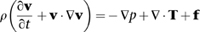
where p is the density of the fluid, v is its velocity field, p is pressure, T determines the stresses, and f represents body forces – forces that act throughout the entire region, not just at its surface. The dot is an operation on vectors, and ∇ is an expression in partial derivatives, namely
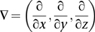
The equation is derived from basic physics. As with the wave equation, a crucial first step is to apply Newton’s second law of motion to relate the movement of a fluid particle to the forces that act on it. The main force is elastic stress, and this has two main constituents: frictional forces caused by the viscosity of the fluid, and the effects of pressure, either positive (compression) or negative (rarefaction). There are also body forces, which stem from the acceleration of the fluid particle itself. Combining all this information leads to the Navier–Stokes equation, which can be seen as a statement of the law of conservation of momentum in this particular context. The underlying physics is impeccable, and the model is realistic enough to include most of the significant factors; this is why it fits reality so well. Like all of the traditional equations of classical mathematical physics it is a continuum model: it assumes that the fluid is infinitely divisible.
This is perhaps the main place where the Navier–Stokes equation potentially loses touch with reality, but the discrepancy shows up only when the motion involves rapid changes on the scale of individual molecules. Such small-scale motions are important in one vital context: turbulence. If you turn on a tap and let the water flow out slowly, it arrives in a smooth trickle. Turn the tap on full, however, and you often get a surging, frothy, foaming gush of water. Similar frothy flows occur in rapids on a river. This effect is known as turbulence, and those of us who fly regularly are well aware of its effects when it occurs in air. It feels as though the aircraft is driving along a very bumpy road.
Solving the Navier–Stokes equation is hard. Until really fast computers were invented, it was so hard that mathematicians were reduced to short cuts and approximations. But when you think about what a real fluid can do, it ought to be hard. You only have to look at water flowing in a stream, or waves breaking on a beach, to see that fluids can flow in extremely complex ways. There are ripples and eddies, wave patterns and whirlpools, and fascinating structures like the Severn bore, a wall of water that races up the estuary of the River Severn in south-west England when the tide comes in. The patterns of fluid flow have been the source of innumerable mathematical investigations, yet one of the biggest and most basic questions in the area remains unanswered: is there a mathematical guarantee that solutions of the Navier–Stokes equation actually exist, valid for all future time? There is a million-dollar prize for anyone who can solve it, one of the seven Clay Institute Millennium Prize problems, chosen to represent the most important unsolved mathematical problems of our age. The answer is ‘yes’ in two-dimensional flow, but no one knows for three-dimensional flow.
Despite this, the Navier–Stokes equation provides a useful model of turbulent flow because molecules are extremely small. Turbulent vortices a few millimetres across already capture many of the main features of turbulence, whereas a molecule is far smaller, so a continuum model remains appropriate. The main problem that turbulence causes is practical: it makes it virtually impossible to solve the Navier–Stokes equation numerically, because a computer can’t handle infinitely complex calculations. Numerical solutions of partial differential equations use a grid, dividing space into discrete regions and time into discrete intervals. To capture the vast range of scales on which turbulence operates – its big vortices, middle-sized ones, right down to the millimetre-scale ones – you need an impossibly fine computational grid. For this reason, engineers often use statistical models of turbulence instead.
The Navier–Stokes equation has revolutionised modern transport. Perhaps its greatest influence is on the design of passenger aircraft, because not only do these have to fly efficiently, but they have to fly, stably and reliably. Ship design also benefits from the equation, because water is a fluid. But even ordinary household cars are now designed on aerodynamic principles, not just because it makes them look sleek and cool, but because efficient fuel consumption relies on minimising drag caused by the flow of air past the vehicle. One way to reduce your carbon footprint is to drive an aerodynamically efficient car. Of course there are other ways, ranging from smaller, slower cars to electric motors, or just driving less. Some of the big improvements in fuel consumption figures have come from improved engine technology, some from better aerodynamics.
In the earliest days of aircraft design, pioneers put their aeroplanes together using back-of-the-envelope calculations, physical intuition, and trial and error. When your aim was to fly more than a hundred metres no more than three metres off the ground, that was good enough. The first time that Wright Flyer I got properly off the ground, instead of stalling and crashing after three seconds in the air, it travelled 120 feet at a speed just below 7 mph. Orville, the pilot on that occasion, managed to keep it aloft for a staggering 12 seconds. But the size of passenger aircraft quickly grew, for economic reasons: the more people you can carry in one flight, the more profitable it will be. Soon aircraft design had to be based on a more rational and reliable method. The science of aerodynamics was born, and its basic mathematical tools were equations for fluid flow. Since air is both viscous and compressible, the Navier–Stokes equation, or some simplification that makes sense for a given problem, took centre stage as far as theory went.
However, solving those equations, in the absence of modern computers, was virtually impossible. So the engineers resorted to an analogue computer: placing models of the aircraft in a wind tunnel. Using a few general properties of the equations to work out how variables change as the scale of the model changes, this method provided basic information quickly and reliably. Most Formula 1 teams today use wind tunnels to test their designs and evaluate potential improvements, but computer power is now so great that most also use CFD. For example, Figure 43 shows a CFD calculation of air flow past a BMW Sauber car. As I write, one team, Virgin Racing, uses only CFD, but they will be using a wind tunnel as well next year.
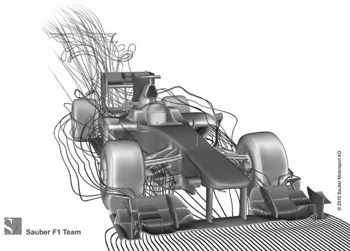
Fig 43 Computed air flow past a Formula 1 car.
Wind tunnels are not terribly convenient; they are expensive to build and run, and they need lots of scale models. Perhaps the biggest difficulty is to make accurate measurements of the flow of air without affecting it. If you put an instrument in the wind tunnel to measure, say, air pressure, then the instrument itself disturbs the flow. Perhaps the biggest practical advantage of CFD is that you can calculate the flow without affecting it. Anything you might wish to measure is easily available. Moreover, you can modify the design of the car, or a component, in software, which is a lot quicker and cheaper than making lots of different models. Modern manufacturing processes often involve computer models at the design stage anyway.
Supersonic flight, where the aircraft goes faster than sound, is especially tricky to study using models in a wind tunnel, because the wind speeds are so great. At such speeds, the air cannot move away from the aircraft as quickly as the aircraft pushes itself through the air, and this causes shockwaves – sudden discontinuities in air pressure, heard on the ground as a sonic boom. This environmental problem was one reason why the joint Anglo-French airliner Concorde, the only supersonic commercial aircraft ever to go into service, had limited success: it was not allowed to fly at supersonic speeds except over oceans. CFD is widely used to predict the flow of air past a supersonic aircraft.
There are about 600 million cars on the planet and tens of thousands of civil aircraft, so even though these applications of CFD may seem hightech, they are significant in everyday life. Other ways to use CFD have a more human dimension. It is widely used by medical researchers to understand blood flow in the human body, for example. Heart malfunction is one of the leading causes of death in the developed world, and it can be triggered either by problems with the heart itself or by clogged arteries, which disrupt the blood flow and can cause clots. The mathematics of blood flow in the human body is especially intractable analytically because the walls of the arteries are elastic. It’s difficult enough to calculate the movement of fluid through a rigid tube; it’s much harder if the tube can change its shape depending on the pressure that the fluid exerts, because now the domain for the calculation doesn’t stay the same as time passes. The shape of the domain affects the flow pattern of the fluid, and simultaneously the flow pattern of the fluid affects the shape of the domain. Pen-and-paper mathematics can’t handle that sort of feedback loop.
CFD is ideal for this kind of problem because computers can perform billions of calculations every second. The equation has to be modified to include the effects of elastic walls, but that’s mostly a matter of extracting the necessary principles from elasticity theory, another well-developed part of classical continuum mechanics. For example, a CFD calculation of how blood flows through the aorta, the main artery entering the heart, has been carried out at the École Polytechnique Féderale de Lausanne in Switzerland. The results provide information that can help doctors get a better understanding of cardiovascular problems.
They also help engineers to develop improved medical devices such as stents – small metal-mesh tubes that keep the artery open. Suncica Canic has used CFD and models of elastic properties to design better stents, deriving a mathematical theorem that caused one design to be abandoned and suggested better designs. Models of this type have become so accurate that the US Food and Drugs Administration is considering requiring any group designing stents to carry out mathematical modelling before performing clinical trials. Mathematicians and doctors are joining forces to use the Navier–Stokes equation to obtain better predictions of, and better treatments for, the main causes of heart attacks.
Another, related, application is to heart bypass operations, in which a vein is removed from elsewhere in the body and grafted into the coronary artery. The geometry of the graft has a strong effect on the blood flow. This in turn affects clotting, which is more likely if the flow has vortices because blood can become trapped in a vortex and fail to circulate properly. So here we see a direct link between the geometry of the flow and potential medical problems.
The Navier–Stokes equation has another application: climate change, otherwise known as global warming. Climate and weather are related, but different. Weather is what happens at a given place, at a given time. It may be raining in London, snowing in New York, or baking in the Sahara. Weather is notoriously unpredictable, and there are good mathematical reasons for this: see Chapter 16 on chaos. However, much of the unpredictability concerns small-scale changes, both in space and time: the fine details. If the TV weatherman predicts showers in your town tomorrow afternoon and they happen six hours later and 20 kilometres away, he thinks he did a good job and you are wildly unimpressed. Climate is the long-term ‘texture’ of weather – how rainfall and temperature behave when averaged over long periods, perhaps decades. Because climate averages out these discrepancies, it is paradoxically easier to predict. The difficulties are still considerable, and much of the scientific literature investigates possible sources of error, trying to improve the models.
Climate change is a politically contentious issue, despite a very strong scientific consensus that human activity over the past century or so has caused the average temperature of the Earth to rise. The increase to date sounds small, about 0.75 degrees Celsius during the twentieth century, but the climate is very sensitive to temperature changes on a global scale. They tend to make the weather more extreme, with droughts and floods becoming more common.
‘Global warming’ does not imply that the temperature everywhere is changing by the same tiny amount. On the contrary, there are large fluctuations from place to place and from time to time. In 2010 Britain experienced its coldest winter for 31 years, prompting the Daily Express to print the headline ‘and still they claim it’s global warming’. As it happens, 2010 tied with 2005 as the hottest year on record, across the globe.1 So ‘they’ were right. In fact, the cold snap was caused by the jet stream changing position, pushing cold air south from the Arctic, and this happened because the Arctic was unusually warm. Two weeks of frost in central London does not disprove global warming. Oddly, the same newspaper reported that Easter Sunday 2011 was the hottest on record, but made no connection to global warming. On that occasion they correctly distinguished weather from climate. I’m fascinated by the selective approach.
Similarly, ‘climate change’ does not simply mean that the climate is changing. It has done that without human assistance repeatedly, mainly on long timescales, thanks to volcanic ash and gases, long-term variations in the Earth’s orbit around the Sun, even India colliding with Asia to create the Himalayas. In the context currently under debate, ‘climate change’ is short for ‘anthropogenic climate change’ – changes in global climate caused by human activity. The main causes are the production of two gases: carbon dioxide and methane. There are greenhouse gases: they trap incoming radiation (heat) from the Sun. Basic physics implies that the more of these gases the atmosphere contains, the more heat it traps; although the planet does radiate some heat away, on balance it will get warmer. Global warming was predicted, on this basis, in the 1950s, and the predicted temperature increase is in line with what has been observed.
The evidence that carbon dioxide levels have increased dramatically comes from many sources. The most direct is ice cores. When snow falls in the polar regions, it packs together to form ice, with the most recent snow at the top and the oldest at the bottom. Air is trapped in the ice, and the conditions that prevail there leave it virtually unchanged for very long periods of time, keeping the original air in and more recent air out. With care, it is possible to measure the composition of the trapped air and to determine the date when it was trapped, very accurately. Measurements made in the Antarctic show that the concentration of carbon dioxide in the atmosphere was pretty much constant over the past 100,000 years – except for the last 200, when it shot up by 30%. The source of the excess carbon dioxide can be inferred from the proportions of carbon-13, one of the isotopes (different atomic forms) of carbon. Human activity is by far the most likely explanation.
The main reason why the skeptics have even faint glimmerings of a case is the complexity of climate forecasting. This has to be done using mathematical models, because it’s about the future. No model can include every single feature of the real world, and, if it did, you could never work out what it predicted, because no computer could ever simulate it. Every discrepancy between model and reality, however insignificant, is music to the skeptics’ ears. There is certainly room for differences of opinion about the likely effects of climate change, or what we should do to mitigate it. But burying our heads in the sand isn’t a sensible option.
Two vital aspects of climate are the atmosphere and the oceans. Both are fluids, and both can be studied using the Navier–Stokes equation. In 2010 the UK’s main science funding body, the Engineering and Physical Sciences Research Council, published a document on climate change, singling out mathematics as a unifying force: ‘Researchers in meteorology, physics, geography and a host of other fields all contribute their expertise, but mathematics is the unifying language that enables this diverse group of people to implement their ideas in climate models.’ The document also explained that ‘The secrets of the climate system are locked away in the Navier–Stokes equation, but it is too complex to be solved directly.’ Instead, climate modellers use numerical methods to calculate the fluid flow at the points of a three-dimensional grid, covering the globe from the ocean depths to the upper reaches of the atmosphere. The horizontal spacing of the grid is 100 kilometres – anything smaller would make the computations impractical. Faster computers won’t help much, so the best way forward is to think harder. Mathematicians are working on more efficient ways to solve the Navier–Stokes equation numerically.
The Navier–Stokes equation is only part of the climate puzzle. Other factors include heat flow within and between the oceans and the atmosphere, the effect of clouds, non-human contributions such as volcanoes, even aircraft emissions in the stratosphere. Skeptics like to emphasise such factors to suggest the models are wrong, but most of them are known to be irrelevant. For example, every year volcanoes contribute a mere 0.6% of the carbon dioxide produced by human activity. All of the main models suggest that there is a serious problem, and humans have caused it. The main question is just how much the planet will warm up, and what level of disaster will result. Since perfect forecasting is impossible, it is in everybody’s interests to make sure that our climate models are the best we can devise, so that we can take appropriate action. As the glaciers melt, the Northwest Passage opens up as Arctic ice shrinks, and Antarctic ice shelves are breaking off and sliding into the ocean, we can no longer take the risk of believing that we don’t need to do anything and it will all sort itself out.