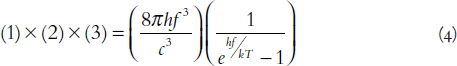The main narrative chronicles Planck’s work on thermal radiation, including his breakthrough of 1900, but it stays with Planck and the limited tools available to him. Here I want to provide a more contemporary understanding of the underlying physics. Even though we’ll wade a bit further into technical waters, I still write this with a general audience in mind, including a hopefully appetizing analogy.
In 1900, Planck didn’t have the benefit of understanding the true nature of light and all electromagnetic radiation. We now know it is composed of massless bits of energy called “photons.”
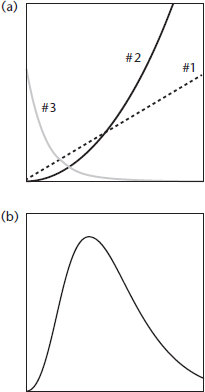
It turns out that the beautiful curve with its narrow peak describes a sort of tug-of-war between fundamental influences—the peak is just a marker for the central knot in the tug-of-war rope. (The curve appears in Figure P.1, for the cosmic microwave background radiation, and in Figure 5.4, for the black bodies examined in the German laboratories of the 1890s.) On one end, we have to figure out all the different ways a photon could exist, given a certain energy. This is roughly like holding a doll, figuring out which joints bend, and then finding all the different poses the doll can hold. The greater the photon energy, the more imaginable ways (or modes) we can imagine for the appearance of a photon. On the other end of the rope, we have a reality check, which is the actual number of available photons reporting for duty at a given temperature. Each of these effects would make a very simple graph on its own, just sloping downward to the left or to the right respectively, but put together, their opposite tendencies result in a “tie,” evidenced by a central peak showing the most popular color of black-body photons at a given temperature.
Our analogy has us sitting and watching a bakery from the outside—that is our black-body experiment. We can’t see inside, but we can observe (and eat) the various types of baked goods that emanate from within it. We want to model exactly the spectrum of goodies produced by the bakery each day—that is the weight of baked goods produced at each specific pastry size, from tiny donut holes to enormous wedding cakes. In this way, we aim to sketch a curve that would show the weight of baked goods per day on the vertical (y) axis versus the individual sizes of different goodies on the horizontal (x) axis. There are three factors that are crucial to figuring out the resulting curve, and if we multiply these three together, we should be able to get something close to the desired curve—literally a radiated bakery spectrum.
1. The individual weight for each pastry size.
2. The total options of possible baked goods that can be made at a certain weight. For example, starting with the smallest item, a donut hole, the baker has two basic options: plain or chocolate. Once you reach the size of a cinnamon roll, you could also have various muffins of the same size. In general, the baker has more and more options as he considers items of greater size. Think of the nearly infinite ways one can scaffold and decorate a wedding cake, versus just the two flavors of donut holes.
3. The internal decision of the bakery concerning how to allocate its limited resources. A bakery could send out infinite cakes and cream puffs if it had infinite ingredients, but the basic weight of ingredients is limited, assuming a fixed budget. The bakery has some kind of internal logic it uses, typically making just a few big cakes and a lot of muffins and rolls, because there is greater demand for items customers can take in hand to a boring morning meeting (or physics class).
Factors 1#1 and 2 increase the output weight of the bakery products as you increase the pastry size, so they would suggest a curve or line with an upward slope on our proposed graph. However, the reality check comes from factor 3. There is a limited amount of dough, and the bakery can’t devote itself to just 600-lb super-cakes. It typically makes more of the smaller items and fewer of the larger items. So if we just plotted factor 3, we would get a curve with a downward slope (Figure A.1).
When we multiply these three factors together, the net effect is to make a hump in the middle (see Figure A.1b). At the low end, the bakery makes dozens of donut holes, but each one is lightweight, so a relatively small collective weight of donut holes rolls out of the bakery every day. On the high end, there are very few enormous wedding cakes produced on the average day, so the collective weight of enormous items is also pretty small. The greatest total output weight of baked goods comes in the form of handheld items like muffins, rolls, and scones. We have lots of different kinds, with a decent heft per item.
This analogy establishes our principal players well enough. The radiation spectrum of a black body shows radiated power on the vertical axis, plotted against frequency on the horizontal axis, and we will multiply three different effects together in order to achieve that full spectrum. The chunks of radiation (which we now call photons) are analogous to pastries.
The energy of each photon is analogous to the weight of each pastry, and the frequency of each photon is analogous to generic pastry size. So the first important function is one of Planck’s most insightful and enduring suggestions, that the energy of radiation from a black body must be related directly to its frequency, or

where E is the photon’s energy, h is Planck’s universal constant, and f is the frequency of the electromagnetic radiation. This equation dates to Planck’s December 1900 presentation, where he claimed that “the most essential point of the whole calculation,” was that energy would be emitted in chunks of energy hf. This was the conception moment for quantum theory, with a granular treatment for energy.1 We finally figured out that the best model of a bakery’s behavior has it selling units of pastries and not just squeezing raw dough into the hands of customers.
(An important note from the chef: Where this analogy leaves a messy kitchen is in the analogy of pastry size to photon frequency. It’s not a clean conceptual fit, but it’s the best I can whip up for now. In the bakery world, it seems obvious that a pastry’s weight tracks its size in a simple way, but equation 1, in the world of physics, was much more surprising.)
Physicists call the second function a “density of states,” and it describes the different options of photons given a certain energy level. In our bakery analogy, this is the number of different types of baked goods that could possibly be made at a certain weight. For light, much like for the baked goods, the number of possible types of photons will increase at greater frequency and energy levels. One way of thinking about the density of states is to consider an apartment building. The larger the building (i.e., the larger the total energy “space”), the more photon housing options we have. The density of states ρ, is given by

where c is the speed of light. For you physics or math students, if the 8π looks like a geometric factor, your intuition serves you well. If our apartment building was spherical, and everyone needed a window unit, the total possible number of different tenants would be proportional to 4πf2, the surface area of the apartment complex. We end up with an extra factor of two for photons because of their so-called polarizations. The photon still has wave-like qualities, and as it moves toward you, it can wiggle up-and-down or side-to-side, and these two options, like vanilla or chocolate, increase the total number of photon options for any frequency, so that’s why the density of states has the factor of 8πf2.
Before we move to the third factor, let’s look at the first two. Based on just the energy per photon and the total photon options at any given frequency, we see both functions just increasing. So given these two, we would expect a black body to radiate more and more photons for an ever-higher frequency of light. In fact, when the classical picture of physics was better refined, by 1911, the young physicist Paul Ehrenfest labeled this expectation the “ultraviolet catastrophe.” Ultraviolet light has higher frequencies than visible light, and classical physics was predicting that even your clothes, at room temperature, would glow a dull blue color to your eyes and then send out enough ultraviolet to give you their own brand of sunburn. Such a catastrophic mismatch between reality and classical theory underlined the need for new thinking, helping motivate the first Solvay conference on quantum theory.
So now we move to the third function, the distribution of photons given a naturally limited amount of available energy. Everything to this point has assumed an infinite supply of available energy, but now we bring in some reality. In our analogy, this is the mysterious way in which a bakery decides to allocate its supply of ingredients. The ambient temperature, much like a supply of bakery ingredients, provides the energy needed to cook up some photons.
Planck intuited this distribution, nature’s own choice of pastries, in his formula of 1900, but it was not well understood for many years. Hendrik Lorentz took an early run at understanding the distribution by 1910, and we must acknowledge the wholly original and now time-tested approach of Albert Einstein in 1917, when he built a new and surprisingly simple theory for analyzing the emission and absorption of radiation.2 In the 1920s, the young Indian physicist Satyendra Nath Bose, in an exchange of letters with Albert Einstein, came to propose the precise distribution function for photons (and similar fundamental critters). So the third factor, buried within Planck’s 1900 formula, is today called the Bose-Einstein distribution.

The k here is Boltzmann’s constant, T is temperature, and f is frequency. Note the important ratio hf/kT; this is simply comparing, by analogy, the weight of one pastry to the total weight of available ingredients, and it determines the whole shape of the resulting function, g. We could write a whole book about the remarkable implications of this function—it contains the magic of thermal radiation and its universal character. Unlike human bakeries, which all make their own unique decisions of how to allocate their dough, every object in the universe obeys the same rules for distributing thermal energy to photons. Though some people bemoan restaurant chains, all of nature’s black-body bakeries practice a hyper-uniformity. And this is precisely why the thermal radiation curves are so universal, and why they are only altered by temperature (i.e., just the amount of dough available).3
Unlike the first two equations, this third equation decreases dramatically as frequency (and therefore energy) increases. The bakery figure’s curve #3 actually shows the correct function. And so the competing effects join in battle. Multiplying all three together, we obtain the thermal radiation curve, as set out perfectly by Max Planck in 1900.
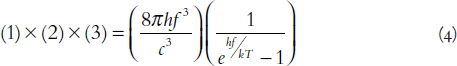
Planck’s first derivation for this was flawed. Because our approximate derivation here benefits from hindsight, it uses ideas and tools (like equation 3) that Planck did not have in his available kit at the time. These tools were also largely unavailable when he penned his so-called second quantum theory in 1912 and 1913.4
While he failed to perfect a derivation from points A to Z, he birthed critically correct and wholly original steps along the path in each attempt, and these steps persist into the present. Equation 1 was a primary result of his first attempted derivation. Just as amazing, but less well appreciated, is a result of his second attempted derivation. In Planck’s second quantum theory, his modified statistical approach created a small artifact: No matter the temperature of an object, and no matter the color of light one examined, there would always be an extra little “chunklet” equal to half of one quantum of energy. It was a trifle and could largely be ignored in most cases. Far from a mistaken slip of Planck’s pen, the effect, the “zero-point energy,” is real. It describes a sort of very low-level but ubiquitous seething of energy in the fabric of the cosmos itself. It was an unavoidable result of Planck’s mathematical approach, and he even apologized for introducing such an ugly wart to quantum theory. He wrote a mea culpa to Paul Ehrenfest in 1915.
I fear that your hatred of the zero-point energy extends to [my theory overall]. But what’s to be done? For my part, I hate discontinuity of energy even more than discontinuity of emission. Warm greetings to you and your wife.5
The zero-point energy lingers in high-level theoretical conversations 100 years later. Astrophysicists are plagued by the obvious but unexplained rapid expansion of the universe. Far from a residual effect of a Big Bang, our universe appears to be expanding faster and faster, like an explosion that is then powered by more and more explosions. In looking to explain the mysterious “dark energy” causing this accelerated expansion, physicists often start with two historical factors, emanating respectively from Einstein and Planck.
The first is Einstein’s “cosmological constant,” his proposal for propping up the universe against gravity. He sought a way to keep everything from collapsing into one enormous clump. The other is Planck’s zero-point energy that fills our quantum reality, giving the great void a “vacuum energy,” always on hand. I refer interested readers to Helge Kragh’s very readable account of how the Berlin chemist Walther Nernst first interjected Planck’s zero-point energy into cosmology just a few year’s after hearing Planck unveil the second quantum theory.6 Either factor could, hypothetically, help explain an outward pressure in the universe, but as of this writing, neither suspect can be blamed for the so-called dark energy we observe.