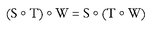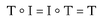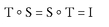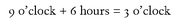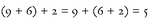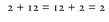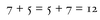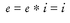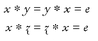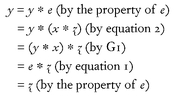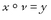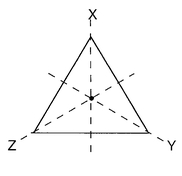In geometry we study patterns of shape. Not any kind of shape, but regular shapes, such as triangles, squares, rectangles, parallelograms, pentagons, hexagons, circles, ellipses, and, in three dimensions, tetrahedra, cubes, octahedra, spheres, ellipsoids, and the like. We see examples of these shapes in the world around us—the circular appearance of the sun and the moon, circular clock faces, circular wheels, triangular, square, and hexagonal floor tiles, cubic boxes, spherical tennis balls, ellipsoidal footballs, and so forth. Geometry studies these shapes in the abstract, removed from any particular real-world example.

Having decided what kinds of shape to study, the geometrician then discovers general facts that apply to all instances of the shape. For example, Pythagoras’s theorem says that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

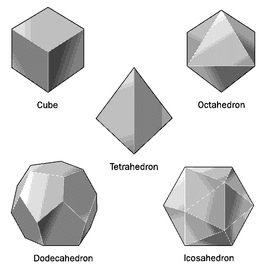
Many of the basic theorems of geometry were collected by the ancient Greek mathematician Euclid in his famous book Elements, written around 350 BC. One of the deepest theorems in Elements concerns the so-called regular polyhedra. These are the three-dimensional analogs of the regular polygons.

A regular polygon is a figure made up of equal straight-line edges, each adjacent pair of which meets at exactly the same angle. The simplest such figure is an equilateral triangle, where the sides are all equal and the angle of each vertex is 60°. Then comes a square; followed by a regular pentagon (a 108° angle between touching edges); a regular hexagon (angle 120°), etc. (see Figure 4.1). A regular polygon may have any number of sides you choose.

FIGURE 4.1 Regular Polygons. A polygon is regular if all its sides are equal and all its interior angles are equal. There are regular polygons of any number of sides greater than two. The first four are shown: the equilateral triangle, the square, the regular pentagon, and the regular hexagon.

A regular polyhedron is a three-dimensional object whose faces are all identical regular polygons, with the angles between all touching faces the same. You might think that, as with the regular polygons, there are regular polyhedra with any number of faces. But this is not true. As was proved in Euclid’s Elements, there are just five regular polyhedra: the regular tetrahedron (four identical equilateral-triangle faces); the cube (six identical square faces); the regular octahedron (eight identical equilateral-triangle faces); the regular dodecahedron (twelve identical regular pentagon faces); and the isocahedron (twenty identical equilateral-triangle faces). These are all illustrated in Figure 4.2. In this instance, the laws of geometry restrict the number of possibilities.

A similar thing happens with wallpaper patterns. The laws of geometry restrict the number of possibilities to seventeen.

FIGURE 4.2 Regular Solids. A polyhedron is regular if all its faces are identical and all its interior angles are equal. There are exactly five regular polyhedra.

Now, whereas most of us are surprised to learn that there are only five regular polyhedra, we are not surprised to find that there is a mathematical theorem about them. Regular polyhedra are just the kind of thing you would expect to find a mathematical theorem about. But wallpaper?

It’s a bit more surprising to learn of a theoretical limit to wallpaper patterns. Surely designers can always come up with new ideas, can’t they? Indeed they can. But the mathematical theorem is not about the fine details of wallpaper patterns. The feature that attracts mathematicians is that wallpaper takes a particular pattern and repeats it without limit. How many different ways are there for a fixed pattern to repeat endlessly? What are the patterns of repetition?

Well, you can simply copy the basic pattern side by side. Or you can move it along, alternately reflecting it left to right. Or maybe you can move it with some kind of rotation? Or maybe...Well, just how many different ways can you do it?

Once you start to think along these lines, asking yourself what exactly is involved in endlessly repeating a fixed, basic pattern, you realize that this too is highly structured, indeed geometric. Just the kind of thing to which mathematics might be applied.

Even so, I still find it surprising that there are exactly seventeen ways to repeat a fixed pattern. Some of those seventeen ways are fairly intricate, but interestingly, designers of rugs, mosaics, and decorative wall tilings had discovered all of them hundreds of years before the mathematicians of the nineteenth century enumerated them all and proved that there were no others. Figure 4.3 gives examples of each of the seventeen possible wallpaper patterns.

The wallpaper-pattern theorem is a good illustration of how mathematics approaches the world. Mathematics is a precise subject that deals with precise patterns. In the case of geometry, the patterns are immediately recognizable—the straight lines, the triangles, the circles, the tetrahedra, the spheres, and so forth. But sometimes you have to find the right way to look at a phenomenon before you discover those precise patterns. In the case of wallpaper design, the right question to ask is: what are the patterns by which a fixed design can repeat endlessly, to cover an entire wall?

FIGURE 4.3 Wallpaper patterns. There are exactly seventeen different ways to repeat a fixed pattern indefinitely to cover the whole plane. The illustrations show one wallpaper pattern that repeats in each of the seventeen different ways.

Of course, until you investigate, you can’t know whether you will discover any interesting (or useful) mathematics. The repeating patterns of wallpaper are mathematical because it is possible to prove a theorem about them. A similar thing happened with the coat patterns of animals.

Although the spots on a leopard or the stripes on a tiger have some regularity, they don’t appear to exhibit the kind of geometrical regularity to which mathematics can be applied. But is there a hidden pattern to animal coat markings to which we can apply mathematics?

Until recently, the answer would have been no. But during the last twenty years, mathematicians have started to develop a “geometry” of living things. One of the results of that new mathematics is the discovery that the coat patterns of animals are every bit as constrained by mathematical laws as are regular polyhedra or wallpaper patterns. The key was to discover the right way to look at the phenomenon. In the case of animal coat patterns, the question to ask is: what is the mechanism that produces the different patterns of spots and stripes?

THE GEOMETRY OF ANIMAL COAT PATTERNS

The idea of applying mathematics to study the form of living things was put forward by the great British thinker D’Arcy Thompson in his book On Growth and Form, first published in 1917. In the 1950s, the English mathematician Alan Turing took up Thompson’s suggestion, proposing a specific mechanism for applying mathematics to study the coat patterns of animals. He called this new field “morphogenesis.”

Turing’s idea was to formulate equations that describe the way animal coat patterns form, based on the biological or chemical processes that generated them. It was a good idea, but for many years no one could make much progress with it. For one thing, biologists had only the beginnings of an understanding of the actual growth processes. For another, the kinds of equations that come from the relevant biology and chemistry cannot be solved in the same way that an equation for, say, a circle or a parabola can, allowing you to draw a picture (a graph) of the curve.

Only with the development of the computer—and computer graphics —was it possible to take up Turing’s suggestion.

In the late 1980s, mathematician James Murray of the University of Oxford embarked on a three-step process to carry out Turing’s program. The first step was to write down equations that described the chemical processes that cause coloration in an animal coat. The second step was to write a computer program to solve these equations. The third step was to use computer graphics techniques to turn those solutions into pictures. If everything worked—and if the equations really did describe the growth patterns—then the resulting pictures should resemble some (all?) of the kinds of animal coat patterns observed in nature.

Murray knew that any coloration of an animal’s coat is caused by a chemical called melanin, which is produced by cells just beneath the surface of the skin. It’s the same chemical that makes fair-skinned people develop a suntan. But why spots on the leopard? Or stripes on the tiger?

Murray began by assuming that certain chemicals stimulated the cells to produce melanin. The visible coat pattern was thus a reflection of an invisible chemical pattern in the skin: high concentrations of the chemicals give rise to melanin coloration, low concentrations leave the skin largely uncolored. The question then was: what caused the melanininducing chemicals to cluster into a regular pattern so that when they “switched on” the melanin, the result was a visible pattern in the skin?

One possible mechanism was provided by so-called reaction-diffusion systems. A reaction-diffusion system is where two or more chemicals in the same solution (or in the same skin) react and diffuse through the solution, fighting with each other for territory. Although first proposed by mathematicians as a theoretical idea in the 1950s, reaction-diffusion systems were only later observed by chemists in the laboratory. Even today, they are still studied more by mathematicians, in a theoretical way, than by chemists in the laboratory.

To keep things as simple as possible, Murray assumed that just two chemicals are produced in the skin, one of which stimulates melanin production, the other which inhibits it. He further assumed that the presence of the stimulating chemical triggers increased production of the inhibitor. Finally, he supposed that the inhibiting chemical diffused through the skin faster than the stimulator. Given these assumptions, if a concentration of the stimulating chemical is formed, triggering production of the inhibitor, then the faster-moving inhibitor would be able to encircle the more slowly diffusing stimulator and prevent further expansion. The result would be a region of stimulator kept in check by an encircling ring of inhibitor. In other words, a spot.

Murray likens this process to the following scenario. Imagine, he says, a very dry forest in which scattered fire crews are stationed with helicopters and firefighting equipment. When a fire breaks out (the stimulator), the firefighters (the inhibitors) spring into action. Traveling in their helicopters, they can move much more quickly than the fire. (The inhibitor diffuses faster than the stimulator.) However, because of the intensity of the fire (the high concentration of the stimulator), the firefighters cannot contain the fire at its core. So, using their greater speed, they outrun the front of the fire and spray fire-resistant chemicals onto the trees. When the fire reaches the sprayed trees, its progress is stopped. Seen from the air, the result will be a blackened spot where the fire burned, surrounded by the green ring of sprayed trees.

Now imagine that several fires break out all over the forest. Seen from the air, the resulting landscape will show patches of blackened, burned trees interspersed with the green of unburned trees. If the fires break out sufficiently far apart, the resulting aerial pattern could be one of black spots in a sea of green. But if nearby fires are able to merge before being contained, different patterns could result. The exact pattern will depend on the number and relative positions of the initial fires and the relative speeds of the fire and the firefighters (the reaction-diffusion rates).

The case of interest to Murray was what the resulting pattern would be if the initial fire pattern was random. How would different reaction-diffusion rates then affect the final pattern? More specifically, were there rates that, starting from a random pattern of fire sources, would lead to recognizable patterns such as spots or stripes? This is where mathematics came in. There are equations that describe how chemicals react and disperse. They involve techniques from calculus and are called partial differential equations. Given the equations, Murray was able to forget the biology and the chemistry and concentrate on mathematics. By putting his equations into a computer, Murray was able to generate pictures on the screen, showing the way the chemicals dispersed. To his surprise, even with the simple scenario of just two chemicals, his equations generated dispersal patterns that looked remarkably like the skins of animals.

In fact, by experimenting with various parameters in his equations, Murray discovered a simple, hitherto unsuspected relationship between the shape and size of the skin area on which the reaction-diffusion process occurs and the coat pattern that results. Very small skin regions, he found, led to no pattern at all; long, thin regions led to stripes perpendicular to the length of the region; and squarish regions of roughly the same overall area gave rise to spots whose exact pattern depended on the region’s dimensions. For larger area he got no pattern at all. (See Figure 4.4.)

The key factor is the shape and size of the animal’s coat at the time the reaction-diffusion process occurs, which for most animals is during embryonic development—not the shape and size of the fully grown adult. For example, there is a four-week period early in the year-long gestation of a zebra during which the embryo is long and pencil-like. Murray’s mathematics predicts that, if the reactions take place during this period, the resulting pattern will be stripes. Leopard embryos, however, are fairly chubby when reaction-diffusion occurs, and Murray’s equations predict spots. Apart, that is, from the tail. The tail is long and pencil-like throughout development, which explains why the tail of the leopard is always striped.

Do Murray’s equations describe what actually happens? Since biologists have not yet observed reaction-diffusion experimentally in embryo skin, we cannot know. Murray chose the simplest case, with just two chemical reagents, so there is no reason to suppose his equations describe the situation exactly. On the other hand, those equations do produce all the coat patterns found in nature.

Some of the most convincing evidence that Murray is on the right track is that his mathematics answers a long-standing question in zoology: why is it that several kinds of animals have spotted bodies and striped tails, but none have striped bodies and spotted tails? There seems to be no evolutionary reason for this curious fact. Murray provides a ridiculously simple explanation: it’s a direct consequence of the fact that many animal embryos have chubby bodies and skinny tails, but no animal embryo has a long skinny body and a chubby tail.

FIGURE 4.4 Animal coat patterns produced mathematically on a computer screen, by solving the equations written down by mathematical biologist James Murray. By changing the value of a single parameter in his equations, Murray could change a spotted tail into a striped one.

If Murray is correct, then we have a marvelous example of how evolution leads to a highly efficient process. The two obvious survival benefits of animal coat patterns are camouflage and appeal to the opposite sex. The question is, how is this achieved?

Instead of coding the entire detailed pattern into the animal’s DNA, nature could more efficiently use the mathematical patterns Murray has discovered. All that would be necessary would be for the DNA to encode instructions telling the skin of the developing embryo (or newly born creature in the case of animals, such as Dalmatian dogs, whose skin pattern appears after birth) when to activate the reaction-diffusion process and when to bring it to a halt. The final coat pattern would then be determined by the shape and size of the skin at that stage of development.

The mathematics of animal coat patterns is just one of several new kinds of “geometry of life” described in my 1998 book Life by the Numbers. Another example I think would be usefully presented here is geometry of flowers.

THE GEOMETRY OF FLOWERS

How do you describe the shape of a flower? You could say a daisy is circular. But no flower is really circular. It only looks that way from a distance. When you take a proper look, you see that the flower is made up of many petals, which trace out a shape much more complicated than a circle. Can mathematics be used to describe the real shape of a daisy? Or how about a flower that is not circular, such as a lilac? Can mathematics describe the shape of a lilac flower?

The question might seem pointless. After all, what possible benefit is to be gained from giving a mathematical description of a flower?

One answer, which history has taught us again and again, is that scientific knowledge generally turns out to be beneficial. For example, in the early nineteenth century, mathematicians began to study the patterns of knots. Their only motivation was curiosity. But during the last twenty-five years, biologists have used the mathematics of knots to help in the fight against viruses, many of which alter the way a DNA molecule wraps around itself to form a knot.

A possible benefit of finding a mathematical description of a lilac is that it could lead to more accurate weather forecasts. Here’s how.

As in the case of wallpaper patterns and animal coat markings, the crucial first step is to find the right way of looking at the phenomenon. In the case of animal coats, the trick was to concentrate not so much on the final markings but on the process that led to those markings. Maybe a similar approach will work for flowers. Can we develop a geometry of flowers by looking at the way nature might create the flower’s shape?

If you look closely at a lilac, you will notice that a small part looks much the same as the entire flower. You see the same phenomenon with certain other flowers, and with some vegetables such as broccoli or cauliflower. Mathematicians refer to this property as self-similarity.

Clouds also have self-similarity. A mathematical way to describe self-similar patterns could be used to study clouds. Given a mathematical description of clouds, we could simulate the formation, growth, and movement of clouds on a computer. Using those simulations, maybe we could improve our ability to forecast severe weather, using our forecasts to protect ourselves better from the consequences of a major storm or a tornado. This is not completely fanciful. Researchers have been carrying out just such investigations for some years.

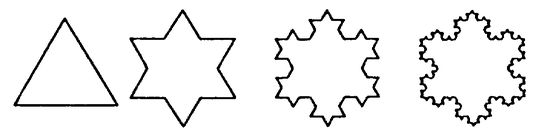
A mathematician named Helge Koch studied self-similarity at the end of the nineteenth century. Koch noticed that if you take an equilateral triangle, add a smaller equilateral triangle to the middle third of each side, then repeat the process of adding smaller and smaller triangles to the middle-thirds of the sides, eventually you will develop the fascinating shape now called the Koch snowflake, shown in Figure 4.5. (To be precise, you delete the middle-third length each time you add a new triangle.)

FIGURE 4.5 The Koch snowflake starts to take shape.

This example shows that a complicated-looking shape can result from the repeated application of a very simple rule. The self-similarity results from using the same rule over and over again. Present-day mathematicians refer to self-similar figures as fractals, a name invented in the 1960s by the mathematician Benoit Mandelbrot, who cataloged and studied many instances of self-similarity in nature.

To obtain a geometric description of a fractal, the mathematician looks for rules that, when used over and over again, produce its self-similar shape. Such a system of repeatable growth rules is called an L-system, after Aristid Lindenmayer, a biologist who, in 1968, developed a formal model for describing the development of plants at the cellular level.

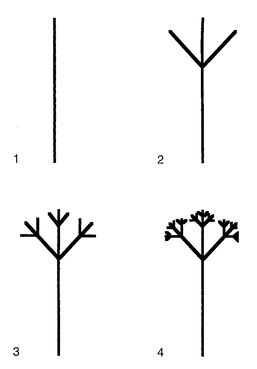
For example, a very simple L-system to produce a tree-like shape might say that if we start with the top part of any branch, that portion forms two new branches, giving three new tops. When we repeat this rule, we find we rapidly get a tree-like shape. It is easy to carry out the first few iterations of this rule using a paper and pencil (see Figure 4.6). But you only start to get something that looks like a real tree when you apply the rule hundreds of times on a computer.

Mathematician Przemyslaw Prusinkiewicz has used such an approach to generate flowers on a computer. To create, say, a lilac, Prusinkiewicz starts with a very simple L-system to generate the skeleton of the flower. Then, by taking careful measurements of an actual lilac, he refines his L-system so that the figure it produces more closely resembles reality. Using his refined L-system, he generates the branching structure of the lilac. He then uses the same technique, with a different L-system, to produce the blossoms. The result? A lilac grows before his eyes. Not a real lilac, but a mathematical one, produced on a computer (see Figure 4.7).

What does one of Prusinkiewicz’s computer-generated lilacs look like? It looks stunningly like a photograph of a real lilac. Just as the animal coat patterns produced by Murray’s equations look just like the real thing.

Both pieces of work show how the complex shapes of nature can result from very simple rules. As Prusinkiewicz says: “A plant is repeating the same thing over and over again. Since it is doing it in so many places, the plant winds up with a structure that looks complex to us. But it’s not really complex; it’s just intricate."

FIGURE 4.6 Repetition of a simple reproduction rule rapidly generates a tree-like structure. The rule is to add two new branches two-thirds of the way up each topmost branch, each one equal to one-third the length of that branch.

Murray and Prusinkiewicz both see a deeply satisfying aesthetic aspect to their work. For instance, Murray says:

When I’m walking in the woods on my own or with my wife or daughter or son, and I have time to look around, I find it quite difficult not to

FIGURE 4.7 An electronic lilac generated on a computer by the iteration of some simple growth rules. Examples such as this demonstrate that much of the seeming complexity of the natural world can be produced by some very simple rules.

look at a fern or the bark of a tree and wonder how it was formed—why is it like that? It doesn’t mean one doesn’t appreciate the beauty of a sunset or of a flower; the ideas or questions are interspersed with that sort of appreciation.

Prusinkiewicz has a similar sense of an enhanced appreciation of life:

When you appreciate the beauty of plant form, it comes not only from the static structure, but often also from the process that led to the structure. To a scientist who appreciates the beauty of this flower or leaf, it is an important aspect of understanding to know how these things were evolving over time. I call it the algorithmic beauty of plants. It’s a little bit of hidden beauty.

THE PATTERNS OF BEAUTY THE EYE CANNOT SEE

In geometry we study some of the visual patterns that we see in the world around us. Those visual patterns can be the “obviously mathematical” shapes studied by the ancient Greeks—triangles, circles, polyhedra, and the like—or the coat patterns of animals and the growth patterns of plants and flowers. (It is really a matter of definition whether you call these more recent studies “geometry.” In any event, they are definitely mathematics, and they deal with visual patterns of shape.)

But our eyes perceive other patterns, patterns not so much of shape but of form. Symmetry is an obvious example. The symmetry of a flower or snowflake is clearly related to its geometric regularity. Yet we do not really see symmetry—at least, not with our eyes; rather, we perceive it, with our minds. The only way to “see” the actual patterns of symmetry (as opposed to symmetrical patterns) is through mathematics. By making visible the otherwise invisible patterns of symmetry that contribute to beauty, the study of symmetry captures one of the deeper, more abstract aspects of shape.

I shall go a bit deeper into this example than I did for animal coat patterns and flowers, and as a result most readers are likely to find the next few pages hard going. Please try to bear with me. As I develop my theme of investigating how human beings acquired the ability to do mathematics (and why many people seem unable to use that ability), I shall use this particular example to illustrate my argument.

The first step is to find a precise way of looking at symmetry—a way that allows the mathematician to start to use formal reasoning and (most likely) to write down formulas and equations. This initial step in developing a new branch of mathematics is often one of the most difficult. Not mathematically difficult. After all, there is no mathematics yet! Rather, the problem is finding a new way to look at the phenomenon.

What is symmetry? In everyday terms, we say an object (a vase, perhaps, or a face) is symmetrical if it looks the same from different sides or from different angles, or when it is reflected in a mirror. These general observations do not exhaust all the possibilities, but they capture the main idea.

First, we take that general idea of “looking the same from several (or many) angles” and put it into concrete form. (By starting with physical objects and viewing symmetry in terms of concrete manipulations of those objects, we will arrive at an abstract, formal definition of symmetry that can apply to totally abstract objects.)

Let’s start by saying what we mean by “looking the same from a different angle.” Imagine you have some object in front of you. It could be a two-dimensional figure or a three-dimensional object. Now imagine that the object is rotated about some line or point (see figures 4.8 and 4.9). Does the object look the same after the manipulation as it did before—are its position, shape, and orientation the same? 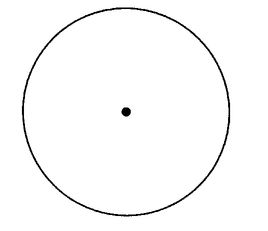If they are, we shall say that the object is “symmetrical” for that particular manipulation.

For example, if we take a circle and rotate it about its center through any angle we please, the resulting figure looks exactly the same as it started out (see Figure 4.8). We say that the circle is symmetrical for any rotation about its center. Of course, unless the rotation is through a full 360° (or a multiple of 360°), any point on the circle will end up in a different location. The circle will have moved. But, even though individual points have moved, the figure looks exactly the same afterward as it did before.

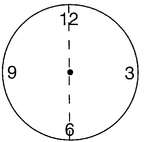
A circle is symmetrical not only for any rotation about its center but also for a reflection in any diameter. Reflection here means swapping each point of the figure with the one directly opposite with respect to the chosen diameter. For example, with a clock face, reflection in the vertical diameter swaps the point at 9 o‘clock with the point at 3 o’clock, the point at 10 o‘clock with the point at 2 o’clock, etc. (see Figure 4.9).

The circle is unusual, in that it has many symmetries—in everyday language, we would call it “highly symmetrical.”

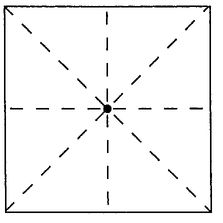
A square, on the other hand, has less symmetry than a circle. If we rotate a square through 90° or through 180° in either direction, it looks the same. But if we rotate it through 45°, it looks different—we see a diamond. Other manipulations of a square that leave it looking the same are reflecting it about either of the two lines through the center point, parallel to an edge. Or we can reflect the square in either of the two diagonals. Figure 4.10 shows that each of these manipulations moves specific points of the square to other positions, but as with the circle, the figure we end with looks exactly the same—in position, shape, and orientation—as it did before.

FIGURE 4.8 The circle looks exactly the same if it is rotated about the center through any angle or reflected in any diameter.

FIGURE 4.9 Reflecting a clock face in the diameter from 12 down to 6 swaps the 3 and the 9.

A human face has symmetry, but not as much as a square. The face looks the same if it is reflected in a vertical line through the middle of the nose (i.e., swap left and right sides), a transformation that is easily achieved with a transparency photograph by simply flipping it left to right. But any other rotation or reflection produces a result that looks different. (I am assuming a perfect face here. In reality, there are no truly symmetrical human faces, just as no physical object is a perfect circle. Mathematics always studies imaginary perfect versions of real-world objects.)

In three dimensions, the human body is symmetrical for a reflection in the plane running vertically down the center of the body, front to back—the reflection that swaps the left side of the body with the right. This symmetry lies behind what at first seems a puzzling feature of mirrors. Namely, when you look in the mirror, you see yourself with your left and right sides swapped around (lift up your left hand, the reflection looking back at you lifts its right hand), and yet your reflection does not have top and bottom swapped. How is it that the mirror swaps left and right but not top and bottom? What happens when you lie down in front of the mirror, with your left side on top and your head on the right?

FIGURE 4.10 The square looks exactly the same after a rotation about the center through one or more right angles or a reflection in any of the dashed lines.

The explanation for this strange phenomenon is that a mirror does not in fact swap anything around. If you wear a watch on your left wrist, then the reflection has a watch on the wrist directly opposite your left one. Likewise, the head of the reflected figure is directly opposite your head. But because of the left-right symmetry of the human body, you see your reflection as if it were another person facing you. Another person facing you would indeed have his or her right hand opposite your left hand.

To continue, we have moved from an everyday idea of “symmetry” to the more precise notion of symmetry with respect to a particular manipulation of the object. The greater the number of manipulations that leave a figure or object looking the same (in position, shape, and orientation), the more “symmetrical” it is in the everyday sense.

Since we want to apply our concept of symmetry to things other than geometric figures or physical objects, we shall begin to use the word “transformation” rather than manipulation from now on. A transformation takes a given object (which may be an abstract object) and transforms it into something else. The transformation might simply be translation (moving the object to another position without rotating it), or it could be rotation (about a point for a two-dimensional figure; about a line for a three-dimensional object) or reflection (in a line for a two-dimensional figure; in a plane for a three-dimensional object). Or it could be something that is not generally possible for a physical object, such as stretching or shrinking.

The key to the mathematical study of symmetry is to look at transformations of objects rather than the objects themselves.

To a mathematician a symmetry of a figure is a transformation that leaves the figure invariant. “Invariant” means that, taken as a whole, the figure looks the same after the transformation, in terms of position, shape, and orientation, as before, even though individual points of the figure may have been moved.

Because translations are included among the possible transformations, the repeating wallpaper patterns we considered earlier are symmetries. In fact, the mathematics of symmetry is what lies behind the proof that there are exactly seventeen possible ways to repeat a particular local pattern. The permissible transformations—the “symmetries” for wallpaper patterns—have to work on the entire wall, not just one part of it. This restriction is what limits the number of symmetries to seventeen.

The proof of the wallpaper-pattern theorem involves a close examination of the ways transformations can be combined to give new transformations, such as performing a reflection followed by a counterclockwise rotation through 90°. It turns out that there is an “arithmetic” of combining transformations, just as there is an arithmetic (the familiar one) for combining numbers. In ordinary arithmetic, you can add two numbers to give a new number, and you can multiply two numbers to give a new number. In the “arithmetic of transformations,” you combine two transformations to give a new transformation by performing one of the transformations followed by the other.

The arithmetic of transformations works in some ways like the arithmetic of numbers. But there are interesting differences. The discovery of this strange new arithmetic in the latter part of the eighteenth century opened the door to a host of dazzling new mathematical results that affected not only mathematics but physics, chemistry, crystallography, medicine, engineering, communications, and computer technology as well.

WHY EVEN MATHEMATICAL LONERS LIKE TO WORK IN GROUPS

When mathematicians talk about “groups,” chances are they are not talking about encounter groups or hot tub parties, but about these powerful new kinds of arithmetic—which mathematicians call by the rather daunting name “group theory.”

Our initial look at symmetry has taken us on a path of increased precision and deeper abstraction. Starting with an intuitive sense of things being “symmetrical,” we were led to formulate a precise notion of a mathematical “symmetry”—a transformation that leaves the overall object or figure invariant, i.e., looking exactly the same. Then we realized that when we combine two such symmetries of a given object or figure, we get another symmetry (of that object or figure). That in turn reminded us of combining two numbers to give a new number in arithmetic, say by adding or multiplying them together.

The next step, which we’ll carry out below, is to see how the pattern of combining symmetries compares with the pattern of adding numbers or the pattern of multiplying numbers.

Notice how, by remaining constantly on the lookout for new patterns (or even more, for familiar patterns in new guises), we keep changing our viewpoint. I am sure that this constant shifting of view and the accompanying steady increase in abstraction (from patterns, to patterns of patterns, to patterns of patterns of patterns) are among the features of advanced mathematics that most people find hardest to cope with. (I certainly do.)

For the eighteenth-century mathematicians who first trod it, the “symmetry path” we are following was very much a journey into the unknown. It took tremendous insight and breathtaking creativity to see that this simple idea of combining symmetry transformations would lead to a powerful new kind of arithmetic: the arithmetic of groups.

Given any figure, the symmetry group of that figure is the collection of all transformations that leave the figure invariant. For example, the symmetry group of the circle consists of all rotations about the center (through any angle, in either direction), all reflections in any diameter, and any combination of such. Invariance of the circle under rotations about the center is referred to as rotational symmetry; invariance with respect to reflection in a diameter is called reflectional symmetry. Both kinds of symmetry are recognizable by sight.

Since it is such a simple example, I’ll use the symmetry group of a circle to show how you do “arithmetic” with a group. This will involve a bit of algebra. It’s a bit like the algebra familiar to you from high school, except that whereas in high school algebra the letters x, y, and z generally denoted unknown numbers, here the letters S, T, and W denote symmetry transformations (of the circle in the first instance).

If you get totally lost, you can always skip ahead to the start of the next chapter. You will still be able to finish the book, although you will not be able to appreciate fully the case I make that mathematical thought is just a variation of other kinds of thought. (Of course, you can always come back later and take another look. By the book’s end, I hope to have convinced you that you really do have the ability to follow such a discussion.) Here goes.

If S and T are two transformations in the circle’s symmetry group, then the result of applying first S and then T is also a member of the symmetry group. (Why? Because, as both S and T leave the circle invariant, so too does the combined application of both transformations.) It is common to denote this double transformation by T ° S. (This is read as “T composed with S.” There is a good reason for the order here, where the transformation applied first is written second, having to do with an abstract pattern that connects groups and other branches of mathematics, but I shall not go into that connection here.)

As I mentioned, this method of combining two transformations to give a third is reminiscent of addition and multiplication, which combine any pair of whole numbers to give a third. To the mathematician, ever on the lookout for patterns and structure, it is natural to want to see which properties of addition and multiplication of whole numbers are echoed by the act of combining symmetry transformations.

First, the operation is what is called associative: if S, T, W are transformations in the symmetry group, then:

What this equation means is that if you want to combine three transformations, it doesn’t matter which two you combine first (as long as you keep them in the same order: S, then T, then W). You can form S _° T first, and then combine the result with W, or you can form T _° W first and then combine S with that result. The answer you get will be the same in both cases. In this respect, this new operation is very much like addition and multiplication of whole numbers.

Second, there is an identity transformation that leaves unchanged any transformation it is combined with. It’s the null rotation, the rotation through angle o. The null rotation, call it I, can be applied along with any other transformation T, to yield:

The rotation I plays the same role here as the number o does in addition (x + 0 = 0 + x = x, for any whole number x) and the number 1 in multiplication (x × 1 = 1 × x = x).

Third, every transformation has an inverse: if T is any transformation, there is another transformation S such that the two combined together give the identity:

The inverse of a rotation is a rotation through the same angle in the opposite direction. The inverse of any reflection is that very same reflection. To obtain the inverse for any finite combination of rotations and reflections, you take the combination of backward rotations and rereflections that exactly undoes its effect: start with the last one, undo it, then undo the previous one, then its predecessor, and so on.

The existence of inverses is another property familiar to us in addition of whole numbers: for every whole number m there is a whole number n such that:

m + n = n + m = 0 (the identity for addition)

The inverse of m is just negative m. That is, n =—m.

The same is not true for multiplication of whole numbers. It is not the case that for every whole number m there is a whole number n such that:

m × n = n × m = 1 (the identity for multiplication)

In fact, only for the whole numbers m = 1 and m =—1 is there another whole number n that satisfies the above equation. Whereas for the first two properties (associativity and the existence of an identity) group arithmetic for the circle is just like both addition and multiplication of whole numbers, for the third property (existence of inverses) group arithmetic is like addition of whole numbers but different from multiplication of whole numbers.

To summarize, any two symmetry transformations of a circle can be combined by the combination operation to give a third symmetry transformation, and this operation has the three properties familiar to many of us from ordinary arithmetic of whole numbers: associativity, identity, and inverses.

Although we were thinking about symmetries of a circle, everything we just observed is true for the group of symmetry transformations of any figure or object. (If you don’t believe me, pick some other figure, say a square, and go back and check.) In other words, the arithmetic of symmetry transformations applies to any object or figure whatsoever. What is more, that arithmetic is like the addition (but not the multiplication) of whole numbers.

Once mathematicians realized that they had found a new kind of arithmetic, they immediately started to study it in a completely abstract fashion. Now, if you think things have become pretty abstract already, you’re right. But abstraction is one of the most powerful weapons in mathematicians’ armory, and it’s one they use whenever the opportunity arises. In the case of groups, the next abstraction step is to forget the actual symmetries and the figure or object they are based on, and just look at the arithmetic. The result is a completely abstract definition of the (abstract) mathematical object called a “group.”

In general, whenever mathematicians have some set, G, of entities (which could be the set of all symmetry transformations of some figure, but need not be) and an operation that combines any two elements x and y in the set G to give a further element x * y in G (read as “x star y” or simply “xy”), they call this collection a group if the following three conditions are met:

G1. For all x, y, z in G, (x * y) * z = x * (y * z).

G2. There is an element e in G such that x * e = e * x = x for all x in G. (e is called an identity element.)

G3. For each element x in G there is an element y in G such that x * y = y * x = e, where e is as in condition G2.

These three conditions (generally called the axioms³ for a group) are just the properties of associativity, identity, and inverses that we already observed for combining symmetry transformations of any figure. Thus the collection of all symmetry transformations of a figure is a group: G is the collection of all symmetry transformations of the figure, and is the operation of combining two symmetry transformations.

It should also be clear that if G is the set of whole numbers and the operation * is addition, then the resulting structure is a group. As we observed, the same is not true for the whole numbers and multiplication. But you should have no trouble convincing yourself that, if G is the set of all rational numbers (i.e., whole numbers and fractions) apart from zero, and * is multiplication, then the result is a group. All you have to do is show that the conditions G1, G2, and G3 above are all valid for the rational numbers when the symbol * denotes multiplication. In that example, the identity element e in axiom G2 is the number i.

The finite arithmetic we use to tell the time is another example of a group. In this arithmetic, the 12-hour clock has the whole numbers 1, ... , 12 (which constitute the set G), and we add them according to the rule that we go back to 1 when we get to past 12. For example, 9 + 6 = 3, which looks a little odd until you remember that:

For this arithmetic, the associativity condition (G1) is valid. For example:

(9 o‘clock + 6 hours) + 2 hours = 9 o’clock + (6 hours + 2 hours) = 5 o’clock

(Just work out each part for yourself). So:

4. All right angles are the same.

5. Given any line and a point not on that line, there is a unique line through that point, parallel to the given line. (Two lines are parallel if they do not meet, no matter how far extended.)

What about an identity? Well, in clock arithmetic, adding 12 takes us back to the same hour. For example,

2 o‘clock + 12 hours = 12 o’clock + 2 hours = 2 o’clock

So G2 holds, with the number 12 being the identity. (Note that clock arithmetic does not have o.) What about condition G3? To get the inverse for any number in G, you simply continue around the clock face until you reach 12. For example, the inverse of 7 is 5, because

and 12 is the identity in 12-hour clock arithmetic. (Thus, in 12-hour clock arithmetic, we get the rather strange-looking equation—7 = 5.)

Clock groups are cute, but not particularly interesting to a mathematician. My purpose in mentioning them was simply to show you that the group concept can arise in many different contexts besides the ones we’ve looked at previously. In fact, groups arise all over the place. The group “pattern” can be found hidden in all sorts of phenomena. This is why the mathematics of groups is taught to every university student of mathematics.

NOW FOR THE REALLY HEAVY STUFF

Before looking at one further example of a symmetry group, it is worth spending a few moments looking at the three conditions that determine whether a given collection of entities and an operation constitute a group.

The question is: what other properties of groups follow automatically from the three group axioms? Anything that we can show to be a logical consequence of the axioms will be automatically true for any particular group.

(This is probably another point where some readers will want to bail out and skip to the next chapter. As I said before, the longer you stick with this chapter, the better you will be able to appreciate my arguments about the nature of mathematical thought. But again, you can always come back later.)

The first condition, G1, the associativity condition, is already very familiar to us in the case of the arithmetic operations of addition and multiplication (although not subtraction or division). I won’t say anything more about that.

Condition G2 asserts the existence of an identity element. In the case of addition of whole numbers, there is only one identity: the number o. Is this true of all groups, or is it something special about whole number arithmetic?

In fact, any group has exactly one identity element. If e and i are both identity elements, applying the G2 property twice in succession gives the equation:

So e and i must be one and the same.

This last observation means in particular that there is only one element e that can figure in condition G3. (G3, remember, says that for each element x in G there is an element y in G such that x * y = y * x = e.) Using that fact, we can go on to show that, for any given element x in G, there is only one element y in G that satisfies the condition in G3. This is a bit harder to prove. Hang on.

Suppose y and z are both related to x as in G3. That is, suppose that:

Then:

So y and z are one and the same. In other words, there is only one such y for a given x.

Since there is precisely one y in G related to a given x as in G3, that y may be given a name: it is called the (group) inverse of x and is often denoted x^—1. And with that, I have just proved a theorem in group theory: in any group, every element has a unique inverse. I proved this by deducing it logically from the group axioms, the three initial conditions, G1, G2, G3.

For most people, the above algebra is already a stretch. But for a mathematician, it is fairly straightforward. (The reason for this difference in comprehension is, of course, one of the things this book sets out to explain.) Whether you find it hard or easy, however, it does illustrate the enormous power of abstraction in mathematics. There are many, many examples of groups in mathematics. Having proved, using only the group axioms, that group inverses are unique, we know that this fact applies to every single example of a group. No further work is required. If tomorrow you come across a quite new kind of mathematical structure, and you determine that what you have is a group, you will know at once that every element of your group has a single inverse. In fact, you will know that your newly discovered structure possesses every property that can be established—in abstract form—on the basis of the group axioms alone.

The more examples there are of a given abstract structure, such as a group, the wider the applications of any theorems you prove about it. The cost of this greatly increased efficiency is that one has to learn to work with highly abstract structures—with abstract patterns of abstract entities. In group theory, it seldom matters what the elements of a group are or what the group operation is. Their nature plays no role. The elements could be numbers, transformations, or other kinds of entities, and the operation could be addition, multiplication, composition of symmetry transformations, or whatever. All that matters is that the objects together with the operation satisfy the group axioms G1, G2, and G3.

One final remark concerning the group axioms is in order. Anyone familiar with the commutative laws of arithmetic might well ask why we did not include it as a fourth axiom:

G4. For all x, y in G, x * y = y * x.

The absence of this law meant that in both G2 and G3, the combinations had to be written two ways. For instance, both x * e and e * x appear in G2. If commutative law were true, we could have written G2 as:

There is an element e in G such that x * e = x for all x in G.

The reason mathematicians do not include an axiom G4 is that it would exclude many of the examples of groups that mathematicians wish to consider. By writing G2 and G3 the way they do, and leaving the commutative law out, the group concept has much wider application than it otherwise would.

Consider, for example, a symmetry group a bit more complicated than a circle—the equilateral triangle shown in Figure 4.11. This triangle has precisely six symmetries. There is the identity transformation, I (the transformation that makes no changes whatsoever), clockwise rotations v and w through 120° and 240°, and reflections x, y, z in the lines X, Y, Z, respectively. (The lines X, Y, Z stay fixed as the triangle moves.) There is no need to list any counterclockwise rotations, since a counterclockwise rotation of 120° is equivalent to a clockwise rotation of 240° and a counterclockwise rotation of 240° has the same effect as a clockwise rotation of 120°.

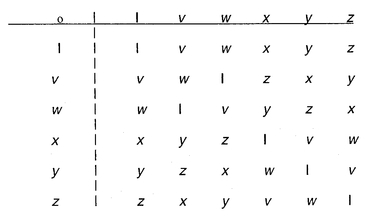
There is also no need to include any combinations of these six transformations, since the result of any such combination is equivalent to one of the six given. The table shown in Figure 4.12 gives the basic transformation that results from applying any two basic transformations. For instance, the transformations x and v combine to give y, which we write as:

FIGURE 4.11 The triangle looks the same if it is rotated about the center through 120° in either direction or if it is reflected in any of the dashed lines marked X, Y, Z.

Again, the result of applying first w and then x, namely the group element x ° w, is z, and the result of applying v twice in succession, v ° v, is w. The group table also shows that v and w are mutual inverses and x, y, z are each self-inverse. Moreover, x ° y = v and y ° x = w, so this group is not commutative.

Since the combination of any two of the given six transformations is another such transformation, it follows that the same is true for any finite combination. You simply apply the pairing rule successively. For example, the combination (w ° x) ° y is equivalent to y ° y, which in turn is equivalent to I.

And there you have the group theorist’s equivalent of the multiplication table that caused you so much trouble in elementary school. For all the abstraction, we have been doing nothing more complicated than elementary school arithmetic.

So why does it feel much more complicated?

FIGURE 4.12 Multiplication table for the symmetry group of an equilateral triangle.

Partly because it seems so much more abstract. Yet I don’t think combining transformations is any more abstract than combining numbers. The only difference is that transformations are processes you perform whereas numbers are based on collections that you count. And that’s not much of a difference. Both can be done concretely—with cardboard cutout figures for symmetry transformations and with collections of counters for arithmetic. Maybe if we were taught the “arithmetic” of symmetry transformations as young children, and encountered numbers only when we were older, we would find groups easier than arithmetic.

This points to a significant factor affecting the way we learn mathematics. Young children have not only a great ability to master abstraction, but an instinct to do so. For that is precisely what is involved in learning to use language, which all young children do with ease. Since children are taught arithmetic at a very young age, they achieve a reasonable mastery of it. By the time they are faced with learning a “different arithmetic”—be it algebra at high school or group theory in college—not only have they lost the ability to master abstraction spontaneously, but even worse, most have also developed an expectation that they cannot master it. And, as with most things in life, we tend to find what we expect.