© Springer Nature Switzerland AG 2019
C. Bocci, L. ChiantiniAn Introduction to Algebraic Statistics with TensorsUNITEXT118https://doi.org/10.1007/978-3-030-24624-2_3

3. Statistical Models

Cristiano Bocci1   and Luca Chiantini1
(1)
Dipartimento di Ingegneria dell’Informazione e Scienze Matematiche, Università di Siena, Siena, Italy
 
 
Cristiano Bocci
Email: cristiano.bocci@unisi.it

3.1 Models

In this chapter, we introduce the concept of model, essential point of statistical inference. The concept is reviewed here by our algebraic interpretation. The general definition is very simple:

Definition 3.1.1

A model on a system S of random variables is a subset M of the space of distributions $$\mathcal {D}(S)$$.

Of course, in its total generality, the previous definition it is not so significant.

The Algebraic Statistics consists of practice in focus only on certain particular types of models.

Definition 3.1.2

A model M  on a system S is called algebraic model  if, in the coordinates of $$\mathcal {D}(S)$$, M corresponds to the set of solutions of a finite system of polynomial equations. If the polynomials are homogeneous, then M si called a homogeneous algebraic model.

It occurs that the algebraic models are those mainly studied by the proper methods of Algebra and Algebraic Geometry.

In the statistical reality, it occurs that many models, which are important for the study of stochastic systems (discrete), are actually algebraic models.

Example 3.1.3

On a system S, the set of distributions with constant sampling is a model M. Such a model is a homogeneous algebraic one.

As a matter of fact, if $$x_1,\dots , x_n$$ are the random variables in S and we identify $$\mathcal {D}_{\mathbb R}(S)$$ with $$\mathbb R^{a_1}\times \dots \times \mathbb R^{a_n}$$, where the coordinates are $$y_{11}, \dots , y_{1a_1}, y_{21}, \dots , y_{2a_2}, \dots , y_{n1}, \dots , y_{na_n}$$, then M is defined by the homogeneous equations:
$$ y_{11}+\dots +y_{1a_1}=y_{21}+\dots +y_{2a_2}=\dots =y_{n1}+\dots +y_{na_n}.$$
The probabilistic distributions form a submodel of the previous model, which is still algebraic, but not homogeneous!

3.2 Independence Models

The most famous class of algebraic models is the one given by independence models. Given a system S, the independence model on S is, in effect, a subset of the space of distributions of the total correlation $$T = \Pi S$$, containing the distributions in which the variables are independent among them. The basic example is Example 2.​3.​13, where we consider a Boolean system S, whose two variables x, y represent, respectively, the administration of the drug and the healing.

This example justifies the definition of a model of independence, for the random systems with two variables (dipoles) , already in fact introduced in the previous chapters.

Definition 3.2.1

Let S be a system with two random variables $$x_1, x_2$$ and let $$T=\Pi S$$. The space of $$K-$$distributions on T is identified with the space of matrices $$K^{a_1,a_2}$$, where $$a_i$$ is the number of states of the variable $$x_i$$.

We recall that a distribution $$D\in \mathcal {D}_K(T)$$ is a distribution of independence if D, as matrix, has rank $$\le 1$$.

The independence model on S is the subset of $$\mathcal {D}_K(T)$$ of distributions of rank $$\le 1$$.

To extend the definition of independence to systems with more variables, consider the following example.

Example 3.2.2

Let S be a random system, having three random variables $$x_1, x_2, x_3$$ representing, respectively, a die and two coins (this time not loaded). Let $$T = \Pi S$$ and consider the $$\mathbb R$$-distribution D on T defined by the tensor

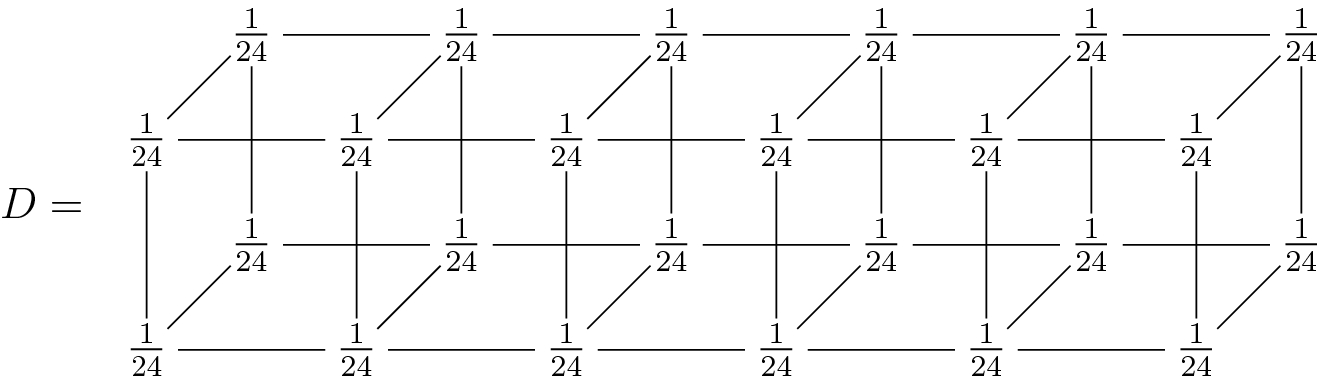
../images/485183_1_En_3_Chapter/485183_1_En_3_Figa_HTML.png

It is clear that D is a distribution of independence and probabilistic. You can read it like the fact that the probability that a d comes out from the die at the same time of the faces (for example, T and H) from the two coins, is the product of the probability $$\frac{1}{6}$$ that d comes out of the die times the probability $$\frac{1}{2}$$ that T comes out of the coin times the probability $$\frac{1}{2}$$ that H comes out of the other coin.

Hence, we can use Definition 6.​3.​3 to define the independence model.

Definition 3.2.3

Let S be a system with random variables $$x_1,\dots , x_n$$ and let $$T=\Pi S$$. The space of K-distributions on T is identified with the space of tensors $$K^{a_1,\dots , a_n}$$, where $$a_i$$ is the number of states of the variable $$x_i$$.

A distribution $$D\in \mathcal {D}_K(T)$$ is a distribution of independence  if D lies in the image of independence connection (see Definition 2.​3.​4), i.e., as a tensor, it has rank 1 (see Definition 6.​3.​3).

The independence model  on X is the subset of $$\mathcal {D}_K(T)$$ consisting of all distributions of independence (that is, of all tensors of rank 1).

The model of independence, therefore, corresponds to the subset of simple (or decomposable) tensors in a tensor space (see Remark 6.​3.​4).

We have seen, in Theorem 6.​4.​13 of the chapter on Tensorial Algebra, how such subset can be described. Since all relations (6.​4.​1) correspond to the vanishing of one (quadratic) polynomial expression in the coefficients of the tensor, we have

Corollary 3.2.4

The model of independence is an algebraic model.

Note that for the tensors $$2 \times 2 \times 2$$, the independence model is defined by 12 quadratic equations (6 faces + 6 diagonal).

The equations corresponding to the equalities (6.​4.​1) describe a set of equations for the model of independence. However such a set, in general, it is not minimal.

The distributions of independence represent situations in which there is no link between the behavior of the various random variables of S, which are, therefore, independent.

There are, of course, intermediate cases between a total link and a null link, as seen in the following:

Example 3.2.5

Let S be a system with 3 random variables. The space of distribution $$\mathcal {D}(\Pi S)$$ consists of tensors of dimension 3 and type $$(d_1,d_2,d_3)$$. We say that a distribution $$D\in \mathcal {D}(\Pi S)$$ is without triple correlation  if there exist three matrices $$A\in R^{d_1,d_2}$$, $$B\in R^{d_1,d_3}$$, $$C\in R^{d_2,d_3}$$ such that for all i, j, k:
$$ D(i,j,k)= A(i,j)B(i,k)C(j, k).$$
An example, when S is Boolean, is given by the tensor
../images/485183_1_En_3_Chapter/485183_1_En_3_Figb_HTML.png
which is obtained by the matrices
$$ A=\begin{pmatrix} 2 &{} 1 \\ 1 &{} 3 \end{pmatrix} \quad B= \begin{pmatrix} 0 &{} 1 \\ -1 &{} 2 \end{pmatrix} \quad C=\begin{pmatrix} 1 &{} -2 \\ 3 &{} 2 \end{pmatrix} \quad $$

3.3 Connections and Parametric Models

Another important example of models in Algebraic Statistics is provided by the parametric models. They are models whose elements have coefficients that vary according to certain parameters. To be able to define parametric models, it is necessary first to fix the concept of connection between two random systems.

Definition 3.3.1

Let S, T be system of random variables. We call K-connection between S and T any function $$\Gamma $$ from the space of K-distributions $$\mathcal {D}_K(S)$$ to the space of K-distributions $$\mathcal {D}_K(T)$$.

As usual, when the field K is understood, we will omit it in the notation.

After all, therefore, connections are nothing more than functions between a space $$K ^ s$$ and a space $$K ^ t$$. The name we gave, in reference to the fact that these are two spaces connected to random systems, serves to emphasize the use we will make of connections: to transport distributions from the system S to the system T.

In this regard, if T has n random variables $$y_1, \dots , y_n$$, and the alphabet of each variable $$y_i$$ has $$d_i$$ elements, then $$\mathcal {D}_K(T) $$ can be identified with $$K^{d_1} \times \dots \times K^{d_n}$$. In this case, it is sometimes useful to think of a connection $$\Gamma $$ as a set of functions $$\Gamma _i:\mathcal {D}(S)\rightarrow K^{d_i}$$.

If $$s_1,\dots , s_a$$ are all possible states of the variables in S, and $$t_{i1},\dots , t_{id_i}$$ are the possible states of the variable $$y_i$$, then we will also write
$$ {\left\{ \begin{array}{ll} t_{i1} &{}= \quad \Gamma _{i1}(s_1,\dots , s_a) \\ ... &{}= \quad ... \\ t_{id_i} &{}= \quad \Gamma _{id_i}(s_1,\dots , s_a) \\ \end{array}\right. } $$
The definition of connection given here, in principle, it is extremely general: no particular properties are required for the $$\Gamma _i$$ functions; not even continuity. Of course, in concrete cases, we will study in particular certain connections having well-defined properties.

It is clear that, in the absence of any property, we cannot hope that the more general connections satisfy many properties.

Let us look at some significant examples of connections.

Example 3.3.2

Let S be a random system and $$S'$$ a subsystem of S. You get a connection from S to $$S'$$, called projection simply by forgetting the components of the distributions which correspond to random variables not contained in $$S'$$.

Example 3.3.3

Let S be a random system and $$T=\Pi S $$ its total correlation. Assume that S has random variables $$x_1,\dots , x_n$$, and each variable $$x_i$$ has $$a_i$$ states, then $$\mathcal {D}_K(S)$$ is identified with $$K^{a_1}\times \dots \times K^{a_n}$$. In Definition 2.​3.​4, we defined a connection $$\Gamma : \mathcal {D}_K(S)\rightarrow \mathcal {D}_K(T)$$, called connection of independence  or Segre connection, in the following way: $$\Gamma $$ sends the distribution
$$ D=((d_{11},\dots , d_{1a_1}),\dots ,(d_{n1},\dots , d_{na_n}))$$
to the tensor (thought as distribution on $$\Pi S$$) $$D'=\Gamma (D)$$ such that
$$ D'_{i_1,\dots , i_n}= d_{1i_1}\cdots d_{ni_n}. $$
It is clear, by construction, that the image of the connection is formed exactly by the distributions of independence on $$ \Pi S $$.

Clearly there are other interesting types of connection. A practical example is the following:

Example 3.3.4

Consider a population of microorganisms in which we have elements of two types, A, B, that can pair together randomly. In the end of the couplings, we will have microorganisms with genera of type AA or BB, or mixed type $$AB = BA$$.

The initial situation corresponds to a Boolean system with a variable (the initial type $$t_0$$) which assumes the values A, B. At the end, we still have a system with only one variable (the final type t) that can assume the 3 values AA, AB, BB.

If we initially insert a distribution with $$a = D(A)$$ elements of type A and $$b=D(B)$$ elements of type B, which distribution we can expect on the final variable t?

An individual has a chance to meet another individual of type A or B which is proportional to (a, b), then the final distribution on t will be $$D'$$ given by $$D'(AA) = a^2 $$, $$D '(AB) = 2ab$$, $$D'(BB) = b^2$$. This procedure corresponds to the connection $$\Gamma : \mathbb R^2 \rightarrow \mathbb R^3$$ $$\Gamma (a, b) = (a^2,2ab, b^2)$$.

Definition 3.3.5

We say that a model $$V\subset \mathcal {D}(T)$$ is parametric if there exists a random system S and a connection $$\Gamma $$ from S to T such that V is the image of S under $$\Gamma $$ in $$\mathcal {D}(T)$$, i.e., $$V=\Gamma (\mathcal {D}(S))$$.

A model is polynomial parametric if $$\Gamma $$ is defined by polynomials.

A model is toric   if $$\Gamma $$ is defined by monomials.

The motivation for defining parametric models should be clear from the representation of a connection. If $$s_1, \dots , s_a$$ are all possible states of the variables in S, and $$t_ {i1}, \dots , t_ {id_i}$$ are the possible states of the variables $$y_i $$ of T, then in the parametric model defined by the connection $$\Gamma $$ we have
$$ {\left\{ \begin{array}{ll} t_{i1} &{}= \quad \Gamma _{i1}(s_1,\dots , s_a) \\ ... &{}=\quad ... \\ t_{id_i} &{}= \quad \Gamma _{id_i}(s_1,\dots , s_a) \\ \end{array}\right. } $$
where the $$\Gamma _{ij}$$’s represent the components of $$\Gamma $$.

The model definition we initially gave is so vast to be generally poorly usable. In reality, the models we will use in the following will always be algebraic models or polynomial parametric.

Example 3.3.6

It is clear from the Example 3.3.3 that the model of independence is given by the image of the independence connection, defined by the Segre map (see the Definition 10.​5.​9), so it is a parametric model.

The tensors T of the independence model have in fact coefficients that satisfy parametric equations
$$\begin{aligned} {\left\{ \begin{array}{ll} \dots \\ T_{i_1\dots i_n} = v_{1i_1}v_{2i_2}\cdots v_{ni_n} \\ \dots \end{array}\right. } \end{aligned}$$
(3.3.1)

From its parametric equations, (3.3.1), we quickly realize that the independence model is a toric model.

Example 3.3.7

The model of Example 3.3.4 is a toric model, since it is defined by the equations
$$ {\left\{ \begin{array}{ll} x &{}= a^2 \\ y &{}= 2ab \\ z &{}= b^2 \end{array}\right. }. $$

Remark 3.3.8

It is evident, but it is good to underline it, that for the definitions we gave, being an algebraic or polynomial parametric model is independent from changes in coordinates. Being a toric model instead it can depend on the choice of coordinates.

Definition 3.3.9

The term linear model  denotes, in general, a model on S defined in $$\mathcal {D}(S)$$ by linear equations.

Obviously, every linear model is algebraic and also polynomial parametric, because you can always parametrize a linear space.

Example 3.3.10

Even if a connection $$\Gamma $$, between the K-distributions of two random systems S and T, is defined by polynomials, the polynomial parametric model that $$\Gamma $$ defines it is not necessarily algebraic!.

In fact, if we consider $$K = \mathbb R$$ and two random systems S and T each having one single random variable with a single state, the connection $$\Gamma : \mathbb R\rightarrow \mathbb R$$, $$\Gamma (s) = s^2$$ certainly determines a polynomial parametric model (even toric) which corresponds to $$\mathbb R_{\ge 0} \subset \mathbb R$$, so it can not be defined in $$\mathbb R$$ as vanishing of polynomials.

We will see, however, that by widening the field of definition of distributions, as we will do in the next chapter switching to distributions on $$\mathbb C$$, under a certain point of view all polynomial parametric models will, in fact, be algebraic models.

The following counterexample is a milestone in the development of so much part of the Modern mathematics. Unlike Example 3.3.10, it cannot be recovered by enlarging our field of action.

Example 3.3.11

Not all algebraic models are polynomial parametric.

We consider in fact a random system S with only one variable having three states. In the distribution space $$\mathcal {D}(S) = \mathbb R^3$$, we consider the algebraic model V defined by the unique equation $$x^3 + y^3-z^3 = 0 $$.

There cannot be a polynomial connection $$\Gamma $$ from a system $$S'$$ to S whose image is V.

In fact, suppose the existence of three polynomials p, q, r, such that $$x = p, y = q, z = r$$. Obviously, the three polynomials must satisfy identically the equation $$p^3 + q^3-r^3 = 0$$. It is enough to verify that there are no three polynomials satisfying the previous relationship. Provided to set values for the other variables, we can assume that p, q, r are polynomials in a single variable t. We can also suppose that the three polynomials do not have common factors. Let us say that $$\deg (p) \ge \deg (q) \ge \deg (r)$$.

Deriving the equation
$$ p(t)^3+q(t)^3-r(t)^3=0, $$
with respect to t, we get
$$ p^2(t)p'(t)+q^2(t)q'(t)-r^2(t)r'(t)=0. $$
The two previous equations give a homogeneous linear system
$$ \begin{pmatrix} p(t) &{} q(t) &{} -r(t) \\ p'(t) &{} q'(t) &{} -r'(t) \end{pmatrix}. $$
The solution $$p^2(t), q^2(t), r^2(t)$$ must be proportional to the $$2\times 2$$-minors of the matrix, hence $$p^2(t)$$ is proportional to $$q(t)r'(t)-q'(t)r(t)$$, and so on. Considering the equality $$p^2(t)(p(t)r'(t)-p'(t)r(t))=q^2(t)(q(t)r'(t)-q'(t)r(t))$$, we get that $$p^2(t)$$ divides $$q(t)r'(t)-q'(t)r(t)$$, hence $$2\deg (p(t))\le \deg (q)+deg(r)-1$$ which contradicts the fact that $$\deg (p) \ge \deg (q) \ge \deg (r)$$.

Naturally, there are examples of models that arise from connections that they do not relate a system and its total correlation.

Example 3.3.12

Let us say we have a bacterial culture in which we insert bacteria corresponding to two types of genome, which we will call A, B.

Suppose, according to the genetic makeup, the bacteria can develop characteristics concerning the thickness of the membrane and of the core. To simplify, let us say that in this example, cells can develop nucleus and membrane large or small.

According to the theory to be verified, the cells of type A develop, in the descent, a thick membrane in $$20\%$$ of cases and develop large core in $$40\%$$ of cases. Cells of type B develop thick membrane in the $$25 \%$$ of cases and a large core in one-third of the cases. Moreover, the theory expects that the two phenomena are independent, in the intuitive sense that developing a thick membrane is not influenced by, nor influences, the development of a large core.

We build two random systems. The first S, which is Boolean, has only one variable random c (= cell) with A, B states. The second T with two boolean variables, m (= membrane) and n (= core). We denote for both with 0 the status “big” and with 1 the status “small”.

The theory induces a connection $$\Gamma $$ between S and T. In the four states of the two variables of T, which we will indicate with $$x_0, x_1, y_0, y_1$$, this connection is defined by
$$ {\left\{ \begin{array}{ll} x_0 &{}= \frac{1}{5} a +\frac{1}{4} b \\ x_1 &{}= \frac{4}{5} a +\frac{3}{4} b \\ y_0 &{}= \frac{2}{5} a +\frac{1}{3} b \\ y_1 &{}= \frac{3}{5} a +\frac{2}{3} b \end{array}\right. } $$
where a, b correspond to the two states of S. As a matter of fact, suppose we introduce 160 cells, 100 of type A, and 60 of type B. This leads to consider a distribution D on S given by $$D=(100,60)\in \mathbb R^2$$.
The distribution on T defined by the connection is given by
$$\Gamma (D)= ((35,125), (60, 100))\in (\mathbb R^2)\times (\mathbb R^2).$$
This reflects the fact that in the cell population (reported at 160) we expect to eventually observe 35 cells with large membrane and 60 cells with a large core.
If the experiment, more realistically, manages to capture the percentage of cells with the two characteristics (shuffled), then we can consider a connection that links S with the total correlation $$\Pi T $$: indicating with $$x_ {00}, x_ {01}, x_ {10}, x_ {11}$$ the variables corresponding to the four states of the only variable of $$\Pi T$$, then such connection $$\Gamma '$$ is defined by
$$ {\left\{ \begin{array}{ll} x_{00} &{}= \frac{(\frac{1}{5} a +\frac{1}{4} b)(\frac{2}{5} a +\frac{1}{3} b)}{(a+b)^2} \\ &{} \\ x_{01} &{}= \frac{(\frac{1}{5} a +\frac{1}{4} b)(\frac{3}{5} a +\frac{2}{3} b)}{(a+b)^2} \\ &{} \\ x_{10} &{}= \frac{(\frac{4}{5} a +\frac{3}{4} b)(\frac{2}{5} a +\frac{1}{3} b)}{(a+b)^2} \\ &{} \\ x_{11} &{}= \frac{(\frac{4}{5} a +\frac{3}{4} b)(\frac{3}{5} a +\frac{2}{3} b)}{(a+b)^2} \end{array}\right. } $$
This connection, starting at D, determines the (approximate) probabilistic distribution on $$\Pi T$$:
$$\Gamma '(D) = (0.082, 0.137, 0.293, 0.488) \in \mathbb R^4.$$
From an algebraic point of view, an experiment will be in agreement with the model if the percentages observed will be exactly those described by the latter connection: $$8.2\%$$ of cells with a thick membrane, nucleus, etc.

In the real world, of course, some tolerance should be expected from experimental data error. The control of this experimental tolerance will be not addressed in this book, as it is a part of standard statistical theories.

3.4 Toric Models and Exponential Matrices

Recall that a toric model is a parametric model on a system T corresponding to a connection from S to T which is defined by monomials.

Definition 3.4.1

Let W be a toric model defined by a connection $$\Gamma $$ from S to T. Let $$s_1, \dots , s_q$$ be all possible states of all the variables of S and let $$t_1, \dots , t_p$$ the states of all the variables of T. One has, for every i, $$t_i = \Gamma _i (s_1, \dots , s_q)$$, where each $$\Gamma _i$$ is a monomial in the $$s_j$$.

We will call exponential matrix  of W the matrix $$E = (e_ {ij})$$, where $$e_ {ij}$$ is the exponent of $$s_j$$ in $$t_i$$.

E is, therefore, a $$p \times q$$ array of nonnegative integers. We will call it complex associated with W the subset of $$\mathbb Z^q$$ formed by the points corresponding to the rows of E.

Proposition 3.4.2

Let W be a toric model defined by a monomial connection $$\Gamma $$ from S to T and let E be its exponential matrix.

Each linear relationship $$\sum a_iR_i = 0 $$ among the $$R_i$$ rows of E corresponds to implicit polynomial equations that are satisfied by all points in W.

Proof

Consider a relation $$\sum a_iR_i = 0$$ among the rows of E. We associate to this relation a polynomial equation
$$ \prod _{a_i \ge 0} t_i^{a_i} - z \prod _{a_j <0} t_j^{a_j} = 0 $$
where, by indicating with $$c(\Gamma _i) $$ the monomial coefficient,
$$ z = \frac{\prod _{a_i \ge 0} c (\Gamma _i)^{a_i}}{\prod _{a_j <0} c(\Gamma _j)^{a_j}} $$
We verify that this polynomial relationship is satisfied by all points in W.

In effect, by replacing $$t_1, \dots , t_p$$ with their expressions in terms of $$\Gamma $$, we get two monomials with equal exponents and opposite coefficients, which are canceled.   $$\square $$

Note that the polynomial equations obtained previously, are in fact binomial.

Definition 3.4.3

The polynomial equations associated with the linear relations between the rows of the exponential matrix of a toric model W define an algebraic model containing W. This model takes the name of algebraic model generated by W.

It is clear from Example 3.3.10 that the algebraic model generated by a toric model W always contains W, but it does not always coincide with W. Let us see a couple of examples about it.

Example 3.4.4

We still consider the example of the model of independence on a dipole S.

Resuming the terminology of the previous section, we indicate with $$t_1, \dots , t_n$$ the states of the first variable T and with $$u_1, \dots , u_m$$ the states of the second variable. The resulting model is parametrically defined, on $$\Pi S$$, by $$y _ {(t_i, u_j)} = t_iu_j$$. It is, therefore, a toric model, whose exponential matrix is given by
../images/485183_1_En_3_Chapter/485183_1_En_3_Equ23_HTML.png
from which we can see all relations, between rows, of the form
$$ R_{qm+h}+R_{pm+k} = R_{qm+k}+R_{pm+h} $$
which define, as equations in $$\mathbb R^{mn}=\mathbb R^{m, n}$$, exactly the $$2\times 2$$-minors of the matrices in the model.

It follows that the algebraic model associated to this connection coincides with the space of matrices of rank $$\le 1$$, which is exactly the image of the connection of independence.

Example 3.4.5

Come back to the connection of Example 3.3.4. It defines a polynomial parametric model W on $$\mathbb R^3$$ given by the parametric equations
$$ {\left\{ \begin{array}{ll} x &{}= a^2 \\ y &{}= 2ab \\ z &{}= b^2 \end{array}\right. } $$
The associated exponential matrix is
$$ \begin{pmatrix} 2 &{} 0 \\ 1 &{} 1 \\ 0 &{} 2 \end{pmatrix} $$
which, as unique relation between rows, satisfies $$R_1+R_3=2R_2$$. Using the formula for the coefficients, we get the equation in $$\mathbb R^3$$:
$$ 4xz = y^2. $$
The algebraic model $$W'$$ defined by this equation does not coincide with W. As a matter of fact, it is clear that the points in W have nonnegative x, z, while the point $$(-1,2,-1)$$ is in $$W'$$.

However, one has $$W= W'\cap B$$ where B is the subset of the points in $$\mathbb R^3$$ with nonnegative coordinates. In fact, if (x, y, z) is a point in B which satisfies the equation, then, posing $$a=\sqrt{x}$$, $$b=\sqrt{z}$$, one has $$y=ab$$.

Remark 3.4.6

The scientific method.

Given a parametric model, defined by a connection $$\Gamma $$ from S to T, if we know an “initial” distribution D over S (the experiment data) and we measure the distribution $$D '= \Gamma (D)$$ that we derive on T (the result of the experiment), we can easily deduce if the hypothesized model fits or not with reality.

But if we have no way of knowing the D distribution and we can only measure the $$D'$$ distribution, as happens in many real cases, then it would be a great help to know some polynomial F that vanishes on the model, that is, to know its implicit equations. In fact, in this case the simple check of the fact that $$F(D') = 0$$ can give us many indications: if the vanishing does not occur, our model is clearly inadequate; instead if it occurs, it gives a clue in favor of the validity of the model.

If we then knew that the model is also algebraic and we knew the equations, their control over many distributions, results of experiments, would give a good scientific evidence on the validity of the model itself.