How to Explain Number Theory at a Dinner Party
THIRD SESSION: CONGRUENCES
The proof of Gauss’ two square theorem, as well as its statement, is based on the distinction between even and odd numbers. But the statement also distinguishes between odd numbers of the form 4k + 1 and those of the form 4k + 3. One should imagine a cyclic classification of numbers into four classes, called congruence classes modulo 4:
These classes can be labeled by their first members: the class of 0 modulo 4, of 1 modulo 4, and so on. One can define congruence classes modulo any number; for example,
are the congruence classes modulo 3. Congruence classes modulo 12 are used to tell time: the clock reads the same after 3 hours as after 15 hours as after 27 hours, and so on. Formally, we say that the integers a and b belong to the same congruence class modulo the integer N if the difference (a − b) is a multiple of N—in other words, if N divides (a − b) without remainder.
The story of congruences is that a problem where the variables can take infinitely many values can be replaced by one in which the variables can take only finitely many values, and it is sometimes enough to solve the latter problem in order to solve the former. This is roughly how the proof of Gauss’ theorem goes, though a great deal of algebra has to be established ahead of time to make this work.
Gauss’ methods show that when p is an odd prime number, then
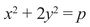
has infinitely many rational solutions when p is congruent to 1 or 3 modulo 8, none when p is congruent to 5 or 7 modulo 8. For example, if p = 17, take (x, y) = (3, 2); if p = 19, take (x, y) = (1, 3). Similarly, has infinitely many rational solutions when p is congruent to 1 modulo 3 but none when p is congruent to 2 modulo 3.
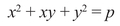
In the next session we’re going to move up to equations of degree 3 in two variables, which is as high a degree as I would ever want to calculate at a dinner party. Motivation will have to wait until the next session; for now, I just want to explain how to count solutions to congruences. Something interesting already happens with equations in a single variable. Suppose p is a prime number and consider the equation of degree p:
It’s obvious that x = 0 and x = 1 are solutions and if p is an odd prime number, then x = −1 is also a solution. It is less obvious, but also true, that these are all the solutions in rational numbers; the proof is based on the same principles as the proof of irrationality of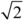 
. However, there is a notion of approximate solutions for each prime number p: we say x is an approximate solution to equation (F) for the prime p if the difference between the right-hand and left-hand sides of the equation is a multiple of p—in other words, if the two sides belong to the same congruence class modulo p. This is determined by dividing the difference between the two sides by p; if there is no remainder, then we have an approximate solution. For example, if p = 7, we can check that x = 2 is an approximate solution: the left-hand side is
which is divisible by 7. But, in fact, we didn’t have to calculate; we could simply have quoted the following.
Fermat’s Little Theorem: Let p be a prime number. Then every integer a is an approximate solution to equation (F): ap − a is always divisible by p.
This curiosity, which is not difficult to prove, was discovered by Fermat in the early seventeenth century and is now presented at the very beginning of any course in modern number theory. We could say that there are infinitely many approximate solutions, since every integer is a solution. For the reasons to be explained shortly, it is more reasonable to count each congruence class modulo p only once; thus equation (F) has p approximate solutions modulo p for any prime number p.
Before we move on to equations in two variables, let’s return briefly to equation (I) of chapter α. It turns out that the equation x2 = 2 has two approximate solutions modulo p if p2 − 1 is divisible by 16, and no approximate solutions modulo p otherwise. So if p = 7, p2 − 1 = 49 − 1 = 48 is divisible by 16; and x = 3 and x = 4 are both approximate solutions to x2 = 2 modulo 7. We check: if x = 3, the left-hand side is 32 = 9, whereas the right-hand side is 2, and 9 − 2 = 7 is a multiple of 7. Again, if x = 4, the left-hand side is 42 = 16, the right-hand side is 2, and 16 − 2 = 14 is again a multiple of 7. The diligent reader can check that there are no other approximate solutions with x between 0 and 6; and an even more diligent reader will check that x2 = 2 has no approximate solutions modulo p when p = 3, p = 5, or p = 11, which is consistent with what we said previously, because 9 − 1 = 8, 25 − 1 = 24, and 121 − 1 = 120 are not divisible by 16.
As for the equations x2 = 3, x2 = 5, x2 = 7, and so on, the quadratic reciprocity theorem, proved by Gauss (in eight different ways), completely determines the number of approximate solutions modulo p for any prime p:
• If p and q are two different odd primes, at least one of which is of the form 4k + 1 (so can be written as the sum of two squares), then x2 = p has two approximate solutions modulo q if and only if x2 = q has two approximate solutions modulo p.
• If both p and q are of the form 4k + 3, then x2 = p has two approximate solutions modulo q if and only if x2 = q has no approximate solutions modulo p.
It looks like the riddle has been answered by another riddle, but the two preceding statements [together with the approximate solutions to equation (I)] contain enough information to solve the problem in all cases.
There is no (obvious) way to count the rational solutions to an equation in two variables, but as with equation (F), there is a notion of approximate solutions for each prime number p. We say x and y are an approximate solution to the equation
for the prime p if the difference between the two sides of the equation x3 − x and y2 is a multiple of p. We can then count approximate solutions to equation (E1) and similar equations, for example,
The number of approximate solutions for each p is written S(p), as follows. I illustrate the procedure for p = 2, p = 3, and p = 5 and expect the reader to get the hang of it in general. Some of the calculations are indicated in the table in figure γ.1: Y means Yes (the pair is a solution), N means No (not a solution). The number of solutions is the number of Ys.
The point is that we have to try only one x in each congruence class and, likewise, one y; replacing x by another number in its congruence class—say, replacing x = 0 by x = 2 for p = 2—gives us no new information. For p = 2, we have to try only four pairs. When x = 0 and y = 0, the equation is
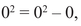
which is true, so we have one solution—a genuine (not approximate) solution. When x = 1 and y = 0, we have another genuine solution. When x = 0 and y = 1, we have y2 = 1 but x3 − x = 0, and the difference is 1, which is not a multiple of 2. Finally, when x = 1 and y = 1, we have y2 = 1 but x3 − x = 0, which is again not a solution. We thus have found two solutions, and we say S(2) = 2.
Next, try p = 3. We still have the two genuine solutions, x = 0, y = 0 and x = 1, y = 0. But now we can try x = 2, y = 0. The left-hand side is x3 − x = 0, whereas the right-hand side is x3 − x = 8 − 2 = 6, and the difference between the sides is 6—which is a multiple of 3! In other words, x = 2, y = 0, while not a genuine solution, is an approximate solution, so we count it as well. We can continue to test all possible combinations where x = 0, 1, or 2 and y = 0, 1, or 2. The only solutions are the first three we found; therefore, S(3) = 3.
Now consider the case p = 5. We have to test x from 0 to 4 (after which the congruence classes repeat), and likewise for y. The first novelty is the case x = 2, y = 1. The left-hand side is y2 = 1; the right-hand side is x3 − x = 6. The difference between these two sides is 5, a multiple of 5. We find that x = 3, y = 2; x = 4, y = 0; and x = 2, y = 4 are all solutions, and there are no others. Thus S(5) = 6.
The last table in figure γ.1 shows the answers for p = 7, and one counts S(7) = 7.
The reader is invited to check the correctness of the table and to determine S(p) for the next few primes: S(11), S(13), S(17),…. The expressions y2 and x3 − x grow quickly as p gets bigger, but not too big for a calculator to handle. But before you get started, you might want to know whether or not there is a pattern to the S(p). The answer is literally: yes and no—explanation next time.1
