chapter 2

How I Acquired Charisma

J’ai glissé dans cette moitié du monde. pour laquelle l’autre n’est qu’un décor.

—Annie Ernaux

My mathematical socialization began during the prodigious summer of 1968. While my future colleagues chanted in the Paris streets by day and ran the printing presses by night, helping to prepare the transition from structuralism to poststructuralism; while headlines screamed of upheavals—The Tet offensive! The Prague spring! Student demonstrations in Mexico City!—too varied and too numerous for my teenage imagination to put into any meaningful order; while cities across America burst into flames in reaction to the assassination of Martin Luther King and continued to smolder, I was enrolled in the Temple University summer program in mathematics for high school students at the suggestion of Mr. Nicholas Grant, who had just guided my class through a two-year experimental course in vector geometry. It was the summer between tenth and eleventh grades and between the presidential primaries and the unforgettable Democratic National Convention in Chicago. Like many of my classmates, I was already a veteran of partisan politics. Over the course of the summer, the certainty of the religious, patriotic, and familial narratives that had accompanied the first fourteen years of my own life were shaken, in some cases to the breaking point. How convenient, then, that a new and timeless certainty was ready and waiting to take their place.1

At Temple that summer, I discovered the Men of Modern Mathematics poster that I subsequently rediscovered in nearly every mathematics department I visited around the world: at Swarthmore, where the marvelous Mr. Grant drove me during my senior year to hear a lecture by Philadelphia native L. J. Mordell, an alumnus of my high school and G. H. Hardy’s successor at Cambridge to the Sadleirian Chair of Pure Mathematics; near the University of Pennsylvania mathematics library, where I did research for a high school project; and through all the steps of my undergraduate and graduate education. The poster was ubiquitous and certainly seemed timeless to my adolescent mind but had, in fact, been created only two years earlier by IBM. Its title alludes to Eric Temple Bell’s Men of Mathematics, the lively but unreliable collection of biographies that served as motivational reading that summer at Temple. You will have noticed at least one problem with the title, and it’s not only that one of the “men” in Bell’s book and (a different) one on the IBM poster are, in fact, women. Whole books can and should be devoted to this problem, but for now let’s just be grateful that something (though hardly enough) has been learned since 1968 and move on to the topic of this chapter: the contours and the hierarchical structure of what I did not yet know would be my chosen profession when I first saw that poster.

It was designed, according to Wikipedia, by the “famous California designer team of Charles Eames and his wife Ray Eames,” with the “mathematical items” prepared by UCLA Professor Raymond Redheffer.”2 Each “man” is framed by a rectangle, with a portrait occupying the left-hand side, a black band running along the top with name and dates and places of scientific activity, and Redheffer’s capsule scientific biography filling the rest of the space, stretched to the length of “his” lifespan. As my education progressed, I began to understand the biographies, but at the time most of the names were unfamiliar to me. With E. T. Bell’s help, we learned some of the more entertaining or pathetic stories attached to these names. That’s when I first heard not only about the work of Nils Henrik Abel and Evariste Galois (see figure 2.1) in connection with the impossibility of trisecting the angle and with the problem of solving polynomial equations of degree 5—they both showed there is no formula for the roots—but also how they both died at tragically young ages, ostensibly³ through the neglect of Augustin-Louis Cauchy, acting as referee for the French Académie des Sciences. What surprised me was that Abel and Galois both had portraits and biographies of standard size, while Cauchy, of whose work I knew nothing at the time, belonged to the very select company of nine Men of Mathematics entitled to supersized entries. The other eight were (I recite from memory) Pierre de Fermat, Sir Isaac Newton, Leonhard Euler, Joseph-Louis Lagrange, Carl Friedrich Gauss (the “Prince of Mathematicians”), Bernhard Riemann, Henri Poincaré, and David Hilbert.

Figure 2.1. Portraits of eminent mathematicians on the wall of the UCLA mathematics department, with Galois in front. (Photo Don Blasius)

Maybe Bell’s book and the IBM poster should have been entitled Giants of Mathematics,4 with a special category of Supergiants, including the nine just mentioned plus Archimedes and a few others from antiquity (the poster’s timeline starts in AD 1000). The hierarchy admitted additional refinements, the Temple professors told us. It was generally agreed—the judgment goes back at least to Felix Klein, if not to Gauss himself—that Archimedes, Newton, and Gauss were the three greatest mathematicians of all time. And who among those three was the very greatest, we asked? One of our professors voted for Newton; the others invited us to make up our own minds.

The field of mathematics has a natural hierarchy. Mathematicians generally work on research problems. There are problems and then there are hard problems. Mathematicians look to publish their work in journals. There are good journals and there are great journals. Mathematicians look to get academic jobs. There are good jobs and great jobs…. It is hard to do mathematics and not care about what your standing is.

In Wall Street every year bonus numbers come out, promotions are made and people are reminded of where they stand. In mathematics, it is no different…. Even in graduate school, I found that everyone was trying to see where they stood.⁵

That’s hedge-fund manager Neil Chriss, explaining why he quit mathematics for Wall Street. But his analogy between finance and mathematics doesn’t quite hold up. For mathematicians, the fundamental comparisons are with those pictures on the wall. “To enter into a practice,” according to moral philosopher Alasdair MacIntyre, “is to enter into a relationship not only with its contemporary practitioners, but also with those who have preceded us….”6 Adam Smith, writing in the eighteenth century, found these relations harmonious:

Mathematicians and natural philosophers … live in good harmony with one another, are the friends of one another’s reputation, enter into no intrigue in order to secure the public applause, but are pleased when their works are approved of, without being either much vexed or very angry when they are neglected.⁷

Two centuries later, one meets a more varied range of personality types:

In the 1950’s there was a math department Christmas party at the University of Chicago. Many distinguished mathematicians were present, including André Weil…. For amusement, the gathered company endeavored to … list … the ten greatest living mathematicians, present company excluded. Weil, however, insisted on being included in the consideration.

The company then turned to the … list of the ten greatest mathematicians of all time. Weil again insisted on being included.

Weil soon moved to the Institute for Advanced Study (IAS) in Princeton, and when, in the mid-1970s, a Princeton University graduate student asked him to name the greatest twentieth-century mathematician, “the answer (without hesitation) was ‘Carl Ludwig Siegel.’ ” Asked next to name the century’s second-greatest mathematician, he “just smiled and proceeded to polish his fingernails on his lapel.”⁸ Fifteen years later my colleagues in Moscow proposed a different ranking: A. N. Kolmogorov was by consensus the greatest mathematician of the twentieth century, with a plurality supporting Alexander Grothendieck for the second spot.

Hierarchy and snobbery are, naturally, not specific to mathematics. “Democracy should be used only where it is in place,” wrote Max Weber in the 1920s. “Scientific training … is the affair of an intellectual aristocracy, and we should not hide this from ourselves.”⁹ In the nineteenth century, Harvard professor Benjamin Peirce, perhaps the first American mathematician to enjoy an international reputation, could “cast himself … as the enemy of sentimental egalitarianism … a pure meritocrat with no democracy about him.”¹⁰ Nowadays, of course, mathematicians are no less committed to democracy than the rest of our university colleagues. But we do seem peculiarly obsessed with ordered lists.¹¹ A lively exchange in 2009 on the collective blog MathOverflow aimed at filling in the gap between the last Giants of Bell’s book and the winners in 1950 of the first postwar Fields Medals, awarded every four years to distinguished mathematicians under 40 and still the most prestigious of mathematical honors. The discussion generated several overlapping lists of “great mathematicians born 1850–1920”¹² and at least one novel graphic representation, as shown in figure 2.2.

Figure 2.2. “Word Cloud” of twentieth-century mathematicians. Generated by José Figueroa-O’Farrill for the StackExchange Web site MathOverflow, based on frequency of references in (Gowers et al. 2008). See http://mathoverflow.net/questions/10103/great-mathematicians-born-1850-1920-et-bells-book-x-fields-medalists/10105#10105. Weil makes a respectable showing on the left, but Kolmogorov is barely visible on the right between Minkowski and Banach. Note the prominence of Einstein, who was not a mathematician.

The MathOverflowers—who mainly treat the blog as a forum for exchanging technical questions and answers—favored the word romanticizable to qualify candidates for inclusion in the list. You read that right: mathematicians are not only individually fit subjects for romantic idealization—we’ll see a lot of that in chapter 6—but romanticizable collectively, as befits the theme of this chapter. This may seem odd if you haven’t read Bell’s book and even odder if you have run through the list of Fields medalists—or winners of prizes created more recently, such as the Wolf Prize (since 1978), the Abel Prize (administered since 2003 by the Norwegian Academy of Science and Letters as an explicit substitute for the missing Nobel Prize in mathematics), or the Shaw Prize (the “Nobel of the East,” awarded in Hong Kong since 2004).13 Few prizewinners are obvious candidates for biographical treatment in Bell’s romantic vein, but the same could have been said of the majority of Bell’s subjects before he got hold of them. Leaving aside the tragic cases of Galois and Abel (after whom the prize is named), perhaps the most authentically romantic figure in Bell’s book was Sofia Kovalevskaia—“scientist, writer, revolutionary” is the subtitle of one of her biographies—the first woman to receive a PhD in mathematics; she traveled to Paris to witness the Commune of 1871 and devoted herself as ener-getically to prose and political activism as to her work on differential equations. Among prizewinners, Fields medalist Laurent Schwartz (1950) surely qualifies as romantic for his long and courageous commitment to human rights; so do Fields medalists Grothendieck (1966) and Grigori Perelman (2006) and (Wolf Prize winner) Paul Erdős, for reasons we will explore at length.¹⁴ And Cédric Villani, with his “romantic” dress code, has been a fixture of Paris talk shows since he won the Fields Medal in 2010 (he’s on the radio again as I write this, talking about ideal gases and how most efficiently to transport croissants to cafés). As for the others, their native romanticism has found no public outlet. This is not an accident.

Weber, writing a few years before Bell, had a romantic vision of science: “Without this strange intoxication, ridiculed by every outsider; without this passion … you have no calling for science and you should do something else.” Did this change after the war? Not for impressionable teenagers, in any case. The romance of a vocation and the mystique of hierarchy intertwined when the undergraduate adviser received me, a first-year student still under the spell of a recent encounter with Cauchy’s residue formula, in one of the alcoves of the Princeton mathematics department common room. His deep voice and distant demeanor made me think of fate incarnate.¹⁵ We talked about course requirements and such, but my only distinct memory of the conversation is that at one point he said, “You want to be the world’s greatest mathematician”; my immediate reaction was to wonder, How can he tell? Even at age 16, though, I had enough sense to recognize this as a sentence he had used before, and this meant there would be competition. My mother used to get birthday cards addressed to the World’s Greatest Grandma, and while there is no more a World’s Greatest Mathematician than there is an international ordered ranking of Grandmas, competition within the acknowledged hierarchy of mathematicians is fundamental to the elaboration of professional self-image, as Neil Chriss understood, in a way it’s not for Grandmas. The aspiration to be something like the World’s Greatest Mathematician is thus one of the concrete forms taken by the initiation into what I am going to call charisma.

Figure 2.3. (a) A “romantic” mathematician of the nineteenth century: Sofya (Sonia) Kovalevskaya on a 1951 Soviet postage stamp. (The text reads: S. V. Kovalevskaya, outstanding Russian mathematician.) (b) A “romantic” mathematician of the twenty-first century: Cédric Villani in one of his trademark lavallière ties.

(© Hervé Thouroude)

Shortly after that common-room meeting I was converted to number theory—there’s no other way to describe the experience—when a professor explained Weil’s idea to count solutions to polynomial equations using topology, the geometric theory of shape. The equations of interest to Weil are like the equation in figure 2.4 (see p. 20) that was the object of Galois’ attention, but they involve lots of variables, not only the single variable x, and thus describe geometric objects.¹⁶ I had already learned what it meant to solve polynomial equations like figure 2.4 in my high school algebra class. I even knew what it meant to solve equations in more than one variable—that was L. J. Mordell’s specialty and the subject of his talk at Swarthmore. The reader, however, may not know or may have forgotten what it means, in which case it is advisable to flip ahead and look at the first few pages of chapter β, which includes a sampling of polynomial equations in two variables, along with pictures (graphs) of their solutions. The use of geometry to understand solutions to polynomial equations and the use of algebra to solve problems in geometry comprise the field of algebraic geometry, whose history can be traced back through Descartes to medieval Islamic algebraists—and specifically to the Persian Omar al-Khayyām, the very first Giant on the IBM chart.¹⁷ Weil’s idea was that solutions to certain kinds of equations could be counted¹⁸ by interpreting them as fixed points, the points that stay put under a motion of a sort of space; these fixed points could then be counted using a fixed point theorem. I had seen some fixed point theorems in one of the books Mr. Grant had advised me to read as a high school junior,¹⁹ but those had to do with spaces that looked like balls or tori that had nothing to do with Weil’s equations, and it was the very incongruity of the visual analogy that I found irresistible.

Be assured that this is not a series of clippings from my autobiography. “When the studies of a philosopher, and especially of a mathematician, have been described, his discoveries recorded, and his writings considered, his history has been written. There is little else to say of such a man: his private life is generally uninteresting and unvaried.”²⁰ Too true! I can’t even begin to imagine what might make for an interesting private life. The “I” of this chapter’s title is not the hateful “I” of Blaise Pascal’s Pensées but rather the hypothetical “I” of a Weberian ideal type. “Type of what?” Maybe we’ll know by the end of this book. In this chapter it’s the type associated with the possession of a specific degree of routinized charisma, with one curious feature: its subject crossed the threshhold relatively late, granting him an unusual and, he likes to think, unbiased perspective on life on both sides of the charisma divide.

The word charisma colloquially means a kind of personal magnetism, often mixed with glamour, but Weber chose the word to designate the quality endowing its bearer with authority (Herrschaft, also translated domination) that is neither traditional nor rational (legally prescribed). Charisma is (in the first place) “a certain quality of an individual personality, by virtue of which he is set apart from ordinary men and treated as endowed with supernatural, superhuman, or at least specifically exceptional powers or qualities,” whose legitimacy is based on “the conception that it is the duty of those subject to charismatic authority to recognize its genuineness and to act accordingly.”21

For mathematicians “acting accordingly” consists in participation in a research program. For example, the Langlands program, established by Robert P. Langlands—one of the great research programs of our time, very much in the way this term was understood by Imre Lakatos²²—benefited from its founder’s meticulous elaboration of the program’s ultimate goals, too distant to serve as more than motivation, as well as a remarkably precise vision of accessible intermediate goals and the steps needed to attain them. In both these respects, the Langlands program, developed in several stages during the 1970s and thus part of my generation’s collective memory, resembled the program promoted by Alexander Grothendieck in the 1960s, whose ultimate goal was to realize the implications of Weil’s ideas about fixed point theorems.

It’s for its subjective, romantic, and not altogether rational associations that I prefer charisma to words like prestige, status, standing, or visibility currently in use in the sociology of science.²³ Weber’s primary target was religious leaders—Jesus, Mohammed, or the Buddha were extreme cases—but even mathematical charisma does not derive from “objective” external considerations. After Weil made his “topological” insight work for algebraic curves—a ten-year undertaking that required a complete rethinking of what he called the Foundations of Algebraic Geometry, the title of the most elaborate of the three books he wrote for the project—he formulated in three conjectures the outlines of a new geometry that would place topology at the center of number theory. For the next twenty-five years, the Weil conjectures served as a focus of charisma, what I would like to call a guiding problem in number theory and algebraic geometry, a challenge to specialists and a test of the rightness of their perspective. Grothendieck, who called them his “principal source of inspiration”24 during his most active period of research, was the first to find a geometry that met Weil’s specifications, proving all but one of Weil’s conjectures and reorienting much of mathematics along the way, number theory in particular, before withdrawing from active mathematical research.

Charisma … is imputed to persons, actions, roles, institutions, symbols, and material objects because of their presumed connection with “ultimate,” “fundamental,” “vital,” order-determining powers. This presumed connection with the ultimately “serious” elements in the universe and in human life is seen as a quality or a state of being, manifested in the bearing or demeanor and in the actions of individual persons; it is also seen as inhering in certain roles and collectivities.

What is alone important is how the individual is actually regarded by those subject to charismatic authority, by his “followers” or “disciples.”²⁵

Of course some mathematicians possess charisma in the colloquial sense as well as charismatic authority within the field.²⁶ Grothendieck was by all accounts such an individual. His close colleague, the French mathematician Jean-Pierre Serre, who received the Fields Medal in 1954, has for more than sixty years been one of the world’s most influential mathematicians. In addition to his original research that literally reshaped at least four central branches of mathematics, he is an exceptionally gifted lecturer and an incomparable clarifier, whose books have been required reading since before I was a graduate student. The Matthew Effect, sociologist Robert K. Merton’s name for the familiar tendency of prizes and honors to accrue to those who have already been honored,²⁷ works both ways: by awarding him the first Abel Prize in 2003, the Norwegian Academy borrowed Serre’s charisma to secure their own legitimacy and to confirm the new prize’s compatibility with community norms.

Serre is known for his effortless personal charm,²⁸ and in France, where politicians routinely point to the many French Fields Medalists as a mark of national glory, he could easily have become a media favorite. But he has limited his field of action to mathematics, apparently agreeing with Weber that the scientist who “steps upon the stage and seeks to legitimate himself through ‘experience,’ asking: How can I prove that I am something other than a mere ‘specialist’ … always makes a petty impression.” It “debases the one who is thus concerned. Instead of this, an inner devotion to the task, and that alone, should lift the scientist to the height and dignity of the subject he pretends to serve.”29

Cambridge professor Sir Timothy Gowers (Fields Medal 1998, knighted in 2012) is not the sort to “step upon the stage,” but unlike Serre, he has chosen to devote time and energy to exploring mathematical communication in a variety of forms. For professional mathematicians and the mathematically informed, he edited the encyclopedic Princeton Companion to Mathematics and runs a popular blog that covers topics of broad interest; for specialists he has pioneered “massively collaborative mathematics” online; and for the general public he has written a Very Short Introduction to Mathematics. He’s very good at communication—he was chosen to give one of the talks in Paris at the meeting organized by the Clay Mathematics Institute for the 100th anniversary of Hilbert’s 1900 Paris lecture—and he has also shown considerable courage, since it’s commonly felt, at least in English-speaking countries, that a mathematician who willingly spends time on anything other than research must be short of ideas.³⁰

“In every age,” according to Northrop Frye, “the ruling social or intellectual class tends to project its ideals in some form of Romance.” Class struggle is a poor guide to the history of mathematics;³¹ it’s more accurate to say that the romantic ideal is projected onto charismatic figures and any “ruling” is as likely as not to be posthumous. What Weber called the routinization of charisma helps explain why mathematical romanticism is mainly to be sought in a legendary (nineteenth-century) past. A professional mathematician will regularly enjoy the privilege of consorting, consulting, lunching, and even partying with Giants of Mathematics. This is consistent with the dynamics of the routinization of charisma, which does not necessarily divide mathematics socially into segregated Weberian “status groups” (Stände): “The very effort of a charismatic elite to stabilize its position and to impose a charismatic order on the society or institution it controls entails … spreading the particular charismatic sensitivity to persons who did not share it previously. This means a considerable extension of the circle of charisma.”³² If we ignore charged verbs such as impose and controls that are misleading in the mathematical context, this sentence helps to understand how charisma can propagate from the “specifically exceptional” individuals to those (like the author of these lines) who occupy “certain roles” or participate in “collectivities.”

“The charismatic leader,” writes Pierre Bourdieu, “manages to be for the group what he is for himself, instead of being for himself, like those dominated in the symbolic struggle, what he is for others. He ‘makes’ the opinion which makes him; he constitutes himself as an absolute by a manipulation of symbolic power which is constitutive of his power since it enables him to produce and impose his own objectification.” It may sound as if Bourdieu is saying that the charismatic leader, and the charismatic academic, in particular, exercises political power over the group. Whether or not this applies to mathematicians, it’s not what I have in mind.33 The bearer of mathematical charisma, consistently with Bourdieu’s model, contributes to producing the objectification—the reality—of the discipline, in the process producing or imposing the objectification of his or her own position within the discipline. The reader can judge whether or not this is compatible with democracy—more material will be provided as the chapter progresses—but I want to stress that there is nothing deliberately misleading or sinister or even mysterious about this process, which is manifested in practice as well as in the perception of the field as a whole:

In mathematics, many details of a proof are omitted because they are considered obvious. But what is “obvious” in a given subject evolves through time. It is the result of an implicit agreement between the reseachers based on their knowledge and experience. A mathematical theory is a social construction.³⁴

The symbolic infrastructure of mathematical charisma is, likewise, a social construction, the result of an implicit agreement. But it is also the “objectification” of mathematics: the common object to which researchers refer, which in turn drives the evolution of aspects of mathematical discourse like the “obviousness” just cited. Does this mean that mathematicians can share only an understanding of mathematical theories and discoveries associated with charismatic individuals? No, but insofar as a mathematical theory is a social construction, one measures the importance of one’s own contributions in terms of an accepted scale of values, which in turn is how charisma is qualified.

In other words, it’s not just a theory’s contents that are defined by a social understanding: so are the value judgments that organize these contents. Caroline Ehrhardt captures this process well in her account of the construction of Galois theory, decades after Galois’ tragic and romantic death (my emphasis added to highlight effects of charisma):

[W]riters of university textbooks not only played the passive role of collectors of research ideas … they also created mathematical knowledge in that when they introduced students to Galois theory, they offered an organisation and a hierarchy of its constitutive elements which were anything but established within the initial, fragmented landscape of local memories. In this way, these authors structured the mathematical field; they redistributed symbolic capital between the authors, they defined which objects are legitimate, which orientations took precedence, and they enabled the constitution of a community of specialists who had received the same kind of training. Mathematical content and practice thus defined the social space corresponding to Galois theory at the end of the 19th century within the mathematical field.35

Galois, you’ll recall, showed that there is no formula for finding the root of a polynomial equation of degree 5 or more, like the one shown in figure 2.4. So did Abel. But Galois, before he died in a duel at the age of 20, did much more for equations: he invented a method for understanding their roots, even in the absence of a formula—the Galois group, which governs what, for want of a more precise term, one would now call the structure of the roots of an equation. Together with his successors who “defined the social space” of Galois theory, he also created a new point of view: that what’s interesting is no longer the centuries-old goal of finding a root of the equation, but rather to understand the structure of all the roots—the Galois group. This is a stage in an ongoing process of abstraction; it is also a change in perspective. Today’s mathematicians, especially number theorists, have taken this process one step further: rather than focus on the Galois group of a single equation, number theorists look at all the Galois groups of all equations simultaneously as a single structure. Is this a paradigm shift or a priority shift?

Figure 2.4. There is no formula for the solutions x of this polynomial equation. But they have a structure determined by the Galois group.

Once it is routinized, charisma can be quantified. These days a popular name for quantifiable academic charisma is excellence, the recent pursuit of which has spawned an immense secondary literature and bureaucratic infrastructure, notably in Europe. The exact day I and all my colleagues at the Université Paris-Diderot acquired excellence is recorded in the French Journal Officiel. The news arrived in my inbox on February 3, 2012, that my university, together with its seven partners, had been chosen as one of eight Initiatives d’excellence. These are the French contribution to an effort to improve the position of European universities in international rankings:

A metric that purports to show the stock and presumed rate of creation of new intellectual capital in those institutions, universities, whose role it is [to] conserve and create it, becomes the equivalent of a stock market quotation, and also an index of national intellectual prestige.36

The League of European Research Universities (LERU) cautioned against attaching too much importance to these metrics, writing that they “promote […] the idea of the university as a supermarket selling modular products that happen currently to be in vogue” and that “It’s about measuring a brand, like Gucci or Chanel. It almost paints universities as a fashion accessory.”³⁷ But excellence is the professed goal, and a system of material rewards and penalties is the means chosen to encourage us to strive for excellence.

The rules of bureaucratic rationalization therefore require quantitative metrics. For scientists the typical metrics count citations, weighted for “impact.” The market in impact factors, jealously guarded by Thomson Reuters and similar commercial services, is rooted in early attempts by Mertonian sociologists to quantify scientific “visibility.” The brothers Jonathan and Stephen Cole, both students of Merton, demonstrated in their statistical analysis of the reward system in physics that honors correlate more highly with quality than with quantity of research; but to reach this conclusion they needed an objective measure of quality, and citation indices were their metrics of choice.³⁸ Mathematicians, whose papers remain relevant for decades, tend to dismiss citation metrics adapted to the experimental sciences, such as the h-index,39 as poor indicators of mathematical influence. Andrew Wiles, for example, proved Fermat’s Last Theorem (see chapter δ) as well as a long list of theorems of the highest importance in number theory (see note 52 for the first of the list) and is undoubtedly the most famous of all living number theorists; but his h-index of 13 would just barely qualify him for tenure if he were a physicist. On the other hand, I doubt my colleagues would have much sympathy for the view, promoted in the 1960s by sociologist Warren Hagstrom and still occasionally cited, that mathematics is Durkheimian rather than Weberian, characterized by anomy [sic] rather than charisma—that mathematicians are so narrowly specialized that we don’t read one another’s papers and couldn’t understand them if we did.⁴⁰

Chapter 10 shows how “excellence”—it is no coincidence that “excellence” is a translation of the Greek word aristos, as in Weber’s “intellectual aristocracy”—colludes with market forces to shape European research budgets. Innovations with immediate practical applications, such as radar, image processing, or cryptography, are obviously subject to external judgments of excellence or profitability or whatever norms are favored by those in a position to impose them. What’s specific to pure mathematics is that it is obliged to create its own value system—and that it has the means to do so. “The essence of mathematics,” Cantor might have written, “lies in its socially constructed freedom.” And because this freedom is inseparable from value judgments, its starting point is the charismatic hierarchy it tends (with revisions) to reproduce.

Of course charisma in mathematics, as in other academic disciplines, brings power in the conventional sense: power to organize one’s time, power to set the research agenda, power to attract talented students and to place them in prominent positions, as well as material perks, including the generous salary that (in the United States, at least) helps distinguish a “great job” from a “good job.” Departmental rankings are broadly charisma based, so that a professor at one of the top U.S. mathematics departments will be perceived as charismatic, and a professorship like Weil’s at the IAS, the pinnacle of pure mathematics research practically since its creation, is presumptive evidence of Gianthood.⁴¹ The Cole brothers argued that “there is substantial overlap in the groups having power and those having prestige” (charisma in my sense). The two overlapping groups are the “scientists who have earned recognition for their outstanding contributions to knowledge and those who hold key administrative positions.” The first group “extends the circle of charisma” by distributing what Bourdieu calls “symbolic capital”: Chriss’s “great jobs,” publication in “great journals”…; the second group distributes material resources (“[t]hey can determine what specific research areas are to receive priority, and what individuals are to receive support for their research programs”).42

Let’s leave the second group to professional sociologists and focus on the first group. A mathematician derives authority from being an author—the two words have the same root—but if one asks, with Michel Foucault, “What is an author?” one begins to get a sense of how peculiar the constellation of power around a charismatic mathematician looks, compared to the authorial aura of a charismatic scientist. Unlike articles in particle physics or biomedicine that can be signed by a thousand authors or contributors, it’s unusual for articles in pure mathematics to have more than two or three authors, and single-author articles are common. Mathematics research, as opposed to mathematics publishing, is, nevertheless, intensely collaborative, and breakthroughs are always prepared by years of preliminary work, whose authors are usually given full credit by specialists and are quickly forgotten by nonspecialists. This communalism, in Merton’s sense, is especially relevant in highly visible research programs like those of Langlands and Grothendieck. Langlands himself has observed that

when the theorem in which the solution is formulated is a result of cumulative efforts by several mathematicians over decades, even over centuries … and when there may have been considerable effort—the more famous the problem the more intense—in the last stages, it is not easy, even for those with considerable understanding of the topic, to determine whose imagination and whose mathematical power were critical.

Langlands contrasts those responsible for “the novelty and insight of the solution” to mathematicians “whose contributions were presented with more aplomb and at a more auspicious moment.”⁴³ So the question of how credit—and, therefore, authority—are apportioned has real consequences, and it is a shame that its sociological and philosophical underpinnings are so poorly understood. Foucault has left a hint. Alongside a mathematical treatise’s historically determinate author and the “I” who serves as the subject of the proofs, with whom the reader identifies by accepting the rules in force, Foucault alludes to a “third self, one that speaks to tell the work’s meaning, the obstacles encountered, the results obtained, and the remaining problems … situated in the field of already existing or yet-to-appear mathematical discourses.”44 This authorial self places each new work in one or more of the discourses instituted by those figures peering down from the (metaphorical) wall. Highly charismatic mathematical authors have a more fundamental responsibility: not only are they in dialogue with the portraits on the wall, whether or not they have a scholarly interest in the details of history; they—and not “nature”—mediate this dialogue for the rest of us, including those who contribute to their research programs.

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

The way a graduate student, barely past 20, chooses a thesis adviser, and, in so doing, nearly always determines a permanent career orientation, has always fascinated me. Is the choice based on an ineffable preexisting harmony or is it true, as Pascal thought, that “chance decides”? Did I ask Barry Mazur to supervise my Harvard PhD because I admired his research style that unites methods and insights in novel and unexpected combinations or because he was (and still is) one of the few people I’ve met who can without hesitation speak engagingly and cogently on practically any topic—because of his personal charisma in the familiar sense? Does it even make sense to separate his personal style from his research style? However I made my choice, I soon found myself caught up in the thrill of the first encounter between two research programs, each of a scope and precision that would have been inconceivable to previous generations, each based on radically new heuristics, each experienced by my teachers’ generation as a paradigm shift. Hilbert, whose quotation opens the previous chapter, pioneered the conception of mathematics as a practice oriented to the future, whose meaning is defined less by what we can prove than by what we expect to be able to prove.⁴⁵ But nothing in Hilbert’s list of twenty-three problems could compare with the detailed predictions of Robert Langlands’s program for number theory in the light of automorphic forms or of the conjectures deriving from Alexander Grothendieck’s hypothetical theory of motives, both on the brink of spectacular expansion when I entered the field, both too complicated to do more than shadow my narrative.

The IHÉS (Institut des Hautes-Études Scientifiques) was created outside Paris in conscious imitation, on a smaller scale, of Princeton’s IAS; Grothendieck was one of the first permanent professors. His IHES seminars in the 1960s, collected in a series of volumes known as SGA—Séminaire de géométrie algébrique, or Seminar of Algebraic Geometry46—were both symbolically and practically the founding acts of a school of experts, mainly Grothendieck’s own students, who wrote most of the text and continued the research program after the leader’s hermetic withdrawal from active research in 1972. Langlands, who joined the IAS as Hermann Weyl Professor that same year, promoted his unifying vision for automorphic forms and number theory for two decades, serving as the focus of research for widening circles of specialists before taking a break to think about physics; over the past fifteen years, he has returned to his guiding role with a “reckless” new approach to his conjectures.

Steven Shapin points out in Scientific Life that the word charisma is “the word used by both participants and commentators” to describe the “personally embodied leadership” exercised by scientific entrepreneurs. Quoting the economist Richard Langlois, Shapin argues that “charismatic authority ‘solves a coordination problem’ … in circumstances of radical normative uncertainty” and that the use of the word charisma in this way “is a consequential, reality-making usage.”⁴⁷ Leaders of mathematical research programs, such as Grothendieck and Langlands, exercise their charismatic authority in a very similar way, even in the absence of entrepreneurial incentives.

Langlands and Grothendieck are both (at least) Giants by any measure, and both were consciously successors of Galois. In his attempt to prove the last of Weil’s conjectures—solved instead by his most brilliant student, 1978 Fields medalist and IAS Professor Pierre Deligne—Grothendieck imagined a theory of elementary particles of algebraic geometry, called motives. The theory, still far from complete, represents one vision of a Galois theory of algebraic geometry, the geometry of equations. The Langlands program is another vision of Galois theory: his unexpected insight was that the structure of the theory of automorphic forms, rooted in a different geometry, the geometry of mechanics, is in large part determined by Galois’ theory of polynomial equations. In a famous article entitled Ein Märchen—a fairy tale—Langlands speculates about a reformulation of number theory, also still incomplete, in terms of elementary particles (automorphic representations) that mirror Grothendieck’s (hypothetical) motives but include additional mysterious particles that—unlike motives—the Galois group is not equipped to detect.⁴⁸

Figure 2.5. Grothendieck lecturing at the Séminaire de Géométrie Algébrique (SGA), IHES, 1962–1964.

Grothendieck, whose relations to the material world (and to his colleagues) are far from straightforward (see chapter 7 and his underground memoirs, Récoltes et Sémailles), may well qualify as the last century’s most romantic mathematician; his life story begs for fictional treatment. Langlands’ life has been by no means as extravagant as Grothendieck’s, but his romanticism is evident to anyone who reads his prose; the audacity of his program, one of the most elaborate syntheses of conjectures and theorems ever undertaken, has few equivalents in any field of scholarship. While neither of them has ever “ruled” in Frye’s sense, their research programs, like Hilbert’s problems, typify charisma by focusing attention and establishing standards of value for specialists. They also provide a way for colleagues in other branches of mathematics to judge the importance of someone’s research: proving a central conjecture of a named research program often suffices to establish one’s charisma in the eyes of such colleagues, who may only dimly apprehend the program as a whole. Three of the seven Clay Millennium Problems, announced at the Clay meeting in Paris in 2000 by an all-star roster of speakers, including Gowers as well as John Tate (Abel Prize 2010) and Sir Michael Atiyah (Fields Medal 1966, Abel Prize 2004), in a conscious echo of Hilbert’s problems—but each offering a million-dollar reward for its solution—predate but are at least loosely connected with one or both of these research programs.

Number theorists began building bridges back from the Langlands program to motives in connection with problems like the Conjecture of Birch and Swinnerton-Dyer (BSD), one of the three Clay problems related to number theory,49 which served as the guiding problem for my own entry into research. Just as Weil’s conjectures were about counting solutions to equations in a situation where the number of solutions is known to be finite, the BSD conjecture concerns the simplest class of polynomial equations—elliptic curves—for which there is no simple way to decide whether the number of solutions is finite or infinite. Here are the equations of two elliptic curves:

We will see these curves again in chapters γ and δ, along with a whole family labeled EN (one for every number N). It can be shown (but not in a simple way) that equation (E1) has only finitely many solutions, while (E5) has infinitely many solutions.

Each of these equations belongs to Grothendieck’s research program—it can be seen as a motive—and to Langlands’ program—it can be seen as an automorphic form.50 The BSD conjecture states roughly that the number of solutions can be determined by properties of this automorphic form. That is not how Birch and Swinnerton-Dyer initially formulated their conjecture, but a few years later, just before I arrived at Harvard, the Langlands perspective was gaining ground. John Tate and Barry Mazur, Harvard’s two number theorists at that time, had both been working on the BSD conjecture; they were also both actively studying Langlands’ work, and their PhD students were encouraged to work on problems connected to Langlands’ program (see chapter 9).

Between 1976 and 1993, there were successive striking partial solutions to the BSD and closely related problems by six groups of authors. Although the full BSD conjecture remains unsolved (and its solution is still worth $1,000,000), each of these authors was immediately and dramatically rewarded—not materially, though material rewards eventually came to some of them—but with an appropriate degree of charismatic authority within the community, in accordance with the general principles of continuity of Kuhn’s “normal” science:

Because the criteria of scientific adequacy and value within any research area are so specialized and subtle, the task of deciding which contributions are acceptable and which are important tends to be given to those who are already recognized as having contributed significantly to the field … scientists who wish to advance their careers and/or to produce acceptable contributions to knowledge must comply with the cognitive standards set and exemplified by these leaders.⁵¹

It goes without saying that their work was published in “great journals,” and (as far as national circumstances allowed) they were offered “great jobs” at institutions where they could hope to advise “great students.”⁵² The gates of authority opened to welcome them to conference committees, journal editorial boards, and prize panels, alongside or replacing their former mentors in accordance with the informal rules maintaining the organizational balance of the discipline’s distinct branches. Hiring and promotion committees solicited their advice—and Deans wanted additional information—in a process that offers valuable insight for a future sociology concerned with the reproduction of the mathematical elite, since the authors in question had without exception spent some of or all their careers studying or teaching at the leading poles of number theory in their respective countries: Oxford, Cambridge, Harvard, Princeton, Bonn, the École Normale Supérieure, Moscow State University, and the University of Tokyo. They spoke at the most important international seminars, where their work was examined and its lessons were absorbed by the most qualified specialists, and at colloquia at peripheral as well as central mathematics institutes, where students and colleagues from all branches of mathematics were invited to share the dreams and aspirations of number theory for the space of an hour. A few of the authors even had the supreme honor of addressing a plenary session of the International Congress of Mathematicians (ICM)—as Hilbert had done in Paris in 1900, when he announced his list of problems. Their names, hyphenated in the case of joint work, became shorthand for breakthroughs and served as titles for intensive study groups around the world, where a new generation of students, by seeking to eliminate unnecessary hypotheses and to streamline arguments, transformed each landmark article into the founding document of a new research program, branches of which persist today as semiautonomous subcultures within the broad scope of the Grothendieck or Langlands program or both at once.

The Langlands program remained in the background in all the work I’ve just mentioned, since less elaborate methods sufficed for the authors’ purposes. But they would not do for the sequel, which is why I gradually moved away from a direct involvement with BSD and began thinking about—thinking by means of—the Langlands program. This lateral movement across subdisciplinary boundaries would have been conceptually impossible without the help of my colleagues—I’ve always been better at learning from conversations than from reading research articles, which is probably not uncommon in the profession—but it would have been materially impossible had I not been encouraged and tutored by a series of professors who occupied leading positions within the respective subdisciplines and were thus in an authoritative position to represent my work as significant from their charismatically enhanced standpoints.53 Concretely, my mentors and validators wrote the letters that convinced the hiring and promotion committees—and ultimately the Deans—that I was on the way to acquiring the charisma I would need to function effectively within the routine at the level of the hierarchy to which I was soon successfully appointed.

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

The Cole brothers’ use of citation indices to quantify visibility and influence is characteristic of the Mertonian school that dominates what, taking a hint from philosopher David Corfield, one might call the encyclopedic tendency in sociology of science. Corfield borrowed the term to adapt Alasdair MacIntyre’s tripartite division of “moral inquiry” to the philosophy of mathematics. Alongside the encyclopedic approach, associated with various strains of positivism, MacIntyre places the genealogical (inspired by Nietzche or Foucault but often conflated with historical relativism) and the tradition-based, which he and Corfield favor in their respective fields. Sociology of science can be similarly divided. Encyclopedic sociologists of science (to oversimplify) follow their philosophical counterparts in leaving unexamined the assumptions of practitioners—or the assumptions philosophers attribute to the latter—and concentrate on factors they are prepared to consider objective, which in practice means quantifiable. For the genealogists, on the other hand, specifically those associated with the Sociology of Scientific Knowledge (SSK) program, everything practitioners say is suspect.54 David Bloor, for example, has written that “[t]he unique, compelling character of mathematics is part of the phenomenology of that subject. An account of the nature of mathematics is not duty-bound to affirm these appearances as truths, but it is bound to explain them as appearances.” Bloor continues, “It is a notable characteristic of some philosophies of mathematics”—he has the encyclopedic approach in mind—“that they uncritically take over the phenomenological data and turn them into a metaphysics.” This implies that “there can be no sociology of mathematics in the sense of the strong programme. What is required is a more critical and naturalistic approach.”⁵⁵

Appearances notwithstanding, my intention in this chapter is not to indulge in amateur sociologizing; but it’s true that the questions I’ve raised are among the topics I’d like to see covered in a sociology of mathematics—a sociology of meaning as opposed to encyclopedists’ exclusive emphasis on the implementation of preexisting consensual norms or the genealogists’ focus on effects of power. Questions of meaning fit best with the tradition-based perspective—or so a participant in the tradition might be expected to say—but the sociology (as opposed to philosophy) of mathematics doesn’t seem to have a tradition-based wing. I find it striking that among the philosophers and the (rare) sociologists who write about the subject, neither encyclopedists nor genealogists actually have much to say about mathematics. Instead, mathematics tends to serve as an excuse either to promote—or, as in the previous Bloor quotation, to strike a blow against—a questionable ideology, promoted by certain philosophers, most long dead.

(Controversies among philosophers, especially encyclopedist philosophers, surrounding the word meaning, which has just made its third appearance in this chapter and which will reappear repeatedly throughout the book, are as lively as they get. My intention in introducing the word is not to enter into these controversies, but rather to give the reader a sense of how it is used by pure mathematicians, even if the reader happens to be a philosopher. One theme of chapter 7 is that this use is fraught with paradox—which doesn’t make it less meaningful.)

The sociological texts I’ve seen specifically devoted to mathematics mainly belong to the genealogical tendency,⁵⁶ but with few exceptions the encyclopedists and genealogists are united by their grounding in what I will be calling philosophy of Mathematics.⁵⁷ Capital-M Mathematics is a purely hypothetical subject invented by philosophers to address (for example) problems of truth and reference, which these days presupposes an outsized concern for logical formalization, with very little attention paid to what matters to mathematicians. The encyclopedic and genealogical tendencies are for the most part variants of the philosophy of Mathematics, the main difference being their differing degree of credulity versus skepticism regarding truth claims.⁵⁸ Philosophy of (small-m) mathematics, on the other hand, takes as its subject of inquiry the activity of mathematicians and other mathematically motivated humans—the basis, one would have thought, of what Bloor calls the “phenomenological data.”⁵⁹

Genealogists are especially concerned with the achievement of epistemic consensus, how mathematicians come to agree on the truth despite the paradoxes and antinomies that plague reason, but ignore charismatic consensus, whereas the encyclopedists treat the latter as a functional question, without looking into content. Christian Greiffenhagen, a sociologist trained in the SSK perspective, observes in a literature review that, thirty years after Bloor wrote the words quoted earlier, “There is almost a complete absence of anthropological or sociological studies of professional mathematics.” By this he means there have been few “laboratory studies” of “science in the making” of the sort pioneered by SSK, and he proposes explanations as to why this might be the case. His own “video ethnography” of “situations in which mathematical competence is accountably visible,” concerned as it is with mathematical communication, necessarily addresses questions of meaning.60

As for the third tendency, when Corfield and MacIntyre use the word tradition they mean it to be read descriptively; MacIntyre makes a point of divesting it of its associations with (traditional) conservatism. Within the tradition-based perspective, Corfield emphasizes the meaning attached to value rather than truth, to ethics rather than epistemology: “[I]f we wish to treat the vital decisions of mathematicians as to how to direct their own and others’ research as more than mere preferences,” he writes—in other words, if we want to treat these decisions as following from “rational considerations”—then value has to be admitted as a matter for rational analysis. “[I]t is the notion of progress toward a telos”—a goal—“that distinguishes genealogy and tradition.”⁶¹

An example may help illustrate how a sociology of meaning can illuminate what Corfield means by telos. If Langlands was alone with a few of his friends and associates during his program’s Act 1, extending, refining, and revising the outlines of his conjectures through calculations and a series of letters, Act 2 mobilized an international cast to verify these conjectures in a restricted situation called endoscopy, where Langlands thought his preferred technique would suffice if elaborated with sufficient diligence and attention.⁶² Twenty years of intense work completed most of the steps required to bring Act 2 to the conclusion Langlands had marked out as an intermediate telos. But one vexing bottleneck remained, a series of calculations of the form

conjectured by Langlands and Diana Shelstad and called the fundamental lemma. The earliest examples of (FL1) could be checked by fairly simple calculations of both sides of the equation, but the calculations quickly became tedious and then intractable, and by the year 2000 experts were convinced that the only sensible way to prove (FL1) was by deriving it from an identification of the form

where G and H are objects in Grothendieck’s geometry. Since Grothendieck’s and Langlands’ programs both emanate from Galois theory, it’s not surprising that they overlap. Pierre Deligne, the Russian Vladimir Drinfel’d, and Langlands himself had been applying Grothendieck’s methods to the questions raised in Act 1 since the 1970s, and two Fields Medals had been awarded for such work (to Drinfel’d in 1990 and to Laurent Lafforgue in 2002) by the time the Vietnamese mathematician Ngô Bảo Châu realized that the geometric objects needed for (FL2) could be built out of the repertoire of mathematical physics.⁶³ Here, by the way, Weil’s and Grothendieck’s original priorities are reversed: instead of using the results of counting to say something about the geometric objects—to pin them down as motives, for example—Grothendieck’s methods provide the quantities of interest from the objects, and the identification (FL2) is used to avoid calculation of the complicated quantities in (FL1)—which brings Act 2 to a close, since in the applications all one needs to know is the equality in (FL1) and not the quantities themselves.

To explain why it was at this point generally agreed that Ngô’s work was worthy of the Fields Medal—which he received in 2010—requires a vocabulary of value, of meaning, of telos. Had he devised the objects G and H and proved (FL2) without reference to the telos of the Langlands program—without the goal of deducing (FL1)—it would have been deep and difficult but unlikely to have attracted much notice; the Grothendieck tradition provides the means for proving any number of identifications like (FL2) but would not have recognized this one as furthering its specific goals. On the other hand, if Ngô had simply proved the experts wrong by displaying enough stamina to calculate the two sides of (FL1) directly—and before you set out to flaunt your own stamina I should warn you that (FL1) is shorthand for infinitely many separate calculations that would somehow have to be carried out simultaneously—he would have completed the telos of Act 2. Rapturous applause and offers of “great jobs” would have greeted the news. But Ngô would probably not have won the Fields Medal. This is because such a calculation has no meaning outside Langlands’ endoscopy project, whereas (FL2)—precisely when it is seen against the background of the Langlands program—is the starting point for a new and open-ended research program (overlapping with Act 3 of the Langlands program, the “reckless” new initiative mentioned previously).

Ngô’s prize-winning achievement was to create a synoptic proof, a proof that made the result “obvious” to those trained to see it, that served a specific telos within the overlapping traditions of the Grothendieck and Langlands research programs, and these programs link him both historically and conceptually to that poster on the wall and specifically to the figure of Galois. The danger of a tradition-based ethic is that it limits both understanding and participation to what David Pimm and Nathalie Sinclair call an “oligarchy” (Weber’s “aristocracy”), whose rule, exercised “through the explicit notion of ‘taste,’” excludes anyone outside the tradition. Asking “[I]n what sense … can mathematics be considered a democratic regime … ” open to all, Pimm and Sinclair quote (Supergiant) Henri Poincaré to the effect that “only mathematicians are privy to the aesthetic sensibilities that enable” the decision of “what is worth studying.”⁶⁴ The article, published in a journal for educators, is motivated by the “view that mathematics can do something for me in a humanistic sense that repays the careful attention and deep engagement it may require; one that may expose students to a fundamental sense and experience of equality … and provide them with another sense of human commonality.”

The concern that mathematics is structured as a gated community to which only professional mathematicians are admitted calls to mind William Stanley Jevons’s advocacy of “the better class of dance music, old English melodies, popular classical songs” as a vehicle for the moral improvement of nineteenth-century Britain’s untutored working classes, who lacked the “long musical training” needed to appreciate “great musical structures,” or the more recent defenders of elite standards against the encroachment of mass culture.⁶⁵ This is a debate mathematicians cannot afford to ignore, but this chapter is concerned only with a more specialized question: whether the hierarchy of values is compatible with democracy within the profession.

Rational authority in mathematics is vested not only in national (and in Europe supranational) administrative bodies reponsible for research funding and orientation, but especially in national professional organizations. Officers of these organizations are elected by the membership; they, in turn, elect the leadership of the International Mathematical Union (IMU), whose functions include the organization every four years of an International Congress and defending the perceived interests of mathematics. The IMU and certain national professional and governmental bodies, including the AMS, SIAM, and NSF66 in the United States, devote substantial resources to improving access for mathematicians from developing countries and for women and (at least in the United States and Britain) minorities in the metropolitan centers—promoting inclusion in mathematics as presently constituted (the term in the United States is diversity)—and fostering the growing awareness of the historical importance of long-standing mathematical traditions outside the European cultural sphere, notably in China, India, Japan, and the Islamic world. The main thrust of this work has been to insist on the underlying unity of mathematics, even in traditions that could not influence one another, rather than to suggest (as sociologists of the genealogical tendency might) that traditional Chinese and Greek mathematics, say, are based on norms that are fundamentally different and, presumably, equally valid. The success of the inclusion of mathematicians from all over the world is ascribed to the field’s universality rather than the victory of the European worldview.

Specialized mathematics institutes and conference centers⁶⁷ display their rational authority by organizing the day-to-day and year-to-year activity of mathematical research, setting priorities by devoting time and resources to areas and problems identified as important by their national or international scientific advisory boards. I started writing this book during a three-month membership at the IAS in Princeton, as a participant in a year-long program on Galois representations and automorphic forms. Unofficial bodies can also exercise a kind of semirational authority. The most celebrated example is the ostensibly secret Bourbaki association, founded in Paris in the 1930s by André Weil and a few of his contemporaries to reform mathematics according to a clear conceptual “architecture.” The Bourbakistes, including Serre, Tate, Grothendieck, and Deligne, just to list those mentioned in this chapter, promoted their program through the collective authorship and publication over sixty years of a series of books entitled Eléments de mathématique—the singular mathématique itself an expression of their vision of the field’s unity—and through the choice of topics at their three-times-yearly (now four-times-yearly) seminar in Paris. Seminars identified with prominent mathematicians in Russia used to fulfill a similar function.

Charismatic and rational authority overlap, but they are not identical. Both came to public attention in the spring of 2012 when Timothy Gowers announced on his blog his decision to boycott mathematical journals published by Elsevier. Commercial firms, relative latecomers to scientific publishing, are driven by economic goals increasingly incompatible with the budgets of the libraries on which the researchers depend in order to produce the articles that publishers sell back to them at a profit. Gowers listed a few of Elsevier’s commercial practices he found inexcusable, and within days a Web site had collected thousands of pledges by mathematicians and scholars in other fields to refuse to publish in or otherwise cooperate with Elsevier’s journals. A statement of purpose (SoP) signed by thirty-four international specialists from all branches of mathematics—including Gowers and fellow Fields medalists Terence Tao and Wendelin Werner, several laureats of other prestigious prizes, and (in their private capacity) past and present top officers of the IMU and the (U.S.-based) SIAM—was posted on the internet and published in several languages in the official organs of national mathematics associations.68

Coming as it did on the heels of the prodigious events of 2011, the boycott inspired talk of an academic spring aimed at democratizating the access to knowledge, just as the Arab spring a year earlier was a revolt against the undemocratic regimes of the Middle East. But while Arab demonstrators stopped far short of calling for the “withering away of the state,” the Elsevier boycott left mathematicians wondering whether the Internet had not made traditional scientific journals obsolete. Two years before Gowers launched the Elsevier boycott, an article entitled “Why hasn’t scientific publishing been disrupted already?” had already pointed out that “While the journal was a brilliant solution to the dissemination problems of the 17th century … dissemination [i.e., making the results of scientific research widely available] is no longer a problem that requires journals.” Mathematicians have for years been posting advance versions of their articles on their home pages or on open Web sites, especially the prepublication server at arxiv.org. Quoting the “disruption” article in one of the discussions spawned by the boycott, Terence Tao—like Gowers, Tao hosts a wide-ranging and popular blog—suggested that the journal form remained necessary only for “validation (certifying correctness and significance of a paper) and designation (providing evidence of research achievement for the purposes of career advancement).” With regard to attempts to incorporate these functions into what some have called a “Math 2.0” framework, Tao wrote that “so far I don’t see how to scale these efforts so that a typical maths research paper gets vetted at a comparable level to what a typical maths journal currently provides, without basically having the functional equivalent of a journal.”69

The still unresolved case of Elsevier raises fascinating questions about the possibility of reconciling the goals of science with the material organization of society. A mathematical tradition unified around charismatic norms maintained by overlapping research programs hardly fits comfortably in the intellectual property regime monitored by the supervisors of globalization. What I find intriguing is the apparent consensus that publishing retains one indispensable function that can’t be automated—the maintenance of the charismatic structure of the field. Given the preponderant role of informal communication even in the 1970s, long before the Internet made delivery of preprints instantaneous, the sociologist Bernard Gustin is convincing when he calls scientific publication a form of “Traditional Ritual.”⁷⁰ “Validation”—the process of peer review—has two aspects in mathematics, as indicated before: “certifying correctness,” the painstaking reading of an article, line by line if possible, to make sure all the arguments are valid; and certifying “significance,” irrelevant to the “Mathematics” of logical empiricist philosophy, but the very life of the “mathematics” of mathematicians. The “good journals” of Chriss’ comment differ from “great journals” by the relative “significance” of what they choose to publish; “designation” in turn relies on the “significance,” as validated by more or less great journals, to assign candidates to the “good” or “great” (or lousy) jobs they are deemed to merit.

The commercial publishing issue points up the arbitrariness or absurdity of inherited social forms: there is no reason to assume traditional forms (like the research journal) are rational. I find it striking that most mathematicians take the logic of the current system for granted. The SoP acknowledges that junior colleagues place themselves at risk when boycotting expensive commercial publishers that hold a monopoly on the crucial fountains—“great journals”71—that dispense the charisma hiring committees (and those omnipotent Deans) need to evaluate before agreeing to award tenure; the SoP encourages senior mathematicians supporting the Elsevier boycott to “do their best to help minimize any negative career consequences.”

“In his later writings,” writes Robert Bellah, “Durkheim identified ‘society’ not with its existing reality but with the ideals that gave it coherence and purpose.”⁷² Some colleagues judge that participation in such networked collective activities as blog discussions and MathOverflow represents a Sociability 2.0, close to mathematical ideals. MathOverflow’s constantly updated register lists the most active contributors, and those who take the time to answer questions are rewarded by a system of “badges” and reputation points, as on amazon.com or Facebook, but much more elaborate (that’s the 2.0 part); so are those who manage to find the right ways to frame questions that are or should be on everyone’s minds. Modesty regarding one’s own standing while displaying one’s expertise is an unwritten rule of good manners on this and similar blogs (there are also written rules of conduct). Gowers leads the gold-badge competition (he has nine) and clocks in with a very impressive 16,608 reputation points (as of November 3, 2012), which still places him well behind logician Joel David Hamkins of CUNY, the current reputation champion (64,313 points!).

“Reputation,” explains the MathOverflow FAQ page, “is earned by convincing other users that you know what you’re talking about.” A few participants in the Math 2.0 blog, launched soon after Gowers announced his Elsevier boycott, wonder why publishing can’t be reorganized along similar lines, eliminating the profit motive and replacing the less democratic features of the charismatic hierarchy by a permanent plebiscite.⁷³ One blogger wrote “some people like ‘elite communities,’ [others] prefer more democratic communities,” suggesting that the latter are in the majority. In contrast, SoP signatories were for the most part explicitly committed to maintaining the “élitist” functions of journals—validation and designation—in what they hoped would be a post-Elsevier era of mathematical publication; some were actively working to create new vehicles for this very purpose. If the content of mathematics is bound up, as I’ve argued, with a hierarchical charismatic structure, something of this sort is inevitable; if journals relinquish these functions, other institutions will take them up.

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

By granting me tenure at the age of twenty-seven, Brandeis University ratified my permanent admission to the community of mathematicians. Thus I was endowed with the routinized charisma symbolized by my institutional position and fulfilled the (rational-bureaucratic) obligations74 incumbent upon one enjoying the privileges befitting my charismatic status. These privileges included and still include regular invitations to research centers like the IAS (where I began writing this book in 2011), the IHES, or the Tata Institute of Fundamental Research (TIFR) in Mumbai (Bombay); to specialized mathematics institutes like the Fields Institute in Toronto, the Mathematical Sciences Research Institute (MSRI) in Berkeley, or the Institut Henri Poincaré (IHP) in Paris, where Cédric Villani is now director; or to speak about my work at picturesque locations like the Mathematisches Forschungsinstitut Oberwolfach, a conference center nestled high in the hills of the Black Forest in Germany, that for nearly seven decades has hosted weekly mathematics meetings.⁷⁵

I could, therefore, end this chapter right now and consider that I have respected the bargain announced in its title. Eleven years after obtaining tenure, however, an unexpected event—a mystic vision, no less—started me on the path to being bumped up a few rungs on the charisma ladder. The incident, recounted in chapter 9, resulted directly in item 34 on my publication list, a premonitory sign of my impending symbolic promotion. The process continued with item 37 and was clinched with the much more substantial item 43, a collaboration with Richard Taylor in the form of a 276-page book published in the highly visible Annals of Mathematics Studies series edited by the mathematics departments of Princeton University and the IAS (where Taylor is now a professor).

My book with Taylor concluded with the proof of a conjecture in a named research program—the local Langlands conjecture, a step in Langlands’ program. Like every mathematical breakthrough, this one was prepared by the extensive work of numerous colleagues, especially my Paris colleague Guy Henniart, who turned a qualitative prediction by Langlands into a precise and optimal quantitative conjecture. Henniart, whose office was across the hall from mine when I began thinking about the question in 1992, was also instrumental in making sense of my first results in the field. So it’s only fitting that his name should be attached to the solution of the problem, and so it is, but—because the rules of charisma almost always severely discount work that stops short of the perceived telos—it’s there on the grounds of the separate proof he found shortly after my announcement with Taylor.76

Ideal-typical honors—the details are unimportant, and anyway some of them are listed on the book jacket—flowed from this and subsequent collaborations with Taylor. Consistently with the Matthew Effect, the prize the French Académie des Sciences awarded my research group, including a substantial research grant, is routinely but inaccurately described as a prize for me alone. I’m sometimes invited to put an ordinary face on the Langlands program’s charisma for the sake of mathematicians in other fields—Langlands can’t be everywhere, and while none of his surrogates can really represent his perspective, he has been a good sport about it. Students with only the vaguest idea of my motivations think they want to work with me; indefatigable Deans solicit my opinions before proceeding with hiring decisions; colleagues I visit often hasten to meet even my tentative requests, as if the Matthew Effect had outfitted me with a built-in megaphone.

And, to cap it off, this book. A friend whose bluntness I cherish told me, “Of course if you’re able to publish this book, it’s because of the kind of mathematician you are.” This is misleading. We’ll see throughout the book quotations by Giants and Supergiants in which they conflate their own private opinions and feelings with the norms and values of mathematical research, seemingly unaware that the latter might benefit from more systematic examination. One of the premises of this chapter is that the generous license granted hieratic figures is of epistemological as well as ethical import.

My own experiments with the expression of what appear to be my private opinions resemble this model only superficially and only because they conform to the prevailing model for writing about mathematics. My friend’s point was that even my modest level of charisma entitles me not only to say in public whatever nonsense comes into my head—at a philosophy meeting, for example, like the one for which I wrote the first version of chapter 7—but even to get it published. Or, to quote Pierre Bourdieu and Jean-Claude Passeron, “There is nothing upon which [the charismatic professor] cannot hold forth … because his situation, his person, and his rank ‘neutralize’ his remarks.”⁷⁷ This book’s ideal (-typical) reader, on the other hand, will know how to neutralize this kind of charisma, will have already recognized its ostensible narrator as little more than a convenient focal point around which to organize the text, and will be attentive to what is being organized.

 

chapter α

How to Explain Number Theory at a Dinner Party

Researcher: So your image of a mathematician—describe a mathematician to me apart from the fact that they’re a maths academic. What are they like physically? What are they, I mean, are they …?

Babs: An old bloke with a big grey beard.1

INTRODUCTION

During the spring of 2008 I was invited by the Columbia University mathematics department to deliver the Samuel Eilenberg lectures—a perfect illustration of the Matthew Effect described in the previous chapter. The appointment involved living away from my family for several months. Working late in the department one Friday evening, I must have looked even more forlorn than usual, because a colleague passing my open door decided on the spot to invite me home to dinner. Several other mathematicians had been invited, along with a neighbor from another department and the neighbor’s visiting friend, a young British woman who turned out to be a performer between jobs—a real, professional actress, with an agent and a long string of film and TV credits as well as a steady and successful career on the stage. She talked about the trials of being an actress, hinting that not all her peers suffered quite so much as she did. The younger men and women among the mathematicians alluded to their own career anxieties, while their tenured colleagues offered reassuring but noncommital replies. The actress glowed enigmatically during this part of the conversation, but when it came time to serve dessert, she turned to me without warning and asked, “What is it you do in number theory, anyway?”

The other mathematicians looked at me in unison, holding their collective breath. I had stumbled into the awkward moment every mathematician dreads, my predicament highlighted by the questioner’s quiet radiance. “If you have ever found yourself next to a mathematician at a dinner party,” Tim Gowers once wrote, “you have probably, out of politeness, or perhaps desperation, asked what he or she works on.” Variants of this scenario take place in cocktail parties, on long-distance flights, more rarely at singles bars. “If you do not have a mathematics degree,” Gowers continued, “you will almost certainly have received a disappointing answer such as, ‘I work in Iwasawa theory, but it would take too long to explain to you what that is.’ ”2

All of us in the room were in our own ways performing artists, of course, but the mathematicians were trapped in the invariable role of emissaries from a distant and reputedly inhospitable planet. In 1952 Helmut Hasse lamented that he often heard (“especially from ladies”) remarks like these: “You mathematicians are all cold, sober rationalists. How can you find satisfaction in an activity that offers nothing for the heart, nothing for the soul?”³ My answer to the actress and the conversation that ensued lasted at most ten minutes. The consensus in the department over the following days was that I didn’t do so badly, given the hopelessness of my situation. But one always feels one could have done better. This chapter, which has been broken up into short sessions in order to impede the accumulation of formulas—each of which, according to publishing wisdom, is enough to scare off 10,000 potential readers—contains what should have been my answer. Those intrepid readers who continue to the end will see that I work my way up to the guiding problem of the Birch-Swinnerton-Dyer conjecture, which concerns equations of degree 3 in two variables, through problems of increasing complexity: equations of degree 2 in one variable in the first session, of degree 3 (or 4) in one variable or degree 2 in two variables in the second session, with a detour through congruences in the third session in order to hint at the substance of the guiding problem in the last session. Parts of what I actually said and of the actress’s reactions have been incorporated into the first of the (otherwise entirely imaginary) dialogues that conclude each session.

FIRST SESSION: PRIMES

One theorem found in nearly every popular book on mathematics, whether or not it is really relevant to the topic at hand, is the irrationality of the square root of 2. This can be stated as a theorem:

Theorem: There is no fraction p/q, where p and q are whole numbers, with the property that

In other words, equation (Q) in the unknown quantities p and q is impossible to solve if p and q are required to be whole numbers. The theorem is easy to state, its proof fits in a few lines, and it’s accompanied by a story about the crisis the discovery of such numbers provoked among the ancient Greeks who concerned themselves with such questions.

There is also a picture: figure α.1.

Figure α.1.

If ABCD is a square with sides of length 1, then the Pythagorean theorem tells us that

Thus the diagonal AC has length , which the theorem tells us is an irrational number, that is, a number that is not a fraction. Here, therefore. is a quantity that one can perceive, or believe one perceives, but that cannot be apprehended rationally, or so the argument goes. The idea is that the rational number p/q can be understood in terms of acts that can be completed in finite time—cutting a unit length into q equal parts and then stringing p of these parts together; maybe this requires cutting several (or several billion) unit lengths in the first step. But cannot be understood in such terms. It can be understood in other terms, say as the diagonal AC of the unit square in figure α.1, or as the number x that satisfies an equation of degree 2 in one variable:

Comparing the ways one can understand this number to the way that the theorem tells us is off limits helps to attenuate the mystery that may be attached to 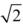. Figure α.1 suggests that can be embedded in what Ludwig Wittgenstein called a “language game” that can be used to talk about geometry, whereas equation (I) tells us that can be embedded in a language game that can be used to talk about algebraic equations. The theorem tells us that the language game of rational fractions has to be expanded in order to accommodate . The square root of 2, and the many numbers like it, thus serve to establish the relations among various language games that arise from different aspects of our experience with mathematics—measuring, counting, dividing up space into geometric figures, and comparing numbers with one another. The square root of 2 is old news, literally ancient history, but it remains true that mathematicians and those drawn to mathematics pay special attention to notions that can serve to link distinct language games—the more distinct, the better.

I borrow Wittgenstein’s metaphor “language games” not because I believe experience is neatly divided up into such games (Wittgenstein certainly believed no such thing) but because it draws attention to the habit mathematicians have of using the word exist in regard to the objects we study when they become the subjects of the stories we tell about them. I have already begun to tell three stories about the square root of 2. The natural continuation of the first of the three stories is the proof of the theorem. Here’s how it goes. We can write the fraction p/q in lowest terms. That means that we can assume that any number that divides p doesn’t also divide q; otherwise, we can remove this factor from both numerator and denominator and simplify the fraction. “Simplifying” fractions is one of the skills we learn as part of learning to use fractions. There is an implicit value judgment that 2/3 is simpler than 10/15 even though they are two ways of writing the same number. Learning that a given number can be written in (infinitely) many ways is a very important step in learning to use numbers at all and contributes to forging their meaning.

In our case, all we really care about is that p and q can’t both be even. What would be the point in writing as the quotient of two even numbers? We can divide both numerator and denominator by 2 as many times as it takes, simplifying over and over again until one or the other is no longer even.

Now we rewrite equation (Q):

All we have done is to convert the equality of fractions into an equality of whole numbers. But now the right-hand side is 2q², which is even. Since this is an equality, p² must also be even.

Now comes the crucial step. If p were an odd number, then p² would also be an odd number. We know that because when you multiply two odd numbers, the result is odd. How do we know that? Undoubtedly, a teacher told us this, we confirmed it by experience if we were curious, and if we were very curious. we eventually cobbled together something resembling a mathematical proof of the fact.

Let’s just accept that we know this fact and resume the arguments. If p were an odd number, then p² would also be odd, but we know this is not the case; hence p must be even. Note the strategic use of that word hence! This is argument by contradiction, a form of argument we all use but that leads to somewhat problematic, or at least controversial, conclusions if applied incautiously.

Anyway, p is even, so it can be divided by 2; say, p = 2n. Now rewrite equation (Q) again:

or again:

or, finally, dividing both sides by 2:

Now we are nearly done. The right-hand side is now even, so q² is even; just as before, this must imply that q is even.

We started out by arranging that p and q would not both be even, but here we have shown that p and q must necessarily both be even. This is a contradiction, which means we must have made a false step somewhere along the way. But our reasoning has been flawless. The false step must therefore have come at the very beginning, when we assumed equation (Q). This shows that equation (Q) has no solution, and that is what the theorem asserts.

I want to return to what I called the crucial step. There were between five and ten steps, depending on how you count. What makes that particular step more crucial than any of the others? You might say it’s less obvious than the others, except that by the time we get to the stage of reading this proof, it’s hard to perceive this difference in obviousness. The crucial step is crucial to what you might call the deep structure of the proof: deep relative to proofs of other theorems that bear some resemblance to the original theorem. One can generate other potential theorems by tinkering with the statement. For example:

Theorem: There is no fraction p/q, where p and q are whole numbers, with the property that

That one is certainly true (and is attributed to the ancient Greek mathematician Thaeatetus, who gave his name to one of Plato’s dialogues), whereas

“Theorem”: There is no fraction p/q, where p and q are whole numbers, with the property that

is certainly false, because 4 = 2²: take p = 2 and q = 1 (of course, the fraction 2/1 is also the whole number 2). The step I identified as crucial is the one that can be imitated to give a proof that (Q3) has no solutions but cannot be twisted to give a proof of the false theorem that (Q4) has no solutions. One needs to replace our notion of “odd” by one adapted to 3. Just as odd is a synonym for not a multiple of 2, the appropriate notion to show that is irrational is not a multiple of 3.

The crucial fact, then, is that if neither of two numbers is a multiple of 3, then their product is again not a multiple of 3. This fact is less familiar than the corresponding fact for odd numbers, but it is true nonetheless. In contrast, neither 2 nor 6 is a multiple of 4, but 2 × 6 = 12 is also 4 × 3.

Armed with this crucial fact for 3, the proof proceeds as before: a solution to (Q3) would yield

forcing us to conclude that p is a multiple of 3—this is what fails if 3 is replaced by 4—and then a few steps later that q is also a multiple of 3, which contradicts the hypothesis that p and q have no common factors.

We can, therefore, divide up the whole numbers (positive integers) into those, like 2 and 3, for which the crucial fact is valid and those, like 4, for which it is not. Say that a positive integer p is prime if, whenever a and b are two numbers that are not divisible by p, the product ab is again not divisible by p. This is not the familiar definition of a prime as a (positive) integer that has no divisors other than 1 and itself, but Euclid already knew that the two definitions are equivalent, and it is the former to which our proof has drawn attention. The first few primes are 2, 3, 5, 7, 11,….

For any prime p, our proof shows that is not a rational number. That is as far as our proof can stretch without modification. For example, 6 = 2 × 3 is not a prime, but is still irrational. The proof requires additional properties of primes that need not be mentioned here, but they are not particularly novel; they were also known at the time of Euclid.

Number theory gets started as a theory of prime numbers, and prime numbers are on the front lines in analyzing any number-theoretic question. One has known at least since Euclid that there are infinitely many prime numbers (another theorem found in nearly every popular book on mathematics).⁴ Another basic fact proved by Euclid is that every number can be factored as a product of prime numbers—for example, 238 = 2 × 7 × 17—and that the factorization is unique.

Most numbers are not primes—no even number other than 2 is prime, for instance—but experiment shows that they are rather evenly distributed among numbers in general. One of the major mathematical problems of the nineteenth century was to prove that the number of primes less than a given number N was roughly N/log(N), which is, even more roughly, N divided by three times the number of digits in N. This claim, the prime number theorem, was proved by two French mathematicians at the turn of the twentieth century and has been re-proved in countless ways since then, but it’s not the last word. One can ask how well the quantity N/log(N) approximates the actual number of primes less than N. The claim that it is statistically an optimal approximation is the import of the Riemann hypothesis, the subject of at least four books for the nonspecialist public,5 considered by most mathematicians to be the outstanding unsolved problem in number theory and indeed in any branch of mathematics; it is one of the seven Clay Millennium Problems, for the solution of which the Clay Mathematical Foundation has offered a $1,000,000 prize.

At least two other well-known problems, simpler to state and therefore more popular with amateurs, concern prime numbers: the twin primes conjecture to the effect that there are infinitely many primes p such that p + 2 is also prime (examples of twin prime pairs: 3, 5; 11, 13; 29, 31; 65,516,468,355 · 2³³³³³³ ± 1; and so on); and Goldbach’s conjecture that every even number can be written as the sum of two primes (for example 8 = 3 + 5, 28 = 11 + 17; 100 = 97 + 3; …), the subject of a popular novel by Apostolos Doxiadis.⁶

PERFORMING ARTIST: I’ve always wondered why the square root of 2 deserved to be called a number. When you count 1, 2, 3, …, you don’t want to stop for the square root of 2, otherwise you would have to let all sorts of other square roots in and you’d never get to 10.

NUMBER THEORIST: You could make the same objection to fractions. Before you get from one fraction to the next you have to pass the one halfway between.

P. A.: Yes, Tom Stoppard made this point in Jumpers:

It was precisely this notion of infinite series which in the sixth century BC led the Greek philosopher Zeno to conclude that since an arrow shot towards a target first had to cover half the distance, and then half the remainder, and then half the remainder after that, and so on ad infinitum, the result was, as I will now demonstrate, that though an arrow is always approaching its target, it never quite gets there, and Saint Sebastian died of fright.

But we’re used to using fractions as numbers. The fraction of this cake that’s being divided—not very evenly, by the way—among nine people, for example. What’s the use of the square root of 2?

N. T.: Well, there’s figure α.1, for a start.

P. A.: But that’s a length. Why does every length deserve to be called a number?

N. T.: You sound suspiciously like a logician. When logicians started worrying about using infinite numbers to count things, they convinced themselves they already didn’t know how to explain what they were doing when they counted finite collections of objects—even one object, for that matter. But then they realized that just because they didn’t know how to count one object, they did, in fact, know how to count zero objects, because that’s how many objects you have counted before you have figured out how to start counting. On that insight, starting with zero the logicians built a whole theory of counting⁷ that includes a place for the square root of 2 as well as any other number you can think of. Some people still claim this is the only reliable way to talk about numbers. But I find it most helpful to think of a number as an answer to a question.

P. A.: I don’t find that at all helpful. Most questions can’t be answered by numbers.

N. T.: Of course not. A number is an answer to a question about numbers.

P. A.: You could just as well explain trains by saying they are answers to questions about trains.

N. T.: I grant that it’s a circular explanation, but trust me, you won’t get a better one, at least not at a dinner party.

P. A.: Remind me when I might have asked a question about numbers.

N. T.: Well, you may wonder how many people attended your last performance. That appears to be a question about people, but it is so only incidentally, since you are considering them only quantitatively and disregarding their individual characteristics. That is a counting question and is in the spirit of the logicians’ approach. But we can also ask questions about measurement—how much space your audience occupied in the theater. Because we can do arithmetic with the answers—because we can add lengths, or multiply them to get areas, for example, and because the arithmetic of measurements follows the same rules as the arithmetic of counting numbers—we decide that the answer to a question about measurement is also a number. If you were to ask the length of the diagonal in figure α.1, the answer would be , which thereby qualifies as a number.

P. A.: My impression is that one hardly needs an advanced degree to answer that sort of question. For that matter, each of your examples looks to me like a question about something else that you, in your self-serving way, have chosen to interpret perversely as a question about numbers.

N. T.: Very much to the point. We could also ask

Question 1: What number, multiplied by itself, yields 2?

This is a question purely about numbers and its answer is, again, the square root of 2. As we have already observed, that number is also the answer to a question about length. But now suppose we asked

Question 2: What number, multiplied by itself and added to 1, yields 0?

Or, at the risk of losing another 10,000 readers, we can ask for the solution to the equation x² + 1 = 0. The answer, which is usually called i, or , can’t be used to count anything, and it’s certainly not the length of anything; all it does is answer the question.

P. A.: But what makes it a number??

N. T.: It’s just as I said, i is the answer to a question about numbers, namely, question 2. May I ask whether you are a devotee of Leopold Kronecker, who once claimed that Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk?*

P. A.: May I ask whether you are trying to distract me from the circularity of your reasoning by bringing up irrelevant theological considerations in German?⁸

N. T.: Not so irrelevant, unfortunately. But you might find my reasoning a little less circular if I mentioned that, just as with lengths, we can do arithmetic with numbers like i. Strictly speaking it’s a new kind of arithmetic: when we want to multiply i by 3 and add, say, , the answer is just . But when we allow ourselves to do that, we find we can answer questions such as

Question 3: What number solves the equation x⁴ + 14x² + 121 = 0?

When you get home you can check that is an answer to question 3.

And, while we’re on the subject of circles, your homework assignment for our next session is to understand the relation between numbers in the language game of arithmetic—for example, whether 1 can be written as the sum of squares of two rational numbers or whether the square root of 2 is rational; numbers in the language game of equations—for example, x² + y² = 1 (or x² = 2); and numbers in the language game of pictures—for example a circle (or whatever picture you can find to go along with x² = 2).

P. A.: So to summarize what you’ve been saying, a number theorist sits at a desk and answers questions about numbers all day, just like the person at the railway station information desk answers questions about trains.

N. T.: Actually, number theorists are not especially interested in answering questions about numbers. We really get excited when we notice that answers seem to be coming out a certain way, and then we try to explain why that is. For example, the equation x⁴ + 14x² + 121 = 0—the question, what number solves that equation?—has not one but four answers: . There’s a pattern: you can permute with and 3i with −3i. What does it mean? What does it tell us about solutions to other equations?

When our ideas about possible explanations are sufficiently clear, we set ourselves the goal of finding the correct explanation and then justifying it.9 In other words, our goal as number theorists is to solve problems, such as the Riemann hypothesis, but in general much easier.

P. A.: I’m not convinced railway staff are especially interested in answering questions about trains either. But I think I understand what you mean by problems. Most of my work as a performer involves solving problems.

N. T.: What kind of problems?

P. A.: About characters, mostly. It’s my job to create the character as a credible presence for the duration of the performance. You may think the playwright has created the characters, and all we have to do is deliver the lines in the right order. If that were all it involved, someone could program a computer to take my place. Someone like you, for instance. As Marilyn Monroe said, “I’m not a Model T … An actor is not a machine, no matter how much they want to say you are.”

N. T.: A familiar dilemma! If you glance at some of the earlier chapters, you might agree that we have quite a bit in common, after all. As it happens, I can’t program a computer to do anything, and in any case I doubt any computer could reproduce your stage presence, even for the duration of this brief sketch. But now it’s your turn to provide an example of what kind of problem you have to solve.

P. A.: For example, when I played Nora in A Doll’s House, there’s a problem that has as much to do with the audience as with the character. Everyone comes to the theater knowing that Nora is trapped by the hypocrisy of the conventions of marriage, and when she slams the door at the end, she is signaling her escape from all that. But the audience doesn’t follow her out the door. One of my main problems is to use the character to create an image of what Nora expects to find on the other side of the door and to make the image real for the audience.

N. T.: That reminds me of a problem I have writing this book.

P. A.: A number theory problem?

N. T.: More like a writing problem.

P. A.: Are you a writer? I thought you were a number theorist.

N. T.: Let’s say it’s the kind of problem I would have if I were a writer.

P. A.: Maybe I can help.

N. T.: I’m afraid I’ll have to solve that one by myself. It’s easy to argue that both the mechanizers and promoters of the “knowledge economy”10 are missing what is most precious about mathematics: namely, that it is a human activity and one of the few remaining human activities not driven by commercial considerations. But to complain that these images of mathematics are stifling and confining, like Nora’s marriage, is merely negative. There’s not much sympathy to be gained in saying what mathematics is not.

On the other hand, maybe you can help me with a smaller problem I need to solve right now, which is to explain complex numbers—expressions like —without turning my readers to stone. Barry Mazur, my thesis adviser, published a 288-page book about a single complex number, the square root of −15, and some people still found it too difficult to grasp.

P. A.: I suppose you want me to ask what question a complex number is designed to answer …

N. T.: More questions than you can possibly imagine!

P. A.: We’d better stick with the questions I can imagine, so I suggest you find a way to connect your complex numbers with literature.

N. T.: Mazur talked about poetry, but he made a convincing case that there are real similarities between what we do when we imagine the square root of −15 and the imagination inspired by reading poetry. I have no such case to make.

P. A.: Even if your literary references are artificial, your readers will put down the book feeling they haven’t been wasting their time, because they’ll at least have seen something that interests them.

---

* “The Good Lord made the whole numbers, all the rest is the work of man.”