chapter 10

No Apologies

 

 

When as teenagers we began our initiation into the values and aspirations of research in pure mathematics, we never tired of quoting to each other—and to the uninitiated—from G. H. Hardy’s A Mathematician’s Apology, especially the parts where he insisted that “I have never done anything ‘useful.’ ” It was our cliché that he had chosen number theory exactly “because of its supreme uselessness” and indeed that “[n]o one has yet discovered any warlike purpose to be served by the theory of numbers….”1 Nowadays the cliché opens with the same Hardy quotations but immediately veers off toward an “ironic” surprise ending:

The irony of [Hardy’s] life is that his “useless” work in obscure number theory and random numbers has found application in cryptography and encryption.

More precisely, “When you enter your credit details on the Internet, they are encrypted using pure mathematics so that only the dealer can decrypt your message and complete the transaction. The entire boom in e-commerce”—now worth $1 trillion worldwide—“would not have been possible without pure mathematics.”² Number theory, in other words, is not merely useful: it is the bedrock of modern shopping.

A word like “useful” is useful not so much because it promises an unambiguous scale against which to measure our ambitions and priorities, but because it provides a marker to divide its users according to priorities that differ radically, depending on the positions they have chosen to occupy, or that have been chosen for them, in the social panorama. After I moved to France, I was grateful for the public-key cryptography, based on the congruences explained in chapter γ, that allowed me to order books in English online with only minimal risk of identity theft; but on each trip back to the United States I found that another bookstore had disappeared, and with it a neighborhood’s cultural focus and the skilled work that kept the store alive, replaced by low-paid and infinitely replaceable jobs in filing, packing, lifting, and data entry. This is practical for many and profitable for a few, but is it “useful”?

Book store owners and record store owners used to be oracles …; you’d go in this dusty old place and they might point you toward something that would change your life. All that’s gone.3

When I reread Hardy’s Apology to prepare for writing this chapter, I was appalled to see what a hearty dose of unapologetic elitism I had imbibed along with Hardy’s mathematical idealism when I was fourteen years old, too young to know any better. “[M]ost people can do nothing at all well,” he wrote, but even a good mathematician “should [n]ever allow himself to forget that mathematics, more than any other art or science, is a young man’s game.”⁴ Graduate students in our early twenties, beneath the gaze of the portraits of Giants and Supergiants on the wall, we aimed for an air of cool arrogance but often reached no higher than anxiety as we trembled and tried to imagine what would become of us if inspiration failed to emerge before the passage of ten or twenty years deprived us of the qualities of youth—persistence, energy, freshness of mind—without which meaningful participation in the fellowship of mathematical research is impossible. This didn’t stop us from scorning or pitying senior colleagues who were now devoting themselves to administration or history or philosophy—or undergraduate teaching—as washed-up renegades. When it began to dawn on me that some of the assumptions I had been taking for granted deserved to be questioned, the reading was buried so deeply in my past that I could not trace these beliefs back to their source. Years later I returned to A Mathematician’s Apology, the book novelist David Foster Wallace acknowledged as one of the inspirations of his own work, “the most lucid English prose work ever on math,”⁵ and there they were.

Hardy’s first paragraphs are a “melancholy” and literal apology for writing about mathematics rather than “do[ing] something”:

[T]here is no scorn more profound, or on the whole more justifiable, than that of the men who make for the men who explain. Exposition, criticism, appreciation, is work for second-rate minds.

… If then I find myself writing, not mathematics, but “about” mathematics, it is a confession of weakness, for which I may rightly be scorned or pitied by younger and more vigorous mathematicians. I write about mathematics because, like any other mathematician who has passed sixty, I have no longer the freshness of mind, the energy, or the patience to carry on effectively with my proper job.

Even as I reproduce these lines I shudder to think how the news of this book will be greeted by whispers in the common room, the speakers perhaps not realizing that they are quoting Hardy. How old do we have to be, I wonder, before we are no longer susceptible to indoctrination?

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

MEPHISTOPHELES: Der ganze Strudel strebt nach oben; Du glaubst zu schieben, und du wirst geschoben.*

When we wanted to proclaim our hostility to utility, we had our pick of quotations, especially from Amir Alexander’s “romantic hero” period. Carl Gustav Jacob Jacobi’s declaration in 1830 that “the sole objective of science is the honor of the human spirit” is a perennial favorite.⁶ And as early as 1808, Carl Friedrich Gauss, “Prince of Mathematicians”—applied no less than pure—considered it to be to be “no good sign of the spirit of the times” that one keeps hearing the “petty, narrowhearted, and lazy” question—“what use is th[is] science?”—symptomatic of “coolness and lack of sense for what is great and honors mankind.”

[Q]ne thinks everything has to be related to our physical needs … one requires a justification, as it were, for involvement with a science, and can’t conceive that there are people who study simply because studying is itself also a need.

“There are sciences,” he continued, “whose study is not encouraged by the prospect of benefits to physical existence” but rather by “a pure, disinterested joy in study.”⁷

Reminding his reader that “science works for evil as well as good,” Hardy thought “both Gauss and less mathematicians may be justified in rejoicing that there is one science at any rate, and that their own, whose very remoteness from ordinary human activities should keep it gentle and clean.” A few of us nevertheless grew up and became aware of how delicately dependent on “external goods” are the “internal goods” of Hardy’s and Jacobi’s idealism, and spend practically all their time (and all of us spend some of our time) keeping open the lines of communication with Powerful Beings. Alexander von Humboldt, explorer, naturalist, and royal chamberlain of Prussia, was the go-to guy in the Germany of Gauss and Jacobi for mathematicians running short of external goods. Here is a well-known excerpt from Jacobi’s letter to Humboldt praising (Johann Peter Gustav) Lejeune-Dirichlet, his contemporary on the IBM timeline and, like Gauss, an early precursor of the Langlands program:

If Gauss says he has proved something, I think it is likely. If Cauchy says it, one may bet as much in favour as against it. If Dirichlet says it, it is for sure…. [Details of his work follow.] Had he stayed in Paris, he would now reign there without competitor, and how different would his ostensible situation be!

“And thus,” writes the historian, “Dirichlet’s income was raised and he remained in Berlin.”8

Power has many addresses nowadays, but its representatives assemble periodically so that they and the mathematicians can remind one another of the mutual benefits of their exchange of internal for external goods. Exemplary in this respect was a “gala event” at the Oberwolfach institute, in the presence of the German Federal Minister of Education and Research, to celebrate the publication of a collection of short essays by heads of major German corporations entitled Mathematik—Motor der Wirtschaft [Mathematics—Motor of the Economy]. “The list of authors in the Springer book reads like a Who’s Who of German DAX companies” (Allianz, Bayer, Daimler, Lufthansa, Siemens, …) and their message “in a nutshell” is that “Mathematics is everywhere, and our economy would not work without it.” Or, as the mathematicians who edited the volume put it, “Mathematics is not merely a fascinating science and the basis of all natural sciences and technical developments; today it has also become … an important factor for economic competitiveness.”⁹

The CEOs used the opportunity to explain just where mathematics fits into their business models. Their explanations were straightforward, technically precise, and mercifully short on the empty generalities one expects to find in this kind of exercise. The editors put in a word for “fundamental research without concrete prospects of applications,” claiming that much of the mathematics used in business was of just this type not so many years ago. Maybe so; Shell claims to be using topology and the geometry of polynomial equations along with their familiar differential equations in their tireless search for oil. But the volume’s summary, written by Helmut Neunzert, an international expert in industrial mathematics, finds that the mathematics corporations use falls mainly under six headings: numerical simulation, optimization and control, modeling of risk and decisions under uncertainty, data analysis and image processing, multiscale modeling and algorithms, and high-performance and grid computing. Apart from computing, these are golden eggs mathematics has been laying for a very long time; they cover the same industrial mathematics specialties one finds on the careers’ page of the Society for Industrial and Applied Mathematics (SIAM) in the United States.10 The main novelty turns out to be Hardy’s useless number theory: crucial for corporate applications to data storage (coding) and data security (encryption).

A 2013 report, prepared by the consulting firm Deloitte MCS Limited on behalf of the British Engineering and Physical Sciences Research Council (EPSRC) and the Council for the Mathematical Sciences (CMS), buries content very similar to Neunzert’s under a mountain of management jargon and arrives at the astounding conclusion that in 2010, £ 556 billion, or 40% of total UK gross value added (GVA) that year, can be attributed to mathematical science research (MSR): £ 208 billion directly, £ 155 billion indirectly, and £ 192 billion “induced.” The top two sectors for direct MSR GVA are banking/finance and computer services. “In 2010, there were over 6.9 million individuals in employment due to the wider ripple effects” of MSR in the United Kingdom. The top sector for MSR ripple employment is retail distribution, followed closely by “hotels, catering, pubs, etc.”¹¹

France’s efforts along these lines are both more elaborate and more ambivalent. Maths à Venir (MAV), whose name is a pun meaning both “math to come” and “math-future,” was a ceremony held in 1987 and again in 2009 in order to propitiate the Powerful Beings known in France as décideurs, literally “deciders,” who are definitely not the same as elected officials but whose power to make decisions is no less universally acknowledged for being based on no discernable mandate. The 1987 MAV reportedly convinced décideurs to toss some welcome external goods in the direction of mathematics, and the hope in 2009 was that this gesture would be repeated. The décideurs to whom one needed to appeal were mostly French counterparts of the German industrialists who attended the Oberwolfach gala. But the 2009 edition of MAV, held at the newly refurbished Maison de la Mutualité in central Paris, was also conceived as an “évènement exceptionnelle,”¹² a public relations extravaganza, a celebration of mathematics’ utility addressed to the décideurs but open to the public. The German government had sent a Minister to Oberwolfach; the French government placed MAV under the sponsorship of Prime Minister François Fillon (a no-show, but he did send a short speech). There were public conversations between mathematicians and high school students, multimedia exhibits, and lavish buffet lunches, as well as the inevitable champagne reception to which I inadvertently managed to get myself invited, all underwritten by a handful of leading French banks and industrial and defense corporations.

Figure 10.1. The impact of mathematics on the UK economy, or the Golden Goose as virtuous circle. (Source: Deloitte 2013)

The Gallic pessimism on display at the Mutualité clashed sharply with the serenity of the Oberwolfach meeting, not to mention the self-congratulatory pomp of the Deloitte report. The president of the Société Mathématique de France hoped the public would leave convinced that “basic research (in particular mathematical research) is an excellent investment for our society,” while recognizing that in an age when everyone has to “prove immediate profitability … it is difficult to justify … research … whose ultimate aim is the extension of human knowledge.” His counterparts in the French societies of statisticians and of Industrial and Applied Mathematics felt less compelled to apologize but spoke along similar lines. Opening the meeting, Philippe Camus, a true décideur—president of Alcatel-Nugent, codirector of Lagardère, and head of MAV’s Comité de parrainage (literally, “Godfathership committee”)—made the stakes clear: The world outside the Mutualité needs to know that “mathematics is alive, it’s useful, it’s practical … and most of all, it’s a strategic resource that needs to be looked after, because it will allow us in the future to preserve our social model, our way of life, and our ethic.”

Mathematicians, pure as well as applied, took part in planning the two-day event, and the most charismatic spoke in plenary sessions and in panels. The organizers noted in their postmortem discussion that the “image of mathematics” presented by the meeting (“strategic resource”—in other words “merely good,” a Golden Goose) “is not exactly the one mathematicians make themselves.” This is consistent with the findings of Zarca’s study. Comments from mathematicians in the audience betrayed distrust of corporations and décideurs in general. For at least some of the décideurs on the final panel, entitled Mathematics, a strategic resource for the future, the distrust was mutual. One of them had long ago decided that “I don’t believe in pure research, nor do I believe … that direct corporate investment in research is the right way to go”; another that “corporations are not responsible for public sector salaries” (in response to a comment on the reasons for declining interest in the profession); and a third that “mathematics for the sake of mathematics is none of the business of corporations.” In the aftermath of MAV, one organizer worried aloud that failing to act on the concluding recommendations “could be worse than the analytical vacuum that, for certain organizers” was their primary motivation.

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Readers who are not mathematicians will mainly know of Hardy, if at all, for his instrumental role in bringing the self-taught Indian mathematical genius, Srinivasa Ramanujan, to Cambridge. Years later, long after both men had died, Ramanujan returned the favor by bringing Hardy, in a straphanger role, to Broadway (in David Freeman’s A First Class Man), to the West End (in Simon McBurney’s play A Disappearing Number), and to four best-seller lists (David Leavitt’s novel The Indian Clerk).

Reviewing one of the Ramanujan & Hardy plays, a New York Times theater critic asked “Is there a more romantic figure in popular culture than the mathematician?”13 We may suspect him of harboring ironic intentions, but professional as well as aspiring mathematicians recognize Hardy, alone or in Ramanujan’s shadow, as one of the field’s most “romanticizable” personalities (if you look closely, you can see his name in the middle of figure 2.2). This is due largely to his Apology, dedicated from beginning to end to answering one question: “What is the proper justification of a mathematician’s life?”

As graduate students in the common room, we told each other that mathematics was different from the natural sciences, that it was actually more like art. That, we’ve seen, is in Hardy too; he contrasted the “real mathematics” that “must be justified as arts” with “the ‘crude’ utility of mathematics,” the kind engineers or doctors (or major German corporations) use: what usually goes by the name of applied mathematics, in contrast to the pure mathematics that is the primary subject of the present book as well as the Apology. It’s not that Hardy found applied mathematics crude: “It is the dull and elementary parts of applied mathematics,” Hardy argues, “as it is the dull and elementary parts of pure mathematics, that work for good or ill.” The interesting parts of mathematics, pure or applied, are what Hardy compares to art. “Beauty is the first test: there is no permanent place in the world for ugly mathematics.” That’s one of Hardy’s most quoted epigrams.¹⁴ He allows that beauty may be “very hard to define,” but he expects his readers to know what he means by art, and to agree that beauty is one of its criteria.

That word beautiful recurs regularly when one speaks of Hardy. He was past fifty and gray-haired when C. P. Snow, author of The Two Cultures and a close friend of Hardy’s, first saw him and found his face “beautiful—high cheek bones, thin nose, spiritual and austere but capable of dissolving into convulsions of internal … amusement.” And Leonard Woolf, like Hardy a member of the very selective secret society of Cambridge Apostles, wrote that Hardy was “one of the strangest and most charming of men”; he “had the eyes of a slightly startled fawn below the very beautiful and magnificent forehead of an infant prodigy.”

The contemporary reader has outlived Hardy and has, therefore, seen art, beauty, and the relation between the two vary in meaning even more than “useful,” which makes them less than ideally useful as justifications for mathematics. Nevertheless, as Herbert Mehrtens observes, the notion that mathematics has its own aesthetic, “that it is itself an ‘art,’ ” remains “a familiar topos in mathematicians’ talk about mathematics,” one whose history “has yet to be written.”15 So it’s an open question whether we still mean what Hardy meant when we recite his claims about beauty.¹⁶ For Walter Pater, a precursor of the late-nineteenth-century Aesthetic Movement, the question would have been beside the point: “What is important … is not that the critic should possess a correct abstract definition of beauty for the intellect, but a certain kind of temperament, the power of being deeply moved by the presence of beautiful objects.” Twice in the Apology, Hardy speaks of a “passion for mathematics;” Pater, comparing objects of passion, declared that “the poetic passion, the desire of beauty, the love of art for art’s sake has most [wisdom].”¹⁷ Since Hardy’s Apology is often applauded or disparaged as a defense of mathematics as “art for art’s sake,” it should be remembered that this was a relatively new notion in Pater’s time. John Ruskin aimed “to exhibit the moral function and end of art … to attach to the artist the responsibility of a preacher.” For Ruskin, the utility of art was in its power of moral uplift, but Ruskin was not a utilitarian, unlike the economist William Stanley Jevons, whose prescription for improving the moral habits of workers was to expose them to music, which promoted “a general removal of the mind from its ordinary course of duties”—Russell’s “lofty habit of mind,” to which Hardy alludes in his Apology—leaving “the body in a perfect state of repose.”18

Pater’s aestheticism echoes in an extraordinary article by George Salmon “explaining” the great algebraist Arthur Cayley to the general public on the occasion of Cayley’s nomination as President of the British Association. Cayley was the first occupant of the Sadleirian Chair of Pure Mathematics at Cambridge, the position Hardy held years later, when he wrote his Apology. In an unpublished thesis submitted in 2004, John Heard speculates that Salmon, realizing that “Cayley’s work was incomprehensible” to the vast majority of his intended readers, “created a clear divide between scientists and pure mathematicians” by choosing to depict Cayley as an artist:

My subject is the life of a great artist who has had courage to despise the allurements of avarice or ambition, and has found more happiness from a life devoted to the contemplation of beauty and truth than if he had striven to make himself richer, or otherwise push himself on in the world…. we can understand that it is often the lowest style of art which will attract round it the largest circle of admirers. So the fact that it is a very limited circle which is capable of appreciating the beauty of the work done by a great mathematician should not prevent men from understanding that it is like the work done by a poet or painter, work done entirely for its own sake, and capable of affording lively pleasure both to the worker himself and his admirers, without any thought of material benefit.

Heard juxtaposes the elitism of Pater and his fellow aesthetes with Salmon’s rhetoric (see figure 10.2) and argues that to affirm “that the value of pure mathematics lay, not in its utility, but in the pleasure [recall Salmon’s “lively pleasure”] that it gave to the elite band of pure mathematicians” did not contradict “the claim that pure mathematics was beautiful and that pure mathematicians were artists.”¹⁹

Britain’s aesthetic movement soon gave way to the promotion of beauty to ethical principle by G. E. Moore and his Bloomsbury followers, with whom Hardy was in close contact, as we’ll see shortly. The “topos” of mathematics as art, however, is only one facet of a much older tradition that defines art and science in contrast to one another. Pater and Ruskin did share the habit of using the word arts primarily in connection with fine arts, and for them, as for Hardy, art and beauty were practically synonymous. But mathematics in the Apology is a science as well as an art: “of all the arts and sciences, the most austere and the most remote” (ch. 28), and it is its status as science that allows Hardy to ask whether mathematics is “ ‘useful,’ directly useful, as other sciences such as chemistry and physiology are” (ch. 6).

Figure 10.2. From Heard 2004.

Early glimmerings of the “familiar topos” of the superiority of “useless” mathematics can be found in Plato and Archimedes (cf. chapter 3, note 31). That mathematics is an art has to be a much newer idea, for the simple reason that “the modern distinction between science and art, as contrasted areas of human skill and effort, with fundamentally different methods and purposes, dates effectively from [the mid-nineteenth century],” and the contemporary identification of art with the fine arts is a relatively recent development.²⁰ Armand Borel’s 1981 lecture Mathematik: Kunst und Wissenschaft [Mathematics: Art and Science] at the Siemens-Stiftung cites Hardy and Poincaré but traces the theme back to the 1845 thesis defense of Leopold Kronecker. In addition to his mathematical thesis, the young Kronecker was required to argue “a number of propositions of varying degrees of seriousness, against ‘opponents’ chosen, partly by the Faculty, partly by the candidate among his own friends.” The third of these “theses” was Mathesis et ars et scientia dicenda [mathematics is both art and science] and the opponent, Gotthold Eisenstein, was said to have argued that mathematics is only art.²¹ A few years later, the Bavarian Maximilian Order for Science and Art inducted its first prestigious group of initiates, and Gauss was among them—for science, not for art.

We will return momentarily to the “beauty question” in mathematics, but we should remember that the status of mathematics as science rather than art was a matter of philosophical consensus for centuries, and beauty had nothing to do with it. Our words science and art derive from the Latin scientia and ars, the equivalents in Roman and scholastic texts of epistêmê and technê, respectively. Aristotle explained how to distinguish epistêmê from technê in his Nicomachean Ethics and elsewhere. For example: Science is less subject than art to doubt; the object of scientific knowledge is necessity; whereas “art is concerned with coming into being … how something may come into being which is capable of either being or not being.”22 On these grounds, the difference between seeing mathematics as art or science might simply map onto the difference between mathematics as invented and mathematics as discovered. But there are more decisive differences. As conceived by Plato and Aristotle, technê is “practical and empirical,” epistêmê is “contemplative (theoretikê) and demonstrative (apodeiktikê) and most importantly is defined by a preexisting ontological domain.” The latter means, for example, that the sciences are separate: “We cannot, for instance, prove geometrical truths by arithmetic.”²³

The Greek distinction between epistêmê and technê underwent re-consideration by medieval Arab philosophers—who called them respectively ‘ilm and sina‘a—before reaching the hands of the scholastics, in large part as a result of al-Khwārizmī’s invention of algebra (al-jabr w’al-muqabala). The typical object in al-Khwārizmī’s “ontological domain” is a shay—the (still) common word for “thing” and the unknown quantity called x in our high school algebra. “When I considered what people generally want in calculating,” al-Khwārizmī wrote on his first page, “I found that it always is a number.” The equations look like this:

Divide [the inheritance] between the two sons; there will be for each of them three dirhems and a half plus two-fifths of thing; and this is equal to one thing. Reduce it by subtracting two-fifths of thing from thing [italics added for emphasis].²⁴

Since al-Fârâbî saw algebra as “common for number and geometry”—“a bastard by cultural as well as by disciplinary standards,” in the words of Jens Høyrup²⁵—it could not be a science, as we’ve seen, but rather a ḥila’, a trick or mechanism or ingenious device. One century after al-Fârâbî, ibn Sīnā (Avicenna) followed Aristotle and included geometry, astronomy, arithmetic, and music in the chapter of his Book of Scientific Knowledge devoted to mathematics but relegated algebra, as we’ve seen, to the list of “secondary parts of arithmetic.”

Aristotelians will agree with al-Fârâbî that algebra can’t be an authentic science because it is defined, not by its objects, but rather by its methods. Since these methods apply indifferently to objects geometric or arithmetic or of any other nature, it cannot reveal the essence of the objects and, therefore, are mere ḥiyal, ingenious procedures—tricks.26 Once again, al-Khayyām dissents. “The most remarkable thing, perhaps, about Omar Khayyam’s methodology is his denial of any essential disciplinary differences between geometry and algebra.” Al-Khayyām opened his treatise on algebra in most unaristotelian fashion: “one of the scientific notions we need in the part of philosophy known as mathematics is the art of al-jabr w’al-muqabala” [my emphasis]. More explicitly:

I say, with the help of God and His good support: The art [sina‘a] of Algebra is a scientific art [sina‘a ‘ilmiya, my emphasis], whose subject is absolute numbers and measurable magnitudes qua unknown but connected with something known which enables one to determine them—and that thing is either a quantity or a ratio—according to a certain way in which nothing participates with them but themselves and to which you are led by examining them. And what it looks for is the accidents which are attached to its subject in that it is a subject of it with the said property. And what makes it complete is the knowledge of the scientific methods whereby one will understand this above-mentioned kind of determination of numerical and geometrical unknowns.²⁷

So by the end of the middle ages—when Cardano was writing up the solution of the cubic equation in his Ars Magna [The Great Art], concluding “So progresses arithmetic subtlety the end of which, as is said, is as refined as it is useless”²⁸—the clear distinction between art and science was completely mixed up, in no small part thanks to the “bastard” status of algebra, Cayley’s future specialty. Then Descartes came along and turned the distinction upside down. In his Rules for the Direction of the Mind it’s now art that is determined by its object “since it is not so easy for the same hand to adapt itself both to agricultural operations and to harp-playing,” but it “is certainly wrong” to say the same of science: “all the sciences are conjoined with each other and interdependent.” Twenty years later, in his conversation with Frans Burman, Descartes insisted that “one needs a mathematical mind which must then be polished by actual practice. Now this mathematical knowledge must be acquired from Algebra.”29 But note that “mind” in “mathematical mind” as well as in Descartes’ Rules … translates as ingenium….

Far from pretending to shed any light on the mathematical artistry of Eisenstein, Cayley, Hardy, or Bombieri, this pseudoarcheological detour reminds us just how hard it is for us to be sure we know what they were talking about. In the long view, even if our Colleges of Arts and Sciences lack “bastard” departments of “scientific arts,” no consistent meaning can be assigned to the contrast between art and science.³⁰ Max Weber thought he had put his finger on the contrast when he wrote “Scientific work is chained to the course of progress; whereas in the realm of art there is no progress in the same sense.”³¹ But progress has no constant meaning either; certainly the “sense” of progress in mathematics is not the same in different places and across generations.

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

When Abraham Flexner opened his Institute for Advanced Sciences … in the early 1930s, he saved the top floor—and the best offices—for mathematicians, and his first permanent position was also given to a mathematician [Oswald Veblen] …. for Flexner, mathematics was the ‘highest’ because of the difficult, abstract work that it involved…. The IAS was for thinkers—and mathematicians were the purest of thinkers.³²

Irving and Marilyn Lavin remind us of Flexner’s “usefulness of useless knowledge,” in their reconstruction of the history of the the IAS Seal.³³ The two allegorical figures (see figure 10.3) are labeled TRUTH (iconographically correct in her nudity, as in Horace’s nuda veritas) and BEAUTY (draped). The fruit of the tree between them is Knowledge presumably the usefully useless kind Flexner favored. (And the IAS is indeed an Eden for those privileged enough to spend even a few weeks there, but I’ll let the reader speculate on what this has to do with the scene on the Seal or, for that matter, with Rites of Love and Math).

Figure 10.3. Truth and Beauty: the IAS seal (Photo by Bruce White, Courtesy of the Institute for Advanced Study).

“The radical nature of Flexner’s twinning of science and humanism with truth and beauty arose in part” according to the Lavins “from the radical nature of his concept for a ‘modern’ university by which he meant a university devoted exclusively to the pursuit of higher learning for its own sake and without regard to practical value.” In the decade before Flexner had materialized his trinity of Truth and Beauty and Useful Uselessness in the form of the IAS, topologist Oswald Veblen, who later left Princeton’s Mathematics Department to become the first IAS professor, had been busy tempting the snake into the garden with visions of Golden Geese. “What” he asked,34 “do industry and engineering owe to mathematics?” Answers included “the development of locomotives, automobiles, airplanes, the telegraph, the telephone, and radio … overcoming ‘formidable natural obstacles, bridging rivers, and damming floods’ … applications to physics, astronomy, economics, and the social sciences.” “[T]he civilization of the future will depend even more on mathematics than does the civilization of the present.”

The Lavins argue that the IAS seal refers intentionally to the “Beauty is truth, truth beauty” from Keats’s Ode on a Grecian Urn, but the IAS could just as well have adopted this motto from Wordsworth when addressing its donors:

Give all thou canst; high Heaven rejects the lore

Of nicely-calculatedless or more;

The lines are from the poem Inside of King’s College Chapel, Cambridge and are a plea for openhandedness in support of “immense and glorious Work of fine intelligence” albeit “for a scanty band/Of white-robed Scholars only.” But did the white-robed scholars and the donors see eye to eye about useful uselessness? It’s hard to find a less consensual topic; the scholars scarcely agreed among themselves from one year to the next:

What is the attitude of the academic man towards his vocation …? He maintains that he engages in ‘science for science’s sake’ and not merely because others, by exploiting science, bring about commercial or technical success and can better feed, dress, illuminate, and govern (Max Weber, 1922).

… an important aim of [British Science Research Council] support for long-term basic research is to enable university departments to give help to industry and Government Departments on shorter-term projects and thus bring more social and industrial relevance to their research and teaching (from the 1970–1971 SRC report)

… science and patents don’t mix any more than oil and water (Stanford physicist D. L. Webster in 1939, in connection with funding by the Sperry Gyroscope Company),

… as scholars, we should not seek knowledge for its own sake (the chancellor of UCSD in 2001).

… between the managerial outlook and the scientific there is a basic conflict in goals (William H. Whyte, 1956).

Through closer ties to the socio-economic universe, new academic, ethical, and moral responsibilities are enriching the role and action of the university in a way that favors building the foundations of the construction of a knowledge society in harmony with a necessary sustainable development.35

Steven Shapin’s Scientific Life reminds us of the stereotypical image of the scientist in the mid-twentieth century, the time of the first stirrings of Mertonian sociology of science and Hardy’s Apology: “Scientists are internally motivated; dedicated, even called, to their work; they are selfless; resistant to convention and authority; intentionally blind to social convention and prejudice; unconcerned for fame and material reward; open. Their virtues are a pastiche of the heroic, chivalric, Stoic, and Christian. Put such people into the moral environment of corporate capitalism, and the resulting tensions are not merely mundane and contingent but ideologically essential.” Karl Compton, physicist and president of MIT, drew on this stereotype when responding to a senator’s question just after the war: “I don’t know of any … group [other than pure scientists] that has less interest in monetary gain.”36 Much of Shapin’s book is, in fact, devoted to deconstructing this image, which needed qualification even before today’s “knowledge society.” Unfortunately, Shapin’s study has nothing to say about mathematicians and doesn’t help us to weigh Yuri Manin’s remark in a 2009 interview addressed to (Russian) mathematicians—

“I always say, ‘Why should we put ourselves on the market? We (a) don’t cost anything, and (b) don’t use up natural resources and don’t spoil the environment.’ Give us salaries, and leave us in peace.”

—against this excerpt from the SIAM report:

“Research often has a serious difficulty: too much understanding and too little transfer.”³⁷

Mehrtens sees mathematicians’ indifference to Golden Geese as part of the modernization process, which saw the “driving out” [verdrängen] of questions connected with applications from “the official consciousness of mathematics.³⁸ But the continuing economic crisis drives them back in again. Several roundtables at that 2009 edition of Maths à Venir, convened during the dark early days of the crisis, addressed the role of finance mathematics. It was even proposed to draw up a charter of mathematical social responsibility, which seems to have been forgotten almost immediately, but none of the speeches at the Paris MAV noted the irony of the choice of venue: the Mutualité, long-time headquarters of the mutual insurance movement dedicated precisely to the ideal of collective solutions to the financial needs ostensibly addressed by the quants. After serving for decades as the scene of massive meetings of radical dissent, the Mutualité was finally handed over to a public-relations multinational and converted to a luxurious convention center, where French President Nicolas Sarkozy had planned to celebrate if he had been reelected in 2012.

Irony has not spoken its last word on the flight from utility, even when utility is understood, with Hardy, as that which “tends to accentuate the existing inequalities in the distribution of wealth.” The thirteen Creative Industries promoted by Britain’s Department of Culture, Media, and Sports were estimated in 2007 to account for 7.3% of the economy, the same proportion as financial services.39 England has changed since Hardy’s day, and it’s not only because online commerce needs prime numbers, nor is it because Hardy’s work in functional analysis gets applied to the Black-Scholes equation: mathematics and art turn out to be useful in much the same way.⁴⁰

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

It is in the abstruser sciences, particularly in the higher parts of mathematics, that the greatest and most admired exertions of human reason have been displayed. But the utility of those sciences, either to the individual or to the public, is not very obvious, and to prove it, requires a discussion which is not always very easily comprehended.⁴¹

I have no idea whose idea it was to invite me to the Ministère de l’Enseignement Supérieur et la Recherche on October 6, 2009, for an immersion in contemporary utilitarian public policy, in the form of a morning seminar on the French National strategy of research and innovation: what projects for the Big National Loan (Grand Emprunt National)? Entrepreneurs sat beside researchers and representatives of voluntary associations⁴² in the seats and the aisles of the auditorium in the grand old École Polytechnique building in the Latin Quarter to listen to Minister Valérie Pécresse outline her hopes for the morning’s four simultaneous roundtable discussions. I failed then and still fail to grasp the historic significance of the Big National Loan, piloted by a committee led by one former Prime Minister from each of the main parties.⁴³ Keywords pronounced by the minister—visibilité, esprit d’entreprise [entrepreneurial mindset], valorisation, gouvernance—resurfaced throughout the morning’s events. In her greetings and again at her concluding speech three hours later, she insisted that basic research not subject to retour sur investissement was “at the heart of our national research and innovation strategy.” My notes have the minister saying that “progress of science must not be neglected” and stressing the parallel between quête de rente [search for profit] and quête de sens [search for meaning].44 There is an “urgency to renew and rationalize research” to confront its “major defect”—the absence of fluidité between research and innovation.

Otherwise basic research was hardly mentioned at all, certainly not at the roundtable I chose to attend, entitled The Big Loan to reinforce the innovation ecosystem. Finally a key concept—ecosystem—that might help me figure out how I fit into the grand national scheme.⁴⁵ A big-enough fish to merit invitation to the seminar, I am nevertheless too small to be a predator—most likely a bottom-feeder. The minister situated the innovation ecosystem in a “new research landscape” characterized by three more key concepts: autonomie, décloisonnement [removing barriers], and the université au coeur de l’innovation [university at the heart of innovation] as a “post-crisis springboard” [tremplin d’après-crise].

Facing a panel too numerous for the space at the table, the innovation ecologists in the audience were a comparatively young and hungry crowd, overflowing the seating in the assigned seminar room (“I’m sorry about these material conditions”) and compulsively consulting their portable communications devices. The session was led by the president of something called the pôle de compétitivité SYSTEM@TIC, who made a distinction I couldn’t quite follow between problèmes de moyens and problèmes soft and introduced the four themes of the presentation, namely,

1.  Getting from emergence de l’idée to création d’un startup;

2.  Technology transfer;

3.  Problèmes de financement;

4.  Décloisonnement de l’écosystème.

Of these, only the fourth theme seemed at all relevant to my situation—the décideurs want to break down the barriers and let me out to swim among the sharks, and vice versa.⁴⁶ Naturally this was the theme dropped from the program for lack of time. But I did learn from the speakers, as well as from décideurs in the audience, that

1.  It is important to focus on people rather than (just) on patents—has the researcher set loose from the cloison made millions or tens of millions of euros?

2.  Research turns money into ideas; innovation turns ideas into money.47

Two recurrent themes—the knowledge economy and competitiveness of the French economy—were repeatedly attributed to then-President Sarkozy. As for my own responsibility in all this, “It’s up to scientists to leave the labs to meet citizens and explain how what they are doing contributes to their well-being.”* Not the scientist’s well-being, of course, but that of the citizen, 49% of whom, according to a 2006 opinion poll, thought that the first responsibility of researchers is to “improve the well-being of humanity,” far ahead of “knowledge,” “French competitiveness,” and “improving everyday life.”⁴⁸ No figure was given for the percentage of French citizens who referred to anything that looked like the “relaxed field” or “internal goods” or telos of a “tradition-based practice.” But we don’t know whether or not mathematics was mentioned in the survey.

Will scientists really meet ordinary citizens, rather than décideurs, on the other side of the cloison? In their concluding remarks (just before the champagne reception), the speakers insisted that, while it was understood that basic research brings no retour sur investissement—in other words, the research laboratory cannot help to repay the Big Loan—basic research must be “associated” with laboratoires d’innovation. “All our research will evolve in the direction of encouraging [public-private] exchanges.” At one point during the ecosystème panel, I was tempted to speak up and point out that, actually, the “entrepreneurial mindset” was not unfamiliar to scientists, and if most of us have chosen to follow a not especially easy path to a not particularly lucrative career, it was because we decided early in our lives that the esprit d’entreprise was a mindset to be avoided at all costs! This is just another way of underscoring our attachment to our “relaxed field,” and you might think the décideurs should hear how the chercheurs feel about the décloisonnement in store for us. But how much time would a marine ecologist have for a soft-shelled creature showing up at the lab, fresh from the sludge, with a point of view? Would the décideurs have understood why Neal Koblitz, coinventor of elliptic curve cryptography, “would have felt queasy” about accepting the $1000 per month consultancy he was offered in 1997 and gave the money away “since there was little that I did … during my five years as consultant that I wouldn’t have been glad to do anyway free of charge,” given that the trillion dollar e-commerce industry has spun off tens if not hundreds of millions for the data security techniques based on Koblitz’s ideas? Or would they have simply disregarded Koblitz’s hopelessly romantic unentrepreneurial mindset?49

“The dichotomy between truth and interest is one of the standard topoi of the logic of scientific authorship,” writes Mario Biagioli, who adds that “truth … has to be priceless because it cannot belong to the logic of interest and its ubiquitous unit of measure—money.” Anyway, you were right to be skeptical about Sarkozy’s claim to authorship of the themes cited earlier. Along with three of Pécresse’s keywords, those themes can be found on the first two pages of the report on the First European Forum on Cooperation between Higher Education and the Business Community, held in Brussels in February 2008 “in line with the European Commission’s initiative of May 2006 on modernizing Higher Education in Europe, a key element of the Lisbon strategy”; Valérie Pécresse had given one of the opening speeches. These same themes and keywords reappear in item 9 of the 2009 European Commission Legislative and Work Program List of Strategic and Priority Initiatives, where one reads that

[t]he Communication of the Commission “Delivering on the Modernisation Agenda for Universities: Education, Research and Innovation” (COM(2006) 208 final) highlights that Universities have to recognize “that their relationship with the business community is of strategic importance and forms part of their commitment to serving the public interest.”⁵⁰

Neither of these documents refers even once to mathematics, but at least one French décideur has seen the connection: Philippe Camus, MAV Godfather, had written on the MAV 2009 Web site that “Mathematics are at the heart of most key technological and economic issues…. It’s more crucial than ever to promote closer ties between the world of mathematical research and the corporate world.”

Back in the United States, the 2012 SIAM Report concurs: “Our economy and that of the developed world is in the midst of a transition from a product-based economy to a knowledge-based economy…. We are convinced that the mathematical and computational sciences have contributed and will continue to contribute to the nation’s economy … Universities will continue to play a key role.” This is true enough and hardly surprising, because the concept of the “knowledge economy” was popularized by U.S. economists long before it became fashionable in Europe. SIAM then goes on to channel the voices of Powerful Beings, recognizable by their use of the word must:

But this will not happen by itself; university faculty must actively encourage students to consider careers in industry and prepare those students for the very different world they will encounter upon graduation.51

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

I don’t know why we are here, but I’m pretty sure that it is not in order to enjoy ourselves.

This unsourced quotation, probably apocryphal but attributed to Wittgenstein on dozens of websites,⁵² may well be in keeping with the European Commission’s Strategic and Priority Initiatives: the écosystème panelists worried that professors and researchers suffer from “soft emotional problems,” such as a reluctance to work on projects that are not their own. But it is belied by mathematicians’ accounts of their experience. Helmut Neunzert and his colleagues published a study in 2004 entitled “Mathematics Dream Job” [Traumjob Mathematik], in which they report that about 80% of their subjects had “fulfilled their occupational dreams.” Neunzert stressed that “this is an unusually high percentage,” but we have seen that an even higher 91% of pure mathematicians in France placed “the pleasure of doing mathematics” at the top of their list of motivations. A 2011 survey in Abu Dhabi reports that mathematics (and chemistry) teachers are the most satisfied of the emirate’s (generally highly satisfied) teaching staff.⁵³

One of the good things the Simons Foundation has done is to record interviews with mathematicians, by mathematicians, and make them freely available on the Internet. Their value as sociology is questionable—the selection is mainly limited to Giants—but you may want to believe that mathematicians speak with greater candor to their peers than to even the most sensitive social scientist. So we watch Paul Sally of Chicago reminisce about his 1968 collaboration with Joe Shalika at IAS: “we would work there eight or ten hours a day, filling every blackboard in the place, just having the time of our lives.” IAS professor Robert MacPherson quotes Kolmogorov’s opinion that “the only way somebody can be a scientist is that somehow their personality gets frozen at an early age … at the playful stage.” Whenever he’s talking with Pierre Deligne, MacPherson feels like “I’m the eight-year old and he’s the kindergartener.” Deligne himself recalls how pleased he was to learn as a student in Brussels that “one could earn one’s living by playing, i.e., by doing research in mathematics.”54

I hope my distinguished but playful colleagues won’t take it as a mark of disrespect if I remind them at this point that, asked about the utility of his discovery of the magnetic field, Michael Faraday supposedly answered, not that we would someday be using it for activities as diverse as data mining and shopping, but rather: “Of what use is a newborn babe?” If you grant the legitimacy of that question, you may be ready to join Alison Gopnik in contemplating the “philosophical baby” in its relaxed field. Note the uncanny resemblance of the “useful uselessness of immaturity” to life at the School of Mathematics at the IAS:

Play is the signature of childhood. It’s a living, visible manifestation of imagination and learning in action. It’s also the most visible sign of the paradoxically useful uselessness of immaturity. By definition, play … has no obvious point or goal or function. It does nothing to advance the basic evolutionary goals of mating and predation, fleeing and fighting. And yet these useless actions—and the adult equivalents we squeeze into our work-day—are distinctively, characteristically human and deeply valuable.⁵⁵

Outside this relaxed field, it’s considered poor form to admit that we are motivated by pleasure. Aesthetics is a way of reconciling this motivation with the “lofty habit of mind,” and it has been that way at least since Plato’s Philebus listed the constituents of “the good,” placing pleasure in fifth and last place, with beauty second, followed by “mind and wisdom” and “sciences and arts and true opinions.”⁵⁶ Nevertheless, the suspicion grows that not only beauty, but goodness (or utility) and truth serve as excuses to talk about pleasure on the sly. Truth’s pleasures are relished more widely than you might think. Henri Cartan, a founder of Bourbaki, confessed that “I greatly enjoyed discovering what was true.” Benedict Gross, coauthor of one of the most influential papers on the Birch-Swinnerton-Dyer conjecture (and part-time installation artist): “When you discover a mathematical truth, everything immediately becomes clear…. The beauty of mathematics is just a pleasure to behold.” Ingrid Daubechies, current president of the IMU, opines that “We like logical thinking as an activity—figuring things out gives us pleasure.”57

The pleasure of “figuring things out” is not so different in mathematics and theoretical physics—Daubechies was originally trained as a physicist—and if we are about to quote Richard Feynman at length, it’s because he was never at a loss for words. In a televised interview, he explained that he “used to enjoy physics and mathematical things because I used to play with it. It was never very important, but I used to do things for the fun of it.” When he was a young physicist at Cornell, Feynman showed a calculation involving the rotation of a Cornell cafeteria dish to his senior colleague Hans Bethe, who told him, “that’s very amusing, but what is the use of it?” No use, Feynman replied, just “the fun of it.”

I relaxed and started to play … with rotation … and that just led me back into quantum electrodynamics … and I continued to play with it in the relaxed fashion … and in very short order I worked out the things for which I later won the Nobel prize⁵⁸ [my emphasis].

David Hume’s Treatise of Human Nature takes for granted that the reasons for “curiosity, or the love of truth,” specifically the “discovery of the proportions of ideas, consider’d as such”—and draws his examples from “mathematics and algebra”—are bound up with pleasure. The relation is not as simple as cause and effect: “‘tis not the justness of our conclusions, which alone gives the pleasure.” Indeed, “to fix our attention or exert our genius” is “of all other exercises of the mind … the most pleasant and agreeable.”

But that’s not all: “The truth we discover must also be of some importance.” Later in this section, Hume uses “importance” and “utility” interchangeably.⁵⁹ When Neunzert was asked “what it is that fascinates me about mathematics,” he summarized his answer in a few words: “That one can do something useful with its playfulness.” Industrial and applied mathematicians in the United States are reported to feel the same way: “In many cases, academic mathematicians derive considerable satisfaction from seeing the technologies they know and love being applied in productive and interesting ways to real-world problems.”60

At Gradgrind’s utilitarian school in Dickens’s Hard Times, pleasure is a world away, more precisely the world of Sleary’s circus. In reality, the historical utilitarians and their immediate followers held pleasure in such high regard that some of them attempted to quantify it as a surrogate for utility. The “exact utilitarianism” of Francis Ysidro Edgeworth’s Mathematical Psychics hypothesized that “Pleasure is the concomitant of Energy;” to understand emigration, for example, Edgeworth thought it would help to write things such as

The happiness of the present generation may be symbolized

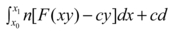
“Inexact” utilitarians, such as Jevons, John Stuart Mill, or Jeremy Bentham, were less keen on mathematical formalism, but all emphasized the centrality of pleasure in their systems—Bentham invented a “hedonic,” or “felicific, calculus”—to the point that it has recently been proposed to define historical “utilitarianism” as “an acceptance of two postulates,” the first of which is “ ‘Social utility’ is an aggregate (estimated or precise) of individual utilities (reflecting individuals’ pleasure, happiness, etc).”⁶¹ In this respect, at least, mathematicians line up with the utilitarians, while the European Commission, with no mention of either pleasure or happiness on any of the 117 pages of their 2009 road map, sides with the Gradgrinds.⁶²

I have already hinted that mathematicians refer to “beauty” when they want to talk about pleasure while maintaining a “lofty habit of mind”; talk about art is loftier still. But let no one be fooled. For Edmund Burke, “the beautiful is founded on mere positive pleasure.” Hume thought it “an universal rule, that their beauty [of every work of art] is chiefly derived from their utility, and from their fitness for that purpose, to which they are destined,” but we have already seen that utility for Hume is also bound up with pleasure. As for Kant, “the feeling of pleasure or displeasure … is precisely the riddle” whose solution required him to write the Critique of Judgment.63

Much as Edgeworth understood pleasure in his Mathematical Psychics on the model of physics, Burke sought physiological grounds for beauty; he was convinced that “beauty acts by relaxing the solids of the whole system…. a relaxation somewhat below the natural tone seems to me to be the cause of all positive pleasure.” The last chapters of part IV of Burke’s On the Sublime and Beautiful are devoted to showing that “the genuine constituents of beauty, have each of them … a natural tendency to relax the fibres.” Neuroimaging now maps Burke’s “solids” and “fibres” in order to trace emotion through the activation of brain regions. Researchers at London’s Wellcome Laboratory report that activation of the medial orbito-frontal cortex (mOFC) is associated with a reported experience of beauty, with the intensity of the experience reflected in the strength of the activation. T. Ishizu and S. Zeki claim to have demonstrated that this correspondence is similar for auditory and visual beauty and that, therefore, “there is a faculty of beauty that is not dependent on the modality through which it is conveyed.” More intriguing, for our present purposes, is the following passage:

[A]ctivity in mOFC correlates with the experience of pleasure and reward, whether real or imagined, and its expectation. This naturally raises, at a neurobiological level, an issue long discussed in the humanities, namely the relationship of aesthetic experience to pleasure.⁶⁴

Now if it turns out that mathematical beauty is also hardwired in the mOFC of the beholder,⁶⁵ it stands to reason that one would want to equip automatic theorem provers with mOFCs. We seem to be back in Steven Pinker’s cheesecake bakery, an uncomfortable spot for mathematicians seeking to frame their apologies. Artist and art critic Roger Fry, a leading member of Bloomsbury, posits a “pure moralist” for whom the “life of the imagination”—the description applies to pure mathematics, though Fry is naturally thinking of the arts—can be justified only if it is “shown not only not to hinder but actually to forward right action, otherwise it is not only useless but, since it absorbs our energies, positively harmful.” What Fry calls “the Puritanical view,” a version of which appears to reign in today’s European Commission, “regards the life of the imagination as no better or worse than a life of sensual pleasure, and therefore entirely reprehensible.” Fry dismisses as “special pleading” a second view, that of “moralists like Ruskin” who argue “that the imaginative life does subserve morality.” Fry’s own “Apology” rests on different tenets:

[M]ost people would, I think, say that the pleasures derived from art were of an altogether different character and more fundamental than merely sensual pleasures, that they did exercise some faculties which are felt to belong to whatever part of us there may be which is not entirely ephemeral and material.

Note that Fry seeks the eternal, not in the foundations of mathematical truth but rather in the “fundamental … pleasures” of art. Like pure mathematics, the imaginative life that art expresses “is separated from actual life by the absence of responsive action.” And, therefore, art isn’t faced with the “moral responsibility” implied by the life of action; instead, “it presents a life freed from the binding necessities of our actual existence.”66 Art, in other words, is a relaxed field, as is the “life of the imagination” more generally. We don’t have to choose between Pinker’s evolutionary determinism and “whatever part of us … is not entirely ephemeral”; we might even choose to see the latter as the focus of a tradition-based aesthetics—and here Fry’s aesthetics shades into ethics, specifically the ethics of the philosopher G. E. Moore, whose Principia Ethica has been called Bloomsbury’s Bible.⁶⁷

Irving Lavin argues in his article on the IAS seal that the theme of the relation of truth and beauty to science first “became explicit and central” in Fry’s essay “Art and Science,” which we quote shortly. “It may be that Fry and Flexner were acquainted,” Lavin speculates. Fry lived a few blocks away from Abraham Flexner while he was Curator of Painting at the Metropolitan Museum in New York, and Fry certainly knew Simon Flexner, Abraham’s older brother. It is known that Flexner was advised—by mathematicians, not by Fry—to recruit Hardy to the IAS but was “readily convinced that there was no way to lure [him] away from Cambridge,” where they met in 1932.⁶⁸

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Grothendieck insists throughout Récoltes et Sémailles on the importance of beauty in his life, in mathematics and beyond. This quotation is typical:

The deepest and most fruitful work is the one that attests to the most liberated sensitivity to apprehending the hidden beauty of things [and a footnote adds: such delicate sensitivity to beauty seems to me intimately linked to something to which I’ve had occasion to refer under the name of making demands (on oneself), or of “rigor” (in the full sense of the term), which I described as “attention to something delicate in ourselves,” an attention to a quality of comprehension of the thing that is probed. This quality of comprehension of a mathematical thing cannot be separated from a more or less intimate, more ore less perfect perception of the particular “beauty” of the thing.].69

Langlands, invited by Notre Dame’s philosophy department to address the question of “beauty in mathematical theories,” was, as usual, more circumspect. After reminding his audience that Jacobi declared his devotion to the “honor of the human spirit” in response to the opinion he attributed to Fourier, that “the main goal of mathematics is public utility and the explanation of natural phenomena,” he continued:

I am not sure it is so easy. I have given a great deal of my life to matters closely related to the theory of numbers, but the honor of the human spirit is, perhaps, too doubtful and too suspect a notion to serve as vindication. The mathematics that Jacobi undoubtedly had in mind when writing the letter, the division of elliptic integrals, remains, nevertheless, to this day unsurpassed in its intrinsic beauty and in its intellectual influence.

Acknowledging that referring as Fourier did to “public utility” is “if not then at least now, often abusive,” Langlands concluded that “it is not easy to find an apology for a life in mathematics.” “Nevertheless,” though we are “only animals,” human beings

have also created—and destroyed—a great deal of beauty, some small, some large, some immediate, some of enormous complexity and fully accessible to no-one. It, even in the form of pure mathematics, partakes a little of our very essence, namely its existence is, like ours, like that of the universe, in the end inexplicable.⁷⁰

Before the Apology shifts to a polemic on utility, Hardy concludes his aesthetic chapters with “a few disjointed remarks” on the nature of mathematical beauty, summarized in a single sentence: “In both theorems [of Euclid and the Pythagoreans, together with their proofs] there is a very high degree of unexpectedness, combined with inevitability and economy.”71 Louis J. Mordell, Hardy’s successor as Sadleirian Professor at Cambridge (and the first professional mathematician I ever met), later added “simplicity of enunciation.” With that, it’s only a slight exaggeration to say that the theorizing of mathematical beauty—on internal, structural grounds—comes to an end.⁷²

Aesthetic judgment in mathematics⁷³ is hampered by its meager lexicon; it doesn’t inspire “lofty” habits in the use of language. Pretty, appealing, attractive, and the like, carry less weight than the all-purpose beautiful and the perennial favorite elegant, and in practice they overlap with words like clever or ingenious that reflect a different set of concerns. Harmonious or symmetric seem to me to beg the question. So in principle Hardy’s trio of unexpectedness, inevitability, and economy should provide a welcome alternative. André Weil’s topological insight, the one that converted me to number theory, qualifies on all three counts; and I recognized these qualities in the dream strategy that lingered with me in Paris in 1992. But after a moment’s thought, we realize that we have made no progress at all toward elucidating what beauty in mathematics has to do with beauty elsewhere. The problem is that unexpectedness, inevitability, and economy are of little help in grasping the beauty of Hardy’s “forehead” or “high cheekbones” or Shakespeare’s “After life’s fitful fever he sleeps well,” quoted in the Apology and a particular favorite of Hardy’s.

Even if we suspect that the word beautiful in mathematics is used mainly in order to express personal approval, we are entitled to ask what kind of approval it expresses and how, if at all, it differs from positive value judgments expressed by words like true or good. Roger Fry had studied mathematics at Cambridge and once attempted to distinguish “esthetic response … from the responses made by us to certain abstract mental constructions such as those of pure mathematics….” His conclusion is reminiscent of Russell’s “stern perfection”: “Perhaps the distinction lies in this, that in the case of works of art the whole end and purpose is found in the exact quality of the emotional state, whereas in the case of mathematics the purpose is the constatation of the universal validity of the relations without regard to the quality of the emotion accompanying apprehension.”74

All three of Hardy’s criteria can be found, with some effort, in Fry. In his Art and Science, for example, Fry returned to the theme of emotion in science: “the recognition of inevitability in thought is normally accompanied by a pleasurable emotion, and … the desire for this mental pleasure is the motive force which impels to the making of scientific theory.” Elsewhere he wrote that “a certain quality of surprise, or at least unexpectedness, is essential to keep our contemplation at full stretch”; and he drew his readers’ attention to Rembrandt’s (and Shakespeare’s) “economy.”⁷⁵ But while each of these qualities meets with Fry’s approval, he mentions them only briefly; they are not central to his aesthetic vision.

Fry, like Hardy, was a Cambridge Apostle, as were Leonard Woolf, Russell, John Maynard Keynes, E. M. Forster, and Lytton Strachey. G. E. Moore was Hardy’s Apostolic sponsor, and you could read the Apology’s aestheticism and cult of uselessness as an expression of the ideal of Moore’s Principia Ethica, which was “that personal affections and aesthetic enjoyments include all the greatest, and by far the greatest, goods we can imagine.”⁷⁶ Thus Moore subordinates aesthetics to ethics. He makes it possible to find an ethical justification for something as useless as pure mathematics, provided it can be framed in terms of “aesthetic enjoyments.” In the Apology, Hardy attempted to do just that.

Clive Bell, Bloomsbury’s other major art critic, agreed with Moore. “To pronounce anything a work of art is … to make a momentous moral judgment,” he wrote. Echoing Moore, he insisted, “The starting point for all systems of aesthetics must be the personal experience of a peculiar emotion.” Bell lists mathematicians alongside mystics and artists as capable of attaining “ecstasy”:

The pure mathematician rapt in his studies … feels an emotion for his speculations which arises from no perceived relation between them and the lives of men, but springs, inhuman or super-human, from the heart of an abstract science…. Before we feel an aesthetic emotion for a combination of forms, do we not perceive intellectually the rightness and necessity of the combination?⁷⁷

Bertrand Russell, rather than Hardy, may have been the mathematician the Bloomsbury critics had in mind. Bell exchanged letters with Russell, and Fry painted Russell’s portrait. My cursory exploration of the available source material, on the other hand, has unfortunately yielded no evidence that Hardy ever talked about art or beauty—or about anything at all, for that matter—with Bell or Fry. All I have been able to establish is an affinity at the level of ideas. Hardy shared with Bell and Fry, as well as with Moore, the readiness to recognize the aesthetic as an intrinsic good; if pressed to categorize Hardy’s three-word aesthetic theory, we would be tempted to call it “formalist,” in the manner of the Bloomsbury critics.

There is also a difference. The emotional response central to Bloomsbury’s aesthetic is absent from Hardy’s discussion of mathematical beauty. “[O]bsessive math is not done by geeks, but by passionate people who feel as much as they think.” This is the lesson David Auburn, author of Proof, a play about fictional mathematicians, wanted to share with his audience after learning in the Apology “about the pleasure, passion, and joy of doing” mathematics. Auburn was right to recognize that Hardy’s book is a work of deeply felt emotion, not limited to the “melancholy” of the Apology’s first lines. But it is telling that the words passion and pleasure hardly figure in the Apology, and joy, not at all. Only once does Hardy’s aesthetic emotion approach ecstasy: “Greek mathematics … is eternal because the best of it may, like the best literature, continue to cause intense emotional satisfaction to thousands of people after thousands of years.”

Hardy did call his research “the one great permanent happiness of my life,” and when we read this we feel the “haunting sadness” that struck Snow and most subsequent readers, because the sixty-three-year-old Hardy told us at the very beginning of his Apology that mathematics is “a young man’s game” and he is no longer a player. The word permanent occurs ten times in the Apology, emotion, three times. Beauty, which recurs throughout the text, is the word Hardy chose to allude to his emotional reaction to mathematics. The Powerful Beings to whom he thought he owed allegiance, he may have felt, would find it more “serious”—the word occurs in nearly every chapter of the Apology—than a direct appeal to emotion. Most mathematicians who have written on the topic have made the same choice, because they also want their aestheticism to be taken seriously. It is, therefore, ironic that aestheticism as a movement, far from permanent, belongs to an increasingly irretrievable past. Even Fry, who could write “[i]f by some miracle beauty could be generated without effort, the whole world would be the richer,” used the word beauty sparingly in connection with art, while Bell preferred to avoid it altogether, opting instead for significant form. More than a century separates us from the time when serious people who were not mathematicians could speak of beauty unfiltered, without apologies. Is it any wonder that, in popular culture’s serious precincts, the mathematician has become the romantic figure of choice?

---

* The whole whirlpool is striving upwards; you think you are pushing, but you are being pushed.

* “Il reste aux scientifiques de sortir du labo à la rencontre du citoyen et d’expliquer comment ce qu’ils font contribuera à son bien-être.”

 

chapter δ

How to Explain Number Theory at a Dinner Party

FOURTH SESSION: ORDER AND RANDOMNESS

In 1801 Gauss published the Disquisitiones Arithmeticae, considered the founding text of modern number theory. Much of the Disquisitiones is concerned with the study of solutions to equations of degree 2 (quadratic equations) in two variables, such as x² + y² = 3 or x² + xy + y² = 11: equations of ellipses or hyperbolas. For our purposes here, quadratic equations (especially equations of ellipses) with integer coefficients are completely understood, thanks to Gauss. This does not mean that one cannot still ask questions about quadratic equations in two variables whose answers are unknown. In this as in all areas of mathematics, our state of knowledge can be determined only relative to the questions we have chosen to ask. Nevertheless, we are here only looking for a way to classify quadratic equations in two variables into two kinds: those that have infinitely many solutions and those that have none at all. Legendre and Gauss explained exactly this dichotomy more than two hundred years ago for quadratic equations.1 When there is at least one solution, there is a formula for writing down all the solutions. So, for the purposes of a dinner party, I can consider this problem to be closed.

Matters are quite different when the degree of the equation is allowed to increase to 3, as with the two equations we considered last time.

These cubic equations in two variables are two examples of elliptic curves.

Figure δ.1 shows a picture of the curve with equation (E5), which should not look at all like an ellipse; the curves do have a distant connection with ellipses, but for number theorists the connection survives only in the name.

Figure δ.1. Graph of the cubic equation y² = x3 − 25x [formula (E5)].

It is a famous theorem of Gerd Faltings, proved in 1983, that equations in two variables of degree 4 and higher almost always have only finitely many solutions in rational numbers, as predicted by (Hardy’s future successor) L. J. Mordell in 1922; when they have infinitely many, it is always for an uninteresting reason, basically because they are the wrong sort of equations—the graph will cross itself like figure δ.2a) or have a sharp cusp like figure δ.2b) rather than be smooth like the one in figure δ.1.

For example, Faltings’s theorem implied that the equation

where n is a positive integer, has only finitely many rational solutions as soon as n is at least 4. If we write

Figure δ.2 (a)

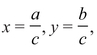
Figure δ.2 (b)

where a, b, and c are whole numbers, then equation (Cn) becomes the more familiar Fermat equation,

and Fermat’s Last Theorem, proved by Andrew Wiles, says that (when n is at least 3) this equation has no solutions when a, b, and c are all positive. At one point in Wiles’s proof of Fermat’s Last Theorem, he makes direct reference to a theorem of Langlands (and a version due to Jerrold Tunnell, whom we already encountered in chapter 9) on automorphic forms; at one point in Faltings’s proof, he also uses automorphic forms (not in the Langlands style); and both Wiles and Faltings were utterly dependent on Grothendieck’s algebraic geometry.

So equations of degree 1 or 2 are easy to understand; equations of degree 4 or more may be complicated, but at least one knows not to look for infinitely many solutions. The degree that continues to obsess number theorists is 3.

Equations (E1) and (E5) are very special examples because they have a direct connection with triangles, as do all equations of the form

where N is any positive whole number [so (E7) has equation y² = x³ − 49x, and so on]. It turns out that equation (EN) has infinitely many solutions in rational numbers precisely when there is a right triangle with area N, all three of whose sides—what we called a, b, and h in session 2—are rational numbers.

If there is such a right triangle, then N is called a congruent number, and so the problem of determining whether or not (EN) has infinitely many solutions is called the congruent number problem. There are many right triangles with area 1, but it can be checked that none of them has all three sides rational (for example if a = 1 and b = 2, then h = 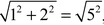, which we have already seen is irrational). Thus 1 is not a congruent number, and, therefore, equation (E1) has only finitely many rational solutions. On the other hand, (E5) has infinitely many rational solutions. The first interesting one is x = −4, y = 6. And you can check that the right triangle with sides a = 9/6, b = 40/6, h = 41/6 (you have seen these numbers before) has area

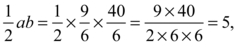
as promised.

I have already made the point that a problem in number theory is interesting when it is the subject of one or more stories. You are right to notice that there is no triangle visible in equation (EN) and that I have not explained why you might think of the N that indexes the equation as the area of anything. It takes a leap of the imagination to see the equation a² + b² = h² in the right triangle, but the leap was taken for us so many years ago that we no longer notice that we are leaping every time we write down the Pythagorean theorem. The story that relates equations (EN) to right triangles is not so well known but is also quite old; it goes back at least to Arab algebraists of the tenth century, and is fascinating in itself. It has been retold many times, most recently in the 1980s by Jerrold Tunnell in a particularly engaging way, one that revealed a close connection with the most contemporary concerns of number theorists. There are infinitely many ways to write equations for elliptic curves, and most (for example y² + y = x³ + x, which has the obvious solution x = y = 1) cannot be attached to such immediately appealing stories. But a web of stories has grown up in the last fifty years or so around the problem of determining whether or not a given elliptic curve has infinitely many points.

The starting point is the method of congruences. In the last session, we introduced the notion of approximate solutions relative to a prime number p, and we used congruences to count the numbers of approximate solutions S(p) to equations (E1) and (E5). One would need to perform a great many calculations (easy with a computer program) and test a great many cubic equations in two variables to appreciate the following theorem.

Theorem (Hasse) For any elliptic curve, and for any prime number p, the number S(p) as just defined is very close to p in the following sense: except for a finite set of exceptional primes p that depends on the elliptic curve in a simple way, the difference between S(p) and p is at most equal to .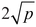

We have been alluding indirectly to Hasse’s theorem practically since the beginning of the book. It was the inspiration for Weil’s idea to count solutions to polynomial equations using topology, which in turn inspired Grothendieck’s new foundations for geometry, which was in turn the basis for Deligne’s solution—using a trick, in Grothendieck’s opinion—to the last of Weil’s conjectures. But Hasse’s theorem is quite remarkable on its own. For example, there are 25 possible pairs x, y for p = 5. Hasse’s theorem says that for most cubic equations in two variables, the number S(5) of approximate solutions modulo 5 is more than 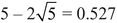and less than 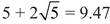Since S(5) is always a whole number, this means, in other words, that there is always at least one approximate solution modulo 5 [unless 5 is one of the exceptional primes, which is usually not the case but is the case for (E5)], and there are also always at least 16 pairs x, y that are not solutions. Similarly, the number S(7) is always at least 2 and at most 12 out of a possible 49 pairs. After calculating the numbers S(p) for a variety of equations, one can easily understand the statement of Hasse’s theorem, but it was the height of sophistication at the time and still requires a good deal of advanced mathematics to prove.

Hasse’s theorem provides a glimpse of order into the mysterious problem of determining whether or not a cubic equation in two variables has finitely or infinitely many rational solutions. If you are heuristically inclined, you might guess that if the equation has infinitely many rational solutions, then S(p) would have a tendency to be at the high end of the allowed range (i.e., closer to 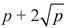than to 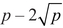). If you try to justify the heuristics, you will soon admit that this is quite a wild guess, but the really tricky part is to make sense of what it means for something like S(p) to “tend” in one way or another. It was the two British mathematicians Bryan Birch and Sir Peter Swinnerton-Dyer who gave a rigorous expression to this wild heuristic guess, providing a very precise notion of how the size of the expressions S(p) can be used to predict whether or not an elliptic curve has infinitely many solutions. This notion is defined in the framework of the prime number theorem mentioned in the first session; it can be considered a substitute for a formula for the number of solutions.

You will remember from chapter 2 that the Birch-Swinnerton-Dyer (BSD) conjecture² was the guiding problem for the first part of my career and that it has the distinction of being one of the seven Clay Millenium Prize Problems, like the Riemann hypothesis, whose solution carries a million dollar price tag. Jeremy Gray’s essay, “A History of Prizes in Mathematics,” written to accompany the Clay Mathematics Institute’s official presentation of the Millennium Problems, traces the tradition of awarding prizes for solving mathematical problems back to the sixteenth century. Not surprisingly, the earliest prize Gray records was given for solving a problem that has already come up during our dinner party. It was awarded in 1535 by Antonio Fior to Niccolò Tartaglia, for (re)discovering Scipione del Ferro’s formula for the three solutions to the cubic equation, and consisted in “thirty dinners to be enjoyed by [Tartaglia] and his friends.”

The BSD conjecture is an attempt to discern order in the apparently unpredictable nature of solutions to elliptic curves, following Hasse’s theorem, which places strict limits on the numbers of approximate solutions for varying p. The “tendency” (also known in the literature as “bias”) to which Birch and Swinnerton-Dyer drew attention is a rather subtle phenomenon. There are coarser ways to measure the difference between p and S(p). In the few examples given before, S(p) was always greater than p, but it is easy to find examples where S(p) is less than p; Hasse’s theorem shows only that there are no examples where S(p) is less than 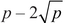. In fact, on the coarse measure it can be seen that it is equally likely that S(p) − p is positive or negative.

You will have noticed that for the curve (E1) we have calculated S(3) = 3 and S(7) = 7. This is not a coincidence. Remember that 3 and 7 are the first two prime numbers that cannot be written as sums of two squares. One can prove that for equation (EN) (any N), we have S(p) = p whenever p is a prime in the congruence class of 3 modulo 4—in other words, whenever p cannot be written as the sum of two squares. There is a reason for this: each of equations (EN) has an extra symmetry. Suppose (x, y) is a solution to equation (EN). If you multiply x by −1 and y by , then you get another solution, as you can verify if you like algebra:

Now you will recall that 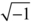, also written i, is an imaginary number, and so the new solution will be in imaginary numbers if the original solution consisted of rational numbers, but this should not obscure the main point, which is the presence of an extra symmetry. Although this is by no means obvious, it turns out that the additional symmetry of the equation imposes a predictable additional structure on the numbers S(p), a reason that permits calculation of some of the S(p) without any additional effort.

Most elliptic curves do not have extra symmetries. For those that do not (for example, the elliptic curve with equation y² + y = x³ + x), it was conjectured by Mikio Sato and John Tate that the only predictable feature of S(p) is that imposed by Hasse’s theorem. In other words, the difference between S(p) and p is at most 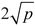, but within that range the difference is as random as possible. What it means to be as random as possible is again framed by the prime number theorem and cannot be explained in a few words. The histogram in figure δ.3 plots the difference p − S(p) for large collections of primes p.³

The Sato-Tate conjecture was proved by Laurent Clozel, Nick Shepherd-Barron, Richard Taylor, and me in a series of papers completed in 2005 and 2006, for a large class of elliptic curves (including the example y² + y = x³ + x and infinitely many others), and then for all elliptic curves in my joint paper with Tom Barnet-Lamb, David Geraghty, and Taylor. Number theorists are interested in detecting patterns.

Figure δ.3. Numerical confirmation of the Sato-Tate conjecture (William Stein).

A perceptible pattern demands explanation. This explanation typically takes the form of a story, expressed in the language of proof, that provides a convincing reason for the existence of the perceived pattern. Where no reason can be found, one expects there to be no pattern—or, rather, as random a pattern as possible. But randomness is also a pattern.

P. A.: I had been thinking of getting a copy of the author’s book for my future in-laws’ coffee table, but I’m finally convinced it would be pointless.

N. T.: Is it because of the formulas? Have they joined the latest exodus of 10,000 potential readers?

P. A.: Formulas are not the problem. On the contrary, it was thanks to a formula that Tartaglia and his friends enjoyed all those dinners. Abel, on the other hand, went hungry after he showed there was no formula and died at 26. Maybe he would have led a happier life if he had found a formula.

N. T.: A formula like Scipione del Ferro’s, like Ed Frenkel’s love formula, gives an immediate impression of control: not only do you know the problem has a solution, you can actually write it down. But mathematicians are equally happy to know there is no formula, provided an alternative structure is available. Once the work of Abel and Galois shifted attention to structural features of solutions, formulas were no longer the goal, and the ones that worked up to degree 4 were consigned to the realm of the routine and predictable. The same thing happened with polynomial equations in two variables: the degree 2 polynomials, like those we saw in chapter β, were central to Gauss’ systematic approach to number theory 200 years ago, but their formulas have long been understood. Now attention is focused on degree 3 polynomials in two variables, where the Birch-Swinnerton-Dyer conjecture offers a very different kind of formula.

P. A.: You are talking as if you agree with André Weil’s comment about achieving “knowledge and indifference at the same time.”

N. T.: I found the part about “furtive caresses” more eloquent.

P. A.: And about the “majestic beauty” that “can no longer excite us.”

N. T.: Jeremy Gray writes in his essay that “A good problem is one that defies existing methods … but whose solution promises a real advance in our knowledge.”⁴

P. A.: Gray could just as well have defined a good problem as one whose solution promises a real advance in our indifference. You are reminding me that the author has given my in-laws excellent reasons for not wanting to read his book, and formulas have nothing to do with it.

N. T.: The author did try to explain that the problem of understanding solutions to equations of degree 3 in two variables is the first really hard problem one encounters in number theory.

P. A.: I’m sure every problem looked hard until it was solved, at which point it didn’t look hard any more; instead, the solution became “routine and predictable.” That’s what I understand by “achieving knowledge and indifference at the same time.” My in-laws have every reason to assume solution of the Birch-Swinnerton-Dyer conjecture will lead inexorably to indifference, in exactly the same way.⁵

N. T.: It’s the first really hard problem those of us encounter who are living in the present, which is when the Clay Millennium Problems were chosen, and it stands to reason that if one can’t solve the first problem, one isn’t going to have much luck with the ones that follow.

P. A.: It’s the first of a series of doors you will need to unlock, and the series is endless, as the author himself wrote. For those of us who stand by and watch your indifference grow after you unlock them, all those doors look alike.

N. T.: Let me try an analogy. You don’t really care about Nora, do you?

P. A.: Of course I care about Nora! If I didn’t care about her, why would anyone in the audience care about her?

N. T.: And yet Maurice Maeterlinck, at the turn of the twentieth century, wrote of his “disgust” at the presence of living human performers on stage, which leads to “the abolition of the symbol, the annihilation of the dream and, consequently, the destruction of art.” He once wrote an essay calling for a “theater of androids” like the figures in a wax museum.6

P. A.: There are now theaters like that, in Disneyland, for example. And cartoon characters can also provoke catharsis. Performing artists, on the other hand, perform, which is different from what mechanical figures or cartoon characters do, and caring about the characters has something to do with that.

N. T.: Maybe the audience comes to watch you care about Nora. It’s no concern of theirs whether you will still be caring about her after they leave the theater or whether you will have moved on to some other problem.

P. A.: But the audience wants to care about Nora, wants to feel pity and fear, at least for the duration of the performance, not just to experience a vicarious catharsis through watching some performer’s caring. Are you saying that the author expects readers to pick up the book just in order to watch mathematicians care about the Birch-Swinnerton-Dyer conjecture?

N. T.: That’s not exactly how I would put it, but it’s not a small matter to be able to care about something like that. Some readers, if not your future in-laws, will have wondered how that’s possible.

P. A.: From the vantage point of page 320, it’s hard to disagree. But what makes you think anyone will read that far?