Glossary of Terms

A portfolio weighting strategy in which the asset classes within a portfolio are weighted equally. It has been argued that such a strategy performs better out of sample than optimized portfolios, but we argue to the contrary in Chapter 7. See also Mean‐variance analysis.

A measure of illiquidity that applies to asset classes that cannot be traded for a specified period of time by contractual agreement or because they are prohibitively expensive to trade within that time frame. See also Partial illiquidity.

A measure of risk concentration that is equal to the fraction of the total variance of a set of asset returns explained or “absorbed” by a fixed number of eigenvectors. See also Eigenvalues, Eigenvectors, and Principal Components Analysis.

The risk‐adjusted return of an asset or portfolio calculated as the asset's or portfolio's excess return net of the risk‐free return less beta times the market's excess return net of the risk‐free return. Alpha is more commonly construed as the difference between an actively managed portfolio's average return and the average return of a benchmark. See also Beta and Capital Asset Pricing Model.

The sum of a series of discrete returns divided by the number of discrete returns in the series. The arithmetic average return is used as the expected return in mean‐variance analysis instead of the geometric average return because, unlike the geometric average return, the arithmetic average return of a portfolio is equal to the weighted sum of the arithmetic averages of the asset classes within the portfolio. See also Geometric average return and Mean return.

The process of allocating a portfolio across a group of asset classes. Investors typically employ mean‐variance analysis to determine the optimal weights for a portfolio. See also 1/N, Asset class, and Tactical asset allocation.

See Policy portfolio.

A stable aggregation of investable units that is internally homogeneous and externally heterogeneous, which, when added to a portfolio, raises its expected utility without benefit of selection skill, and which can be accessed cost effectively in size. See also Asset allocation, Expected utility, Externally heterogeneous, and Internally homogeneous.

The association between values of a random variable and its prior values. First‐degree autocorrelation measures the association of successive observations. Second‐degree autocorrelation measures the association among every other observation. See also Cross‐correlation.

A regression model that relates values of random variables such as returns to their prior values. See also Autocorrelation.

In currency hedging, a put option that protects a portfolio's collective currency exposure. A basket option is less expensive than a portfolio of put options because diversification across currencies reduces the volatility of the basket. However, it provides less protection than a portfolio of options because it pays off only if the currencies collectively breach the chosen strike price. See also Put option.

A search algorithm designed to find transition probabilities of a hidden Markov model. The algorithm works both forward and backward to determine the probabilities of transitions from one regime to another. See also Hidden Markov model.

A method for combining views with empirical observations. It defines the “posterior” probability as the probability that a variable will take on a specified value given the fact that we observe a particular sample of data. The posterior probability is equal to our “prior” belief about the probability that the parameter will take on that value, multiplied by the likelihood of observing the data given that we hold that prior belief.

A procedure for mitigating the impact of estimation error when forming portfolios in which each estimate is blended with a prior view such as the cross‐sectional mean or the estimate associated with the minimum‐risk portfolio. See also Estimation error.

A measure of an asset's or portfolio's relative volatility with a reference portfolio, such as the market portfolio. It is estimated as the slope of a regression line relating an asset's or portfolio's excess return over the risk‐free return to a reference portfolio's excess return over the risk‐free return. Within the context of the Capital Asset Pricing Model, beta, when squared and multiplied by the market's variance, represents an asset's or portfolio's nondiversifiable risk. See also Alpha, Capital Asset Pricing Model, and Market portfolio.

An estimate of covariance that is a blend of covariances from different regimes such as a calm regime and a turbulent regime. It is designed to address an investor's expectation of the relative likelihood of a particular regime or the investor's attitude toward a particular regime. See also Financial turbulence.

A procedure by which new samples are generated from an original data set by randomly selecting observations with replacement from the original data. See also Monte Carlo simulation.

An option that grants its owner the right but not the obligation to purchase an underlying asset at a previously agreed upon price at or up to a specified future date (American) or only at a specified future date (European). See also Put option.

A theory of market equilibrium that partitions risk into two sources: that caused by changes in the market portfolio, which cannot be diversified away, and that caused by nonmarket factors, which can be diversified away. An asset's nondiversifiable risk is equal to its beta squared multiplied by the market portfolio's variance. The CAPM implies that investors should incur only nondiversiable risk because they are not compensated for bearing diversifiable risk. The CAPM was developed simultaneously and independently by John Lintner, Jan Mossin, William Sharpe, and Jack Treynor. See also Alpha, Beta, and Market portfolio.

A demand for cash from a portfolio to fund benefit payments, investment opportunities associated with capital committed to private equity and real estate funds, or consumption needs. See also Absolute illiquidity and Partial illiquidity.

In dimensions of expected return (vertical axis) and standard deviation (horizontal axis), a straight line emanating from the risk‐free rate on the vertical axis and progressing with an upward slope to a point of tangency on the efficient frontier and beyond. The segment of the capital market line between the risk‐free rate and the point of tangency represent combinations of the risk‐free asset (lending) and the tangent portfolio. The segment of the capital market line beyond the point of tangency represents combinations of the tangency portfolio and borrowing at the risk‐free rate. See also Efficient frontier and Tangency portfolio.

The principle that the distribution of the sum or average of independent random variables, which are not necessarily individually normally distributed, will approach a normal distribution as the number of variables increases. See also Normal distribution.

A certain outcome that conveys the same amount of expected utility as the utility associated with a risky gamble. See also Expected utility.

A distribution of the sum of the squares of a specified number of independent standard random normal variables. It is used to evaluate the significance of the difference between an empirically observed distribution and a theoretical distribution, for example. See also Jarque‐Bera test.

A description of investor preferences that assumes utility increases with wealth but at a diminishing rate, implying that investors derive a smaller increase in utility for a particular increase in wealth than the disutility they suffer from a decrease in wealth of the same amount. See also Expected utility, Kinked utility function, Log‐wealth utility function, Power utility function, and S‐shaped utility function.

In asset allocation, the notion of increasing a portfolio's expected return by allocating the portfolio to a fewer number of asset classes with higher expected returns, instead of using leverage to increase expected return. See also Asset allocation, Asset class, and Leverage.

A measure of risk aversion which holds that investors prefer to maintain the same absolute amount of their wealth in risky assets irrespective of changes to their wealth. See also Constant relative risk aversion, Log‐wealth utility function, and Power utility function.

A measure of risk aversion which holds that investors prefer to maintain the same proportion of their wealth in risky assets as their wealth grows. See also Constant absolute risk aversion, Log‐wealth utility function, and Power utility function.

In asset allocation, a maximum or minimum limit on the allocation to a particular asset class or group of asset classes. See also Asset allocation, Asset class, Mean‐variance‐tracking error optimization, and Wrong and alone.

In currency hedging, a put option that pays off only if the currencies within the portfolio breach a chosen strike price and, at the same time, either the foreign component of the portfolio or the total portfolio also breaches a chosen strike price. See also Put option.

A probability distribution in which there are an infinite number of observations covering all possible values along a continuous scale. See also Discrete probability distribution and Probability distribution.

The rate of return that, if compounded continuously or instantaneously, would generate the corresponding discrete return. It is equal to the natural logarithm of the quantity, 1 plus the discrete return. See also Discrete return, e, and Natural logarithm.

See Continuous return.

A measure of the association between two variables. It ranges in value from 1 to –1. If one variable's values are higher than its average when another variable's values are higher than its average, for example, the correlation will be positive, somewhere between 0 and 1. Alternatively, if one variable's values are lower than its average when another variable's values are higher than its average, then the correlation will be negative. See also Covariance.

A measure of the comovement of the returns of two assets that accounts for the magnitude of the moves. It is equal to the correlation between the two assets' returns times the first asset's standard deviation times the second asset's standard deviation. Combinations of assets that have low covariances are desirable because they offer greater diversification. See also Correlation, Standard deviation, and Variance.

A matrix used in portfolio optimization, sometimes called a variance‐covariance matrix, with an equal number of rows and columns, which contains the variances of a group of asset classes in the cells along the diagonal of the matrix and the covariances of the asset classes in the off‐diagonal cells. See also Covariance and Variance.

The association between the values of two random variables at various lags relative to each other. See also Autocorrelation.

In currency hedging, the practice of using a forward contract on one currency to hedge a portfolio's exposure to another currency. See also Overhedging.

A probability distribution that measures, for example, the probability that a variable is less than or equal to a specified value. For a discrete distribution, the cumulative probability is calculated by summing the relative frequencies up to and including the value of interest. See also Probability density function and Probability distribution.

The rate of return that is equal to the product of the quantities, 1 plus the discrete returns, minus 1, or, equivalently, an asset's ending value divided by its beginning value minus 1, assuming reinvestment of income and controlling for contributions and disbursements. See also Continuous return and Discrete return.

A contractual obligation between two parties to exchange a currency at a future date for a set price. The buyer of the forward contract agrees to pay the set price and take delivery of the currency on the agreed date, and is said to be long the forward contract. The seller of the forward contract agrees to deliver the currency at the set price on the agreed date, and is said to be short the forward contract. Usually these contracts are settled by a payment of cash rather than an exchange of the currencies.

The practice of searching for associations or patterns within a set of data using numerical search procedures rather than first hypothesizing an association or pattern and then testing for its presence.

See Policy portfolio.

With regard to a continuous probability distribution, the relative likelihood that a random variable takes on a given value. See also Probability distribution.

In optimization, the number of distinct units, such as asset classes, factors, or securities, to be optimized. See also Mean‐variance analysis.

A probability distribution that shows the percentage of observations falling within specified ranges, which collectively account for all of the observations. See also Continuous probability distribution.

The income produced by an asset during a specified period plus its change in price during that period, all divided by its price at the beginning of the period. Also called periodic return. See also Continuous return.

A decision‐making process that provides solutions to problems that involve multistage decisions in which the decisions made in prior periods affect the choices available in later periods. Dynamic programming is particularly suitable to portfolio rebalancing because whether or not we rebalance today influences what happens to our portfolio in the future. Dynamic programming was introduced by Richard Bellman in 1952, the same year that Markowitz published his landmark article on portfolio selection.

The base of the natural logarithm and the limit of the function (1 + 1/n)ⁿ as n goes to infinity after (1 + 1/n)ⁿ. To five decimal places, it equals 2.71828. When e is raised to the power of a continuous return, it is equal to 1 plus the discrete return. See also Continuous return, Discrete return, and Natural logarithm.

A continuum of portfolios plotted in dimensions of expected return and standard deviation that offer the highest expected return for a given level of risk or the lowest risk for a given expected return. See also Efficient surface, E‐V maxim, Expected return, Mean‐variance analysis, and Standard deviation.

A portfolio that resides on the efficient frontier. It has the highest expected return for its given level of risk. See also Efficient frontier, E‐V maxim, and Mean‐variance analysis.

A representation of portfolios plotted in dimensions of expected return, standard deviation, and tracking error. It is bounded on the upper left by the traditional mean‐variance efficient frontier, which comprises efficient portfolios in dimensions of expected return and standard deviation. The right boundary of the efficient surface is the mean‐tracking error efficient frontier comprising portfolios that offer the highest expected return for varying levels of tracking error. The lower boundary of the efficient surface comprises combinations of the minimum‐risk asset and the benchmark portfolio. See also Efficient frontier and Tracking error.

In Principal Components Analysis, the amount of variance associated with a given eigenvector. See also Eigenvector and Principal Components Analysis.

In Principal Components Analysis, a linear combination of assets, comprising both long and short positions, that explains a fraction of the covariation in the assets' returns. See also Eigenvalue and Principal Components Analysis.

In two dimensions (two asset classes), a distribution whose observations are evenly distributed along the boundaries of ellipses that are centered on the mean observation of the scatter plot. It therefore has no skewness, but it may have nonnormal kurtosis. This concept extends to distributions with more than two dimensions, though it cannot be visualized beyond three. Mean‐variance optimization assumes either that returns are elliptically distributed or that investor preferences are well approximated by mean and variance. See also Kurtosis, Mean‐variance analysis, Normal distribution, Skewness, and Symmetric distribution.

A measure of the likelihood that a portfolio will incur a particular percentage of loss as of the end of a specified investment horizon. See also End‐of‐horizon value at risk, Within‐horizon probability of loss, and Within‐horizon value at risk.

At a given probability the maximum loss or minimum gain that could occur at the end of a specified investment horizon. See also End‐of‐horizon probability of loss, Within‐horizon probability of loss, and Within‐horizon value at risk.

The asset class return that is expected to prevail when the asset classes within a market are fairly priced. It is equal to the risk‐free return plus beta times the excess return of the market portfolio. It is often used as the default expected return in mean‐variance analysis. See also Capital Asset Pricing Model, Expected return, and Mean‐variance analysis.

The notion that mean‐variance analysis, by construction, favors assets for which return is overestimated and risk is underestimated. This bias leads to two problems. First, the expected return of the optimized portfolio is overstated, while its risk is understated. Second, assets for which return is underestimated and risk is overestimated are underweighted in the optimized portfolio, while assets with opposite errors are overweighted. We argue in Chapter 5 that error maximization is not as problematic to asset allocation as some would have us believe. However, we discuss procedures for addressing estimation error in Chapter 13. See also Estimation error and Mean‐variance analysis.

The difference between estimated values for expected returns, standard deviations, and correlations and the realizations of these values out of sample or, in the case of interval error, within the same sample but at different intervals. Estimation error can be partitioned into independent‐sample error, interval error, mapping error, and small‐sample error. See also Error maximization, Independent‐sample error, Interval error, Mapping error, Mean‐variance analysis, and Small‐sample error.

The ordinary, straight‐line distance between two points. In defining a turbulent risk regime, it is contrasted to the Mahalanobis distance, which is a measure of statistical unusualness. Observations with the same Mahalanobis distance may have different Euclidean distances.

The proposition by Harry Markowitz that investors choose portfolios that offer the highest expected return for a given level of variance. See also Efficient frontier, Efficient portfolio, and Mean‐variance analysis.

The notion that for a given finite number of bets there is a partial sum of them that is acceptable even though the bets individually are unacceptable. See also Law of large numbers and Time diversification.

That part of return that exceeds the risk‐free return. See also Risk‐free return.

Modified unit trusts or mutual fund–type investment funds characterized by a dual trading process. Fund shares are created or redeemed through the deposit of securities to, or the delivery of securities from, the fund's portfolio. Secondary trading takes place on a stock exchange. The dual trading process permits the fund shares to trade very close to net asset value at all times.

The average or probability weighted value of all possible returns. The process of compounding causes the expected return to exceed the median return. Thus, there is less than a 50 percent chance of exceeding the expected return. See also Arithmetic average return, Geometric average return, Lognormal distribution, and Skewness.

The average or probability weighted utility or measure of satisfaction associated with all possible wealth levels. See also Expected utility maximization and Utility function.

The process of identifying the asset class weights within a portfolio that yield the highest possible expected utility. If investor utility is a quadratic function or returns are elliptically distributed, expected utility maximization is equivalent to mean‐variance analysis. See also Elliptical distribution, Full‐scale optimization, Mean‐variance analysis, and Quadratic function.

A function that converts a continuous return to a discrete return by raising e to the power of the continuous return and subtracting 1. For example, 1.10 is the exponential of e raised to the power 0.0953. Thus, 10 percent is the discrete counterpart of the continuous return, 9.53 percent. See also Continuous return, Discrete return, e, and Natural logarithm.

A measure of the dissimilarity of an asset class from other asset classes or combinations of other asset classes within a portfolio. This attribute is a necessary but not sufficient condition for a group of assets to be considered an asset class. See also Asset class and Internally homogeneous.

An economic variable such as inflation or a group of securities with a particular attribute such as capitalization, or an eigenvector derived through Principal Components Analysis, that is believed to reflect a particular risk. See also Eigenvector, Factor exposure, and Factor‐mimicking portfolio.

The comovement of the returns of a portfolio or asset class with changes in the value of a factor, usually measured by regressing the portfolio or asset class returns on changes in the factor value. See also Factor and Factor‐mimicking portfolio.

A group of securities or asset classes that are selected and weighted to minimize tracking error between its returns and movements of a factor value. See also factor and factor‐mimicking portfolio.

The practice of estimating the value of an asset for which market prices are unavailable. These valuations are usually positively autocorrelated because current valuations are usually anchored to prior valuations. The observed standard deviation of a series of returns estimated from fair values, therefore, is likely to understate the true risk of these assets.

A probability distribution in which there are more extreme observations than would be expected under a normal distribution. Fat‐tailed distributions are called leptokurtic. See also Kurtosis, Leptokurtic distribution, Normal distribution, and Platykurtic distribution.

A measure of the statistical unusualness of a cross section of returns during a particular period, taking into account extreme price moves, the convergence of uncorrelated assets, and the decoupling of correlated assets. It is measured as the Mahalanobis distance.

A probability that measures the likelihood of a value penetrating a threshold at any time during a specified time horizon. See also Within‐horizon probability of loss and Within‐horizon value at risk.

Given a particular utility function and sample of returns, an optimization technique that maximizes expected utility by repeatedly testing different asset mixes to determine the utility‐maximizing portfolio. Full‐scale optimization may be preferable to mean‐variance analysis if the return sample is not elliptically distributed and the investor's utility function is not well approximated by mean and variance. See also Elliptical distribution, Genetic search, Mean‐variance analysis, and Skewness.

An economic variable, such as inflation or industrial production, that is thought to explain differences in the returns and risk of assets. See also Eigenvector and Security attribute.

A numerical search procedure inspired by evolutionary biology and used to implement full‐scale optimization. This method starts with an “initial population” of weight vectors. Next, it introduces random mutations and combinations of existing vectors to form the next “generation,” and proceeds by “mating” the most promising (highest utility) offspring until a dominant solution is found. See also Full‐scale optimization.

The average annual return that, when compounded forward, converts an initial value to an ending value. It is equal to the product of the quantities, 1 plus the annual discrete returns, raised to the power, 1 over the number of discrete returns, less 1. When based on historical returns, an initial value compounded forward at the geometric average return yields the median value. The natural logarithm of the quantity, 1 plus the geometric average return, equals the continuous return. Also called annualized return or constant rate of return. See also Continuous return, Discrete return, and Expected return.

A model of the distribution of a variable, such as a financial indicator or asset return, that assumes the observed values come from multiple distributions that switch according to a hidden regime variable. Each regime has a degree of persistence from one period to the next. For example, if we are in regime A this month, regime A might be more likely to prevail next month, too. But there is also a chance that the regime will shift abruptly from A to B. The term “Markov” refers to the assumption that the underlying regime variable follows a Markov process in that next period's regime probability depends only on the regime we are in today. See also Baum‐Welch algorithm.

A central moment of a distribution beyond the first and second central moments that measures nonnormality. A central moment is the average of all deviations from the mean raised to a specified power. The third central moment measures asymmetry and is called skewness, and the fourth central moment measures peakedness and is called kurtosis. See also Kurtosis, Moment, Normal distribution, and Skewness.

In matrix algebra, a square matrix with 1s in the diagonal elements and 0s in the off‐diagonal elements. A matrix multiplied by its inverse will yield the identity matrix. See also Inverse matrix, Invertible matrix, and Matrix algebra.

The inability to trade an asset within a specified period of time without significantly and adversely affecting its price. See also Absolute illiquidity, Illiquidity, and Partial illiquidity.

A condition in which successive draws from a population are independent of one another and generated from the same underlying distribution, implying that the parameters of an IID distribution are constant across all draws. See also Random variable.

The differences in the average returns, standard deviations, and correlations of two nonoverlapping samples. See also Estimation error, Interval error, Mapping error, and Small‐sample error.

See Continuous return.

A function that gives the area under the curve of the graph of another function. It is used to estimate a probability, given a continuous distribution of returns. See also Probability distribution.

A measure of the similarity of the components within an asset class. This attribute is a necessary but not sufficient condition for a group of assets to be considered an asset class. See also Asset class and Externally heterogeneous.

The differences in the standard deviations and correlations estimated from longer‐interval returns and their values implied by estimating them from shorter‐interval returns and converting them to longer‐interval estimates. Standard deviations estimated from shorter‐interval returns are typically converted to standard deviations of longer‐interval returns by multiplying them by the square root of the number of shorter intervals within the longer interval, but this rule will give an incorrect answer if the returns have nonzero autocorrelations. Correlations are typically assumed to be invariant to the return interval used to calculate them, but this invariance will not hold if either of the return series has nonzero autocorrelations or if they have nonzero lagged cross‐correlations. See also Autocorrelation, Cross‐correlation, Estimation error, Independent‐sample error, Interval error, and Mapping error.

A continuous probability distribution that permits only positive values and is suitable to represent the distribution that contains an unknown variance. It can also be represented as a scaled inverse chi‐squared distribution.

In matrix algebra, a matrix that is analogous to a reciprocal in simple algebra. A matrix multiplied by its inverse yields an identity matrix. An identity matrix includes 1s along its diagonal and 0s in all of the other elements. It is analogous to the number 1 in simple algebra, in that a matrix multiplied by an identity matrix yields itself. Multiplying a vector or matrix by the inverse of another matrix is analogous to multiplying a number by the reciprocal of another number; hence, the analogy with division. See also Identity matrix, Invertible matrix, and Matrix algebra.

In matrix algebra, a square matrix for which an inverse exists such that the inverse matrix times the original matrix times a vector gives back the same vector. In portfolio optimization, the covariance matrix is inverted to solve for the vector of optimal asset class weights. See also Covariance matrix, Identity matrix, Inverse matrix, and Matrix algebra.

In dimensions of standard deviation and tracking error, a curve comprising portfolios that all have the same expected return but different combinations of standard deviation and tracking error. See also Mean‐variance‐tracking error optimization.

A test used to determine whether departures from normality are significant, given the number of observations in the sample from which they are estimated. The test statistic is a function of skewness squared and excess kurtosis squared. See also Chi‐squared distribution.

A utility function that is kinked because, for a small change in wealth at a particular threshold, utility changes abruptly rather than smoothly. See also Constant relative risk aversion, Log‐wealth utility function, S‐shaped utility function, and Utility function.

A measure of a distribution's peakedness. It is computed by raising the deviations from the mean to the fourth power and taking the average of these values. It is usually represented as the ratio of this value to the standard deviation raised to the fourth power. A normal distribution has a kurtosis value equal to 3. See also Higher moment, Normal distribution, and Skewness.

In optimization, a variable introduced to facilitate a solution when there are constraints. It does not always lend itself to economic interpretation.

The principle that, as a sample becomes large, measures of its central tendency and dispersion become more accurate. See also Central limit theorem, Eventual acceptance property, and Time diversification.

A distribution with a narrow peak and wide tails. Compared to a normal distribution, a larger proportion of the returns are located near the extremes rather than the mean of the distribution. It is also called a fat‐tailed distribution. See also Higher moment, Kurtosis, Normal distribution, and Platykurtic distribution.

In asset allocation, the notion of increasing a portfolio's expected return by borrowing and using the proceeds to increase investment in the tangency portfolio, as opposed to concentrating the portfolio in higher‐expected‐return asset classes in order to raise its expected return. See also Asset allocation, Asset class, and Concentration.

In currency hedging, a strategy that uses currency forward or futures contracts to offset the embedded currency exposure of a portfolio. This hedging strategy is called a linear hedging strategy because the portfolio's return is a linear function of the performance of the currencies to which the portfolio is exposed. See also Nonlinear hedging strategy.

The power to which a base must be raised to yield a particular number. For example, the logarithm of 100 to the base 10 equals 2, because 10² equals 100. Prior to the advent of calculators, logarithms were convenient because, with an implement called a slide rule, one could multiply numbers by adding their logarithms. See also e and Natural logarithm.

See Continuous return.

A distribution of returns that is positively skewed as a result of compounding. Compared to a normal distribution, which is symmetric, a lognormal distribution has a longer right tail than left tail and an average value that exceeds the median value. A lognormal distribution of discrete returns corresponds to a normal distribution of their continuous counterparts. See also Normal distribution and Skewness.

A concave utility function that assumes utility is equal to the logarithm of wealth. It is one of a family of utility functions that assume investors have constant relative risk aversion. For investors with a log‐wealth utility function, as wealth increases, utility also increases but at a diminishing rate. See also Constant relative risk aversion, Natural logarithm, and Utility function.

The notion that aggregations of securities such as asset classes are priced efficiently. Paul A. Samuelson famously argued that investment markets are microefficient and macroinefficient. See also Microefficiency and Samuelson dictum.

A multivariate measure of the difference between one group and another. It was originally conceived of by the statistician Prasanta Mahalanobis to distinguish between the skulls of people belonging to different castes in India. It is applied to asset returns to distinguish turbulent periods from stable periods. See also Financial turbulence.

In factor replication, the out‐of‐sample differences between the returns, standard deviations, and correlations of factor values and the returns, standard deviations, and correlations of the portfolio of securities designed to mimic their behavior. See also Estimation error, Factor‐mimicking portfolio, Independent‐sample error, Interval error, and Small‐sample error.

The change in expected utility given small changes in the weights of asset classes within a portfolio. It is computed as the derivative of expected utility with respect to an asset class weight. See also Expected utility maximization.

In portfolio theory, the portfolio of all tradeable securities held according to their relative capitalization. According to the Capital Asset Pricing Model, it is the tangency portfolio that joins the capital market line with the efficient frontier. In practice, it is usually approximated by a broad index of stocks and bonds. See also Capital Asset Pricing Model, Capital market line, Efficient frontier, and Tangency portfolio.

In portfolio rebalancing, an approximation of expected future costs resulting from rebalancing trades and suboptimal weights. It equals squared differences between the current portfolio weights and the optimal portfolio weights times a constant that is calibrated through simulation.

Algebraic operations performed on matrices to solve systems of linear equations. See also Identity matrix, Inverse matrix, Invertible matrix, Matrix transpose, and Positive‐semidefinite.

In matrix algebra, for a given matrix, a new matrix whose rows are the columns of the original matrix. See also Matrix algebra.

In asset allocation, a numerical procedure that gives the statistically most likely covariances of asset classes with short return histories compared to other asset classes under consideration. It is based on the returns that prevailed for the periods that are common to all asset classes, together with the returns of the asset classes with longer histories. See also Covariance.

The tendency of an above average return to be followed by another above average return and a below average return to be followed by another below average return, resulting in a higher incidence of trends than would be expected from a random process. See also Mean reversion and Random variable.

The arithmetic average return. See also Arithmetic average return.

The tendency of an above average return to be followed by a below average return and a below average return to be followed by an above average return, resulting in a higher incidence of reversals than would be expected from a random process. See also Mean aversion and Random variable.

A continuum of portfolios plotted in dimensions of expected return and tracking error that offers the highest expected return for a given level of tracking error or the lowest tracking error for a given expected return. See also Efficient frontier, Efficient surface, E‐V maxim, Expected return, Mean‐variance analysis, and Standard deviation.

An asset allocation process that identifies combinations of asset classes that offer the highest expected return for a given level of risk. See also Efficient frontier, E–V maxim, Expected return, Standard deviation, and Variance.

See Efficient frontier.

See Mean‐variance analysis.

An asset allocation process that identifies portfolios that offer the highest expected return for a given combination of standard deviation and tracking error, or the lowest standard deviation for a given combination of expected return and tracking error, or the lowest tracking error for a given combination of expected return and standard deviation. It is suitable for investors who care about both absolute performance and relative performance. See also Efficient surface and Mean‐variance analysis.

The notion that individual securities are priced efficiently. Paul A. Samuelson famously argued that investment markets are microefficient and macroinefficient. See also Macroefficiency and Samuelson dictum.

A currency hedge ratio equal to 50 percent of a portfolio's currency exposure. It is argued that this hedge ratio minimizes regret should a strategy to hedge fully or not to hedge at all deliver the best performance. See also Minimum‐variance hedge ratio and Universal hedge ratio.

The currency hedge ratio that is designed to minimize a portfolio's variance by explicitly accounting for the covariances among the currency forward contracts and between the currency forward contracts and the portfolio. See also Minimum‐regret hedge ratio and Universal hedge ratio.

A measure of the shape of a distribution. It is the average of all observations (in the case of a raw moment) or all deviations from the mean (in the case of a central moment) raised to a specified power. The first raw moment is the mean. The second central moment is variance. The third and fourth central moments, after normalizing, are skewness and kurtosis, respectively. See also Higher moment, Kurtosis, Normal distribution, Probability distribution, Skewness, and Variance.

A process used to simulate the performance of an investment strategy by randomly selecting returns from an underlying theoretical distribution such as a normal or lognormal distribution and subjecting the investment strategy to these randomly selected returns. See also Bootstrap simulation, Lognormal distribution, Normal distribution, and Random variable.

The joint probability distribution of two or more random variables such as asset class returns. See also Probability distribution.

The power to which the value 2.71828 (e) must be raised to yield a particular number. Natural logarithms have a special property. The natural logarithm of the quantity, 1 plus a discrete return, equals the continuous return. For example, the natural logarithm of 1.10 equals 9.53 percent. If one invests $1.00 at a continuously compounded annual rate of 9.53 percent for one year, it would grow to $1.10 by the end of the year. See also Continuous return, Discrete return, e, and Natural logarithm.

The random variability around an expected value such as expected return.

In currency hedging, a strategy that uses put options to protect a portfolio from the devaluation of currencies to which the portfolio is exposed. This hedging strategy is called a nonlinear hedging strategy because the portfolio's return is a nonlinear function of the performance of the currencies to which the portfolio is exposed. See also Linear hedging strategy.

A procedure for statistical inference that does not depend on the use of a stylized function with parameters to describe the distribution of observations.

A continuous probability distribution that often arises from the summation of a large number of random variables. It has the convenient property that its mean, median, and mode are all equal. Also, approximately 68 percent of its area falls within a range of the mean plus and minus one standard deviation, and approximately 95 percent of its area falls within a range of the mean plus and minus two standard deviations. See also Central limit theorem and Lognormal distribution.

Within the context of asset allocation, behavior that describes what an investor should do rather than what an investor actually does. See also Positive.

An iterative search process that is used to solve problems that cannot be solved analytically, which is to say, cannot be solved by using a formula.

A portfolio that maximizes an investor's expected utility, or, more prosaically, a portfolio that best balances an investor's desire to grow wealth with the investor's aversion to loss.

In currency hedging, the practice of selling currency forward contracts in amounts that exceed the portfolio's exposure to the currencies either individually or collectively. See also Cross‐hedging.

An investment or activity that does not require capital, such as a forward contract or a shadow allocation. See also Shadow asset and Shadow liability.

A measure of illiquidity that applies to asset classes that are tradeable without prohibitive delay or expense. See also Absolute illiquidity.

See Discrete return.

A distribution with thin tails and a wider, flatter center. Relative to a normal distribution, a greater fraction of its returns are clustered near the center of the distribution, and a smaller fraction lie in the extremes. See also Higher moment, Kurtosis, Leptokurtic distribution, and Normal distribution.

In asset allocation, activities that are intended to preserve the expected utility of a portfolio, such as portfolio rebalancing. See also Playing offense.

In asset allocation, activities that are intended to increase the expected utility of a portfolio beyond what would be expected by holding the composition of the portfolio constant, such as tactical asset allocation. See also Playing defense.

In the absence of views about the relative valuation of asset classes, the default portfolio an investor would hold. It is designed to balance an investor's desire to grow wealth with the investor's aversion to loss, and typically serves as the benchmark against which tactical asset allocation decisions are evaluated. See also Asset allocation, Asset class, Mean‐variance analysis, Security selection, and Tactical asset allocation.

The science that describes how investors form efficient portfolios and choose the optimal portfolio. Portfolio theory was introduced in 1952 with the publication of Portfolio Selection by Harry Markowitz. See also Efficient frontier, Efficient portfolio, E‐V maxim, Expected utility maximization, and Mean‐variance analysis.

In asset allocation, behavior that describes what an investor actually does rather than what an investor should do. See also Normative.

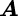A necessary and sufficient condition to preclude a matrix, images

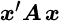, from generating a negative number from the quadratic form images

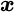for any possible vector images

. In mean‐variance analysis, it ensures the absence of negative variances. It is a necessary condition because, given the correlation between asset classes A and B, and between A and C, the correlation between B and C is restricted to a particular range of values. See also Mean‐variance analysis.

A utility function in which utility is equal to wealth raised to a power less than 1. Investors whose preferences are defined by a power utility function have constant relative risk aversion. See also Constant relative risk aversion, Expected utility, Log‐wealth utility function, and Utility function.

An approach to valuation in which the value of an asset is invariant to investors' particular preferences with respect to risk. Instead, value is determined by the absence of arbitrage.

See Eigenvector.

A statistical process that transforms a set of correlated variables into a new and comprehensive set of uncorrelated variables called eigenvectors or principal components. This transformation can be performed on a covariance matrix or a correlation matrix.

A function that defines the probability distribution of a random variable. By integrating this function between two points, we identify the probability that the random variable will take on a value within the specified interval. See also Probability distribution and Random variable.

A description of the linkage between each potential outcome of a random variable, such as an asset class return, and its probability of occurrence. See also Normal distribution.

See End‐of‐horizon probability of loss.

An option that grants its owner the right but not the obligation to sell an underlying asset at a previously agreed upon price at or up to a specified future date (American) or only at a specified future date (European). See also Call option.

A function that forms a parabola. Mean‐variance analysis, strictly speaking, assumes that investors have a utility function that is quadratic, which implies that utility rises at a diminishing rate with increases in wealth, but eventually peaks and then falls with further increases in wealth. It has been shown, however, that within a wide range of returns, mean and variance can be used to approximate other concave utility functions in which utility always rises with increases in wealth. See also Expected utility, Mean‐variance analysis, and Utility function.

See Markowitz–van Dijk heuristic.

A variable that takes on a value influenced by chance, such as the toss of a coin or next year's return on the stock market. See also Random walk.

A stochastic process in which future values of a random variable are unrelated to its current value. Variables that are believed to follow a random walk are said to be independent and identically distributed. See also Independent and identically distributed and Random variable.

A statistical process for measuring the relationships between a dependent variable and one or more independent variables. See also Alpha and Beta.

A description of the linkage between each potential return and its probability of occurrence. See also Normal distribution and Probability distribution.

Technically, a preference for a certain prospect over an uncertain prospect of equal value. More generally, risk aversion equals an investor's dislike for uncertainty. See also Risk aversion coefficient.

In mean‐variance analysis, a coefficient that multiplies portfolio risk to trade off the utility an investor receives from increases in expected return with the utility an investor loses from increases in portfolio variance. See also Expected utility, Expected utility maximization, Mean‐variance analysis, and Risk aversion.

A period in which the return distribution of a set of asset classes differs significantly from the distribution of the entire sample. For example, it is common to partition return samples into calm risk regimes when returns, standard deviations, and correlations are similar to their historical averages, and turbulent regimes when returns, standard deviations, and correlations depart substantially from their historical averages. The Mahalanobis distance is often used to separate calm risk regimes from turbulent risk regimes. See also Financial turbulence and Mahalanobis distance.

The return available from an asset class that is assumed to be risk free, such as Treasury bills. Because Treasury bills do have some variability as well as reinvestment risk, they are not entirely risk free. Over longer investment horizons, and taking inflation into account, TIPS are thought to be the least risky asset class. See also Capital Asset Pricing Model.

The exchange of asset classes that have the same cash flows.

An optimization procedure that considers a wide set of expected returns and risk and selects the portfolio that suffers the least in the most adverse scenario. This approach is sometimes called “minimax” optimization; it aims to minimize the maximum loss.

A summary of the degree of error present in a data sample. Errors are typically defined as differences between predictions and realizations. Squaring the errors ensures that they are all positive, taking their average (or mean) summarizes the extent of the errors, and taking the square root converts the result back to units of the original errors, as opposed to their squared values. If errors are defined relative to the mean of a given data set, the root‐mean‐squared error equals the standard deviation. We use root‐mean‐squared errors to quantify estimation error in Chapter 13.

A statistic, such as mean or standard deviation, that is estimated from a finite sample of returns, and therefore is vulnerable to estimation error. See also Estimation error.

The notion, proposed by Paul A. Samuelson, that investment markets are microefficient and macroinefficient. Samuelson argued that if an individual security is a mispriced, a smart investor will notice and trade to exploit the mispricing, and by doing so will correct the mispricing. However, if an aggregation of securities such as an asset class is mispriced and a smart investor trades to exploit the asset class mispricing, the investor will not have the scale to revalue the entire asset class. It is typically revalued when an exogenous shock jolts a large number of investors to act in concert. Hence, microinefficiencies are fleeting and thus difficult to exploit, whereas macroinefficiencies tend to persist, thus allowing investors time to exploit them. See also Macroefficiency and Microefficiency.

A feature such as capitalization or price/earnings multiple that distinguishes securities from one another. Securities with particular attributes are believed to carry risk premiums.

The activity of choosing individual securities within an asset class based on views about their relative valuation or other attributes that are believed to affect their performance, for the purpose of improving a portfolio's performance. See also Tactical asset allocation.

The standard deviation calculated using only the subsample of returns that fall below the full‐sample mean. See also Standard deviation.

The principle, put forth by James Tobin, that the investment process can be separated into two distinct steps: (1) the choice of a unique optimal portfolio along the efficient frontier, and (2) the decision to combine this portfolio with a risk‐free investment. See also Capital Asset Pricing Model, Capital market line, and Efficient frontier.

See Shadow asset and Shadow liability.

An implicit allocation to an activity, defined in units of expected return and risk, that does not require capital and is expected to raise the expected utility of a portfolio, such as internally implemented tactical asset allocation. It is attached to the liquid asset classes within a portfolio that enable the activity. See also Shadow liability.

A penalty, defined in units of expected return and risk, that is attached to illiquid asset classes within a portfolio that prevent an investor from fully preserving the expected utility of a portfolio. For example, a shadow liability would be attached to illiquid asset classes that prevent an investor from rebalancing a portfolio to its optimal weights after price changes force the portfolio away from its optimal weights. See also Shadow asset.

An asset, asset class, or portfolio's expected return in excess of the risk‐free return, all divided by its standard deviation. It is used to compare mutually independent investment alternatives. See also Beta, Capital Asset Pricing Model, and Standard deviation.

The third central moment of a distribution. It measures the asymmetry of a distribution. A positively skewed distribution has a long right tail, and its mean exceeds its median, which in turn exceeds its mode. Both the mean and the median are located to the right of the peak, which represents the mode. Although there are more returns below the mean, they are of smaller magnitude than the fewer returns above the mean. The exact opposite properties hold for a negatively skewed distribution. Skewness is measured as the average of the cubed deviations from the mean. However, it is usually represented as the ratio of this value to standard deviation cubed. A normal distribution has skewness equal to 0. See also Higher moment, Kurtosis, Lognormal distribution, and Normal distribution.

The differences between the average returns, standard deviations, and correlations of a small subsample selected from within a large sample and the average returns, standard deviations, and correlations of the large sample. See also Estimation error, Independent‐sample error, Interval error, and Mapping error.

An asset's or portfolio's expected return in excess of the risk‐free return, all divided by its semi–standard deviation. See also Semi–standard deviation and Sharpe ratio.

A utility function that assumes investors are risk seeking when they face losses and risk averse when they face gains. See also Kinked utility function, Log‐wealth utility function, and Power utility function.

An asset allocation process that relies on a sample of returns that has been adjusted to account for the effect of estimation error on the shape of the return distribution. It treats the relative stability of covariances as a distinct component of risk. See also Estimation error, Independent‐sample error, Interval error, and Small‐sample error.

A distribution of returns that is reshaped by estimation error and accounts for the relative stability of covariances. See also Estimation error and Stability‐adjusted optimization.

A measure of dispersion that is commonly used to measure an asset's riskiness. It is equal to the square root of the average of the squared deviations from the mean, and it is the square root of variance. Approximately 68 percent of the observations under a normal distribution fall within the mean plus and minus one standard deviation. See also Normal distribution and Variance.

The number of standard deviation units a particular value is away from the mean under a normal distribution. It is equal to the difference between the value of interest and the mean, divided by the standard deviation. A normal distribution converts a standardized variable into the corresponding area under a normal distribution by rescaling the distribution to have a mean of 0 and a standard deviation of 1. Also called normal deviate. See also Normal distribution.

See Eigenvector.

A probability distribution that has no skewness. Unlike a normal distribution, it may have nonnormal kurtosis. And, unlike an elliptical distribution, it allows for return pairs in a two‐dimensional scatter plot to be unevenly distributed along the boundaries of ellipses that are centered on the mean observation of the scatter plot as long as they are distributed symmetrically. A symmetric distribution that is nonelliptical would apply to a return sample that comprises subsamples with substantially different correlations. See also Elliptical distribution, Kurtosis, Normal distribution, and Skewness.

The activity of shifting a portfolio's asset class weights away from the policy portfolio based on views about the relative valuation of asset classes or changes in their risk, for the purpose of improving a portfolio's performance. See also Asset allocation, Asset class, and Security selection.

The portfolio located at the point of tangency of the capital market line with the efficient frontier. See also Capital market line, Efficient frontier, and Separation theorem.

A polynomial function in which successive terms of x raised to a larger power are added to continually refine the approximation of any chosen function at a particular input value, based on the derivatives of that function at that value. This method was used by Levy and Markowitz to approximate power utility functions with mean and variance. See also Power utility function.

The notion that above average returns tend to offset below average returns over long time horizons. It does not follow, however, that time reduces risk. Although the likelihood of a loss decreases with time for investments with positive expected returns, the potential magnitude of a loss increases with time. See also Law of large numbers.

See Tactical asset allocation.

A measure of dispersion that is commonly used to measure an asset class's relative risk. It is equal to the square root of the average of an asset class's or portfolio's squared deviations from a benchmark's returns. See also Standard deviation.

An investor's dislike for the uncertainty of a portfolio's returns relative to a benchmark's returns. See also Risk aversion.

A single hedge ratio for all investors, proposed by Fischer Black, that applies to a portfolio's exposure to all currencies and is optimal if all investors have the same aversion to risk, the same portfolio composition, and the same wealth. See also Minimum‐regret hedge ratio and Minimum‐variance hedge ratio.

The relationship between varying levels of wealth and the happiness or satisfaction imparted by the different wealth levels. A commonly invoked utility function for financial analysis is the log‐wealth utility function, which implies that utility increases at a decreasing rate as wealth increases. See also Constant relative risk aversion, Kinked utility function, Log‐wealth utility function, Power utility function, and S‐shaped utility function.

The axioms and principles that describe how investors relate wealth and changes in wealth to their perception of well‐being. See also Expected utility, Expected utility maximization, and Utility function.

See End‐of‐horizon value at risk.

A measure of dispersion used to characterize an asset's riskiness. It is equal to the average of the squared deviations from the mean, and its square root is the standard deviation. See also Standard deviation.

An array of variables such as returns.

A measure of the likelihood that a portfolio will incur a particular percentage of loss within a specified investment horizon, assuming the portfolio is monitored continuously throughout the horizon. It is estimated as a first passage time probability. See also End‐of‐horizon probability of loss, End‐of‐horizon value at risk, First passage time probability, and Within‐horizon value at risk.

At a given probability, the maximum loss or minimum gain a portfolio could experience at any time throughout a specified investment horizon, assuming the portfolio is monitored continuously throughout the horizon. It is estimated numerically using a first passage time probability. See also End‐of‐horizon probability of loss, End‐of‐horizon value at risk, First passage time probability, and Within‐horizon probability of loss.

A situation in which an investor produces poor absolute performance and underperforms the benchmark at the same time. We argue that aversion to this dual failure compels investors to constrain their portfolios from deviating too far from the perceived norm.