2
The Anonymous Codebreaker

The Vigenère cipher,
why cryptographers seldom get
credit for their breakthroughs
and a tale of buried treasure

For centuries, the simple monoalphabetic substitution cipher had been sufficient to ensure secrecy. The subsequent development of frequency analysis, first in the Arab world and then in Europe, destroyed its security. The execution of Mary Queen of Scots was a dramatic illustration of the weaknesses of monoalphabetic substitution, and in the battle between cryptographers and cryptanalysts it was clear that the cryptanalysts had gained the upper hand. Anybody sending an encrypted message had to accept that an expert enemy codebreaker might intercept and decipher their most precious secrets.

The burden was clearly on the cryptographers to concoct a new, stronger cipher, something that could outwit the cryptanalysts. Although such a cipher would not emerge until the end of the sixteenth century, its origins can be traced back to the fifteenth-century Florentine polymath Leon Battista Alberti. Born in 1404, Alberti was one of the leading figures of the Renaissance – a painter, composer, poet and philosopher, as well as the author of the first scientific analysis of perspective, a treatise on the housefly and a funeral oration for his dog. He is probably best known as an architect, having designed Rome’s first Trevi Fountain and having written De re aedificatoria, the first printed book on architecture, which acted as a catalyst for the transition from Gothic to Renaissance design.

Sometime in the 1460s, Alberti was wandering through the gardens of the Vatican when he bumped into his friend Leonardo Dato, the pontifical secretary, who began chatting to him about some of the finer points of cryptography. This casual conversation prompted Alberti to write an essay on the subject, outlining what he believed to be a new form of cipher. At the time, all substitution ciphers required a single cipher alphabet for encrypting each message. However, Alberti proposed using two or more cipher alphabets and switching between them during encipherment, thereby confusing potential cryptanalysts.

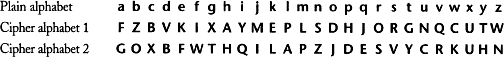
For example, here we have two possible cipher alphabets, and we could encrypt a message by alternating between them. To encrypt the message hello, we would encrypt the first letter according to the first cipher alphabet, so that h becomes A, but we would encrypt the second letter according to the second cipher alphabet, so that e becomes F. To encrypt the third letter we return to the first cipher alphabet, and to encrypt the fourth letter we return to the second alphabet. This means that the first l is enciphered as P, but the second l is enciphered as A. The final letter, o, is enciphered according to the first cipher alphabet and becomes D. The complete ciphertext reads AFPAD. The crucial advantage of Alberti’s system is that the same letter in the plaintext does not necessarily appear as the same letter in the ciphertext, so the repeated l in hello is enciphered differently in each case. Similarly, the repeated A in the ciphertext represents a different plaintext letter in each case, first h and then l.

Blaise de Vigenère, a French diplomat born in 1523, became acquainted with the writings of Alberti when, at the age of twenty-six, he was sent to Rome on a two-year mission. To start with, his interest in cryptography was purely practical and was linked to his work. Then, at the age of thirty-nine, Vigenère decided that he had accumulated enough money to be able to abandon his career and concentrate on a life of study. It was only then that he examined Albertu’s idea and turned it into a coherent and powerful new cipher, now known as the Vigenère cipher. The strength of the Vigenère cipher lies in its use of not one or two but twenty-six distinct cipher alphabets to encrypt a message. The first step in encipherment is to draw up a so-called Vigenère square, as shown in Table 3, a plaintext alphabet followed by twenty-six cipher alphabets, each shifted by one letter with respect to the previous alphabet. Hence, row 1 represents a cipher alphabet with a Caesar shift of 1, which means that it could be used to implement a Caesar shift cipher in which every letter of the plaintext is replaced by the letter one place further on in the alphabet. Similarly, row 2 represents a cipher alphabet with a Caesar shift of 2, and so on. The top row of the square, in lowercase, represents the plaintext letters. You could encipher each plaintext letter according to any one of the twenty-six cipher alphabets. For example, if cipher alphabet number 2 is used, then the letter a is enciphered as C, but if cipher alphabet number 12 is used, then a is enciphered as M.

Figure 10 Blaise de Vigenère.

If the sender were to use just one of the cipher alphabets to encipher an entire message, this would effectively be a simple Caesar cipher, which would be a very weak form of encryption, easily deciphered by an enemy interceptor. However, in the Vigenère cipher a different row of the Vigenère square (a different cipher alphabet) is used to encrypt different letters of the message. In other words, the sender might encrypt the first letter according to row 5, the second according to row 14, the third according to row 21, and so on.

To unscramble the message, the intended receiver needs to know which row of the Vigenère square has been used to encipher each letter, so there must be an agreed system of switching between rows. This is achieved by using a keyword. To illustrate how a keyword is used with the Vigenère square to encrypt a sample message, let us encipher divert troops to east ridge, using the keyword WHITE. First of all, the keyword is spelled out above the message and repeated over and over again, so that each letter in the message is associated with a letter from the keyword, as shown on page 56. The ciphertext is then generated as follows. To encrypt the first letter, d, begin by identifying the key letter above it, W, which in turn defines a particular row in the Vigenère square. The row beginning with W, row 22, is the cipher alphabet that will be used to find the substitute letter for the plaintext d. We look to see where the column headed by d intersects the row beginning with W, which turns out to be at the letter Z.

Table 3 A Vigenère square.

Consequently, the letter d in the plaintext is represented by Z in the ciphertext.

To encipher the second letter of the message, i, the process is repeated. The key letter above i is H, so it is encrypted via a different row in the Vigenère square: the H row (row 7), which is a new cipher alphabet. To encrypt i, we look to see where the column headed by i intersects the row beginning with H, which turns out to be at the letter P. Consequently, the letter i in the plaintext is represented by P in the ciphertext. Each letter of the keyword indicates a particular cipher alphabet within the Vigenère square, and because the keyword contains five letters, the sender encrypts the message by cycling through five rows of the Vigenère square. The fifth letter of the message is enciphered according to the fifth letter of the keyword, E, but to encipher the sixth letter of the message we have to return to the first letter of the keyword. A longer keyword, or perhaps a keyphrase, would bring more rows into the encryption process and increase the complexity of the cipher. Table 4 shows a Vigenère square, highlighting the five rows (i.e., the five cipher alphabets) defined by the keyword WHITE.

The great advantage of the Vigenère cipher is that it is invulnerable to the frequency analysis described in Chapter 1. For example, a cryptanalyst applying frequency analysis to a piece of ciphertext would usually begin by identifying the most common letter in the ciphertext, which in the case above is Z, and then assume that this represents the most common letter in English, e. In fact, the letter Z represents three different letters, d, r and s, but not e. This is clearly a problem for the cryptanalyst. The fact that a letter that appears several times in the ciphertext can represent a different plaintext letter on each occasion generates tremendous ambiguity. Equally confusing is the fact that a letter that appears several times in the plaintext can be represented by different letters in the ciphertext. For example, the letter o is repeated in troops, but it is substituted by two different letters – the oo is enciphered as HS.

Table 4 A Vigenère square with the rows defined by the keyword WHITE highlighted. Encryption is achieved by switching among the five highlighted cipher alphabets, defined by W, H, I, T and E.

As well as being invulnerable to frequency analysis, the Vigenère cipher has an enormous number of keys. The sender and receiver can agree on any word in the dictionary or any combination of words, or even fabricate words. A cryptanalyst would be unable to crack the message by searching all possible keys because the number of options is simply too great.

The traditional forms of substitution cipher, those that existed before the Vigenère cipher, were called monoalphabetic substitution ciphers because they used only one cipher alphabet per message. In contrast, the Vigenère cipher belongs to a class known as polyalphabetic because it employs several cipher alphabets per message.

In 1586 Vigenère published his work in A Treatise on Secret Writing. Although some people continued to use traditional ciphers (Appendix D), use of the Vigenère cipher spread during the seventeenth and eighteenth centuries, and the arrival of the telegraph in the nineteenth century suddenly made it popular within the business community.

The polyalphabetic Vigenère cipher was clearly the best way to ensure secrecy for important business communications that were transmitted via a telegraph operator, who would otherwise be able to read the contents of the message. The cipher was considered unbreakable, and became known as le chiffre indéchiffrable: the uncrackable cipher. Cryptographers had, for the time being at least, a clear lead over the cryptanalysts.

MR BABBAGE VERSUS THE VIGENÈRE CIPHER

The most intriguing figure in nineteenth-century cryptanalysis is Charles Babbage, the eccentric British genius best known for developing the blueprint for the modern computer. He was born in 1791, the son of Benjamin Babbage, a wealthy London banker. When Charles married without his father’s permission, he no longer had access to the Babbage fortune, but he still had enough money to be financially secure, and he pursued the life of a roving scholar, applying his mind to whatever problem tickled his fancy. His inventions include the speedometer and the cowcatcher, a device that could be fixed to the front of steam locomotives to clear cattle from railway tracks. In terms of scientific breakthroughs, he was the first to realize that the width of a tree ring depended on that year’s weather, and he deduced that it was possible to determine past climates by studying ancient trees. He was also intrigued by statistics, and as a diversion he drew up a set of mortality tables, a basic tool for today’s insurance industry.

The turning point in Babbage’s scientific career came in 1821, when he and the astronomer John Herschel were examining a set of mathematical tables, the sort used as the basis for astronomical, engineering and navigational calculations. The two men were disgusted by the number of errors in the tables, which in turn would generate flaws in important calculations. One set of tables, the Nautical Ephemeris for Finding Latitude and Longitude at Sea, contained over a thousand errors. Indeed, many shipwrecks and engineering disasters were blamed on faulty tables.

These mathematical tables were calculated by hand, and the mistakes were simply the result of human error, causing Babbage to exclaim, “I wish to God these calculations had been executed by steam!” This marked the beginning of an extraordinary endeavour to build a machine capable of faultlessly calculating the tables to a high degree of accuracy. In 1823 Babbage designed Difference Engine No. 1, a magnificent calculator consisting of twenty-five thousand precision parts, to be built with government funding. Although Babbage was a brilliant innovator, he was not a great implementer. After ten years of toil, he abandoned Difference Engine No. 1, cooked up an entirely new design and set to work building Difference Engine No. 2.

When Babbage abandoned his first machine, the government lost confidence in him and decided to cut its losses by withdrawing from the project – it had already spent £17,470, enough to build a pair of battleships. It was probably this withdrawal of support that later prompted Babbage to make the following complaint: “Propose to an Englishman any principle, or any instrument, however admirable, and you will observe that the whole effort of the English mind is directed to find a difficulty, a defect, or an impossibility in it. If you speak to him of a machine for peeling a potato, he will pronounce it impossible: if you peel a potato with it before his eyes, he will declare it useless, because it will not slice a pineapple.”

Figure 11 Charles Babbage.

Lack of government funding meant that Babbage never completed Difference Engine No. 2. The scientific tragedy was that Babbage’s machine would have offered a stepping-stone to the Analytical Engine, which, rather than merely calculating a specific set of tables, would have been able to solve a variety of mathematical problems depending on the instructions that it was given. In fact, the Analytical Engine provided a template for modern computers. The design included a “store” (memory) and a “mill” (processor), which would allow it to make decisions and repeat instructions, which are equivalent to the IF … THEN … and LOOP commands familiar in modern programming.

A century later, during the course of the Second World War, the first electronic incarnations of Babbage’s machine would have a profound effect on cryptanalysis, but in his own lifetime, Babbage made an equally important contribution to codebreaking: he succeeded in breaking the Vigenère cipher, and in so doing he made the greatest breakthrough in cryptanalysis since the Arab scholars of the ninth century broke the monoalphabetic cipher by inventing frequency analysis. Babbage’s work required no mechanical calculations or complex computations. Instead, he employed nothing more than sheer cunning.

Babbage had become interested in ciphers at a very young age. In later life, he recalled how his childhood hobby occasionally got him into trouble: “The bigger boys made ciphers, but if I got hold of a few words, I usually found out the key. The consequence of this ingenuity was occasionally painful: the owners of the detected ciphers sometimes thrashed me, though the fault lay in their own stupidity.” These beatings did not discourage him, and he continued to be enchanted by cryptanalysis. He wrote in his autobiography that “deciphering is, in my opinion, one of the most fascinating of arts.”

While most cryptanalysts had given up all hope of ever breaking the Vigenère cipher, Babbage was inspired to attempt a decipherment by an exchange of letters with John Hall Brock Thwaites, a dentist from Bristol with a rather innocent view of ciphers. In 1854, Thwaites claimed to have invented a new cipher, which, in fact, was equivalent to the Vigenère cipher. He wrote to the Journal of the Society of Arts with the intention of patenting his idea, apparently unaware that he was several centuries too late. Babbage too wrote to the society, pointing out that “the cypher … is a very old one, and to be found in most books.” Thwaites was unapologetic and challenged Babbage to break his cipher. Whether or not it was breakable was irrelevant to whether or not it was new, but Babbage’s curiosity was sufficiently aroused for him to embark on a search for a weakness in the Vigenère cipher.

Table 5 A Vigenère square used in combination with the keyword KING. The keyword defines four separate cipher alphabets, so that the letter e may be encrypted as O, M, R or K.

Cracking a difficult cipher is akin to climbing a sheer cliff face: the cryptanalyst is seeking any nook or cranny that could provide the slightest foothold. In a monoalphabetic cipher the cryptanalyst will latch on to the frequency of the letters, because the commonest letters, such as e, t and a, will stand out no matter how they have been disguised. In the polyalphabetic Vigenère cipher the frequencies are much more balanced, because the keyword is used to switch between cipher alphabets. Hence, at first sight, the rock face seems perfectly smooth.

Remember, the great strength of the Vigenère cipher is that the same letter will be enciphered in different ways. For example, if the keyword is KING, then every letter in the plaintext can potentially be enciphered in four different ways, because the keyword contains four letters. Each letter of the keyword defines a different cipher alphabet in the Vigenère square, as shown in Table 5. The e column of the square has been highlighted to show how it is enciphered differently, depending on which letter of the keyword is defining the encipherment:

If the K of KING is used to encipher e, then the resulting ciphertext letter is O.
If the I of KING is used to encipher e, then the resulting ciphertext letter is M.
If the N of KING is used to encipher e, then the resulting ciphertext letter is R.
If the G of KING is used to encipher e, then the resulting ciphertext letter is K.

Similarly, whole words will be enciphered in different ways: the word the, for example, could be enciphered as DPR, BUK, GNO or ZRM, depending on its position relative to the keyword. Although this makes cryptanalysis difficult, it is not impossible. The important point to note is that if there are only four ways to encipher the word the, and the original message contains several instances of the word the, then it is inevitable that some of the four possible encipherments will be repeated in the ciphertext. This is demonstrated in the following example, in which the line the sun and the man in the moon has been enciphered using the Vigenère cipher and the keyword KING.

Keyword	K I N G K I N G K I N G K I N G K I N G K I N G
Plaintext	t h e s u n a n d t h e m a n i n t h e m o o n
Ciphertext	D P R Y E V N T N B U K W I A O X B U K W W B T

The word the is enciphered as DPR in the first instance, and then as BUK on the second and third occasions. The reason for the repetition of BUK is that the second the is displaced by eight letters with respect to the third the, and eight is a multiple of the length of the keyword, which is four letters long. In other words, the second the was enciphered according to its relationship to the keyword (the is directly below ING), and by the time we reach the third the, the keyword has cycled around exactly twice, to repeat the relationship, and hence repeat the encipherment.

Babbage realized that this sort of repetition provided him with exactly the foothold he needed in order to conquer the Vigenère cipher. He was able to define a series of relatively simple steps that could be followed by any cryptanalyst to crack the hitherto uncrackable cipher. To demonstrate his brilliant technique, let us imagine that we have intercepted the ciphertext shown in Figure 12. We know that it was enciphered using the Vigenère cipher, but we know nothing about the original message, and the keyword is a mystery.

The first stage in Babbage’s cryptanalysis is to look for sequences of letters that appear more than once in the ciphertext.

Figure 12 The ciphertext, enciphered using the Vigenère cipher.

There are two ways that such repetitions could arise. The most likely is that the same sequence of letters in the plaintext has been enciphered using the same part of the key. Alternatively, there is a slight possibility that two different sequences of letters in the plaintext have been enciphered using different parts of the key, coincidentally leading to the identical sequence in the ciphertext. If we restrict ourselves to long sequences, then we largely discount the second possibility, and in this case we shall consider repeated sequences only if they consist of four letters or more. Table 6 is a log of such repetitions, along with the spacing between the repetition. For example, the sequence E-F-I-Q appears in the first line of the ciphertext and then in the fifth line, shifted forward by ninety-five letters.

As well as being used to encipher the plaintext into ciphertext, the keyword is used by the receiver to decipher the ciphertext back into plaintext. Hence, if we could identify the keyword, deciphering the text would be easy. At this stage we do not have enough information to work out the keyword, but Table 6 does provide some very good clues as to its length. Having listed which sequences repeat themselves and the spacing between these repetitions, the rest of the table is given over to identifying the factors of the spacing – the numbers that will divide into the spacing. For example, the sequence W-C-X-Y-M repeats itself after twenty letters, and the numbers 1, 2, 4, 5,10 and 20 are factors, because they divide perfectly into 20 without leaving a remainder. These factors suggest six possibilities:

1. The key is 1 letter long and is recycled 20 times between encryptions.
2. The key is 2 letters long and is recycled 10 times between encryptions.
3. The key is 4 letters long and is recycled 5 times between encryptions.
4. The key is 5 letters long and is recycled 4 times between encryptions.
5. The key is 10 letters long and is recycled 2 times between encryptions.
6. The key is 20 letters long and is recycled 1 time between encryptions.

The first possibility can be excluded, because a key that is only 1 letter long gives rise to a monoalphabetic cipher – only one row of the Vigenère square would be used for the entire encryption, and the cipher alphabet would remain unchanged; it is unlikely that a cryptographer would do this. To indicate each of the other possibilities, a check mark is placed in the appropriate column of Table 6. Each check mark indicates a potential key length.

Table 6 Repetitions and spacings in the ciphertext.

To identify whether the key is two, four, five, ten or twenty letters long, we need to look at the factors of all the other spacings. Because the keyword seems to be twenty letters or smaller, Table 6 lists those factors that are 20 or smaller for each of the other spacings. There is a clear tendency toward a spacing divisible by 5. In fact, every spacing is divisible by 5. The first repeated sequence, E-F-I-Q, can be explained by a keyword of length five recycled nineteen times between the first and second encryptions. The second repeated sequence, P-S-D-L-P, can be explained by a keyword of length five recycled just once between the first and second encryptions. The third repeated sequence, W-C-X-Y-M, can be explained by a keyword of length five recycled four times between the first and second encryptions. The fourth repeated sequence, E-T-R-L, can be explained by a keyword of length five recycled twenty-four times between the first and second encryptions. In short, everything is consistent with a five-letter keyword.

Assuming that the keyword is indeed five letters long, the next step is to work out the actual letters of the keyword. For the time being, let us call the keyword L₁-L₂-L₃-L₄-L₅, such that L₁ represents the first letter of the keyword, and so on. The process of encipherment would have begun with enciphering the first letter of the plaintext according to the first letter of the keyword, L₁. The letter L₁ defines one row of the Vigenère square and effectively provides a monoalphabetic substitution cipher alphabet for the first letter of the plaintext. However, when it comes to encrypting the second letter of the plaintext, the cryptographer would have used L₂ to define a different row of the Vigenère square, effectively providing a different monoalphabetic substitution cipher alphabet. The third letter of plaintext would be encrypted according to L₃, the fourth according to L₄, and the fifth according to L₅. Each letter of the keyword is providing a different cipher alphabet for encryption. However, the sixth letter of the plaintext would once again be encrypted according to L₁, the seventh letter of the plaintext would once again be encrypted according to L₂, and the cycle repeats itself thereafter. In other words, the polyalphabetic cipher consists of five monoalphabetic ciphers, each monoalphabetic cipher is responsible for encrypting one-fifth of the entire message and, most importantly, we already know how to cryptanalyze monoalphabetic ciphers.

We proceed as follows. We know that one of the rows of the Vigenère square, defined by L₁, provided the cipher alphabet to encrypt the first, sixth, eleventh, sixteenth … letters of the message. Hence, if we look at the first, sixth, eleventh, sixteenth … letters of the ciphertext, we should be able to use old-fashioned frequency analysis to work out the cipher alphabet in question. Figure 13 shows the frequency distribution of the letters that appear in the first, sixth, eleventh, sixteenth … positions of the ciphertext, which are W, I, R, E … At this point, remember that each cipher alphabet in the Vigenère square is simply a standard alphabet shifted by between one and twenty-six spaces. Hence, the frequency distribution in Figure 13 should have similar features to the frequency distribution of a standard alphabet, except that it will have been shifted by some distance. By comparing the L₁ distribution with the standard distribution, it should be possible to work out the shift. Figure 14 shows the standard frequency distribution for a piece of English plaintext.

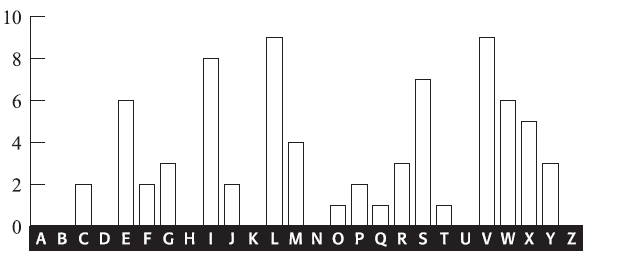
Figure 13 Frequency distribution for letters in the ciphertext encrypted using the L₁ cipher alphabet (number of occurrences).

Figure 14 Standard frequency distribution (number of occurrences based on a piece of plaintext containing the same number of letters as in the ciphertext).

The standard distribution has peaks, plateaus and valleys, and to match it with the L₁ cipher distribution we look for the most outstanding combination of features. For example, the three spikes at R-S-T in the standard distribution (Figure 14) and the long depression to its right that stretches across six letters from U to Z together form a very distinctive pair of features. The only similar features in the L₁ distribution (Figure 13) are the three spikes at V-W-X, followed by the depression stretching six letters from Y to D. This would suggest that all the letters encrypted according to L₁ have been shifted four places, or that L₁ defines a cipher alphabet that begins E, F, G, H… In turn, this means that the first letter of the keyword, L₁ is probably E. This hypothesis can be tested by shifting the L₁ distribution back four letters and comparing it with the standard distribution. Figure 15 shows both distributions for comparison. The match between the major peaks is very strong, implying that it is safe to assume that the keyword does indeed begin with E.

Figure 15 The L₁ distribution shifted back four letters (top), compared with the standard frequency distribution (bottom). All major peaks and troughs match.

To summarize, searching for repetitions in the ciphertext has allowed us to identify the length of the keyword, which turned out to be five letters long. This allowed us to split the ciphertext into five parts, each one enciphered according to a monoalphabetic substitution as defined by one letter of the keyword. By analyzing the fraction of the ciphertext that was enciphered according to the first letter of the keyword, we have been able to show that this letter, L₁, is probably E. This process is repeated in order to identify the second letter of the keyword. A frequency distribution is established for the second, seventh, twelfth, seventeenth … letters in the ciphertext. Again, the resulting distribution, shown in Figure 16, is compared with the standard distribution in order to deduce the shift.

Figure 16 Frequency distribution for letters in the ciphertext encrypted using the L₂ cipher alphabet (number of occurrences).

This distribution is harder to analyze. There are no obvious candidates for the three neighbouring peaks that correspond to R-S-T. However, the depression that stretches from G to L is very distinct and probably corresponds to the depression we expect to see stretching from U to Z in the standard distribution. If this were the case, we would expect the three R-S-T peaks to appear at D, E and F, but the peak at E is missing. For the time being, we shall dismiss the missing peak as a statistical glitch and go with our initial hunch, which is that the depression from G to L is a recognizably shifted feature. This would suggest that all the letters encrypted according to L₂ have been shifted twelve places, or that L₂ defines a cipher alphabet that begins M, N, O, P … and that the second letter of the keyword, L₂, is M. Once again, this hypothesis could be tested by shifting the L₂ distribution back twelve letters and comparing it with the standard distribution.

I shall not continue the analysis; suffice it to say that analyzing the third, eighth, thirteenth … letters implies that the third letter of the keyword is I; analyzing the fourth, ninth, fourteenth … letters implies that the fourth letter is L, and analyzing the fifth, tenth, fifteenth … letters implies that the fifth letter is Y. The keyword is EMILY. It is now possible to reverse the Vigenère cipher and complete the cryptanalysis. The first letter of the ciphertext is W, and it was encrypted according to the first letter of the keyword, E. Working backwards, we look at the Vigenère square and find W in the row beginning with E, and then we find which letter is at the top of that column. The letter is s, which must make it the first letter of the plaintext. By repeating this process, we see that the plaintext begins sittheedownandhavenoshamecheekbyjowl. By inserting suitable word breaks and punctuation, we eventually get:

Sit thee down, and have no shame,
Cheek by jowl, and knee by knee:
What care I for any name?
What for order or degree?

Let me screw thee up a peg:
Let me loose thy tongue with wine:
Callest thou that thing a leg?
Which is thinnest? thine or mine?

Thou shalt not be saved by works:
Thou hast been a sinner too:
Ruined trunks on withered forks,
Empty scarecrows, I and you!

Fill the cup, and fill the can:
Have a rouse before the morn:
Every moment dies a man,
Every moment one is born.

These are verses from a poem by Alfred, Lord Tennyson entitled “The Vision of Sin’. The keyword happens to be the first name of Tennyson’s wife, Emily Sellwood. I chose to use a section from this particular poem as an example for cryptanalysis because it inspired some curious correspondence between Babbage and the great poet. Being an avid statistician and compiler of mortality tables, Babbage was irritated by the lines “Every moment dies a man / Every moment one is born”, which are the last lines of the plaintext above. Consequently, he offered a correction to Tennyson’s “otherwise beautiful” poem:

It must be manifest that if this were true, the population of the world would be at a standstill … I would suggest that in the next edition of your poem you have it read – “Every moment dies a man, Every moment 1¹⁄₁₆ is born”… The actual figure is so long I cannot get it onto a line, but I believe the figure 1¹⁄₁₆ will be sufficiently accurate for poetry.

I am, Sir, yours, etc.,

Charles Babbage.

Babbage’s successful cryptanalysis of the Vigenère cipher was probably achieved in 1854, soon after his spat with Thwaites, but his discovery went completely unrecognized because he never published it. The discovery came to light only in the twentieth century, when scholars examined Babbage’s extensive notes. In the meantime, his technique was independently discovered by Friedrich Wilhelm Kasiski, a retired Prussian army officer. Ever since 1863, when he published his cryptanalytic breakthrough in Die Geheimschriften und die Dechiffrirkunst (Secret Writing and the Art of Deciphering), the technique has been known as the Kasiski test, and Babbage’s contribution has been largely ignored.

And why did Babbage fail to publicize his cracking of such a vital cipher? He certainly had a habit of not finishing projects and not publishing his discoveries, which might suggest that this is just one more example of his lackadaisical attitude. However, there is an alternative explanation for his anonymity. His discovery occurred soon after the outbreak of the Crimean War, and one theory is that it gave the British a clear advantage over their Russian enemy. It is quite possible that the British military demanded that Babbage keep his work secret, thus providing them with a nine-year head start over the rest of the world. If this was the case, then it would fit in with the longstanding tradition of hushing up codebreaking achievements in the interests of national security, a practice that continued into the twenty-first century.

FROM AGONY COLUMNS TO BURIED TREASURE

The development of the telegraph, which had driven a commercial interest in cryptography, was also responsible for generating public interest in cryptography. The public became aware of the need to protect personal messages of a highly sensitive nature, and they would use encryption if necessary, even though it then took more time to send the message, which added to the cost of the telegram.

As people became comfortable with encipherment, they began to express their cryptographic skills in a variety of ways. For example, young lovers in Victorian England were often forbidden from publicly expressing their affection, and could not even communicate by letter in case their parents intercepted and read the contents. This resulted in lovers sending encrypted messages to each other via the personal columns of newspapers. These “agony columns”, as they became known, provoked the curiosity of cryptanalysts, who would scan the notes and try to decipher their titillating contents. Charles Babbage is known to have indulged in this activity, along with his friend Sir Charles Wheatstone. On one occasion, Wheatstone deciphered a note in The Times from an Oxford student, suggesting to his true love that they elope. A few days later, Wheatstone inserted his own message, encrypted in the same cipher, advising the couple against this rebellious and rash action. Shortly afterwards there appeared a third message, this time unencrypted and from the lady in question: “Dear Charlie, Write no more. Our cipher is discovered.”

Another example of the public’s familiarity with cryptography was the widespread use of pinprick encryption. The ancient Greek historian Aeneas the Tactician suggested conveying a secret message by pricking tiny holes under particular letters in an apparently innocuous page of text. Those letters would spell out a secret message, easily read by the intended receiver. However, any intermediary who stared at the page would probably be oblivious to the barely perceptible pinpricks and would probably be unaware of the secret message. Two thousand years later, British letter writers used exactly the same method, not to achieve secrecy but to avoid paying excessive postage costs. Before the overhaul of the postage system in the mid-1800s, sending a letter cost about a shilling for every hundred miles, beyond the means of most people. However, newspapers could be posted free of charge, and this provided a loophole for thrifty Victorians. Instead of writing and sending letters, people began to use pinpricks to spell out a message on the front page of a newspaper. They could then send the newspaper through the post without having to pay a penny.

The public’s growing fascination with cryptographic techniques meant that codes and ciphers soon found their way into nineteenth-century literature. In Jules Verne’s Journey to the Centre of the Earth, the decipherment of a parchment filled with runic characters prompts the first step on the epic journey. The characters are part of a substitution cipher that generates a Latin script, which in turn makes sense only when the letters are reversed: “Descend the crater of the volcano of Sneffels when the shadow of Scartaris comes to caress it before the calends of July, audacious voyager, and you will reach the centre of the Earth.” In 1885, Verne also used a cipher as a pivotal element in his novel Mathias Sandorff. In Britain, one of the finest writers of cryptographic fiction was Sir Arthur Conan Doyle. Not surprisingly, Sherlock Holmes was an expert in cryptography and, as he explained to Dr. Watson, was “the author of a trifling monograph upon the subject in which I analyze one hundred and sixty separate ciphers.” The most famous of Holmes’ decipherments is told in “The Adventure of the Dancing Men”, which involves a cipher consisting of stick men, each pose representing a distinct letter.

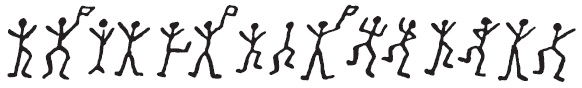
Figure 17 A section of the ciphertext from The Adventures of the Dancing Men, a Sherlock Holmes adventure by Sir Arthur Conan Doyle.

On the other side of the Atlantic, Edgar Allan Poe was also developing an interest in cryptanalysis. Writing for Philadelphia’s Alexander Weekly Messenger, he issued a challenge to readers, claiming that he could decipher any monoalphabetic substitution cipher. Hundreds of readers sent in their ciphertexts, and he successfully deciphered them all. Although this required nothing more than frequency analysis, Poe’s readers were astonished by his achievements. One adoring fan proclaimed him “the most profound and skilful cryptographer who ever lived.”

In 1843, hoping to exploit the interest he had generated, Poe wrote a short story about ciphers that is widely acknowledged by professional cryptographers to be the finest piece of fictional literature on the subject. “The Gold Bug” tells the story of William Legrand, who discovers an unusual beetle, the gold bug, and collects it using a scrap of paper lying nearby. That evening he sketches the gold bug upon the same piece of paper, and then holds his drawing up to the light of the fire to check its accuracy. However, his sketch is obliterated by an invisible ink, which has been developed by the heat of the flames. Legrand examines the characters that have emerged and becomes convinced that he has in his hands the encrypted directions for finding Captain Kidd’s treasure. The remainder of the story is a classic demonstration of frequency analysis, resulting in the decipherment of Captain Kidd’s clues and the discovery of his buried treasure.

Although “The Gold Bug” is pure fiction, there is a true nineteenth-century story containing many of the same elements. The case of the Beale ciphers involves Wild West escapades, a cowboy who amassed a vast fortune, a buried treasure worth $20 million and a mysterious set of encrypted papers describing its whereabouts. Much of what we know about this story, including the encrypted papers, is contained in a pamphlet published in 1885. Although only twenty-three pages long, the pamphlet has baffled generations of cryptanalysts and captivated hundreds of treasure hunters.

The story begins at the Washington Hotel in Lynchburg, Virginia, sixty-five years before the publication of the pamphlet. According to the pamphlet, the hotel owner, Robert Morriss, was held in high regard: “His kind disposition, strict probity, excellent management, and well ordered household, soon rendered him famous as a host, and his reputation extended even to other States.” In January 1820 a stranger by the name of Thomas J. Beale rode into Lynchburg and checked into the Washington Hotel. “In person, he was about six feet in height,” recalled Morriss, “with jet black eyes and hair of the same color, worn longer than was the style at the time. His form was symmetrical, and gave evidence of unusual strength and activity; but his distinguishing feature was a dark and swarthy complexion.” Although Beale spent the rest of the winter with Morriss and was “extremely popular with every one, particularly the ladies”, he never spoke about his background, his family or the purpose of his visit. Then, at the end of March, he left as suddenly as he had arrived.

Two years later, in January 1822, Beale returned to the Washington Hotel, “darker and swarthier than ever”. Once again, he spent the rest of the winter in Lynchburg and disappeared in the spring, but not before he entrusted Morriss with a locked iron box, which he said contained “papers of value and importance”. Morriss placed the box in a safe and thought nothing more about it or its contents until he received a letter from Beale, dated May 9, 1822, sent from St Louis. After a few pleasantries and a paragraph about an intended trip to the plains “to hunt the buffalo and encounter the savage grizzlies”, Beale’s letter revealed the significance of the box:

It contains papers vitally affecting the fortunes of myself and many others engaged in business with me, and in the event of my death, its loss might be irreparable. You will, therefore, see the necessity of guarding it with vigilance and care to prevent so great a catastrophe. Should none of us ever return you will please preserve carefully the box for the period of ten years from the date of this letter, and if I, or no one with authority from me, during that time demands its restoration, you will open it, which can be done by removing the lock. You will find, in addition to the papers addressed to you, other papers which will be unintelligible without the aid of a key to assist you. Such a key I have left in the hand of a friend in this place, sealed and addressed to yourself, and endorsed not to be delivered until June 1832. By means of this you will understand fully all you will be required to do.

Morriss dutifully continued to guard the box, waiting for Beale to collect it, but the swarthy man of mystery never returned to Lynchburg. He disappeared without explanation, never to be seen again. Ten years later, Morriss could have followed the letter’s instructions and opened the box, but he seems to have been reluctant to break the lock. Beale’s letter had mentioned that a note would be sent to Morriss in June 1832, and this was supposed to explain how to decipher the contents of the box. However, the note never arrived, and perhaps Morriss felt that there was no point opening the box if he could not decipher what was inside it. Eventually, in 1845, Morriss’ curiosity got the better of him and he cracked open the lock. The box contained three sheets of enciphered characters, and a note written by Beale in plain English.

The intriguing note revealed the truth about Beale, the box and the ciphers. It explained that in April 1817, almost three years before his first meeting with Morriss, Beale and twenty-nine others had embarked on a journey across America. After travelling through the rich hunting grounds of the western plains, they arrived in Santa Fe, and spent the winter in the “little Mexican town”. In March they headed north and began tracking an “immense herd of buffaloes”, picking off as many as possible along the way. Then, according to Beale, they struck lucky:

Figure 18 The title page of The Beale Papers, the pamphlet that contains all we know about the mystery of the Beale treasure.

One day, while following them, the party encamped in a small ravine, some 250 or 300 miles north of Santa Fé, and, with their horses tethered, were preparing their evening meal, when one of the men discovered in a cleft of the rocks something that had the appearance of gold. Upon showing it to the others it was pronounced to be gold, and much excitement was the natural consequence.

The letter went on to explain that Beale and his men, with help from the local tribe, mined the site for the next eighteen months, by which time they had accumulated a large quantity of gold, as well as some silver that was found nearby. In due course they agreed that their newfound wealth should be moved to a secure place, and decided to take it back home to Virginia, where they would hide it in a secret location. In 1820, Beale travelled to Lynchburg with the gold and silver, found a suitable location, and buried it. It was on this occasion that he first lodged at the Washington Hotel and made the acquaintance of Morriss. When Beale left at the end of the winter, he rejoined his men, who had continued to work the mine during his absence.

After another eighteen months Beale revisited Lynchburg with even more to add to his stash. This time there was an additional reason for his trip:

Before leaving my companions on the plains it was suggested that, in case of an accident to ourselves, the treasure so concealed would be lost to their relatives, without some provision against such a contingency. I was, therefore, instructed to select some perfectly reliable person, if such could be found, who should, in the event of this proving acceptable to the party, be confided in to carry out their wishes in regard to their respective shares.

Beale believed that Morriss was a man of integrity, which is why he trusted him with the box containing the three enciphered sheets, the so-called Beale ciphers. Each enciphered sheet contained an array of numbers (reprinted here as Figures 19, 20 and 21), and deciphering the numbers would reveal all the relevant details; the first sheet described the treasure’s location, the second outlined the contents of the treasure and the third listed the relatives of the men who should receive a share of the treasure. When Morriss read all of this, it was some twenty-three years after he had last seen Thomas Beale. Working on the assumption that Beale and his men were dead, Morriss felt obliged to find the gold and share it among their relatives. However, without the promised key, he was forced to decipher the ciphers from scratch, a task that troubled his mind for the next twenty years, and which ended in failure.

In 1862, at the age of eighty-four, Morriss knew that he was coming to the end of his life, and that he had to share the secret of the Beale ciphers, otherwise any hope of carrying out Beale’s wishes would die with him. Morriss confided in a friend, but unfortunately the identity of this person remains a mystery. All we know about Morriss’ friend is that it was he who wrote the pamphlet in 1885, so hereafter I will refer to him simply as the author. The author explained the reasons for his anonymity within the pamphlet:

I anticipate for these papers a large circulation, and, to avoid the multitude of letters with which I should be assailed from all sections of the Union, propounding all sorts of questions, and requiring answers which, if attended to, would absorb my entire time, and only change the character of my work, I have decided upon withdrawing my name from the publication, after assuring all interested that I have given all that I know of the matter, and that I cannot add one word to the statements herein contained.

Figure 19 The first Beale cipher.

Figure 20 The second Beale cipher.

Figure 21 The third Beale cipher.

To protect his identity, the author asked James B. Ward, a respected member of the local community and the county’s road surveyor, to act as his agent and publisher.

Everything we know about the strange tale of the Beale ciphers is published in the pamphlet, and so it is thanks to the author that we have the ciphers and Morriss’ account of the story. In addition to this, the author is also responsible for successfully deciphering the second Beale cipher. Like the first and third ciphers, the second cipher consists of a page of numbers, and the author assumed that each number represented a letter. However, the range of numbers far exceeds the number of letters in the alphabet, so the author realized that he was dealing with a cipher that uses several numbers to represent the same letter. One cipher that fulfills this criterion is the so-called book cipher, in which a book, or any other piece of text, is the key.

First, the cryptographer sequentially numbers every word in the book (or keytext). Thereafter, each number acts as a substitute for the initial letter of its associated word. ¹For ²example, ³if ⁴the ⁵sender ⁶and ⁷receiver ⁸agreed ⁹that ¹⁰this ¹¹sentence ¹²was ¹³to ¹⁴be ¹⁵the ¹⁶keytext, ¹⁷then ¹⁸every ¹⁹word ²⁰would ²¹be ²²numerically ²³labelled, ²⁴each ²⁵number ²⁶providing ²⁷the ²⁸basis ²⁹for ³⁰encryption. Next, a list would be drawn up matching each number to the initial letter of its associated word:

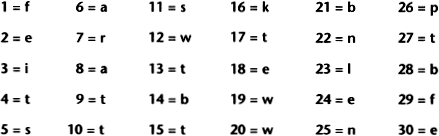
A message can now be encrypted by substituting letters in the plaintext for numbers according to the list. In this list, the plaintext letter f would be substituted with 1, and the plaintext letter e could be substituted with either 2, 18, 24 or 30. Because our keytext is such a short sentence, we do not have numbers that could replace rare letters such as x and z, but we do have enough substitutes to encipher the word beale, which could be 14-2-8-23-18. If the intended receiver has a copy of the keytext, then deciphering the encrypted message is trivial. However, if a third party intercepts only the ciphertext, then cryptanalysis depends on somehow identifying the keytext. The author of the pamphlet wrote, “With this idea, a test was made of every book I could procure, by numbering its letters and comparing the numbers with those of the manuscript; all to no purpose, however, until the Declaration of Independence afforded the clue to one of the papers, and revived all my hopes.”

The Declaration of Independence turned out to be the keytext for the second Beale cipher, and by numbering the words in the Declaration it is possible to unravel it. Figure 22 shows the start of the Declaration of Independence, with every tenth word numbered to help the reader see how the decipherment works. Figure 20 shows the ciphertext – the first number is 115, and the 115th word in the Declaration is instituted, so the first number represents i. The second number in the ciphertext is 73, and the 73rd word in the Declaration is hold, so the second number represents h. Here is the whole decipherment, as printed in the pamphlet:

I have deposited in the county of Bedford, about four miles from Buford’s, in an excavation or vault, six feet below the surface of the ground, the following articles, belonging jointly to the parties whose names are given in number “3,” herewith:

The first deposit consisted of one thousand and fourteen pounds of gold, and three thousand eight hundred and twelve pounds of silver, deposited November, 1819. The second was made December, 1821, and consisted of nineteen hundred and seven pounds of gold, and twelve hundred and eighty-eight pounds of silver; also jewels, obtained in St. Louis in exchange for silver to save transportation, and valued at $13,000.

The above is securely packed in iron pots, with iron covers. The vault is roughly lined with stone, and the vessels rest on solid stone, and are covered with others. Paper number “1” describes the exact locality of the vault, so that no difficulty will be had in finding it.

It is worth noting that there are some errors in the ciphertext. For example, the decipherment includes the words “four miles”, which relies on the 95th word of the Declaration of Independence, beginning with the letter u. However, the 95th word is inalienable. This could be the result of Beale’s sloppy encryption, or it could be that Beale had a copy of the Declaration in which the 95th word was unalienable, which does appear in some versions dating from the early nineteenth century. Either way, the successful decipherment clearly indicated the value of the treasure – at least $20 million at today’s bullion prices.

Not surprisingly, once the author knew the value of the treasure, he spent increasing amounts of time analyzing the other two cipher sheets, particularly the first Beale cipher, which describes the treasure’s location. Despite strenuous efforts, he failed, and the ciphers brought him nothing but sorrow:

When, in the course of human events, it becomes ¹⁰necessary for one people to dissolve the political bands which ²⁰have connected them with another, and to assume among the ³⁰powers of the earth, the separate and equal station to ⁴⁰which the laws of nature and of nature’s God entitle ⁵⁰them, a decent respect to the opinions of mankind requires ⁶⁰that they should declare the causes which impel them to ⁷⁰the separation.

We hold these truths to be self-evident, ⁸⁰that all men are created equal, that they are endowed ⁹⁰by their Creator with certain inalienable rights, that among these ¹⁰⁰are life, liberty and the pursuit of happiness; That to ¹¹⁰secure these rights, governments are instituted among men, deriving their ¹²⁰just powers from the consent of the governed; That whenever ¹³⁰any form of government becomes destructive of these ends, it ¹⁴⁰is the right of the people to alter or to ¹⁵⁰abolish it, and to institute a new government, laying its ¹⁶⁰foundation on such principles and organizing its powers in such ¹⁷⁰form, as to them shall seem most likely to effect¹⁸⁰their safety and happiness. Prudence, indeed, will dictate that governments ¹⁹⁰long established should not be changed for light and transient ²⁰⁰causes; and accordingly all experience hath shewn, that mankind are ²¹⁰more disposed to suffer, while evils are sufferable, than to ²²⁰right themselves by abolishing the forms to which they are ²³⁰accustomed.

But when a long train of abuses and usurpations, ²⁴⁰pursuing invariably the same object evinces a design to reduce ²⁵⁰them under absolute despotism, it is their right, it is ²⁶⁰their duty, to throw off such government, and to provide ²⁷⁰new Guards for their future security. Such has been the ²⁸⁰patient sufferance of these Colonies; and such is now the ²⁹⁰necessity which constrains them to alter their former systems of ³⁰⁰government. The history of the present King of Great Britain ³¹⁰is a history of repeated injuries and usurpations, all having ³²⁰in direct object the establishment of an absolute tyranny over ³³⁰these States. To prove this, let facts be submitted to ³⁴⁰a candid world.

Figure 22 The first three paragraphs of the Declaration of Independence, with every tenth word numbered. This is the key for deciphering the second Beale cipher.

In consequence of the time lost in the above investigation, I have been reduced from comparative affluence to absolute penury, entailing suffering upon those it was my duty to protect, and this, too, in spite of their remonstrations. My eyes were at last opened to their condition, and I resolved to sever at once, and forever, all connection with the affair, and retrieve, if possible, my errors. To do this, as the best means of placing temptation beyond my reach, I determined to make public the whole matter, and shift from my shoulders my responsibility to Mr. Morriss.

Thus the ciphers, along with everything else known by the author, were published in 1885. Although a warehouse fire destroyed most of the pamphlets, those that survived caused quite a stir in Lynchburg. Among the most ardent treasure hunters attracted to the Beale ciphers were the Hart brothers, George and Clayton. For years they pored over the two remaining ciphers, mounting various forms of cryptanalytic attack, occasionally fooling themselves into believing that they had a solution. A false line of attack will sometimes generate a few tantalizing words within a sea of gibberish, which then encourages the cryptanalyst to devise a series of caveats to excuse the gibberish. To an unbiased observer the decipherment is clearly nothing more than wishful thinking, but to the all-consumed treasure hunter it makes complete sense. One of the Harts’ tentative decipherments encouraged them to use dynamite to excavate a particular site; unfortunately, the resulting crater yielded no gold. Although Clayton Hart gave up in 1912, George continued working on the Beale ciphers until 1952.

Professional cryptanalysts have also embarked on the Beale treasure trail. Herbert O. Yardley, who founded the U.S. Cipher Bureau (known as the American Black Chamber) at the end of the First World War, was intrigued by the Beale ciphers, as was Colonel William Friedman, the dominant figure in American cryptanalysis during the first half of the twentieth century. While he was in charge of the Signal Intelligence Service, he made the Beale ciphers part of the training programme, presumably because, as his wife once said, he believed the ciphers to be of “diabolical ingenuity, specifically designed to lure the unwary reader”. The Friedman archive, established after his death in 1969 at the George C. Marshall Research Centre, is frequently consulted by military historians, but the great majority of visitors are eager Beale devotees, hoping to follow up some of the great man’s leads. More recently, one of the major figures in the hunt for the Beale treasure has been Carl Hammer, retired director of computer science at Sperry Univac and one of the pioneers of computer cryptanalysis. According to Hammer, “the Beale ciphers have occupied at least ten per cent of the best cryptanalytic minds in the country. And not a dime of this effort should be begrudged. The work – even the lines that have led into blind alleys – has more than paid for itself in advancing and refining computer research.”

You might be surprised by the strength of the unbroken Beale ciphers, especially bearing in mind that when we left the ongoing battle between codemakers and codebreakers, it was the codebreakers who were on top. Babbage and Kasiski had invented a way of breaking the Vigenère cipher, and codemakers were struggling to find something to replace it. How did Beale come up with something that is so formidable? The answer is that the Beale ciphers were created under circumstances that gave the cryptographer a great advantage. The messages were not intended to be part of a series, and because they related to such a valuable treasure, Beale might have been prepared to create a special keytext for the first and third ciphers. Indeed, if the keytext was penned by Beale himself, this would explain why searches of published material have not revealed it. We can imagine that Beale might have written a two-thousand-word private essay on the subject of buffalo hunting, of which there was only one copy. Only the holder of this essay, the unique keytext, would be able to decipher the first and third Beale ciphers. Beale mentioned that he had left the key in “the hand of a friend” in St Louis, but if the friend lost or destroyed the key, then cryptanalysts might never be able to crack the Beale ciphers.

Creating a keytext specifically for one message is much more secure than using a key based on a published book, but it is practical only if the sender has the time to create the keytext and is able to convey it to the intended recipient, requirements that are not feasible for routine, day-to-day communications. In Beale’s case, he could compose his keytext at leisure, deliver it to his friend in St Louis whenever he happened to be passing through, and then have it posted or collected at some arbitrary time in the future, whenever the treasure was to be reclaimed.

It is possible that the treasure was found many years ago and that the discoverer spirited it away without being spotted by local residents. Beale enthusiasts with a fondness for conspiracy theories have suggested that the National Security Agency (NSA) has already found the treasure. America’s central government cipher facility has access to the most powerful computers and some of the most brilliant minds in the world, and they may have discovered something about the ciphers that has eluded everybody else. The lack of any announcement would be in keeping with the NSA’s hush-hush reputation – it has been proposed that NSA stands not for “National Security Agency”, but rather for “Never Say Anything” or “No Such Agency”.

Finally, we cannot exclude the possibility that the Beale ciphers are an elaborate hoax and that Beale never existed. Sceptics have suggested that the unknown author, inspired by Poe’s “The Gold Bug”, fabricated the whole story and published the pamphlet as a way of profiting from the greed of others.

One of the foremost nonbelievers is the cryptographer Louis Kruh, who claims to have found evidence that the pamphlet’s author also wrote Beale’s letters, the one supposedly sent from St Louis and the one supposedly contained in the box. He performed a textual analysis on the words attributed to the author and the words attributed to Beale to see if there were any similarities. Kruh compared aspects such as the percentage of sentences beginning with the, of and and, the average number of commas and semicolons per sentence, and the writing style—the use of negatives, negative passives, infinitives, relative clauses and so on. In addition to the author’s words and Beale’s letters, the analysis also took in the writing of three other nineteenth-century Virginians. Of the five sets of writing, those authored by Beale and the pamphlet’s author bore the closest resemblance, suggesting that they may have been written by the same person. In other words, this suggests that the author faked the letters attributed to Beale and fabricated the whole story.

On the other hand, evidence favouring the validity of the ciphers comes from historical research, which can be used to verify the story of Thomas Beale. Peter Viemeister, a local historian, has gathered much of the research in his book The Beale Treasure – History of a Mystery. Viemeister began by asking if there was any evidence that Thomas Beale actually existed. Using the census of 1790 and other documents, Viemeister has identified several Thomas Beales who were born in Virginia and whose backgrounds fit the few known details. Viemeister has also attempted to confirm the other details in the pamphlet, such as Beale’s trip to Santa Fe and his discovery of gold. For example, there is a Cheyenne legend dating from around 1820 that tells of gold and silver being taken from the West and buried in eastern mountains. Also, the 1820 postmaster’s list in St Louis contains a Thomas Beall, which fits in with the pamphlet’s claim that Beale passed through the city in 1820 on his journey westward after leaving Lynchburg. The pamphlet also says that Beale sent a letter from St Louis in 1822. So there does seem to be a basis for the tale of the Beale ciphers, and consequently it continues to enthrall cryptanalysts and treasure hunters.

Having read the tale of the Beale ciphers, you might be encouraged to take up the challenge yourself. The lure of an unbroken nineteenth-century cipher, together with a treasure worth $20 million, might prove irresistible. However, before you set off on the treasure trail, take heed of the advice given by the author of the pamphlet:

Before giving the papers to the public, I would say a word to those who may take an interest in them, and give them a little advice, acquired by bitter experience. It is, to devote only such time as can be spared from your legitimate business to the task, and if you can spare no time, let the matter alone … Again, never, as I have done, sacrifice your own and your family’s interests to what may prove an illusion; but, as I have already said, when your day’s work is done, and you are comfortably seated by your good fire, a short time devoted to the subject can injure no one, and may bring its reward.