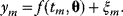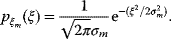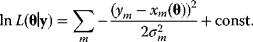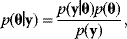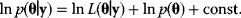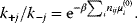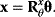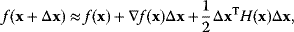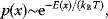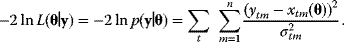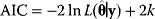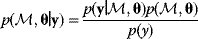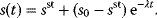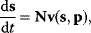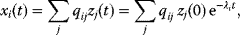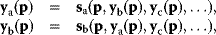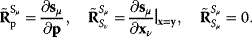6
Model Fitting, Reduction, and Coupling
- Introduction
- 6.1 Parameter Estimation
- 6.2 Model Selection
- 6.3 Model Reduction
- 6.4 Coupled Systems and Emergent Behavior
- Exercises
- References
- Further Reading
Introduction
Cells and organisms are incredibly complex, and the only way to understand them is through simplified pictures. Simplicity comes from omitting irrelevant details. For instance, we may picture a pathway in isolation, pretending that its environment is given and constant, or we may neglect microscopic details within a system: Instead of considering all reaction events between single molecules, we average over them and see a smooth behavior of macroscopic concentrations.
Simplified models will be approximations, but approximations are exactly what we are aiming at: models that provide a good level of details and are easy to work with. Keeping in mind that cells are much more complex than our models (and that effective quantities like free energies summarize a lot of microscopic complexity in a single number), we can move between models of different scope whenever necessary. If models turn out to be too simple, we zoom in and consider previously neglected details, or zoom out and include parts of the environment into our model.
Early biochemical models were simple and mostly used for studying general principles, for example, the emergence of oscillations from feedback regulation. With increasing amounts of data, models of metabolism, cell cycle, or signaling pathways have become more complex, more accurate, and more predictive. As more data are becoming available, biochemical models are increasingly used to picture biological reality and specific experimental situations.
Building a useful model is usually a lengthy process. Based on literature studies and collected data, one starts by developing hypotheses about the biological system. Which objects and processes (e.g., substances, reactions, cell compartments) are relevant? Which mathematical framework is appropriate (continuous or discrete, kinetic or stochastic, spatial or nonspatial model)? Sometimes, model structures must meet specific criteria, for example, known robustness properties. The bacterial chemotaxis system, for instance, shows a precise adaptation to external stimuli, and a good model should account for this fact; models that implement perfect adaptation by their network structure will be even more plausible than models that require a fine-tuning of parameters (see Section 10.2).
Modeling often involves several cycles of model generation, fitting, testing, and selection [1,2]. To choose between different model variants, new experiments may be required. In practice, the choice of a model depends on various factors: Does a model reflect the basic biological facts about the system? Is it simple enough to be simulated and fitted? Does it explain known observations and can it predict previously unobserved behavior? Sometimes, a model's structure (e.g., stoichiometric matrix and rate laws) is already known, while the parameter values (e.g., rate constants or external concentrations) still have to be determined. They can be obtained by fitting the model outputs (e.g., concentration time series) to a set of experimental data. If the model is structurally identifiable (a property that will be explained below), if enough data are available, and if the data are free of errors, this procedure should allow us to determine the true parameter set: For all other parameter sets, data and model output would differ. In reality, however, these conditions are rarely met. Therefore, modelers put large efforts in parameter estimation and in developing efficient optimization algorithms.
Without comprehensive data, many parameters remain nonidentifiable and there will be a risk of overfitting. This calls for models that are simple enough to be fully validated by existing data, which limits the degree of details in realistic models. The process of model simplification can be systematized: Different hypotheses and simplifications may lead to different model variants, and statistical methods can help us select based on data. Using optimal experimental design [3], and based on preliminary models, one may devise experiments that are most likely to yield the information needed to select between possible models. This cycle of experiments and modeling enables us to overcome many limitations of one-step model selection. Model selection can be insightful: For instance, the fact that fast equilibrated processes cannot be resolved using data can tell us that also the cellular machinery may take these fast processes “for granted” when controlling processes on slower time scales.
6.1 Parameter Estimation
In mathematical models, for example, the kinetic models discussed before, each possible parameter set 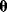 is mapped to a set of predicted data values
is mapped to a set of predicted data values  via a function
via a function 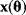 . If measurement data are given, we can try to invert this procedure and reconstruct the unknown parameter set
. If measurement data are given, we can try to invert this procedure and reconstruct the unknown parameter set 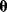 from the data. There are three possible cases: (i) the parameters are uniquely determined; (ii) the parameters are overdetermined (i.e., no parameter set corresponds to the data) because data are noisy or the model is wrong; (iii) the parameters are underdetermined, that is, several or many parameter sets explain the data equally well.
from the data. There are three possible cases: (i) the parameters are uniquely determined; (ii) the parameters are overdetermined (i.e., no parameter set corresponds to the data) because data are noisy or the model is wrong; (iii) the parameters are underdetermined, that is, several or many parameter sets explain the data equally well.
Case (i) is mainly theoretical; in reality, when simple models are applied to complex phenomena, we do not expect perfect predictions. Cases (ii) and (iii) are what we normally encounter. Pragmatically, it is common to assume that a model is correct and that discrepancies between data and model predictions are caused by measurement errors. This resolves the problem of overdetermined parameters (case (ii)) and allows us to fit model parameters and to compare different models by their data fits. We can use data and statistical methods to obtain parameter estimates that approximate the true parameter values, as well as the uncertainty of the estimates [4]. Underdetermined parameters (case (iii)) can either be accepted as a fact or specific parameters can be chosen by additional regularization criteria. Common modeling tools such as COPASI [5] support parameter estimation.
6.1.1 Regression, Estimators, and Maximal Likelihood
6.1.1.1 Regression
Linear regression is a typical example of parameter estimation. A linear regression problem is shown in Figure 6.1: A number of data points 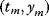 have to be approximated by a straight line
have to be approximated by a straight line 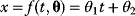 . If the data points are indeed located exactly on a line, we can choose a parameter vector
. If the data points are indeed located exactly on a line, we can choose a parameter vector 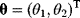 such that
such that 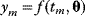 holds for all data points
holds for all data points  . In practice, measured data will scatter, and we search for a regression line as close as possible to the data points. If the deviation between line and data is scored by the sum of squared residuals (SSR),
. In practice, measured data will scatter, and we search for a regression line as close as possible to the data points. If the deviation between line and data is scored by the sum of squared residuals (SSR),  , the regression problem can be seen as a minimization problem for the function
, the regression problem can be seen as a minimization problem for the function  .
.
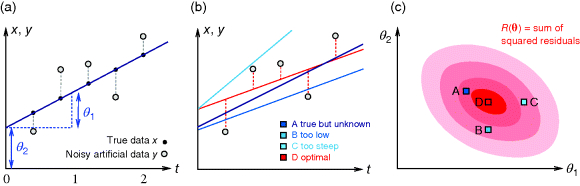
Figure 6.1 Linear regression. (a) Artificial data 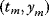 (gray) are generated by computing data points (black) from a model
(gray) are generated by computing data points (black) from a model 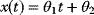 (straight line) and adding Gaussian noise. Each possible line is characterized by two parameters, slope
(straight line) and adding Gaussian noise. Each possible line is characterized by two parameters, slope 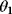 and offset
and offset 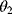 . The aim in linear regression is to reconstruct the unknown parameters from noisy data (in this case, artificial data
. The aim in linear regression is to reconstruct the unknown parameters from noisy data (in this case, artificial data 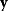 ). (b) The deviation between a possible line (four lines A, B, C, and D are shown) and data can be measured by the sum of squared residuals. Residuals are shown for line D (dashed lines). (c) Each of the lines A, B, C, and D corresponds to a point
). (b) The deviation between a possible line (four lines A, B, C, and D are shown) and data can be measured by the sum of squared residuals. Residuals are shown for line D (dashed lines). (c) Each of the lines A, B, C, and D corresponds to a point 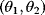 in parameter space. The SSR as a function
in parameter space. The SSR as a function 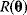 in parameter space can be pictured as a landscape (shades of pink; dark pink indicates small SSR, that is, a good fit). Line D minimizes the SSR value. Small SSR values correspond to a large likelihood.
in parameter space can be pictured as a landscape (shades of pink; dark pink indicates small SSR, that is, a good fit). Line D minimizes the SSR value. Small SSR values correspond to a large likelihood.
6.1.1.2 Estimators and Maximal Likelihood
The use of the SSR as a distance measure is justified by statistical arguments, assuming that the data stem from some generative model with unknown parameters and additional random errors. As an example, we consider a curve 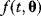 with an independent variable
with an independent variable 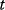 (e.g., time) and curve parameters
(e.g., time) and curve parameters 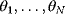 . For a number of time points
. For a number of time points 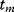 , the model yields the output values
, the model yields the output values 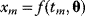 , which can be seen as a vector
, which can be seen as a vector 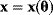 . By adding random errors
. By adding random errors 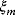 , we obtain the noisy data:
, we obtain the noisy data:
If the errors follow independent Gaussian distributions with mean 0 and variance 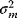 , each data point
, each data point 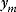 is a Gaussian-distributed random number with mean
is a Gaussian-distributed random number with mean 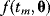 and variance
and variance 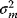 .
.
In parameter estimation, we revert this process: Starting with a model (characterized by a function 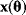 and noise variances
and noise variances 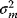 ) and a set of noisy data
) and a set of noisy data 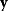 (some realization of Eq. (6.1)), we try to infer the unknown parameter set
(some realization of Eq. (6.1)), we try to infer the unknown parameter set 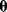 . A function
. A function 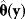 mapping each data set
mapping each data set 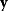 to an estimated parameter vector
to an estimated parameter vector 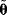 is called an estimator.
is called an estimator.
Practical and fairly simple estimators follow from the principle of maximum likelihood. The likelihood of a model is the conditional probability to observe the actually observed data 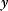 if the model is correct. For instance, if a model predicts “Tomorrow, the sun will shine with 80% probability,” and sunshine is indeed observed, the model has a likelihood of 0.8. Accordingly, if a model structure is given, each possible parameter set
if the model is correct. For instance, if a model predicts “Tomorrow, the sun will shine with 80% probability,” and sunshine is indeed observed, the model has a likelihood of 0.8. Accordingly, if a model structure is given, each possible parameter set 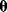 has a likelihood
has a likelihood 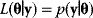 . To compute likelihood values for a biochemical model, we need to specify our assumptions about possible measurement errors. From a generative model like Eq. (6.1), the probability density
. To compute likelihood values for a biochemical model, we need to specify our assumptions about possible measurement errors. From a generative model like Eq. (6.1), the probability density 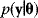 to observe the data
to observe the data 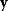 , given the parameters
, given the parameters 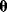 , can be computed. The maximum likelihood estimator
, can be computed. The maximum likelihood estimator
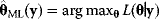
yields the parameter set that would maximize the likelihood given the observed data. If the maximum point is not unique, the model parameters cannot be identified by maximum likelihood estimation.
6.1.1.3 Method of Least Squares
To see how likelihood functions can be computed in practice, we return to the model Eq. (6.1) with additive Gaussian noise. If our model yields a true value 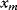 , the observable noisy value
, the observable noisy value 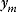 has a probability density
has a probability density 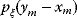 , where
, where 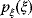 is the probability density of the error term. If the variables
is the probability density of the error term. If the variables 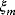 are independently Gaussian-distributed with mean 0 and variance
are independently Gaussian-distributed with mean 0 and variance 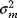 , their density reads
, their density reads
Given one data point 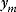 , we obtain the likelihood function:
, we obtain the likelihood function:
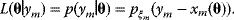
Given all data points and assuming that random errors are independent, the probability to observe the data set 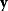 is the product of all probabilities for individual data points. Hence, the likelihood reads
is the product of all probabilities for individual data points. Hence, the likelihood reads
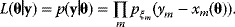
By inserting the Gaussian probability density (6.3) and taking the logarithm, we obtain
If all random errors 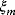 have the same variance
have the same variance 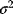 , the logarithmic likelihood reads
, the logarithmic likelihood reads
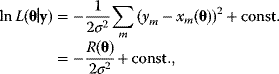
where 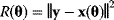 is the sum of squared residuals. Thus, maximum likelihood estimation with the error model (6.3) is equivalent to a minimization of weighted squared residuals. This justifies the method of least squares. The same argument holds for data on logarithmic scale. Additive Gaussian errors on logarithmic scale correspond to multiplicative log-normal errors for the original, nonlogarithmic data. In this case, a uniform variance
is the sum of squared residuals. Thus, maximum likelihood estimation with the error model (6.3) is equivalent to a minimization of weighted squared residuals. This justifies the method of least squares. The same argument holds for data on logarithmic scale. Additive Gaussian errors on logarithmic scale correspond to multiplicative log-normal errors for the original, nonlogarithmic data. In this case, a uniform variance 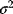 for all data points means that all nonlogarithmic data points have the same range of relative errors. According to the Gauss–Markov theorem, the least-squares estimator is a best linear unbiased estimator if the model is linear and if the errors
for all data points means that all nonlogarithmic data points have the same range of relative errors. According to the Gauss–Markov theorem, the least-squares estimator is a best linear unbiased estimator if the model is linear and if the errors 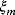 for different data points are linearly uncorrelated and have the same variance. The error distribution
for different data points are linearly uncorrelated and have the same variance. The error distribution 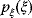 need not be Gaussian.
need not be Gaussian.
6.1.2 Parameter Identifiability
If a likelihood function is seen as a landscape in parameter space, the maximum likelihood estimate 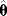 is the maximum point in this landscape. According to Eq. (6.6), this point corresponds to a minimum of the weighted SSR (compare with Figure 6.1). In a single isolated maximum, the logarithmic likelihood function
is the maximum point in this landscape. According to Eq. (6.6), this point corresponds to a minimum of the weighted SSR (compare with Figure 6.1). In a single isolated maximum, the logarithmic likelihood function 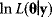 has strictly negative curvatures and can be approximated using the local curvature matrix
has strictly negative curvatures and can be approximated using the local curvature matrix 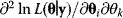 . Directions with weak curvatures correspond to parameter variations that have little effect on the likelihood.
. Directions with weak curvatures correspond to parameter variations that have little effect on the likelihood.
If several parameter sets fit the data equally well, the maximum likelihood criterion does not yield a unique solution, and the estimation problem is underdetermined (Figure 6.2). In particular, the likelihood function may be maximal on an entire curve or surface in parameter space. This can have different reasons: structural or practical nonidentifiability.
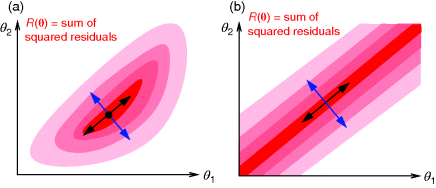
Figure 6.2 Identifiability. (a) In identifiable models, the sum of squared residuals (SSR, shown in pink) has a single minimum point (dot). The curvatures (i.e., second derivatives) of the SSR form a matrix. Its eigenvectors point toward directions of maximal (blue) and minimal curvatures (black). (b) In the nonidentifiable model shown, the SSR is minimized on a line in parameter space. A linear combination of parameters (blue arrow) is identifiable from the data, while another one (black arrow) is nonidentifiable, visible from the vanishing curvatures along this direction.
6.1.2.1 Structural Nonidentifiability
If two parameters 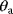 and
and 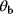 in a model appear only as a product
in a model appear only as a product 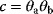 , they are underdetermined: For any choice of
, they are underdetermined: For any choice of 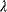 , the pair
, the pair 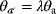 and
and 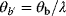 will yield the same result
will yield the same result 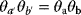 and lead to the same model predictions. Thus, maximum likelihood estimation (which compares model predictions with data) can determine the product
and lead to the same model predictions. Thus, maximum likelihood estimation (which compares model predictions with data) can determine the product 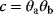 , but not the individual values
, but not the individual values 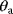 and
and 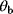 . Such models are called structurally nonidentifiable. To resolve this problem, we may replace the product
. Such models are called structurally nonidentifiable. To resolve this problem, we may replace the product 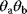 by a new identifiable parameter
by a new identifiable parameter 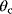 . Structural nonidentifiability can arise in various ways and may be difficult to detect and resolve.
. Structural nonidentifiability can arise in various ways and may be difficult to detect and resolve.
6.1.2.2 Practical Nonidentifiability
Even structurally identifiable models may be practically nonidentifiable with respect to some parameters if data are insufficient, that is, if too few or the wrong kind of data are given. In particular, if the number of parameters exceeds the number of data points, the parameters cannot be identified. Let us assume that each possible parameter set 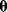 would yield a prediction
would yield a prediction 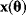 and that the mapping
and that the mapping 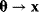 is continuous. If the dimensionality of
is continuous. If the dimensionality of 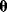 is larger than the dimensionality of
is larger than the dimensionality of  , it is impossible to invert the function
, it is impossible to invert the function 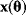 and to reconstruct the parameters from the given data. Rules for the minimum numbers of experimental data needed to reconstruct differential equation models can be found in Ref. [6].
and to reconstruct the parameters from the given data. Rules for the minimum numbers of experimental data needed to reconstruct differential equation models can be found in Ref. [6].
If a model is nonidentifiable, numerical parameter optimization with different starting points will yield different estimates 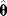 , all located on the same manifold in parameter space. In the example above, the estimates for
, all located on the same manifold in parameter space. In the example above, the estimates for 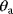 and
and 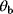 would differ, but they would all satisfy the relation
would differ, but they would all satisfy the relation 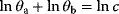 with a fixed value for
with a fixed value for  . On logarithmic scale, the estimates would lie on a straight line (provided that all other model parameters are identifiable).
. On logarithmic scale, the estimates would lie on a straight line (provided that all other model parameters are identifiable).
Problems like parameter identification in which the procedure of model simulation is reverted are called inverse problems. If the solution of an inverse problem is not unique, the problem is ill-posed and additional assumptions are required for a unique solution. For instance, we may postulate that the sum of squares of all parameter values should be minimized. Such requirements can help us select a particular solution; the method is called regularization.
6.1.3 Bootstrapping
From a noisy data set 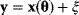 , we cannot determine the true model parameters
, we cannot determine the true model parameters 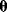 ; we only obtain an estimate
; we only obtain an estimate 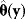 . Different realizations of the random error
. Different realizations of the random error 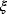 lead to different possible sets of noisy data, and thus different estimates
lead to different possible sets of noisy data, and thus different estimates 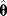 . Ideally, the mean value
. Ideally, the mean value 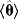 of these estimates should yield the true parameter value (in this case, the estimator is called “unbiased”), and their variance should be small. In practice, only a single data set is available, and we obtain a single point estimate
of these estimates should yield the true parameter value (in this case, the estimator is called “unbiased”), and their variance should be small. In practice, only a single data set is available, and we obtain a single point estimate  . Bootstrapping [7] is a way to assess, at least approximately, the statistical distributions of such estimates. First, hypothetical data sets of the same size as the original data set are generated from the original data by resampling with replacement (see Figure 6.3). Then, a parameter estimate
. Bootstrapping [7] is a way to assess, at least approximately, the statistical distributions of such estimates. First, hypothetical data sets of the same size as the original data set are generated from the original data by resampling with replacement (see Figure 6.3). Then, a parameter estimate  is calculated for each of these data sets. The empirical distribution of these estimates is taken as an approximation of the true distribution of
is calculated for each of these data sets. The empirical distribution of these estimates is taken as an approximation of the true distribution of  . The bootstrapping method is asymptotically consistent, that is, the approximation becomes exact as the size of the original data set goes to infinity.
. The bootstrapping method is asymptotically consistent, that is, the approximation becomes exact as the size of the original data set goes to infinity.
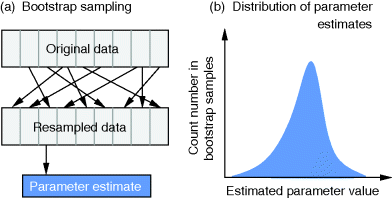
Figure 6.3 Bootstrapping with resampled data. (a) A hypothetical data set is generated by sampling values with replacement from the original data. Each resampled data set yields one parameter estimate  . (b) The distribution of parameter estimates obtained from bootstrap samples approximates the true distribution of the estimator
. (b) The distribution of parameter estimates obtained from bootstrap samples approximates the true distribution of the estimator  . For a good approximation, the original data set should be large.
. For a good approximation, the original data set should be large.
6.1.3.1 Cross-Validation
There is a fundamental difference between model fitting and prediction. If a model has been fitted to a given data, we enforce an agreement with exactly these training data, and the model is likely to fit them better than it will fit test data that have not been used during model fitting. The fitted model will fit the data even better than the true model itself – a phenomenon called overfitting. However, overfitted models will predict new data less reliably than the true model, and their parameter values may differ strongly from the true parameter values. Therefore, overfitting should be avoided.
We have seen an example of overfitting in Figure 6.1: The least-squares regression line yields a lower SSR than the true model – because a low SSR is what it is optimized for. The apparent improvement is achieved by fitting the noise, that is, by adjusting the line to the specific realization of random errors in the data. However, this precise fit does not lead to better predictions; here, the true model will be more reliable.
How can we test whether models are overfitted? In theory, we would need new data that have not been used during model fitting. In cross-validation (see Figure 6.4), to mimic this test, an existing data set is split into two parts: a training set for fitting and a test set for evaluating the model predictions. This procedure is repeated many times with different parts of the data used as test sets. From the prediction errors, we can judge how the model predicts new data on average, when fitted to  data points (size of the training set). The average prediction error is an important quality measure and allows us to reject models prone to overfitting. Cross-validation, just like bootstrapping, can be numerically demanding because many estimation runs must be performed.
data points (size of the training set). The average prediction error is an important quality measure and allows us to reject models prone to overfitting. Cross-validation, just like bootstrapping, can be numerically demanding because many estimation runs must be performed.
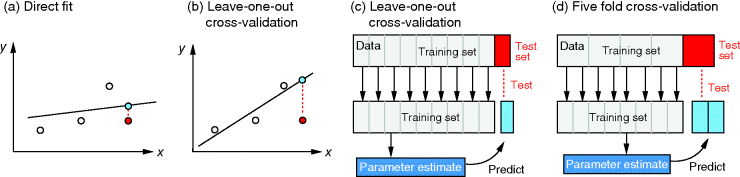
Figure 6.4 Cross-validation as a way to detect overfitting. (a) In linear regression, a straight line is fitted to data points (gray and red). The fitting error (dotted red line) is the distance between a data point (red) and the corresponding height of the regression line (blue). The regression line is chosen such that fitting errors are minimized. (b) In a leave-one-out cross-validation, we pretend that one point (red) is unknown and attempt to predict it from the model. The regression line is fitted to the remaining (gray) points, and the prediction error for the red data point will be larger than the fitting error shown in part (a). (c) Scheme of leave-one-out cross-validation. The model is fitted to all data points except for one (training set) and the remaining data point (test set) is predicted. This procedure is repeated for each data point to be predicted and yields an estimate of the average prediction error. (d) In 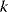 -fold cross-validation, the data are split into
-fold cross-validation, the data are split into 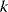 subsets. In every run,
subsets. In every run, 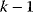 subsets serve as training data, while the remaining subset is used as test data.
subsets serve as training data, while the remaining subset is used as test data.
6.1.4 Bayesian Parameter Estimation
In maximum likelihood estimation, we search for a single parameter set representing the true parameters. Bayesian parameter estimation, an alternative approach, is based on a different premise: The parameter set 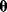 is formally treated as a random variable. In this context, randomness describes a subjective uncertainty due to lack of information. Once more data become available, the parameter distribution can be updated and uncertainty will be reduced. By choosing a prior parameter distribution, we state how plausible certain parameter sets appear in advance. Given a parameter set
is formally treated as a random variable. In this context, randomness describes a subjective uncertainty due to lack of information. Once more data become available, the parameter distribution can be updated and uncertainty will be reduced. By choosing a prior parameter distribution, we state how plausible certain parameter sets appear in advance. Given a parameter set 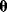 , we assume that a specific data set
, we assume that a specific data set 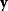 will be observed with a probability density (likelihood)
will be observed with a probability density (likelihood) 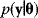 . Hence, parameters and data are described by a joint probability distribution with density
. Hence, parameters and data are described by a joint probability distribution with density 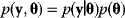 (see Figure 6.5).
(see Figure 6.5).
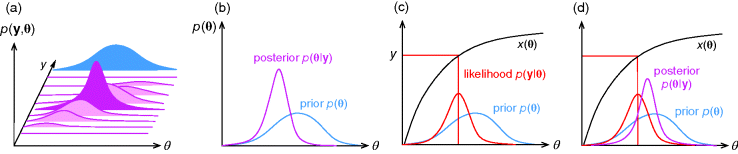
Figure 6.5 Bayesian parameter estimation. (a) In Bayesian estimation, parameters 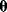 and data
and data 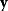 are described by a joint probability distribution with density
are described by a joint probability distribution with density 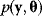 . The marginal density
. The marginal density 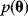 of the parameters (blue) is called prior, while the conditional density
of the parameters (blue) is called prior, while the conditional density 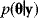 given a certain data set (magenta) is called posterior. (b) The posterior is narrower than the prior (blue), reflecting the information gained by the data. (c) Prior and likelihood. A variable
given a certain data set (magenta) is called posterior. (b) The posterior is narrower than the prior (blue), reflecting the information gained by the data. (c) Prior and likelihood. A variable 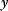 is given by the output
is given by the output 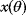 of a generative model (black line) plus Gaussian measurement errors. A given observed value
of a generative model (black line) plus Gaussian measurement errors. A given observed value 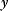 gives rise to the likelihood function
gives rise to the likelihood function 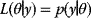 in parameter space. (d) The posterior is the product of prior and likelihood function, normalized to a total probability of 1.
in parameter space. (d) The posterior is the product of prior and likelihood function, normalized to a total probability of 1.
Given a data set 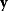 , we can determine the conditional probabilities of θ given
, we can determine the conditional probabilities of θ given 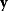 , called posterior probabilities. According to the Bayes formula,
, called posterior probabilities. According to the Bayes formula,
the posterior probability density 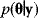 is proportional to likelihood and prior density. Since the data
is proportional to likelihood and prior density. Since the data 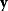 are given, the denominator
are given, the denominator 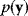 is a constant; it is used for normalization only. Bayesian estimation can also be applied recursively, that is, the posterior from one estimation can serve as a prior for another estimation with new data.
is a constant; it is used for normalization only. Bayesian estimation can also be applied recursively, that is, the posterior from one estimation can serve as a prior for another estimation with new data.
Maximum likelihood estimation and Bayesian parameter estimation differ in their practical use and in how probabilities are interpreted. In the former, we ask: Under which hypothesis about the parameters would the data appear most probable? In the latter, we directly ask: How probable does each parameter set appear given the data? Moreover, the aim in Bayesian statistics is not to determine parameters precisely, but to characterize their posterior 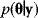 (e.g., to compute marginal distributions for individual parameters or probabilities for quantitative predictions). For complicated models, the posterior cannot be computed analytically; instead, it is common to sample parameter sets from the posterior, for instance, by using the Metropolis–Hastings algorithm described below.
(e.g., to compute marginal distributions for individual parameters or probabilities for quantitative predictions). For complicated models, the posterior cannot be computed analytically; instead, it is common to sample parameter sets from the posterior, for instance, by using the Metropolis–Hastings algorithm described below.
Bayesian priors are used to encode general beliefs or previous knowledge about the parameter values. In practice, they can serve as regularization terms that make models identifiable. By taking the logarithm of Eq. (6.8), we obtain the logarithmic posterior:
If the logarithmic likelihood has no unique maximum (as in Figure 6.2b), the model will not be identifiable by maximum likelihood estimation. By adding the logarithmic prior 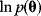 in Eq. (6.9), we can obtain a unique maximum in the posterior density.
in Eq. (6.9), we can obtain a unique maximum in the posterior density.
6.1.4.1 Bayesian Networks
Bayesian statistics is commonly used in probabilistic reasoning [10,11] to study relationships between uncertain facts. Facts are described by random variables (binary or quantitative), and their (assumed) probabilistic dependencies are represented as a directed acyclic graph 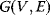 , called Bayesian network [10,12,13]. Vertices
, called Bayesian network [10,12,13]. Vertices 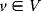 correspond to random variables
correspond to random variables 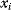 and edges
and edges 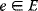 encode conditional dependencies between these variables: A variable, given the variables represented by its parent vertices, is conditionally independent on all other variables. Bayesian networks can also define a joint probability distribution precisely. Each variable
encode conditional dependencies between these variables: A variable, given the variables represented by its parent vertices, is conditionally independent on all other variables. Bayesian networks can also define a joint probability distribution precisely. Each variable 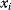 is associated with a conditional probability
is associated with a conditional probability 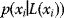 , where
, where 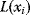 denotes the parents of variable
denotes the parents of variable 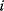 , that is, the set of variables having a direct probabilistic influence on
, that is, the set of variables having a direct probabilistic influence on 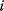 . Together, these conditional probabilities define a joint probability distribution via the formula
. Together, these conditional probabilities define a joint probability distribution via the formula 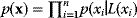 . Notably, the shape of a Bayesian network is not uniquely defined by a dependence structure: Instead, the same probability distribution can be represented by different equivalent Bayesian networks, which cannot be distinguished by observation of the variables
. Notably, the shape of a Bayesian network is not uniquely defined by a dependence structure: Instead, the same probability distribution can be represented by different equivalent Bayesian networks, which cannot be distinguished by observation of the variables  [13].
[13].
Bayesian networks have, for instance, been used to infer gene regulation networks from gene expression data. Variables 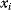 belonging to the vertices
belonging to the vertices 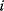 are a measure of gene activity, for example, the expression level of a gene or the amount of active protein. The assumption is that statistical information (given the expression of gene
are a measure of gene activity, for example, the expression level of a gene or the amount of active protein. The assumption is that statistical information (given the expression of gene 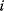 , the expression of gene
, the expression of gene 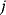 is independent of other genes) reflects mechanistic causality (gene product
is independent of other genes) reflects mechanistic causality (gene product 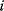 is the only regulator of gene
is the only regulator of gene 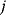 ).
).
Generally, Bayesian conditioning can be applied in different ways: to search for networks or network equivalence classes that best explain measured data; to learn the parameters of a given network; or a network can be used to predict data, for example, possible gene expression profiles. In any case, to resolve causal interactions, time series data or data from intervention experiments are needed. In dynamic Bayesian networks, time behavior is modeled explicitly: In this case, the conditional probabilities describe the state of a gene in one moment given the states of genes in the moment before [14].
6.1.5 Probability Distributions for Rate Constants
The values of rate constants, an important requisite for kinetic modeling, can be obtained in various ways: from the literature, from databases like Brenda [15] or Sabio-RK [16], from fits to dynamic data, from optimization for other objectives, or from simple guesses. Based on data, we can obtain parameter distributions. Parameters that have been measured can be described by a log-normal distribution representing the measured value and error bar; if experimental conditions are not exactly comparable, the error bar may be artificially increased. If a parameter has not been measured, one may describe it by a broader distribution. The empirical distribution of Michaelis constants in the Brenda database, which is roughly log-normal, can be used to describe a specific, but unknown Michaelis constant. Such probability distributions can be helpful for both uncertainty analysis and parameter estimation. In maximum likelihood estimation, on can restrict the parameters to biologically plausible values and reduce the search space for parameter fitting. In Bayesian estimation, knowledge encoded in prior distributions is combined with information from the data.
6.1.5.1 Distributions of Enzymatic Rate Constants
If we neglect all possible interdependencies, we can assume separate distributions for all parameters in a kinetic model. According to Bayesian views, a probability distribution reflects what we can know about some quantity, based on data or prior beliefs. The shapes of such distributions may be chosen by the principle of minimal information (see Section 10.1) [17]: For instance, given a known mean value and variance (and no other known characteristics), we should assume a normal distribution. If we apply this principle to logarithmic parameters, the parameters themselves will follow log-normal distributions.
What could constitute meaningful mean values and variances, specifically for rate constants? This depends on what knowledge we intend to represent, namely, values for specific parameters (e.g., the 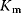 value of some enzyme, with measurement error) or types of parameters (
value of some enzyme, with measurement error) or types of parameters (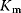 values in general, characterized by median value and spread). In the latter case, we may consult the distributions of measured rate constants, possibly broken down to specific enzyme classes (see Figure 6.6). Thermodynamic and enzyme kinetic parameters can be found in publications or databases like NIST [18], Brenda [15], or Sabio-RK [16]. With more information about model elements, for example, molecule structures, improved parameter estimates can be obtained from molecular modeling or machine learning [19].
values in general, characterized by median value and spread). In the latter case, we may consult the distributions of measured rate constants, possibly broken down to specific enzyme classes (see Figure 6.6). Thermodynamic and enzyme kinetic parameters can be found in publications or databases like NIST [18], Brenda [15], or Sabio-RK [16]. With more information about model elements, for example, molecule structures, improved parameter estimates can be obtained from molecular modeling or machine learning [19].
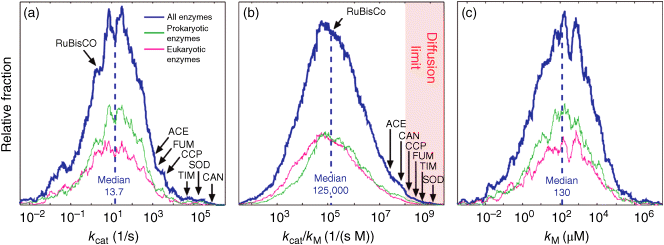
Figure 6.6 Distribution of enzymatic rate constants from the Brenda database [15]. (a) 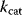 values in the Brenda database. (b)
values in the Brenda database. (b) 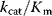 ratios. (c)
ratios. (c) 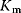 values. The values of RuBisCo and some prominent enzymes in E. coli are indicated. From Ref. [20].
values. The values of RuBisCo and some prominent enzymes in E. coli are indicated. From Ref. [20].
6.1.5.2 Thermodynamic Constraints on Rate Constants
Whenever kinetic constants are fitted, optimized, or sampled, we should ensure that only valid parameter combinations are used. In metabolic networks with mass-action kinetics, for instance, the rate constants 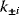 and the equilibrium constant
and the equilibrium constant 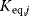 in a reaction
in a reaction 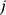 are related by
are related by 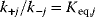 . The equilibrium constants, in turn, depend on standard chemical potentials
. The equilibrium constants, in turn, depend on standard chemical potentials  via
via 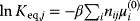 , with
, with 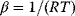 , which yields the condition
, which yields the condition
Thus, a choice of rate constants 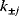 will only be feasible if there exists a set of standard chemical potentials
will only be feasible if there exists a set of standard chemical potentials 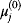 satisfying Eq. (6.12). If a metabolic network contains loops, it is unlikely that this test will be passed by randomly chosen rate constants.
satisfying Eq. (6.12). If a metabolic network contains loops, it is unlikely that this test will be passed by randomly chosen rate constants.
Instead of excluding parameter sets by hindsight, based on condition (6.12), one may directly construct parameter sets that satisfy it automatically [21,22]. The equation itself shows us how to proceed: The chemical potentials 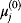 are calculated or sampled from a Gaussian distribution and used to compute the equilibrium constants. Prefactors
are calculated or sampled from a Gaussian distribution and used to compute the equilibrium constants. Prefactors 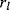 are then sampled from a log-normal distribution, and the kinetic constants are set to
are then sampled from a log-normal distribution, and the kinetic constants are set to 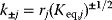 . This procedure yields rate constants
. This procedure yields rate constants 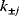 with dependent log-normal distributions, which are feasible by construction. For Michaelis–Menten-like rate laws (e.g., convenience kinetics [23] or the modular rate laws [24]), this works similarly: Velocity constants, defined as the geometric means
with dependent log-normal distributions, which are feasible by construction. For Michaelis–Menten-like rate laws (e.g., convenience kinetics [23] or the modular rate laws [24]), this works similarly: Velocity constants, defined as the geometric means 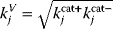 of
of 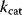 values, can be used as independent basic parameters; and feasible
values, can be used as independent basic parameters; and feasible 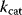 values, satisfying the Haldane relationships, can be computed from equilibrium constants, Michaelis constants, and velocity constants [24].
values, satisfying the Haldane relationships, can be computed from equilibrium constants, Michaelis constants, and velocity constants [24].
6.1.5.3 Dependence Scheme for Model Parameters
Dependencies between rate constants can be an obstacle in modeling, but they can also be helpful: On the one hand, measured values, when inserted into models, can lead to contradictions. On the other hand, dependencies reduce the number of free parameters, allowing us to infer unknown parameters from the other given parameters. How can we account for parameter dependencies in general, for example, when formulating a joint parameter distribution? Parameters that satisfy linear equality constraints can be expressed in terms of independent basic parameters, and their dependencies can be depicted in a scheme with separate layers for basic and derived parameters (see Figure 6.7). For instance, the vector of logarithmic rate constants in a model (vector  ) can be computed from a set of basic (logarithmic) parameters (in a vector
) can be computed from a set of basic (logarithmic) parameters (in a vector 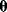 ) by a linear equation:
) by a linear equation:
The dependence matrix 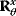 follows from the structure of the network [21,23,24,25]. In kinetic models with reversible standard rate laws (e.g., convenience kinetics [23] or thermodynamic–kinetic rate laws [22]), this parametrization can be used to guarantee feasible parameter sets. Dependence schemes cover not only rate constants but also other quantities, in particular metabolite concentrations and thermodynamic driving forces (see Figure 6.7).
follows from the structure of the network [21,23,24,25]. In kinetic models with reversible standard rate laws (e.g., convenience kinetics [23] or thermodynamic–kinetic rate laws [22]), this parametrization can be used to guarantee feasible parameter sets. Dependence schemes cover not only rate constants but also other quantities, in particular metabolite concentrations and thermodynamic driving forces (see Figure 6.7).
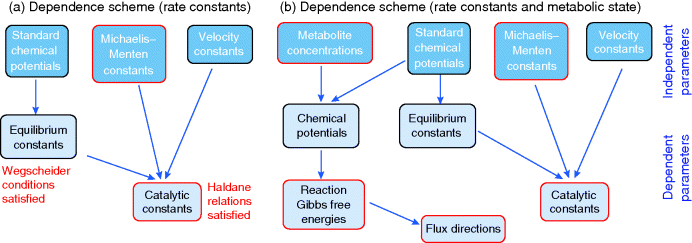
Figure 6.7 Dependence scheme for rate constants and metabolic state. (a) Dependence scheme for rate constants. To obtain consistent Michaelis–Menten constants and catalytic constants 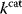 for a kinetic model, one treats them as part of a larger dependence scheme. In the scheme, basic parameters (top) can be chosen at will and derived parameters (center and bottom) are computed from them by linear equations. Parameters appearing in the model are marked by red frames. (b) Dependence scheme for a kinetic model in a specific metabolic state. The scheme additionally includes metabolite concentrations, chemical potentials, and reaction Gibbs free energies, which predefine the flux directions.
for a kinetic model, one treats them as part of a larger dependence scheme. In the scheme, basic parameters (top) can be chosen at will and derived parameters (center and bottom) are computed from them by linear equations. Parameters appearing in the model are marked by red frames. (b) Dependence scheme for a kinetic model in a specific metabolic state. The scheme additionally includes metabolite concentrations, chemical potentials, and reaction Gibbs free energies, which predefine the flux directions.
A dependence scheme can help us define a joint probability distribution of all parameters. We can describe the basic parameters by independent normal distributions; the dependent parameters (which are linear combinations of them) will then be normally distributed as well. We obtain a multivariate Gaussian distribution for logarithmic parameters, and each parameter, on nonlogarithmic scale, will follow a log-normal distribution. The chosen distribution should match our knowledge about rate constants. But what can we do if standard chemical potentials (as basic parameters) are poorly determined, although equilibrium constants (as dependent parameters) are almost precisely known? To express such knowledge by a joint distribution, we need to assume correlated distributions for the basic parameters. Such distributions can be determined from collected kinetic data by parameter balancing.
6.1.5.4 Parameter Balancing
Parameter balancing [9,25] is a method for estimating consistent parameter sets in kinetic models based on kinetic, thermodynamic, and metabolic data as well as prior assumptions and parameter constraints. Based on a dependence scheme, all model parameters are described as linear functions of some basic parameters with known coefficients. Using this as a linear regression model, the basic parameters can be estimated from observed parameter values using Bayesian estimation (Figure 6.8). General expectations about parameter ranges can be formulated in two ways: as prior distributions (for basic parameters) or as pseudo-values (for derived parameters). Pseudo-values appear formally as data points, but represent prior assumptions [25], providing a simple way to define complex correlated priors, for example, priors for standard chemical potentials that entail a limited variation of equilibrium constants.
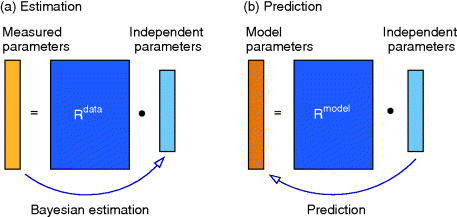
Figure 6.8 Parameter balancing. (a) Based on measured rate constants, and using a dependence scheme represented by a matrix 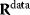 , the independent parameters are estimated by Bayesian multivariate regression. (b) From the posterior distribution of the basic parameters, a joint posterior of all model parameters is obtained.
, the independent parameters are estimated by Bayesian multivariate regression. (b) From the posterior distribution of the basic parameters, a joint posterior of all model parameters is obtained.
To set up the regression model, we use Eq. (6.13), but consider on the left only parameters for which data exist: 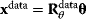 . Inserting this relation into Eq. (6.11) and assuming priors for the basic parameters, we obtain the posterior covariance and mean for the basic parameters:
. Inserting this relation into Eq. (6.11) and assuming priors for the basic parameters, we obtain the posterior covariance and mean for the basic parameters:
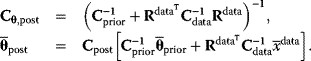
Using Eq. (6.13) again, we obtain the posterior distribution for all parameters, characterized by
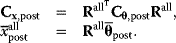
Parameter balancing does not yield a point estimate, but a multivariate posterior distribution for all model parameters. The posterior describes typical parameter values, uncertainties, and correlations between parameters, based on what is known from data, constraints, and prior expectations. Priors and pseudo-values keep the parameter estimates in meaningful ranges even when few data are available. Parameter balancing can also account for bounds on single parameters and linear inequalities for parameter combinations. With such constraints, the posterior becomes restricted to a region in parameter space.
Model parameters for simulation can be obtained in two ways: by using the posterior mode (i.e., the most probable parameter set) or by sampling them from the posterior distribution. By generating an ensemble of random models and assessing their dynamic properties, we can learn about potential behavior of such models, given all information used during parameter balancing. Furthermore, the posterior can be used as a prior in subsequent Bayesian parameter estimation, for example, when fitting kinetic models to flux and concentration time series [9].
Being based on linear regression and Gaussian distributions, parameter balancing is applicable to large models with various types of parameters. Flux data cannot be directly included because rate laws, due to their mathematical form, do not fit into the dependence scheme. However, if a thermodynamically feasible flux distribution is given, one can impose its signs as constraints on the reaction affinities and obtain solutions in which rate laws and metabolic state match the given fluxes (see Section 6.4) [26].
6.1.6 Optimization Methods
Parameter fitting typically entails optimization problems:
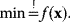
In the method of least squares, for instance,  denotes the parameter vector
denotes the parameter vector 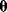 and
and  is the sum of squared residuals. The allowed choices of
is the sum of squared residuals. The allowed choices of  may be restricted by constraints such as
may be restricted by constraints such as 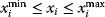 . Global and local minima of
. Global and local minima of 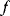 are defined as follows. A parameter set
are defined as follows. A parameter set 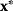 is a global minimum point if no allowed parameter set
is a global minimum point if no allowed parameter set  has a smaller value for
has a smaller value for 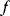 . A parameter set
. A parameter set  is a local minimum point if no other allowed parameter set
is a local minimum point if no other allowed parameter set  in a neighborhood around
in a neighborhood around 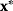 has a smaller value. To find such optimal points numerically, algorithms evaluate the objective function
has a smaller value. To find such optimal points numerically, algorithms evaluate the objective function 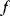 (and possibly its derivatives) in a series of points
(and possibly its derivatives) in a series of points  , leading to increasingly better points until a chosen convergence criterion is met.
, leading to increasingly better points until a chosen convergence criterion is met.
6.1.6.1 Local Optimization
Local optimizers are used to find a local optimum in the vicinity of some starting point. Gradient descent methods are based on the local gradient 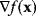 , a vector that indicates the direction of the strongest increase of
, a vector that indicates the direction of the strongest increase of 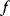 . A sufficiently small step in the opposite direction will lead to lower function values:
. A sufficiently small step in the opposite direction will lead to lower function values:
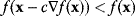
for sufficiently small coefficients  . In gradient descent methods, we iteratively jump from the current point
. In gradient descent methods, we iteratively jump from the current point 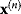 to a new point by
to a new point by
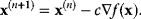
The coefficient  can be adapted in each step, for example, by a numerical line search:
can be adapted in each step, for example, by a numerical line search:
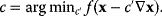
Newton's method is based on a local second-order approximation of the objective function:
with the curvature matrix 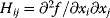 (also called Hessian matrix). If we neglect the approximation error in Eq. (6.20), a direct jump
(also called Hessian matrix). If we neglect the approximation error in Eq. (6.20), a direct jump 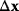 to an optimum would require that
to an optimum would require that
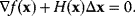
In the iterative Newton method, we approximate this and jump from the current point 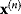 to a new point:
to a new point:
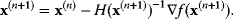
The second term can be multiplied by a relaxation coefficient 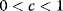 : With smaller jumps, the iteration process will converge more stably.
: With smaller jumps, the iteration process will converge more stably.
6.1.6.2 Global Optimization
Theoretically, global optimum points of a function 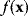 can be found by scanning the space of
can be found by scanning the space of  values with a very fine grid. However, for a problem with
values with a very fine grid. However, for a problem with  parameters and
parameters and 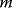 grid values per parameter, this would require
grid values per parameter, this would require 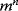 function evaluations, which soon renders the problem intractable. In practice, most global optimization algorithms scan the parameter space by random jumps (Figure 6.9). The aim is to find high-quality solutions (preferably, close to a global optimum) in a short computation time or with an affordable number of function evaluations. To surmount the basins of attraction of local solutions, algorithms should allow for jumps toward worse solutions during the search. Among the many global optimization algorithms [27,28], popular examples are simulated annealing and genetic algorithms.
function evaluations, which soon renders the problem intractable. In practice, most global optimization algorithms scan the parameter space by random jumps (Figure 6.9). The aim is to find high-quality solutions (preferably, close to a global optimum) in a short computation time or with an affordable number of function evaluations. To surmount the basins of attraction of local solutions, algorithms should allow for jumps toward worse solutions during the search. Among the many global optimization algorithms [27,28], popular examples are simulated annealing and genetic algorithms.

Figure 6.9 Global optimization. (a) A function may have different local minima with different function values. (b) The Metropolis–Hastings algorithm samples points  by an iterative jump process: Points are sampled with probabilities
by an iterative jump process: Points are sampled with probabilities 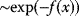 , reflecting their function values
, reflecting their function values 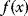 . Tentative jumps toward lower
. Tentative jumps toward lower 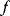 values (A → B) are always accepted, while upward jumps (A → C) are accepted only with probability
values (A → B) are always accepted, while upward jumps (A → C) are accepted only with probability 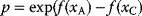 .
.
Aside from purely local and global methods, there are hybrid methods [29,30] that combine the robustness of global optimization algorithms with the efficiency of local methods. Starting from points generated in the global phase, they apply local searches that can accelerate the convergence to optimal solutions up to some orders of magnitude. Hybrid methods usually prefilter their candidate solutions to avoid local searches leading to known optima.
6.1.6.3 Sampling Methods
Simulated annealing, a popular optimization method based on sampling, is inspired by statistical thermodynamics. To use a physical analogy, we consider a particle with position  (scalar or vectorial) that moves by stochastic jumps in an energy landscape
(scalar or vectorial) that moves by stochastic jumps in an energy landscape 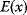 . In a thermodynamic equilibrium ensemble at temperature
. In a thermodynamic equilibrium ensemble at temperature 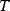 , the particle position
, the particle position  follows a Boltzmann distribution with density
follows a Boltzmann distribution with density
where 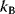 is Boltzmann's constant (see Section 16.6). In the Metropolis–Hastings algorithm [31,32], this Boltzmann distribution is realized by a jump process (Monte Carlo Markov chain):
is Boltzmann's constant (see Section 16.6). In the Metropolis–Hastings algorithm [31,32], this Boltzmann distribution is realized by a jump process (Monte Carlo Markov chain):
- Given the current position
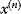 with energy
with energy 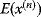 , choose a new potential position
, choose a new potential position 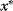 at random.
at random. - If
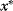 has an equal or a lower energy
has an equal or a lower energy 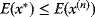 , accept the jump and set
, accept the jump and set 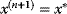 .
. - If
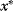 has a higher energy
has a higher energy 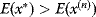 , accept the jump with probability
, accept the jump with probability
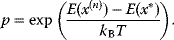
To accept or reject a potential jump, we draw a uniform random number
 between 0 and 1; if
between 0 and 1; if 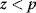 , we accept the jump and set
, we accept the jump and set 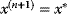 ; otherwise, we set
; otherwise, we set 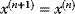 , keeping the particle at its old position.
, keeping the particle at its old position.
Programming the Metropolis–Hastings algorithm is easy. The random rule for jumps in step 1 can be chosen at will, with only one restriction: The transition probability for potential jumps from state 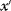 to state
to state 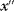 must be the same as for potential jumps from
must be the same as for potential jumps from 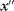 to
to 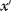 . If this condition does not hold, the unequal transition probabilities must be compensated by a modified acceptance function in step 3. Nevertheless, the rule in step 1 must be carefully chosen: Too large jumps will mostly be rejected; too small jumps will cause the particle to stay close to its current position; in both cases, the distribution will converge very slowly to the Boltzmann distribution. Convergence can be improved by adapting the jump rule to previous movements and, thus, to the energy landscape itself [8].
. If this condition does not hold, the unequal transition probabilities must be compensated by a modified acceptance function in step 3. Nevertheless, the rule in step 1 must be carefully chosen: Too large jumps will mostly be rejected; too small jumps will cause the particle to stay close to its current position; in both cases, the distribution will converge very slowly to the Boltzmann distribution. Convergence can be improved by adapting the jump rule to previous movements and, thus, to the energy landscape itself [8].
According to the Boltzmann distribution (6.23), a particle will spend more time and yield more samples in positions with low energies: The preference for low energies becomes more pronounced if the temperature is low. At temperature 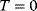 , only jumps to lower or same energies will be accepted and the particle reaches, possibly after a long time, a global energy minimum. The Metropolis–Hastings algorithm has two important applications:
, only jumps to lower or same energies will be accepted and the particle reaches, possibly after a long time, a global energy minimum. The Metropolis–Hastings algorithm has two important applications:
- Sampling from given probability distributions In Bayesian statistics, a common method for sampling the posterior distribution is Metropolis–Hastings sampling with fixed temperature (6.8): We set
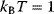 and choose
and choose 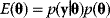 , ignoring the constant factor
, ignoring the constant factor 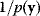 . From the resulting samples, we can compute, for instance, the posterior mean values and variances of individual parameters
. From the resulting samples, we can compute, for instance, the posterior mean values and variances of individual parameters 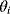 .
. - Global optimization by simulated annealing For global optimization by simulated annealing [33],
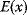 is replaced by some function
is replaced by some function 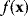 to be minimized,
to be minimized, 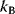 is set to 1, and the temperature is varied during the optimization process. Simulated annealing starts with a high temperature, which is then continuously lowered during the sampling process. If the temperature falls slowly enough, the system will reach a global optimum almost certainly (i.e., with probability 1). In practice, finite run times require a faster cooling, so convergence to a global optimum is not guaranteed.
is set to 1, and the temperature is varied during the optimization process. Simulated annealing starts with a high temperature, which is then continuously lowered during the sampling process. If the temperature falls slowly enough, the system will reach a global optimum almost certainly (i.e., with probability 1). In practice, finite run times require a faster cooling, so convergence to a global optimum is not guaranteed.
6.1.6.4 Genetic Algorithms
Genetic algorithms like differential evolution [34] are inspired by biological evolution. As we shall see in Section 11.1, genetic algorithms do not iteratively improve a single solution (as in simulated annealing), but simulate a whole population of possible solutions (termed “individuals”). In each step, the function value of each individual is evaluated. Individuals with high values (in relation to other individuals in the population) can have offspring, which form the following generation. In addition, mutations (i.e., small random changes) or crossover (i.e., random exchange of properties between individuals) allow the population to explore large regions of the parameter space in a short time. In problems with constraints, the stochastic ranking method [35] provides an efficient way to trade the objective function against the need to satisfy the constraints. Genetic algorithms are not proven to find global optima, but they are popular and have been successfully applied to various optimization problems.
6.2 Model Selection
A biochemical system can be described by multiple model variants, and choosing the right variant is a major challenge in modeling. Different model variants may cover different pathways, different substances or interactions within a pathway, different descriptions of the same process (e.g., different kinetic laws, fixed or variable concentrations), and different levels of details (e.g., subprocesses or time scales). Together, such choices can lead to a combinatorial explosion of model variants. To choose between models in a justified way, statistical methods for model selection are needed [36,37]. In fact, model fitting and model selection are very similar tasks: In both cases, we look for models that agree with biological knowledge and match experimental data; in one case, we choose between possible parameter sets, and in the other case between model structures. Moreover, model selection can involve parameter estimation for each of the candidate models.
A philosophical principle called Ockham's razor (Entia non sunt multiplicanda praeter necessitatem: Entities should not be multiplied without necessity) claims that theories should be free of unnecessary elements. Statistical model selection relies on a similar principle: Complexity in models – for example, additional substances or interactions in the network – should be avoided unless it is supported, and thus required, by data. If two models achieve equally good fits, the one with fewer free parameters should be chosen. With limited and inaccurate data, we may not be able to pinpoint a single model, but we can at least rule out models that contradict the data or for which there is no empirical evidence. With data values being uncertain, notions like “contradiction” and “evidence” can only be understood in a probabilistic sense, which calls for statistical methods.
6.2.1 What Is a Good Model?
Good models need not describe a biological system in all details. J.L. Borges writes in a story [38]: “In that empire, the art of cartography attained such perfection that the map of a single province occupied the entirety of a city, and the map of the empire, the entirety of a province. In time, those unconscionable maps no longer satisfied, and the cartographers guilds struck a map of the empire whose size was that of the empire, and which coincided point for point with it.” Similarly, systems biology models range from simple to complex “maps” of the cell, and like in real maps, details must be omitted. Otherwise, models would be as hard to understand as the biological systems described.
Models are approximations of reality or, as George Box put it, “Essentially, all models are wrong, but some are useful” [39]. In model selection, we have to make this specific and ask: useful for what? Depending on their purpose, models will have to meet various, sometimes contrary, requirements (see Figure 6.10):
- In data fitting, we start from data and describe them by some mathematical function. A reason to do this can be simple economy of description: Instead of specifying many data pairs
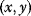 on a curve, we specify much fewer curve parameters (e.g., offset and slope for a straight line). If data points deviate from our curve, we may attribute the discrepancy to measurement errors. In the context of model fitting, a dynamical model is just one specific way to define predicted curves. Given a model structure, for example, a differential equation system, we can fit the model parameters, for instance, by minimizing the sum of squared residuals.
on a curve, we specify much fewer curve parameters (e.g., offset and slope for a straight line). If data points deviate from our curve, we may attribute the discrepancy to measurement errors. In the context of model fitting, a dynamical model is just one specific way to define predicted curves. Given a model structure, for example, a differential equation system, we can fit the model parameters, for instance, by minimizing the sum of squared residuals. - To serve for prediction, a model should not just fit existing data, but also remain valid for future observations. In the language of statistical learning, it should generalize well to new data.
- Realistic models are supposed to picture processes “as they happen in reality.” Since there is a limit to detailing, models have to focus on certain pathways and describe them to reasonable details. Simplifying assumptions and model reduction (see Section 6.3) can be used to simplify models to a tractable level.
- To highlight key principles of biological processes, models need to be simple. Simplicity makes models useful as didactic or prototypic examples. This holds not only for computational models but also for example cases in general, for instance, the lac operon as an example of microbial gene regulation.
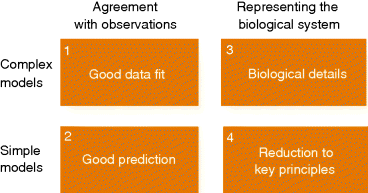
Figure 6.10 Possible requirements for good models.
Only few of these requirements can be tested formally, as described in Section 5.4. Moreover, different criteria can either entail or compromise each other. A good data fit, for instance, may suggest that a model is mechanistically correct and sufficiently complete. However, it may also arise in models with a very implausible structure, as long as they are flexible enough to fit various data. As a rule of thumb, models with more free parameters can fit data more easily (“With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” J. von Neumann, quoted in Ref. [40]). In this case, even though the fit becomes better, the average amount of experimental information per parameter decreases and the parameter estimates become poorly determined. This, in turn, compromises prediction. The overfitting problem notoriously occurs when many free parameters are fitted to few data points or when a large set of models is prescreened for good data fits (Freedman's paradox [41]).
6.2.2 The Problem of Model Selection
In modeling, one typically gets to a point at which a number of model variants have been proposed and the best model is chosen by comparing model predictions with experimental data. The procedure resembles parameter fitting, as described in the previous chapter; now it is the model structure that needs to be chosen – which possibly entails parameter estimation for each of the model variants.
6.2.2.1 Likelihood and Overfitting
The quality of models can be assessed by their likelihood, that is, the probability that a model assigns to experimental observations. Let us assume that a model is correct in its structure and parameters; then, data values 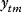 (component
(component 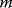 , at time point
, at time point 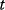 ) will be Gaussian random variables with mean values
) will be Gaussian random variables with mean values 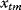 and variances
and variances 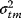 . According to Eq. (6.6), the logarithmic likelihood is related to the weighted sum of squared residuals (wSSR) as
. According to Eq. (6.6), the logarithmic likelihood is related to the weighted sum of squared residuals (wSSR) as
The wSSR itself, as a sum of standard Gaussian distributions, follows a 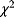 -distribution with
-distribution with  degrees of freedom. This fact can be used for a statistical test: If the weighted SSR for the given data falls in the upper 5% quantile of the
degrees of freedom. This fact can be used for a statistical test: If the weighted SSR for the given data falls in the upper 5% quantile of the 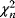 -distribution, we can reject the model on a 5% confidence level. If we do reject it, we conclude that the model is wrong. Importantly, a negative test – one in which the model is not rejected – does not prove that the model is correct; it only shows that there is not enough evidence to disprove the model. Also, note that this test works only for data that have not previously been used to fit the model.
-distribution, we can reject the model on a 5% confidence level. If we do reject it, we conclude that the model is wrong. Importantly, a negative test – one in which the model is not rejected – does not prove that the model is correct; it only shows that there is not enough evidence to disprove the model. Also, note that this test works only for data that have not previously been used to fit the model.
A high likelihood can serve as a criterion for model selection provided that the likelihood is evaluated with new data, that is, data that have not been used for fitting the model before. For instance, the statement “Tomorrow, the sun will shine with 80% probability” (obtained by some model A) can be compared with the statement “Tomorrow, the sun will shine with 50% probability” (obtained from another model B). If sunshine is observed, model A has a higher likelihood (Prob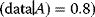 than model B (Prob
than model B (Prob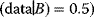 and will be chosen by the likelihood criterion.
and will be chosen by the likelihood criterion.
However, there is one big problem: When posing the question “which model fits our data best,” we usually do not compare models with given parameters, but fit candidate models to data and then compare them by their maximized likelihood values. In doing so, we use the same data twice: first for fitting the model and then for assessing its quality. This would be a wrong usage of statistics and leads to overfitting. A direct comparison by likelihood values is justified only if model parameters have been fixed in advance and without using the test data.
6.2.2.2 Methods for Model Selection
This is the central problem in model selection: We try to infer model details based on data fits, but we know that good data fits can also arise from overfitting. To counter this risk, models with more free parameters must satisfy stricter requirements regarding the goodness of fit; or, following Ockham's principle, we should choose the most simple model variant unless others are clearly better supported by data. The problem of overfitting in model selection can be addressed in a number of ways:
- Cross-validation In cross-validation, models are tested with data that have not been used for fitting. Like a normal goodness of fit, the mean prediction error from cross-validation can be used as a criterion to select parameters or structures of models. Notably, the cross-validation error after this selection will again be biased. To prove that the selected model is free of overfitting, one would need to run a nested cross-validation: an inner cross-validation loop for selecting a model, and an outer cross-validation loop to check the selected model for overfitting in an unbiased way.
- Statistical tests In statistical tests, we compare a more complex model with a simpler background model. Our null hypothesis states that both models perform equally well. Only if the predictions of the more complex model are strikingly better, we reject this hypothesis. If we perform a test with confidence level
 , and if the null hypothesis is indeed correct, there will be an
, and if the null hypothesis is indeed correct, there will be an 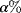 chance that we wrongly reject it.
chance that we wrongly reject it. - Selection criteria A given set of candidate models can be scored by selection criteria [42,43,44,45]. Selection criteria are mathematical score functions that trade agreement with experimental data against model complexity: To compensate the advantage of complex models in fitting, they penalize high numbers of free parameters. Selection criteria can be used to rank models, to choose between them, and to weight predictions from different models when computing weighted averages.
- Tests with artificial data It can be helpful to test model fitting and selection procedures with artificial data obtained from model simulations. Knowing the true model behind the data, we can judge more easily if a model selection method is able to recover the original model.
A second problem arises when we have several models to compare. If we test many models, we are likely to find some models that fit the data well just by chance. In such cases of multiple testing, stricter significance criteria must be applied: Predefining the false discovery rate is a good strategy for choosing sensible significance levels. But let us now describe likelihood ratio test and selection criteria in more detail.
6.2.3 Likelihood Ratio Test
The likelihood ratio test [46] compares two models A and B (with 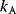 and
and 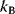 free parameters) by their maximized likelihood values
free parameters) by their maximized likelihood values 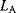 and
and 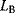 . Like in Eq. (6.25), the models must be nested, that is, model B must be a special case of model A with some of the parameters fixed. As a null hypothesis, we assume that both models explain the data equally well. However, even if the null hypothesis is true, model A is likely to show a higher observed likelihood because its additional parameters make it easier to fit the noise. The statistical test accounts for this fact. As a test statistic, we consider the expression
. Like in Eq. (6.25), the models must be nested, that is, model B must be a special case of model A with some of the parameters fixed. As a null hypothesis, we assume that both models explain the data equally well. However, even if the null hypothesis is true, model A is likely to show a higher observed likelihood because its additional parameters make it easier to fit the noise. The statistical test accounts for this fact. As a test statistic, we consider the expression 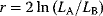 . Assuming that the number of data points is large and that measurement errors are independent and Gaussian distributed, this statistic will asymptotically follow a
. Assuming that the number of data points is large and that measurement errors are independent and Gaussian distributed, this statistic will asymptotically follow a 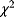 -distribution with
-distribution with  degrees of freedom. In the test, we consider the empirical value of
degrees of freedom. In the test, we consider the empirical value of  ; if it is significantly high, we reject the null hypothesis and accept model A. Otherwise, we accept the simpler model B. The likelihood ratio test can be sequentially applied to more than two models, provided that they are subsequently nested. Likelihood ratio tests, like other statistical tests, can only tell us whether to a reject the null hypothesis model: If the test result is negative, we cannot reject the null model, that is, model A may still be the better one, but we cannot prove it.
; if it is significantly high, we reject the null hypothesis and accept model A. Otherwise, we accept the simpler model B. The likelihood ratio test can be sequentially applied to more than two models, provided that they are subsequently nested. Likelihood ratio tests, like other statistical tests, can only tell us whether to a reject the null hypothesis model: If the test result is negative, we cannot reject the null model, that is, model A may still be the better one, but we cannot prove it.
The likelihood values and, thus, the result of the likelihood ratio test depend on the data values and their standard errors. If standard errors are known to be small, the data require an accurate fit. Accordingly, if we simply shrink all error bars, the likelihood ratio becomes larger and complex models have better chances to be selected.
6.2.4 Selection Criteria
Nonnested models can be compared by using selection criteria. As we saw, if the likelihood value were not biased, it could directly be used as a criterion for model selection. However, the likelihood after fitting is biased due to overfitting. The average bias 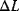 is unknown, but estimates for it have been proposed. By adding these estimates to the log-likelihood, we obtain supposedly less biased score functions, the so-called selection criteria. By minimizing these functions instead of the log-likelihood, we can reduce the impact of overfitting. The Akaike information criterion [47]
is unknown, but estimates for it have been proposed. By adding these estimates to the log-likelihood, we obtain supposedly less biased score functions, the so-called selection criteria. By minimizing these functions instead of the log-likelihood, we can reduce the impact of overfitting. The Akaike information criterion [47]
directly penalizes the number 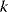 of free parameters. If we assume additive Gaussian measurement noise of width 1, the term
of free parameters. If we assume additive Gaussian measurement noise of width 1, the term 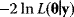 in Eq. (6.27) equals the sum of squared residuals
in Eq. (6.27) equals the sum of squared residuals 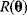 and we obtain
and we obtain
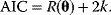
A correction for small sample sizes [48] leads to
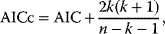
where  is the number of data. The Schwarz criterion (Bayesian information criterion) [49]
is the number of data. The Schwarz criterion (Bayesian information criterion) [49]
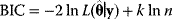
penalizes free parameters more strongly. In contrast to AIC, the BIC is consistent, that is, as the number of data  goes to infinity, the true model will be selected with probability 1. Selection criteria can be used for ranking and selecting models, but the statistical significance of such a model selection cannot be assessed.
goes to infinity, the true model will be selected with probability 1. Selection criteria can be used for ranking and selecting models, but the statistical significance of such a model selection cannot be assessed.
Table 6.1 Selection criteria calculated for Example 6.5.
 Large Large |
 Small Small |
|||
| Model A | Model B | Model A | Model B | |
| n | 3 | 2 | … | |
| k | 9 | 9 | ||
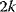 |
6 | 4 | … | |
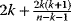 |
4.67 | 2.33 | ||
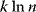 |
6.59 | 4.39 | ||
| wSSR | 4.98 | 6.13 | 4.99 | 19.81 |
| AIC | 10.98 | 10.13 | 10.99 | 23.81 |
| AICc | 9.64 | 8.46 | 9.66 | 22.14 |
| BIC | 11.57 | 10.52 | 11.58 | 24.20 |
| The upper rows show characteristics of the models compared. For each criterion (weighted sum of squared residuals (SSR), Akaike information criteria (AIC and AICc) and Schwarz criterion (BIC)), the selected model variant is marked in bold. | ||||
In some cases, selection criteria may suggest that none of the models is considerably better than the others. In such cases, instead of selecting a single model, we may combine predictions from several models. For example, to estimate a model parameter 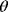 , we may average over the estimates
, we may average over the estimates 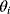 obtained from several models
obtained from several models 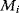 , giving higher weights to estimates from more reliable models. Weighting factors can be constructed from the selection criteria by heuristic methods like the following [45]. We compute, for each model
, giving higher weights to estimates from more reliable models. Weighting factors can be constructed from the selection criteria by heuristic methods like the following [45]. We compute, for each model 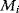 , the Akaike information criterion
, the Akaike information criterion 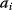 and translate it into a likelihood score
and translate it into a likelihood score 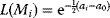 , where
, where 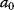 is the minimum value among the
is the minimum value among the 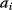 . Models can be compared by their evidence ratios
. Models can be compared by their evidence ratios 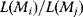 and the normalized scores
and the normalized scores 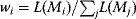 , called Akaike weights, can be used to weight numerical results. If no single model is strongly supported by the data (e.g.,
, called Akaike weights, can be used to weight numerical results. If no single model is strongly supported by the data (e.g., 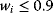 for all models), the Akaike weights may be used to compute weighted parameter averages
for all models), the Akaike weights may be used to compute weighted parameter averages 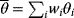 or variances. Numerical model predictions (e.g., concentration curves) can be scored or averaged accordingly.
or variances. Numerical model predictions (e.g., concentration curves) can be scored or averaged accordingly.
6.2.5 Bayesian Model Selection
The logic of maximum likelihood estimation contradicts our everyday reasoning. We do not usually ask: “Under which explanation do our observations appear most likely?” Rather we ask: “What is the most plausible explanation for our observations?” Furthermore, the maximum likelihood criterion may force us to accept explanations even if they are implausible: Imagine that you toss a coin, you obtain heads, and are asked to choose between statement A: “The coin always shows heads” and statement B: “It shows heads and tails with equal probability.” According to the maximum likelihood criterion, you should choose explanation A, even if you know that usual coins do not always show heads.
Bayesian statistics provides model selection methods that are more intuitive [50,51]. We saw in Section 6.1.6 how model parameters can be scored by posterior probabilities. This concept can be extended to entire models (considering their structure 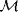 and possibly their parameters
and possibly their parameters  ). Our hypotheses about plausible model structures – before observing any data – are expressed by prior probabilities
). Our hypotheses about plausible model structures – before observing any data – are expressed by prior probabilities 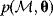 . In the previous example, for instance, the prior could define the (very small) probability to encounter a coin that always shows heads. The posterior follows from Bayes' theorem:
. In the previous example, for instance, the prior could define the (very small) probability to encounter a coin that always shows heads. The posterior follows from Bayes' theorem:
as the product of likelihood 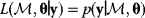 (which quantifies how well the model explains the data) and prior (which describes how probable the model appears in general). The marginal probability
(which quantifies how well the model explains the data) and prior (which describes how probable the model appears in general). The marginal probability 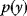 acts as a normalization constant. After taking the logarithm, we can rewrite Eq. (6.31) as a sum:
acts as a normalization constant. After taking the logarithm, we can rewrite Eq. (6.31) as a sum:
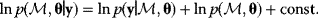
The purpose of Bayesian estimation is not to select a single model, but to assign probabilities to different models. From these probabilities, we can obtain distributions of single parameters, probabilities for structural features in different models, or probabilities for quantitative model predictions.
In practice, it is often impossible to compute the posterior density (Eq. (6.31)) analytically. However, Monte Carlo methods [50] allow us to sample representative models and parameter sets from the posterior. From a sufficient number of samples, all statistical properties of the model can be estimated to arbitrary accuracy. By considering many possible models and weighting them by their probabilities, we can obtain reliable probabilities for structural model features even if the model cannot be precisely determined in all its details. As a criterion for model selection, we can compare two models by the ratio of their posterior probabilities, given all data. With equal priors 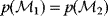 for models
for models  and
and  , this so-called Bayes' factor reads
, this so-called Bayes' factor reads
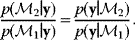
Unlike the likelihood ratio, the Bayes factor does not score models based on a single optimized parameter set; instead, it is computed from weighted averages over all possible parameter vectors 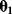 and
and  :
:
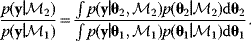
For complicated models, these integrals can be approximated by Monte Carlo sampling.
Our choice of priors (for model structures and parameter values) can strongly affect the posterior distribution. The choice of the prior can reflect both our expectations about biological facts and our demands for simplicity. In any case, Bayesian statistics forces modelers to explicitly state their assumptions about system structure. With a uniform prior (i.e., using the same prior probability for all models), the posterior will be proportional to the likelihood. Priors can also be used, like the above-mentioned selection criteria, to penalize models with many parameters.
Pragmatically, the prior probability can also be used as a regularization term. When the data are not sufficient to identify parameter sets or model structures, model selection becomes an ill-posed problem; however, if we employ a prior, the posterior may have, at least, a unique optimum point. If we select this single model – which is, in fact, a rather “non-Bayesian” use of the posterior – the problem of model selection becomes well determined.
6.3 Model Reduction
6.3.1 Model Simplification
In modeling, we must find a good compromise between biological complexity and the simplicity needed for understanding and practical use. The choice of models depends on both the data and biological knowledge and the questions to be addressed. Smaller models – with fewer equations and parameters – provide some advantages: They are better to understand, easier to simulate, and make model fitting more reliable. It is always good to follow A. Einstein's advice: “Make everything as simple as possible, but not simpler.”
Some systematic ways to simplify models [52] are shown in Figure 6.12. A first rule is to omit all elements that have little influence on model predictions, for instance, reactions with negligible rates. Some elements that cannot be omitted may be described, for the conditions or time scales of interest, by effective variables. For instance, we may assume constant concentrations or flux ratios, use effective rate laws fitted to measured data, or linearize nonlinear kinetics for usage in the physiological range. All such simplifications need to be justified: A reduced model should yield a good approximation of the original model for certain quantities of interest, a certain time scale, and certain conditions (for a range of parameter values, in the vicinity of a certain steady state, or regarding some qualitative behavior under study).
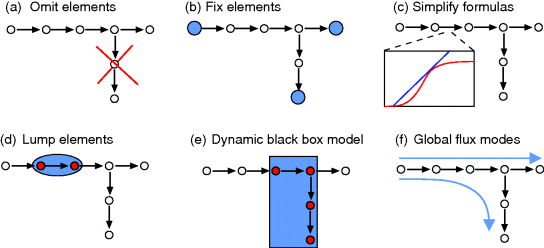
Figure 6.12 Simplification of biochemical models. The scheme shows different types of model reduction in a branched pathway (metabolites shown as circles). (a) Omitting substances and reactions. (b) Predefining concentration or flux values or relations between them. (c) Simplifying mathematical expressions (e.g., omitting terms in a rate law, using simplified rate laws [53], neglecting insensitive parameters [54]). (d) Lumping substances (e.g., similar metabolites, protonation states of a metabolite, or metabolite concentrations in different compartments). Likewise, subsequent reactions in a pathway or elementary steps in a reaction can be replaced by a single reaction of the same velocity; for parallel reactions, for example, reactions catalyzed by isoenzymes, the velocities are summed up. (e) Replacing parts of a model by a dynamic black-box model that mimics the input–output behavior [55]. (f) Describing dynamic behavior by global modes (e.g., elementary flux modes or eigenvectors of the Jacobian matrix).
Model simplification facilitates model building and simulation because it reduces the number of equations, variables, and parameters, replaces differential equations by algebraic equations, and can remove stiff differential equations. But apart from being a practical tool, model, reduction also brings up fundamental questions about what models are and how they can represent reality. The same simplifications that we apply to existing models, in model reduction, can also be directly employed as model assumptions. In fact, any model can be seen as a simplified form of more complex, hypothetical models, which, although faithfully representing reality, would be intractable in practice. Accordingly, the methods for model reduction discussed in this chapter can also be read as a justification of model assumptions in general and, thus, of our mental pictures of reality.
Another important lesson can be learned from model reduction. If we omit all unnecessary details from a model, the resulting model will describe our biological systems in two ways: in a positive way, by the choice of processes described and the details given in the model; and in a negative way, by the choice of processes omitted, simplified, or treated as constant. The positive facts about the system are those stated explicitly; the negative ones – which may be just as important, and possibly much harder to prove when a model is built – are those implicit in the model assumptions.
6.3.2 Reduction of Fast Processes
Cell processes occur on time scales from microseconds to hours. The time scales of enzymatic reactions, for instance, can differ strongly due to different enzyme concentrations and kinetic constants. Time scales in biochemical systems leave their mark on both the system's internal dynamics (e.g., relaxation to steady state, periodic oscillations) and their susceptibility to external fluctuations. If processes occupy very different time scales, the number of differential equations can be reduced with acceptable errors: Slow processes are approximately treated as constant and fast processes can be effectively described by time averages or fixed relationships between quantities, for example, a quasi-equilibrium between metabolites or quasi-steady-state value for an individual metabolite. For instance, in a model of gene expression, binding and unbinding of transcription factors can occur on the order of microseconds, changes in transcription factor activity on the order of minutes, and culture conditions may change much more slowly. In the model, we may assume a fast equilibrium for transcription factor binding, a dynamical model for signal transduction and gene expression, and constant values for the culture conditions.
6.3.2.1 Time Scale Separation
In numerical simulations, a fast process in a model, for example, a rapid conversion between two substances  as shown in Figure 6.13b, can force numerical solvers to use very small time steps during integration. If the same model also contains slow processes, a long total time interval may have to be simulated and the numerical effort can become enormous. Luckily, the dynamics of fast reactions can often be neglected: The concentration ratio
as shown in Figure 6.13b, can force numerical solvers to use very small time steps during integration. If the same model also contains slow processes, a long total time interval may have to be simulated and the numerical effort can become enormous. Luckily, the dynamics of fast reactions can often be neglected: The concentration ratio  will remain close to the equilibrium constant and if we assume an exact equilibrium in every moment in time, we can replace the reaction by the algebraic relation
will remain close to the equilibrium constant and if we assume an exact equilibrium in every moment in time, we can replace the reaction by the algebraic relation 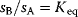 , thereby omitting the stiff differential equation that caused the big numerical effort.
, thereby omitting the stiff differential equation that caused the big numerical effort.
Figure 6.13 Time scale separation. (a) A system's dynamics can be depicted by its trajectories in state space. If the system state is attracted by a submanifold (in the two-dimensional case, a curve), all trajectories (red) will rapidly approach this manifold (blue). Later, the system moves slowly along the manifold, thus satisfying an algebraic equation. (b) A small reaction system with different time scales. A fast conversion between metabolites A and B keeps their concentration ratio 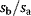 close to the equilibrium constant
close to the equilibrium constant 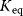 , while slow production and degradation of A only change the sum
, while slow production and degradation of A only change the sum 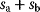 . (c) Schematic trajectories for the system shown in part (b). For any initial condition, the concentrations
. (c) Schematic trajectories for the system shown in part (b). For any initial condition, the concentrations 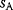 and
and 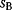 rapidly approach the line
rapidly approach the line 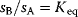 and then move slowly toward the steady state.
and then move slowly toward the steady state.
A justification for such an algebraic equation is shown in Figure 6.13: In state space, fast processes may bring the system state rapidly close to a submanifold on which certain relationships hold (e.g., an equilibrium between different concentrations). After a short relaxation phase, the system state remains close to this manifold and changes slowly. In our approximation, the system moves exactly on the manifold. In general, there can be a hierarchy of such manifolds related to different time scales [56].
6.3.2.2 Relaxation Time and Other Characteristic Time Scales
The time scales of biochemical processes can differ strongly depending on the rate constants involved. To capture them by numbers, we can define characteristic times for different kinds of processes. Such time constants typically describe how fast systems return to equilibrium or steady states after a perturbation. Let us start with the return to equilibrium. As an example, we consider an isolated first-order reaction:
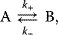
with rate constants  and equilibrium concentrations satisfying
and equilibrium concentrations satisfying 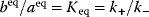 . If the concentrations
. If the concentrations 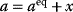 and
and 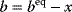 are out of equilibrium (e.g., after a small shift in temperature), the deviation
are out of equilibrium (e.g., after a small shift in temperature), the deviation  will decrease in time as
will decrease in time as
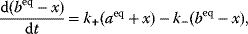
which results in
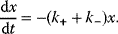
Integration leads to
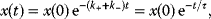
with a relaxation time 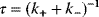 for the decrease of
for the decrease of  from its initial value to the
from its initial value to the 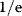 -fold value. Accordingly, we can define
-fold value. Accordingly, we can define 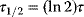 for a decrease to 1/2 of the initial value. Similarly, we can observe how systems relax to steady state. As an example, consider a substance produced at a rate
for a decrease to 1/2 of the initial value. Similarly, we can observe how systems relax to steady state. As an example, consider a substance produced at a rate  and linearly degraded with rate constant
and linearly degraded with rate constant 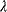 ; its concentration
; its concentration  satisfies the rate equation:
satisfies the rate equation:
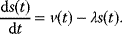
If the production rate  is constant, the concentration
is constant, the concentration  relaxes from an initial value
relaxes from an initial value 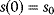 to the steady-state value
to the steady-state value 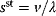 as
as
Again, the response time 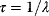 is the time after which the initial deviation
is the time after which the initial deviation 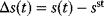 has decreased by a factor
has decreased by a factor 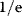 , and response half time
, and response half time 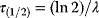 is defined accordingly. A more general response time for single reactions is defined as [57]:
is defined accordingly. A more general response time for single reactions is defined as [57]:
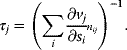
This definition also applies to reactions with several substrates or products and with nonlinear rate expressions. Time constants for metabolite concentrations can be defined in different ways. Reich and Sel'kov [58] defined the turnover time as the time that is necessary to convert a metabolite pool once:
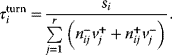
Every reaction is split into partial forward ( ) and reverse (
) and reverse ( ) reactions. Accordingly, stoichiometric coefficients are assigned to individual reaction directions (
) reactions. Accordingly, stoichiometric coefficients are assigned to individual reaction directions (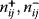 ). To define a transition time for entire pathways, Easterby [59] considered a pathway in which enzymes, but no metabolites, are initially present. The transition time after addition of substrate describes how fast intermediate pools reach their steady-state concentrations. For each intermediate,
). To define a transition time for entire pathways, Easterby [59] considered a pathway in which enzymes, but no metabolites, are initially present. The transition time after addition of substrate describes how fast intermediate pools reach their steady-state concentrations. For each intermediate, 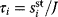 , where
, where 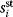 and
and 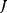 denote concentration and flux, respectively, in the final steady state. The transition time of the pathway is the sum
denote concentration and flux, respectively, in the final steady state. The transition time of the pathway is the sum 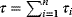 of all these transition times. Another time constant, as defined by Heinrich and Rapoport, measures the time necessary to return to a steady state after a small perturbation [60]. Let
of all these transition times. Another time constant, as defined by Heinrich and Rapoport, measures the time necessary to return to a steady state after a small perturbation [60]. Let 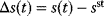 be the deviation from steady-state concentrations
be the deviation from steady-state concentrations 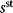 . Then the transition time is defined as
. Then the transition time is defined as
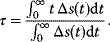
This definition applies only if 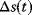 vanishes asymptotically for large
vanishes asymptotically for large 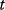 . Lloréns et al. [61] have generalized this definition. Let
. Lloréns et al. [61] have generalized this definition. Let 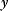 denote an output quantity, for example, a flux or concentration, that is analyzed after a perturbation. Using the absolute derivative
denote an output quantity, for example, a flux or concentration, that is analyzed after a perturbation. Using the absolute derivative 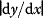 as a probability weight, a characteristic time can be calculated as
as a probability weight, a characteristic time can be calculated as
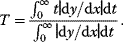
This definition applies even to damped oscillations after a perturbation.
6.3.3 Quasi-Equilibrium and Quasi-Steady State
In systems with several different time scales, various kinds of simplifications are possible: (i) In molecular dynamics, we may focus on slow changes of a thermodynamic ensemble: Then, fast molecular movements (e.g., fast jittering atom movements versus slow conformation changes in proteins) average out. (ii) If there is fast diffusion, leading to homogeneous concentrations, spatial structures can be neglected. (iii) In the quasi-equilibrium approximation, we assume that the substrates and products of a reaction are practically equilibrated; then their concentration ratio is given, in every moment, by the equilibrium constant. A quasi-equilibrium requires that the equilibrium reaction be reversible and much faster than all other processes considered. An example is the permanent protonation and deprotonation of acids: Since this process is much faster than the usual enzymatic reactions, the protonation states of a substance need not be treated separately, but can be effectively captured by a quasi-species. Another example is transcription factor binding (see Section 10.3), which can be treated as an equilibrium process to derive effective gene regulation functions. (iv) In the quasi-steady-state approximation, we assume that production and consumption of a substance are balanced. If the consuming reactions are irreversible, the substance concentration will be directly determined by the production rate. Quasi-equilibrium and quasi-steady-state approximations can be used, for instance, to derive the Michaelis–Menten rate law from an enzyme mechanism with elementary mass-action steps (see Section 4.1).
6.3.4 Global Model Reduction
If a system is constrained to a submanifold in state space (as shown in Figure 6.13a), its movement on this manifold can be described by a smaller set of variables. Constraints can arise, for instance, from linear conservation relations between metabolite concentrations (see Section 3.1.4): If rows of the stoichiometric matrix 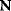 are linearly dependent, the vector of metabolite concentrations is confined to a linear subspace and the system state can be described by independent metabolite concentrations from which all other concentrations can be directly computed. Other constraints can arise from fast processes, like in the quasi-steady-state and quasi-equilibrium approximation. Unlike the original concentrations, effective variables need not refer to individual substances: A linear manifold can be spanned by linear combinations of all substance concentrations, representing global modes of the system's dynamics. Such modes can appear, for instance, in metabolic systems linearized around a steady state: Each mode represents a specific pattern of metabolite levels (actually, their deviations from steady state) with a specific temporal dynamics (e.g., exponential relaxation).
are linearly dependent, the vector of metabolite concentrations is confined to a linear subspace and the system state can be described by independent metabolite concentrations from which all other concentrations can be directly computed. Other constraints can arise from fast processes, like in the quasi-steady-state and quasi-equilibrium approximation. Unlike the original concentrations, effective variables need not refer to individual substances: A linear manifold can be spanned by linear combinations of all substance concentrations, representing global modes of the system's dynamics. Such modes can appear, for instance, in metabolic systems linearized around a steady state: Each mode represents a specific pattern of metabolite levels (actually, their deviations from steady state) with a specific temporal dynamics (e.g., exponential relaxation).
6.3.4.1 Linearization of Biochemical Models
Linear control theory is concerned with dynamic models of the general form:
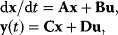
with vectors of input variables 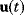 , internal variables
, internal variables  , and observable outputs
, and observable outputs 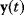 (see Section 15.5). In practice, the output variables in
(see Section 15.5). In practice, the output variables in 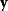 represent variables that can be observed, that affect other systems, or that determine the objective in some optimal control problem. Biochemical models are usually nonlinear, but many of them can be linearized around a steady state. Consider a kinetic model:
represent variables that can be observed, that affect other systems, or that determine the objective in some optimal control problem. Biochemical models are usually nonlinear, but many of them can be linearized around a steady state. Consider a kinetic model:
with concentration vector  , stoichiometric matrix
, stoichiometric matrix 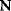 , reaction rate vector
, reaction rate vector  , and parameter vector
, and parameter vector 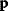 . We assume that for given parameter sets
. We assume that for given parameter sets 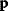 , the system shows a stable steady state
, the system shows a stable steady state 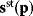 . To linearize Eq. (6.51), we determine the steady state
. To linearize Eq. (6.51), we determine the steady state 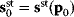 at a reference parameter vector
at a reference parameter vector  and compute the elasticity matrices
and compute the elasticity matrices 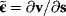 and
and 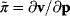 (see Section 4.2). For small deviations of concentrations
(see Section 4.2). For small deviations of concentrations 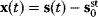 and parameters
and parameters 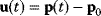 , linearizing Eq. (6.51) leads to
, linearizing Eq. (6.51) leads to
with the Jacobian matrix 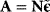 and the matrix
and the matrix 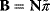 . In general, the approximation (6.52) is valid only near the expansion point, and its accuracy decreases for larger deviations
. In general, the approximation (6.52) is valid only near the expansion point, and its accuracy decreases for larger deviations  or
or  . Moreover, linearized models may not be able to reproduce certain kinds of dynamic behavior, for example, stable limit cycles.
. Moreover, linearized models may not be able to reproduce certain kinds of dynamic behavior, for example, stable limit cycles.
Closely related to this linear approximation, we can consider the input–output relation 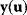 between static parameter deviations
between static parameter deviations  and steady output variables
and steady output variables  such as fluxes or concentrations. For instance, consider a stable system under small parameter perturbations: If the perturbations are slow enough, the entire system will follow them in a quasi-steady state. Therefore, the system's input–output relation – even for complicated systems – can be described by a function and approximated by simple functions with fitted parameters. After linearization, this becomes relatively simple: By setting the time derivative in Eq. (6.52) to zero, assuming a small static perturbation
such as fluxes or concentrations. For instance, consider a stable system under small parameter perturbations: If the perturbations are slow enough, the entire system will follow them in a quasi-steady state. Therefore, the system's input–output relation – even for complicated systems – can be described by a function and approximated by simple functions with fitted parameters. After linearization, this becomes relatively simple: By setting the time derivative in Eq. (6.52) to zero, assuming a small static perturbation  , solving for
, solving for  , and computing
, and computing  , we obtain
, we obtain 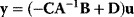 , which is nothing else but the linear response:
, which is nothing else but the linear response:
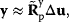
with response matrix  , well known from metabolic control analysis. The effects of oscillating parameter perturbations [62,63], as well as the effects of stationary perturbations on transient behavior [64], can be treated accordingly (see Sections 10.1.5 and 15.5).
, well known from metabolic control analysis. The effects of oscillating parameter perturbations [62,63], as well as the effects of stationary perturbations on transient behavior [64], can be treated accordingly (see Sections 10.1.5 and 15.5).
6.3.4.2 Linear Relaxation Modes
In the linearized system (Eq. (6.52)), the general model behavior can be represented by a superposition of global modes  , each corresponding to an eigenvector of
, each corresponding to an eigenvector of 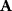 (see Section 15.2). For constant system parameters (
(see Section 15.2). For constant system parameters (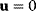 ), a small deviation
), a small deviation 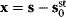 will follow
will follow
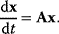
Now we assume that the Jacobian is diagonalizable, 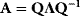 with a diagonal matrix
with a diagonal matrix 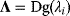 and a transformation matrix
and a transformation matrix 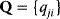 , and that all eigenvalues
, and that all eigenvalues 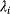 have negative (or, at least, vanishing) real parts. We introduce the transformed vector
have negative (or, at least, vanishing) real parts. We introduce the transformed vector 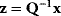 , which follows the equation
, which follows the equation
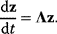
Thus, whenever 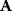 is diagonalizable, we obtain an equation
is diagonalizable, we obtain an equation
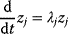
for each global mode 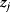 . The behavior of the original variables
. The behavior of the original variables 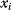 can be written as
can be written as
with initial value 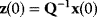 . Each mode is characterized by a response time similar to Eq. (6.40). If the eigenvalue
. Each mode is characterized by a response time similar to Eq. (6.40). If the eigenvalue 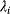 is a real number,
is a real number, 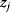 relaxes exponentially to a value of 0, with a response time
relaxes exponentially to a value of 0, with a response time 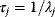 . A pair of complex conjugate eigenvalues, in contrast, leads to a pair of oscillatory modes with time constant
. A pair of complex conjugate eigenvalues, in contrast, leads to a pair of oscillatory modes with time constant 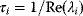 . An eigenvalue
. An eigenvalue 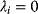 (corresponding to infinitely slow modes) can arise, for instance, from linear conservation relations. Modes in biochemical dynamics are comparable to the harmonics of a guitar string. Each of the harmonics displays a characteristic spatial pattern and, as a simple temporal behavior, a sine wave modulation of its amplitude. All possible movements of the string, at least for small amplitudes that justify our linear approximation, can be obtained by linear superposition of these modes.
(corresponding to infinitely slow modes) can arise, for instance, from linear conservation relations. Modes in biochemical dynamics are comparable to the harmonics of a guitar string. Each of the harmonics displays a characteristic spatial pattern and, as a simple temporal behavior, a sine wave modulation of its amplitude. All possible movements of the string, at least for small amplitudes that justify our linear approximation, can be obtained by linear superposition of these modes.
6.3.4.3 Model Reduction
In model reduction, we assume that fast modes (with small  ) in the sum (6.57) relax immediately. If we neglect these modes, the accuracy in describing rapid changes is reduced, but no metabolite or reaction is omitted from the model. Like in Figure 6.13, the system state is projected to a space of slow modes. Even in cases where
) in the sum (6.57) relax immediately. If we neglect these modes, the accuracy in describing rapid changes is reduced, but no metabolite or reaction is omitted from the model. Like in Figure 6.13, the system state is projected to a space of slow modes. Even in cases where  cannot be diagonalized, the state space can be split into subspaces related to fast and slow dynamics, and by neglecting the fast subspace, the number of variables can be reduced. This method can be applied adaptively during computer simulations [65]. Powerful methods for linear model reduction, such as balanced truncation [66,55], have been developed in control engineering. Using such methods, we can mimic the external behavior of a complex biochemical model, that is, its responses to perturbations, by linearized, dynamic black-box models with similar input–output relations (see Section 16.5.5). However, these methods operate on the system as a whole and are not directly related to the quasi-steady-state and quasi-equilibrium approximations for single network elements. A model reduction for selected network elements can be achieved by the computational singular perturbation method that identifies such elements automatically during a simulation and can be used in the software tool COPASI [67].
cannot be diagonalized, the state space can be split into subspaces related to fast and slow dynamics, and by neglecting the fast subspace, the number of variables can be reduced. This method can be applied adaptively during computer simulations [65]. Powerful methods for linear model reduction, such as balanced truncation [66,55], have been developed in control engineering. Using such methods, we can mimic the external behavior of a complex biochemical model, that is, its responses to perturbations, by linearized, dynamic black-box models with similar input–output relations (see Section 16.5.5). However, these methods operate on the system as a whole and are not directly related to the quasi-steady-state and quasi-equilibrium approximations for single network elements. A model reduction for selected network elements can be achieved by the computational singular perturbation method that identifies such elements automatically during a simulation and can be used in the software tool COPASI [67].
6.4 Coupled Systems and Emergent Behavior
To understand cells, we need to consider their parts, the interactions between these parts, and the global dynamics that emerges from the interactions. Molecules and biochemical processes have been studied in great detail, and systems biology builds on a wealth of knowledge from biochemistry, molecular biology, and molecular genetics. A basic credo of systems biology says that analysis (taking apart) and synthesis (putting together) must be combined.
There are two contrary approaches, bottom-up and top-down modeling. Both proceed from simplicity to complexity, but in opposite ways. In bottom-up modeling [68,69], one considers elementary processes and aggregates them to larger models. Since there is no guarantee that models will remain valid when combined with others, parameters may have to be refitted after model construction. In top-down modeling, a model is based on a coarse-grained picture of the entire system, which can then be iteratively refined. If a model structure is biologically plausible, such models, even though lacking many details, may yield accurate predictions. Bottom-up and top-down approaches pursue different goals: A bottom-up model is constructed to explore how high-level behaviors emerge from the interaction of many molecular components; a top-down model, on the other hand, is designed to accurately predict high-level behavior regardless of molecular correctness. Generally, it is difficult to construct models that are both molecularly detailed and globally correct.
Recently, researchers developed the first whole-cell model [70] of Mycoplasma genitalium, a pathogenic bacterium known for its small genome size (525 genes). This constituted a major step forward in modular cell modeling. In this model, a variety of cellular processes – including genome-wide transcription and translation, DNA repair, DNA replication, metabolism, cell growth, and cell division – were represented by a total of 28 coupled submodels. Accomplishing this task involved overcoming several challenges. First, a huge number of cell components were modeled in detail. For example, DNA-binding proteins were described by their precise position on the chromosome, and the specific function of every annotated gene product was represented. Second, the submodels were expressed using multiple mathematical formalisms, including differential equations, stochastic particle simulations, and dynamic flux balance analysis (FBA). These submodels were coupled together using an Euler-type integration scheme in which submodels are repeatedly simulated independently for 1 s intervals and coupled by updating a set of global state variables (see Figure 6.15). To allow processes in different submodels to consume the same shared resources (e.g., ATP, which is involved in many processes described), the available resources are partitioned before each integration step. At each iteration, each submodel obtains a fraction of each resource for potential consumption. The M. genitalium model was fitted and validated with various types of biological data and can now be used to simulate numerous biological behaviors, including the movement and collisions of DNA-binding proteins, the global allocation of energy to different functional subsystems (see Section 8.3), and the detailed effects of single-gene disruptions on the growth rate and macromolecule synthesis.
Figure 6.15 Modular whole-cell model of M. genitalium [70]. The model consists of 28 submodels (blue boxes), each of which represents a distinct cellular process. Submodels are coupled via global state variables (yellow box), which represent the instantaneous configuration of a single cell. To simulate the life cycle of a single cell, the state variables are first initialized corresponding to the beginning of the cell cycle. Second, the submodels are simulated for 1 s of real (i.e., the cell's) time. Next, the global state variables are updated. The submodels are repeatedly simulated and the global variables are repeatedly updated until the in silico cell cycle has been completed. The modular model structure allows the model to simultaneously employ multiple mathematical modeling formalisms, including differential equations, particle-based stochastic models, and dynamic FBA.
6.4.1 Modeling of Coupled Systems
6.4.1.1 Modeling the System Boundary
When building a model, we separate a system of interest (which is explicitly modeled) from its environment, which is either not modeled or described very roughly. This distinction is artificial, but hard to avoid. The model is bounded by quantities like external substance levels or fluxes whose values are set as model assumptions. If the boundary variables are fixed, the system is modeled as if it were isolated. To justify this assumption at least approximately, one should carefully consider experimental details and pay attention to the choice of boundary variables. The system boundary should be chosen such that interactions between system and environment are weak, constant in time, or average out (because they are fast or random). If boundary variables (concentrations or fluxes) change dynamically, their time courses may be predefined based on experimental data or computed from a separate environment model. If the environment responds dynamically to the system, it needs to be described within the model: either by effective algebraic relationships [71] or by simplified dynamic black-box models [72].
6.4.1.2 Coupling of Submodels
If a model is composed of submodels, the submodels are connected through variables such as shared metabolite concentrations. As shown in Figure 6.16, a submodel can take metabolite concentrations as inputs and yield reaction rates as an output. These reaction rates in turn contribute to the rate equations of the boundary metabolites. Submodels affect each other only through these interfaces, and if time curves of the communicating variables were fixed and given, each module could be simulated independently. Thus, communicating variables connect submodules and separate them at the same time. One advantage of this modular structure is that submodels can be based on different mathematical formalisms or be simulated in parallel on separate computers. If the influences between modules form an acyclic graph, we can simulate their dynamics sequentially. We begin with the upstream modules, compute their outputs, and use them as inputs for the downstream modules. In contrast, if the coupling involves loops, all modules need to be simulated together, with the communicating variables as shared variables and all other variables as “private” variables of the modules. If global variables are updated in intervals – as in the Mycoplasma model in Figure 6.15, then the dynamics of the shared global variables should be slow in relation to the updating intervals.
Figure 6.16 Model reduction applied to a schematic biochemical network model. (a) A metabolic system is split into a pathway of interest (left half) and its environment (right half). Both subsystems interact via communicating metabolites (belonging to the pathway of interest) and reactions (belonging to the environment). (b) To simplify numerical simulations, the environment model has been replaced by a reduced black-box model (see Ref. [72]).
6.4.1.3 Supply–Demand Analysis
Metabolic pathways need to match input and output fluxes, and thus supply and demand [73,74]. In a metabolic pathway, the steady-state flux depends on the initial substrate concentration. However, if rate laws are reversible or if enzymes are allosterically regulated, the end product will also exert control on the flux. Supply–demand analysis [73] splits metabolism into blocks that are coupled by matching their supply and demand variables at the boundaries. The elasticities of supply and demand reactions, which can be measured for the individual blocks, are then used to describe the behavior, control, and regulation of metabolism.
6.4.1.4 Hierarchical Regulation Analysis
An important question, one that concerns the interplay of metabolic systems and the underlying transcriptional or posttranslational regulation of enzymes, is whether flux changes are mainly caused by changes in metabolite levels or by enzymatic changes; and, in turn, whether these enzymatic changes are mainly caused by expression changes or by posttranslational modification. This varies from case to case and has consequences for time scales (posttranslational modification being much faster than expression changes) and cellular economics (different underlying changes will be associated with different costs and benefits). In metabolic control analysis, one would address such questions by considering an initial perturbation, for example, an expression change, tracing its effects in the system, and predicting the resulting flux change. This, however, would require a comprehensive model of the system. A much simpler procedure is provided by hierarchical regulation analysis [75]. Here one starts from the effect – namely, the flux changes – and traces back to its possible causes. For the reaction in question, we assume a rate law of the following form:
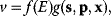
with rate  , enzyme level
, enzyme level 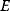 , substrate levels
, substrate levels  , product levels
, product levels 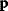 , and effector levels
, and effector levels  . The maximal velocity
. The maximal velocity 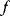 is typically given by
is typically given by 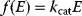 . Now we consider a change in conditions, where
. Now we consider a change in conditions, where  ,
,  ,
,  , and
, and  may change at the same time. The resulting change in logarithmic reaction rate (where a positive flux is assumed without loss of generality) reads
may change at the same time. The resulting change in logarithmic reaction rate (where a positive flux is assumed without loss of generality) reads
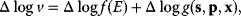
which implies
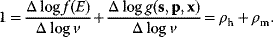
The hierarchical regulation coefficient  describes which fraction of the log-rate change is caused by changes in maximal velocity, and thus by changes in the gene expression cascade. Given a hierarchical model of expression (including transcription, translation, and posttranslational modification), the coefficient can further be split into contributions of these individual processes. The metabolic regulation coefficient
describes which fraction of the log-rate change is caused by changes in maximal velocity, and thus by changes in the gene expression cascade. Given a hierarchical model of expression (including transcription, translation, and posttranslational modification), the coefficient can further be split into contributions of these individual processes. The metabolic regulation coefficient  describes the fraction of log-rate change caused by changes in metabolite levels, capturing the enzyme's interaction with the rest of metabolism. Regulation coefficients can be directly determined from flux and expression data and can yield direct information about regulation without the need for complex quatitative models.
describes the fraction of log-rate change caused by changes in metabolite levels, capturing the enzyme's interaction with the rest of metabolism. Regulation coefficients can be directly determined from flux and expression data and can yield direct information about regulation without the need for complex quatitative models.
6.4.2 Combining Rate Laws into Models
Once models for several reactions, pathways, or cellular subsystems have been built, they can be combined to form more complex models. One may even start from individual reaction kinetics measured in vitro: Pioneering this modeling approach, Teusink et al. [68] built a model of yeast glycolysis from in vitro rate laws. In general, in vitro measurements allow for an exact characterization and manipulation of enzyme parameters, but they will not reflect the precise biochemical conditions – such as pH or ion concentrations – existing in living cells. Nevertheless, the yeast glycolysis model, without further adaptation, yielded a plausible steady state.
In this way, metabolic network models can be constructed by inserting collected rate laws into known network structures. In theory, a network with correct rate laws should yield a consistent model; in reality, however, such models, for given external metabolite levels and enzyme levels, may show unrealistic states or no steady state at all because, for instance, the parameters obtained from different experiments simply do not fit. In particular, thermodynamic correctness may not be ensured because equilibrium constants do not fit together. This can be tested by simulating the model with all metabolites and cofactors treated as internal. In a thermodynamically correct model, this simulation should lead to an equilibrium state with vanishing fluxes. However, if no attention has been paid to consistent equilibrium constants, the simulation may instead result in steady fluxes, contradicting the laws of thermodynamics and representing a perpetuum mobile.
To avoid these issues, Stanford et al. [76] proposed a systematic way to construct models with reversible rate laws, using the network structure as a scaffold. The model variables are determined step-by-step: (i) Choose the intended flux distribution (which must be thermodynamically feasible, but need not be stationary). (ii) Choose equilibrium constants satisfying the Wegscheider conditions. (iii) Choose metabolite concentrations such that the thermodynamic forces (i.e., negative reaction Gibbs free energies) follow the flux directions (see Section 16.6). (iv) Choose reversible rate laws (e.g., modular rate laws) with rate constants satisfying the Haldane relationships (e.g., by parameter balancing). (v) Set all enzyme levels to 1 and compute the resulting reaction rates; by construction, the rates will have the same signs as the predefined fluxes. (vi) Adjust the enzyme levels (or generally  values) such that reaction rates match the previously defined fluxes. An open problem in such models is how to choose suitable rate laws for biomass production; a possibility would be to use rate laws for polymerization reactions [77], treating biomass – which actually comprises protein, polynucleotides, lipids, and many other substances – as a single hypothetical polymer, produced after a template sequence.
values) such that reaction rates match the previously defined fluxes. An open problem in such models is how to choose suitable rate laws for biomass production; a possibility would be to use rate laws for polymerization reactions [77], treating biomass – which actually comprises protein, polynucleotides, lipids, and many other substances – as a single hypothetical polymer, produced after a template sequence.
6.4.3 Modular Response Analysis
When dynamic systems are coupled, be they biological systems or mathematical models describing them, mutual interactions can drastically change the dynamic behavior. Metabolic control analysis allows us to study the global behavior emerging from many coupled reactions. Modular response analysis [78,79], one of its variants, addresses the coupling of larger modules, for example, interacting signaling pathways, and predicts emergent global behavior from the effective input–output behavior of single modules. In modular response analysis (see Figure 6.17a), a communicating variable is an output of one module that acts as a parameter in other modules. All other system parameters are collected in the external parameter vector  , and modules are not connected by fluxes.
, and modules are not connected by fluxes.
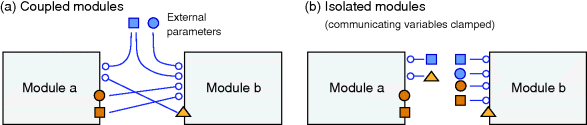
Figure 6.17 Modular response analysis. (a) Two network modules, described by kinetic models, interact through communicating variables. (b) To study the behavior of isolated modules, the communicating variables are treated as controllable parameters. A sensitivity analysis yields the local response coefficients. These coefficients, together with the wiring scheme of the communicating variables in part (a), allow us to compute the global response coefficients for scenario (a).
To calculate response coefficients for the entire system, we first consider the single modules and compute their local response coefficients, assuming that the communicating variables are clamped and the modules are isolated from each other. The dynamics of a module 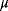 depends, in general, on the external parameter vector
depends, in general, on the external parameter vector 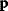 and on the output vectors
and on the output vectors 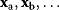 of the other modules. Its steady-state output
of the other modules. Its steady-state output 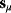 can be written as a function
can be written as a function 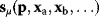 , where the argument list contains all module outputs except for
, where the argument list contains all module outputs except for 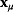 itself (see Figure 6.17b). Next, we consider the modules coupled to one another. We assume that the coupled system reaches a stable steady state in which the values
itself (see Figure 6.17b). Next, we consider the modules coupled to one another. We assume that the coupled system reaches a stable steady state in which the values 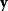 of the output variables satisfy
of the output variables satisfy
and so on. The modules' local response coefficients in this steady state are defined by
The global response coefficients – the sensitivities of the coupled system to small external parameter changes – are defined as
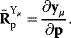
If we collect the response matrices in large block matrices:
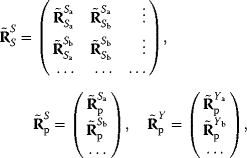
the global response coefficients can be computed from the local ones by
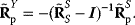
Thus, to compute global steady-state responses to small perturbations, the internal details of the modules need not be known. We only need to know the local response coefficients, that is, the modules' effective input–output behavior for the communicating variables. Modular response analysis only applies to steady-state perturbations. To treat dynamic small-amplitude perturbations instead, the submodels could be approximated by dynamical black-box models obtained by linear model reduction (see Figure 6.16) [72].
6.4.4 Emergent Behavior in Coupled Systems
In Section 5.4, we saw how biochemical models can be formally combined and which technical and conceptual problems may arise on the way. However, if we couple two models, how will this affect their dynamic behavior? If models influence each other sequentially, their overall dynamics can be simulated step-by-step. However, if models interact in both ways or in a circle, this may change their qualitative behavior. The following examples illustrate how new behavior can emerge in coupled systems.
The two possible descriptions – treating systems as isolated, or treating them as dynamically coupled – are characteristic of two general perspectives on complex systems. In reductionist approaches, one studies the parts of a system in isolation and in great detail. This view is dominant in molecular biology and biochemistry. A holistic perspective, in contrast, focuses on global dynamic behavior that emerges in the coupled system. Instead of tracing causal chains across the network, it emphasizes how the system dynamics, as a whole, responds to changes of external conditions. In the examples above, we saw that fundamental notions for describing biochemical dynamics (bistable system; steady-state flux) rely on holistic explanations.
Whether behavior is caused locally or globally can be hard to decide: Yeast cells, for instance, communicate by exchanging chemicals, and this interaction can lead to synchronized glycolytic oscillations. Spontaneous oscillations of this sort are observed in experiments and models [80,81,82]. Experiments with desynchronized populations suggest that individual yeast cells oscillate by themselves, and that the main effect of their coupling is to synchronize preexisting oscillations, which would otherwise go unnoticed in most experiments. Thus, the overall oscillations rely on a local dynamics (namely, the oscillations in individual cells), but only the coupling between cells enables them to emerge as a global phenomenon.
6.4.5 Causal Interactions and Global Behavior
What are the roles of reductionism and holism in biochemical modeling? We can see this by looking at how kinetic models are built and solved in practice. Obviously, models rely on strong simplifications on the level of structure (by omitting elements from the model), dynamics (by deciding which interactions exist in a model), and function (by assigning specific functions to molecules, pathways, or organs). In particular, we assume that our biological system can be described in isolation, and that it can be subdivided into simple interacting components. We thus choose a number of substances and reactions to be modeled and postulate direct causal interactions between them. These causalities define our network.
Starting from this causal model, we study how local interactions translate into global behavior. When integrating the model, we trace the local interactions step-by-step. This becomes visible in the Euler method for integration of differential equations: In each time step, we consider direct influences between neighboring elements; then, however, perturbations propagate step-by-step throughout the network. A steady state, even though it may look simple, can be difficult to understand from a causal point of view: It is a state in which elements are tightly interacting, but with a zero net effect in terms of dynamic changes. In metabolic analysis, the transition from direct influences (described by differential equations) to systemic behavior (described by control coefficients) is achieved by a matrix inversion (in the calculation of control coefficients). Also in this case, we move from local interactions to a global, systemic behavior, which can then be compared with cell behavior in experiments or with phenomenological cell models. Finally, a network can be subdivided into pathways for convenience, for instance, in modular response analysis; since there is no “objective truth” about these modules, they may simplify our understanding, but should not change the result of the calculations.
Exercises
Section 6.1
- Linear regression. A data set
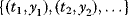 has been generated by a linear model:
has been generated by a linear model:
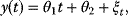
with random errors ξt. (a) Given the vectors t = (t1, t2,…)T and y = (y1, y2,…)T, estimate the model parameters θ1 and θ2 by maximizing the likelihood. Assume that the errors ξt are independent Gaussian random variables with mean 0 and variance σ2.
- Bootstrapping procedure for the empirical mean. The expected value of a random number X can be estimated by the empirical mean value
 of n realizations x(1),…, x(n). (a) Compute the mean and variance of the estimator
of n realizations x(1),…, x(n). (a) Compute the mean and variance of the estimator  . (b) Choose a distribution of X and approximate the mean and the variance of
. (b) Choose a distribution of X and approximate the mean and the variance of 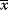 numerically by repeatedly drawing samples (x(1),…, x(n)). (c) Implement a bootstrapping procedure and assess the distribution of the estimate
numerically by repeatedly drawing samples (x(1),…, x(n)). (c) Implement a bootstrapping procedure and assess the distribution of the estimate 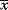 based on a single sample (x(1),…, x(n)). (d) Explain why these three results differ.
based on a single sample (x(1),…, x(n)). (d) Explain why these three results differ. - One-norm and two-norm. The method of least squares can be derived from the maximum likelihood estimator under the assumption of independent standard Gaussian errors. (a) Assume that measurement errors
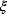 are not Gaussian, but follow an exponential distribution with density
are not Gaussian, but follow an exponential distribution with density 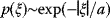 . Find the minimization principle that replaces the method of least squares in this case. (b) Assume that a model is fitted to the same data set (i) by the principle of least squares or (ii) by the minimization principle derived in (a). How will the two fitting results differ qualitatively?
. Find the minimization principle that replaces the method of least squares in this case. (b) Assume that a model is fitted to the same data set (i) by the principle of least squares or (ii) by the minimization principle derived in (a). How will the two fitting results differ qualitatively? - Local and global optimization. (a) Why is it important in parameter estimation to find a global optimum rather than a suboptimal local one? Do local optimum points also have a relevance?
Section 6.2
- Experimental design. A kinetic model has been fitted to an experimental concentration time series. An additional data point can be measured, and you can choose the time point at which the measurement will take place. How would you choose the best time point for the measurement, and what circumstances would influence your choice?
- Selection criteria. Three models A, B, and C have been fitted to experimental data (n = 10 data points) by a maximum likelihood fit. The numbers k of free parameters and the optimized likelihood values are given below. (a) Calculate the selection criteria AIC, AICc, and BIC, and use these results to choose between the models. (b) Assume that the models are nested, that is, A is a submodel of B, and B is a submodel of C. Decide for one of the models by using the likelihood ratio test.
Model A B C k
In L2
10.03
5.04
2.0 - Model selection. Models A and B are supposed to explain a given experimental time series. Model A contains more free parameters than B and fits the data better. Discuss reasons for choosing model A or model B. What would you do to choose between them in practice, and how could you verify your choice?
- Bayesian parameter estimation. A measured quantity
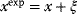 consists of a true value x and an additive error ξ. Compute the posterior distribution of x given a measured value
consists of a true value x and an additive error ξ. Compute the posterior distribution of x given a measured value 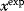 ; assume that the error ξ is Gaussian distributed with mean value 0 and standard deviation σξ and that the prior distribution of x is also Gaussian, with mean value µprior and standard deviation σprior.
; assume that the error ξ is Gaussian distributed with mean value 0 and standard deviation σξ and that the prior distribution of x is also Gaussian, with mean value µprior and standard deviation σprior.
Section 6.3
- Fast buffering. A metabolite appears in a kinetic model in two forms, either free or bound to proteins; there is a fast conversion between both forms, and only the free form participates in chemical reactions. Explain how the model could be modified to describe the metabolite only by its total concentration.
- Complete cell models. Does the notion of a complete cell model make any sense? (a) Speculate about possible definitions of “complete models.” (b) Estimate roughly the number of variables and parameters in models of living cells. Consider the following types of model: (i) Kinetic model of whole-cell metabolism without spatial structure. (ii) Compartment model including organelles. (iii) Particle-based model describing single molecules and their complexes in different conformation states. (iv) Model with atomic resolution.
- All models are wrong. Discuss the phrase by George Box “Essentially, all models are wrong, but some are useful.” What do you think of it? Does it give any helpful advice for modeling?
- Quasi-steady state. Consider a metabolic pathway A → B → C → with irreversible mass-action kinetics. The concentrations of B and C are described by the differential equation system:
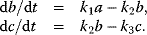
Assume that the second reaction is much faster than the other reactions,
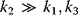 . Use the quasi-steady-state approximation to replace the first differential equation by an algebraic equation.
. Use the quasi-steady-state approximation to replace the first differential equation by an algebraic equation. - Quasi-equilibrium. Consider the same pathway, with the second reaction being fast and reversible. The differential equation system reads
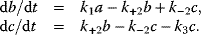
The conversion between B and C is much faster than the other reactions,
 ; use the quasi-equilibrium approximation to express b by an algebraic equation.
; use the quasi-equilibrium approximation to express b by an algebraic equation.
Section 6.4
- Holism and reductionism. (a) Discuss Aristotle's proposition “The whole is more than the sum of its parts.” in the context of biochemical systems and mathematical models describing them. (b) Speculate about the advantages and disadvantages of reductionist and holistic approaches in systems biology.
- Oscillations by interactions. Consider a pair of dynamical systems with the following properties: Each system, operating in isolation, shows a stable steady state; when coupled, both systems show stable oscillations. Describe how such oscillations can arise, find real-world examples, and formulate a biochemical model with these properties.
- Modular response analysis. Derive Eq. (6.65) from (Eqs. 6.64).
References
- 1. Vanrolleghem, P.A. and Heijnen, J.J. (1998) A structured approach for selection among candidate metabolic network models and estimation of unknown stoichiometric coefficients. Biotechnol. Bioeng., 58 (2–3), 133–138.
- 2. Wiechert, W. (2004) Validation of metabolic models: concepts, tools, and problems, in Metabolic Engineering in the Post Genomic Era (eds. B.N. Kholodenko and H.V. Westerhoff), Horizon Bioscience, Taylor & Francis.
- 3. Takors, R., Wiechert, W., and Weuster-Botz, D. (1997) Experimental design for the identification of macrokinetic models and model discrimination. Biotechnol. Bioeng., 56, 564–567.
- 4. Seber, G.A.F. and Wild, C.J. (2005) Nonlinear Regression, Wiley-Interscience.
- 5. Hoops, S., Sahle, S., Gauges, R., Lee, C., Pahle, J., Simus, N., Singhal, M., Xu, L., Mendes, P., and Kummer., U. (2006) COPASI: a complex pathway simulator. Bioinformatics, 22 (24), 3067–3074.
- 6. Sontag, E.D. (2002) For differential equations with r parameters, 2r+1 experiments are enough for identification. J. Non Linear Sci., 12 (6), 553–583.
- 7. Efron, B. and Tibshirani, R. (1993) An Introduction to the Bootstrap, Chapman & Hall/CRC.
- 8. Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. (1997) Bayesian Data Analysis, Chapman & Hall, New York.
- 9. Liebermeister, W. and Klipp, E. (2006) Bringing metabolic networks to life: integration of kinetic, metabolic, and proteomic data. Theor. Biol. Med. Model., 3, 42.
- 10. Heckerman, D. (1998) A tutorial on learning with Bayesian networks. Learning in Graphical Models, Kluwer Academic Publishers.
- 11. Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, Morgan Kaufmann Publishers, Inc.
- 12. Jensen, F.V. (2001) Bayesian Networks and Decision Graphs, Springer, New York.
- 13. Friedman, N., Linial, M., Nachman, I., and Pe'er, D. (2000) Using Bayesian networks to analyze expression data. J. Comput. Biol., 7 (3–4), 601–620.
- 14. Perrin, B.E., Ralaivola, L., Mazurie, A., Bottani, S., Mallet, J., and d'Alché Buc, F. (2003) Gene networks inference using dynamic Bayesian networks. Bioinformatics, 19 (ii), 138–148.
- 15. Schomburg, I., Chang, A., Ebeling, C., Gremse, M., Heldt, C., Huhn, G., and Schomburg, D. (2004) Brenda, the enzyme database: updates and major new developments. Nucleic Acids Res., 32 (Database Issue), D431–D433.
- 16. Wittig, U., Golebiewski, M., Kania, R., Krebs, O., Mir, S., Weidemann, A., Anstein, S., Saric, J., and Rojas, I. (2006) SABIO-RK: integration and curation of reaction kinetics data, in Data Integration in the Life Sciences: Proceedings of the 3rd International Workshop on (DILS'06) Hinxton, UK (eds. U. Leser, F. Naumann, and B. Ekman), Lecture Notes in Computer Science, vol. 4075, pp. 94–103.
- 17. Jaynes, E.T. (1957) Information theory and statistical mechanics. Phys. Rev. A, 106, 620–630.
- 18. Goldberg, R.N. (1999) Thermodynamics of enzyme-catalyzed reactions: Part 6–1999 update. J. Phys. Chem. Ref. Data, 28, 931.
- 19. Liebermeister, W. (2005) Predicting physiological concentrations of metabolites from their molecular structure. J. Comp. Biol., 12 (10), 1307–1315.
- 20. Bar-Even, A., Noor, E., Savir, Y., Liebermeister, W., Davidi, D., Tawfik, D.S., and Milo, R. (2011) The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry, 21, 4402–4410.
- 21. Liebermeister, W. and Klipp, E. (2005) Biochemical networks with uncertain parameters. IEE Proc. Syst. Biol., 152 (3), 97–107.
- 22. Ederer, M. and Gilles, E.D. (2007) Thermodynamically feasible kinetic models of reaction networks. Biophys. J., 92, 1846–1857.
- 23. Liebermeister, W. and Klipp, E. (2006) Bringing metabolic networks to life: convenience rate law and thermodynamic constraints. Theor. Biol. Med. Model., 3, 41.
- 24. Liebermeister, W., Uhlendorf, J., and Klipp, E. (2010) Modular rate laws for enzymatic reactions: thermodynamics, elasticities, and implementation. Bioinformatics, 26 (12), 1528–1534.
- 25. Lubitz, T., Schulz, M., Klipp, E., and Liebermeister, W. (2010) Parameter balancing for kinetic models of cell metabolism. J. Phys. Chem. B, 114 (49), 16298–16303.
- 26. Stanford, N.J., Lubitz, T., Smallbone, K., Klipp, E., Mendes, P., and Liebermeister, W. (2013) Systematic construction of kinetic models from genome-scale metabolic networks. PLoS One, 8 (11), e79195.
- 27. Mendes, P. and Kell, D.B. (1998) Non-linear optimization of biochemical pathways: application to metabolic engineering and parameter estimation. Bioinformatics, 14 (10), 869–883.
- 28. Moles, C.G., Mendes, P., and Banga, J.R. (2003) Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome Res., 13 (11), 2467–2474.
- 29. Rodriguez-Fernandeza, M., Mendes, P., and Banga, J.R. (2006) A hybrid approach for efficient and robust parameter estimation in biochemical pathways. Biosystems, 83 (2–3), 248–265.
- 30. Rodriguez-Fernandez, M., Egea, J.A., and Banga, J.R. (2006) Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinformatics, 7, 483.
- 31. Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., and Teller, E. (1953) Equations of state calculations by fast computing machines. J. Chem. Phys., 21 (6), 1087–1092.
- 32. Hastings, W.K. (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika, 57 (1), 97–109.
- 33. Kirkpatrick, S., Gelatt, C.D., and Vecchi, M.P. (1983) Optimization by simulated annealing. Science, 220 (4598), 671–680.
- 34. Storn, R. and Price, K. (1997) Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim., 11, 341–359.
- 35. Runarsson, T.P. and Yao, X. (2000) Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput., 4 (3), 284–294.
- 36. Wiechert, W. (2004) Validation of metabolic models: concepts, tools, and problems, in Metabolic Engineering in the Post Genomic Era (eds. B.N. Kholodenko and H.V. Westerhoff), Horizon Bioscience, Taylor & Francis.
- 37. Haunschild, M., Freisleben, B., Takors, R., and Wiechert, W. (2005) Investigating the dynamic behaviour of biochemical networks using model families. Bioinformatics, 21, 1617–1625.
- 38. Borges, J.L. (1999) Suarez Miranda, Viajes de varones prudentes, Libro IV, Cap. XLV, Lerida, 1658, in Jorge Luis Borges: Collected Fictions, Penguin.
- 39. Box, G.E.P. and Draper, N.R. (1987) Empirical Model-Building and Response Surfaces, John Wiley & Sons, Inc., New York.
- 40. Dyson, F. (2004) A meeting with Enrico Fermi. Nature, 427, 297.
- 41. Freedman, D.A. (1983) A note on screening regression equations. Am. Stat., 37 (2), 152–155.
- 42. Atkinson, A.C. (1981) Likelihood ratios, posterior odds and information criteria. J. Econom., 16, 15–20.
- 43. Ghosh, J.K. and Samanta, T. (2001) Model selection: an overview. Curr. Sci., 80 (9), 1135.
- 44. Hansen, M.H. and Yu, B. (2001) Model selection and the principle of minimum description length. J. Am. Stat. Assoc., 454, 746–774.
- 45. Johnson, J.B., and Omland, K.S. (2004) Model selection in ecology and evolution. Trends Ecol. Evol., 19 (2), 101–108.
- 46. Vuong, Q.H. (1989) Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica, 57 (2), 307–333.
- 47. Akaike, H. (1974) A new look at the statistical model identification. IEEE Trans. Automat. Contr., 19 (6), 716–723.
- 48. Hurvich, C.M. and Tsai, C.-L. (1989) Regression and time series model selection in small samples. Biometrika, 76, 297–307.
- 49. Schwarz, G. (1978) Estimating the dimension of a model. Ann. Stat., 6 (2), 461–464.
- 50. Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. (1997) Bayesian Data Analysis, Chapman & Hall, New York.
- 51. Stewart, W.E., and Henson, T.L. (1996) Model discrimination and criticism with single-response data. AIChE J., 42 (11), 3055.
- 52. Okino, M.S. and Mavrovouniotis, M.L. (1998) Simplification of mathematical models of chemical reaction systems. Chem. Rev., 98 (2), 391–408.
- 53. Visser, D., Schmid, J.W., Mauch, K., Reuss, M., and Heijnen, J.J. (2004) Optimal re-design of primary metabolism in Escherichia coli using linlog kinetics. Metab. Eng., 6 (4), 378–390.
- 54. Degenring, D., Fromel, C., Dikta, G., and Takors, R. (2004) Sensitivity analysis for the reduction of complex metabolism models. J. Process Control, 14, 729–745.
- 55. Liebermeister, W., Baur, U., and Klipp, E. (2005) Biochemical network models simplified by balanced truncation. FEBS J., 272 (16), 4034–4043.
- 56. Roussel, M.R. and Fraser, S.J. (2001) Invariant manifold methods for metabolic model reduction. Chaos, 11 (1), 196–206.
- 57. Higgins, J.J. (1965) Dynamics and control in cellular systems, in Control of Energy Metabolism (eds. B. Chance, R.W. Estabrok, and J.R. Williamson), Academic Press, New York, p. 13.
- 58. Reich, J.G. and Sel'kov, E.E. (1975) Time hierarchy, equilibrium and non-equilibrium in metabolic systems. BioSystems, 7, 39–50.
- 59. Easterby, J.S. (1981) A generalized theory of the transition time for sequential enzyme reactions. Biochem. J., 199, 155–161.
- 60. Heinrich, R. and Rapoport, T.A. (1975) Mathematical analysis of multienzyme systems: II. Steady state and transient control. BioSystems, 7, 130–136.
- 61. Lloréns, M., Nuno, J.C., Rodríguez, Y., Meléndez-Hevia, E., and Montero, F. (1999) Generalization of the theory of transition times in metabolic pathways: a geometrical approach. Biophys. J., 77, 23–36.
- 62. Ingalls, B.P. (2004) A frequency domain approach to sensitivity analysis of biochemical systems. J. Phys. Chem. B, 108, 1143–1152.
- 63. Liebermeister, W. (2005) Response to temporal parameter fluctuations in biochemical networks. J. Theor. Biol., 234 (3), 423–438.
- 64. Ingalls, B.P. and Sauro, H.M. (2003) Sensitivity analysis of stoichiometric networks: an extension of metabolic control analysis to non-steady state trajectories. J. Theor. Biol., 222 (1), 23–36.
- 65. Zobeley, J., Lebiedz, D., Ishmurzin, A., and Kummer, U. (2005) A new time-dependent complexity reduction method for biochemical systems, in Transactions on Computational Systems Biology (ed. C. Prami et al.), Lecture Notes in Computer Science, vol. 3380, Springer, pp. 90–110.
- 66. Moore, B.C. (1981) Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans. Automat Contr., 26, 17–32.
- 67. Surovtsova, I., Simus, N., Hübner, K., Sahle, S., and Kummer, U. (2012) Simplification of biochemical models: a general approach based on the analysis of the impact of individual species and reactions on the systems dynamics. BMC Syst. Biol., 6, 14.
- 68. Teusink, B., Passarge, J., Reijenga, C.A., Esgalhado, E., van der Weijden, C.C., Schepper, M., Walsh, M.C., Bakker, B.M., van Dam, K., Westerhoff, H.V., and Snoep, J.L. (2000) Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem., 267, 5313–5329.
- 69. Chassagnole, C., Raïs, B., Quentin, E., Fell, D.A., and Mazat, J. (2001) An integrated study of threonine-pathway enzyme kinetics in Escherichia coli. Biochem. J., 356, 415–423.
- 70. Karr, J.R., Sanghvi, J.C., Macklin, D.N., Gutschow, M.V., Jacobs, J.M., Bolival, B., Assad-Garcia, N., Glass, J.I., and Covert, M.W. (2012) A whole-cell computational model predicts phenotype from genotype. Cell, 150 (2), 389–401.
- 71. Petersen, S., Lieres, E.v., de Graaf, A.A., Sahm, H., and Wiechert, W. (2004) A multi-scale approach for the predictive modeling of metabolic regulation, in Metabolic Engineering in the Post Genomic Era (eds. B.N. Kholodenko and H.V. Westerhoff), Horizon Bioscience, Taylor & Francis.
- 72. Liebermeister, W., Baur, U., and Klipp, E. (2005) Biochemical network models simplified by balanced truncation. FEBS J., 272 (16), 4034–4043.
- 73. Hofmeyr, J.-H.S. and Cornish-Bowden, A. (2000) Regulating the cellular economy of supply and demand. FEBS Lett., 476 (1–2), 47–51.
- 74. He, F., Fromion, V., and Westerhoff, H.V. (2013) (Im)Perfect robustness and adaptation of metabolic networks subject to metabolic and gene-expression regulation: marrying control engineering with metabolic control analysis. BMC Syst. Biol., 7, 131.
- 75. van Eunen, K., Rossell, S., Bouwman, J., Westerhoff, H.V., and Bakker, B.M. (2011) Quantitative analysis of flux regulation through hierarchical regulation analysis. Methods Enzymol., 500, 571–595.
- 76. Stanford, N.J., Lubitz, T., Smallbone, K., Klipp, E., Mendes, P., and Liebermeister, W. (2013) Systematic construction of kinetic models from genome-scale metabolic networks. PLoS One, 8 (11), e79195.
- 77. Hofmeyr, J.S., Gqwaka, O.P.C., and Rohwer, J.M. (2013) A generic rate equation for catalysed, template-directed polymerisation. FEBS Lett., 587, 2868–2875.
- 78. Schuster, S., Kahn, D., and Westerhoff, H.V. (1993) Modular analysis of the control of complex metabolic pathways. Biophys. Chem., 48, 1–17.
- 79. Bruggeman, F., Westerhoff, H.V., Hoek, J.B., and Kholodenko, B. (2002) Modular response analysis of cellular regulatory networks. J. Theor. Biol., 218, 507–520.
- 80. Wolf, J. and Heinrich, R. (2000) Effect of cellular interaction on glycolytic oscillations in yeast: a theoretical investigation. Biochem. J., 345, 312–334.
- 81. Wolf, J., Sohn, H.-Y., Heinrich, R., and Kuriyama, H. (2001) Mathematical analysis of a mechanism for autonomous metabolic oscillations in continuous culture of Saccharomyces cerevisiae. FEBS Lett., 499, 230–234.
- 82. du Preez, F.B., van Niekerk, D.D., Kooi, B., Rohwer, J.M., and Snoep, J.L. (2012) From steady-state to synchronized yeast glycolytic oscillations I: model construction. FEBS J., 279, 2810–2822.
Further Reading
- Modular Response Analysis: Bruggeman, F., Westerhoff, H.V., Hoek, J.B., and Kholodenko, B. (2002) Modular response analysis of cellular regulatory networks. J. Theor. Biol., 218, 507–520.
- Bottom-Up Modeling (Threonine Pathway Model): Chassagnole, C., Raïs, B., Quentin, E., Fell, D.A., and Mazat, J. (2001) An integrated study of threonine-pathway enzyme kinetics in Escherichia coli. Biochem. J., 356, 415–423.
- Bootstrap: Efron, B. and Tibshirani, R. (1993) An Introduction to the Bootstrap, Chapman & Hall/CRC.
- Bayesian Data Analysis: Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. (1997) Bayesian Data Analysis, Chapman & Hall, New York.
- Metabolic Response to Periodic Perturbations: Ingalls, B.P. (2004) A frequency domain approach to sensitivity analysis of biochemical systems. J. Phys. Chem. B, 108, 1143–1152.
- Metabolic Response for Time Series: Ingalls, B.P. and Sauro, H.M. (2003) Sensitivity analysis of stoichiometric networks: an extension of metabolic control analysis to non-steady state trajectories. J. Theor. Biol., 222 (1), 23–36.
- Modular Whole-Cell Model of Mycoplasma genitalium: Karr, J.R., Sanghvi, J.C., Macklin, D.N., Gutschow, M.V., Jacobs, J.M., Bolival, B., Jr., Assad-Garcia, N., Glass, J.I., and Covert, M.W. (2012) A whole-cell computational model predicts phenotype from genotype. Cell, 150 (2), 389–401.
- Flux-Based Model Construction: Stanford, N.J., Lubitz, T., Smallbone, K., Klipp, E., Mendes, P., and Liebermeister, W. (2013) Systematic construction of kinetic models from genome-scale metabolic networks. PLoS One, 8 (11), e79195.
- Bottom-Up Modeling (Glycolysis Model): Teusink, B., Passarge, J., Reijenga, C.A., Esgalhado, E., van der Weijden, C.C., Schepper, M., Walsh, M.C., Bakker, B.M., van Dam, K., Westerhoff, H.V., and Snoep, J.L. (2000) Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem., 267, 5313–5329.
- Hierarchical Regulation Analysis: van Eunen, K., Rossell, S., Bouwman, J., Westerhoff, H.V., and Bakker, B.M. (2011) Quantitative analysis of flux regulation through hierarchical regulation analysis. Methods Enzymol., 500, 571–595.