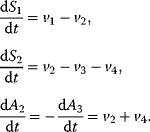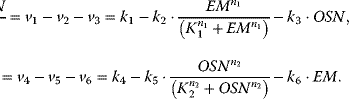2
Modeling of Biochemical Systems

2.1 Overview of Common Modeling Approaches for Biochemical Systems
2.2 ODE Systems for Biochemical Networks
1. Basic Components of ODE Models
2. Illustrative Examples of ODE Models
References
Further Reading

Over the last two decades, formulation of formal (often mathematical) concepts and computational modeling have become more and more familiar in biology, although they have been applied much earlier. Leonardo of Pisa used in his book from 1202 the Fibonacci numbers to describe the growth of a rabbit population. Lotka and Volterra characterized population dynamics of lynx and hares (predators and preys) with their famous equation in the 1920s. Michaels and Menten developed a model to determine the rate for kinetic reactions in 1913. In the mid of the last century, Ludwig von Bertalanffy became famous for his work on biophysics of open systems, thermodynamics of living systems, and the introduction of the notion of “Fließgleichgewicht,” roughly translated with dynamic equilibrium.

Since that time, many different approaches have been introduced and applied for in-depth understanding of biology, to relate independent biological observations to each other (what has the protein content measured in one experiment to do with the mRNA amounts measured independent of another technique?). Concepts from physics and engineering have fruitfully invaded biological research, one example being concepts of control systems for gene regulation. Biology is on its way to a quantitative science like physics, chemistry, or geography. It requires numbers and mathematical predictions to complement biological measurements and to derive useful predictions from them. We can compare it, in some sense, with the weather forecast: Data are combined with models and evaluated by computers to predict tomorrow's weather. The forecast is often not precise, but getting better. However, biology is much more complicated with different species, different cell types making a higher organism, and processes of development and evolution. Nevertheless, many promising results indicate that it is worth trying to provide a mathematical description of biological systems.

Here, we will give a short and cursory introduction to model concepts and how to formulate a first model for the process of interest. More detailed explanations of construction and analysis procedures for models follow in the later chapters.

2.1 Overview of Common Modeling Approaches for Biochemical Systems

Understanding a biological system is not a straight, unidirectional process. It requires understanding of its topology or the structure of the system. It involves analyses of its dynamical behavior and the control mechanisms at play. Also, it requires interpreting how its design and function relate one another in the overall context. The major guiding principles for model building are as follows: What question is the model supposed to answer? Is it built to explain a surprising observation? Is it built to relate separate observations with each other and with previous knowledge? Is it built to make predictions, for example, about the effect of specific perturbations? Often, a major function of models is to make assumptions about the underlying process explicit and, hence, testable. Only if we have a formal description of the system at hand, we can prove formal relations or falsify certain assumptions.

A mathematical model of a biological system can describe very different aspects and, hence very different approaches are employed. Let us consider the following three major types of computational models, which are further explained below:

Network-based models
Rule-based models
Statistic models

Network-based models describe and analyze properties, states, or dynamics of networks, that is, components and their interactions. Typical and frequently used network-centered modeling frameworks are as follows:

Systems of ordinary differential equations for biochemical reaction networks
Stochastic description of biochemical reaction networks and other state change processes, for example, for birth–death processes or reaction networks with small compound numbers
Boolean models, for example, for gene regulatory networks
Petri net models, for example, for metabolic networks or for transitions in complex systems

In classical cases, the model has instances for a set of compounds, for example, genes, RNAs, proteins, or small molecules contributing to a process. These compounds can be represented simply by a node or by a set of variables describing their amount or activity or states. The mathematical description suitable for the variables depends on the chosen modeling framework. The topology of the network, that is, the ensemble of all compounds (or nodes of the network) and interactions between them, can be derived from different experiments to identify interactions. These experiments range from classical biochemical methods to more recent high-throughput techniques such as protein–protein interactions by yeast two-hybrid analysis, DNA–protein interactions by chip-on-chip, or gene coexpression profiling (a survey on experimental techniques for systems biology is given in Chapter 14). Since a considerable amount of data is available in publications, an alternative or addition to new experiments is exhaustive literature research, including text mining as well as systematic screening of databases.

A sensible description of the network topology already allows a set of topological analyses: Are compounds densely or loosely connected? Do we have single important hubs or are all nodes equally well connected? What is the shortest path to get from one node to another node? These questions are answered in Chapter 8. They can provide an understanding of how information is transmitted in a network, how robust it is against changes of its topology (e.g., by knockout of a node or cutting of a connection), or how it may have emerged and changed during evolution.

Based on the completed network topology, it is possible to add more detailed information about the nature of the connections or the nodes. This can be kinetic laws for individual reactions or instructions for combining input information arriving at a node from different edges as in Boolean networks. Again, the type of additional information to add depends on the choice of the model framework, which in turn is largely determined by the question that the model is supposed to answer.

Concerning the choice of modeling framework, we have a number of alternatives. The most important ones are the following:

For the variables describing the states of the compounds, we can consider either discrete or continuous values. An example of discrete values is the pair of 0 and 1 used in Boolean networks (Section 7.1) to characterize on/off states of genes due to the presence or absence of transcription factors, respectively. Another example is the set of all natural numbers indicating the number of molecules. Continuous variable values are used to describe compound concentrations or physical properties such as temperature, pressure, or chemical potential.
For the behavior of the system in time, we may on one side assume that it essentially does not depend on time but is static (as, for example, metabolic fluxes in flux balance analysis) (Section 3.3). In dynamic networks, on the other hand, states of variables can be updated either on a continuous time axis or in discrete time steps. Ordinary differential equation (ODE) systems make use of continuous time, while model approaches with discrete variable values typically also employ discrete time schemes.
The update of states over time can proceed deterministically, that is, according to fixed rules that always lead to the same outcome when start conditions are identical. Examples are again ODE systems or classical Boolean networks. Alternatively, state updates may be realized in a stochastic fashion, where events occur with a certain probability, leading to different outcomes for different simulation runs, even under identical initial conditions. Stochastic models are explained in detail in Section 7.2.

Rule-based models or agent-based models represent a different approach of modeling biological phenomena (and, of course, also phenomena in other areas). In rule-based models, every compound of the system can update its state according to a set of rules. For example, a rule could express that protein X is phosphorylated if its kinase Y is activated and its inhibitor Z is not present. Rule-based modeling lists all potential state changes of the individual compounds, but not all potentially occurring states. That is why it can be computationally less demanding than an ODE system, for example, for signaling systems, where compounds may have many degrees of phosphorylation or involve in various complexes. Cellular automata are regular grids of cells (here cells in the sense of abstract location or unit, not of a biological entity), which can assume a finite number of states. States are updated based on rules that depend on the states of neighboring cells. Cellular automata can create complex phenomena, including the classical Game of Life. More complex are the agent-based models, in which all individual compounds such as proteins or cells are considered as autonomous agents with their own rules. The agents move freely in the containing space and update their states according to their rules and the environmental conditions. They can be used to describe many processes such as (i) signaling pathways in models accounting for spatial and structural properties of the cell or (ii) cell states in models describing differentiation or (iii) the interplay of different cells of the immune system or (iv) the interaction of parasites with the occupied host tissue.

In the light of massive data production by the different omics technologies, statistical models are very important in systems biology. Statistical models establish relations between measured data and provide a guide to extracting underlying structures of the biological system that gave rise to the data. Examples are the detection of linear or multilinear relationships such as linear regression or ANOVA. One may also perform a comparison of the measured data distribution with well-understood distributions such as binomial distribution, Gaussian distribution, Poisson distribution, and others. Clustering of measurement data is used to find groups of data that behave similarly in some aspects (e.g., in their dynamics). It is frequently applied for the output of networks such as gene expression data and may reveal common regulation patterns. Other methods have been developed to categorize data. An example is support vector machines, which are learning algorithms that are supposed to divide a number of objects into classes with maximal distance. These classes may or may not reflect biological mechanisms or structures, but often provide a good indication of underlying principles.

If you want to build a theoretical model for a biological process, you would like to use the following short recipe:

Define the question that the model shall help to answer.
Seek available information:
1. Read the literature.
2. Look at the available experimental data.
3. Talk to experts in the field.
Formulate a mental model.
Decide on the modeling concept (network-based or rule-based, deterministic or stochastic, etc.)
Formulate the first (simple) mathematical model.
Test the model performance in comparison to the available data.
Refine the model, estimate parameters.
Analyze the system (parameter sensitivity, static and temporal behaviors, etc.)
Make predictions for scenarios not used to construct the model such as
1. gene knockout or overexpression,
2. application of different stimuli or perturbations.
Compare predictions and experimental results.

If model predictions and the new experimental data are in agreement, it indicates that the model may have covered correctly important aspects of the described system and can be used to make further predictions. Models are never “right,” but can be appropriate and helpful. If predictions and experimental tests differ, it may be even more interesting. It tells you that important aspects of the biological process have not been understood correctly, not been presented appropriately, or have been completely ignored. The model is falsified (at least in its current state), leading to an interesting journey of finding missing links, alternative explanations, or better parameter sets to explain the observations.

2.2 ODE Systems for Biochemical Networks

2.2.1 Basic Components of ODE Models

To formulate an ODE model for a dynamic biochemical reaction network, we need the following information:

The basic building blocks are all compounds and all reactions converting these compounds into each other. A list of the reactions and their substrates and products gives us the stoichiometry of the network. This approach is further detailed in Chapter 3.
The modeler must set the boundary of the system. Which components should the model follow? They become internal components. Which components are not considered relevant for the model? They are completely left out. Which components determine the model behavior, but are not changed by its dynamics? They are called external components. For a metabolic pathway, for example, all metabolites within the pathway may be internal metabolites, while the concentration of a nutrient provided in the medium at fixed experimental conditions may be an external metabolite. All other cellular components may be ignored for that specific study.
For all reactions that are part of the model, assign kinetic laws (see Chapter 4).
Determine the values of the kinetic parameters used in the kinetic laws. They can be taken either from databases or literature or they can be fitted to experimental data (Chapter 6).
On the basis of the well-formulated model, we can perform different analysis steps:
Find out whether the system has a steady state or not. Is the steady state uniquely defined or do we obtain several steady states depending on the parameter values? Calculate steady state concentrations and reaction rates.
Simulate the time course for a given set of parameter values and initial conditions (tools and techniques are introduced in Chapter 5).
Analyze the effect of perturbations. The impact of small changes of parameter values is studied by sensitivity analysis and – for biochemical networks – by metabolic control analysis (see Section 4.2). One may also test the effect of complete knockouts of enzymes catalyzing the individual reactions or of knockdowns or overexpression.

2.2.2 Illustrative Examples of ODE Models

To illustrate the steps introduced above, we consider two little models: one for a metabolic network and the other for a small regulatory network.

2.2.2.1 Metabolic Example

Metabolism serves the uptake of nutrients to convert them into energy, mostly in the form of ATP, and into building blocks such as amino acids and lipids. All metabolic reactions are catalyzed by enzymes. The metabolic network in Figure 2.1 resembles the first steps in glycolysis, a major catabolic pathway for the uptake and initial phosphorylation of glucose, which is afterward distributed to other catabolic and anabolic pathways to provide building blocks and energy. Let us call extracellular glucose S₀ and its concentration S₀. Intracellular glucose is S₁, singly phosphorylated glucose (glucose-6-phosphate, G6P) is S₂, and doubly phosphorylated fructose (fructose-1,6-bisphosphate, F16P₂) is S₄. G6P is provided for other synthetic pathways producing S₃. Phosphorylation is carried out by consuming ATP (A₃) and converting it into ADP (A₂).

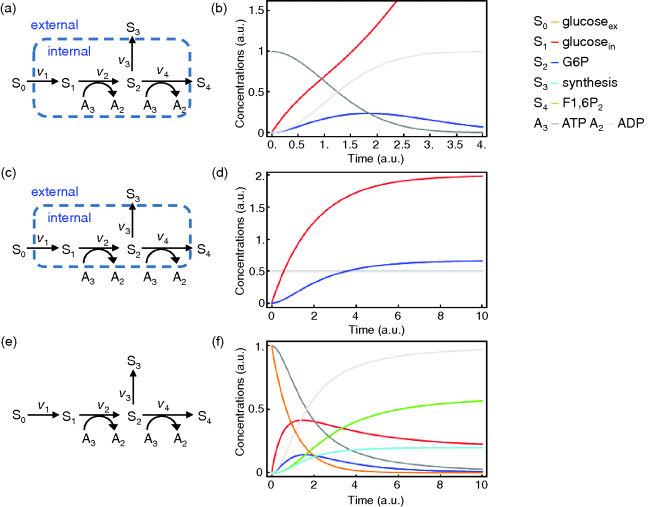
**Figure 2.1** Example of a metabolic model. (a) Network representation with S₀ and S₃ considered external and S₁, S₂ as well as A₂ and A₃ treated as internal variables. (b) Time course resulting from dynamic simulation of the network shown in part (a). (c) The same network as in part (a), but here A₂ and A₃ are also treated as external. (d) Time course resulting from dynamic simulation of the network shown in part (c). (e) Network representation with all components considered as internal and, therefore, dynamic. (f) Dynamics of the network shown in part (e). The dynamics and kinetics are listed in Eqs. (2.1) and (2.2). Parameter values: ().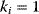

We can describe the dynamics of the network in Figure 2.1a by a set of ordinary differential equations as follows:

(2.1)

When we assign kinetics to the reactions, we can simulate the system. A simple choice of kinetics is mass action kinetics, where the reaction rate is proportional to the concentration of its substrates:

(2.2)

You can find more information on kinetic laws in Chapter 4. We will now use this set of equations to simulate the dynamic behavior of the network. Starting with an ATP concentration of 1, an ADP concentration of 0, and zero concentrations of the internal sugars (S₁, S₂), we find that ATP is consumed and ADP is produced. S₁ is produced in an unlimited fashion through the uptake reaction v₁, but S₂ is produced only as long as ATP is available, afterward it declines. Since there is unlimited supply of S₀, the system has no steady state, that is, no state with .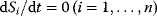

A steady state with 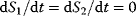can be obtained if we consider that ATP and ADP are kept constant by other cellular processes, that is, 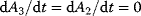. Then we can consider them as external variables, as shown in Figure 2.1c with the dynamics represented in Figure 2.1d.

If S₀, S₃, and S₄ were internal variables that can change (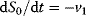, , 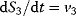, 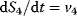respectively), then the mass provided by S₀ remains within the system and it approaches a state where S₀, A₃, and S₂ decline to 0, while A₂ reaches 1, S₁ and S₄ approach about 0.2, and S₃ about 0.6. However, the model will never reach a true steady state (Figure 2.1e and f).

2.2.2.2 Regulatory Network Example

Stem cell research is of increasing importance in biological research and of great interest in health care. Besides many other promises, it provides the hope that in the future many diseases can be cured by administration of healthy cells of a specific tissue to a diseased person that have been grown out of reprogrammed induced pluripotent stem cells (iPS cells) originating from the same person. The three genes (and gene products) considered as the main regulators of stemness of cells are Oct4, Sox2, and Nanog. They activate each other, but they are controlled by epigenetic marking and by growth factors. Cellular differentiation is accompanied by hypermethylation of their promoters and by downregulation of their gene expression. In order to create iPS cells, many experimental procedures have been tested. The addition of viral plasmid containing four factors – Sox2, Oct4, c-Myc, and the microRNA Klf4 – that was introduced by Takahashi and Yamanaka in 2006 [2] was most successful.

Here, we will use a simple model to study some basic properties of that system. Let us first assume that Oct4, Sox2, and Nanog stabilize each other. Their expression is suppressed by the epigenetic marking (the DNA methylation), but the proteins also prevent DNA methylation (see Figure 2.2). This mutual inhibition can be described on different levels of detail (e.g., including the joint stabilization of the proteins or not). We will use the following differential equation system that focuses on the collective effect of stemness markers on epigenetic marking and vice versa, that is, the double negative feedback (resulting in a positive feedback) that each component has on itself:

(2.3)

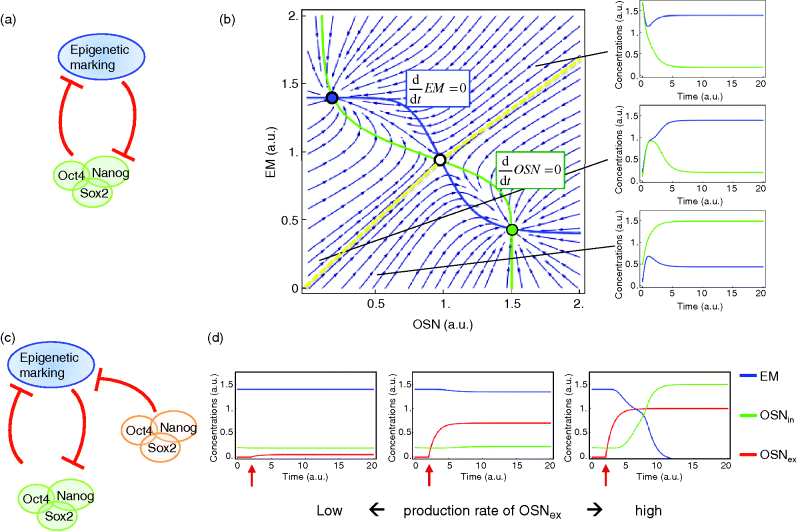
**Figure 2.2** Network and dynamics of a model for epigenetic regulation of stemcellness. (a) Epigenetic regulation (EM) and the three factors Oct4, Sox2, and Nanog (OSN) responsible for pluripotency. The dynamics is described with the ordinary differential system (equations system 2.3). (b) The phase plan showing a plot of EM against *OSN* represents the three steady states of this system, one stable state for high values of EM (indicated in blue), one stable state for high values of *OSN* (indicated in green), and one in-between. The state in-between is unstable. The small light blue arrows indicate the actual flow of the system at each point in the phase plan. The green line is the line with no change (nullcline) of *OSN*; hence, the flow arrows cross it always vertically. The blue line for steady values of EM is always crossed horizontally. The dashed yellow line is called separatrix since it separates the basin of attraction for the steady state featuring high EM and low *OSN* (blue dot) from the basin of attraction for the steady state with high *OSN* and low EM (green dot). The small time plots to the right exemplify that any starting condition within these basins of attraction leads to the respective stable state. (c) The system can be pushed out of its current stable state by supply of another component, here by OSN transcribed from an exogenous vector, which inhibits EM but is not regulated by it. (d) The effect depends on the expression strength of external OSN; only if it is expressed strongly enough and for sufficient time, it can reverse the cellular decision from high EM to high *OSN* (and low EM).

OSN denotes the common activity of the stemness markers Oct4, Sox2, and Nanog. EM represents the level of epigenetic marking. The activity of OSN increases linearly, but EM inhibits it in a fashion described with a Hill function (see Chapter 4). Its basal degradation is proportional to its current concentration. The respective rules hold for EM with OSN as inhibitor. The behavior is illustrated in Figure 2.2. It shows that the system has three steady states. One steady state is unstable, the other two steady states feature either low levels of epigenetic marking and high expression of the stemness factors, indicating that the cell is a stem cell, or high levels of epigenetic marking and low levels of Oct4, Sox2, and Nanog, indicating differentiation. In isolation, the system will always reach one of these states, depending on the initial conditions, and then remain there. It can only be moved out of this state by external cues. Under natural conditions, stem cells are forced into differentiation by external signaling compounds such as Wnt or growth factors. When trying to reprogram cells away from the differentiated state toward induced pluripotency, the strategy introduced by Takahashi and Yamanaka favors OSN through the expression from a viral vector. This has the effect that these four compounds are expressed and active, for example, in regulating epigenetic marking, but they are not under epigenetic regulation themselves. If their expression is strong and long enough, they push the cells back into conditions featuring pluripotency with high expression also of endogenous stem cell factors.

Cellular reprogramming with viral vectors has provided many opportunities to study the reprogramming process in detail and determine the contribution of individual regulatory mechanisms, such as cell cycle progression. It is less suited for long-term application in human patients, which is an interesting medical aim, since it implies using viral material and since the uncontrolled expression of pluripotency factors can also lead to unintended side effects such as cancerogenesis. Hence, the search for alternative ways for reprogramming is ongoing, for example, by using small molecules.

References

1. Klipp, E., Liebermeister, W., Helbig, A., Kowald, A., and Schaber, J. (2007) Systems biology standards: the community speaks. Nat. Biotechnol., 25, 390–391.
2. Takahashi, K. and Yamanaka, S. (2006) Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. Cell, 126, 663–676.