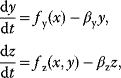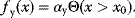8
Network Structure, Dynamics, and Function
- 8.1 Structure of Biochemical Networks
- 8.2 Regulation Networks and Network Motifs
- 8.3 Modularity and Gene Functions
- Cell Functions Are Reflected in Structure, Dynamics, Regulation, and Genetics
- Metabolics Pathways and Elementary Modes
- Epistasis Can Indicate Functional Modules
- Evolution of Function and Modules
- Independent Systems as a Tacit Model Assumption
- Modularity and Biological Function Are Conceptual Abstractions
- Exercises
- References
- Further Reading
Cells use thousands of proteins to produce and convert substances, to sense environmental stimuli and internal cell states, and to transmit and process this information. Even bacteria contain several thousands of genes, so the number of enzyme-catalyzed reactions (including transcription and translation for all genes) and the number of compounds involved are on the order of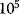 
. A way to deal with such highly complex systems is to disregard all their quantitative details and to simply depict them as networks.
Whenever complex information is reduced to discrete elements and their relations, it can be displayed as a network. Biological networks may describe very different things: causal or mechanistic effects (reaction–metabolite network, transcriptional regulation network), molecule interactions (protein–protein or protein–DNA binding), statistical relationships (Bayesian networks for gene expression, correlated metabolite fluctuations), or functional or evolutionary relatedness.
Many networks are inferred statistically, for example, from high-throughput data or text mining screens, and represent things such as statistical correlations or even co-occurrence in scientific articles. Based on quantitative relationships, which can be formally seen as distances or similarities, networks can be constructed by thresholding: An edge is drawn whenever a correlation exceeds some threshold value or is statistically significant. Such inferred networks may be related to biological networks, but need not represent them directly. In particular, they often capture indirect interactions (e.g., genes influencing each others' expression via changes of the metabolic state) instead of specified mechanisms (e.g., gene products acting directly as transcription factors).
A focus on network structures and omission of quantitative details can be fruitful. Sometimes, the dynamic properties of a system depend mostly on its network structure and less on the dynamics of individual elements. Negative feedback loops, for instance, can have typical effects independent of their physical realization. Thus, even models with an inaccurate dynamics but correct network structure may be helpful to simulate system behavior. However, a main usage of networks is visualization: Networks can highlight structures that would otherwise go unnoticed. When patterns stand out, we may analyze them closely and try to find reasons for them in the system's dynamics or evolution.
8.1 Structure of Biochemical Networks
The prominent biochemical networks in cells – metabolic networks, transcription networks, and signal transduction networks – perform different functions and evolve in different ways. Metabolic networks allow cells to produce and convert metabolites; they support the metabolic fluxes, which vary depending on supply and demand. The network structure is, in principle, determined by the enzymes encoded in an organism's genome, and many metabolic networks have been reconstructed [1]. Depending on the organism's ecological niche, these networks range from small sizes, in intracellular parasites, to very large sizes, for instance, in plants. However, central pathways such as glycolysis are widely conserved and all organisms use a core set of important cofactors. A commonly used reconstruction of the Escherichia coli metabolic network [2] contains 1260 genes, 1148 unique functional proteins, and 1039 unique metabolites. The 2077 reactions are assigned to different compartments (cytoplasm, periplasm, or the extracellular space) and include 1387 chemical and 690 transport reactions. A current reconstruction of the human metabolic network contains 7440 reactions and 2626 metabolites (which, differentiated by cell compartments, yield 5063 molecule species), and has been used to construct 65 cell-type-specific submodels [3].
Transcription networks, as shown in Figure 8.1a, describe the regulation of gene expression by transcription factors; their structure is biochemically determined by transcription factor binding sites. Signal transduction networks rely mostly on interactions between proteins, for example, kinases or phosphatases, which can mutually phosphorylate and dephosphorylate each other. Physical interactions between proteins in cells, such as binding and complex formation, can be derived from yeast two-hybrid screens (see Chapter 14.10) and visualized in protein–protein interaction networks (see Figure 8.1b).
Figure 8.1 Biological networks. (a) Transcription network in E. coli. Genes are shown by colored segments. Arcs show different kinds of regulation (blue: activation, red: inhibition, green: dual regulation). Traces around the circle indicate autoregulation. (Courtesy of S. Ortiz, L. Rico, and A. Valencia.) (b) Protein–protein binding interactions. The network shown contains about 80% of all protein species in yeast. Node colors indicate the phenotypic effects of removing a protein (red: lethal; green: nonlethal; orange: slow growth; yellow: unknown). (From Ref. [4].)
Biological networks can contain repetitive or prominent local structures, which may work as functional units and can be detected with statistical methods. To understand how such structures emerge, we need to see how networks can change during evolution. Bacterial promoter sequences, for instance, can evolve relatively rapidly, so edges in their transcription networks (implemented by transcription factor binding sites) may easily get lost by mutations. If we know how mutations, without selection for network function, would rewire a network, we can compare the structures in actual networks with such random structures. The comparison can point us to network structures that may have been conserved for specific biological functions. Such structures can be candidates for further biological study.
8.1.1 Random Graphs
8.1.1.1 Mathematical Graphs
Networks in which edges point from nodes to nodes (and not to other edges) can be described by mathematical graphs. A graph consists of a discrete set of nodes and a set of edges, defined as pairs of nodes. In directed graphs, edges are ordered pairs represented by arrows. In undirected graphs, edges are unordered pairs and displayed by lines. Examples are shown in Figure 8.2.
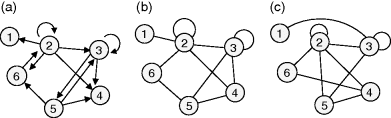
Figure 8.2 Simple graphs. (a) Directed graph. (b) Undirected graph with the same topology. (c) Rewired variant of graph (b) where all degrees (number of edges per node) are preserved.
The structure of a graph can be represented by an adjacency matrix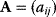 
: Edges from node 
to node 
are represented by matrix elements 
, all other elements have values of 0. For undirected graphs, the adjacency matrix is symmetric. A directed graph with 
nodes can have maximally 
edges (corresponding to elements of the adjacency matrix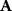 
), 
of which would be self-edges (diagonal elements of 
). In a directed graph, a cycle is a sequence of arrows that starts from a node, follows the arrows in their proper direction, and returns to the first node; graphs without cycles are called acyclic.
When graphs are drawn, the arrangement of nodes and edges is a matter of convenience. Larger biological networks are usually nonplanar – that is, edge intersections cannot be avoided – and designing well-drawn layouts can be a challenge [5]. In metabolic charts, cofactors are often omitted or displayed multiple times, which greatly simplifies the layout. A unique graph layout, suited to visually compare networks by their statistical properties, is provided by hive plots (www.hiveplot.net).
A graph can be characterized by some basic statistical properties (see Table 8.1). Nodes sharing an edge with node 
are called its neighbors, and the number of neighbors is called the degree or node size 
. In directed graphs, we distinguish between in-degrees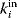 
and out-degrees 
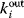, referring to incoming and outgoing edges, respectively. In finite graphs – graphs with a finite number of nodes – the count numbers of nodes with degree 
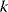form the degree sequence 
. A directed graph with 
nodes and 
edges has an average degree of 
, and the probability that two randomly chosen nodes share an edge is 
. In infinite graphs, the probabilities 
for randomly picked nodes to have degree 
are called the degree distribution.
Table 8.1 Statistical properties of graphs.
Source: Data from Ref. [8].
| Graph |  |
 |
 |
 |
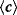| Example Figure 8.2b | 6 | 3 | 23/15 | 1/5 |
| E. coli metabolite graph [6] | 282 | 7.35 | 2.9 | 0.32 |
| Movie actors [7] | 225 226 | 61 | 3.65 | 0.79 |
| Power grid [7] | 4941 | 2.67 | 18.7 | 0.08 |
Graphs can be characterized by node number  , average degree  , diameter  , and average clustering coefficient 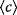 . Numbers refer to different real-world graphs. |
||||
8.1.1.2 Random Graphs
A random graph, similar to a random number, is defined as a probability distribution over a set of graphs. The single graphs are called realizations. For brevity, we sometimes refer to random graph realizations as “random graphs” and call the random graph an “ensemble.” In some random graphs, the probabilities are specified by a general rule: For instance, to define a random graph with 
nodes, we may assign equal probabilities to all possible graphs with exactly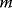 
edges and zero probability to other graphs. Another way to define probabilities is by a random process for graph construction: For instance, we may start with a set of unconnected nodes and add edges according to some probabilistic rule.
8.1.1.3 Erdös–Rényi Random Graphs
An Erdös–Rényi random graph 
is a random graph with 
nodes in which possible edges are realized independently and with probability 
. The elements of the adjacency matrix are independent binary variables with probabilities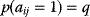 
. The number of edges in an Erdös–Rényi graph follows a binomial distribution 
with a maximum edge number 
; similarly, the out-degrees follow a binomial distribution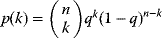 
. This distribution has a peak at the mean degree 
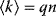and a standard deviation 
. For large graphs (
) with a fixed average degree, the degree distribution becomes a Poisson distribution, showing an exponential tail for large degrees.
In an Erdös–Rényi graph, a possible 
-node graph has the probability 
, which depends only on its edge number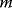 
. The edge number follows a binomial distribution 
with mean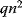 
and standard deviation 
. The mean degree (number of edges per node) reads 
, and for large graphs (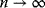
), the standard deviation becomes negligible. Therefore, a large Erdös–Rényi random graph can be approximated by a random graph 
with fixed edge number 
. Here, in each realization, 
edges are randomly distributed over the 
possible pairs of nodes. If we consider large directed graphs (
) with predefined mean degree 
, both types of random graph yield similar results; the parameters must be chosen such that 
.
8.1.1.4 Geometric Random Graphs
The topologies of some networks reflect an underlying spatial structure. For instance, the connections between nerve cells (which can be depicted as a graph) may reflect cell distances in space. Geometric random graphs [9] are defined based on such spatial relationships: Nodes correspond to points in a space (e.g., in the plane 
) with geometric distances 
. Two nodes are connected with a probability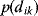 
depending on their geometric distance. Assuming a Gaussian probability density 
, typical random graph realizations will contain many local connections, but very few connections between distant points.
8.1.1.5 Random Graphs with Predefined Degree Sequence
For statistical tests, we need random graphs that resemble a given network in its basic statistical properties. Random graphs preserving the in- and out-degrees of all nodes can be constructed by a random flipping of edges [10]: In each step, two edges are chosen at random and replaced by two edges with the same origin nodes, but with their target nodes flipped. This flipping changes the graph, but leaves the degree of each node unchanged (see Figure 8.2b and c). After many iterations, we obtain a randomized graph in which in- and out-degrees are unchanged, but more complex structures have been destroyed. Other random graphs, in which more complicated properties are preserved, can be obtained by simulated annealing [10].
8.1.2 Scale-Free Networks
Many real-world networks, including metabolic networks, social networks, and the Internet, show degree distributions with characteristic power laws [11]:
and scaling exponents 
(see Section 10.2.5). By taking logarithms on both sides, we obtain
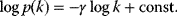
In a double-logarithmic histogram plot, power-law distributions show a simple linear decrease (see Figure 8.3). If a network shows this linearity over several orders of magnitude, in particular for large degrees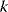 
, a power-law distribution may be suspected. It can be vigorously tested by statistical model selection [12].
Figure 8.3 Scale-free degree distributions in real-world networks. (a) Collaborating movie actors (
). In the network, two actors are linked if they have played together in a movie. (b) World Wide Web (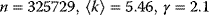
). (c) Power grid data (
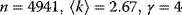). (From Ref. [11].)
Power-law distributions exist, for instance, in word frequencies (Zipf's law: The frequency of words in natural language is inversely proportional to the words' count number ranks) and economy (Pareto's law: The number of people with income larger than 
scales with 
according to a power law). The power-law distribution (8.1) is self-similar under a rescaling of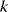 
, satisfying 
(see Section 10.2.5). Therefore, it does not define a typical range (or “scale”) for the degrees: For finite networks, the mean value 
increases with the network size, and for infinite networks, it diverges. This is why power-law distributions are called scale-free.
Scale-free networks contain a few very large (i.e., high-degree) nodes called hubs, many nodes with very small degrees, and a hierarchy of differently sized nodes in between. However, this hierarchy arises only for scaling exponents 
. For small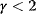 
, a “hub-and spokes” network with a single hub will arise. For larger 
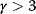, hubs are not relevant and the network resembles an Erdös–Rényi network. Erdös–Rényi networks show a different, peaked degree distribution with a mean degree 
: Most nodes have relatively similar degree, and nodes with large degrees practically do not exist. The mean degree 
and the degree dispersion 
follow from the binomial distribution of degrees, independent of the graph size. In scale-free networks, both quantities increase with the network size.
8.1.2.1 Preferential Attachment Model
Many real-world networks show scale-free degree distributions that distinguish them from Erdös–Rényi random graphs. A possible explanation for these structures refers to the ways in which networks are growing. In the preferential attachment model [11], a network grows by successive addition of nodes: A new node attaches randomly to one of the nodes, but with a preference for nodes that have many connections already. Therefore, nodes with large degrees have higher chances to increase their degree (“the rich get richer”). In simulations, preferential attachment with a linear relation between preference and node size leads to graphs with scale-free degree distributions. If the preference increases more strongly than linearly, a single node will become connected to almost all other nodes, while these share very few connections among themselves.
Can scale-free degree distributions in biochemical networks be explained by preferential attachment? In metabolic networks, this growth model would require that newly evolving enzymes metabolize compounds that are already widely used. This has not been shown directly, but the fact that existing hub metabolites have arisen early in evolution [6] supports the preferential attachment assumption. In protein–protein interaction networks, preferential attachment can be realized by gene duplication [13,14]. If the gene for a protein A is duplicated in a genome, all its interaction partners B will obtain one more edge. Now assume that genes are duplicated at random: If a protein B has many interaction partners, it is likely that one of them will be duplicated next; if B has few interaction partners, this is less probable. Thus, the probability of obtaining new interaction partners is proportional to the number of existing interaction partners, just as required for preferential attachment.
The evolution of real-world networks is much more complex, involving specific preferences between nodes, dynamic rewiring, and removal of nodes and edges. However, the idea of preferential attachment shows that scale-free networks can emerge from a simple evolutionary mechanism without selection. Therefore, statistical network features that would automatically arise in any scale-free networks cannot be taken as a proof of evolutionary selection.
8.1.3 Connectivity and Node Distances
8.1.3.1 Clustering Coefficient
In geometric random graphs, the neighbors of a node have a higher chance to be connected as well. This phenomenon, called clustering, also appears in many real-world graphs and can be quantified by the mean clustering coefficient. For a node 
, the number 
counts all connections between its neighboring nodes, or in other words, the triangles (three loops) comprising node 
. In undirected graphs, a node with degree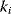 
can maximally have a value of 
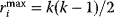. Watts and Strogatz [7] defined the clustering coefficient of node 
as the ratio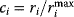 
, that is, the fraction of possible edges between neighbors that are actually realized. Self-edges are not counted in the clustering coefficient. Graphs with scale-free degree distributions and strong clustering can be constructed with the hierarchical network model [15].
If graphs are clustered, this may indicate an underlying similarity relation between nodes. In social networks, people who live nearby or share similar interests (small distances in physical space or in some abstract “interest space”) are more likely to share other relationships as well; these relationships will therefore be clustered. Clustering arises automatically when bipartite graphs are collapsed (see Figure 8.4): A bipartite graph contains two types of nodes (e.g.,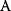 
and 
, black or white), and edges connect nodes of different types. In the collapsed graph, all nodes of type 
are removed and the neighbors of a removed node become connected by edges. An example is the graph of collaborating movie actors in Figure 8.3, which stems from a bipartite graph of actors and movies. When collapsing a bipartite graph, each collapsed node gives rise to a fully connected subgraph, realizing a clustering coefficient of 1.
Figure 8.4 Metabolic pathways represented by graphs. (a) Three reactions from upper glycolysis (see Section 4.2.2) shown as a bipartite graph of metabolites and reactions. (b) Collapsed metabolite graph. (c) Collapsed reaction graph. HK: hexokinase; PG: phosphoglucoisomerase; PFK: phosphofructokinase; Glc: glucose; G6P: glucose 6-phosphate; F6P: fructose 6-phosphate; FBP: fructose 1,6-bisphosphate.
8.1.3.2 Small-World Networks
The topological distance of two nodes is defined as the length of the shortest path between them. For some node pairs, the distance may not be defined, and in directed graphs it is not a symmetric function. An example of a topological distance is the “Erdös number,” the collaborative distance of mathematicians to the mathematician Paul Erdös, the father of Erdös–Rényi random graphs. People who published together with Erdös (504 people) have an Erdös number of 1, while those who did not, but published with persons who published with Erdös, have an Erdös number of 2, and so on. Typical Erdös numbers are relatively small (mean 4.65, maximum 15 among mathematicians with a finite Erdös number). Incidentally, low Erdös numbers have been offered at eBay.
The diameter of a graph is the longest distance between two nodes in the network. How will this distance depend on the number of nodes and on the graph structure? In Erdös–Rényi random graphs with 
nodes and average degree 
, the diameter scales logarithmically with 
: In a simple approximation, a node has approximately 
neighbors, 
second neighbors, 
third neighbors, and so on. The number of reachable nodes grows exponentially with the node distance, and virtually any point of the network can be reached after relatively few steps.
For clustered networks, the expectation would be different: Compared to Erdös–Rényi random graphs with the same average degree, we expect larger diameters; when counting the first, second, or higher neighbors, we are likely to remain close to our starting point and to count the same nodes several times. However, some real-world networks show a clustered structure and a small diameter (compared to Erdös–Rényi graphs with the same average degree). Watts and Strogatz [7] called such networks “small-world” networks and showed that they can be generated from locally structured networks by adding relatively few global connections.
8.1.4 Network Motifs and Significance Tests
8.1.4.1 Network Motifs
Many real-world networks contain characteristic local wiring patterns. If a pattern is significantly abundant, it is called a network motif [18]. Since their discovery in transcription networks, network motifs have been explored in many real-world networks and networks have been classified by motifs they contain [19]. Characteristic motifs in transcription networks, such as self-inhibition and the feed-forward loop (FFL) [20,21], will be discussed in Section 8.2.
To test if a pattern is significantly abundant in a network, the network is compared with a random graph that serves as a background model. In each realization of the random graph, the pattern will appear with a certain count number; this defines a probability distribution 
for the count number 
. If the count number in the original network is larger than that in 95% of the random graphs, the pattern, as a motif, is significant at a 5% confidence level. For Erdös–Rényi random graphs, the probabilities of local structures can be computed analytically. The same type of significance test also applies to other kinds of network structures, for instance, to highly connected subgraphs called network modules [22].
8.1.4.2 Null Hypotheses for Detecting Network Structures
We saw that networks can be characterized by statistical properties such as degree distribution, occurrence of motifs, or highly connected subgraphs. For statistical reasons, some of these properties may be related, and prominent structures like modules can result from basic features such as the degree sequence.
To focus our significance tests on structures that are not simply by-products of some basic network statistics, we need to compare the original network with random graphs with the same basic statistics. These random graphs represent a specific null hypothesis, the hypothesis that our structure is in fact a by-product of basic statistical properties. Again, if less than 5% of realization meets our criterion for detecting the structure, the structure is taken to be significant at the 5% confidence level. So, which kinds of random graphs should we choose to compute the significance of network motifs? A geometric random graph contains more self-inhibition loops than an Erdös–Rényi graph with the same mean degree. Using one or the other random graph as a null model would lead to different results; the number of self-inhibitions in a real-world graph could be significant in one case, but not in the other. The selection of background model depends on which network features we take for granted.
Here is an example. The structure of transcription networks is determined by binding sites for transcription factors, and it evolves by mutation or duplication of promoter sequences [23]. However, the possible network topologies seem to be restricted: In-degrees (numbers of regulators per gene) are typically small, whereas out-degrees (number of targets per regulator) can be larger. To study motifs in transcription networks, Milo et al. [10] constructed random graphs in which all node degrees from the original network were preserved. If motifs are significant with this background model, they do not simply follow from the degree distribution. With the random graph representing a scenario of neutral evolution, network motifs, being significantly unlikely structures, can be taken as signs of selection at work.
8.1.5 Explanations for Network Structures
Many structures in biological networks can be explained by evolutionary history or biological function. However, structures like power-law distributions or network motifs also appear in completely different types of networks such as social networks, food webs, public transport networks, or the Internet; there must be other, nonbiological principles behind their emergence. In general, four groups of principles can be considered:
- Definition of the network Network structures can arise from how networks are defined or mathematically constructed. For instance, networks that reflect distances (e.g., the wiring scheme of neurons) or similarities (e.g., correlations between gene expression profiles) or that are obtained by collapsing a bipartite graph will also show clustering.
- Material constraints Network structures can result from material constraints. Transcription factors, for instance, can have many binding sites in the genome, but the number of binding sites per promoter may be limited. In metabolic networks, chemical reactions are constrained by the conservation of atom numbers.
- Common origin or similar growth processes Some structures may reflect the ways in which networks evolve. On the one hand, common features (e.g., the cofactors used in metabolic networks) may stem from common ancestors. Once many processes rely on some feature, this feature cannot be changed anymore and will be conserved (once-forever selection). Also, the growth process itself can induce structure: If biological, social, and technical networks grow by preferential attachment – maybe for very different reasons – this may result in a common degree distribution, which can then induce further similarities.
- Analogous function and shaping for optimality Another possible explanation for network structures is a selection for usefulness or cost-efficiency. Systems with similar tasks can evolve independently toward analogous structures. The feed-forward loop motif, for instance, appears in many transcription networks, but also in neural connections of the worm Caenorhabditis elegans. In both cases, loops may evolve because they can perform specific signal processing tasks with a low material effort. Generally, since network connections (e.g., enzymes establishing chemical reactions, or streets connecting cities) are costly, cost pressures may lead to sparse networks and short connections between central nodes.
Each of the explanations follows a different logic: Aristotle proposed that “why” –questions can be answered by four different types of explanations, traditionally called “causes.” Our explanations of network structures exemplify these types: Network structures arise from the mathematical forms of networks (causa formalis: “formal cause”); from their realization by physical objects (causa materialis: “material cause”); from factors that shaped networks in evolution or in their construction (cause efficiens: “effective cause”); or because of a network's usefulness, for example, as a communication or transport system (causa finalis: “final cause”). These explanations are complementary, and linking them can provide new insights. For instance, scale-free degree distributions in protein–protein interaction networks may stem from preferential attachment and provide robustness against node failure. This could mean that preferential attachment itself is a favorable mode of network evolution because it promotes favorable network properties.
8.1.5.1 The Network Picture Revisited
We saw that networks emphasize the structure of interactions while neglecting the nature of the elements and the dynamics of the system. Such an abstraction can be useful for various reasons: (i) Networks may be good starting points to describe systems when little quantitative information is available. (ii) Networks, especially in their graphical representation, are better understandable than detailed quantitative descriptions. (iii) Studies of network structure may reveal similarities between apparently unrelated systems. (iv) Studies of network structure may show which structural features can emerge from basic features such as the degree distribution. (v) Some dynamical processes (e.g., spreading of diseases) [24] depend much more on network structures than on the details of the quantitative process. (vi) Studies of network evolution show how structures emerge from network growth or rewiring and can help to infer selection pressures on specific biological functions. A comparison with random networks may indicate that certain structures are under selection.
In any case, a convincing explanation of network structures must refer to the underlying dynamical systems and evolutionary processes. In particular, networks constructed from statistical correlations should not be overinterpreted: For example, correlated metabolite fluctuations need not imply that the involved metabolites participate in the same pathway. To relate “data networks” to the biological systems behind them, mechanisms and dynamics need to be understood.
8.2 Regulation Networks and Network Motifs
Summary
The various cellular processes are orchestrated by a complex regulation system. Apart from a direct allosteric regulation of enzymes, there exist signaling pathways, specialized circuits for cell cycle control, growth regulation, or stress response, and a transcription network that adjusts protein levels to current demands. Metabolism, signaling systems, and transcriptional regulation form a large feedback loop, and within this loop, regulation occurs on multiple levels and time scales: A metabolite can, for example, inhibit its own production pathway via either direct allosteric regulation or slower transcriptional regulation. The signaling system is very complex, but we can focus on parts, which we frame as signaling pathways, and see how they process information.
Signaling molecules engage in molecular interactions such as complex formation, protein phosphorylation, or binding to DNA. Specific interactions, enabled by the shapes and binding properties of proteins, can be seen as a form of recognition. In evolution, the strength and specificity of these interactions can be adapted by genetic changes of protein or promoter sequences. Signaling substances or complexes, possibly in different modification states, can be represented as nodes of a network. Edges, possibly with plus or minus signs for activation or inhibition, indicate that substances affect each other, for example, by catalyzing each other's production or degradation. If several arrows point to one node, multiple input values must be processed at this node, and the processing may be described by Boolean functions. Substances are often regulated by opposing processes such as synthesis and degradation or phosphorylation and dephosphorylation. Compared to metabolic networks, regulation networks can be rewired rather easily by adding or removing individual arrows or by varying their strengths.
Signaling Systems Process Information
Signaling systems translate input stimuli (e.g., the concentration of an extracellular ligand) into output signals (e.g., active transcription factors binding to DNA). Information can be encoded in concentrations, modifications, and localization of proteins, and either in stationary levels or in temporal patterns. Signaling pathways can sense such signals and transmit, process, and integrate this information. On the one hand, signals are transmitted from one place in the cell to the other (e.g., from a receptor at the cell surface to the transcription machinery in the nucleus). On the other hand, the input–output relations of signaling systems can realize information processing tasks such as discrimination, regression, data compression, or filtering of temporal signals, providing informative inputs for downstream processes.
The output of a signaling pathway contains information about the input. Here the term “information” can be taken literally, in the sense of Shannon information: Knowing the output signals would reduce our uncertainty about the input signals. Information transmission through signaling pathways can be measured in units of bits or Shannons [25]. Apart from the statistical Shannon information, signaling systems also provide useful information, enabling other systems to respond in adequate ways to the current situation – for example, to express stress response proteins when cells are under threat. Pragmatic information, that is, information supporting advantageous decisions, is quantified by the value of information, a concept from Bayesian decision theory (see Section 10.3) [26,27]. In terms of function, regulation networks could also be seen as optimal controllers, for instance, controllers steering metabolic pathways (see Sections 11.1 and 15.5).
8.2.1 Structure of Transcription Networks
Transcription networks describe how gene expression is regulated by transcription factors. Nodes represent genes and arrows indicate that transcription factors (which are again encoded by genes) can bind to a gene's promoter region and, possibly, regulate its expression. In quantitative models, the arrows are described more precisely by gene regulation functions (see Section 9.3). The network structure is determined by binding sites in the genes' promoter regions. Binding site sequences of many transcription factors are known [28], and transcription factor binding can be measured in vivo on a genome-wide scale [29–31].
When the transcription network of E. coli bacteria (Figure 8.1b) is reduced to transcription factors and properly arranged, a clear functional design becomes visible [32]. As shown in Figure 8.5, information is processed in three subsequent layers: An input layer, formed by two-component systems, feeds signals about the cell's state or environment into the network. A second, densely connected layer – resembling an artificial neural network – generates various outputs that integrate the input information. The third layer consists of target genes that are regulated directly or through feed-forward loops. The entire system consists of parallel blocks related to general cell functions. Each block contains a dense overlapping regulon as its core, which responds to some input stimuli and controls the expression of functionally related genes [32]. One such subnetwork, which regulates the expression of five sugar utilization pathways and contains a large number of feed-forward loops, is shown in Figure 8.6.
Figure 8.5 Regulation network of transcription factors in E. coli bacteria. Extracted from the transcription network (see Figure 8.1a) and arranged in blocks, the network highlights functional subsystems. Information is processed in three layers: Input signals are received via two-component systems, processed and integrated in dense overlapping regulons, and converted into output signals, often through feed-forward loops (marked by triangles). Major cell functions (indicated on top) are controlled by large separate blocks. Activation and repression edges are shown in blue and red, respectively. (From Ref. [32].)
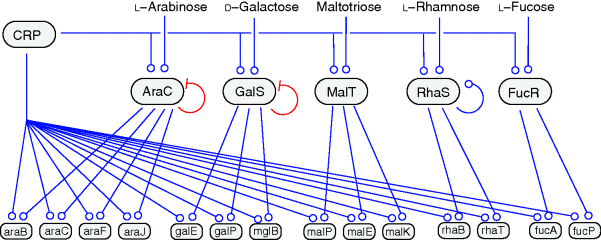
Figure 8.6 Transcriptional regulation of sugar utilization genes in E. coli bacteria. Transcription factors signal the availability of specific sugars and control the corresponding pathway genes; all genes are also controlled by CRP, a proxy for energy demand (see Section 9.3). (From Ref. [33].)
Transcription networks contain typical motifs such as negative autoregulation or feed-forward loops [34–37]. Larger clusters formed by such motifs can be described as generalized motifs [38]. The network motifs found in E. coli also appear in other organisms. To reconstruct the transcription network in the yeast Saccharomyces cerevisiae, Lee et al. [29] studied the binding of transcription factors to DNA in vivo by chromatin immunoprecipitation. The reconstructed network contains about 4000 interactions between regulators and promoter regions, with an average of 38 target promoters per regulator. The network motifs include the motifs previously found in E. coli (examples in Figure 8.7).
Figure 8.7 Network motifs in the transcription network of the yeast S. cerevisiae. Gene names refer to specific examples in the network. (a) Autoregulation: a transcription factor regulating its own expression. (b) Multicomponent loop: a cycle involving two or more factors. (c) Feed-forward loop. (d) Regulator chain. (e) Single-input module: one regulator controlling several genes. (f) Multi-input motif (dense overlapping regulon): several regulators controlling a number of target genes. (Redrawn from Ref. [29].)
Positive and Negative Regulation
Regulation edges can represent activation (+, shown in blue) or repression (−, shown in red), or they can show both modes of regulation (dual regulation) (Figure 8.8). Activating an activator and repressing a repressor lead to net activation, while activating a repressor and repressing an activator lead to repression. When signals pass through a series of edges, the overall sign of the response depends on the number of repressions (even or odd) along the way. Thus, there are multiple ways to realize the same overall response; for example, transcriptional repression of a metabolic pathway by its own product can be realized in two ways: The pathway product, as a ligand, can activate an inducer or inhibit a repressor (see Section 10.3). In theory, both types of regulation should yield the same result. However, evolved networks seem to show preferences: According to Savageau's demand rule [39], genes that are usually expressed (in an organism's common environment) are typically controlled by activators, while genes that are usually not expressed are controlled by repressors. In both cases, the binding site is typically occupied. One explanation is that occupied sites reduce the variation in expression levels. Thus, regulation structures following Savageau's rule may contribute to insulation, that is, to making expression levels robust against biochemical noise [40].
Figure 8.8 Potential regulation patterns with one, two, or three nodes. (a) Positive and negative autoregulation. (b) Possible two-node patterns. (c) Three-node patterns can contain up to six arrows. The incoherent feed-forward loop type I (bottom) is a motif in transcription networks (also see Figure 8.12).
Regulation Structures and Network Motifs
Instead of studying regulation networks in their full complexity, we may study small circuits within such networks. For some of them, dynamic behaviors and functions in signal processing have been proposed [41], and some have been realized as genetic circuits in synthetic biology [42–46]. Next, we may study layered networks as in Figure 8.5 and trace how information (encoded in steady-state values or time curves) is transmitted from layer to layer.
When looking for regulation circuits of biological interest, we may focus on patterns appearing in large numbers, that is, network motifs [34,47,48]. If some of the possible local patterns (see Figure 8.8) are highly abundant in transcription networks, what could be the reasons? One explanation is that the network's statistical properties (e.g., the degree distribution) enforce certain structures as by-products; for network motifs, this sort of explanation can be excluded by choosing the right sort of random graphs in the statistical test. A functional explanation would state that certain circuits underlie active selection during evolution. In fact, some transcription motifs perform specific functions in signal processing [49]. Moreover, network motifs can stabilize networks against dynamic perturbations, which may constitute an additional selection advantage [50,51].
To make such claims, we need to assume that a motif's dynamic behavior is mostly determined by its structure, while kinetic details play a minor role. This, of course, needs to be verified. A first step is to simulate a motif with different rate laws and parameters. Next, it can be simulated under perturbations, or even implemented as a genetic circuit in living cells to see if it performs its predicted behavior robustly. Preferably, the motif should also be minimal, in the sense that it requires lower material efforts than other structures performing similar tasks.
If a regulation circuit promotes favorable behavior, it may appear in different places. For instance, two genes that inhibit each other can form a bistable genetic switch (see Section 6.4 and the example in Figure 2.2). Such a switch can also be useful in other contexts; if it works in transcription networks, it could also be realized, for instance, by mutual inhibitions between immune cells [52].
8.2.2 Regulation Edges and Their Steady-State Response
Before we study regulation circuits, let us see how single edges can be modeled as little dynamic systems. An arrow connects an input S (signal) to an output R (response). Examples of such signal/response elements are kinase/target protein, transcription factor/target gene, and mRNA/protein. In a dynamical model, we can describe signal and response by their strengths 
and 
, following a rate equation:
For each input value 
, the steady-state condition 
yields a stationary value of 
, and the resulting steady-state response curve 
is the input–output relation for this arrow.
Regulation arrows can symbolize different reaction patterns. Figure 8.9 shows three such patterns, which may serve as building blocks for larger network models. Their steady-state response 
in the three systems depends on both their reaction scheme and the rate laws (Table 8.2). A linear mechanism with linear kinetics leads to a linear response. Saturable responses can be obtained by Michaelis–Menten kinetics or by a reaction loop with linear kinetics and a conservation relation 
for different forms of R (Figure 8.9b). The same loop, with Michaelis–Menten kinetics, yields a sigmoid response curve (Goldbeter–Koshland kinetics). All types of responses (linear, hyperbolic, and sigmoid) depend gradually on the signal strength. Moreover, the steady-state output depends only on the current input signal and not on its previous history. As soon as the signal S stops, the response is switched off: There is no hysteresis.
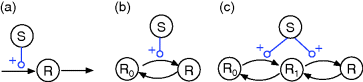
Figure 8.9 An activation arrow S → R can represent different underlying reaction patterns. (a) Linear pattern: A substance S (signal) induces the production of R (response). (b) In a loop pattern (e.g., a phosphorylation cycle), S converts inactive R0 into the active form R. (c) In a double-loop pattern (e.g., double phosphorylation), R is activated in two steps. Black arrows indicate chemical reactions, blue catalysis.
Table 8.2 Kinetic implementation of signaling arrows.
| Structure | Kinetics | Response |  | |
| Linear | Linear |  |
Linear |  |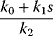
| MM |  |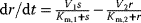
Hyperbolic |  | |
| Loop | Linear |  |
Hyperbolic |  |
 |
||||
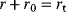| MM |  |
Sigmoid |  | |
 |
||||
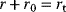| Double loop | Linear |  |
Sigmoid |  |
 |
||||
 |
||||
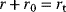Formulas correspond to the network structures in Figure 8.9. Linear kinetics and Michaelis–Menten (MM) kinetics lead to different response curves. The Goldbeter–Koshland function 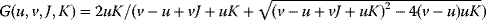 is used to model ultrasensitive behavior [53,54]. |
||||
8.2.3 Negative Feedback
Negative feedback is common in transcription networks and as a regulation pattern in metabolic pathways. In synthesis pathways, the first enzyme is often inhibited by the pathway product. This prevents overproduction and stabilizes the product level against fluctuations caused by varying demands. The feedback can be realized by allosteric inhibition, by transcriptional repression of enzymes, or both. Ideally, a feedback system should receive its input exactly from the output variable to be controlled. If this is impossible (as is the case for metabolic fluxes), other variables can be sensed as proxies. For instance, fructose bisphosphate can act as a flux sensor, representing by its concentration the glycolytic flux in E. coli [55].
Feedback regulation is used on many levels of physiology: For instance, the stable and material-saving shapes of bones and trees arise from growth processes under feedback regulation by sensed stresses [56–59]. In signaling networks, negative feedback has different functions: It can stabilize a steady state against external and internal fluctuations [43], produce pulse-like overshoots, induce sustained oscillations, and speed up responses [60].
Some of these phenomena can be observed in the pathway model shown in Figure 8.10 (for a detailed analysis, see Ref. [61]). In the model, all reactions follow irreversible mass-action kinetics 
, internal metabolites start at levels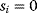 
, and after the external substrate is raised to a constant level 
, the metabolite concentrations approach a new steady state after a short transition period (Figure 8.10a). We also consider variants of this model in which the first reaction is allosterically inhibited by one of the downstream metabolites: The inhibition is implemented by a modified rate law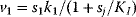 
. If the second metabolite is the inhibitor, the first metabolite shows an overshooting response (Figure 8.10b). With a longer ranging feedback, that is, longer time delays, this effect becomes more pronounced and damped oscillations arise (Figure 8.10c).
Figure 8.10 Negative feedback in a metabolic pathway. (a) Concentration time series in a chain of reactions. After substrate (- -) becomes available (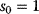
) at time 
, the curves rise with different time delays. (b) Negative feedback via the second metabolite decreases the steady-state level and speeds up the response. (c) Negative feedback via the last metabolite leads to an overshoot and damped oscillations. All mass-action constants 
have values of 1.
The example shows the double nature of negative feedback. A feedback inhibition can shift the eigenvalues of the Jacobian matrix in the complex plane (see Section 15.5). This can stabilize the system state, but a delayed feedback can also lead to damped or sustained oscillations and destabilize the steady state. Metabolic oscillations are observed in reality, but whether they have particular functions, or arise simply from stabilization mechanisms gone wild, is still a matter of debate [62,63].
Figure 8.10 also shows that negative autoregulation can speed up system responses. The response time 
– the time at which the last metabolite 
reaches its half-maximal level – decreases from (a) to (c). In the arbitrary units used, the values read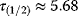 
(no feedback), 
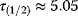(short-ranging feedback from second metabolite), and 
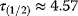(long-ranging feedback from last metabolite). A similar effect has been shown experimentally in transcription networks: Protein expression responds faster to a stimulus if the protein inhibits its own expression [60]. Fast responses can be crucial for cells in rapidly changing environments. They could also be reached by a faster protein turnover, but this would increase the costs for protein production. Negative autoregulation, in contrast, saves this cost: Initially, protein production is high, but when self-inhibition kicks in, protein synthesis is interrupted and no further production costs arise.
8.2.4 Adaptation Motif
An important characteristic of signaling systems is their transient response to step-like input signals. The system in Figure 8.11 shows a remarkable behavior called perfect adaptation: After a step of the input value, it shows some transient dynamics, but after a while, the output returns exactly to its initial value. Perfect adaptation makes systems sensitive to temporal changes, but insensitive to the baseline input value. As we will see in Section 10.2.1, this plays a vital role in the bacterial chemotaxis pathway.
Figure 8.11 Adaptation motif. (a) A signal substance X catalyzes the production of Y and Z, while Y catalyzes the degradation of Z. The reactions follow mass-action kinetics. (b) Temporal dynamics of the adaptation motif. A step-like input level 
(black) evokes a sustained response of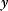 
(red); the output level 
(blue) shows a transient response and returns to its steady-state value (all rate constants set to values of 1).
In the adaptation motif (Figure 8.11), the input X activates the production of Z, but also inhibits it via activation of Y. With mass-action kinetics and linear activation, the levels of Y and Z follow the equations
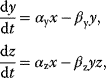
which for x > 0 lead to the steady state
In steady state, activation and inactivation cancel out and the level of Z is determined only by rate constants. However, when the input changes, the activation responds faster than the inactivation. This creates a transient peak (Figure 8.11b).
8.2.5 Feed-Forward Loops
The feed-forward loop shown in Figure 8.12 is a common motif in transcription networks [35–37,64]. It consists of three genes that regulate each other: Gene product X regulates gene Z directly and via an intermediate gene Y. Each arrow can represent activation (+) or inhibition (−). In Boolean models, the two inputs of Z can be processed by logical AND or OR functions. In the feed-forward loop, eight sign combinations are possible, but only two are abundant in transcription networks: the so-called coherent FFL type 1 and the incoherent FFL type 1 (Figure 8.12). In a coherent FFL type 1, all regulations are activating, while in the incoherent FFL type 1, the edge from Y to Z becomes inhibiting.
Figure 8.12 Feed-forward loops. An input gene X regulates an output gene Z in two ways: directly and via an intermediate gene Y. (a) Coherent feed-forward loop type 1 with AND gate. (b) Incoherent feed-forward loop type 1 with AND gate. (c) Possible reaction scheme behind a coherent feed-forward loop. X is activated by rapid ligand binding (circle denotes the ligand, X* its active form). Blue edges represent transcriptional regulation of Y and Z; transcription and translation are lumped into one reaction.
At first sight, the second branch, via gene Y, has no obvious function: In the coherent FFL, it seems redundant; in the incoherent FFL, it even cancels the effect of the direct branch. However, this holds only in steady-state situations. If the input X in the incoherent FFL is switched on, gene Y turns up with a delay, so Z is first activated via the direct branch and only later inhibited by Y. Due to the time delay, a step in the input X is translated into a peak of the output Z. Thus, a possible function of feed-forward loops could be the processing of temporal signals [36]: If an external signal (e.g., a ligand concentration) changes the activity of X, the FFL translates the time profile of X into a specific peak profile of Z, which then can serve as an input for downstream processes. Dynamical models and measurements in gene circuits in E. coli have shown that feed-forward loops can realize sign-sensitive delays, generate temporal pulses, and accelerate the response to input signals. Moreover, incoherent FFL can create nonmonotonic effective input functions for the target gene 
[65]. The precise behavior of an FFL depends on kinetic parameters or, in the Boolean paradigm, on the signs and the logic regulation function for Z.
Dynamic Model of Feed-Forward Loops
To study the dynamics of feed-forward loops in a simple model, we assume that the product of gene X is expressed constitutively, that it can be rapidly activated by a ligand, and that activities of Y and Z depend directly on their expression levels. Lumping transcription and translation into one step, we obtain the following rate equations:
where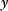 
and 
denote the protein levels of Y and Z,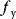 
and 
are the production rates, and 
and 
are degradation constants. For a realistic model, protein production could be described by measured gene regulation functions (see Section 9.3). Here we keep the model simple and use a step-like gene regulation function [35]:
The step function 
yields a value of 1 if 
is larger than 
and a value of 0 otherwise. Thus, when 
is below the threshold value 
, Y is not transcribed; otherwise, Y is transcribed at a constant rate 
. We consider two types of FFL, a coherent and an incoherent one, both with logical AND functions. The regulation functions for gene Z read
Figure 8.13 shows simulation results from the model (8.6) with piecewise constant regulation functions (8.7) and (8.8) and predefined input pulses.
Figure 8.13 Dynamic behavior of feed-forward loops (FFLs). (a) Coherent FFL type 1 with AND logic (see Figure 8.12a). Time curves show the active input X (top), intermediate gene Y (center), and output Z (bottom) in arbitrary units. Short pulses are filtered out; the response to a longer pulse is delayed, but the response to the end of the pulse is immediate. (b) Incoherent FFL type 1 with AND logic. The onset of each input pulse leads to a pulse in Z with a fixed maximal length. Model parameters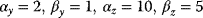 
.
Functions of Feed-Forward Loops
The simulations illustrate characteristic features of the feed-forward loop. The coherent-AND FFL shows a delayed response to the onset and an immediate response to the end of pulses, so short input pulses are filtered out. The incoherent-AND FFL, in contrast, responds immediately to an input pulse, but the response stops after a while: Larger input pulses are translated into standard pulses of similar length. We know this behavior from the adaptation motif, which in fact can be seen as an incoherent feed-forward loop. The dynamics of feed-forward loops in the E. coli transcription network has been verified experimentally [36,37,64].
Tightly interlinked feed-forward loops constitute the sporulation system in the bacterium Bacillus subtilis. In response to harsh environmental conditions, cells can transform themselves into spores, which can then survive for a long time without metabolic activity. The process, called sporulation, involves several waves of gene expression. In the network, these waves are generated upon stimulation of the sigma factor 
by five entangled FFLs (see Figure 8.14).
Figure 8.14 Gene network coordinating the process of sporulation. B. subtilis bacteria can transform themselves into spores to survive harmful environmental conditions. When sporulation is triggered, a large number of genes are differentially expressed in subsequent waves. The waves are created and coordinated by the regulation network shown [66]. It contains a number of feed-forward loops that activate the downstream target genes. Activation of the master regulator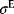 
triggers waves of expression in different groups of target genes (denoted by 
). (Redrawn from Ref. [66].)
Paradoxical Regulation
The examples above show that a simultaneous activation and inhibition of the same target – which appears paradoxical at first sight – can be functional to signal processing. The same phenomenon appears in the communication between immune cells [52]: Different cell types can influence each others' growth and death via chemical signal molecules called cytokines. Thus, the growth dynamics of cell types may serve as a signaling device analogous to the expression dynamics of protein levels inside a cell. Unlike the dynamics of protein levels, however, the growth dynamics of cells is inherently unstable because rapidly growing cell types would outcompete all others. In this situation, self-regulation and mutual regulation via cytokines are key to ensure homeostatic cell concentrations, and interaction schemes between cell types (e.g., feed-forward loops) can realize similar dynamics as in gene networks. Thus, apparently paradoxical actions of cytokines (i.e., causing cell proliferation and death at the same time) can be functionally important.
8.3 Modularity and Gene Functions
In a modular description, a system is seen as composed of subsystems with characteristic dynamics, specific functions, or sparse or weak connections between them [67]. In nonmodular systems, in contrast, parts are tightly connected and functions are distributed over the system. Modular designs are common in technical systems: Computers, for instance, consist of standardized parts that exert distinct and defined functions, operate more or less autonomously, communicate via standard interfaces, and can be repeated, replaced, or transferred as independent units. A modular design keeps machines manageable and ensures that parts can be reused in different combinations or be replaced in case of failure.
Modules can be a helpful concept in studies of complex systems: In biology, modules can concern the structure, dynamics, regulation, genetics, and function or organisms. Organisms contain physical modules on various levels: organs, cells, organelles, protein complexes, or single molecules that bear specific functions and can retain them in new contexts (e.g., organs can be transplanted and proteins can be transfected into different cells). Also in cellular networks, we observe modules such as metabolic pathways, signaling pathways, or dense overlapping regulons, which give the transcription network of E. coli its pronounced modular structure (see Figure 8.5).
To obtain an overview of how a cell functions, we may first consider general tasks it needs to perform – such as DNA replication, metabolism, transcription and translation, and signal processing. Subdividing these general systems into more specific ones (e.g., metabolic pathways or signaling systems), we obtain a hierarchical classification of cell functions and systems that perform them. Many such classifications exist [68–70], and if proteins are associated with specific functions – for example, catalyzing a reaction, sensing a specific ligand, or acting as a transporter or molecular motor – they can be placed in a functional hierarchy.
Proteomaps [71] visualize proteome data by Voronoi treemaps based on proteins' functional assignments. Figure 8.15 shows how E. coli cells allocate their protein resources to different possible functions: A large fraction of the protein mass (as measured by mass spectrometry) is devoted to metabolic enzymes, and another substantial fraction to transcription, translation, and protein processing. Breaking the protein fractions down into more specialized systems, we observe large investments in glycolysis, transporters, and ribosomes, as well as individual highly abundant proteins.
Figure 8.15 Protein investment in different cell functions. The abundance of proteins in E. coli bacteria [72], determined by mass spectrometry and arranged by functions, is shown by proteomaps (www.proteomaps.net) [71]. Small polygons represent single proteins; sizes correspond to mass abundance (molecule number multiplied by protein chain length) and give a broad overview of protein investments. The arrangement in larger areas represents a functional hierarchy. The four maps show the same data on different hierarchy levels. In reality, proteins have more than one function; our function assignments are, to an extent, arbitrary.
8.3.1 Cell Functions Are Reflected in Structure, Dynamics, Regulation, and Genetics
Biological modules appear on several levels, including network structure, dynamics, regulation, and genetics. In bacterial operons, functionally related proteins (e.g., parts of a metabolic pathway) are encoded by a common strand of mRNA and controlled by the same gene promoter. These proteins share very similar expression profiles, and the entire system together with its regulatory region can be transferred to other cells, where it will exert its function in a different biochemical context. The fact that operon structures are established and maintained in evolution suggests a selection advantage – so evolutionary theory should explain how such modules arise.
Notions of function reflect established biochemical knowledge and imply that cell physiology is modular, that is, separate systems exist for metabolism, for processing signals, for establishing cell structure, and so on. Functional assignments are based on evidence from genetics, cell biology, biochemistry, or comparisons between species. Various criteria have been proposed for defining pathways or modules in cellular networks, ranging from network topologies [73–76] to correlated dynamics [77], regulation systems [78], correlations in high-throughput data [79], and phylogenetic profiles [80]. We can define modularity on the levels of structure, dynamics, regulation, and genetics:
- Structure Based on network topology, we can define different kinds of modules: dense subnetworks with few external connections [76], subnetworks that are connected only via hub elements [73], or recurrent structures such as motifs, single-input modules, or dense overlapping regulons.
- Dynamic behavior In dynamic systems, we can define modules by requiring that there is a strong dynamic coupling within, and weak dynamic coupling between modules. Biochemical subnetworks without mass flows between them can be seen as regulation modules. A more empirical criterion is a strongly correlated dynamics within modules [77]: The resulting division into modules may change during the course of a simulation, and there may be a hierarchy of modules defined on different time scales.
- Regulation Gene or protein modules can be defined based on coregulation, either as operons or as the regulon, that is, the target gene set, of a common transcription factor.
- Gene exchange and reuse Due to genetic mechanisms, gene sequences can evolve in modular ways: Chromosomes are inherited as units, but become differently combined in sexual reproduction; in bacteria, DNA sequences can be exchanged between cells by horizontal gene transfer. Mobile elements can copy and duplicate DNA sequences, including coding regions, regulatory elements, or even entire operons. After a gene duplication, and being put into new genetic or functional contexts, genes can become further specialized.
A modularity on various levels is exemplified by bacterial operons. Operons act as regulatory and genetic modules, and the encoded proteins often form a common pathway. The fact that functionally related genes are located in close vicinity and expressed together can have several advantages:
- To ensure an optimal resource allocation, enzymes must be expressed in appropriate ratios. Otherwise, material and energy would be wasted. Stable expression ratios can be ensured if enzymes share a common regulation system; this reduces uncorrelated fluctuations in their expression. Correlated fluctuations are less problematic because their downstream effects can be compensated by special pathway designs (see Section 10.2).
- Some bacteria can exchange pieces of DNA (horizontal gene transfer). If genes encoding a pathway are colocalized in the genome, they may be transferred as one unit. However, a successful transfer also requires that the pathway remains functional in cells with a different genetic background. Thus, its dynamics should be relatively robust against changes in the state of the cell in which it resides.
- If an organism loses a gene by mutation, a second loss-of-function mutation in the same pathway will have little additional fitness effects. This phenomenon, called buffering epistasis, will be discussed below. If a pathway is already incomplete, there will be little selection pressure on preserving the remaining genes: Thus, genes in a pathway should be conserved together or disappear together. This is why a correlated appearance of genes, visible in phylogenetic profiles [80], can be taken as a sign of functional association.
8.3.2 Metabolic Pathways and Elementary Modes
Metabolism can be described in terms of pathways, that is, physiological routes between key metabolites. Metabolic pathways, which also appear in the protein classification in Figure 8.15, can overlap and are linked by cofactors such as ATP. In tightly connected networks, what counts as a pathway is a matter of definition. There are various possible criteria.
First, pathways and modules can be defined based on network connectivity. One possibility is to choose subgraphs with dense internal connections [76]. Another possibility is to eliminate all hub metabolites, for example, metabolites participating in more than four reactions. If enough of these hubs – among them, many cofactors – are removed from the stoichiometric matrix, the remaining network will be split into disjoint blocks [73]. To justify this procedure, we may see the hubs as external metabolites with fixed concentrations, assuming that hub metabolites are either abundant (and therefore insensitive to fluxes), strongly buffered (because stable concentrations are important for many biological processes) or their fluctuations average out (because they participate in many reactions).
Second, metabolic pathways can be defined on the basis of possible fluxes; this leads to notions such as basic pathways [81] or elementary flux modes [82] (see Section 3.1.3). A flux mode is a set of reactions (i.e., a subnetwork) that can support a stationary flux distribution, possibly obeying restrictions on reaction directions. A flux mode is called elementary if it does not contain any smaller flux modes; different elementary modes can be overlapping. Elementary modes can be computed from the stoichiometric matrix, but for larger networks their number grows rapidly. To avoid a combinatorial explosion, one may decompose a network by removing the hub metabolites and then compute elementary modes for the modules [73]. In contrast to textbook pathways, elementary modes are defined not only based on network topology but also by considering stationary fluxes through the entire network.
Flux distributions on elementary flux modes, called elementary fluxes, can be seen as modules in the space of possible chemical conversions: Each of them can convert some external substrates into external products. All stationary flux distributions can be obtained from linear superpositions of elementary fluxes, with arbitrary coefficients for the nondirected modes and nonnegative coefficients for the directed ones. However, this decomposition is not unique; moreover, elementary fluxes and their linear combinations are not guaranteed to respect thermodynamic constraints. A survey of the thermodynamically feasible elementary modes is a good way to characterize the general capabilities of a metabolic network [83].
8.3.3 Epistasis Can Indicate Functional Modules
Can functional associations between genes be inferred objectively, without presupposing any particular gene functions? In fact, deletion experiments can provide such information. If two proteins can compensate for each other's loss, deleting one of them will have little effect on the cell's fitness; however, the effect of a double deletion will be relatively strong. On the contrary, if both proteins are essential for a pathway, a single deletion would already disrupt the pathway's function, and the second deletion would have little effect. Thus, by comparing the fitness losses caused by multiple gene deletions, functional relationships among proteins may be inferred.
Epistasis describes how the fitness effects of gene mutations depend on the presence or absence of other genes. To quantify it, we compare the fitness of a wild-type organism – for example, the growth rate of a bacteria culture – with the fitness of single- and double-deletion mutants. A single-gene deletion (for gene 
) will change the fitness (e.g., the growth rate) from the wild-type value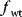 
to a value 
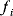, typically giving rise to a growth defect 
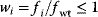. For a double deletion of functionally unrelated genes 
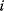and 
, we expect a multiplicative effect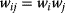 
. If a double deletion is even more severe (
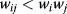), we call the epistasis “aggravating”; if it is less severe, we call it “buffering.” In both cases, we can conclude that the genes are functionally associated.
An example can help us understand why the “naive” expectation – that functionally unrelated genes have multiplicative effects – may be justified: The reproduction rate of an organism is proportional to both (i) the probability to reach the age of reproduction and (ii) the mean number of offspring when this age has been reached. If gene A affects only (i) and gene B affects only (ii), we would consider them functionally unrelated, and their effect on reproduction is in fact multiplicative.
To study epistasis between metabolic enzymes in the yeast S. cerevisiae, Segrè et al. [84] predicted growth rates by flux balance analysis. Based on predicted relative growth rates 
and 
after single and double deletions, they computed an epistasis measure
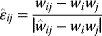
for each pair of genes. The term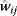 
is defined as follows: In case of buffering interactions, it represents extreme buffering (
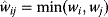), where the less severe deletion does not play a role; in case of aggravating interactions, it represents extreme aggravation (
), where double mutations are lethal. The statistical distribution of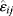 
, obtained from the FBA simulation, has a strong peak around 
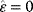, that is, the growth defects are approximately multiplicative in most cases. However, some gene pairs show strong aggravation (lethal phenotypes) or complete buffering.
To further analyze the epistasis values, genes were grouped into functional categories (see Figure 8.16). In fact, the epistatic effects were strongly related to functional groups, and, with few exceptions, the epistatic effects between two groups are either aggravating or buffering, but not both (monochromatic interactions). This result shows that genes contribute to biological fitness through their roles in functional subsystems. The same kind of analysis can be used to establish functional groups based on measured growth rates.
Figure 8.16 Epistatic interactions. (a) Schematic examples of buffering and aggravating epistasis. (b) Epistatic effects reflect functional subsystems. Circles show how many pairs of genes belonging to specific subsystems (rows and columns) are engaged in epistatic interactions. Circle radii represent numbers of epistatic interactions. Fractions of aggravating and buffering interactions are shown in red and green. (From Ref. [84].)
8.3.4 Evolution of Function and Modules
In engineering, modularity helps developers share their work and facilitates repair because stand-alone parts can more easily be replaced. Most machine parts have one specific function (even though exceptions exist – the wings of a plane are also used to store fuel). Even in cases where nonmodular designs would perform better, a modular design may still be preferable because it keeps machines or software understandable.
Does this also concern modules in biology? Biological systems are not designed, but shaped by mutation and selection, which constantly change them by small modifications. Existing structures can be modified, rewired, and reused for new purposes. This process resembles tinkering rather than engineering [85]: Starting from organisms that already function, gene recombination and mutations introduce innovations or reshape existing structures. Under selection pressures, these random changes can lead to functional adaptations. Natural selection is likely to choose solutions that work best, no matter whether they are understandable to us, and the resulting biological systems may look very different from the solutions that engineers would conceive. The contrast between engineered networks (e.g., in computer chips) and evolved networks (e.g., transcriptional regulation networks) resembles the contrast between structured computer programs and artificial neural networks: A trained neural network may be able to solve complex computational problems of various kinds, but will not reflect the logical structure of these problems in an understandable way.
Evolution of Modularity
Biological systems like the transcription network in Figure 8.5 show modules and recurrent structures and seem to be specialized for particular functions. What could be the reasons for modularity to evolve? A possible explanation is that such modularity can contribute to robustness. The very existence of cells is a good example: Separated from each other by membranes, cells in a tissue can undergo apoptosis without affecting the functioning of neighboring cells. However, modularity also relies on robustness: To be used in various biochemical contexts (cell states or cell types), biological modules, for example, signaling pathways, need to be robust against typical variation in cells.
A second-order selection advantage ensues from the fact that modules can contribute to evolvability [86]. In a simulation study [87], Kashtan and Alon evolved hypothetical electronic circuits by random mutation and selection, realizing an optimal performance in two signal processing tasks. In an evolution scenario with one constant task, evolution leads to different, highly optimal circuits, which were nonmodular. In a second scenario, the task consisted of two subtasks that appeared in varying combinations. Now modular circuits emerged in the evolution: Although being suboptimal for each of the tasks, they were better evolvable because small genetic changes were sufficient for switching from one task to the other. Also, in other computational evolution scenarios, varying modular goals helped speed up evolution toward well-adapted solutions [88].
Evolution of Analogous Traits
A second question, apart from the emergence of modules, is how recurrent structures such as the feed-forward loop can evolve. A possible explanation for this is analogy. Even though evolution is eventually based on random mutations, it is also strongly restricted by functional constraints on the phenotypes. Therefore, species under similar selection pressures may evolve similar traits. Wings, for instance, have independently evolved in birds and bats and show similar shapes due to their common functions and constraints (biomechanics, aerodynamics, and energy balance). Network motifs, which appeared many times independently, are another example of analogous evolution [87,89,90].
Convergence toward optimal performance may also explain the analogies between biological and technical systems: Although being physically very different, biological and technical systems share requirements such as robustness and cost-efficiency, so that optimization may lead to similar structures (in the case of chemical reaction systems versus electronic circuits, regulatory feedback; in the case of wings, the aerodynamic shapes). Technical metaphors can thus improve our understanding of biological systems in terms of function and physical constraints [89,91].
8.3.5 Independent Systems as a Tacit Model Assumption
A tacit assumption in pathway modeling is that networks surrounding a pathway of interest can be neglected. Ideally, experiments should be designed in such a way that this assumption is justified in later modeling.
The model (8.10), for example, makes predictions about an isolated, deterministic system. Details of transcription and translation, as well as chemical noise due to small particle numbers, are ignored; the dynamics of the protein level 
depends only on 
, while interactions with other processes are neglected; the model parameters are assumed to be constant. In reality, the parameters depend on the cell state, are noisy, or depend on 
, which implies additional feedback loops.
Becskei and Serrano [92] have implemented this feedback loop as an engineered genetic circuit in living cells, and the experiment confirmed the predicted stabilizing effect. At first sight, this may not be very surprising – but this only means that we trust the tacit model assumptions. The main insight from the experiment is not that feedback can lead to stability (which is well known), but that the feedback system can be implemented in cells in such a way that the pathway is affected only little by the surrounding cell. This is a precondition for using such circuits as recombinable building blocks.
8.3.6 Modularity and Biological Function Are Conceptual Abstractions
Are modules in cells and organisms real, or just a construct we use for description? Are the biological functions we attribute to proteins or organs well defined? When describing cells verbally, we cannot avoid using reifying terms such as “pathway,” “cell cycle phase,” or “function”; our language and thinking are based on distinct concepts, and so are our mathematical models. However, if we imagine how complex and flexible cell physiology actually is, we will admit that notions such as “module” or “biological function” are strong simplifications that enable, but may also limit, our understanding. For example, associating brain functions with specific parts of the brain may help understand physiology; yet, functional areas are flexible, common actions such as speech involve many areas simultaneously, and a functional brain relies on connections between areas as much as on the areas themselves. The same holds for cell physiology: Even if we distinguish biochemical processes in our descriptions, we still know that the processes are tightly coupled; that cell states fluctuate; that proteins can be involved in many processes (which we acknowledge when calling them “multifunctional”); and that their functions may keep on changing in evolution.
If we use modular models to describe cells, and if we focus our research on (apparently) modular systems, are we not bound to simply find what we are looking for? In fact, we cannot take for granted that evolution favors modular physiology. Cells function the way they do, and evolution selects for the most functional and evolvable phenotypes. However, if modular and specialized systems provide fitness advantages or contribute to evolvability (see Section 8.2), they may be favored in evolution. In this case, our notions of modules and function are “good to think with” not only because they are simple but also because they capture the evolutionary selection for things that work.
The same holds for our notion of “function”: To define a protein's function, we may ask about its effects – how will the cell state or the cell fitness change when the component is over- or underexpressed? If a component has specific effects, and if these effects depend specifically on this component, the component will be under a selection pressure; thus, specialized components may be selected, which eventually justifies our notion of function.
That modularity is not just an invented concept is supported by several facts: First, modules can be independently defined based on genome analysis, high-throughput data, and cell physiology, and we observe clear correspondences between these modules. Second, if there was no modularity in biological systems, many of our methods would fail: Not only models, but also most experimental methods in molecular biology and biochemistry rely on the fact that genes, molecules, or cells can be treated as discrete, modular systems (see Section 6.4.2). Finally, synthetic biology, where proteins and their regulatory elements are expressed in new combinations and across different cell types, is an ongoing test of the modularity hypothesis [93].
Exercises
Section 8.1
- 1) Adjacency matrix. Determine the adjacency matrices for the graphs in Figure 8.2. Compute the degree and clustering coefficient of each node in parts (b) and (c). How many feed-foward loops are contained in the directed graph? Show that the topological distance in the directed graph is not a symmetric mathematical function.
- 2) Degree distribution in metabolic networks. According to Ref. [16], the degrees of metabolites, that is, the number of reactions in which each metabolite is involved, follow good approximation to a power law. In E. coli bacteria, the exponent is α ≈ 2.2. About 1% of the metabolites have a degree k = 10. Which percentage of metabolites have a degree k = 20?
- 3) Self-inhibition in E. coli transcription network. The transcription network of E. coli in Ref. [20] contains 424 transcription factors, connected by 519 edges. Among these transcription factors, 42 show self-inhibition. Is this number surprisingly large or would you expect it to appear by chance?
- 4) Dynamic systems behind networks. Explain the meaning of arrows in metabolic networks, transcription networks, and protein–protein interaction networks. How can the different types of arrows be confirmed or ruled out experimentally?
Section 8.2
- 5) Network motifs. What are network motifs? How would you determine them for a given network? Choose a network motif that appears in transcription networks, describes its dynamic properties, and speculate about its biological function. Explain why network motifs might emerge during evolution of biological networks.
- 6) Sporulation in B. subtilis. Consider the genetic network controlling sporulation in B. subtilis (Figure 8.14). Find all feed-forward loops in the scheme and determine their types. Assume a dynamic model of this system with piecewise linear kinetics, all thresholds set to values of 1/2, and all other model parameters set equal to 1. Sketch the time-dependent regulator concentrations after the sigma factor σE exceeds its threshold value. What qualitative behavior do you expect for the four groups of target genes X1, X2, X3, and X4 in terms of pulses and delays?
- 7) Incoherent feed-forward loop type 1. Draw and explain the dynamic response of an incoherent feed-forward loop type 1 to short and long input pulses. Discuss possible biological functions of this behavior.
- 8) Simple cascade and feed-forward loop. Consider three genes X, Y, Z, that activate each other in a cascade X → Y → Z. The temporal behavior of x(t) is given and the levels of Y and Z are described by rate equations:
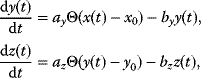
with threshold values x0 and y0. The step function Θ is defined by Θ(x ≥ 0) = 1, Θ(x < 0) = 0. (a) Assume a constant x < x0 and y(0) > 0, and draw y(t). How do the parameters ay and by affect the curve? (b) Assume a constant value x > x0 and an initial value y(0) = 0, and draw y(t). (c) Let x(t) show a profile as in Figure 8.13, with a maximal value larger than x0, and ay = az = 0.1 µM min−1, by = bz = 0.1 min−1, x0 = ythr bz = 0.5 µM. Draw y(t) and z(t) schematically and explain how their shapes arise from the dynamics. (d) In a feed-forward loop, Z is regulated by both X and Y. Synthesis of Z requires that both X and Y are above their threshold values
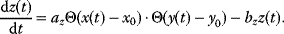
Draw z(t) schematically (after the onset of x) and discuss the influence of the parameters ay, az, by, bz, x0, and y0.
Section 8.3
- 9) Living systems. Discuss how notions of mechanism, dynamics, regulation, and optimality help us describe inanimate natural systems, living systems, and technical systems. Which similarities and differences do you see between these systems? Is there a need to describe them by different forms of mathematical models?
- 10) Convergent evolution. Find examples of homology and analogy in (i) shapes or organs of animals, (ii) biochemical processes and structures on the molecular level, and (iii) biological network structures.
- 11) Epistasis. Explain why epistasis between genes may indicate functional association. State the main assumptions on which your argument is based.
- 12) Synthetic biology. What insights can be gained from constructing a genetic circuit (e.g., a bistable switch) if similar systems exist already in wild-type cells?
- 13) Modularity. How would you define a modular system? Discuss possible criteria for modularity that apply to biological systems. Can modularity convey a selection advantage? How can modular systems emerge in evolution?
References
- 1. Henry, C.S., DeJongh, M., Best, A.A., Frybarger, P.M., Linsay, B., and Stevens, R.L. (2010) High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol., 28, 977–982.
- 2. Feist, A.M., Henry, C.S., Reed, J.L., Krummenacker, M., Joyce, A.R., Karp, P.D., Broadbelt, L.J., Hatzimanikatis, V., and Palsson, B.Ø. (2007) A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol., 3, 121.
- 3. Thiele, I. et al. (2013) A community-driven global reconstruction of human metabolism. Nat. Biotechnol., 31 (5), 419–427.
- 4. Jeong, H., Mason, S.P., Barabási, A.-L., and Oltvai, Z.N. (2001) Lethality and centrality in protein networks. Nature, 411, 41–42.
- 5. Suderman, M. and Hallett, M. (2007) Tools for visually exploring biological networks. Bioinformatics, 23 (20), 2651–2659.
- 6. Wagner, A. and Fell., D.A. (2001) The small world inside large metabolic networks. Proc. Biol. Sci., 268 (1478), 1803–1810.
- 7. Watts, D.J. and Strogatz., S.H. (1998) Collective dynamics of ‘small-world’ networks. Nature, 393, 440–442.
- 8. Albert, R. and Barabási, A.-L. (2002) Statistical mechanics of complex networks. Rev. Mod. Phys., 74, 47–97.
- 9. Itzkovitz, S. and Alon, U. (2005) Subgraphs and network motifs in geometric networks. Phys. Rev. E, 71, 026117.
- 10. Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002) Network motifs: simple building blocks of complex networks. Supramol. Sci., 298, 824–827.
- 11. Barabási, A.-L. and Albert, R. (1999) Emergence of scaling in random networks. Supramol. Sci., 286, 509.
- 12. Edwards, A.M. et al. (2007) Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature, 449, 1044–1048.
- 13. Pastor-Satorras, R., Smith, E., and Solé, R.V. (2003) Evolving protein interaction networks through gene duplication. J. Theor. Biol., 222 (2), 199–210.
- 14. Wagner, A. (2003) How the global structure of protein interaction networks evolves. Proc. Biol. Sci., 270 (1514), 457–466.
- 15. Ravasz, E., Somera, A.L., Mongru, D.A., Oltvai, Z.N., and Barabási, A.-L. (2002) Hierarchical organization of modularity in metabolic networks. Supramol. Sci., 297, 1551–1555.
- 16. Jeong, H., Tombor, B., Albert, R., Oltvai, Z., and Barabási, A.-L. (2000) The large-scale organization of metabolic networks. Nature, 407, 651–654.
- 17. Arita, M. (2004) The metabolic world of Escherichia coli is not small. Proc. Natl. Acad. Sci. USA, 101 (6), 1543–1547.
- 18. Alon, U. (2007) Network motifs: theory and experimental approaches. Nat. Rev. Genet., 8, 450–461.
- 19. Milo, R., Itzkovitz, S., Kashtan, N., Levitt, R., Shen-Orr, S., Ayzenshtat, I., Sheffer, M., and Alon, U. (2004) Superfamilies of designed and evolved networks. Supramol. Sci., 303, 1538–1542.
- 20. Shen-Orr, S., Milo, R., Mangan, S., and Alon, U. (2002) Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet., 31, 64–68.
- 21. Lee, T.I., Rinaldi, N.J., Robert, F., Odom, D.T., Bar-Joseph, Z., Gerber, G.K., Hannett, N.M., Harbison, C.T., Thompson, C.M., Simon, I., Zeitlinger, J., Jennings, E.G., Murray, H.L., Gordon, D.B., Ren, B., Wyrick, J.J., Tagne, J.B., Volkert, T.L., Fraenkel, E., Gifford, D.K., and Young, R.A. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae. Supramol. Sci., 298, 799–804.
- 22. Guimera, R. and Nunes Amaral, L.A. (2005) Functional cartography of complex metabolic networks. Nature, 433, 895.
- 23. Dekel, E. and Alon, U. (2005) Optimality and evolutionary tuning of the expression level of a protein. Nature, 436, 588–692.
- 24. Brockmann, D. and Helbing, D. (2013) The hidden geometry of complex, network-driven contagion phenomena. Supramol. Sci., 342, 1337.
- 25. Cheong, R., Rhee, A., Wang, C.J., Nemenman, I., and Levchenko, A. (2011) Information transduction capacity of noisy biochemical signaling networks. Science, 334, 354.
- 26. Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, Morgan Kaufmann Publishers, Inc.
- 27. Rivoire, O. and Leibler, S. (2011) The value of information for populations in varying environments. J. Stat. Phys., 142 (6), 1124–1166.
- 28. Robison, K., McGuire, A.M., and Church, G.M.A. (1998) A comprehensive library of DNA-binding site matrices for 55 proteins applied to the complete Escherichia coli K12 genome. J. Mol. Biol, 284 (2), 241–254.
- 29. Lee, T.I., Rinaldi, N.J., Robert, F., Odom, D.T., Bar-Joseph, Z., Gerber, G.K., Hannett, N.M., Harbison, C.T., Thompson, C.M., Simon, I., Zeitlinger, J., Jennings, E.G., Murray, H.L., Gordon, D.B., Ren, B., Wyrick, J.J., Tagne, J.B., Volkert, T.L., Fraenkel, E., Gifford, D.K., and Young, R.A. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae. Science, 298, 799–804.
- 30. Salgado, H., Gama-Castro, S., Martínez-Antonio, A., Díaz-Peredo, E., Sánchez-Solano, F., Peralta-Gil, M., Garcia-Alonso, D., Jiménez-Jacinto, V., Santos-Zavaleta, A., Bonavides-Martínez, C., and Collado-Vides, J. (2004) RegulonDB (version 4.0): transcriptional regulation, operon organization and growth conditions in Escherichia coli K-12. Nucleic Acids Res., 32, 303–306.
- 31. Keseler, I.M., Collado-Vides, J., Gama-Castro, S., Ingraham, J., Paley, S., Paulsen, I.T., Peralta-Gil, M., and Karp, P.D. (2005) EcoCyc: a comprehensive database resource for Escherichia coli. Nucleic Acids Res., 39, D583–D590.
- 32. Shen-Orr, S., Milo, R., Mangan, S., and Alon, U. (2002) Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet., 31, 64–68.
- 33. Kaplan, S., Bren, A., Zaslaver, A., Dekel, E., and Alon, U. (2008) Diverse two-dimensional input functions control bacterial sugar genes. Mol. Cell, 29, 786–792.
- 34. Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002) Network motifs: simple building blocks of complex networks. Science, 298, 824–827.
- 35. Mangan, S. and Alon, U. (2003) Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA, 100, 11980–11985.
- 36. Mangan, S., Zaslaver, A., and Alon, U. (2003) The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks. J. Mol. Biol., 334, 197–204.
- 37. Kalir, S., Mangan, S., and Alon, U. (2005) A coherent feed-forward loop with a sum input function prolongs flagella expression in Escherichia coli. Mol. Syst. Biol., 1. doi: 10. 1038/msb4100010
- 38. Itzkovitz, S., Levitt, R., Kashtan, N., Milo, R., Itzkovitz, M., and Alon, U. (2005) Coarse-graining and self-dissimilarity of complex networks. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys., 71 (1 Part 2), 016127.
- 39. Savageau, M.A. (1998) Demand theory of gene regulation. Genetics, 149, 1665–1691.
- 40. Sasson, V., Shachrai, I., Bren, A., Dekel, E., and Alon, U. (2012) Mode of regulation and the insulation of bacterial gene expression. Mol. Cell, 46, 399–407.
- 41. Tyson, J.J., Chen, K.C., and Novak, B. (2003) Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol., 15 (2), 221–231.
- 42. Elowitz, M.B. and Leibler, S. (2000) A synthetic oscillatory network of transcriptional regulators. Nature, 403, 335–338.
- 43. Becskei, A. and Serrano, L. (2000) Engineering stability in gene networks by autoregulation. Nature, 405, 590–592.
- 44. Hasty, J., McMillen, D., and Collins, J.J. (2002) Engineered gene circuits. Nature, 420, 224–230.
- 45. Elowitz, M. et al. (2002) Stochastic gene expression in a single cell. Science, 297, 1183.
- 46. Pedraza, J.M. and van Oudenaarden, A. (2005) Noise propagation in gene networks. Science, 307, 1965–1969.
- 47. Alon, U. (2006) An Introduction to Systems Biology: Design Principles of Biological Circuits, CRC Mathematical & Computational Biology, Chapman & Hall.
- 48. Alon, U. (2007) Network motifs: theory and experimental approaches. Nat. Rev. Genet., 8, 450–461.
- 49. Mangan, S. and Alon, U. (2003) Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA, 100 (21), 11980–11985.
- 50. Prill, R.J., Iglesias, P.A., and Levchenko, A. (2005) Dynamic properties of network motifs contribute to biological network organization. PLoS Biol., 3 (11), 1881–1892.
- 51. Klemm, K. and Bornholdt, S. (2005) Topology of biological networks and reliability of information processing. Proc. Natl. Acad. Sci. USA, 102 (51), 18414–18419.
- 52. Hart, Y., Antebi, Y.E., Mayo, A.E., Friedman, N., and Alon, U. (2012) Design principles of cell circuits with paradoxical components. Proc. Natl. Acad. Sci. USA, 109 (21), 8346–8351.
- 53. Goldbeter, A. and Koshland, D.E., Jr (1981) An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA, 78, 6840–6844.
- 54. Goldbeter, A. and Koshland, D.E., Jr (1984) Ultrasensitivity in biological systems controlled by covalent modification. J. Biol. Chem., 259, 14441–14447.
- 55. Kochanowski, K., Volkmer, B., Gerosa, L., Haverkorn van Rijsewijka, B.R., Schmidt, A., and Heinemann, M. (2013) Functioning of a metabolic flux sensor in Escherichia coli. Proc. Natl. Acad. Sci. USA, 110 (3), 1130–1135.
- 56. Huiskes, R. et al. (2000) Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature, 405, 704–706.
- 57. Frost, H.M. (2001) From Wolff's law to the Utah paradigm: insights about bone physiology and its clinical applications. Anat. Rec., 262, 398–419.
- 58. Nowlan, N.C., Murphy, P., and Prendergast, P.J. (2007) Mechanobiology of embryonic limb development. Ann. N.Y. Acad. Sci., 1101, 389–411.
- 59. Weinkamer, R. and Fratzl, P. (2011) Mechanical adaptation of biological materials: the examples of bone and wood. Mater. Sci. Eng., 31, 1164–1173.
- 60. Rosenfeld, N., Elowitz, M.B., and Alon, U. (2002) Negative autoregulation speeds the response times of transcription networks. J. Mol. Biol., 323 (5), 785–793.
- 61. He, F., Fromion, V., and Westerhoff, H.V. (2013) (Im)Perfect robustness and adaptation of metabolic networks subject to metabolic and gene-expression regulation: marrying control engineering with metabolic control analysis. BMC Syst. Biol., 7, 131.
- 62. Klevecz, R.R., Bolen, J., Forrest, G., and Murray, D.B. (2004) A genomewide oscillation in transcription gates DNA replication and cell cycle. Proc. Natl. Acad. Sci. USA, 101 (5), 1200–1205.
- 63. Machné, R. and Murray, D. (2012) The yin and yang of yeast transcription: elements of a global feedback system between metabolism and chromatin. PLoS One, 7 (6), e37906.
- 64. Mangan, S., Zaslaver, A., and Alon, U. (2006) The incoherent feed-forward loop accelerates the response time of the GAL system in E. coli. J. Mol. Biol., 356, 1073–1082.
- 65. Kaplan, S., Bren, A., Erez Dekel, E., and Alon, U. (2008) The incoherent feed-forward loop can generate non-monotonic input functions for genes. Mol. Syst. Biol., 4 (203), 203.
- 66. Eichenberger, P., Fujita, M., Jensen, S.T., Conlon, E.M., Rudner, D.Z., Wang, S.T., Ferguson, C., Haga, K., Sato, T., Liu, J.S., and Losick, R. (2004.) The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis. PLoS Biol., 2 (10), e328.
- 67. Hartwell, L.H., Hopfield, J.J., Leibler, S., and Murray, A.W. (1999) From molecular to modular cell biology. Nature, 402 (6761 Suppl.), C47–C52.
- 68. Mewes, H.W., Dietmann, S., Frishman, D., Gregory, R., Mannhaupt, G., Mayer, K.F.X., Münsterkötter, M., Ruepp, A., Spannagl, M., Stümpflen, V., and Rattei, T. (2008) MIPS: analysis and annotation of genome information in 2007. Nucleic Acids Res., 36, D196–D201.
- 69. Kanehisa, M., Goto, S., Kawashima S, S., and Nakaya, A. (2002) The KEGG databases at GenomeNet. Nucleic Acids Res., 30, 42–46.
- 70.The Gene Ontology Consortium (2000) Gene ontology: tool for the unification of biology. Nat. Genet., 25, 25–29.
- 71. Liebermeister, W., Noor, E., Flamholz, A., Davidi, D., Bernhardt, J., and Milo, R. (2014) Visual account of protein investment in cellular functions. Proc. Natl. Acad. Sci. USA, 111 (23), 8488–8493.
- 72. Arike, L., Valgepea, K., Peil, L., Nahku, R., Adamberg, K., and Vilu, R. (2012) Comparison and applications of label-free absolute proteome quantification methods on Escherichia coli. J. Proteomics, 75 (17), 5437–5448.
- 73. Schuster, S., Pfeiffer, T., Moldenhauer, F., Koch, I., and Dandekar, T. (2002) Exploring the pathway structure of metabolism: decomposition into subnetworks and application to Mycoplasma pneumoniae. Bioinformatics, 18 (2), 351–361.
- 74. Ravasz, E., Somera, A.L., Mongru, D.A., Oltvai, Z.N., and Barabási, A.-L. (2002) Hierarchical organization of modularity in metabolic networks. Supramol. Sci., 297, 1551–1555.
- 75. Shen-Orr, S., Milo, R., Mangan, S., and Alon, U. (2002) Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet., 31, 64–68.
- 76. Guimera, R. and Nunes Amaral, L.A. (2005) Functional cartography of complex metabolic networks. Nature, 433, 895.
- 77. Ederer, M., Sauter, T., Bullinger, E., Gilles, E., and Allgöwer, F. (2003) An approach for dividing models of biological reaction networks into functional units. Simulation, 79 (12), 703–716.
- 78. Segal, E., Shapira, M., Regev, A., Pe'er, D., Botstein, D., Koller, D., and Friedman, N. (2003) Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat. Genet., 34 (2), 166–176.
- 79. Tanay, A., Sharan, R., and Shamir, R. (2002) Discovering statistically significant biclusters in gene expression data. Bioinformatics, 18 (Suppl. 1), S136–S144.
- 80. Pellegrini, M., Marcotte, E.M., Thompson, M.J., Eisenberg, D., and Yeates, T.O. (1999) Assigning protein functions by comparative genome analysis: protein phylogenetic profiles. Proc. Natl. Acad. Sci. USA, 96 (8), 4285–4288.
- 81. Schilling, C.H. and Palsson, B.Ø. (1998) The underlying pathway structure of biochemical reaction networks. Proc. Natl. Acad. Sci. USA, 95 (8), 4193–4198.
- 82. Schuster, S., Fell, D., and Dandekar, T. (2000) A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol., 18, 326–332.
- 83. Jol, S.J., Kümmel, A., Terzer, M., Stelling, Jörg., and Heinemann, M. (2012) System-level insights into yeast metabolism by thermodynamic analysis of elementary flux modes. PLoS Comput. Biol., 8 (3), e1002415.
- 84. Segrè, D., DeLuna, A., Church, G.M., and Kishony, R. (2005) Modular epistasis in yeast metabolism. Nat. Genet., 37, 77–83.
- 85. Alon, U. (2003) Biological networks: the tinkerer as an engineer. Supramol. Sci., 301, 1866–1867.
- 86. Kirschner, M. and Gerhart, J. (1998) Evolvability. Proc. Natl. Acad. Sci. USA, 95 (15), 8420–8427.
- 87. Kashtan, N. and Alon, U. (2005) Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. USA, 102 (39), 13773–13778.
- 88. Kashtan, N., Noor, E., and Alon, U. (2007) Varying environments can speed up evolution. Proc. Natl. Acad. Sci. USA, 104 (34), 13711–13716.
- 89. Csete, M.E. and Doyle, J.C. (2002) Reverse engineering of biological complexity. Supramol. Sci., 295 (5560), 1664–1669.
- 90. Conant, G.C. and Wagner, A. (2003) Convergent evolution of gene circuits. Nat. Genet., 34, 264–266.
- 91. Lazebnik, Y. (2002) Can a biologist fix a radio? or, what I learned while studying apoptosis. Cancer Cell, 2, 179–182.
- 92. Becskei, A. and Serrano, L. (2000) Engineering stability in gene networks by autoregulation. Nature, 405, 590–592.
- 93. Hasty, J., McMillen, D., and Collins, J.J. (2002) Engineered gene circuits. Nature, 420, 224–230.
Further Reading
- Network motifs: Alon, U. (2006) An Introduction to Systems Biology: Design Principles of Biological Circuits, CRC Mathematical & Computational Biology, Chapman & Hall.
- Network motifs: Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002) Network motifs: simple building blocks of complex networks. Supramol. Sci., 298, 824–827.
- Networks: Barabási, A.-L. (2002) Linked: The New Science of Networks, Perseus Publishing.
- Networks: Barabási, A.-L. and Oltvai, Z.N. (2004) Network biology: understanding the cell's functional organization. Nat. Rev. Genet., 5, 101–113.
- Repressilator: Elowitz, M.B. and Leibler, S. (2000) A synthetic oscillatory network of transcriptional regulators. Nature, 403, 335–338.
- Stochastic gene expression: Elowitz, M. et al. (2002) Stochastic gene expression in a single cell. Supramol. Sci., 297, 1183.
- Metabolic network reconstruction: Henry, C.S., DeJongh, M., Best, A.A., Frybarger, P.M., Linsay, B., and Stevens, R.L. (2010) High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol., 28, 977–982.
- Signaling networks: Atlas of Cancer Signalling Networks (acsn.curie.fr/).
- Human metabolic network: Thiele, I. et al. (2013) A community-driven global reconstruction of human metabolism. Nat. Biotechnol., 31 (5), 419–427.
- Regulation motifs: Tyson, J.J., Chen, K.C., and Novak, B. (2003) Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol., 15 (2), 221–231.
- Interactome networks: Vidal, M. et al. (2011) Interactome networks and human disease. Cell, 144 (6), 986–998.