GRAPH THEORY

Graph Theory is the study of how things are interconnected. This includes how computers are connected to each other in your house and on the Internet, how to efficiently place power plants to provide electricity in cities, the best locations to put fast food restaurants so that no one is too far from their favorite junk food, how to plan airplane flight paths, and more.

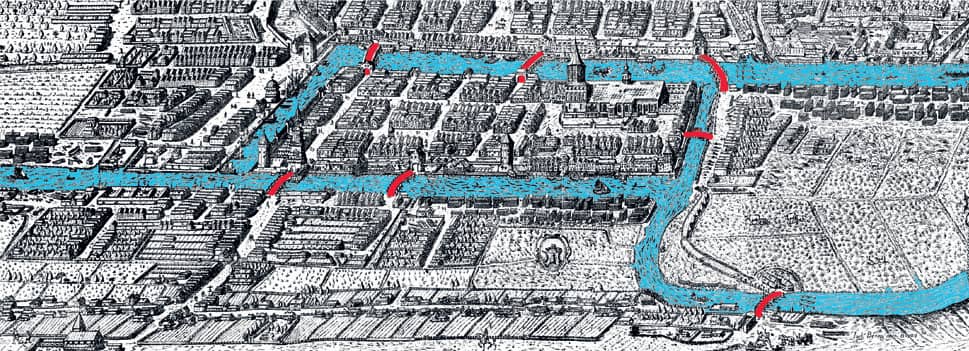
In 1736, mathematician Leonhard Euler solved the Bridges of Königsberg problem (see below), inventing Graph Theory in the process.

Think About It

One of the most famous Graph Theory problems involves the city of Königsberg. Spanning both sides of a river, it has two islands, which are connected to the rest of the city by seven bridges. Citizens challenged each other to find a path that started and ended in the same place and crossed each of the seven bridges exactly once. Can you find such a path?

LAB 33

EULERIAN CIRCUITS

Learn how to trace shapes without lifting your pencil. To trace every line of the figure eight (left) without lifting your pencil, trace in the direction of the arrows as shown on the bottom.

Materials

Pencil

Paper

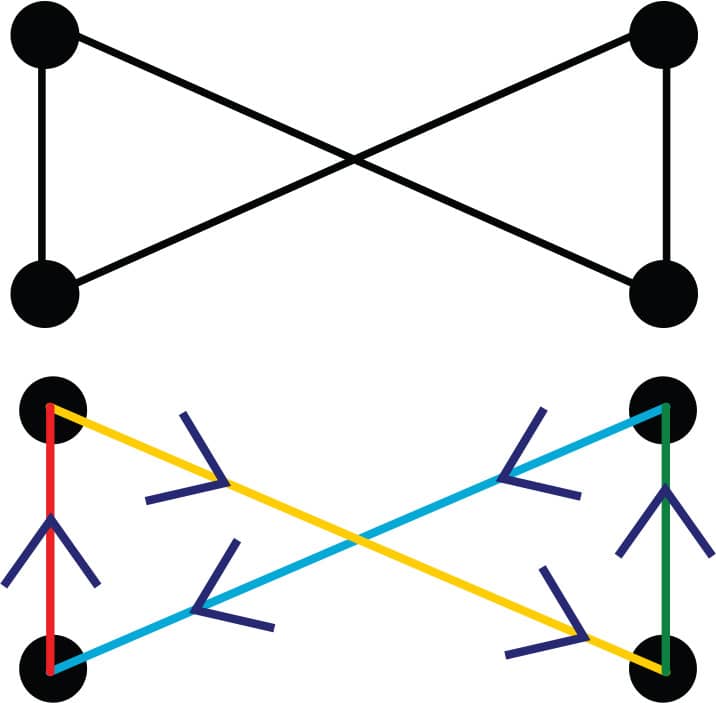
You can avoid lifting your pencil by following the direction of the arrows when tracing the figure eight.

MATH FACT

In math, a graph is a set of dots, called vertices, connected by lines, called edges. You can also think of a vertex (the singular of vertices) as a corner. Note that edges don’t have to be straight.

TRACING EULERIAN CIRCUITS

The paths we draw in this lab travel over every edge of the entire graph, start and end on the same vertex, and don’t retrace any edges. Mathematicians call these paths Eulerian circuits.

Important: Lines are allowed to cross but you can’t trace over the same line twice.

1. Can you trace a five-point star without lifting your pencil or going over the same line twice (fig. 1)?

2. It’s possible to trace all the shapes on the next page starting and ending at the same vertex without lifting your pencil or going over the same line twice (figs. 2–6). Can you find the paths?

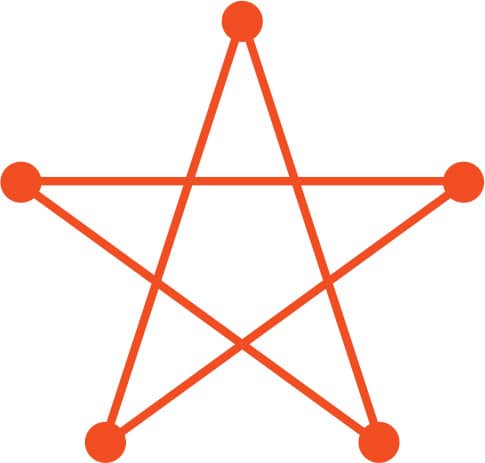
FIG. 1: A five-point star.

FIG. 2: A simple house shape.

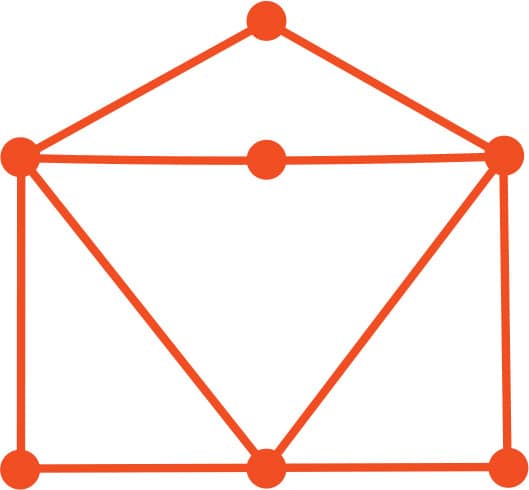
FIG. 3: An open envelope.

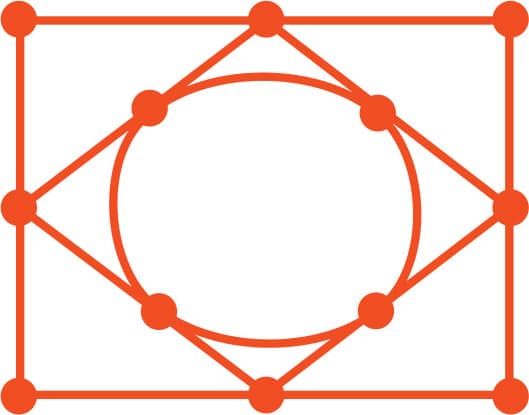
FIG. 4: Nested shapes.

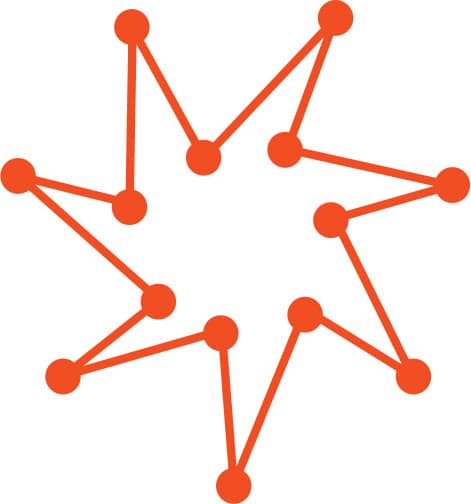
FIG. 5: A seven-point star.

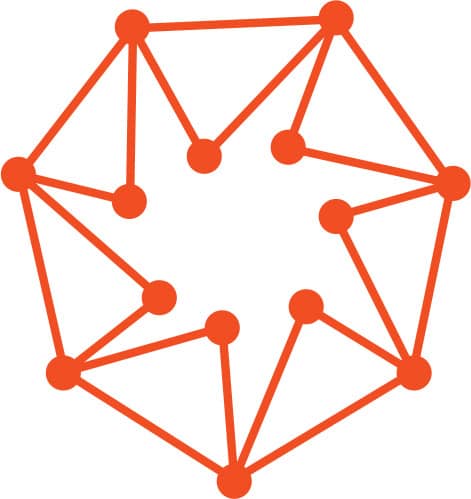
FIG. 6: A seven-point star inside out.

MEET THE MATHEMATICIAN FAN CHUNG

Fan Chung is an American mathematician who was born in Taiwan. She is a Distinguished Professor of Mathematics and Computer Science at the University of California San Diego. Her main area of research is Graph Theory, including graphs of very large networks such as the Internet. In college, she met many female mathematicians. They all talked about math and helped each other, which encouraged her to become a mathematician. Fan says, “Frequently a good problem from someone else will give you a push in the right direction, and the next thing you know you have another good problem. You make mathematical friends and share the fun!”

The Power Grid Graph
Photo by Derrick Benzanson and Fan Chung

LAB 34

SECRETS OF EULERIAN CIRCUITS REVEALED

What will you discover about the mathematically mysterious Eulerian circuits?

Materials

Pencil

Paper

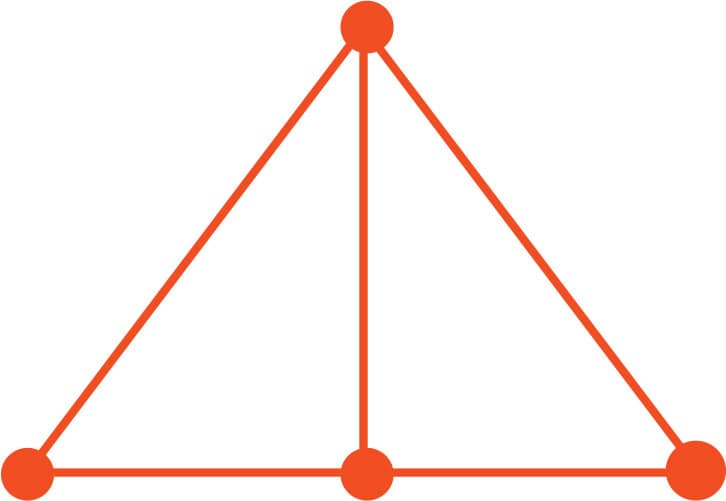
FIG. 1: A triangle graph with no Eulerian circuit.

A SECRET SHORTCUT

In Lab 33, we discovered three rules for creating an Eulerian circuit:

1. Start and end from the same vertex.

2. Don’t lift your pencil.

3. Don’t retrace any edges.

In this lab, we’ll learn a shortcut for figuring out if a graph has an Eulerian circuit.

1. You cannot follow the rules for creating an Eulerian circuit to draw this shape (fig. 1). Try it and you’ll see it’s impossible.

2. What about figs. 2–6? Some of them have Eulerian circuits and others do not. Circle the ones that have an Eulerian circuit and put an “X” next to the ones that don’t.

3. As we discovered, some graphs have no Eulerian circuit. Can you figure out a rule that will tell you if a shape has an Eulerian circuit?

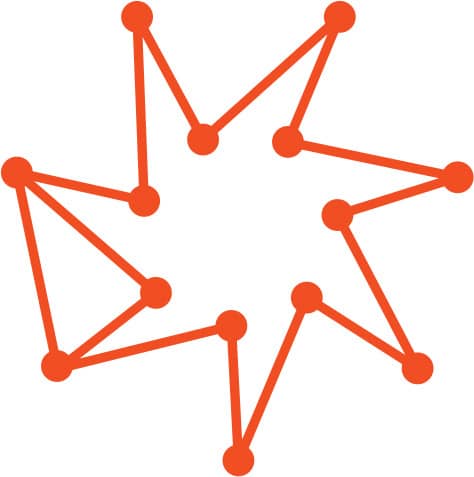
FIG. 2: A modified seven-point star.

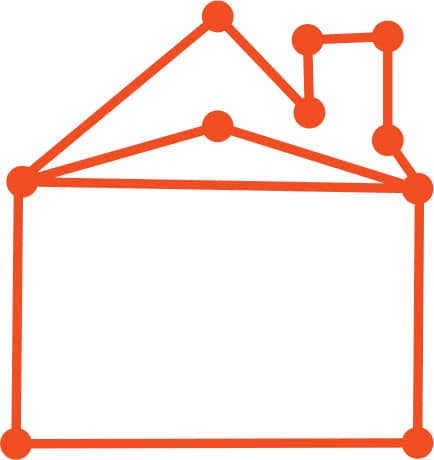
FIG. 3: A fancy house.

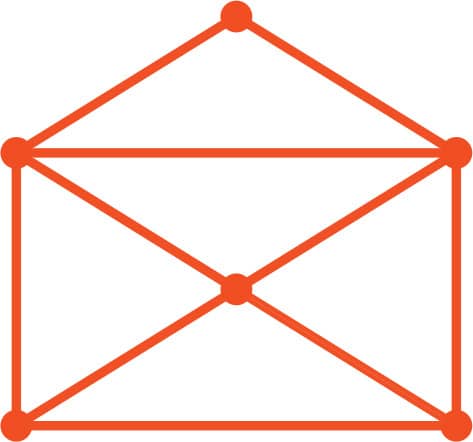
FIG. 4: An envelope.

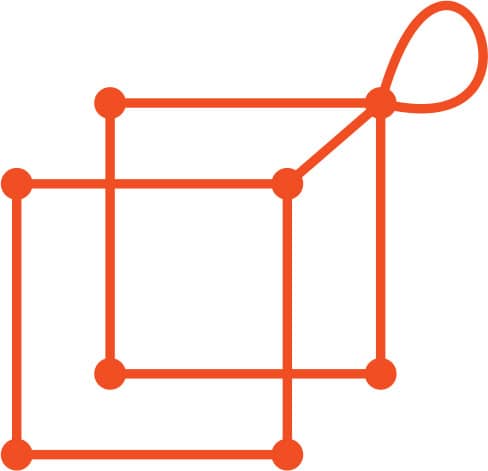
FIG. 5: A cube-like shape.

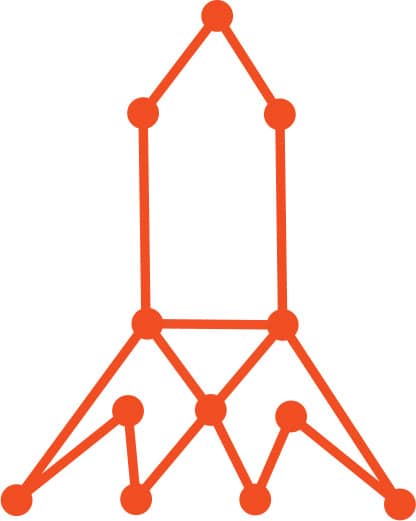
FIG. 6: A rocket.

What’s Going On?

For every graph in Labs 33 and 34, write the number of edges coming out of each vertex next to the vertex. (Hint: Every graph in Lab 33 does have an Eulerian circuit.) For example:

Do you see a pattern? Is there something that all the graphs with an Eulerian circuit have in common? Is there something that all the graphs without an Eulerian circuit have in common? Stop here and think about it.

Here’s the answer: If there is an Eulerian circuit, then every time you go to a vertex, you leave it on a different edge until you get back to the beginning vertex. This means there must be an even number of edges (2, 4, 6, etc.) at every vertex. If any vertex connects an odd number of edges, you automatically know that the graph does not have an Eulerian circuit. An exciting discovery is that if every vertex in a graph has an even number of edges, the graph does have an Eulerian circuit.

LAB 35

BRIDGES OF KÖNIGSBERG

Now that you know so much about Graph Theory, let’s solve the Bridges of Königsberg problem from the Think About It.

Materials

Map of Königsberg (see below)

Pencil

What’s Going On?

Even if you can’t find a path that crosses every bridge in Königsberg exactly once and ends up where you started, that doesn’t mean no path exists! To solve the problem, we have to prove that there cannot be a path. We’ll learn how to do a mathematical proof in this lab.

GOING FROM MAP TO GRAPH

1. Turn the map below into a graph, as shown in fig. 1. Each area you can visit becomes a vertex of a graph. Each bridge between areas becomes an edge connecting those vertices.

2. The Bridges of Königsberg challenge is the same as finding an Eulerian circuit on the graph we just drew. Can you find an Eulerian circuit on this graph? If you get stuck, go on to the next step.

3. Hmm, maybe there isn’t an Eulerian circuit. Let’s label every vertex with the number of edges it connects (fig. 2).

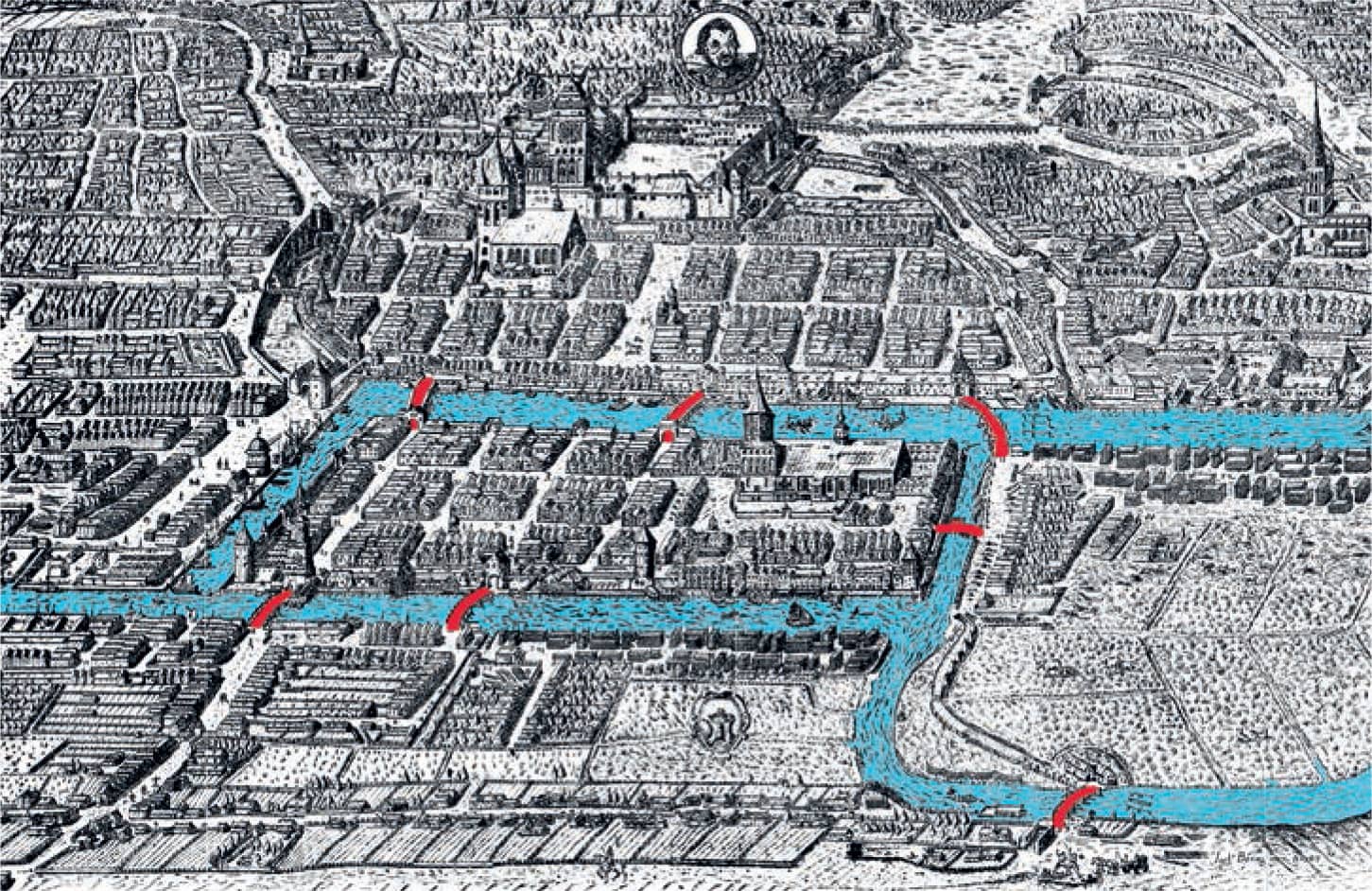
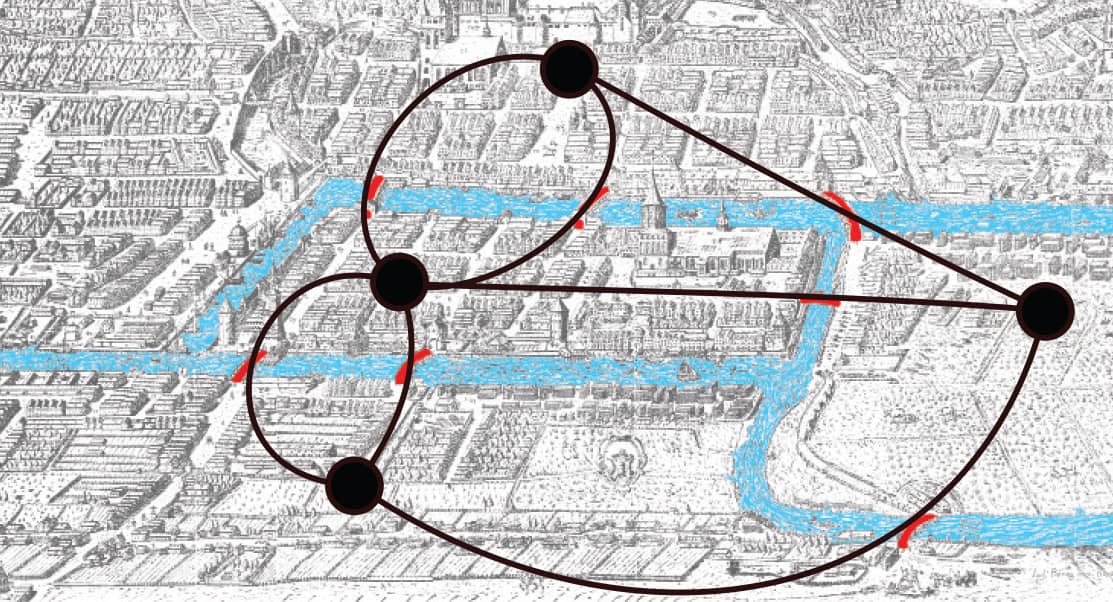
FIG. 1: Turn the map into a graph.

Now we know we weren’t imagining it—there’s no Eulerian circuit Remember, in Lab 34, we learned that if any vertex connects an odd number of edges, the graph does not have an Eulerian circuit. Here, all of the vertices connect an odd number of edges. Congratulations, you just did a proof by contradiction!

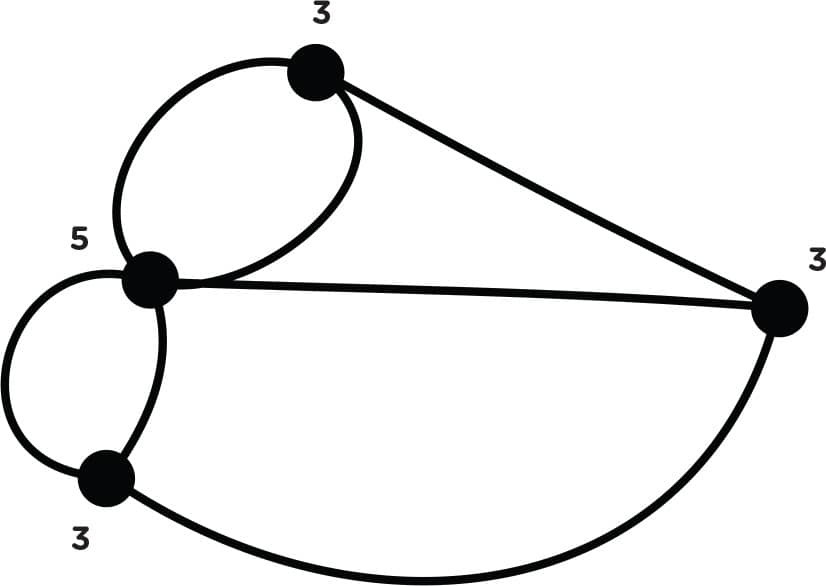
FIG. 2: Label every vertex with the number of edges it connects.

MATH TECHNIQUE

Proof by Contradiction

A mathematical proof is a series of logical arguments showing that something is true. There are many kinds of proofs. We explore two in this chapter (see Lab 36).

A proof by contradiction uses a series of arguments to show that if one thing is true, this means a second thing must be true. But here’s the trick: If we can show that the second thing is actually false, that means that the first thing must have been false as well!

For example, for the Bridges of Königsberg problem, we know that if there is a path around the city, the graph will have an Eulerian circuit. We also know that if the graph has an Eulerian circuit, then all vertices must have an even number of edges coming out of it. But we showed that none of the vertices had an even number of edges! That means there cannot be a path that crosses every bridge exactly once and returns to where it started, so we’ve proven that a path cannot exist.

LAB 36

THE EULER CHARACTERISTIC

Learn an interesting relationship between vertices, edges, and regions.

Materials

Pencil

Paper

COUNTING VERTICES, REGIONS, AND EDGES

Earlier, we said that a graph is a set of dots, called vertices, connected by lines, called edges. The paper you draw the graph on is divided into regions, each surrounded by edges. The space outside the graph also counts as a region. In the picture below, there are 10 vertices (colored black), 7 regions (colored yellow or green), and 15 edges (colored blue).

Leonhard Euler noticed something interesting about graphs when he counted

 

(number of vertices) + (number of regions) − (number of edges)

Let’s count the number of vertices, edges, and regions in some graphs and see if we can figure out what he noticed.

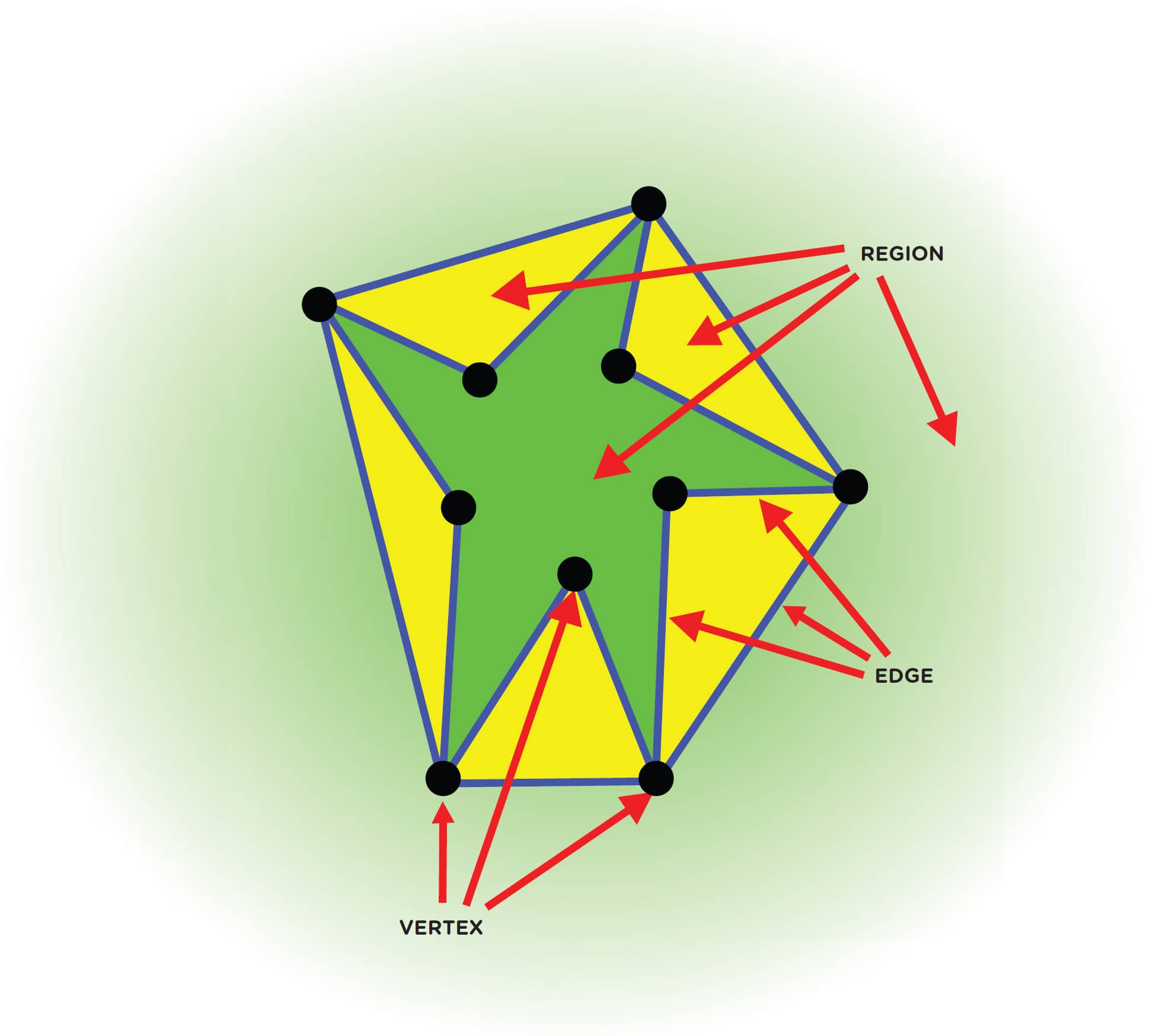
1. Figs. 1–3 show some examples where we’ve counted the vertices, edges, and regions of some graphs. You count them too and make sure your counts match ours! Remember to count the “outside” region.

Once we’ve counted V, R, and E, we’ll add the number of vertices and regions together, subtract the number of edges, and see what we get!

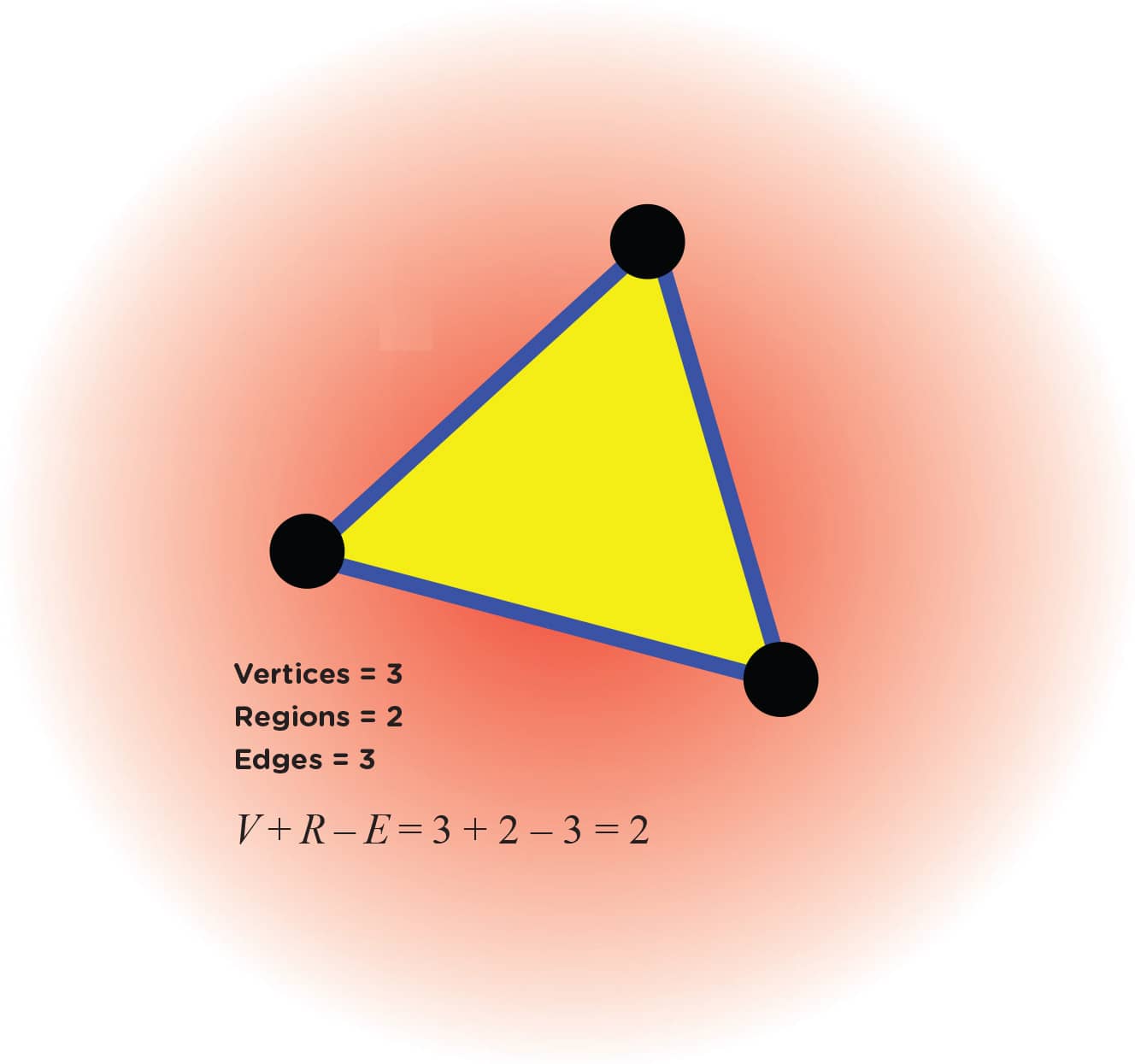
FIG. 1: Count the vertices, edges, and regions.

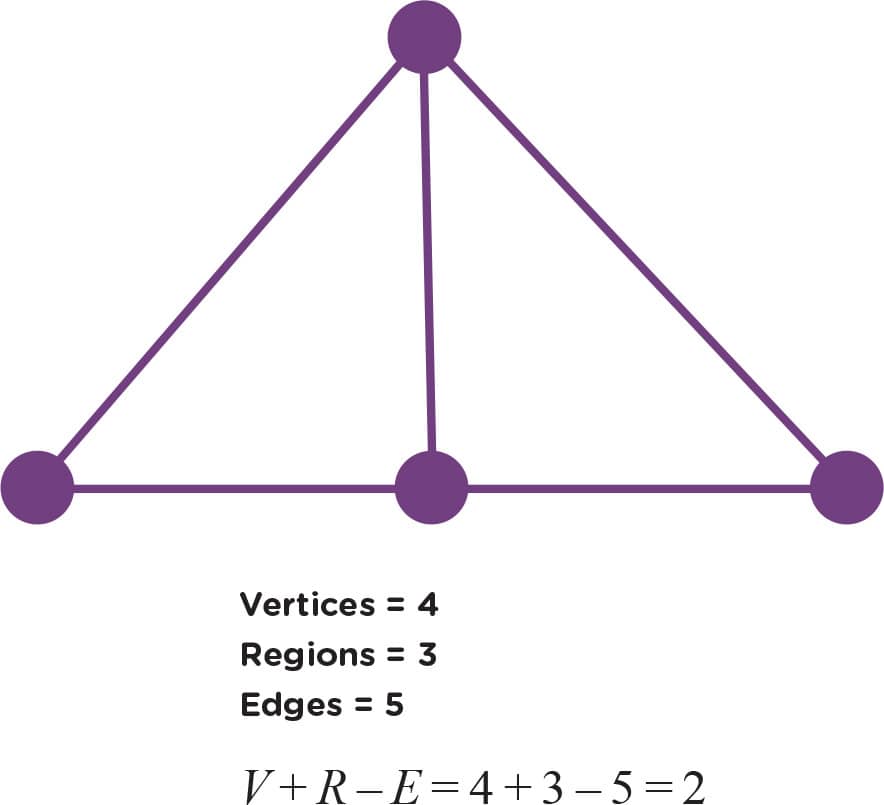
FIG. 2: Remember to count the “outside” region.

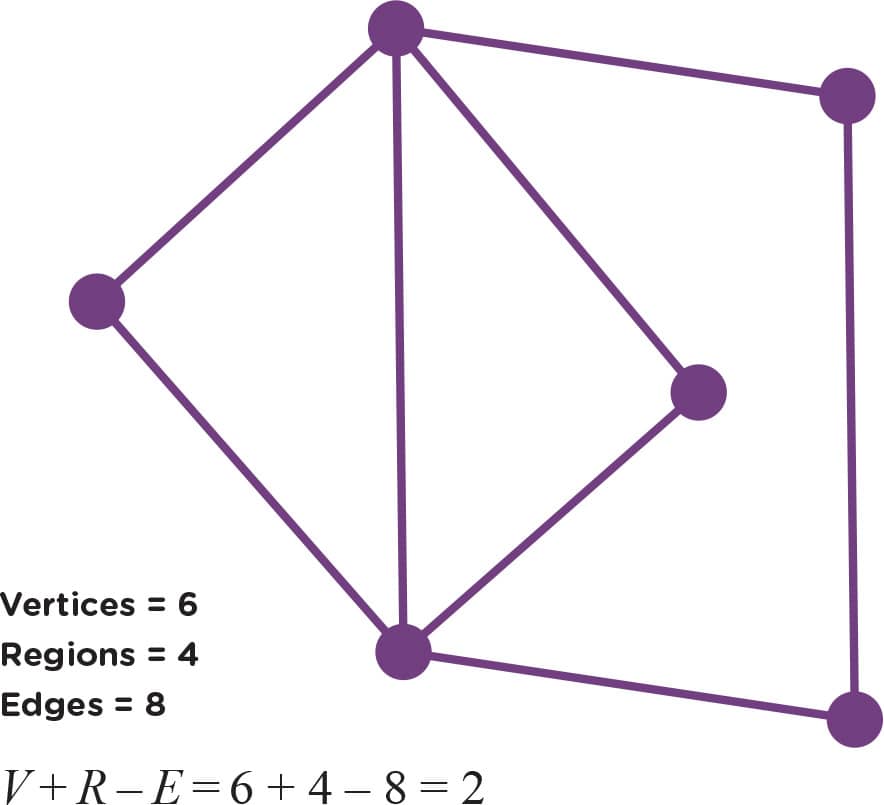
FIG. 3: Do your counts match ours?

2. Now you try counting yourself (figs. 4–10). Don’t forget to count the “outside” region. How many vertices, edges, and regions do the following graphs have? Also calculate V + R − E for each graph. Hint: The graphs in figs. 9 and 10 only have one region: the “outside” region.

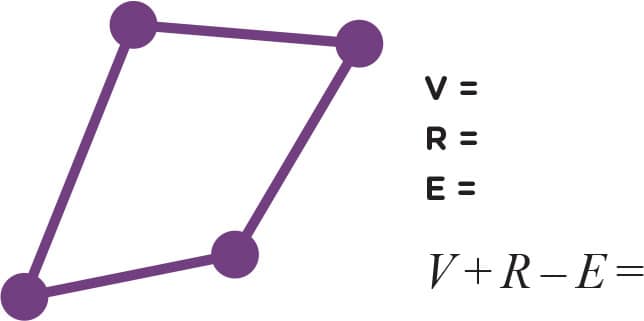
FIG. 4

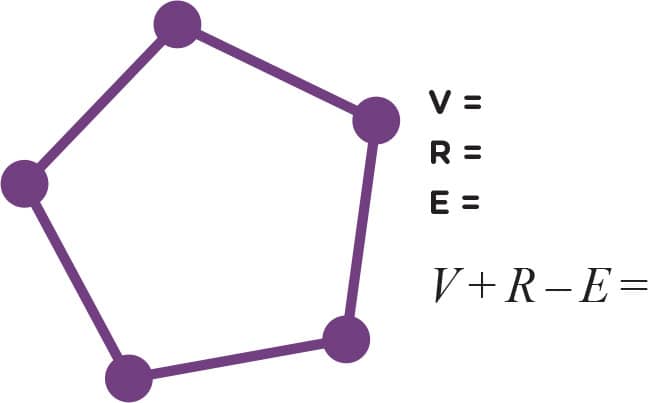
FIG. 5

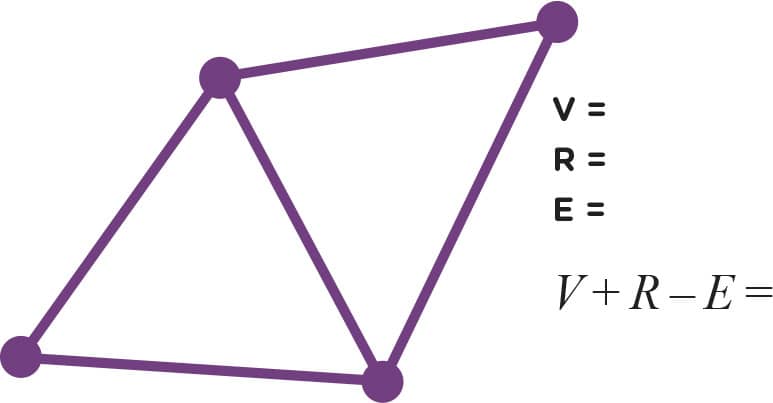
FIG. 6

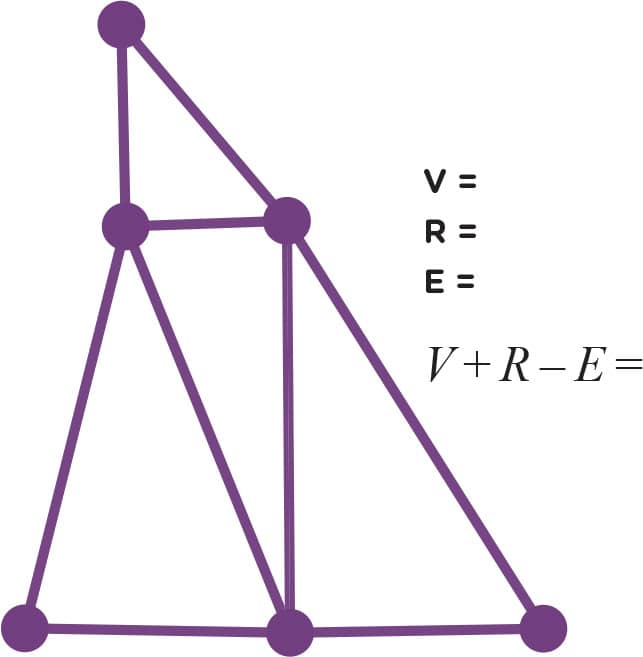
FIG. 7

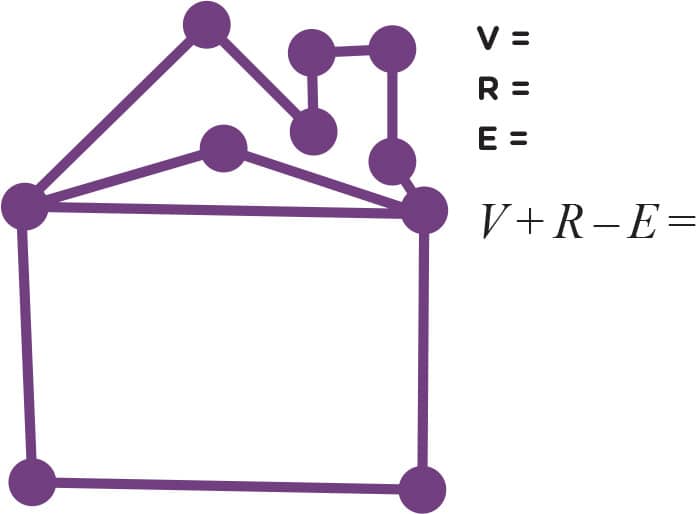
FIG. 8

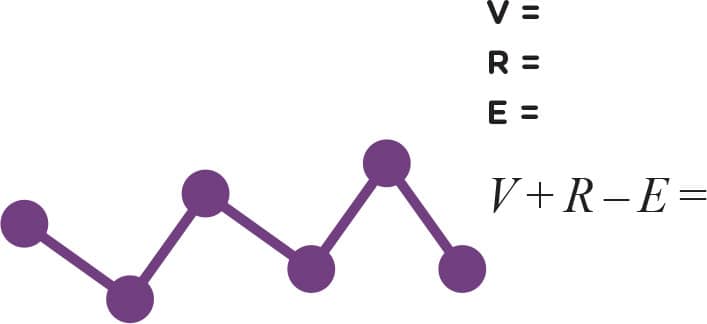
FIG. 9

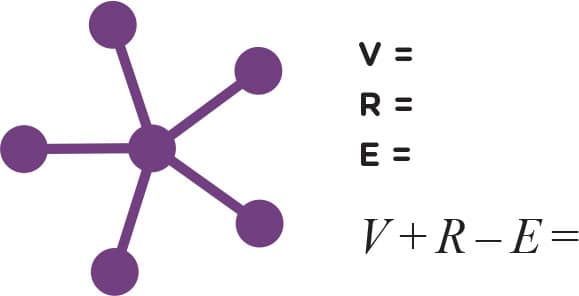
FIG. 10

SOLUTION: In every example, V + R − E = 2. That’s pretty amazing. Do you think it’s always true? (You might want to think about this for a bit before you continue on.)

Requirements for the Euler Characteristic to Be 2

Calculate the Euler Characteristic (V + R – E) of this graph:

This graph is not connected. (Some vertices have no path between them.) We can connect it by adding an edge. Calculate the Euler Characteristic of the newly connected graph.

You got 2, right?

In the graph below, the two inside edges cross but there’s no vertex where they cross. (Don’t worry about why one edge is a different color quite yet.) What is the Euler Characteristic of this graph?

In Graph Theory, a planar graph has no crossing edges. (If there is a vertex where two edges meet, that’s not considered crossing edges and it’s still a planar graph.) Let’s move the red edge outside as below so the graph becomes planar. What is the Euler Characteristic of the newly planar graph?

Now Euler’s characteristic is 2 again!

LAB 37

A PROOF ABOUT THE EULER CHARACTERISTIC

In a PROOF BY INDUCTION, you first show that the simplest case (called the BASE CASE) is true. Next you prove the INDUCTION STEP, showing that a general case being true means that the following case is also true. Now you have a recipe showing how to get from any size to any other size (repeating the induction step as many times as needed, even going on forever), so you know it’s always true. (This is college-level math, so don’t worry if you find it a bit confusing.) Let’s show that the Euler Characteristic is 2 for all planar, connected graphs!

Materials

Pencil

Paper

CHALLENGE!: PROOF BY INDUCTION

1. Base case: Calculate V + R – E in the case of a single vertex and no edges (fig. 1). It’s 2, right?

2. Calculate V + R – E when we add a new edge and a new vertex (fig. 2). It’s still 2. We added one new vertex and one new edge, so they canceled each other out.

3. Calculate V + R – E before and after we add a new edge but not a new vertex (figs. 3–4). It’s still 2, because when we add a new edge but no new vertex, we end up adding a new region, which cancels out the new edge. Try adding one edge to some of the graphs from earlier in this chapter. Do you see how we always add one region when we add one edge? Thus, V + R – E stays the same.

4. We can build any planar connected graph by adding vertices and/or edges as in the steps above. Try adding edges and/or vertices to the graphs in figs. 5–7. Calculate V + R – E before and after.

5. Add some vertices and/or edges to a few graphs you make up yourself. Calculate V + R – E before and after. You can try this on any planar connected graph, not just the simple ones from steps 1 and 2.

If you add just an edge, that ends up adding a new region. If you add a new vertex, you have to add the edge to connect it to the existing graph. Thus, at every step of building a planar connected graph, V + R – E = 2. Amazing!

You have just done a mathematical proof by induction. Congratulations!

FIG. 1: Calculate V + R – E in the case of a single vertex and no edges.

FIG. 2: Calculate V + R – E when we add a new edge and a new vertex.

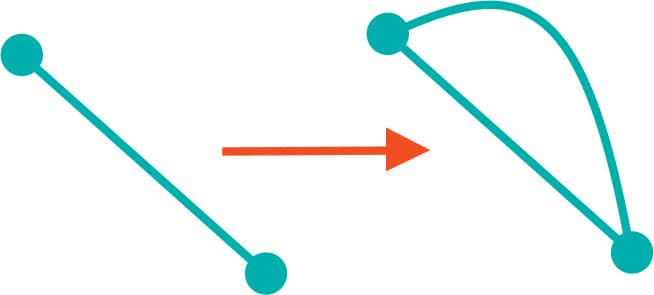
FIG. 3: Calculate V + R – E before and after we add a new edge.

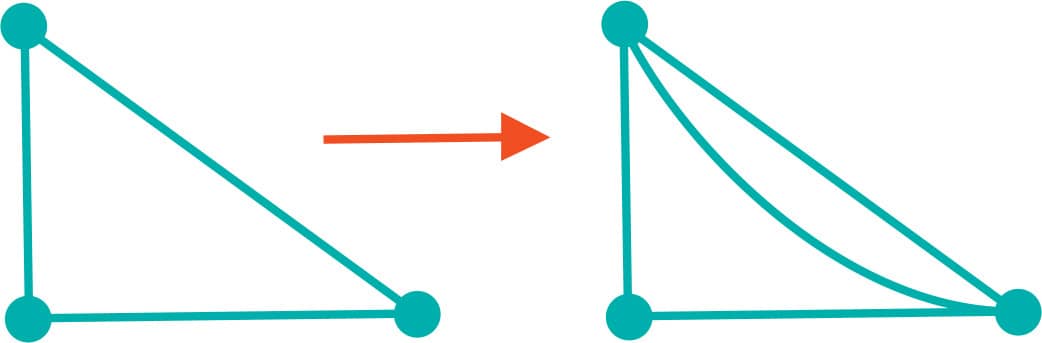
FIG. 4: Calculate V + R – E before and after we add a new edge.

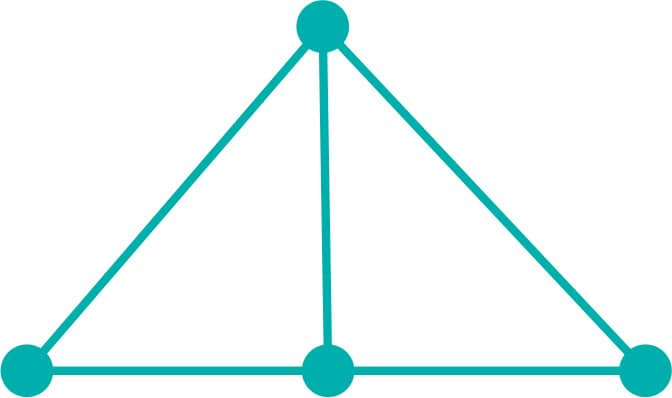
FIG. 5: Calculate V + R – E before and after adding vertices and edges.

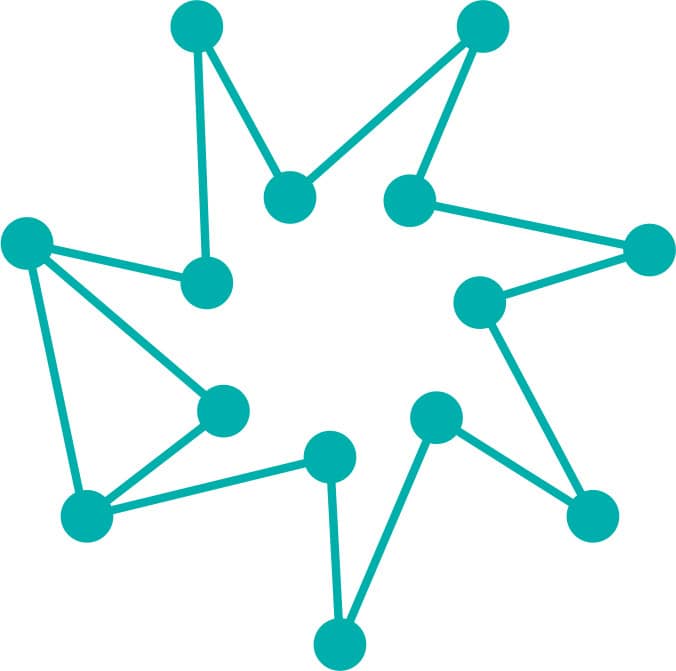
FIG. 6: Calculate V + R – E before and after adding vertices and edges.

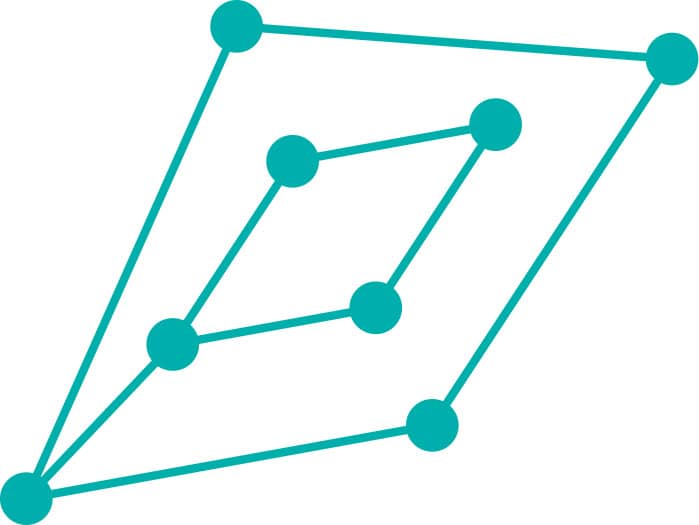
FIG. 7: Calculate V + R – E before and after adding vertices and edges.