Stacks and Queues

This chapter covers stacks and queues; both are versatile data structures commonly used in the implementation of other, more complex data structures. You will learn what stacks and queues are, how and when they are used, and how to implement them. Finally, the exercises will help you to understand these concepts as well as when to apply stacks and queues to an algorithmic problem.

Stacks

A stack is a data structure in which only the last inserted element can be removed and accessed (see Figure 12-1). Think about stacking plates on a table. To get to the bottom one, you must remove all the other ones on the top. This is a principle known as last in, first out(LIFO). A stack is great because it is fast. Since it is known that the last element is to be removed, the lookup and insertion happen in a constant time of O(1). Stacks should be used over arrays when you need to work with data in the LIFO form where the algorithm needs to access only the last-added element. The limitation of stacks is that they cannot access the non-last-added element directly like arrays can; in addition, accessing deeper elements requires you to remove the elements from the data structure.

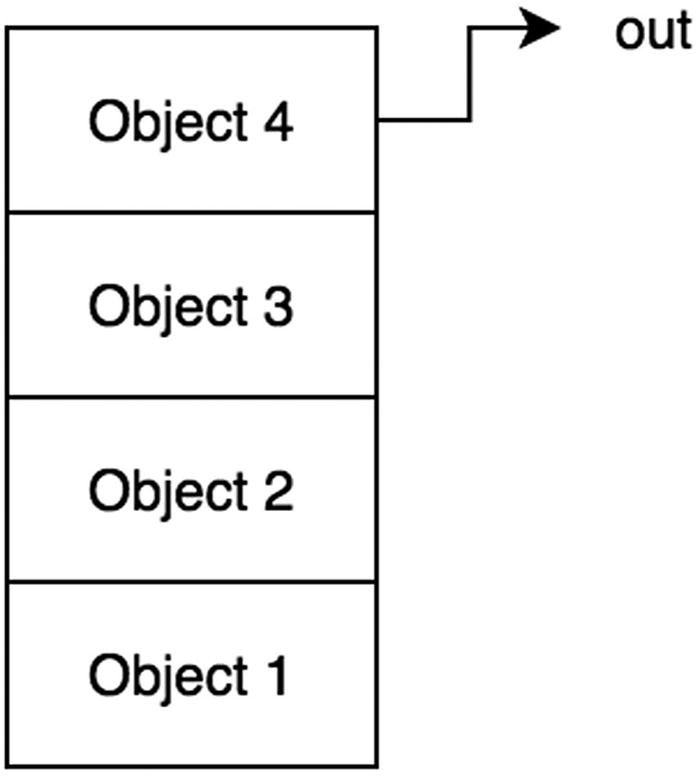
../images/465726_1_En_12_Chapter/465726_1_En_12_Fig1_HTML.jpg — Figure 12-1
Stack, LIFO

In JavaScript, arrays have methods that define the stack class: pop and push (as discussed in Chapter 5). With this, a stack can be easily implemented.

Here is some skeleton code to start. You can find the code on GitHub.¹

1 function Stack(array){

2 this.array = [];

3 if(array) this.array = array;

4 }

6 Stack.prototype.getBuffer = function(){

7 return this.array.slice();

8 }

10 Stack.prototype.isEmpty = function(){

11 return this.array.length == 0;

12 }

14 //instance of the stack class

15 var stack1 = new Stack();

17 console.log(stack1); // {array: []}

Let’s first consider “peeking” at the most recently added element. This can be done simply by using the largest index of the array.

Peek

Peeking at the last added element of the stack means returning the last-added element without removing it from the data structure. Peeking is often used to compare the last-added element to some other variable and to evaluate whether the last-added element should be removed from the data structure.

1 Stack.prototype.peek = function(){

2 return this.array[this.array.length-1];

3 }

4 stack1.push(10);

5 console.log(stack1.peek()); // 10

6 stack1.push(5);

7 console.log(stack1.peek()); // 5

Time Complexity: O(1)

Insertion

Inserting into a stack can be done via the push function natively supported with JavaScript arrays.

1 Stack.prototype.push = function(value){

2 this.array.push(value);

3 }

5 stack1.push(1);

6 stack1.push(2);

7 stack1.push(3);

8 console.log(stack1); // {array: [1,2,3]}

Time Complexity: O(1)

Deletion

Deletion can also be implemented using a native JavaScript array method, called pop.

1 Stack.prototype.pop = function() {

2 return this.array.pop();

3 };

5 stack1.pop(1);

6 stack1.pop(2);

7 stack1.pop(3);

9 console.log(stack1); // {array: []}

Time Complexity: O(1)

Access

Accessing specific elements in a data structure is important. Here, let’s take a look at how to access an element based on order.

To access the nth node from the top, you need to call popn number of times.

1 function stackAccessNthTopNode(stack, n){

2 var bufferArray = stack.getBuffer();

3 if(n<=0) throw 'error'

5 var bufferStack = new Stack(bufferArray);

7 while(--n!==0){

8 bufferStack.pop();

9 }

10 return bufferStack.pop();

11 }

13 var stack2 = new Stack();

14 stack2.push(1);

15 stack2.push(2);

16 stack2.push(3);

17 stackAccessNthTopNode(stack2,2); // 2

Time Complexity: O(n)

Search will be implemented in a similar way .

Search

Searching the stack data structure for a specific element is a critical operation. To do this, you must first create a buffer stack so that pop can be called on that buffer stack. This way, the original stack is not mutated, and nothing is removed from it.

1 function stackSearch(stack, element) {

2 var bufferArray = stack.getBuffer();

4 var bufferStack = new Stack(bufferArray); // copy into buffer

6 while(!bufferStack.isEmpty()){

7 if(bufferStack.pop()==element){

8 return true;

9 }

10 }

11 return false;

12 }

Time Complexity: O(n)

Queues

A queue is also a data structure, but you can remove only the first added element (see Figure 12-2). This is a principle known as first in, first out(FIFO). A queue is also great because of the constant time in its operations. Similar to a stack, it has limitations because only one item can be accessed at a time. Queues should be used over arrays when you need to work with data in the FIFO form where the algorithm only needs to access the first added element.

../images/465726_1_En_12_Chapter/465726_1_En_12_Fig2_HTML.jpg — Figure 12-2
Queue, FIFO

In JavaScript, arrays have methods that define the queue class: shift() and push() (as discussed in Chapter 5). Recall that the shift() method on an array in JavaScript removes and returns the first element of the array. Adding to a queue is commonly known as enqueuing , and removing from a queue is known as dequeuing . shift() can be used for the dequeue, and .push() can be used for the enqueue.

Here is some skeleton code to start. You can find the code on GitHub.²

1 function Queue(array){

2 this.array = [];

3 if(array) this.array = array;

4 }

6 Queue.prototype.getBuffer = function(){

7 return this.array.slice();

8 }

10 Queue.prototype.isEmpty = function(){

11 return this.array.length == 0;

12 }

14 //instance of the queue class

15 var queue1 = new Queue();

17 console.log(queue1); // { array: [] }

Peek

The peek function looks at the first item without popping it from the queue. In the stack implementation, the last element in the array was returned, but a queue returns the first element in the array because of FIFO.

1 Queue.prototype.peek = function(){

2 return this.array[0];

3 }

Insertion

As mentioned, insertion for a queue is known as enqueue. Since an array is used to hold the stack data, the push() method can be used to implement enqueue.

1 Queue.prototype.enqueue = function(value){

2 return this.array.push(value);

3 }

Time Complexity: O(1)

Deletion

As mentioned, deletion for a queue also is known as dequeue. Since an array is used to hold the stack data, the shift() method can be used to remove and return the first element in the queue.

1 Queue.prototype.dequeue = function() {

2 return this.array.shift();

3 };

5 var queue1 = new Queue();

7 queue1.enqueue(1);

8 queue1.enqueue(2);

9 queue1.enqueue(3);

11 console.log(queue1); // {array: [1,2,3]}

13 queue1.dequeue();

14 console.log(queue1); // {array: [2,3]}

16 queue1.dequeue();

17 console.log(queue1); // {array: [3]}

Time Complexity: O(n)

Because the shift() implementation removes the element at zero indexes and then shifts remaining indexes down consecutively, all other elements in the array need to have their indexes altered, and this takes O(n). With a linked-list implementation, as covered in Chapter 13, this can be reduced to O(1) .

Access

Unlike an array , items in a queue cannot be accessed via index. To access the nth last-added node, you need to call dequeuen number of times. A buffer is needed to prevent modification to the original queue.

1 function queueAccessNthTopNode(queue, n){

2 var bufferArray = queue.getBuffer();

3 if(n<=0) throw 'error'

5 var bufferQueue = new Queue(bufferArray);

7 while(--n!==0){

8 bufferQueue.dequeue();

9 }

10 return bufferQueue.dequeue();

11 }

Time Complexity: O(n)

Search

You might need to search a queue to check whether an element exists within a queue. Again, this involves creating a buffer queue first to avoid modifications to the original queue.

1 function queueSearch(queue, element){

2 var bufferArray = queue.getBuffer();

4 var bufferQueue = new Queue(bufferArray);

6 while(!bufferQueue.isEmpty()){

7 if(bufferQueue.dequeue()==element){

8 return true;

9 }

10 }

11 return false;

12 }

Time Complexity: O(n)

Summary

Both stacks and queues support peek, insertion, and deletion in O(1). The most important distinction between a stack and a queue is that a stack is LIFO and a queue is FIFO. Table 12-1 summarizes the time complexity.

Table 12-1

Queue and Stack Time Complexity Summary

	Access	Search	Peek	Insertion	Deletion
Queue	O(n)	O(n)	O(1)	O(1)	O(n)³
Stack	O(n)	O(n)	O(1)	O(1)	O(1)

Exercises

All the code for the exercises can be found on GitHub.⁴

DESIGN A STACK USING ONLY QUEUES AND THEN DESIGN A QUEUE USING ONLY STACKS

Stack Using Queues

A queue can be made with two stacks. A queue is a data structure that returns the first-added element with the dequeue() method. A stack is a data structure that returns the last-added element via pop. In other words, a queue removes elements in the reverse direction of a stack.

For example, examine a stack array with [1,2,3,4,5].

To reverse the order, all of the elements could be pushed onto a second stack and pop that second stack. So, the second stack array will look like this: [5,4,3,2,1].

When this is popped off, the last element is removed, which is 1. So, 1 is originally the first element. Hence, a queue was implemented using only two stacks.

1 function TwoStackQueue(){

2 this.inbox = new Stack();

3 this.outbox= new Stack();

4 }

6 TwoStackQueue.prototype.enqueue = function(val) {

7 this.inbox.push(val);

8 }

10 TwoStackQueue.prototype.dequeue = function() {

11 if(this.outbox.isEmpty()){

12 while(!this.inbox.isEmpty()){

13 this.outbox.push(this.inbox.pop());

14 }

15 }

16 return this.outbox.pop();

17 };

18 var queue = new TwoStackQueue();

19 queue.enqueue(1);

20 queue.enqueue(2);

21 queue.enqueue(3);

22 queue.dequeue(); // 1

23 queue.dequeue(); // 2

24 queue.dequeue(); // 3

Queue Using Stacks

A stack can be made with two queues. A stack is a data structure that returns the last element. To implement this using a queue, simply enqueue all the elements inside the main queue except for the last element. Then return that last element.

1 function QueueStack(){

2 this.inbox = new Queue(); // first stack

3 }

5 QueueStack.prototype.push = function(val) {

6 this.inbox.enqueue(val);

7 };

9 QueueStack.prototype.pop = function() {

10 var size = this.inbox.array.length-1;

11 var counter =0;

12 var bufferQueue = new Queue();

14 while(++counter<=size){

15 bufferQueue.enqueue(this.inbox.dequeue());

16 }

17 var popped = this.inbox.dequeue();

18 this.inbox = bufferQueue;

19 return popped

20 };

22 var stack = new QueueStack();

24 stack.push(1);

25 stack.push(2);

26 stack.push(3);

27 stack.push(4);

28 stack.push(5);

30 console.log(stack.pop()); // 5

31 console.log(stack.pop()); // 4

32 console.log(stack.pop()); // 3

33 console.log(stack.pop()); // 2

34 console.log(stack.pop()); // 1

DESIGN A CASHIER CLASS THAT TAKES IN A CUSTOMER OBJECT AND HANDLES FOOD ORDERING ON A FIRST-COME, FIRST-SERVED BASIS

Here are the requirements:

1.
The cashier requires a customer name and order item for the order.
2.
The customer who was served first is processed first.

Here are the required implementations:

addOrder(customer): Enqueues a customer object to be processed by deliverOrder()
deliverOrder(): Prints the name and order for the next customer to be processed

For this exercise, the Cashier class should enqueue customer class objects with a queue and dequeue them when finished.

1 function Customer(name, order){

2 this.name = name;

3 this.order = order;

4 }

6 function Cashier(){

7 this.customers = new Queue();

8 }

10 Cashier.prototype.addOrder = function (customer){

11 this.customers.enqueue(customer);

12 }

14 Cashier.prototype.deliverOrder = function(){

15 var finishedCustomer = this.customers.dequeue();

17 console.log(finishedCustomer.name+", your "+finishedCustomer.order+" is ready!");

18 }

20 var cashier = new Cashier();

21 var customer1 = new Customer('Jim',"Fries");

22 var customer2 = new Customer('Sammie',"Burger");

23 var customer3 = new Customer('Peter',"Drink");

25 cashier.addOrder(customer1);

26 cashier.addOrder(customer2);

27 cashier.addOrder(customer3);

29 cashier.deliverOrder(); // Jim, your Fries is ready!

30 cashier.deliverOrder(); // Sammie, your Burger is ready!

31 cashier.deliverOrder(); // Peter, your Drink is ready!

DESIGN A PARENTHESIS VALIDATION CHECKER USING A STACK

((())) is a valid parentheses set, while ((() and ))) are not. A stack can be used to check the validity of parentheses by storing the left parenthesis and using push and triggering pop when the right parenthesis is seen.

If there is anything left in the stack afterward, it is not a valid parentheses set. Also, it is not a valid parentheses set if more right parentheses are seen than left ones. Using these rules, use a stack to store the most recent parenthesis.

1 function isParenthesisValid(validationString){

2 var stack = new Stack();

3 for(var pos=0;pos<validationString.length;pos++){

4 var currentChar = validationString.charAt(pos);

5 if(currentChar=="("){

6 stack.push(currentChar);

7 }else if(currentChar==")"){

9 if(stack.isEmpty())

10 return false;

12 stack.pop();

13 }

14 }

15 return stack.isEmpty();

16 }

17 isParenthesisValid("((()"); // false;

18 isParenthesisValid("(((("); // false;

19 isParenthesisValid("()()"); // true;

Time Complexity: O(n)

This algorithm processes a string character by character. Hence, its time complexity is O(n), where n is the length of the string.

DESIGN A SORTABLE STACK

The idea is to have two stacks, one that is sorted and one that is nonsorted. When sorting, pop from the unsorted stack, and when any number smaller (if descending order) or bigger (if ascending order) on the sorted stack is on top, that sorted stack element should move back to unsorted because it is out of order. Run a loop until the stack is all sorted.

1 function sortableStack(size){

2 this.size = size;

4 this.mainStack = new Stack();

5 this.sortedStack = new Stack();

7 // let's initialize it with some random ints

8 for(var i=0;i<this.size;i++){

9 this.mainStack.push(Math.floor(Math.random()*11));

10 }

11 }

13 sortableStack.prototype.sortStackDescending = function(){

14 while(!this.mainStack.isEmpty()){

15 var temp = this.mainStack.pop();

16 while(!this.sortedStack.isEmpty() && this.sortedStack.peek()< temp){

17 this.mainStack.push(this.sortedStack.pop());

18 }

19 this.sortedStack.push(temp);

20 }

21 }

23 var ss = new sortableStack(10);

24 console.log(ss); // [ 8, 3, 4, 4, 1, 2, 0, 9, 7, 8 ]

25 ss.sortStackDescending();

26 console.log(ss.sortedStack); // [ 9, 8, 8, 7, 4, 4, 3, 2, 1, 0 ]

Time Complexity: O(n²)

This algorithm involves a reshuffling of the elements between two stacks, which in the worst possible case takes O(n²), where n is the number of elements to be sorted.

12. Stacks and Queues

Stacks

Peek

Insertion

Deletion

Access

Search

Queues

Peek

Insertion

Deletion

Access

Search

Summary

Exercises

DESIGN A STACK USING ONLY QUEUES AND THEN DESIGN A QUEUE USING ONLY STACKS

DESIGN A CASHIER CLASS THAT TAKES IN A CUSTOMER OBJECT AND HANDLES FOOD ORDERING ON A FIRST-COME, FIRST-SERVED BASIS

DESIGN A PARENTHESIS VALIDATION CHECKER USING A STACK

DESIGN A SORTABLE STACK