© Sammie Bae 2019
Sammie BaeJavaScript Data Structures and Algorithmshttps://doi.org/10.1007/978-1-4842-3988-9_8

8. Recursion

Sammie Bae1 
(1)
Hamilton, ON, Canada
 

This chapter introduces the concept of recursion and recursive algorithms. First, the definition of recursion and fundamental rules for recursive algorithms will be explored. In addition, methods of analyzing efficiencies of recursive functions will be covered in detail using mathematical notations. Finally, the chapter exercises will help solidify this information.

Introducing Recursion

In math, linguistics, and art, recursion refers to the occurrence of a thing defined in terms of itself. In computer science, a recursive function is a function that calls itself. Recursive functions are often elegant and solve complex problems through the “divide-and-conquer” method. Recursion is important because you will see it again and again in the implementation of various data structures. Figure 8-1 shows a visual illustration of recursion where the picture has smaller pictures of itself.
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig1_HTML.jpg
Figure 8-1

Recursion illustrated

Rules of Recursion

When recursive functions are implemented incorrectly, it causes fatal issues because the program will get stuck and not terminate. Infinite recursive calls result in stack overflow. Stack overflow is when the maximum number of call stacks of the program exceeds the limited amount of address space (memory).

For recursive functions to be implemented correctly, they must follow certain rules so that stack overflow is avoided. These rules are covered next.

Base Case

In recursion, there must be a base case (also referred to as terminating case). Because recursive methods call themselves, they will never stop unless this base case is reached. Stack overflow from recursion is most likely the result of not having a proper base case. In the base case, there are no recursive function calls.

Let’s examine the following function, which prints numbers counting down from n to 0 as an example:
 1   function countDownToZero(n) {
 2       // base case. Stop at 0
 3       if (n < 0) {
 4           return; // stop the function
 5       } else {
 6           console.log(n);
 7           countDownToZero(n - 1); // count down 1
 8       }
 9   }
10   countDownToZero(12);

The base case for this function is when n is smaller or equal to 0. This is because the desired outcome was to stop counting at 0. If a negative number is given as the input, it will not print that number because of the base case. In addition to a base case, this recursive function also exhibits the divide-and-conquer method.

Divide-and-Conquer Method

In computer science, the divide-and-conquermethod is when a problem is solved by solving all of its smaller components. With the countdown example, counting down from 2 can be solved by printing 2 and then counting down from 1. Here, counting down from 1 is the part solved by “dividing and conquering.” It is necessary to make the problem smaller to reach the base case. Otherwise, if the recursive call does not converge to a base case, a stack overflow occurs.

Let’s now examine a more complex recursive function known as the Fibonacci sequence .

Classic Example: Fibonacci Sequence

The Fibonacci sequence is a list of infinite numbers, each of which is the sum of the past two terms (starting with 1).

  • 1, 1, 2, 3, 5, 8, 13, 21 …

How might you program something to print the Nth term of the Fibonacci sequence?

Iterative Solution: Fibonacci Sequence

An iterative solution using a for loop may look something like this:
 1   function getNthFibo(n) {
 2       if ( n <= 1)  return n;
 3       var sum = 0,
 4           last = 1,
 5           lastlast = 0;
 6
 7       for (var i = 1; i < n; i++) {
 8           sum = lastlast + last;
 9           lastlast = last;
10           last = sum;
11       }
12       return sum;
13   }

A for loop can be used to keep track of the last two elements of the Fibonacci sequence, and its sum yields the Fibonacci number.

Now, how might this be done recursively?

Recursive Solution: Fibonacci

The following shows the recursive solution:
1   function getNthFibo(n) {
2       if (n <= 1) {
3           return n;
4       } else {
5           return getNthFibo(n - 1) + getNthFibo(n - 2);
6       }
7   }

Base case: The base case for the Fibonacci sequence is that the first element is 1.

Divide and conquer: By definition of the Fibonacci sequence, the Nth Fibonacci number is the sum of the (n-1)th and (n-2)th Fibonacci numbers. However, this implementation has a time complexity of O(2n), which is discussed in detail later in this chapter. We will explore a more efficient recursive algorithm for the Fibonacci sequence using tail recursion in the next section.

Fibonacci Sequence: Tail Recursion

A tail recursivefunction is a recursive function in which the recursive call is the last executed thing in the function. First let’s look at the iterative solution:
 1   function getNthFibo(n) {
 2       if ( n <= 1)  return n;
 3       var sum = 0,
 4           last = 1,
 5          lastlast = 0;
 6
 7       for (var i = 1; i < n; i++) {
 8           sum = lastlast + last;
 9           lastlast = last;
10           last = sum;
11       }
12       return sum;
13   }
At each iteration, the following update happens: (lastlast, last) = (last, lastlast+last). With this structure, the following recursive function can be formed:
1   function getNthFiboBetter(n, lastlast, last) {
2       if (n == 0) {
3           return lastlast;
4       }
5       if (n == 1) {
6           return last;
7       }
8       return getNthFiboBetter(n-1, last, lastlast + last);
9   }

Time Complexity: O(n)

At most, this function executes n times because it’s decremented by n-1 each time with only single recursive call.

Space Complexity: O(n)

The space complexity is also O(n) because of the stack call used for this function . This will be further explained in the “Recursive Call Stack Memory” section later in this chapter.

To conclude the rules of recursion, let’s examine another example, which is more complex.

Pascal’s Triangle

In this example, a function for calculating a term of Pascal’s triangle will be explored. Pascal’s triangle is a triangle whose element value is the summation of its top two (left and right) values, as shown in Figure 8-2.
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig2_HTML.jpg
Figure 8-2

Pascal’s triangle

Base case: The base case for Pascal’s triangle is that the top element (row=1, col=1) is 1. Everything else is derived from this fact alone. Hence, when the column is 1, return 1, and when the row is 0, return 0.

Divide and conquer: By the mathematical definition of Pascal’s triangle, a term of Pascal’s triangle is defined as the sum of its upper terms . Therefore, this can be expressed as the following: pascalTriangle(row - 1, col) + pascalTriangle(row - 1, col - 1).
 1   function pascalTriangle(row, col) {
 2       if (col == 0) {
 3           return 1;
 4       } else if (row == 0) {
 5           return 0;
 6       } else {
 7           return pascalTriangle(row - 1, col) + pascalTriangle(row - 1, col - 1);
 8       }
 9   }
10   pascalTriangle(5, 2); // 10

This is the beauty of recursion! Look next at how short and elegant this code is.

Big-O for Recursion

In Chapter 1, Big-O analysis of recursive algorithms was not covered. This was because recursive algorithms are much harder to analyze. To perform Big-O analysis for recursive algorithms, its recurrence relations must be analyzed.

Recurrence Relations

In algorithms implemented iteratively, Big-O analysis is much simpler because loops clearly define when to stop and how much to increment in each iteration. For analyzing recursive algorithms, recurrence relations are used. Recurrence relations consist of two-part analysis: Big-O for base case and Big-O for recursive case.

Let’s revisit the naive Fibonacci sequence example:
function getNthFibo(n) {
    if (n <= 1) {
        return n;
    } else {
        return getNthFibo(n - 1) + getNthFibo(n - 2);
    }
}
getNthFibo(3);
The base case has a time complexity of O(1). The recursive case calls itself twice. Let’s represent this as T (n) = T (n − 1) + T (n − 2) + O(1).

  • Base case:T (n) = O(1)

  • Recursive case:T (n) = T (n − 1) + T (n − 2) + O(1)

Now, this relation means that since T (n) = T (n − 1) + T (n − 2) + O(1), then (by replacing n with n−1), T (n − 1) = T (n − 2) + T (n − 3) + O(1). Replacing n−1 with n−2 yields T (n − 2) = T (n − 3) + T (n − 4) + O(1). Therefore, you can see that for every call, there are two more calls for each call. In other words, this has a time complexity of O(2n).

It helps to visualize it as such:
F(6)                * <-- only once
F(5)                *
F(4)                **
F(3)               ****
F(2)             ********
F(1)         ****************         <-- 16
F(0) ******************************** <-- 32

Calculating Big-O this way is difficult and prone to error. Thankfully, there is a concept known as the master theorem to help. The master theorem helps programmers easily analyze the time and space complexities of recursive algorithms.

Master Theorem

The master theorem states the following:

  • Given a recurrence relation of the form T (n) = aT (n/b) + O(nc) where a >= 1 and b >=1, there are three cases.

a is the coefficient that is multiplied by the recursive call. b is the “logarithmic” term, which is the term that divides the n during the recursive call. Finally, c is the polynomial term on the nonrecursive component of the equation.

The first case is when the polynomial term on the nonrecursive component O(nc) is smaller than logb(a).

  • Case 1:c < logb(a) then T (n) = O(n(logb(a))).

  • For example, T (n) = 8T (n/2) + 1000n2

  • Identify a, b, c:a = 8, b = 2, c = 2

  • Evaluate:log2(8) = 3. c < 3 is satisfied.

  • Result:T (n) = O(n3)

The second case is when c is equal to logb(a).

  • Case 2:c = logb(a) then T (n) = O(nclog(n)).

  • For example, T (n) = 2T (n/2) + 10n.

  • Identify a, b, c:a = 2, b = 2, c = 1

  • Evaluate:log2(2) = 1. c = 1 is satisfied.

  • Result:T (n) = O(nclog(n)) = T (n) = O(n1log(n)) = T (n) = O(nlog(n))

The third and final case is when c is greater than logb(a).

  • Case 3:c > logb(a) then T (n) = O(f (n)).

  • For example, T (n) = 2T (n/2) + n2.

  • Identify a,b,c: a = 2, b = 2, c = 2

  • Evaluate:log2(2) = 1. c > 1 is satisfied.

  • Result:T (n) = f (n) = O(n2)

This section covered a lot about analyzing the time complexity of recursive algorithms. Space complexity analysis is just as important. The memory used by recursive function calls should also be noted and analyzed for space complexity analysis.

Recursive Call Stack Memory

When a recursive function calls itself, that takes up memory, and this is really important in Big-O space complexity analysis.

For example, this simple function for printing from n to 1 recursively takes O(n) in space:
1   function printNRecursive(n) {
2       console.log(n);
3       if (n > 1){
4           printNRecursive(n-1);
5       }
6   }
7   printNRecursive(10);
A developer can run this on a browser or any JavaScript engine and will see the result shown in Figure 8-3 in the call stack.
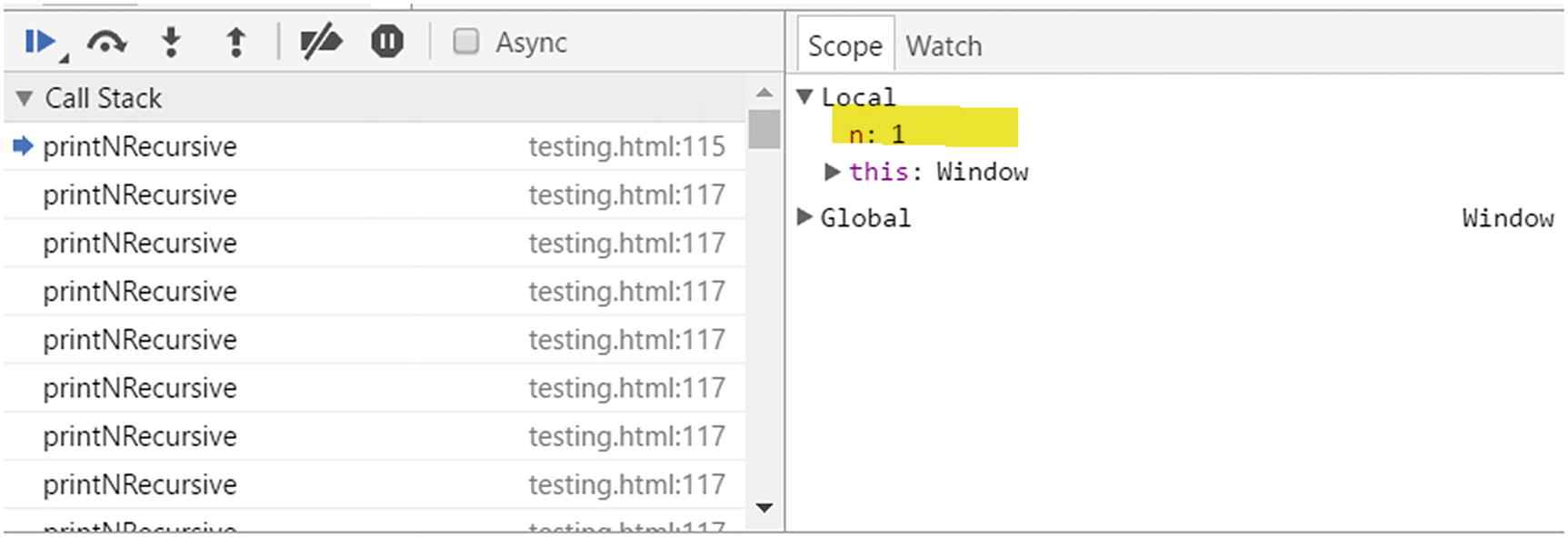
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig3_HTML.jpg
Figure 8-3

Call stack in Developer Tools

As shown in Figures 8-3 and 8-4, each recursive call must be stored in memory until the base case is resolved. Recursive algorithms take extra memory because of the call stack.
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig4_HTML.jpg
Figure 8-4

Call stack memory

Recursive functions have an additional space complexity cost that comes from the recursive calls that need to be stored in the operating system’s memory stack. The stack is accumulated until the base case is solved. In fact, this is often why an iterative solution may be preferred over the recursive solution. In the worst case, if the base case is implemented incorrectly, the recursive function will cause the program to crash because of a stack overflow error that occurs when there are more than the allowed number of elements in the memory stack.

Summary

Recursion is a powerful tool to implement complex algorithms. Recall that all recursive functions consist of two parts: the base case and the divide-and-conquer method (solving subproblems).

Analyzing the Big-O of these recursive algorithms can be done empirically (not recommended) or by using the master theorem. Recall that the master theorem needs the recurrence relation in the following form: T (n) = aT (n/b) +O(nc). When using the master theorem, identify a, b, and c to determine which of the three cases of the master theorem it belongs to.

Finally, when implementing and analyzing recursive algorithms, consider the additional memory caused by the call stack of the recursive function calls. Each recursive call requires a place in the call stack at runtime; when the call stack accumulate n calls, then the space complexity of the function is O(n).

Exercises

These exercises on recursion cover varying problems to help solidify the knowledge gained from this chapter. The focus should be to identify the correct base case first before solving the entire problem. You will find all the code for the exercises on GitHub.1

CONVERT DECIMAL (BASE 10) TO BINARY NUMBER

To do this, keep dividing the number by 2 and each time calculate the modulus (remainder) and division.

Base case: The base case for this problem is when the n is less than 2. When it is less than 2, it can be only 0 or 1.
 1   function base10ToString(n) {
 2       var binaryString = "";
 3
 4       function base10ToStringHelper(n) {
 5           if (n < 2) {
 6               binaryString += n;
 7               return;
 8           } else {
 9               base10ToStringHelper(Math.floor(n / 2));
10               base10ToStringHelper(n % 2);
11           }
12       }
13       base10ToStringHelper(n);
14
15       return binaryString;
16   }
17
18   console.log(base10ToString(232)); // 11101000

Time Complexity: O(log2(n))

Time complexity is logarithmic because the recursive call divides the n by 2, which makes the algorithm fast. For example, for n = 8, it executes only three times. For n=1024, it executes 10 times.

Space Complexity: O(log2(n))

PRINT ALL PERMUTATIONS OF AN ARRAY

This is a classical recursion problem and one that is pretty hard to solve. The premise of the problem is to swap elements of the array in every possible position.

First, let’s draw the recursion tree for this problem (see Figure 8-5).
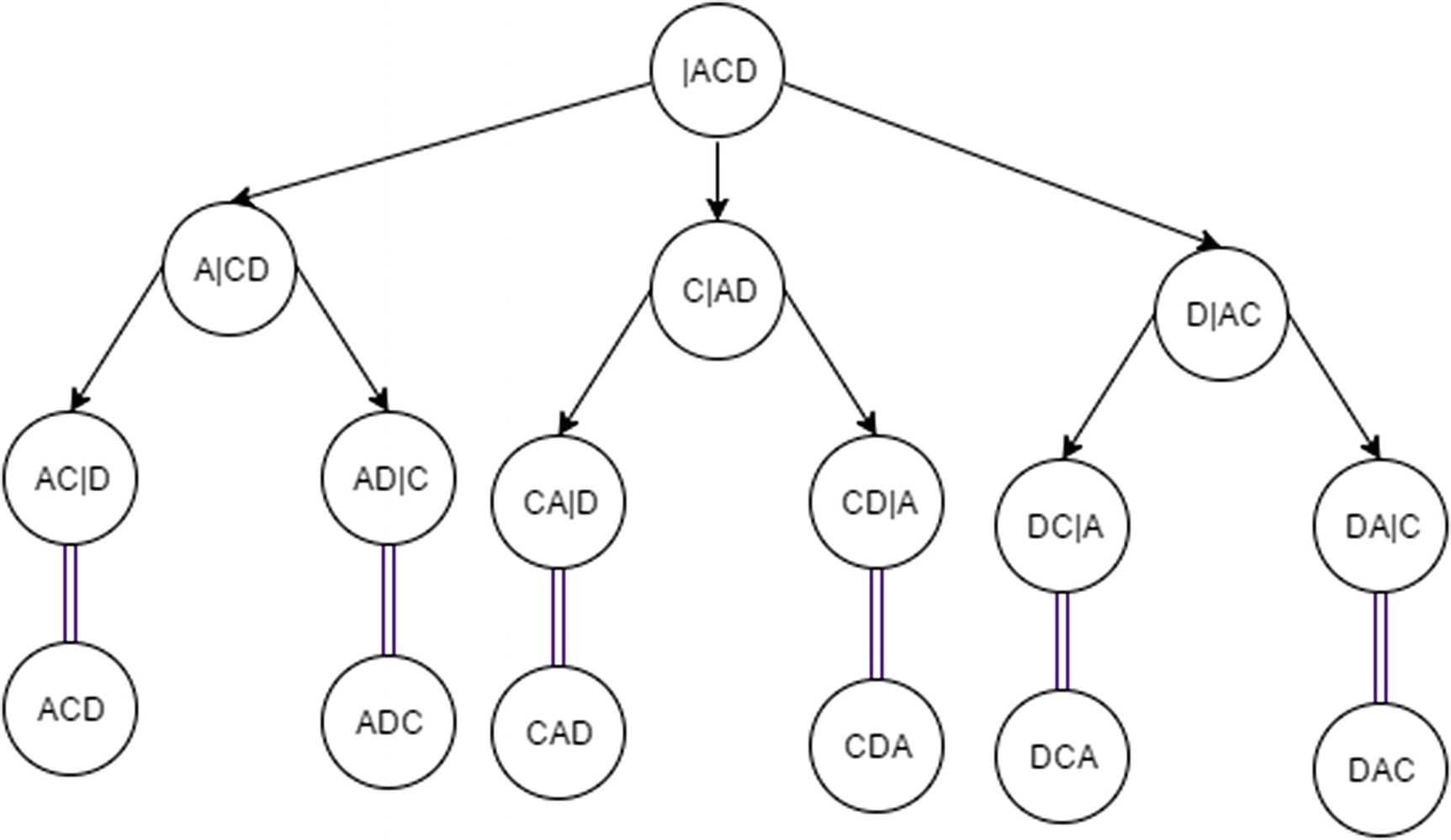
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig5_HTML.jpg
Figure 8-5

Permutation of array recursion tree

Base case: beginIndex is equal to endIndex.

When this occurs, the function should print the current permutation.

Permutations: We will need a function to swap elements:
 1   function swap(strArr, index1, index2) {
 2       var temp = strArr[index1];
 3       strArr[index1] = strArr[index2];
 4       strArr[index2] = temp;
 5   }
 1   function permute(strArr, begin, end) {
 2       if (begin == end) {
 3           console.log(strArr);
 4       } else {
 5           for (var i = begin; i < end + 1; i++) {
 6               swap(strArr, begin, i);
 7               permute(strArr, begin + 1, end);
 8               swap(strArr, begin, i);
 9           }
10       }
11   }
12
13   function permuteArray(strArr) {
14       permute(strArr, 0, strArr.length - 1);
15   }
16
17   permuteArray(["A", "C", "D"]);
18   // ["A", "C", "D"]
19   // ["A", "D", "C"]
20   // ["C", "A", "D"]
21   // ["C", "D", "A"]
22   // ["D", "C", "A"]
23   // ["D", "A", "C"]

Time Complexity: O(n!)

Space Complexity: O(n!)

There are n! permutations , and it creates n! call stacks.

FLATTEN AN OBJECT

Given a JavaScript array like this:
 1   var dictionary = {
 2       'Key1': '1',
 3       'Key2': {
 4           'a' : '2',
 5           'b' : '3',
 6           'c' : {
 7               'd' : '3',
 8               'e' : '1'
 9           }
10       }
11   }
flatten it into {'Key1': '1', 'Key2.a': '2','Key2.b' : '3', 'Key2.c.d' : '3', 'Key2.c.e' : '1'}, where the child is denoted by . between the parent and child (see Figure 8-6).
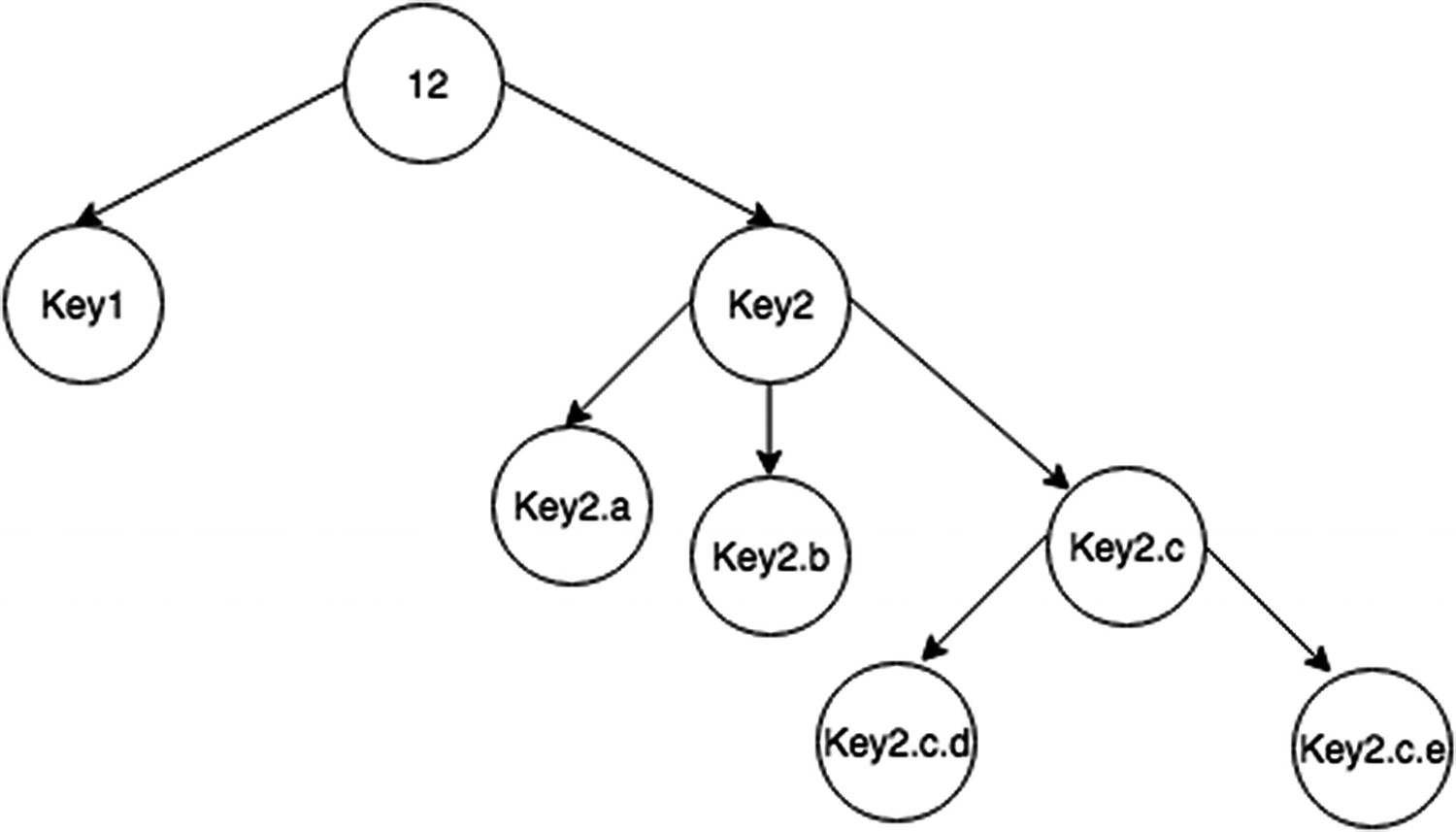
../images/465726_1_En_8_Chapter/465726_1_En_8_Fig6_HTML.jpg
Figure 8-6

Flatten a dictionary recursion tree

To do this, iterate over any property and recursively check it for child properties, passing in the concatenated string name.

Base case: The base case for this problem is when input is not an object.
 1   function flattenDictionary(dictionary) {
 2       var flattenedDictionary = {};
 3
 4       function flattenDitionaryHelper(dictionary, propName) {
 5           if (typeof dictionary != 'object') {
 6               flattenedDictionary[propName] = dictionary;
 7               return;
 8           }
 9           for (var prop in dictionary) {
10               if (propName == "){
11                   flattenDitionaryHelper(dictionary[prop], propName+prop);
12               } else {
13                   flattenDitionaryHelper(dictionary[prop], propName+'.'+prop);
14               }
15           }
16       }
17
18       flattenDitionaryHelper(dictionary, ");
19       return flattenedDictionary;
20   }

Time Complexity: O(n)

Space Complexity: O(n)

Each property is visited only once and stored once per nproperties.

WRITE A PROGRAM THAT RECURSIVELY DETERMINES IF A STRING IS A PALINDROME

A palindrome is a word spelled the same backward and forward such as deified, racecar, testset, and aibohphobia (the fear of palindromes).
 1   function isPalindromeRecursive(word) {
 2       return isPalindromeHelper(word, 0, word.length-1);
 3   }
 4
 5   function isPalindromeHelper(word, beginPos, endPos) {
 6       if (beginPos >= endPos) {
 7           return true;
 8       }
 9       if (word.charAt(beginPos) != word.charAt(endPos)) {
10           return false;
11       } else {
12           return isPalindromeHelper(word, beginPos + 1, endPos - 1);
13       }
14   }
15
16   isPalindromeRecursive('hi'); // false
17   isPalindromeRecursive('iii'); // true
18   isPalindromeRecursive('ii'); // true
19   isPalindromeRecursive('aibohphobia'); // true
20   isPalindromeRecursive('racecar'); // true

The idea behind this one is that with two indexes (one in front and one in back) you check at each step until the front and back meet.

Time Complexity: O(n)

Space Complexity: O(n)

Space complexity here is still O(n) because of the recursive call stack. Remember that the call stack remains part of memory even if it is not declaring a variable or being stored inside a data structure.