Polymorphism is the ability to associate different specific behaviors with a single generic notation.1 Polymorphism is also a cornerstone of the object-oriented programming paradigm, which in C++ is supported mainly through class inheritance and virtual functions. Because these mechanisms are (at least in part) handled at run time, we talk about dynamic polymorphism. This is usually what is thought of when talking about plain polymorphism in C++. However, templates also allow us to associate different specific behaviors with a single generic notation, but this association is generally handled at compile time, which we refer to as static polymorphism. In this chapter, we review the two forms of polymorphism and discuss which form is appropriate in which situations.
Note that Chapter 22 will discuss some ways to deal with polymorphism after introducing and discussing some design issues in between.
Historically, C++ started with supporting polymorphism only through the use of inheritance combined with virtual functions.2 The art of polymorphic design in this context consists of identifying a common set of capabilities among related object types and declaring them as virtual function interfaces in a common base class.
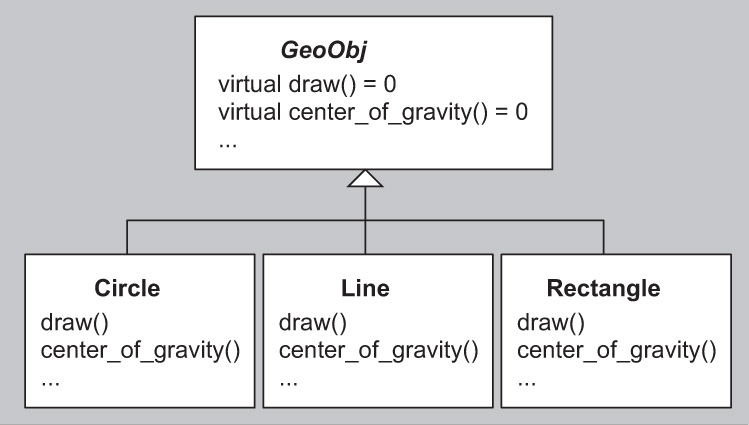
The poster child for this design approach is an application that manages geometric shapes and allows them to be rendered in some way (e.g., on a screen). In such an application, we might identify an abstract base class (ABC) GeoObj, which declares the common operations and properties applicable to geometric objects. Each concrete class for specific geometric objects then derives from GeoObj (see Figure 18.1):
Figure 18.1. Polymorphism implemented via inheritance

poly/dynahier.hpp
#include "coord.hpp"
// common abstract base class GeoObj for geometric objects
class GeoObj {
public:
// draw geometric object:
virtual void draw() const = 0;
// return center of gravity of geometric object:
virtual Coord center_of_gravity() const = 0;
…
virtual ~GeoObj() = default;
};
// concrete geometric object class Circle
// - derived from GeoObj
class Circle : public GeoObj {
public:
virtual void draw() const override;
virtual Coord center_of_gravity() const override;
…
};
// concrete geometric object class Line
// - derived from GeoObj
class Line : public GeoObj {
public:
virtual void draw() const override;
virtual Coord center_of_gravity() const override;
…
};
…
After creating concrete objects, client code can manipulate these objects through references or pointers to the common base class by using the virtual function dispatch mechanism. Calling a virtual member function through a pointer or reference to a base class subobject results in an invocation of the appropriate member of the specific (“most-derived”) concrete object being referred to.
In our example, the concrete code can be sketched as follows:

poly/dynapoly.cpp
#include "dynahier.hpp"
#include <vector>
// draw any GeoObj
void myDraw (GeoObj const& obj)
{
obj.draw(); // call draw() according to type of object
}
// compute distance of center of gravity between two GeoObjs
Coord distance (GeoObj const& x1, GeoObj const& x2)
{
Coord c = x1.center_of_gravity() - x2.center_of_gravity();
return c.abs(); // return coordinates as absolute values
}
// draw heterogeneous collection of GeoObjs
void drawElems (std::vector<GeoObj*> const& elems)
{
for (std::size_type i=0; i<elems.size(); ++i) {
elems[i]->draw(); // call draw() according to type of element
}
}
int main()
{
Line l;
Circle c, c1, c2;
myDraw(l); // myDraw(GeoObj&) => Line::draw()
myDraw(c); // myDraw(GeoObj&) => Circle::draw()
distance(c1,c2); // distance(GeoObj&,GeoObj&)
distance(l,c); // distance(GeoObj&,GeoObj&)
std::vector<GeoObj*> coll; // heterogeneous collection
coll.push_back(&l); // insert line
coll.push_back(&c); // insert circle
drawElems(coll); // draw different kinds of GeoObjs
}
The key polymorphic interface elements are the functions draw() and center_of_gravity(). Both are virtual member functions. Our example demonstrates their use in the functions mydraw(), distance(), and drawElems(). The latter functions are expressed using the common base type GeoObj. A consequence of this approach is that it is generally unknown at compile time which version of draw() or center_of_gravity() must be called. However, at run time, the complete dynamic type of the objects for which the virtual functions are invoked is accessed to dispatch the function calls.3 Hence, depending on the actual type of a geometric object, the appropriate operation is performed: If mydraw() is called for a Line object, the expression obj.draw() calls Line::draw(), whereas for a Circle object, the function Circle::draw() is called. Similarly, with distance(), the member functions center_of_gravity() appropriate for the argument objects are called.
Perhaps the most compelling feature of this dynamic polymorphism is the ability to handle heterogeneous collections of objects. drawElems() illustrates this concept: The simple expression
elems[i]->draw()
results in invocations of different member functions, depending on the dynamic type of the element being iterated over.
Templates can also be used to implement polymorphism. However, they don’t rely on the factoring of common behavior in base classes. Instead, the commonality is implicit in that the different “shapes” of an application must support operations using common syntax (i.e., the relevant functions must have the same names). Concrete classes are defined independently from each other (see Figure 18.2). The polymorphic power is then enabled when templates are instantiated with the concrete classes.

Figure 18.2. Polymorphism implemented via templates
For example, the function myDraw() in the previous section:
void myDraw (GeoObj const& obj) // GeoObj is abstract base class
{
obj.draw();
}
could conceivably be rewritten as
template<typename GeoObj>
void myDraw (GeoObj const& obj) // GeoObj is template parameter
{
obj.draw();
}
Comparing the two implementations of myDraw(), we may conclude that the main difference is the specification of GeoObj as a template parameter instead of a common base class. There are, however, more fundamental differences under the hood. For example, using dynamic polymorphism, we had only one myDraw() function at run time, whereas with the template we have distinct functions, such as myDraw<Line>() and myDraw<Circle>().
We may attempt to recode the complete example of the previous section using static polymorphism. First, instead of a hierarchy of geometric classes, we have several individual geometric classes:
poly/statichier.hpp
#include "coord.hpp"
// concrete geometric object class Circle
// - not derived from any class
class Circle {
public:
void draw() const;
Coord center_of_gravity() const;
…
};
// concrete geometric object class Line
// - not derived from any class
class Line {
public:
void draw() const;
Coord center_of_gravity() const;
…
};
…
Now, the application of these classes looks as follows:

poly/staticpoly.cpp
#include "statichier.hpp"
#include <vector>
// draw any GeoObj
template<typename GeoObj>
void myDraw (GeoObj const& obj)
{
obj.draw(); // call draw() according to type of object
}
// compute distance of center of gravity between two GeoObjs
template<typename GeoObj1, typename GeoObj2>
Coord distance (GeoObj1 const& x1, GeoObj2 const& x2)
{
Coord c = x1.center_of_gravity() - x2.center_of_gravity();
return c.abs(); // return coordinates as absolute values
}
// draw homogeneous collection of GeoObjs
template<typename GeoObj>
void drawElems (std::vector<GeoObj> const& elems)
{
for (unsigned i=0; i<elems.size(); ++i) {
elems[i].draw(); // call draw() according to type of element
}
}
int main()
{
Line l;
Circle c, c1, c2;
myDraw(l); // myDraw<Line>(GeoObj&) => Line::draw()
myDraw(c); // myDraw<Circle>(GeoObj&) => Circle::draw()
distance(c1,c2); //distance<Circle,Circle>(GeoObj1&,GeoObj2&)
distance(l,c); // distance<Line,Circle>(GeoObj1&,GeoObj2&)
// std::vector<GeoObj*> coll; //ERROR: no heterogeneous collection possible
std::vector<Line> coll; // OK: homogeneous collection possible
coll.push_back(l); // insert line
drawElems(coll); // draw all lines
}
As with myDraw(), GeoObj can no longer be used as a concrete parameter type for distance(). Instead, we provide for two template parameters, GeoObj1 and GeoObj2, which enables different combinations of geometric object types to be accepted for the distance computation:
distance(l,c); // distance<Line,Circle>(GeoObj1&,GeoObj2&)
However, heterogeneous collections can no longer be handled transparently. This is where the static part of static polymorphism imposes its constraint: All types must be determined at compile time. Instead, we can easily introduce different collections for different geometric object types. There is no longer a requirement that the collection be limited to pointers, which can have significant advantages in terms of performance and type safety.
Let’s categorize and compare both forms of polymorphism.
Dynamic and static polymorphism provide support for different C++ programming idioms:4
• Polymorphism implemented via inheritance is bounded and dynamic:
– Bounded means that the interfaces of the types participating in the polymorphic behavior are predetermined by the design of the common base class (other terms for this concept are invasive and intrusive).
– Dynamic means that the binding of the interfaces is done at run time (dynamically).
• Polymorphism implemented via templates is unbounded and static:
– Unbounded means that the interfaces of the types participating in the polymorphic behavior are not predetermined (other terms for this concept are noninvasive and nonintrusive).
– Static means that the binding of the interfaces is done at compile time (statically).
So, strictly speaking, in C++ parlance, dynamic polymorphism and static polymorphism are shortcuts for bounded dynamic polymorphism and unbounded static polymorphism. In other languages, other combinations exist (e.g., Smalltalk provides unbounded dynamic polymorphism). However, in the context of C++, the more concise terms dynamic polymorphism and static polymorphism do not cause confusion.
Dynamic polymorphism in C++ exhibits the following strengths:
• Heterogeneous collections are handled elegantly.
• The executable code size is potentially smaller (because only one polymorphic function is needed, whereas distinct template instances must be generated to handle different types).
• Code can be entirely compiled; hence no implementation source must be published (distributing template libraries usually requires distribution of the source code of the template implementations).
In contrast, the following can be said about static polymorphism in C++:
• Collections of built-in types are easily implemented. More generally, the interface commonality need not be expressed through a common base class.
• Generated code is potentially faster (because no indirection through pointers is needed a priori and nonvirtual functions can be inlined much more often).
• Concrete types that provide only partial interfaces can still be used if only that part ends up being exercised by the application.
Static polymorphism is often regarded as more type safe than dynamic polymorphism because all the bindings are checked at compile time. For example, there is little danger of inserting an object of the wrong type in a container instantiated from a template. However, in a container expecting pointers to a common base class, there is a possibility that these pointers unintentionally end up pointing to complete objects of different types.
In practice, template instantiations can also cause some grief when different semantic assumptions hide behind identical-looking interfaces. For example, surprises can occur when a template that assumes an associative operator + is instantiated for a type that is not associative with respect to that operator. In practice, this kind of semantic mismatch occurs less often with inheritance-based hierarchies, presumably because the interface specification is more explicitly specified.
Of course, you could combine both forms of polymorphism. For example, you could derive different kinds of geometric objects from a common base class to be able to handle heterogeneous collections of geometric objects. However, you can still use templates to write code for a certain kind of geometric object.
The combination of inheritance and templates is further described in Chapter 21. We will see (among other things) how the virtuality of a member function can be parameterized and how an additional amount of flexibility is afforded to static polymorphism using the inheritance-based curiously recurring template pattern (or CRTP).
One argument against static polymorphism with templates is that the binding of the interfaces is done by instantiating the corresponding templates. This means that there is no common interface (class) to program against. Instead, any usage of a template simply works if all instantiated code is valid. If it is not, this might lead to hard-to-understand error messages or even cause valid but unintended behavior.
For this reason, C++ language designers have been working on the ability to explicitly provide (and check) interfaces for template parameters. Such an interface is usually called a concept in C++. It denotes a set of constraints that template arguments have to fulfill to successfully instantiate a template.
Despite many years of work in this area, concepts are still not part of standard C++ as of C++17. Some compilers provide experimental support for such a feature,5 however, and concepts will likely be part of the next standard after C++17.
Concepts can be understood as a kind of “interface” for static polymorphism. In our example, this might look as follows:
poly/conceptsreq.hpp
#include "coord.hpp"
template<typename T>
concept GeoObj = requires(T x) {
{ x.draw() } -> void;
{ x.center_of_gravity() } -> Coord;
…
};
Here, we use the keyword concept to define a concept GeoObj, which constrains a type to have callable members draw() and center_of_gravity() with appropriate result types.
Now, we can rewrite some of our example templates to include a requires clause that constrains the template parameters with the GeoObj concept:

poly/conceptspoly.hpp
#include "conceptsreq.hpp"
#include <vector>
// draw any GeoObj
template<typename T>
requires GeoObj<T>
void myDraw (T const& obj)
{
obj.draw(); // call draw() according to type of object
}
// compute distance of center of gravity between two GeoObjs
template<typename T1, typename T2>
requires GeoObj<T1> && GeoObj<T2>
Coord distance (T1 const& x1, T2 const& x2)
{
Coord c = x1.center_of_gravity() - x2.center_of_gravity();
return c.abs(); // return coordinates as absolute values
}
// draw homogeneous collection of GeoObjs
template<typename T>
requires GeoObj<T>
void drawElems (std::vector<T> const& elems)
{
for (std::size_type i=0; i<elems.size(); ++i) {
elems[i].draw(); // call draw() according to type of element
}
}
This approach is still noninvasive with respect to the types that can participate in the (static) polymorphic behavior:
// concrete geometric object class Circle
// - not derived from any class or implementing any interface
class Circle {
public:
void draw() const;
Coord center_of_gravity() const;
…
};
That is, such types are still defined without any specific base class or requirements clause and can still be fundamental data types or types from independent frameworks.
Appendix E includes a more detailed discussion of concepts for C++, as they are expected for the next C++ standard.
The availability of static polymorphism in C++ leads to new ways of implementing classic design patterns. Take, for example, the Bridge pattern, which plays a major role in many C++ programs. One goal of using the Bridge pattern is to switch between different implementations of an interface.

Figure 18.3. Bridge pattern implemented using inheritance
According to [DesignPatternsGoF], this is usually done using an interface class that embeds a pointer to refer to the actual implementation and delegating all calls through this pointer (see Figure 18.3).
However, if the type of the implementation is known at compile time, we exploit the power of templates instead (see Figure 18.4). This leads to more type safety (in part, by avoiding pointer conversions) and better performance.

Figure 18.4. Bridge pattern implemented using templates
Static polymorphism leads to the concept of generic programming. However, there is no single agreed-on definition of generic programming (just as there is no single agreed-on definition of object-oriented programming). According to [CzarneckiEiseneckerGenProg], definitions go from programming with generic parameters to finding the most abstract representation of efficient algorithms. The book summarizes:
Generic programming is a subdiscipline of computer science that deals with finding abstract representations of efficient algorithms, data structures, and other software concepts, and with their systematic organization.… Generic programming focuses on representing families of domain concepts. (pp. 169-170)
In the context of C++, generic programming is sometimes defined as programming with templates (whereas object-oriented programming is thought of as programming with virtual functions). In this sense, just about any use of C++ templates could be thought of as an instance of generic programming. However, practitioners often think of generic programming as having an additional essential ingredient: Templates have to be designed in a framework for the purpose of enabling a multitude of useful combinations.
By far the most significant contribution in this area is the Standard Template Library (STL), which later was adapted and incorporated into the C++ standard library). The STL is a framework that provides a number of useful operations, called algorithms, for a number of linear data structures for collections of objects, called containers. Both algorithms and containers are templates. However, the key is that the algorithms are not member functions of the containers. Instead, the algorithms are written in a generic way so that they can be used by any container (and linear collection of elements). To do this, the designers of STL identified an abstract concept of iterators that can be provided for any kind of linear collection. Essentially, the collection-specific aspects of container operations have been factored out into the iterators’ functionality.
As a consequence, we can implement an operation such as computing the maximum value in a sequence without knowing the details of how values are stored in that sequence:
template<typename Iterator>
Iterator max_element (Iterator beg, //refers to start of collection
Iterator end) //refers to end of collection
{
// use only certain Iterator operations to traverse all elements
// of the collection to find the element with the maximum value
// and return its position as Iterator
…
}
Instead of providing all useful operations such as max_element() by every linear container, the container has to provide only an iterator type to traverse the sequence of values it contains and member functions to create such iterators:
namespace std {
template<typename T, …>
class vector {
public:
using const_iterator = …; // implementation-specific iterator
… // type for constant vectors
const_iterator begin() const; // iterator for start of collection
const_iterator end() const; // iterator for end of collection
…
};
template<typename T, …>
class list {
public:
using const_iterator = …; // implementation-specific iterator
… // type for constant lists
const_iterator begin() const; // iterator for start of collection
const_iterator end() const; // iterator for end of collection
…
};
}
Now, we can find the maximum of any collection by calling the generic max_element() operation with the beginning and end of the collection as arguments (special handling of empty collections is omitted):

poly/printmax.cpp
#include <vector>
#include <list>
#include <algorithm>
#include <iostream>
#include "MyClass.hpp"
template<typename T>
void printMax (T const& coll)
{
// compute position of maximum value
auto pos = std::max_element(coll.begin(),coll.end());
// print value of maximum element of coll (if any):
if (pos != coll.end()) {
std::cout << *pos << ’\n’;
}
else {
std::cout << "empty" << ’\n’;
}
}
int main()
{
std::vector<MyClass> c1;
std::list<MyClass> c2;
…
printMax(c1);
printMax(c2);
}
By parameterizing its operations in terms of these iterators, the STL avoids an explosion in the number of operation definitions. Instead of implementing each operation for every container, we implement the algorithm once so that it can be used for every container. The generic glue is the iterators, which are provided by the containers and used by the algorithms. This works because iterators have a certain interface that is provided by the containers and used by the algorithms. This interface is usually called a concept, which denotes a set of constraints that a template has to fulfill to fit into this framework. In addition, this concept is open for additional operations and data structures.
You’ll recall that we described a concepts language feature earlier in Section 18.4 on page 377(and in more detail in Appendix E), and indeed, the language feature maps exactly onto the notion here. In fact, the term concept in this context was first introduced by the designers of the STL to formalize their work. Soon thereafter, work commenced to try to make these notions explicit in our templates.
The forthcoming language feature will help us to specify and double check requirements on iterators (since there are different iterator categories, such as forward and bidirectional iterators, multiple corresponding concepts would be involved; see Section E.3.1 on page 744). In today’s C++, however, the concepts are mostly implicit in the specifications of our generic libraries (and the standard C++ library in particular). Some features and techniques (e.g., static_assert and SFINAE) do permit some amount of automated checking, fortunately.
In principle, functionality such as an STL-like approach could be implemented with dynamic polymorphism. In practice, however, it would be of limited use because the iterator concept is too lightweight compared with the virtual function call mechanism. Adding an interface layer based on virtual functions would most likely slow down our operations by an order of magnitude (or more).
Generic programming is practical precisely because it relies on static polymorphism, which resolves interfaces at compile time. On the other hand, the requirement that the interfaces be resolved at compile time also calls for new design principles that differ in many ways from object-oriented design principles. Many of the most important of these generic design principles are described in the remainder of this book. Additionally, Appendix E delves deeper into generic programming as a development paradigm by describing direct language support for the notion of concepts.
Container types were a primary motivation for the introduction of templates into the C++ programming language. Prior to templates, polymorphic hierarchies were a popular approach to containers. A popular example was the National Institutes of Health Class Library (NIHCL), which to a large extent translated the container class hierarchy of Smalltalk (see Figure 18.5).

Figure 18.5. Class hierarchy of the NIHCL
Much like the C++ standard library, the NIHCL supported a rich variety of containers as well as iterators. However, the implementation followed the Smalltalk style of dynamic polymorphism: Iterators used the abstract base class Collection to operate on different types of collections:
Bag c1;
Set c2;
…
Iterator i1(c1);
Iterator i2(c2);
…
Unfortunately, the price of this approach was high in terms of both running time and memory usage. Running time was typically orders of magnitude worse than equivalent code using the C++ standard library because most operations ended up requiring a virtual call (whereas in the C++ standard library, many operations are inlined, and no virtual functions are involved in iterator and container interfaces). Furthermore, because (unlike Smalltalk) the interfaces were bounded, built-in types had to be wrapped in larger polymorphic classes (such wrappers were provided by the NIHCL), which in turn could lead to dramatic increases in storage requirements.
Even in today’s age of templates, many projects still make suboptimal choices in their approach to polymorphism. Clearly, there are many situations in which dynamic polymorphism is the right choice. Heterogeneous iterations are an example. However, in the same vein, many programming tasks are naturally and efficiently solved using templates, and homogeneous containers are an example of this.
Static polymorphism lends itself well to code fundamental computing structures. In contrast, the need to choose a common base type implies that a dynamic polymorphic library will normally have to make domain-specific choices. It’s no surprise then that the STL part of the C++ standard library never included polymorphic containers, but it contains a rich set of containers and iterators that use static polymorphism (as demonstrated in Section 18.6 on page 380).
Medium and large C++ programs typically need to handle both kinds of polymorphism discussed in this chapter. In some situations, it may even be necessary to combine them very intimately. In many cases, the optimal design choices are clear in light of our discussion, but spending some time thinking about long-term, potential evolutions almost always pays off.
1 Polymorphism literally refers to the condition of having many forms or shapes (from the Greek polymorphos).
2 Strictly speaking, macros can also be thought of as an early form of static polymorphism. However, they are left out of consideration because they are mostly orthogonal to the other language mechanisms.
3 That is, the encoding of polymorphic base class subobjects includes some (mostly hidden) data that enables this run-time dispatch.
4 For a detailed discussion of polymorphism terminology, see also Sections 6.5 to 6.7 of [CzarneckiEiseneckerGenProg].
5 GCC 7, for example, provides the option -fconcepts.