
IN CONTEXT
Physics
1761 Joseph Black discovers latent heat – the heat taken up by ice to melt and water to boil without changing temperature. He also studies specific heat – required by substances to raise their temperature by a certain amount.
1783 Antoine Lavoisier and Pierre-Simon Laplace measure latent heat and specific heat.
1824 By developing the first theory of heat engines, which turn heat energy into mechanical energy, Nicolas Sadi Carnot provides the foundations for the theory of thermodynamics.
1834 Émile Clapeyron shows that energy must always become more diffuse, formulating the second law of thermodynamics.
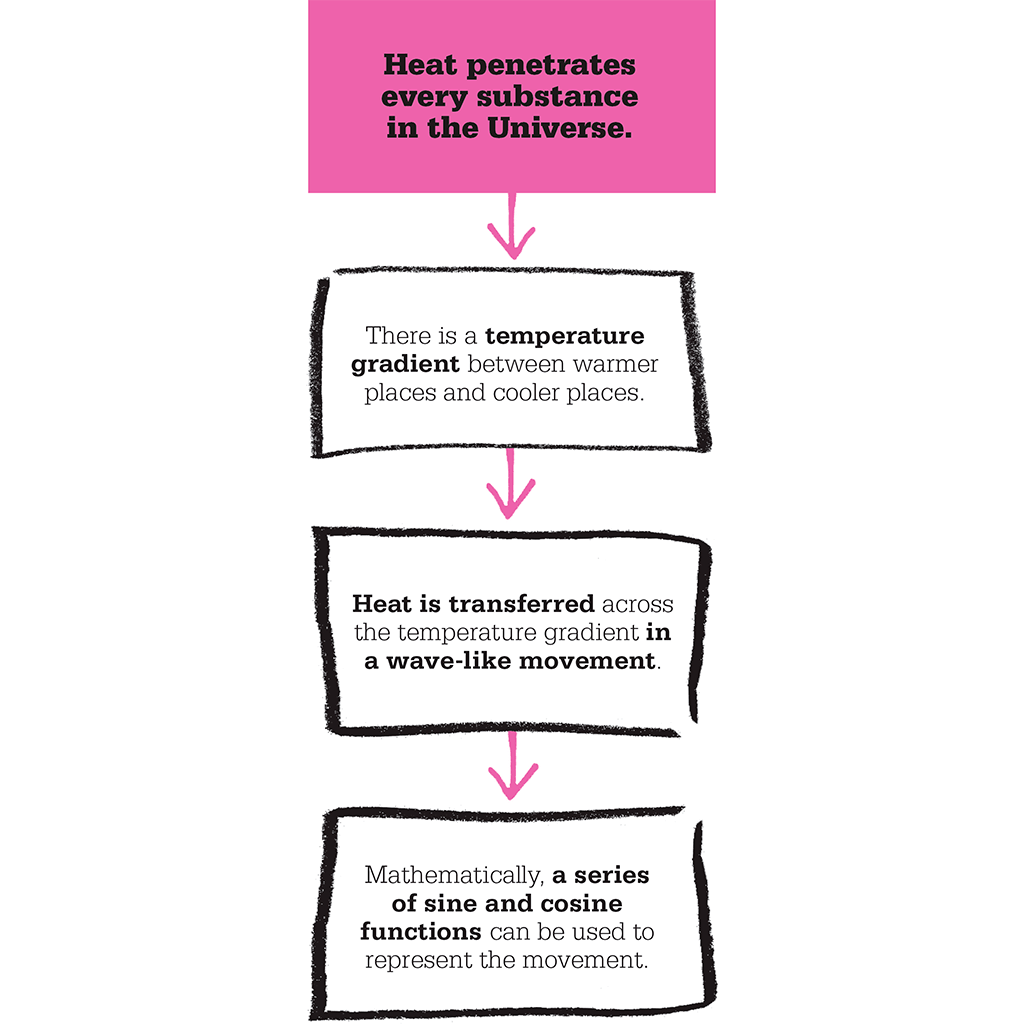
Today, one of the most fundamental laws of physics is that energy is neither created nor destroyed, but only changes from one form to another or moves from one place to another. French mathematician Joseph Fourier was a pioneer in the study of heat and how heat moves from warm places to cool places.
Fourier was interested in both how heat diffused through solids by conduction and how things cooled down by losing heat. His compatriot Jean-Baptiste Biot had imagined the spread of heat as “action at a distance”, in which it spreads by jumping from warm places to cool. Biot represented the heat flow in a solid as a series of slices, which allowed it to be studied with conventional equations showing the heat jumping from one slice to the next.
Temperature gradients
Fourier looked at heat flow in an entirely different way. He focused on temperature gradients – continuous gradations between warm and cool places. These could not be quantified with conventional equations, so he devised new mathematical techniques.
Fourier focused on the idea of waves, and finding a way to represent them mathematically. He saw that every wave-like movement, which is what a temperature gradient is, can be approximated mathematically by adding together simpler waves, whatever the shape of the wave to be represented. The simpler waves that are to be added together are sines and cosines, derived from trigonometry, and can be written out mathematically as a series. These individual waves each move uniformly from a peak to a trough. Adding more and more of these simple waves together produces increasing complexity that can approximate any other type of wave. These infinite series are now called Fourier series.
Fourier published his idea in 1807, but it attracted criticism, and it was not until 1822 that his work was finally accepted. Continuing his study of heat, in 1824, Fourier examined the difference between the heat that Earth gains from the Sun and the heat it loses to space. He realized that the reason Earth is pleasantly warm, considering how far it is from the Sun, is because gases in its atmosphere trap heat and stop it from being radiated back into space – the phenomenon now called the greenhouse effect.
Today, Fourier analysis is applied not only to heat transfer but also to a host of problems at the cutting edge of science, ranging from acoustics, electrical engineering, and optics to quantum mechanics.
"Mathematics compares the most diverse phenomena and discovers the secret analogies that unite them."
Joseph Fourier
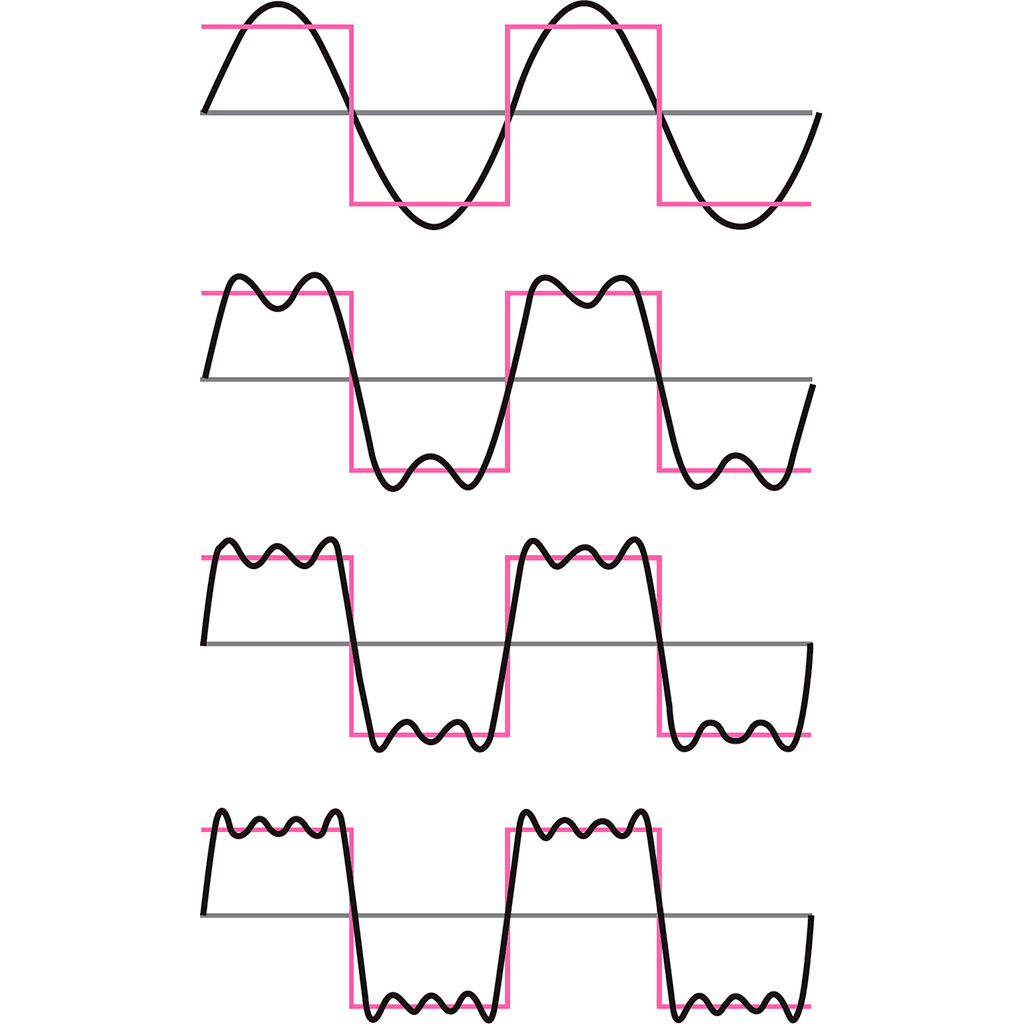
A Fourier series can approximate a wave of any shape – even a square one (shown here in pink). Adding more sine waves to the series gives a closer and closer approximation of the square wave. The first four approximations in the series (shown here in black) each incorporate an extra sine wave.
JOSEPH FOURIER

The son of a tailor, Joseph Fourier was born in Auxerre, France. Orphaned at the age of 10, he was taken into a local convent before going on to a military school, where he excelled at mathematics. France was in the throes of revolution, and during the Terror of 1794, he was briefly imprisoned after falling out with fellow revolutionaries.
After the Revolution, Fourier accompanied Napoleon on an expedition to Egypt in 1798. He was made governor of Egypt and put in charge of the study of ancient Egyptian relics. Returning to France in 1801, Fourier was made governor of Isère in the Alps. In between administrative duties overseeing road building and drainage schemes, he published a groundbreaking study of ancient Egypt and started his studies of heat. He died in 1831 after tripping and falling down a flight of stairs.
Key works
1807 On the Propagation of Heat in Solid Bodies
1822 The Analytic Theory of Heat
See also: Isaac Newton • Joseph Black • Antoine Lavoisier • Charles Keeling