
IN CONTEXT
Artificial intelligence
1950 Alan Turing suggests a test to measure machine intelligence (the Turing Test).
1955 American programmer Arthur Samuel improves his program to play draughts by writing one that learns to play.
1956 The term “artificial intelligence” is coined by American John McCarthy.
1960 American psychologist Frank Rosenblatt makes a computer with neural networks that learn from experience.
1968 MacHack, the first chess program to achieve a good level of skill, is created by American Richard Greenblatt.
1997 World chess champion Garry Kasparov is defeated by IBM’s Deep Blue computer.
Computers in 1961 were mostly mainframes the size of a room. Minicomputers would not arrive until 1965 and microchips as we know them today were several years in the future. With computer hardware so huge and specialized, British research scientist Donald Michie decided to use simple physical objects for a small project on machine learning and artificial intelligence – matchboxes and glass beads. He selected a simple task, too – the game of noughts-and-crosses, also known as tic-tac-toe. Or, as Michie called it “tit-tat-to”. The result was the Matchbox Educable Noughts And Crosses Engine (MENACE).
Michie’s main version of MENACE comprised 304 matchboxes glued together in a chest-of-drawers arrangement. A code number on each box was keyed into a chart. The chart showed drawings of the 3x3 game grid with various arrangements of Os and Xs, corresponding to possible layout permutations as the game progressed. There are actually 19,683 possible layout combinations but some can be rotated to give others, and some are mirror-images of, or symmetrical to, each other. This made 304 permutations an adequate working number.
In each matchbox box were beads of nine different kinds, distinguished by colour. Each colour of bead corresponded to MENACE putting its O on a certain one of the nine squares. For example, a green bead meant O in the lower left square, a red one designated O in the central square, and so on.
"Can machines think? The short answer is “Yes: there are machines which can do what we would call thinking, if it were done by a human being.”"
Donald Michie
Mechanics of the game
MENACE opened the game using the matchbox for no Os or Xs in the grid – the “first move” box. In the tray of each matchbox were two extra pieces of card at one end forming a “V” shape. To play, the tray was removed from the box, jiggled, and tilted so the V was at the lower end. The beads randomly rolled down and one nestled into the apex of the V. Thus chosen, this bead’s colour determined the position of MENACE’s first O in the grid. This bead was then put aside, and the tray replaced in its box but left slightly open.
Next, the opponent positioned their first X. For the second turn of MENACE, the matchbox was selected that corresponded to the positions of the X and O on the grid at this time. Again the matchbox was opened, the tray shaken and tilted, and the colour of the randomly selected bead determined the position of MENACE’s second O. The opponent placed their second X. And so on, recording MENACE’s sequence of beads and so moves.
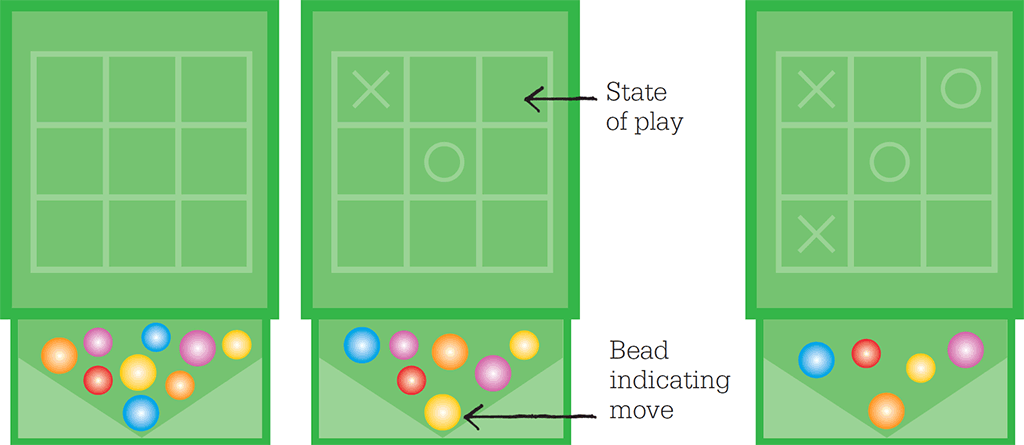
Each of the 304 matchboxes in MENACE represented a possible state of the board. The beads inside the boxes represented each possible move for that state. The bead at the bottom of the “V” determined the move. As games went on, winning beads were reinforced and losing ones removed, allowing MENACE to learn from its experience.
Win, lose, draw
Eventually there came a result. If MENACE won, it received reinforcement or a “reward”. The removed beads showed the sequence of winning moves. Each of these beads was put back in its box, identified by the code number and slightly open tray. The tray also received three extra “bonus” beads of the same colour. As a consequence, in a future game, if the same permutation of Os and Xs occurred on the grid, this matchbox would come into play again – and it had more of the beads that previously led to a win. The chances of choosing that bead, and so the same move and another possible win, were increased.
If MENACE lost it was “punished” by not receiving back the removed beads, which represented the losing sequence of moves. But this was still positive. In future games, if the same permutation of Xs and Os cropped up, the beads designating the same move as the previous time were either fewer in number or absent, thereby lessening the chance of another loss.
For a draw, each bead from that game was replaced in its relevant box, along with a small reward, one bonus bead of the same colour. This increased the chances of that bead being selected if the same permutation came round again, but not so much as the win with three bonus beads.
Michie’s aim was that MENACE would “learn from experience”. For given permutations of Os and Xs, when a certain sequence of moves had been successful, it should gradually become more likely, while moves that led to losses would become less likely. It should progress by trial and error, adapt with experience, and with more games, become more successful.

Colossus, the world’s first electronic programmable computer, was made in 1943 to crack codes at Bletchley Park in England. Michie trained staff to use the computer.
Controlling variables
Michie considered potential problems. What if the selected bead from a tray decreed that MENACE’s O should be placed on a square already occupied by an O or X? Michie accounted for this by ensuring that each matchbox contained only beads corresponding to empty squares for its particular permutation. So the box for the permutation of O top left and X bottom right did not contain beads for putting the next O on those squares. Michie considered that putting beads for all nine possible O positions in every box would “complicate the problem unnecessarily”. It meant MENACE would not only learn to win or draw, it would also have to learn the rules as it went along. Such start-up conditions might lead to one or two early disasters that collapsed the whole system. This demonstrated a principle: machine learning does well to start simple and gradually add more sophistication.
Michie also pointed out that when MENACE lost, its last move was the 100 per cent fatal one. The move before contributed to the loss, as though backing the machine into a corner, but less so – usually it still left open the possibility of escaping defeat. Working back towards the start of the game, each earlier move contributed less to the final defeat – that is, as moves accumulate, the probability that each becomes the final one increases. Therefore as the total number of moves grows, it becomes more important to get rid of choices that have proved fatal.
Michie simulated this by having different numbers of beads for each move. So for MENACE’s second move (third move overall), each box that could be called upon to play – those with permutations of one O and one X already in the grid – had three of each kind of bead. For MENACE’s third move, there were two beads of each kind, and for its fourth (seventh move overall), just one. A fatal choice on the fourth move would result in removal of the only bead specifying that position on the grid. Without that bead, the same situation could not recur.
"Expert knowledge is intuitive; it is not necessarily accessible to the expert himself."
Donald Michie
Human vs MENACE
So what were the results? Michie was MENACE’s first opponent in a tournament of 220 games. MENACE began shakily but soon settled down to draw more often, then notch up some wins. To counter, Michie began to stray from safe options and employ unusual strategies. MENACE took time to adapt but then began to cope with these too, coming back to achieve more draws, then wins. At one point in a series of 10 games, Michie lost eight.
MENACE provided a simple example of machine learning and how altering variables could affect the outcome. Michie’s description of MENACE was, in fact, part of a longer account that went on to compare its performance with trial-and-error animal learning, as Michie explained:
‘“Essentially, the animal makes more-or-less random movements and selects, in the sense that it subsequently repeats, those which produced the ‘desired’ result. This description seems tailor-made for the matchbox model. Indeed, MENACE constitutes a model of trial-and-error learning in so pure a form, that when it shows elements of other categories of learning we may reasonably suspect these of contamination with a trial-and-error component.”

New computer technology has led to a rapid development in AI, and in 1997, the chess machine Deep Blue defeated world champion Garry Kasparov. The computer learned strategy by analysing thousands of past games.
Turning point
Before developing MENACE, Donald Michie had pursued a distinguished research career in biology, surgery, genetics, and embryology. After MENACE, he moved into the fast-developing area of artificial intelligence (AI). He developed his machine learning ideas into “industrial-strength tools” applied in hundreds of situations, including assembly lines, factory production, and steel mills. As computers spread, his artificial intelligence work was used to design computer programs and control structures that could learn in ways perhaps not even guessed at by their human originators. Michie demonstrated that careful application of human intelligence empowered machines to make themselves smarter. Recent developments in AI use similar principles to develop networks that mirror the neural networks of animals’ brains.
Michie also conceived the notion of memoization, in which the result of each set of inputs in a machine or computer was stored as a reminder or “memo”. If the same set of inputs recurred, the device would at once activate the memo and recall the answer, rather than recalculating afresh, thereby saving time and resources. He contributed the memoization technique to computer programming languages such as POP-2 and LISP.
"He had this concept that he wanted to try out that he thought might possibly solve computer chess…It was the idea of reaching a steady state."
Kathleen Spracklen
DONALD MICHIE

Born in 1923 in Rangoon, Burma (Myanmar), Michie won a scholarship to Oxford in 1942, but instead assisted in the war effort by joining the code-breaking teams at Bletchley Park, becoming a close colleague of the computing pioneer Alan Turing.
In 1946, he returned to Oxford to study mammalian genetics. However, he had a growing interest in artificial intelligence, and by the 1960s it had become his main pursuit. He moved to the University of Edinburgh in 1967, and became the first Chairman of the Department of Machine Intelligence and Perception. He worked on the FREDDY series of visually-enabled, teachable research robots. In addition, he ran a series of prestigious artificial intelligence projects and founded the Turing Institute in Glasgow.
Michie continued as an active researcher into his eighties. He died in a car accident while travelling to London in 2007.
Key work
1961 Trial and Error
See also: Alan Turing