IN CONTEXT

BRANCH

Meteorology

BEFORE

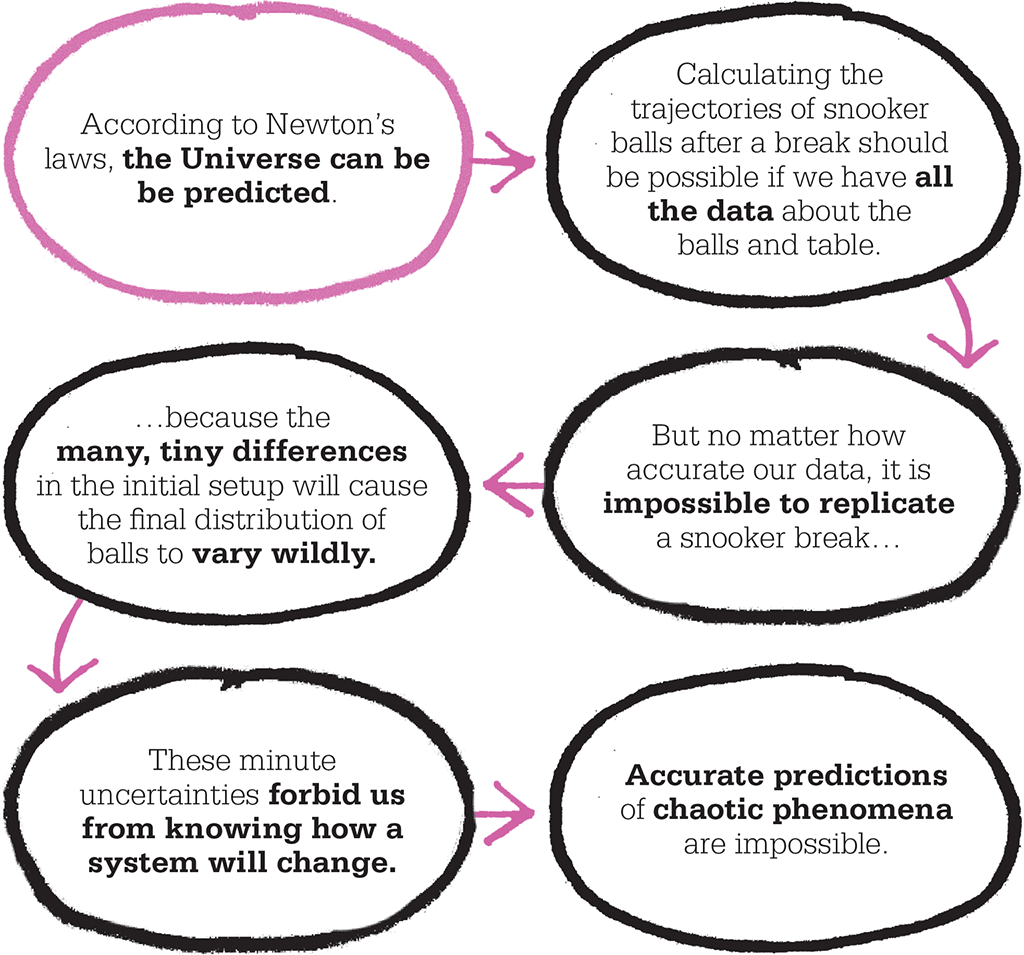
1687 Newton’s three laws of motion hold that the Universe is predictable.

1880s Henri Poincaré shows that the motion of three or more bodies interacting gravitationally is generally chaotic and unpredictable.

AFTER

1970s Chaos theory is used to model traffic flow, digital encryption, function, and in designs for cars and aircraft.

1979 Benoît Mandelbrot discovers the Mandelbrot set, which shows how complex patterns can be created using very simple rules.

1990s Chaos theory is thought of as a subset of complexity science, which seeks to explain complex natural phenomena.

Much of the history of science has been devoted to developing simple models that predict the behaviour of systems. Certain phenomena in nature, such as planetary motion, lend themselves readily to this schema. With a description of the initial conditions – the mass of a planet, its position, velocity, and so on – future configurations can be calculated. However, the behaviour of many processes, such as waves crashing on a beach, smoke rising from a candle, or weather patterns, is chaotic and unpredictable. Chaos theory seeks to explain such unpredictable phenomena.

Three-body problem

The first strides towards chaos theory were taken in the 1880s, when French mathematician Henri Poincaré worked on the “three-body problem”. Poincaré showed that for a planet with a satellite orbiting a star – an Earth-Moon-Sun system – there is no solution for a stable orbit. Not only was the gravitational interaction between bodies far too complex to calculate, Poincaré found that tiny differences in initial conditions resulted in large and unpredictable changes. However, his work was largely forgotten.

A surprise discovery

Few further developments occurred in the field until the 1960s, when scientists began to use new, powerful computers to predict the weather. Surely, they reasoned, given enough data on the state of the atmosphere at a given time and enough computational power to crunch the data, it should be possible to know how weather systems evolve. Working on the assumption that ever-larger computers would increase the range of predictions, Edward Lorenz, an American meteorologist at the Massachusetts Institute of Technology (MIT), tested simulations involving just three simple equations. He ran the simulation several times, each time inputting the same initial state and expecting to see the same results. Lorenz was astounded when the computer returned hugely different outcomes each time. Checking his figures again, he found that the program had rounded up the numbers from six decimal places to three. This tiny alteration to the initial state had a major impact on the end result. This sensitive dependence on initial conditions was named the “butterfly effect” – the idea that a small change in a system, as trivial as a teaspoonful of air molecules moved by a butterfly flapping its wings in Brazil, can be amplified over time to create unpredictable outcomes, such as a tornado in Texas.

  Edward Lorenz defined the limits of predictability, explaining that the impossibility of knowing what will happen is actually written into the rules that govern a chaotic system. Not only weather, but many real-world systems are chaotic – traffic systems, stock market fluctuations, the flow of fluids and gases, the growth of galaxies – and they have all been modelled using chaos theory.

Here, turbulence forms at the tip of a vortex left in the wake of an aircraft’s wing. Study of the critical point beyond which a system creates turbulence was key to the development of chaos theory.

EDWARD LORENZ

Born in West Hartford, Connecticut, in 1917, Edward Norton Lorenz received his MSc in mathematics from Harvard in 1940. During World War II he served as a meteorologist, forecasting the weather for the US Army Air Corps. After the war, he studied meteorology at Massachusetts Institute of Technology (MIT).

  Lorenz’s discovery of sensitive dependency on initial conditions (SDIC) was accidental – and one of the great “eureka” moments in science. Running simple computer simulations of weather systems he found that his model was churning out wildly different outcomes, despite being supplied with almost identical starting conditions. His seminal 1963 paper showed that perfect weather prediction was a pipe dream. Lorenz remained physically and academically active all his life, contributing academic papers, and hiking and skiing until shortly before his death in 2008.

Key work

1963 Deterministic Nonperiodic Flow

See also: Isaac Newton • Benoît Mandelbrot