in which spacetime is viewed as
curved on Sundays and flat on Mondays,
and horizons are made from
vacuum on Sundays and charge on Mondays,
but Sunday’s experiments and Monday’s experiments
agree in all details
Is spacetime really curved? Isn’t it conceivable that spacetime is actually flat, but the clocks and rulers with which we measure it, and which we regard as peifect in the sense of Box 11.1, are actually rubbery? Might not even the most perfect of clocks slow down or speed up, and the most perfect of rulers shrink or expand, as we move them from point to point and change their orientations? Wouldn’t such distortions of our clocks and rulers make a truly flat spacetime appear to be curved?
Yes.
Figure 11.1 gives a concrete example: the measurement of circumferences and radii around a nonspinning black hole. On the left is shown an embedding diagram for the hole’s curved space. The space is curved in this diagram because we have chosen to define distances as though our rulers were not rubbery, as though they always hold their lengths fixed no matter where we place them and how we orient them. The rulers show the hole’s horizon to have a circumference of 100 kilometers A circle of twice this circumference, 200 kilometers, is drawn around the hole, and the radial distance from the horizon to that circle is measured with a perfect ruler; the result is 37 kilometers. If space were flat, that radial distance would have to be the radius of the outside circle, 200/π kilometers, minus the radius of the horizon, 100/π kilometers; that is, it would have to be 200/π – 100/π = 16 kilometers (approximately). To accommodate the radial distance’s far larger, 37-kilometer size, the surface must have the curved, trumpet-horn shape shown in the diagram
Perfection of Rulers and Clocks
By “perfect clocks” and “perfect rulers” I shall mean, in this book, clocks and rulers that are perfect in the sense that the world’s best clock makers and ruler makers understand: Perfection is to be judged by comparison with the behaviors of atoms and molecules.
More specifically, perfect clocks must tick at a uniform rate when compared with the oscillations of atoms and molecules. The world’s best atomic clocks are designed to do just that. Since the oscillations of atoms and molecules are controlled by what I called in earlier chapters the “rate of flow of time,” this means that perfect clocks measure the “time” part of Einstein’s curved spacetime.
The markings on perfect rulers must have uniform and standard spacings when compared to the wavelengths of the light emitted by atoms and molecules, for example, uniform spacings relative to the “21-centimeter-wavelength” light emitted by hydrogen molecules. This is equivalent to requiring that when one holds a ruler at some fixed, standard temperature (say, zero degrees Celsius), it contain always the same fixed number of atoms along its length between markings; and this, in turn, guarantees that perfect rulers measure the spatial lengths of Einstein’s curved space-time.
The body of this chapter introduces the concept of “true” times and “true” lengths. These are not necessarily the times and lengths measured by perfect clocks and perfect rulers, that is, not necessarily the times and lengths based on atomic and molecular standards, that is, not necessarily the times and lengths embodied in Einstein’s curved spacetime.
If space is actually flat around the black hole, but our perfect rulers are rubbery and thereby fool us into thinking space is curved, then the true geometry of space must be as shown on the right in Figure 11.1, and the true distance between the horizon and the circle must be 16 kilometers, as demanded by the flat-geometry laws of Euclid. However, general relativity insists that our perfect rulers not measure this true distance. Take a ruler and lay it down circumferentially around the hole just outside the horizon (curved thick black strip with ruler markings in right part of Figure 11.1). When oriented circumferentially like this, it does measure correctly the true distance. Cut the ruler off at 37 kilometers length, as shown. It now encompasses 37 percent of the distance around the hole. Then turn the ruler so it is oriented radially (straight thick black strip with ruler markings in Figure 11.1). As it is turned, general relativity requires that it shrink. When pointed radially, its true length must have shrunk to 16 kilometers, so it will reach precisely from the horizon to the outer circle. However, the scale on its shrunken surface must claim that its length is still 37 kilometers, and therefore that the distance between horizon and circle is 37 kilometers. People like Einstein who are unaware of the ruler’s rubbery nature, and thus believe its inaccurate measurement, conclude that space is curved. However, people like you and me, who understand the rubberiness, know that the ruler has shrunk and that space is really flat.
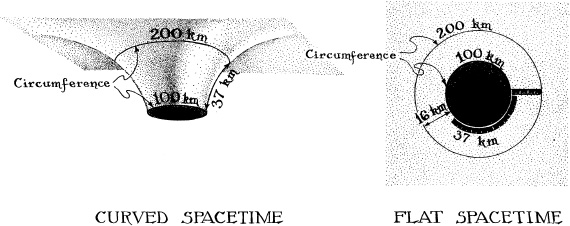
11.1 Length measurements in the vicinity of a black hole from two different viewpoints. Left: Spacetime is regarded as truly curved, and perfect rulers measure precisely the lengths of the true spacetime. Right: Spacetime is regarded as truly flat and perfect rulers are rubbery. A 57-km-Iong perfect ruler, when oriented in a circumferential direction, measures precisely the lengths of the true, flat spacetime. However, when oriented radially, it shrinks by an amount that is greater the nearer it is to the hole, and therefore it reports radial lengths that are larger than the true ones (it reports 37 km rather than the true 16 km in the case shown).
What could possibly make the ruler shrink, when its orientation changes? Gravity, of course. In the flat space of the right half of Figure 11.1 there resides a gravitational field that controls the sizes of fundamental particles, atomic nuclei, atoms, molecules, everything, and forces them all to shrink when laid out radially. The amount of shrinkage is great near a black hole, and smaller farther away, because the shrinkage-controlling gravitational field is generated by the hole, and its influence. declines with distance.
The shrinkage-controlling gravitational field has other effects. When a photon or any other particle flies past the hole, this field pulls on it and deflects its trajectory. The trajectory is bent around the hole; it is curved, as measured in the hole’s true, flat spacetime geometry. However, people like Einstein, who take seriously the measurements of their rubbery rulers and clocks, regard the photon as moving along a straight line through curved spacetime.
What is the real, genuine truth? Is spacetime really flat, as the above paragraphs suggest, or is it really curved? To a physicist like me this is an uninteresting question because it has no physical consequences. Both viewpoints, curved spacetime and flat, give precisely the same predictions for any measurements performed with perfect rulers and clocks, and also (it turns out) the same predictions for any measurements performed with any kind of physical apparatus whatsoever. For example, both viewpoints agree that the radial distance between the horizon and the circle in Figure 11.1, as measured by a perfect ruler, is 37 kilometers. They disagree as to whether that measured distance is the “real” distance, but such a disagreement is a matter of philosophy, not physics. Since the two viewpoints agree on the results of all experiments, they are physically equivalent. Which viewpoint tells the “real truth” is irrelevant for experiments; it is a matter for philosophers to debate, not physicists. Moreover, physicists can and do use the two viewpoints interchangeably when trying to deduce the predictions of general relativity.
The mental processes by which a theoretical physicist works are beautifully described by Thomas Kuhn’s concept of a paradigm Kuhn, who received his Ph.D. in physics from Harvard in 1949 and then became an eminent historian and philosopher of science, introduced the concept of a paradigm in his 1962 book The Structure of Scientific Revolutions—one of the most insightful books I have ever read.
A paradigm is a complete set of tools that a community of scientists uses in its research on some topic, and in communicating the results of its research to others. The curved spacetime viewpoint on general relativity is one paradigm; the flat spacetime viewpoint is another. Each of these paradigms includes three basic elements: a set of mathematically formulated laws of physics; a set of pictures (mental pictures, verbal pictures, drawings on paper) which give us insight into the laws and help us communicate with each other; and a set of exemplars—past calculations and solved problems, either in textbooks or in published scientific articles, which the community of relativity experts agrees were correctly done and were interesting, and which we use as patterns for our future calculations.
The curved spacetime paradigm is based on three sets of mathematically formulated laws: Einstein’s field equation, which describes how matter generates the curvature of spacetime; the laws which tell us that perfect rulers and perfect clocks measure the lengths and the times of Einstein’s curved spacetime; and the laws which tell us how matter and fields move through curved spacetime, for example, that freely moving bodies travel along straight lines (geodesics). The flat spacetime paradigm is also based on three sets of laws: a law describing how matter, in flat spacetime, generates the gravitational field; laws describing how that field controls the shrinkage of perfect rulers and the dilation of the ticking rates of perfect clocks; and laws describing how the gravitational field also controls the motions of particles and fields through flat spacetime.
The pictures in the curved spacetime paradigm include the embedding diagrams drawn in this book (for example, the left half of Figure 11.1) and the verbal descriptions of spacetime curvature around black holes (for example, the “tornado-like swirl of space around a spinning black hole”). The pictures in the flat spacetime paradigm include the right half of Figure 11.1, with the ruler that shrinks when it turns from circumferential orientation to radial, and the verbal description of “a gravitational field controlling the shrinkage of rulers.”
The exemplars of the curved spacetime paradigm include the calculation, found in most relativity textbooks, by which one derives Schwarzschild’s solution to the Einstein field equation, and the calculations by which Israel, Carter, Hawking, and others deduced that a black hole has no “hair.” The flat spacetime exemplars include textbook calculations of how the mass of a black hole or other body changes when gravitational waves are captured by it, and calculations by Clifford Will, Thibault Damour, and others of how neutron stars orbiting each other generate gravitational waves (waves of shrinkage-producing field).
Each piece of a paradigm—its laws, its pictures, and its exemplars—is crucial to my own mental processes when I’m doing research. The pictures (mental and verbal as well as on paper) act as a general compass. They give me intuition as to how the Universe probably behaves; I manipulate them, along with mathematical doodlings, in search of interesting new insights. If I find, from the pictures and doodlings, an insight worth pursuing (for example, the hoop conjecture in Chapter 7), I then try to verify or refute it by careful mathematical calculations based on the paradigm’s mathematically formulated laws of physics. I pattern my careful calculations after the paradigm’s exemplars. They tell me what level of calculational precision is likely to be needed for reliable results. (If the precision is too poor, the results may be wrong; if the precision is too high, the calculations may eat up valuable time unnecessarily.) The exemplars also tell me what kinds of mathematical manipulations are likely to get me through the morass of mathematical symbols to my goal. Pictures also guide the calculations; they help me find shortcuts and avoid blind alleys. If the calculations verify or at least make plausible my new insight, I then communicate the insight to relativity experts by a mixture of pictures and calculations, and I communicate to others, such as readers of this book, solely with pictures—verbal pictures and drawings.
The flat spacetime paradigm’s laws of physics can be derived, mathematically, from the curved spacetime paradigm’s laws, and conversely. This means that the two sets of laws are different mathematical representations of the same physical phenomena, in somewhat the same sense as 0.001 and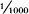 
are different mathematical representations of the same number. However, the mathematical formulas for the laws look very different in the two representations, and the pictures and exemplars that accompany the two sets of laws look very different.
As an example, in the curved spacetime paradigm, the verbal picture of Einstein’s field equation is the statement that “mass generates the curvature of spacetime.” When translated into the language of the flat spacetime paradigm, this field equation is described by the verbal picture “mass generates the gravitational field that governs the shrinkage of rulers and the dilation of the ticking of clocks.” Although the two versions of the Einstein field equation are mathematically equivalent, their verbal pictures differ profoundly.
It is extremely useful, in relativity research, to have both paradigms at one’s fingertips. Some problems are solved most easily and quickly using the curved spacetime paradigm; others, using flat spacetime. Black-hole problems (for example, the discovery that a black hole has no hair) are most amenable to curved spacetime techniques; gravitational-wave problems (for example, computing the waves produced when two neutron stars orbit each other) are most amenable to flat spacetime techniques. Theoretical physicists, as they mature, gradually build up insight into which paradigm will be best for which situation, and they learn to flip their minds back and forth from one paradigm to the other, as needed. They may regard spacetime as curved on Sunday, when thinking about black holes, and as flat on Monday, when thinking about gravitational waves. This mind-flip is similar to that which one experiences when looking at a drawing by M. C. Escher, for example, Figure 11.2.
Since the laws that underlie the two paradigms are mathematically equivalent, we can be sure that when the same physical situation is analyzed using both paradigms, the predictions for the results of experiments will be identically the same. We thus are free to use the paradigm that best suits us in any given situation.
This freedom carries power. That is why physicists were not content with Einstein’s curved spacetime paradigm, and have developed the flat spacetime paradigm as a supplement to it.
Newton’s description of gravity is yet another paradigm. It regards space and time as absolute, and gravity as a force that acts instantaneously between two bodies (“action at a distance,” Chapters 1 and 2).
The Newtonian paradigm for gravity, of course, is not equivalent to Einstein’s curved spacetime paradigm; the two give different predictions for the outcomes of experiments. Thomas Kuhn uses the phrase scientific revolution to describe the intellectual struggle by which Einstein invented his paradigm and convinced his colleagues that it gives a more nearly correct description of gravity than the Newtonian paradigm (Chapter 2). Physicists’ invention of the flat spacetime paradigm was not a scientific revolution in this Kuhnian sense, because the flat spacetime paradigm and the curved spacetime paradigm give precisely the same predictions.
11.2 A drawing by M. C. Escher. One can experience a mind-flip by looking at this drawing, first from one point of view (for example, with the flowing stream at the same height as the waterfall’s top) and then from another (with the stream at the height of the waterfall’s bottom). This mind-flip is somewhat like the one a theoretical physicist experiences when switching from the curved spacetime paradigm to the flat spacetime paradigm. [© 1961 M. C. Escher Foundation–Baarn-Holland. All rights reserved.]
When gravity is weak, the predictions of the Newtonian paradigm and Einstein’s curved spacetime paradigm are almost identical, and correspondingly the two paradigms are very nearly mathematically equivalent. Thus it is that, when studying gravity in the solar system, physicists often switch back and forth with impunity between the Newtonian paradigm, the curved spacetime paradigm, and also the flat spacetime paradigm, using at any time whichever one strikes their fancy or seems the more insightful.1
Sometimes people new to a field of research are more open-minded than the old hands. Such was the case in the 1970s, when new people had insights that led to a new paradigm for black holes, the membrane paradigm.
In 1971 Richard Hanni, an undergraduate at Princeton University, together with Remo Ruffini, a postdoc, noticed that a black hole’s horizon can behave somewhat like an electrically conducting sphere. To understand this peculiar behavior, recall that a positively charged metal pellet carries an electric field which repels protons but attracts electrons. The pellet’s electric field can be described by field lines, analogous to those of a magnetic field. The electric field lines point in the direction of the force that the field exerts on a proton (and oppositely to the force exerted on an electron), and the density of field lines is proportional to the strength of the force. If the pellet is alone in flat spacetime, its electric field lines point radially outward (Figure 11.3a). Correspondingly, the electric force on a proton points radially away from the pellet, and since the density of field lines decreases inversely with the square of the distance from the pellet, the electric force on a proton also decreases inversely with the square of the distance.
Now bring the pellet close to a metal sphere (Figure 11.3b). The sphere’s metal surface is made of electrons that can move about on the sphere freely, and positively charged ions that cannot. The pellet’s electric field pulls a number of the sphere’s electrons into the pellet’s vicinity, leaving excess ions everywhere else on the sphere; in other words, it polarizes2 the sphere.
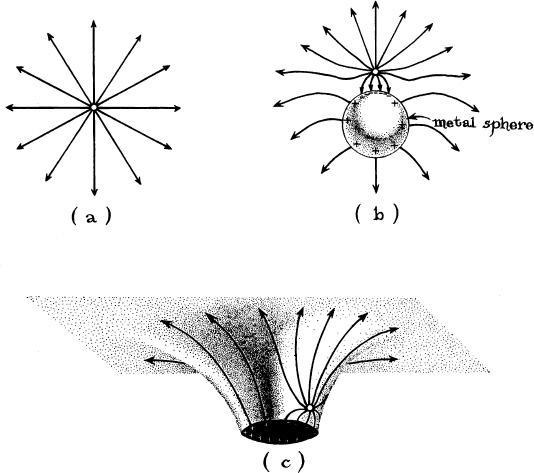
11.3 (a) The electric field lines produced by a positively charged metal pellet at rest, alone, in flat spacetime. (b) The electric field lines when the pellet is at rest just above an electrically conducting, metal sphere in flat spacetime. The pellet’s electric field polarizes the sphere. (c) The electric field lines when the pellet is at rest just above the horizon of a black hole. The pellet’s electric field appears to polarize the horizon.
In 1971 Hanni and Ruffirti, and independently Robert Wald of Princeton University and Jeff Cohen of the Princeton Institute for Advanced Study, computed the shapes of the electric field lines produced by a charged pellet near the horizon of a nonspinning black hole. Their computations, based on the standard curved spacetime paradigm, revealed that the curvature of spacetime distorts the field lines in the manner shown in Figure 11.3c. Hanni and Ruffini, noticing the similarity to the field lines in Figure 11.3b [look at diagram (c) from below, and it will be nearly the same as diagram (b)], suggested that we can think of a black hole’s horizon in the same manner as we think of a metal sphere; that is, we can regard the horizon as a thin membrane composed of positively and negatively charged particles, a membrane similar to the sphere’s metal. Normally there are equal numbers of positive and negative particles everywhere on the membrane, that is, there is no net charge on any region of the membrane. However, when the pellet is brought near the horizon, excess negative particles move into the region below the pellet, leaving excess positive particles everywhere else on the membrane; the horizon’s membrane thereby gets polarized; and the total set of field lines produced by the pellet’s charges and the horizon’s charges takes the form of diagram (c).
When I, as an old hand at relativity theory, heard this story, I thought it ludicrous. General relativity insists that, if one falls into a black hole, one will encounter nothing at the horizon except spacetime curvature. One will see no membrane and no charged particles. Thus, the Hanni–Ruffini description of why the pellet’s electric field lines are bent can have no basis in reality. It is pure fiction. The cause of the field lines’ bending, I was sure, is spacetime curvature and nothing else: The field lines bend down toward the horizon in diagram (c) solely because tidal gravity pulls on them, and not because they are being attracted to some polarized charge in the horizon. The horizon cannot possess any such polarized charge; I was sure of it. I was wrong.
Five years later Roger Blandford and a graduate student, Roman Znajek, at Cambridge University discovered that magnetic fields can extract the spin energy of a black hole and use it to power jets (the Blandford-Znajek process, Chapter 9 and Figure 11.4a). Blandford and Znajek also found by curved spacetime calculations that, as the energy is extracted, electric currents flow into the horizon near the hole’s poles (in the form of positively charged particles falling inward), and currents flow out of the horizon near the equator (in the form of negatively charged particles falling inward). It was as though the black hole were part of an electric circuit.
The calculations showed, moreover, that the hole behaved as though it were a voltage generator in the circuit (Figure 11.4b). This black-hole voltage generator drove current out of the horizon’s equator, then up magnetic field lines to a large distance from the hole, then through plasma (hot, electrically conducting gas) to other field lines near the hole’s spin axis, then down those field lines and into the horizon. The magnetic field lines were the wires of the electric circuit, the plasma was the load that extracts power from the circuit, and the spinning hole was the power source.
From this viewpoint (Figure 11.4b), it is the power carried by the circuit that accelerates the plasma to form jets. From the viewpoint of Chapter 9 (Figure 11.4a), it is the spinning magnetic field lines, whipping around and around, that accelerate the plasma. The two viewpoints are just different ways of looking at the same thing. The power comes ultimately from the hole’s spin in both cases. Whether one thinks of the power as carried by the circuit or as carried by the spinning field lines is a matter of taste.
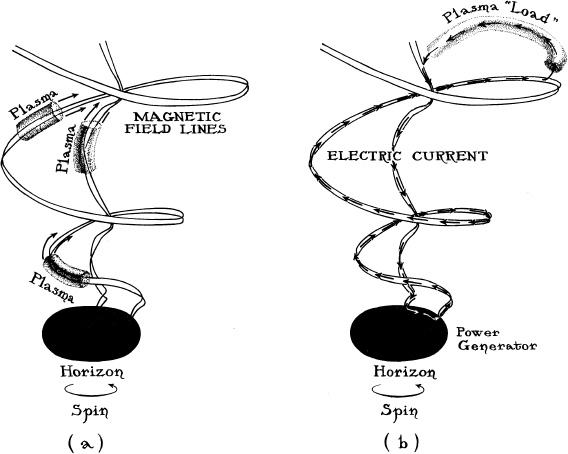
11.4 Two viewpoints on the Blandford–Znajek process by which a spinning, magnetized black hole can produce jets. (a) The hole’s spin creates a swirl of space which forces magnetic fields threading the hole to spin. The spinning fields’ centrifugal forces then accelerate plasma to high speeds (compare with Figure 9.7d). (b) The magnetic fields and the swirl of space together generate a large voltage difference between the hole’s poles and equator; in effect, the hole becomes a voltage and power generator. This voltage drives current to flow in a circuit. The circuit carries electrical power from the black hole to the plasma, and that power accelerates the plasma to high speeds.
The electric circuit description, although based on the standard curved spacetime laws of physics, was totally unexpected, and the flow of current through the black hole—inward near the poles and outward near the equator—seemed very peculiar. During 1977 and 1978, Znajek and, independently, Thibault Damour (a recent PhD at the Obser-vatoire de Paris in France) puzzled over this peculiarity. While trying to understand it, they independently translated the curved spacetime equations, which describe the spinning hole and its plasma and magnetic field, into an unfamiliar form with an intriguing pictorial interpretation: The current, when it reaches the horizon, does not enter the hole. Instead, it attaches itself to the horizon, where it is carried by the kinds of horizon charges previously imagined by Hanni and Ruffini. This horizon current flows from the pole to the equator, where it exits up the magnetic field lines. Moreover, Damour and Znajek discovered, the laws that govern the horizon’s charge and current are elegant versions of the flat spacetime laws of electricity and magnetism: They are Gauss’s law, Ampère’s law, Ohm’s law, and the law of charge conservation (Figure 11.5).
Damour and Znajek did not assert that a being who falls into the black hole will encounter a membrane-like horizon with electric charges and currents. Rather, they asserted that if one wishes to figure out how electricity, magnetism, and plasmas behave outside a black hole, it is useful to regard the horizon as a membrane with charges and currents.
When I read the technical articles by Damour and Znajek, I suddenly understood: They, and Hanni and Ruffini before them, were discovering the foundations of a new paradigm for black holes. The paradigm was fascinating. It captivated me. Unable to resist its allure, I spent much of the 1980s, together with Richard Price, Douglas Mac-donald, Ian Redmount, Wai-Mo Suen, Ronald Crowley, and others, bringing it into a polished form and writing a book on it, Black Holes: The Membrane Paradigm
The laws of black-hole physics, written in this membrane paradigm, are completely equivalent to the corresponding laws of the curved spacetime paradigm—so long as one restricts attention to the hole’s exterior. Consequently, the two paradigms give precisely the same predictions for the outcomes of all experiments or observations that anyone might make outside a black hole—including all astronomical observations made from Earth. When thinking about astronomy and astrophysics, I find it useful to keep both paradigms at hand, membrane and curved spacetime, and to do Escher-type mind-flips back and forth between them. The curved spacetime paradigm, with its horizons made from curved empty spacetime, may be useful on Sunday, when I am puzzling over the pulsations of black holes. The membrane paradigm, with horizons made from electrically charged membranes, may be useful on Monday, when I am puzzling over a black hole’s production of jets. And since the predictions of the two paradigms are guaranteed to be the same, I can use each day whichever one best suits my needs.
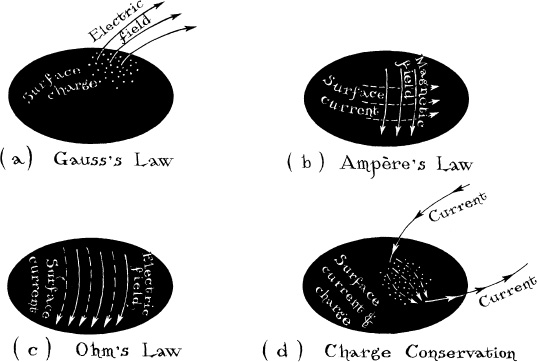
11.5 The laws governing electric charge and current on a black hole’s membrane-like horizon: (a) Gauss’s law—the horizon has precisely the right amount of surface charge to terminate all electric field lines which intersect the horizon, so they do not extend into the hole’s interior; compare with Figure 11.3. (b) Ampere’s law—the horizon has precisely the right amount of surface current to terminate that portion of the magnetic field which is parallel to the horizon, so there is no parallel field below the horizon. (c) Ohm’s law—the surface current is proportional to the part of the electric field which is tangential to the surface; the proportionality constant is a resistivity of 377 ohms. (d) Charge conservation—no charge is ever lost or created; all positive charge that enters the horizon from the outside Universe becomes attached to the horizon, and moves around on it, until it exits back into the outside Universe (in the form of negative charge falling inward to neutralize the positive charge).
Not so inside a black hole. Any being who falls into a hole will discover that the horizon is not a charge-endowed membrane, and that inside the hole the membrane paradigm completely loses its power. However, infalling beings pay a price to discover this: They cannot publish their discovery in the scientific journals of the outside Universe
1. pare with the last section of Chapter 1, “The Nature of Physical Law.”
2. This is a different usage of the word “polarize” from that of “polarized gravitational waves” and “polarized light” (Chapter 10).