The Mystery of the White Dwarfs
in which Eddington and Chandrasekhar do battle
over the deaths of massive stars;
must they shrink when they die,
creating black holes?
or will quantum mechanics save them?
The year was 1928; the place, southeast India, the city of Madras on the Bay of Bengal. There, at Presidency College, a seventeen-year-old Indian boy named Subrahmanyan Chandrasekhar was immersed in the study of physics, chemistry, and mathematics. Chandrasekhar was tall and handsome, with regal bearing and pride in his academic achievements. He had recently read Arnold Sommerfeld’s classic textbook Atomic Structure and Spectral Lines and was now overjoyed that Sommerfeld, one of the world’s great theoretical physicists, had come from his home in Munich to visit Madras.
Eager for personal contact, Chandrasekhar went to Sommerfeld’s hotel room and asked for an interview. Sommerfeld granted an appointment for several days hence.
On the day of his appointment Chandrasekhar, filled with pride and confidence in his mastery of modern physics, walked up to Sommerfeld’s hotel room and knocked on the door. Sommerfeld greeted him politely, inquired about his studies, then deflated him. “The physics you have been studying is a thing of the past. Physics has all changed in the five years since my textbook was written,” he explained. He went on to describe a revolution in physicists’ understanding of the laws that govern the realm of the small: the realm of atoms, molecules, electrons, and protons. In this realm, the Newtonian laws had been found to fail in ways that relativity had not anticipated. Their replacement was a radically new set of physical laws—laws that were called quantum mechanics1 because they deal with the behavior (the “mechanics”) of particles of matter (“quanta”). Though only two years old, the new quantum mechanical laws were already having great success in explaining how atoms and molecules behave.
Chandrasekhar had read in Sommerfeld’s book about the first, tentative version of the new laws. But the tentative quantum laws had been unsatisfactory, Sommerfeld explained to him. Although they agreed well with experiments on simple atoms and molecules such as hydrogen, the tentative laws could not account for the behaviors of more complicated atoms and molecules, and they did not mesh in a logically consistent way with each other or with the other laws of physics. They were little more than a mishmash of unaesthetic, ad-hoc rules of computation.
The new version of the laws, though radical in form, looked far more promising. It explained complicated atoms and complicated molecules, and it seemed to be meshing quite nicely with the rest of physics.
Chandrasekhar listened to the details, entranced.
Quantum Mechanics and the Guts of White Dwarfs
When they parted, Sommerfeld gave Chandrasekhar the galley proofs of a technical article that he had just written. It contained a derivation of the quantum mechanical laws that govern large collections of electrons squeezed together into small volumes, in a metal for instance.
Chandrasekhar read Sommerfeld’s galley proofs with fascination, understood them, and then spent many days in the University library studying all the research articles he could find relating to them. Especially interesting was an article entitled “On Dense Matter” by the English physicist R. H. Fowler, published in the 10 December 1926 issue of Monthly Notices of the Royal Astronomical Society. Fowler’s article pointed Chandrasekhar to a most fascinating book, The Internal Constitution of the Stars, by the eminent British astrophysicist Arthur S. Eddington, in which Chandrasekhar found a description of the mystery of white-dwarf stars.
“White dwarfs were a type of star that astronomers had discovered through their telescopes. The mysterious thing about white dwarfs was the extremely high density of the matter inside them, a density far greater than humans had ever before encountered. Chandrasekhar had no way of knowing it when he opened Eddington’s book, but the struggle to unravel the mystery of this high density would ultimately force him and Eddington to confront the possibility that massive stars, when they die, might shrink to form black holes.
“White dwarfs are probably very abundant,” Chandrasekhar read in Eddington’s book. “Only three are definitely known, but they are all within a small distance of the Sun.... The most famous of these stars is the Companion of [the ordinary star] Sirius,” which has the name Sirius B. Sirius and Sirius B are the sixth and seventh nearest stars to the Earth, 8.6 light-years away, and Sirius is the brightest star in our sky. Sirius B orbits Sirius just as the Earth orbits the Sun, but Sirius B requires 50 years to complete an orbit, the Earth only one.
Eddington described how astronomers had estimated, from telescopic observations, the mass and circumference of Sirius B. The mass was that of 0.85 Sun; the circumference, 118,000 kilometers. This meant that the mean density of Sirius B was 61,000 grams per cubic centimeter—61,000 times greater density than water and just about a ton to the cubic inch. “This argument has been known for some years,” Eddington wrote. “I think it has generally been considered proper to add the conclusion ‘which is absurd.’ “ Most astronomers could not take seriously a density so much greater than ever encountered on Earth—and had they known the real truth, as revealed by more modern astronomical observations Ca mass of 1.05 Suns, a circumference of 31,000 kilometers, and a density of 4 million grams per cubic centimeter or 60 tons per cubic inch), they would have considered it even more absurd; see Figure 4.1.
Eddington went on to describe a key new observation that reinforced the “absurd” conclusion. If Sirius B were, indeed, 61,000 times denser than water, then according to Einstein’s laws of gravity, light climbing out of its intense gravitational field would be shifted to the red by 6 parts in 100,000—a shift 30 times greater than for light emerging from the Sun, and therefore easier to measure. This redshift prediction, it seemed, had been tested and verified just before Eddington’s book went to press in 1925, by the astronomer W. S. Adams at Mount Wilson Observatory on a mountaintop above Pasadena, California.2 “Professor Adams has killed two birds with one stone,” Eddington wrote; “he has carried out a new test of Einstein’s general theory of relativity and he has confirmed our suspicion that matter 2000 times denser than platinum is not only possible, but is actually present in the Universe.”
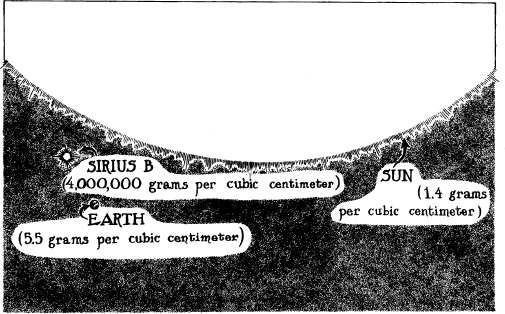
4.1 Comparison of the sizes and mean densities of the Sun, the Earth, and the white-dwarf star Sirius B, using modern values.
Further on in Eddington’s book, Chandrasekhar found a description of how the internal structure of a star, such as the Sun or Sirius B, is governed by the balance of internal pressure against gravitational squeeze. This squeeze/pressure balance can be understood (though this was not Eddington’s way) by analogy with squeezing a balloon in your hands (left half of Figure 4.2): The inward force of your squeezing hands is precisely counterbalanced by the outward force of the balloon’s air pressure—air pressure that is created by air molecules inside the balloon bombarding the balloon’s rubber wall.
4.2 Left: The balance between the squeeze of your hands and the pressure inside a balloon. Right: The analogous balance between the gravitational squeeze (weight) of an outer shell of stellar matter and the pressure of an inner ball of stellar matter.
For a star (right half of Figure 4.2) the analogue of your squeezing hands is the weight of an outer shell of stellar matter, and the analogue of the air in the balloon is the spherical ball of matter inside that shell. The boundary between the outer shell and inner ball can be chosen anywhere one wishes—a meter deep into the star, a kilometer deep, a thousand kilometers deep. Wherever one chooses the boundary, it must fulfill the requirement that the weight of the outer shell squeezing on the inner ball (the outer shell’s “gravitational squeeze”) is precisely counterbalanced by the pressure of the inner ball’s molecules bombarding the outer shell. This balance, enforced at each and every location inside the star, determines the star’s structure,. that is, it determines the details of how the star’s pressure, gravity, and density vary from the star’s surface down to its center.
Eddington’s book also described a troubling paradox in what was then known about the structures of white-dwarf stars. Eddington believed—indeed all astronomers believed in 1925—that the pressure of white-dwarf matter, like that in your balloon, must be caused by its heat. Heat makes the matter’s atoms fly about inside the star at high speed, bombarding each other and bombarding the interface between the star’s outer shell and its inner ball. If we take a “macroscopic” viewpoint, too coarse to detect the individual atoms, then all we can measure is the total bombardment force of all the atoms that hit, say, one square centimeter of the interface. That total force is the star’s pressure.
As the star cools by emitting radiation into space, its atoms will fly about more slowly, their pressure will go down, and the weight of the star’s outer shell will then squeeze its inner ball into a smaller volume. This compression of the ball, however, heats it up again, raising its pressure so a new squeeze/pressure balance can be achieved—one with the star slightly smaller than before. Thus, as Sirius B continues gradually to cool by radiating heat into interstellar space, it must gradually shrink in size.
How does this gradual shrinkage end? What will be the ultimate fate of Sirius B? The most obvious (but wrong) answer, that the star will shrink until it is so small that it becomes a black hole, was anathema to Eddihgton; he refused even to consider it. The only reasonable answer, he asserted, was that the star must ultimately turn cold and then support itself not by thermal pressure (that is, heat-induced pressure), but rather by the only other type of pressure known in 1925: the pressure that one finds in solid objects like rocks, a pressure due to repulsion between adjacent atoms. But such “rock pressure” was only possible, Eddington believed (incorrectly), if the star’s matter has a density something like that of a rock, a few grams per cubic centimeter—10,000 times less than the present density of Sirius B.
This line of argument led to Eddington’s paradox. In order to reexpand to the density of rock and thereby be able to support itself when it turns cold, Sirius B would have to do enormous work against its own gravity, and physicists did not know of any energy supply inside the star adequate for such work. “Imagine a body continually losing heat but with insufficient energy to grow cold!” Eddington wrote. “It is a curious problem and one may make many fanciful suggestions as to what actually will happen. We here leave aside the difficulty as not necessarily fatal.”
Chandrasekhar had found the resolution of this 1925 paradox in R. H. Fowler’s 1926 article “On Dense Matter.” The resolution lay in the failure of the laws of physics that Eddington used. Those laws had to be replaced by the new quantum mechanics, which described the pressure inside Sirius B and other white dwarfs as due not to heat, but instead to a new, quantum mechanical phenomenon: the degenerate motions of electrons, also called electron degeneracy.3
Electron degeneracy is somewhat like human claustrophobia. When matter is squeezed to a density 10,000 times higher than that of rock, the cloud of electrons around each of its atomic nuclei gets squashed 10,000-fold. Each electron thereby gets confined to a “cell” with 10,000 times smaller volume than the one it previously was allowed to move around in. With so little space available to it, the electron, like a claustrophobic human, starts to shake uncontrollably. It flies about its tiny cell at high speed, kicking with great force against adjacent electrons in their cells. This degenerate motion, as physicists call it, cannot be stopped by cooling the matter. Nothing can stop it; it is forced on the electron by the laws of quantum mechanics, even when the matter is at absolute zero temperature.
This degenerate motion is a consequence of a feature of matter that Newtonian physicists never dreamed of, a feature called wave/particle duality: Every kind of particle, according to quantum mechanics, sometimes behaves like a wave, and every kind of wave sometimes behaves like a particle. Thus, waves and particles are really the same thing, a “thing” that sometimes behaves like a wave and sometimes like a particle; see Box 4.1.
Electron degeneracy is easily understood in terms of wave/particle duality. When matter is compressed to high densities, and each electron inside the matter gets confined to an extremely small cell squeezed up against neighboring electrons’ cells, the electron begins to behave in part like a wave. The wavelength of the electron wave (the distance between its crests) cannot be larger than the electron’s cell; if it were, the wave would extend beyond the cell. Now, particles with very short wavelengths are necessarily highly energetic. (A common example is the particle associated with an electromagnetic wave, the photon. An X-ray photon has a wavelength far shorter than that of a photon of light, and as a result X-ray photons are far more energetic than photons of light. Their higher energies enable the X-ray photons to penetrate human flesh and bone.)
In the case of an electron inside very dense matter, the electron’s short wavelength and accompanying high energy imply rapid motion, and this means that the electron must fly around inside its cell, behaving like an erratic, high-speed mutant: half particle, half wave. Physicists say that the electron is “degenerate,” and they call the pressure that its erratic high speed motion produces “electron degeneracy pressure.” There is no way to get rid of this degeneracy pressure; it is an inevitable consequence of confining the electron to such a small cell. Moreover, the higher the matter’s density, the smaller the cell, the shorter the electron wavelength, the higher the electron energy, the faster the electron’s motion, and thus the larger its degeneracy pressure. In ordinary matter with ordinary densities, the degeneracy pressure is so tiny that one never notices it, but at the huge densities of white dwarfs it is enormous.
A Brief History of Wave/Particle Duality
Already in Isaac Newton’s time (the late 1600s), physicists were struggling over the issue of whether light is made of particles or waves. Newton, though equivocal about the issue, leaned toward particles and called them corpuscles, while Christiaan Huygens argued for waves. Newton’s particle view prevailed until the early 1800s, when the discovery that light can interfere with itself (Chapter 10) converted physicists to Huygens’ wave viewpoint. In the mid-1800s, James Clerk Maxwell put the wave description on a firm footing with his unified laws of electricity and magnetism, and physicists then thought the issue had finally been settled. However, that was before quantum mechanics.
In the 1890s Max Planck noticed hints, in the shape of the spectrum of the light emitted by very hot objects, that something might be missing in physicists’ understanding of light. Einstein, in 1905, showed what was missing: Light sometimes behaves like a wave and sometimes like a particle (now called a photon). It behaves like a wave, Einstein explained, when it interferes with itself; but it behaves like a particle in the photoelectric effect: When a dim beam of light shines on a piece of metal, the beam ejects electrons from the metal one at a time, precisely as though individual particles of light (individual photons) were hitting the electrons and knocking them out of the metal’s surface one by one. From the electrons’ energies, Einstein inferred that the photon energy is always inversely proportional to the light’s wavelength. Thus, the photon and wave properties of light are intertwined; the wavelength is inexorably tied to the photon energy. _Einstein’s discovery of the wave/particle duality of light, and the tentative quantum mechanical laws of physics that he began to build around this discovery, won him the 1921 Nobel Prize in 1922.
Although Einstein almost single-handedly formulated general relativity, he was only one among many who contributed to the laws of quantum mechanics—the laws of the “realm of the small.”
When Einstein discovered the wave/particle duality of light, he did not realize that an electron or proton might also behave sometimes like a particle and sometimes like a wave. Nobody recognized it until the mid-1920s when Louis de Broglie raised it as a conjecture and then Erwin Schrödinger used it as a foundation for a full set of quantum mechanical laws, laws in which an electron is a wave of probability. Probability for what? For the location of a particle. These “new” quantum mechanical laws (which have been enormously successful in explaining how T electrons, protons, atoms, and molecules behave) will not concern us much in this book. However, from time to time a few of their features will be important. In this chapter, the important feature is electron degeneracy.
When Eddington wrote his book, electron degeneracy had not yet been predicted, and it was not possible to compute correctly how rock or other materials will respond if compressed to the ultra-high densities of Sirius B. With the laws of electron degeneracy in hand such computations were now possible, and they had been conceived and carried out by R. H. Fowler in his 1926 article.
According to Fowler’s computations, because the electrons in Sirius B and other white-dwarf stars have been compressed into such tiny cells, their degeneracy pressure is far larger than their thermal (heat-induced) pressure. Accordingly, when Sirius B cools off, its minuscule thermal pressure will disappear, but its enormous degeneracy pressure will remain and will continue to support it against gravity.
Thus, the resolution of Eddington’s white-dwarf paradox was twofold: (1) Sirius B is not supported against its own gravity primarily by thermal pressure as everyone had thought before the advent of the new quantum mechanics; rather, it is supported primarily by degeneracy pressure. (2) When Sirius B cools off, it need not reexpand to the density of rock in order to support itself; rather, it will continue to be supported quite satisfactorily by degeneracy pressure at its present density of 4 million grams per cubic centimeter.
Chandrasekhar, reading these things and studying their mathematical formulations in the library in Madras, was enchanted. This was his first contact with modern astronomy, and he was finding here, side by side, deep consequences of the two twentieth-century revolutions in physics: Einstein’s general relativity, with its new viewpoints on space and time, was showing up in the gravitational redshift of light from Sirius B; and the new quantum mechanics, with its wave/particle duality, was responsible for Sirius B’s internal pressure. This astronomy was a fertile field in which a young man could make his mark.
As he continued his university studies in Madras, Chandrasekhar explored further the consequences of quantum mechanics for the astronomical Universe. He even wrote a small article on his ideas, mailed it to England to R. H. Fowler, whom he had never met, and Fowler arranged for it to be published.
Finally, in 1930 at age nineteen, Chandrasekhar completed the Indian equivalent of an American bachelor’s degree, and in the last week of July he boarded a steamer bound for far-off England. He had been accepted for graduate study at Cambridge University, the home of his heroes, R. H. Fowler and Arthur Eddington.
The Maximum Mass
Those eighteen days at sea, steaming from Madras to Southampton, were Chandrasekhar’s first opportunity in many months to think quietly about physics without the distraction of formal studies and examinations. The solitude of the sea was conducive to thought, and Chandrasekhar’s thoughts were fertile. So fertile, in fact, that they would help to win him the Nobel Prize, but only fifty-four years later, and only after a great struggle to get them accepted by the world’s astronomical community.
Aboard the steamer, Chandrasekhar let his mind reminisce over white dwarfs, Eddington’s paradox, and Fowler’s resolution. Fowler’s resolution almost certainly had to be correct; there was none other in sight. However, Fowler had not worked out the full details of the balance between degeneracy pressure and gravity in a white-dwarf star, nor had he computed the star’s resulting internal structure—the manner in which its density, pressure, and gravity change as one goes from its surface down to its center. Here was an interesting challenge to help ward off boredom during the long voyage.
As a tool in working out the star’s structure, Chandrasekhar needed to know the answer to the following question: Suppose that white-dwarf matter has already been compressed to some density (for example, a density of a million grams per cubic centimeter). Compress the matter (that is, reduce its volume and increase its density) by an additional 1 percent. The matter will protest against this additional compression by raising its pressure. By what percentage will its pressure go up? Physicists use the name adiabatic index for the percentage increase in pressure that results from a 1 percent additional compression. In this book I shall use the more graphic name resistance to compression or simply resistance. (This “resistance to compression” should not be confused with “electrical resistance”; they are completely different concepts.)
Chandrasekhar worked out the resistance to compression by examining step by step the consequences of a 1 percent increase in the density of white-dwarf matter: the resulting decrease in electron cell size, the decrease in electron wavelength, the increase in electron energy and speed, and finally the increase in pressure. The result was clear: A 1 percent increase in density produced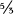 
of a percent (1.667 percent) increase in pressure. The resistance of white-dwarf matter, therefore, was .
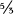Many decades before Chandrasekhar’s voyage, astrophysicists had computed the details of the balance of gravity and pressure inside any star whose matter has a resistance to compression that is independent of depth in the star-that is, a star whose pressure and density increase in step with each other, as one moves deeper and deeper into the star, with a 1 percent increase in density always accompanied by the same fixed percentage increase in pressure. The details of the resulting stellar structures were contained in Eddington’s book The Internal Constitution of the Stars, which Chandrasekhar had brought on board the ship because he treasured it so much. Thus, when Chandrasekhar discovered that white-dwarf matter has a resistance to compression of 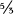, independent of its density, he was pleased. He could now go directly to Eddington’s book to discover the star’s internal structure: the manner in which its density and pressure changed from surface to center.
Among the things that Chandrasekhar discovered, by combining the formulas in Eddington’s book with his own formulas, were the density at the center of Sirius B, 360,000 grams per cubic centimeter (6 tons per cubic inch), and the speed of the electrons’ degeneracy motion there, 57 percent of the speed of light.
This electron speed was disturbingly large. Chandrasekhar, like R. H. Fowler before him, had computed the resistance of white-dwarf matter using the laws of quantum mechanics, but ignoring the effects of relativity. However, when any object moves at almost the speed of light, even a particle obeying the laws of quantum mechanics, the effects of special relativity must become important. At 57 percent of the speed of light, relativity’s effects might not be too terribly big, but a more massive white dwarf with its stronger gravity would require a larger central pressure to support itself, and the random speeds of its electrons would be correspondingly higher. In such a white dwarf the effects of relativity surely could not be ignored. So Chandrasekhar returned to the starting point of his analysis, the calculation of the resistance to compression for white-dwarf matter, vowing to include the effects of relativity this time around.
To include relativity in the computation would require meshing the laws of special relativity with the laws of quantum mechanics—a mesh that the great minds of theoretical physics were only then working out. Alone on the steamer and barely graduated from university, Chandrasekhar could not produce that full mesh. However, he was able to produce enough to indicate the principal effects of high electron speeds.
Quantum mechanics insists that when already dense matter is compressed a bit, making each electron’s cell smaller than it was, the electron’s wavelength must decrease and correspondingly the energy of its degeneracy motion must increase. However, Chandrasekhar realized, the nature of the additional electron energy is different, depending on whether the electron is moving slowly compared to light or at close to light speed. If the electron’s motion is slow, then, as in everyday life, an increase of energy means more rapid motion, that is, higher speed. If the electron is already moving at close to light speed, however, there is no way its speed can go up much (if it did, it would exceed the speed limit!), so the energy increase takes a different form, one unfamiliar in everyday life: The additional energy goes into inertia; that is, it increases the electron’s resistance to being speeded up-it makes the electron behave as though it had become a bit heavier. These two different fates of the added energy (added speed versus added inertia) produce different increases in the electron’s pressure, and thus different resistances to compression, Chandrasekhar deduced: at low electron speeds, a resistance of 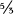the same as he had computed before; at high speeds, a resistance of 
.
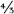By combining his 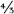resistance for relativistically degenerate matter (that is, matter so dense that the degenerate electrons move at nearly the speed of light) with the formulas given in Eddington’s book, Chandrasekhar then deduced the properties of high-density, high-mass white dwarfs. The answer was astonishing: The high-density matter would have difficulty supporting itself against gravity—sufficient difficulty that only if the star’s mass were less than that of 1.4 Suns could the squeeze of gravity be counterbalanced This meant that no white dwarf could ever have a mass exceeding 1.4 solar masses!
With his limited knowledge of astrophysics, Chandrasekhar was deeply puzzled about the meaning of this strange result. Time and again Chandrasekhar checked his calculations, but he could find no error. So, in the last few days of his voyage, he wrote two technical manuscripts for publication. In one he described his conclusions about the structure of low-mass, low-density white dwarfs such as Sirius B. In the other he explained, very briefly, his conclusion that no white dwarf can ever be heavier than 1.4 Suns.
When Chandrasekhar arrived in Cambridge, Fowler was out of the country. In September, when Fowler returned, Chandrasekhar eagerly went to his office and gave him the two manuscripts. Fowler approved the first one and sent it to Philosophical Magazine for publication, but the second one, the white-dwarf maximum mass, puzzled him. He could not understand Chandrasekhar’s proof that no white dwarf can be heavier than 1.4 Suns; but then, he was a physicist rather than an astronomer, so he asked his colleague, the famous astronomer E. A. Milne, to look at it. When Milne couldn’t understand the proof either, Fowler declined to send it for publication.
Chandrasekhar was annoyed. Three months had passed since his arrival in England, and Fowler had been sitting on his paper for two months. This was too long to wait for approval to publish. So, piqued, Chandrasekhar abandoned his attempts to publish in Britain and mailed the manuscript to the Astrophysical Journal in America.
After some weeks there came a response from the editor at the University of Chicago: The manuscript had been sent to the American physicist Carl Eckart for refereeing. In the manuscript Chandrasekhar stated, without explanation, the result of his relativistic and quantum mechanical calculation, that the resistance to compression is 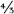at ultra-high densities. This 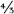resistance was essential to the limit on how heavy a white dwarf can be. If the resistance were larger than 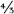, then white dwarfs could be as heavy as they wished—and Eckart thought it should be larger. Chandrasekhar fired off a reply containing a mathematical derivation of the 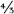resistance; Eckart, reading the details, conceded that Chandrasekhar was right and approved his paper for publication. Finally, a full year after Chandrasekhar had written it, his paper got published.4
The response of the astronomical community was deafening silence. Nobody seemed interested. So Chandrasekhar, wanting to complete his Ph.D. degree, turned to other, more acceptable research.
Three years later, with his Ph.D. finished, Chandrasekhar visited Russia to exchange research ideas with Soviet scientists. In Leningrad a young Armenian astrophysicist, Viktor Amazapovich Ambartsumian, told Chandrasekhar that the world’s astronomers would not believe his strange limit on the masses of white dwarfs unless he computed, from the laws of physics, the masses of a representative sample of white dwarfs and demonstrated explicitly that they were all below his claimed limit. It was not enough, Ambartsumian asserted, that Chandrasekhar had analyzed white dwarfs with rather low densities and resistances of 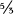, and white dwarfs with extremely high densities and resistances of 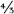; he needed also to analyze a goodly sample of white dwarfs with densities in between and show that they, too, always have masses below 1.4 Suns. Upon returning to Cambridge, Chandrasekhar took up Ambartsumian’s challenge.
One foundation that Chandrasekhar would need was the equation of state of white-dwarf matter over the entire range of densities, running from low to extremely high. (By the “state” of the matter, physicists mean the matter’s density and pressure—or equivalently its density and its resistance to compression, since from the resistance and the density one can compute the pressure. By “equation of state” is meant the relationship between the resistance and the density, that is, the resistance as a function of density.)
In late 1934, when Chandrasekhar took up Ambartsumian’s challenge, the equation of state for white-dwarf matter was known, thanks to calculations by Edmund Stoner of Leeds University in England and Wilhelm Anderson of Tartu University in Estonia. 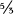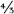The Stoner–Anderson equation of state showed that, as the density of the white-dwarf matter is squeezed higher and higher, moving from the nonrelativistic regime of low densities and low electron speeds into the relativistic domain of extremely high densities and electron speeds near the speed of light, the matter’s resistance to compression decreases smoothly from to (left half of Figure 4.3). The resistance could not have behaved more simply.
To meet Ambartsumian’s challenge, Chandrasekhar had to combine this equation of state (this dependence of resistance on density) with the star’s law of balance between gravity and pressure, and thereby obtain a differential equation5 describing the star’s internal structure—that is, describing the variation of its density with distance from the star’s center. He then had to solve that differential equation for a dozen or so stars that have central densities spanning the range from low to extremely high. Only by solving the differential equation for each star could he learn the star’s mass, and see whether it is less than 1.4 Suns.
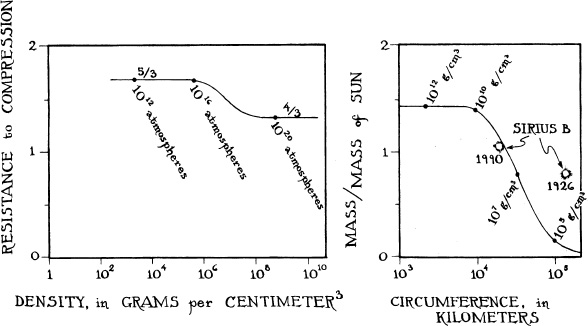
4.3 Left: The Stoner–Anderson equation of state for white-dwarf matter, that is, the relationship between the matter’s density and its resistance to compression. Plotted horizontally is the density to which the matter has been squeezed. Plotted vertically is its resistance (the percentage increase of pressure that accompanies a 1percent increase of density). Along the curve is marked the squeeze pressure (equal to internal pressure), in multiples of the pressure of the Earth’s atmosphere. Right: The circumferences (plotted horizontally) and masses (plotted vertically) of white-dwarf stars as computed by Chandrasekhar using Eddington’s Braunschweiger mechanical calculator. Along the curve is marked the density of the matter at the center of the star, in grams per cubic centimeter.
For stars with low or extremely high central density, which Chandrasekhar had studied on the steamer, he had found the solution to the differential equation and the resulting stellar structures in Eddington’sbook; but for stars with intermediate densities Eddington’s book was of no help and, despite great effort, Chandrasekhar was not able to deduce the solution using mathematical formulas. The mathematics was too complicated. There was no recourse but to solve his differential equation numerically, on a computer.
Now, the computers of 1934 were very different from those of the 1990s. They were more like the simplest of pocket calculators: They could only multiply two numbers at a time, and the user had to enter those numbers by hand, then turn a crank. The crank set into motion a complicated morass of gears and wheels which performed the multiplication and gave the answer.
Such computers were precious machines; it was very hard to gain access to one. But Arthur Eddington owned one, a “Braunschweiger” about the size of an early 1990s desk-top personal computer; so Chandrasekhar, who by now had become well acquainted with the great man, went to Eddington and asked to borrow it. Eddington at the time was embroiled in a controversy with Milne over white dwarfs and was eager to see the full details of white-dwarf structure worked out, so he let Chandrasekhar cart the Braunschweiger off to the rooms in Trinity College where Chandrasekhar was living.
The calculations were long and tedious. Each evening after dinner Eddington, who was a fellow of Trinity College, would ascend the stairs to Chandrasekhar’s rooms to see how they were coming and to give him encouragement.
At last, after many days, Chandrasekhar finished. He had met Ambartsumian’s challenge. For each of ten representative white-dwarf stars, he had computed the internal structure, and then from it the star’s total mass and its circumference. All the masses were less than 1.4 Suns, as he had firmly expected. Moreover, when he plotted the stars’ masses and circumferences on a diagram and “connected the dots,” he obtained a single, smooth curve (right half of Figure 4.3; see also Box 4.2), and the measured masses and circumferences of Sirius B and other known white dwarfs agreed with that curve moderately well. (With improved, modern astronomical observations, the fit has become much better; note the new, 1990 values of the mass and circumference of Sirius B in Figure 4.3.) Proud of his results and anticipating that the world’s astronomers would finally accept his claim that white dwarfs cannot be heavier than 1.4 Suns, Chandrasekhar was very happy.
Especially gratifying would be the opportunity to present these results to the Royal Astronomical Society in London. Chandrasekhar was scheduled for a presentation on Friday, 11 January 1935. Protocol dictated that the details of the meeting’s program be kept secret until the meeting started, but Miss Kay Williams, the assistant secretary of the Society and a friend of Chandrasekhar’s, was in the habit of sending him programs secretly in advance. On Thursday evening when the program arrived in the mail, he was surprised to discover that immediately following his own talk there would be a talk by Eddington on the subject of “Relativistic Degeneracy.” Chandrasekhar was a little annoyed. For the past few months Eddington had been coming to see him at least once a week about his work and had been reading drafts of the articles he was writing, but never once had Eddington mentioned doing any research of his own on the same subject!
Box 4.2
An Explanation of the Masses and Circumferences of White-Dwarf Stars
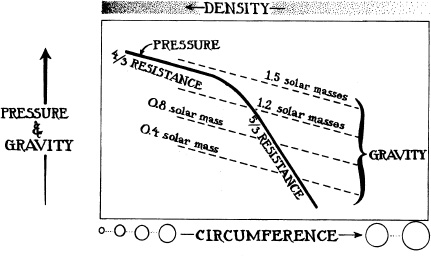
To understand qualitatively why white dwarfs have the masses and circumferences shown in Figure 4.3, examine the drawing below. It shows the average pressure and gravity inside a white dwarf (plotted upward) as functions of the star’s circumference (plotted rightward) or density (plotted leftward). If one compresses the star, so its density increases and its circumference decreases (leftward motion in the drawing), then the star’s pressure goes up in the manner of the solid curve, with a sharper rise at low densities where the resistance to compression is 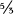, and a slower rise at high densities where it is 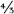. This same compression of the star causes the star’s surface to move in toward its center, thereby increasing the strength of the star’s internal gravity in the manner of the dashed lines. The rate of gravity’s increase is analogous to a 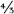resistance: There is a 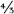percent increase in gravity’s strength for each 1 percent compression. The drawing shows several dashed gravity lines, one for each value of the star’s mass, because the greater the star’s mass, the stronger its gravity.
Inside each star, for example a 1.2-solar-mass star, gravity and pressure must balance each other. The star, therefore, must reside at the intersection of the dashed gravity line marked “1.2 solar masses” and the solid pressure curve; this intersection determines the star’s circumference (marked on bottom of graph). If the circumference were larger, then the star’s dashed gravity line would be above its solid pressure curve, gravity would overwhelm pressure, and the star would implode. If the circumference were smaller, pressure would overwhelm gravity, and the star would explode.
The intersections of the several dashed lines with the solid curve correspond to the masses and circumferences of equilibrium white dwarfs, as shown in the right half of Figure 4.3. For a star of small mass (lowest dashed line), the circumference at the intersection is large. For a star of higher mass (higher dashed lines), the circumference is smaller. For a star with mass above 1.4 Suns, there is no intersection whatsoever; the dashed gravity line is always above the solid pressure curve, so gravity always overwhelms pressure, no matter what the star’s circumference may be, forcing the star to implode.
Suppressing his annoyance, Chandrasekhar went down to dinner. Eddington was there, dining at high table, but protocol dictated that, just because’ you knew so eminent a man, and just because he had been expressing an interest in your work, you did not thereby have a right to go bother him about such a matter as this. So Chandrasekhar sat down elsewhere and held his tongue.
After dinner Eddington himself sought Chandrasekhar out and said, “I’ve asked Smart to give you half an hour tomorrow instead of the customary fifteen minutes.” Chandrasekhar thanked him and waited for him to say something about his own talk, but Eddington just excused himself and left. Chandrasekhar’s annoyance acquired an anxious twinge.
The next morning Chandrasekhar took the train down to London and a taxi to Burlington House, the home of the Royal Astronomical Society. While he and a friend, Bill McCrea, were waiting for the meeting to start, Eddington came walking by, and McCrea, having just read the program, asked, “Well, Professor Eddington, what are we to understand by ‘Relativistic Degeneracy’?” Eddington, in reply, turned to Chandrasekhar and said, “That’s a surprise for you,” and walked off leaving Chandrasekhar even more anxious.
Left: Arthur Stanley Eddington in 1932. Right: Subrahmanyan Chandrasekhar in 1934. [Left: courtesy UPI/Bettmann; right: courtesy S. Chandrasekhar.]
At last the meeting started. Time dragged by as the Society president made various announcements, and various astronomers gave miscellaneous talks. At last it was Chandrasekhar’s turn. Suppressing his anxiety, he gave an impeccable presentation, emphasizing particularly his maximum mass for white dwarfs.
After polite applause from the fellows of the Society, the president invited Eddington to speak.
Eddington began gently, by reviewing the history of white-dwarf research. Then, gathering steam, he described the disturbing implications of Chandrasekhar’s maximum-mass result:
In Chandrasekhar’s diagram of the mass of a star plotted vertically and its circumference plotted horizontally (Figure 4.4), there is only one set of masses and circumferences for which gravity can be counterbalanced by nonthermal pressure (pressure that remains after the star turns cold): that of white dwarfs. In the region to the left of Chandrasekhar’s white-dwarf curve (shaded region; stars with smaller circumferences), the star’s nonthermal degeneracy pressure completely overwhelms gravity. The degeneracy pressure will drive any star in the shaded region to explode. In the region to the right of the white-dwarf curve (white region; stars with larger circumferences), gravity completely overwhelms the star’s degeneracy pressure. Any cold star which finds itself in this region will immediately implode under gravity’s squeeze.
The Sun can live in the white region only because it is now very hot; its thermal (heat-induced) pressure manages to counterbalance its gravity. However, when the Sun ultimately cools down, its thermal pressure will disappear and it no longer will be able to support itself. Gravity will force it to shrink smaller and smaller, squeezing the Sun’s electrons into smaller and smaller cells, until at last they protest with enough degeneracy pressure (nonthermal pressure) to halt the shrinkage. During this shrinkage “death,” the Sun’s mass will remain nearly constant, but its circumference will decrease, so it will move leftward on a horizontal line in Figure 4.4, finally stopping on the white-dwarf curve—its grave. There, as a white dwarf, the Sun will continue to reside forever, gradually cooling and becoming a black dwarf—a cold, dark, solid object about the size of the Earth but a million times heavier and denser.
This ultimate fate of the Sun seemed quite satisfactory to Eddington. Not so.the ultimate fate of a star more massive than Chandrasekhar’s white-dwarf limit of 1.4 solar masses-for example, Sirius, the 2.3-solar-mass companion of Sirius B. If Chandrasekhar were right, such a star could never die the gentle death that awaits the Sun. When the radiation it emits into space has carried away enough heat for the star to begin to cool, its thermal pressure will decline, and gravity’s squeeze will make it shrink smaller and smaller. For so massive a star as Sirius, the shrinkage cannot be halted by nonthermal degeneracy pressure. This is clear from Figure 4.4, where the shaded region does not extend high enough to intercept Sirius’s shrinking track. Eddington found this prediction disturbing.
“The star has to go on radiating and radiating and contracting and contracting,” Eddington told his audience, “until, I suppose, it gets down to a few kilometers radius, when gravity becomes strong enough to hold in the radiation, and the star can at last find peace.” (In the words of the 1990s, it must form a black hole.) “Dr. Chandrasekhar had got this result before, but he has rubbed it in in his last paper; and, when discussing it with him, I felt driven to the conclusion that this was almost a reductio ad absurdum of the relativistic degeneracy formula. Various accidents may intervene to save the star, but I want more protection than that. I think there should be a law of Nature to prevent a star from behaving in this absurd way!”
Then Eddington argued that Chandrasekhar’s mathematical proof of his result could not be trusted because it was based on an inadequately sophisticated meshing of special relativity with quantum mechanics. “I do not regard the offspring of such a union as born in lawful wedlock,” Eddington said. “1 feel satisfied myself that [if the meshing is made correctly], the relativity corrections are compensated, so that we come back to the ‘ordinary’ formula” (that is, to a resistance, which would permit white dwarfs to be arbitrarily massive and thereby would enable pressure to halt the contraction of Sirius at the hypothetical dotted curve in Figure 4.4). Eddington then sketched how he thought special relativity and quantum mechanics should be meshed, a rather different kind of mesh than Chandrasekhar, Stoner, and Anderson had used, and a mesh, Eddington claimed, that would save all stars from the black-hole fate.
Chandrasekhar was shocked. He had never expected such an attack on his work. Why had Eddington not discussed it with him in advance? And as for Eddington’s argument, to Chandrasekhar it looked specious—almost certainly wrong.
Now, Arthur Eddington was the great man of British astronomy. His discoveries were almost legendary. He was largely responsible for as tronomers’ understanding of normal stars like the Sun and Sirius, their interiors, their atmospheres, and the light that they emit; so, naturally, the fellows of the Society, and astronomers throughout. the world, listened with great respect. Clearly, if Eddington thought Chandrasekhar’s analysis incorrect, then it must be incorrect.
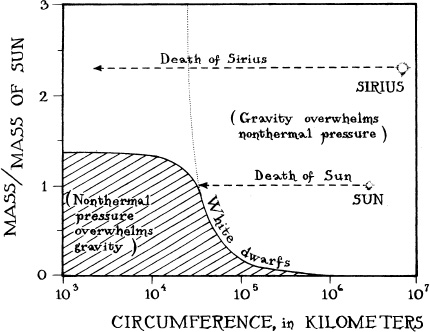
4.4 When a normal star such as the Sun or Sirius (not Sirius B) starts to cool off, it must shrink, moving leftward in this diagram of mass versus circumference. The shrinkage of the Sun will stop when it reaches the edge of the shaded region (the white-dwarf curve). There degeneracy pressure balances gravity’s squeeze. The shrinkage of Sirius, by contrast, cannot be so stopped because it never reaches the edge of the shaded region. See Box 4.2 for a different depiction of these conclusions. If, as Eddington claimed, white-dwarf matter’s resistance to compression were always 5/3, that is, if relativity did not reduce it to 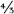at high densities, then the graph of mass versus circumference would have the form of the faint dotted curve, and the shrinkage of Sirius would stop there.
After the meeting, one fellow after another came up to Chandrasekhar to offer condolences. “I feel it in my bones that Eddington is right,” Milne told him.
The next day, Chandrasekhar began appealing to his physicist friends for help. To Leon Rosenfeld in ‘Copenhagen, he wrote, “If Eddington is right, my last four months’ work all goes in the fire. Could Eddington be right? I should very much like to know Bohr’s opinion.” (Niels Bohr was one of the fathers of quantum mechanics and the most respected physicist of the 1930s.) Rosenfeld replied two days later, with assurances that he and Bohr both were convinced that Eddington was wrong and Chandrasekhar right. “I may say that your letter was some surprise for me,” he wrote, “for nobody had ever dreamt of questioning the equations [that you used to derive the 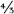resistance] and Eddington’s remark as reported in your letter is utterly obscure. So I think you had better cheer up and not let you scare [sic] so much by high priests.” In a follow-up letter on the same day, Rosenfeld wrote, “Bohr and I are absolutely unable to see any meaning in Eddington’s statements.”
But for astronomers, the matter was not so clear at first. They had no expertise in these issues of quantum mechanics and relativity, so Eddington’s authority held sway amongst them for several years. Moreover, Eddington stuck to his guns. He was so blinded by his opposition to black holes that his judgment was totally clouded. He so deeply wanted there to “be a law of Nature to prevent a star from behaving in this absurd way” that he continued to believe for the rest of his life that there is such a law—when, in fact, there is none.
By the late 1930s, astronomers, having talked to their physicist colleagues, understood Eddington’s error, but their respect for his enormous earlier achievements prevented them from saying so in public. In a lecture at an astronomy conference in Paris in 1939, Eddington once again attacked Chandrasekhar’s conclusions. As Eddington attacked, Chandrasekhar passed a note to Henry Norris Russell (a famous astronomer from Princeton University in America), who was presiding. Chandrasekhar’s note asked for permission to reply. Russell passed back a note of his own saying, “I prefer you don’t,” even though earlier in the day Russell had told Chandrasekhar privately, “Out there we don’t believe in Eddington.”
With the world’s leading astronomers having finally—at least behind Eddington’s back—accepted Chandrasekhar’s maximum mass for white dwarfs, were they then ready to admit that black holes might exist in the real Universe? Not at all. If nature provided no law against them of the sort that Eddington had sought, then nature would surely find another way out: Presumably, every massive star would eject enough matter into interstellar space, as it ages or during its death throes, to reduce its mass below 1.4 Suns and thereby enter a safe, white-dwarf grave. This was the view to which most astronomers turned when Eddington lost his battle, and they adhered to it through the 1940s and 1950s, and into the early 1960s.
As for Chandrasekhar, he was badly burned by the controversy with Eddington. As he recalled some forty years later, “I felt that astronomers without exception thought that I was wrong. They considered me as a sort of Don Quixote trying to kill Eddington. As you can imagine, it was a very discouraging experience for me—to find myself in a controversy with the leading figure of astronomy and to have my work completely and totally discredited by the astronomical community. I had to make up my mind as to what to do. Should I go on the rest of my life fighting? After all I was in my middle twenties at that time. I foresaw for myself some thirty to forty years of scientific work, and I simply did not think it was productive to constantly harp on something which was done. It was much better for me to change my field of interest and go into something else.”
So in 1939 Chandrasekhar turned his back on white dwarfs and stellar death, and did not return to them for a quarter century (Chapter 7).
And what of Eddington? Why did he treat Chandrasekhar so badly? To Eddington, the treatment may not have seemed bad at all. Roughand- tumble, freewheeling intellectual conflict was a way of life for him. Treating young Chandrasekhar in this manner may have been, in some sense, a measure of respect, a sign that he was accepting Chandrasekhar as a member of the astronomical establishment. In fact, from their first confrontation in 1935 until Eddington’s death in 1944, Eddington displayed warm personal affection for Chandrasekhar, and Chandrasekhar, though burned by the controversy, reciprocated.
1. For a clear discussion of the laws of quantum mechanics, see The Cosmic Code by Heinz Pagels (Simon and Schuster, 1982).
2. It is dangerously easy, in a delicate measurement, to get the result that one thinks one is supposed to get. Adams’s gravitational redshift measurement is an example. His result agreed with the predictions, but the predictions were severely wrong (five times too small) due to errors in astronomers’ estimates of the mass and circumference of Sirius B.
3. This usage of the word “degenerate” does not have its origins in the concept of “moral degeneracy” (the lowest possible level of morality), but rather in the concept of the electrons having reached their lowest possible levels of energy.
4. In the meantime, Edmund C. Stoner had independently derived and published the existence of the white-dwarf maximum mass, but his derivation was rather less convincing than Chandrasekhar’s because it pretended the star had a constant density throughout its interior.
5. A differential equation is one that combines in a single formula various functions and their rates of change, that is, the functions and their “derivatives.” In Chandrasekhar’s differential equation, the functions were the star’s density and pressure and the strength of its gravity, and they were functions of distance from the star’s center. The differential equation was a relation between these functions and the rate that they change as one moves outward through the star. By “solve the differential equation” is meant “compute the functions themselves from this differential equation.”