APPENDIX A
CHRONOLOGY OF RENNES-LE-CHÂTEAU
The authors and publishers are very grateful to Paul Smith, one of the most accurate and painstaking of all the Rennes-le-Château researchers, for permission to include his Chronology.
c410 |
Possible Rhedae, major Visigothic strategic outpost in Septimania. (Rennes-le-Château, Châteaux de Blanchefort and Bézu/“Albedun” are all constructed on Visigothic foundations forming an isosceles triangle with angles 36°, 72°, 72°. |
1210 |
Destruction of the Château de Blanchefort, during the Crusade against the Cathars. |
1633 |
Guillaume de Catel's account, stating that workers were imported all the way from Germany to excavate the mines by Rennes-les-Bains (Mémoires de l'Histoire du Languedoc, Tome I, p. 51). |
1645 |
Legend of the shepherd “Jean” (Folklore (Aude), Nr. 8, p. 137, 1938). Legend of the shepherd Ignace Paris (Noël Corbu, Essai Historique sur Rennes-le-Château, 1962). |
1709 |
Antiquités des Bains de Monferran communement appelés les Bains de Rennes by Abbé Antoine Delmas, vicar at Rennes-les-Bains. |
1732 |
Marriage of Marie de Nègre d'Ables to François d'Hautpoul, first Marquis de Blanchefort. |
1780 |
Jean-Baptiste Siau, notary at Espéraza, refused to give the Hautpoul family will to Pierre Françoise d'Hautpoul, under the pretext: “It would be unwise of me to let a will of such great consequence out of my hands”. (Rennes et ses derniers seigneurs by René Descadeillas, pp. 7-8) |
c1780 |
Legend of the “Devil's Treasure” (Voyages à Rennes-les-Bains by Auguste de Labouisse-Rochefort, pp. 469-471, 1832). |
1781 |
Death of Marie de Nègre d'Ables, Countess Hautpoul-Blanchefort: the mysterious epitaph on her tombstone containing errors which point out the words MORT épée (Excursion de 25 Juin 1905 à Rennes-le-Château by Elie Tisseyre, Bulletin de la Société d'études Scientifiques de l'Aude, Tome XVII, pp. 98-106, 1906). |
“1872” |
“Death” of Abbé Jean Vié, vicar at Rennes-les-Bains, whose epitaph reveals that he was named priest when 32, and “died” 32 years later (the chessboard motif: 32 “white years” before becoming priest, then 32 “black years” as a priest). |
1880 |
“In the Middle Ages it was believed that the precious metals extracted from the Blanchefort mine came, not from a vein in the rock, but from a store of gold and silver ingots buried in the dungeons of the fortress by its first masters, the Visigothic kings.” (Histoire du comté de Razes et du diocèse d'Alet, by Louis Fédié). |
1885 |
François-Bérenger Saunière (1852-1917) appointed Parish Priest of Rennes-le-Château, at the Church of St. Mary Magdalen. |
1886 |
Saunière temporarily transferred to the Seminary at Narbonne for delivering anti-Republican, right-wing sermons during the elections. |
1887 |
Saunière reinstated at Rennes-le-Château: began renovating his church — moved the “Knight's Stone” which lay face-down before the main Altar (which was probably the entrance to the Hautpoul family burial vault beneath the church), and made his fateful discovery… Church renovation details (1887-1900) are introduced by the character as below.
|
1890-91 |
Saunière in charge by interim at Antugnac, near Rennes-le-Château. |
1891 |
Visigothic Pillar/Statue of the Lourdes Virgin: ceremony June 21st. “Lettre de Granès. Découverte d'un tombeau, le soir pluie.” (Saunière's diary, September 21st). “Vu curé de Névian — Chez Gélis — Chez Carrière — Vu Cros en secret.” (Saunière's diary, September 29th).
|
1892 |
Treasurer of the Conseil de Fabrique resigned stating he found the duties of the post contrary to his beliefs; replaced by Guillaume Dénarnaud. (The Church's income rose from 239.60Frs 1886 to 1914.80Frs in 1888, returning to its original level in 1893). |
1893 |
Confessional (700Frs; M. Mestre, Limoux). |
1895 |
Letters of complaint sent against Saunière to the Préfet de l'Aude, regarding his clandestine activities in the cemetery. |
1897 |
|
1898 |
Collecting-trunk made from oak (400Frs; M. Mestre, Limoux). |
c1900 |
Bas-Relief of St. Mary Magdalen at the foot of the Altar (reverse image of a stained-glass window from Puichéric church). |
1902 |
Mgr. Paul-Félix Beuvain de Beauséjour replaces Mgr. Félix-Arsène Billard as Bishop of Carcassonne. |
1901-05 |
Villa Béthanie; Tour Magdala; gardens and terraces, etc. |
New Altar (700Frs; F. D. Monna, Toulouse)| Owner: | Mlle. Marie Dénarnaud | |
| Promoter: | Abbé Berénger Saunière | |
| Architect: | Tiburce Caminade (Limoux) | |
| Master-Builder: | Elie Bot (Luc-sur-Aude) | |
| Plasterer: | Tisseyre | |
| Carpenters: | Oscar Vila (Couiza) | |
| Jean Idrac (Toulouse) | ||
| Painters: | Georges Castex (Limoux) | |
| V. Laffon | ||
| Ironmonger: | Charles Dénarnaud (Alet) | |
| Papers/Paints: | Duchesne (Paris) | |
| Tile-Flooring: | Taillefer (Trèbes) | |
| Materials: | Sté des Chaux et Ciments d'Albi Ciments Bethelot de Grenoble |
“1903”(?) |
Galibert family erect the “Poussin-Tomb” at Les Pontils m Peyrolles (dismantled April 9th 1988). |
1905-06 |
Separation of the Church from State in France. Saunière's superiors demand he show his accounts and give an explanation of his source of wealth. |
1909 |
Saunière transferred to Coustouge: replaced by Abbé Marty at Rennes-le-Château; but he refused his nomination and built a private altar in the Villa Béthanie. |
1910-11 |
Saunière's trial before the Carcassonne Bishopric, to account for his source of wealth. |
1911 |
Bishop of Carcassonne issues a strong warning against Saunière, accusing him of simony and forbidding him to administer the Sacraments: Carcassonne February 1st (Semaine Religieuse de Carcassonne, February 3rd). Following three sentences against him (dated July 23rd 1910, November 5th 1910 and December 5th 1911), Saunière sought assistance from Rome, unsuccessfully. He never regained his position as Parish Priest of Rennes-le-Château. |
1915 |
Reminder to the local population of Saunière's interdiction in Semaine Religieuse de Carcassonne, July 3rd. |
1917 |
Death of Saunière, his interdiction being lifted only in articulo mortis (“at the moment of death”). He is not described as a priest in the obituary column of Semaine Religieuse de Carcassonne of January 27th. |
1931 |
Pamphlet version of Elie Tisseyre's 1906 article deposited in the Municipal Library of Carcassonne, by “Marty”. |
1946 |
Noël Corbu purchases Saunière's old estate held m Marie Dénarnaud's name. |
1953 |
Marie Dénarnaud dies aged 85; Noël Corbu inherits her archives relating to Bérenger Saunière. |
1956 |
First popular account of the Saunière mystery: La Fabuleuse Découverte du Curé aux Milliards de Rennes-le-Château by Albert Salamon (appearing in La Dépêche du Midi, January 12th, 13th and 14th). |
1962 |
Essai Historique sur Rennes-le-Château by Noël Corbu (5-page MS deposited in the Archives de l'Aude, Carcassonne); possible transcript of a 1955/56 tape-recording made for the tourists to Rennes-le-Château. |
1964 |
Henri Buthion acquires Saunière's old estate. |
1968 |
Noël Corbu tragically killed in a car crash. |
1974 |
Mythologie du Trésor de Rennes: Histoire véritable de l'Abbé Saunière, Curé de Rennes-le-Château by René Descadeillas (Mémoires de la Société des Arts et des Sciences de Carcassonne, Années 1971-72, 4me série, Tome VU, 2me partie). |
1983 |
Le Fabuleux Trésor de Rennes-le-Château! Le Secret de l'Abbe Saunière by Jacques Rivière (Éditions Bélisane). |
1985 |
Histoire du Trésor de Rennes-le-Château by Pierre Jarnac (Éditions Bélisane). L'Héritage de l'Abbé Saunière by Claire Corbu and Antoine Captier (Éditions Bélisane). |
1987 |
Les Archives de Rennes-le-Château, Tome 1 by Pierre Jamac (Éditions Bélisane). |
1988 |
Les Archives de Rennes-le-Château, Tome 2 by Pierre Jamac (Éditions Bélisane). |
1989 |
Formation of Association Terre de Rhedae (May), devoted to historical research of the mystery. Its President, Antoine Captier, is curator of the Saunière Museum at Rennes. |
APPENDIX B
GERVASE OF TILBURY'S ACCOUNT OF “SHIPPING THE DEAD” TO ARLES (CIRCA 1210)
The Anglo-Latin writer, priest, scholar and adventurer, Gervase of Tilbury, was related to Patrick, Earl of Salisbury. Before 1177 Gervase taught Law in Bologna. Later he worked for Henry fitz Henry in England, for William of Champagne (the Cardinal Archbishop of Rheims) and William II of Sicily. Shortly before 1200 he was employed by Emperor Otto IV, who promoted him to be Marshall of the Kingdom of Arles, where, despite being in holy orders, he married a rich and beautiful young heiress.
His Otia Imperialia trilogy was written for the Emperor in 1211. It is a fascinating mixture of political theory, geography, history and folklore.
Cathars, Templars and the Knights of St. John were all flourishing in the vicinity of Arles at the time. The famous Venus of Arles was discovered in the remains of the Roman Theatre there in 1651 – during the period when Poussin was painting. Marie de Nègre's tombstone records her as “Dame d'Arles”.
What Gervase says about floating corpses and treasure could be linked to M. Patin's ideas about Rennes-le-Château being laid out to resemble a “ship of the dead” bearing a giant warrior.
Gervase's text (Otia Imperialia, Decisio iii, c.90) follows, in both the original Latin and in an English translation. The authors wish to thank Father Martin I. Williams, Vicar of the parish of St. German, Roath, for advice on the mediaeval Latin.
Insigne mirum ac ex divina virtute miraculum audi, Princeps Sacratissime. Caput regni Burgundionum, quod Arelatense dicitur, civitas est Arelas, antiquissimis dotata privilegiis. Hanc ordinatus ab Apostolis Petro et Paulo, Trophimus, qui…deliberavit coemeterium solemne ad meridianam urbis partem constituere, in quo omnium orthodoxorum corpora sepulturae traderentur, ut, sicut ab Arelatensi ecclesia tota Gallia fidei sumsit exordium, ita et mortui in Christo undecunque advecti sepulturae communis haberent beneficium. Facta itaque consecratione solemni per manus sanctissimorum antistitum ad Orientalem Portam, ubi nunc est ecclesia ab ipsis in honorem B. Virginis consecrata, illis Christus, pridem in came familiariter agnitus, apparuit, opus eorum sua benedictione profundens, dato coemeterio ac illis sepeliendis munere, ut quicunque inibi sepelirentur, nullas in cadaveribus suis paterentur diabolicas illusiones. Ex hujusmodi ergo Dominicae benedictionis munere, apud omnes majoris auctoritatis Galliarum principes ac clericos inolevit, quod maxima patentum pars illuc sepulturam habent, et quidam in plaustris, alii in curribus, nonnulli in equis, plurimi per dependulum fluentis Rhodani ad coemeterium Campi Elisii deferebantur. Est ergo omni admiratione dignissimum, quod nullus in thecis positus mortuus ultimos civitatis Arelatensis terminos, quod Rochestam nominant, quantalibet vi ventorum aut tempestate compulsus praeterit, sed infra semper subsistens in aqua rotatur donec applicet, aut ad ripam fluminis ductus coemeterio sacro inferatur. Mirandis magis miranda succedunt, quae oculis conspeximus sub innumera utriusque sexus hominum multitudine. Solent, ergo praemisimus, mortui in doliis bituminatis ac in thecis corpora mortuorum a longinquis regionibus fluminis Rhodani dimitti cum pecunia sigillata, quae coemeterio tam sacro, nomine eleemosynae, confertur. Uno aliquo die, nondum decennio delapso, dolium cum mortuo suo descendit inter illud angustum, quod ex alternis ripis castrum Tarasconense et castrum Belliquadri prospectant. Exilientes adolescentes Belliquadri dolium ad terram trahunt, et relicto mortuo pecuniam reconditam rapiunt. Depulsum dolium inter impetuosi amnis fluctus subsistit, et nec vi fluminis praecipitis nec juvenum impulsibus potuit descendere, verum rotans et in se revolvens, eosdem circinabat fluminis fluctus…Tandem, restituto censu, confestim mortuus sine omni impellentis adjutorio viam aggreditur, et infra modicam horam apud civitatem Arelatensem applicans, sepulturae honorifice traditur. |
Most Sacred Prince, let me tell you of a remarkable wonder and miracle of divine power. The capital of the kingdom of Burgundy (known as the Arlesian kingdom) is the city of Arles, the recipient of ancient privilege. It was Trophimus, who had been ordained by the Apostles Peter and Paul, who…determined to set aside a proper cemetery in the central part of the city, in which the bodies of all the faithful could be brought for burial, that as the whole of Gaul received the faith initially from the church of Arles, so also the dead in Christ by being brought there from all over the country might have the benefit of a common burial ground. The solemn consecration was therefore performed at the hands of the most holy bishops at the East Gate, where the church consecrated by them in honour of the Blessed Virgin now stands. To them Christ himself appeared, as of old he was intimately recognisable in human flesh; he lavished his blessing on their work, granting to the cemetery and to its occupants that whoever might be buried there should suffer in their corpse no mockery of the devil. As a result, therefore, of this gift of the Lord's benediction, it was borne in upon all the principalrulers and clergy of Gaul that the great majority of those to whom they had access had right of burial there. And so some in wagons, others in chariots, a number on horse back, but the majority borne downstream on the River Rhone, were brought to the cemetery of the Elysian Field. It is quite astonishing that no dead person placed in a coffin ever overshot the outer boundary of the City of Arles (which they call Rocheta), driven by whatever force of wind or tempest, but remaining close to the shore, the coffin circles in the water until it lands, orelse is borne into the sacred cemetery by the direct current of the river. Marvels succeed to marvels which we have seen with our own eyes in the case of innumerable multitudes of people of either sex. As we have said, the dead are usually sent in vessels of bitumen and in coffins from distant reaches of the river Rhone, with figured coinage, which is of fered as alms to so sacred a cemetery. On one occasion, less than ten years ago, a vessel with its corpse came downstream into that strait which is overlooked on one side by the camp of the Tarasconians and on the other by that of the Belliquadri. Some youths of Belliquadri jumped out and dragged the vessel to shore, and, leaving the dead body, seized the money laid within it. The vessel having been pushed out again into the river stood still amidst its fierce currents, and neither the force of the headlong flood nor the thrusts of the young men could make it go downstream. Turning and turning about on itself, it circled those same waves of the stream…At last, when the whole sum of money was restored, the body forthwith pursued its way without the help of anyone impelling it, and within a short space of time, landing at Arles, was given an honourable burial. |
APPENDIX C
THE KOGI OF COLOMBIA
Before the Spanish Conquest, the ancient, indigenous Chibcha peoples were the dominant race in what is now Colombia. Their population of close to 500,000 seems to have been concentrated in the high valleys around the modem cities of Bogotá and Tunja. They were intensive agriculturalists, craftsmen and traders: fruit, vegetables, pottery and cotton cloth changed hands at the weekly markets in their larger villages. Trade with their neighbours brought in large quantities of gold which they used for religious ceremonies, personal adornment and ornaments.
Descent was matrilineal: chiefs and religious leaders were succeeded by sons of their sisters. Land, however, was inherited patrilineally.
The present-day Kogi of northern Colombia were recently visited for the first time by Alan Ereira (whom they call “Mr. BBC”). The brilliant and thought-provoking documentary which he produced as a result of that visit was shown on BBC 1 on Tuesday, December 4th, 1990.
In essence, Ereira's programme revealed that the Kogi are descended in an undisturbed line from an ancient South American civilisation who had learned to live with nature, to cooperate (as some might rephrase it) with Gaia herself Their simplistically wise priest-rulers believe that the Kogi, high on their secret mountain, are the Elder Brothers: they refer to the rest of humanity as the Younger Brothers. The Kogi asked Alan Ereira to broadcast a solemn warning to the world — a request which his superb documentary fulfilled with great clarity and dignity. Fundamentally, Kogi priest-rulers believe that mining and other world-wide industrial exploitation are mortally wounding the Great Earth Mother (Gaia?) on whom we all depend — Elder Brothers and Younger Brothers alike.
If the strange “natural pentagon” at Rennes-le-Château is one of Gaia's “sensory organs” or “communication channels”, is the secret mountain of the Kogi another?
Is it only by the strangest of coincidences that the River Magdalena runs close by the Kogi's mountain citadel, and that the city of Santa Marta (surely the Hispanic rendering of St. Martha, sister of Mary of Bethany, who might also have been Mary Magdalen) is only a few miles away?
Is there the remotest possibility that the hypothetical refugees who might have established themselves on Oak Island were a group of the Kogi's ancestors escaping with their gold and their strange nature secrets from the sixteenth century Spanish invaders?
Could the mysterious Colombian Kogi, and their belief in the Great Earth Mother, have any connection — however remote — with Jean Robin and von Däniken's ideas about tunnels under South America?
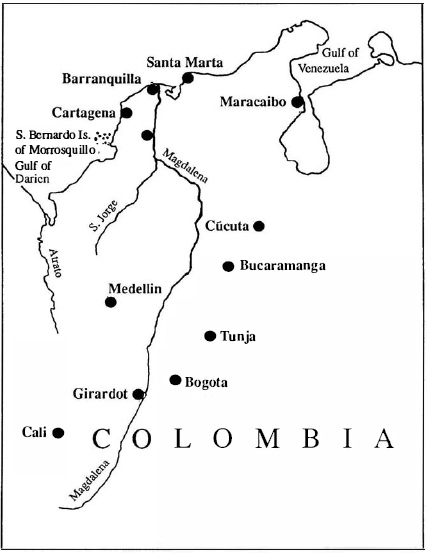
Map of Colombia showing Bogota, Tunja and the Magdalena River.
APPENDIX D
THE VIGENÉRE SQUARE CIPHER
In Chapter 6 (Codes, Ciphers and Cryptograms), an entirely new approach to the decipherment of the long coded inscription was made using the purely numerical “position value” method. This obviated the old Tableau Vigenère technique. However, since the Vigenère system has become almost traditional as an aid to decoding the tombstone and parchment ciphers, its use is explained briefly in this Appendix.
To produce a French Vigenère table, write out the 25-letter French alphabet (the same as our own alphabet with the letter W removed) twenty-five times in the form of a square. The first horizontal line is written normally from A to Z; the line below it begins with B and ends with A, Z in this line being the penultimate letter; the twenty-fifth and last line begins with Z followed by A, and ends with Y.
It will be seen that the uppermost horizontal line and the first (far left) vertical line are normal alphabets. To use the square to decode a message write out the key words (MORT épée in the case of the tombstone) over and over again below the ciphered version. The key word indicates which of the horizontal alphabets is to be used to find the letter.
For example, suppose that the key word is SAUNIERE and that the cipher reads:
B R J F G N M O B A X Q F J M O
Copy the key word as of ten as necessary until every letter of the cipher is covered by a letter of the repeated key word.
| Cipher: | B R J F G N M O B A X Q F J M O… |
| Key Word: | S A U N I E R E S A U N I E R E… |
Locate the letter B (the letter from the encoded message) along the top row of the square, then follow that column vertically until you reach the row with S (the first letter from the keyword) leftmost. The letter found at the intersection of that column and row is T, which becomes the first letter of the plaintext. The second letter is R, found in column R, row A—which row is just the unshifted alphabet at the top of the square. Similarly, column J, row U gives E, the third letter of the message. Continuing to the end gives the decoded message Trésor est à Rennes…
| Cipher: | B R J F G N M O B A X Q FJ M O… |
| Key Word: | S A U N I E R E S A U N I E R E… |
| Clear: | T R E S O R E S T A R E N N E S… |
It is important to note that letter changes via a Tableau Vigenère can be effected in two ways: either by the method demonstrated above, i.e. by finding the alphabet indicated by the keyword, looking for the cipher letter along the top line and then finding its partner by descending vertically into the keyword alphabet, or the other way round.
Note that the Tableau Vigenère system is not equivalent to the position value addition system described in Chapter 6. The Trésor est à Rennes message emerged from the position value system from a different original:
A Q I E F M L N A Z V P E I L N
Let us see what happens when we attempt to decipher this by the Vig-enère method, using the same keyword SAUNIERE:
| Cipher: | A Q I E F M L N A Z V P E I L N… |
| Key Word: | S A U N I E R E S A U N I E R E… |
| “Clear”: | S Q D R N Q D R S Z Q D M M D R… |
It doesn't work! Complete decipherment requires that one slight refinement be performed on the text — one of the “alphabetic shifts” that feature so prominently in the Vigenère analysis of the long coded inscription given below. We replace each letter with the next letter in the alphabet, i.e., S becomes T, Q becomes R, etc. Only when this is done is the plain message Trésor est à Rennes revealed.
Let us consider again the long coded inscription. In their original form, the 128 letters of the coded inscription run as follows:
V C P S J Q R O V Y M Y Y D L T P E F R B O X T O D J L B K N J F Q U E P A J Y N P P B F E I E L R G H I I R Y B T T C V T G D L U C C V M T E J H P N P G S V Q J H G M L F T S V J L Z Q M T O X A N P E M U P H K O R P K H V J C M C A T L V Q X G G N D T
The key word is MORTépée, which has to be written sixteen times below the letters like this:
| Cipher: | V C P S J Q R O V Y M Y Y D L T P E F R B O X T… |
| Key word: | M O R T E P E E M O R T E P E E M O R T E P E E… |
The key letter M directs us to the M alphabet line of the Tableau Vigenère which changes V into I; the key letter O directs us to the O alphabet line of the Tableau Vigenère which changes C into Q; the key letter R directs us to the R alphabet line of the Tableau Vigenère which changes P into H…and so on. The letter transformation, using the Vigenère method, begins like this:
| Cipher: | V C P S J Q R O V Y M Y Y D L T P E f R B O X T… |
| Key word: | M O R T E P E E M O R T E P E E M O R T E P E E… |
| Stage 1: | I Q H M N G V S I M E R C S P Y C S X L F E B Y… |
The full text at this stage is:
I Q H M N G V S I M E R C S P Y C S X L F E B Y B R B F F A R N R F M Y T P N C A E H U J T M I Y G Y B M Y V C N I L V A J K H Y J T V A C Y I V V H H T V X A D Y Z A Q B J Y F K B F D G Q Y B L R H T T Q Z C V C I V F O L I Y T G G P Y P I F O A K D H Y
The next complication is an alphabetic shift as described above. Following this alphabet shift we have the Stage 2 text — a whole new string of 128 letters:
J R I N O H X T J N F S D T Q Z D T Y M G F C Z C S C G G B S O S G N Z U Q O D B F I V K U N J Z H Z C N Z X D O J M X B K L I Z K U X B D Z J X X I I U X Y B E Z A B R C K Z G L C G E H R Z C M S I U U R A D X D J X G P M J Z U H H Q Z Q J G P B L E I Z
Now we have to use a different keyword: the whole of the inscription from the gravestone of Marie de Nègre, including the “(P. S.)” and “prae cum”. To complicate matters still further, this new keyword has to be used backwards. We start in the bottom right-hand corner and work from right to left and from the lowest line upwards:-
| Cipher: | J R I N O H X T J N F S D T Q Z Z Q J G P B L E I Z… |
| Keyword: | M U C E A R P S P E C A P N I T E L B O N T I G T C… |
| Stage3: | V M K R O Z M M Z R H S S H Z S D C K U D U T K C B… |
The full text at this stage is:
V M K R O Z M M Z R H S S H Z S D V Q Q O A S D T B Z D D M H Q V S F D D M C D K N Q R H Z Z N D K D E R C P Q O D C B T O F V Z H D L T H C N B D I C M L D F L B N B D D O C R G Q V Z H Z C G Z S L N Z D R D A H B D K D Q M D D Z H D D C K U D U T K C B
Next comes yet another alphabet shift, giving the Stage 4 text:
X N L S P A N N A S I T T I A T E X R R P B T E U C A E E N I R X T G E E N D E L O R S I A A O E L E F S D Q R P E D C U P G X A I E M U I D O C E J D N M E G M C O C E E P D S H R X A I A D H A T M O A E S E B I C E L E R N E E A I E E DL V E V U L D C
This brings us to precisely the same point as the more efficient position value method given in Chapter 6. There a single decipherment stage was used, in place of the four stages given above. By either method, the text is now ready for the knight's tour transformation.
APPENDIX E
THE TOWNSEND CIPHER
So much has been written about the complexity of the hypothetical codes on the parchments which Saunière is said to have found in or near the Visigothic altar pillar, that an antidote to their complexity makes a refreshing change — not to mention a challenge to a lot of conventional thinking about the secret of Rennes-le-Château.
It is no exaggeration to say that Paul Townsend, the compiler of this appendix, is a computer genius with few equals, but his alternative hypothesis, and the spoof “tombstone code” which he has concocted, bring esoteric cryptographers down to earth with something of a bump.
We present his hypothesis without comment — other than to reiterate that he is an extremely able man, and his ideas are well worth careful consideration.
An Enquiry into the Affairs of Joe Bloggs (Deceased)
The story begins with the tombstone of the proverbial Joe Bloggs, a reproduction of which is shown below. He was well-known as the brother of the equally proverbial Fred, but his recently discovered tombstone gives some further details of his family and – most importantly – reveals that he was probably Supreme Grand Master of the Priory of Sion.
Spoof tombstone
As with the Rennes tombstone, there are several “funnies” in the inscription:
(a) Three letters – the P of “JOSEPH”, the O of “BELOVED” and the E of “AGED” — are in lower case.
(b) The H of “LIETH” and the A of “ANDREW” are missing their crossbars.
(c) The F of “FREDERICK” is detached from the rest of the name, isolated on the previous line.
(d) The T of “NINETEEN” has a spurious crossbar approximately halfway up.
(e) The first N of “NINTH” and the R of “YEARS” have been carved in mirror-image form.
The above imperfections in the inscription highlight the letters A,E,F,H,N,O,P,R,T. There has been much speculation regarding what these letters represent, but the most likely rendering is FANTHORPE, the surname of a priest from Wales and one of the co-authors of at least one book about the Rennes mystery.
The Long Coded Inscription
We have heard of the following inscription, corresponding to the long coded manuscript alleged to have been found behind the altar at Rennes:
AS I FWALKED THKROUGH THE WFILDERNESS POF THIS WOKRLD TI LIGHTEZD ON A ICERTIAIN PLACEN WHERE WASB A DEN AVND I LAID MEH DOWN NIN THAT PLACWE TO SLEEP SAND AS IZ SLEPT ID DREAMED AL DREAM I QDREAMED ANCD BEHOLD NI SAW AA MAN CPLOTHEVD WITH RAGIS STANDIFNGP IN AR CERTAIN PKLACE WITAH HIS FAGCE FROM HIVSOWN HOUWSE A XBOOK INN HIS HHAND ANDN AW GREAT BRURDEN UPAON HIS BACK TI LOOKIED AND SAEW HIM OPEN MTHE BOOGK AND READV THEREIN ANTD AS HE READL HE WEWPT AND KTREMBLERD AND NOT FBEINGZ ABLEP LONGER TOJ CONTAIN HQE BRAKE OUYT WITH A LAFMENTABKLE CRY SUAYING WHXAT SHDALL I DOL IN THISL PLIGHKT THERPEFORE CHE WENT OHOME AND RRESTRAVINEDL HIMTSELF BAS LONG ASH HE COULZD THATZ HIS WIFE RAND CHILIDREN SHOULED NOT PHERCEVIVE HIZS DISTRESS UBUT HE COULRD NOT BJE SILENTT LONG BECIAUSE THAPT HIS TROUBYLE IYNCREASED WHEDREFORE ABT LENGTH XHE BRAKER HIS MIND TOL HIS WIZFE ANVD CHGILDRENW AND TPHUS HE BWEGANH TO TGALK TOJ THEM O TMYF DEAR WIIFE SAAID HE ATND YOU TTHE CHILFDREN OF MUY BOWELS I XYOUR DEIAR FRYIEND AMB INU MYSELF UNDOONE BYP REASON SOF A HBURDEN THAT QLIETH HARD JUPON MEW MOREOVER HI AM FORZ CERTAINR INFORMED NTHAT THIS OAUR CITHY WIXLL BE BNURNED LWITH FIKRE FROM HQEAVEN INX WHICRH FEARFULW OVERTHROZW BOTH MYLSELF WITH STHEE MY WFIFE AND YOUS MY SWVEET BABESP SHALL MTISERABLY COFME TO RSUIN AEXCEPT XTHE WHICH YEST I LSEE NOT SHOME WAYR OF MESCAPNE CAN HBE FOUEND WVHEREBYS WE JMAY BE DELIVERED
One recognises the opening paragraphs of John Bunyan's Pilgrim's Progress, into which some one hundred and sixty-two additional letters have been inserted. The number 162 is significant – it is the same number of letters as on our concocted tombstone inscription.
There are three main steps to decoding the message. Firstly, the letters of the message have to be extracted. Here they are shown in upper case, with all the remaining letters rendered into lower case for clarity:
as i Fwalked thKrough the wFildemess Pof this woKrld Ti lighteZd on a Icertlain placeN where wasB a den aVnd i laid meH down Nin that placWe to sleep Sand as iZ slept iD dreamed aL dream i Qdreamed anCd behold Ni saw aA man cPlotheVd with ragIs standiFngP in aR certain pKlace witAh his faGce from hiVs own houWse a Xbook inN his Hhand andN aW great bRurden upAon his back Ti lookIed and saEw him open Mthe booGk and readV therein anTd as he readL he weWpt and KtrembleRd and not FbeingZ ableP longer toJ contain hQe brake ouYt with a laFmentabKle cry sUaying whXat shDall i doL in thisL plighKt therPefore Che went Ohome and rRestraVinedL himTselfBas long asH he coulZd thatZ his wife Rand chilIdren shoulEd not pHerceVive hiZs distress Ubut he coulRd not bJe silenTt long becIause thaPt his troubYle iYncreased wheDrefore aBt length Xhe brakeR his mind toL his wiZfe anVd chGildrenW and tPhus he bWeganH to tGalk toJ them o TmyF dear wilfe sAaid he aTnd you Tthe chilFdren of mUy bowels i Xyour deIar frYiend amB inU myselfundOone byP reason Sofa Hburden that Qlieth hard Jupon meW moreover Hi am forZ certainR informed Nthat this oAur citHy wiXll be bNumed Lwith fiKre from hQeaven inX whicRh fearfulW overthroZw both myLself with Sthee my wFife and youS my swVeet babesP shall mTiserably coFme to rSuin Aexcept Xthe which yeSt i Lsee not sHome wayR of MescapNe can Hbe fouEnd wVherebyS we Jmay be delivered
The number of additional letters, 162, is twice the square of9. We write the letters, taking them in the order in which they appear in the inscription, into a double 9 x 9 grid, filling up the left grid and then the right:
A suitable transposition is now required. We remain with the double 9 x 9 grid, and this time generate a 9 x 9 magic square in the left grid using a standard technique, as described in A Number for Your Thoughts by Malcolm E. Lines (Adam Hilger Ltd., Bristol, 1986), section 13. The right grid contains a mirror-image duplicate of the same magic square:
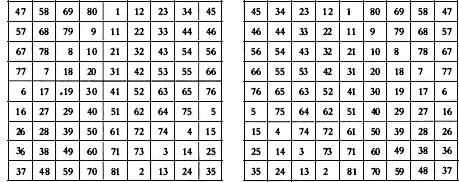
We now read the letters off in the order specified by the numbering of the squares in the above magic squares, the left grid then the right. This gives:
K R R X Z H R C H N N T I V D G N K W A A W Z E L P V J T R G P S I H L T L Q L A V V Z I D F B K Y W T W I X F N K H P F K I R E N L B F Z C K O U F M P Q V P Z J N T X Z H Y T L J R R M P Q K W I J X G X U R V S L F N Q U H B Z H L J S S X H F W D V Y Y S X L H S T P T W G P V A Z A P N O A I V I E S W F R R U B F Z T H
When this sequence of letters is decoded using the Vigenère Square technique (using the English alphabet, and the keyword FANTHORPE), the following highly suggestive message is revealed:
FREE STANDING POPPY GRAND SQUARE TENIERS HOLDS THE KEY FOR RICHES FAR ABOVE MEASURING JUSTICE AVENGES THE HERETIC THE EXTENDED HAND BANISHES FEAR FORTY FEET BELOW TWO MILLION POUNDS ARE BURIED
Yes – very suggestive, particularly in the reference to Teniers and including a copy of a familiar inscription — that alleged to be the meaning of the mysterious carvings on the Money Pit tablet. This final message is (as the reader may wish to check) a perfect anagram of the tombstone inscription.
Explanation
Well, of course, it is all concocted. Unfortunately, it was not possible to get anything better than a series of disjointed phrases as above out of the tombstone letters, but that does not matter. The original BERGERE PAS DE TENTATION message is no better in this respect.
The first germ of my hypothesis is a curious “flaw” in the original Rennes tombstone message — reproduced in my concoction. This is that the anagram uses all the letters on the tombstone, even those of MORT pe'e [FANTHORPE] itself. It seems rather odd to decode a message and find within it the keyword to use for the decoding! One does not expect a locked safe to contain its own key.
Secondly, the Rennes encipherment was so complex, involving two Vigenère transformations with different keywords, plus transpositions and further alphabetic shifts, that I do not believe that Saunière — or anybody else in his time – would have been able to decipher the message had it been genuine. In our own century, the wartime codebreakers did manage to “crack” the ciphers produced by the German “Enigma” machine (a mechanical implementation of a multi-stage Vigenère square), but they required their own machinery in the form of Colossus (a purpose-built electro-mechanical computer) with various sundry pieces of additional equipment, knowledge of the Enigma machine itself, and a fair idea of what the contents of the messages would be (e.g. weather reports, or particular lightships being destroyed).1
I therefore began with the idea that Saunière had gone the other way, and enciphered the message. I therefore set out to determine how difficult (or, as it turned out, how easy) it would be to construct something similar, beginning with a concocted tombstone inscription containing some “funny” letters which gave the keyword when taken together. Finding the anagram only required an hour or so with modem technological aid (an anagram-exploring program running on an IBM-compatible Personal Computer) to turn up the “FREE STANDING POPPY” nonsense. In Saunière's time, the easiest way to play with the letters would have been to write them on small pieces of paper and attempt to arrange them all into a series of sensible words. (Was this the inspiration for the game of Scrabble?!)
My hypothesis is, therefore, that the BERGERE PAS DE TENTATION anagram is a red herring, devised, probably by Saunière himself, to supply an ostensible “use” for the letters MORT épée of the tombstone inscription once he had become aware of its survival despite his obliteration of it from the tombstone itself; and thereby detract attention from further research on the real meaning of MORT épée. Saunière (or whoever) should have excluded the key letters MORT épée from the anagram and attempted to concoct some meaningful-looking nonsense from the 120 remaining letters.
APPENDIX F
THE ASIMOV-ECO CONNECTION
Isaac Asimov
The authors gratefully acknowledge a fascinating idea which was sent to them by Chris Kirk of New Oscott, Birmingham, shortly after their first volume on the Rennes mystery was published in 1982.
Chris made a detailed study of Isaac Asimov's Foundation trilogy after reading our 1982 comments about the similarity of names in the Rennes mystery and those used by Tolkien in Lord of the Rings. If Tolkien, he wondered, why not Asimov?
Chris's first point is that Asimov's books refer to an open Foundation of physical scientists, and a secret or hidden Foundation (the Second Foundation) whose aim is the preservation of the “Seldon Plan” to form a new galactic empire. Is this a parallel of the Open and Closed Orders of the Knights Templar, he asks.
Kirk's second point is that the background to Asimov's Foundation trilogy is a crumbling galactic empire and a lineage of emperors. On page 140 of Volume Two in the Panther edition, entitled Foundation and Empire, the Emperor Dagobert IX is mentioned. His son, Dagobert X, is later killed by a character called The Mule. A heroine in Volume Three (page 71 in the Panther edition) is called Arcadia. The instigator of the whole plot is a character called Hari Seldon. The name is an anagram of “Sion Herald”!
As an afterthought, Chris adds that the transmutation of base metals into gold features prominently in Part IV of Volume I, Foundation, especially on page 122 of the Panther edition.
So, is it possible to add Isaac Asimov to the list of writers (so far including Victor Hugo, Jules Verne, George MacDonald, J. R. R. Tolkien, Charles Williams and C. S. Lewis) who might have known about Rennes and dropped a few hints to that effect into their work?
Umberto Eco
If anything, even more probable than an Asimov connection, is the possibility that Umberto Eco is dropping extremely erudite and subtle hints first in The Name of the Rose and later in Foucault's Pendulum?
The very word “Rose” in the first title may be significant. The mystery is set in an ancient monastery and centres on a curious lost work of philosophy. Strangely, one of the monks is called Berengar— the second case we have come across (after Prof. Beringer in Chapter 12) of somebody who bears a name similar to that of Bérenger Saunière. Even more strangely, there is almost an element of anticlimax in the dénouement. Jorge, the grim, blind librarian, has kept secret the second book of the Poetics of Aristotle because it dealt with laughter. The explanation isn't really adequate. The secret was guarded so carefully. Men died to keep it safe. The reader is left asking why.
Is Eco doing what Lewis Carroll and Boudet perhaps did? Is the “secret” not really hidden in Aristotle's treatise on humour? Is there some subtle camouflage within the camouflage? Eco's towering intellect is more than capable of that sort of double concealment.
What then of Foucault's Pendulum?
Jean Bernard Leon Foucault was born in Paris on September 18th, 1819. His father was a publisher. Jean Bernard studied medicine and then turned his attention to experimental physics. With Armand Fizeau, who was also born in September 1819, Foucault carried out a series of important experiments concerned with the behaviour of heat and light: forms of energy.
Perhaps Foucault's most memorable achievement was the demonstration of the diurnal motion of the earth using a long, heavy, freely suspended pendulum, which was subsequently named after him. He also invented the gyroscope (which still seems to possess some only partially explained power to defy gravity!). Foucault died of paralysis in 1868 in Paris, but his friend and collaborator, Armand Fizeau, lived on until 1896 – well into Saunière's time.
Eco's second book, like his first, has the underlying and persistent theme of a secret that is no secret: the paradox of a mystery which in one sense does not exist. His text swings like Foucault's Pendulum itself, seemingly independent of the earth and those who crawl about their mundane business across its surface. Yet scattered throughout the whole work are intriguing hints and innuendoes, suggestions of dark secret societies and their relentless pursuit of arcane knowledge. There are whispers of alchemists…of transmutation…and of much, much more…
APPENDIX G
ON THE TRAIL OF THE PAINTINGS
Among the many subsidiary mysteries that surround Rennes-le-Château is that of who is misinformed about the various so-called “significant” paintings, who is responsible for such misinformation as appears to be circulating, and whether there is some secret, sinister reason for it, or whether it's just one more good old-fashioned human error laced up with a bit of honest, understandable and forgivable record bungling?
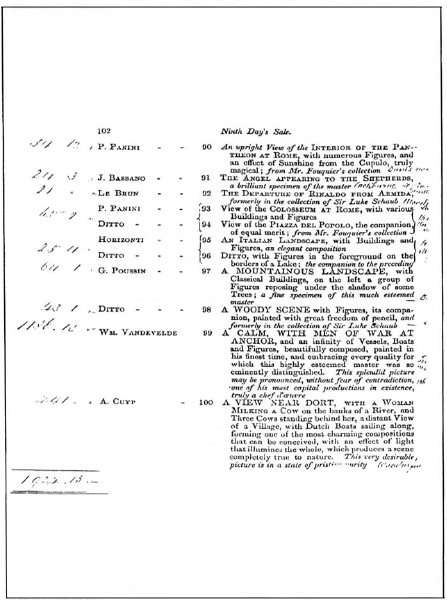
Prior to the great ninth day picture sale of August 10th, 1842, there were in Shugborough Hall, Staffordshire, one or two paintings by Teniers, Guercino and Poussin — at least, they were there according to the auctioneer's catalogue.
When we wrote to the Louvre as long ago as November 1976, we were told that the second version of “The Shepherds of Arcadia”, which Henri Buthion had told us about, did not exist — although he had shown us what certainly looked like a reproduction of a slightly modified Poussin canvas. When our expedition photographer of the time, Peter Rice of Ipswich, called in person one Saturday and asked to see it, he was told that it did exist but that it couldn't be seen at weekends!
The Shugborough sale catalogue and the subsequent “hunt-the-Poussin” correspondence make interesting reading.
APPENDIX H
THE MYSTERY OF SAUNIÉRE'S BEDROOM CEILING
One of the most intriguing things about Rennes-le-Château is that information about the mystery comes in small instalments from many unsuspected sources. The tale of Saunière's bedroom ceiling comes via a very roundabout route.
The Russian Revolution led to the murder of the Tsar's family on July 17th, 1918. At that time a loyal old Cossack named Basile Kikof fled from Russia. He married a girl named Anastasia. The two exiles arrived in France in 1928 and worked wherever they could until 1950, when they reached Rennes-le-Château. Here, Anastasia Kik of befriended the eighty-year-old Marie Dénarnaud, and the two women became friends and confidantes.
According to what Anastasia said to a reporter, whose article appeared in Littoral on June 10th, 1983, what was left of the treasure was concealed in the false ceiling of Saunière's bedroom. With the collaboration of other local residents at the time, the Kikof family searched the ceiling: there was nothing there. Had it once been there? The question cannot now be answered satisfactorily…but it does provide one more microscopic clue to the Rennes mystery.
APPENDIX I
THE MANDELBROT ENIGMA AND THE RIDDLE OF THE TESSERACT
In this Appendix, written mostly by our friend Paul Townsend, M.Sc, we discuss two mathematical constructions – the Mandelbrot set (with some variations upon it) and the Tesseract, both of which refer back to points raised in the main text of this book, and both of which involve extensions to the mathematics of the ‘real world’. The authors and publishers wish to express their grateful thanks to Paul Townsend for writing graphic programs showing the “Bearskin Rug” pattern and an animated tesseract on screen, and for his kind permission to reproduce photographs and line illustrations generated by these programs.
Complex Numbers — The Mandelbrot Set and Others
Through the ages, mathematicians have bestowed derogatory tags upon concepts which, at first, seemed to be blemishes upon the ideally spotless face of the Queen of Sciences. We speak, for example, of a division of two whole numbers which does not produce a whole number answer. as being a “vulgar” fraction. Gradually, of course, the new concept is integrated into mathematics and gains general acceptance – the vulgar fraction is now usually known by the more polite expression ratio. When it was found that the division of the diagonal of a square by its side could not be expressed even as a ratio, this and similar quantities were termed irrational— a word which originally meant simply “without ratio”, but has entered general currency with the meaning “odd”, “eccentric” or “illogical”.
The name “complex numbers” is a similar misnomer, and is particularly unfortunate since, far from complicating mathematics, the use of complex numbers simplifies and unifies a large number of concepts. For example, every quadratic equation has exactly two solutions (no dependence on b2-4ac or other such parameters), and such diverse concepts as the sine and cosine functions of trigonometry, and the raising of one number to the power of another, join into a single larger whole – the de Moivre function.
The mathematics of complex numbers seems to have begun in the 16th century with the Italian mathematician Cardan. Cardan's original problem was to find two numbers which gave the sum 10 when added, and the product 40 when multiplied together.
Two numbers which add to 10 may be represented by the expressions (5+P) and (5-P), where P is some number. For example, setting P=2 gives the numbers 7 and 3. When these two expressions are added, the +P and -P cancel each other out, leaving only the two S's which add to 10.
The two expressions are recognised as a case of the “difference of two squares” theorem: their product is given by:
(5 + P)(5-P) = 52-P2
Since 52 is the unalterable constant 25, our hope of finding a solution to Cardan's problem rests in the P2 term. Unfortunately, for 5 -P2 to have the value 40 requires that P2 equals -15. Since all numbers, whether positive or negative, have positive squares, Cardan's problem seems impossible to solve.
But mathematicians don't like a problem being branded “impossible” so quickly. It was soon determined that a whole new class of numbers, namely those with negative squares, could be introduced into mathematics without at the same time introducing any contradictions. Since such numbers did not appear to fit into the “real world”, they were branded “imaginary” — another instance of the derogatory tags referred to above. The imaginary numbers could be combined with the ordinary “real” numbers to produce the compound numbers referred to as “complex”. Mathematicians now give the solution to Cardan's problem as the pair of complex numbers:
5 +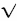 
– 15 and 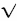5 – – 15
Just as the real numbers can be plotted on a line, representing the magnitude of the number by the length of the line from a given origin, so complex numbers can be plotted on a plane, usually referred to as the Argand diagram, where the real component is plotted horizontally and the imaginary component plotted vertically. The complex number 5 + 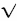– 15 is represented by a point 5 units east, and 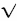15 (nearly 4) units north, of the origin. By Pythagoras' theorem, the distance of this point from the origin (known as the modulus of the number) along a straight line is 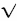40 (approximately 6.3), the appearance of “40” reflecting the conditions of Cardan's problem.
Quadratic equations can be solved directly, simply by inserting the a, b and c parameters into a formula and pulling out the two answers. However, such cases are rare — there is no formula, for example, for solving more typical equations such as:
2z – 2 – z Ln(z) = 0
This one appeared in the doctoral thesis of the authors' daughter Stephanie. Its solution (z = 4.921554 to six decimal places) had to be found by numerical techniques. In such circumstances, mathematicians resort to an iteration scheme, constructed as follows:
(1) Express the equation in the form:
x = [some expression involving x]
which is more elegantly written (“f” is read “function of”):
x = f(x)
(2) Estimate (or guess) an approximate solution.
(3) Evaluate f(x) for the approximate solution.
(4) Use the result from step 3 as the new approximate solution.
(5) Return to step 3.
It is hoped that, eventually, the value of f(x) computed from step 3 will be equal to the value of x that went into the expression. The iteration scheme is then said to converge to this final value, which may be computed as accurately as desired by running the iteration scheme enough times. Unfortunately, a badly constructed iteration scheme, or an initial estimate too far from the true solution, will result in x moving further and further from the solution, eventually heading to infinity. Such a scheme is said to diverge.
Consider the equation:
x2 – x + c == 0
where c is some constant. Although this is a simple quadratic, solvable using the formula, we use it here as an illustration of the iteration scheme. Step 1 requires that the equation be transformed into the form x==f(x). The following is the simplest of many such transformations:
x = x2 + c
We shall examine below two cases of this equation, using two different values of c: -0.5 and +0.5. In each case, our initial guess at the solution will be zero.
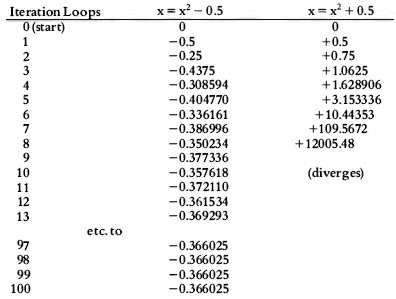
We find that, whereas x2- 0.5 converged to a single value, x2+ 0.5 diverged. The next term of the latter sequence (not shown in the table) exceeded 140,000,000 and in subsequent terms the number of digits in the number doubled each time.
Further experimentation shows that convergence to a single value is found for values of c in the range -0.75 to +0.25 inclusive. Divergence is found for c more negative than -2, or more positive than +0.25. Between the limits of -2 and -0.75 comes a more complicated regime: the values of x do not converge to a single value, but to a series of two or more different values which appear in turn. However, such behaviour can still be classed as “finite” since the x values do not diverge to infinity.
To sum up the above discussion, we find that only real values of c falling between the limits of -2 and +0.25 remain finite, while all other numbers diverge.
We now introduce Mandelbrot and his set. The “Mandelbrot Set” emerged as a solution to a problem in “fractal geometry”, a branch of mathematics too complicated to outline in any great detail. Basically, it is concerned with the mathematics of infinite complexity. To give the stock example, how long is the coastline of Britain? Even if no allowance is made for tides, erosion and other dynamical factors, the answer still depends on your scale of measurement. If you measure the coastline as shown on a road map with a scale of, say, five miles to the inch, features less than 100 yards across would be below the resolution of the printing process, and could not be shown with any great accuracy. It would not, therefore, be surprising if the answer were significantly less than that obtained if you were to tour the entire coast of Britain armed with (a) a metre rule, (b) a suitably long piece of string, (c) a gauge capable of tracking the contours of the smallest pebble with 1/100” accuracy, (d) an apparatus perhaps based on an electron microscope which could plot the surfaces of the tiniest grain of sand down to the atomic scale.
The Mandelbrot Set is the set of constants c which remain finite under the iteration scheme x=x2+c which we have discussed above, with the twist that complex values are admitted for c. When the entire Argand diagram is checked for divergence under this iteration scheme, with points that remain finite coloured in while points which diverge are left blank, the pattern that emerges is one of infinite complexity. Nowhere is the boundary between finite and divergent behaviour absolutely smooth, but smaller and smaller “nodules” are visible, upon infinitely finer and finer scales. No matter how much the diagram is magnified, there is always detail below the resolution of the picture. The set even contains miniatures of itselfl We have the paradoxical situation of a figure of finite area (since the entire set must lie within a circle of radius 2 drawn about the origin) but with an infinitely long surface. A beautiful series of successively magnified views of the Mandelbrot Set is shown in the colour plates in James Gleick's excellent book Chaos: Making a New Science (Heinemann, London, 1988).
What has all this to do with our subject? We take up the reference in Chapter 5 to Bayley and Campbell's exposition of the curious properties of the number five. It is found that, when the power in the iteration scheme x=x2+c is raised above 2, totally different patterns emerge. The pattern of interest here is that which results from plotting those values of c which remain finite under the iteration scheme x=x6+c. The resulting pattern has fivefold rotational symmetry (i.e. it can be rotated by one-fifth of a turn and look the same as before). Each of the major branches of the pattern terminates in what looks very much like a “foot” with five “toes”.
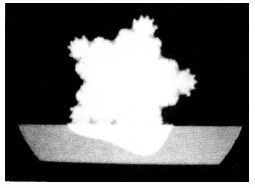
When this pattern appeared for the first time on our friend Paul Townsend's computer display, he immediately dubbed it the “bearskin rug”. Is this the “Quinotaur” of Chapter 2, the name arising from the pentagonal symmetry and its resemblance to the fattened-out skin of some kind of animal?
When magnified, the pattern shows similar fivefold divisions down to infinitely finer scales. Is the approximate fivefold symmetry of higher lifeforms, mentioned by Campbell, simply a variation on this pattern? Does the x=x6+c iteration scheme have this physical significance, just as the classic Mandelbrot set emerges unexpectedly as the shape of the physical boundary between magnetised and nonmagnetised regions in metals as discovered by Peitgen and Richter (Chaos p.236)?
Four-Dimensional Space — The Tesseract
In classical Euclidean geometry: a point has no magnitude; an infinite number of points make a line, which has length but no breadth; an infinite number of lines make a plane, which has length and breadth but no thickness; and an infinite number of planes make a three dimensional or “solid” figure. In the “real world”, that is as far as we go.
To specify a position on a flat, two dimensional shape (e.g. a map), we need two sets of imaginary lines running at right-angles to one another (e.g. parallels of latitude and lines of longitude). To specify positions in a “solid” we have to introduce a third set of lines running at right angles to both the other dimensions — the pilot of an aircraft will want to know not only his position (latitude and longitude) but also his height.
If there were four dimensions of space — not merely the three with which we are familiar from our everyday life experiences — the fourth dimension would have to go off at right-angles to each of the other three.
Because our minds are understandably circumscribed by the three-dimensional world in which we have always lived, most of us find it impossible to imagine such a shape as a four-dimensional hypercube. Pure mathematics is, however, equal to the task and can readily elucidate the properties of spaces of four, five, six or more dimensions.2
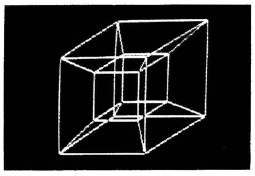
Although a true four-dimensional figure cannot be constructed, it is perfectly possible to build a three-dimensional model of a four-dimensional hypercube.
Suppose we constructed a cube from twelve equal lengths of wire representing its edges. Looking at this cube from above one of its faces, we would see a large square (i.e., the top face) containing a smaller square (i.e., the bottom face) within it, and the outer comers of the inner square would be joined to the corresponding inner comers of the outer square by lines (i.e., the four vertical edges).
The three-dimensional model of the hypercube — the tesseract—usually takes the analogous form of a cube inside a cube, where the external comers of the smaller internal cube are connected to the internal comers of the larger, enveloping cube. In this way four spatial dimensions can be represented in three, much as a two-dimensional shadow can be cast on a flat surface by a three-dimensional human being standing in a patch of sunlight. Although some of the edges and faces of the hypercube as represented appear to be larger than others, this effect must be regarded as a perspective distortion – all edges and faces are “really” equal in four-dimensional space. The four-dimensional hypercube has 16 vertices, 32 edges, 24 faces and 8 bounding cubes.
The arrangement of the edges of the hypercube – four edges meeting at each comer – permit a re-entrant tour of all the edges, reminiscent of the knight's tours of the chessboard which featured so largely in the chapter on codes and ciphers. In such a tour, all 32 edges are traversed once each, and each comer is visited twice before we return to the starting point. No such complete tour of the edges is possible on an ordinary cube – at best only nine of the twelve edges may be traversed.
There is some interesting evidence that a thirteenth century Catalonian mystic and numerologist drew a two dimensional sketch of a tesseract – or, perhaps, built a three dimensional model of one – and achieved an altered state of mind by contemplating it. Some modem investigations into psi-powers at universities with research departments interested in extrasensory perception have seemed to suggest that prolonged gazing at a tesseract (or a sketch of one) may induce a state of mind in which psychic abilities in certain “sensitive” individuals are enhanced.
The tesseract, supercube or hypercube may be no more than an interesting and unusual mathematical diversion: it could just be part of the key to something extremely interesting and mysterious.
1An excellent account of AUied codebreaking activities during WWII is contained in Chapter 6 of The Secret War by Brian Johnson (Arrow Books, London, 1979). This book accompanied a series of BBC documentary programmes transmitted in 1978.
2For further discussion of the geometry of hyperspaces, the reader is referred to Martin Gardner's excellent recreational mathematics books, published in the Pelican series: Mathematical Carnival, Chapter 4, “Cubes and Hypercubes,” and Mathematical Circus, Chapter 3, “Spheres and Hyperspheres.” PVST