In the multiple-choice section, this topic appears in about 10 out of 75 questions. In the free-response section, this topic appears every year.
S. A. Arrhenius defined an acid as a substance that ionizes in water and produces hydrogen ions (H+ ions). For instance, HCl is an acid.
HCl → H+ + Cl–
He defined a base as a substance that ionizes in water and produces hydroxide ions (OH– ions). For instance, NaOH is a base.
NaOH → Na+ + OH–
J. N. Brønsted and T. M. Lowry defined an acid as a substance that is capable of donating a proton, which is the same as donating an H+ ion, and they defined a base as a substance that is capable of accepting a proton.
Look at the reversible reaction below.
HC2H3O2 + H2O C2H3O2– + H3O+
According to Brønsted-Lowry
HC2H3O2 and H3O+ are acids.
C2H3O2– and H2O are bases.
Now look at this reversible reaction.
NH3 + H2O ![]() NH4+ + OH–
NH4+ + OH–
According to Brønsted-Lowry
NH3 and OH– are bases.
H2O and NH4+ are acids.
So in each case, the species with the H+ ion is the acid, and the same species without the H+ ion is the base; the two species are called a conjugate pair. The following are the acid-base conjugate pairs in the reactions above:
HC2H3O2 and C2H3O2–
NH4+ and NH3
H3O+ and H2O
H2O and OH–
Notice that water can act either as an acid or a base.
G. N. Lewis focused on electrons, and his definitions are the most broad of the acid-base definitions. Lewis defined a base as an electron pair donor and an acid as an electron pair acceptor; according to Lewis’s rule, all of the Brønsted-Lowry bases above are also Lewis bases, and all of the Brønsted-Lowry acids are Lewis acids.
The following reaction is exclusively a Lewis acid-base reaction:
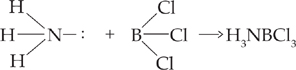
NH3 is the Lewis base, donating its electron pair, and BCl3 is the Lewis acid, accepting the electron pair.
Many of the concentration measurements in acid-base problems are given to us in terms of pH and pOH.
p (anything) = –log (anything)
pH = –log [H+]
pOH = –log [OH–]
pKa = –log Ka
pKb = –log Kb
In a solution
It is important to remember that increasing pH means decreasing [H+], which means that there are fewer H+ ions floating around and the solution is less acidic. Alternatively, decreasing pH means increasing [H+], which means that there are more H+ ions floating around and the solution is more acidic.
When a weak acid is placed in water, a small fraction of its molecules will dissociate into hydrogen ions (H+) and conjugate base ions (B–). Most of the acid molecules will remain in solution as undissociated aqueous particles.
The dissociation constants, Ka and Kb, are measures of the strengths of weak acids and bases. Ka and Kb are just the equilibrium constants specific to acids and bases.
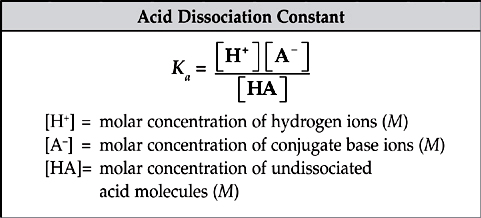
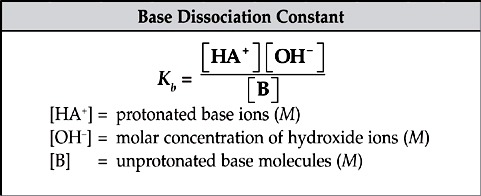
The greater the value of Ka, the greater the extent of the dissociation of the acid and the stronger the acid. The same thing goes for Kb.
If you know the Ka for an acid and the concentration of the acid, you can find the pH. For instance, let’s look at 0.20-molar solution of HC2H3O2, with Ka = 1.8 × 10–5.
First we set up the Ka equation, plugging in values.
HC2H3O2 → H+ + C2H3O2–
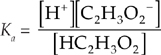
Therefore, the ICE (Initial, Change, Equilibrium) table for the above problem is:
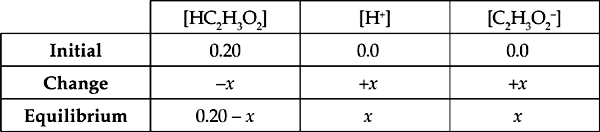
Because every acid molecule that dissociates produces one H+ and one C2H3O2–,
[H+] = [C2H3O2–] = x
and because, strictly speaking, the molecules that dissociate should be subtracted from the initial concentration of HC2H3O2, [HC2H3O2] should be (0.20 M – x). In practice, however, x is almost always insignificant compared with the initial concentration of acid, so we just use the initial concentration in the calculation.
[HC2H3O2] = 0.20 M
Now we can plug our values and variable into the Ka expression.
![]()
Solve for x.
x = [H+] = 1.9 × 10–3
Now that we know [H+], we can calculate the pH.
pH = –log [H+] = –log (1.9 × 10–3) = 2.7
This is the basic approach to solving many of the weak acid/base problems that will be on the test.
Strong acids dissociate completely in water, so the reaction goes to completion and they never reach equilibrium with their conjugate bases. Because there is no equilibrium, there is no equilibrium constant, so there is no dissociation constant for strong acids or bases.

Because the dissociation of a strong acid goes to completion, there is no tendency for the reverse reaction to occur, which means that the conjugate base of a strong acid must be extremely weak.
Oxoacids are acids that contain oxygen. The greater the number of oxygen atoms attached to the central atom in an oxoacid, the stronger the acid. For instance, HClO4 is stronger than HClO3, which is stronger than HClO2. That’s because increasing the number of oxygen atoms that are attached to the central atom weakens the attraction that the central atom has for the H+ ion.
It’s much easier to find the pH of a strong acid solution than it is to find the pH of a weak acid solution. That’s because strong acids dissociate completely, so the final concentration of H+ ions will be the same as the initial concentration of the strong acid.
Let’s look at a 0.010-molar solution of HCl.
HCl dissociates completely, so [H+] = 0.010 M
pH = –log [H+] = –log (0.010) = –log (10–2) = 2
So you can always find the pH of a strong acid solution directly from its concentration.
Water comes to equilibrium with its ions according to the following reaction:
H2O(l) ![]() H+(aq) + OH–(aq) Kw = 1 × 10–14 at 25°C.
H+(aq) + OH–(aq) Kw = 1 × 10–14 at 25°C.
Kw = 1 × 10–14 = [H+][OH–]
pH + pOH = 14
The common ion effect tells us that the hydrogen ion and hydroxide ion concentrations for any acid or base solution must be consistent with the equilibrium for the ionization of water. That is, no matter where the H+ and OH– ions came from, when you multiply [H+] and [OH–], you must get 1 × 10–14. So for any aqueous solution, if you know the value of [H+], you can find out the value of [OH–] and vice versa.
The acid and base dissociation constants for conjugates must also be consistent with the equilibrium for the ionization of water.
Kw = 1 × 10–14 = KaKb
pKa + pKb = 14
So if you know Ka for a weak acid, you can find Kb for its conjugate base and vice versa.
A salt solution can be acidic or basic, depending on the identities of the anion and cation in the salt.
That’s because neither ion will react in water because, as you may recall, the conjugates of strong acids and bases are very weak and unreactive.
When NH4Cl ionizes in water, the Cl– ions won’t react at all, but the NH4+ will dissociate to some extent to produce some H+ ions, as shown in the reaction below, making the solution acidic.
NH+ + H2O→ NH3 + H3O+
NaC2H3O2(s) → Na+(aq) + C2H3O2–(aq) pH > 7
When NaC2H3O2 ionizes in water, the Na+ ions don’t react at all, but the C2H3O2– ions will react with water according to the following reaction:
C2H3O2–(aq) + H2O(l) → HC2H3O2(aq) + OH–(aq)
This is an acid-base reaction, which produces some OH– ions and increases the pH.
Calculations with salts aren’t much different from regular acid-base calculations, except that you may need to convert between Ka and Kb and between pH and pOH.
Remember:
KaKb = 1 × 10–14, and pH + pOH = 14
Let’s find the pH of a 0.10-molar solution of NaC2H3O2. Ka for HC2H3O2 is 1.8 × 10–5. The solution will be basic, so let’s find Kb for C2H3O2–.
![]()
Therefore, the ICE table for the above equation is:
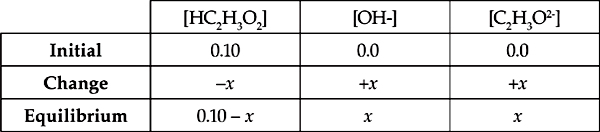
Now we can use the base dissociation expression.
![]()
Every C2H3O2– polyatomic ion that reacts with a water molecule produces one HC2H3O2 and one OH–, so
[HC2H3O2] = [OH–] = x
Again, we assume that x is insignificant compared with the initial concentration of C2H3O2–; 0.10 M, so
[C2H3O2–] = (0.10 M – x) = 0.10 M
Now we can plug our values and variable into the Kb expression.
![]()
Solve for x.
x = [OH–] = 7.5 × 10–6
Once we know the value of [OH–], we can calculate the pOH.
pOH = –log [OH–] = –log (7.5 × 10–6) = 5.1
Now we use pOH to find pH.
pH = 14 – pOH = 14 – 5.1 = 8.9
A buffer is a solution with a very stable pH. You can add acid or base to a buffer solution without greatly affecting the pH of the solution. The pH of a buffer will also remain unchanged if the solution is diluted with water or if water is lost through evaporation.
A buffer is created by placing a large amount of a weak acid or base into a solution along with its conjugate, in the form of salt. A weak acid and its conjugate base can remain in solution together without neutralizing each other. This is called the common ion effect.
When both the acid and the conjugate base are together in the solution, any hydrogen ions that are added will be neutralized by the base, while any hydroxide ions that are added will be neutralized by the acid, without this having much of an effect on the solution’s pH.
When dealing with buffers, it is useful to rearrange the equilibrium constant to create the Henderson-Hasselbalch equation.

Let’s say we have a buffer solution with concentrations of 0.20 M HC2H3O2 and 0.50 M C2H3O2–. The acid dissociation constant for HC2H3O2 is 1.8 × 10–5. Let’s find the pH of the solution.
We can just plug the values we have into the Henderson-Hasselbalch equation for acids.
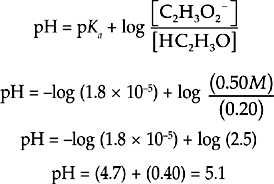
Now let’s see what happens when [HC2H3O2] and [C2H3O2–] are both equal to 0.20 M.
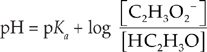
pH = –log (1.8 × 10–5) + log (1)
pH = (4.7) + (0) = 4.7
Notice that when the concentrations of acid and conjugate base in a solution are the same,
pH = pKa (and pOH = pKb). When you choose an acid for a buffer solution, it is best to pick an acid with a pKa that is close to the desired pH. That way you can have almost equal amounts of acid and conjugate base in the solution, which will make the buffer as flexible as
possible in neutralizing both added H+ and OH–.
Some acids, such as H2SO4 and H3PO4, can give up more than one hydrogen ion in solution. These are called polyprotic acids.
Polyprotic acids are always more willing to give up their first protons than later protons. For example, H3PO4 gives up an H+ ion (proton) more easily than does, so H3PO4 is a stronger acid. In the same way, is a stronger acid than.
Substances that can act as either acids or bases are called amphoteric substances.
For instance
An acid anhydride is a substance that combines with water to form an acid. Generally, oxides of nonmetals are acid anhydrides.
CO2 + H2O → H2CO3
SO3 + H2O → H+ +
A basic anhydride is a substance that combines with water to form a base. Generally, oxides of metals are basic anhydrides.
CaO + H2O → Ca(OH)2
Na2O + H2O → 2 Na+ + 2 OH–
When an acid and a base are mixed, a neutralization reaction occurs. Neutralization reactions can be written in the following form:
Acid + Base → Water + Salt
Neutralization reactions are generally performed by titration, where a base of known concentration is slowly added to an acid (or vice versa). The progress of a neutralization reaction can be shown in a titration curve. The diagram below shows the titration of a strong acid by a strong base.

In the diagram above, the pH increases slowly but steadily from the beginning of the titration until just before the equivalence point. The equivalence point is the point in the titration when exactly enough base has been added to neutralize all the acid that was initially present. Just before the equivalence point, the pH increases sharply as the last of the acid is neutralized. The equivalence point of a titration can be recognized through the use of an indicator. An indicator is a substance that changes color over a specific pH range. When choosing an indicator, it’s important to make sure the equivalence point falls within the pH range for the color change.
For this titration, the pH at the equivalence point is exactly 7 because the titration of a strong acid by a strong base produces a neutral salt solution.
The following diagram shows the titration of a weak acid by a strong base:
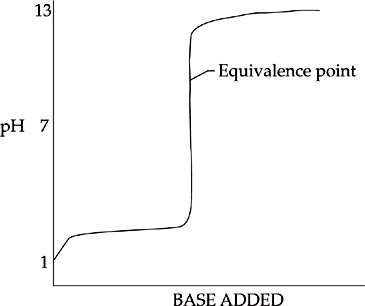
In this diagram, the pH increases more quickly at first, then levels out into a buffer region. At the center of the buffer region is the half-equivalence point. At this point, enough base has been added to convert exactly half of the acid into conjugate base; here the concentration of acid is equal to the concentration of conjugate base (pH = pKa). The curve remains fairly flat until just before the equivalence point, when the pH increases sharply. For this titration, the pH at the equivalence point is greater than 7 because the titration of a weak acid by a strong base produces a basic salt solution.
The following diagram shows the titration curve of a polyprotic acid:
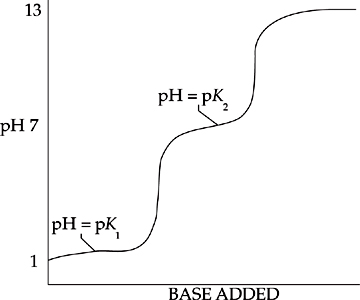
For a polyprotic acid, the titration curve will have as many bumps as there are hydrogen ions to give up. The curve above has two bumps, so it represents the titration of a diprotic acid.
Questions 1–4
The diagram below shows the titration of a weak monoprotic acid by a strong base.
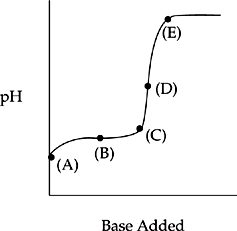
1. At this point in the titration, the pH of the solution is equal to the pKa of the acid.
2. This is the equivalence point of the titration.
3. Of the points shown on the graph, this is the point when the solution is most basic.
4. At this point the solution is buffered.
Questions 5–8
(A) 1
(B) 3
(C) 7
(D) 11
(E) 13
5. The pH of a solution with a pOH of 11
6. The pH of a 0.1-molar solution of HCl
7. The pH of a 0.001-molar solution of HNO3
8. The pH of a 0.1-molar solution of NaOH
Questions 9–12
(A) HNO3
(B) HCN
(C) H2CO3
(D) HF
(E) H2O
9. This is a strong electrolyte.
10. This substance can act as a Lewis base.
11. A 0.1-molar solution of this substance will have the lowest pH of the substances listed.
12. This substance is formed when carbon dioxide is dissolved in water.
14. What is the volume of 0.05-molar HCl that is required to neutralize 50 ml of a 0.10-molar Mg(OH)2 solution?
(A) 100 ml
(B) 200 ml
(C) 300 ml
(D) 400 ml
(E) 500 ml
15. Which of the following best describes the pH of a 0.01-molar solution of HBrO? (For HBrO, Ka = 2 × 10–9)
(A) Less than or equal to 2
(B) Between 2 and 7
(C) 7
(D) Between 7 and 11
(E) Greater than or equal to 11
16. A 0.5-molar solution of which of the following salts will have the lowest pH?
(A) KCl
(B) NaC2H3O2
(C) NaI
(D) KNO3
(E) NH4Cl
17. Which of the following salts will produce a solution with a pH of greater than 7 when placed in distilled water?
(A) NaCN
(B) KCl
(C) NaNO3
(D) NH4NO3
(E) KI
18. A laboratory technician wishes to create a buffered solution with a pH of 5. Which of the following acids would be the best choice for the buffer?
(A) H2C2O4, Ka = 5.9 × 10–2
(B) H3AsO4, Ka = 5.6 × 10–3
(C) H2C2H3O2, Ka = 1.8 × 10–5
(D) HOCl, Ka = 3.0 × 10–8
(E) HCN, Ka = 4.9 × 10–10
20. How many liters of distilled water must be added to 1 liter of an aqueous solution of HCl with a pH of 1 to create a solution with a pH of 2?
(A) 0.1 L
(B) 0.9 L
(C) 2 L
(D) 9 L
(E) 100 L
21. A 1-molar solution of a very weak monoprotic acid has a pH of 5. What is the value of Ka for the acid?
(A) Ka = 1 × 10–10
(B) Ka = 1 × 10–7
(C) Ka = 1 × 10–5
(D) Ka = 1 × 10–2
(E) Ka = 1 × 10–1
22. The value of Ka for HSO![]() is 1 × 10–2. What is the value of Kb for SO
is 1 × 10–2. What is the value of Kb for SO![]() ?
?
(A) Kb = 1 × 10–12
(B) Kb = 1 × 10–8
(C) Kb = 1 × 10–2
(D) Kb = 1 × 102
(E) Kb = 1 × 105
23. How much 0.1-molar NaOH solution must be added to 100 milliliters of a 0.2-molar H2SO3 solution to neutralize all of the hydrogen ions in H2SO3?
(A) 100 ml
(B) 200 ml
(C) 300 ml
(D) 400 ml
(E) 500 ml
24. The concentrations of which of the following species will be increased when HCl is added to a solution of HC2H3O2 in water?
I. H+
II. C2H3O2–
III. HC2H3O2
(A) I only
(B) I and II only
(C) I and III only
(D) II and III only
(E) I, II, and III
25. Which of the following species is amphoteric?
(A) HNO3
(B) HC2H3O2
(C) HSO4–
(D) H3PO4
(E) ClO4–
26. If 0.630 grams of HNO3 (molecular weight 63.0) are placed in 1 liter of distilled water at 25oC, what will be the pH of the solution? (Assume that the volume of the solution is unchanged by the addition of the HNO3.)
(A) 0.01
(B) 0.1
(C) 1
(D) 2
(E) 3
27. Which of the following procedures will produce a buffered solution?
I. Equal volumes of 0.5 M NaOH and 1 M HCl solutions are mixed.
II. Equal volumes of 0.5 M NaOH and 1 M HC2H3O2 solutions are mixed.
III. Equal volumes of
1 M NaC2H3O2 and 1 M HC2H3O2 solutions are mixed.
(A) I only
(B) III only
(C) I and II only
(D) II and III only
(E) I, II, and III
28. Which of the following compounds will most likely act as a Lewis acid?
(A) AlBr3
(B) CH4
(C) NH3
(D) PCl3
(E) Xe
29. The following titration curve shows the titration of a weak base with a strong acid:
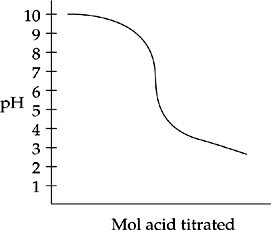
Which of the following values most accurately approximates the pKb of the weak base?
(A) 9.8
(B) 8.4
(C) 7
(D) 3.3
(E) 4.2
30. Which of the following expressions is equal to the hydrogen ion concentration of a
1-molar solution of a very weak monoprotic acid, HA, with an ionization constant Ka?
(A) Ka
(B) Ka2
(C) 2Ka
(D) 2Ka2
(E) ![]()
1. A beaker contains 100 milliliters of a solution of hypochlorous acid, HOCl, of unknown concentration.
(a) The solution was titrated with 0.100 molar NaOH solution, and the equivalence point was reached when 40.0 milliliters of NaOH solution was added. What was the original concentration of the HOCl solution?
(b) If the original HOCl solution had a pH of 4.46, what is the value of Ka for HOCl?
(c) What percent of the HOCl molecules were ionized in the original solution?
(d) What is the concentration of OCl– ions in the solution at the equivalence point reached in (a)?
(e) What is the pH of the solution at the equivalence point?
2. A vessel contains 500 milliliters of a 0.100-molar H2S solution. For H2S, K1 = 1.0 × 10–7 and
K2 = 1.3 × 10–13.
(a) What is the pH of the solution?
(b) How many milliliters of 0.100-molar NaOH solution must be added to the solution to create a solution with a pH of 7?
(c) What will be the pH when 800 milliliters of 0.100-molar NaOH has been added?
(d) What is the value of Keq for the following reaction?
H2S(aq) ![]() 2H+(aq) + S2-(aq)
2H+(aq) + S2-(aq)
3. A 100 milliliter sample of 0.100-molar NH4Cl solution was added to 80 milliliters of a 0.200-molar solution of NH3. The value of Kb for ammonia is 1.79 × 10–5.
(a) What is the value of pKb for ammonia?
(b) What is the pH of the solution described in the question?
(c) If 0.200 grams of NaOH were added to the solution, what would be the new pH of the solution? (Assume that the volume of the solution does not change.)
(d) If equal molar quantities of NH3 and NH4+ were mixed in solution, what would be the pH of the solution?
4. H3PO4
![]() H+ + H2PO4– K1 = 7.5 × 10–3
H+ + H2PO4– K1 = 7.5 × 10–3
H2PO4–
![]() H+ + HPO
H+ + HPO![]() K2 = 6.2 × 10–8
K2 = 6.2 × 10–8
HPO42–
![]() H+ + PO
H+ + PO![]() K3 = 2.2 × 10–13
K3 = 2.2 × 10–13
(a) Choose an amphoteric species from the reactions listed above, and give its conjugate acid and its conjugate base.
(b) Explain why the dissociation constant decreases with each hydrogen ion lost.
(c) Of the acids listed above, which would be most useful in creating a buffer solution with a pH of 7.5?
(d) Sketch the titration curve that results when H3PO4 is titrated with excess NaOH and label the two axes.
5. Use the principles of acid-base theory to answer the following questions:
(a) Predict whether a 0.1-molar solution of sodium acetate, NaC2H3O2, will be acidic or basic, and give a reaction occurring with water that supports your conclusion.
(b) Predict whether a 0.1-molar solution of ammonium chloride, NH4Cl, will be acidic or basic, and give a reaction occurring with water that supports your conclusion.
(c) Explain why buffer solutions are made with weak acids instead of strong acids.
(d) Explain why, although oxygen occupies the same position in both KOH and HBrO, KOH is a base and HBrO is an acid.
6. Identify which one of the acids listed in pairs below is the stronger of the two, and explain why.
(a) HF and HCl
(b) H2SO3 and HSO3–
(c) HNO3 and HNO2
(d) HClO4 and HBrO4
1. B At this point, sometimes called the half-equivalence point, enough base has been added to neutralize half of the weak acid. That means that at this point, the concentration of the acid—let’s call it HA—will be equal to the concentration of the conjugate base, A–.
Now let’s look at the equilibrium expression.
![]()
If [HA] = [A–], then they cancel and Ka = [H+].
So pH = pKa.
2. D The point in the middle of the steep rise in a titration curve is the equivalence point. That’s the point when exactly enough base has been added to neutralize all of the acid that was originally in the solution.
3. E This is the point with the highest pH, so at this point, the solution is most basic.
4. B A buffered solution resists changes to its pH, so the flat part of the titration curve is the buffer region because the pH of the solution is changing very little even when base is being added.
At (B), the solution contains a large quantity of both the acid HA, which absorbs added base, and its conjugate base, A–, which absorbs added acid.
5. B In any aqueous solution at 25°C, pH + pOH = 14.
So pH + 3 = 14 and pH = 3.
6. A HCl is a strong acid and dissociates completely, so the hydrogen ion concentration is equal to the molarity.
So [H+] = 0.1 M
pH = –log[H+] = –log(0.1) = 1
7. B HNO3 is a strong acid and dissociates completely, so the hydrogen ion concentration is equal to the molarity.
So [H+] = 0.001 M
pH = –log[H+] = –log(0.001) = 3
8. E NaOH is a strong acid and dissociates completely, so the hydroxide ion concentration [OH–] is equal to the molarity.
So [OH–] = 0.1 M
pOH = –log[OH–] = –log(0.1) = 1
Now, pH + pOH = 14
So pH + 1 = 14 and pH = 13
9. A A strong electrolyte is a substance that dissociates to form a lot of ions. HNO3 is the only substance listed that ionizes completely in solution.
10. E Water can act as a Lewis base by donating an electron pair to a hydrogen ion to form H3O+.
11. A HNO3 is the only strong acid listed, meaning that it is the only acid listed that ionizes completely, so it will have the lowest pH. By the way, in a 0.1 M solution of a strong acid, the hydrogen ion concentration will be 0.1 M, so the pH will be equal to 1.
12. C H2CO3, carbonic acid, is formed in the reaction between CO2 and H2O.
13. E NaOH is a strong base, so it can be assumed to dissociate completely. That means that the OH– concentration will also be 0.01 M.
pOH = –log[OH–], so pOH = 2, but we’re looking for the pH.
In an aqueous solution, pH + pOH = 14, so pH = 12.
14. B Every mole of Mg(OH)2 molecules dissociates to produce 2 moles of OH– ions, so a 0.10 M Mg(OH)2 solution will be a 0.20 M OH– solution.
The solution will be neutralized when the number of moles of H+ ions added is equal to the number of OH– ions originally in the solution.
Moles = (molarity)(volume)
Moles of OH– = (0.20 M)(50 ml) = 10 millimoles = moles of H+ added
Volume = ![]()
Volume of HCl = ![]() = 200 ml
= 200 ml
15. B You can eliminate (C), (D), and (E) by using common sense. HBrO is a weak acid, so an HBrO solution will be acidic, with a pH of less than 7.
To choose between (A) and (B) you have to remember that HBrO is a weak acid. If HBrO were a strong acid, it would dissociate completely and [H+] would be equal to 0.01-molar, for a pH of exactly 2. Because HBrO is a weak acid, it will not dissociate completely and [H+] will be less than 0.01-molar, which means that the pH will be greater than 2. So by POE, (B) is the answer.
16. E To find the lowest pH, we should look for the salt that produces an acidic solution.
The salt composed of the conjugate of a weak base (NH4+ is the conjugate of NH3) and the conjugate of a strong acid (Cl– is the conjugate of HCl) will produce an acidic solution.
As for the other choices, (A), (C), and (D) are composed of conjugates of strong acids and bases and will produce neutral solutions.
(B) is composed of the conjugate of a strong base (Na+) and the conjugate of a weak acid (C2H3O2–) and will produce a basic solution.
17. A A pH of greater than 7 means that the solution is basic.
The salt composed of the conjugate of a strong base (Na+ is the conjugate of NaOH) and the conjugate of a weak acid (CN– is the conjugate of HCN) will produce a basic solution.
As for the other choices, (B), (C), and (E) are composed of conjugates of strong acids and bases and will produce neutral solutions.
(D) is composed of the conjugate of a weak base (NH4+) and the conjugate of a strong acid (NO3–) and will produce an acidic solution.
18. C The best buffered solution occurs when pH = pKa. That happens when the solution contains equal amounts of acid and conjugate base. If you want to create a buffer with a pH of 5, the best choice would be an acid with a pKa that is as close to 5 as possible. You shouldn’t have to do a calculation to see that the pKa for choice (C) is much closer to 5 than that of any of the others.
19. C An amphoteric species can act either as an acid or a base, gaining or losing a proton.
HCO3– can act as an acid, losing a proton to become CO32–, or it can act as a base, gaining a proton to become H2CO3.
20. D We want to change the hydrogen ion concentration from 0.1 M (pH of 1) to 0.01 M (pH of 2).
The HCl is completely dissociated, so the number of moles of H+ will remain constant as we dilute the solution.
Moles = (molarity)(volume) = Constant
(M1)(V1) = (M2)(V2)
(0.1 M)(1 L) = (0.01 M)(V2)
So, V2 = 10 L, which means that 9 L must be added.
21. A A pH of 5 means that [H+] = 1 × 10–5
![]()
For every HA that dissociates, we get one H+ and one A–, so [H+] = [A–] = 1 × 10–5.
The acid is weak, so we can assume that very little HA dissociates and that the concentration of HA remains 1-molar.
![]()
22. A For conjugates, (Ka)(Kb) = Kw = 1 × 10–14
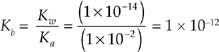
23. D First let’s find out how many moles of H+ ions we need to neutralize.
Every H2SO3 will produce 2 H+ ions, so for our purposes, we can think of the solution as a
0.4-molar H+ solution.
Moles = (molarity)(volume)
Moles of H+ = (molarity)(volume) = (0.4 M)(100 ml) = 40 millimoles = moles of OH– required
Volume of NaOH = ![]() =
= ![]() = 400 ml
= 400 ml
24. C Let’s look at the equilibrium expression for the dissociation of HC2H3O2.

When HCl is added to the solution, H+ ions are added and [H+] will increase, so (I) is correct.
Because of Le Châtelier’s law, the equilibrium will shift to consume some of the added H+ ions, so some of the H+ ions will combine with C2H3O2– ions to form more HC2H3O2.
So [C2H3O2–] will decrease, making (II) wrong, and [HC2H3O2] will increase, making (III) correct.
25. C An amphoteric species can act either as a base and gain an H+ or as an acid and lose an H+.
HSO4– can lose an H+ to become SO42– or it can gain an H+ to become H2SO4.
HNO3 (A), HC2H3O2 (B), and H3PO4 (D) can only lose an H+.
ClO4– (E) can only gain an H+.
26. D Every unit of HNO3 added to the solution will place 1 unit of H+ ions in the solution. So first find the moles of HNO3 added.
Moles = ![]()
Moles of H+ = ![]() = 0.01 moles
= 0.01 moles
Now it’s easy to find the H+ concentration.
Molarity = ![]()
[H+] = ![]() = 0.01 M
= 0.01 M
pH = –log [H+] = – log(0.01) = 2
27. D A buffered solution can be prepared by mixing a weak acid with an equal amount of its conjugate or by adding enough strong base to neutralize half of the weak acid present in a solution.
In (I), equal amounts of a strong acid and base are mixed. They’ll neutralize each other completely to produce salt water, which is not a buffer.
In (II), enough strong base is added to neutralize half of the weak acid. This will leave equal amounts of weak acid and its conjugate base, producing a buffered solution.
In (III), equal amounts of a weak acid and its conjugate base are mixed. This will produce a buffered solution.
28. A A Lewis acid must be able to accept a pair of electrons. By drawing the Lewis structure of AlBr3, shown below, one can see that Al lacks a full octet and therefore is a very strong Lewis acid.
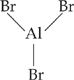
NH3 is a good Lewis base, since it has a lone pair of electrons to donate. Both CH4 and Xe have full octets, and will not accept more electrons. The compound PCl3 looks a lot like NH3, and has a lone pair of electrons and acts as a Lewis base.
29. E The half equivalence point of this titration, shown in the plot below, is around pH = 9.8.
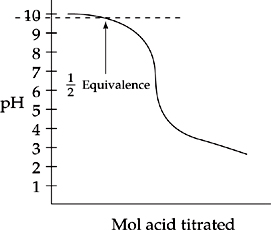
However, this is not the pKb of the weak base. Remember that the Henderson-Hasselbalch equation relates pH with pKa, not pKb. At the half equivalence point shown, the amount of base (which we can call [A–] as we do when talking about acids and pH values) is equal to the neutralized base [HA]. When these two quantities are equal, the H-H
equation tells us that the pH = the pKa of the acid form, which when subtracted from 14 gives the pKb of the base. So, the pKa of the acid form is 9.8, so the pKb of the base is 4.2.
30. E Use the equilibrium expression
![]()
For every HA that dissociates, we get one H+ and one A–, so [H+] = [A–] = y.
The acid is weak, so we can assume that very little HA dissociates and that the concentration of HA remains 1-molar.
So [H+] = y = ![]()
1. (a) First let’s find out how many moles of NaOH were added.
Moles = (molarity)(volume)
Moles of NaOH = (0.100 M)(.040 L) = 0.004 moles
Every OH– ion neutralizes one H+ ion, so at the equivalence point, the number of moles of NaOH added is equal to the number of moles of HOCl originally present.
(moles of NaOH) = (moles of HOCl) = 0.004 moles
Now we can find the original concentration of the HOCl solution.
Molarity = ![]()
[HOCl] = ![]() = 0.040 M
= 0.040 M
(b) Use the equilibrium expression.
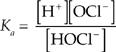
[H+] = 10–pH = 10–4.46 = 3.47 × 10–5
M
[H+] = [OCl–] = 3.47 × 10–5
M
[HOCl] = 0.040 M
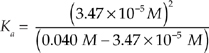
0.040 is much larger than 3.47 × 10–5, so we can simplify the expression.
Ka=  = 3.00 × 10–8M
= 3.00 × 10–8M
(c) The percent of molecules ionized is given by the following expression:
% ionized = ![]() = 0.087%
= 0.087%
(d) At the equivalence point, all of the HOCl initially present has been converted into OCl– ions.
From (a), we know that there were initially 0.004 moles of HOCl, so at equivalence, there are 0.004 moles of OCl–.
At equivalence, we have added 40 ml to the 100 ml of solution originally present, so we must take this into account in our concentration calculation.
Molarity = ![]()
[OCl–] = ![]() = 0.029 M
= 0.029 M
(e) We know the Ka for HOCl, so we can use it to find the Kb for OCl–.
Kb = ![]() = 3.33 × 10–7
= 3.33 × 10–7
Now use the Kb expression.
![]()
[HOCl] = [OH–] = x
[OCl–] = 0.029 M
3.33 × 10–7 = ![]()
Let’s assume that 0.029 M is much larger than x. This simplifies the expression.
3.33 × 10–7 = ![]()
x2 = (3.33 × 10–7)(0.029 M) = 9.67 × 10–9
x = 9.83 × 10–5 = [OH–]
pOH = –log[OH–] = 4
pH = 14 – pOH = 14 – 4 = 10
2. (a) Use the equilibrium expression for H2S to find [H+].
![]()
[H+] = [HS–] = x
[H2S] = 0.100 M
K1 = 1.0 × 10–7
1.0 × 10–7 = ![]()
Let’s assume that 0.100 is much larger than x. That simplifies the expression.
1.0 × 10–7 = ![]()
x2 = (1.0 × 10–7)(0.100) M2 = 1.0 × 10–8
M2
x = 1.0 × 10–4
M = [H+]
pH = –log[H+] = –log(1.0 × 10–4) = 4.0
(b) At the midpoint, pH = pK1
Let’s look at the Henderson-Hasselbalch expression.
pH = pK + log ![]()
When pH = pK, [HS–] must be equal to [H2S], making ![]() equal to one and log
equal to one and log ![]() equal to zero.
equal to zero.
For every molecule of H2S neutralized, one unit of HS– is generated, so we must add enough NaOH to neutralize half of the HS– initially present. (We are assuming that the further dissociation of HS– into H+ and S2– is negligible and can be ignored.)
Let’s find out how many moles of H2S were initially present.
Moles = (molarity)(volume)
Moles of H2S = (0.100 M)(0.500 L) = 0.050 moles
We need to neutralize half of that, or 0.025 moles, so we need 0.025 moles of NaOH.
Volume of NaOH = ![]() = 0.250 L = 250 ml
= 0.250 L = 250 ml
(c) The concentrations of the H2S solution and NaOH solution are both 0.100 M, so the first 500 ml of NaOH solution will completely neutralize the H2S. The final 300 ml of NaOH solution will neutralize HS– molecules.
Initially, there were 0.050 moles of H2S, so after 500 ml of NaOH solution was added, there were 0.050 moles of HS–.
By adding 300 ml more of NaOH solution, we added (0.100 M)(0.300 L) = 0.030 moles of NaOH. [Moles = (molarity)(volume)]
Every unit of NaOH added neutralizes one unit of HS–, so when all the NaOH has been added, we have 0.030 moles of S2– and (0.050 moles) – (0.030 moles) = 0.020 moles of HS–.
Now we can use the Henderson-Hasselbalch expression to find the pH. We can use the number of moles we just calculated (0.030 for S2– and 0.020 for HS–) instead of concentrations because in a solution the concentrations are proportional to the number of moles.
pH = pK + log ![]()
pK = –log(1.3 × 10–13) = 12.9
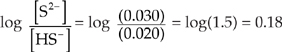
pH = 12.9 + 0.18 = 13.1.
(d) The reaction (H2S ![]() 2 H+ + S2–) is the sum of the two acid dissociation reactions below.
2 H+ + S2–) is the sum of the two acid dissociation reactions below.
H2S ![]() H+ + HS–
H+ + HS–
HS–
![]() H+ + S2–
H+ + S2–
If one reaction is the sum of two other reactions, then its equilibrium constant will be the product of the equilibrium constants for the other two reactions.
So Keq = K1K2 = (1.0 × 10–7)(1.3 × 10–13) = 1.3 × 10–20
3. (a) pKb = –log Kb = –log(1.79 × 10–5) = 4.75
(b) This is a buffered solution, so we’ll use the Henderson-Hasselbalch expression.
First let’s find [NH4+] and [NH3].
Moles = (molarity)(volume)
Moles of NH4+ = (0.100 M)(0.100 L) = 0.010 moles
Moles of NH3 = (0.200)(0.080 L) = 0.016 moles
When we mix the solutions, the volume becomes (0.100 L) + (0.080 L) = 0.180 L.
Molarity = ![]()
[NH4+] = ![]() = 0.056 M
= 0.056 M
[NH3] = ![]() = 0.089 M
= 0.089 M
Now we can use the Henderson-Hasselbalch expression for bases.
pOH = pK + log![]()
pK = 4.75
![]()
pOH = 4.75 + (–0.20) = 4.55
pH = 14 – pOH = 14 – 4.55 = 9.45
(c) First let’s find out how many moles of NaOH were added.
Moles = ![]()
Moles of NaOH = ![]() = 0.005 mol
= 0.005 mol
When NaOH is added to the solution, the following reaction occurs:
NH4+ + OH– → NH3 + H2O
So for every unit of NaOH added, one ion of NH4+ disappears and one molecule of NH3 appears. We can use the results of the molar calculations we did in part (b).
Moles of NH4+ = (0.010) – (0.005) = 0.005 moles
Moles of NH3 = (0.016) + (0.005) = 0.021 moles
Now we can use the Henderson-Hasselbalch expression. We can use the number of moles we just calculated (0.005 for NH4+ and 0.021 for NH3) instead of concentrations because in a solution the concentrations will be proportional to the number of moles.
pOH = pK + log ![]()
pK = 4.75
![]()
pOH = 4.75 + (–0.62) = 4.13
pH = 14 – pOH = 14 – 4.13 = 9.87
(d) When equal quantities of a base (NH3) and its conjugate acid (NH4+) are mixed in a solution, the pOH will be equal to the pKb.
From (a), pOH = pKb = 4.75
pH = 14 – pOH = 14 – 4.75 = 9.25
4. (a) An amphoteric species can act either as an acid or base.
H2PO![]() is amphoteric.
is amphoteric.
Conjugate base: HPO![]()
Conjugate acid: H3PO4
or
HPO![]() is amphoteric.
is amphoteric.
Conjugate base: PO![]()
Conjugate acid: H2PO![]()
(b) The smaller the dissociation constant, the more tightly the acid holds its hydrogen ions and the weaker the acid becomes.
After a hydrogen ion has been removed, the remaining species has a negative charge that attracts the remaining hydrogen ions more strongly.
(c) H2PO4–
![]() H+ + HPO
H+ + HPO![]() K2 = 6.2 × 10–8
K2 = 6.2 × 10–8
For H2PO4–, pKa = –log(6.2 × 10–8) = 7.2
The best buffer solution is made with an acid whose pKa is approximately equal to the desired pH.
(d)

The axes should have the correct labeling (pH and NaOH added).
The curve should show rising pH, and it should have three bumps.
5. (a) The solution will be basic. A salt composed of the conjugate of a strong base (Na+) and the conjugate of a weak acid (C2H3O2–) will create a basic solution in water.
NaC2H3O2 dissociates into Na+ and C2H3O2–.
Na+ does not react with water but C2H3O2– does.
C2H3O2– + H2O ![]() HC2H3O2 + OH–
HC2H3O2 + OH–
(b) The solution will be acidic. A salt composed of the conjugate of a strong acid (Cl–) and the conjugate of a weak base (NH4+) will create an acidic solution in water.
NH4Cl dissociates into NH4+ and Cl–.
Cl– does not react with water but NH4+ does.
NH4+ + H2O ![]() NH3 + H3O+
NH3 + H3O+
(c) For a buffer solution, it is necessary for both an acid (HA) and its conjugate base (A–) to be present in the solution.
By definition, strong acids dissociate completely, so the conjugate base will be too weak to accept any hydrogen atoms that are added to the solution.
Weak acids do not dissociate completely, so it is possible to have a solution that contains both undissociated acid (HA) and conjugate base (A–). The undissociated acid can react with added hydroxide, and the conjugate base can react with added hydrogen ions.
(d) KOH separates into K+ and OH– in water because the ionic bond between O and K in the unit can be broken by water, which is a polar solvent.
HBrO separates into H+ and BrO– because the covalent O–Br bond pulls electrons away from the O–H bond. This makes the O–H bond more polar and more easily broken by water, a polar solvent.
6. (a) HCl is the stronger acid. The bond between H and Cl is weaker than the bond between H and F, so HCl dissociates more easily.
(b) H2SO3 is stronger. As a polyprotic acid gives up hydrogen ions, it becomes negatively charged, causing it to hang onto its remaining hydrogen ions more tightly, which weakens it as an acid.
(c)

HNO3 is stronger. As more oxygens are added to the central atom of an oxyacid, the oxidation number of the central atom increases.
In HNO2, the central atom, N, has an oxidation state of +3.
In HNO3, N has an oxidation state of +5.
The increased oxidation state of N makes the N–O bond stronger. This draws electrons away from the O–H bond, making it more polar or weaker. The weakness of the O–H bond makes the acid stronger.
(d)

HClO4 is stronger. Cl has greater electronegativity than Br, so Cl draws electrons away from O in the Cl–O bond; this makes the O–H bond more polar or weaker. A weak O–H bond makes for a strong acid.