In the multiple-choice section, this topic appears in about 3 out of 75 questions. In the free-response section, this topic appears almost every year.
In thermodynamics, you determine whether a reaction will occur spontaneously, based on the relative states of the reactants and products. Kinetics deals with the rate at which a reaction occurs between those states. The rate of a chemical reaction is determined experimentally by measuring the rate at which a reactant disappears or a product appears. So reaction rates are generally measured in moles/time or M/time.
The rate law for a reaction describes the dependence of the initial rate of a reaction on the concentrations of its reactants. It includes the Arrhenius constant, k, which takes into account the activation energy for the reaction and the temperature at which the reaction occurs. The rate of a reaction is described in terms of the rate of appearance of a product or the rate of disappearance of a reactant. The rate law for a reaction cannot be determined from a balanced equation; it must be determined from experimental data, which is presented on the test in table form.
The data below were collected for the following hypothetical reaction:
A + 2 B + C → D

The rate law always takes the following form, using the concentrations of the reactants:
Rate = k[A]x[B]y[C]z
The greater the value of a reactant’s exponent, the more a change in the concentration of that reactant will affect the rate of the reaction. To find the values for the exponents x, y, and z, we need to examine how changes in the individual reactants affect the rate. The easiest way to find the exponents is to see what happens to the rate when the concentration of an individual reactant is doubled.
Let’s look at [A]
From experiment 3 to experiment 4, [A] doubles while the other reactant concentrations remain constant. For this reason, it is useful to use the rate values from these two experiments to calculate x (the order of the reaction with respect to reactant A).
As you can see from the table, the rate quadruples from experiment 3 to experiment 4, going from 0.02 M/sec to 0.08 M/sec.
We need to find a value for the exponent x that relates the doubling of the concentration to the quadrupling of the rate. The value of x can be calculated as follows:
(2)x = 4, so x = 2
Because the value of x is 2, the reaction is said to be second order with respect to A.
Rate = k[A]2[B]y[C]z
From experiment 1 to experiment 3, [B] doubles while the other reactant concentrations remain constant. For this reason it is useful to use the rate values from these two experiments to calculate y (the order of the reaction with respect to reactant B).
As you can see from the table, the rate doubles from experiment 1 to experiment 3, going from 0.01 M/sec to 0.02 M/sec.
We need to find a value for the exponent y that relates the doubling of the concentration to the doubling of the rate. The value of y can be calculated as follows:
(2)y = 2, so y = 1
Because the value of y is 1, the reaction is said to be first order with respect to B.
Rate = k[A]2[B][C]z
From experiment 1 to experiment 2, [C] doubles while the other reactant concentrations remain constant.
The rate remains the same at 0.01 M.
The rate change is (2)z = 1, so z = 0.
Because the value of z is 0, the reaction is said to be zero order with respect to C.
Rate = k[A]2[B]
Because the sum of the exponents is 3, the reaction is said to be third order overall.
Once the rate law has been determined, the value of the rate constant can be calculated using any of the lines of data on the table. The units of the rate constant are dependent on the order of the reaction, so it’s important to carry along units throughout all rate constant calculations.
Let’s use experiment 3.

You should note that we can tell from the coefficients in the original balanced equation that the rate of appearance of D is equal to the rate of disappearance of A and C because the coefficients of all three are the same. The coefficient of D is half as large as the coefficient of B, however, so the rate at which D appears is half the rate at which B disappears.
It’s also useful to have rate laws that relate the rate constant k to the way that concentrations change over time. The rate laws will be different depending on whether the reaction is first, second, or zero order, but each rate law can be expressed as a graph that relates the rate constant, the concentration of a reactant, to the elapsed time.
The rate of a first-order reaction depends on the concentration of a single reactant raised to the first power.
Rate = k[A]
As the concentration of reactant A is depleted over time, the rate of reaction will decrease with a characteristic half-life. This is the same curve you’ve seen used for nuclear decay, which is also a first-order process.
The rate law for a first-order reaction uses natural logarithms.

The use of natural logarithms in the rate law creates a linear graph comparing concentration and time. The slope of the line is given by –k and the y-intercept is given by ln[A]o.
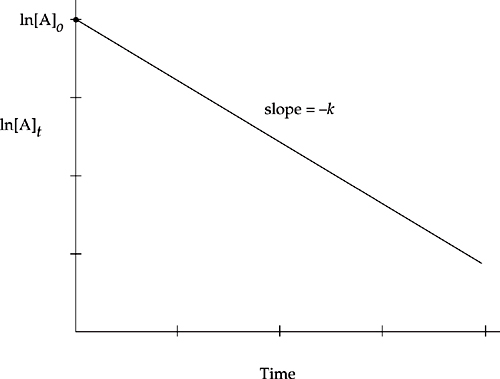
If you are asked to give the half-life of a first-order reaction, you can usually figure it out by looking at the graph or table given in the problem, but it’s worth your while to know the equation that gives the half-life in terms of the rate constant.
![]()
Let’s try an example based on the data below.
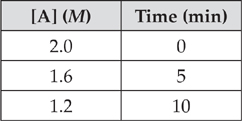
(a) Let’s find the value of k. We’ll use the first two lines of the table.
ln[A]t – ln[A]o = –kt
ln(1.6) – ln(2.0) = –k(5 min)
–0.22 = –(5 min)k
k = 0.045 min–1
(b) Now let’s use k to find [A] when 20 minutes have elapsed.
ln[A]t – ln[A]o = –kt
ln[A]t – ln(2.0) = –(0.045 min–1)(20 min)
ln[A]t = –0.21
[A]t = e–0.21 = 0.81 M
(c) Now let’s find the half-life of the reaction.
We can look at the answer (b) to see that the concentration dropped by half (1.6 M to 0.8 M) from 5 minutes to 20 minutes. That makes the half-life about 15 minutes. We can confirm this using the half-life equation.
![]()
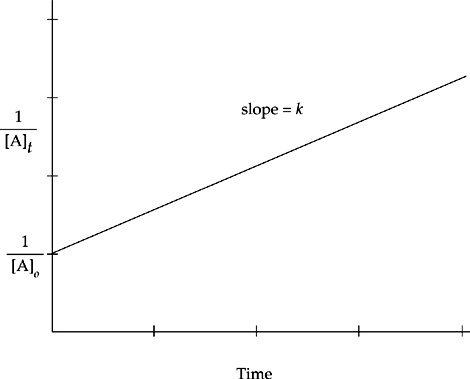
The rate of a second-order reaction depends on the concentration of a single reactant raised to the second power.
Rate = k[A]2
The rate law for a second-order reaction uses the inverses of the concentrations.

The use of inverses in the rate law creates a linear graph comparing concentration and time. Notice that the line moves upward as the concentration decreases. The slope of the line is given by k and the y-intercept is given by ![]() .
.
The rate of a zero-order reaction does not depend on the concentration of reactants at all, so the rate of a zero-order reaction will always be the same at a given temperature.
Rate = k
The graph of the change in concentration of a reactant of a zero-order reaction versus time will be a straight line with a slope equal to –k.
According to collision theory, chemical reactions occur because reactants are constantly moving around and colliding with one another.
When reactants collide with sufficient energy (activation energy, Ea), a reaction occurs. These collisions are referred to as effective collisions, because they lead to a chemical reaction. Ineffective collisions do not produce a chemical reaction. At any given time during a reaction, a certain fraction of the reactant molecules will collide with sufficient energy to cause a reaction between them.
Reaction rate increases with increasing concentration of reactants because if there are more reactant molecules moving around in a given volume, then more collisions will occur.
Reaction rate increases with increasing temperature because increasing temperature means that the molecules are moving faster, which means that the molecules have greater average kinetic energy. The higher the temperature, the greater the number of reactant molecules colliding with each other with enough energy (Ea) to cause a reaction.
The Boltzmann distribution diagram below is often used to show that increasing temperature increases the fraction of reactant molecules above the activation energy.
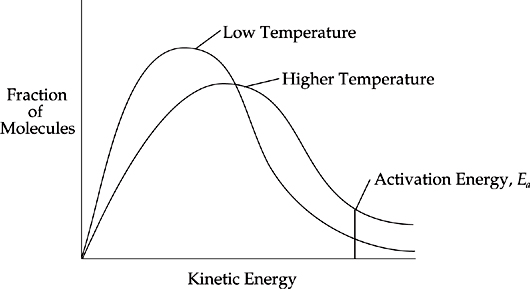
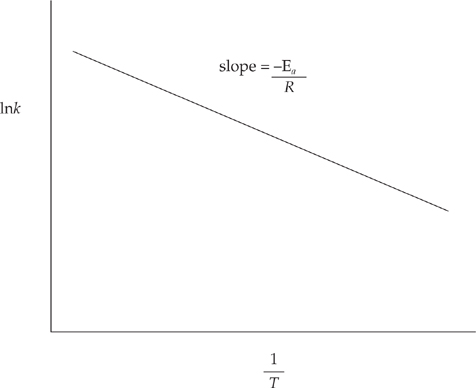
The rate constant will increase when temperature is increased. The relationship between temperature and the rate constant is given by the Arrhenius equation, ![]() . This equation is generally rewritten using natural logarithms.
. This equation is generally rewritten using natural logarithms.

When lnk is graphed versus ![]() , it makes a straight line with a slope of
, it makes a straight line with a slope of ![]() . It’s a little difficult to see, but the graph below shows that k is increasing as the temperature increases.
. It’s a little difficult to see, but the graph below shows that k is increasing as the temperature increases.
Many chemical reactions are not one-step processes. Rather, the balanced equation is the sum of a series of simple steps. Three molecules will not collide simultaneously very often, so steps of a reaction mechanism involve only one or two reactants at a time.
For instance, the following hypothetical reaction:
![]()
could take place by the following three-step mechanism:
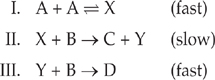
Species X and Y are called intermediates because they appear in the mechanism, but they cancel out of the balanced equation. The steps of a reaction mechanism must add up to equal the balanced equation, with all intermediates cancelling out.
Let’s show that the mechanism above is consistent with the balanced equation by adding up all the steps.
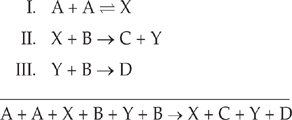
Cancel species that appear on both sides.
![]()
By adding up all the steps, we get the balanced equation for the overall reaction, so this mechanism is consistent with the balanced equation.
As in any process where many steps are involved, the speed of the whole process can’t be faster than the speed of the slowest step in the process, so the slowest step of a reaction is called the rate-determining step. Because the slowest step is the most important step in determining the rate of a reaction, the slowest step and the steps leading up to it are used to see if the mechanism is consistent with the rate law for the overall reaction.
Let’s look at the reaction and the three-step mechanism again.
![]()
The reaction above takes place by the following three-step mechanism.
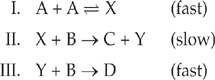
Let’s show that the reaction mechanism is consistent with the rate law (Rate = k[A]2[B]).
The slowest step is the rate-determining step, so we should start with the rate law for step II:
Rate = k2[X][B]
But X is an intermediate, which means that it can’t appear in the overall rate law. To eliminate X from the rate law, we need to look at the equilibrium reaction in step I. We can assume that the reaction in step I comes to equilibrium quickly. At equilibrium the rate of the forward reaction is equal to the rate of the reverse reaction, so we get
kf [A][A] = kr[X]
Now we can solve for [X].
![]()
Once we have solved our equilibrium rate expression for [X] in terms of [A], we can substitute for [X] in our step II rate law.
![]()
Now we have a rate law that contains only reactants from the overall equation and that’s consistent with the experimentally derived rate law that we were given. You can always eliminate intermediates from the rate-determining step by this process.
As we mentioned earlier in the book, a catalyst increases the rate of a chemical reaction without being consumed in the process; catalysts do not appear in the balanced equation. In some cases, a catalyst is a necessary part of a reaction because in its absence, the reaction would proceed at too slow a rate to be at all useful.
A catalyst increases the rate of a chemical reaction by providing an alternative reaction pathway with a lower activation energy.
There is a relationship between the rate constants for the forward and reverse directions of a particular reaction and the equilibrium constant for that reaction.

Questions 1–3
A + B → C
The following are possible rate laws for the hypothetical reaction given above.
(A) Rate = k[A]
(B) Rate = k[A]2
(C) Rate = k[A][B]
(D) Rate = k[A]2[B]
(E) Rate = k[A]2[B]2
1. This is the rate law for a first order reaction.
2. This is the rate law for a reaction that is second order with respect to B.
3. This is the rate law for a third order reaction.
Questions 4–6
A + B → C
The following are possible rate laws for the hypothetical reaction given above.
(A) Rate = k[A]
(B) Rate = k[B]2
(C) Rate = k[A][B]
(D) Rate = k[A]2[B]
(E) Rate = k[A]2[B]2
4. When [A] and [B] are doubled, the initial rate of reaction will increase by a factor of eight.
5. When [A] and [B] are doubled, the initial rate of reaction will increase by a factor of two.
6. When [A] is doubled and [B] is held constant, the initial rate of reaction will not change.
7. A multistep reaction takes place by the following mechanism:
A + B → C + D
A + C → D + E
Which of the species shown above is an intermediate in the reaction?
(A) A
(B) B
(C) C
(D) D
(E) E
8. 2 NOCl → 2 NO + Cl2
The reaction above takes place with all of the reactants and products in the gaseous phase. Which of the following is true of the relative rates of disappearance of the reactants and appearance of the products?
(A) NO appears at twice the rate that NOCl disappears.
(B) NO appears at the same rate that NOCl disappears.
(C) NO appears at half the rate that NOCl disappears.
(D) Cl2 appears at the same rate that NOCl disappears.
(E) Cl2 appears at twice the rate that NOCl disappears.
9. H2(g) + I2(g) → 2 HI(g)
When the reaction given above takes place in a sealed isothermal container, the rate law is
Rate = k[H2][I2]
If a mole of H2 gas is added to the reaction chamber, which of the following will be true?
(A) The rate of reaction and the rate constant will increase.
(B) The rate of reaction and the rate constant will not change.
(C) The rate of reaction will increase and the rate constant will decrease.
(D) The rate of reaction will increase and the rate constant will not change.
(E) The rate of reaction will not change and the rate constant will increase.
10. A + B → C
When the reaction given above takes place, the rate law is
Rate = k[A]
If the temperature of the reaction chamber were increased, which of the following would be true?
(A) The rate of reaction and the rate constant will increase.
(B) The rate of reaction and the rate constant will not change.
(C) The rate of reaction will increase and the rate constant will decrease.
(D) The rate of reaction will increase and the rate constant will not change.
(E) The rate of reaction will not change and the rate constant will increase.
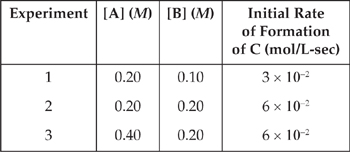
11. A + B → C
Based on the following experimental data, what is the rate law for the hypothetical reaction given above?
(A) Rate = k[A]
(B) Rate = k[A]2
(C) Rate = k[B]
(D) Rate = k[B]2
(E) Rate = k[A][B]
12. A + B → C + D
The rate law for the hypothetical reaction shown above is as follows:
Rate = k[A]
Which of the following changes to the system will increase the rate of the reaction?
I. An increase in the concentration of A
II. An increase in the concentration of B
III. An increase in the temperature
(A) I only
(B) I and II only
(C) I and III only
(D) II and III only
(E) I, II, and III
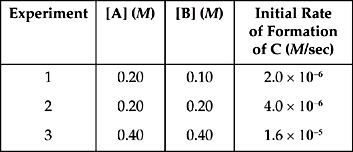
13. A + B → C
Based on the following experimental data, what is the rate law for the hypothetical reaction given above?
(A) Rate = k[A]
(B) Rate = k[A]2
(C) Rate = k[B]
(D) Rate = k[B]2
(E) Rate = k[A][B]
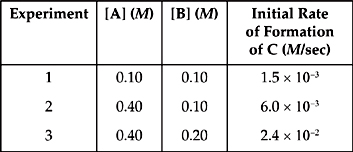
14. A + B → C
Based on the following experimental data, what is the rate law for the hypothetical reaction given above?
(A) Rate = k[A]
(B) Rate = k[A]2
(C) Rate = k[A][B]2
(D) Rate = k[B]2
(E) Rate = k[A]2[B]2
| Time (Hours) | [A] M |
| 0 | 0.40 |
| 1 | 0.20 |
| 2 | 0.10 |
| 3 | 0.05 |
Reactant A underwent a decomposition reaction. The concentration of A was measured periodically and recorded in the chart above. Based on the data in the chart, which of the following is the rate law for the reaction?
(A) Rate = k[A]
(B) Rate = k[A]2
(C) Rate = 2k[A]
(D) Rate = k[A]
(E) Rate = k
1. A + 2B → 2C
The following results were obtained in experiments designed to study the rate of the reaction above:
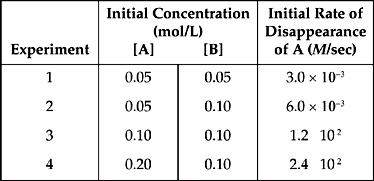
(a) Determine the order of the reaction with respect to each of the reactants, and write the rate law for the reaction.
(b) Calculate the value of the rate constant, k, for the reaction. Include the units.
(c) If another experiment is attempted with [A] and [B], both 0.02-molar, what would be the initial rate of disappearance of A?
(d) The following reaction mechanism was proposed for the reaction above:
A + B → C + D
D + B → C
(i) Show that the mechanism is consistent with the balanced reaction.
(ii) Show which step is the rate-determining step, and explain your choice.
2. 2 NO(g) + Br2(g) → 2 NOBr(g)
The following results were obtained in experiments designed to study the rate of the reaction above:
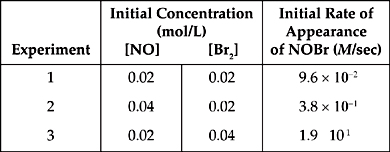
(a) Write the rate law for the reaction.
(b) Calculate the value of the rate constant, k, for the reaction. Include the units.
(c) In experiment 2, what was the concentration of NO remaining when half of the original amount of Br2 was consumed?
(d) Which of the following reaction mechanisms is consistent with the rate law established in (a)? Explain your choice.
| I. NO + NO |
(fast) |
| N2O2 + Br2 → 2 NOBr | (slow) |
| II. Br2 → Br + Br | (slow) |
| 2(NO + Br → NOBr) | (fast) |
3. N2O5(g) → 4NO2(g) + O2(g)
Dinitrogen pentoxide gas decomposes according to the equation above. The first-order reaction was allowed to proceed at 40°C and the data below were collected.
| [N2O5] (M) | Time (min) |
| 0.400 | 0.0 |
| 0.289 | 20.0 |
| 0.209 | 40.0 |
| 0.151 | 60.0 |
| 0.109 | 80.0 |
(a) Calculate the rate constant for the reaction using the values for concentration and time given in the table. Include units with your answer.
(b) After how many minutes will [N2O5] be equal to 0.350 M?
(c) What will be the concentration of N2O3 after 100 minutes have elapsed?
(d) Calculate the initial rate of the reaction. Include units with your answer.
(e) What is the half-life of the reaction?
4. 2 A + B → C + D
The following results were obtained in experiments designed to study the rate of the reaction above:
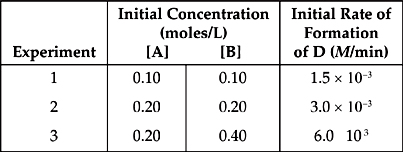
(a) Write the rate law for the reaction.
(b) Calculate the value of the rate constant, k, for the reaction. Include the units.
(c) If experiment 2 goes to completion, what will be the final concentration of D? Assume that the volume is unchanged over the course of the reaction and that no D was present at the start of the experiment.
(d) Which of the following possible reaction mechanisms is consistent with the rate law found in (a)?
| I. A + B → C + E | (slow) |
| A + E → D | (fast) |
| II. B → C + E | (slow) |
| A + E → F | (fast) |
| A + F → D | (fast) |
(e) Calculate the half-life of reactant B.
5. A(g) + B(g) → C(g)
The reaction above is second order with respect to A and zero order with respect to B. Reactants A and B are present in a closed container. Predict how each of the following changes to the reaction system will affect the rate and rate constant and explain why.
(a) More gas A is added to the container.
(b) More gas B is added to the container.
(c) The temperature is increased.
(d) An inert gas D is added to the container.
(e) The volume of the container is decreased.
6. Use your knowledge of kinetics to answer the following questions. Justify your answers.
(a)
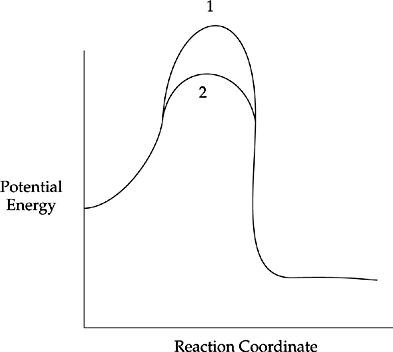
The two lines in the diagram above show different reaction pathways for the same reaction. Which of the two lines shows the reaction when a catalyst has been added?
(b)

Which of the two lines in the energy distribution diagram shows the conditions at a higher temperature?
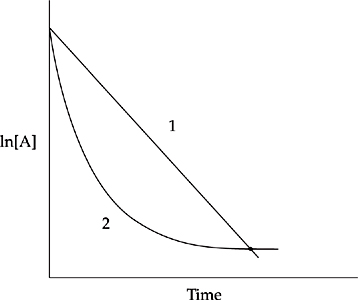
Which of the two lines in the diagram above shows the relationship of ln[A] to time for a first order reaction with the following rate law?
Rate = k[A]
(d)

Which of the two graphs above shows the changes in concentration over time for the following reaction?
A → B
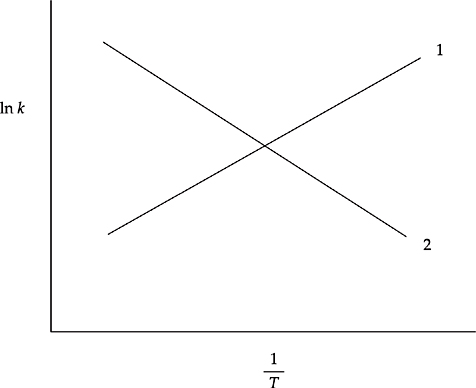
Which of the two lines in the diagram above shows the relationship of ln k to ![]() for a reaction? How is the slope of the line related to the activation energy for the reaction?
for a reaction? How is the slope of the line related to the activation energy for the reaction?
7. Use your knowledge of kinetics to explain each of the following statements:
(a) An increase in the temperature at which a reaction takes place causes an increase in reaction rate.
(b) The addition of a catalyst increases the rate at which a reaction will take place.
(c) A catalyst that has been ground into powder will be more effective than a solid block of the same catalyst.
(d) Increasing the concentration of reactants increases the rate of a reaction.
1. A In a first-order reaction, the exponents of all the reactants present in the rate law add up to 1.
Rate = k[A]1
2. E The exponent for B in this rate law is 2, so the reaction is second order with respect to B.
Rate = k[A]2[B]2
3. D In a third-order reaction, the exponents of all the reactants present in the rate law add up to 3.
Rate = k[A]2[B]1
4. D Let’s say that [A] = [B] = 1. Then Rate = k.
Now if we double [A] and [B], that is, we make [A] = [B] = 2, here’s what we get for each of the answer choices.
(A) Rate = k(2) = 2k
(B) Rate = k(2)2 = 4k
(C) Rate = k(2)(2) = 4k
(D) Rate = k(2)2(2) = 8k
(E) Rate = k(2)2(2)2 = 16k
So in (D), the rate increases by a factor of 8.
5. A Let’s say that [A] = [B] = 1. Then Rate = k.
Now if we double [A] and [B], that is, we make [A] = [B] = 2, here’s what we get for each of the answer choices.
(A) Rate = k(2) = 2k
(B) Rate = k(2)2 = 4k
(C) Rate = k(2)(2) = 4k
(D) Rate = k(2)2(2) = 8k
(E) Rate = k(2)2(2)2 = 16k
So in (A), the rate increases by a factor of 2.
6. B We need to find the rate law that is independent of changes in [A].
The only choice listed that does not include [A] is choice (B), Rate = k[B]2.
7. C C is created and used up in the reaction, so it will not be present in the balanced equation.
8. B For every two NO molecules that form, two NOCl molecules must disappear, so NO is appearing at the same rate that NOCl is disappearing. Choices (D) and (E) are wrong because for every mole of Cl2 that forms, two moles of NOCl are disappearing, so Cl2 is appearing at half the rate that NOCl is disappearing.
9. D From the rate law given in the question (Rate = k[H2][I2]), we can see that increasing the concentration of H2 will increase the rate of reaction. The rate constant, k, is not affected by changes in the concentration of the reactants.
10. A When temperature increases, the rate constant increases to reflect the fact that more reactant molecules are likely to have enough energy to react at any given time. So both the rate constant and the rate of reaction will increase.
11. C From a comparison of experiments 1 and 2, when [B] is doubled while [A] is held constant, the rate doubles. That means that the reaction is first order with respect to B.
From a comparison of experiments 2 and 3, when [A] is doubled while [B] is held constant, the rate doesn’t change. That means that the reaction is zero order with respect to A and that A will not appear in the rate law.
So the rate law is Rate = k[B].
12. C An increase in the concentration of A will increase the rate, as shown in the rate law for the reaction, so (I) is correct. Reactant B is not included in the rate law, so an increase in the concentration of B will not affect the rate; therefore, (II) is wrong. An increase in temperature causes more collisions with greater energy among reactants and always increases the rate of a reaction, so (III) is correct.
13. E From a comparison of experiments 1 and 2, when [B] is doubled while [A] is held constant, the rate doubles. That means that the reaction is first order with respect to B.
From a comparison of experiments 2 and 3, when both [A] and [B] are doubled, the rate increases by a factor of 4. We would expect the rate to double based on the change in B; because the rate is in fact multiplied by 4, the doubling of A must also change the rate by a factor of 2, so the reaction is also first order with respect to A.
So the rate law is Rate = k[A][B].
14. C From a comparison of experiments 1 and 2, when [A] is quadrupled while [B] is held constant, the rate quadruples. That means that the reaction is first order with respect to A.
From a comparison of experiments 2 and 3, when [B] is doubled while [A] is held constant, the rate quadruples. That means that the reaction is second order with respect to B.
So the rate law is Rate = k[A][B]2.
15.
A The key to this question is to recognize that reactant A is disappearing with a characteristic half-life. This is a signal that the reaction is first order with respect to A. So the rate law must be
Rate = k[A].
1. (a) When we compare the results of experiments 3 and 4, we see that when [A] doubles, the rate doubles, so the reaction is first order with respect to A.
When we compare the results of experiments 1 and 2, we see that when [B] doubles, the rate doubles, so the reaction is first order with respect to B.
Rate = k[A][B]
(b) Use the values from experiment 3, just because they look the simplest.
k = ![]() = 1.2 M–1sec–1 = 1.2 L/mol-sec
= 1.2 M–1sec–1 = 1.2 L/mol-sec
(c) Use the rate law.
Rate = k[A][B]
Rate = (1.2 M–1sec–1)(0.02 M)(0.02 M) = 4.8 × 10–4
M/sec
D + B → C
The two reactions add up to
A + 2 B + D → 2 C + D
D’s cancel, and we’re left with the balanced equation.
A + 2 B → 2 C
(ii) A + B → C + D (slow)
D + B → C (fast)
The first part of the mechanism is the slow, rate-determining step because its rate law is the same as the experimentally determined rate law.
2. (a) When we compare the results of experiments 1 and 2, we see that when [NO] doubles, the rate quadruples, so the reaction is second order with respect to NO.
When we compare the results of experiments 1 and 3, we see that when [Br2] doubles, the rate doubles, so the reaction is first order with respect to Br2.
Rate = k[NO]2[Br2]
(b) Use the values from experiment 1, just because they look the simplest.
k = ![]() = 1.2 × 104
M–2sec–1 = 1.2 × 104 L2/mol2-sec
= 1.2 × 104
M–2sec–1 = 1.2 × 104 L2/mol2-sec
(c) In experiment 2, we started with [Br2] = 0.02 M, so 0.01 M was consumed.
From the balanced equation, 2 moles of NO are consumed for every mole of Br2 consumed. So 0.02 M of NO are consumed.
[NO] remaining = 0.04 M – 0.02 M = 0.02 M
(d) Choice (I) agrees with the rate law.
NO + NO N2O2 (fast)
N2O2 + Br2 → 2 NOBr (slow)
The slow step is the rate-determining step, with the following rate law:
Rate = k[N2O2][Br2]
We can replace the intermediate (N2O2) by assuming that the first step reaches equilibrium instantaneously and remembering that at equilibrium, the rates of the forward and reverse reactions are equal.
kf [NO]2 = kr[N2O2]
Now solve for [N2O2].
![]()
Now we can substitute the rate law for the rate determining step.
![]()
This matches the experimentally determined rate law. By the way, the mechanism in choice (II) would have a rate law of Rate = k[Br2].
3. (a) Use the first-order rate law and insert the first two lines from the table.
ln[N2O5]t – ln[N2O5]o = –kt
ln(0.289) – ln(0.400) = –k(20.0 min)
–.325 = –k(20.0 min)
k = 0.0163 min–1
(b) Use the first-order rate law.
ln[N2O5]t – ln[N2O5]o = –kt
ln(0.350) – ln(0.400) = –(0.0163 min–1)t
–0.134 = –(0.0163 min–1)t
t = 8.19 min
(c) Use the first-order rate law.
ln[N2O5] – ln[N2O5]o = –kt
ln[N2O5] – ln(0.400) = –(0.0163 min–1)(100 min)
ln[N2O5] + 0.916 = 1.63
ln[N2O5] = –2.55
[N2O5] = e–2.55
M = 0.078 M
(d) For a first-order reaction, Rate = k[N2O5] = (0.0163 min–1)((0.400 M) = 0.0652 M/min)
(e) You can see from the numbers on the table that the half-life is slightly over 40 min. To calculate it exactly, use the formula
![]()
4. (a) When we compare the results of experiments 2 and 3, we see that when [B] doubles, the rate doubles, so the reaction is first order with respect to B.
Experiments 2 and 3 prove that the rate must double when [B] doubles. Knowing this, we can see that when the rate doubles from experiment 1 to 2, it must be because of B, and the change in A has no effect. So the reaction is zero order with respect to A.
Rate = k[B]
(b) Take the values from experiment 1.
![]()
(c) In experiment 2, there are equal concentrations of A and B, but A is consumed twice as fast, so A is the limiting reagent.
0.2 M of A is consumed.
According to the balanced equation, for every 2 moles of A consumed, 1 mole of D is produced.
So if 0.2 M of A is consumed, 0.1 M of D is produced.
(d) The reaction mechanism in choice (II) is consistent with the rate law.
| B → C + E | (slow) |
| A + E → F | (fast) |
| A + F → D | (fast) |
The slow, rate-determining step gives the proper rate law:
Rate = k[B]
By the way, choice (I) gives a rate law of Rate = k[A][B]
(e) The reaction is first order with respect to B, so use the half-life formula.
![]()
5. (a) The rate of the reaction will increase because the rate depends on the concentration of A as given in the rate law: Rate = k[A]2.
The rate constant is independent of the concentration of the reactants and will not change.
(b) The rate of the reaction will not change. If the reaction is zero order with respect to B, then the rate is independent of the concentration of B.
The rate constant is independent of the concentration of the reactants and will not change.
(c) The rate of the reaction will increase with increasing temperature because the rate constant increases with increasing temperature.
The rate constant increases with increasing temperature because at a higher temperature more gas molecules will collide with enough energy to overcome the activation energy for the reaction.
(d) Neither the rate nor the rate constant will be affected by the addition of an inert gas.
(e) The rate of the reaction will increase because decreasing the volume of the container will increase the concentration of A. Rate = k[A]2
The rate constant is independent of the concentration of the reactants and will not change.
6. (a) Line 2 is the catalyzed reaction. Adding a catalyst lowers the activation energy of the reaction, making it easier for the reaction to occur.
(b) Line 2 shows the higher temperature distribution. At a higher temperature, more of the molecules will be at higher energies, causing the distribution to flatten out and shift to the right.
(c) Line 1 is correct. ln[reactant] for a first order reaction changes in a linear fashion over time, as shown in the following equation.
ln[A]t = –kt + ln[A]o
y = mx + b
Notice the similarity to the slope-intercept form for a linear equation.
(d) Graph 1 is correct, showing a decrease in the concentration of A as it is consumed in the reaction, and a corresponding increase in the concentration of B as it is produced.
(e) Line 2 is correct. The rate constant k increases with increasing temperature, so the line will slope downward when graphed against ![]() . The slope of the line is proportional to the activation energy (slope =
. The slope of the line is proportional to the activation energy (slope = ![]() ).
).
7. (a) An increase in temperature means an increase in the energy of the molecules present. If the molecules have more energy, then more of them will collide more often with enough energy to overcome the activation energy required for a reaction to take place, causing the reaction to proceed more quickly.
(b) A catalyst offers a reaction an alternative pathway with a lower activation energy. If the activation energy is lowered, then more molecular collisions will occur with enough energy to overcome the activation energy, causing the reaction to proceed more quickly.
(c) The effectiveness of a solid catalyst depends on the surface area of the catalyst that is exposed to the reactants. Grinding a solid into powder greatly increases its surface area.
(d) Increasing the concentration of reactants crowds the reactants more closely together, making it more likely that they will collide with one another. The more collisions that occur, the more likely that collisions that will result in reactions will occur.