This chapter, like the preceding one, is sufficiently general and abstract to apply to gambling problems based on any set of fortunes. Here the study of strategies, which in Chapter 2 played a role subsidiary to that of policies, is pursued. This chapter is entirely independent of Chapter 4, which might well be read first, and though this chapter is logically preliminary to much beyond Chapter 4, it is not quite so basic as most of Chapter 2.
Strategies are closely akin to policies. The main reason for considering both is that, while policies are simpler to work with, strategies are conceptually simpler and optimal policies rarely exist.
If the kinship is to be close, a strategy, like a policy, must be assigned a utility. We do not intend to appraise a strategy σ in terms of the utilities of fortunes visited early, nor would it be appropriate to penalize σ for visits to fortunes of low utility however frequent, if these serve as stepping stones to fortunes of high utility. These considerations, together with the remark, in Section 2.11, that stop rules, as functions from H to the integers, are naturally partially ordered, suggest this definition:
The “lim sup” here means, of course, the supremum of those numbers c such that for every t there is a t′ with t′(h) ≥ t(h) for all h and u(σ, t′) ≥ c.
The definition (1) would be unsatisfactory if it did not permit this theorem:
Proof: Equation (2.10.2) says that
For a given stop rule t and positive 
, and for all f, let t′(f) be a stop rule such that t′(f) ≥ t[f] and u(σ[f], 
. There is a stop rule t′ defined by the condition t′(fh) = t′(f)(h) + 1; equivalently, t′[f] = t′(f) for all f. Clearly, t′ ≥ t, and, according to (3),
Therefore, u(σ) ≥ ∫ u(σ[f]) dσ0(f).
On the other hand, for each and f there is a stop rule t(f) such that u(σ[f], 
for t′(f) as large as t(f). If t is the stop rule for which t(fh) = t(f)(h) + 1 for all h, then t[f] = t(f), and, for t′ ≥ t, t′[f] ≥ t(f) for all f. If t′ ≥ t,
The notion of a gambler’s ceasing to gamble after the partial history p = (f1, · · ·, fn) can be given two technical interpretations. First, it can mean that he is employing a policy which terminates at time n after that partial history. Second, it can mean that the continuation of his strategy after p is such that, with probability 1, the fortune remains fn time after time. As this section and the next will show, these two senses of ceasing are so close to each other in their effects that each policy can be imitated by a strategy. Moreover, as the next section makes evident, provided δ(f) ∈ Γ(f) for all f, a strategy σ that imitates π is available in Γ at f if π is.
A gambling house Γ is leavable if δ(f) ∈ Γ(f) for all f. We had so little spontaneous interest in nonleavable gambling houses that we were tempted to make leavability part of the official definition of a gambling house. We find, however, that the more general concept leads to better insight into the special one of main interest and, as Chapter 12 indicates, some problems of current interest are most naturally handled in the theory of not necessarily leavable houses.
In this chapter, and in some later contexts where the distinction makes a difference, we shall consider not only the utility U of a gambling house Γ but also the strategic utility V, where V(f) = sup u(σ) over all σ available in Γ at f. Comparison with the definition of U by (2.10.3) and with the definition of the utility of a strategy in Section 2 shows immediately that U majorizes V. Pictorially speaking, U reflects the possible achievements of a gambler who is free to go home when he pleases, whereas V represents the achievements of a gambler who is subject to detention in the gambling house for an arbitrarily long time and who must even select his σ before he is informed of the length of his detention. If the gambling house is leavable, then V and U are the same, as Corollary 2 states. When the gambling house is obviously leavable, we ordinarily write U rather than V. The notion of “gambler’s problem” introduced in Section 2.10 is now modified to mean the determination of V and of optimal or nearly optimal strategies.
With the aid of Theorem 2.1, it is as easy to prove that V is excessive for Γ as it was to prove the corresponding fact (Theorem 2.14.1) for U. Similarly, if Q is excessive for Γ and Q(σ) ≥ u(σ) for all σ available in Γ, then it is easy to paraphrase the proof of Theorem 2.12.1 to conclude that Q majorizes V. These remarks and one lemma easily pave the way to extensions to V of the basic facts about U as a function excessive for Γ.
For each nonvacuous partial history p = (f1, · · ·, fn), let l(p) = fn.
LEMMA 1. For all f and all σ available in Γ at f, V(σ) ≥ u(σ).
Proof: The two general formulas,
and
are applicable to any bounded functions u and V of fortunes, as is easily verifiable by induction. (Compare with the related formula (2.9.6) and Theorem 2.1.) In the special case that V is the V of a Γ, and σ is in Γ at some f, V(l(p)) ≥ u(σ[p]) for all p. Consequently, V(σ, t) = V(π) ≥ u(σ) for all t; so V(σ) ≥ u(σ).
THEOREM 1. V is the smallest of all those functions Q that are excessive for Γ and for which Q(σ) ≥ u(σ) for every σ available in Γ (at any f).
COROLLARY 1. If V ≥ u, then V is U.
COROLLARY 2. If Γ is leavable, V is U.
Let ΓL, the leavable closure of Γ, be the smallest leavable Γ that includes Γ. That is, ΓL(f) = Γ(f) ∪ {δ(f)} for every fortune f.
COROLLARY 3. The U of any gambling house Γ is the V of ΓL.
As Theorem 1 and its corollaries suggest, it would have been mathematically more efficient to begin with the concept V and regard that of U as auxiliary. We thought it better, however, to present U first—in imitation of our own experience—because, in the problems that interest us most, Γ is leavable.
COROLLARY 4. If σ is a strategy available in Γ at f, and t and t′ are stop rules with t ≤ t′, then
This section shows that, for every fortune f′, there is a strategy σ′ that imitates the act of accepting the initial fortune f′ without actually embarking on a policy and, for every policy π, there is some strategy σ that imitates π. For every u, u(σ′) = u(f′) and u(σ) = u(π). The strategy σ′ is available in every leavable Γ at f′, and, for every leavable Γ and fortune f, σ is available in Γ at f if π is. These facts go beyond the assertion of Corollary 3.2 that U is V for every leavable Γ.
If, for some h and σ, every finitary set has probability 1 or 0 according as h is or is not in the set, a (or, more accurately, the measure determined by σ) is the one-point measure δ(h) at h. If F has more than one element, no one-point set of histories is finitary according to Corollary 2.7.1. Yet the finitary sets (and even those of finite structure) are adequate to separate points. Therefore, if δ(h) = δ(h′), then h = h′. (Of course, different strategies σ can determine the same measure σ, which can, in particular, be a one-point measure.)
THEOREM 1. The following conditions are equivalent:
(a) σ = δ(h).
(b) σg = g(h)for all inductively integrable g.
(c) σg = g(h) for all inductively integrable g that depend on only finitely many coordinates, that is, are of finite structure.
(d) σ0 = δ(f1) and σn(f1, · · ·, fn) = δ(fn+1) for all positive n (where h = (f1, f2, · · ·)).
(e) For each n, the probability under σ that the n th fortune is fn is 1.
(f) For each stop rule t, the probability under σ that t = t(h) is 1.
(g) For each t, the σ-probability that ft = ft(h) is 1.
(h) σ0 = δ(f1) and σ[f1] = δ(h′), where h′ = (f2, f3, · · ·).
Of course, the components of the strategy σ along histories other than h have no bearing on whether the measure σ is δ(h).
Let hf be the history (f, f, f, · · ·). If the measure σ is δ(hf), the strategy σ stagnates immediately at f. For σ to stagnate immediately at f it is necessary and sufficient that u(σ, t) = u(f) for all t and u. If the conditional strategy σ[f1, · · ·, fn] (defined in Section 2.5) is δ(hfn), that is, if σ[f1, · · ·, fn] stagnates immediately at fn, the strategy σ stagnates (at n) at (f1, · · ·, fn) The gambler here decides after (f1, · · ·, fn) to remain at fn with probability 1 on his (n + l)st gamble, to do so again at his (n + 2)nd if he finds himself at fn (which he is almost certain to), and so on.
Stagnation is closely akin to termination. In particular, if stagnation occurs at a given partial history (f1, · · ·, fn) and if the stop rule t stops then or later, the terminal fortune given the first n coordinates (f1, · · ·, fn) is fn with probability 1, as the next theorem formally asserts.
THEOREM 2. If σ stagnates at (f1, · · ·, fn) and if tf1f2· · · fn ≥ n, then
Proof: The measure concerned is the one-point measure on the history h = (fn, fn, · · ·), and the set concerned contains this h, since ftf1· · · fn(h) = fn. 
With each σ associate the (possibly) incomplete stop rule tσ such that tσ (h) is the first n, if any, for which a stagnates at (f1, · · ·, fn); failing such an n, tσ(h) = ∞. We intend that tσ(h) = 1 if σ stagnates immediately or at time 1 at f1. According to the definition of tσ, tσ[f] = tσf − 1, unless σ[f] stagnates immediately at f, in which case tσ[f] = tσf = 1.
As the following theorem says formally, it is immaterial when a gambler leaves the gambling house once he has decided to remain inactive.
THEOREM 3. For any utility u and policy (σ, t),
Proof: Recall the convention that u(σ[f], 0) = u(f) implied in the paragraph containing (2.10.2), so that (2.3) is valid without exception. Then proceed by induction on the structure α(ft), calculating thus.
If tσ is a (complete) stop rule, σ is stagnant.
COROLLARY 1. If there is a stop rule t for which t ≥ tσ, then σ is stagnant and u(σ, t) = u(σ, tσ).
COROLLARY 2. If σ is stagnant, then u(σ) = u(σ, tσ).
Just as it is immaterial to u(π) where termination occurs, provided it is not before stagnation, so, too, the behavior of the strategy after termination is immaterial.
THEOREM 4. If 
and if, for all h = (f1, f2, · · ·) and all n < t(h), 
, then u(σ′, t) = u(σ, t) for all u.
For each history h = (f1, f2, · · ·) and stop rule t, if t(h) > n, t terminates after p = (f1, · · ·, fn); if t(h) ≤ n, t terminates by p.
For each policy π = (σ, t), there is a strategy σ′ closely equivalent to π in its effects. The natural candidate for σ′ is σπ defined by σπ(p) = σ(p) or δ(l(p)) according as t terminates after p or by p. (Recall that l(p) is the last coordinate of p.)
THEOREM 5. For all π, σπ is a stagnant strategy with t(σπ) ≤ t; σπ is available in any leavable gambling house Γ at f for which σ is; and u(σπ, t) = u(π) = u(σ, t) = u(σπ).
If the set of histories where tσ is finite has (Eudoxian) probability 1 under σ, then σ stagnates almost certainly; u(σ, tσ) is then defined in accordance with Section 2.11.
THEOREM 6. If σ stagnates almost certainly, u(σ) = u(σ, tσ). In fact, limt u(σ, t) = u(σ, tσ).
Proof: If t ≥ tσ on a finitary set A with complement Ā and 
, let t′ = min (t, tσ).
The right side of (3) is arbitrarily small for all sufficiently large t.
THEOREM 7. If u assumes only 0 and 1 as values, and if σ stagnates at (f1, · · ·, fn) whenever u(fn) = 1, then u(σ, t) is nondecreasing in t; consequently, u(σ) = limt u(σ, t).
This section and the following three form a sort of subchapter about optimal strategies. This section introduces and makes a preliminary study of optimal strategies. Optimality is shown to be the intersection of two other properties. The next two sections study the two properties separately. A fourth section brings together some of the conclusions about optimal strategies implicit in the first three.
From the point of view that led to the definition of U in Section 2.10, a good behavior on the part of a gambler with initial fortune f is to adopt a policy π for which u(π) is very close to U(f) or to settle for u(f), if that is very close to U(f). If, however, all behavior is to be expressed in terms of strategies, which the preceding sections indicate can be done without mathematical loss, then good behavior at f is any strategy σ available in Γ at f for which u(σ) is very close to V(f). So far as optimal, as opposed to merely good, behavior is concerned, we here focus attention on optimal strategies only. Optimal policies are rare and have not proved very interesting. In studying optimal strategies, we emphasize the general theory of not necessarily leavable gambling houses, so that V is not necessarily the same as U. At the same time, examples and counterexamples will be chosen from among leavable gambling houses.
A strategy σ available in Γ at f is optimal at f if u(σ) = V(f). Though this does seem the almost inevitable definition of “optimal”, an optimal strategy is not necessarily quite without blemish. Even in the presence of countable additivity, an optimal strategy might permit bad behavior with probability 0; in the absence of countable additivity, bad behavior may occur along every partial history.
Example 1. Let F consist of the positive integers i. Let each Γ(i) be the same for all i and consist of every gamble on F. Let u(i) = 1 − i−1.A strategy σ that begins with a diffuse gamble γ and then stagnates is available at every fortune i and is optimal there. Yet σ[j], the conditional continuation of σ after the initial gamble γ results in j, is not optimal.
A strategy σ that is optimal at f might be called thoroughly optimal at f if, for each partial history p, the conditional strategy σ[p] is optimal at l(p). Some concepts intermediate between optimal and thoroughly optimal are suggested by the expression “almost thoroughly optimal”, but we refrain from exploration of any concepts stronger than that of optimality. The strategy σ in Example 1 is of course optimal but not thoroughly optimal, though the gambling house Γ of that example abounds in thoroughly optimal strategies.
The following reformulation of optimality is obvious in the light of Corollary 3.4.
THEOREM 1. A σ available in Γ at f is optimal there if and only if V(f) = V(σ) and V(σ) = u(σ).
Theorem 1 displays the strategies optimal for u in Γ at f among those available in Γ at f as just those that have two properties that can be viewed as aspects of optimality. The next section investigates the strategies which have one of these properties, and the one after that, those which have the other.
The next theorem is immediate from Theorem 3.1.
THEOREM 2. If u ≤ u′ ≤ V, then V′ = V, and a strategy optimal for u in Γ at f is also optimal for u′ in Γ at f.
A strategy can, of course, be optimal for u′ without being optimal for u.
The purpose of this section is to continue the exploration of optimal strategies by studying those strategies σ that are thrifty for the V of a gambling house at some fortune f, that is, those for which V(f) = V(σ).
It is convenient, however, to replace this by a superficially more general problem: Among the strategies σ for which an arbitrary bounded function V is excessive, which σ are thrifty for V at f? Therefore, whenever a σ, V, and f are mentioned in the rest of this section, it is to be understood that V is excessive for σ at f, and it is also to be remembered that the conclusions have an immediate application to the situation in which V is the V of a gambling house Γ and σ is available in Γ at f. Examples and counterexamples will be so constructed that the strategy σ will be available in a leavable gambling house Γ the U of which is V.
All but the final inequality in Corollary 3.4 depend only on the fact that V is excessive for Γ at f. Therefore, for t ≤ t′,
A reformulation of thriftiness flows immediately from (1).
LEMMA 1. V(σ) = V(f) if and only if V(σ, t) = V(f) for all stop rules t.
If γV ≥ V(f), γ conserves V at f; if σ0 conserves V at f and σj(f1, · · ·, fj) conserves V at fj for 1 ≤ j < n, σ conserves V at f along h = (f1, f2, · · ·) up to n For each stop rule t, the event that σ conserves V at f up to t is finitary. If, for every t, this event has σ-probability 1, then σ persistently conserves V at f.
LEMMA 2. If the probability that σ conserves V at f up to t is 
, then 
.
Proof: Consider as a function of σ and f and use induction on the structure of ft.
(We thank Manish Bhattacharjee for Lemma 2.)
THEOREM 1. If σ persistently conserves V at f, then V(σ) = V(f); that is, σ is thrifty for V at f.
(If σ persistently conserves V at f, then the set of histories along which σ conserves V up to ∞ that is, up to every n, has outer probability 1. But its inner probability may be 0 even if F is finite; even more, it may include no nonempty finitary subset.
Example 1. Let F = {0, 1, 2}; Γ(0) = {δ(0)}, Γ(1) = {δ(0), δ(1), δ(2)}, Γ(2) = {δ(2)}; u(0) = u(1) = 0, u(2) = 1; σ0 = δ(2), σn(f1, · · ·, fn) = δ(fn) if fn = 0 or 2, and δ(0) if fn = 1.)
A converse to Theorem 1 for countably additive situations is indicated below, but the full converse is in conflict with the next example.
Example 2. Let F consist of the ordered pairs of integers f = (i, j), with i = 1 and 2 and j ≥ 1. Let Γ(1, 1) consist of δ(1, 1) and a diffuse γ on the fortunes (1, j) (that is, for all k,
for all other f whose first coordinate is 1, let Γ(f) consist of δ(f) and δ(g) for all g whose first coordinate is 2; for all f whose first coordinate is 2, let Γ(f) contain only δ(f). Let u(i, j) = 0 or 1 − j−1 according as i = 1 or 2. Then U(i, j) = 1 for i = 1, and 1 − j−1 for i = 2; γ is the only nontrivial gamble that conserves U. Any σ in Γ that first uses γ and then, when the first coordinate is 1, uses any nontrivial gamble that does not decrease the second coordinate is optimal at (1, 1) and therefore thrifty at (1, 1), but σ does not persistently conserve U.
Though σ need not persistently conserve in order to be thrifty, it must approximately do so. A gamble γ -conserves V at f if 
; if σ0 -conserves V at f and σj(f1, · · ·, fj) -conserves V at fj for 1 ≤ j < n, then σ -conserves V at f along h = (f1, f2, · · ·) up to n. If, for each stop rule t, σ -conserves V at f up to t with σ-probability 1, then σ persistently -conserves V at f.
LEMMA 3. If α is the σ-probability that σ -conserves V at f up to t, then
Proof: Use induction on the structure of ft thus. If σ0 does not -conserve V at f, then V(σ, t) ≤ σ0V according to (1), and 
. If σ0 is -conserving, use formula (2.10.2), Theorem 2.9.3, and the inductive hypothesis.
THEOREM 2. If σ is thrifty for V at f, then, for each positive , σ is persistently -conserving. (Of course, the assertion cannot be made for 
.)
COROLLARY 1. If σ is thrifty for V at f and the partial history (f1, · · ·, fn) occurs with positive probability, then the gamble σn(f1, · · ·, fn) conserves V at fn.
Theorem 1 states a sufficient condition that σ be thrifty, which was seen in Example 2 not to be necessary. Theorem 2 states a necessary condition, which, as the next example shows, is not sufficient. We have not succeeded in closing this gap in the theory of thriftiness and optimal strategies.
Example 3. Let F be the set of ordered pairs of positive integers f = (i, j), with i ≥ j. Define a γ(f) for each f thus: γ(1, 1) is any diffuse gamble on the fortunes (i, 1)’, γ(i, j) = δ(i, j + 1) if j < i; γ(i, i) = δ(i, i) if i > 1. Let Γ(f) = {δ(f), γ(f)} and u(f) = −j/i. It is easy to verify that U(1, 1) = 0 and U(f) = u(f) if f ≠ (1, 1). Define a stagnant σ available in Γ at (1, 1) thus: σ0 = γ(1, 1), σn(f1, · · ·, fn) = γ(fn). Define t(h) as the first coordinate of f1. Though σ is persistently -conserving, U(σ) ≤ U(π) = −1 < U(1, 1) = 0.
In the presence of countable additivity, σ persistently -conserves V at f for every positive if and only if it does so for 
. In this important environment, then, Theorem 1 and Theorem 2 establish a condition necessary and sufficient for thriftiness. In order to avoid a technical discussion of measurability, the presentation of this fact is here limited to a special case, which is more than adequate for the applications in Chapters 5 and 6.
As usual, a gamble γ is discrete if there is a countable sequence of fortunes f1, f2, · · · for which Σ γ{fi} = 1. A strategy σ is (persistently) discrete if, for every stop rule t, with σ-probability 1, the only gambles σ(p) used prior to termination are discrete.
THEOREM 3. If σ is discrete, then V(σ) = V(f) (that is, a is thrifty for V at f) if and only if σ0 conserves V at f and σ(p) conserves V at l(p) for every nonvacuous partial history p that occurs with positive σ-probability.
This section continues the study of optimal strategies for a gambling house Γ and in Theorem 2 characterizes those σ that equalize u and V, that is, those for which u(σ) = V(σ).
Consonant with Section 2.6, for each function g on H and each p = (f1, · · ·, fn), gp evaluated at 
is
If g is inductively integrable, B is a subset of partial histories, and A = {h: pt(h) ∈ B}, then
where η is the distribution of pt under σ, as is verifiable by induction on the structure of pl.
LEMMA 1. If w is the indicator function of a set of fortunes and σ is any strategy (in Γ or not) for which w(σ) > 0, then, for every δ > 0, there is a partial history p for which w(σ[p]) > 1 − δ.
Proof: For any positive and 
, and any stop rule t′′, there is a t′ > t′′ for which
as the next two paragraphs show.
Choose t′ > t′′ such that 
. Let A = {h: w(ft′(h)) = 0 and 
, and let Ā be its complement.
If t′ does not satisfy (2), then 
; so 
. Clearly,
For each p, let t*(p) be a stop rule for which w(σ[p]), 
. Let t** be the composition of t′ with the family t* as in (2.9.2). According to (1),
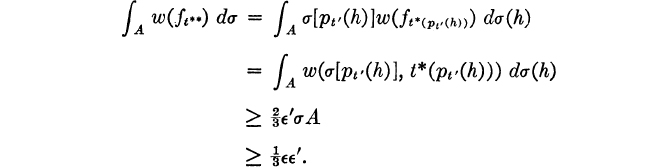
If h is in A, let t(h) = t**(h); if h is not in A, let t(h) = t′(h). This defines a stop rule t, and
which is impossible. Therefore t′ does satisfy (2).
in view of (3.1).
In consequence of (2) and (3), were w(σ[p]) bounded by 1 − δ, w(σ) would not exceed 
for 
and sufficiently close to 0.
(Incidentally, Lemma 1 can, with some effort, be strengthened into a general (that is, finitely additive) version of Lévy’s (1937, Section 41) martingale theorem, and even Doob’s (1953, Theorem VII 4.1) martingale convergence theorem can be so generalized.)
For each 
, a fortune f is -unstable if 
. Under any available strategy, the gambler’s fortune is unlikely to be e-unstable far in the future.
THEOREM 1. Let 
be the indicator of the -unstable fortunes. If σ is available in Γ, then 
for each positive .
Proof: Otherwise, according to Lemma 1, for each δ > 0 there is a strategy σ′, available in Γ, for which 
. So, for each stop rule t, there is a stop rule t′ ≥ t such that, with σ′ probability at least 1 − δ, 
. Consequently, 
, where M and m are upper and lower bounds for u and hence for V. For δ sufficiently small, 
, contradictory to Lemma 3.1.
A fortune f is -adequate if 
and adequate if it is 0-adequate, or u(f) ≥ V(f).
THEOREM 2. Let 
be the indicator of the -adequate fortunes. For σ available in Γ, u(σ) = V(σ) or σ equalizes u and V, if and only if for every 
, 
.
Proof: As is trivial to verify, this condition implies u(σ) ≥ V(σ). Lemma 3.1 asserts the reverse inequality. On the other hand, if u(σ) = V(σ) and 
, Theorem 1 plainly implies that 
.
COROLLARY 1. If σ is available in Γ and almost certainly stagnates, then u(σ) ≥ V(σ) if and only if, for each 
, the fortune at stagnation is -adequate with probability 1.
The 
in Theorem 2, unlike the one in Theorem 6.2, enters not because of finite additivity.
Example 1. Let F be the positive integers; Γ(f) = {δ(f), δ(f + 1)}; and u(f) = 1 − f−1. Then U ≡ 1; no fortune is 0-adequate; the strategy σ of moving forward step by step from any f0 is optimal, and u(σ) = U(σ) = 1.
But if F is finite, the 
in Theorem 2 can be eliminated.
COROLLARY 2. Suppose that F is finite. Then u(σ) = V(σ) if and only if, for every stop rule t and positive δ, there is a stop rule t′ ≥ t such that, with σ-probability at least 1 − δ, ft′, is adequate.
In a countably additive application, such as Corollary 2, the t in Theorem 2 need range over bounded stop rules only, but this is not so in general.
Example 2. Let: F be the pairs of integers f = (i, j), with i = 0, 1 and j ≥ 0; γ be a diffuse gamble on the fortunes (1, j); Γ(f) = {δ(0, j), δ(1, j), γ} for all f; σ0 = γ, and σn(f1, · · ·, fn) = σ(fn) or δ(0, jn) according as n < j1 or n ≥ j1; and u(i, j) = i. Check that: σ is stagnant and in Γ at every f; u(σ) = 0; U ≡ 1; and yet σ{h: fn is adequate} = 1 for all n ≥ 1.
As is emphasized by Theorem 5.1, every fact about thrifty and equalizing strategies has an implication for optimal strategies. A few of the implications of the preceding three sections that are not quite automatic, and some other facts, are here put on record.
THEOREM 1. If no gamble in Γ(f), other than possibly δ(f), conserves V at f, and if u(f) < V(f), then there is no optimal strategy for u in Γ at f.
THEOREM 2. If σ is available in Γ at f, persistently conserves V at f, and almost surely stagnates at an adequate fortune, then σ is optimal at f.
Proof: Apply Corollary 7.1, Theorem 6.1, and Theorem 5.1.
There may be no optimal strategies even if each Γ(f) includes only a finite number of γ and each γ is countably additive.
Example 1. Let F be all integers greater than − 2. Let u(0) = 1, and u(i) = 0 for i ≠ 0. For i = 0 and i = −1, Γ(i) contains only δ(i). For all other i, Γ(i) = {δ(i), δ(i + 1), γ(i)}, where γ(i) assigns to 0 probability 1 − i−1 and to −1 probability i−1 Then U(i) = 1 for i ≥ 0, but for i ≥ 1, clearly no optimal strategies exist.
Even if F is finite, provided that it has as many as three elements, there may exist no optimal strategies at some f.
Example 2. Let F = {0, l, 2}; Γ(0) = {δ(0)}, Γ(1) = {δ(1), (1 − n−1) δ(2) + n−1δ(0) for n = 1, 2, · · · }, Γ(2) = {δ(2)}; u(i) = i, i = 0, 1, 2. There is no optimal strategy available in Γ at 1.
The notation |p| is sometimes convenient for the number of coordinates of the partial history p, as in the proof of the next theorem.
THEOREM 3. For each f, there is a strategy σ available in Γ at f such that, for every partial history p (including the null one), u(σ[p]) ≥ inf U, and therefore inf V = inf U.
Proof: Without real loss in generality, assume that the infimum of U is 0. For each f and n, there is then a policy πn(f) for which u(πn(f)) > −1/n. Construct a new sequence of families of policies 
by induction, thus: Let 
be π1(f), and for each f and n ≥ 1, let 
be the policy obtained by following the policy 
until it terminates, say at f′, and by then continuing with the family of policies πn+1(f′) in accordance with Section 2.9. For each f, the sequence of policies 
, · · · is such that for all n, all m > n, and all partial histories p, if 
does not terminate by p, then 
. In particular, for each p and all sufficiently large n, all 
prescribe the same gamble after p, say σ(f)(p).
To verify that u(σ(f)[p]) ≥ 0, let t′ be an arbitrary stop rule and n a large integer. Let m(h) be the first integer as large as n for which 
, and let 
. Plainly, t is a stop rule, and t ≥ t′. As is easy to see, u(σ(f)[p], t) ≥ − (n + 1)−1. For (σ(f)[p], t) is the composition of a policy π′′ with the family πm(h)+1(f′), and u(πm(h)+1(f′)) ≥ − (n + 1)−1 In fact, 
.
COROLLARY 1. If V is constant, there is, at each f, an optimal strategy available in Γ.
THEOREM 4. There is, at each f, a σ available in Γ that equalizes u and V, that is, for which u(σ) = V(σ).
Proof: Let u′ = u − V. Then V′ ≡ 0, and Corollaries 1 and 3.4 apply.
LEMMA 1. If u is an indicator, σ is a strategy available at some f, and u(σ[p]) ≥ δ for some δ > 0 and all partial histories p, then u(σ) = 1.
Proof: For any 
, there is a stop rule t such that 
and for all t′ ≥ t, 
. Let t′ = t where u(ft) = 1. Elsewhere let t′ be the composition of t with a family t*(·), where 
. Then 
. So 
, which is impossible unless u(σ) is 1.
THEOREM 5. If u is an indicator function and V is bounded away from 0, then V ≡ 1, and at each f there is an optimal strategy.
Proof: Apply Theorem 3 and Lemma 1.
A family of strategies 
was denned as a mapping from fortunes to strategies; 
is stationary if, for some gamble-valued function 
, 
is 
unless p is the empty partial history, in which case it is 
. Intuitively, it would seem that a gambler at his nth decision ought not to benefit from knowledge of his past fortunes fm for m < n. So perhaps there is (at least in every leavable Γ) a stationary family of nearly optimal strategies.
A single strategy σ is stationary if σ[f], or more logically σ[·], is a stationary family. Therefore, whether a single strategy σ is stationary does not depend on σ0.
There can be, at each f, a stationary optimal strategy and yet be no stationary family of optimal strategies.
Example 1. Let: F be the integers; γ be a diffuse gamble on the positive integers; Γ(j) = {δ(j), γ, δ(−j)} for j ≥ 0, Γ(j) = {δ(j)} for j < 0; u(j) = 0 for j ≥ 0, u(j) = 1 + j−l for j < 0.
Four lemmas prepare for the first of several theorems on the existence of stationary families of optimal and near optimal strategies.
LEMMA 1. For any f and positive there is available in Γ at f a policy π = (σ, t) such that, with positive σ-probability, ft is -adequate and σ conserves V at f up to t.
LEMMA 2. If F is finite, then, for some sufficiently small positive , every -adequate f is adequate. If also each Γ(f) is finite, then can be so chosen that also, for every f, every γ in Γ(f) that -conserves V at f conserves V at f.
LEMMA 3. Let 
be a stationary family of strategies. If for each positive there is a family 
of stop rules for which the 
-probability that 
is -adequate is uniformly positive in f, then 
for all f.
Proof: Let 
be the gamble-valued function corresponding to 
. Apply Theorem 8.5 to the gambling problem for which 
and for which u′ is the indicator of the -adequate fortunes and conclude that V′ ≡ 1 and therewith that 
. Theorem 7.2 now applies to 
as a strategy available in Γ at f.
LEMMA 4. If F is finite and at each f there is available in Γ a policy π(f) = (σ(f), t(f)) such that, with positive σ(f)-probability, ft(f) is an adequate fortune and σ(f) conserves V at f up to t(f), then there exists a stationary family of optimal strategies.
Proof: Every stop rule is bounded according to Theorem 2.9.1. If f is adequate, let d(f) be 0; otherwise let d(f) be the least integer such that, for some π(f) of the postulated kind, t(f) ≤ d(f). From now on, let π(f) be of the postulated kind; and let it be so chosen that t(f) ≤ d(f), unless f is adequate. Let 
be the initial gamble of σ(f); 
plainly must conserve V at f.
The stationary family of strategies 
determined by 
is optimal. Why? If d(f) > 0, the 
-probability of those fortunes f′ for which d(f′) < d(f) is positive. Since F is finite and d is bounded, there is an 
and a family of stop rules 
, one stop rule for each f, such that, with 
-probability at least 
is adequate. Lemma 3 now shows that each 
equalizes u and V. Theorems 5.1 and 6.1 imply that each 
is optimal.
THEOREM 1. If F is finite and each Γ(f) is finite, then there is a stationary family of optimal strategies.
Proof: Choose as in the second part of Lemma 2. With this , choose π(f) as in Lemma 1. The hypotheses of Lemma 4 are then satisfied.
The finiteness of both F and Γ(f) is essential for Theorem 1, as the examples in Section 8 amply illustrate. Still more, even if F is finite, no stationary strategy available at some f may be at all good.
Example 2. Let: F = {0, 1}; u(i) = i for i = 0 and 1; Γ(0) = {δ(0)}, and Γ(1) be the set of all γ such that, for some 
, 
and 
. For any stationary σ available at 1, u(σ) = 0. But V(1) = 1, as is easily seen.
We believe that if Γ is leavable then there does exist a stationary family of nearly optimal strategies, but we have established this only in certain special cases.
THEOREM 2. If Γ is leavable and F is finite, then for each positive there is available in Γ a stationary family of strategies 
such that 
for all f.
Proof: For each f, let π(f) be available in Γ at f and such that 
. Since, according to Theorem 2.9.1, every stop rule is bounded, only a finite number of gambles are used by the family π(f). Let Γ′ be the smallest leavable subhouse of Γ for which Γ′(f) includes all γ used by any π(f′) at f. Theorem 1 applied to Γ′ yields a stationary family 
available in Γ′ such that 
. Of course, 
is available in Γ too.
Donald Ornstein has extended Theorem 2 to the situation in which F is countable and each γ ∈ Γ(f) is countably additive but has not yet published his proof. Whether Theorem 2 can be further extended to uncountable F or to finitely additive γ is not known.
THEOREM 3. If F is finite and there is an optimal strategy at each f, then there is a stationary family of optimal strategies.
Proof: Let σ(f) be optimal at f, and let 
satisfy the first part of Lemma 2. Theorem 7.2 assures the existence of a stop rule t(f) such that (σ(f), t(f)) terminates with positive probability at an -adequate fortune which, here, is necessarily adequate. According to Theorem 6.3, with σ(f)-probability 1, σ(f) conserves V at f up to t(f). Consequently, the hypotheses of Lemma 4 are satisfied.
The finiteness of F is essential for Theorem 3. For infinite F there can be optimal strategies at every f and yet no stationary optimal strategy at any f. This can happen even if every gamble is a one-point gamble and Γ is leavable.
Example 3. Let: F be the integers; Γ(j) = {δ(j), δ(j + 1), δ(−j)} for j ≥ 0; Γ(j) = {δ(j), δ(j + 1)} for j < 0; u(j) = 0 for j ≥ 0, u(j) = 1 + j−1 for j < 0.
The finiteness of F in Theorem 3 cannot be relaxed even if Γ is leavable and there is an optimal policy (not merely an optimal strategy) at each f, and even if the conclusion is weakened to assert only the existence of an optimal stationary strategy at each f.
Example 4. Let F be the pairs of integers f = (i, j), with i = 0, 1, 2, and j ≥ 1. Let γ be a gamble that attaches probability 2−i to f = (1, i) and γ′ be a diffuse gamble on the fortunes (1, j). Let Γ(0, j) = {δ(0, j), δ(2, j), γ}, Γ(1, j) = {δ(1, j), δ(2, j), γ′}, and Γ(2, j) = {δ(2, j)}. Let u(i, j) = i − j−1 Let σ0 = γ, σ1(f1) = γ′ if i1 = 1 and δ(f1) otherwise; σ2(f1, f2) = δ(2, j2); σn(f1, · · ·, fn) = δ(fn) if n > 2. The strategy σ thus defined is available in Γ at (0, j) and u(σ) = 2 = sup u; so σ is optimal. In fact, optimal policies for each initial f are easily defined. But no stationary strategy in Γ at (0, j) is optimal.
If there is complete absence of any stochastic element, the gambler can restrict himself to stationary families without macroscopic penalty. A house Γ is deterministic if each γ in every Γ(f) is δ(g) for some g. A strategy a available in Γ at f is strongly optimal at f, if lim u(σ, t) (not only lim sup u(σ, t)) is V(f).
THEOREM 4. If Γ is deterministic, then the existence of a stationary family of optimal strategies is implied by each of these two conditions:
(a) u assumes only a finite number of values.
(b) There is at each f a strongly optimal strategy.
Proof: Since the two parts of this theorem have similar proofs, only that of Part (b) (which is, if anything, the more difficult) is given here.
Every strategy available in Γ is δ(h) for some history h = (f1, f2, · · ·). Choose for each f0 a strongly optimal strategy δ(h).
Suppose first that for each f′ there are at most a finite number of n for which fn = f′. Define a sequence 
inductively, thus: Let, 
, and let, 
be fj, where j is the smallest integer such that 
for all i ≥ 0. As is easily verified: 
for 0 ≤ i < j; for each i, there is a j such that 
and 
; and δ(h*) is a stationary strategy that is strongly optimal for f0, where 
.
Suppose next that there is an f′ such that, for an infinite number of n, fn = f′. Since δ(h) is strongly optimal, u(f′) = V(f0). It requires but modest effort to define a sequence 
with the following properties: (i) 
; (ii) for every i there is a j such that 
and 
; (iii) if 
, then 
; and (iv) for an infinite number of i, 
. Let 
. Then (i) and (ii) imply that δ(h*) is available at f0 since δ(h) is. According to (iii), δ(h*) is stationary, and δ(h*) is seen to be optimal according to (iv). Thus, there is a stationary family of optimal strategies defined at least for a nonempty subset G of F. By Zorn’s lemma (Kelley 1955), there exists a maximal such family. It is easy to see that such a maximal family is necessarily defined for all of F.
Since any bounded u can be approached uniformly from below by a u′ with only a finite number of values, Part (a) of Theorem 4 has this corollary:
COROLLARY 1. If T is deterministic and is positive, there is available a stationary family of strategies 
such that 
for all f.
Example 3 illustrates the need for some condition like (a) or (b) in Theorem 4. If Γ in Theorem 4 is also leavable, the proof is simplified, and (b) then implies the existence of a stationary family of strongly optimal strategies. But without leavability the conclusion cannot be thus strengthened, as easy examples show.
Theorem 4 can of course be interpreted as facts about directed graphs. These facts may previously have been observed in that context.
THEOREM 5. If each Γ(f) contains at most one gamble α(f) in addition to δ(f), then the stationary family determined by
is optimal.
Since this theorem is so special and will not be used in this book, we do not give a proof. There may be no optimal strategy at some f if some Γ(f) contains as many as three elements, as is illustrated by Example 8.1.
The next theorem, though immediate from earlier results, is recorded because it is applicable to the two-armed (or n-armed) bandit problems with future incomes discounted as described in Section 12.5.
THEOREM 6. If at each f there is available a V-conserving γ, as for example when there are only a finite number of γ available at each f, and if every available strategy equalizes u and V, then there is a stationary family of optimal strategies.
