SIMP. Non potrà esser se non quella che tocca il cerchio nel punto della separazione, perché tutte l’altre mi par che, prolungate, segherebbono la circonferenza, e però conterrebber con essa qualche angolo.

SALV. Voi benissimo avete discorso, e vi sete dimostrato mezo geometra. Ritenete dunque in memoria che il vostro concetto reale si spiega con queste parole: cioè che il proietto acquista impeto di muoversi per la tangente l’arco⁶¹ descritto dal moto del proiciente nel punto della separazione di esso proietto dal proiciente.⁶²

SIMP. Intendo benissimo, e quest’è quel ch’io volevo dire.

SALV. D’una linea retta che tocchi un cerchio, quale de’ suoi punti è il più vicino di tutti al centro di quel cerchio?

SIMP. Quel del contatto senza dubbio; perché quello è nella circonferenza del cerchio, e gli altri fuora, ed i punti della circonferenza son tutti egualmente lontani dal centro.

SALV. Adunque un mobile partendosi dal contatto e movendosi per la retta tangente, si va continuamente discostando dal contatto ed anco dal centro del cerchio.

SIMP. Così è sicuramente.

SALV. Or, se voi avete tenuto a mente le proposizioni che mi avete dette, ricongiugnetele insieme, e ditemi ciò che se ne raccoglie.

SIMP. Io non credo però d’esser tanto smemorato, ch’io non me n’abbia Proietto si muove
per la tangente il
cerchio del moto
precedente nel punto
della
separazione.a ricordare. Dalle cose dette si raccoglie che il proietto, mosso velocemente in giro dal proiciente, nel separarsi da quello ritiene impeto di continuare il suo moto per la linea retta che tocca il cerchio descritto dal moto del proiciente nel punto della separazione; per il qual moto il proietto si va sempre discostando dal centro del cerchio descritto dal moto del proiciente.

SALV. Voi dunque sin ora sapete la ragione del venir estrusi i gravi aderenti alla superficie d’una ruota mossa velocemente; estrusi, dico, e lanciati oltre alla circonferenza, sempre più lontani dal centro.

SIMP. Di questo mi par di restar assai ben capace; ma questa nuova cognizione più tosto mi accresce che mi scemi l’incredulità che la Terra possa muoversi in giro con tanta velocità, senza estruder verso il cielo le pietre, gli animali, etc.

SALV. Nell’istesso modo che voi avete saputo sin qui, saprete, anzi sapete, anco il resto: e co ’l pensarvi sopra ve ne ricordereste ancora da per voi; ma, per abbreviar il tempo, vi aiuterò io a ricordarvelo. Sin qui avete per voi stesso saputo che il moto circolare del proiciente imprime nel proietto impeto di muoversi (quando avviene ch’e’ si separino) per la retta tangente il cerchio del moto nel punto della separazione, e, continuando per essa il moto, vien sempre allontanandosi dal proiciente; ed avete detto che per tal linea retta continuerebbe il proietto di muoversi, quando dal proprio peso non gli fusse aggiunta inclinazione all’in giù, dalla quale deriva l’incurvazione della linea del moto. Parmi ancora che voi abbiate saputo da per voi che questa piegatura tende sempre verso il centro della Terra, perché là tendon tutti i gravi. Ora passo un poco più avanti, e vi domando se il mobile dopo la separazione, nel continuar il suo moto retto, si va sempre allontanando egualmente dal centro, o volete dalla circonferenza, di quel cerchio del qual il moto precedente fu parte; che tanto è a dir se un mobile che partendosi dal punto della tangente, e movendosi per essa tangente, si allontani egualmente dal punto del contatto e dalla circonferenza del cerchio.

SIMP. Signor no, perché la tangente vicino al punto del contatto si scosta pochissimo dalla circonferenza, con la quale ella contiene un angolo strettissimo, ma nell’allontanarsi più e più, l’allontanamento cresce sempre con maggior proporzione: sì che in un cerchio che avesse, v. g., dieci braccia di diametro, un punto della tangente che fusse lontano dal contatto due palmi, si troverebbe lontano dalla circonferenza del cerchio tre o quattro volte più che un punto che fusse discosto dal toccamento un palmo; e ’l punto che fusse lontano mezo palmo, parimente credo che a pena si discosterebbe la quarta parte della distanza del secondo; sì che vicino al contatto per un dito o due, appena si scorge che la tangente sia separata dalla circonferenza.

SALV. Talché il discostamento del proietto dalla circonferenza del precedente moto circolare in su ’l principio è piccolissimo?

SIMP. Quasi insensibile.

SALV. Or ditemi un poco: il proietto che dal moto del proiciente riceve impeto di muoversi per la retta tangente, e che vi andrebbe ancora se il proprio peso non lo tirasse in giù, quanto sta, doppo la separazione, a cominciar a declinare a basso?

SIMP. Credo che cominci subito, perché non avendo chi lo sostenti, non può esser che la propria gravità non operi.

Proietto grave,
subito che è separato
dal proiciente, comincia
a declinare.

SALV. Talché, se quel sasso che scagliato da quella ruota mossa in giro con velocità grande, avesse così propension naturale di muoversi verso il centro dell’istessa ruota sì come e’ l’ha di muoversi verso il centro della Terra, sarebbe facil cosa che e’ ritornasse alla ruota, o più tosto che e’ non se ne partisse; perché essendo, su ’l principio della separazione, l’allontanamento tanto minimissimo, mediante l’infinita acutezza dell’angolo del contatto, ogni poco poco d’inclinazione che lo ritirasse verso il centro della ruota, basterebbe a ritenerlo sopra la circonferenza.

SIMP. Io non ho dubbio alcuno che, supposto quello che non è né può essere, cioè che l’inclinazione di quei corpi gravi fusse di andare al centro di quella ruota, e’ non verrebbero estrusi né scagliati.

SALV. Né io ancora suppongo, né ho bisogno di supporre, quel che non è, perché non voglio negare che i sassi vengano scagliati; ma dico così per supposizione, acciò voi mi diciate il resto. Figuratevi ora che la Terra sia la gran ruota, che, mossa con tanta velocità, abbia a scagliar le pietre. Già voi mi avete molto ben saputo dire che il moto proietto dovrà esser per quella linea retta che toccherà la Terra nel punto della separazione: e questa tangente come si va ella allontanando notabilmente dalla superficie del globo terrestre?

SIMP. Credo che in mille braccia non s’allontani un dito.

SALV. Ed il proietto non dite voi che, tirato dal proprio peso, declina dalla tangente verso il centro della Terra?

SIMP. Hollo detto: e dico anco il resto, e intendo perfettamente che la pietra non si separerà dalla Terra, poiché il suo allontanarsene su ’l principio sarebbe tanto e tanto minimo, che ben mille volte più vien ad esser l’inclinazione che ha il sasso di muoversi verso il centro della Terra; il qual centro in questo caso è anco il centro della ruota. E veramente è forza concedere che le pietre, gli animali e gli altri corpi gravi non posson esser estrusi: ma mi fanno ora nuova difficultà le cose leggierissime, le quali hanno debolissima inclinazione di calare al centro, onde, mancando in loro la facultà di ritirarsi alla superficie, non veggo che elle non avessero a esser estruse; voi poi sapete che ad destruendum sufficit unum.⁶³

SALV. Daremo sodisfazione anco a questo. Però ditemi in prima quel che voi intendete per cose leggiere, cioè se voi intendete materie così leggiere veramente che vadano all’insù, o pur non assolutamente leggiere, ma così poco gravi che ben vengano a basso, ma lentamente; perché se voi intendete delle assolutamente leggiere, ve le lascerò esser estruse più che voi non volete.⁶⁴

SIMP. Io intendo di queste seconde, quali sarebbono penne, lana, bambagia e simili, a sollevar le quali basta ogni minima forza: tuttavia si veggono starsene in Terra molto riposatamente.

SALV. Come questa penna abbia qualche natural propensione di scender verso la superficie della Terra, per minima ch’ella sia, vi dico che ell’è bastante a non la lasciar sollevare; e questo non è ignoto né anco a voi. Però ditemi: quando la penna fusse estrusa dalla vertigine della Terra, per che linea si moverebb’ella?

SIMP. Per la tangente nel punto della separazione.

SALV. E quando ella dovesse tornar a riunirsi, per qual linea si muoverebbe?

SIMP. Per quella che va da lei al centro della Terra.

SALV. Talché qui cascano in considerazione due moti: uno della proiezione, che comincia dal punto del contatto e segue per la tangente; e l’altro dell’inclinazione all’ingiù, che comincia dal proietto e va per la segante verso il centro: ed a voler che la proiezione segua, bisogna che l’impeto per la tangente prevaglia all’inclinazione per la segante: non sta così?

SIMP. Così mi pare.

SALV. Ma che cosa pare a voi che sia necessaria che si trovi nel moto proiciente, acciò che e’ prevaglia a quel dell’inclinazione, onde ne segua lo staccamento e l’allontamento della penna dalla Terra?

SIMP. Io non lo so.

SALV. Come non lo sapete? qui il mobile è il medesimo, cioè la medesima penna; or come può il medesimo mobile superare nel moto e prevalere a sé stesso?

SIMP. Io non intendo che e’ possa prevalere o cedere a sé medesimo nel moto, se non co ’l muoversi or più veloce e or più tardo.

SALV. Ecco dunque che voi pur lo sapevi. Se dunque deve seguir la proiezione della penna e prevalere il suo moto per la tangente al moto per la segante, quali bisogna che sieno le velocità loro?

SIMP. Bisogna che il moto per la tangente sia maggior di quell’altro per la segante. Oh povero a me! o non è egli anco centomila volte maggiore, e non solamente del moto in giù della penna, ma anco di quello della pietra? ed io, ben da semplice davvero, mi ero lasciato persuadere che le pietre non potrebber esser estruse dalla vertigine della Terra! Torno dunque a ridirmi, e dico che quando la Terra si muovesse, le pietre, gli elefanti, le torri e le città volerebbero verso il cielo per necessità; e perché ciò non segue, dico che la Terra non si muove.

SALV. Oh, Sig. Simplicio, voi vi sollevate così presto, ch’io comincerò a temer più di voi che della penna. Quietatevi un poco, e ascoltate. Se per ritener la pietra o la penna annessa alla superficie della Terra ci fusse di bisogno che ’l suo descender a basso fusse più o tanto quanto è il moto fatto per la tangente, voi areste ragione a dir che bisognasse che ella si movesse altrettanto o più velocemente per la segante all’ingiù che per la tangente verso levante: ma non mi avete voi detto poco fa, che mille braccia di distanza per la tangente dal contatto non rimuovono appena un dito dalla circonferenza? Non basta, dunque, che il moto per la tangente, che è quel della vertigine diurna, sia semplicemente più veloce del moto per la segante, che è quel della penna all’ingiù; ma bisogna che quello sia tanto più veloce, che ’l tempo che basta a condur la penna, v. g., mille braccia per la tangente, sia poco per il muoversi un sol dito all’ingiù per la segante: il che vi dico che non sarà mai, fate pur quel moto veloce, e questo tardo, quanto vi piace.

SIMP. E perché non potrebbe esser quello per la tangente tanto veloce, che non desse tempo alla penna d’arrivar alla superficie della Terra?

SALV. Provate a mettere il caso in termini, ed io vi risponderò. Dite adunque quanto vi par che bastasse far quel moto più veloce di questo.

SIMP. Dirò, per esempio, che quando quello fusse un milion di volte più veloce di questo, la penna e anco la pietra verrebbero estruse.

SALV. Voi dite così, e dite il falso, solo per difetto non di logica o di fisica o di metafisica, ma di geometria: perché, se voi intendeste solo i primi elementi, sapreste che dal centro del cerchio si può tirare una retta linea sino alla tangente, che la tagli in modo che la parte della tangente tra ’l contatto e la segante sia uno, due e tre milioni di volte maggior di quella parte della segante che resta tra la tangente e la circonferenza; e di mano in mano che la segante sarà più vicina al contatto, questa proporzione si fa maggiore in infinito: onde non è da temere che, per veloce che sia la vertigine e lento il moto in giù, la penna, o altro più leggiero, possa cominciare a sollevarsi, perché sempre l’inclinazione in giù supera la velocità della proiezione.

SAGR. Io non resto interamente capace di questo negozio.

Dimostrazione
geometrica per provare
l’impossibilità
dell’estrusione mediante
la vertigine
terrestre.

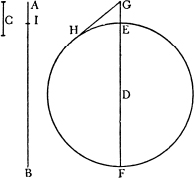
SALV. Io ve ne farò una dimostrazione universalissima, e anco assai facile. Sia data proporzione quella che ha la BA alla C, e sia BA maggior di C quanto esser si voglia; e sia il cerchio il cui centro D, dal quale bisogni tirare una segante, sì che la tangente ad essa segante abbia la proporzione che ha BA alla C: prendasi delle due BA, C la terza proporzionale AI, e come BI ad IA, così si faccia il diametro FE ad EG, e dal punto G tirisi la tangente GH^*: dico esser fatto quanto bisognava, e come BA a C, così essere HG a GE. Imperocché, essendo come BI ad IA così FE ad EG, sarà, componendo, come BA ad AI così FG a GE; e perché la C è media proporzionale tra BA, AI, e la GH è media tra FG, GE, però come BA a C così sarà FG a GH, cioè HG a GE, che è quel che bisognava fare.

SAGR. Resto capace di questa dimostrazione; tuttavia non mi si toglie interamente ogni scrupolo, anzi mi sento rigirar per la mente certa confusione, la quale, a guisa di nebbia densa ed oscura, non mi lascia discerner, con quella lucidità che suole esser propria delle ragioni matematiche, la chiarezza e necessità della conclusione. E quello in che io mi confondo, è questo. È vero che gli spazii tra la tangente e la circonferenza si vanno diminuendo in infinito verso ’l contatto; ma è anco vero, all’incontro, che la propensione del mobile al descendere si va facendo in esso sempre minore quanto egli si trova più vicino al primo termine della sua scesa, cioè allo stato di quiete, sì come è manifesto da quello che voi ci dichiaraste, mostrando che il grave descendente partendosi dalla quiete debbe passar per tutti i gradi di tardità mezani tra essa quiete e qualsivoglia segnato grado di velocità, li quali sono minori e minori in infinito. Aggiugnesi che essa velocità e propensione al moto si va per un’altra ragione diminuendo pure in infinito,⁶⁵ e ciò avviene dal potersi in infinito diminuire la gravità di esso mobile: talché le cagioni che diminuiscono la propensione allo scendere, ed in conseguenza favoriscono la proiezione, son due, cioè la leggerezza del mobile e la vicinità al termine di quiete, ed amendue agumentabili in infinito; le quali hanno, all’incontro, il contrasto di una sola causa del far la proiezione, la quale, benché essa parimente agumentabile in infinito, non comprendo come essa sola non possa restar vinta dall’unione ed accoppiamento dell’altre, che son due pure agumentabili in infinito.

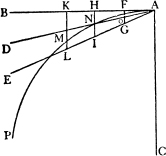
SALV. Dubitazione degna del Sig. Sagredo; e per dilucidarla, sì che più chiaramente venga da noi compresa, poiché voi ancora dite d’averla in confuso, la verremo distinguendo con ridurla in figura, la quale anco forse ci arrecherà agevolezza nel risolverla. Segniamo dunque una linea perpendicolare verso il centro, e sia questa AC, ed ad essa sia ad angoli retti la orizontale AB, sopra la quale si farebbe il moto della proiezione e vi continuerebbe d’andare il proietto con movimento equabile, quando la gravità non lo inclinasse a basso. Intendasi ora dal punto A prodotta una linea retta, la quale con la AB contenga qualsivoglia angolo, e sia questa AE, e notiamo sopra la AB alcuni spazii eguali AF, FH, HK, e da essi tiriamo le perpendicolari FG, HI, KL sino alla AE. E perché, come altra volta si è detto, il grave cadente, partendosi dalla quiete, va acquistando sempre maggior grado di velocità di tempo in tempo, secondo che l’istesso tempo va crescendo, possiamo figurarci gli spazii AF, FH, HK rappresentarci tempi eguali, e le perpendicolari FG, HI, KL gradi di velocità acquistati in detti tempi, sì che il grado di velocità acquistato in tutto il tempo AK sia come la linea KL rispetto al grado HI acquistato nel tempo AH, e ’l grado FG nel tempo AF, li quali gradi KL, HI, FG hanno (come è manifesto) la medesima proporzione che i tempi KA, HA, FA; e se altre perpendicolari si tireranno da i punti ad arbitrio notati nella linea FA, sempre si troverranno gradi minori e minori in infinito, procedendo verso il punto A, rappresentante il primo instante del tempo e il primo stato di quiete: e questo ritiramento verso A ci rappresenta la prima propensione al moto in giù, diminuita in infinito per l’avvicinamento del mobile al primo stato di quiete, il quale avvicinamento è agumentabile in infinito. Troveremo adesso l’altra diminuzion di velocità, che pure si può fare in infinito per la diminuzion della gravità del mobile; e questo si rappresenterà col produrre altre linee dal punto A, le quali contengano angoli minori dell’angolo BAE, qual sarebbe questa AD, la quale, segando le parallele KL, HI, FG ne’ punti M, N, O, ci figura i gradi FO, HN, KM acquistati ne i tempi AF, AH, AK, minori de gli altri gradi FG, HI, KL acquistati ne i medesimi tempi, ma questi come da un mobile più grave, e quelli da un più leggiero. Ed è manifesto che col ritirar la linea EA verso AB, ristrignendo l’angolo EAB (il che si può fare in infinito, sì come la gravità in infinito si può diminuire), si vien parimente a diminuire in infinito la velocità del cadente, ed in conseguenza la causa che impediva la proiezione: e però pare che dall’unione di queste due ragioni contro alla proiezione, diminuite in infinito, non possa ella esser impedita. E riducendo tutto l’argomento in brevi parole, diremo: Col ristrigner l’angolo EAB si diminuiscono i gradi di velocità LK, IH, GF; ed in oltre col ritirar le parallele KL, HI, FG verso l’angolo A si diminuiscono pure i medesimi gradi, e l’una e l’altra diminuzione si estende in infinito: adunque la velocità del moto in giù si potrà ben diminuir tanto e tanto (potendosi doppiamente diminuire in infinito), che ella non basti per restituire il mobile sopra la circonferenza della ruota, e per fare, in conseguenza, che la proiezione venga impedita e tolta. All’incontro poi, per far che la proiezion non segua, bisogna che gli spazii per i quali il proietto deve scendere per riunirsi alla ruota, si facciano così brevi ed angusti, che per tarda, anzi pur diminuita in infinito, che sia la scesa del mobile, ella pur basti a ricondurvelo; e però bisognerebbe che si trovasse una diminuzione di essi spazii non solo fatta in infinito, ma di una infinità tale che superasse la doppia infinità che si fa nella diminuzion della velocità del cadente in giù. Ma come si diminuirà una magnitudine più di un’altra che si diminuisce doppiamente in infinito? Ora noti il Sig. Simplicio quanto si possa ben filosofare in natura senza geometria! I gradi della velocità diminuiti in infinito, sì per la diminuzion della gravità del mobile sì per l’avvicinamento al primo termine del moto, cioè allo stato di quiete, sempre son determinati, e proporzionatamente rispondono alle parallele comprese tra due linee rette concorrenti in un angolo, conforme all’angolo BAE o BAD o altro in infinito più acuto, ma però sempre rettilineo; ma la diminuzione degli spazii per li quali il mobile ha da ricondursi sopra la circonferenza della ruota è proporzionata ad un’altra sorte di diminuzione, compresa dentro a linee che contengono un angolo infinitamente più stretto ed acuto di qualsivoglia acuto rettilineo, quale sarà questo. Piglisi nella perpendicolare AC qualsivoglia punto C, e fattolo centro, descrivasi con l’intervallo CA un arco AMP, il quale taglierà le parallele determinatrici de i gradi di velocità, per minime che elle siano e comprese dentro ad angustissimo angolo rettilineo; delle quali parallele le parti che restano tra l’arco e la tangente AB sono le quantità de gli spazii e de i ritorni sopra la ruota, sempre minori, e con maggior proporzione minori quanto più s’accostano al contatto, minori, dico, di esse parallele, delle quali son parti. Le parallele comprese tra le linee rette, nel ritirarsi verso l’angolo, diminuiscono sempre con la medesima proporzione, come, v. g., essendo divisa la AH in mezo nel punto F, la parallela HI sarà doppia della FG, e suddividendo la FA in mezo, la parallela prodotta dal punto della divisione sarà la metà della FG, e continuando la suddivisione in infinito, le parallele sussequenti saranno sempre la metà delle prossime precedenti: ma non così avviene delle linee intercette tra la tangente e la circonferenza del cerchio; imperocché, fatta l’istessa suddivisione nella FA e posto, per esempio, che la parallela che vien dal punto H fusse doppia di quella che vien da F, questa sarà poi più che doppia della seguente, e continuamente quanto verremo verso il toccamento A troveremo le precedenti linee contenere le prossime seguenti tre, quattro, dieci, cento, mille, centomila, e cento milioni, e più in infinito. La brevità, dunque, di tali linee si riduce a tale, che di gran lunga supera il bisogno per far che il proietto, per leggerissimo che sia, ritorni, anzi pur si mantenga, sopra la circonferenza.⁶⁶

SAGR. Io resto molto ben capace di tutto il discorso e della forza con la quale egli strigne: tuttavia mi pare che chi volesse travagliarlo ancora, potrebbe muoverci qualche difficultà, con dire che delle due cause che rendono la scesa del mobile più e più tarda in infinito, è manifesto che quella che depende dalla vicinità al primo termine della scesa, cresce sempre con la medesima proporzione, sì come sempre mantengono l’istessa proporzione tra di loro le parallele etc.; ma che la diminuzion della medesima velocità dependente dalla diminuzion della gravità del mobile (che era la seconda causa) si faccia essa ancora con la medesima proporzione, non par così manifesto. E chi ci assicura che ella non si faccia secondo la proporzione delle linee intercette tra la tangente e la circonferenza, o pur anco con proporzion maggiore?

SALV. Io avevo preso come per vero che le velocità de i mobili naturalmente descendenti seguitassero la proporzione delle loro gravità, in grazia del Sig. Simplicio e d’Aristotile, che in più luoghi l’afferma come proposizione manifesta; voi, in grazia dell’avversario, ponete ciò in dubbio, ed asserite poter esser che la velocità si accresca con proporzion maggiore, ed anco maggiore in infinito, di quella della gravità, onde tutto il discorso passato vadia per terra; resta a me, per sostenerlo, il dire che la proporzione delle velocità è molto minore di quella delle gravità, e così non solamente sollevare, ma fortificare, quanto si è detto: e di questo ne adduco per prova l’esperienza, la quale ci mostrerà che un grave anco ben trenta e quaranta volte più di un altro, qual sarebbe, per esempio, una palla di piombo ed una di sughero, non si moverà né anco a gran pezzo più veloce il doppio.⁶⁷ Ora, se la proiezione non si farebbe quando ben la velocità del cadente si diminuisse secondo la proporzione della gravità, molto meno si farà ella tutta volta che poco si scemi la velocità per molto che si detragga del peso. Ma posto anco che la velocità si diminuisse con proporzione assai maggiore di quella con che si scemasse la gravità, quando ben anco ella fusse quella stessa con la quale si diminuiscono quelle parallele tra la tangente e la circonferenza, io non penetro necessità veruna che mi persuada doversi far la proiezione di materie quanto si vogliano leggierissime, anzi affermo pure che ella non si farà, intendendo però di materie non propriamente leggierissime, cioè prive di ogni gravità e che per lor natura vadano in alto, ma che lentissimamente descendano ed abbiano pochissima gravità: e quello che mi muove a così credere è che la diminuzione di gravità, fatta secondo la proporzione delle parallele tra la tangente e la circonferenza, ha per termine ultimo ed altissimo la nullità di peso, come quelle parallele hanno per ultimo termine della lor diminuzione l’istesso contatto, che è un punto indivisibile; ora la gravità non si diminuisce mai sino al termine ultimo, perché così il mobile non sarebbe grave; ma ben lo spazio del ritorno del proietto alla circonferenza si riduce all’ultima piccolezza, il che è quando il mobile posa sopra la circonferenza nell’istesso punto del contatto, talché per ritornarvi non ha bisogno di spazio quanto: e però, sia quanto si voglia minima la propensione al moto in giù, sempre è ella più che a bastanza per ricondurre il mobile su la circonferenza, dalla quale ei dista per lo spazio minimo, cioè per niente.

SAGR. Veramente il discorso è molto sottile, ma altrettanto concludente; ed è forza confessare che il voler trattar le quistioni naturali senza geometria è un tentar di fare quello che è impossibile ad esser fatto.

SALV. Ma il Sig. Simplicio non dirà così; se bene io non credo ch’ei sia di quei Peripatetici che dissuadono i lor discepoli dallo studio delle mattematiche, come quelle che depravano il discorso e lo rendono meno atto alla contemplazione.

SIMP. Io non farei questo torto a Platone, ma direi bene con Aristotile che ei s’immerse troppo e troppo s’invaghì di quella sua geometria; perché finalmente queste sottigliezze mattematiche, Sig. Salviati, son vere in astratto, ma applicate alla materia sensibile e fisica non rispondono: perché dimostrerranno ben i mattematici con i lor principii, per esempio, che sphaera tangit planum in puncto,⁶⁸ proposizione simile alla presente; ma come si viene alla materia, le cose vanno per un altro verso: e così voglio dire di quest’angoli del contatto e di queste proporzioni, che tutte poi vanno a monte quando si viene alle cose materiali e sensibili.

SALV. Adunque voi non credete altrimenti che la tangente tocchi la superficie del globo terrestre in un punto?

SIMP. Non solo in un punto, ma credo che molte e molte decine e forse centinaia di braccia vadia una linea retta toccando la superficie anco dell’acqua, non che della Terra, prima che separarsi da lei.

SALV. Ma s’io vi concedo questa cosa, non v’accorgete voi che tanto peggio è per la causa vostra? perché, se posto che la tangente, da un sol punto in fuori, fusse separata dalla superficie della Terra, si è ad ogni modo dimostrato che per la grande strettezza dell’angolo della contingenza (se però si deve chiamar angolo) il proietto non si separerebbe, quanto meno avrà egli causa di separarsi se quell’angolo si chiuda affatto e la superficie e la tangente procedano unitamente? Il vero talora
acquista forze dalle
contradizioni.Non vedete voi che a questo modo la proiezione si farebbe su l’istessa superficie della Terra, che tanto è quanto a dire che ella non si farebbe? Vedete adunque qual sia la forza del vero, che mentre voi cercate d’atterrarlo, i vostri medesimi assalti lo sollevano e l’avvalorano. Ma già che vi ho tratto di questo errore, non vorrei già lasciarvi in quest’altro, che voi stimaste che una sfera materiale non tocchi un piano in un sol punto; e vorrei pur che la conversazione, ancor che di poche ore, avuta con persone che hanno qualche cognizion di geometria vi facesse comparir un poco più intelligente tra quei che non ne sanno niente. Or, per mostrarvi quanto sia grande l’error di coloro che dicono che una sfera, v. g. di bronzo, non tocca un piano, v. g. d’acciaio, in un punto, ditemi qual concetto voi vi formeresti di uno che dicesse e costantemente asseverasse che la sfera non fusse veramente sfera.

SIMP. Lo stimerei per privo di discorso affatto.

SALV. In questo stato è colui che dice che la sfera materiale non tocca un piano, pur materiale, in un punto, perché il La sfera, benché
materiale, tocca ’l
piano materiale in
un sol punto.dir questo è l’istesso che dire che la sfera non è sfera. E che ciò sia vero, ditemi in quello che voi costituite l’essenza della sfera, cioè che cosa è quella che fa differir la sfera da tutti gli altri corpi solidi.

SIMP. Credo che l’essere sfera consista nell’aver tutte le linee rette, prodotte dal suo centro sin alla circonferenza, eguali.

SALV. Talché quando tali linee non fussero eguali, quel tal solido non sarebbe altrimenti una sfera.

Definizione della
sfera.

SIMP. Signor no.

SALV. Ditemi appresso, se voi credete che delle molte linee che si posson tirar tra due punti, ve ne possa essere altro che una retta sola.

SIMP. Signor no.

SALV. Ma voi intendete pure che questa sola retta sarà poi per necessità la brevissima di tutte l’altre.

SIMP. L’intendo, e ne ho anche la dimostrazion chiara, arrecata da un gran filosofo peripatetico;⁶⁹ e parmi, se ben mi ricorda, ch’ei la porti riprendendo Archimede, che la suppone come nota, potendola dimostrare.

SALV. Questo sarà stato un gran matematico, avendo potuto dimostrar quel che né seppe né potette dimostrare Archimede; e se ve ne sovvenisse la dimostrazione, la sentirei volentieri, perché mi ricordo benissimo che Archimede ne i libri della sfera e del cilindro⁷⁰ mette cotesta proposizione tra i postulati, e tengo per fermo che l’avesse per indimostrabile.

SIMP. Credo che mi sovverrà, perch’ella è assai facile e breve.

SALV. Tanto sarà maggior la vergogna d’Archimede, e la gloria di cotesto filosofo.

SIMP. Io farò la sua figura. Tra i punti A, B tira la linea retta AB D i m o s t r a z i o n e
d’un Peripatetico
per provar che la
linea retta è la
brevissima di tutte.e la curva ACB, delle quali ei vuol provare la retta esser più breve; e la prova è tale. Nella curva piglia un punto, che sarebbe C, e tira due altre rette AC, CB, le quali due sono più lunghe della sola AB, che così dimostra Euclide; ma la curva ACB è maggiore delle due rette AC, CB; adunque a fortiori la curva ACB sarà molto maggiore della retta AB, che è quello che si doveva dimostrare.

Paralogismo del
medesimo
Peripatetico, che prova
ignotum per
ignotius.

SALV. Io non credo che a cercar tutti i paralogismi del mondo si potesse trovare il più accomodato di questo per dare un esempio della più solenne fallacia che sia tra tutte le fallacie, cioè di quella che prova ignotum per ignotius.⁷¹

SIMP. In che modo?

SALV. Come in che modo? la conclusione ignota, che voi volete provare, non è che la curva ACB sia più lunga della retta AB? il mezo termine, che si piglia per noto, non è che la curva ACB sia maggior delle due AC, CB, le quali è noto esser maggior della AB? e se vi è ignoto che la curva sia maggiore della sola retta AB, come non sarà egli assai più ignoto che ella sia maggiora delle due rette AC, CB, che si sa esser maggiore della sola AB? e voi lo prendete per noto?

SIMP. Io non intendo ancor bene dove consista la fallacia.

SALV. Come le due rette sien maggiori della AB (sì come è noto per Euclide), tuttavolta che la curva sia maggior delle due rette ACB,⁷² non sarà ella molto maggiore della sola retta AB?

SIMP. Signor sì.

SALV. Esser maggiore la curva ACB della retta AB è la conclusione, più nota del mezo termine, che è l’esser la medesima curva maggior delle due rette AC, CB: ora, quando il mezo è manco noto della conclusione, si domanda provare ignotum per ignotius. Or torniamo al nostro proposito: basta che voi intendete, la retta esser la brevissima di tutte le linee che si posson tirare fra due punti. E quanto alla principal conclusione, voi dite che la sfera materiale non tocca il piano in un sol punto: qual è dunque il suo contatto?

SIMP. Sarà una parte della sua superficie.

SALV. E il contatto parimente d’un’altra sfera eguale alla prima, sarà pure una simil particella della sua superficie?

SIMP. Non ci è ragione che non deva esser così.

Dimostrazione
come la sfera tocca
’l piano in un sol
punto.

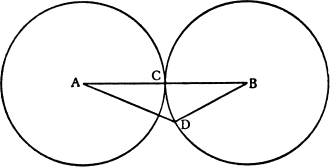
SALV. Adunque ancor le due sfere, toccandosi, si toccheranno con le due medesime particelle di superficie, perché, adattandosi ciascheduna di esse all’istesso piano, è forza che si adattino ancor fra di loro. Imaginatevi ora le due sfere, i cui centri A, B, che si tocchino, e congiungansi i lor centri con la retta linea AB, la quale passerà per il toccamento. Passi per il punto C, e preso nel toccamento un altro punto D, congiungansi le due rette AD, BD, sì che si constituisca il triangolo ADB, del quale i due lati AD, DB saranno eguali all’altro solo ACB, contenendo, tanto quelli quanto questi, due semidiametri, che per la definizion della sfera sono tutti eguali: e così la retta AB, tirata tra i due centri A, B, non sarà la brevissima di tutte, essendoci le due AD, DB eguali a lei; il che per le vostre concessioni è assurdo.

SIMP. Questa dimostrazione conclude delle sfere in astratto, e non delle materiali.

SALV. Assegnatemi dunque in che cosa consiste la fallacia del mio argomento, già che non conclude nelle sfere materiali, ma sì bene nelle immateriali e astratte.

Perché la sfera in
astratto tocchi il
piano in un punto,
ma non la materiale e
in concreto.

SIMP. Le sfere materiali son soggette a molti accidenti, a i quali non soggiacciono le immateriali. E perché non può esser che, posandosi una sfera di metallo sopra un piano, il proprio peso non calchi in modo che il piano ceda qualche poco, o vero che l’istessa sfera nel contatto si ammacchi? In oltre, quel piano difficilmente potrà esser perfetto, quando non per altro, almeno per esser la materia porosa; e forse non sarà men difficile il trovare una sfera così perfetta, che abbia tutte le linee dal centro alla superficie egualissime per l’appunto.

SALV. Oh tutte queste cose ve le concedo io facilmente, ma elle sono assai fuor di proposito; perché mentre voi volete mostrarmi che una sfera materiale non tocca un piano materiale in un punto, voi vi servite d’una sfera che non è sfera e d’un piano che non è piano, poiché, per vostro detto, o queste cose non si trovano al mondo, o se si trovano si guastano nell’applicarsi a far l’effetto. Era dunque manco male che voi concedeste la conclusione, ma condizionatamente, cioè che se si desse in materia una sfera e un piano che fussero e si conservassero perfetti, si toccherebber in un sol punto, e negaste poi ciò potersi dare.

SIMP. Io credo che la proposizione de i filosofi vadia intesa in cotesto senso, perché non è dubbio che l’imperfezion della materia fa che le cose prese in concreto non rispondono alle considerate in astratto.

SALV. Come non si rispondono? Anzi quel che voi stesso dite al presente prova che elle rispondon puntualmente.

SIMP. In che modo?

SALV. Non dite voi che per l’imperfezion della materia quel corpo che dovrebbe esser perfetto sferico, e quel piano che dovrebbe esser perfetto piano, non riescono poi tali in concreto quali altri se gli immagina in astratto?

SIMP. Così dico.

SALV. Adunque, tuttavolta che in concreto voi applicate una sfera materiale a un piano materiale, voi applicate una sfera non perfetta a un piano non perfetto; e questi dite che non si toccano in un punto. Ma io vi dico che anco in astratto una sfera immateriale, che non sia sfera perfetta, può toccare un piano immateriale, che non sia piano perfetto, non in un punto, ma con parte della sua superficie; talché sin qui quello che accade in concreto, accade nell’istesso modo in astratto: e sarebbe ben nuova cosa che i computi e le ragioni fatte in Le cose in astratto
riescono precisamente
quali in
concreto. numeri astratti, non rispondessero poi alle monete d’oro e d’argento e alle mercanzie in concreto. Ma sapete, Sig. Simplicio, quel che accade? Sì come a voler che i calcoli tornino sopra i zuccheri, le sete e le lane, bisogna che il computista faccia le sue tare di casse, invoglie ed altre bagaglie, così, quando il filosofo geometra vuol riconoscere in concreto gli effetti dimostrati in astratto, bisogna che difalchi gli impedimenti della materia; che se ciò saprà fare, io vi assicuro che le cose si riscontreranno non meno aggiustatamente che i computi aritmetici. Gli errori dunque non consistono né nell’astratto né nel concreto, né nella geometria o nella fisica, ma nel calcolatore, che non sa fare i conti giusti.⁷³ Però, quando voi aveste una sfera ed un piano perfetti, benché materiali, non abbiate dubbio che si toccherebbero in un punto; e se questo era ed è impossibile ad aversi, molto Toccarsi in un
punto non è proprio
delle sfere perfette
solamente, ma
di tutte le figure
curve.fuor di proposito fu il dire che sphaera aenea non tangit in puncto.⁷⁴ Ma più vi aggiungo, Sig. Simplicio: concedutovi che non si possa dare in materia una figura sferica perfetta nè un piano perfetto, credete voi che si possano dare due corpi materiali di superficie in qualche parte e in qualche modo incurvata, anco quanto si voglia irregolatamente?

SIMP. Di questi non credo che ce ne manchino.

SALV. Come ve ne siano di tali, questi ancora si toccheranno in un punto, ché il toccarsi in un sol punto non è È più difficile il
trovar figure, che si
tocchino con parte
di lor superficie, che
con un punto solo.miga privilegio particolare del perfetto sferico e del perfetto piano. Anzi chi più sottilmente andasse contemplando questo negozio, troverebbe che più difficile assai è il trovar due corpi che si tocchino con parte delle lor superficie, che con un punto solo: perché a voler che due superficie combagino bene insieme, bisogna o che amendue sieno esattamente piane, o che se una è colma, l’altra sia concava, ma di una incavatura che per appunto risponda al colmo dell’altra; le quali condizioni son molto più difficili a trovarsi, per la lor troppo stretta determinazione, che le altre, che nella casual larghezza son infinite.

SIMP. Adunque voi credete che due pietre o due ferri, presi a caso e accostati insieme, il più delle volte si tocchino in un sol punto?

SALV. Ne gli incontri casuali⁷⁵ credo di no, sì perché per lo più sopra essi sarà qualche poco d’immondizia cedente, sì perché non si usa diligenza in applicargli insieme senza qualche percossa, ed ogni poca basta a far che l’una superficie ceda qualche poco all’altra, sì che scambievolmente si figurino, almeno in qualche minima particella, l’una all’impronta dell’altra: ma quando le superficie loro fussero ben terse, e che posati amendue sopra una tavola, acciocché l’uno non gravasse sopra all’altro, si spingessero pian piano l’uno verso l’altro, io non ho dubbio che potrebbero condursi al semplice contatto in un sol punto.

SAGR. Egli è forza che con vostra licenza io proponga certa mia difficultà, natami nel sentir proporre al Sig. Simplicio la impossibilità che è nel potersi trovare un corpo materiale e solido che abbia perfettamente la figura sferica, e nel veder il Sig. Salviati prestargli in certo modo, non contradicendo, l’assenso. Però vorrei sapere se la medesima difficultà si trovi nel figurare un solido di qualche altra figura, cioè, per dichiararmi meglio, se maggior difficultà si trovi in voler ridurre un pezzo di marmo in figura d’una sfera perfetta, che d’una perfetta piramide o d’un perfetto cavallo o d’una perfetta locusta.

SALV. Per questa prima, risposta la darò io: e prima mi scuserò dell’assenso che vi pare ch’io abbia prestato al Sig. Simplicio, il quale era Figura sferica più
facilmente s’imprime
di ogn’altra.solamente per a tempo, perché io ancora avevo in animo, avanti che entrare in altra materia, dir quello che per avventura sarà l’istesso o assai conforme al vostro pensiero. E rispondendo alla vostra prima interrogazione, dico che se figura alcuna si può dare a un solido, la sferica è la facilissima sopra tutte l’altre, sì come è anco la semplicissima e tiene tra le figure solide quel luogo che il cerchio tiene tra le superficiali: la descrizion Figura circolare posta
sola tra i
postulati.del qual cerchio, come più facile di tutte le altre, essa sola è stata giudicata da i matematici degna d’esser posta tra i postulati attenenti alle descrizioni di tutte l’altre figure. Ed è talmente facile la formazion della sfera, che se in una piastra piana di metallo duro si caverà un vacuo circolare, dentro al quale si Figure sferiche di
diverse grandezze
si possono formare
con un solo
strumento.vadia rivolgendo casualmente qualsivoglia solido assai grossamente tondeggiato, per sé stesso senz’altro artifizio si ridurrà in figura sferica, quanto più sia possibile perfetta, purché quel tal solido non sia minore della sfera che passasse per quel cerchio; e quel che ci è anche di più degno di considerazione è che dentro a quel medesimo incavo si formeranno sfere di diverse grandezze. Quello poi che ci voglia per formare un cavallo o (come voi dite) una locusta, lo lascio giudicare a voi, che sapete che pochissimi scultori si troverranno al mondo atti a poterlo fare; e credo che il Sig. Simplicio in questo particolare non dissentirà da me.

SIMP. Non so se io dissenta punto da voi. L’oppinion mia è che nessuna delle nominate figure si possa perfettamente ottenere; ma per avvicinarsi quanto si possa al più perfetto grado, credo che incomparabilmente sia più agevole il ridurre il solido in figura sferica, che in forma di cavallo o di locusta.

SAGR. E questa maggior difficultà da che credete voi che ella dependa?

Forme irregolari
difficili a
introdursi.

SIMP. Sì come la grand’agevolezza nel formar la sfera deriva dalla sua assoluta semplicità ed uniformità, così la somma irregolarità rende difficilissimo l’introdur l’altre figure.

SAGR. Adunque, come l’irregolarità è causa di difficultà, anco la figura di un sasso rotto con un martello a caso sarà delle difficili a introdursi, essendo essa ancora irregolare forse più di quella del cavallo?

SIMP. Così deve essere.

SAGR. Ma ditemi: quella figura, qualunque ella si sia, che ha quel sasso, hall’egli perfettissimamente o pur no?

SIMP. Quella che egli ha, l’ha tanto perfettamente, che nessun’altra le si assesta tanto puntualmente.

SAGR. Adunque, se delle figure irregolari, e perciò difficili a conseguirsi, pur se ne trovano infinite perfettissimamente ottenute, con qual ragione si potrà dire che la semplicissima, e per ciò facilissima più di tutte, sia impossibile a ritrovarsi?

SALV. Signori, con vostra pace, mi par che noi siamo entrati in una disputa non molto più rilevante che quella della lana caprina, e dove che i nostri ragionamenti dovrebber continuar di esser intorno a cose serie e rilevanti, noi Costituzione dell’universo
è dei più
nobili problemi.consumiamo il tempo in altercazioni frivole e di nessun rilievo. Ricordiamoci in grazia che il cercar la costituzione del mondo è de’ maggiori e de’ più nobil problemi che sieno in natura, e tanto maggior poi, quanto viene indrizzato allo scioglimento dell’altro, dico della causa del flusso e reflusso del mare, cercata da tutti i grand’uomini che sono stati sin qui e forse da niun ritrovata: però, quando altro non ci resti da produrre per l’assoluto scioglimento dell’instanza presa dalla vertigine della Terra, che fu l’ultima portata per argomento della sua immobilità circa il proprio centro, potremo passare allo scrutinio delle cose che sono in pro e contro al movimento annuo.

SAGR. Non vorrei, Sig. Salviati, che voi misuraste gl’ingegni di noi altri con la misura del vostro: voi, avvezzo sempre ad occuparvi in contemplazioni altissime, stimate frivole e basse tal una di quelle che a noi paiono degno cibo de’ nostri intelletti; però talvolta, per sodisfazione nostra, non vi sdegnate di abbassarvi a concedere qualcosa alla nostra curiosità. Quanto poi allo scioglimento dell’ultima instanza, presa dallo scagliamento della vertigine diurna, per sodisfare a me bastava assai meno di quello che si è prodotto; tuttavia le cose che si son dette soprabbondantemente, mi son parse tanto curiose, che non solo non mi hanno stancata la fantasia, ma me l’hanno con le loro novità trattenuta sempre con diletto tale che maggior non saprei desiderarne: però se qualche altra specolazione resta a voi da aggiugnervi, producetela pure, ch’io per la parte mia molto volentieri la sentirò.

SALV. Io nelle cose trovate da me ho sempre sentito grandissimo diletto, e doppo questo, che è il massimo, provo gran piacere nel conferirle con qualche amico che le capisca e che mostri di gustarle: or, poiché voi sete uno di questi, allentando un poco la briglia alla mia ambizione, che gode dentro di sé quando io mi mostro più perspicace di qualche altro reputato di acuta vista, produrrò, per colmo e buona misura della discussion passata, un’altra fallacia de i seguaci di Tolomeo e d’Aristotile, presa nel già prodotto argomento.

SAGR. Ecco che io avidamente mi apparecchio a sentirla.

SALV. Noi aviamo sin qui trapassato e conceduto a Tolomeo come effetto indubitabile, che procedendo lo scagliamento del sasso dalla velocità della ruota mossa intorno al suo centro, tanto si accresca la causa di esso scagliamento, quanto la velocità della vertigine si agumenta; dal che si inferiva che essendo la velocità della terrestre vertigine sommamente maggiore di quella di qualsivoglia macchina che noi artifiziosamente possiam far girare, l’estrusione in conseguenza delle pietre e de gli animali etc. dovesse esser violentissima. Ora io noto che in questo discorso è una grandissima fallacia, mentre noi indifferentemente ed assolutamente paragoniamo le velocità tra di loro. È vero che s’io fo comparazione delle velocità La causa della
proiezione non
cresce secondo la
proporzione della
velocità accresciuta per
far la ruota
maggiore.della medesima ruota o di due ruote eguali tra di loro, quella che più velocemente sarà girata, con maggior impeto scaglierà le pietre, e crescendo la velocità, con la medesima proporzione crescerà anco la causa della proiezione; ma quando la velocità si facesse maggiore non con l’accrescer velocità nell’istessa ruota, che sarebbe co ’l fargli dar numero maggiore di conversioni in tempi eguali, ma co ’l crescere il diametro e far la ruota maggiore, sì che ritenendo il medesimo tempo di una conversione tanto nella piccola quanto nella gran ruota, e solo nella grande la velocità fusse maggiore per esser la sua circonferenza maggiore, non sia chi creda che la causa dello scagliamento nella gran ruota crescesse secondo la proporzione della velocità della sua circonferenza verso la velocità della circonferenza della minor ruota, perché questo è falsissimo, come per adesso una speditissima esperienza ci potrà mostrar così alla grossa: ché tal pietra potremmo noi scagliare con una canna lunga un braccio, che con una lunga sei braccia non potremo, ancorché il moto dell’estremità della canna lunga, cioè della pietra incastratavi, fusse più veloce il doppio del moto della punta della canna più corta; che sarebbe quando le velocità fussero tali, che nel tempo di una conversione intera della canna maggiore, la minore ne facesse tre.

SAGR. Questo, Sig. Salviati, che voi mi dite, già comprendo io dovere necessariamente succeder così; ma non mi sovvien già prontamente la causa perché eguali velocità non abbiano a operare egualmente in estruder i proietti, ma assai più quella della ruota minore che l’altra della ruota maggiore: però vi prego a dichiararmi come il negozio cammina.

SIMP. Voi, Sig. Sagredo, questa volta vi sete dimostrato dissimile a voi medesimo, che solete in un momento penetrar tutte le cose, ed ora trapassate una fallacia posta nell’esperienza delle canne, la quale ho io potuto penetrare; e questa è la diversa maniera di operare nel far la proiezione or con la canna breve ed or con la lunga: perché a voler che la pietra scappi fuor della cocca, non bisogna continuar uniformemente il suo moto, ma allora ch’egli è velocissimo, convien ritenere il braccio e reprimer la velocità della canna, perloché la pietra, che già è in moto velocissimo, scappa e con impeto si muove; ma tal ritegno non si può far nella canna maggiore, la quale, per la sua lunghezza e flessibilità, non ubbidisce interamente al freno del braccio, ma, continuando di accompagnare il sasso per qualche spazio, co ’l dolcemente frenarlo se lo ritien congiunto, e non, come se in un duro intoppo avesse urtato, da sé lo lascia fuggire: ché quando amendue le canne urtassero in un ritegno che le fermasse, io credo che la pietra parimente scapperebbe dall’una e dall’altra, ancorché i movimenti loro fussero egualmente veloci.

SAGR. Con licenzia del Sig. Salviati, risponderò io alcuna cosa al Sig. Simplicio, poiché egli a me si è rivoltato: e dico che nel suo discorso vi è del buono e del cattivo; buono, perché quasi tutto è vero; cattivo, perché non fa in tutto al proposito nostro. Verissimo è, che quando quello che con velocità porta le pietre, urtasse in un ritegno immobile, esse con impeto scorrerebbero innanzi, seguendone quell’effetto che tutto il giorno si vede accadere in una barca che, scorrendo velocemente, arreni o urti in qualche ostacolo, che tutti quelli che vi son dentro, colti all’improvviso, repentinamente traboccano e cascano verso dove correva il navilio; e quando il globo terrestre incontrasse Dato che la vertigine
diurna fusse
della Terra, e che
ella per qualche
repentino ostacolo o
intoppo si fermasse,
le fabbriche e le
montagne stesse e
forse tutto ’l globo si
dissolverebbe.un intoppo tale che del tutto resistesse alla sua vertigine e la fermasse, allora sì ch’io credo che non solamente le fiere, gli edifizii e le città, ma le montagne, i laghi e i mari si sovvertirebbero, e pur che il globo stesso non si dissipasse: ma niente di questo fa al proposito nostro, che parliamo di quel che possa seguire al moto della Terra girata uniformemente e placidamente in sé stessa, ancorché con velocità grande. Quello parimente che voi dite delle canne, è in parte vero, ma non fu portato dal Sig. Salviati come cosa che puntualmente si assesti alla materia di cui trattiamo, ma solamente come un esempio che così alla grossa possa destarci la mente a più accuratamente considerare, se crescendosi la velocità in qualsivoglia modo, con l’istessa proporzione si accresca la causa della proiezione, sì che, v. g., se una ruota di dieci braccia di diametro, movendosi in maniera che un punto della sua circonferenza passasse in un minuto d’ora cento braccia, e perciò avesse impeto di scagliare una pietra, tale impeto si accresce centomila volte in una ruota che avesse un milion di braccia di diametro: il che nega il Sig. Salviati, ed io inclino a creder l’istesso; ma non ne sapendo la ragione, l’ho da esso richiesta, e con desiderio la sto attendendo.

SALV. Eccomi per darvi quella sodisfazione che dalle mie forze mi sarà conceduta; e benché nel mio primo parlare vi sia per parer ch’io vadia ricercando cose aliene dal proposito nostro, tuttavia credo che nel progresso del ragionamento troverremo che pur non saranno tali. Però dicami il Sig. Sagredo in quali cose egli ha osservato consister la resistenza di alcun mobile all’esser mosso.

SAGR. Io per adesso non veggo esser nel mobile resistenza interna all’esser mosso se non la sua naturale inclinazione e propensione al moto contrario, come ne’corpi gravi, che hanno propensione al moto in giù, la resistenza è al moto in su: ed ho detto resistenza interna, perché di questa credo che voi intendiate, e non dell’esterne, che sono accidentali e molte.

SALV. Così ho voluto dire, e la vostra perspicacità ha prevalso al mio avvedimento. Ma s’io sono stato scarso nell’interrogare, dubito che il Sig. Sagredo non abbia, con la risposta, adequata a pieno la domanda, e che L’inclinazione de i
gravi al moto in giù
eguale alla resistenza
al moto in su.nel mobile, oltre alla naturale inclinazione al termine contrario, sia un’altra pure intrinseca e naturale qualità che lo faccia renitente al moto. Però ditemi di nuovo: non credete voi che l’inclinazione, v. g., de i gravi di muoversi in giù sia eguale alla resistenza de i medesimi all’essere spinti in su?

SAGR. Credo che ella sia tale per l’appunto; e per questo veggo nella bilancia due pesi eguali restar fermi nell’equilibrio, resistendo la gravità dell’uno all’esser alzato alla gravità con la quale l’altro, premendo in giù, alzar lo vorrebbe.

SALV. Benissimo; sì che a voler che l’uno alzasse l’altro, bisognerebbe accrescer peso al premente, o scemarlo all’altro. Ma se nella sola gravità consiste la resistenza al moto in su, onde avviene che nella bilancia di braccia diseguali, cioè nella stadera, talvolta un peso di cento libbre, co ’l suo gravare in giù, non è bastante a alzarne uno di quattro libbre, che gli contrasterà; e potrà questo di quattro, abbassandosi, alzare quello di cento? ché tale è l’effetto del romano verso il grave peso che noi vogliam pesare. Se la resistenza all’esser mosso risiede nella sola gravità, come può il romano, co ’l suo peso di quattro libbre sole, resistere al peso di una balla di lana o di seta, che sarà ottocento o mille, anzi pure potrà egli vincere co ’l suo momento⁷⁶ la balla e sollevarla? Bisogna pur, Sig. Sagredo, dire che qui si lavori con altra resistenza e con altra forza, che con quella della semplice gravità.

SAGR. È necessario che sia così: però ditemi qual è questa seconda virtù.

SALV. È quello che non era nella bilancia di braccia eguali. Considerate qual novità è nella stadera, ed in questa di necessità consiste la causa del nuovo effetto.

SAGR. Credo che ’l vostro tentare mi abbia fatto sovvenir non so che. In amendue gli strumenti si lavora co ’l peso e co ’l moto: nella bilancia i movimenti sono eguali, e però l’un peso bisogna che superi l’altro in gravità per muoverlo; nella stadera il peso minore non moverà il maggiore se non quando questo si muova poco, essendo appeso nella minor distanza, e quello si muova molto, pendendo da distanza maggiore: bisogna dunque dire che ’l minor peso superi la resistenza del maggiore co ’l muoversi molto, mentre l’altro si muova poco.

SALV. Che tanto è quanto a dire che la velocità del mobile meno grave compensa la gravità del mobile più grave e meno veloce.

La maggior velocità
compensa
precisamente la
maggior gravità.

SAGR. Ma credete voi che la velocità ristori per l’appunto la gravità? cioè che tanto sia il momento e la forza di un mobile, v. g., di quattro libbre di peso, quanto quella di un di cento, qualunque volta quello avesse cento gradi di velocità e questo quattro gradi solamente?

SALV. Certo sì, come io vi potrei con molte esperienze mostrare: ma per ora bastivi la confermazione di questa sola della stadera, nella quale voi vedrete il poco pesante romano allora poter sostenere ed equilibrare la gravissima balla, quando la sua lontananza dal centro, sopra il quale si sostiene e volgesi la stadera, sarà tanto maggiore dell’altra minor distanza dalla quale pende la balla, quanto il peso assoluto⁷⁷ della balla è maggior di quel del romano. E di questo non poter la gran balla co ’l suo peso sollevare il romano, tanto men grave, altro non si vede poterne esser cagione che la disparità de i movimenti che e quella e questo far dovrebbero, mentre che la balla con l’abbassarsi un sol dito facesse alzare il romano cento dita (posto che la balla pesasse per cento romani, e la distanza del romano dal centro della stadera fusse cento volte più della distanza tra ’l medesimo centro e ’l punto della sospension della balla): il muoversi poi lo spazio di cento dita il romano, nel tempo che la balla si muove per un sol dito, è l’istesso che ’l dire, esser la velocità del moto del romano cento volte maggior della velocità del moto della balla. Ora fermatevi bene nella fantasia, come principio vero e notorio, che la resistenza che viene dalla velocità del moto compensa quello che depende dalla gravità d’un altro mobile: sì che, in conseguenza, tanto resiste all’esser frenato un mobile d’una libbra, che si muova con cento gradi di velocità, quanto un altro mobile di cento libbre, la cui velocità sia d’un grado solo; ed all’esser mossi due mobili eguali resisteranno egualmente, se si avranno a far muovere con egual velocità; ma se uno doverà esser mosso più velocemente dell’altro, farà maggior resistenza, secondo la maggior velocità che se gli vorrà conferire. Dichiarate queste cose, venghiamo all’esplicazion del nostro problema; e per più facile intelligenza 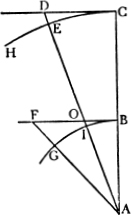facciamone un poco di figura. E siano due ruote diseguali intorno a questo centro A, e della minore sia la circonferenza BG, e della maggiore CEH, ed il semidiametro ABC sia eretto all’orizonte, e per i punti B, C segniamo le rette linee tangenti BF, CD, e ne gli archi BG, CE sieno prese due parti eguali BG, CE; ed intendasi le due ruote esser girate sopra i lor centri con eguali velocità, sì che due mobili, li quali sariano, v. g., due pietre, poste ne’ punti B e C vengano portate per le circonferenze BG, CE con eguali velocità, talché nell’istesso tempo che la pietra B scorrerebbe per l’arco BG, la pietra C passerebbe l’arco CE: dico adesso che la vertigine della minor ruota è molto più potente a far la proiezion della pietra B, che non è la vertigine della maggior ruota della pietra C. Imperocché dovendosi, come già si è dichiarato, far la proiezione per la tangente, quando le pietre B, C dovessero separarsi dalle lor ruote e cominciare il moto della proiezione da i punti B, C, verrebbero dall’impeto concepito dalla vertigine scagliate per le tangenti BF, CD: per le tangenti dunque BF, CD hanno, le due pietre, eguali impeti di scorrere, e vi scorrerebbero se da qualche altra forza non ne fussero deviate. Non sta così, Sig. Sagredo?

SAGR. Così mi par che cammini il negozio.

SALV. Ma qual forza vi par che possa esser quella che devii le pietre dal muoversi per le tangenti, dove l’impeto della vertigine veramente le caccia?

SAGR. È o la propria gravità, o qualche colla che le ritien posate o attaccate sopra le ruote.

SALV. Ma a deviare un mobile dal moto dove egli ha impeto, non ci vuol egli maggior forza o minore, secondo che la deviazione ha da esser maggiore o minore? cioè, secondoché nella deviazione egli dovrà nell’istesso tempo passar maggiore o minore spazio?

SAGR. Sì, perché già di sopra fu concluso che a far muovere un mobile, con quanta maggior velocità si ha da far muovere, tanto bisogna che sia maggiore la virtù movente.

SALV. Ora considerate come per deviar la pietra della minor ruota dal moto della proiezione, che ella farebbe per la tangente BF, e ritenerla attaccata alla ruota, bisogna che la propria gravità la ritiri per quanto è lunga la segante FG, o vero la perpendicolare tirata dal punto G sopra la linea BF; dove che nella ruota maggiore il ritiramento non ha da esser più che si sia la segante DE, o vero la perpendicolare tirata dal punto E sopra la tangente DC, minor assai della FG, e sempre minore e minore secondo che la ruota si facesse maggiore: e perché questi ritiramenti si hanno a fare in tempi eguali, cioè mentre che si passano li due archi eguali BG, CE, quello della pietra B, cioè il ritiramento FG, doverà esser più veloce dell’altro DE, e però molto maggior forza si ricercherà per tener la pietra B congiunta alla sua piccola ruota, che la pietra C alla sua grande; ch’è il medesimo che dire, che tal poca cosa impedirà lo scagliamento nella ruota grande, che non lo proibirà nella piccola. È manifesto, dunque, che quanto più si cresce la ruota, tanto si scema la causa della proiezione.⁷⁸

SAGR. Da questo che ora intendo mercé del vostro lungo sminuzzamento, mi par di poter far restar pago il mio intelletto con assai breve discorso: perché, venendo dalla velocità eguale delle due ruote impresso impeto eguale in amendue le pietre per le tangenti, si vede la gran circonferenza, co ’l poco separarsi dalla tangente, andar secondando in un certo modo e con dolce morso suavemente raffrenando nella pietra l’appetito, per così dire, di separarsi dalla circonferenza, sì che qualunque piccol ritegno, o della propria inclinazione o di qualche glutine, basta a mantenervela congiunta; il quale poi resta invalido a ciò poter fare nella piccola ruota, la quale, co ’l poco secondare la direzione della tangente, con troppa ingorda voglia cerca ritenere a sé la pietra, e non essendo il freno e ’l glutine più gagliardo di quello che manteneva l’altra pietra unita con la maggior ruota, si strappa la cavezza, e si corre per la tangente. Per tanto io non solamente resto capace dell’aver tutti quelli errato, che hanno creduto crescersi la cagione della proiezione secondo che si accresce la velocità della vertigine; ma di più vo considerando, che scemandosi la proiezione nell’accrescersi la ruota, tuttavoltaché si mantenga la medesima velocità in esse ruote, forse potrebbe esser vero che a voler che la gran ruota scagliasse come la piccola, bisognasse crescerle tanto di velocità, quanto se le cresce di diametro, che sarebbe quando le intere conversioni si finissero in tempi eguali: e così si potrebbe stimare che la vertigine della Terra non più fusse bastante a scagliare le pietre, che qualsivoglia altra piccola ruota che tanto lentamente si girasse, che in ventiquattr’ore desse una sola rivolta.⁷⁹

SALV. Non voglio per ora che noi cerchiamo tant’oltre; basta che assai abbondantemente abbiamo (s’io non m’inganno) mostrato l’inefficacia dell’argumento, che nel primo aspetto pareva concludentissimo, e tale era stato stimato da grandissimi uomini: ed assai bene speso mi parrà il tempo e le parole, se anco nel concetto del Sig. Simplicio averò guadagnato qualche credenza, non dirò della mobilità della Terra, ma almanco del non esser l’opinion di coloro che la credono, tanto ridicola e stolta, quanto le squadre de’ filosofi comuni la tengono.

SIMP. Le soluzioni addotte sin qui all’instanze fatte contro a questa diurna revoluzion della Terra, prese da i gravi cadenti dalla sommità d’una torre, e da i proietti a perpendicolo in su o secondo qualsivoglia inclinazione lateralmente, verso oriente, occidente, mezzogiorno o settentrione etc., mi hanno in qualche parte scemata l’antiquata incredulità concepita contro a tale opinione: ma altre maggiori difficultà mi si aggirano adesso per la fantasia, dalle quali io assolutamente non mi saprei mai sviluppare, nè forse credo che voi medesimi ve ne potrete disciorre; e può anco essere che venute non vi sieno all’orecchie, perché sono assai moderne. E queste sono le opposizioni di due autori che ex professo scrivono contro al Copernico: le prime si leggono in un libretto di conclusioni naturali;⁸⁰ le altre sono d’un gran filosofo e matematico insieme, inserte in un trattato che egli fa in grazia d’Aristotile e della sua opinione intorno all’inalterabilità del cielo,⁸¹ Altre opposizioni di
due autori
moderni contro al
Copernico.dove ei prova che non pur le comete, ma anco le stelle nuove, cioè quella del settantadua in Cassiopea e quella del seicentoquattro nel Sagittario,⁸² non erano altrimenti sopra le sfere de i pianeti, ma assolutamente sotto il concavo della Luna⁸³ nella sfera elementare; e ciò dimostra egli contro a Ticone, Keplero e molti altri osservatori astronomi, e gli abbatte con le loro armi medesime, cioè per via delle parallassi. Io, se vi è in piacere, produrrò le ragioni dell’uno e dell’altro, perché le ho lette più d’una volta con attenzione; e voi potrete esaminar la lor forza e dirne il vostro parere.

SALV. Essendoché il nostro principal fine è di produrre e ponderar tutto quello che è stato addotto in pro e contro a i due sistemi Tolemaico e Copernicano, non è bene passar cosa alcuna delle scritte in cotal materia.

Prima opposizione
dell’autor moderno
del libretto delle
conclusioni.

SIMP. Comincerò dunque dall’instanze contenute nel libretto delle conclusioni, e poi verrò all’altre. Primieramente, dunque, l’autore con grand’acutezza va calcolando quante miglia per ora fa un punto della superficie terrestre posto sotto l’equinoziale, e quante si fanno da altri punti posti in altri paralleli; e non contento di investigar tali movimenti in tempi orarii, gli trova anco in un minuto d’ora, né contento del minuto, lo ritrova sino a uno scrupolo secondo; ma più, e’ va insino a mostrar apertissimamente quante miglia farebbe in tali tempi una palla d’artiglieria, posta nel concavo dell’orbe lunare, suppostolo anco tanto grande quanto l’istesso Copernico se lo figura, per levar tutti i sutterfugii all’avversario: e fatta Una palla d’artiglieria
consumerebbe
più di sei giorni nel
cader dal concavo
della Luna sino al
centro della Terra,
secondo l’opinione
dell’autor moderno
delle conclusioni.quest’ingegnosissima ed esquisitissima supputazione, dimostra che un grave cadente di lassù consumerebbe assai più di sei giorni per arrivar sino al centro della Terra, dove naturalmente tendono tutte le cose gravi. Ora, quando dall’assoluta potenza divina o da qualche angelo fusse miracolosamente trasferita lassù una grossissima palla di artiglieria, e posta nel nostro punto verticale e di lì lasciata in sua libertà, è ben, per suo e mio parere, incredibilissima cosa che ella nel descendere a basso si andasse sempre mantenendo nella nostra linea verticale, continuando di girare con la Terra intorno al suo centro per tanti giorni, descrivendo sotto l’equinoziale una linea spirale nel piano di esso cerchio massimo, e sotto altri paralleli linee spirali intorno a coni, e sotto i poli cadendo per una semplice linea retta. Stabilisce poi e conferma questa grand’improbabilità co ’l promover, per modo di interrogazioni, molte difficultà impossibili a rimuoversi da i seguaci del Copernico; e sono, se ben mi ricorda…

SALV. Piano un poco: di grazia, Sig. Simplicio, non vogliate avvilupparmi con tante novità in un tratto; io ho poca memoria, e però mi bisogna andar di passo in passo. E perché mi sovviene aver già voluto calcolare in quanto tempo un simil grave, cadendo dal concavo della Luna, arriverebbe nel centro della Terra, e mi par ricordare che il tempo non sarebbe sì lungo, sarà bene che voi ci dichiate con qual regola quest’autore abbia fatto il suo computo.

SIMP. Hallo fatto, per provare il suo intento a fortiori, vantaggioso assai per la parte avversa, supponendo che la velocità del cadente per la linea verticale verso il centro della Terra fusse eguale alla velocità del suo moto circolare fatto nel cerchio massimo del concavo dell’orbe lunare, al cui ragguaglio verrebbe a fare in un’ora dodicimila seicento miglia tedesche,⁸⁴ cosa che veramente ha dell’impossibile; tuttavia, per abbondare in cautela e dar tutti i vantaggi alla parte, ei la suppone per vera, e conclude il tempo della caduta dovere ad ogni modo esser più di sei giorni.

SALV. E quest’è tutto il suo progresso? e con questa dimostrazione prova, il tempo di tal cascata dover esser più di sei giorni?

SAGR. Parmi che e’ si sia portato troppo discretamente, poiché essendo in poter del suo arbitrio dar qual velocità gli piaceva a un tal cadente, ed in conseguenza farlo venire in Terra in sei mesi ed anco in sei anni, si è contentato di sei giorni. Ma di grazia, Sig. Salviati, racconciatemi un poco il gusto co ’l dirmi in qual maniera procedeva il vostro computo, già che voi dite averlo altra volta fatto; ché ben son sicuro che se ’l quesito non ricercava qualche operazione spiritosa, voi non vi areste applicata la mente.

SALV. Non basta, Sig. Sagredo, che la conclusione sia nobile e grande, ma il punto sta nel trattarla nobilmente. E chi non sa che nel resecar le membra di un animale si possono scoprir meraviglie infinite della provida e sapientissima natura? tuttavia, per uno che il notomista ne tagli, mille ne squarta il beccaio; ed io, nel cercar ora di sodisfare alla vostra domanda, non so con quale delli due abiti sia per comparire in scena: pur, preso animo dalla comparsa dell’autor del Sig. Simplicio, non resterò di recitarvi (se mi sovverrà) il modo che io tenevo. Ma prima ch’io metta mano ad altro, non posso lasciar di dire che dubito grandemente che il Sig. Simplicio non abbia fedelmente referito il modo co ’l quale questo suo autore trova che la palla d’artiglieria, nel venir dal concavo della Luna sino al centro della Terra, consumerebbe più di sei giorni; perché, s’egli avesse supposto che la sua velocità nello scendere fusse stata eguale a quella del concavo (come dice il Sig. Simplicio che e’ suppone), si sarebbe dichiarato ignudissimo anco delle prime e più semplici cognizioni di geometria: anzi mi maraviglio che l’istesso Sig. Simplicio nell’ammetter la supposizione ch’egli dice, non vegga l’esorbitanza immensa che in quella si contiene.

SIMP. Ch’io abbia equivocato nel riferirla, potrebbe essere; ma che io vi scuopra dentro fallacia, non è sicuramente.

SALV. Forse non ho ben appreso quel che avete riferito. Non dite voi che quest’autore fa la velocità del moto della palla nello scendere eguale a quella ch’ell’aveva nello andare in volta, stando nel concavo lunare, e che calando con tal velocità si condurrebbe al centro in sei giorni?

SIMP. Così mi par ch’egli scriva.

Esorbitanza
immensa nell’argomento
preso dalla
palla cadente dal
concavo della Luna.

SALV. E non vedete un’esorbitanza sì grande? Ma voi certo la dissimulate: ché non può esser che non sappiate che ’l semidiametro del cerchio è manco che la sesta parte della circonferenza; e che in conseguenza il tempo nel quale il mobile passerà il semidiametro, sarà manco della sesta parte del tempo nel quale, mosso con la medesima velocità, passerebbe la circonferenza; e che però la palla, scendendo con la velocità con la quale si muoveva nel concavo, arriverà in manco di quattr’ore al centro, posto che nel concavo compiesse una revoluzione in ore ventiquattro, come bisogna ch’ei supponga per mantenersi sempre nella medesima verticale.

SIMP. Intendo ora benissimo l’errore; ma non glie lo vorrei attribuire immeritamente, ed è forza ch’io abbia errato nel recitar il suo argomento: e per fuggir di non gli n’addossar de gli altri, vorrei avere il suo libro, e se ci fusse chi andasse a pigliarlo, l’averei molto caro.

SAGR. Non mancherà un lacchè, che anderà volando; ed appunto si farà senza perdimento di tempo, ché intanto il Sig. Salviati ci favorirà del suo computo.

SIMP. Potrà andare, che lo troverà aperto su ’l mio banco insieme con quello dell’altro che pur argomenta contro al Copernico.

SAGR. Faremo portar quello ancora, per più sicurezza; ed in tanto il Sig. Salviati farà il suo calculo. Ho spedito un servitore.

Computo fatto del
tempo della caduta
della palla d’artiglieria
dal concavo
della Luna sino al
centro della Terra.

SALV. Avanti di ogni altra cosa, bisogna considerare come il movimento de i gravi descendenti non è uniforme, ma partendosi dalla quiete vanno continuamente accelerandosi; effetto conosciuto ed osservato da tutti, fuor che dal prefato autore moderno, il quale, non parlando di accelerazione, Accelerazione del
moto naturale de i
gravi si fa secondo i
numeri impari,
cominciando
dall’unità.lo fa equabile. Ma questa general cognizione è di niun profitto, quando non si sappia secondo qual proporzione sia fatto questo accrescimento di velocità, conclusione stata sino a i tempi nostri ignota a tutti i filosofi, e primieramente ritrovata e dimostrata dall’Accademico, nostro comun amico: il quale, in alcuni suoi scritti non ancor pubblicati,⁸⁵ ma in confidenza mostrati a me ed ad alcuni altri amici suoi, dimostra come l’accelerazione del moto retto de i gravi si fa secondo i numeri impari cioè che segnati quali e quanti si voglino tempi eguali, se nel primo tempo, partendosi il mobile dalla quiete, averà passato un tale spazio, come, per esempio, una canna, nel secondo tempo passerà tre canne, nel terzo cinque, nel quarto sette, e così conseguentemente secondo i succedenti numeri caffi; che in somma è l’istesso che il dire che gli spazii passati Gli spazii passati
dal grave cadente
sono come i
quadrati de’ tempi.dal mobile, partendosi dalla quiete, hanno tra di loro proporzione duplicata di quella che hanno i tempi ne’ quali tali spazii son misurati, o vogliam dire che gli spazii passati son tra di loro come i quadrati de’ tempi. ab unitate,⁸⁶

SAGR. Mirabil cosa sento dire. E di questo dite esserne dimostrazion matematica?

SALV. Matematica purissima, e non solamente di questa, ma di molte altre bellissime passioni attenenti a i moti naturali e a i proietti ancora, tutte ritrovate e Intera e nuova
scienza dell’Accademico
intorno al
moto locale.dimostrate dall’amico nostro: ed io le ho vedute e studiate tutte con mio grandissimo gusto e meraviglia, vedendo suscitata una nuova cognizione intera, intorno ad un suggetto del quale si sono scritti centinaia di volumi; e né pur una sola dell’infinite conclusioni ammirabili che vi son dentro, è stata osservata e intesa da alcuno prima che dal nostro amico.

SAGR. Voi mi fate fuggir la voglia d’intender più oltre de i nostri cominciati discorsi, e solo sentire alcuna delle dimostrazioni che mi accennate: però, o ditemele al presente, o almeno datemi ferma parola di farne meco una particolare sessione, ed anco presente il Sig. Simplicio, se avrà gusto di sentire le passioni ed accidenti del primario effetto della natura.

SIMP. Averollo indubitatamente, ancorché, per quanto appartiene al filosofo naturale, io non credo che il descendere a certe minute particolarità sia necessario, bastando una general cognizione della definizion del moto e della distinzione di naturale e violento, equabile e accelerato, e simili; ché quando questo non fusse bastato, io non credo che Aristotile avesse pretermesso di insegnarci tutto quello che fusse mancato.

SALV. Può essere. Ma non perdiamo più tempo in questo, ch’io prometto spenderci una meza giornata appartatamente per vostra sodisfazione, anzi pur ora mi sovviene avervi un’altra volta promesso di darvi questa medesima sodisfazione. E tornando al nostro cominciato calcolo del tempo nel quale il grave cadente verrebbe dal concavo della Luna sino al centro della Terra, per proceder non arbitrariamente e a caso, ma con metodo concludentissimo, cercheremo prima di assicurarci, con l’esperienza più volte replicata, in quanto tempo una palla, v. g., di ferro venga in Terra dall’altezza di cento braccia.

SAGR. Pigliando però una palla di un tal determinato peso, e quella stessa sopra la quale noi vogliamo far il computo del tempo della scesa dalla Luna.

SALV. Questo non importa niente, perché palle di una, di dieci, di cento, di mille libbre, tutte misureranno le medesime cento braccia nell’istesso tempo.

SIMP. Oh questo non cred’io, né meno lo crede Aristotile, che scrive che le velocità de i gravi descendenti hanno tra di loro la medesima proporzione delle loro gravità.⁸⁷

SALV. Come voi, Sig. Simplicio, volete ammetter cotesto per vero, bisogna che voi crediate ancora, che lasciate nell’istesso momento cader due palle della medesima materia, una di cento libbre e l’altra d’una,Errore d’Aristotile
nell’affermare, i
gravi cadenti muoversi
secondo la proporzione
delle gravità
loro. dall’altezza di cento braccia, la grande arrivi in Terra prima che la minore sia scesa un sol braccio: ora accomodate, se voi potete, il vostro cervello a imaginarsi di veder la gran palla giunta in Terra quando la piccola sia ancora a men d’un braccio vicina alla sommità della torre.

SAGR. Che questa proposizione sia falsissima, io non ne ho un dubbio al mondo; ma che anco la vostra sia totalmente vera, non ne son ben capace: tuttavia la credo, poiché voi risolutamente l’affermate; il che son sicuro che non fareste quando non ne aveste certa esperienza o ferma dimostrazione.

SALV. Honne l’una e l’altra, e quando tratteremo la materia de i moti separatamente, ve la comunicherò: intanto, per non avere occasione di più interrompere il filo, ponghiamo di voler fare il computo sopra una palla di ferro di cento libbre, la quale per replicate esperienze scende dall’altezza di cento braccia in cinque minuti secondi d’ora.⁸⁸ E perché, come vi ho detto, gli spazii che si misurano dal cadente, crescono in duplicata proporzione, cioè secondo i quadrati de’ tempi, essendoché il tempo di un minuto primo è duodeclupo del tempo di cinque secondi, se noi multiplicheremo le cento braccia per il quadrato di 12, cioè per 144, averemo 14400, che sarà il numero delle braccia che il mobile medesimo passerà in un minuto primo d’ora; e seguitando la medesima regola, perché un’ora è 60 minuti, multiplicando 14400, numero delle braccia passate in un minuto, per il quadrato di 60, cioè per 3600, ne verrà 51840000, numero delle braccia da passarsi in un’ora, che sono miglia 17280. E volendo sapere lo spazio che si passerebbe in 4 ore, multiplicheremo 17280 per 16 (che è il quadrato di 4), e ce ne verranno miglia 276480: il qual numero è assai maggiore della distanza dal concavo lunare al centro della Terra, che è miglia 196000, facendo la distanza del concavo 56 semidiametri terrestri, come fa l’autor moderno, ed il semidiametro della Terra 3500 miglia di braccia 3000 l’uno, quali sono le nostre miglia italiane. Adunque, Sig. Simplicio, quello spazio dal concavo della Luna al centro della Terra, che il vostro computista diceva non potersi passare se non in assai più di sei giorni, vedete come, facendo il computo sopra l’esperienza e non su per le dita, si passerebbe in assai meno di 4 ore; e facendo il computo esatto, si passa in ore 3, minuti primi 22 e 4 secondi.

SAGR. Di grazia, caro Signor, non mi defraudate di questo calculo esatto, perché bisogna che sia cosa bellissima.

SALV. Tale è veramente. Però, avendo (come ho detto) con diligente esperienza osservato come un tal mobile passa, cadendo, l’altezza di 100 braccia in 5 secondi d’ora, diremo: Se 100 braccia si passano in 5 secondi, braccia 588000000 (che tante sono 56 semidiametri della Terra) in quanti secondi si passeranno? La regola per quest’operazione è che si multiplichi il terzo numero per il quadrato del secondo; ne viene 14700000000, il quale si deve dividere per il primo, cioè per 100, e la radice quadrata del quoziente, che è 12124, è il numero cercato, cioè 12124 minuti secondi d’ora, che sono ore 3, minuti primi 22 e 4 secondi.⁸⁹

SAGR. Ho veduta l’operazione, ma non intendo niente della ragione del così operare, né mi par tempo adesso di domandarla.

SALV. Anzi ve la voglio dire, ancorché non la ricerchiate, perché è assai facile. Segniamo questi tre numeri con le lettere A primo, B secondo, C terzo; A, C sono i numeri de gli spazii, B è ’l numero del tempo: si cerca il quarto numero, pur del tempo. E perché noi sappiamo, che qual proporzione ha lo spazio A allo spazio C, tale deve avere il quadrato del tempo B al quadrato del tempo che si cerca, però, per la regola aurea,⁹⁰ si multiplicherà il numero C per il quadrato del numero B, ed il prodotto si dividerà per il numero A, ed il quoziente sarà il quadrato del numero che si cerca, e la sua radice quadrata sarà l’istesso numero cercato. Or vedete come è facile da intendersi.⁹¹

SAGR. Tali sono tutte le cose vere, doppo che son trovate; ma il punto sta nel saperle trovare. Io resto capacissimo, e vi ringrazio; e se altra curiosità vi resta in questa materia, vi prego a dirla, perché, s’io debbo parlar liberamente, dirò, con licenzia del Sig. Simplicio, che da i vostri discorsi imparo sempre qualche bella novità, ma da quelli de’ suoi filosofi non so d’aver sin ora imparato cose di gran rilievo.

SALV. Pur troppo ci resterebbe da dire in questi movimenti locali; ma conforme al convenuto ci riserberemo ad una sessione appartata, e per ora dirò qualche cosa attenente all’autor proposto dal Sig. Simplicio: al quale par d’aver dato un gran vantaggio alla parte nel concederle che quella palla d’artiglieria, nel cader dal concavo della Luna, possa venir con velocità eguale alla velocità con la quale si sarebbe mossa in giro restando lassù e movendosi alla conversion diurna. Ora io gli dico che quella palla, cadendo dal concavo sino al centro, acquisterà grado di velocità assai più che doppio della velocità del moto diurno del concavo lunare; e questo mostrerò io con supposti verissimi, e non arbitrarii. Dovete dunque sapere, come il grave cadendo, ed acquistando sempre velocità nuova secondo la proporzione già detta, in qualunque luogo egli si trovi della linea del suo moto, ha in sé tal grado di velocità, che se ei continuasse di muoversi con quella uniformemente, senza più crescerla, in altrettanto tempo quanto è stato quello della sua scesa passerebbe spazio doppio del passato nella linea del precedente moto in giù: e così, per esempio, se quella palla nel venir dal concavo della Luna al suo centro ha consumato ore 3, minuti primi 22 e 4 secondi, dico che giunta al centro si trova costituita in tal grado di velocità, Il mobile cadente,
quando si movesse,
col grado di velocità
acquistato, per
altrettanto tempo con
moto uniforme,
passerebbe spazio
doppio del passato col
moto accelerato.che se con quella, senza più crescerla, continuasse di muoversi uniformemente, passerebbe in altre ore 3, minuti primi 22 e 4 secondi il doppio di spazio, cioè quant’è tutto ’l diametro intero dell’orbe lunare. E perché dal concavo della Luna al centro sono miglia 196000, le quali la palla passa in ore 3, minuti primi 22 e 4 secondi, adunque (stante quello ch’è detto) continuando la palla di muoversi con la velocità che si trova avere nell’arrivare al centro, passerebbe, in altre ore 3, minuti primi 22 e 4 secondi, spazio doppio del detto, cioè miglia 392000: ma la medesima, stando nel concavo della Luna, che ha di circuito miglia 1232000, e movendosi con quello al moto diurno, farebbe nel medesimo tempo, cioè in ore 3, minuti primi 22 e 4 secondi, miglia 172880, che sono assai manco che la metà delle miglia 392000. Ecco dunque come il moto nel concavo non è qual dice l’autor moderno, cioè di velocità impossibile a participarsi dalla palla cadente, etc.

SAGR. Il discorso camminerebbe benissimo e mi quieterebbe, quando mi fusse saldata quella partita del muoversi il mobile per doppio spazio del passato cadendo, in altro tempo eguale a quel della scesa, quando e’ continuasse di muoversi uniformemente co ’l massimo grado della velocità acquistata nel descendere: proposizione anco un’altra volta da voi supposta per vera, ma non dimostrata.⁹²

SALV. Quest’è una delle dimostrate dal nostro amico, e la vedrete a suo tempo; ma intanto voglio con alcune conietture, non insegnarvi cosa nuova, ma rimuovervi da una certa opinione contraria, mostrandovi che forse così possa essere. Sospendendosi con un filo lungo e sottile, legato al palco, una palla di piombo, se noi la allontaneremo dal perpendicolo, lasciandola poi in libertà, non avete voi osservato che ella declinando passerà spontaneamente di là dal perpendicolo poco meno che altrettanto?

SAGR. L’ho osservato benissimo, e veduto (massime se la palla sarà grave assai) che ella sormonta tanto poco meno della scesa, che ho talvolta creduto che l’arco ascendente sia eguale al descendente, e però dubitato Il moto de i penduli
gravi si perpetuerebbe,
rimossi gl’impedimenti.che le sue vibrazioni potessero perpetuarsi; e crederò che lo farebbero se si potesse levar l’impedimento dell’aria, la quale, resistendo all’esser aperta, ritarda qualche poco ed impedisce il moto del pendolo: ma l’impedimento è ben poco; di che è argomento il numero grande delle vibrazioni che si fanno avanti che il mobile si fermi del tutto.

SALV. Non si perpetuerebbe il moto, Sig. Sagredo, quando ben si levasse totalmente l’impedimento dell’aria, perché ve n’è un altro più recondito assai.

SAGR. E qual è? ché altro non me ne sovviene.

SALV. Vi gusterà il sentirlo, ma ve lo dirò poi; intanto seguitiamo. Io vi ho proposta l’osservazione di questo pendolo, acciò che voi intendiate che l’impeto acquistato nell’arco descendente, dove il moto è naturale, è per sé stesso potente a sospignere di moto violento la medesima palla per altrettanto spazio nell’arco simile ascendente; è tale, dico, per sé stesso, rimossi tutti gl’impedimenti esterni. Credo anco che senza dubitarne s’intenda, che sì come nell’arco descendente si va crescendo la velocità sino al punto infimo del perpendicolo, così da questo per l’altro arco ascendente si vadia diminuendo sino all’estremo punto altissimo, e diminuendo con l’istesse proporzioni con le quali si venne prima agumentando, sì che i gradi delle velocità ne i punti egualmente distanti dal punto infimo sieno tra di loro eguali. Di qui parmi (discorrendo con una certa convenienza) di poter credere, che quando il globo terrestre fusse perforato per il centro,⁹³ una palla d’artiglieria scendendo per tal pozzo acquisterebbe sino al centro tal impeto di velocità, che trapassato il centro la spignerebbe in su per Quando il globo
terrestre fusse perforato,
un grave descendente
per tal foro
passerebbe, ascendendo
poi oltre al
centro, per altrettanto
spazio quanto fu quel della
scesa.altrettanto spazio quanto fusse stato quello della caduta, diminuendo sempre la velocità oltre al centro con decrementi simili a gl’incrementi acquistati nello scendere; ed il tempo che si consumerebbe in questo secondo moto ascendente credo che sarebbe eguale al tempo della scesa. Ora, se il mobile co ’l diminuir successivamente, sino alla totale estinzione, il sommo grado della velocità che ebbe nel centro, conduce il mobile in tanto tempo per tanto spazio per quanto in altrettanto tempo era venuto con l’acquisto di velocità dalla total privazione di essa sino a quel sommo grado; par ben ragionevole che quando si movesse sempre co ’l sommo grado di velocità, trapassasse in altrettanto tempo amendue quelli spazii: perché se noi andremo con la mente dividendo quelle velocità in gradi crescenti e calanti, come, v. g., questi numeri, sì che i primi sino al 10 sieno i crescenti, e gli altri sino all’1 i calanti, e quelli, del tempo della scesa, e gli altri, del tempo della salita, si vede che, congiunti tutti insieme, fanno tanto quanto se una delle due parti di loro fusse stata tutta di gradi massimi; e però tutto lo spazio passato con tutti i gradi delle velocità crescenti e calanti (che è tutto il diametro intero) dev’esser eguale allo spazio passato dalle velocità massime che in numero sono la metà dell’aggregato delle crescenti e delle calanti. Io mi conosco essermi assai duramente spiegato, e Dio voglia ch’io mi lasci intendere.⁹⁴

SAGR. Credo d’avere inteso benissimo, ed anco di poter in brevi parole mostrar ch’io ho inteso. Voi avete voluto dire, che cominciando il moto dalla quiete ed andando successivamente crescendo la velocità con agumenti eguali, quali sono quelli de’ numeri conseguenti, cominciando dall’unità, anzi dal zero, che rappresenta lo stato di quiete, disponendogli così, e conseguentemente quanti ne piacesse, sì che il minimo grado sia il zero e ’l massimo, v. g., 5, tutti questi gradi di velocità, con i quali il mobile si è mosso, fanno la somma di 15; ma quando il mobile si movesse con tanti gradi in numero quanti son questi, e che ciascheduno fusse eguale al massimo, che è 5, l’aggregato di tutte queste velocità sarebbe doppio dell’altre, cioè 30: e però movendosi il mobile per altrettanto tempo, ma con velocità equabile e qual è quella del sommo grado 5, doverà passare spazio doppio di quello che passò nel tempo accelerato, che cominciò dallo stato di quiete.

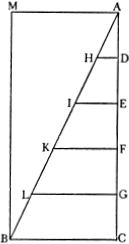
SALV. Voi, conforme alla vostra velocissima e sottilissima apprensiva, avete spiegato il tutto assai più lucidamente di me, e fattomi anco venire in mente di aggiugnere alcuna cosa di più. Imperocché, essendo nel moto accelerato l’agumento continuo, non si può compartire i gradi della velocità, la quale sempre cresce, in numero alcuno determinato, perché, mutandosi di momento in momento, son sempre infiniti: però meglio potremo esemplificare la nostra intenzione figurandoci un triangolo, qual sarebbe questo ABC, pigliando nel lato AC quante parti eguali ne piacerà, AD, DE, EF, FG, e tirando per i punti D, E, F, G linee rette parallele alla base BC; dove voglio che ci imaginiamo, le parti segnate nella linea AC esser tempi eguali, e le parallele tirate per i punti D, E, F, G rappresentarci i gradi delle velocità accelerate e crescenti egualmente in tempi eguali, ed il punto A esser lo stato di quiete, dal quale partendosi il mobile abbia, v. g., nel tempo AD acquistato il grado di velocità DH, nel seguente tempo aver cresciuta la velocità sopra il grado DH sino al grado EI, e conseguentemente fattala maggiore ne i tempi succedenti, secondo i crescimenti delle linee FK, GL, etc. Ma perché l’accelerazione si fa continuamente di momento in momento, e non L’accelerazione de i
gravi naturalmente
descendenti cresce
di momento in momento.intercisamente di parte quanta di tempo in parte quanta, essendo posto il termine A come momento minimo di velocità, cioè come stato di quiete e come primo instante del tempo susseguente AD, è manifesto che avanti l’acquisto del grado di velocità DH, fatto nel tempo AD, si è passato per altri infiniti gradi minori e minori, guadagnati ne gli infiniti instanti che sono nel tempo DA, corrispondenti a gli infiniti punti che sono nella linea DA: però per rappresentare la infinità de i gradi di velocità che precedono al grado DH, bisogna intendere infinite linee sempre minori e minori, che si intendano tirate da gl’infiniti punti della linea DA, parallele alla DH, la qual infinità di linee ci rappresenta in ultimo la superficie del triangolo AHD;⁹⁵ e così intenderemo, qualsivoglia spazio passato dal mobile con moto che, cominciando dalla quiete, si vadia uniformemente accelerando, aver consumato ed essersi servito di infiniti gradì di velocità crescenti, conforme all’infinite linee, che, cominciando dal punto A, si intendono tirate parallele alla linea HD ed alle IE, KF, LG, BC, continuandosi il moto quanto ne piace.

Ora finiamo l’intero parallelogrammo AMBC, e prolunghiamo sino al suo lato BM non solo le parallele segnate nel triangolo, ma la infinità di quelle che si intendono prodotte da tutti i punti del lato AC. E sì come la BC era massima delle infinite del triangolo, rappresentanteci il massimo grado di velocità acquistato dal mobile nel moto accelerato, e tutta la superficie di esso triangolo era la massa e la somma di tutta la velocità con la quale nel tempo AC passò un tale spazio, così il parallelogrammo viene ad esser una massa ed aggregato di altrettanti gradi di velocità, ma ciascheduno eguale al massimo BC, la qual massa di velocità viene a esser doppia della massa delle velocità crescenti del triangolo, sì come esso parallelogrammo è doppio del triangolo; e però, se il mobile che cadendo si è servito de i gradi di velocità accelerata, conforme al triangolo ABC, ha passato in tanto tempo un tale spazio, è ben ragionevole e probabile che servendosi delle velocità uniformi, e rispondenti al parallelogrammo, passi con moto equabile nel medesimo tempo spazio doppio al passato dal moto accelerato.

SAGR. Resto interamente appagato. E se voi chiamate questo un discorso probabile, quali saranno le dimostrazioni necessarie? Volesse Dio che in tutta la comune filosofia se ne trovasse pur una delle sì concludenti!

Nelle scienze naturali
non si deve
ricercar l’evidenza
matematica.

SIMP. Non bisogna nella scienza naturale ricercar l’esquisita evidenza matematica.

SAGR. Ma questa del moto non è quistion naturale? e pur non trovo che di esso Aristotile mi dimostri pur un minimo accidente. Ma non divertiamo più il nostro ragionamento; e voi, Sig. Salviati, non mancate in grazia di dirmi quello che mi accennaste esser cagione del fermare il pendolo, oltre alla resistenza del mezo all’esser aperto.

Il pendente da corda
più lunga fa le
sue vibrazioni più
rade, che il pendolo
da corda breve.

SALV. Ditemi: di due pendenti da distanze diseguali, quello che è attaccato a più lunga corda non fa le sue vibrazioni più rare?

SAGR. Sì, quando si movessero per eguali distanze dal perpendicolo.

Vibrazioni del
medesimo pendolo si
fanno con la
medesima frequenza,
siano esse grandi o
piccole.

SALV. Cotesto allontanarsi più o meno non importa niente, perché il medesimo pendolo fa le sue reciprocazioni sempre sotto tempi eguali, sieno quelle lunghissime o brevissime, cioè rimuovasi il pendolo assaissimo o pochissimo dal perpendicolo;⁹⁶ e se pur non sono del tutto eguali, son elleno Cagione che impedisce
il pendolo e lo riduce
alla quiete.insensibilmente differenti, come l’esperienza vi può mostrare; ma quando ben le fussero molto diseguali, non disfavorirebbe, ma favorirebbe la causa nostra. Imperocché segniamo il perpendicolo AB, e penda dal punto A nella corda AC un peso C, ed un altro pur nella medesima più alto, che sia E; e discostata la corda AC dal perpendicolo, e lasciata poi in libertà, i pesi C, E si moveranno per gli archi CBD, EGF: ed il peso E, come pendente da minor distanza, ed anco come (per vostro detto) allontanato meno, vuol 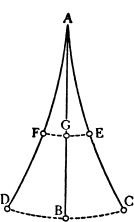ritornare indietro più presto e far le sue vibrazioni più frequenti che il peso C, e però gli impedirà il trascorrere tant’oltre verso il termine D quanto farebbe se fusse libero; e così, recandogli in ogni vibrazione continuo impedimento, finalmente lo ridurrà alla quiete. Ora, la corda medesima (levando i pesi di mezo) è un composto di molti pendoli gravi, cioè ciascheduna delle sue parti è un tal pendolo, attaccato più e più vicino al punto A⁹⁷ e però disposto a far le sue vibrazioni sempre più e più frequenti; ed in conseguenza è abile ad arrecare un continuo impedimento al peso C. Segno di questo ne è, che se noi osserveremo la corda AC, la vedremo distesa non rettamente, ma in arco; e se noi in cambio di corda piglieremo una catena, vedremo tale effetto assai più manifesto, e massime Corda o catena dove
è attaccato il pendolo,
si piega in arco
nelle vibrazioni di
quello, e non si
distende dirittamente.con l’allontanar assai il grave C dal perpendicolo AB: imperocché, per esser la catena composta di molte particelle snodate, e ciascheduna assai grave, gli archi AEC, AFD si vedranno notabilmente incurvati. Per questo dunque, che le parti della catena, secondo che son più vicine al punto A, voglion far le lor vibrazioni più frequenti, non lasciano scorrer le più basse quanto naturalmente farebbero; e con il continuo detrar dalle vibrazioni del peso C, finalmente lo fermano, quando ben l’impedimento dell’aria si potesse tor via.

SAGR. Appunto sono arrivati i libri. Pigliate, Sig. Simplicio, e trovate il luogo del quale si dubita.

SIMP. Eccolo qui, dove egli incomincia ad argumentar contro al moto diurno della Terra, avendo egli prima confutato l’annuo: Motus Terrae annuus asserere Copernicanos cogit conversionem eiusdem quotidianam; alias idem Terrae hemispherium continenter ad Solem esset conversum, obumbrato semper averso;⁹⁸ e così la metà della Terra non vedrebbe mai il Sole.

SALV. Parmi, per questo primo ingresso, che quest’uomo non si sia ben figurata la posizion del Copernico; perché s’egli avesse avvertito come e’ fa star l’asse del globo terrestre perpetuamente parallelo a sé stesso, non arebbe detto che la metà della Terra non vedrebbe mai il Sole, ma che l’anno sarebbe stato un sol giorno naturale, cioè che per tutte le parti della Terra si sarebbe auto sei mesi di giorno e sei mesi di notte, come ora accade a gli abitatori sotto ’l polo. Ma questo siagli perdonato, e venghiamo al resto.

SIMP. Segue: Hanc autem gyrationem Terrae impossibilem esse, sic demonstramus.⁹⁹ Questo appresso è la dichiarazione della seguente figura, dove si veggono dipinti molti gravi descendenti, e leggieri ascendenti, e uccelli che si trattengono per aria, etc.

SAGR. Mostrate, di grazia. Oh che belle figure, che uccelli, che palle, e che altre belle cose son queste?

SIMP. Queste son palle che vengono dal concavo della Luna.

SAGR. E questa che è?

SIMP. È una chiocciola, che qua a Venezia chiaman buovoli, che ancor essa vien dal concavo della Luna.

SAGR. Sì, sì: quest’è che la Luna ha così grand’efficacia sopra questi pesci ostreacei, che noi chiamiamo pesci armai.

SIMP. Quest’è poi quel calcolo ch’io dicevo, di questo viaggio in un giorno naturale, in un’ora, in un minuto primo ed in un secondo, che farebbe un punto della Terra posto sotto l’equinoziale, ed anco nel parallelo di 48 gradi.¹⁰⁰ E poi segue questo, dov’io dubito non avere errato nel referirlo; però leggiamolo: His positis, necesse est, Terra circulariter mota, omnia ex aëre eidem etc. Quod si hasce pilas aequales ponemus pondere, magnitudine, gravitate, et in concavo spherae lunaris positas libero descensui permittamus, si motum deorsum aequemus celeritate motui circum (quod tamen secus est, cum pila A etc.), elabentur minimum (ut multum cedamus adversariis) dies sex: quo tempore sexies circa Terram etc.¹⁰¹

SALV. Voi pur troppo avevi fedelmente referita l’instanza di quest’uomo. Di qui potete comprender, Sig. Simplicio, con quanta cautela dovrebber andar quelli che vorrebber dar a credere altrui quelle cose che forse non credono essi medesimi: perché mi pare impossibil cosa che quest’autore non si avesse ad accorgere ch’e’ si figurava un cerchio, il cui diametro, che appresso i matematici è manco che la terza parte della circonferenza, fusse più di 12 volte maggiore della medesima; errore che pone esser assai più di 36 quello ch’è manco d’uno.¹⁰²

SAGR. Forse che queste proporzioni matematiche, che son vere in astratto, applicate poi in concreto a cerchi fisici ed elementari non rispondon così per appunto: se ben mi pare che i bottai, per trovare il semidiametro del fondo da farsi per la botte, si servono della regola in astratto de’ matematici, ancorché tali fondi sien cose assai materiali e concrete. Però dica il Sig. Simplicio la scusa di quest’autore, e se gli pare che la fisica possa differir tanto dalla matematica.

SIMP. La ritirata non mi par suffiziente, perché lo svario è troppo grande; e in questo caso non saprei che dire altro, se non che quandoque bonus etc.¹⁰³ Ma posto che il calcolo del Sig. Salviati sia più giusto, e che il tempo della scesa della palla non fusse più di tre ore, parmi ad ogni modo che venendo dal concavo della Luna, distante per sì grand’intervallo, mirabil cosa sarebbe che ella avesse instinto da natura di mantenersi sempre sopra ’l medesimo punto della Terra al quale nella sua partita ella soprastava, e non più tosto restar in dietro per lunghissimo intervallo.

SALV. L’effetto può esser mirabile, e non mirabile, ma naturale e ordinario, secondo che sono le cose precedenti. Imperocché, se la palla (conforme a’ supposti che fa l’autore) mentre si tratteneva nel concavo della Luna aveva il moto circolare delle ventiquattr’ore insieme con la Terra e co ’l resto del contenuto dentro ad esso concavo, quella medesima virtù che la faceva andare in volta avanti lo scendere, continuerà di farla andar anco nello scendere; e tantum abest che ella non sia per secondare il moto della Terra, ma debba restare indietro, che più tosto dovrebbe prevenirlo, essendoché nell’avvicinarsi alla Terra il moto in giro ha da esser fatto continuamente per cerchi minori: talché, mantenendosi nella palla quella medesima velocità che ell’aveva nel concavo, dovrebbe anticipare, come ho detto, la vertigine della Terra.¹⁰⁴ Ma se la palla nel concavo mancava della circolazione, non è in obbligo nello scendere di mantenersi perpendicolarmente sopra quel punto della Terra che gli era sottoposto quando la scesa cominciò; né il Copernico né alcuno de’ suoi aderenti lo dirà.

SIMP. Ma l’autore farà instanza, come voi vedete, domandando da qual principio dependa questo moto circolare de’ gravi e de’ leggieri, cioè se da principio interno o esterno.

SALV. Stando nel problema di che si tratta, dico che quel principio che faceva andar la palla in volta mentre era nel concavo lunare, è il medesimo che gli mantiene la circolazione anco nello scendere: lascerò poi che l’autore lo faccia interno o esterno a modo suo.

SIMP. L’autore proverà che non può esser né interno né esterno.

SALV. Ed io risponderò che la palla nel concavo non si muoveva, e sarò libero dal dover dichiarare come discendendo resti sempre verticale al medesimo punto, attesoché ella non vi resterà.

SIMP. Bene; ma come i gravi e i leggieri non possono aver principio né interno né esterno di muoversi circolarmente, né anco il globo terrestre si muoverà di moto circolare; e così avremo l’intento.

SALV. Io non ho detto che la Terra non abbia principio né esterno né interno al moto circolare, ma dico che non so qual de’ dua ella si abbia; ed il mio non lo sapere non ha forza di levarglielo. Ma se questo autore sa da che principio sieno mossi in giro altri corpi mondani, che sicuramente si muovono, dico che quello che fa muover la Terra è una cosa simile a quella per la quale si muove Marte, Giove, e che e’ crede che si muova anco la sfera stellata; e se egli mi assicurerà chi sia il movente di uno di questi mobili, io mi obbligo a sapergli dire chi fa muover la Terra. Ma più, io voglio far l’istesso s’ei mi sa insegnare chi muova le parti della Terra in giù.¹⁰⁵

SIMP. La causa di quest’effetto è notissima, e ciaschedun sa che è la gravità.

Non si ha maggior
cognizione di chi
muova i gravi
all’ingiù, che di chi
muova le stelle in
giro, né di queste
cause sappiamo altro
che i nomi,
impostigli da noi.

SALV. Voi errate, Sig. Simplicio; voi dovevi dire che ciaschedun sa ch’ella si chiama gravità. Ma io non vi domando del nome, ma dell’essenza della cosa: della quale essenza voi non sapete punto più di quello che voi sappiate dell’essenza del movente le stelle in giro, eccettuatone il nome, che a questa è stato posto e fatto familiare e domestico per la frequente esperienza che mille volte il giorno ne veggiamo; ma non è che realmente noi intendiamo più, che principio o che virtù sia quella che muove la pietra in giù, di quel che noi sappiamo chi la muova in su, separata dal proiciente, o chi muova la Luna in giro, eccettoché (come ho detto) il nome, che più singulare e proprio gli abbiamo assegnato di gravità, doveché a quello con termine più generico assegnamo virtù impressa, a quello diamo intelligenza, o assistente, o informante, ed a infiniti altri moti diamo loro per cagione la natura.¹⁰⁶

SIMP. Parmi che quest’autore domandi assai manco di quello a che voi negate la risposta; poiché e’ non vi chiede qual sia particolarmente e nominatamente il principio che muove i gravi e i leggieri in giro, ma, qualunque e’ si sia, cerca solamente se voi lo stimate intrinseco o estrinseco: che se bene, v. g., io non so che cosa sia la gravità, per la quale la Terra descende, so però ch’ell’è principio interno, poiché, non impedito, spontaneamente muove; ed all’incontro so che il principio che la muove in su, è esterno, ancorché io non sappia che cosa sia la virtù impressale dal proiciente.

SALV. In quante quistioni bisognerebbe divertire, se noi volessimo decidere tutte le difficultà che si vengono attaccando l’una in conseguenza dell’altra! Voi chiamate principio esterno, ed anco lo chiamerete preternaturale e violento, quello che muove il proietto grave all’insù; ma forse non è egli meno interno e naturale La virtù che conduce
i proietti gravi
in alto, non gli è
men naturale che
la gravità che gli
muove al basso.che quello che lo muove in giù: può chiamarsi per avventura esterno e violento mentre il mobile è congiunto co ’l proiciente; ma separato, che cosa esterna rimane per motore della freccia o della palla? Bisogna pur necessariamente dire che quella virtù che la conduce in alto, sia non meno interna che quella che la muove in giù; ed io ho così per naturale il moto in su de i gravi per l’impeto concepito, come il moto in giù dependente dalla gravità.

SIMP. Questo non ammetterò io mai; perché questo ha il principio interno naturale e perpetuo, e quello, esterno violento e finito.

SALV. Se voi vi ritirate dal concedermi che i principii de i moti de i gravi in giù ed in su sieno egualmente interni e naturali, che fareste s’io vi dicessi che e’ potessero anco essere il medesimo in numero?

SIMP. Lo lascio giudicare a voi.

Principii contrarii
non possono riseder
naturalmente
nel medesimo
suggetto.

SALV. Anzi voglio io voi stesso per giudice. Pero ditemi: credete voi che nel medesimo corpo naturale possano riseder principii interni che siano tra di loro contrarii?

SIMP. Credo assolutamente di no.

SALV. Della terra, del piombo, dell’oro, ed in somma delle materie gravissime, quale stimate voi che sia la lor naturale intrinseca inclinazione, cioè a qual moto credete voi che ’l lor principio interno le tiri?

SIMP. Al moto verso il centro delle cose gravi, cioè al centro dell’universo e della Terra, dove, non impedite, si condurrebbero.

SALV. Talché, quando il globo terrestre fusse perforato da un pozzo che passasse per il centro di esso, una palla d’artiglieria lasciata cader per esso, mossa da principio naturale ed intrinseco, si condurrebbe al centro; e tutto questo moto farebbe ella spontaneamente e per principio intrinseco: non sta così?

SIMP. Così tengo io per fermo.

SALV. Ma giunta al centro, credete voi ch’ella passasse più oltre, o pur che quivi cesserebbe immediatamente dal moto?

SIMP. Credo che ella continuerebbe di muoversi per lunghissimo spazio.

SALV. Ma questo moto oltre al centro non sarebb’egli all’insù e, per vostro detto, preternaturale e violento? e da qual altro principio lo farete voi dependere, salvoché da quell’istesso che ha condotta la palla al centro, e che voi avete chiamato intrinseco e naturale? trovate voi un proiciente esterno, che gli sopraggiunga di nuovo per cacciarla in su. E questo che si dice del moto per il centro, si vede anco quassù da noi: imperocché l’impeto interno di un grave cadente per una Il moto naturale si
converte per sé stesso
in quello che si
chiama preternaturale
e violento.superficie declive, se la medesima, piegandosi da basso, si refletterà in su, lo porterà, senza punto interrompere il moto, anco all’insù. Una palla di piombo pendente da uno spago, rimossa dal perpendicolo, descende spontaneamente, tirata dall’interna inclinazione, e senza interpor quiete trapassa il punto infimo, e senz’altro sopravvegnente motore si muove in su. Io so che voi non negherete che tanto è naturale ed interno de i gravi il principio che gli muove in giù, quanto de i leggieri quello che gli muove in su: onde io vi metto in considerazione una palla di legno, la quale scendendo per aria da grande altezza, e però movendosi da principio interno, giunta sopra una profondità d’acqua, continua la sua scesa, e senz’altro motore esterno per lungo tratto si sommerge; e pure il moto in giù per l’acqua gli è preternaturale, e con tutto ciò depende da principio che è interno, e non esterno della palla. Eccovi dunque dimostrato come un mobile può esser mosso, da uno stesso principio interno, di movimenti contrarii.¹⁰⁷

SIMP. Io credo che a tutte queste instanze ci sieno risposte, benché per ora non mi sovvengano. Ma comunque ciò sia, continua l’autor di domandar da qual principio dependa questo moto circolare de i gravi e de i leggieri, cioè se da principio interno o esterno, e seguendo dimostra che non può esser né l’uno né l’altro, dicendo: Si ab externo, Deusne illum excitat per continuum miraculum? an vero angelus? an aër? Et hunc quidem multi assignant. Sed contra….¹⁰⁸

SALV. Non vi affaticate in legger l’instanze, perch’io non son di quelli che attribuisca tal principio all’aria ambiente. Quanto poi al miracolo o all’angelo, più tosto inclinerei in quella parte; perché quello che comincia da divino miracolo o da operazione angelica, qual è la trasportazione d’una palla d’artiglieria nel concavo della Luna, non ha dell’improbabile che in virtù del medesimo principio faccia anco il resto. Ma quanto all’aria, a me basta che ella non impedisca il moto circolare de i mobili che per essa si dice che si muovono; e per ciò fare, basta (né più si ricerca) che essa si muova dell’istesso moto, e che con la medesima velocità finisca le sue circolazioni che il globo terrestre.

SIMP. Ed egli insurgerà parimente contro a questo, domandando chi conduce intorno l’aria, la natura o la violenza? e confuta la natura, con dire che ciò è contro alla verità, all’esperienza, all’istesso Copernico.

SALV. Contro al Copernico non è altrimenti, il quale non scrive tal cosa, e quest’autor glie l’attribuisce con troppo eccesso di cortesia: anzi egli dice, e per mio parer dice bene, che la parte dell’aria vicina alla Terra, essendo più presto evaporazion terrestre, può aver la medesima natura, e naturalmente seguire il suo moto, o vero, per essergli contigua, seguirla in quella maniera che i Peripatetici dicono che la parta superiore e l’elemento del fuoco seguono il moto del concavo della Luna;¹⁰⁹ sì che a loro tocca a dichiarare se cotal moto sia naturale o violento.

SIMP. Replicherà l’autore, che se ’l Copernico fa muovere una parte dell’aria inferiore solamente, mancando di cotal moto la superiore, non potrà render ragione come quell’aria quieta sia per poter condur seco i medesimi gravi e fargli secondare il moto della Terra.

SALV. Il Copernico dirà che questa propension naturale de i corpi elementari di seguire il moto terrestre ha una limitata sfera, fuor della quale cesserebbe tal naturale La propensione de
i corpi elementari
in seguir la Terra
ha una limitata
sfera.inclinazione:¹¹⁰ oltreché, come ho detto, non è l’aria quella che porta seco i mobili, i quali, sendo separati dalla Terra, seguano il suo moto; sì che cascano tutte le instanze che questo autor produce per provar che l’aria può non cagionar cotali effetti.

SIMP. Come dunque ciò non sia, bisognerà dire che tali effetti dependano da principio interno; contro alla qual posizione oboriuntur difficillimae, immo inextricabiles, quaestiones secundae, che sono le seguenti: Principium illud internum vel est accidens, vel substantia: si primum, quale nam illud? nam qualitas loco motiva circum hactenus nulla videtur esse agnita.¹¹¹

SALV. Come non si ha notizia di alcuna? non ci sono queste, che muovon intorno tutte queste elementari materie, insieme con la Terra? Vedete come quest’autore suppon per vero quello ch’è in quistione.

SIMP. Ei dice che ciò non si vede, e parmi che abbia ragione in questo.

SALV. Non si vede da noi, perché andiamo in volta insieme con loro.

SIMP. Sentite l’altra instanza: Quae etiam si esset, quomodo tamen inveniretur in rebus tam contrariis? in igne ut in aqua? in aëre ut in terra? in viventibus ut in anima carentibus?¹¹²

SALV. Posto per ora che l’acqua e il fuoco sien contrarii, come anche l’aria e la terra (che pur ci sarebbe da dire assai), il più che da questo ne possa seguire, sarà che ad essi non possono esser comuni i moti che tra loro sien contrarii; sì che, v. g., il moto in su, che naturalmente compete al fuoco, non possa competere all’acqua, ma che, sì come essa è per natura contraria al fuoco, così a lei convenga quel moto che è contrario al moto del fuoco, che sarà il moto deorsum: ma il moto circolare, che non è contrario né al sursum né al deorsum, anzi che si può mescolare con amendue, come il medesimo Aristotile afferma, perché non potrà egualmente competere a i gravi ed a i leggieri? I moti poi che non posson esser comuni a i viventi ed a i non viventi, son quelli che dependon dall’anima; ma quelli che son del corpo, in quanto egli è elementare, ed in conseguenza participante delle qualità degli elementi, perché non hanno ad esser comuni al cadavero ed al vivente? E però, quando il moto circolare sia proprio degli elementi, dovrà esser comune de i misti ancora.

SAGR. È forza che quest’autor creda, che cadendo una gatta morta da una finestra, non possa esser che anco viva ci potesse cadere, non essendo cosa conveniente che un cadavero partecipi delle qualità che convengono ad un vivente.

SALV. Non conclude, dunque, il discorso di quest’autore contro a chi dicesse, il principio del moto circolare de i gravi e de i leggieri esser un accidente interno. Non so quanto e’ sia per dimostrare che non possa esser una sustanza.

SIMP. Insurge contro a questo con molte opposizioni, la prima delle quali è questa: Si secundum (nempe si dicas, tale principium esse substantiam), illud est aut materia, aut forma, aut compositum: sed repugnant iterum tot diversae rerum naturae, quales sunt aves, limaces, saxa, sagittae, nives, fumi, grandines, pisces, etc., quae tamen omnia, specie et genere differentia, moverentur a natura sua circulariter, ipsa naturis diversissima, etc.¹¹³

SALV. Se queste cose nominate sono di nature diverse, e le cose di nature diverse non possono aver un moto comune, bisognerà, quando si debba sodisfare a tutte, pensar ad altro che a due moti solamente in su e in giù; e se se ne deve trovar uno per le freccie, uno per le lumache, un altro per i sassi, uno per i pesci, bisognerà pensare anco a i lombrichi e a i topazii e all’agarico, che non son men differenti di natura tra di loro che la gragnuola e la neve.

SIMP. Par che voi ve ne burliate di questi argomenti.

SALV. Anzi no, Sig. Simplicio; ma già si è risposto di sopra, cioè che se un moto in giù o vero in su può convenire alle cose nominate, potrà non meno convenir loro un circolare. E stando nella dottrina peripatetica, non porrete voi diversità maggiore tra una cometa elementare e una stella celeste, che tra un pesce e un uccello? e pur quelle si muovono amendue circolarmente. Or seguite il secondo argumento.

SIMP. Si Terra staret per voluntatem Dei, rotarentne caetera annon? si hoc, falsum est a natura gyrari: si illud, redeunt priores quaestiones; et sane mirum esset, quod gavia pisciculo, alauda nidulo suo et corvus limaci petraeque, etiam volens, imminere non posset.¹¹⁴

SALV. Io per me darei una risposta generale: che, dato per volontà di Dio che la Terra cessasse dalla vertigine diurna, quegli uccelli farebber tutto quello che alla medesima volontà di Dio piacesse. Ma se pur cotesto autore desiderasse una più particolar risposta, gli direi che e’ farebber tutto l’opposito di quello che e’ facessero quando, mentre eglino separati dalla Terra si trattenesser per aria, il globo terrestre per volontà divina si mettesse inaspettatamente in un moto precipitosissimo: tocca ora a quest’autore ad assicurarci di quello che in tal caso accaderebbe.

SAGR. Di grazia, Sig. Salviati, concedete a mia richiesta a quest’autore, che fermandosi la Terra per volontà di Dio, l’altre cose da quella separate continuasser d’andar in volta del natural movimento loro, e sentiamo quali impossibili o inconvenienti ne seguirebbero: perché io per me non so veder disordini maggiori di questi che produce l’autor medesimo, cioè che l’allodole, ancorché le volessero, non si potrebber trattener sopra i nidi loro, né i corbi sopra le lumache o sopra i sassi; dal che ne seguirebbe che a i corbi converrebbe patirsi la voglia delle lumache, e gli allodolini si morrebber di fame e di freddo, non potendo esser né imbeccati né covati dalle lor madri: questa è tutta la rovina ch’io so ritrar che seguirebbe, stante il detto dell’autore. Vedete voi, Sig. Simplicio, se maggiori inconvenienti seguir ne dovessero.

SIMP. Io non ne so scorger di maggiori, ma è ben credibile che l’autore ci scorga, oltre a questi, altri disordini in natura, che forse per suoi degni rispetti non ha volsuti produrre. Seguirò dunque la terza instanza: Insuper, quî fit ut istae res tam variae tantum moveantur ab occasu in ortum parallelae ad aequatorem? ut semper moveantur, numquam quiescant?¹¹⁵

SALV. Muovonsi da occidente in oriente, parallele all’equinoziale, senza fermarsi, in quella maniera appunto che voi credete che le stelle fisse si muovano da levante a ponente, parallele all’equinoziale, senza fermarsi.

SIMP. Quare quo sunt altiores celerius, quo humiliores tardius?¹¹⁶

SALV. Perché in una sfera o in un cerchio che si volga intorno al suo centro, le parti più remote descrivono cerchi maggiori, e le più vicine gli descrivono nell’istesso tempo minori.

SIMP. Quare quae aequinoctiali propiores in maiori, quae remotiores in minori, circulo feruntur?¹¹⁷

SALV. Per immitar la sfera stellata, nella quale le più vicine all’equinoziale si muovon in cerchi maggiori che le più lontane.

SIMP. Quare pila eadem sub aequinoctiali tota circa centrum Terrae ambitu maximo, celeritate incredibili, sub polo vero circa centrum proprium gyro nullo, tarditate suprema, volveretur?¹¹⁸

SALV. Per immitar le stelle del firmamento, che farebbon l’istesso se ’l moto diurno fusse loro.

SIMP. Quare eadem res, pila v. g. plumbea, si semel Terram circuivit descripto circulo maximo, eamdem ubique non circummigret secundum circulum maximum, sed translata extra aequinoctialem in circulis minoribus agetur?¹¹⁹

SALV. Perché così farebbero, anzi pure hanno fatto in dottrina di Tolomeo, alcune stelle fisse, che già erano vicinissime all’equinoziale e descrivevan cerchi grandissimi, ed ora, che ne son lontane, gli descrivon minori.

SAGR. Oh s’io potessi tenere a mente tutte queste belle cose, mi parrebbe pur d’aver fatto il grand’acquisto! Bisogna, Sig. Simplicio, che voi me lo prestiate questo libretto, perché egli è forza che perentro vi sia un mare di cose peregrine ed esquisitissime.

SIMP. Io ve ne farò un presente.

SAGR. Oh questo no, io non ve ne priverei mai. Ma son finite ancora le interrogazioni?

SIMP. Signor no; sentite pure: Si latio circularis gravibus et levibus est naturalis, qualis est ea quae fit secundum lineam rectam? nam si naturalis, quomodo et is motus qui circum est, naturalis est, cum specie differat a recto? si violentus, quî fit ut missile ignitum, sursum evolans, scintillosum caput sursum a Terra, non autem circum, volvatur, etc.?¹²⁰

Del moto misto, noi
non veggiamo la
parte circolare, perché
di quella siamo
partecipi.

SALV. Già mille volte si è detto che il moto circolare è naturale del tutto e delle parti, mentre sono in ottima disposizione: il retto è per ridurr’all’ordine le parti disordinate; se ben meglio è dire che mai, né ordinate né disordinate, non si muovon di moto retto, ma di un moto misto, che anco potrebb’esser circolare schietto; ma a noi resta visibile e osservabile una parte sola di questo moto misto, cioè la parte del retto, restandoci l’altra parte del circolare impercettibile, perché noi ancora lo participiamo: e questo risponde a i razzi, li quali si muovono in su e in giro, ma noi non possiamo distinguer il circolare, perché di quello ci moviamo noi ancora. Ma quest’autore non credo che abbia mai capita questa mistione, poiché si vede come egli resolutamente dice che i razzi vanno in su a diritto e non vanno altrimenti in giro.

SIMP. Quare centrum spherae delapsae sub aequatore spiram describit in eius plano, sub aliis parallelis spiram describit in cono? sub polo descendit in axe, lineam gyralem decurrens in superficie cylindrica consignatam?¹²¹

SALV. Perché delle linee tirate dal centro alla circonferenza della sfera, che son quelle per le quali i gravi descendono, quella che termina nell’equinoziale disegna un cerchio, e quelle che terminano in altri paralleli descrivon superficie coniche, e l’asse non descrive altro, ma si resta nell’esser suo. E se io vi debbo dire il mio parer liberamente, dirò che non so ritrarre da tutte queste interrogazioni costrutto nissuno che rilievi contro al moto della Terra; perché s’io domandassi a quest’autore (concedutogli che la Terra non si muova) quello che accaderebbe di tutti questi particolari, dato che ella si movesse come vuole il Copernico, son ben sicuro che e’ direbbe che ne seguirebbon tutti questi effetti, che egli adesso oppone come inconvenienti per rimuover la mobilità; talché nella mente di quest’uomo le conseguenze necessarie vengon reputate assurdi. Ma, di grazia, se ci è altro, spediamoci da questo tedio.

SIMP. In questo che segue, ci è contro al Copernico e suoi seguaci, che voglion che il moto delle parti, separate dal suo tutto, sia solo per riunirsi al suo tutto, ma che naturale assolutamente sia il muoversi circolarmente alla vertigine diurna; contro a i quali instà dicendo che, conforme all’oppinion di costoro, si tota Terra, una cum aqua, in nihilum redigeretur, nulla grando aut pluvia e nube decideret, sed naturaliter tantum circumferretur; neque ignis ullus aut igneum ascenderet, cum, illorum non improbabili sententia, ignis nullus sit supra.¹²²

SALV. La providenza di questo filosofo è mirabile e degna di gran lode, attesoché e’ non si contenta di pensare alle cose che potrebbon accadere stante il corso della natura, ma vuol trovarsi provvisto in occasione che seguissero di quelle cose che assolutamente si sa che non sono mai per seguire. Io voglio dunque, per sentir qualche bella sottigliezza, concedergli che quando la Terra e l’acqua andassero in niente, né le grandini né la pioggia cadessero più, né le materie ignee andasser più in alto, ma si trattenesser girando: che sarà poi? e che mi opporrà il filosofo?

SIMP. L’opposizione è nelle parole che seguono immediatamente; eccole qui: Quibus tamen experientia et ratio adversatur.¹²³

SALV. Ora mi convien cedere, poiché egli ha sì gran vantaggio sopra di me, qual è l’esperienza, della quale io manco; perché sin ora non mi son mai incontrato in vedere che ’l globo terrestre, con l’elemento dell’acqua, sia andato in niente, sì ch’io abbia potuto osservare quel che in questo piccol finimondo faceva la gragnuola e l’acqua. Ma ci dic’egli almanco, per nostra scienza, quel che facevano?

SIMP. Non lo dice altrimenti.

SALV. Pagherei qualsivoglia cosa a potermi abboccar con questa persona, per domandargli, se quando questo globo sparì, e’ portò via anco il centro comune della gravità, sì com’io credo; nel qual caso, penso che la grandine e l’acqua restassero come insensate e stolide tra le nugole, senza saper che farsi di loro. Potrebbe anco esser che, attratte da quel grande spazio vacuo, lasciato mediante la partita del globo terrestre, si rarefacesser tutti gli ambienti, ed in particolar l’aria, che è sommamente distraibile, e concorressero con somma velocità a riempierlo; e forse i corpi più solidi e materiali, come gli uccelli, che pur di ragione ne dovevano esser molti per aria, si ritirarono più verso il centro della grande sfera vacua (che par ben ragionevole che alle sustanze che sotto minor mole contengono assai materia, sieno assegnati i luoghi più angusti, lasciando alle più rare i più ampli), e quivi, mortisi finalmente di fame e risoluti in terra, formassero un nuovo globettino, con quella poca di acqua che si trovava allora tra’ nugoli.¹²⁴ Potrebbe anco essere che le medesime materie, come quelle che non veggon lume, non s’accorgessero della partita della Terra, e che alla cieca scendessero al solito, pensando d’incontrarla, e a poco a poco si conducessero al centro, dove anco di presente andrebbero se l’istesso globo non l’impedisse. E finalmente, per dare a questo filosofo una meno irrisoluta risposta, gli dico che so tanto di quel che seguirebbe dopo l’annichilazione del globo terrestre, quanto egli avrebbe saputo che fusse per seguir di esso ed intorno ad esso avanti che fusse creato: e perché io son sicuro ch’e’ direbbe che non si sarebbe né anco potuto immaginare nissuna delle cose seguite, delle quali la sola esperienza l’ha fatto scienziato, dovrà non mi negar perdono e scusarmi s’io non so quel che egli sa delle cose che seguirebbero doppo l’annichilazione di esso globo, atteso che io manco di quest’esperienza che egli ha. Dite ora se ci è altra cosa.

SIMP. Ci è questa figura, che rappresenta il globo terrestre con una gran cavità intorno al suo centro, ripiena d’aria; e per mostrare che i gravi non si muovono in giù per unirsi co ’l globo terrestre, come dice il Copernico, costituisce questa pietra nel centro, e domanda, posta in libertà quel che ella farebbe; ed un’altra ne pone nella concavità di questa gran caverna, e fa l’istessa interrogazione, dicendo quanto alla prima: Lapis in centro constitutus aut ascendet ad Terram in punctum aliquod, aut non: si secundum, falsum est partes ob solam seiunctionem a toto ad illud moveri; si primum, omnis ratio et experientia renititur, neque gravia in suae gravitatis centro conquiescent. Item, si suspensus lapis liberatus decidat in centrum, separabit se a toto, contra Copernicum; si pendeat, refragatur omnis experientia, cum videamus integros fornices corruere.¹²⁵

SALV. Risponderò, benché con mio disavvantaggio grande, già che son alle mani con chi ha veduto per esperienza ciò Prima sono le cose
gravi che il centro
della gravità.che fanno questi sassi in questa gran caverna, cosa che non ho veduta io, e dirò che credo che prima siano le cose gravi che il centro comune della gravità, sì che non un centro, che altro non è che un punto indivisibile, e però di nessuna efficacia, sia quello che attragga a sé le materie gravi,¹²⁶ ma che esse materie, cospirando naturalmente all’unione, si formino un comun centro, che è quello intorno al quale consistono parti di eguali momenti: onde stimo, che trasferendosi il grande aggregato de i gravi in qualsivoglia luogo, le particelle che dal tutto fusser separate lo seguirebbero, Trasponendosi il
grand’aggregato de
i gravi, le particelle
separate da esso lo
seguirebbono.e non impedite lo penetrerebbero sin dove trovassero parti men gravi di loro, ma pervenute sin dove s’incontrassero in materie più gravi, non scenderebber più. E però stimo che nella caverna ripiena d’aria tutta la volta premerebbe, e solo violentemente si sostenterebbe sopra quell’aria, quando la durezza non potesse esser superata e rotta dalla gravità; ma sassi staccati credo che scenderebbero al centro, e non soprannoterebbero all’aria: né per ciò si potrebbe dire che non si movessero al suo tutto, movendosi là dove tutte le parti del tutto si moverebbero, quando non fussero impedite.

SIMP. Quel che resta è certo errore ch’ei nota in un seguace del Copernico, il quale, facendo che la Terra si muova del moto annuo e del diurno in quella guisa che la ruota del carro si muove sopra il cerchio della Terra ed in sé stessa, veniva a fare o il globo terrestre troppo grande o l’orbe magno¹²⁷ troppo piccolo; attesoché 365 revoluzioni dell’equinoziale son meno assai che la circonferenza dell’orbe magno.

SALV. Avvertite che voi equivocate, e dite il contrario di quello che bisogna che sia scritto nel libretto: imperocché bisogna dire che quel tale autore veniva a fare il globo terrestre troppo piccolo o l’orbe magno troppo grande, e non il terrestre troppo grande e l’annuo troppo piccolo.

SIMP. L’equivoco non è altrimenti mio: ecco qui le parole del libretto: Non videt quod vel circulum annuum aequo minorem, vel orbem terreum iusto multo fabricet maiorem.¹²⁸

SALV. Se il primo autore abbia errato, io non lo posso sapere, poiché l’autor del libretto non lo nomina; ma ben è manifesto e inescusabile l’error del libretto, abbia o non abbia errato quel primo seguace del Copernico, poiché quel del libretto trapassa senza accorgersi un error sì materiale, e non lo nota e non lo emenda.¹²⁹ Ma questo siagli perdonato, come errore più Non repugna il
potersi con la circonferenza
di un cerchio
piccolo, e poche
volte rivoltato, misurare
e descrivere una
linea maggiore di
qual si voglia grandissimo
cerchio.tosto d’inavertenza che d’altro. Oltre che, se non ch’io sono omai stracco e sazio di più lungamente occuparmi e consumare il tempo con assai poca utilità in queste molto leggieri altercazioni, potrei mostrare come non è impossibile che un cerchio, anco non maggior d’una ruota d’un carro, co ’l dar non pur 365, ma anco meno di 20 revoluzioni, può descrivere o misurare la circonferenza non pur dell’orbe magno, ma di uno mille volte maggiore: e questo dico per mostrare che non mancano sottigliezze assai maggiori di questa, con la quale quest’autore nota l’error del Copernico. Ma, di grazia, respiriamo un poco, per venir poi a quest’altro filosofo, oppositor del medesimo Copernico.

SAGR. Veramente ne ho bisogno io ancora, benché abbia solamente affaticato gli orecchi; e quando io pensassi di non aver a sentir cose più ingegnose in quest’altro autore, non so s’io mi risolvessi a andarmene a i freschi in gondola.

SIMP. Credo che sentirete cose di maggior polso, perché quest’è filosofo consumatissimo, e anco gran matematico, ed ha confutato Ticone in materia delle comete e delle stelle nuove.

SALV. È egli forse l’autor medesimo dell’Antiticone?

SIMP. È quello stesso:¹³⁰ ma la confutazione contro alle stelle nuove non è nell’Antiticone, se non in quanto e’ dimostra che elle non erano progiudiziali all’inalterabilità ed ingenerabilità del cielo, sì come già vi dissi; ma doppo l’Antiticone, avendo trovato per via di parallasse modo di dimostrare che esse ancora son cose elementari e contenute dentro al concavo della Luna, ha scritto quest’altro libro: De tribus novus stellis etc., ed inseritovi anco gli argomenti contro al Copernico. Io l’altra volta vi produssi quello ch’egli aveva scritto circa queste stelle nuove nell’Antiticone, dove egli non negava che le fussero nel cielo, ma dimostrava che la lor produzione non alterava l’inalterabilità del cielo, e ciò facev’egli con discorso puro filosofico, nel modo ch’io vi dissi; e non mi sovvenne di dirvi come di poi aveva trovato modo di rimuoverle dal cielo, perché, procedendo egli in questa confutazione per via di computi e di parallassi, materie poco o niente comprese da me, non l’avevo lette, e solo avevo fatto studio sopra queste instanze contro al moto della Terra, che son pure naturali.

SALV. Intendo benissimo, e converrà, doppo che avremo sentite le opposizioni al Copernico, che sentiamo, o veggiamo almeno, la maniera con la quale per via di parallasse dimostra essere state elementari quelle nuove stelle, che tanti astronomi di gran nome costituiron tutti altissime e tra le stelle del firmamento; e come quest’autore conduce a termine una tanta impresa, di ritirar di cielo le nuove stelle sin dentro alla sfera elementare, sarà ben degno d’esser grandemente esaltato e trasferito esso tra le stelle, o almeno che per fama sia tra quelle eternato il suo nome. Però spediamoci quanto prima da questa parte, che oppone all’oppinion del Copernico, e cominciate a portare le sue instanze.

SIMP. Queste non occorrerà leggerle ad verbum, perché sono molto prolisse; ma io, come vedete, nel leggerle attentamente più volte, ho contrassegnato nella margine le parole dove consiste tutto il nervo della dimostrazione, e quella basterà leggere. Il primo argomento comincia qui: Et primo, si opinio Copernici recipiatur, criterium naturalis philosophiae, ni prorsus tollatur, vehementer saltem labefactari videtur.¹³¹ Nella opinion del
Copernico si
guasta il criterio della
filosofia.Il qual criterio vuole, secondo l’opinione di tutte le sette de’ filosofi, che il senso e l’esperienza siano le nostre scorte nel filosofare; ma nella posizion del Copernico i sensi vengono a ingannarsi grandemente, mentre visibilmente scorgono da vicino, in mezi purissimi, i corpi gravissimi scender rettamente a perpendicolo, né mai deviar un sol capello dalla linea retta; con tutto ciò per il Copernico la vista in cosa tanto chiara s’inganna, e quel moto non è altrimenti retto, ma misto di retto e circolare.

SALV. Questo è il primo argomento che Aristotile e Tolomeo e tutti i lor seguaci producono: al quale si è abbondantemente risposto, e mostrato il paralogismo, ed assai apertamente dichiarato come il moto comune a noi ed a gli Il moto comune è
come se non fusse.altri mobili è come se non fusse. Ma perché le conclusioni vere hanno mille favorevoli rincontri che le confermano, voglio, in grazia di questo filosofo, aggiunger qualche altra cosa; e voi, Sig. Simplicio, facendo la parte sua, Si confuta in altra
maniera l’argomento
preso da i
cadenti a perpendicolo.rispondetemi alle domande. E prima, ditemi: che effetto fa in voi quella pietra la quale, cadendo dalla cima della torre, è cagione che voi di tal movimento vi accorgiate? perché se ’l suo cadere nulla di più o di nuovo operasse in voi di quello che si operava la sua quiete in cima della torre, voi sicuramente non vi accorgereste della sua scesa, né distinguereste il suo muoversi dal suo star ferma.

SIMP. Comprendo il suo discendere in relazione alla torre, perché or la veggo a canto a un tal segno di essa torre, poi ad un basso, e così successivamente, sin che la scorgo giunta in Terra.

SALV. Adunque, se quella pietra fusse caduta da gli artigli d’una volante aquila e scendesse per la semplice aria invisibile, e voi non aveste altro oggetto visibile e stabile con chi far parallelo di quella, non potreste il suo moto comprendere?

Onde si comprenda
il moto di un
cadente.

SIMP. Anzi pur me n’accorgerei, poiché, per vederla mentre è altissima, mi converrebbe alzar la testa, e secondo ch’ella venisse calando, mi bisognerebbe abbassarla, ed in somma muover continuamente o quella o gli occhi, secondando il suo moto.

SALV. Ora avete data la vera risposta. Voi conoscete dunque la quiete di quel sasso, mentre senza muover punto l’occhio ve lo vedete sempre avanti, e conoscete ch’ei si muove, quando, per non lo perder di vista, vi convien muover l’organo della vista, cioè l’occhio. Il moto dell’occhio
ci arguisce il moto
dell’oggetto veduto.Adunque, tuttavoltaché senza muover mai l’occhio voi vi vedeste continuamente un oggetto nell’istesso aspetto, sempre lo giudichereste immobile.

SIMP. Credo che così bisognasse necessariamente.

SALV. Figuratevi ora d’esser in una nave, e d’aver fissato l’occhio alla punta dell’antenna: credete voi che, perché la nave si muovesse anco velocissimamente, vi bisognasse muover l’occhio per mantener la vista sempre alla punta dell’antenna e seguitare il suo moto?