7
The Wonder of it All
When Alice was in the Looking-Glass land, Tweedledee recited a poem for her:
The Walrus and the Carpenter
Were walking close at hand;
They wept like anything to see
Such quantities of sand:
‘If this were only cleared away’
They said, it WOULD be grand!’
‘If seven maids with seven mops
Swept it for half a year,
Do you suppose,’ the Walrus said,
‘That they could get it clear?’
‘I doubt it’ said the Carpenter,
And shed a bitter tear.
Seven in German is sieben, the same word as for a sieve. Seven needs sifting and sorting out. If you need seven things from the shops, it is wise to make a list. ‘Seventhly’, it is said, is the most depressing word in oratory. Seven is one over the top, a bridge too far. The heptagon cannot be constructed by knowing 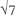 . The seventh harmonic is the poorest fit to the equal temperament scale, and the natural horn’s seventh was always problematic in classical music. The transition to romantic sound, with the whole orchestra singing as a single voice, needed the technological horn of the 1820s. In Vaughan Williams’s Third Symphony, a subtle mourning for the First World War, the horn is instructed at one point to play its natural seventh harmonic as an unintegrated, unresolved, unsmoothed sadness.
. The seventh harmonic is the poorest fit to the equal temperament scale, and the natural horn’s seventh was always problematic in classical music. The transition to romantic sound, with the whole orchestra singing as a single voice, needed the technological horn of the 1820s. In Vaughan Williams’s Third Symphony, a subtle mourning for the First World War, the horn is instructed at one point to play its natural seventh harmonic as an unintegrated, unresolved, unsmoothed sadness.
Seven is also a celebrity, with many fans: vices, virtues, league boots, year itches, and of course dwarves. My favourite celebrities are the legendary Seven Sleepers who slumbered in a cave through the whole of the fascinating fourth century. They woke up to find the world had given up all the stories, symbols and rites of what the Romans called religio. Unlike Christiane Kerner in the wonderful movie Goodbye Lenin!, who underwent a shorter coma, these troglodytic Christians were delighted by the turn of events.
But Seven is not usually so easily satisfied. Seven is the awkward customer who demands one over the odds, and comes back with the complaint that what they bought yesterday doesn’t fit after all. Seven is the number of Nature, which has so far refused to be cleared up.
Sixes and sevens
A little noted aspect of the Seven Sleepers’ time travel is that they dropped off in the old Roman world of the Ides of March and all that, and awoke on what was perhaps a Monday, or a Thursday morning. Constantine, in establishing Christianity as politically correct, had also made official the days of the week, with the dies Solis as its holiday. Astrology is the key to that cycle of seven names, which apparently have been found in Pompeii, and so known to be popular long before they were made official. An odd fact is that the old gods survived in them, despite the Church’s efforts to eradicate them, and so live on in most European languages today. It is a fair guess that the Babylonian weeks, from which the subsequent systems seem to spring, evolved because seven days roughly mark a phase of the Moon and of the menstrual cycle. The pagan planets, translated into Latin or Germanic languages, gave the cycle of Sun, Moon, Mars, Mercury, Jupiter, Venus and Saturn, and now dictate the cycle from Sunday to Saturday. Indeed, their modulo-7 arithmetic dictates the frenetic work-week and market-trading spasms of the entire globalised world.
Astrology, like magic, is a first attempt, or at least a noughth attempt, at science. Given the splendour and drama of the night sky of antiquity (compared with the tiny world of streetlamps, shop windows and mobile phones now available to megalopolitan youth), a thesis of celestial involvement in the minutiae of human doings is a perfectly reasonable noughth impression of the cosmos. More thoughtful first impressions show a tendency to find not Seven-ness but Six-ness in the basis of the cosmos, perhaps from the 360-and-a-bit days of the year, and the perfection of 1 + 2 + 3 = 1 × 2 × 3. The Mayans’ 144000-day units, the Hindu age of 432000 years, and the great age of 622080000000000 = 65 × 80 billion years are examples. Six occurs in the twelve signs of the Zodiac, the calendar months, and the Babylonian 60-based numbers from which we inherit minutes and seconds of angle, and with them the minutes and seconds of time.
But 365 is that tiresome bit bigger than 360, which spoils the perfect party. The year is not even exactly 365 days, requiring the Gregorian fix of 146097 days in 400 years so as to keep the western Christmas where it was at the time of Constantine, a few days after the solstice. (The Orthodox feast will slowly migrate into the spring, a remote consequence of his division of the Empire.) The lunar cycle pushes in its non-fitting sevens, but is itself not quite 28 days, whichever way you measure it. These baffling ratios confronted early cultures with a puzzle of a truly TRICKY standard. Finding integers to make a solar calendar is difficult enough, like the problem of fitting  , but to find a calendar that suits both Sun and Moon is as difficult as reconciling the inconsistent harmonic ratios of music.
, but to find a calendar that suits both Sun and Moon is as difficult as reconciling the inconsistent harmonic ratios of music.
As it happens, nineteen plays a role in the sacred calendar as it does in music, though for some reason this has never given it any of the glamour of Seven. (Nineteen has a famous song, but for a completely different reason.) The Sun-Moon system almost fits over nineteen years, during which the moon orbits 235 times. This coincidence determines the date of the Christian Easter, as formulated in the sixth century. The Byzantine monk Dionysius Exiguus adopted the period of 19 × 7 × 4 = 532 years as the basis of the Christian calendar, and set out a scheme of modulo-19 arithmetic for using it. This was a rare spark in the European dark age of number, while so much more important things happened in India and Persia.
Fixing the date of Easter was apparently far more important than finding historical evidence for the miracle it marks, and a similar remark could be made for the Nativity. It’s worth noting that AD1 was fixed (more or less) by Dionysius Exiguus some five hundred years after the supposed events. The gospels themselves indicate that fulfilment of prophecy counted far more than historical details, and that mathematical pattern added extra value. Stretching a point, the three wise men are the nearest thing to scientists: as following a star is physically impossible, the story must refer to the supposed power of astrological prediction. A modern-day equivalent might be a supercomputer prediction by three top intelligence chiefs. Perhaps the only reference to number factorisation by the evangelists relates Seven-ness to the tricky question of Jesus’sY chromosome. Their genealogies give two (different) descents from King David in fourteen generations—strangely through Joseph who one might suppose had nothing to do with it. Leaving aside the fascinating debates on how these ancestral lines might be reconciled, the common thread is the numerology in which the letters DVD sum to fourteen. (By chance, Bach had the same number, and probably embedded it in the B Minor Mass.) The longer genealogy goes back in 3 × 14 = 42 generations to Adam. Six and seven make a perfect multiplication.
The famous six days of the creationists likewise celebrate Seven as another augmented sixth. Adding on one to perfection allows the creator to rest on the Babylonian day of Saturn. But Nature, the awkward customer, never quite fitted the simple story. Second impressions began in that unplanned and unexpected European revolution, when mathematics made its comeback from Asia.
Sorted
Copernicus killed the classical Seven, swapping the roles of the Earth and the Sun and demoting the Moon. When Herschel identified Uranus in 1781, seven planets were temporarily restored. (Uranus had been recorded earlier, and so presumably had been seen, though not noted as a planet, by the naked eye of antiquity.) But it was not to be for long; there were puzzles in the orbit of Uranus which were solved by the observation of Neptune, thus adding an eighth. The next problem was a tiny discrepancy in the orbit of Mercury: some people thought there must likewise be a ninth planet, very close to the sun. But Einstein, in what by this count must be about the seventh impression of the cosmos, was able to explain Mercury’s orbit by a wonderful calculation from his new theory of general relativity. This superseded Newton’s law of gravity, with the gravitational constant now dictating the curvature of space-time by mass.
The triumphs of unification in physics are often emphasised: Newton for terrestrial and celestial gravity, Faraday and Maxwell for electricity, magnetism and optics. But perhaps as important is the abandonment of attempts at simple explanations for other, more complex phenomena. For astronomy this meant a slow acceptance that there is no simple law about which planets must exist. The solar system has essentially random elements in its formation, and so very complicated details governed by deeper and simpler laws of physics. Kepler had a theory that the planetary distances fitted the classical platonic solids. It was a beautiful theory, but now seen not merely as untrue, but as being on quite the wrong level on which to expect such simplicity. Newton himself probably did not accept this abandonment, being a last medievalist, a would-be Magus of the East, fascinated by patterns in historical chronology. A trace of this numerology is suggested by Newton’s inclusion of the Indian ‘indigo’ in the spectrum to augment the six to seven colours. Indigo, the blue-jeans dye that few would clearly distinguish from blue, is no more distinct a colour than cyan or yellow-green but it makes the visible spectrum parallel the seven notes from A to G.
There is continuity, not discreteness, in the spectrum of sunlight, and astrophysics now likewise sees continuity and chance in the solar system and its collisions: observations of other stars have now confirmed that it is just one of many solar systems. The line-up of nearby stars is also a matter of chance, so that the constellations, despite all the striking anthropomorphy of Orion, are random effects; the twelve-ness of signs in the plane of the solar system is a product of the eye. The patterns of nearby galaxies, clusters of galaxies and superclusters are similar. It is necessary to go further and deeper to find simple structure: back to the uniformity of the Big Bang with its just sufficient primitive fluctuations to explain the present universe’s lumpiness.
Going back to the beginning is not as long a journey as some have conceived. At 13.7 billion years, the universe has turned out ridiculously young by Hindu standards, being only about five times older than some of the DNA sequences which we are the latest things to replicate. Life could hardly have started much quicker; it only had to wait for some earlier star to explode to generate the heavy elements. Astronomy is a story of dynamic change, and even now the universe ages, expands and cools by more than 1 part in a billion during a human lifetime. The light from remote galaxies is therefore slightly dimmer than it was in antiquity.
Nevertheless, the Pleiades shine as brightly now as ever the Seven Sisters did, and as the nearest star-cluster in the galaxy, form a vital link in the huge problem of establishing astronomical distances and that 13.7-billion-year figure. Out of centuries of such meticulous and ingenious measurements come Just Six Numbers, in the title of Martin Rees’s book, which characterise the shape and form of the cosmos, and all springing from its origin. They total a tidy six: but they still present an unsatisfied Seven-ness of untidy loose ends and unsolved questions.
Six is also to be found in the fundamental physics which can be explored in terrestrial experiment. The element uranium was identified in 1789 and named in honour of recently discovered Uranus. Over the next 100 years, it was found to end a roughly periodic table of 92 apparently indestructible elements with various gaps and anomalies, but an integer pattern. Then, in the luminescence of fin-de-siècle France, Becquerel and the Curies recalled the banished transmutations of the alchemists. Breaking down the nucleus explained why atomic weights were sometimes not nearly integers (because of isotopes) and even those of pure isotopes not quite integers (because of binding energy and E = mc2). Now the zoo of 92 elements is not expected to be neat and tidy in its mathematical properties.
Instead, after another 100 years, the sprawling pages of chemical properties can at least in principle all be explained as complex effects of six pairs of more primitive beasts, three electron-like pairs and three quark pairs. As it happens, there are also six dimensions for the forces: one for electromagnetic force, two for the weak force (which has a broken two-dimensional symmetry called isospin) and three for the colour force of quantum chromodynamics. This is the Standard Model.
But—seventhly—there is the question of the masses and strengths of the particles and forces in the Standard Model. These also involve numbers, and they are not neat integers. Heigh ho! The restless materialist Morlocks have to work even on the seventh day.
Stoney ground
What are these masses and strengths? Ultimately all physical measurements are ratios just as 28 and 365 are based on ratios. Superficially, there are sixes and sevens in the statement that Newton’s gravitational constant G is about 6.6742 × 10−11 m3 kg−1 s−2. But they have no fundamental significance; this is as much a statement about metres and kilograms as about gravity, and these are arbitrary human conventions. (The metre was originally based on the distance from the pole to the equator through Paris.) By changing the units of length, mass and time, G can be made to take any value you like. You may choose units to make it 1, and the speed of light also to be 1. In 1881 the Irish physicist George Stoney realised that another natural choice could be derived from electricity. This was quite a magic guess as the electrons had not then been measured directly, but he was a fine guesser and it was he who gave the hypothetical electron its name. Using these choices, there are natural units for length, time and mass. Any other physical quantity can be expressed in terms of these units as a dimensionless ratio, a pure number.
Just such a new physical quantity arose in 1899—1900 when Max Planck defined the quantum, and thereby his own set of natural physical units. I have earlier called the Planck quantum the fundamental unit of ‘existence’. The proper technical term is ‘action’, but this meaningless word does not convey its radicalism as a four-dimensional idea. It measures a quantity of energy persisting for a quantity of time. H. G. Wells in 1896 had a preview of the necessity of a four-dimensional measure of reality in The Time Machine, where the inventor asks: ‘Can a cube that does not last for any time at all have a real existence?’ Quantum mechanics shows that it is ‘action’—not energy, but energy times duration—which comes in integer units. High energy goes with very short time, and so very short wavelengths.
The early years of the twentieth century showed how the Planck quantum related to both light and matter and explained much that was previously inexplicable. Did this unity cohere with Stoney’s units? It was not far off, but not identical either. In the early days of quantum physics, the Planck quantum seemed to be 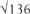 in Stoney units. Equivalently, the strength of electric charge was 1/
in Stoney units. Equivalently, the strength of electric charge was 1/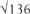 in Planck units.
in Planck units.
The mathematical physicist Arthur Eddington was particularly impressed by this integer 136. His underlying idea was that it must be fixed by timeless and logically absolute properties of mathematics, or as Eddington put it poetically in his writing for the public, God is a pure mathematician. After he had explained why it must be 136, the number turned out to be 137. Eddington famously added on one to the divine creation, and explained this augmented 136 instead. More accurate measurement has shown it not to be an integer at all, but about 137.036. This was a magic guess which did not come off.
Other people have since made guesses at a mathematical origin for this number, which is so basic to the properties of all the matter we see and touch, but as yet these have not served to give a theory explaining it. One problem with isolated formulas is that any number whatsoever could be fitted, to a good approximation, by some plausible-looking combination. It is a much denser wood for walking in than we met in fitting fractions to  . The 137 question continues to fascinate, but in a modern context it is only one item in a long menu of seven-ish problems. Foremost amongst these is why the masses are so small, as can be seen by expressing them in Planck’s units.
. The 137 question continues to fascinate, but in a modern context it is only one item in a long menu of seven-ish problems. Foremost amongst these is why the masses are so small, as can be seen by expressing them in Planck’s units.
The Planck length gives the scale of a black hole which fits inside its own quantum wavelength: this is very small at 10−33 cm, 10−20 of a nuclear diameter. In scale it relates to a nucleus as a nucleus does to a laboratory. That length scale gives a bound below which nothing sensible can be said about space-time: at this level space-time seems to break down into a froth of quantum black holes. It is a signal that some new theory, embracing both gravity and quantum theory, is needed. The Planck time, 10−43 seconds, is similar. In contrast, the Planck mass, which is the mass of such a quantum black hole, is so large that it is on the edge of our awareness. It is the mass of a speck of dust: a flea has a mass of about 4000 Planck units. By E = mc2, the corresponding Planck energy is well within the human scale: it is that of a car bomb, about 500kg of TNT.
By the standards of electrons, these are gigantic masses and energies. This observation is better put the other way: the masses of electrons are inexplicably, absurdly small at around 10−22 Planck units. Although we usually say gravity is extremely ‘weak’, it only seems so because the masses of particles are so small. Not all are as small as the electron: the proton has a mass about 1836 times greater, the neutron slightly more, but by Planck’s absolute standard these are still very small. In fact, through the success of the quark theory described in Chapter 3, the masses of the proton and neutron are no longer fundamental; the quark masses are now more relevant, and the lowest quark masses are closer to the electron mass. But this does not yet bring the scheme into a recognisable pattern, nor explain the overall small scale: the spectrum of masses still runs from neutrinos (with mass parameters perhaps 10−6 that of an electron) to the top quark (of order 105 greater than an electron).
One simplification of this picture came in the 1970s from combining electromagnetism and the weak force. But the unified ‘electro-weak’ force still requires many pieces of information to describe its properties. The neutrinos, like shadows of the electron with no charge and almost no mass, but essential to the weak force, are particularly mysterious and hard to measure.
Another important development allows the masses of all the different particles to be interpreted in terms of their interaction with a single field, that of the ‘Higgs boson’, with zero spin. This means that the mysterious overall small scale of the masses can be related to the properties of this one boson. But the Higgs boson is not seen directly and is very different from other entities in quantum field theory, so this is much more indirect and theoretical a statement. It gives new predictions and is one area where there may be major advances in the light of new experiments with the powerful Large Hadron Collider at CERN.
At present there are still some 29 numbers, counting ten for unmeasured neutrino masses, which are essentially unexplained. The colour force is perfectly symmetric but the weak force is all over the place. Not all pure mathematicians would agree, on the evidence so far, that this mess is just divine. However, Eddington’s view is not the only possible interpretation of the Standard Model: there is another in which it is not pure mathematics at all.
Meaning of life
All atoms, all the physical and chemical properties of matter, depend in a complicated way on the values of these Standard Model parameters. The properties of carbon, gases, liquids, rocks and bones are all functions of them. There are reasonable arguments that, for this reason, life forms could not be very different from those seen on Earth. I once heard a talk by John Barrow explaining this and cunningly making the number 42 appear as the key parameter. As everyone knew from the Hitchhiker’s Guide to the Galaxy, 42 gives the answer to the meaning of life. Naturally it is: the product of a perfect 6 and an awkward 7, the symbol of science.
Maybe that 42, and so human existence, comes from pure mathematics alone, as Eddington thought. But there is a radically different possible explanation. These numbers might arise as a selection effect, in that conscious beings could never see anything very different. It turns out that certain crucial features of the universe we see are strongly dependent on the values of the Standard Model numbers: having stars at all depends on that electromagnetic constant being very near that 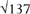 . This point of view was formalised and explored by John Barrow and Frank Tipler in the early 1980s as The Anthropic Cosmological Principle.
. This point of view was formalised and explored by John Barrow and Frank Tipler in the early 1980s as The Anthropic Cosmological Principle.
This principle suggests that the parameters of fundamental physics could have been quite different, but if they had been different there would have been no anthropos to see them. We no longer expect the solar system to be based on simple integers, but we do know it must have properties which allow life to exist on one planet, otherwise we should not see it. In the anthropic view, the important thing about 137.036 is that it defines a universe in which conscious beings can evolve to witness it.
The universe, in this view, is like just one of many possible Sudoku puzzles. But in what sense could there be ‘other’ universes, with other solutions, if the universe (in German, das All) is all there is? There are several possible versions. One is that of a creator who chose just the right values out of all those other universes that could have been chosen. Less flatteringly, we could be the by-product of some far more important experiment going on somewhere else; it might be a dry run, or a failed trial. With around a hundred billion galaxies, each with around a hundred billion stars, and with trillions of years yet to go, it is hard to imagine that it was all organised for our benefit. Others imagine game players, rather like the squabbling gods of classical antiquity, experimenting with the universe. The late humorist Miles Kington, who wrote a canny column for the British newspaper The Independent, used to supply regular updates on the committee meetings of the United Deities. Given that the Standard Model looks rather like something designed by a committee, with compromise clauses and apparently purposeless last-minute amendments, Kington’s picture might offer a clue to how it came about. But rather than assume a Designer Universe, there are other possibilities. There could be innumerable disconnected bubbles of space-time, of which our universe is just one, within a still vaster universe behind the scenes. The physical parameters would take different, random, values in each bubble. Alternatively, such universes might come into being one after another, or exist in some parallel ‘multiverse’.
The anthropic principle does not seem to me a complete answer. Even if the values of the parameters could be explained by such a selection principle, what explanation can be given for the ambient 29-dimensional space? What are the Sudoku rules to which this universe is a particular randomly generated, or divinely hand-crafted, or computer-game-played solution? Why, for instance, is there a Six-ness of the integers one, two, three for forces, and three generations of particles? Is that Six-ness some logical necessity? There might be as yet unseen connections between the parameters, and so not 29 parameters but many fewer. Or there might be more para-meters, as yet unseen because they are small or zero. It is a puzzle that the strong force, unlike the weak force, is symmetric in time: is that symmetry a random zero, a selected zero or something that must be zero? Going further, the very word ‘random’ requires some theory of a probability distribution for what the values could have been, and hence some grander theory behind the universe, analogous to the laws of physics behind the solar system.
In the dark
Recent surprises on the large scale show the danger of premature guessing.
Although the question goes back to the 1930s, it came to a head in the 1990s. The gravitational motion of the galaxies cannot be explained by the masses of their stars and other visible matter. There seems to be much more mass in them than shows up in anything visible. The consistency and detail now achieved through space telescopes and gigantic computer calculations, gives a firm picture of the existence throughout the universe of ‘dark matter’—perhaps better called transparent or invisible matter—which is still completely mysterious, as it seems to interact only through gravity. Dark matter had never been predicted as an aspect of the Standard Model. It is a real embarrassment and a warning against scientific hubris: a huge awkward Seventh form of matter to add to the neat six, which makes up as much as 90% of the total mass of the universe.
Analysis of very distant galaxies has also made it possible to measure the accelerating pace of the universe’s expansion, explicable only by a further feature of the cosmos known as ‘dark energy’. This is a completely different story, going back to Einstein, and a good example of how noughth, first, second, and third impressions of science can succeed each other, for even Einstein had to revise in light of increasing knowledge, and now ideas are being revised back again. Climate change sceptics often pour scorn on the apparent revision from questions of a forthcoming next ice age to an urgent prediction of warming; one can only say that it is the nature of science that new evidence may completely supersede the old.
In 1917, Einstein put forward a picture of the cosmos consistent with his 1915 equations for general relativity. But to fit a universe whose shape did not change with time, as then seemed sensible, he added an extra term to the equations. At that time nothing was known of the galaxies beyond our Milky Way, but in the 1920s astronomy rapidly revealed them and the overall expansion of the universe. Einstein’s original equations now fitted these discoveries much better and the motivation for the added ‘cosmological’ term was lost. Einstein is said to have described it as his greatest mistake. Nevertheless, that extra term had a good rationale: it was the one modification consistent with the principle of depending only on the absolute properties of the geometry. This extra term says that space-time possesses an intrinsic curvature: nothing to do with matter, just pure geometry. From the 1920s to the 1990s it was taken into account and regarded as a theoretically possible, but probably not significant extension of general relativity. The amazing fine detail revealed by space-telescope observations since the late 1990s points clearly to exactly this term being needed after all. The curvature involved is extremely slight, of the order of ten billion light years, but the effect is cumulative and has come to dominate the geometry of the universe at its present age.
For some reason it is thought very important not to prejudge the issue by identifying the astronomical observations as a clear confirmation of the effect Einstein allowed for. The non-commital term ‘dark energy’ is used, and much effort is made in the analysis to keep all options open. But it is to my mind misleading: the observed curvature effect is quite different, requiring a gigantic ‘negative pressure’, from anything produced by the energy of matter.
So it appears that Planck’s length of 10−33cm, identified as fundamental for over 100 years, has recently been joined by an equally fundamental 1028cm cosmological radius. There is a new duality of beginning and end, large and small, emerging from this music of the spheres. From bass to treble this range covers some 200 octaves of frequency, with a tune more like Stockhausen than Mozart, and the particles tinkling in about 40 still inexplicable octaves in the upper middle register. As it happens, the expression ‘sphere’ is apposite. The most fundamental Planck unit seems to be that of the spherical area of a Planck-mass black hole. Curvature is also naturally expressed in terms of area, so Einstein’s cosmological constant is also most naturally thus expressed. The ratio of these two areas gives a pure number of the order of 10123. At present, this gigantic number seems to be the most fundamental fact of physics, more basic than the famous 137, characterising the very nature of space-time even before particles come into it, but completely unexplained: a super-sized Seven to be sorted.
There is a further surprise: the combined effect of known matter, dark matter, and the intrinsic curvature makes the universe spatially flat on a cosmic scale. This might appear to contradict the idea of curved space-time. It does not: the four-dimensional space-time is indeed curved, and the universe everywhere is bumpy and wavy and holey with its stars and galaxies. But large-scale slices through the universe, obtained by looking at sections with the same age and temperature, seem to form an overall flat three-dimensional space. In particular, it is not the 3-sphere that would be just as consistent with Einstein’s equations. Martin Rees’s Just Six Numbers emphasises that such flatness is needed to get a long enough time for galaxies and stars to form but not to collapse. This zero spatial curvature, one of his ‘six numbers’, is an unexplained zero, and seems to be a knife-edge coincidence. The mechanism of cosmic inflation is supposed to explain this flatness as something fixed at the Planck-time age of the universe, but this cannot yet be called a complete theory.
Maybe there are surprises to be found also at the small scale.
In the quark?
The awkward Seven-ness of particles and forces suggests that there may be a deeper layer to be found. Just as the 92 elements have yielded to a simpler Standard Model of electrons and quarks, it is possible that these in turn may be reduced to a yet more fundamental level, from which the puzzling numbers can be explained. Such deeper structure is relevant whether or not an ‘anthropic’ answer is expected.
It’s like going to sea in a sieve, buoyed up by the success of earlier inspired guesses, but as yet without a basis in experiment. Stoney’s electron, Planck’s constant, Bohr’s atomic model, general relativity, quarks and much else started life on the basis of simplicity of explanation rather than on massive databases. String theory dominates this latest voyage of discovery.
The effect on mathematics is striking; to read Constance Reid’s survey of number theory in 1956 is to see how it lacked the invigoration and challenge that has come from this ever-expanding programme of research. Physicists’ voracious appetite for advanced mathematical structure has brought together aspects of new geometry and algebra that might too easily have remained isolated in tunnel vision. It has restored a kind of creative magic and adventure to mathematical vision.
Some express impatience with the fact that despite 30 years of this effervescence, no definitive explanatory theory has emerged. The prominent physicist Lee Smolin, for instance, has said that string theory should be given up. But his own suggestion is still something similar, being based on the idea which takes off from the success of general relativity: to get everything into geometry. He favours a theory of braids to explain the Six-ness of the quarks and electrons: these are stringy knots—knotted surfaces rather than knotted circles. It is hard not to make the comparison with Kelvin’s elegant (but completely wrong) theory of chemical elements as discretely different knots, before the truth was found in quantum theory. There are other ‘preon’ theories which are not based on strings. Hong-Mo Chan and Sheung-Tsun Tsou have a ‘Model behind the Standard Model’ with the idea of breaking electrons and quarks down into a deeper level, based on their Six-ness. This scheme, which reduces the number of parameters, is commended by Roger Penrose in his book The Road to Reality, in the course of criticism of the assumption that string theory in its present form must hold the answer.
The power of mathematical synthesis is such that what now look like either/or contradictions or doublethink may fade when seen in a new light. The radically different twistor description, as mentioned in Chapter 4, offers the possibility of such a new way of looking at the Standard Model. The Higgs boson description of mass has the effect of defining a theory which is in a sense a more fundamental level of the Standard Model, and which is, like light, scale-independent. The usual space-time description does not express this symmetry efficiently; nor does it express the asymmetry of the weak force well. Twistor space could be looked at more seriously as the right framework for this more fundamental level.
Often it is wrongly assumed that only light-like entities can be expressed in terms of twistors. This is not true: the point is that the breaking of conformal invariance is made explicit by twistor geometry. It is seen in the ‘line at infinity’—something finitely described by twistor space, very like the horizon in perspective drawing. The concept of a constant mass or length, as well as the origin and final shape of the universe, must go into that horizon. Witten’s use of twistors in string theory has only used the simplest connection of twistors with Minkowski space, not using their full potential. The same is true, so far, of the twistor-based system described in Chapter 4 for working out simple colour-force processes. But if there is to be serious use of twistor space, then full attention must be given to this structure ‘at infinity’, which has completely new features, different from anything in space-time. Physicists are so far understandably reluctant to adopt such an unfamiliar perspective, and place more trust in the assumed reality of space-time points. Perhaps a turn of thought greater than that of 1989, greater than that of the fourth century, would be needed.
The scientific record of the past century suggests that this chapter will soon look like faded pages from Eddington, and that another hundred years could bring a synthesis currently unimaginable. A more pessimistic reading of the historical record suggests a desertified, flooded, depleted, cluster-bombed, radioactive planet for 2107. Looking on the bright side, there are plenty more galaxies and lots of time, so the All is not lost.
The final reckoning
‘Seventhly’ is demanding enough on the reader—and ‘eighthly’ would be unbearable. I will mention only that eight-dimensional supersymmetry gives an approach to quantum gravity which seems to hold some vital clue, though still on the magic guessing level. So maybe Eight will be the number of a final unification of the Four-ness of gravity with the Two-ness of quantum mechanics. But we will turn to another and simpler Eight, again by going back to the wonders of antiquity. The sifting of the world’s intractable sand began then—quite literally, as Archimedes started to measure the universe with its grains. His Sand-Reckoner initiated the idea that has now evolved into 10123—sorting out the ratio of very large to very small.
The words Ten thousand times ten thousand, in sparkling raiment bright suggest an unusual influence in Christian hymnody, anomalous as the pagan gods obstinately resisting eviction from the days of the week. This is because that figure is not three-based but eight-based. It is the myriad of myriads which Archimedes used as the basis of his description of large numbers—far larger than the small-town vision of 144,000 in the Christian revelation. Archimedes was able to define numbers up to the myriad-myriadth power of a myriad myriads, in modern notation 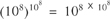 —a one followed by 800 million noughts. For the volume of the universe, Archimedes then derived a figure. The space extending out to the stars could be reckoned as equal to 1057 grains of sand.
—a one followed by 800 million noughts. For the volume of the universe, Archimedes then derived a figure. The space extending out to the stars could be reckoned as equal to 1057 grains of sand.
Astronomical numbers are generally within the range of a googol, this being defined as 10100. The googol has never actually been used in any serious context. It is famous for being famous, being quoted and requoted from one popular book to another, especially after its homonym became the business of billionaires. But it gives a reasonable picture of the scale of the material world. Such is the present reckoning, an updating of Archimedes. And the idea of reckoning leads to a new angle on numbers and the physical world. The gateway, which has also made a trillion-dollar business, is the computer, based on—
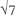 . The seventh harmonic is the poorest fit to the equal temperament scale, and the natural horn’s seventh was always problematic in classical music. The transition to romantic sound, with the whole orchestra singing as a single voice, needed the technological horn of the 1820s. In Vaughan Williams’s Third Symphony, a subtle mourning for the First World War, the horn is instructed at one point to play its natural seventh harmonic as an unintegrated, unresolved, unsmoothed sadness.
. The seventh harmonic is the poorest fit to the equal temperament scale, and the natural horn’s seventh was always problematic in classical music. The transition to romantic sound, with the whole orchestra singing as a single voice, needed the technological horn of the 1820s. In Vaughan Williams’s Third Symphony, a subtle mourning for the First World War, the horn is instructed at one point to play its natural seventh harmonic as an unintegrated, unresolved, unsmoothed sadness. , but to find a calendar that suits both Sun and Moon is as difficult as reconciling the inconsistent harmonic ratios of music.
, but to find a calendar that suits both Sun and Moon is as difficult as reconciling the inconsistent harmonic ratios of music.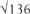 in Stoney units. Equivalently, the strength of electric charge was 1/
in Stoney units. Equivalently, the strength of electric charge was 1/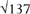 . This point of view was formalised and explored by John Barrow and Frank Tipler in the early
. This point of view was formalised and explored by John Barrow and Frank Tipler in the early 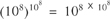 —a one followed by 800 million noughts. For the volume of the universe, Archimedes then derived a figure. The space extending out to the stars could be reckoned as equal to 1057 grains of sand.
—a one followed by 800 million noughts. For the volume of the universe, Archimedes then derived a figure. The space extending out to the stars could be reckoned as equal to 1057 grains of sand.