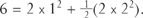. This means its outer shell of electrons is just half-complete, and it can share four electrons. Oxygen, element 8, has just two places free. Because 2 × 2 = 4, they bond in carbon dioxide.Everyone knows that two and two make four. Not everyone sees that two and two make four in several different ways:
2 + 2 = 4, 2 × 2 = 4, 22 = 4.
In short, four is the square of two. Musically, a beat of four, in two twos, gives common time. This rhythm is the first to have an internal structure, a double duality, a micro-drama to every bar. Hidden under the surface, this beat will be found in the numbers.
Squares are special. The periodic table of the chemical elements shows that the elements are built up from certain magic numbers: 2, 8, 18, 32. These numbers all come from squares: 2 × 1, 2 × 4, 2 × 9, 2 × 16, although the usual layout of the table fails to make this plain. The factor of two is the factor of spin already described in Chapter 2. Quantum mechanics is also responsible for the pattern of squares. They count the number of possible states for the electrons with the greater energies required for larger atoms.
So the chemistry of elements follows from the properties of squares. Carbon, in particular, being element 6, is just halfway along the sequence of eight that forms the second tier of elements, because . This means its outer shell of electrons is just half-complete, and it can share four electrons. Oxygen, element 8, has just two places free. Because 2 × 2 = 4, they bond in carbon dioxide.
An n × n Latin square consists of n copies of the numbers 1 to n, placed in n rows and n columns such that each row and each column contains all the numbers just once. Does this puzzle sound familiar? A Sudoku solution is a 9 × 9 Latin square, with an extra condition on the 3 × 3 subsquares.
Latin squares can be used for devising a duty roster for n dirty jobs in a houseshare of n people. Or, for comparing the effect of n drugs on n animals in some doubtless vital trial. Who said mathematics wasn’t useful? Similar ideas lead to the error-correcting codes which make it possible for computers to communicate reliably. Or, for that matter, to football leagues, speed-dating nights, and the plot lines for Desperate Housewives.
Latin squares are also connected with another kind of square, presenting an even more complicated challenge: this is the multiplication table beloved of Britian’s Department of Education.
For some reason, much emphasis is placed on children learning it in a one-dimensional sequential order, when in fact the whole point of a table is to see it in two dimensions. Rote-learning misses the vital point that a × b = b × a, which you can see at a glance in a table. This symmetry is equivalent to the fact that you can reflect the picture in the NW-SE diagonal. Another symmetry comes to light if you ignore everything but the last figure of each entry. These last figures make the pattern:
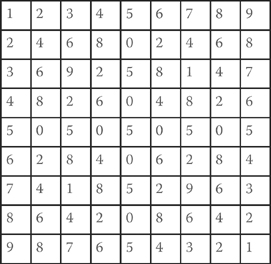
showing another symmetry on the NE-SW diagonal. This second symmetry shows up in the way the nine-times table runs 9, 18, 27, 36 … with the last figure always decreasing. Together, they give a four-fold symmetry of multiplication.
The pattern is not a Latin square, but you can find patterns like Latin squares inside it:
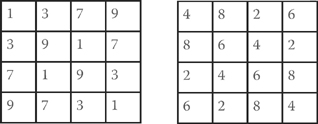
You could study these patterns of the multiplication table in any number base. There is always a four-fold symmetry. Every number base has a different pattern, which tells a story about how it breaks down into factors. In a prime number base, the whole table is a Latin square.
Gauss found a subtle pattern in the numbers appearing in the diagonal of the square, which contains the last figures of the square numbers. In base 10, these are (1, 4, 5, 6, 9). In base 8, as you can see from Chapter 1, they are (0, 1, 4). Each base has its own selection of diagonal numbers, which at first sight look completely random. It took Gauss until he was nineteen before he found the key to the pattern, which we will come to a little later. This is why the multiplication table is a rather difficult subject for eight-year-olds.
At school you’re told you must never divide by zero. So young people with any self-respect will do it to see what happens. As usual the Pet Shop Boys are right on target with Two Divided by Zero: there is a problem. The problem arises because division is the inverse of multiplication. But a multiplication by zero cannot be undone: there is a broken symmetry.
If you are a drug dealer, you are probably good at dividing things into fractions. If two customers turn up, you know how to divide your stock in two. If you have no supply and two customers, that’s also easy, if unprofitable. If you do have a supply but there are no customers, it’s impossible to get rid of it. So 1/0 has no possible meaning. If you have no supply and no customers, then you can allocate a million deals to them all and it makes no difference. So 0/0 can be anything you like.
Constance Reid dealt carefully with 1/0 and 0/0 (though not using quite the same practical illustration) in Chapter 0 of her book. But she omitted the very question that makes 0/0 so interesting: it leads to the differential calculus, which describes how continuous things can change. Newton was sinfully dividing zero by zero all the time, to create this modern idea. He was ticked off by philosophers, but his calculus still worked wonders. It was not until well into the nineteenth century that this kind of 0/0 was given a satisfactory explanation.
In this book, as in hers, such questions of change and continuity must remain off-topic. But we do need a few basic terms to extend the discussion of adding and multiplying and taking powers.
Squaring a number—multiplying it by itself—gives a first interesting example of a function. That technical word ‘function’ is equivalent to a graph, where if the value of one thing is given, the value of another can be read off. A graph turns formulas for functions into pictures which suit the two-dimensional eye.
Taking the cube of a number is also a function, and so is the nth power—multiplying a number by itself n times. There is a pattern to powers: 2m × 2n = 2m+n, and to be consistent with this, the power 0 is defined so that 20 = 1. It is also consistently true that (2a)b = 2aXb. Halving is the inverse of doubling, and it is consistent to write:.
2−1 = 1/2, 2−n = 1/2n.
Then 10−3 metres is a thousandth of a metre, a millimetre; 10−9 metres is a billionth of a metre, a nanometre.
The next step is to go from squares to square roots, which means undoing a square. A graph gives a new way of looking at the duality of doing and undoing. It turns it into a reflection in the diagonal line:
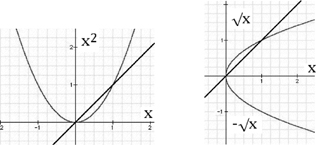
The number 4 has a square root: 2. But there is no integer which when squared gives 2. If asked for 
, a calculator will give an answer like 1.41421356, opening up a problem which we will soon put under a microscope. Another way of thinking of is this: a multiplication by is just halfway to doubling. So can be written consistently as 21/2.
GENTLE: If your shares go up 41.42%, and then increase again by 41.42%, they will (almost exactly) double.
Likewise the cube root can be seen as undoing the cube function, and the cube root of 2 written as 21/3.
This notation naturally extends so that 22/3 means the square of cube root, 2m/n the mth power of the nth root. The fuller picture involves the fact that there are two numbers whose square is 2, because (−)2 is also 2. This can also be read off from the graph. These complications fall into place when the theory is extended to complex numbers, and the graphs become surfaces in 2 + 2 = 4 dimensions!
The logarithm is another example of an inverse operation. It has a subtle relationship to roots. If b is the nth power of a, then the inverse statement is that a is the nth root of b: it answers the question, what number when raised to the nth power gives b? But there is another inverse, which arises from the question, to what power must a be raised to obtain b? The number n, which has this property, is called the logarithm to base a of b, written loga(b).
The statement that 103 = 1000 can be put in reverse by saying that 3 is the logarithm of 1000 to base 10. Likewise, because 210 = 1024, 10 is the logarithm of 1024 to base 2.
Logarithms are natural in describing the scale or ‘order of magnitude’ of a number. Roughly speaking, the logarithm to base 10 of a number measures its length when written in base 10. If you have a kiss-and-tell story to sell, and negotiate a six-figure sum, that means that the logarithm of your earnings, to base 10, lies (probably an appropriate verb) between 5 and 6.
Logarithmic charts are useful in scanning the stock market for speculative purposes. Eurotunnel shares, for instance, once went up from 500p to 1000p; now they are worth pennies. But if they now rise from 20p to 40p, that is just as good an opportunity for making a profit; logarithmic charts show this best by portraying a doubling as the same distance on the chart no matter what the price is. (If you invested your life savings in Eurotunnel, however, logarithms won’t help you dig your way out.)
Logarithms also come into the ‘magnitudes’ of stars and earthquakes. (No one seems yet to have invented a scale for celebrities.) The Richter scale is logarithmic: for every two points on the scale there is a thousand-fold increase in energy. Size 12 would destroy the Earth. If the Earth moves for you and your partner, on the other hand, the energy involved is a shock of about minus 2 on the Richter scale. A pin dropping, or a passionless peck, has the impact of a Richter scale shock of magnitude about minus 4.
Decibels and speaker gain are logarithmic. So indeed are the music notes themselves; the names ABC…, the ‘third’ and ‘fifth’ and so on, the blobs on staves, the numberings of guitar chords, are all roughly logarithms of frequency. The idea that multiplying a frequency by some ratio is equivalent to adding notes in a scale, is just the idea of the logarithm. Writing a careers advice column in the Independent newspaper, the singer Billy Bragg probably spoke for many when he said he had rejected science at school because ‘I didn’t see the point of logarithms’. But he did.
MODERATE: If a virus doubles its numbers every day, how many days does it take to increase by a million? If 22 = 4, what is the logarithm of 4 to base 2? What is the logarithm of 2 to base 4?
TRICKY: Why is log10 2 very close to 0.3?
Constance Reid wisely left alone the even naughtier question of what 00 means. According to a school maths website, ‘x0 = 1 (unless x = 0, then x0 = 0)’. The ‘rule’ that 00 = 0 has perhaps been arrived at like this: you can say that the square root of 0 is 0, and likewise 01/n = 0; so 0m/n = 0, so 0x = 0 for all x, so 00 = 0. But you could equally well argue that x0 = 1 for all x, and that it cannot suddenly jump when x becomes 0. This is a good example of the difficulties in the concepts of continuity and limits that had to be sorted out in the late nineteenth century for the calculus to make sense. The full story involves studying powers and logarithms for complex numbers, but it does not produce an answer for 00, which is as ill-defined as 0/0.
Powers and logarithms provide the Western solution to the problem of musical scales. The solution is a fudge, a creative accountancy called equal temperament, but a fiddle commended by Bach and Mozart commands respect. The secret of the equal-temperament musical scale lies in fractional powers. If twelve equal semitones make an octave, a doubling of frequency, then the semitone ratio must be given by the twelfth root of two, which is about 1.059463. If the note A has a frequency of 440 cycles per second, then B
is at 440 × 21/12, B at 440 × 22/12 and so on.
Equal temperament is another example of synthesis overcoming a deadlocked either/or. The price paid is that not a single interval, except the octave, is correctly in tune. Each one is a just-tolerable approximation. But harmony is thereby established on Western terms. Is this a familiar puzzle?
The major third is approximated by four equal-tempered semitones, giving a ratio equal to 21/3, the cube root of two. This is very close to 1.26, and so less than 1% sharp of the pure harmonic third given by the ratio 5/4 = 1.25. Equivalently, log2(5/4) is near 1/3. Put together with the eight-semitone interval, this gives the augmented triad with its three-way symmetry. Richard Strauss used this triad as the fugue subject in his 1896 tone-poem Also Sprach Zarathustra, and thereby expressed the relentless progress of cold soulless science etc. etc. etc.
The square root of two, equivalent to six equal-tempered semitones, is the interval remotest from the simple harmonics. The interval is tame as a pussy-cat when sitting in the comfy lap of the dominant seventh chord, but standing alone it is what eighteenth-century writers called the diabolus in musica, certainly the devil to sing.
An interval of three equal-tempered semitones corresponds to 21/4, the fourth root of two, about 1.189. This is to be compared with a pure minor third, with harmonic ratio 6/5 = 1.2. It differs by less than 1%. A chord of four such intervals is called the diminished seventh, exploited in classical-classical music for its melodramatic misery and unique four-way symmetry between four keys, which allows for entering it from one key and leaving in another. Mozart used this symmetry in an amazing passage, the end of the ‘Confutatis maledictis’ of his Requiem, emphasised by four dramatic bass leaps of the diabolus in musica. Probably one of the last passages he wrote, it is as free in its ever-shifting tonality as the Vier letzte Lieder (Four Last Songs) of Richard Strauss 150 years later.
Indian and Arabic musical scales have far more subtle and varied tuning solutions for melody, but it is western polyphonic harmony, like African rhythm, that has globalised, through the twelfth roots of 2. It is possible that the Arabic scale went into the Islamic African culture that, enslaved in the Americas, gave rise to blue notes. If so, the call of the muezzin, which had little impact on classical Europe, has morphed into one of America’s major cultural exports. Meanwhile European art music of the early twentieth century got carried away by twelfth roots, abandoning the base in harmonics, and drove itself into a tiny niche. But the avantgarde use of electronically generated sound in the 1960s made a great hit and rapidly found its way into popular music.
Electronic synthesis extends all options, of tonality, melody and harmony, rhythm and timbre. On the electronic scale of nanoseconds, a single sound wave takes a long, languorous age and can be constructed at leisure. Particularly popular is the construction of low sounds which, at the borderline of sonic and tactile, in pre-electronic days, needed a huge investment in vast pipes like church organs. Now you can do this in your house: hence dance music. Music technology creates sound spaces of virtually unlimited numbers of dimensions. The banks of controls and switches and MIDI channels of synthetic music are, in their prolific generosity, a picture of the huge numbers of parameters available.
The space of possibilities for sound is based on the theory of waveforms. Joseph Fourier, who founded this theory in the 1820s, developed it not for music but for the study of heat, making strong use of the duality of growth and oscillation. He also applied his theory of heat to give the first theory of the Earth’s temperature—though in those days, before infrared radiation was understood, it was only guesswork. His work gave the first suggestion of an atmospheric ‘greenhouse effect’. This illustrates the unity and unexpectedness of mathematical exploration. Science needs synthesis as well as music.
Creating sound with electronic synthesisers is not so different in principle from fooling the eye with pigments. But in the class war of the arts, the former counts for little, and the latter counts for much. A philosopher rashly claimed the Pet Shop Boys, leading expositors of synthesised sound, had made only a ‘minimal contribution’ to their music, and that ‘sound engineers’ had done it all. He underestimated these artists. They sued. He paid up. This kind of judgment overlooks the relationship between artistic composition and the mathematics of sound. Mozart also needed instrument makers who could engineer twelfth roots.
The roots of 2 are also vital for literary composition. When I was first asked to write a column about numbers for the Observer, I faced a blank sheet of paper and came up with—a blank sheet of paper. More precisely, a sheet of A4 paper, as is now used in all the non-Canadian and un-American world: it has been a German standard since 1922. The defining property of the series A0, A1, A2, A3, A4, A5 … is that each size can be obtained by cutting the larger one in half—efficient both for manufacture and for photocopying—and that they all have the same shape.
If you wanted to create such a shape, without using a calculator, how would you do it? First, suppose you are given a square of paper, and are asked to find a square with just half its area. You can do it all by folding: first find the mid-points of the sides by folding and then fold along diagonals:
Then the inner square clearly has the required property. What is the length of its side, compared with the sides of the original square? If the original square had a side of 2 units, then the inner square must have an area half of 4, which is 2, and so its side must be .
The A4 rectangle shape then comes from using the length of the diagonal as the shorter side and the side of the square as the longer side. Or, equally well, the length of the diagonal as the longer side and half the side of the square as the shorter side. You can check this by laying three A4 pages together like this:
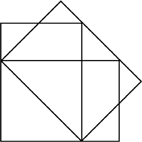
An additional property is that an A0 sheet has an area of 1 square metre. This leads to a complete formula for the size of An paper: Long side: 21/4-n/2 m, short side 2−1/4-n/2 m, area 2−nm2.
The B paper sizes are such that Bn is A(n − 1/2). Organ pipes with lengths taken from A and B paper sides will play a perfect chord of the diminished seventh. This is an example of what Wagner saw as the union of the arts.
But what, exactly, is the square root of two? So far I have avoided this question by saying it is ‘about’ some value. A calculator will give a value like 1.41421356, depending on its precision. But however many decimal places the calculator offers, what it says will never be exact. We know this because if it were exactly the decimal 1.414, for instance, it would be an exact fraction 1414/1000. But it cannot be any such ratio of natural numbers. The ancient Greek mathematicians knew this and gave a proof without the benefit of A4 paper—or decimals, for that matter. It is a famous model of logical argument involving a proof by contradiction, quoted by Hardy in his 1940 Apology as a perfect example of its kind.
The argument, like much in this chapter, depends on the fact that 2 × 2 = 4. It goes like this. Square numbers are either even or odd. If they are even then they are squares of an even number, and that means they are divisible not just by 2 but by 4. Now suppose if possible is equal to an exact fraction m/n, where m and n are not both even numbers. (If they are both even, divide both by 2 and carry on until one of them is not.) Then 2 = m2/n2, so 2n2 = m2, so m is even, so m2 is divisible by 4, so n2 is divisible by 2, so n is even. This is a contradiction. So no such numbers m, n can exist.
This shows that irrational numbers—numbers which are not ratios of integers—are inescapable in any discussion of space. It also points to wider issues, which took millennia to sort out. Is geometry a purely logical theory of the continuum of numbers, or a physical theory of space? Even Gauss does not seem to have been clear, and these concepts only gradually separated in the nineteenth century. By 1900, they were both ready for different and radical developments. The numbers, separated from physical embodiment, were ready for the logical analysis of Russell and Gödel. Physical space, separated from Euclid’s geometry, was ready for Einstein. Nowadays the conceptual distinction is clear, and yet in practice, mathematics interweaves as freely as ever. I shall let the number Four emphasise these interconnections.
How does the calculator work out its approximation? I would be surprised if it used the method for square roots that was taught in schools in pre-calculator days. This was based on the following idea: that by squaring, you find 1.4 too small, 1.5 too large, then 1.41 too small, but 1.42 too large, and so on. Although this can be usefully streamlined, it requires much laborious work. For a quicker method it is better to draw the following picture.
As you pass by a forestry plantation with a rectangular grid of trees, you may encounter avenues of light opening up in different directions. In the grid below, there are obviously vertical avenues and horizontal avenues, and there are also diagonal avenues (one up for one along) clearly visible. There are less obvious and narrower avenues corresponding to every rational slope—every slope that goes an integer m up for an integer n along. But if we take a line of slope , the argument above shows it does not have any such rational slope. However many avenues we explore, we shall never find it. If we draw such a line through one tree, at 0, it cannot pass through any other tree. Thus, on a clear day you can see forever, as long as you look in an irrational direction.
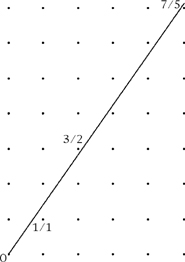
In this picture, good approximations to appear as trees which are close to the line. The fractions 1/1, 3/2 and 7/5 on the grid are the first such nearby trees. The sequence continues: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985…
Each tree gives an approximation which is about six times better than the last, as you can check with a calculator.
These are very efficient because there is a simple rule: each fraction gives the next by (m, n)→ (m + 2xn, m + n). Even better, you can jump the queue, going immediately to a point twice as far along in the sequence, by using the rule (m, n)(m2+2 × n2, 2 × m × n). This does a little better than doubling the number of correct decimal places every time you apply it.
DIFFICULT: Show that is approximately 886731088897/627013566048, correct to 22 decimal places.
The pairs of numbers (m, n) have a special property. There are no integers m, n that satisfy m2 = 2 × n2, but these pairs come as near as possible to doing it: you will find with a calculator that m2 differs from 2 × n2 by 1 or −1 alternately. The problem of finding integer solutions to equations of this kind is called a Diophantine problem, after Diophantus, who wrote a text of problems and answers in the third century CE A Killer Sudoku puzzle is an example of a simple Diophantine problem which only involves addition.
FIENDISH: See why there are not any numbers m, n, with the square of m only differing by 1 from twice the square of n, except those appearing in the sequence above.
The twelve-tone scale uses the approximations log23 = 19/12, log25 = 7/3. One can look for alternative equal-temperament scales by using a similar walk-in-the-woods picture of approximating the irrational logarithms by nearby rationals. A scale with 19 equally separated notes is the next possible candidate. It does better than the twelve-note scale with the approximation log25 = 44/19. Scales of 31 and 53 are the next possibilities, and for microtonal enthusiasts, these observations are only a glimpse of the subtleties of tonality which can be explored.
There is another way of looking at that folded square of A4 paper. It can be seen as an illustration of the theorem attributed to Pythagoras, which can be espressed as follows: given a rectangle of sides a and b, the length of its diagonal is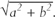 
This is perhaps the simplest thing about squares that is not at all obvious to the eye. The most famous example uses the fact that 32 + 42 = 9 + 16 = 25 = 52, and shows that the diagonal of a 3 × 4 rectangle is 5. Why is this true? From the modern point of view, in which geometry is a theory of continuous numbers, not a scientific account of physical space, Pythagoras’s theorem is a definition of what is meant by distance. So the following picture is not a proof of it, but an illustration showing that it is consistent with what we expect of squares. In this case it won’t suffice just to fold the square; it needs some surgery and rearrangement.
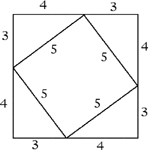
The area of the large square is 72 = 49. The four triangles at the corners can be rearranged into two 3 × 4 rectangles, and so have area 24. This leaves 25 for the inner square, agreeing with its side being 5, as marked. The same argument will illustrate Pythagoras’s Theorem in general, using the fact that (a + b)2 − 2 × a × b = a2 + b2.
A classic Diophantine problem is that of finding all such triples of integers (a, b, c) such that a2 + b2 = c2. Mark Haddon’s popular novel The Curious Incident of the Dog in the Night-Time gives an astonishingly long discussion of it. Here are some puzzles about other related patterns:
DIFFICULT: The following figures are right-angled triangles that have two sides nearly equal: (3, 4, 5), (20, 21, 29), (119, 120, 169), (696, 697, 985) … Find a rule for finding more of these. (Hint: this is closely related to the approximations for .)
MODERATE: Another famous story about the young Gauss is that when told at school to add up all the numbers from 1 to 100, he did it quickly by seeing a pattern. In Killer Sudoku you often need to know and use the sum of the numbers 1+2+3+4+5+6+7+8+9. One way of seeing it is to draw it as a triangle
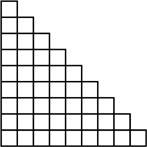
By putting two triangles like this together show that the sum is ½(9 × 10) = 45. Then show that the numbers from 1 to 100 add up to 5050.
FIENDISH: The triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 … Of these, 1 and 36 are also square numbers. What other triangular numbers are also square? (Hint: this is also closely related to the approximations for .)
There is a Diophantine equation which is very simple to write down, but is famous for resisting centuries of attack. This is the equation of the great seventeenth-century mathematician, Pierre de Fermat: an + bn = cn. When n = 2 there are many solutions given by Pythagorean triples. But squares are special: there are no solutions for higher powers. That is, as Fermat asserted, there are no two cubes which sum to a cube, no two fourth powers that sum to a fourth power, and so on. It is famous mainly because Fermat apparently claimed a marvellous proof of this fact, but gave no indication of what it was except that it was too long for the margin of his edition of Diophantus. Fermat was not always right, and we would now say it was almost certainly only a conjecture, which like Poincaré’s could only be justified very much later. It was proved by Andrew Wiles only in 1995, using advanced ideas in algebraic geometry of which the walk-in-the-woods gives only the faintest glimpse, and with which few mathematicians are familiar.
Another Diophantine problem leads in a different (and easier) direction. If you draw a rectangle with sides a and b which are integers, then a2 + b2 is usually not a square integer, so the diagonal will have an irrational length. We can draw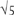 
as the diagonal of a rectangle with sides 1 and 2. But 
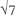cannot be formed immediately in this way. Which square roots can arise as the diagonal of a rectangle, and which can’t?
In other words, which numbers are like 2 and 5 in being sums of two squares? The answer is far from obvious: it lies in looking at the prime numbers and the music of common time, a beat of four.
Count off the numbers to a four-four rhythm: ONE two Three four | FIVE six Seven eight | NINE ten Eleven twelve | THIRTEEN … Then we have on-beat odd numbers and offbeat odd numbers. It turns out that their properties are sharply distinguished. Apart from 2, the prime numbers divide into on-beat (5, 13, 17, 29, 37…) and off-beat (3, 7, 11, 19, 23, 31…). There are infinitely many of each kind. The on-beat primes can always be written as the sum of two squares: 5 = 22 +12, 13 = 32 +22, 17 = 42 + 12, 29 = 52 + 22, 37 = 62 + 12 … The off-beat primes can never be so represented. This was discovered by two great mathematicians: announced by Fermat in 1640, but with a proof first published by Leonhard Euler, Gauss’s predecessor, 100 years later.
Gauss’s discovery about the diagonals of multiplication tables is a key to this deeper level to the numbers. It is useful first to think of those multiplication tables in another way. The cell that says 1 is the last figure of 3 × 7 also says that if you multiply any number ending in 3 by any number ending in 7, the result is a number ending in 1. The table is really about these classes of numbers, which are called congruence classes. Two integers are said to be congruent (modulo 10) if they end in the same figure. Equivalently, two integers are congruent (modulo 10) if they differ by a multiple of 10.
In the same way, all odd numbers are congruent to each other (modulo 2), and all even numbers are congruent to each other (modulo 2). The on-beat odd numbers are those that are congruent to 1 (modulo 4), and the off-beat odd numbers are congruent to 3 (modulo 4).
You are already familiar with congruence classes (modulo 7) from the days of the week. If the 1st of January is a Wednesday, what is the 30th of January? Because 30 is congruent to 2 (modulo 7), the question is the same as asking which day of the week the 2nd of January falls on, which is a Thursday.
Now we can state Gauss’s discovery in terms of congruences. Take two primes p, q, not 2. Consider the multiplication table for numbers modulo p, and the table for numbers modulo q. If p and q are both off-beat, either p (modulo q) appears in the diagonal of the q-table, or q (modulo p) appears in the diagonal of the p-table, but not both. If one of p or q is on-beat, then either they both appear in each other’s diagonals, or both are absent.
This is called the Law of Quadratic Reciprocity: the name reflects that it is an intricate duality of dualities. It shows that the primes form a hidden infinite Sudoku of consistency, all fitting in with each others’ diagonals.
Numbers which are built up by multiplying on-beat primes (and 2) also have the sum-of-two-squares property. For instance 5 and 29 are on-beat primes, and 145 = 29 × 5 also has the two-square property because 145 = 64 + 81 = 82 + 92.
There is a way of seeing why this is so. When the number 2 makes an appearance, the complex numbers are quite likely to lurk behind the scenes. The two-square property means that on-beat primes can be thought of as factorising into complex integer pairs: thus 5 = (2, 1) × (2, −1), 29 = (5, 2) × (5, −2). From this point of view they are not actually primes at all!
In this light, we can look again at their product 145 as (5, 2) × (5,-2) × (2, 1) × (2,-1) = ((5, 2) × (2, 1)) × ((5, −2) × (2,-1)) by reordering the complex factors this can be expressed as= (8, 9) × (8, −9) = 82 + 92.
In fact, this completely answers the question of which numbers are the sum of two squares: all numbers which break down entirely into on-beat primes. The underlying algebra can also be expressed by a formula that doesn’t mention complex numbers:
(a2 + b2)(c2 + d2) = (a × c − b × d)2 + (a × d + b × c)2.
At this point we go into fourth gear, and speed up. It turns out that every integer can be written as the sum of just four squares. There is also a corresponding formula:
To save space I have left out multiplication signs. The important feature is the pattern of plus and minus signs. It does not have the symmetry you might expect. Although it is a picture of a hidden double duality that lies inside the sequence of integers, it does not break the numbers into two pairs. It breaks that symmetry and exploits a deep but easier fact: 2 × 2 = 1 + 3.
Does a sum of four squares have some analogue of the factorisation of a sum of two squares into complex numbers? It does indeed: it can be thought of as splitting into quadruplets called quaternions. In Dublin, a plaque bearing the date of 16 October 1843 marks where the Irish mathematician William Hamilton ‘in a flash of genius discovered the fundamental formula for quaternion multiplication’. But the quaternion multiplication that Hamilton discovered is not like the multiplication of numbers. The splitting of 2 × 2 = 1 + 3 reflects the fact that multiplying quaternions is like combining three-dimensional rotations.
This moment in Dublin marks a milestone in the process of writing new symbols for entities going beyond numbers. Hamilton’s work was also of great importance for starting the description of physical systems in terms of spaces of possibilities, such as Poincaré later used, and which turned out to be vital to quantum mechanics.
This may seem abstruse, but quaternions have a direct application. They are needed for the huge industry of computer games or, if you prefer, animated training software like Brain Surgery for Beginners. Three-dimensional graphics need three-dimensional rotations, and quaternions code them efficiently. A more macho example would be the efficient handling of roll, pitch and yaw in aircraft or spacecraft. In the coding of rotations by quaternions, there is a pernickety point to observe. If Q is a quaternion coding a rotation, then −Q codes the same rotation. It is an inconvenient Two, but there is no getting rid of it: it is so.
That Two has a meaning. It is just the same as the Two-ness defining electron spin. That connection turns out to be highly significant, and so does that 2 × 2 = 1 + 3. A splitting of four into one and three is so familiar that it might go unnoticed. It is there implicitly in a statement about a date and place in Dublin: there is one dimension of time, and three dimensions of space. The next step in exploring the number Four requires some investigation of how time and space are connected.
H. G. Wells’s 1895 novel The Time Machine was not really about time at all, but about class society, with more than a hint of how arts-educated persons, parasitic on science and technology—the world of the subterranean Morlocks in his story—might one day get come-uppance. Nevertheless, Wells wrote a very striking introduction to the scientific concept of time as a dimension. ‘There is no difference between Time and any of the three dimensions of Space except that our consciousness moves along it,’ explains the fictional inventor, showing ‘a portrait of a man at eight years old, another at fifteen, another at seventeen, another at twenty-three, and so on. All these are evidently sections, as it were, Three-Dimensional representations of his Four-Dimensioned being.’ Ancestral trees are a simplified form of what Wells was suggesting, showing the time dimension as if it were a space dimension. Perhaps Wells was influenced by seeing the first reels revolving in a cinema, turning space into time.
But time is not the same as space. Something new and different has to come in, and that is what Einstein provided just ten years later. Pythagoras’s Theorem is still the key.
First we must see how Pythagoras’s Theorem extends from two to three space dimensions. As an example, suppose you are smuggling ancient Peruvian artefacts out of that country. You have a carved rod of length 13.5 units, and a rectangular box of length, width and height given by 12, 3 and 4 units. Obviously the rod will not fit in the box lengthwise, but can the other two dimensions be used to make room for it? We need to know the length of the complete diagonal of the box, i.e. the distance of a corner from the most remote opposite corner. Except when moving furniture through narrow doors, you may well not have had much cause to think about how such lengths are related. The answer comes from applying Pythagoras’s theorem twice. First, see that the small faces of the box have a diagonal of 
units. Now, take a rectangular slice through the box based on this 5-unit diagonal, and the 12-unit length of the box. The diagonal of this slice, which is the complete diagonal of the box, is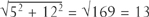 
units. Fortunately for Peru, the rod will not fit. In general, for a box of sides a, b, and c units, the complete diagonal has length 
units.
Although for simplicity I cunningly chose lengths (3, 4, 12) which ended up with an integer value for the complete diagonal, we are now thinking of lengths which may take any value. With this in mind, here are two useful formulas which show a pattern:
x2 + y2 = 1 is the equation of a unit circle: a one-dimensional space sitting in two dimensions. It accounts for all the points (x, y) that are at distance 1 from (0, 0).
x2 + y2 + z2 = 1 is the equation of a unit sphere: a two-dimensional space sitting in three dimensions. It accounts for all the points (x, y, z) that are at distance 1 from (0, 0, 0).
The natural next step is to write:
x2 +y2 + z2 + w2 = 1 is the equation of a unit 3-sphere: a three-dimensional space sitting in four dimensions. It accounts for all the points (x, y, z, w) that are at distance 1 from (0, 0, 0, 0).
This is the 3-sphere already mentioned in Chapters 2 and 3, but now given a definition. A practical use for this four-dimensional measure of distance comes in applying it to the 3-space of rotations parameterised by quaternions. A computer game could use it to roll something smoothly from one position to another.
A measure of distance is called a metric. There are many possible metrics on a space. If you are a supermarket chief you might, however unhealthily, want to give more weight to chocolate bars than to lettuce and muesli when choosing a metric on stock-control space. For the three-dimensional colour space, the question of a metric correctly measuring how close one colour seems to another would be a serious and difficult question in experimental psychology.
But what is the right metric for one physical dimension of time (t) and three of space (x, y, z)? Which metric is respected by the laws governing matter and forces? In H. G. Wells’s picture, t is said to be just the same as x, y, z. If this were true then the measurement of distance should treat them alike, as t2 + x2 + y2 + z2. But time is plainly not just the same as space: The Time Machine is fiction. It turns out that there is a simple difference between fiction and fact. The right expression is: t2 − x2 − y2 − z2. That simple change of plus signs to minus signs is an enormous, radical step. By making that splitting of four into one and three, it expresses the Theory of Relativity.
The M-I-N-I-M-A-L contribution of the PSB has it right: ‘ … light and shade, time and space.’
The word ‘relativity’ has given rise to endless sermonising on twentieth-century moral relativism, the loss of absolute authority etc. etc. etc. It is a pity that this word became the keynote, because Einstein did not introduce the idea that ‘everything is relative’ at all. On the contrary, he showed how to give an absolute meaning to crucial physical ideas, which until then had seemed to depend on how you looked at them.
You may find it convenient to run 10km relative to a moving treadmill mat. Psychologically, the daytime television and air-conditioning of a gym may be very different from the breezes, birdsong and traffic hazards of a 10km road run. But the principle of the treadmill is still sound, because it is the principle of relativity. The physical effort you must make is essentially the same: it does not depend on what is going on around you or how you look at it. The problem for physicists before Einstein was that they could not see how to extend this basic idea to electricity, magnetism and light. These were beautifully unified with each other, but the unified theory was not consistent with Newton’s laws.
Einstein achieved this extension by abandoning a Newtonian assumption which had always seemed natural, but was in fact unwarranted. If two people synchronise their watches, then move around in different ways, and then meet up again, will their watches agree? They will not. This is not a question about making accurate watches—we can assume them perfectly accurate. It is a question about the existence of a universal time that all perfect watches will tell. There is no such time co-ordinate.
‘At this moment of time’, anchorpersons say, to an audience ‘out there’. To illustrate the difficulty of defining a universal time, something which defines ‘this’ moment of time at all places, imagine the breakfast show broadcast to the whole solar system. Far out there, near Jupiter, when astronauts catch Earth News, what are they to make of ‘this’ moment in time? They must allow for the time taken by the radio signal, which travelling at the speed of light takes several hours—but how many hours depends on their distance. The natural way to measure that is by sending yet more radio signals—just like police speed cameras making radar measurements of speed and distance, only on a larger scale. To establish time and distance requires a system of sending signals back and forth and doing calculations, and in no way is ‘this moment of time’ a primary, fundamental observation of reality. It is the signal itself that is fundamental; this is electromagnetic, and travels at the speed of light. The light-signal becomes the foundation of Einstein’s theory.
Once this assumption of a universal time is dropped, the problem of ‘relativity’ disappears. The laws of electricity, magnetism and light, including the constant speed of light, are just the same whether you do experiments while running on a treadmill, or while running along a road. They become absolute laws, which do not depend on how you look at them.
Einstein’s radicalism succeeded where others had shrunk back. Even Poincaré had failed to cut the Gordian knot. But it was not Einstein who gave the first statement of that simple metric in four dimensions which embodies and streamlines his ideas. This was done in 1907 by the mathematician Hermann Minkowski. His formula stated an absolute measurement of the separation between two events, (0, 0, 0, 0) and (t, x, y, z). The rule is this: you take t2 − x2 − y2 − z2. If this is positive, its square root gives the absolute time difference between them. If it is negative then 
gives the absolute spatial distance between them. If it is zero, then they are separated by a light ray, and are thus in immediate contact by a light signal. Minkowski said, ‘Space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.’
It is more usual to write the rule using c2t2 − x2 − y2 − z2, where c is the speed of light. I have simplified it by assuming the use of units such that c is 1. If space is measured in feet and time in nanoseconds this is almost exactly right, and worth thinking about. Light is usually thought of as incredibly fast—a second from the Earth to the Moon. But for computer engineering, it is the slow speed of light that dominates everything. It forces the miniaturisation of computer chips, for which a nanosecond is nowadays a painfully long epoch. Computers now make a trillion operations in a second, so light crawls less than a millimetre when one is made, and this is why the chips must be tiny. For anything involving time coordination to this degree of accuracy, such as the Global Positioning System for navigation, engineering must absorb Minkowski’s metric. The idea of ‘now’ lingers on poetically like the four-squareness, four corners, or four winds of a flat Earth. It is adequate for everyday purposes where light seems instantaneous, just as for many purposes it makes no difference that the Earth is round. But for anything serious, the correct metric must be used.
We are all doing time travel. For we all travel into the future. Yet some travel faster than others. Minkowski’s metric implies that the closer you get to the speed of light, the faster you travel into the future. In principle you can get to the year 802,701 to see if Wells’s dystopia will come true—but unlike his time traveller, you cannot then return to tell the tale to spellbound listeners. That is because time is not the same as space; it has only one dimension and it leaves no room to turn round and come back.
Unfortunately, fantastic accelerations (and so fantastic rocket science) are needed to achieve any significant effect. If you could run round at a circuit at 98% of the speed of light (like particles sent round cyclotrons) then after what seemed to you ten minutes, the rest of the gym would have experienced 50 minutes. To get 800,000 years ahead of the rest of the world, while only living a normal span of life, would require acceleration to 99.999999995% of the speed of light.
The so-called ‘twin paradox’ makes a puzzle out of this. The ‘paradox’ is supposed to be that if you are whizzing round relative to the gym, the gym is whizzing around relative to you, and that the argument can be applied in reverse. This misunderstanding comes from misguided talk about everything being relative. Acceleration is not a relative but an absolute concept. Far from being paradoxical, and far from heralding moral laxity, the lesson of Minkowski’s metric is a very Victorian ethic: you get ahead only with hard work.
By modern standards, the Earth’s wobbly rotation is far too irregular for telling the time. The second is defined by atomic clocks, and Earth-time has to be adjusted now and then by a ‘leap second’. The atomic clock depends on electrons and protons being absolutely reliable clocks, thanks to constant rest-masses. That rest-mass is the m in that most famous formula with a square: E = mc2. Here E stands for energy, c for the speed of light, so the formula asserts that there is an equivalence between mass and energy.
Nowadays, that equation is seen as just one aspect of adopting Minkowski’s metric. It is not the whole story, but is valid for isolated, non-interacting point particles, often called ‘dust’. If you are a desperate house-spouse, then you may like to think of the meaning of the equation as you do your socially atomised housework. Dust settles in houses at about 6mg/m2 every day; for a room of 10m2 this is 60mg in a day. E = mc2 tells you that if this were converted to explosive energy it would yield about 5 × 1012 joules, equivalent to about 1000 tons of TNT. It is a curious fact that the explosion of a gram of TNT has the same energy as a calorie of the kind you count or don’t count for diets. It also releases about the same energy as a bang measuring (−2) on the Richter scale. So your room collects 109 calories of dust, enough to feed 400,000 people. It would power a similar number of light-bulbs, or make a tremor measuring 4 on the Richter scale.
This is fun to work out but also as unlikely as a plot in (dare I say?) the third series of Desperate Housewives. Quantum mechanics—more correctly, its extension to Quantum Field Theory—places severe restrictions on how mass and energy can be traded. It is like a barter economy where you can only trade in a rather limited line of goods. This conversion to energy could only be complete in the unlikely event of half of the dust actually being anti-dust made of anti-matter, perhaps shed by visiting aliens dropping by.
Richard Feynman, the American physicist and mathematician in the Second World War nuclear bomb project, did much to create quantum field theory in the aftermath. He devised an exact accounting system for the barter of energy. Feynman diagrams, as they are called, could well be described as ‘Feynman accounts’. They are book-keeping accounts, making sure that energy balances, but also stories, telling you what happens to particles and forces. With time running up the page, here are three typical Feynman accounts, examples of the very limited possibilities for trade.
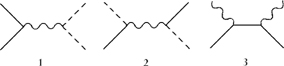
(1) Dust to dust, ashes to ashes, with an electromagnetic interaction between them (2) Dust to ashes, ashes to dust, with a weak interaction between them which can change the type of particle (3) Dust and anti-dust annihilate, leaving electromagnetic energy. In these accounts, ‘dust’ and ‘ashes’ stand for quarks or electrons of some flavour.
These basic meetings and partings build up into the more complicated orgies of interaction that occur in actual experiments when particles collide.
In units such that c = 1, the famous formula is just E = m. This robs it of its glamour, but says something simple and right. What you see in a particle, as its rest-mass, is the most you can possibly get out of it. There is no secret store of energy inside. As with other aspects of ‘relativity’ this is actually more absolute than pre-Einstein physics. To be more precise, Einstein did not actually write E = mc2 in 1905, but he got within an ace of asserting this absolute and finite measure of potential energy.
Before Einstein’s observation, exchanging energy was rather like going shopping: you could pop out and trade small bits and pieces, but no one had any idea what a house was worth. E = mc2 tells you what the capital value of a particle is, and that it can buy a huge load of shopping. But it can only be tested by selling up and moving—actually changing from one rest-mass to another—and this needs the weak force which transmutes particles. In 1905 this was still poorly understood, but Einstein had a good guess: ‘The mass of a body is a measure of its energy-content … it is not impossible that with bodies whose energy-content is variable to a high degree (e.g. with radium salts) the theory may be successfully put to the test.’ For Forty years later that test was successfully made.
Nuclear bombs are not a direct consequence of realising the simple truth of E = mc2. They also need the quantum mechanics of the nucleus. Arguably, E = mc2 might not have been needed: the exponentially growing uranium-235 chain reaction could conceivably have been discovered without a full understanding of mass and energy. Certain uranium ores in Gabon formed a natural nuclear reactor two billion years ago; these might have shown the way. But in practice E = mc2 did pave the way to nuclear fission. And Einstein himself started things off by writing to President Roosevelt in 1939 about the danger posed by German access to uranium. Thus began the superpower.
Popular science books also often say that Einstein’s 1905 theory did not account for accelerations, but only dealt with constant motion. This is nonsense: his theory specifically concerned the accelerations induced by electromagnetic forces. What was missing in 1905 was a consistent account of gravity, and this is what Einstein supplied ten years later as the general theory of relativity. Again, the word ‘relativity’ is misleading. Far from ‘everything being relative’, Einstein’s theory started out from the principle that physical reality cannot depend on how it is described, only on its absolute characteristics. It should be like classic Sudoku, pure pattern, independent of names.
Finding such absolute characteristics is not as easy as it sounds. The full theory of curved four-dimensional manifolds had taken decades for Gauss’s successor Bernhard Riemann and others to work out. But it is not too difficult to see the general idea from the way that navigators use charts of the Earth’s surface, making corrections for its curvature when calculating distances. Riemann’s work showed how all such corrections could be brought systematically into a more general kind of Pythagoras’s Theorem, still based on squaring. General relativity then incorporates and supersedes another famous square, Newton’s inverse square law of gravity.
In this picture, gravity is not a force at all. Instead, the Earth’s mass curves the geometry of space-time in such a way that the Earth’s surface is always accelerating upwards at 9.81 m/sec2 and so presses on your feet. Weight doesn’t exist, but the Earth’s electromagnetic forces push harder on fat boys than on slim. This sounds crazy, but it is no crazier than the fact that if you steam straight ahead on a sphere you will end up back where you started. Such things are made possible by curvature.
Gravity, as space-time curvature, affects everything alike, and has a mutually attractive effect because there is no such thing as negative mass. That gives it a One-ness quite unlike electromagnetism with its cancelling plus and minus charges. A single particle only makes the most imperceptible change in the curvature of space-time, but gravitational effects are cumulative, and for a large body its One-ness outweighs and overwhelms the Two-ness of electromagnetism.
Yet the most important number involved in gravity is not One but Four. There are two ways to see why. One is to learn the quite tricky theory of curvature which was worked out by Gauss’s successors. The other, a little easier, is to lie on the beach. Then you will notice the common-time rhythm of the tides every day: in, out, in, out. If you can see why the tides play a rhythm of four you are doing pretty well, because Galileo got the answer wrong.
If you made the very intelligent guess that it is four because there are four dimensions of space-time, you are, unfortunately, also wrong. The Four of the tides is a quite different Four. But the way that those fours coincide gives general relativity its very special character, in particular with the emergence of black holes where matter disappears from view and time comes to a dead stop. Einstein never believed in the reality of black holes; but his theory was more right than he was.
The structure of space-time, as elucidated by Einstein, could be called ‘only a theory’, but after nearly a hundred years it is as completely verified as anything in science. The effect of gravity in acting like a lens in intergalactic space is now as real as anything else in astronomy. A new space experiment is currently verifying the very subtle and small effect due to the Earth’s rotation. Black holes are often described as mysterious objects found in space which baffle astronomers. This is the reverse of the truth: black holes were described in detail and extremely well understood before astronomical observations indicated that they actually exist. This understanding has relied on taking Einstein’s theory far beyond its base in observations, but so far this extrapolation has been completely justified by new discoveries. Even so, physicists still find it hard to adjust to the universe as a full-scale curved space-time; it is all too natural to think of it as flat, needing merely minor corrections.
One reason why it is hard to adjust to four-dimensional space-time as a unity, as Minkowski wanted, is that it is hard to square with the apparent advance and asymmetry of time, so closely connected with the appearance of consciousness and freedom of will. There seems to be more to time than a minus sign. Minkowski wrote that time and space could be related by the square root of minus one, but although this points correctly to the emergence of complex numbers in modern theory, this doesn’t help the reconciliation with conscious experience. It is even more difficult when time and space are muddled up inextricably in a curved manifold. Einstein’s equations treat space-time as a big lumpy cake, in which time and space directions behave alike. Yet a conscious being seems to experience life like sliced bread, with one damned thing after another, and an intense asymmetry of future and past.
There is another missing link. Complex-number quantum wave functions do not, as they stand, fit into Einstein’s account of gravity. Nor is it clear how Planck’s quantum of existence, which applies alike to forces and particles, should extend also to the ripples of space-time. There are some incomplete pictures of how gravity and quantum mechanics combine. Stephen Hawking found a theory of how black holes can evaporate through quantum mechanics, and this suggests a connection between gravity, entropy and the quantum measurement operation. The ideal of a unified field theory, a theory of everything, as Einstein himself hoped for, still seems remote. But a deeper structure may emerge in some unexpectedly simple way. Hope springs four-dimensionally.
Where might this deeper structure lie? Since the 1950s, ideas about time and space have moved even further towards thinking of light rays as primary. The rays at a point of Minkowski’s space-time form a two-dimensional space, already introduced as the sphere of sight, or the sky. This is where the quaternions come back into the picture. The key idea is to combine them with Minkowski’s observation about relating space and time by the square root of minus one. When this is done, they show how light ray directions can be thought of in a much simpler way. The sphere of sight can be identified with the complex numbers.
This should recall the electron with its spherical space of quantum states. This is the right connection, because the complex numbers perform an amazing double duty: they can define light ray directions and define electron states. This very unobvious structure, linking relativity and quantum mechanics in four dimensions, is rather like the hidden four-based structure of the integers.
These ideas use the equation 2 × 2 = 1 + 3 in reverse, finding a secret Two-ness in the one-plus-three of space-time. There is a much more radical step, which exploits this undercover connection to the full. It was discovered in the 1960s by the British mathematician Roger Penrose, at about the same time that he showed why the formation of black holes from collapsing stars was an inescapable aspect of general relativity. He gave his discovery the name of twistor space.
A complex number can label the sphere of light rays arriving at one point. To describe the space of all light rays, consider a light ray as a streak across space-time, and imagine that its track is actually visible. Choose any two points in space-time, and take a photograph of the sky at each. The track of the light ray will show up as a point on each of the skies. Each point determines a complex number, and the pair of complex numbers then gives an elegantly M-I-N-I-M-A-L description of the light ray. It is rather like the principle of surveying, or of binocular vision. The way that the brain receives a picture from each of two eyes, and puts them together, gives a rough picture of the Four-ness of twistor space.
There is a further step to take. To represent not a light ray, but a quantum photon, an extra ‘twist’ is required. It is achieved by a natural extension of twistor space to four complex numbers: this is a new Four, not connected in any simple way with the original four of time and space. The duality of electricity and magnetism, with its rhythm of four, is also naturally connected with these four dimensions.
There are two different ways of making this extension from light rays to quantum photons, a left-handed and a right-handed way. Choosing one rather than the other means breaking the symmetry of space and time. Twistors are therefore asymmetric and so the weird asymmetry of the weak force may have a more natural expression in a twistor-based theory of physics. In fact, Penrose always hoped to use twistor space not just as another description of space-time, but to replace space-time as the fundamental description of reality.
Behind this two-blue-skies research there are strange, almost surreal ways of looking at spaces to discover hidden symmetries. Back in the 1960s there was a weekly British television comedy show, a sort of genteel precursor of Monty Python’s Flying Circus, called It’s a Square World. At the time of the first manned space missions, it had a sketch where the astronauts looked out to see, to their surprise, a square world—or more precisely, a cube world. The kind of projection or perspective drawing that turns a sphere into a cube is a bit like the surreal transformations which bring to light unexpected properties of the physical world.
A simple example is that of dilation or change of scale. Putting a magnifying glass to a light wave—expanding both space and time by the same factor—gives a light wave of longer wavelength; it still looks like light. This is a size-doesn’t-matter property which also applies to some aspects of gravity. It expresses something deep about the world which is more primitive than the metric—it does not need protons and electrons as clocks. One of Penrose’s many ideas is that this hidden ‘conformal’ symmetry is fundamental, even though it is broken by gravity and by the restmass of particles. The symmetry is made transparent in the twistor description.
The primary importance of light rays has been accepted generally in the development of fundamental physics since the 1950s. But few people took much notice of the extension of this idea to twistor space. In the opinion of vast majorities, the united theory of everything was expected to emerge from something quite different. This, also starting in the 1960s, was string theory. The fundamental idea is that if a quantum entity has a structure based on a line, rather than a point, then its track in space-time traces out a picture which is not like a tree, but a two-dimensional surface. This gives the possibility of uniting two (or more) kinds of Feynman accounts into one, very roughly:
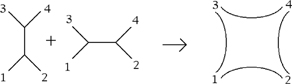
Strings gave a new way to put two and two together and make four. For some 30 years an enormous amount of work has gone into exploring these ideas, hoping to unite gravity and quantum field theory, and also to show the observed particles arising as harmonics played on this string instrument. But there was no apparent connection with Penrose’s twistors. One reason for this is that twistors are absolutely based on the number Four, whilst string theory rejects the four-dimensionality of space-time, demanding that there must be further hidden dimensions.
But in 2003, the leading mathematical physicist Edward Witten drew together strings and twistors in a new geometrical picture, and applied them to something else: the colour force. Physicists had encountered considerable difficulty in analysing the three-based interactions of the colour force, but Witten showed how twistor geometry could usefully cut through the complexity as well as suggesting something more fundamental. For most physicists, unlikely to know anything about twistors, this was something very new.
It was also a revelation for me, because I had for some time been trying to express quantum field theory in twistor geometry, but had not realised how close the structures I had found were to the colour force problem. Essentially, the colour force can take the place of light, and instead of twistor space charting the possibilities for photons, it can do the same for the ‘gluons’ of quantum chromodynamics. One very important factor is that the conformal symmetry of the colour force is exploited in the twistor description, and this greatly simplifies the calculation of how it interacts.
I began writing this book in Canada, during a visit to the Perimeter Institute, Waterloo, Ontario, where I was explaining these new pictures of the colour force. They result from taking the Feynman accounts, and translating them into twistor geometry using ideas which Penrose initiated long ago. They look remarkably like strings built out of squares.
This is a twistor picture of four interacting colour forces. It shows the trading of spin and colour rather than of energy, and makes a string-like surface rather than a network of lines:
In more complicated interactions, millions of Feynman accounts boil down to sewing squares into a quilt, of which an example is:
The expression coded by these pictures involves supersymmetry. In fact it needs four dimensions of supersymmetry. This further Four-ness is another link between twistors and strings.
These twistor accounts are not a complete theory—they are somewhere on the edge of providing a new kind of physical explanation. One important remaining problem is how to account for more advanced kinds of interaction where—to draw an analogy with the more advanced type of parties—uninvited guests turn up. These correspond to loops in the Feynman accounts, and holes in strings. But my belief is that these pictures offer a good clue to a deeper structure in quantum field theory.
The two times two of the twistor picture is incomplete, because it does not yet express the full content of Einstein’s gravity. It is an inspired guess, showing how mathematical imagination can go beyond the immediate Four-ness of the world to—
