You too, Brutus? I and you, ich und du, are number one and number two. You are my equal, but you are not identical to me. Symmetry is about sameness, but the breaking of symmetry is about differences.
A perfect symmetry means that two things are effectively identical. Take a simple Sudoku and reverse it, as if seen in a mirror. The new puzzle is solved by mirror reflections of the steps used in the original problem.
Killer Sudoku shares that mirror symmetry. It has another less obvious symmetry, which is of value in solving it. The Times gives a ‘top tip’ for solutions, which is to ‘start with the smallest totals’. This is a poor hint, because you could equally well attend to the highest totals first. Low and high are related by symmetry. Any Killer Sudoku problem has a dual obtained by swapping 1 with 9, 2 with 8, 3 with 7, 4 with 6, and adjusting the sum totals likewise: the sum S for an n-cell group changes to 10 × n − S. Every tip and rule for Killer Sudoku has its dual: the fact that a two-cell 16 can only be 7 + 9 has the dual truth that a two-cell 4 must be 1 + 3. A four-cell 11 must be 1 + 2 + 3 + 5; a four-cell 29 must be 9 + 8 + 7 + 5. This hidden symmetry in Sudoku gives a picture of the symmetries to be uncovered in the infinite puzzle of the numbers.
Part of the Killer Sudoku from Chapter 1, with its dual.
A broken symmetry arises when there is enough common structure to make a comparison, and that comparison reveals differences. To consider Two-ness is to confront broken symmetries in a world crammed with them. The first is that of yes or no, true or false, the life-or-death dichotomy of Shakespeare’s famous two-letter words.
Considering how galling it is to be wrong about anything, science is quite good at recognising error and even the eating of hats. By definition, almost anything a scientist says will be superseded by a later and more complete theory. Science is a dynamic process, and it is not only about observing and interpreting data. ‘The popular view that scientists proceed from well-established fact to well-established fact, never being influenced by any unproved conjecture, is quite mistaken.’ So wrote Alan Turing, the British mathematician of whom there will be more in later chapters.
Yet Turing’s own mathematics might seem to epitomise the dogmatic yes-or-no ‘fundamentalism’ that its critics ascribe to science—and which, indeed, scientists may hold against mathematics. It lacks the flexibility of all human statements, with their irony, ambiguity, hypocrisy and deceptiveness. It leaves no room for drama-documentaries, press releases, and other grey areas at the margins of fact and fiction; no room for how you feel about Two, for a new Two, for improving the image of Two, or a more inclusive Two. The yin-yang of the Korean flag, with its many symmetries and broken symmetries, suggests a world of subtle complementarities, but mathematical symbols are defined so as to make dualities as aridly exact and inflexible as possible. ‘All is not lost’, people say, but the mathematical NOT must precisely negate the ‘all’, not the ‘lost’. That NOT (NOT A) is the same as A also requires this peculiar precision. Alan Turing suggested explaining it by saying, ‘It’s like crossing the road. You cross it, and then you cross it again, and you’re back where you started.’ But in real life, we often can’t get no such logical satisfaction. Two wrongs make no rights, and doing those things we ought not to have done is not the same as not doing those things we ought to have done.
The OR of mathematics must be identified precisely as the ‘inclusive or’: A OR B means ‘A or B or both’. An ‘exclusive or’, as in the either/or of ‘To Be or Not to Be’, needs a different symbol, usually written XOR. Sudoku logic has this precision: a four-cell group that sums to 28 is (9+8+6+5) XOR (9+8+7+4); if it is not one then it must be the other.
The world of propositional logic, which defines this either/or dichotomy, is a small precise world of Two-ness, without the ambitions or contradictions involved in defining infinite sets. But its questions are far from trivial. For instance, how many independent logical relations are needed? We could dispense with XOR by defining A XOR B as (A OR B) AND NOT(A AND B) or (A AND NOT B) OR (B AND NOT A). OR itself is redundant because A OR B can be defined as NOT(NOT A AND NOT B).
DIFFICULT: NOR can be defined so as to generate all of NOT, AND, and OR.
In computer science, the truth or falsity of a statement is stored as a Boolean variable. The term comes from George Boole, an extraordinary individualist of Victorian England who found ways to encapsulate logical arguments that had escaped Aristotle and Leibniz, the defining figures of earlier epochs. Computer ‘logic circuits’ are based on the essential duality he codified, and computers also exploit the fact that arithmetic in base 2 is very close to the logic of NOT and AND.
It might save a lot of trouble if such logical exactitude were used in legal language. But an either/or mentality is not so obviously helpful to more constructive human thought. The way computers work (or don’t work) accentuates the impression that human minds must be doing something quite different. ‘To Be or Not to Be’ is not about logic but about life and death. Boole called his logical calculus the ‘Laws of Thought’ but the love (or unlove) of life seems to know no such binary laws. How can there be anything imaginative or creative in a world of pure right and wrong?
Sudoku-solvers will already have part of the answer: there is an art to asking the right questions. The starting point lies in asking ‘Where can the nine go in this row?’ and ‘What can be in the ninth square?’, but more sophisticated questions emerge. Advanced guides to Sudoku explain quite elaborate theorems in propositional logic, aided by the efficiency of the two-dimensional eye in pattern-spotting. Chapter 1 has already shown a more serious example of such creative discovery. Gödel’s argument was entirely based on either/or logic, but showed something completely new and unsuspected.
Logic itself is open to exploration. The logic of intuition-ism, for instance, rejects the classical assumption that A OR (NOT A) is always true. It has a ‘Not Proven’ verdict as in Scottish law. Intuitionism is closer to the idea of actually doing something to prove a result, rather than the Platonic idea that ‘it is so’. Multivalued logic can embody options like the spectrum from Strongly Agree to Strongly Disagree on tireseome questionnaires. Fuzzy logic—as in search engines unfazed by spelling errors—refutes the claim that computers are incapable of coping with grey areas.
The huge area of probability and statistics should also give the lie to any claim that mathematics is concerned only with certainties. It can measure degrees of uncertainty. And speaking of uncertainty, twentieth-century mathematics has opened up a completely new picture of physical reality, shaking up logic, number and the concepts of being and not-being. This, the theory of quantum mechanics, is intimately bound up with the number Two. But first, we shall look at some more approachable dualities.
Who do you think you are? This is not a reference to the cogito ergo sum question of One-ness, nor to l’être et le Néant, but to something altogether more concrete. A BBC series of this title, stimulated by the now enormous genealogical resources available on the Web, has made a great success of presenting the powers of Two.
This is an opportunity to introduce a convention that time always runs up the page, so that some significant events look like like this:
A typical genealogy, drawn this way, is a tree with ancestral roots:
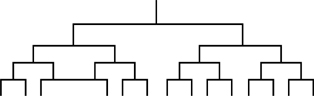
Even ignoring the problem of tracing cousins, genealogical research quickly gets out of hand if every root-line is followed. Two parents, four grandparents, eight great-grandparents and so on with 2n+2 greatn-grandparents, add up to an ever-growing problem. The index n here is a power or ‘exponent’, and the proliferation of ancestors is an example of exponential growth.
Go back some eighty generations, to the year that ought to be numbered 0, and it is obvious that the world did not have room for your 280 great78-grandparents, for that is about a trillion trillion people. The solution to this puzzle is apparent from the genealogies of royal families, where cousin marriages of various degrees are commonplace. We are all inbred in some more remote and more common way.
Exponential growth also places in question the antiquated notions of ‘a family’ with ‘a bloodline’. There has recently been much interest in ‘holy blood’—direct decendants of Jesus—but after 80 generations, ancestral DNA is diluted to one part in 280, as meaningless as a homeopathic remedy. In practice, common usage relies on the patriarchal concept of sonship being the bloodline. It is indeed the carrier of the Y chromosome, but this carries only 23 proteins. If Jesus existed, and had DNA, then there would exist cousins of some degree today, about 80 times removed, who would effectively have as much shared DNA as any direct descendants would. More realistically, DNA analysis, and the Y chromosome in particular, has led to new discoveries about the migration of ancient populations and the human relationship to other primates.
For the broken symmetry between XX and XY chromosomes, the reader is referred to literature and to religion, which applies enormous attention to the various anatomical differences of detail. The dichotomy is actually not as clear-cut as it superficially appears, for one thing because of the many gender assignment operations performed at birth. Instead, we will look at the much greater asymmetry in the vertical direction: time.
The one-dimensionality of time means that the present divides the future from the past. But ‘the’ past and ‘the’ future are puzzling concepts, depending on awareness of an ever-changing present. Historians must remember that what is now the familiar past was once the unknown future. Likewise I must remember (with the moving Now approaching the deadline) that what I am now choosing to write will soon be in the unchangeable past. Yet the asymmetry of time does not depend on choosing a Now moment. To an eternal mind seeing all time at once, the direction or arrow of time would still be distinct. This arrow is naturally connected with the idea of undoing, inverting, or reversing a process, which is one of the most basic dualities in life and in mathematics, and generally a broken symmetry.
To undo multiplication, we must divide. The idea of fractions allows for any natural number to be divided by any other. The inverse of addition is subtraction. But a large number cannot be subtracted from a small number. The Lord giveth, and the Lord taketh away, but even the Lord cannot take away that which was never given. Instead, the Lord can call it a loan, and set up a debit account. Defining negative numbers on this model creates a new symmetry of plus and minus. Indian and Arab mathematicians led the way with a negative symbol.
Again, Europe was reluctant to follow suit. It was not until the eighteenth century that negative numbers entered wholesale into mathematics, and it is hard to understand the reluctance. European culture was full of credit and debt, positive and negative. Thou art weighed in the balance and found wanting!—the Good Book is full of Good Book-keeping, with an emphasis on the negative attributes of the ungodly and their fate. Dante’s vision of the broken symmetry of sheep and goats is a picture of the integers from −9 to 9, in which Brutus languishes at the negative end. ‘Redemption’ is Latin for buying back, undoing a debt. It is naturally written −(−1) = 1 using negative numbers. But it seems that writing proved an even more difficult step than writing 0, and confusion persisted until the nineteenth century.
Negative money, though real enough as an overdraft, does not come in the form of coins. It would surely be more blessed to receive negative money than to give, yet one might, if sufficiently unethical, be tempted to throw negative money away when no one was looking. Alas, such greediness seems bound up with the desire to make the future better than the past, and so brings us back to the puzzle of the asymmetric arrow of time.
A film shown backwards (as used in special-effect sequences) shows apparently miraculous events. The dead arise, umbrellas are found. Water spurts from the plughole, fills the sink, and neatly aims itself at the tap. What is the reason for this asymmetry?
The reason for the virtual impossibility of such events runs contrary to intuition. It is not because ‘gravity pulls water down’. At the level of individual water molecules, every motion could be reversed. The impossibility arises because the large-scale splashiness of the water leads to energy being dissipated as random molecular motions—heat—in your sink. The Second Law of Thermodynamics is the principle governing the asymmetry. It says that disorder increases with time: that on the large scale, the dissipation of heat is never seen in reverse. Strictly speaking, the Second Law speaks of probabilities, but the larger the system, the closer to certainty it is.
Conversely (although not usually put this way) the Second Law says that order increases in the past, and so must be greatest at the outset of the universe. The night sky looks dark; yet deep into the infra-red it is glowing with radiation left over from its early explosion. The glow from that era is now investigated in detail by space telescopes, and its ordered uniformity is indeed a major puzzle. The totally different nature of Beginning and End to the universe is still a major mystery of Two-ness.
It is hard to reconcile the dualities of youth and age, innocence and experience, with the song of the Earth that physics sings. If disorder increases, how can genetic information evolve from primitive to more complex organisms? How can an individual increase knowledge—or money? For some reason the Second Law is often treated with particular solemnity. C. P. Snow used it as a touchstone of scientific literacy, and Arthur Eddington, who did much in the early days of relativity and quantum mechanics, put it on a pedestal of undeniability. Richard Dawkins recently repeated what Eddington said. Yet it is a very odd law, unlike anything else in physics—literally odd, dividing 2 into an asymmetric 1 + 1. Given that it seems to contradict everything in can-do philosophy, I am surprised there aren’t more neo-con skeptics.
Skeptics can be answered: the Second Law applies only to closed systems, but plants and animals are not closed. Life dices with heat-death, but manages to keep going by one chemical contrivance after another, cunningly getting rid of disorder or entropy by sending infra-red rays into space. The concept of temperature is closely bound up with entropy, and that is one reason why the question of global warming is not easily settled by common sense, nor just by measuring quantities of energy. As a matter of fact, the problems usually described as energy crises are more properly described as entropy crises. The Earth receives copious energy from the Sun; the difficulty lies in getting it into a form which is useful for human life, which means getting rid of entropy. Unfortunately, it appears that in creating this text, at the cost of computer power used, trees felled and coffee beans burnt, I am throwing out that extra CO2 which will interfere with the dumping of entropy into space.
Temperature is often used to give examples of how to use negative numbers, since one of the few places where they come into common speech is to express the iciness of the weather. But this makes a poor example of the duality of plus and minus. It depends on conventional scales, where a zero is determined by freezing water (C) or freezing salt water (F). These artificial zeroes do not mark any actual nothingness. The real absolute zero of temperature is at −273°C, which corresponds to a (notional) complete absence of motion. Absolute temperature can have no negative value.
By the end of the nineteenth century it was possible to use this concept to tell us what was happening to the temperature of the Earth. Consequently we could deduce that ‘greenhouse gases’, which prevent infra-red rays going out into space, made it about 30 degrees warmer than what it would be without them. In 1896, Svante Arrhenius, a Swedish chemist, estimated that doubling the CO2 content of this blanket would increase ground temperature by around 5 degrees. Although this is in basic agreement with modern predictions, it is an object lesson in how science can change its mind in the light of better evidence. For the first half of the twentieth century, Arrhenius was held to have made an erroneous prediction. Experiments suggested that the atmosphere was already as opaque to infra-red as it could get, so that adding more CO2 would make no difference. Only in the 1950s, using computers, was this assumption shown to be unjustified. It was also expected that the oceans would absorb any surplus CO2, and more generally assumed that the Earth’s system would keep itself in balance. Again, only detailed observation and computation in the 1950s showed these assumptions to be unjustified.
It is a natural assumption that everything has its opposite in the great yin-yang of Nature. But it doesn’t—there is no negative temperature. Mass is similar: all matter has positive mass. Nor is there such a concept as anti-gravity. But there is one perfect duality in Nature, to be found in the symmetry of electric charge.
The + and − on the ends of batteries are not just conventional signs. Electric charge gives the simplest example of where positive and negative numbers directly represent physical quantities. If you ask how anything can be less than nothing, an electron seems to say ‘look at me!’ The duality is exact: like charges repel, opposites attract, in a way that would satisfy fans of the strictest kind of nuclear family without a flicker of bi-curiosity. The duality of electrical + and − also supplies a natural binary storage medium for computers, giving another reason for using base-2 arithmetic.
Electric charge is not usually directly experienced. Shocks of static and bolts of lightning are unusual in showing its raw strength. Everything about chemistry depends on the electric charges in the atom, but it has equal numbers of positive and negative charges and their effects mainly cancel themselves out in the large—exactly because + and − cancel to give 0. We experience only indirect, second-order consequences.
Those indirect effects include the transmission of energy from the Sun, and our ability to see, because light consists of electromagnetic waves. Infra-red waves emitted by the Earth’s surface, and our bodies, are the same but of longer wavelength. They carry a greater ratio of entropy to energy, and that, quite counter-intuitively, is how life manages to struggle on. Even longer waves exist: these are radio waves, now back in fashion as wi-fi and wireless connections. Shorter waves than those of visible light arise as the sun-burning ultra-violet, and even shorter are penetrating X-rays.
The term ‘electromagnetism’ arises because the great simplification achieved in nineteenth-century physics showed that electricity and magnetism turn out to be two aspects of same thing. This is a good point to introduce Carl Friedrich Gauss (1777-1855), whose name lives on in the phrase ‘degaussing of ships’. Degaussing is getting rid of magnetism, but there would be a good use for the inverse concept of ‘gaussing’. For once Gauss had touched something, it became a lodestone for the modern world. I have already mentioned the observation of Ceres in 1801: it was Gauss who computed its orbit and who helped devise the world’s first telegraph at Göttingen in 1833. The full unification of electromagnetism and light remained a task for others, including Faraday, Maxwell and Einstein, but it was Gauss who first gave it mathematical life.
Within the unified theory of electromagnetism, there is a subtle symmetry between its electricity and magnetism; this is not at all obvious in the ingenious coils of motors and dynamos, but comes out much more clearly in light waves. It is a broken symmetry, because electrons and protons have electric charges, but nothing we know of has a magnetic charge. And the symmetry is not a simple swap of electric and magnetic forces. You must swap them and then reverse the positive and negative of electricity. This appears as a cycle (B, E) → (−E, B) → (−B, −E) → (E, −B) → (B, E) … when the conventional letters B and E are used for magnetism and electricity. This gives an enhanced slant on the duality of BEing or not BEing, but as this depends on the advanced idea of 2 × 2 it must wait until Chapter 4 for a further comment.
When cleaning your teeth in the time-asymmetric sink, you can reflect that your electric toothbrush depends upon yet another broken symmetry. This is that the universe is not symmetric between positive and negative charges: protons carry positive charge and electrons carry negative charge, but they are completely different; in particular, protons are nuclear particles 1836 times as massive as the non-nuclear electron. In wires and motors, chips and screens, the positive-charge protons are stuck in their atomic nuclei whilst the negative-charge electrons are free to wander. But that asymmetry of protons and electrons tells a deeper story.
The electron has an exact dual, the positron or anti-electron, which has positive charge—but a positive mass, the same as that of the electron. Likewise there is an anti-proton with negative charge. These and other anti-particles can make anti-atoms. There is nothing, in principle, to prevent the existence of anti-toothbrushes which would use electricity exactly the other way round (though they would only work on anti-teeth, otherwise there would be gigantic explosions). But the universe we see in the large is completely dominated by matter of one type—electrons and protons, not anti-electrons and anti-protons. The reason for this gross asymmetry would seem to lie right back at the origin of the universe, and is just as mysterious as the direction of time.
Because space is three-dimensional, it does not divide into two parts, so we do not see a left half and a right half. Indeed some people don’t have an intuitive sense of left and right. But da Vinci types apart, most people would only have to hold up this book to a mirror to be aware that there is an orientation to space.
MODERATE: Explain why a mirror exchanges right and left, but not up and down.
If you’re a dentist you may be highly aware of a broken symmetry in those left and right One to Eights, but otherwise, if you look in the mirror while cleaning your teeth, it may not be so obvious. Generally the human body looks remarkably symmetric on the outside, even if you choose to send subtly asymmetric signals for action or passion with hairstyle or piercings. But inside, the asymmetry, especially of brain function, is striking. Left, right, left, right! Walking or marching gives an on-off duality which is different from the monotony of the heart: it is the natural asymmetry from which music starts.
That broken symmetry, with more people being right-handed, is much magnified in so-dominant culture: right is associated with the number One, and anyway means correct, this being just one of those numerous crusty Indo-European r-g-t words which enshrine rules and rectitude: reign, regulate, directorship, righteousness, royalties (yes please!), Dieu et mon droit. At the right hand of the Father: the Christian creed elevates together the two broken symmetries of spatial orientation and gender. Ironically, the language of human rights has attempted to redress the balance for left-overs, the second-fiddle worlds of poverty, race and sex.
Again, although an outward and visible asymmetry in plants like twisting convolvulus is easily seen, it is less obvious that glucose, vital to metabolism, is used by biology only in one (‘dextrose’) form; its mirror image molecule is useless. A walk into Alice’s looking-glass world would leave you starving. Deep down, the DNA helix has also maintained its asymmetry over billions of years. Mirror-images of these molecules would have worked just as well but, for some reason, evolution went with one asymmetrical form rather than with the other.
You may notice a possible analogy: in each country, there is a convention about driving either on the right or on the left. (Not quite: for China is one country with two systems. Hong Kong is still on the left while the rest is on the right.) The origin of the choice typically lies in a small and arbitrary historical decision. It makes only a minor difference what the convention is, but as everyone else is using it, you must conform or die. The great biological asymmetry could likewise have arisen by small chance events, and then have become universal by the dynamics of majority rule. But it is conceivable that those events were influenced by an even deeper asymmetry, the asymmetry of fundamental physics.
This may surprise you, for it is far from obvious that the physical world is asymmetric at a fundamental level. Electromagnetism is mirror-symmetric. So is the geometry underlying gravity, and so is the strong force holding nuclei together, which will be described in Chapter 3. But the weak force, so-called, is another story. The name ‘weak’ is rather—well, weak—for the force which gives the universe so much of its character. The weak force is the transmutation force, seriously interfering with everything it touches. As such it helps keep the Earth hot inside with radioactivity and hence supplies the world’s underfloor heating of about 60Kw per square kilometre (slightly more than the world’s power consumption). This, however, is dwarfed by 5000 times more energy coming from the Sun, where again the weak force plays an essential part in turning hydrogen into helium. It is the weakness of the weak force that makes this a very slow process, and so keeps the Sun going for billions of years, giving enough time for evolution.
It is a weak but also a profoundly weird force, with an extraordinary property: it is asymmetric. The weak force knows left from right just as definitely as does a helix of DNA. This was only shown unequivocally by Chien-Shiung Wu in 1956. Her experiment, though it has never become a popular icon of science, marks a major step in the understanding of space and its Two-ness.
The weak force is now far more systematically accounted for, but its underlying asymmetry remains awkwardly expressed and without any fundamental explanation. It has another asymmetry, subtler and harder to detect: the weak force is unlike the other forces in knowing the direction of time. This asymmetry does not appear to have anything to do with the Second Law: it is an exact effect at the level of individual particles.
If you look at particle interactions in a mirror, you will see something that can’t happen in the real world. If you film them and play it backwards, again you see something impossible. There is another duality we have already noted: that of changing particles to anti-particles. Under this duality, symmetry is again broken. Yet these three broken symmetries fit together: if you apply all of them—anti-particles in a mirror, run backwards—you find an unbroken symmetry, at least for the microscopic world of colliding particles. This unbroken symmetry relies on the fundamental properties of quantum mechanics, and the Two-ness embodied in it.
If you have ever heard the word ‘duality’ used in connection with mysteries of quantum mechanics it might well be from something that is not really a Two-ness at all: so-called wave-particle duality. This is a much vaguer use of the word, not a two-fold symmetry, but rather expressing the idea that neither ‘particle’ nor ‘wave’ adequately describes what happens on the quantum level. There is, however, a direct and fundamental connection between quantum physics and the number Two, and that is the inescapable role of complex numbers. I will put forward the modern point of view, rather than the long historical groping towards them. Complex numbers are simply pairs of numbers.
If you think of a positive number as a forward march, and a negative number as taking an about-turn and marching backwards, then a complex number can be thought of as corresponding to leaving the road and turning right or left. Complex numbers extend the duality of positive and negative with a second duality. They are defined by the following rules for adding and multiplying pairs. The first rule is unsurprising, but the second is highly unobvious:
(a, b) + (c, d) = (a + c, b + d)
(a, b) × (c, d) = (a × c − b × d, a × d + b × c).
The natural numbers 1, 2, 3 … can be identified with the pairs (1, 0), (2, 0), (3, 0) … and for these, the new addition and multiplication coincides with what we had before. The same goes for the fractions and decimals: 1/2 is (1/2, 0) and π is (π, 0). It goes for negative numbers too: so (−1, 0) is the same as −1. But something new happens when the second element in the pair is used. Following the rules,
(0, 1) × (0, 1) = (−1, 0).
The pair (0, 1) behaves as a square root of minus one.
The most famous roots are in genealogy, where everyone (in the present state of genetic technology) has unique roots in parents and greatn-grandparents. But you may have no children, or may have many children, so the inverse relationship is different. With squares it is the other way round: every number has its square, but not every number has a square root.
The square of 2, 2 × 2, is 4, so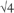 
, the square root of 4, is 2. Likewise 
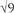= 3. If you ask your calculator for 
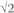, the square root of 2, you will get an answer such as 1.41421356, which we will look at in Chapter 4. But ask for 
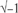, the square root of minus one, and only a highly sophisticated calculator will respond with something better than a blank look and a sad squawk. It is easy to show that there can be no number whose square is −1: the square of any positive number is positive, the square of any negative number is positive, and 0 squared is 0. This looks like the end of the argument. And yet, by going into this second dimension of numbers, allowing these complex numbers, there is a square root of −1 after all. It is (0, 1). More precisely, there are two square roots, because (0, −1) does just as well.
GENTLE: Find a square root of (−4).
The definition of complex numbers is, literally, an example of lateral thinking in mathematics. Instead of going up and down the scale of numbers, we move sideways. Thus the most logic-bound of disciplines can transcend its apparent limitations.
Addition and multiplication, as defined by the formulas above, behave just like the addition and multiplication of single numbers. In fact, the pairs behave, more perfectly than any human coupling, as if they were one number. This extension of number properties is special to Two. There is no such extension to three numbers. There is a special structure for quadruplets of numbers, which will appear in Chapter 4, but it does not make them behave like single numbers.
The extension is also perfectly complete, in that no further extensions are needed in order to get a square root of (0, 1), and the square root of that, and so on. This is a consquence of the Fundamental Theorem of Algebra, to which Gauss made a major contribution in 1799.
TRICKY: Find a square root of (0, 1). (Hint: 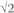is involved.)
The first and second numbers of a complex-number pair are called ‘real’ and ‘imaginary’. The ‘real’ numbers are the numbers we started with, by marching up and down a line. The ‘imaginary’ numbers then arise as the effect of turning to left and right. It is natural to plot the whole scope of complex numbers as an infinite plane, labelled by points (a, b). Amongst these, the numbers (a,0) can be called the ‘real’ numbers, and behave just like the single numbers that we started with, corresponding to real measurements. But the words ‘real’ and ‘imaginary’ are just names. There is a way of thinking of complex numbers which emphasises that the ‘imaginary’ parts also have real significance.
The term ‘positive feedback’ describes situations where an effect accentuates its cause. If ice melts, the increased area of dark water absorbs more sunlight than did the white reflective ice, and so increases the absorption of energy from the sun. Such positive feedback is also expected to arise as warmer soils release more methane and carbon dioxide.
Such an effect, in isolation, and unchecked—never the real situation—implies an escalating, runaway outcome. It increases faster and faster, doubling and redoubling like the ancestors, in fact with exponential growth. Microphone feedback squawks and compound interest are other examples of such spiralling out of control. Equally well, however, positive feedback may lead to exponential decay, in which an effect diminishes, and so does the rate at which it fades. A simple example is of radioactivity: the more atoms decay, the fewer are left, and so the radioactivity decreases. Just as the genealogy research problem doubles for every 25 years or so that you try to go back, radioactivity halves in a certain time—the half-life. In short, exponential growth or decay behaves as do the powers of ‘real’ numbers. A saying from the Gospels summarises both exponential growth and decay: ‘That unto every one which hath shall be given; and from him that hath not, even that he hath shall be taken away from him.’
But there is another situation of great importance, associated with anything that vibrates or oscillates. To-and-fro cycles naturally occur when an effect counteracts its own cause. This is negative feedback. A piano wire is like a spring: the more it is displaced, the greater is the tensile force that pulls it back: this restoring force leads to it vibrating. This is typical of behaviour near a stable equilibrium, which a piano wire exemplifies. It is the self-regulation once believed to hold for the state of the Earth. A genuine example in the context of climate change is that increased air temperature may mean more humid and so cloudier skies, which then shade the Earth (although the actual effect of clouds seems much more complicated). If such a negative feedback were the dominating feature of the atmosphere, our dear Gaia could look after herself. (The formation of rock carbonates gives a negative feedback on a geological timescale, but that will not help the coming century.) The powers of (0, 1) run in a cycle: (0, 1), (−1, 0), (0, −1), (1, 0), (0, 1) … and for this reason, any kind of rotational or vibrational motion is naturally described by the powers of ‘imaginary’ numbers.
This positive feedback leads to exponential growth or decay, and is associated with the ‘real’ axis. Negative feedback leads to oscillating cycles, and is associated with the ‘imaginary’ axis. Both effects can occur at once, and that corresponds to the pairing of real and imaginary parts in a complex number.
Economists refer to positive feedbacks as vicious or virtuous circles, depending on the desirability of the outcome. From the precarious standpoint of a polar bear, the melting of the ice is unwelcome, but it is an ill wind that blows no one any good and a sunny issue of Newsweek in April 2007 hailed the business opportunities arising from global warming. Compound interest on your debt may seem a vicious thing but to your bank it is of great virtue. Radioactive decay is a virtuous circle if you are hoping to dispose of nuclear waste, but if you were counting on polonium to poison your enemies, I suppose you would consider it vicious. But moral judgments of vice and virtue do not enter into the mathematical concepts. They have no axes of evil, square roots of all evil, or arcs of extremism. The numbers lie beyond good and evil.
Returning to reality, there is a non-obvious but pervasive duality between growth and rotation, and this is a first secret of Two. Take a soap film between two parallel circular rings, and stretch it out. Its shape illustrates the duality perfectly. Between the circular rings its shape is that of an exponentially increasing curve.
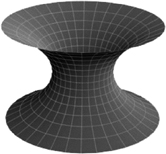
In the nineteenth century many such physical effects were encapsulated using complex-number methods. They were ready and waiting, thoroughly Gaussed, for the twentieth century. After 1900, quantum mechanics revealed that complex numbers do not just supply a method for pairing numbers and properties together; they are the actual medium in which the world works.
Quantum mechanics goes right against the either/or logic of common sense. One cannot think of an electron as an object that either is or is not at some point. In fact the ontology—the ‘To Be or Not to Be’—of electrons is a highly contentious question. They are described by ‘wave functions’ or ‘quantum states’ which are nothing like everyday objects. It is not even valid to speak of ‘two electrons’ with the usual sense of Two-ness applied to counting two separate things. There is no way of telling which is which; they are ‘entangled’ and form something more like a Two-ness of electronicity. Strictly speaking, all the electrons in the universe are entangled in a field of electronicity. But the mathematics of complex numbers can successfully cope with describing this breakdown of ordinary logic.
The strangeness of quantum mechanics is making an impact on practical yes-or-no questions of logic, information and communication. As computers get smaller and faster, they are heading towards a point where their operations will depend on very small numbers of electrons. This threatens the accuracy of the either/or binary logic, because electrons are not either/or entities.
But since the 1980s, much progress has been made towards building quantum computers, to take advantage of the very features of quantum mechanics which seem problematic. A quantum computer can use a new kind of quantum-mechanical Two-ness (a ‘qubit’) instead of the discrete yes-or-no ‘bit’ of computer logic, in a way that makes it possible to pursue many calculations at once. The related engineering of quantum communication can make constructive use of entanglement to pass information across space in a way that would be impossible otherwise. Quantum Two-ness is real, although it is not reality as we know it.
Quantum mechanics supplies the invisible infrastructure of everything we know. After 1800, vague alchemical guesswork about natures and affinities was turned into crisp laws about how chemicals combine, expressed in terms of integers. From the mid-1920s it was clear where these integers came from: the quantum mechanics of the atom. The essential mechanisms of life likewise depend on quantum mechanics. This was appreciated before the structure of DNA was identified. In 1943, the physicist Erwin Schrödinger pointed out in an essay called ‘What is Life’ that the One-ness of the quantum makes possible the encoding of enduring, reliable information. This was verified ten years later when the famous double helix was elucidated. The Two-ness of the helix is a quantum mechanical Two.
The nineteenth-century calculation of the effect of CO2 was done without knowing why it was opaque to infra-red radiation. Later, quantum mechanics explained it as a general property of larger molecules of which CO2, water and methane are examples. So it is for reasons involving the nature of electrons that global temperature is expected to increase. The fact that quantum mechanics is involved is another reason why the predictions will not necessarily coincide with intuitive convictions about the weather always being unpredictable, CO2 being good for plants, the Earth being too big for mere humans to affect it, that what goes up must come down, and so forth.
If complex numbers are so intrinsic to reality, why are we unaware of them? Why don’t we visualise complex qubits rather than Boolean bits of 0 and 1? The standard answer is that measurements break the complex numbers down into classical yes-or-no logic and real numbers. But this is far from being fully understood. How and when do measurements happen, and how are they related to the mind’s perception of the world? There seems to be perfect randomness involved in the process, but what is its origin? How is this connected with time direction, entropy and the Second Law? If quantum mechanics is about small systems, how large is small? Schrödinger devised a famous thought-experiment to ask just this: in modern terms it amounts to asking what happens when a qubit in a quantum computer is measured and turned into an either/or bit of information in an ordinary computer. Schrödinger dramatised the situation by imagining using the computer bit to kill a cat—nothing to do with real animal experiments! The question of whether the cat is To Be or Not to Be goes to the heart of this open question about Two-ness.
To look a little deeper at the Two-ness of quantum mechanics, it is handy to examine something that sighted people use all the time, but do not necessarily ever think about: the Two-ness of the sphere. Visual information comes through the Two-ness of the retina, collecting from a two-dimensional sky of light; nerves fan out to a two-dimensional skin interface with the tactile world, and the brain is largely a folded two-dimensional surface. No more than a portion of the sphere of light can be seen at once, and it is the brain’s putting together those portions of the sphere that creates our visual sense of space. It’s not obvious why animals have not developed all-round vision, analogous to hearing; if we could see from the backs of our necks we might have a different sense of space.
The complete geometry of the sphere is not so easy to grasp, for ‘up’ and ‘round’ are not precise, and East meets West everywhere. Are you sure you know why summer days are longer as you go further north? Can you guess the direction of Mecca from Hawaii? There is a particular problem with time zones at the poles, with choosing an international date line, and defining a truly round-the-world adventure. These difficulties correspond to genuine mathematical problems with describing the Two-ness of the sphere.
As it happens, the Two-ness of the sphere gives the best picture of quantum-mechanical Two-ness. Although I have described complex numbers as if on a plane, with a real and imaginary axis, a simple quantum-mechanical system is actually better described by the geometry of a sphere. This is because it is properly defined by the ratio of two complex numbers, rather than by one complex number. This is not quite the same thing and it curls up a plane into a sphere. A qubit of quantum computing can be thought of as a point on a sphere.
There is something even less obvious about spheres, which reveals a more secret aspect of Two. We return to the picture of a sphere as the sphere of eyesight. If you adopt a new point of view just by moving your head, what changes can you make in your field of vision?
You may never have noticed that this involves a three-dimensional space of possibilities. First, you can move your head to right or left, then move it up and down, to make any direction you like the centre of your field of view. Then (admittedly, with some limitations, unless you are extremely athletic) you can rotate your head while keeping constant this centre of the visual field. This makes three parameters. Some people will be acquainted with this Three-ness as roll, pitch, and yaw, the terms for the three different ways in which a ship or aircraft can rotate, but the more nautically challenged probably lack a name for them.
What is the shape of this three-dimensional space? You are familiar with it from every waking moment; it is the space of your seeing, looking, searching, probing consciousness; you actively navigate it, and yet you are unlikely to have been aware of it needing any conscious description. You are likely to be completely unaware of its shape. It is a finite space, but without any edge, so it is nothing like any three-dimensional object. It actually has almost the shape of a 3-sphere, which means the analogue of a sphere in four dimensions. In Chapter 4 I shall define this properly, but here we need only one thing, the significance of that word ‘almost’. The space of visual possibilities is actually only half such a 3-sphere.
The factor of Two is the inner secret of space, which has only been known since the 1920s, but is vital to the nature of matter. It is the two that appears in the ‘half’ when an electron is said to have a spin-half, meaning a spin of 1/2 of Planck’s quantum of existence. Here is a shoe-string experiment which gives you a way of seeing that factor of two directly.
MODERATE: Tie a pair of shoes to each other with (suitably long) shoe-laces. Now rotate one shoe completely round, so that the laces get twisted too. Rotate again, in the same direction, so the laces are doubly twisted. You will find that you can untwist the laces by passing the shoe between them, without rotating it at all. Only a double rotation can be undone like this.
Electrons are embodied in space in just such a way, as if with strings attached. This follows from their nature as complex-number entities. When given a single rotation, an electron is not back where it started: its virtual laces are twisted. Only when rotated a second time, do they become untwisted. This factor of two is consistent with saying that the electron has spin 1/2. It also gives the electron a double ration of possible states, and this factor of two is the fundamental fact of chemistry. The first place it shows up is in the inertness of helium.
The helium nucleus, emerging at 100 million degrees from fusing two protons together, is vital to the process by which the Sun pours out energy. There is another, gentler, cooler story about Two that comes from investigating helium as a chemical element, complete with its two electrons matching and cancelling the electric charge of its two protons. In the early nineteenth century it was completely unknown. It went undetected on the Earth because it is virtually inert chemically: it bonds with nothing. After the birth of quantum mechanics this complete lack of chemistry could be explained. Helium has a complete set of both of the two possible electron states, one for each state of spin, leaving it with nothing to share. This is the start of a pattern which runs through the table of the elements, and dominates their chemistry.
To say that helium is inert because it is ‘complete’ with two electrons makes an implicit appeal to the idea of there being just two places available for just two electrons. This needs to be made explicit.
Electrons cannot be thought of as objects with ‘places’. They are in ‘quantum states’, which do not correspond to anything in ordinary experience. However, there is one aspect of a quantum state which does correspond to what we expect of something called a ‘particle’: roughly speaking, a state either has one electron in it or none; it cannot have two. There is a genuine ‘To Be or Not to Be’ for electrons, called the ‘exclusion principle’. It turns out to be a logical consequence of its spin-1/2, and so of complex numbers. For the helium atom, there are just two possible states of lowest energy, one for each spin, and if these states are filled then there is indeed no room for more.
Protons and neutrons in the nucleus have the same exclusiveness, and it is this that gives matter its hard and unyielding quality. But this is not the end of the story. At the atomic level, forces also must be considered as quantum states. Electricity, magnetism and light, when interacting with electrons and protons, must be described in terms of photon states. But photons have no such exclusion principle. There can be limitless numbers in the same state: an intense laser beam gives a picture of what this is like.
Particle-like entities are called fermions (for the Italian, Enrico Fermi) and the force-like entities bosons (for the Indian, Satyendra Nath Bose). The properties of fermions and bosons are very different. Yet their equations differ only through choices of plus and minus signs. One reason for this simplicity is that they are united by Planck’s constant, the One-ness of the quantum, which has the same value for both forces and particles. In the 1970s, physicists began to express this duality by a new idea: supersymmetry.
Supersymmetry swaps those plus and minus signs. It must be a highly broken symmetry, because we don’t see any fermions related to the photon by supersymmetry. The Large Hadron Collider at CERN, the European particle laboratory near Geneva, will soon start to look for evidence of new heavy particles which, if found, would make more sense of it. But at present it remains mysterious, and shows how the logical either/or of mathematics is not the whole story. It is a new Two-ness, and different people feel different things about it. Physicists have used it to give simple proofs which, to mathematicians, don’t seem to make complete sense.
The story of Two is not finished. Negative and complex numbers seemed crazy at first. Mathematicians eventually found a consistent logical framework for them, while physicists found them in electricity and quantum mechanics. With supersymmetry, physics seems to be a step ahead. The number Two is not completely understood in itself, and needs a bigger picture of the world. The sphere of sight naturally leads us on to look at—