 and
and 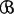 be finite or countably infinite classes such that
be finite or countably infinite classes such that  =
= 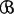 [P]. Then the following three conditions must hold:
[P]. Then the following three conditions must hold:Theorem 3-10B
Let  and
and 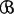 be finite or countably infinite classes such that
be finite or countably infinite classes such that  =
= 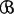 [P]. Then the following three conditions must hold:
[P]. Then the following three conditions must hold:

PROOF Condition 3 follows from condition 3 of Theorem 3-10A. Condition 1 is established by the following calculations:

since P(AiBic) = 0 for every i (Theorem 3-10.4).
Interchanging the role of Ai and Bi gives the same expression for  .
.
Now
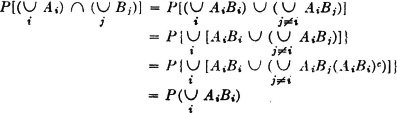
since P[AiBj(AiBi)c] = P[AiBj(Aic ∪ Bic)] = 0 for every i, j.
We have thus established the equalities required by the definition.
Condition 2 follows by considering complements, since
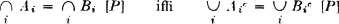
The theorem follows from conditions 1 and 3, which are established. 
Theorem 3-10C
If a finite or countably infinite class  has the properties
has the properties

then there exists a partition 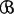 such that
such that  =
= 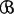 [P].
[P].
PROOF Suppose the events of the class  are numbered to form a sequence A1, A2, …, An, …. First, consider the case in which the union of the Ai is the whole space. Put
are numbered to form a sequence A1, A2, …, An, …. First, consider the case in which the union of the Ai is the whole space. Put
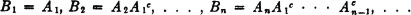
Then it is easy to see that the class 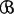 = {Bi: i ∈ J} is a partition, for the sets are disjoint and their union is the whole space. We note, further, that
= {Bi: i ∈ J} is a partition, for the sets are disjoint and their union is the whole space. We note, further, that

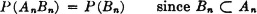
Thus the class 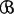 is a partition which is equal with probability 1 to the class
is a partition which is equal with probability 1 to the class  . If the union of the class
. If the union of the class  is not the whole space, we simply consider the set A0, which is the complement of this union and whose probability is zero, and take as B1 the union of A1 and A0. It is evident that in this case B1 = A1 [P].
is not the whole space, we simply consider the set A0, which is the complement of this union and whose probability is zero, and take as B1 the union of A1 and A0. It is evident that in this case B1 = A1 [P]. 
Theorem 3-10D
Consider two simple random variables X(·) and Y(·) with ranges T1 and T2, respectively. Let T = T1 ∪ T2, ti ∈ T. Put Ai = { : X(
: X( ) = ti} and Bi = {
) = ti} and Bi = { : Y(
: Y( ) = ti}. Then X(·) = Y(·) [P] iffi Ai = Bi [P] for each i.
) = ti}. Then X(·) = Y(·) [P] iffi Ai = Bi [P] for each i.
PROOF We note that if ti is not in T1, Ai = 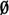 , and if ti is not in T2, Bi =
, and if ti is not in T2, Bi = 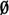 .
.
1. Given X(·) = Y(·) [P]. To show Ai = Bi [P]. Put D = { : X(
: X( ) ≠ Y(
) ≠ Y( )}. P(D) = 0.
)}. P(D) = 0.
Let  . Now on Di we must have X ≠ Y, so that Di ⊂ D. This implies P(Di) = 0 and hence that Ai = Bi [P]. The argument holds for any i.
. Now on Di we must have X ≠ Y, so that Di ⊂ D. This implies P(Di) = 0 and hence that Ai = Bi [P]. The argument holds for any i.
2. If Ai = Bi [P], then P(Di) = 0. Since 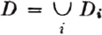 , we have
, we have 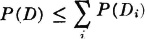 = 0, so that X(·) = Y(·) [P].
= 0, so that X(·) = Y(·) [P]. 
Theorem 3-10E
Consider two random variables X(·) and Y(·). Put EM = { : X(
: X( ) ∈ M} = X−1(M) and FM = {
) ∈ M} = X−1(M) and FM = { : Y(
: Y( ) ∈ M} = Y−1(M) for any Borel set M. Then, (A) X(·) = Y(·) [P] iffi (B) EM = FM [P] for each Borel set M.
) ∈ M} = Y−1(M) for any Borel set M. Then, (A) X(·) = Y(·) [P] iffi (B) EM = FM [P] for each Borel set M.
PROOF
1. To show (A) implies (B) we consider

from which it follows that P(A) = P(AS1) + P(AS1c) = P(AS1) for every event A. Moreover, a little reflection shows that EMS1 = FMS1 = EMFMS1 for any Borel set M. We thus obtain the fact that P(EM) = P(FM) = P(EMFM), which is the defining condition for EM = FM [P].
2. To show (B) implies (A), we consider first the case that X(·) and Y(·) are simple functions. Define the sets T1, T2, T, Ai, and Bi as in the previous theorem. Then Ai = X−1({ti}) and Bi = Y−1({ti}). By hypothesis, Ai = Bi [P], which, by Theorem 3-10D, above, implies X(·) = Y(·) [P].
In the general case, X(·) is the limit of a sequence Xn(·), and Y(·) is the limit of a sequence Yn(·), n = 1, 2, …. Under hypothesis (B) and the construction of the approximating functions Xn(·) and Yn(·), Xn−1({tin}) = X−1[M(i, n)] and Yn−1({tin}) = Y−1[M(i, n)] are equal with probability 1. Thus Xn(·) = Yn(·) [P]. If we put Cn = { : Xn(
: Xn( ) ≠ Yn(
) ≠ Yn( )}, we must have P(Cn) = 0. Let
)}, we must have P(Cn) = 0. Let 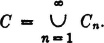 Then P(C) = 0. On the complement Cc we have Xn(
Then P(C) = 0. On the complement Cc we have Xn( ) = Yn(
) = Yn( ) for all n, so that the two sequences approach the same limit for each
) for all n, so that the two sequences approach the same limit for each  in Cc. This means that X(
in Cc. This means that X( ) = Y(
) = Y( ) for all
) for all  in Cc. Since P(Cc) = 1, the theorem is proved.
in Cc. Since P(Cc) = 1, the theorem is proved. 
Suppose X(·) and Y(·) are two nonnegative random variables. Then (A) X(·) = Y(·) [P] iffi (B) there exist nondecreasing sequences of simple random variables {Xn(·): 1 ≤ n < ∞} and {Yn(·): 1 ≤ n < ∞} satisfying the three conditions:
1. Xn(·) = Yn(·) [P], 1 ≤ n < ∞
2. 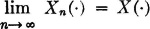
3. 
PROOF
1. To show (A) implies (B), we form the simple functions according to the scheme described in Sec. 3-3. Let the points in the subdivision for the nth approximating functions be tin. Put E(i, n) = { : Xn(
: Xn( ) = tin] and E′(i, n) = {
) = tin] and E′(i, n) = { : Yn(
: Yn( ) = tin}. By Theorem 3-10E (proved above), we must have E(i, n) = E′(i, n) [P] for each i, n, so that Xn(·) = Yn(·) [P] for every n. By Theorem 3-3A, properties 2 and 3 must hold.
) = tin}. By Theorem 3-10E (proved above), we must have E(i, n) = E′(i, n) [P] for each i, n, so that Xn(·) = Yn(·) [P] for every n. By Theorem 3-3A, properties 2 and 3 must hold.
2. To show (B) implies (A), let Dn = { : Xn(
: Xn( ) ≠ Yn(
) ≠ Yn( )}. Then P(Dn) = 0, so that, if
)}. Then P(Dn) = 0, so that, if 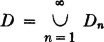 , we must have P(D) = 0. On Dc, Xn(
, we must have P(D) = 0. On Dc, Xn( ) = Yn(
) = Yn( ) for each
) for each  , n, so that
, n, so that 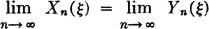 for each
for each  ∈ Dc. Thus X(·) = Y(·) on Dc, so that the set on which these fail to be equal must be a subset of D and thus have probability zero.
∈ Dc. Thus X(·) = Y(·) on Dc, so that the set on which these fail to be equal must be a subset of D and thus have probability zero. 
Theorem 6-1F
Suppose the class of random variables {Xi(·): 1 ≤ i < ∞} is pairwise independent and each random variable in the class has the same distribution with  [Xi] =
[Xi] =  . The variance may or may not exist. Then
. The variance may or may not exist. Then  for any
for any 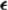 > 0.
> 0.
PROOF The proof makes use of a classical device known as the method of truncation. Let δ be any positive number. For each pair of positive integers i, n, define the random variables Zin(·) and Win(·) as follows:

First we show the Zin(·) are pairwise independent for any given n. Let
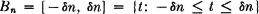
For any Borel set M, we must have
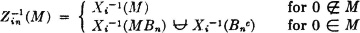
For any distinct pair of integers i, j, the pairwise independence of the variables Xi(·) and Xj(·) ensures the independence conditions necessary to apply Theorem 2-6G. We may thus assert the independence of  and
and 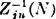 for any Borel sets M and N, which is the condition for independence of the random variables Zin(·) and Zjn(·). We may assert further that
for any Borel sets M and N, which is the condition for independence of the random variables Zin(·) and Zjn(·). We may assert further that

Hence, given any 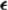 ≥ 0 and δ ≥ 0, there is an n0 such that
≥ 0 and δ ≥ 0, there is an n0 such that
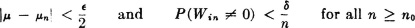
For simplicity of writing, put  . By the Chebyshev inequality,
. By the Chebyshev inequality,

Now | –
–  n| <
n| < 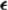 /2 and
/2 and 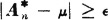 implies
implies

so that in this case
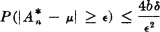
Also, for n sufficiently large,
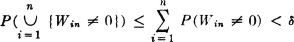
Thus, for any 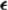 , δ, arbitrarily chosen, there is an n1 such that, for all n > n1,
, δ, arbitrarily chosen, there is an n1 such that, for all n > n1,

The arbitrariness of δ implies the limit asserted. 