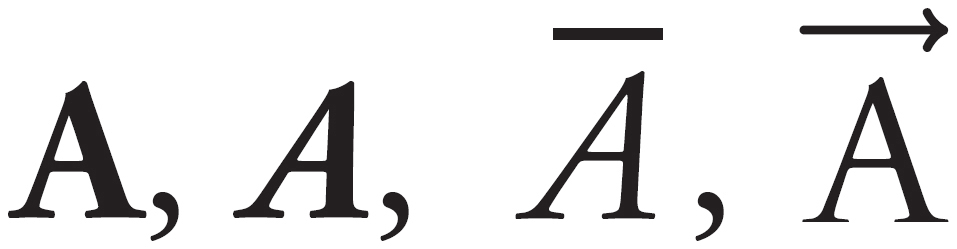
Vectors will show up all over the place in our study of physics. Some physical quantities that are represented as vectors are displacement, velocity, acceleration, force, momentum, and electric and magnetic fields. Since vectors play such a recurring role, it’s important to become comfortable working with them; the purpose of this chapter is to provide you with a mastery of the fundamental vector algebra we’ll use in subsequent chapters. For now, we’ll restrict our study to two-dimensional vectors (that is, ones that lie flat in a plane).
A vector is a quantity that involves both magnitude and direction. A quantity that does not involve direction is a scalar. For example, the quantity 55 miles per hour is a scalar, while the quantity 55 miles per hour to the north is a vector. Other examples of scalars include mass, work, energy, power, temperature, and electric charge.
Vectors can be denoted in several ways, including:
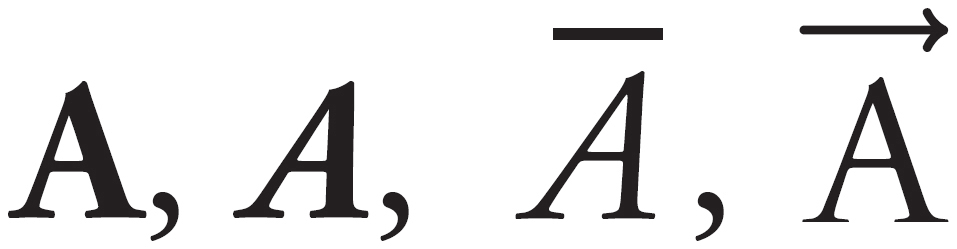
In textbooks, you’ll usually see one of the first two, but when it’s handwritten, you’ll see one of the last two.
Displacement (which is net distance traveled including direction) is an example of a vector:
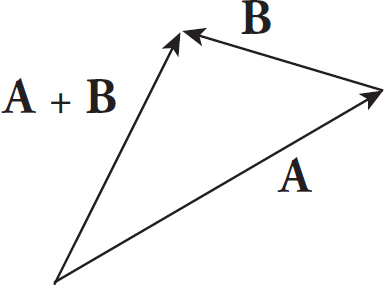
Vectors obey the Commutative Law for Addition, which states:
Commutative Law for Addition
A + B = B + A
The vector sum A + B means the vector A followed by B. The vector sum of B + A means the vector B followed by A, and the result is an identical vector to A + B. Vectors are always added tail to end to find their sum, so A + B or B + A—both are examples of tail to end.
Two vectors are equal when they have the same magnitude and the same direction.
Example 1 Add the following two vectors:
Solution. Place the tail of B at the tip of A and connect them:
Also Worth Noting!
Scalar multiplication indicates a change in magnitude by the numerical multiple, and direction if there is a negative sign only (negative sign indicates opposite direction). An example of this is that of a car travelling east at a velocity of 100 km per hour. When multiplied by k = −2, the car’s new velocity is 200 km per hour WEST.
A vector can be multiplied by a scalar (that is, by a number), and the result is a vector. If the original vector is A and the scalar is k, then the scalar multiple kA is as follows:
Scalar Multiplication
magnitude of 
(magnitude of A)
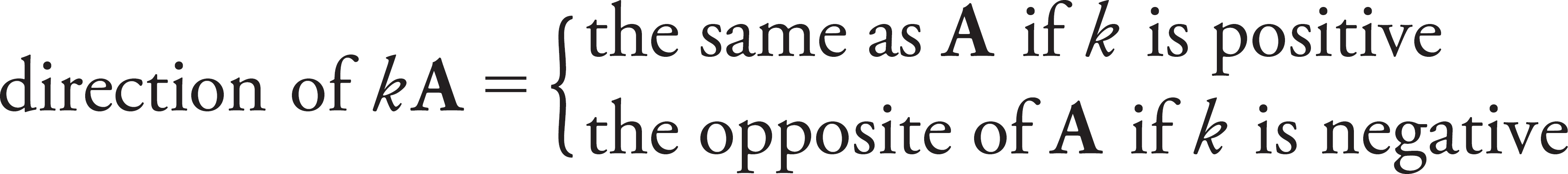
Example 2 Sketch the scalar multiples 2A, 
A, −A, and −3A of the vector A:
Solution.
To subtract one vector from another, for example, to get A − B, simply form the vector −B, which is the scalar multiple (−1)B, and add it to A:
A − B = A + (−B)
Example 3 For the two vectors A and B, find the vector A − B.
Solution. Flip B around (thereby forming −B) and add that vector to A:
It is important to know that vector subtraction is not commutative; you must perform the subtraction in the order stated in the problem.
Two-dimensional vectors are vectors that lie flat in a plane and can be written as the sum of a horizontal vector and a vertical vector. For example, in the following diagram, the vector A is equal to the horizontal vector B plus the vertical vector C:
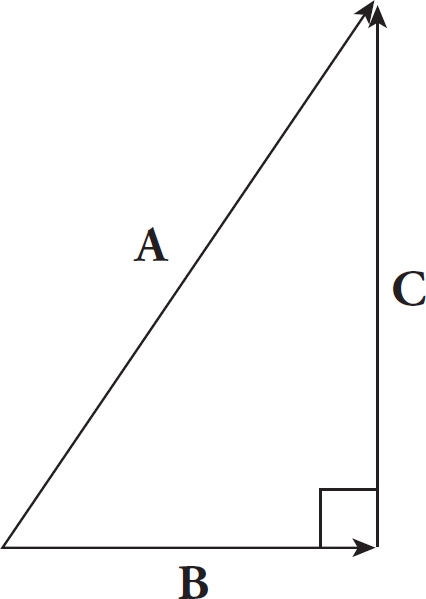
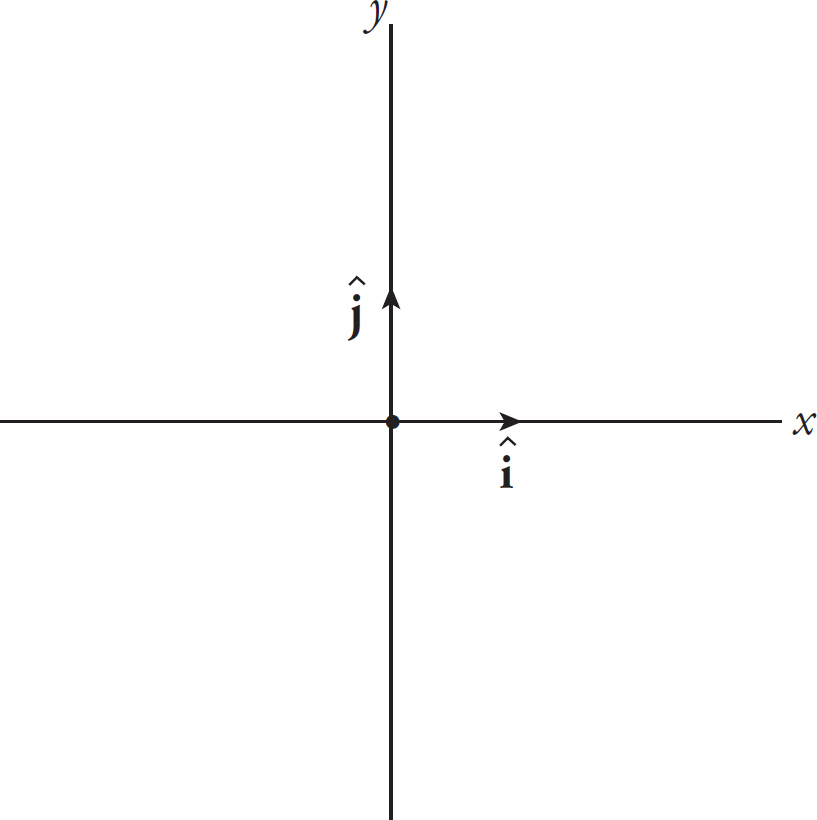
The horizontal vector is always considered a scalar multiple of what’s called the horizontal basis vector, i, and the vertical vector is a scalar multiple of the vertical basis vector, j. Both of these special vectors have a magnitude of 1, and for this reason, they’re called unit vectors. Unit vectors are often represented by placing a hat (caret) over the vector; for example, the unit vectors i and j are sometimes denoted î and ĵ.
For instance, the vector A in the figure below is the sum of the horizontal vector B = 3î and the vertical vector C = 4ĵ.
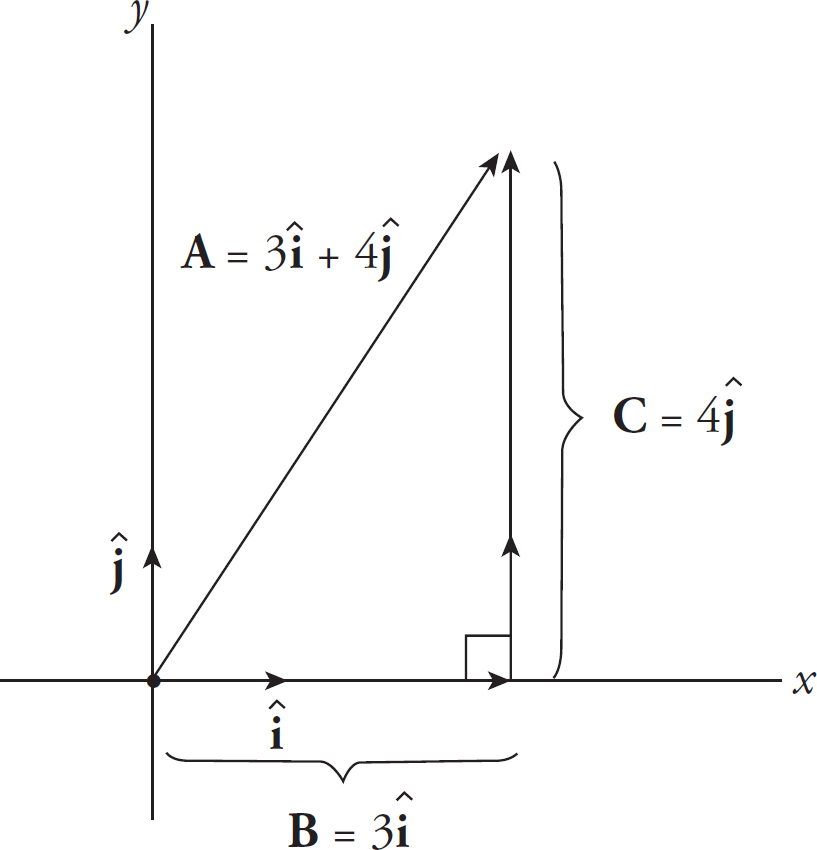
The vectors B and C are called the vector components of A, and the scalar multiples of î and ĵ which give A—in this case, 3 and 4—are called the scalar components of A. So vector A can be written as the sum Axî + Ayĵ, where Ax and Ay are the scalar components of A. The component Ax is called the horizontal scalar component of A, and Ay is called the vertical scalar component of A. In general, any vector in a plane can be described in this manner.
The use of components makes the vector operations of addition, subtraction, and scalar multiplication pretty straightforward:
Vector addition: Add the respective components.
A + B = (Ax + Bx)î + (Ay + By)ĵ
Vector subtraction: Subtract the respective components.
A − B = (Ax − Bx)î + (Ay − By)ĵ
Scalar multiplication: Multiply each component by k.
kA = (kAx)î + (kAy)ĵ
Example 4 If A = 2î − 3ĵ and B = −4î + 2ĵ, compute each of the following vectors: A + B, A − B, 2A, and A + 3B.
Solution. It’s very helpful that the given vectors A and B are written explicitly in terms of the standard basis vectors î and ĵ:
A + B = (2 − 4)î + (−3 + 2)ĵ = −2î − ĵ
A − B = [2 − (−4)]î + (−3 −2)ĵ = 6î − 5ĵ
2A = 2(2)î + 2(−3)ĵ = 4î − 6ĵ
A + 3B = [2 + 3(−4)]î + [−3 + 3(2)]ĵ = −10î + 3ĵ
The magnitude of a vector can be computed with the Pythagorean Theorem. The magnitude of vector A can be denoted in several ways: A or 
or 
. In terms of its components, the magnitude of A = Axî + Ayĵ is given by the equation
which is the formula for the length of the hypotenuse of a right triangle with sides of lengths Ax and Ay.
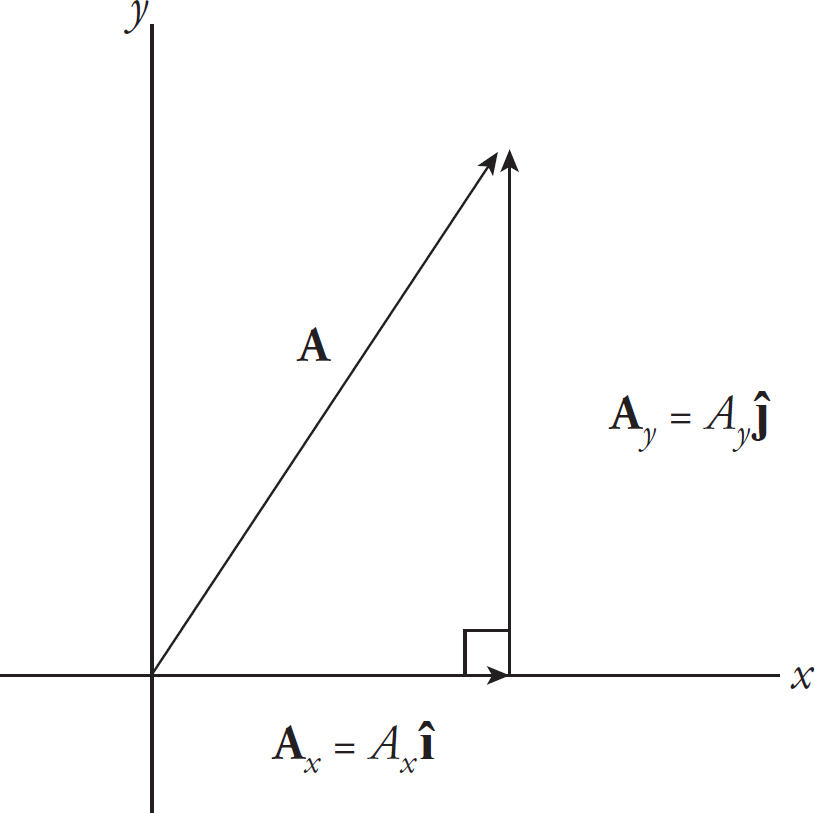
The direction of a vector can be specified by the angle it makes with the positive x-axis. You can sketch the vector and use its components (and an inverse trig function) to determine the angle. For example, if θ denotes the angle that the vector A = 3î + 4ĵ makes with the +x-axis, then tan θ = 4/3, so θ = tan−1(4/3) = 53.1°.
In general, the axis that θ is made to is known as the adjacent axis. The adjacent component is always going to get the cos θ. For example, if A makes the angle θ with the +x-axis, then its x- and y-components are A cos θ and A sin θ, respectively (where A is the magnitude of A).
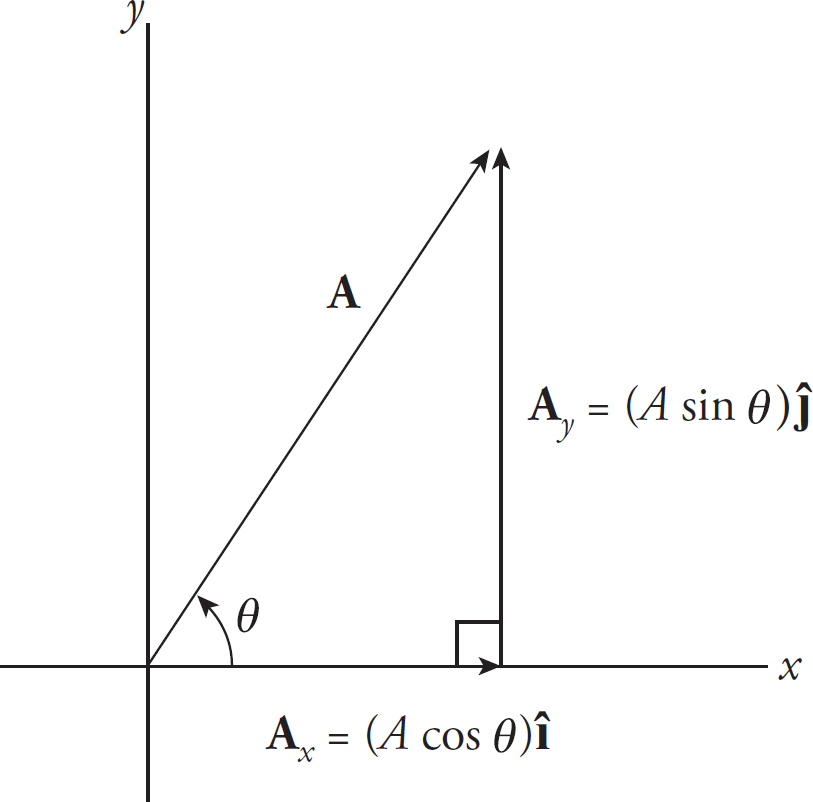
In general, any vector in the plane can be written in terms of two perpendicular component vectors. For example, vector W (shown below) is the sum of two component vectors whose magnitudes are W cos θ and W sin θ:
Answers and explanations can be found in Chapter 13.
1. Two vectors, A and B, have the same magnitude, m, but vector A points north whereas vector B points east. What is the sum, A + B ?
(A) m, northeast
(B) 
northeast
(C) northwest
(D) 2m, northwest
2. If F1= −20ĵ, F2= −10î, and F3 = 5î + 10ĵ, what is the sum F1 + F2 + F3 ?
(A) −15î + 10ĵ
(B) −5î − 10ĵ
(C) 5î
(D) 5î − 10ĵ
3. Both the x- and y-components of a vector are doubled. Which of the following describes what happens to the resulting vector?
(A) Magnitude increases by a factor of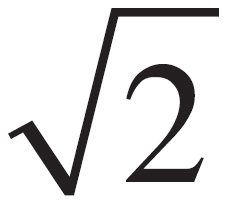 
(B) Magnitude increases by a factor of 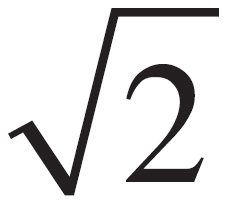and the direction changes.
(C) Magnitude increases by a factor of 2.
(D) Magnitude increases by a factor of 2, and the direction changes.
4. If vectors 
north and 
south, what is 
?
(A) 
(B) 
(C) 
(D) 
5. The magnitude of vector A is 10. Which of the following could be the components of A ?
(A) Ax = 5, Ay = 5
(B) Ax = 6, Ay = 8
(C) Ax = 7, Ay = 9
(D) Ax = 10, Ay = 10
6. If the vector A = î − 2ĵ and the vector B = 4î − 5ĵ, what angle does A + B form with the x-axis?
(A) 
(B) 
(C) 
(D)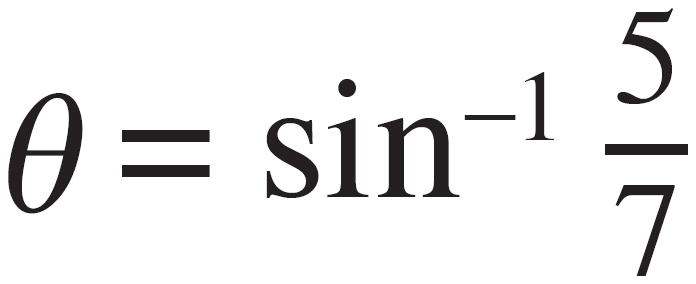 
7. An object travels along the vector d1 = 4m î + 5m ĵ and then along the vector d2 = 2m î − 3m ĵ. How far is the object from where it started?
(A) 6.3 m
(B) 8 m
(C) 10 m
(D) 14 m
8. If A = 
and B = 
, which of the following best represents the direction of A − B ?
(A) 
(B) 
(C) 
(D) 
9. The x-component of vector A is −42, and the angle it makes with the positive x-direction is 130°. What is the y-component of vector A ?
(A) −65.3
(B) −50.1
(C) 50.1
(D) 65.3
10. If two non-zero vectors are added together, and the resultant vector is zero, what must be true of the two vectors?
(A) They have equal magnitude and are pointed in the same direction.
(B) They have equal magnitude and are pointed in opposite directions.
(C) They have different magnitudes and are pointed in opposite directions.
(D) It is not possible for the sum of two non-zero vectors to be zero.
1. Let the vectors, A, B, and C be defined by: A = 3î + 6ĵ, B = −î + 4ĵ, and C = 5î − 2ĵ.
(a) What is the magnitude of vector A?
(b) Sketch the vector subtraction problem B − C and find the components of the resultant vector.
(c) Find the components of A + 2B.
(d) Express A − B − C as a magnitude and angle relative to the horizontal.
2. An ant walks 20 cm due north, 30 cm due east, and then 14 cm northeast.
(a) Assuming that each portion of the ant’s journey is a vector, sketch the ant’s path.
(b) How far has the ant travelled from its original position?
(c) If the ant does not want to travel farther than 80 cm from its original position, how march farther north could it walk?
3. Consider an airplane taking off at an angle of 10° relative to the horizontal. After 2 s, the airplane has travelled a total of 140 m through the air.
(a) Express the position, p, of the airplane compared with the point of liftoff as a vector using components and the î and ĵ basis vectors.
(b) If the airplane had been taking off in a headwind, the position of the airplane would instead have been p′ = p + w, in which the impact of the wind, w, is the vector w = −30î. Draw a sketch to show the relationship between the vectors p′, p, and w.
(c) What angle would the plane make with the horizontal as a result of the headwind after 2 s?
4. As a boat travels in a river, its velocity, v, is determined by the current, c, and its relative velocity compared to the water, r. For instance, at one point in the boat’s journey, these vectors are related in the following way:
(a) Write a vector equation that shows how v is related to c and r.
(b) If the angle between v and c is 90°, as shown, write an equation for the magnitude of v as a function of c and r.
(c) At a different point in the boat’s journey, if the current is flowing due east at 5 m/s and the boat wants to travel due south at 10 m/s, what should the captain set its relative velocity to be (magnitude and direction)?
Vectors are quantities that have both magnitude and direction. Many important physical quantities such as forces and velocities are vector quantities.
Vectors can be represented graphically with an arrow, numerically with a magnitude and direction, or numerically with components.
Vectors can be added (or subtracted) graphically by drawing the first vector and then starting the tail of the second vector at the end of the first (remembering to flip the direction of the second vector for subtraction).
Vectors can be added (or subtracted) numerically by adding (or subtracting) individual components.
Multiplying a vector by a scalar can change the length of the vector or flip the direction by 180° if the scalar is negative.
If the magnitude, A, and angle relative to the horizontal, θ, are known, the x- and y-components can be calculated using:
If the components, Ax and Ay are known, the magnitude, A, and angle relative to the horizontal, θ, can be calculated using:
