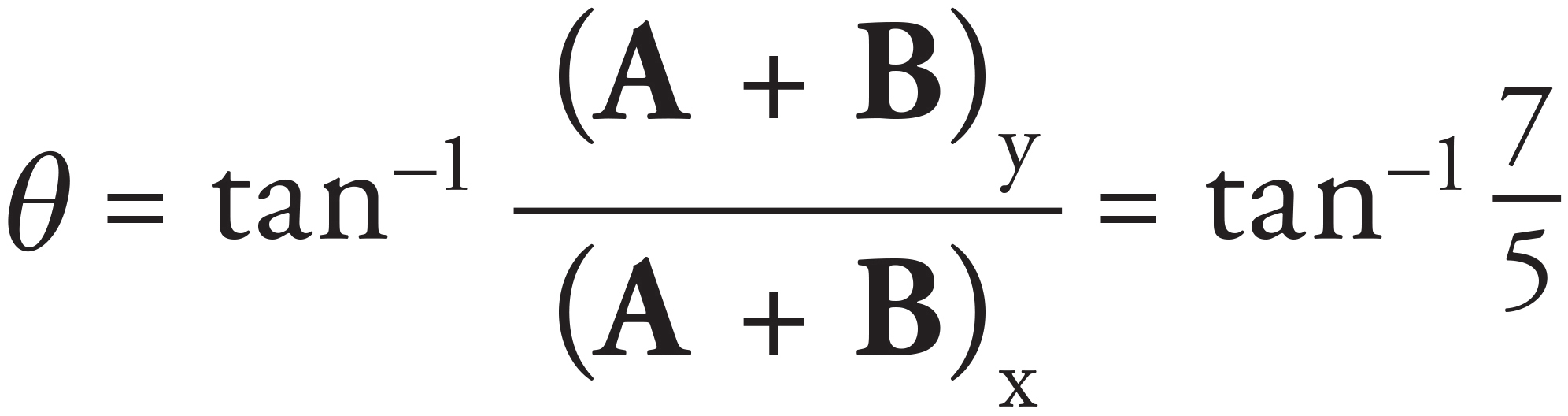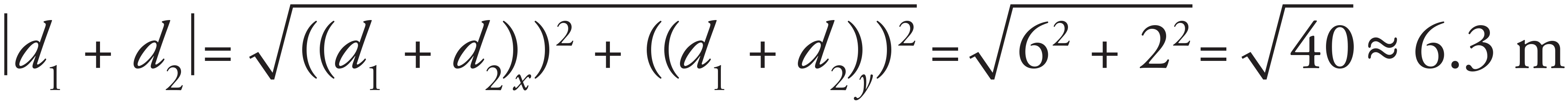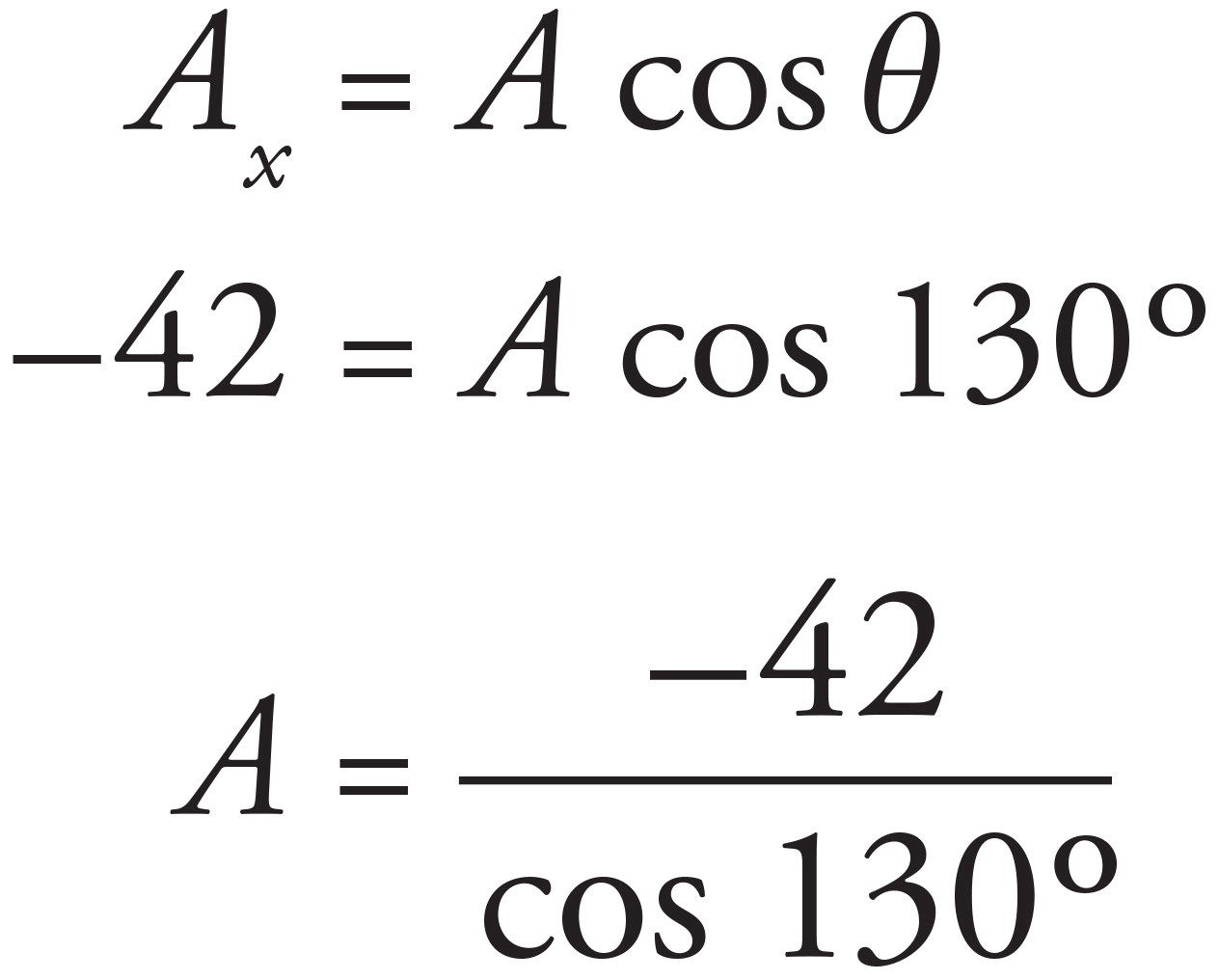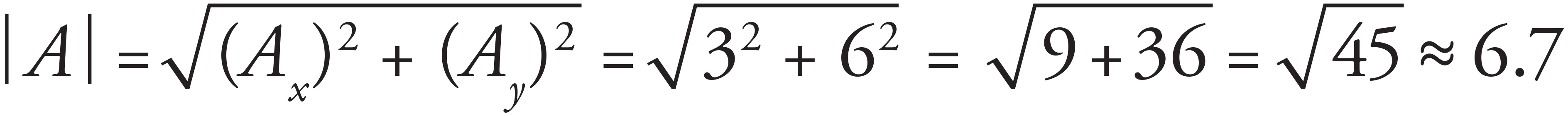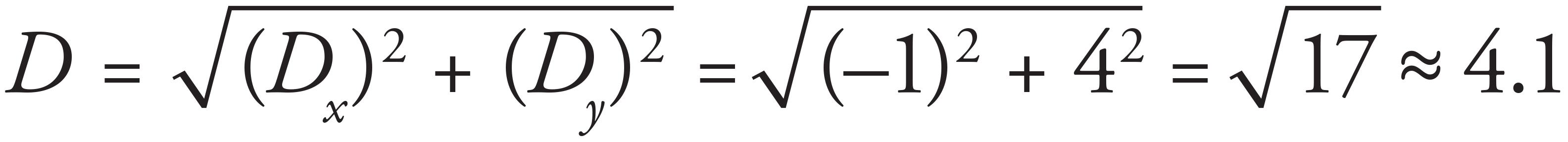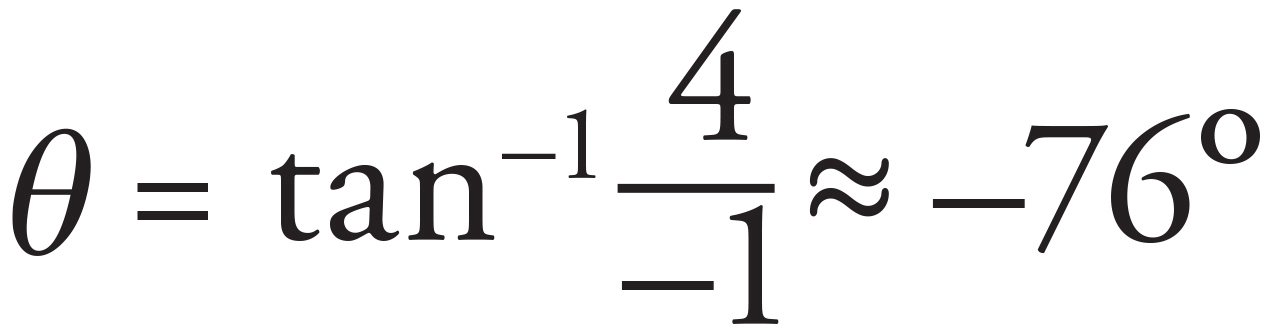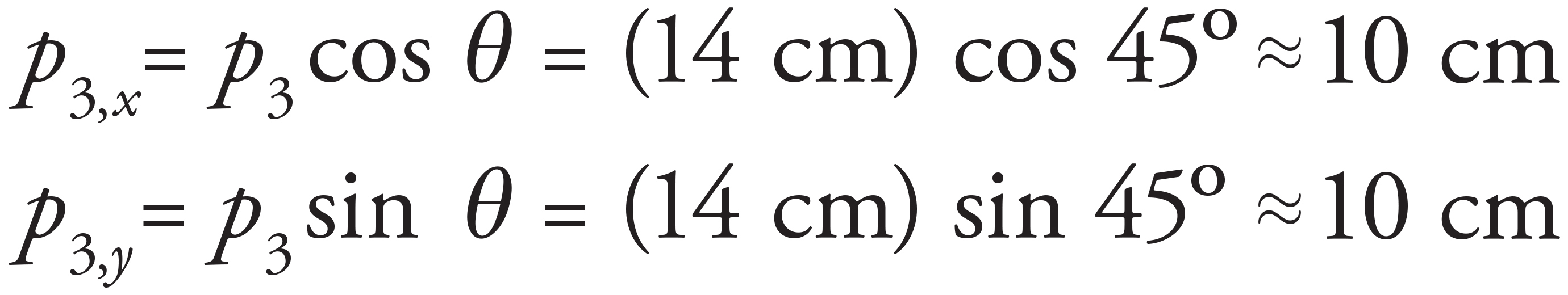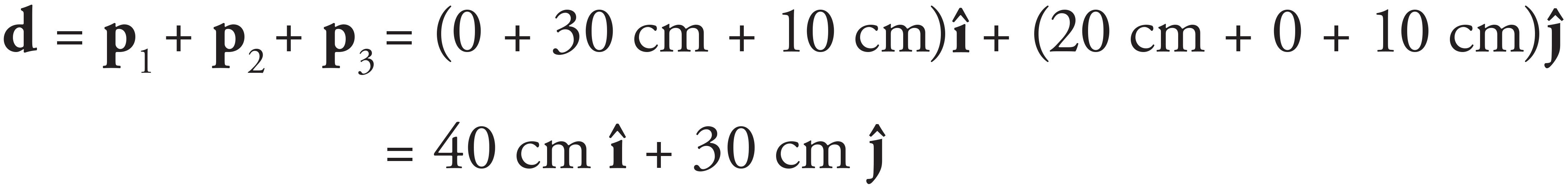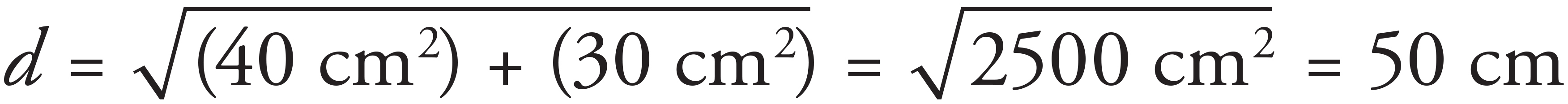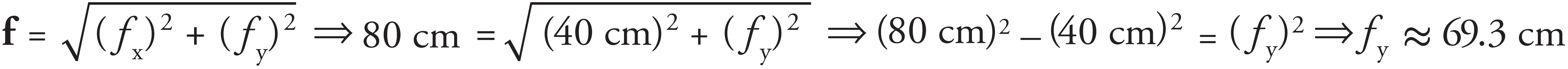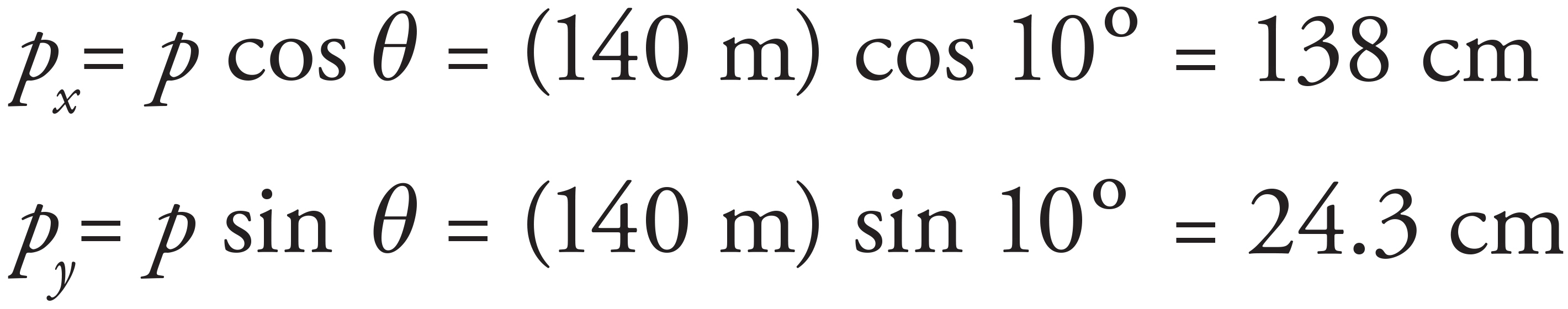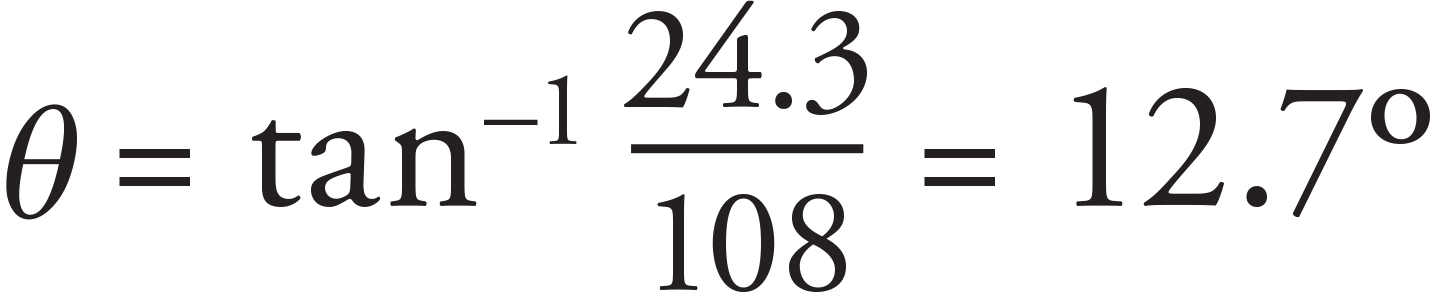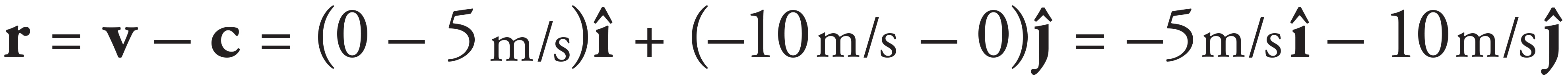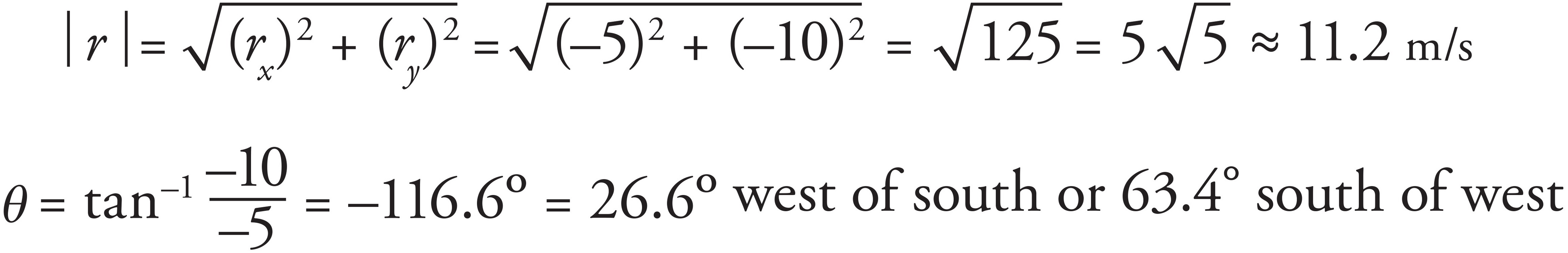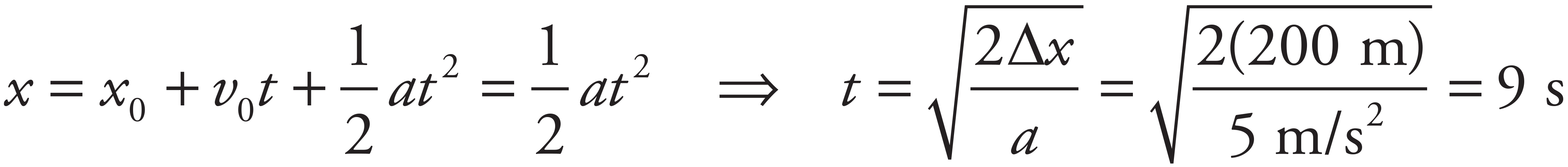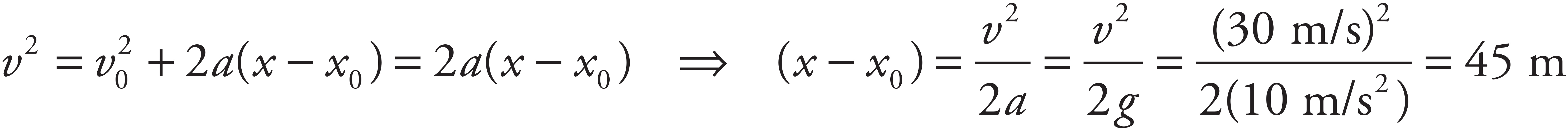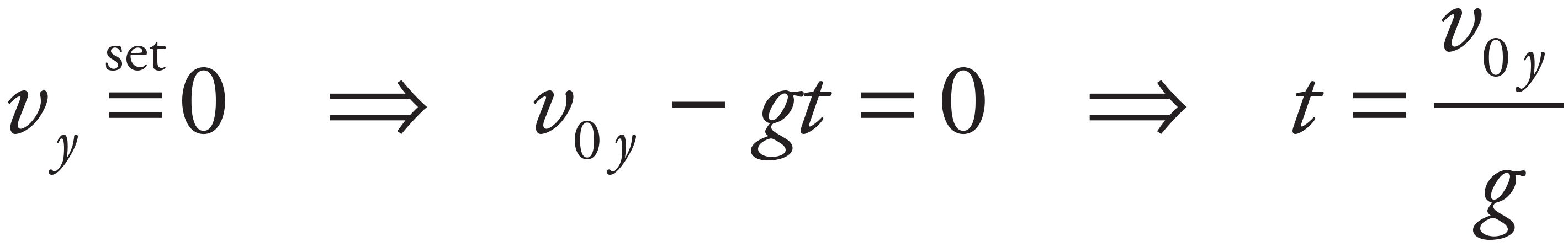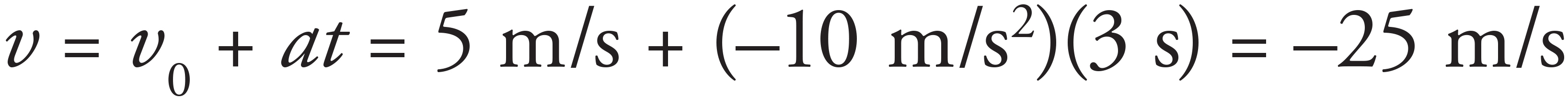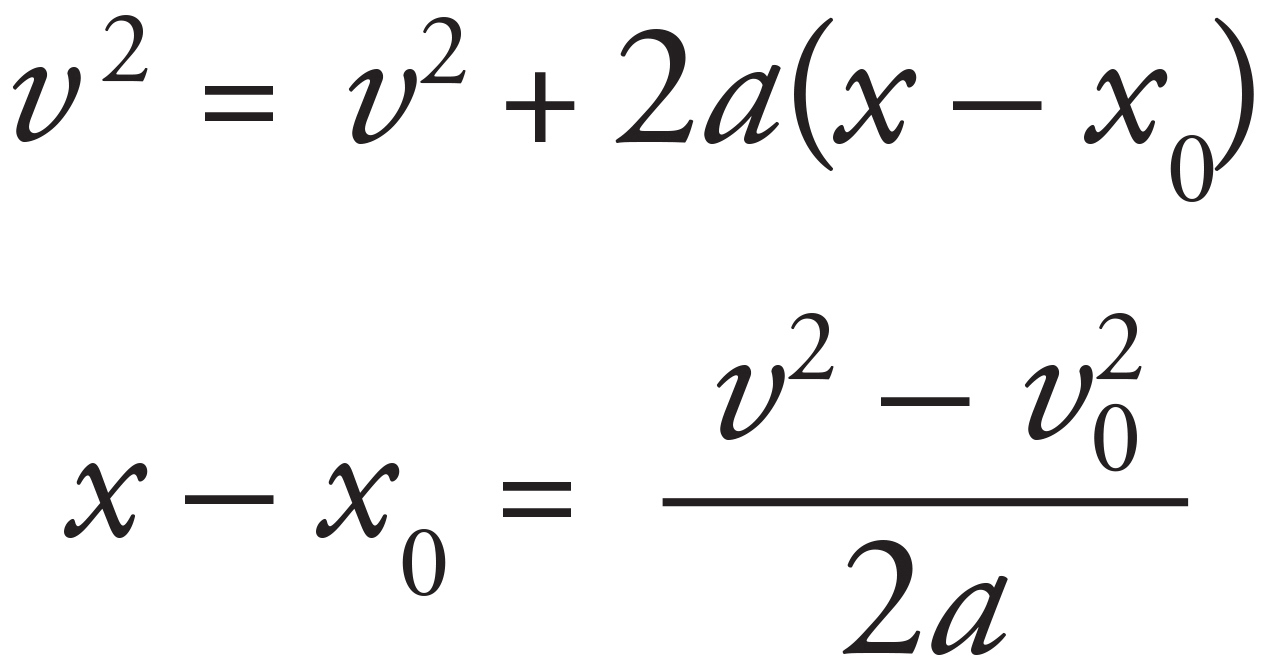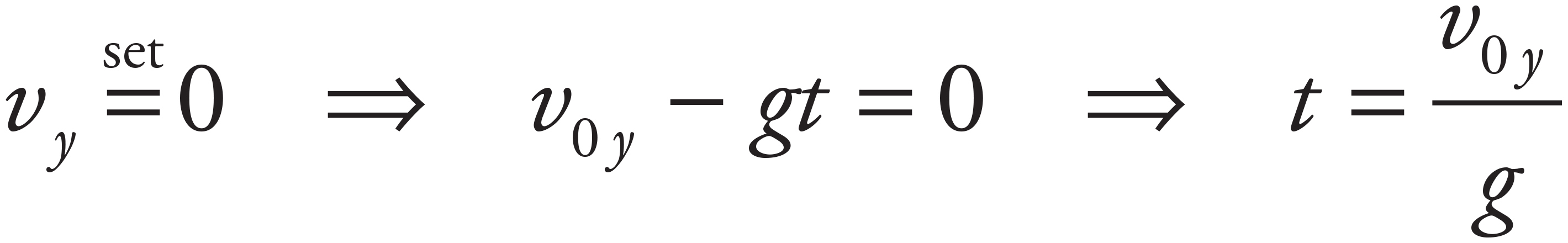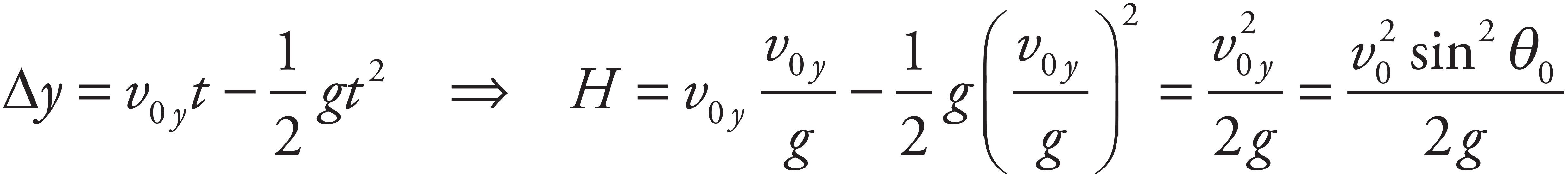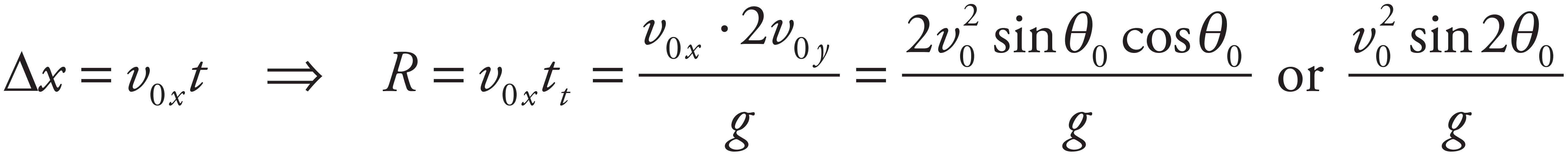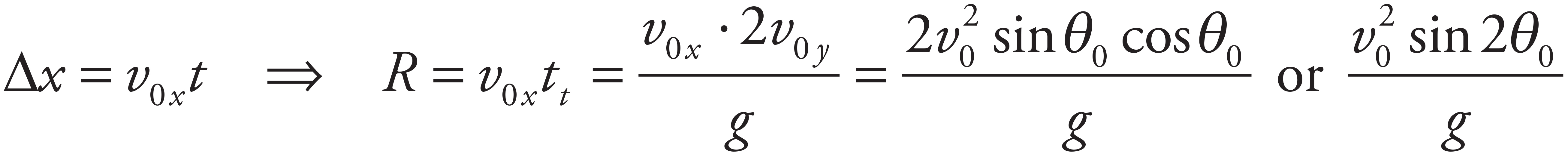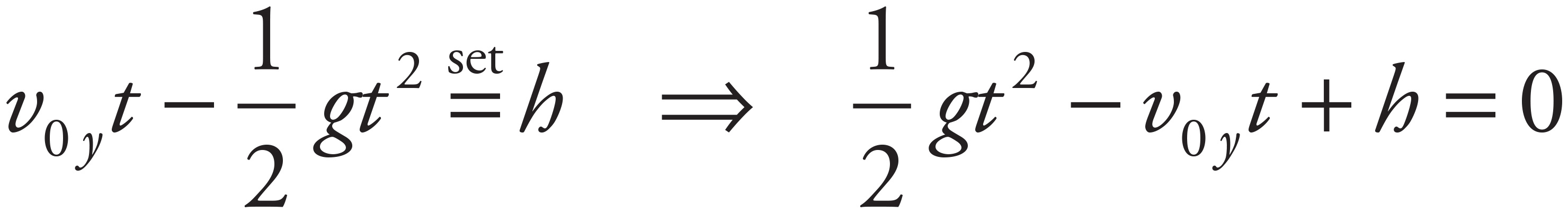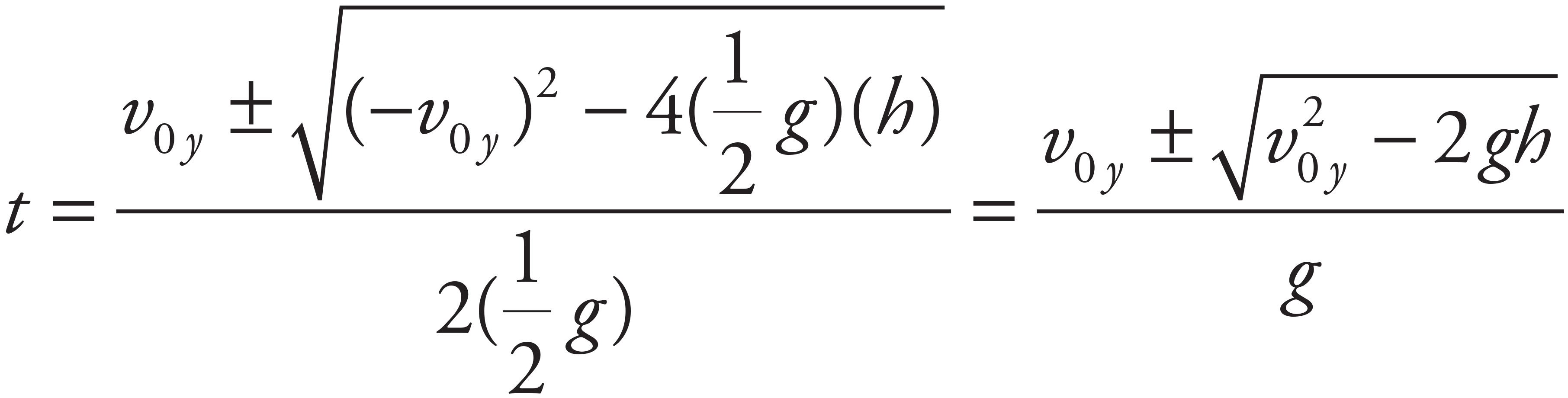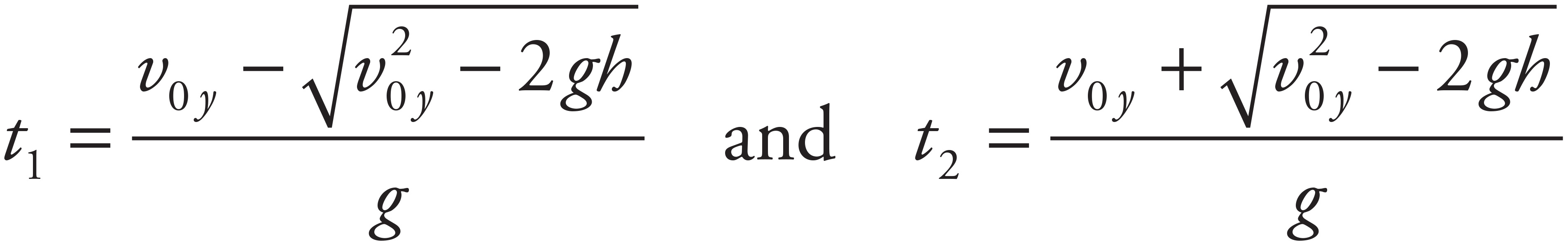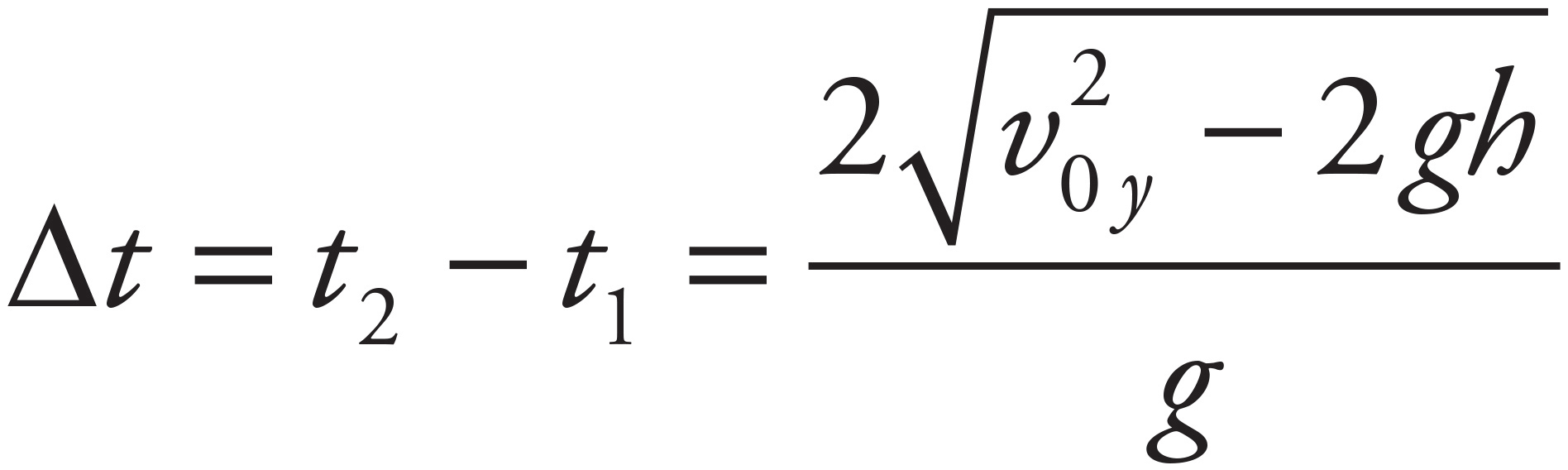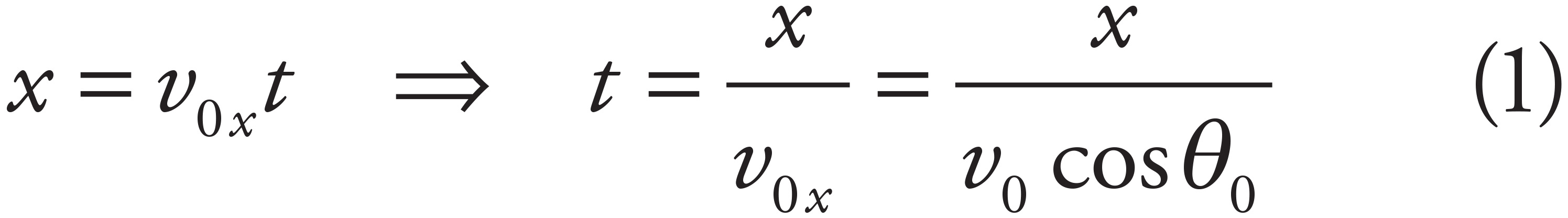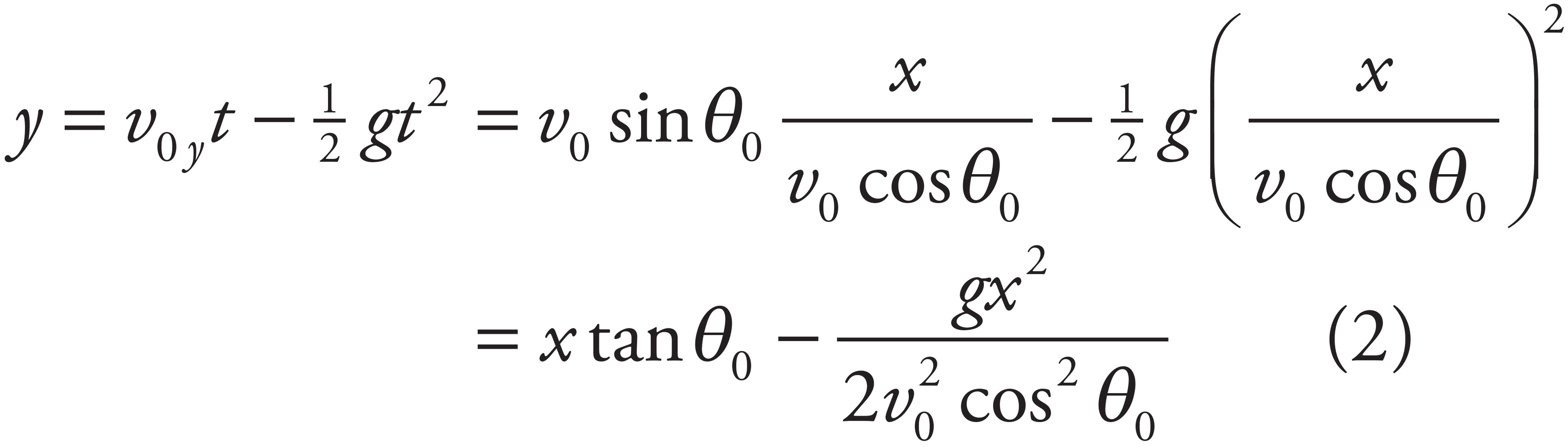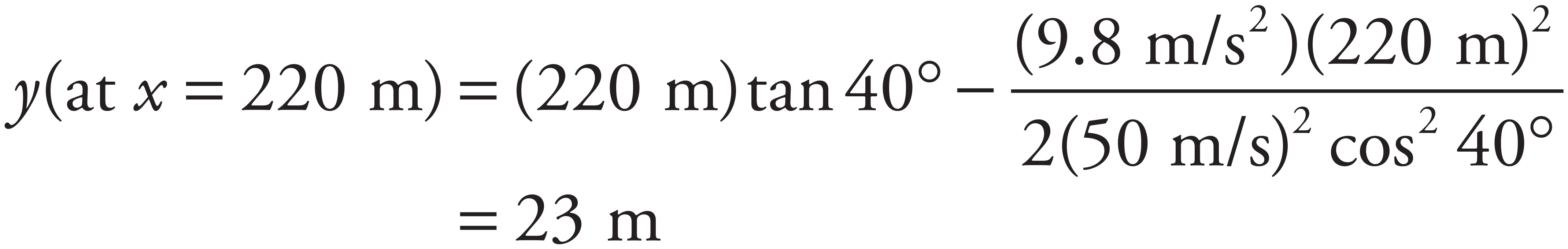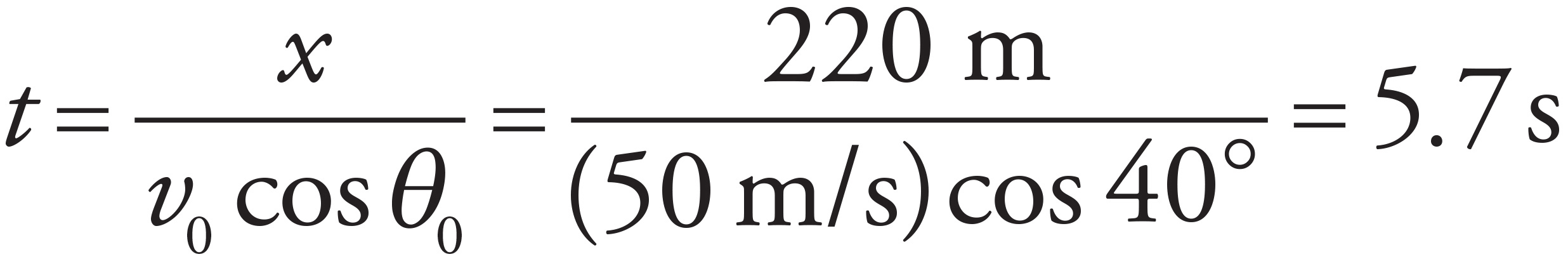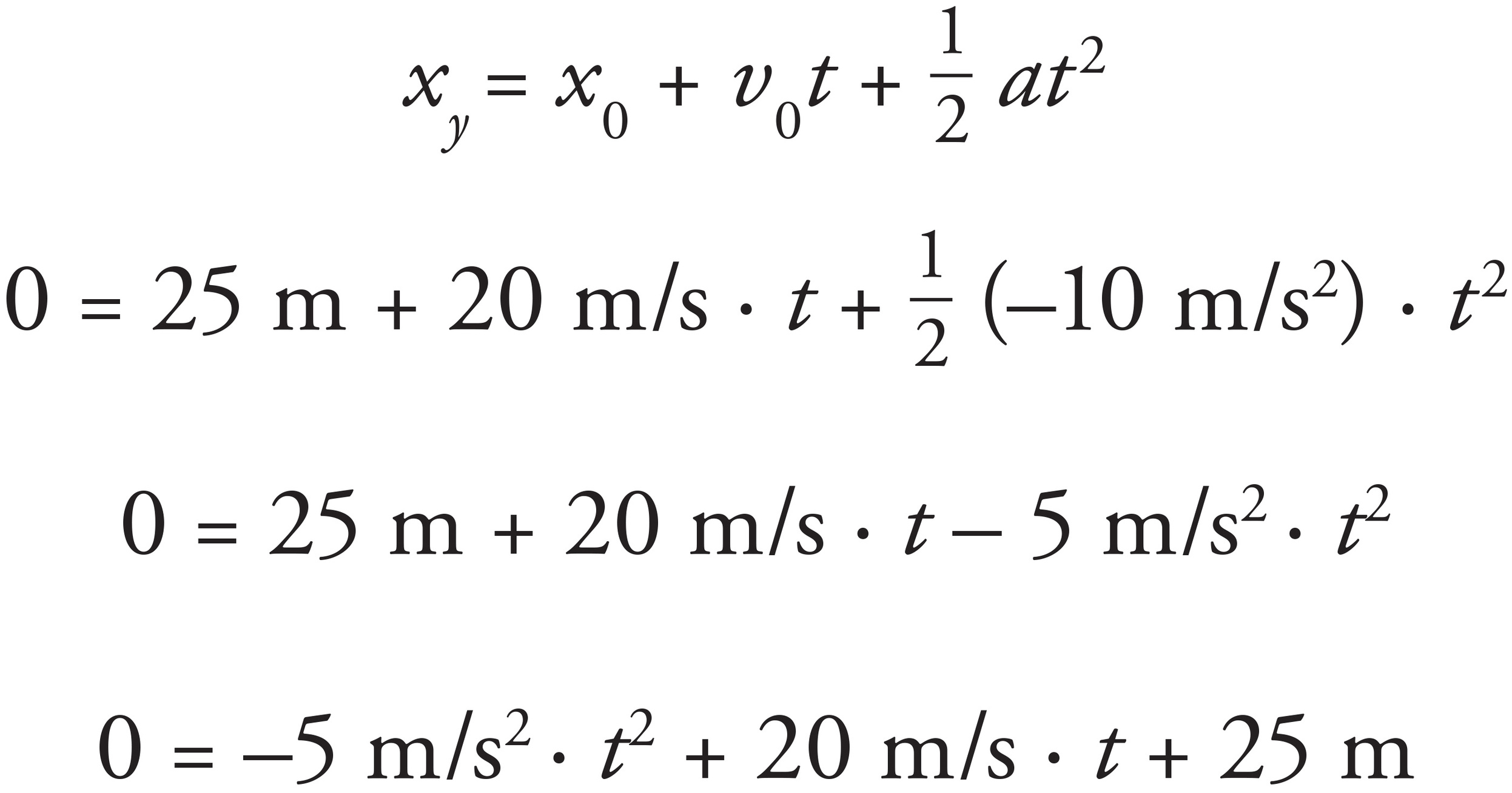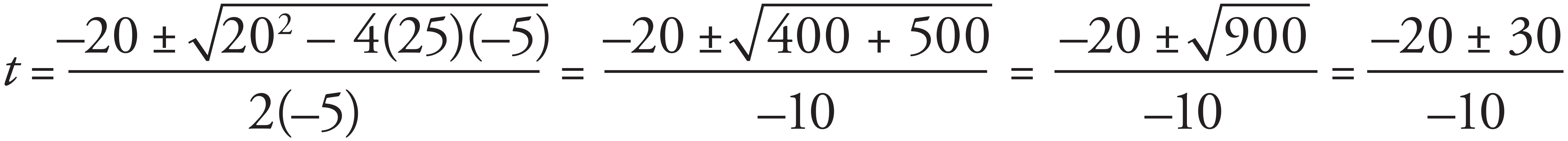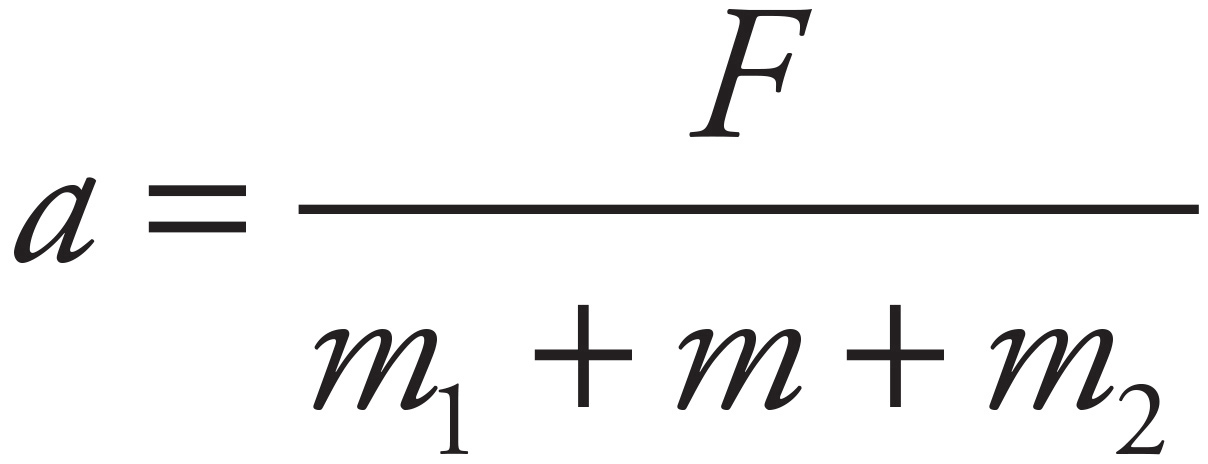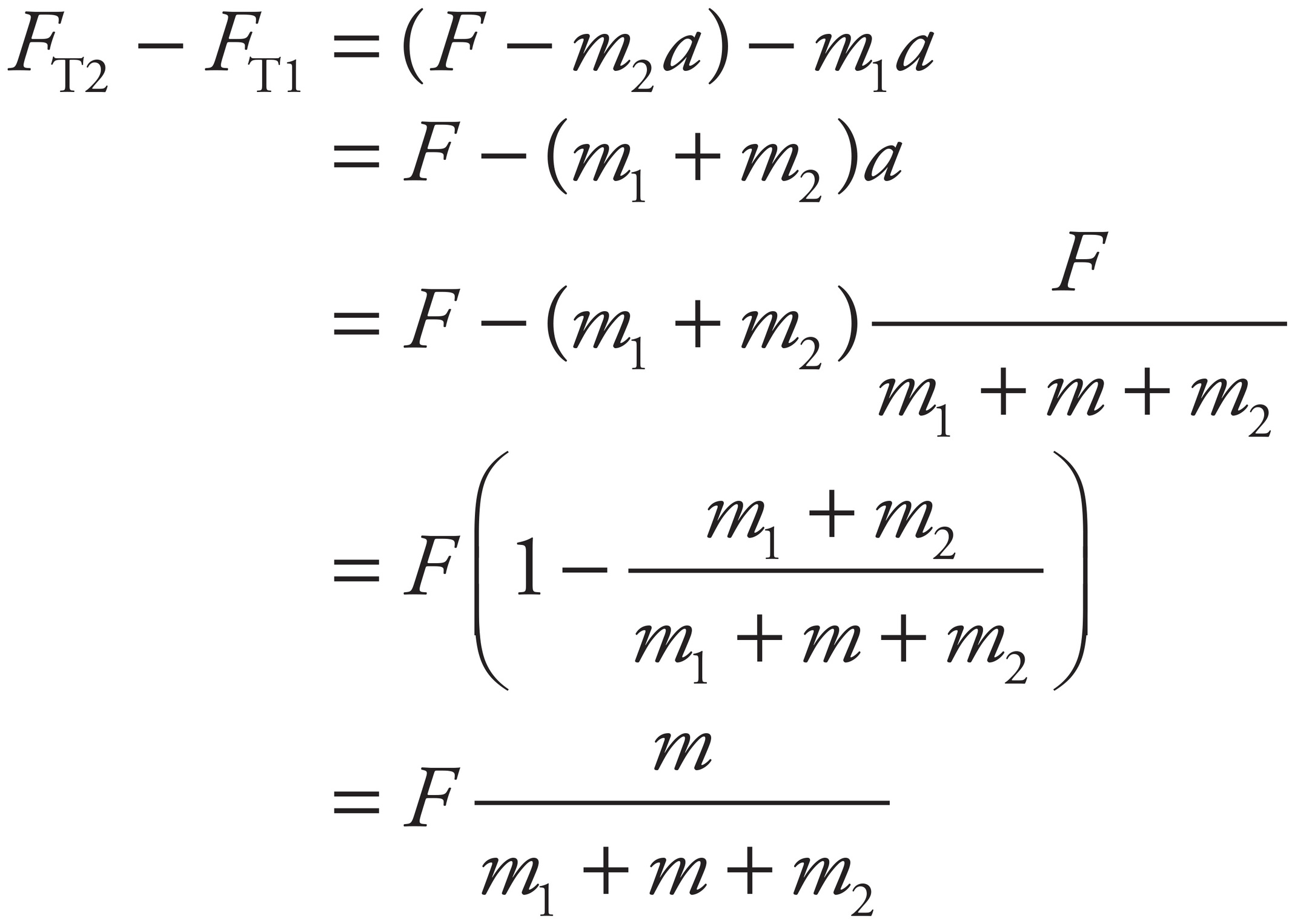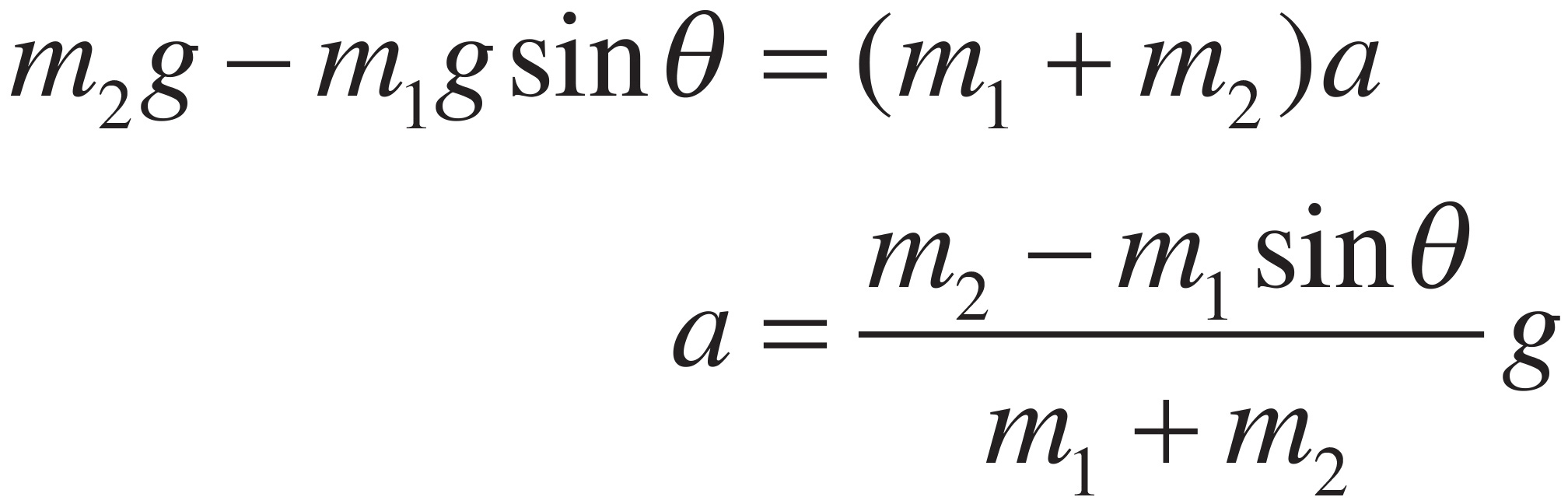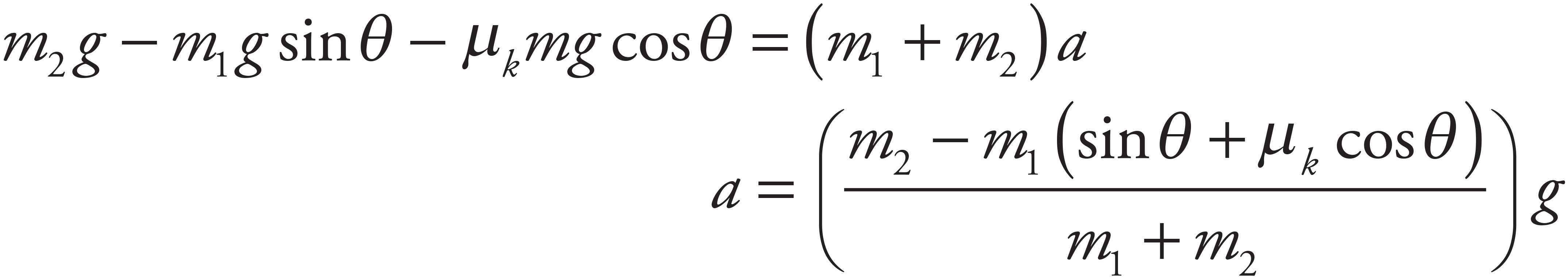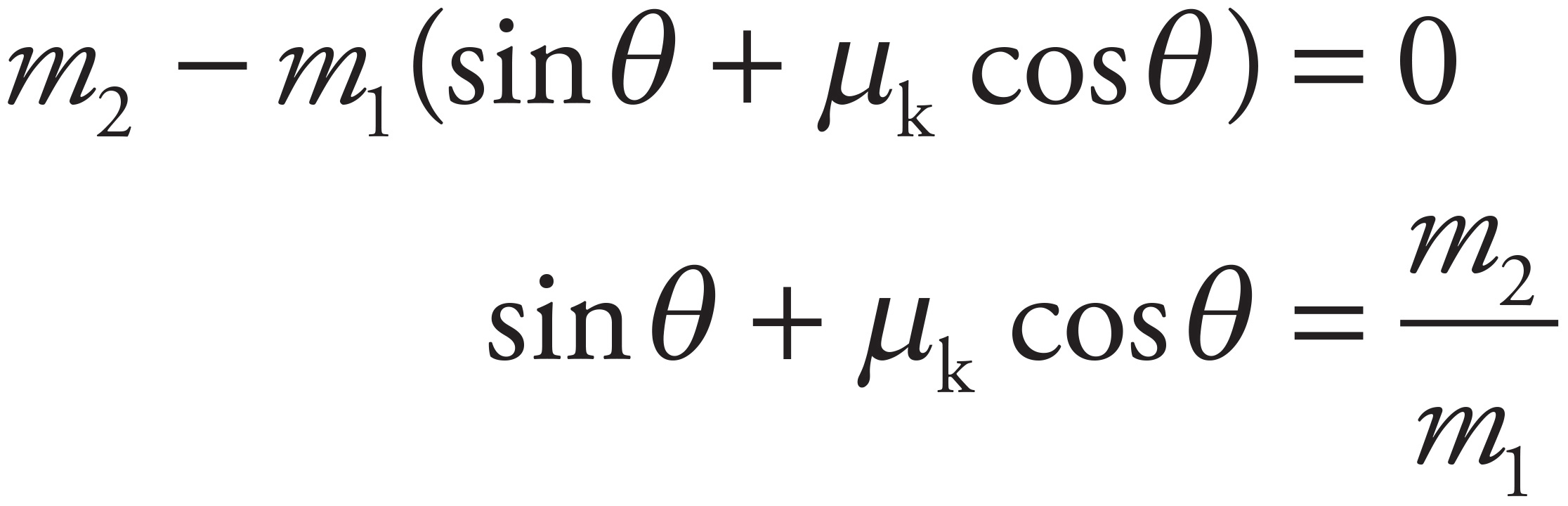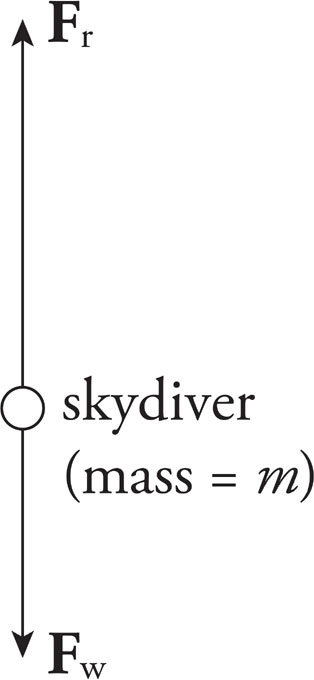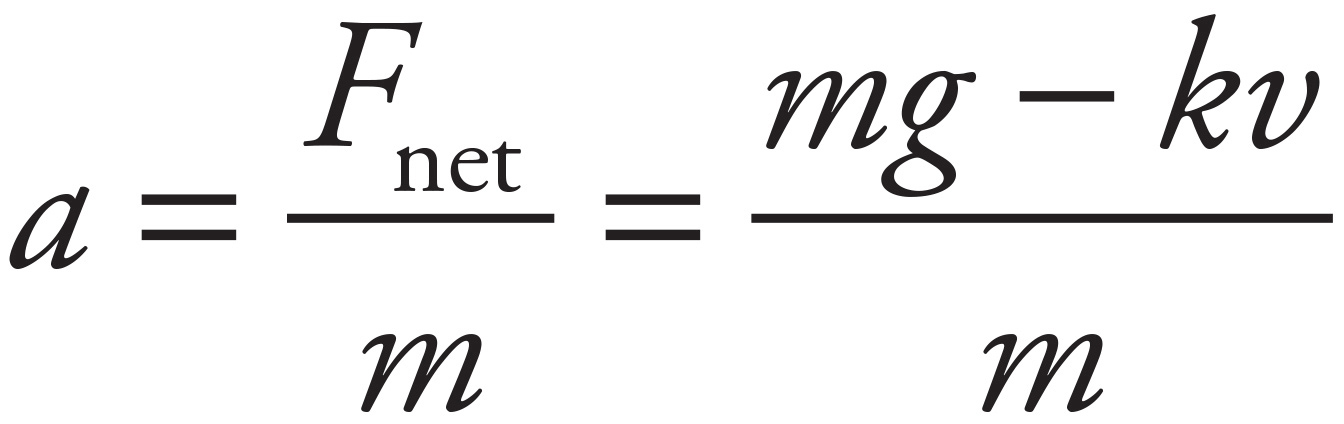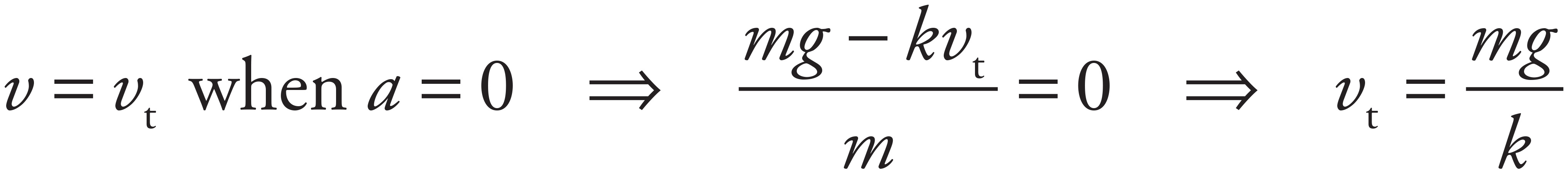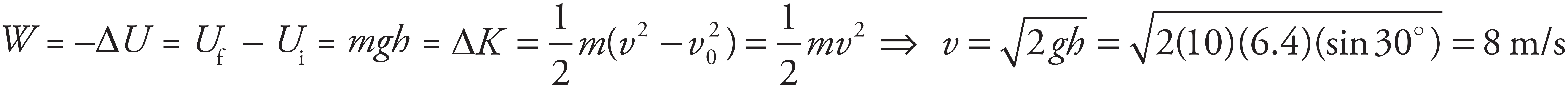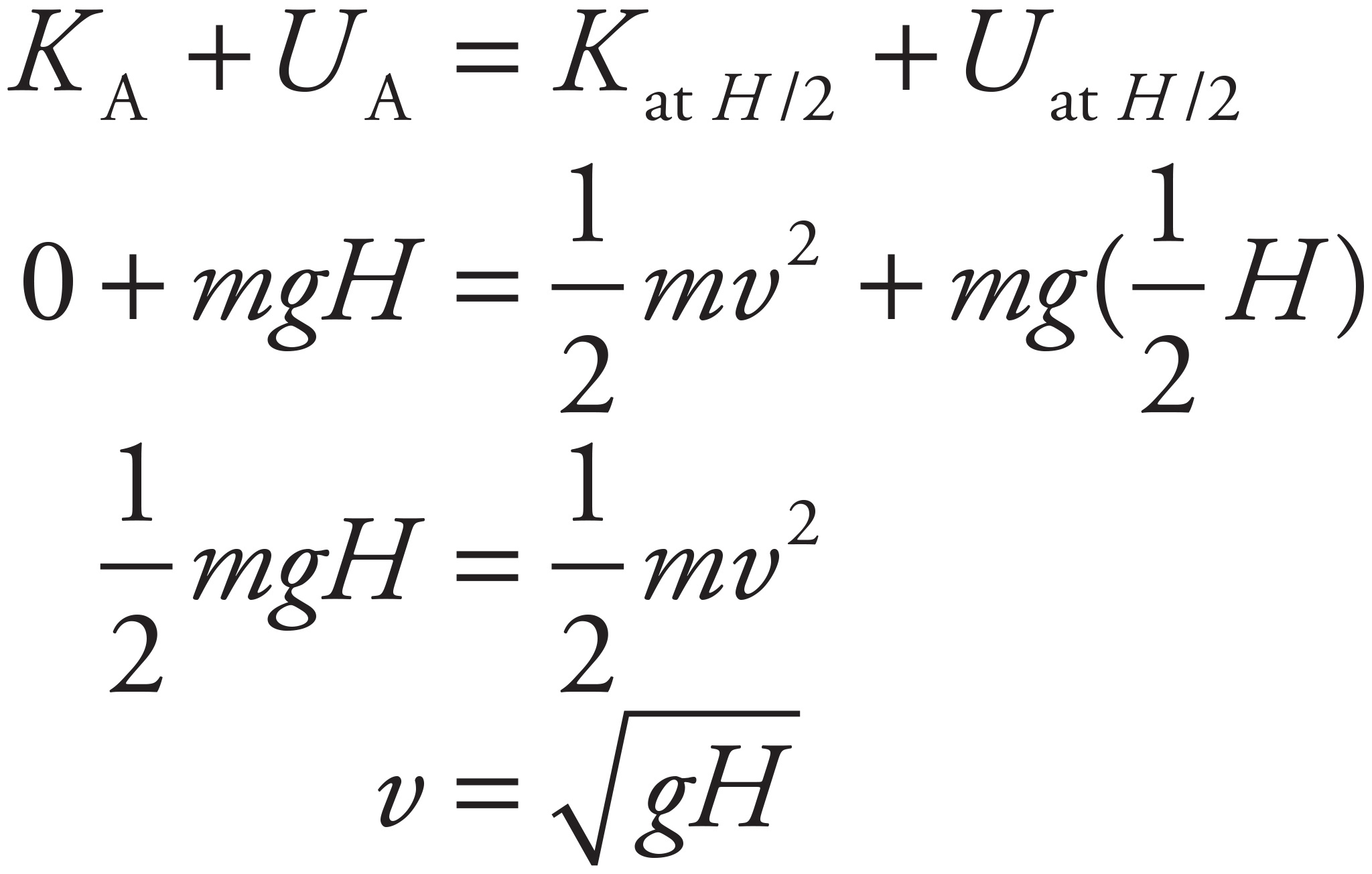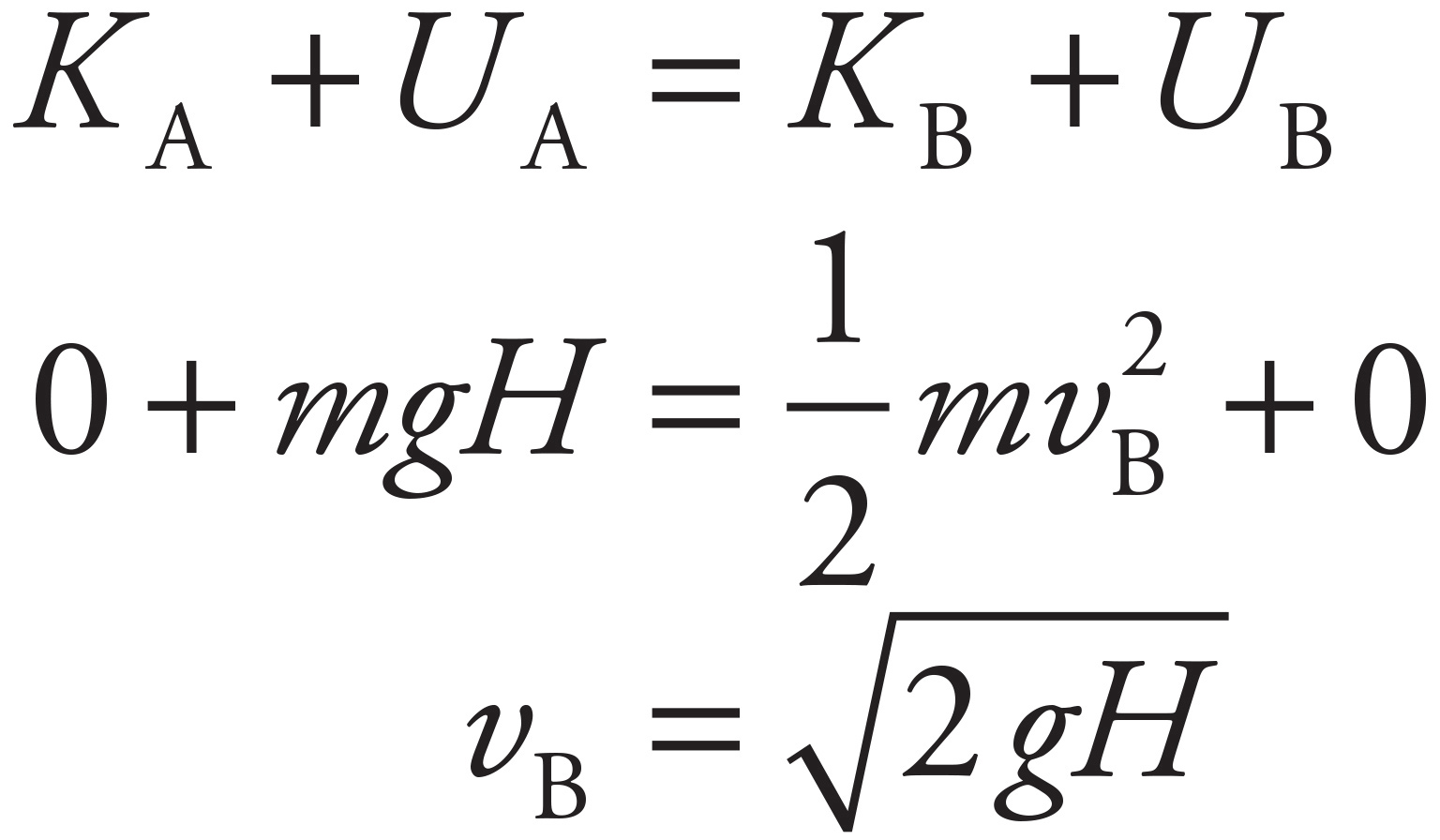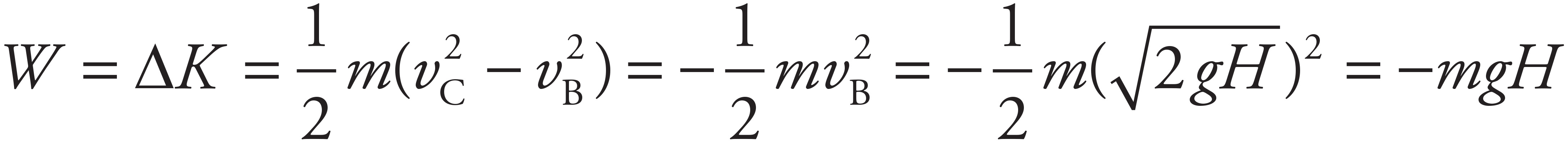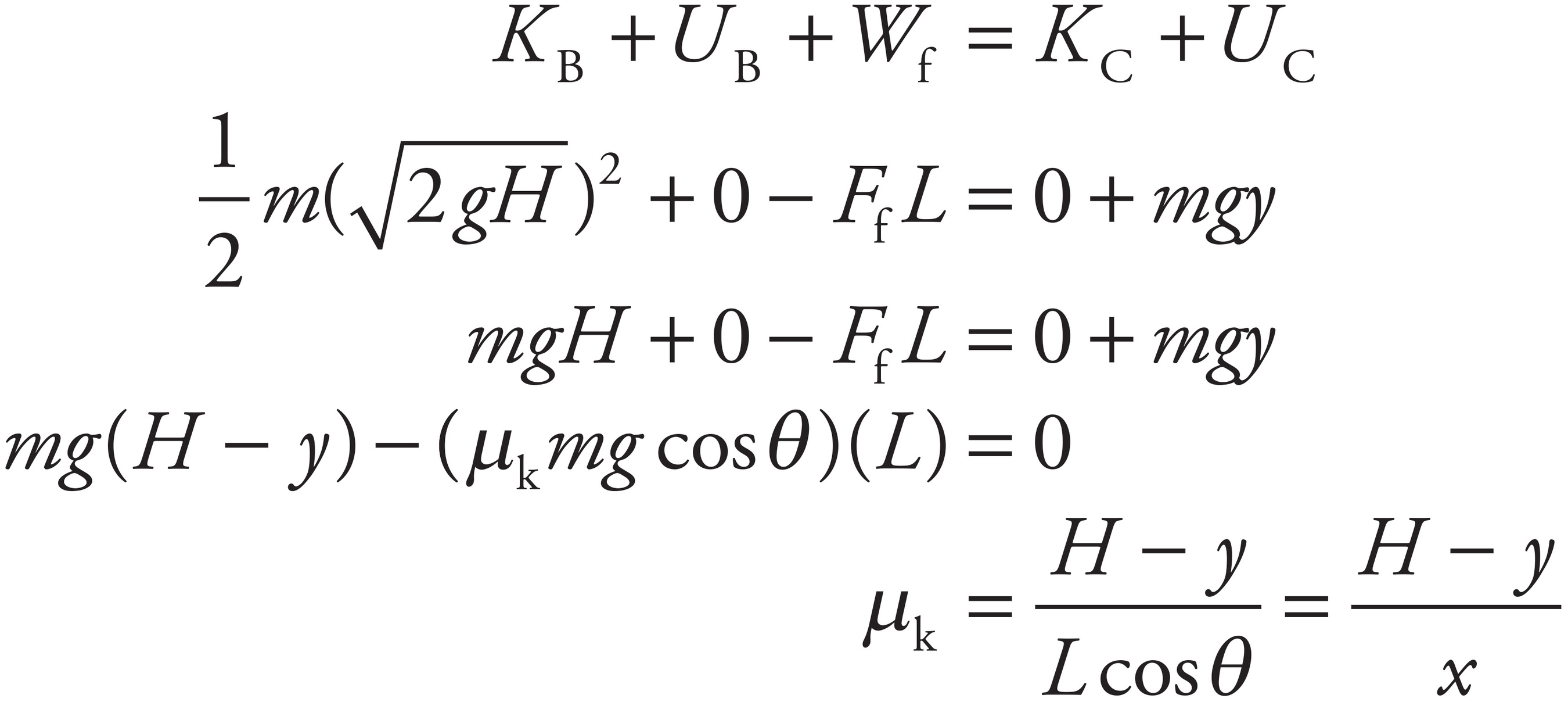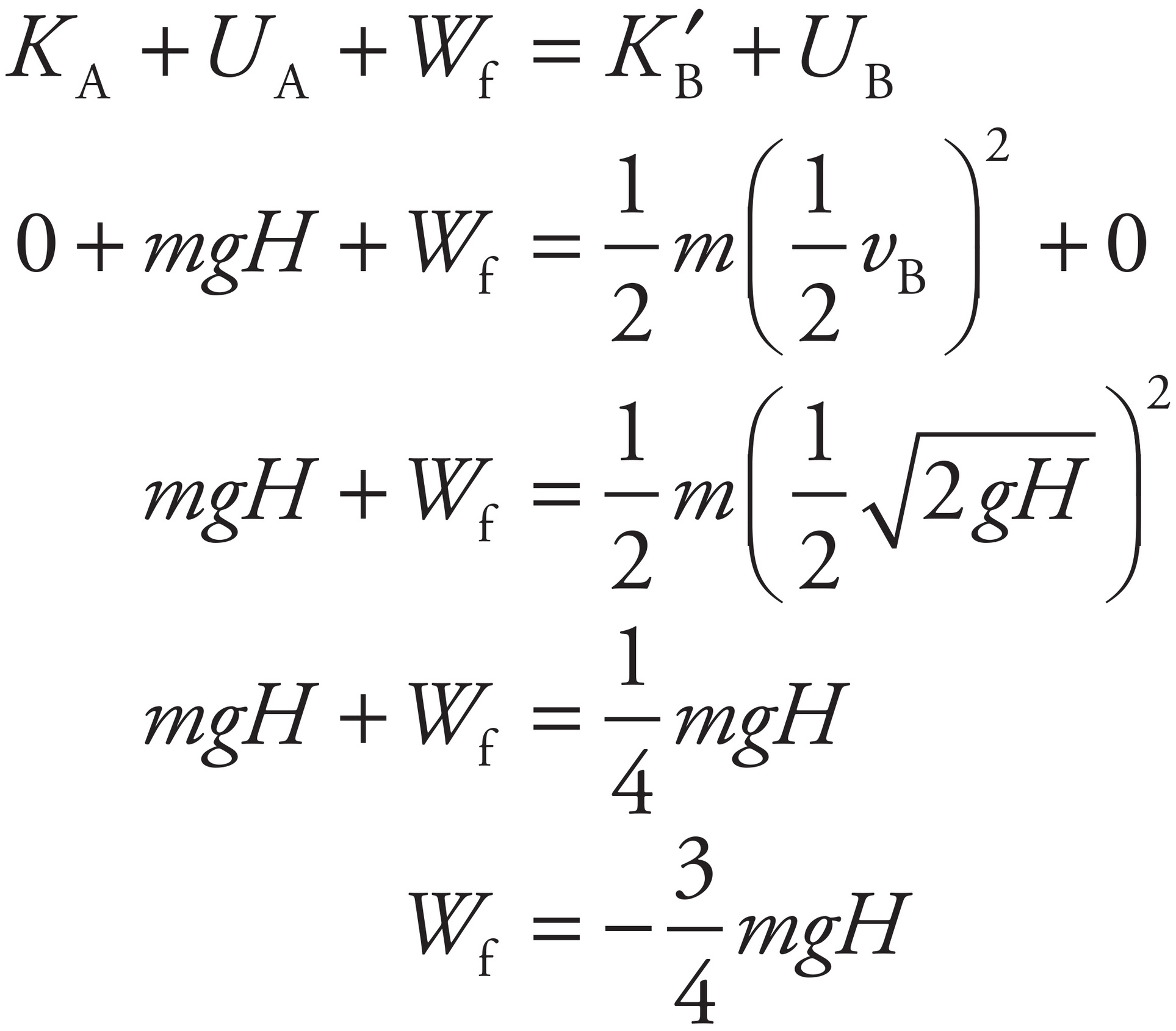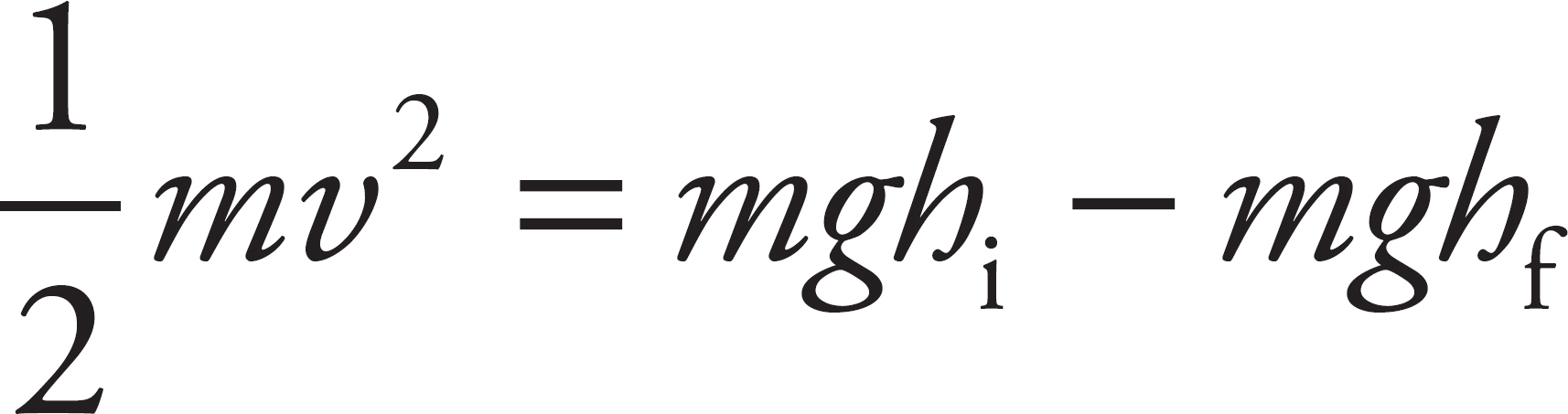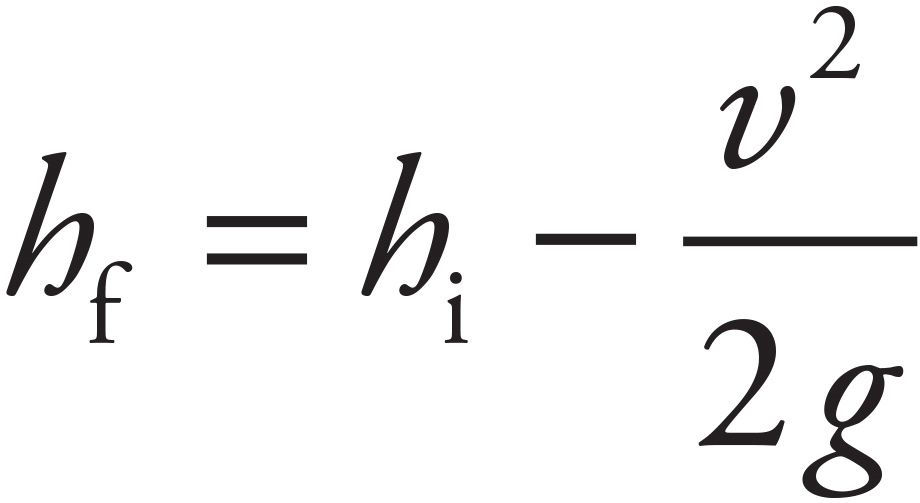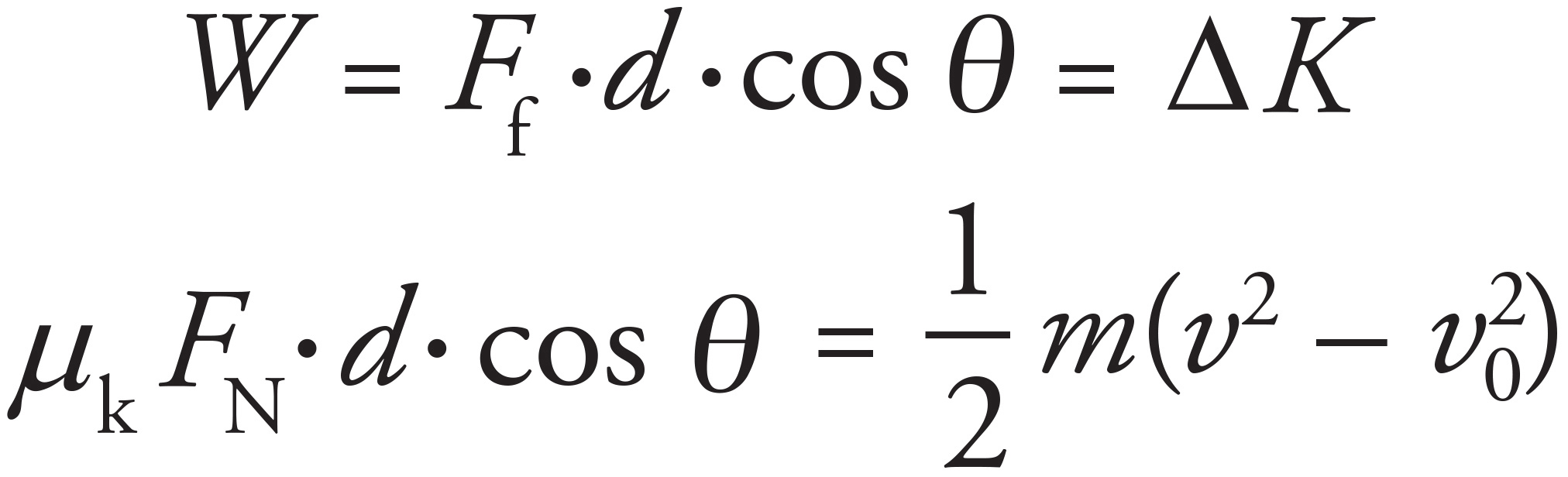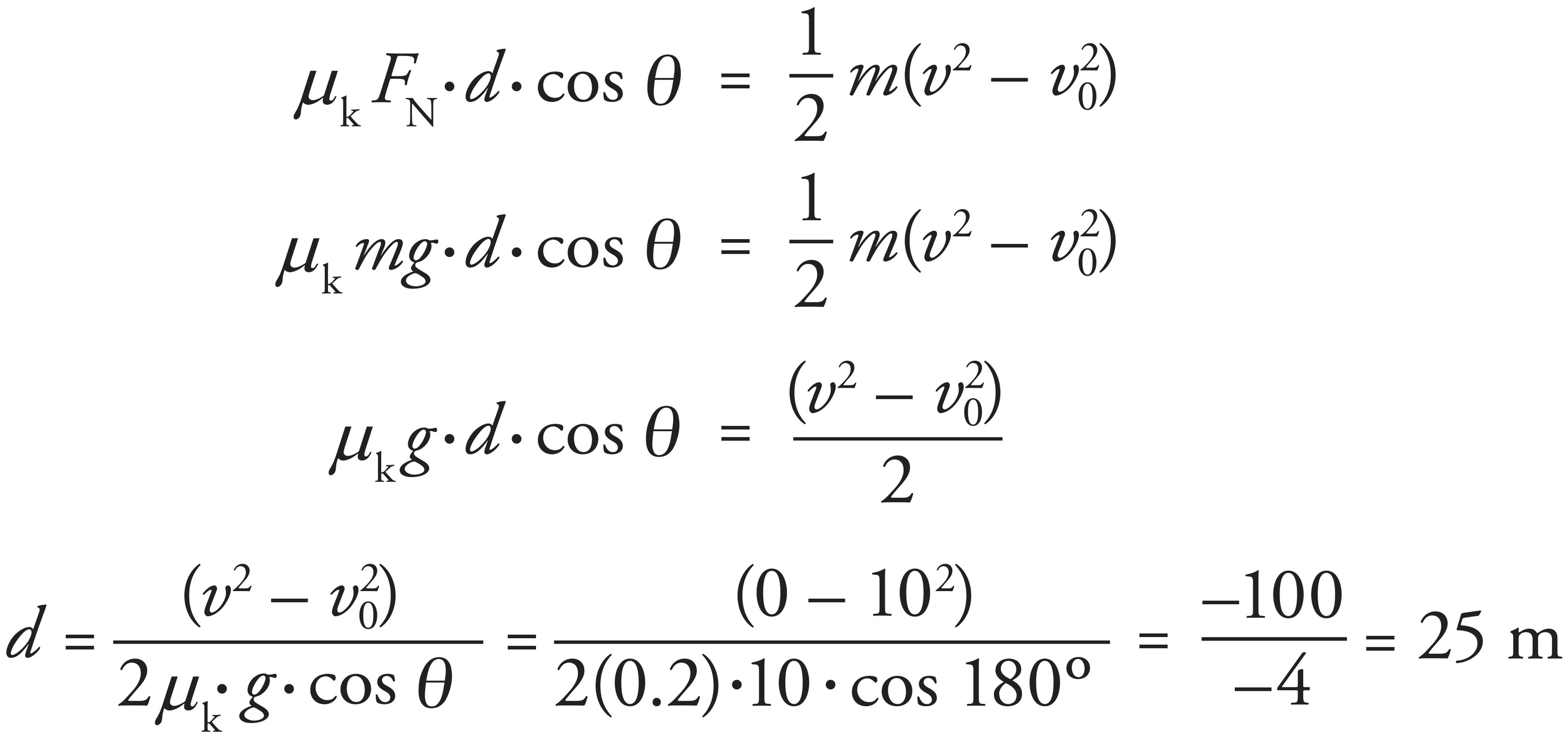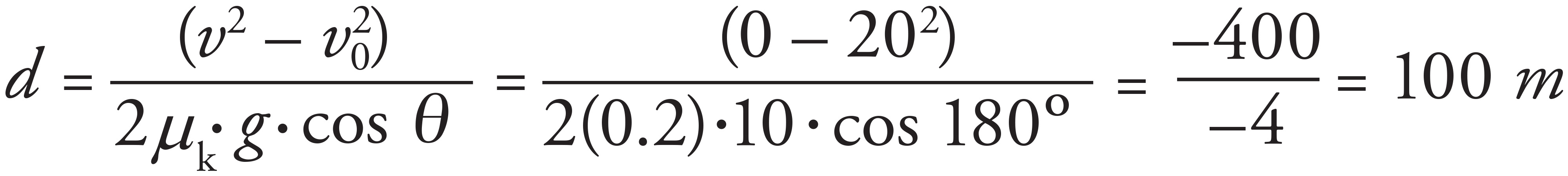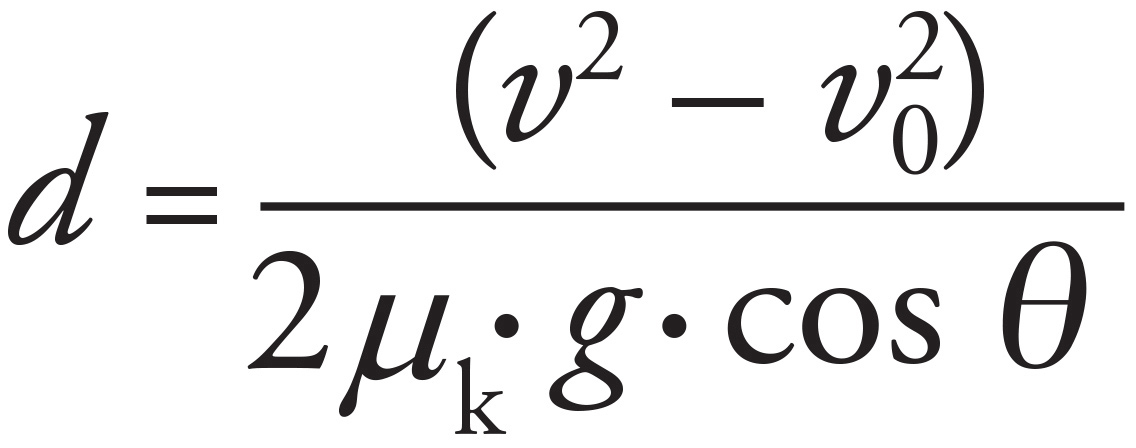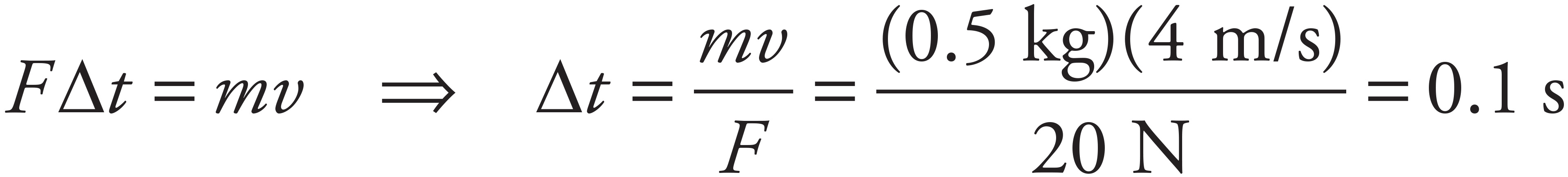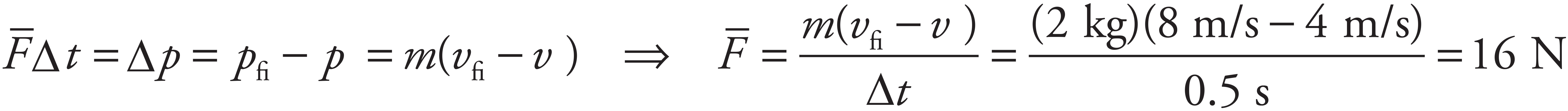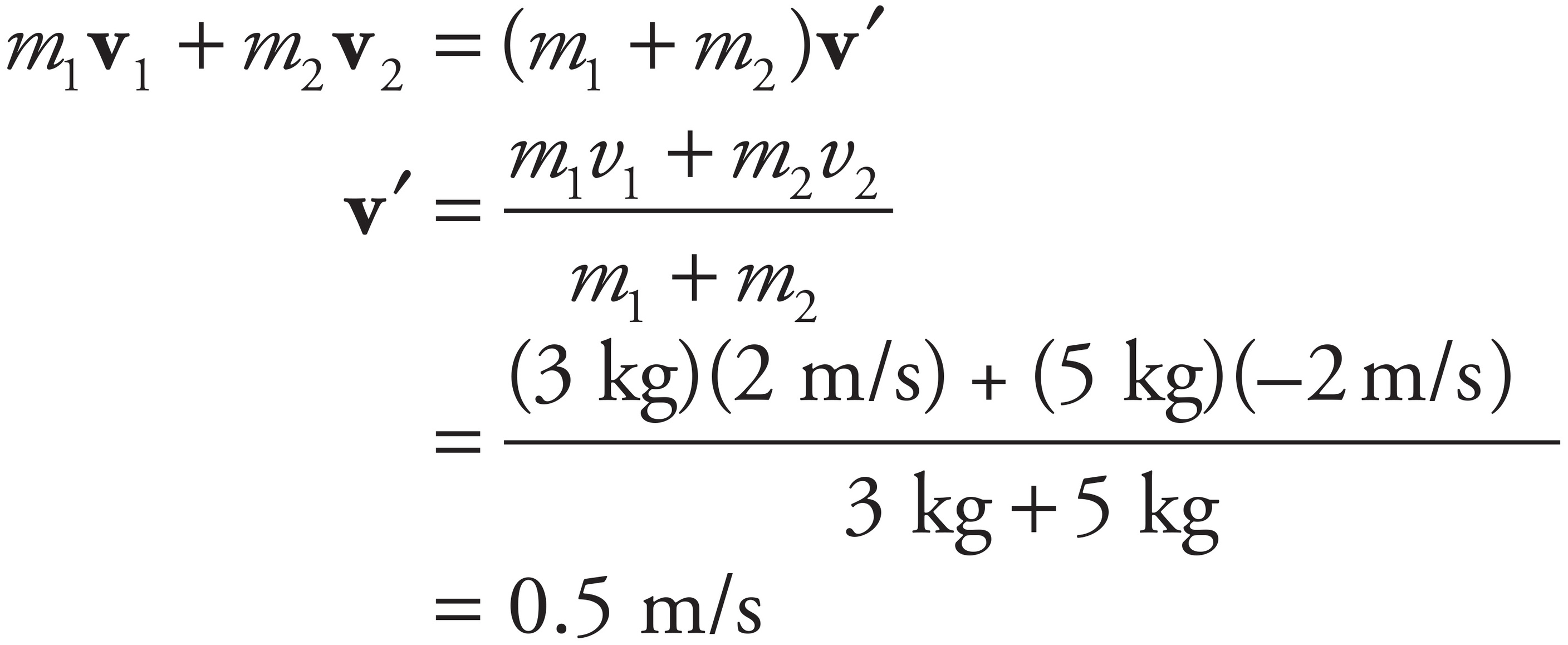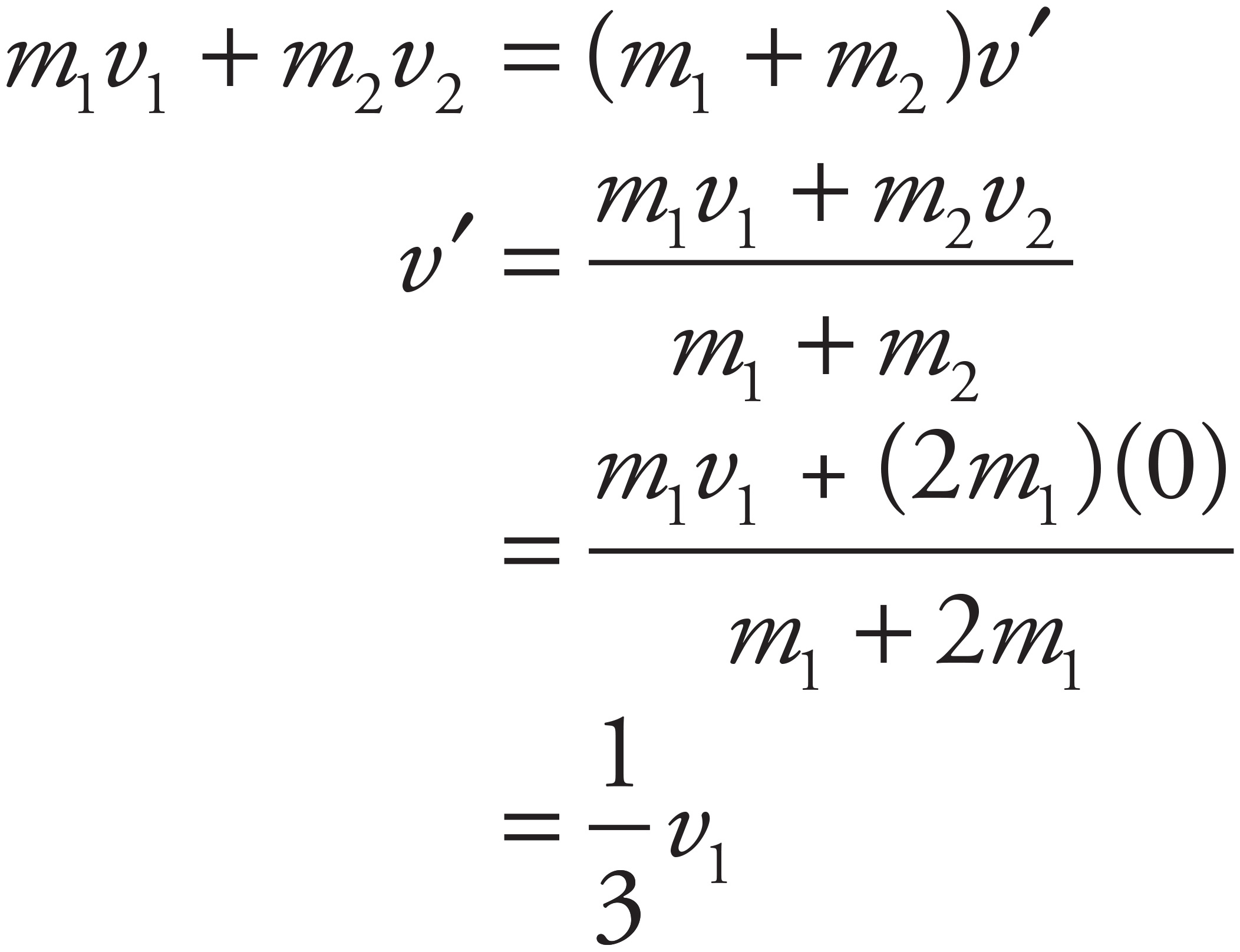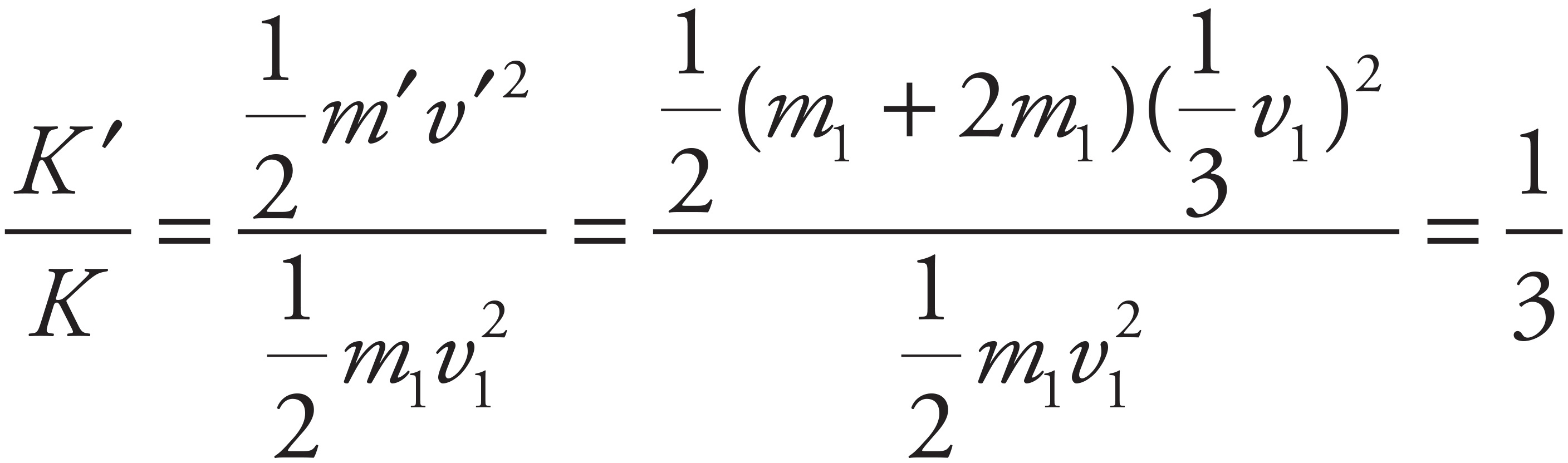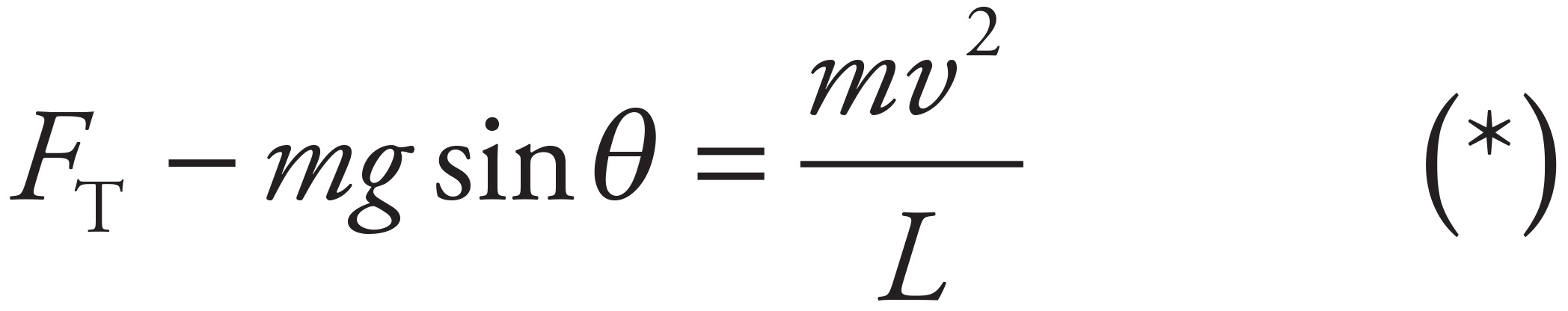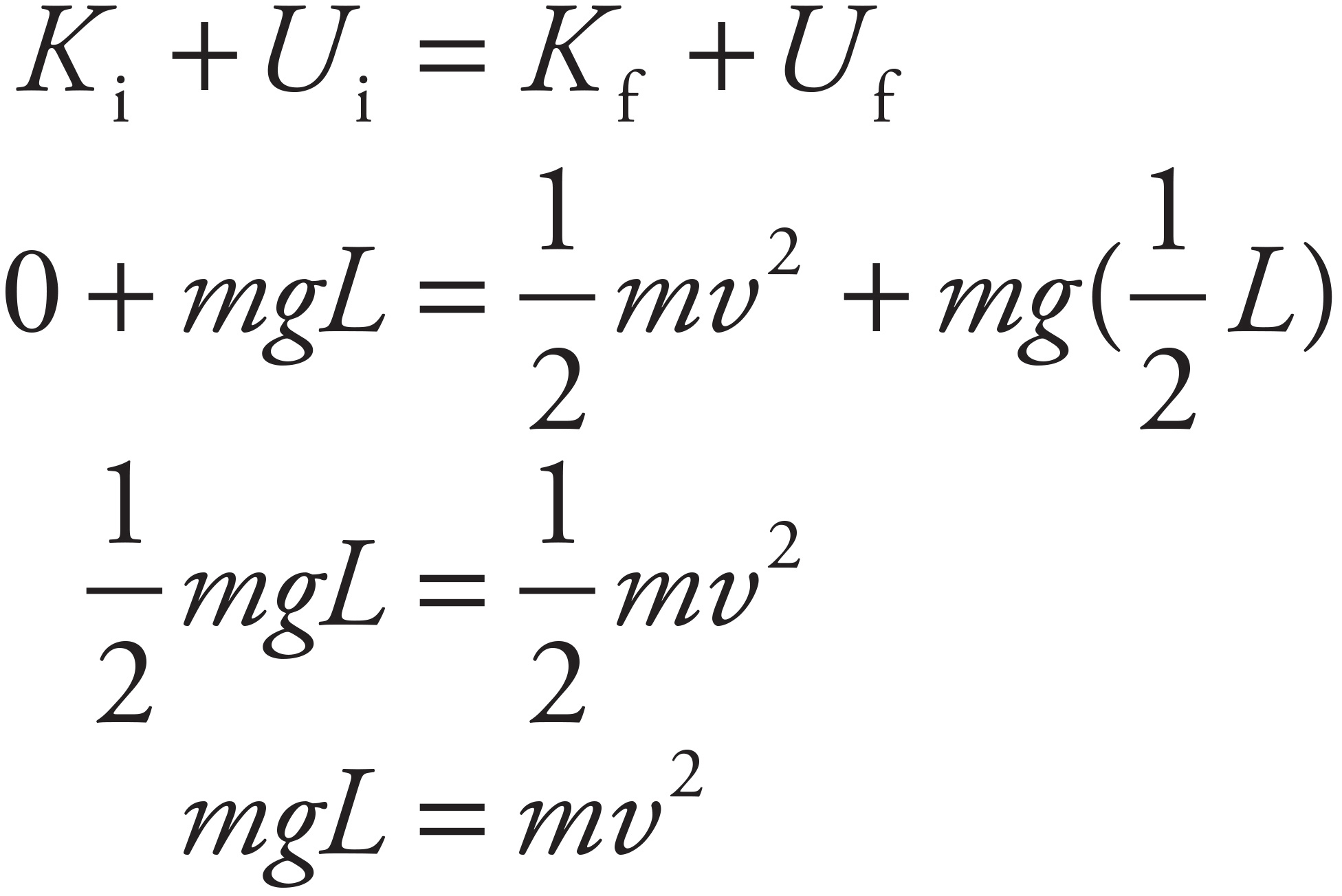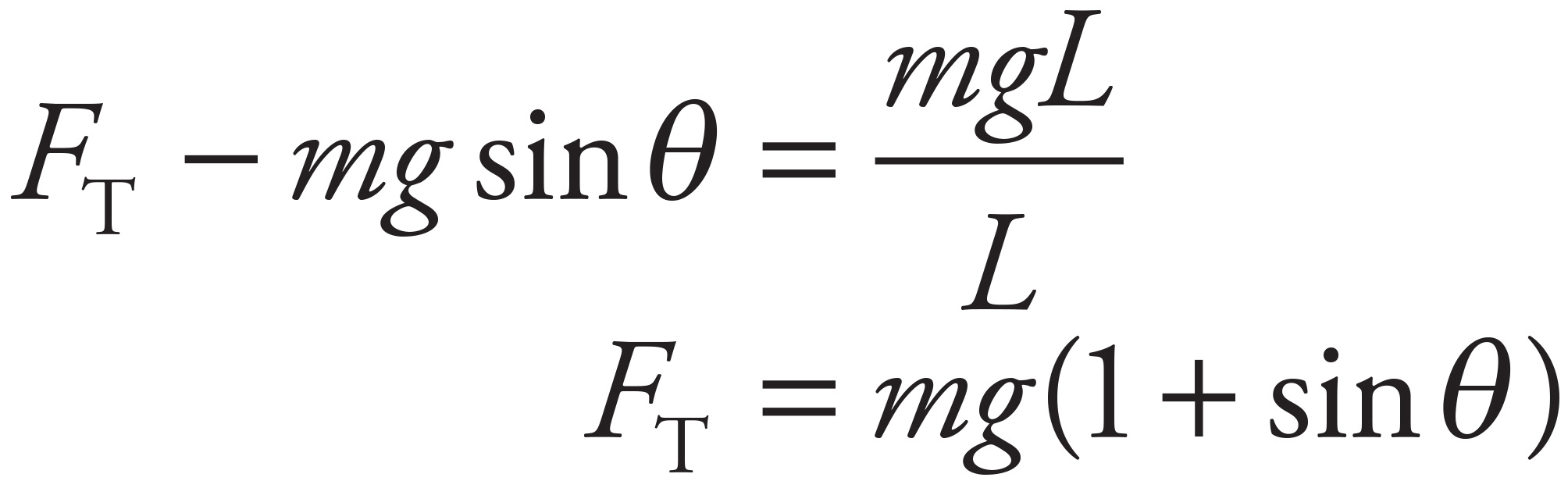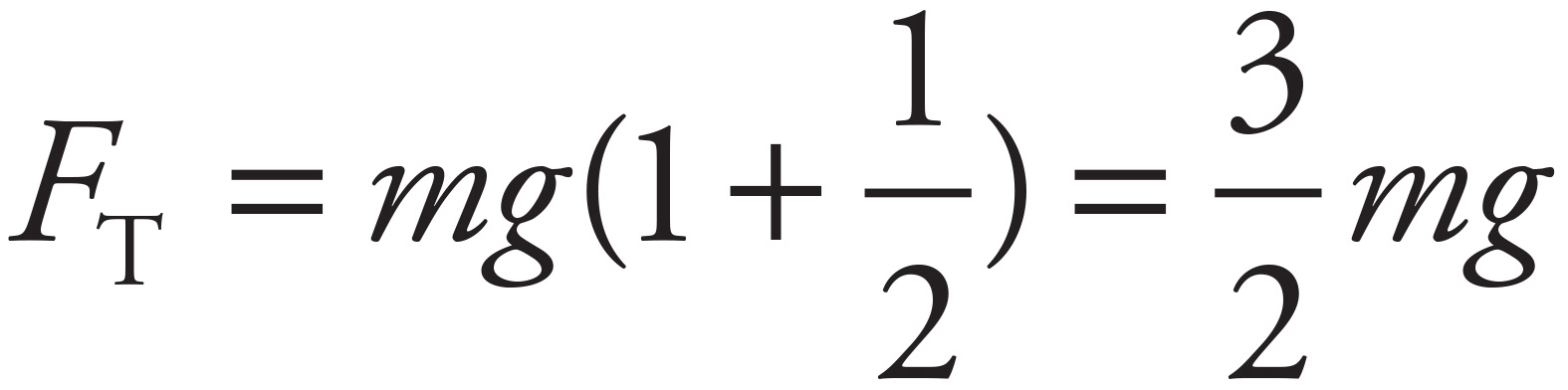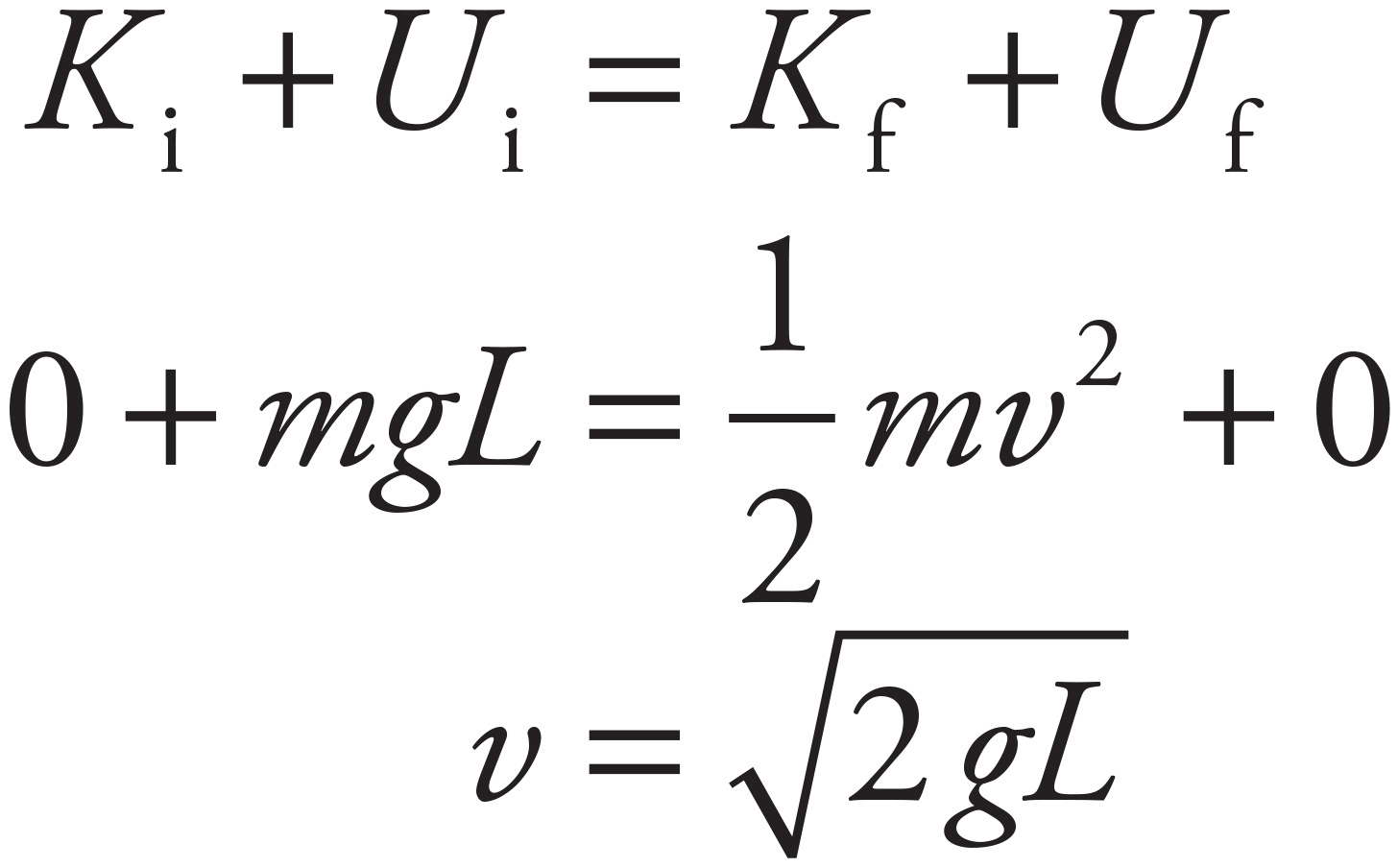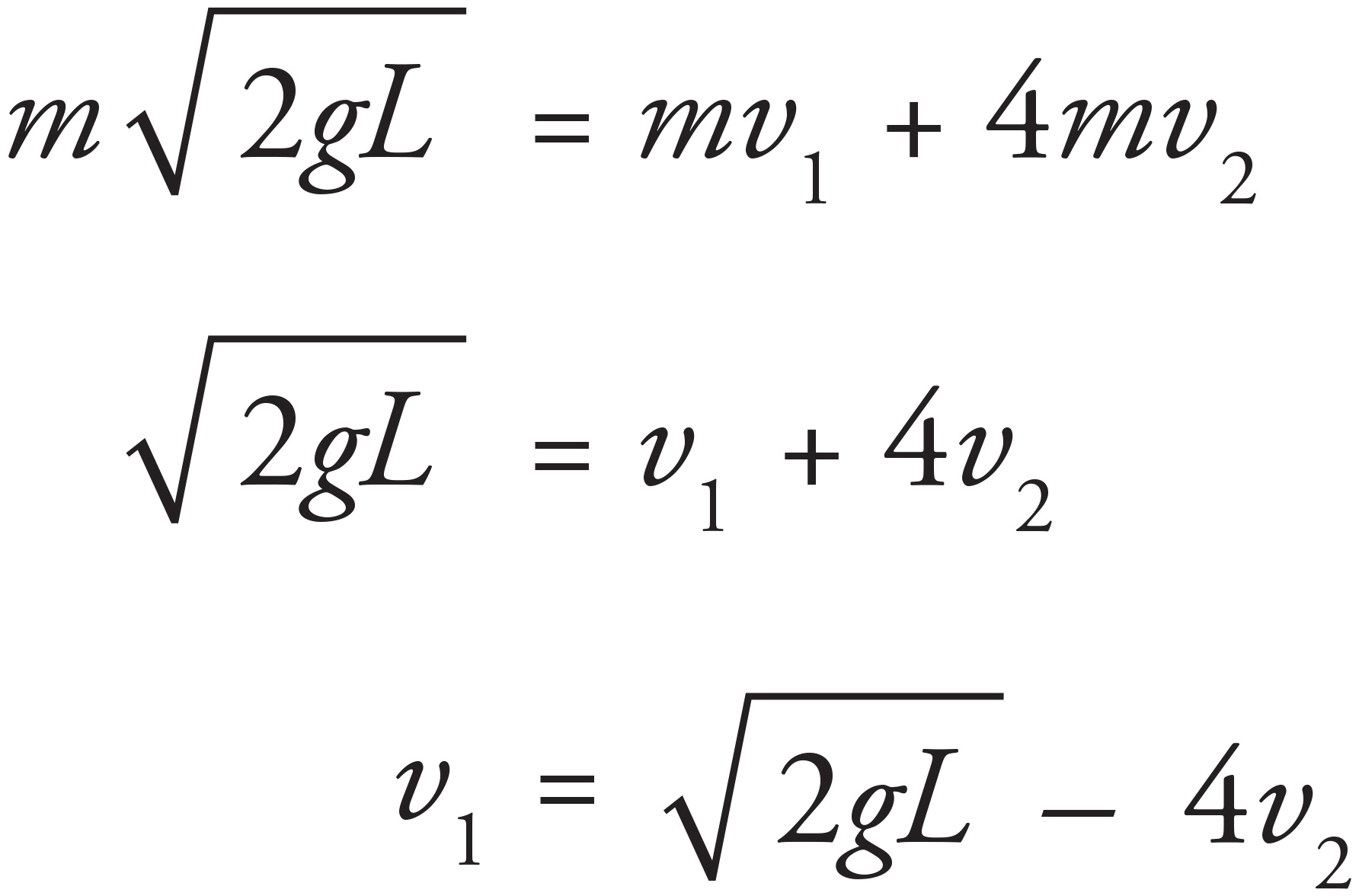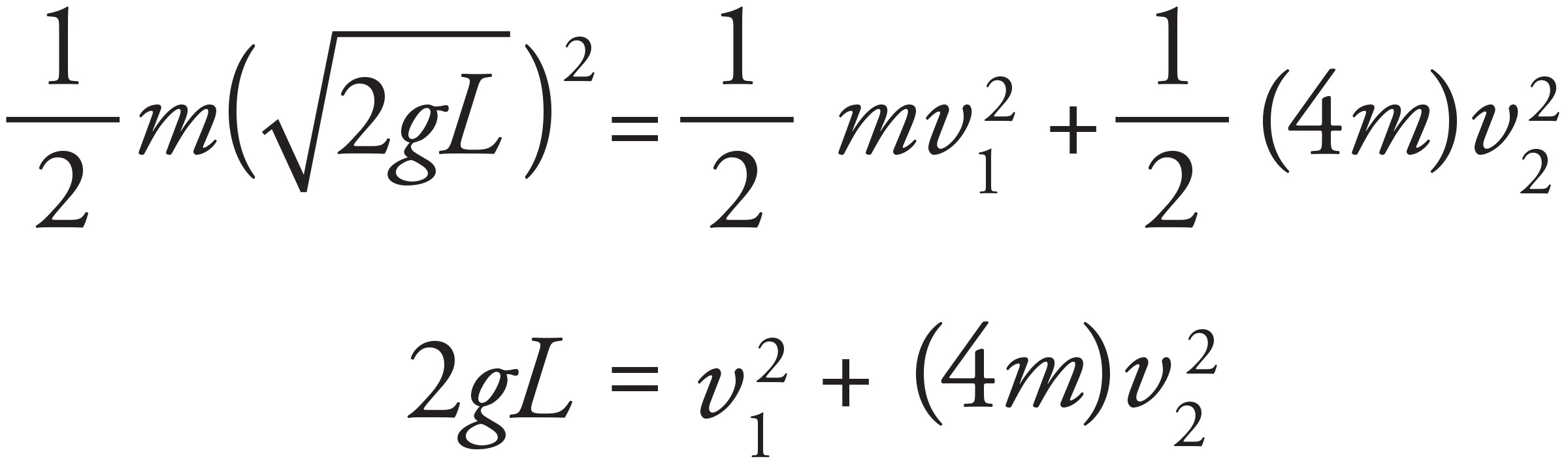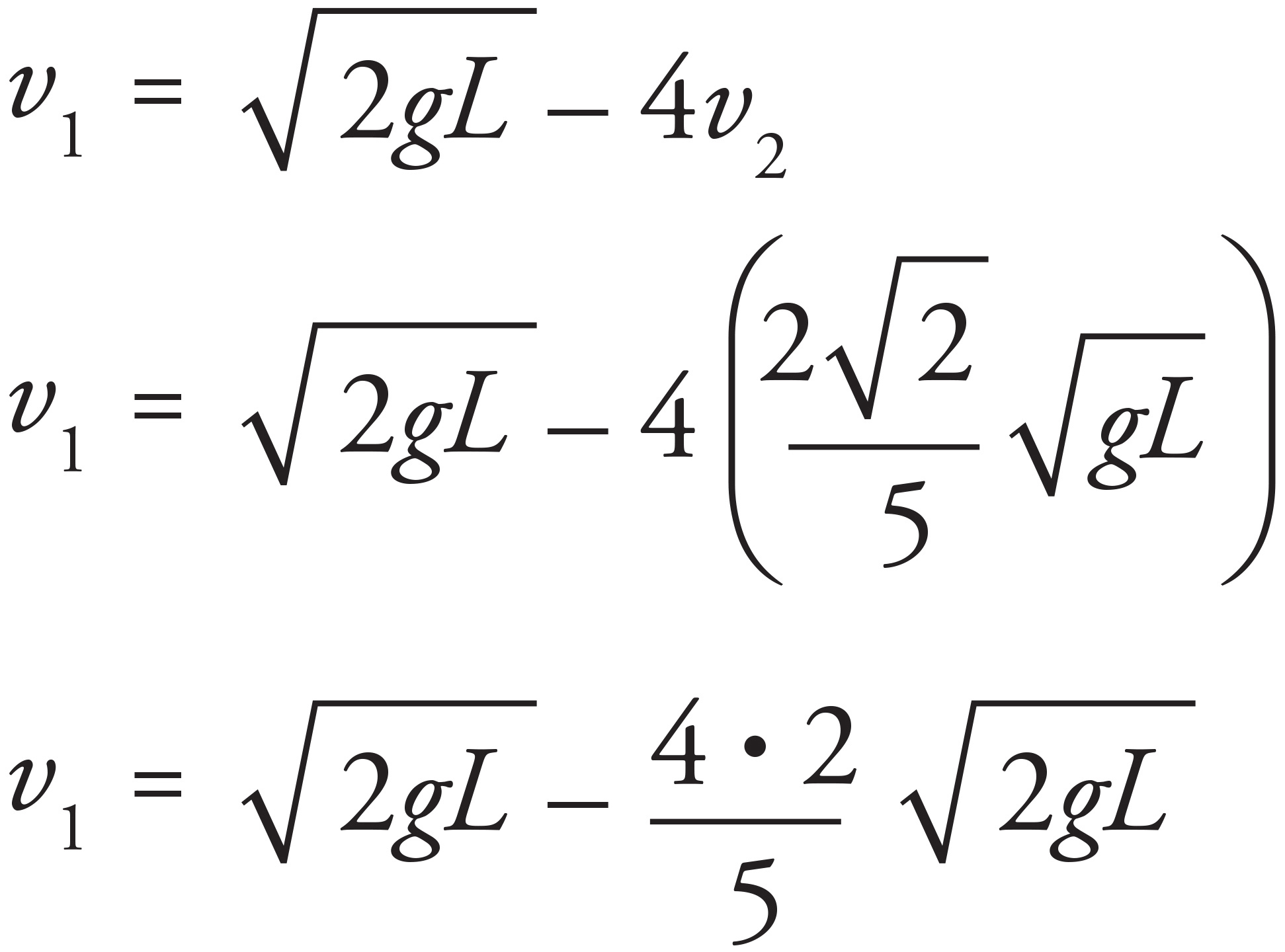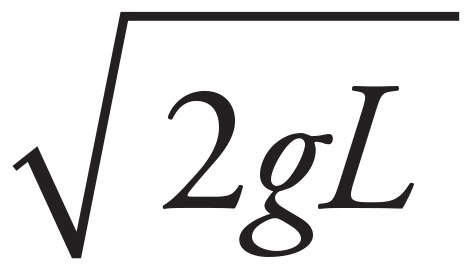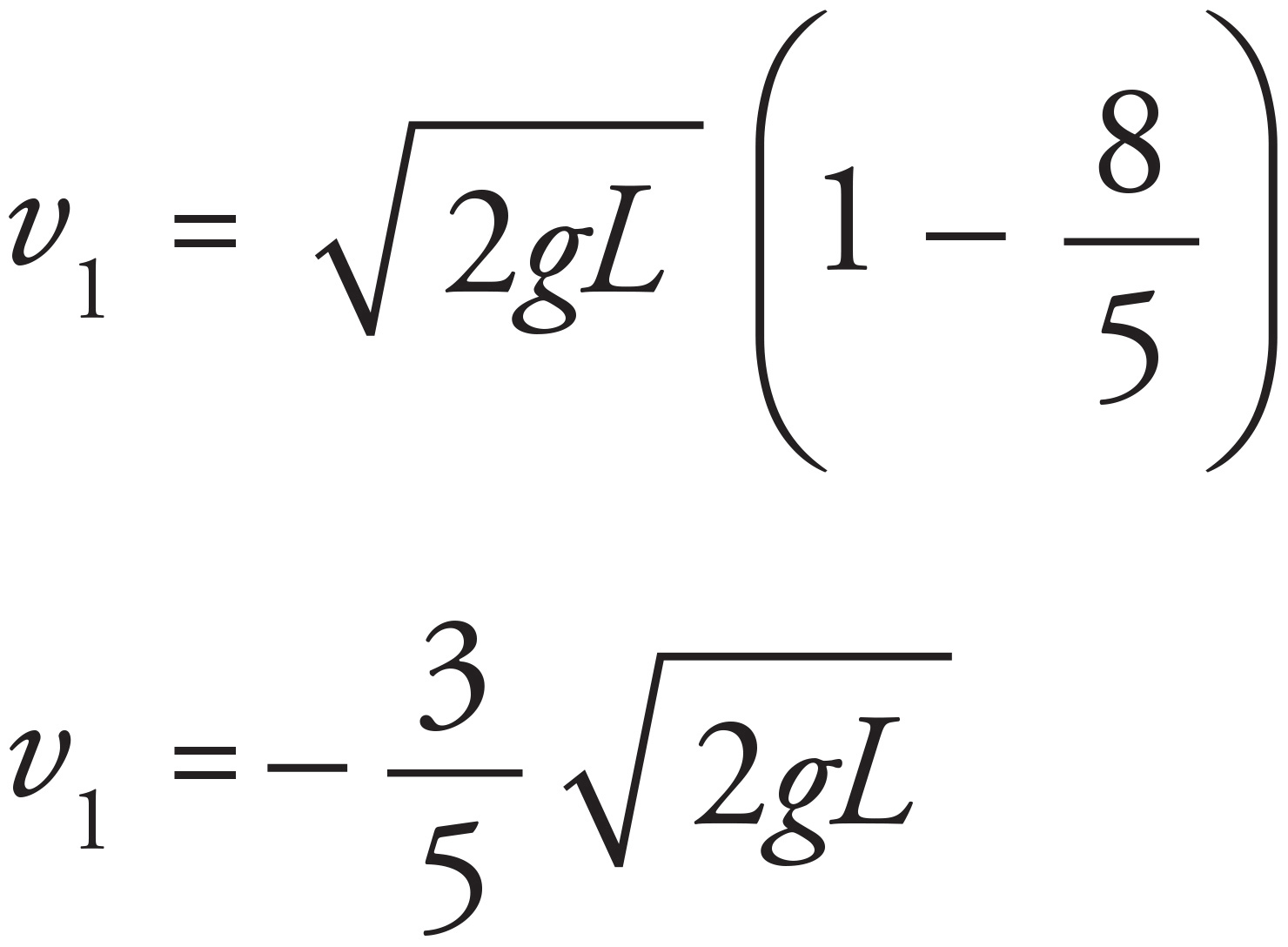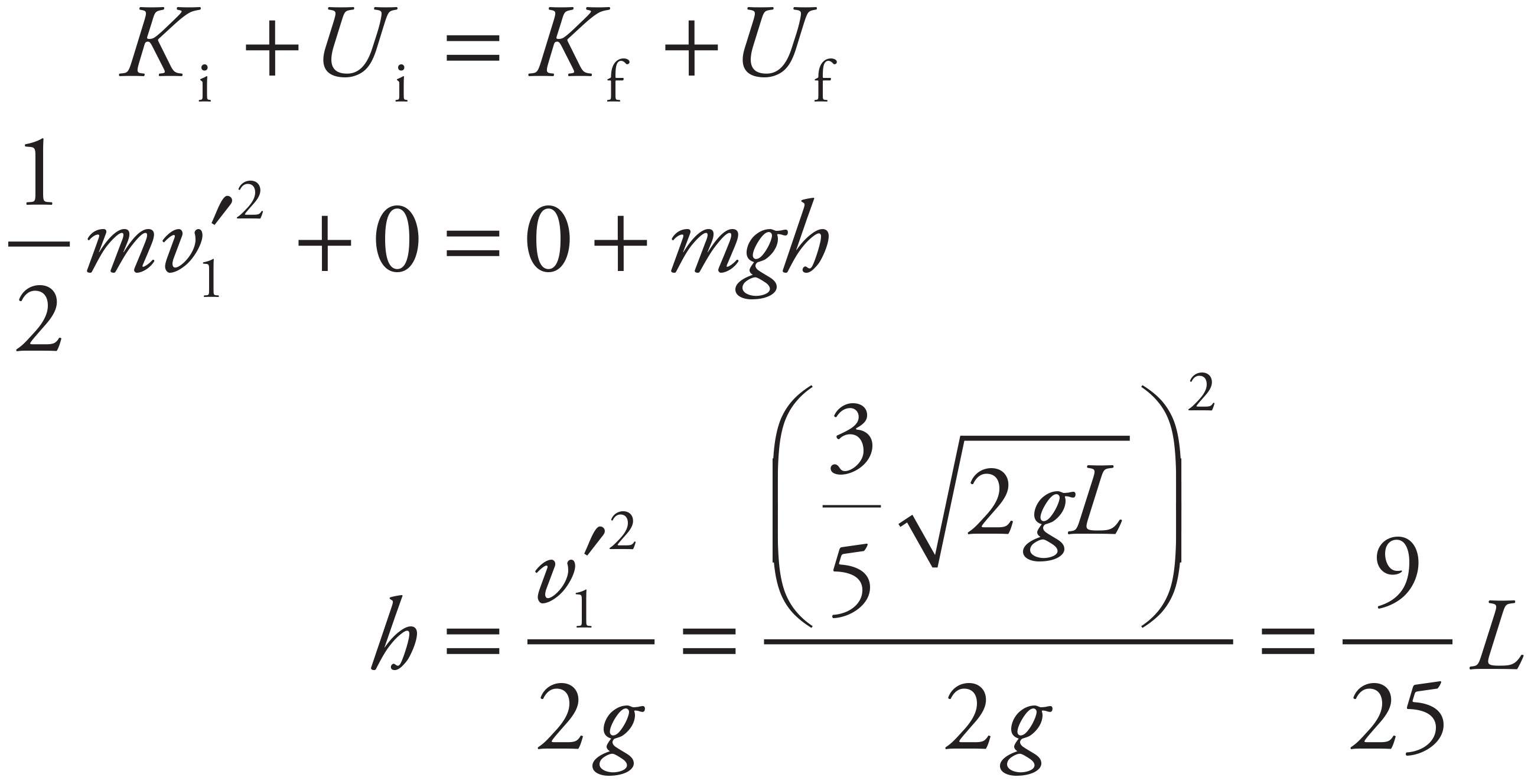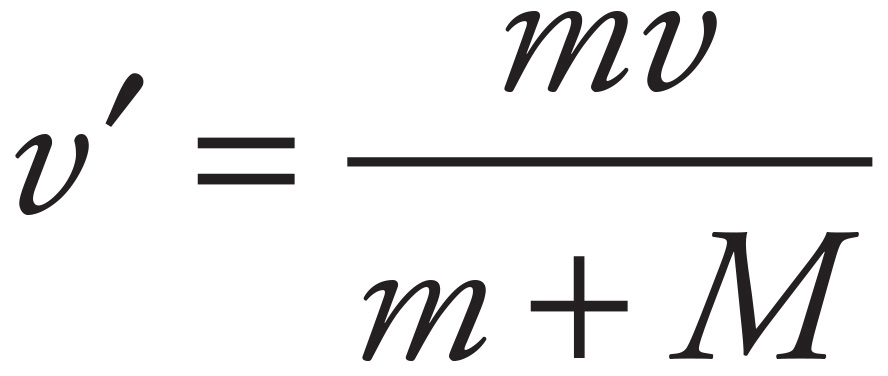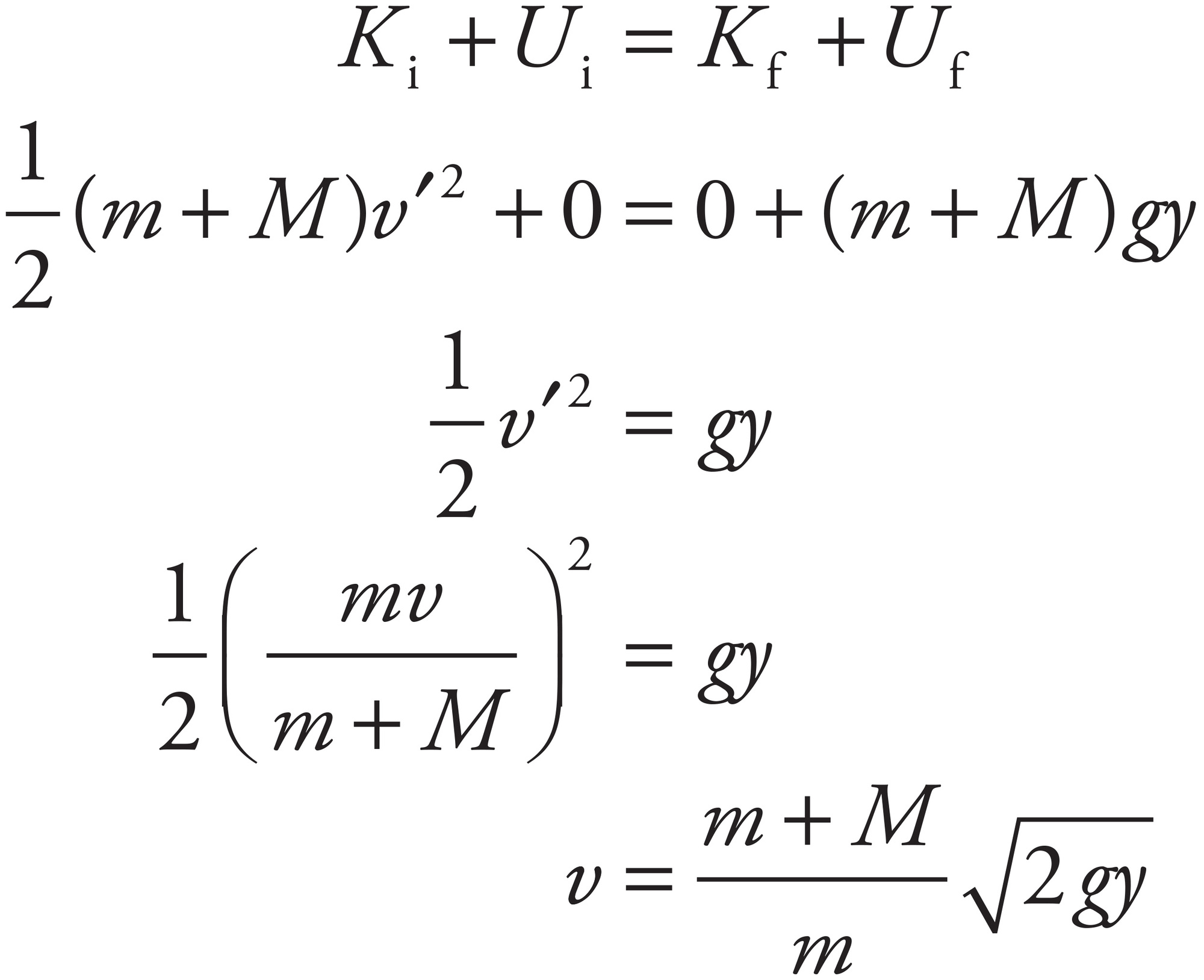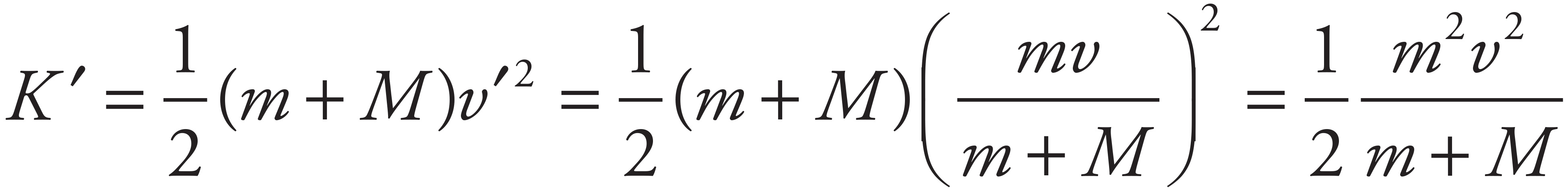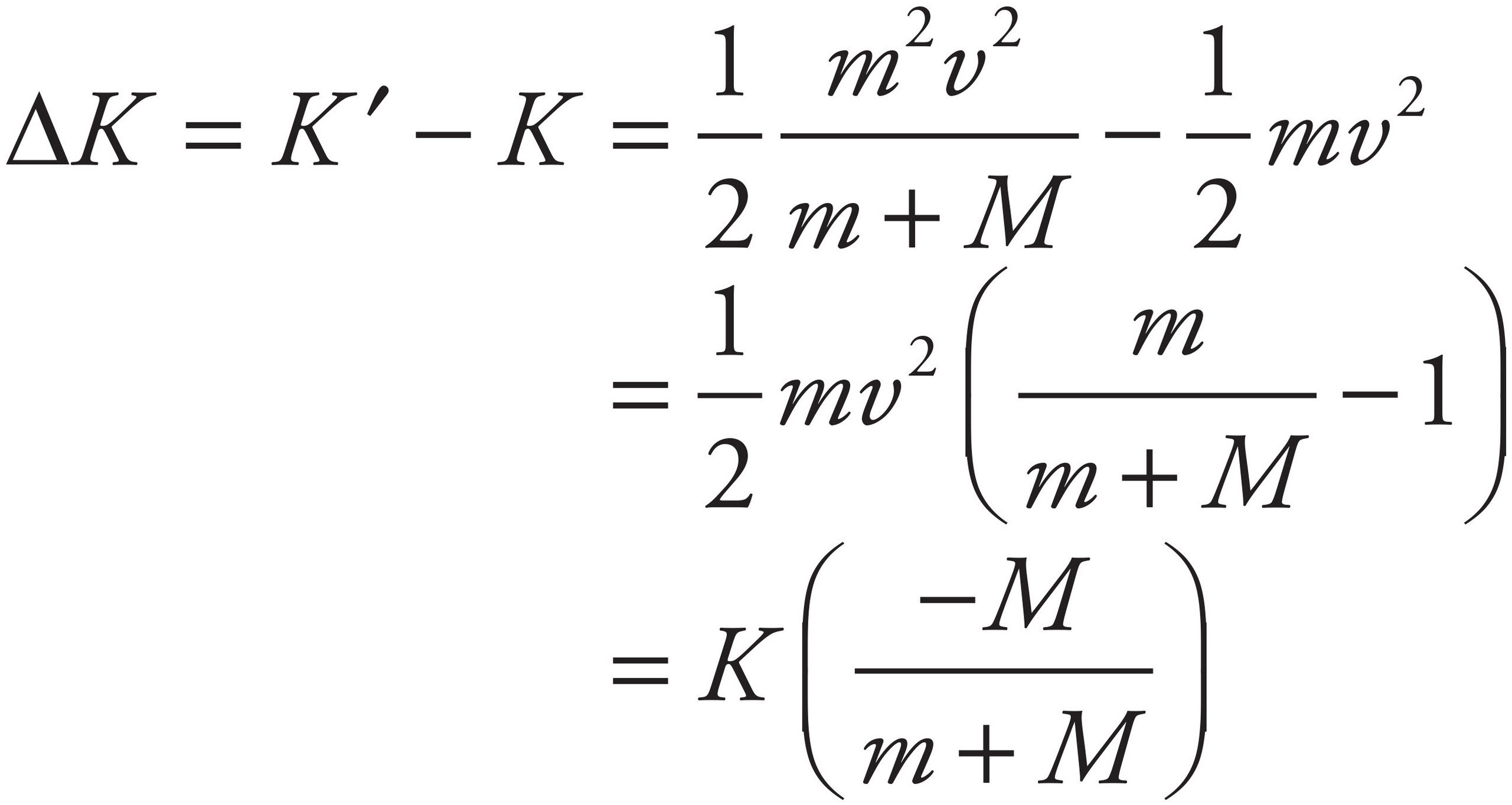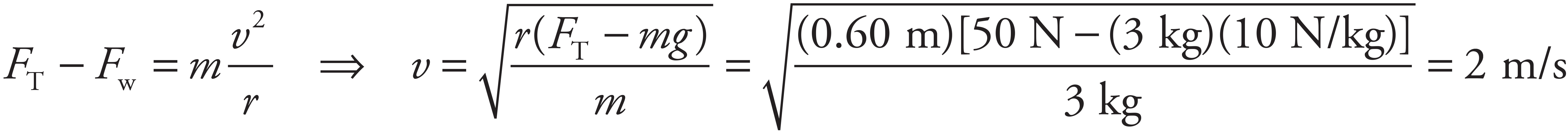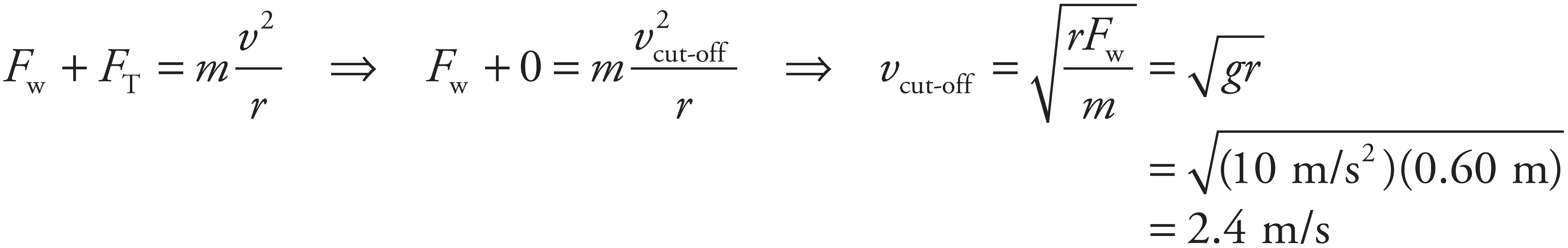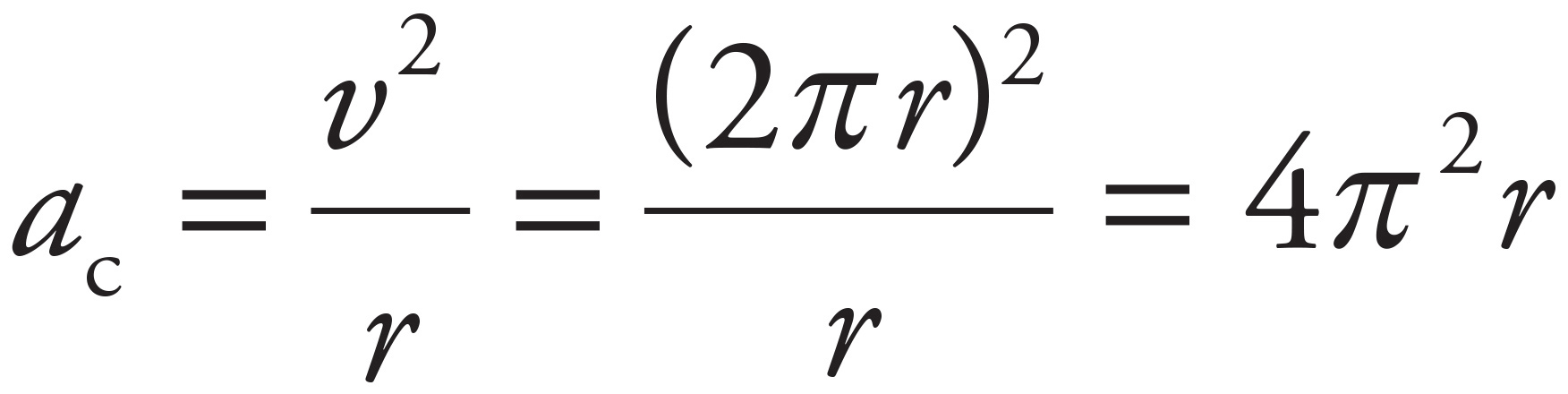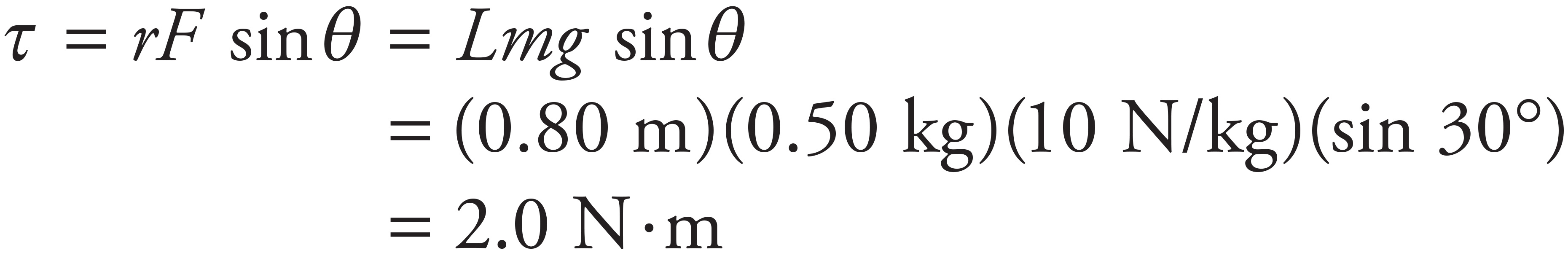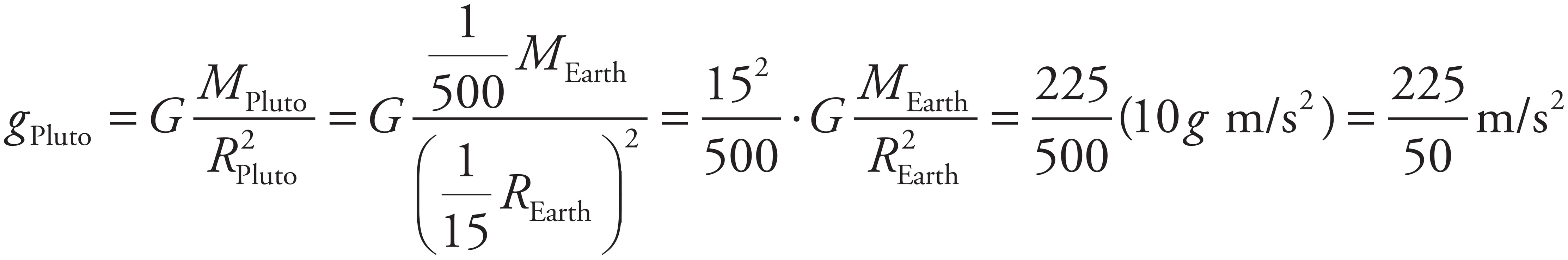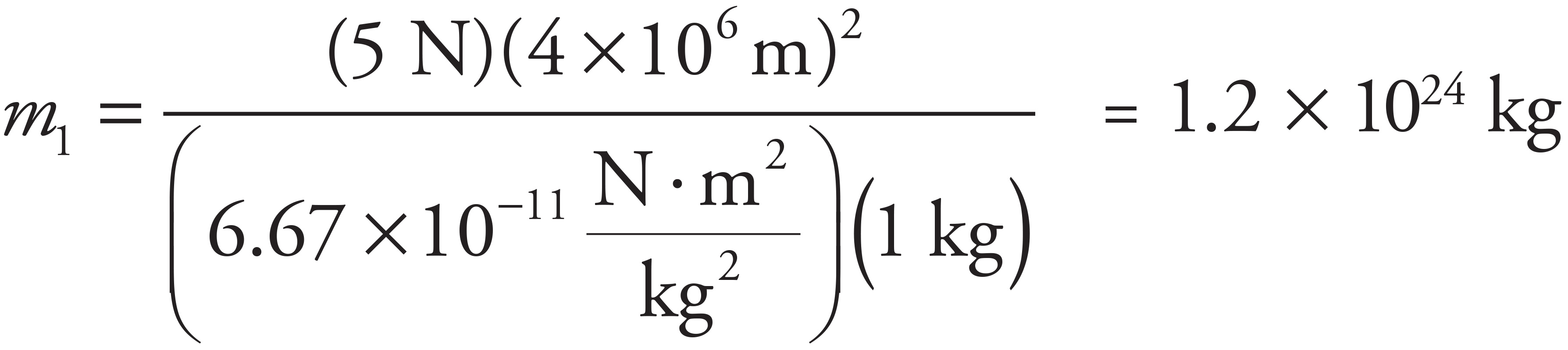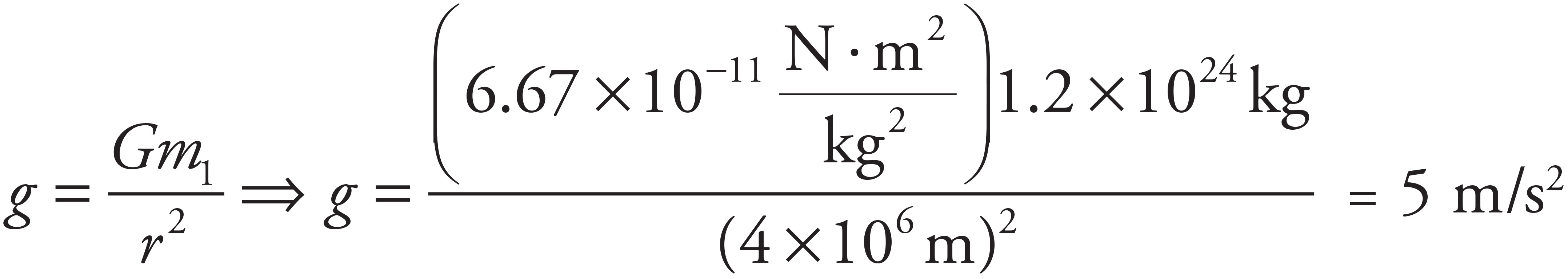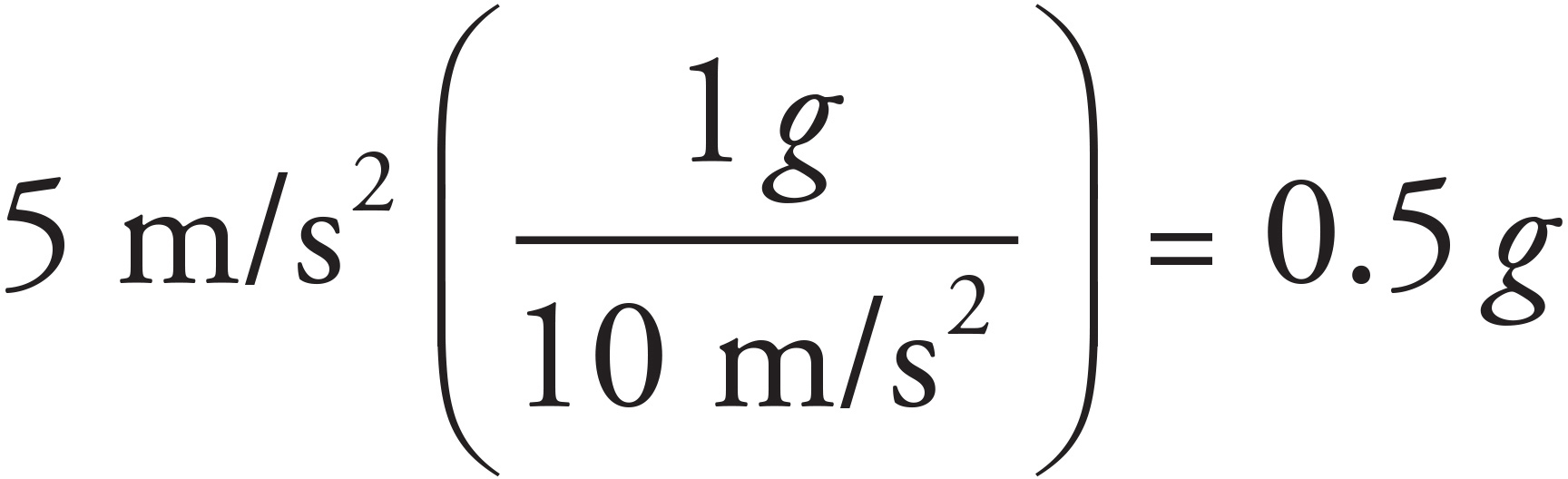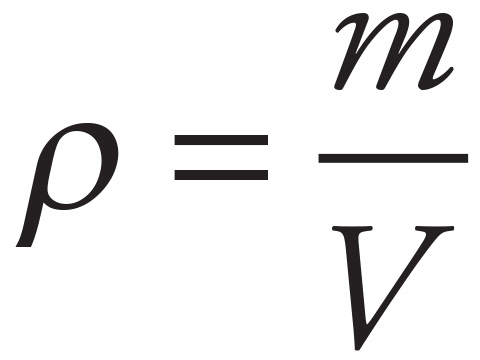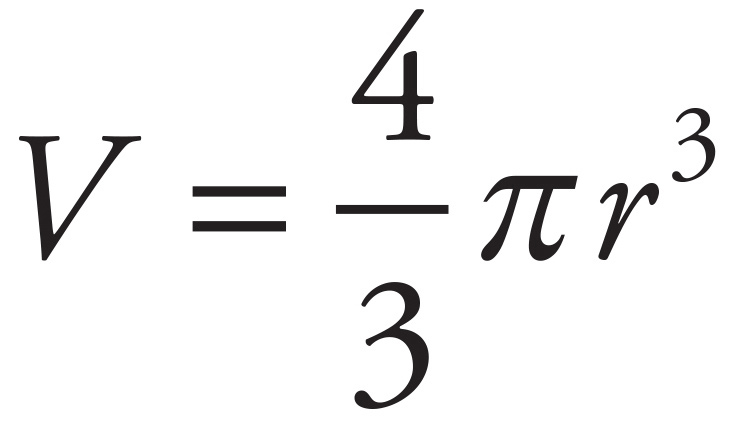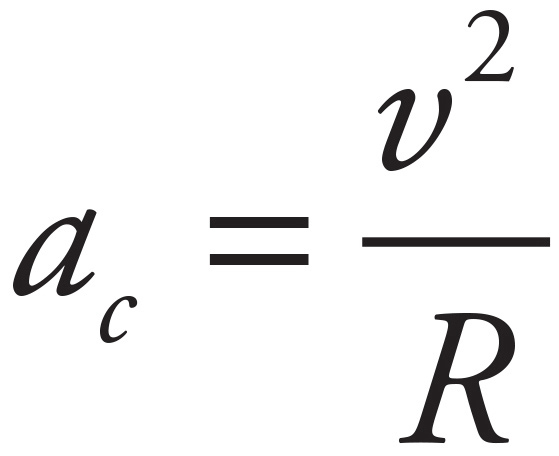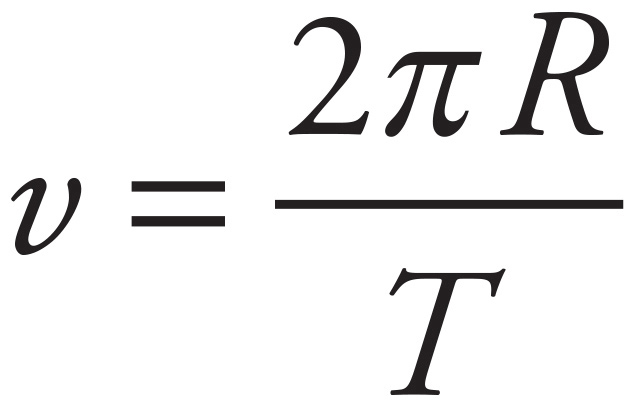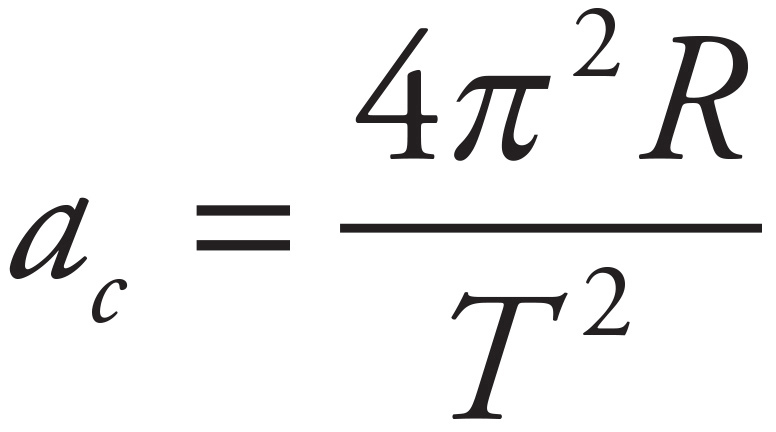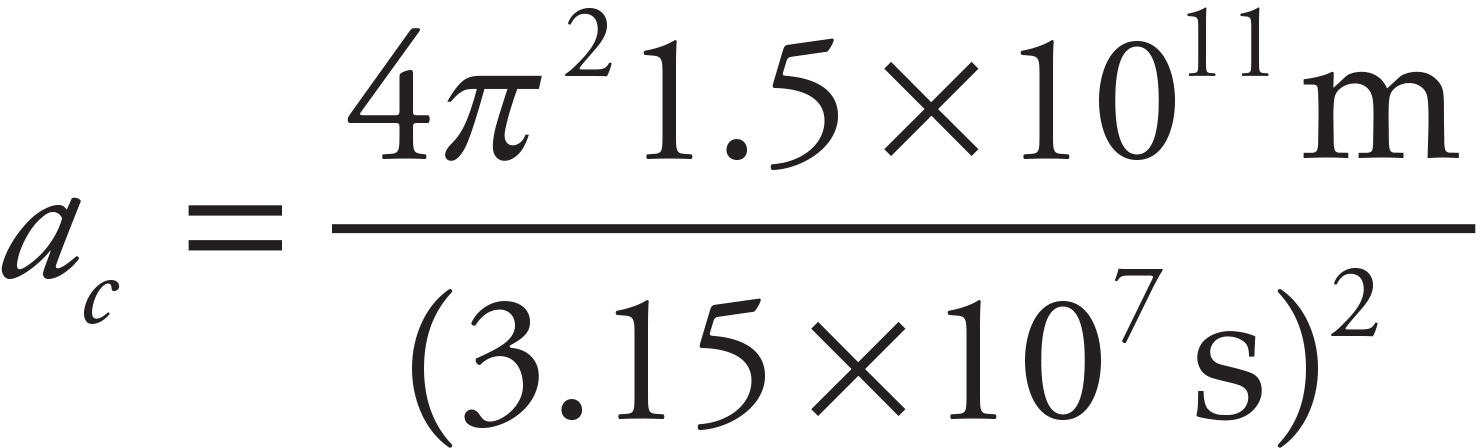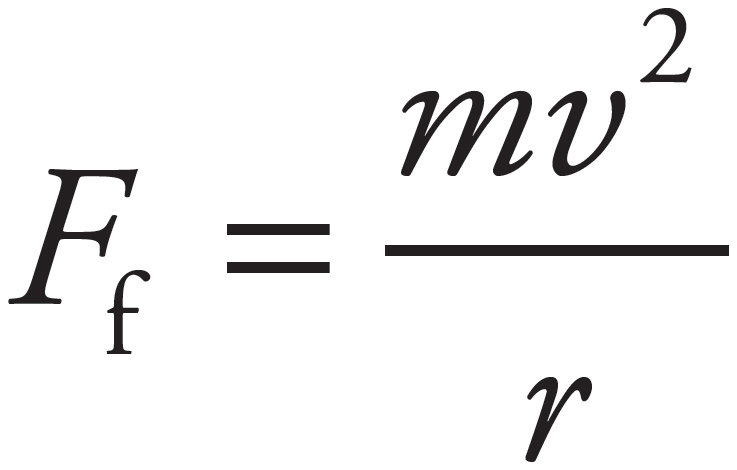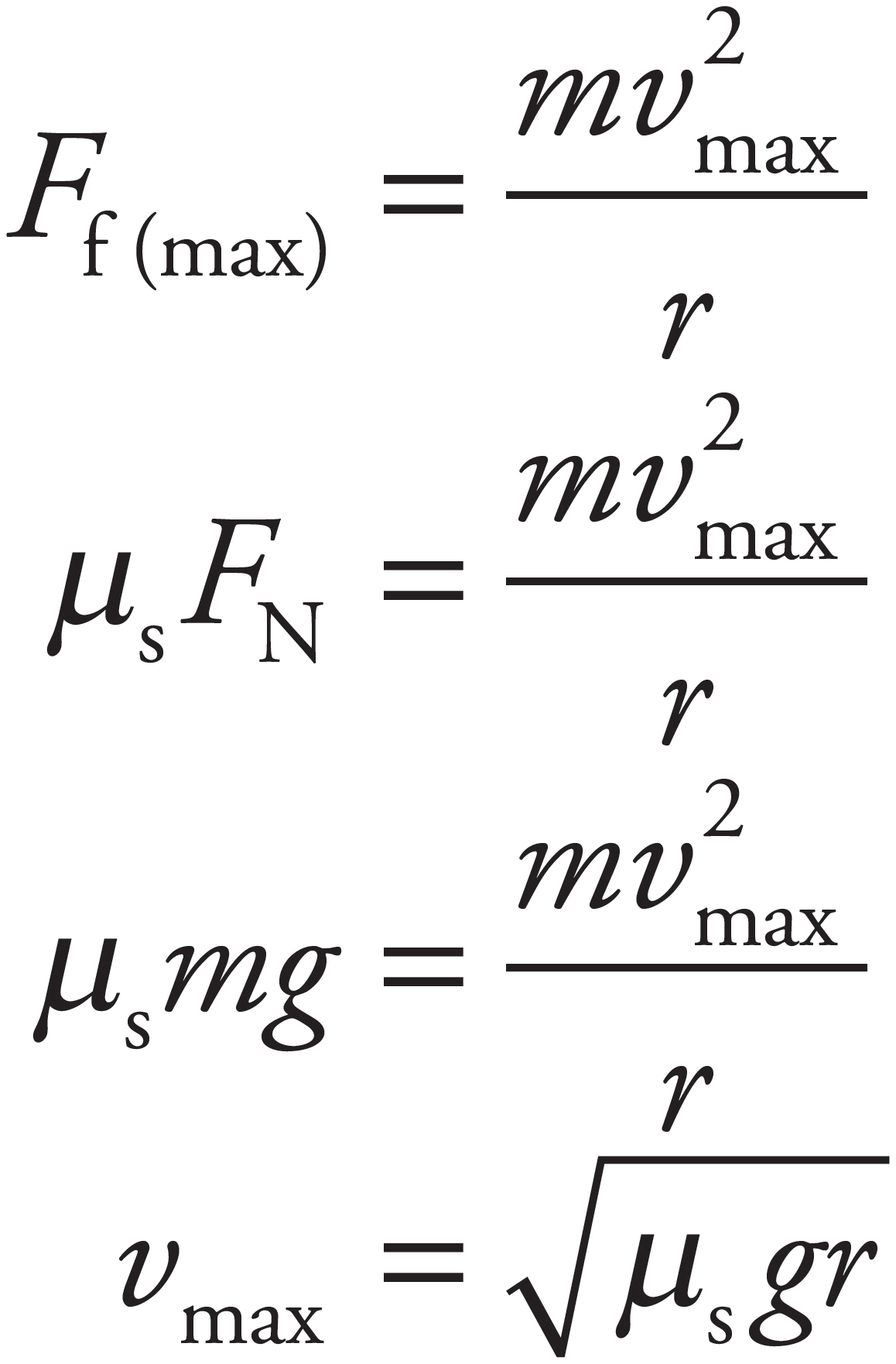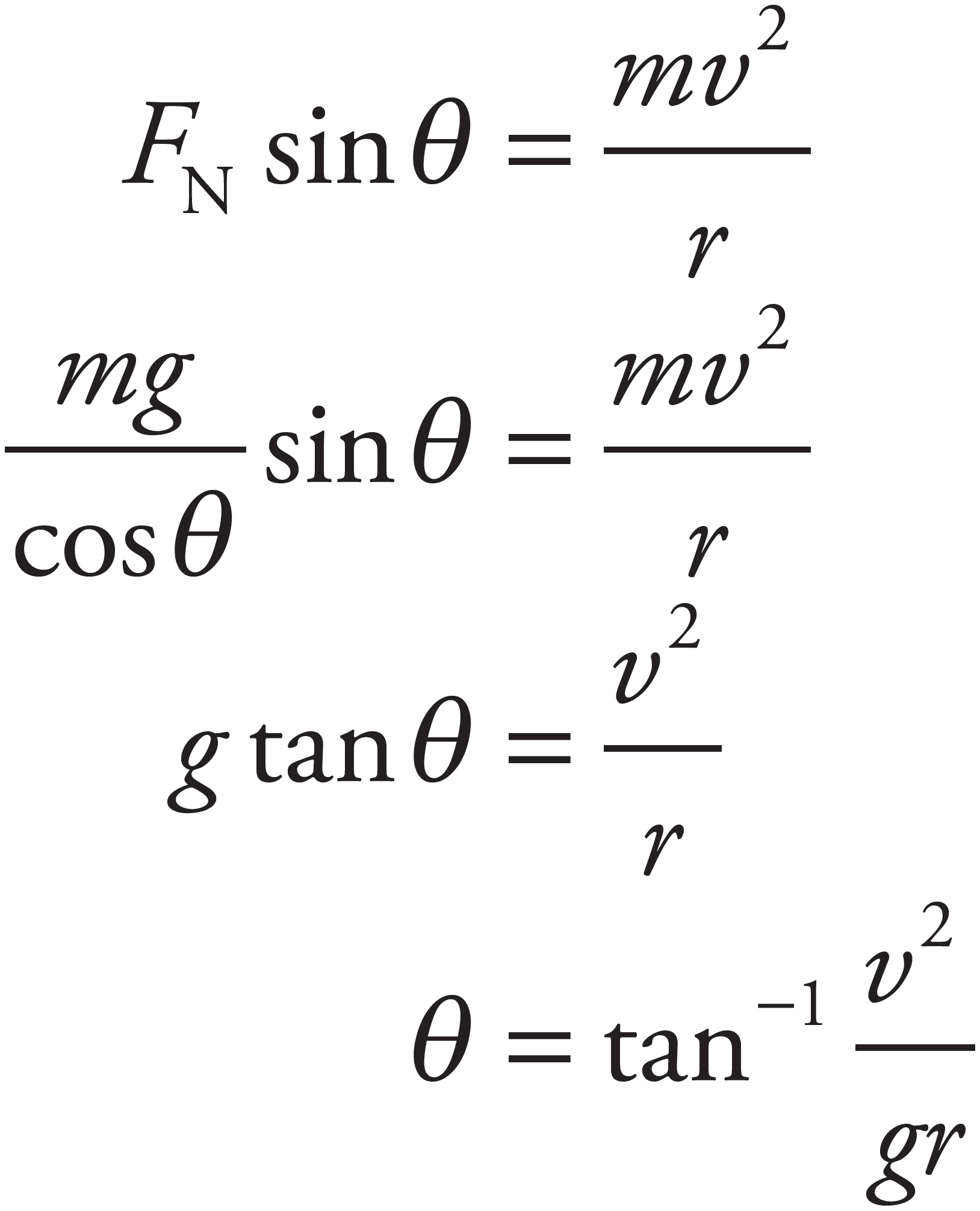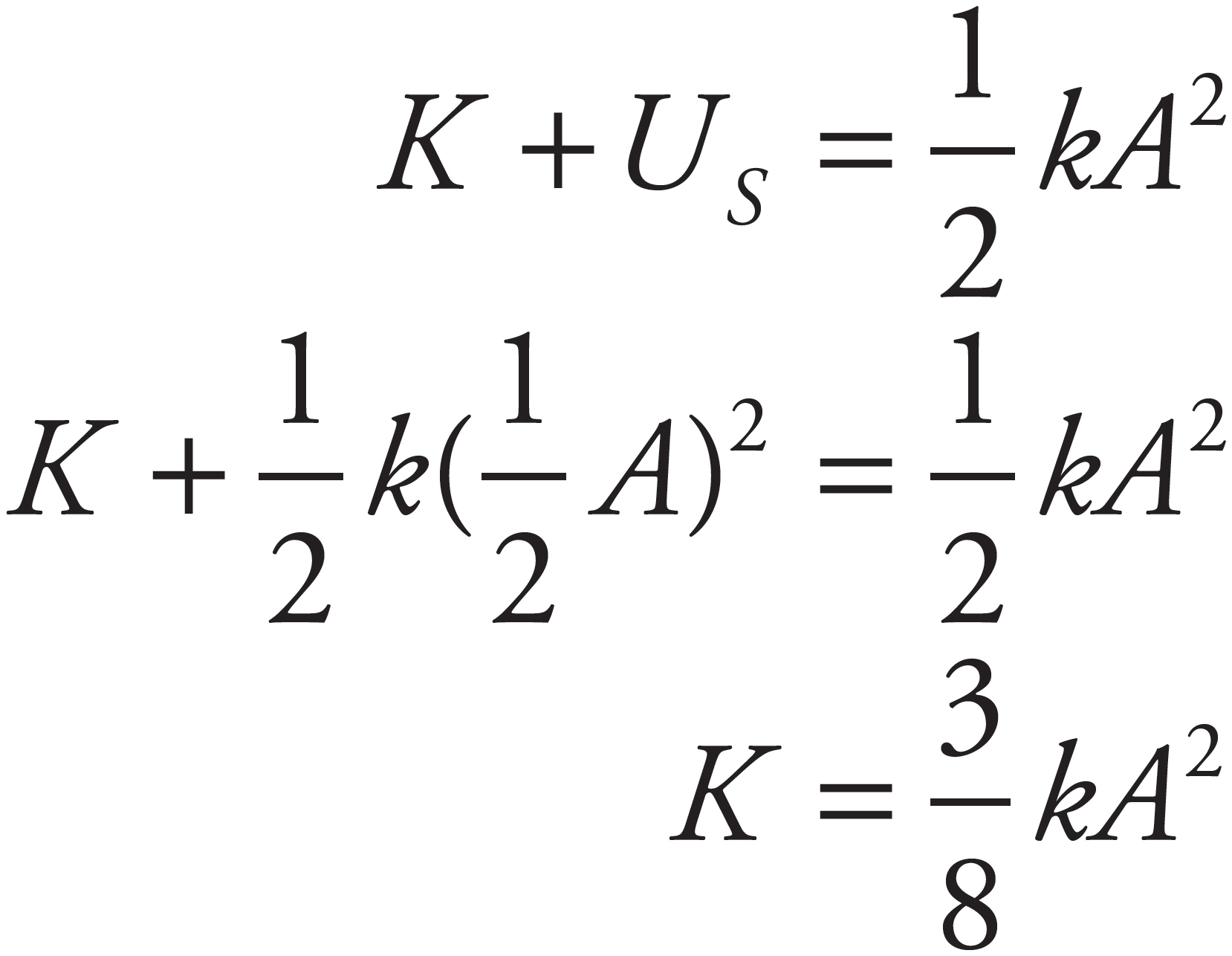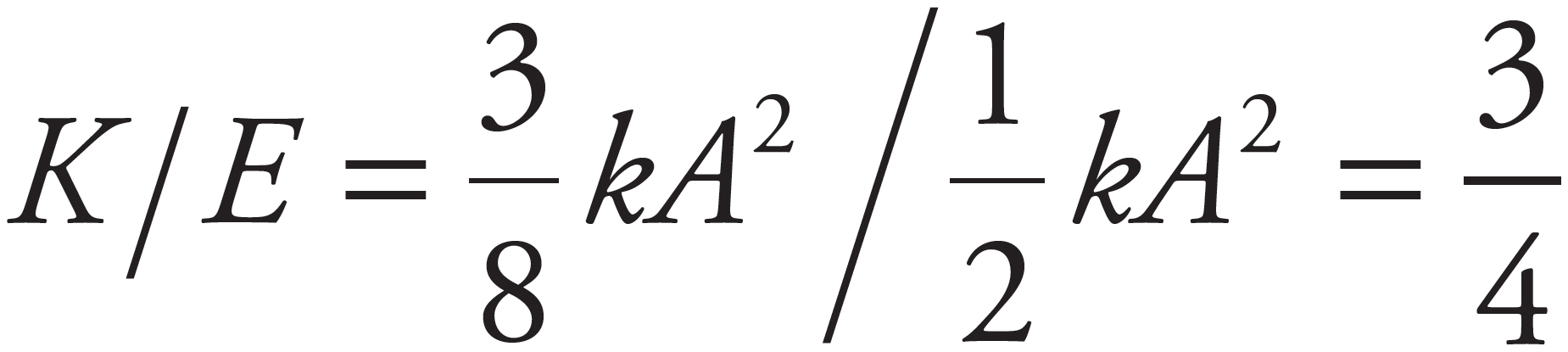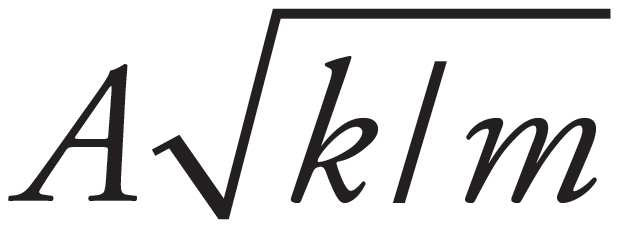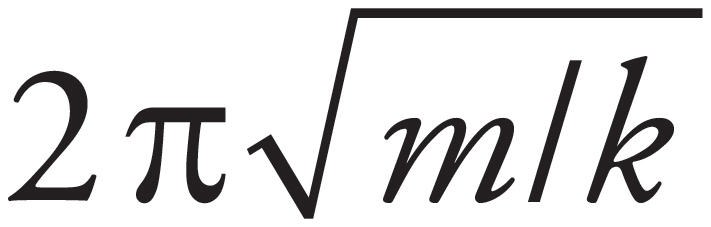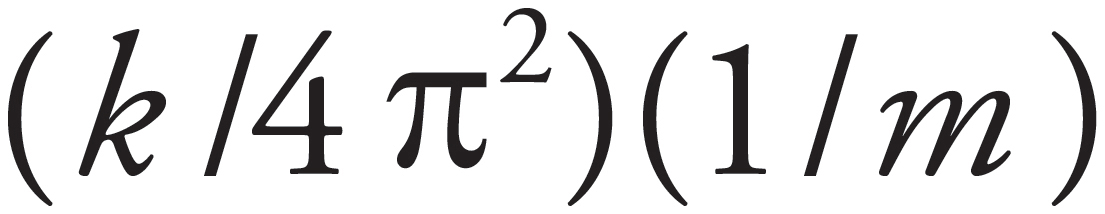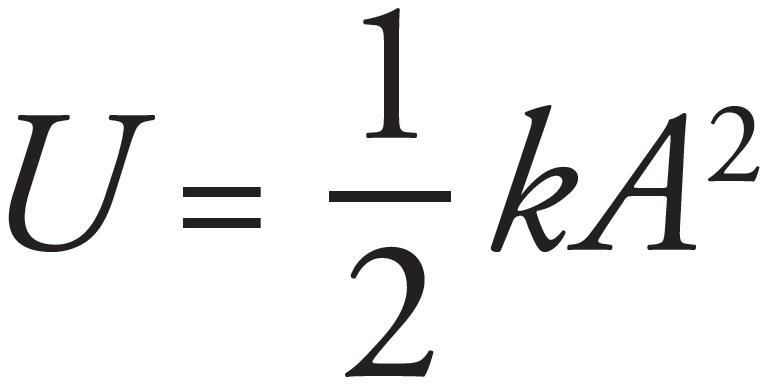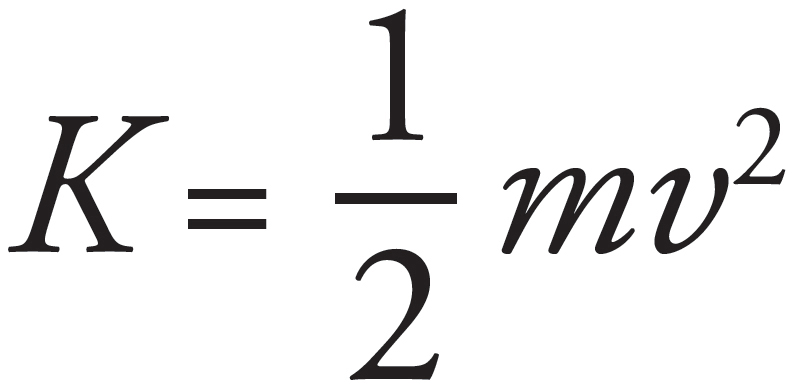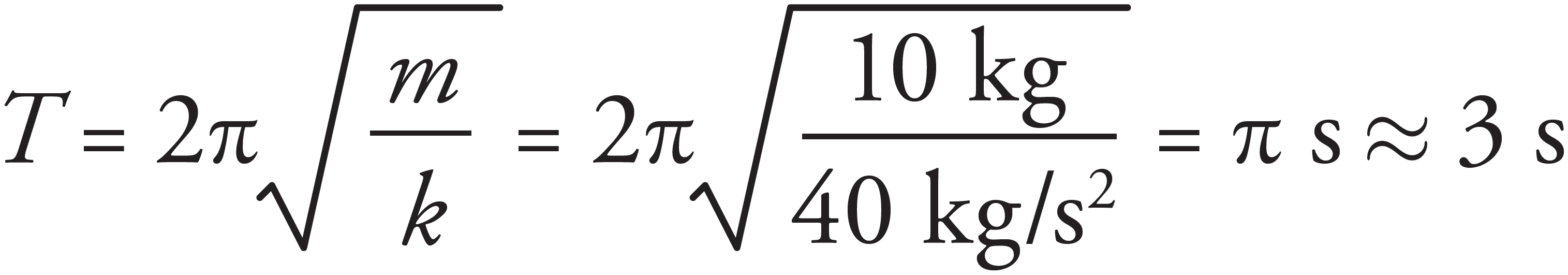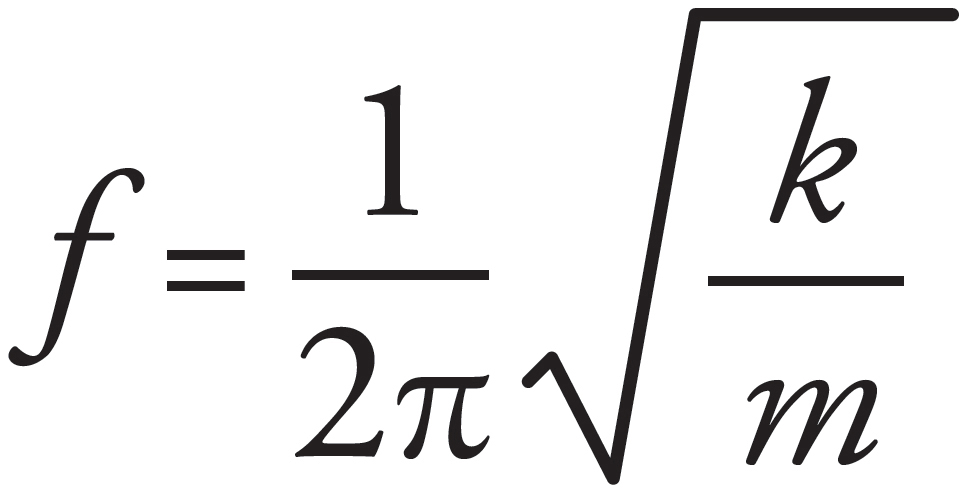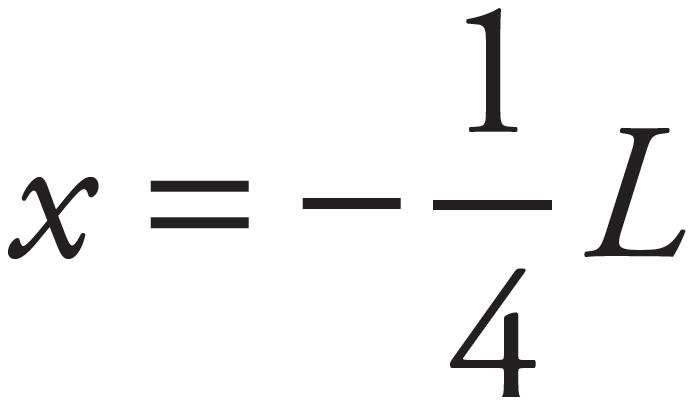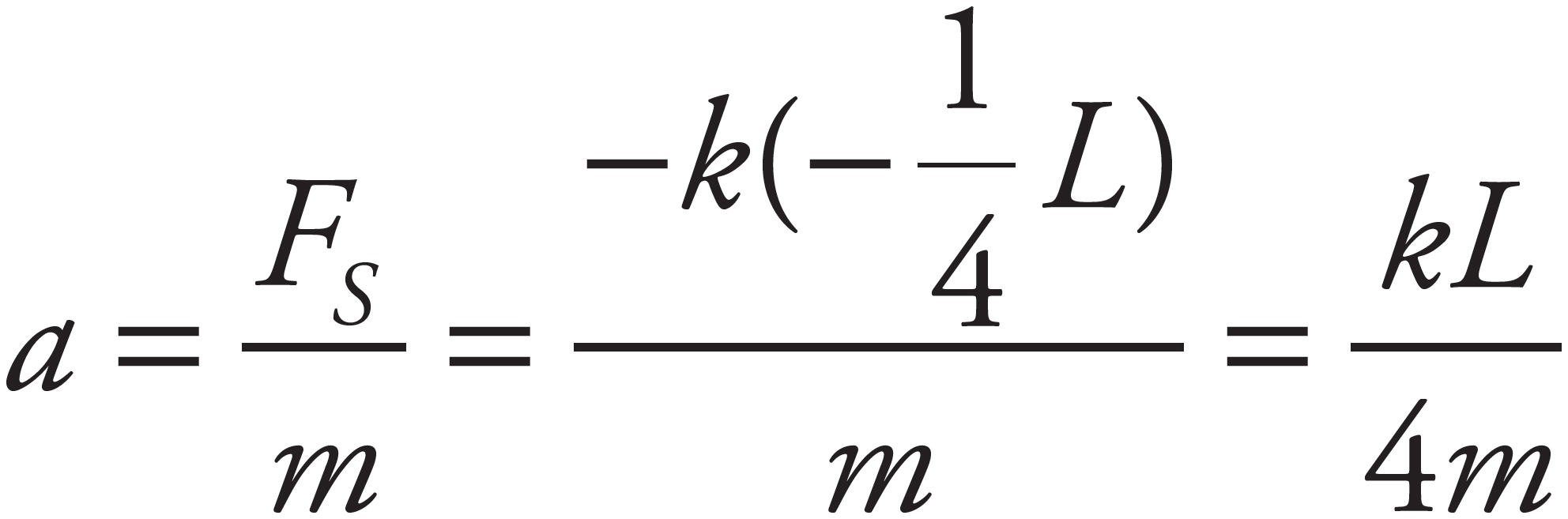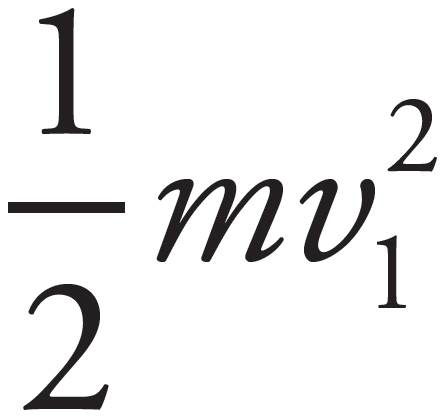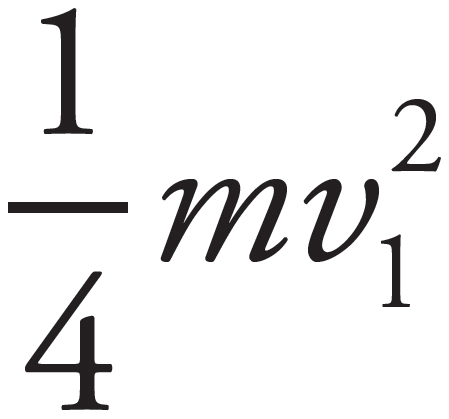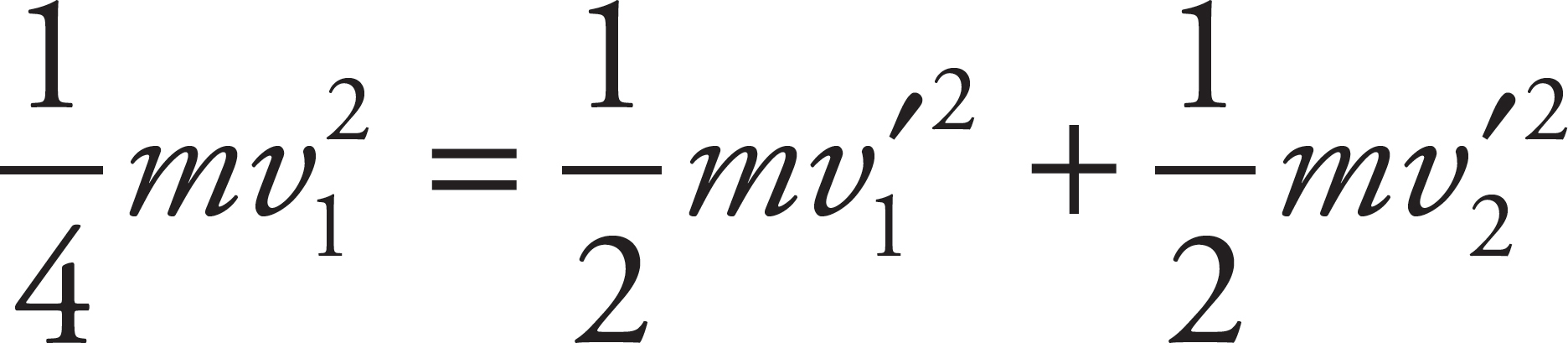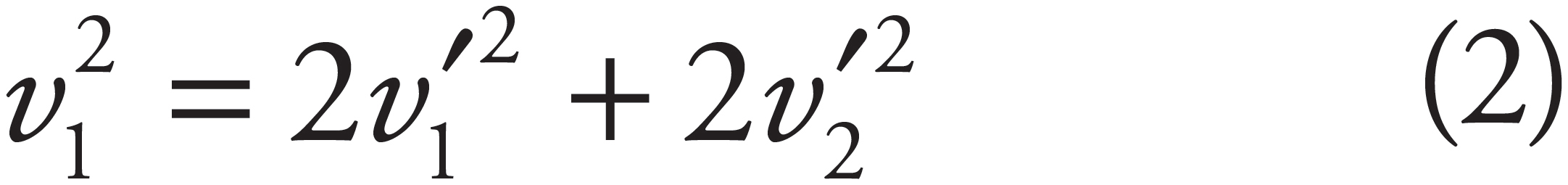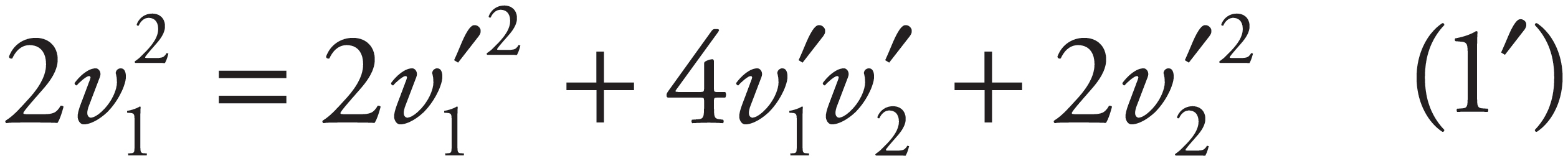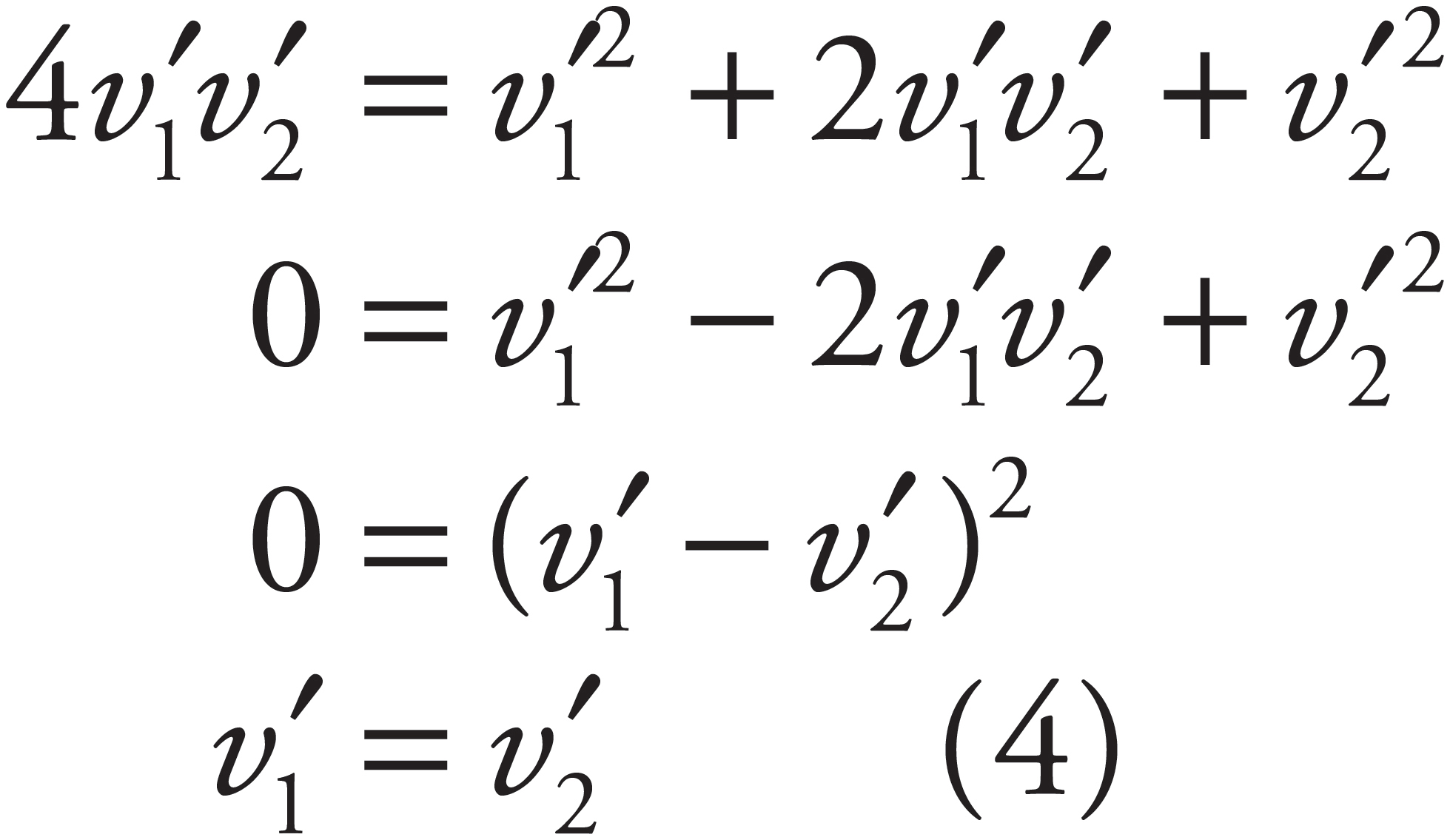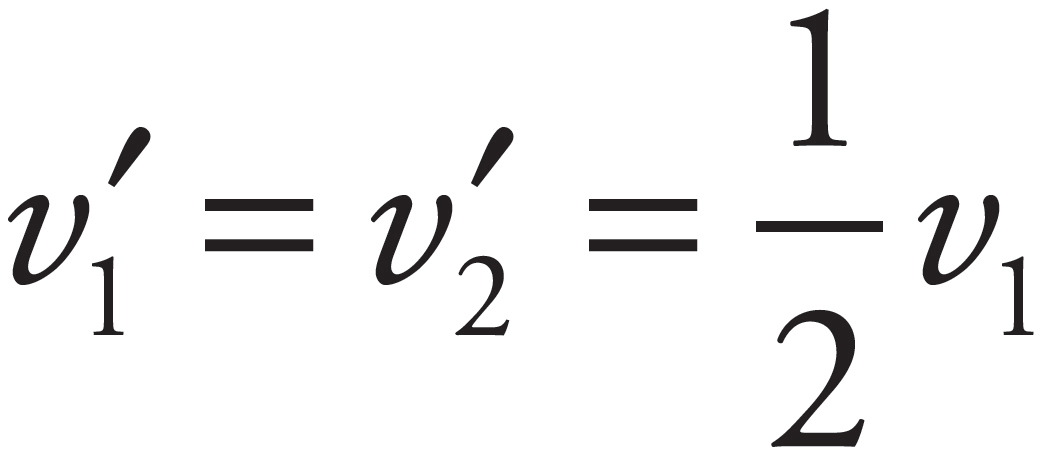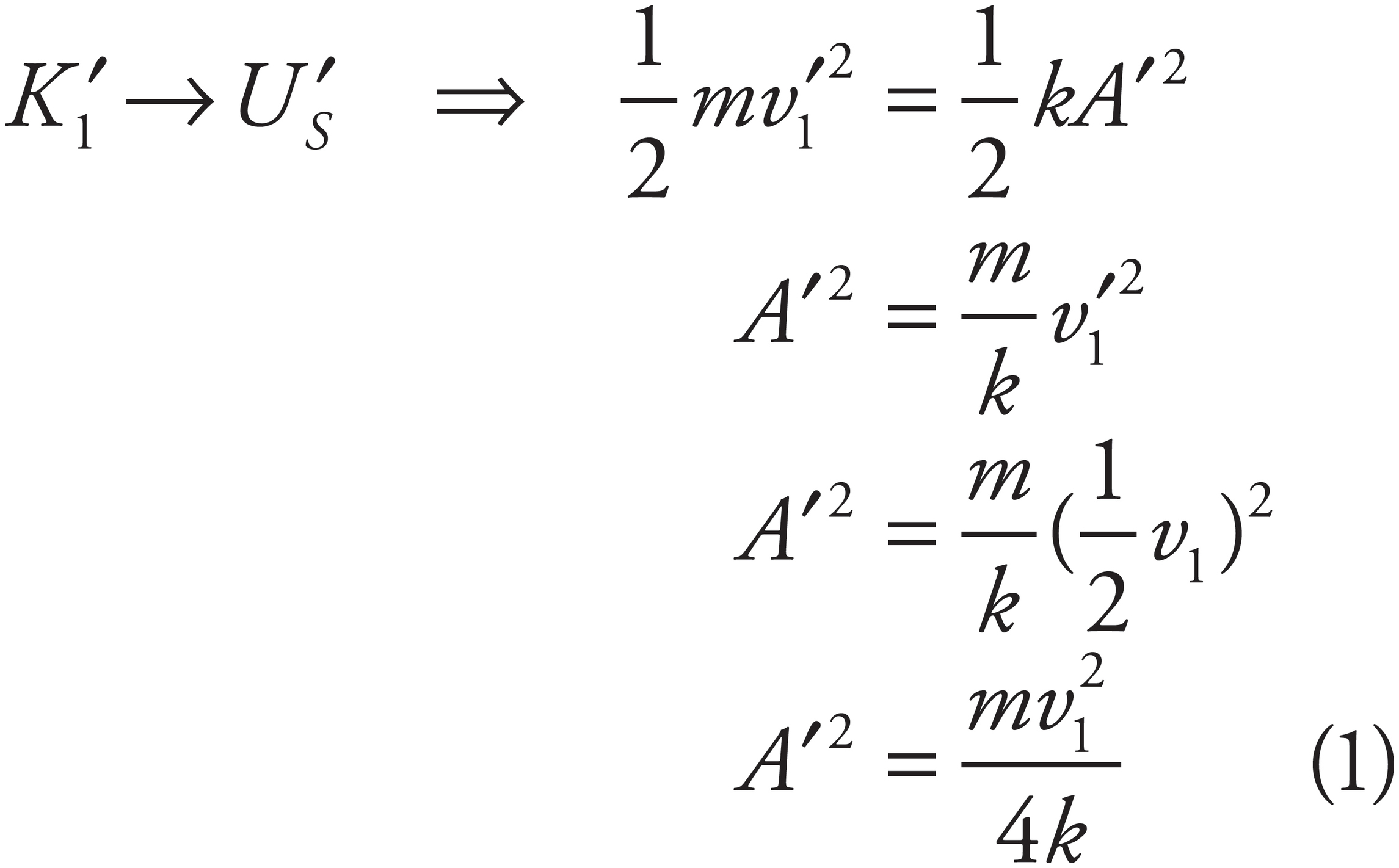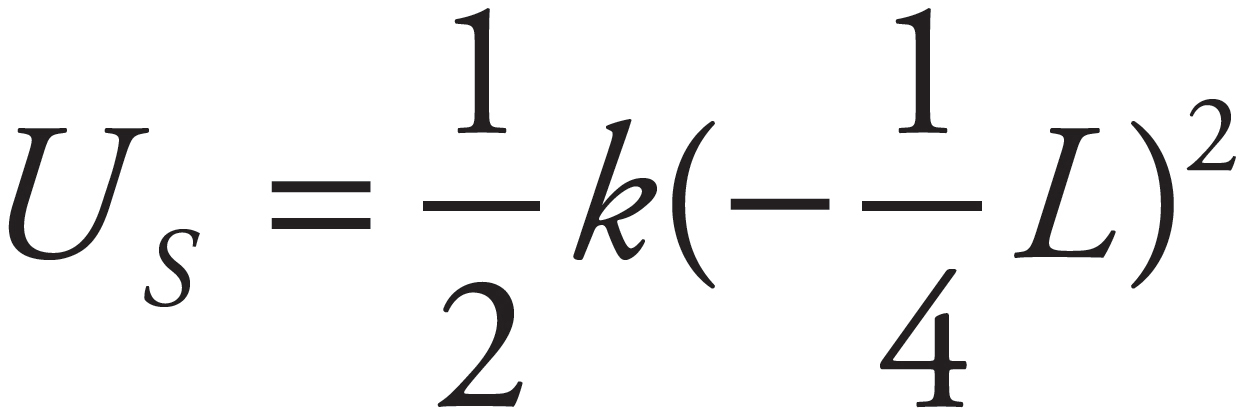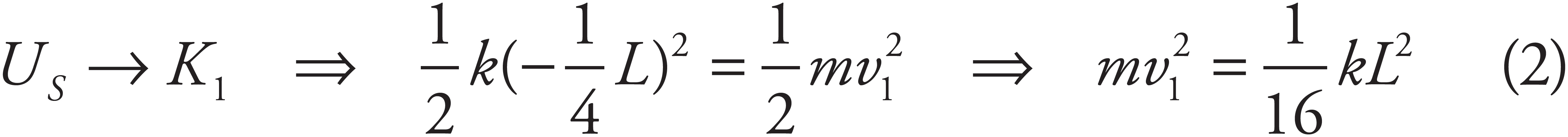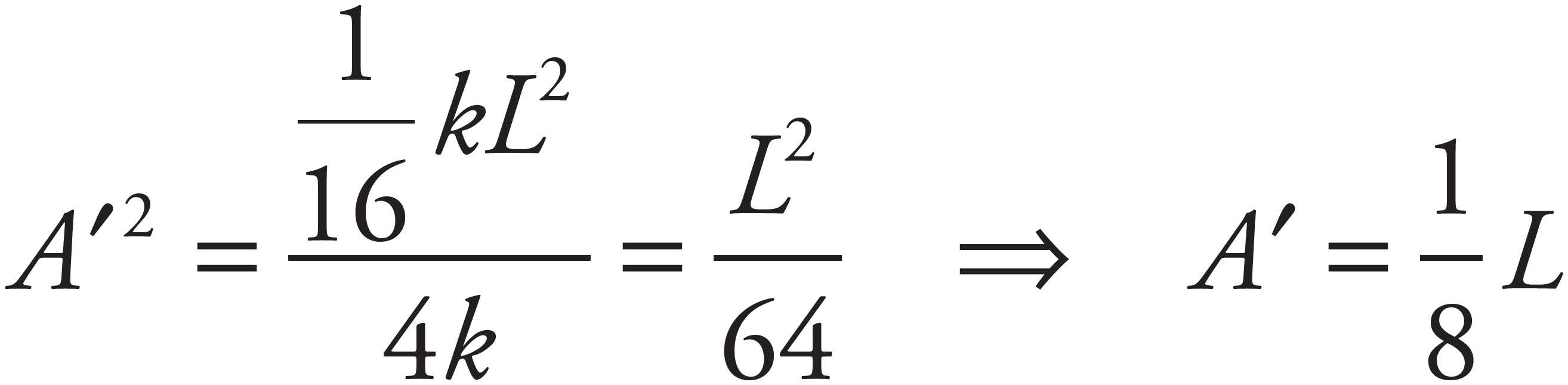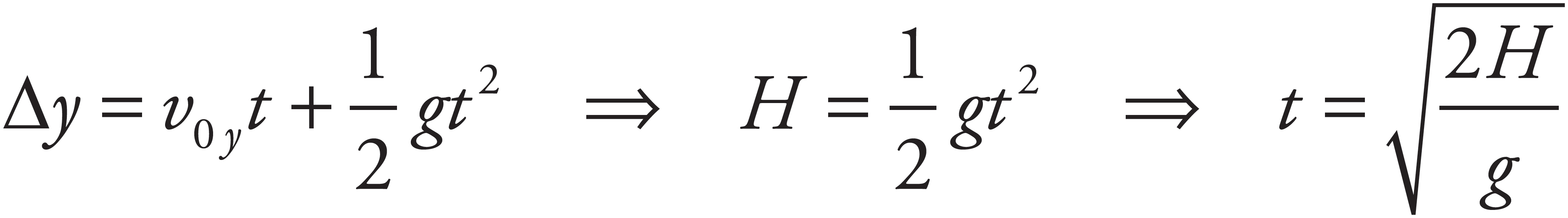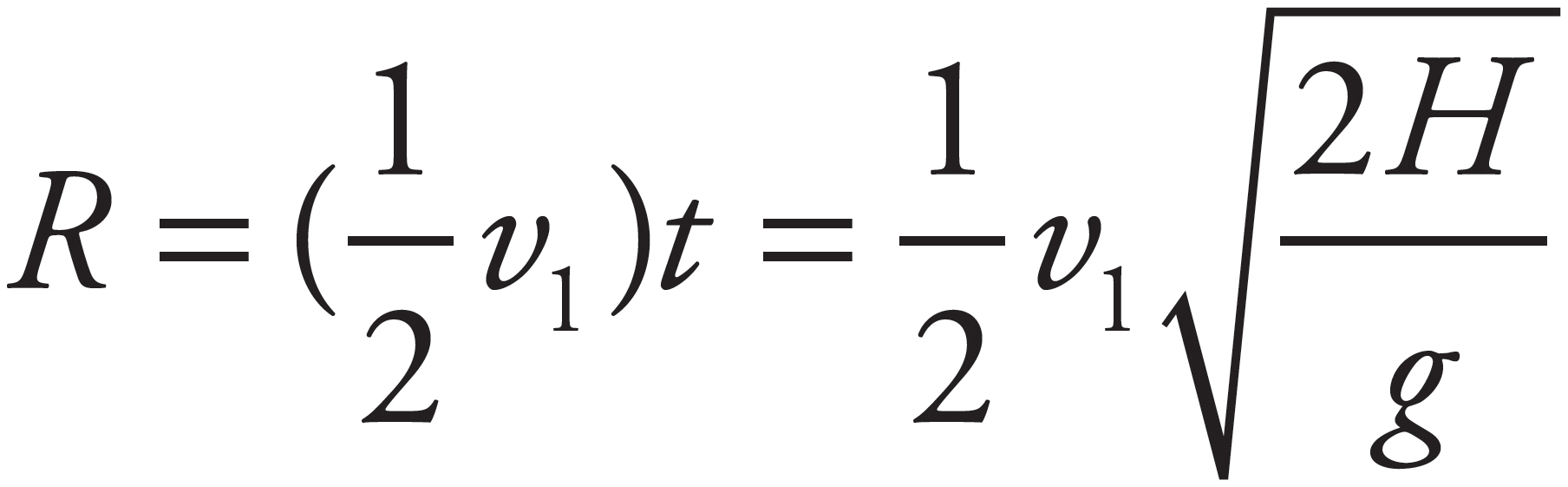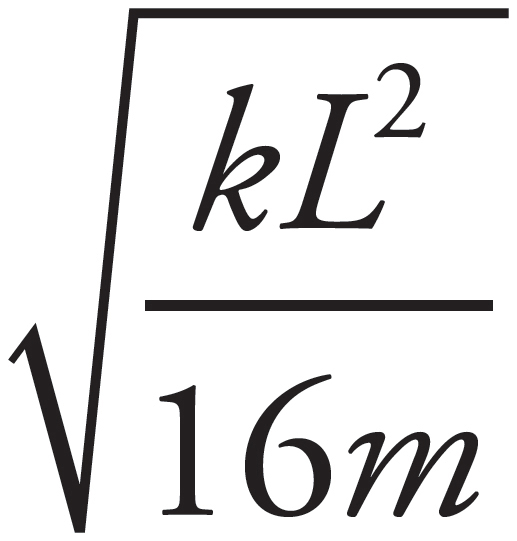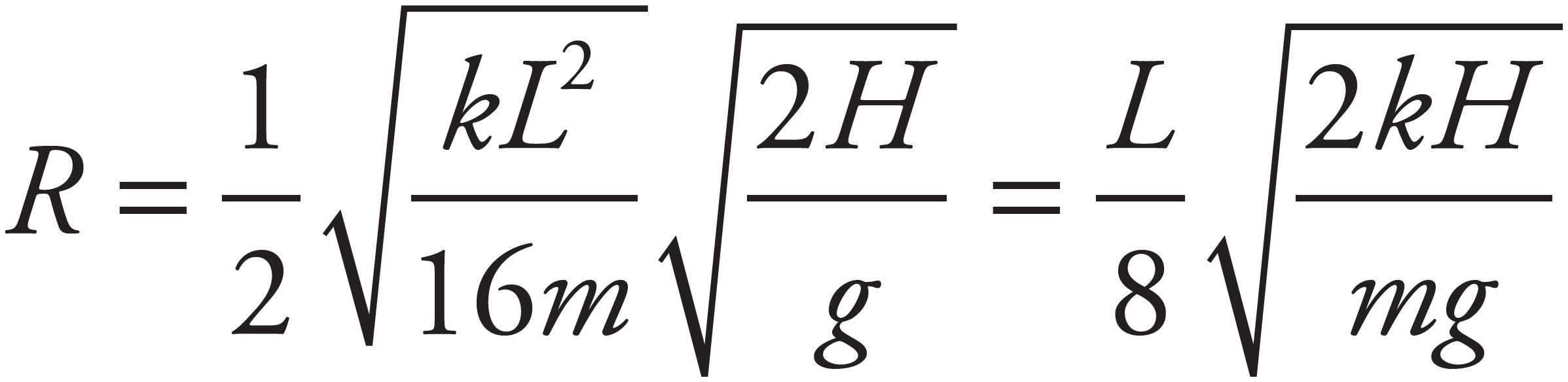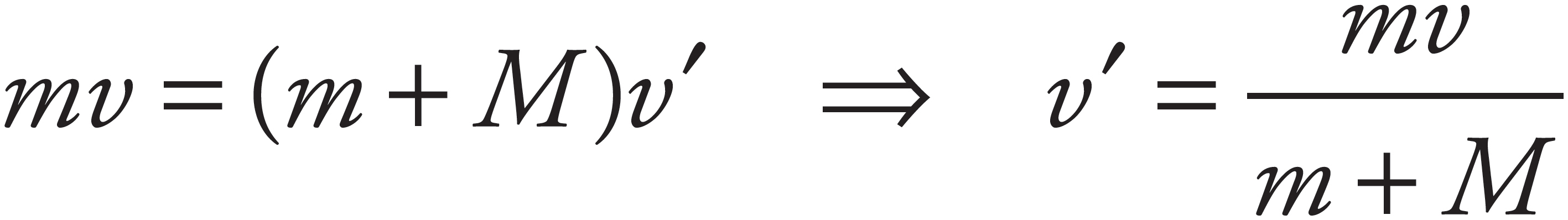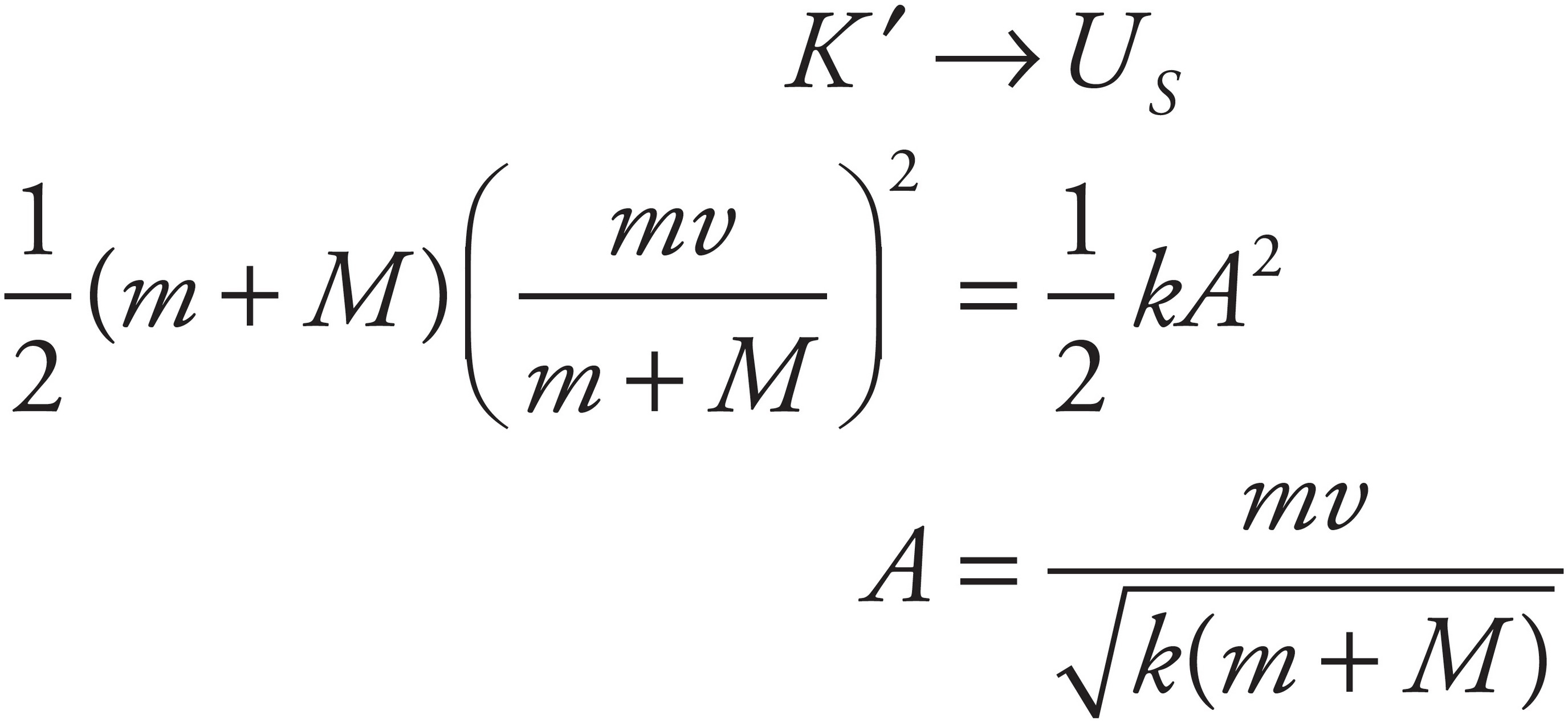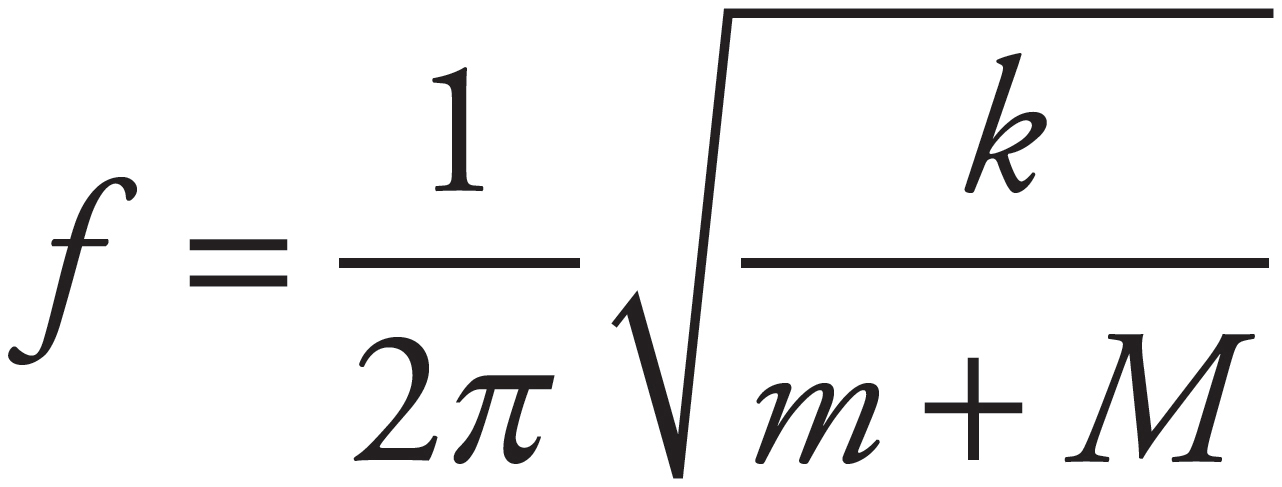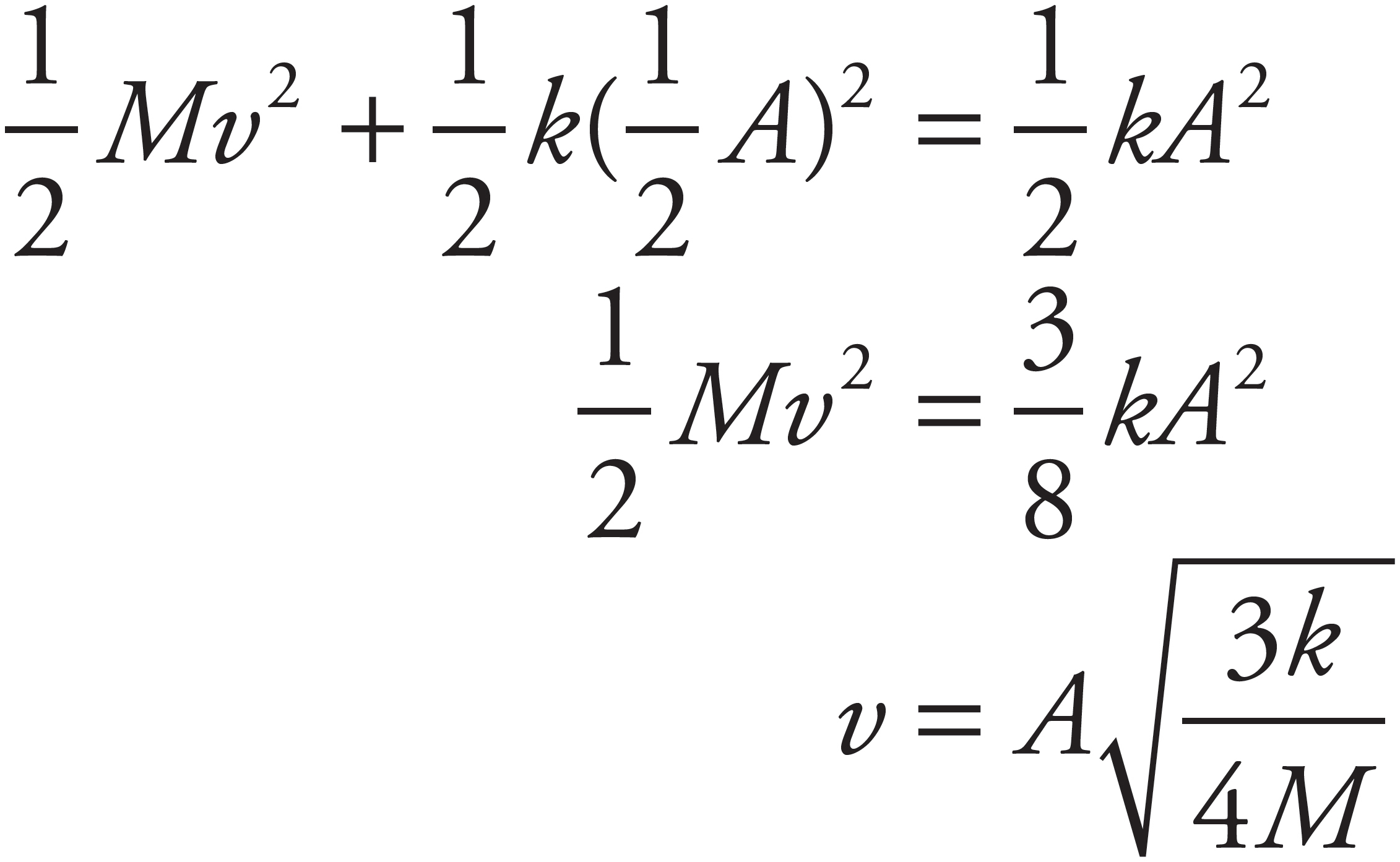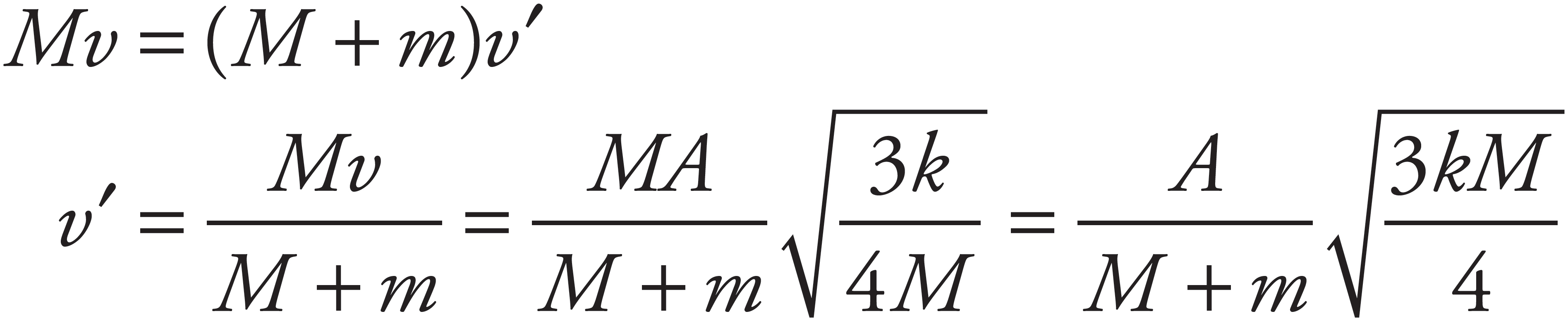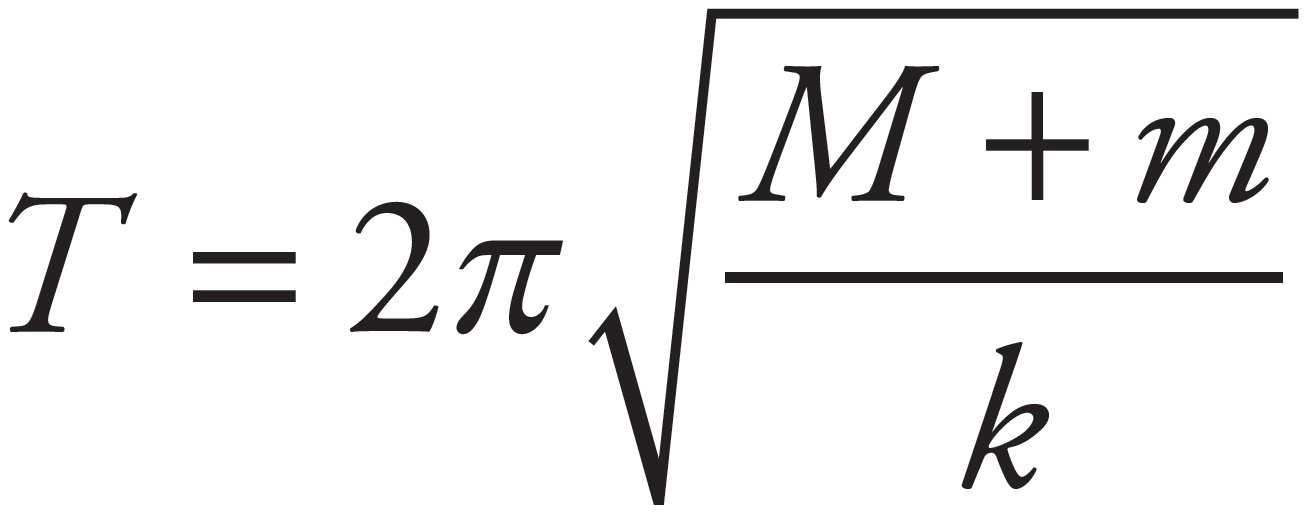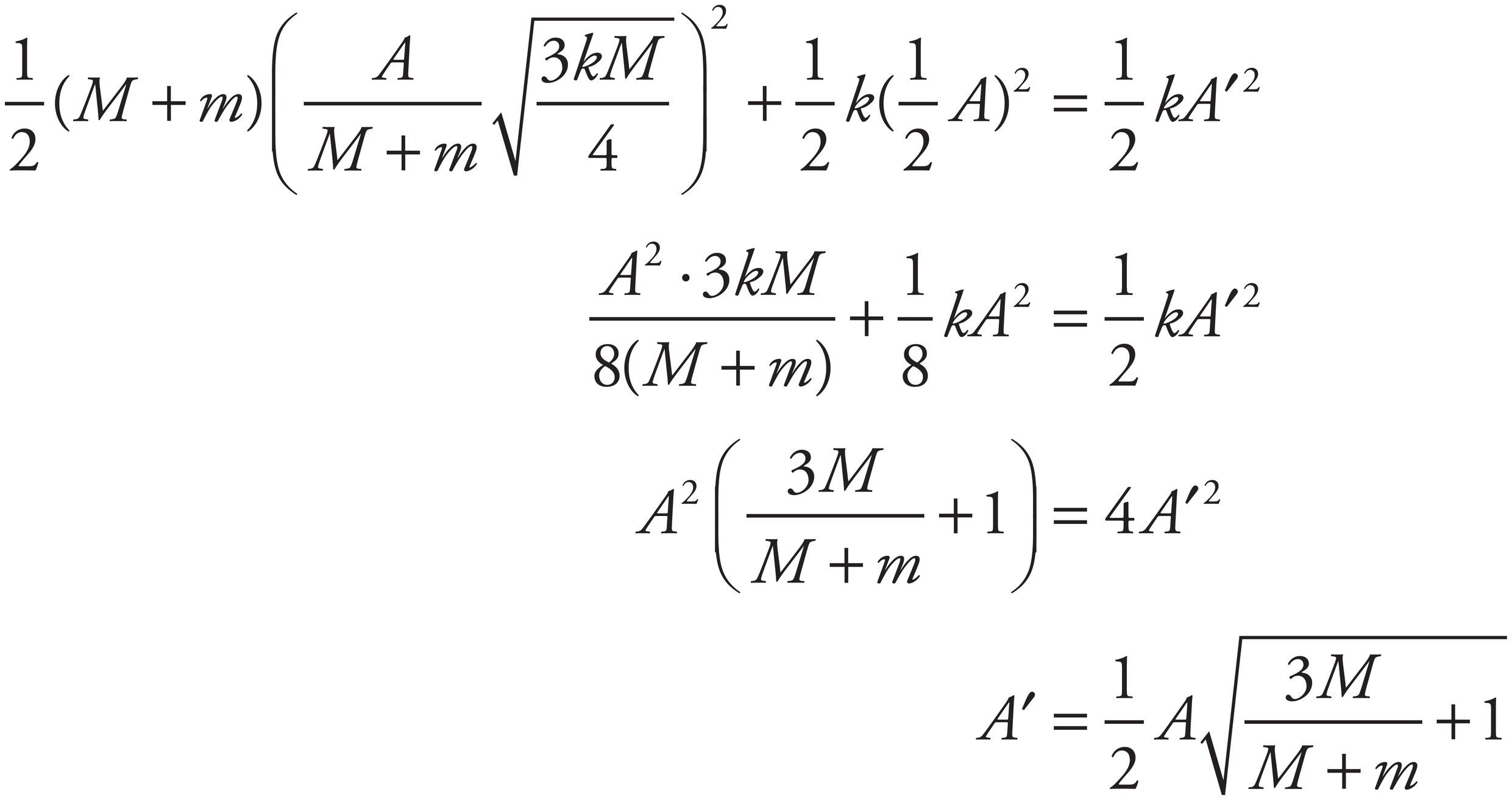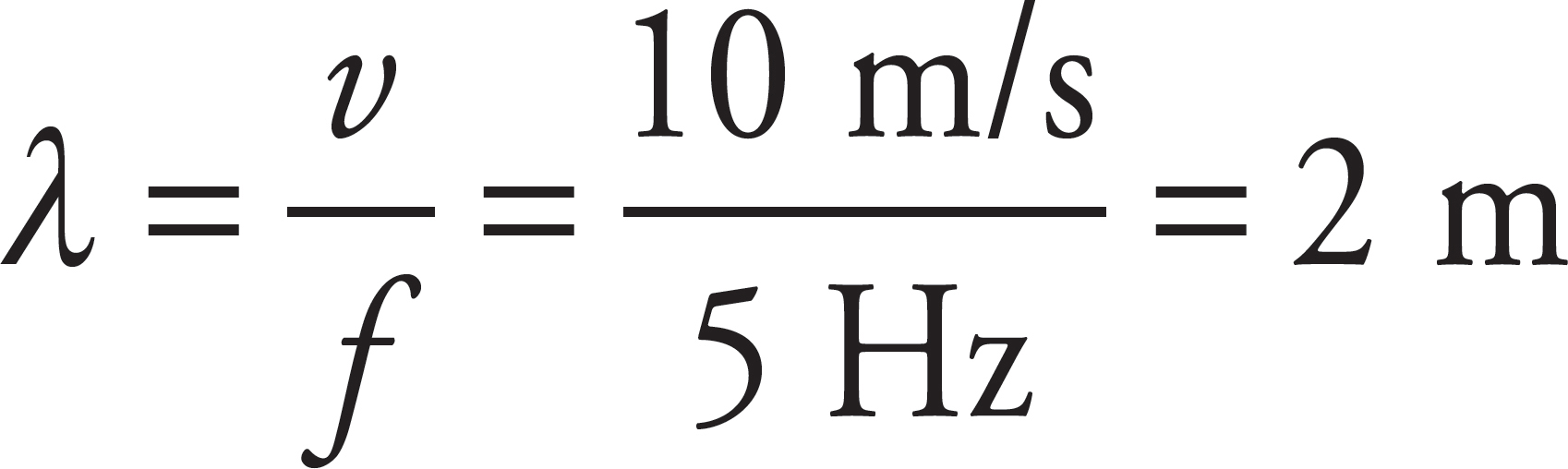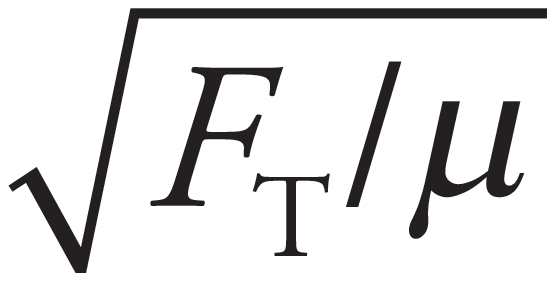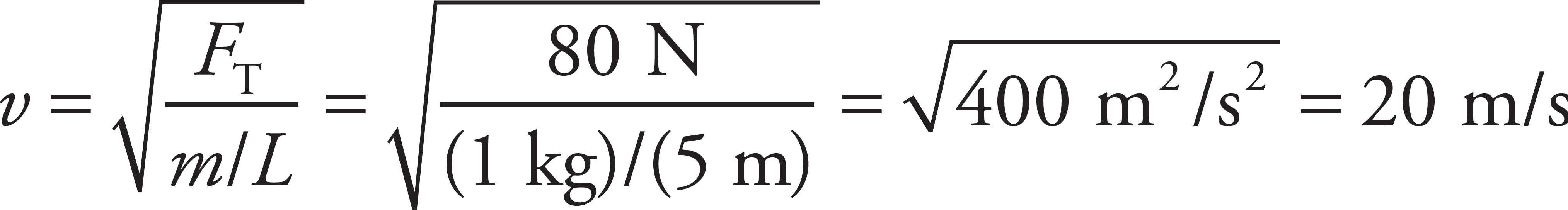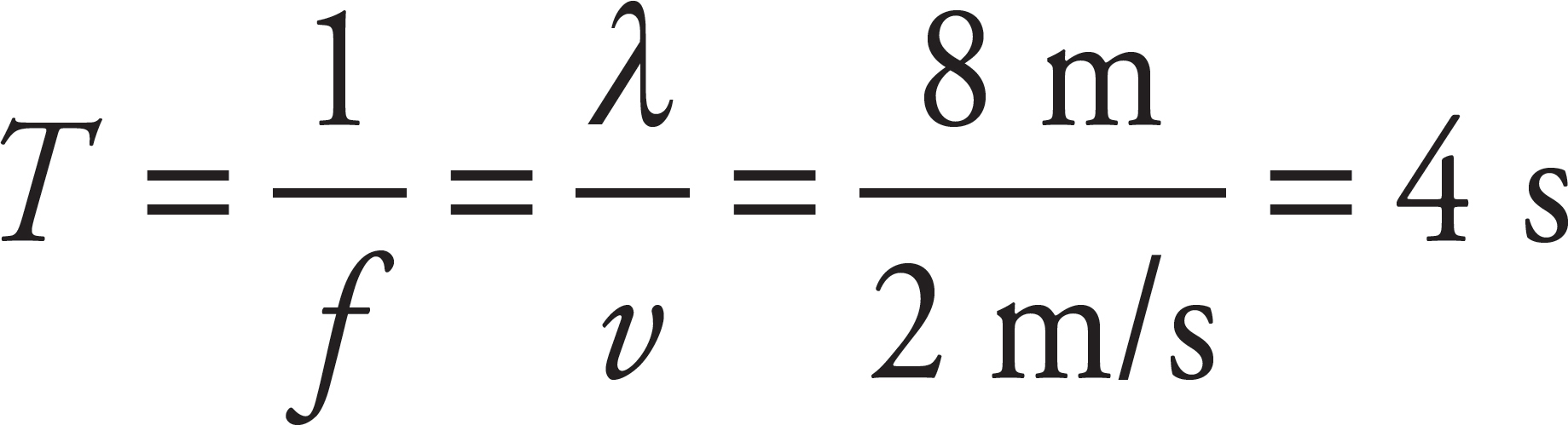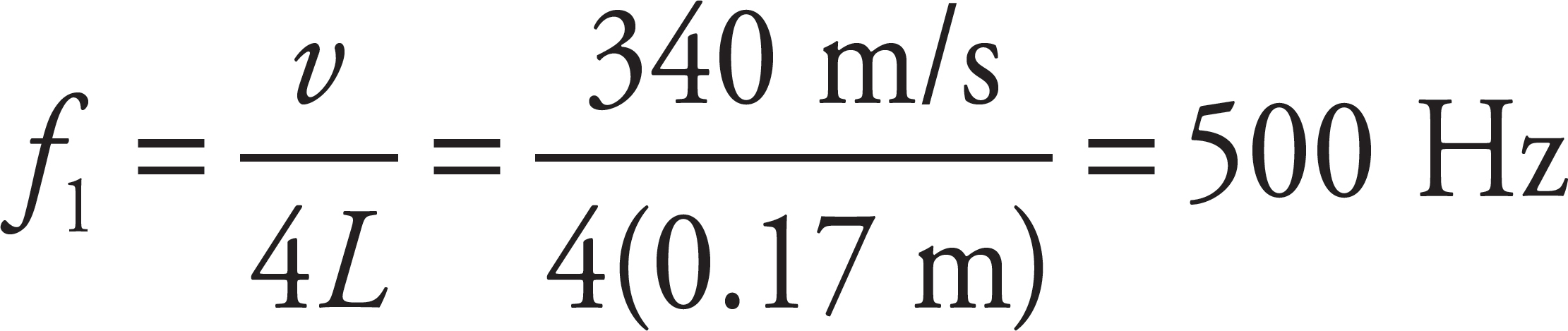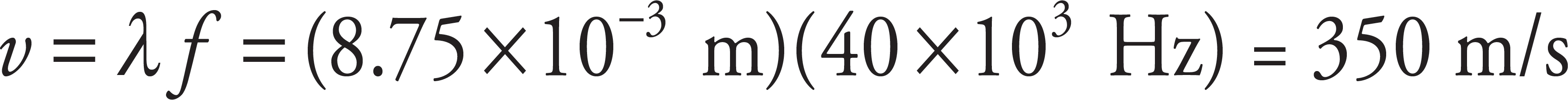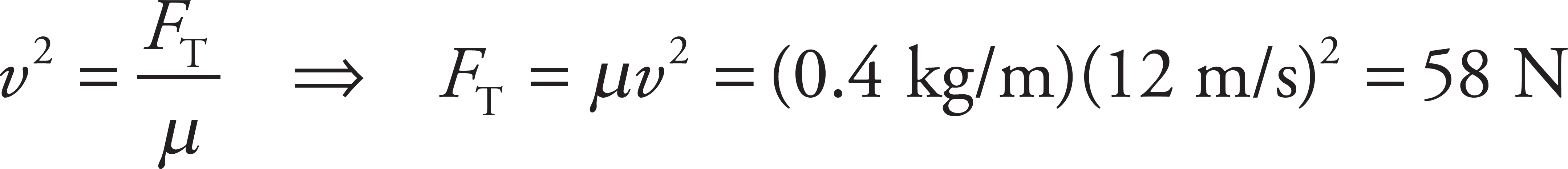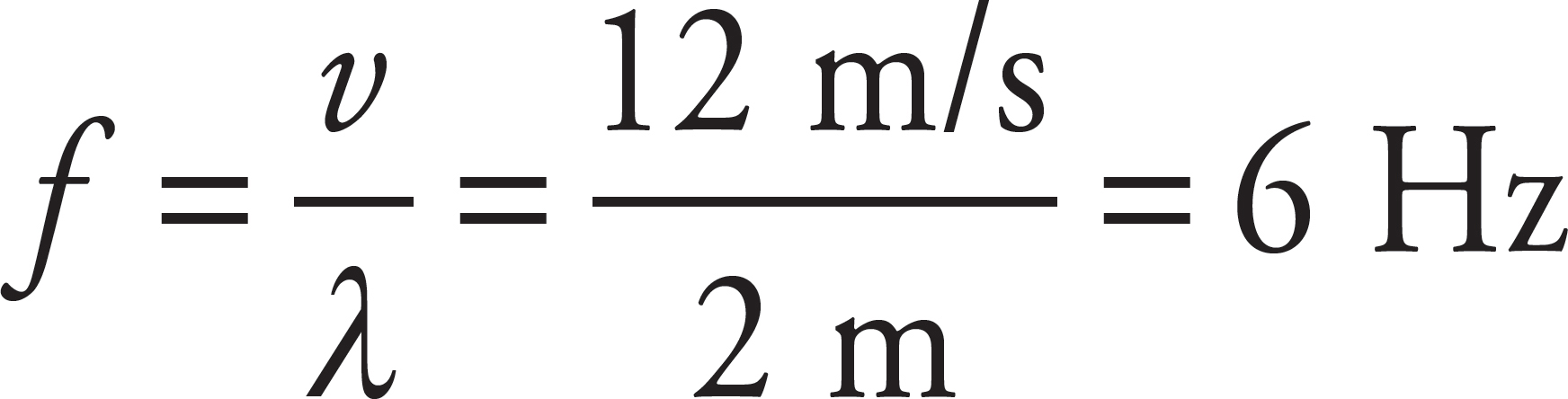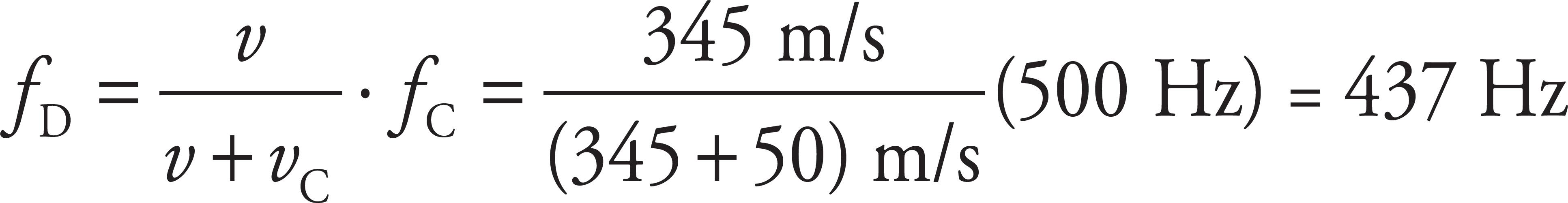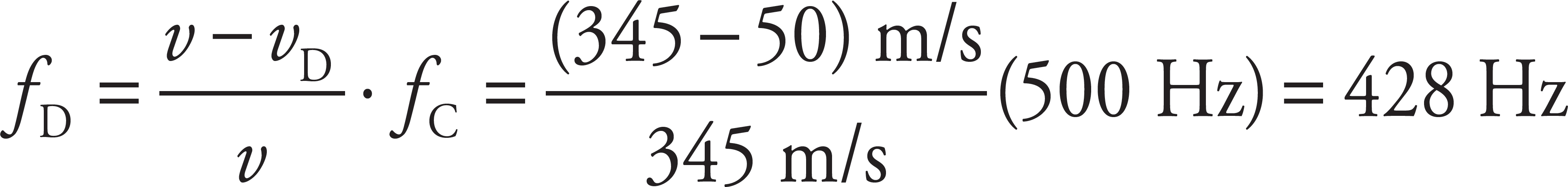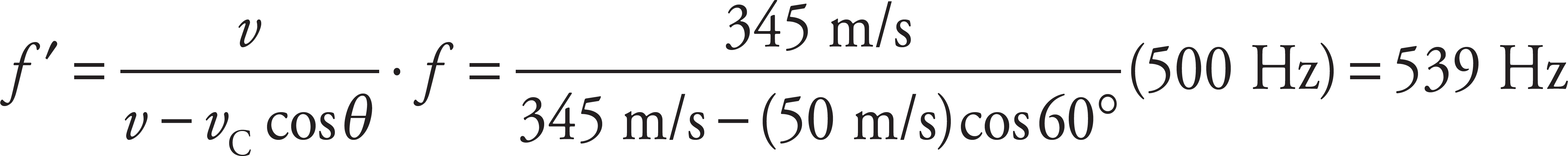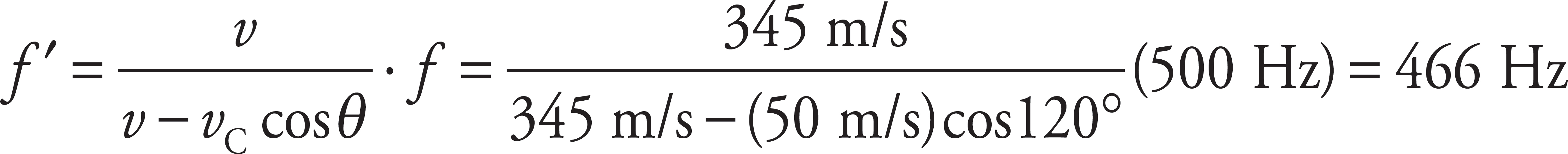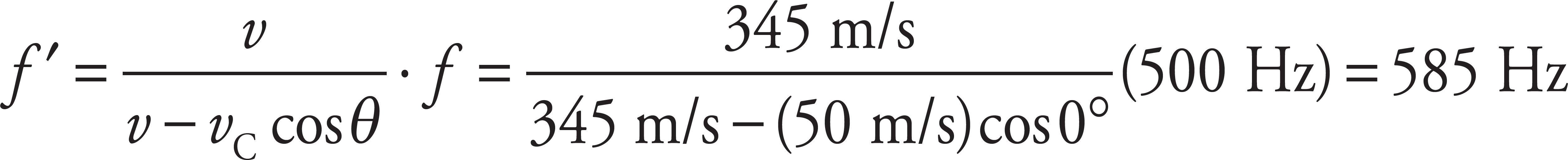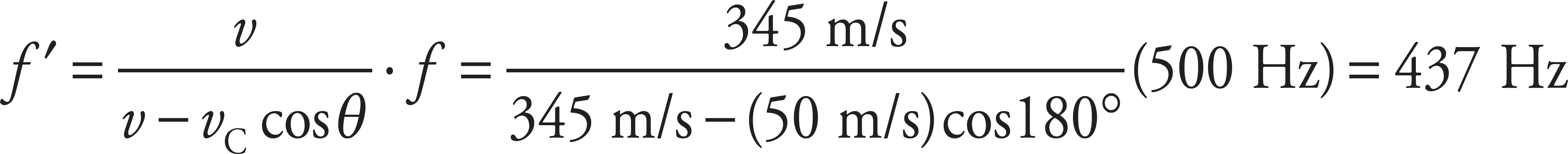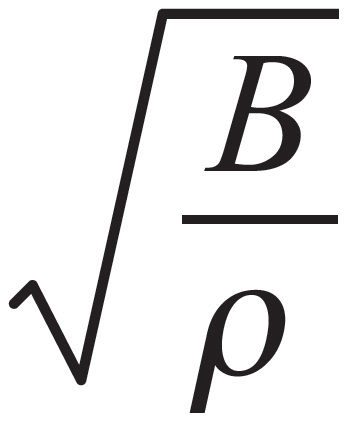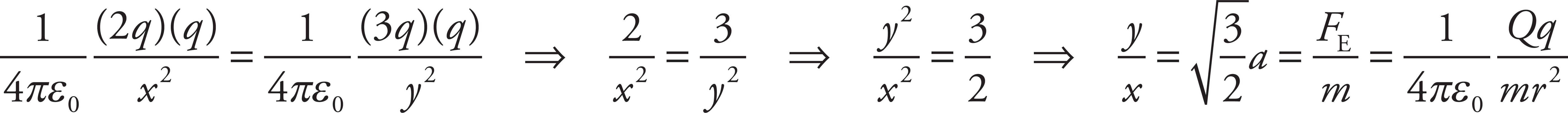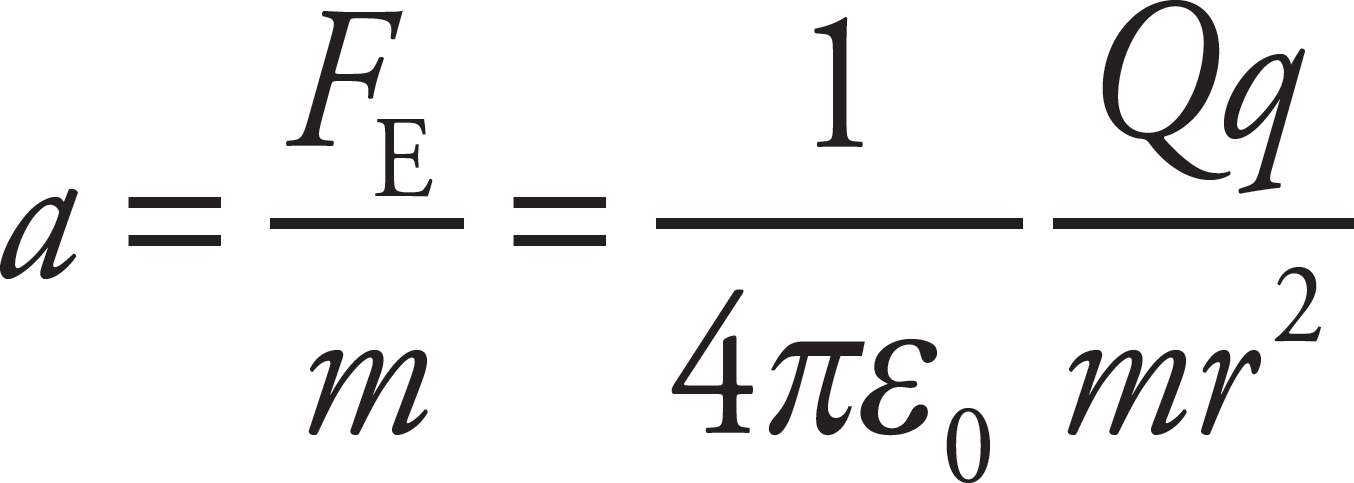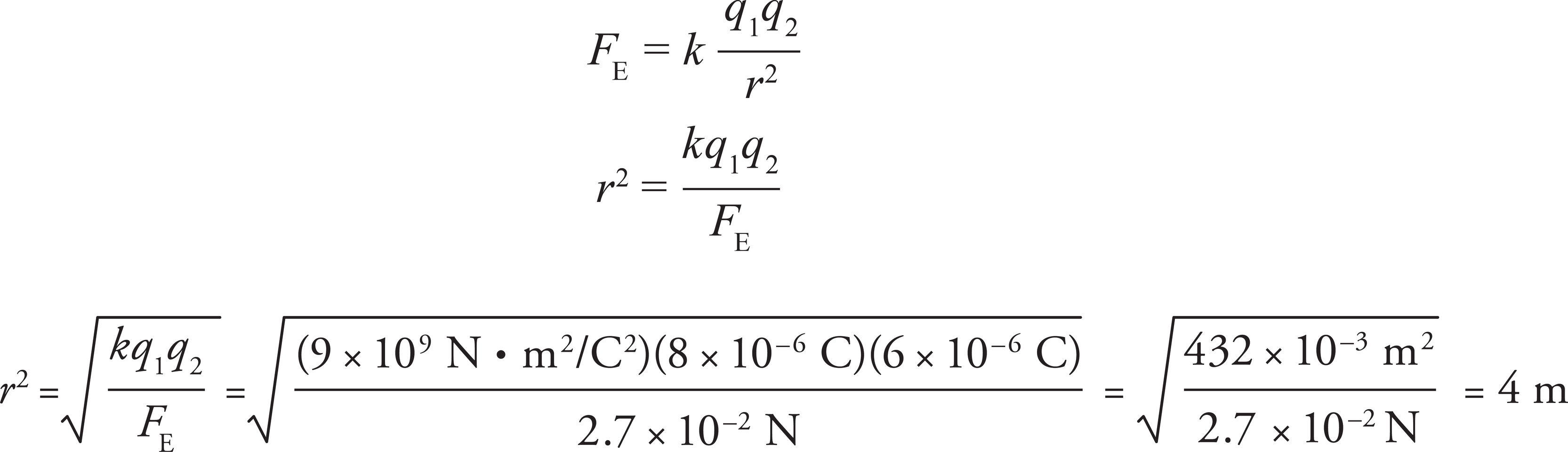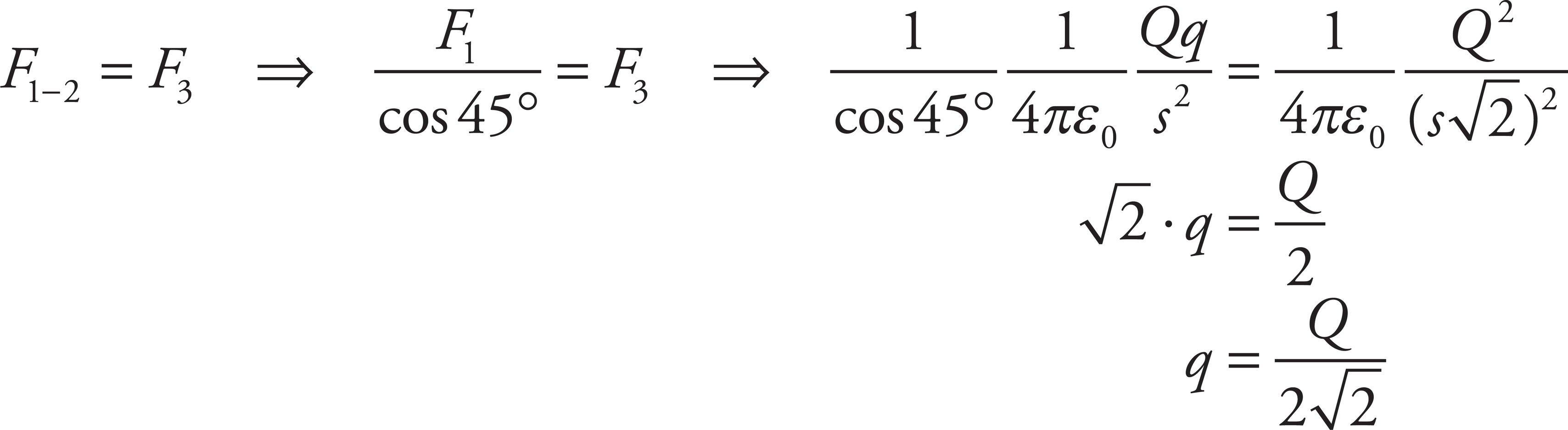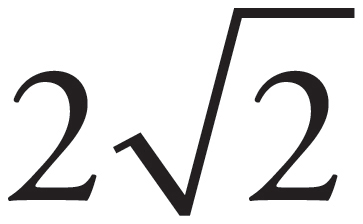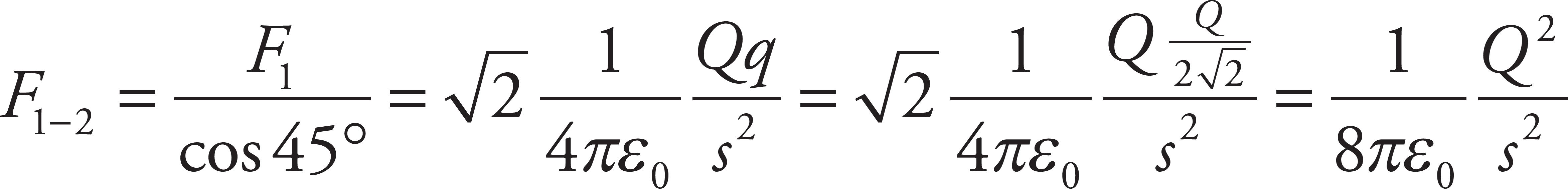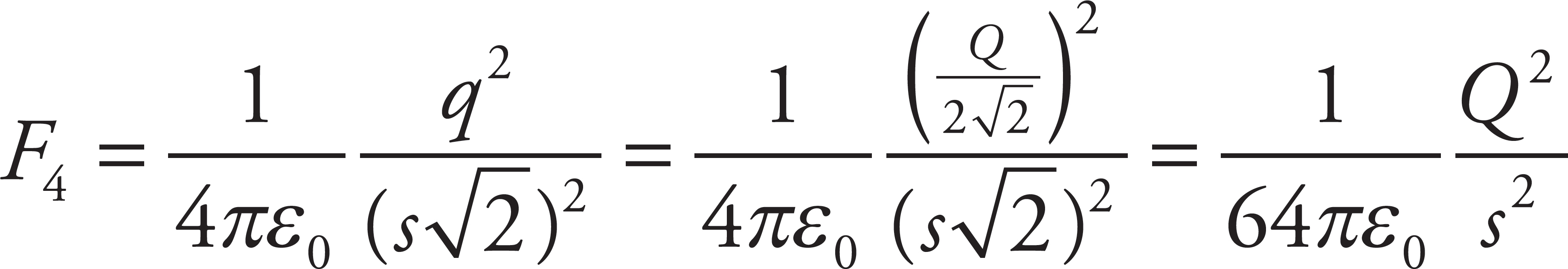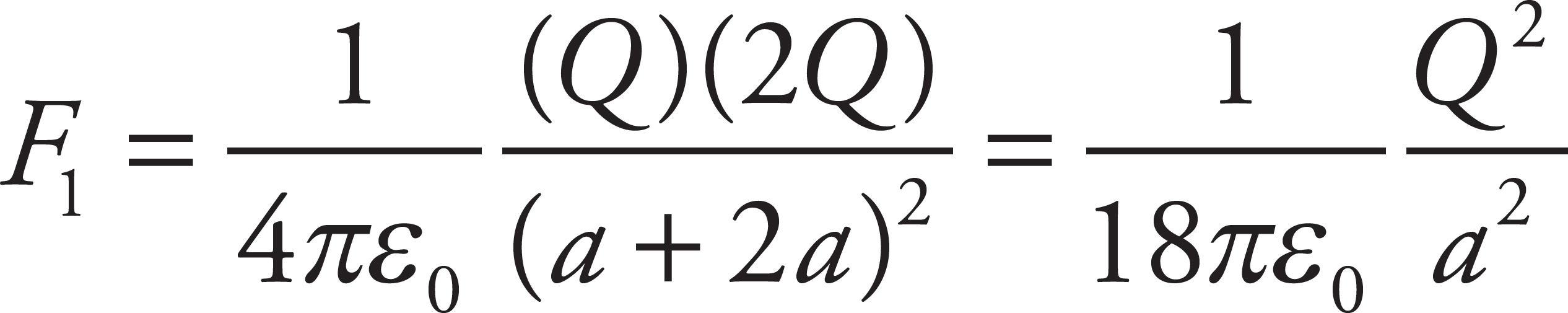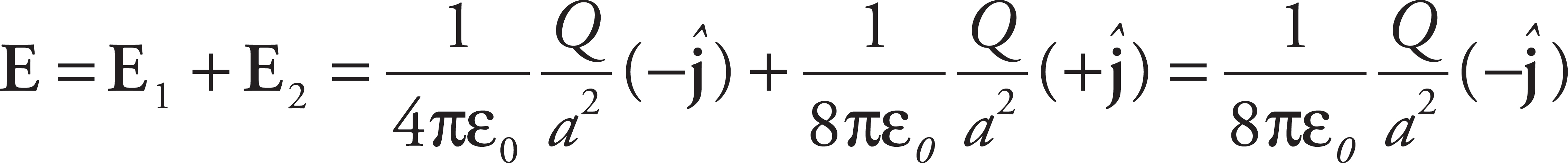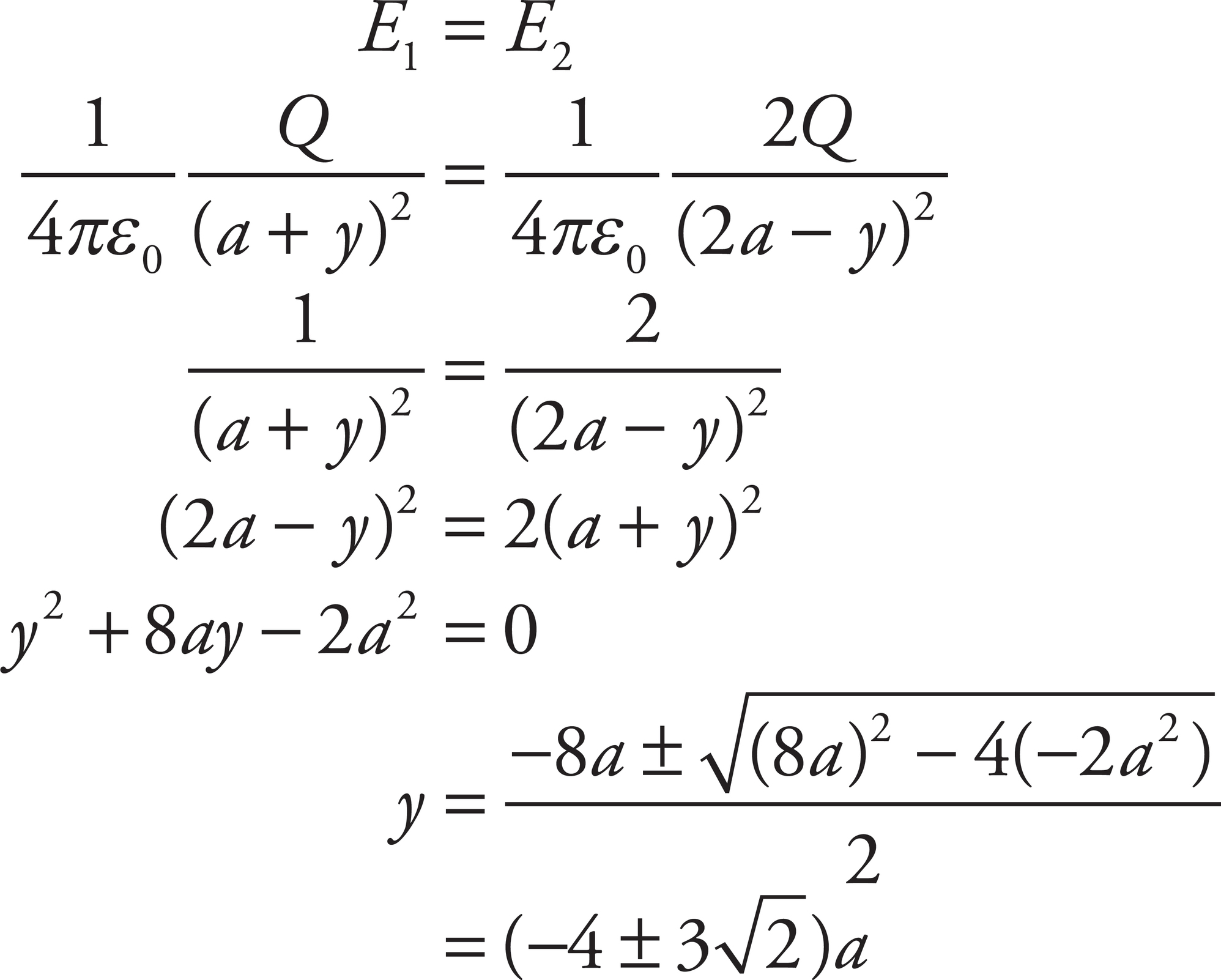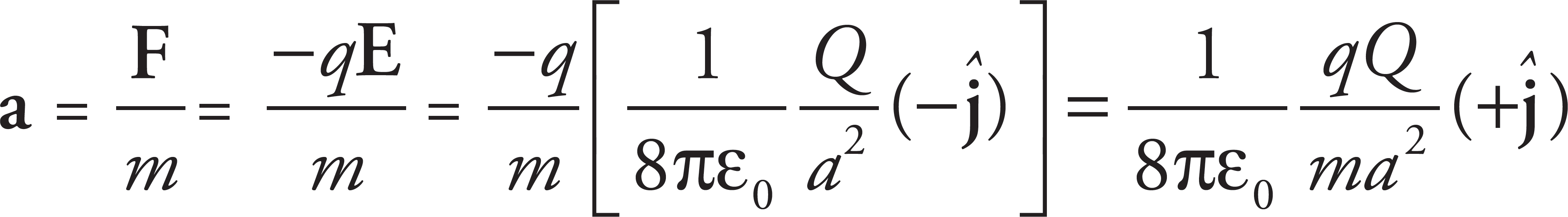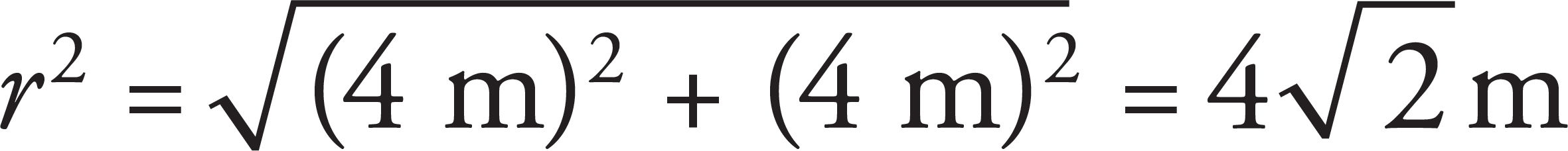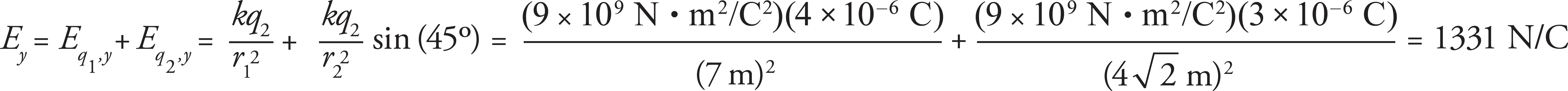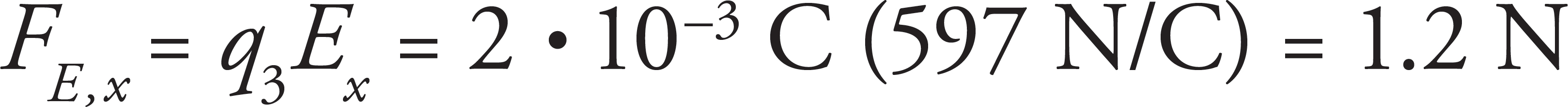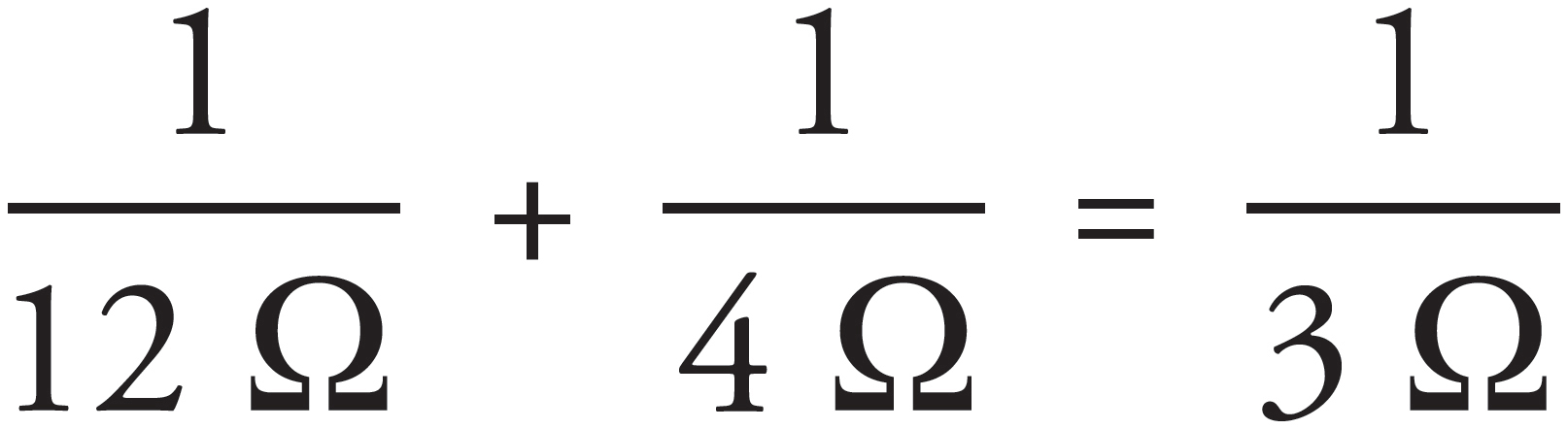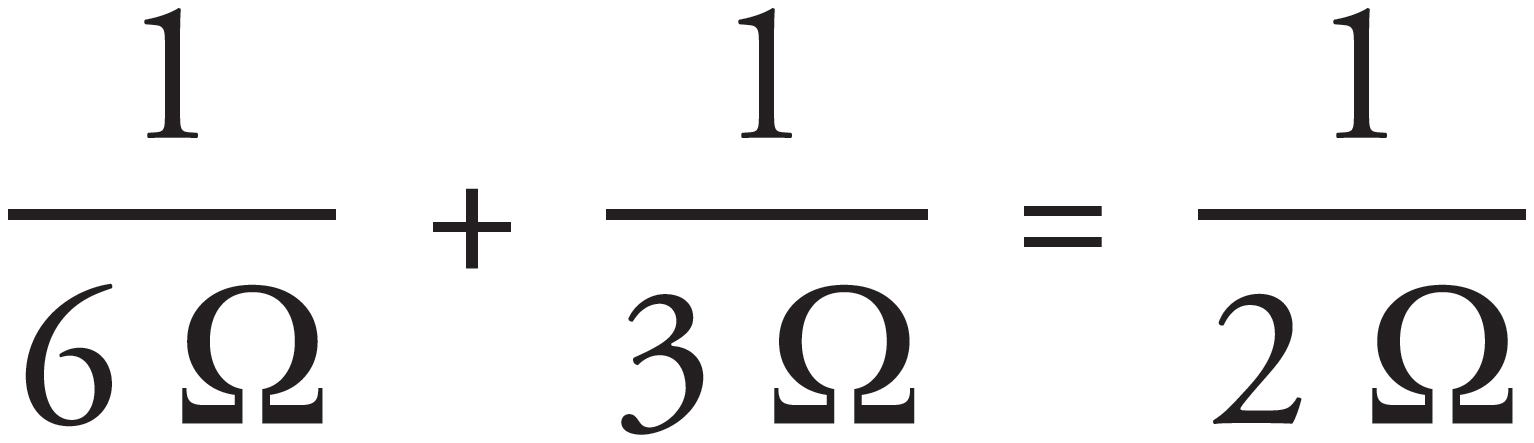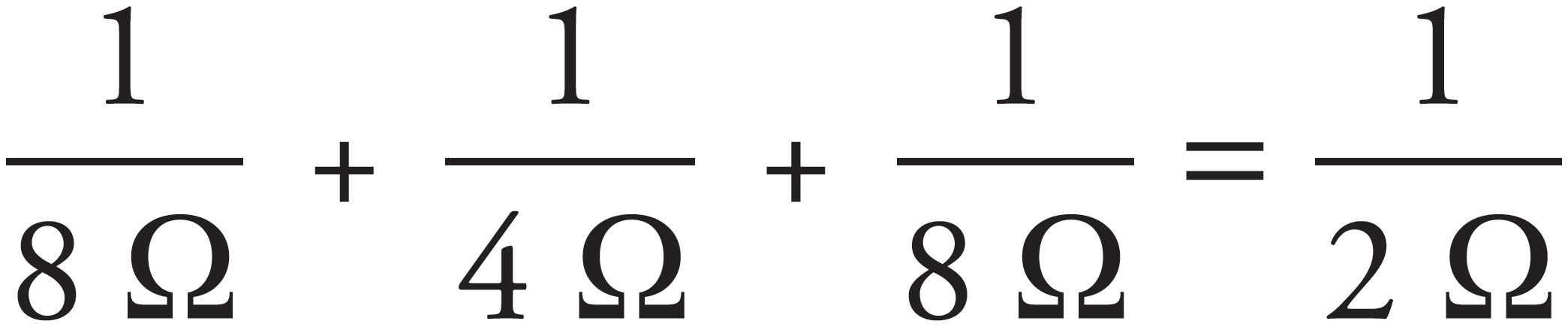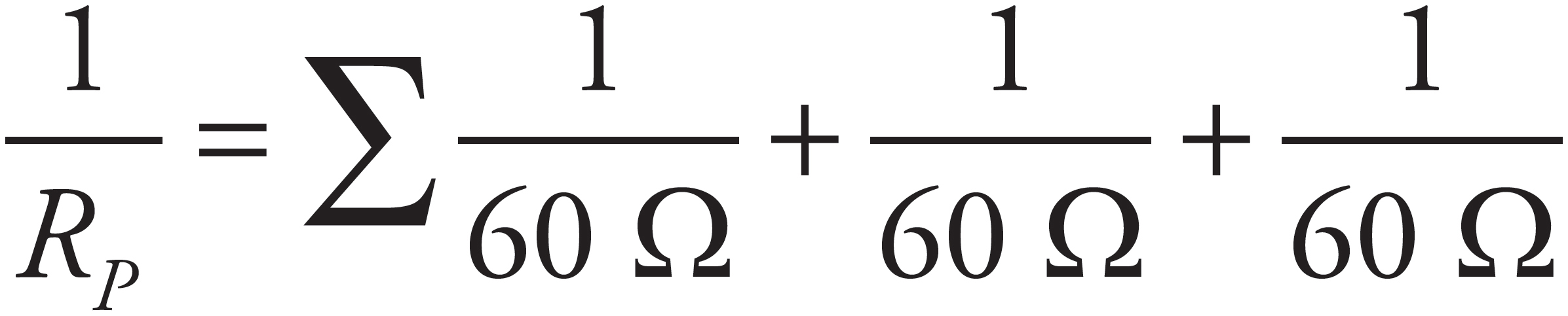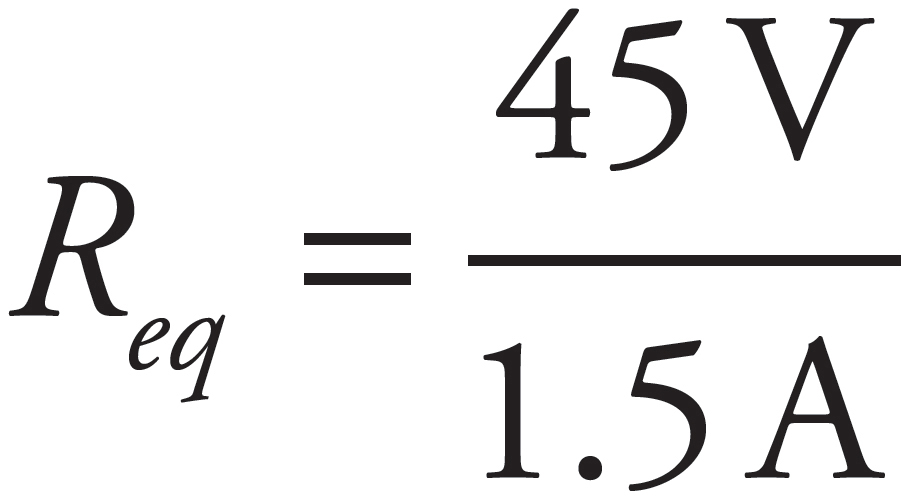1. B
To add the vectors, draw the first vector and then from the end of the first draw the second. The resultant vector is from the beginning of the first vector to the end of the second:
The direction of the resultant vector is therefore northeast, eliminating (C) and (D). Since vectors A and B are perpendicular to each other and equal in magnitude, the magnitude of the resultant vector can be found using the Pythagorean Theorem:
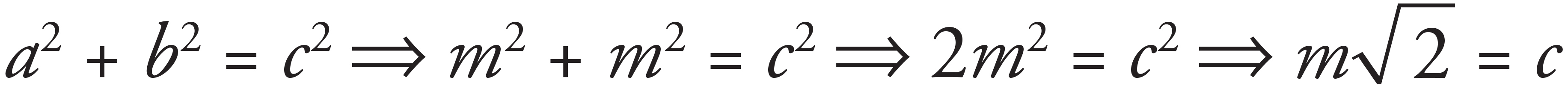
This makes (B) correct.
2. B
To add the three vectors, add their components separately:
F1 + F2 + F3 = (0 − 10 + 5)î + (−20 + 0 + 10)ĵ = −5î − 10ĵ
3. C
The magnitude of a vector is given by
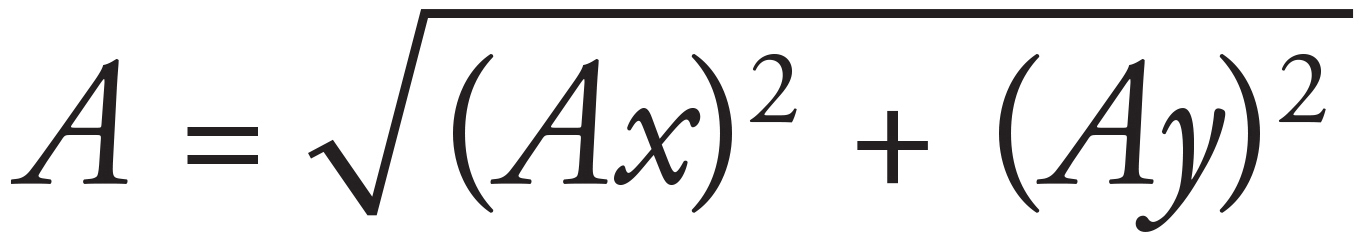
If both components of the vector are doubled, the new magnitude, A′, will be
So the magnitude of the vector will also be doubled.
The angle/direction of a vector is given by
As can be observed in this equation, doubling the magnitude of both components of the vector will have no effect on the direction of the vector.
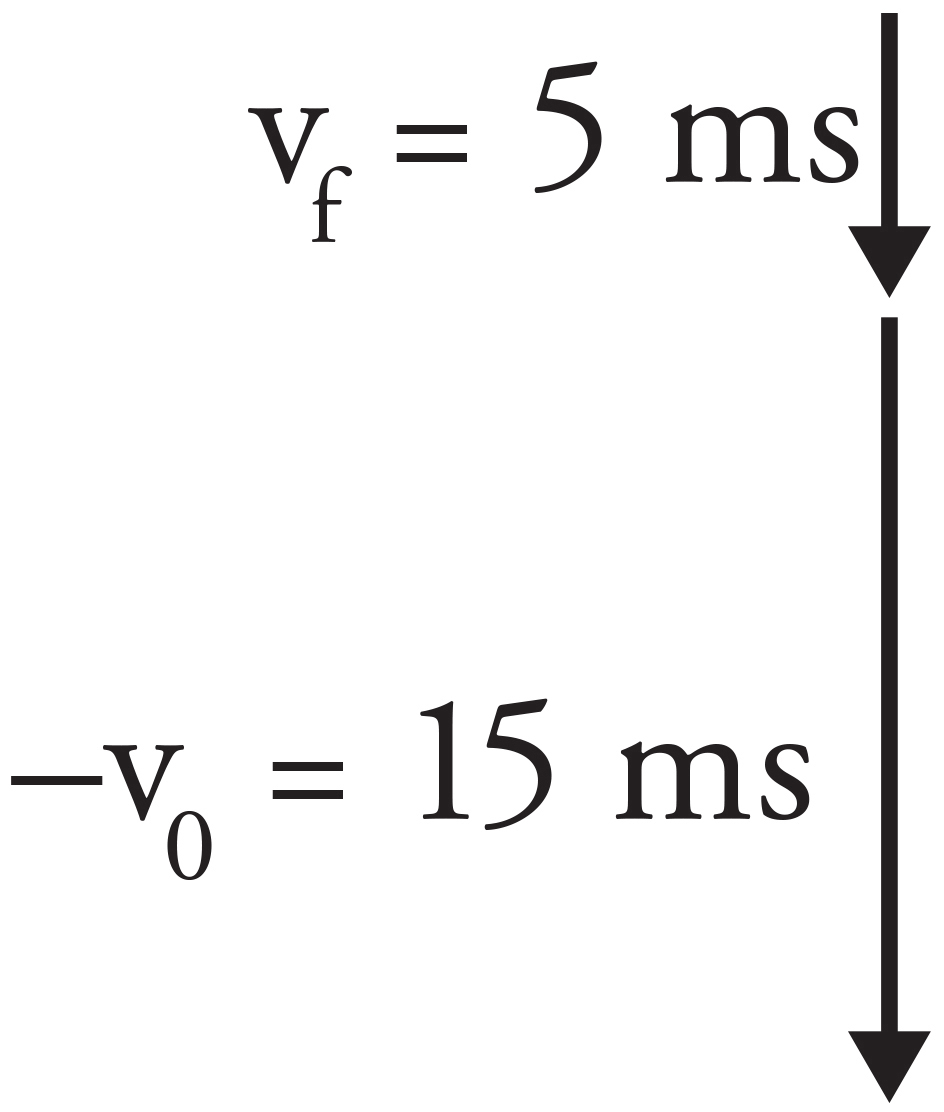
4. D
Subtracting the vector v0 is equivalent to adding the negative of v0 to vf. Since vf and −v0 both point south, adding the two vectors results in a vector that is the sum of their two magnitudes and also points south:
This corresponds to (D).
5. B
The components of the vector must satisfy the equation:
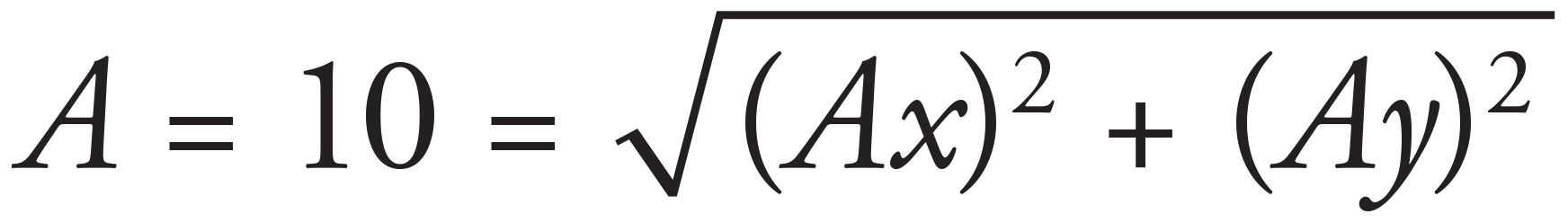
The only answer choice with components that satisfy this equation is (B): 
.
6. B
The vector sum A + B can be found by adding the individual components:
A + B = (1 + 4)î + (−2 − 5)ĵ = 5î − 7ĵ
The angle that this vector makes with the x-axis is then found with
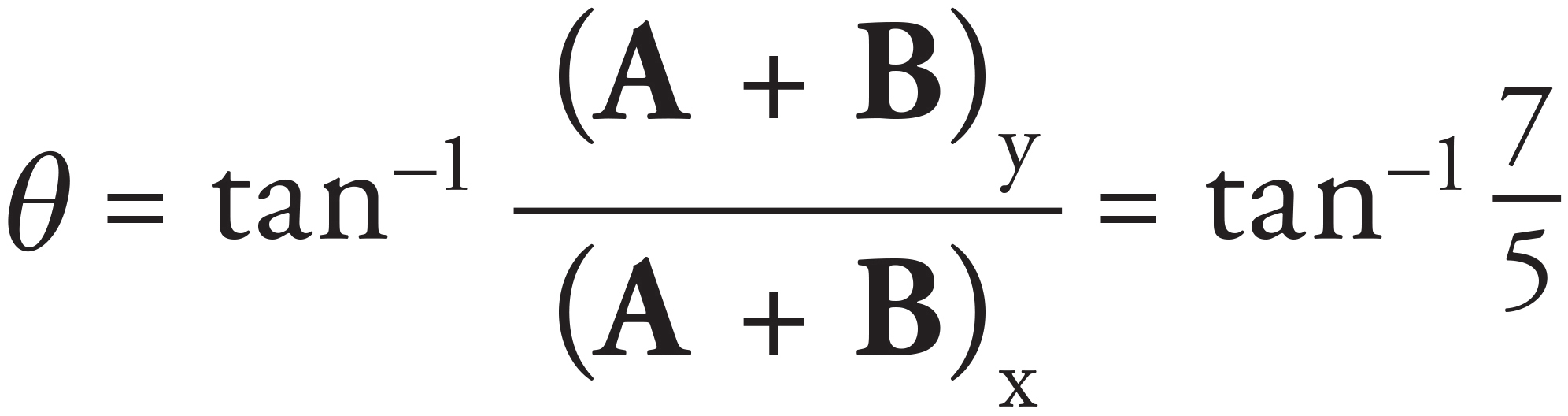
This matches (B).
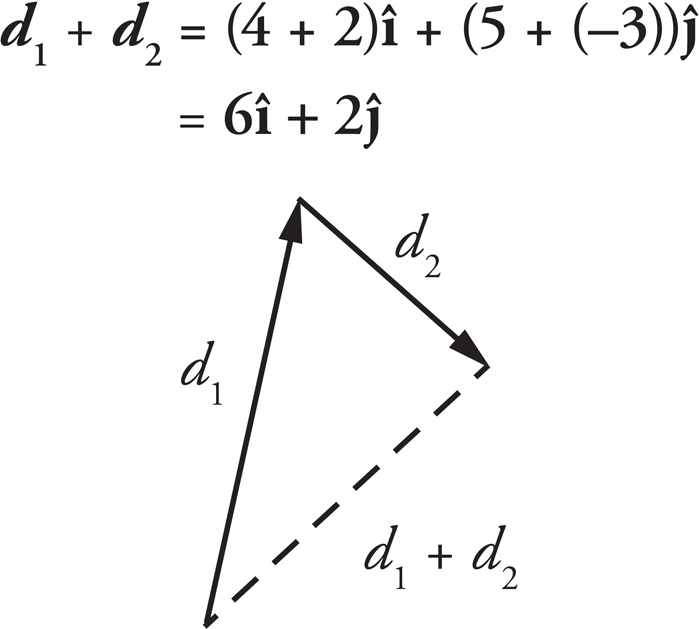
7. A
If the object travels along the vectors d1 and then d2, then the total distance travelled with be the sum of the two vectors d1 + d2:
The total distance of the object from the starting position is therefore the magnitude d1 + d2:
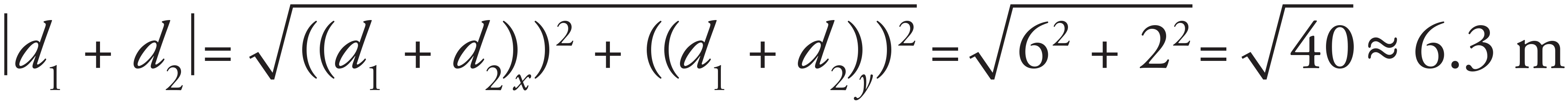
That’s (A).
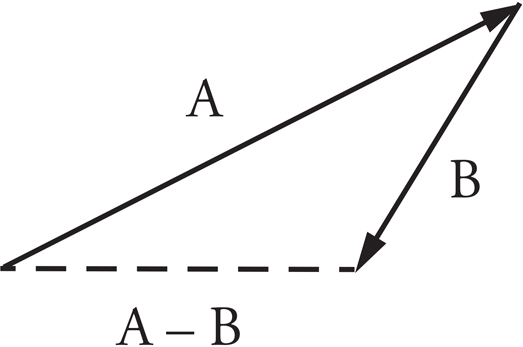
8. A
Subtracting vector B from A is equivalent to adding the negative of the second vector to the first:
This results in a vector pointing the direction of (A).
9. C
The x-component of vector A can be used to calculate the magnitude of A:
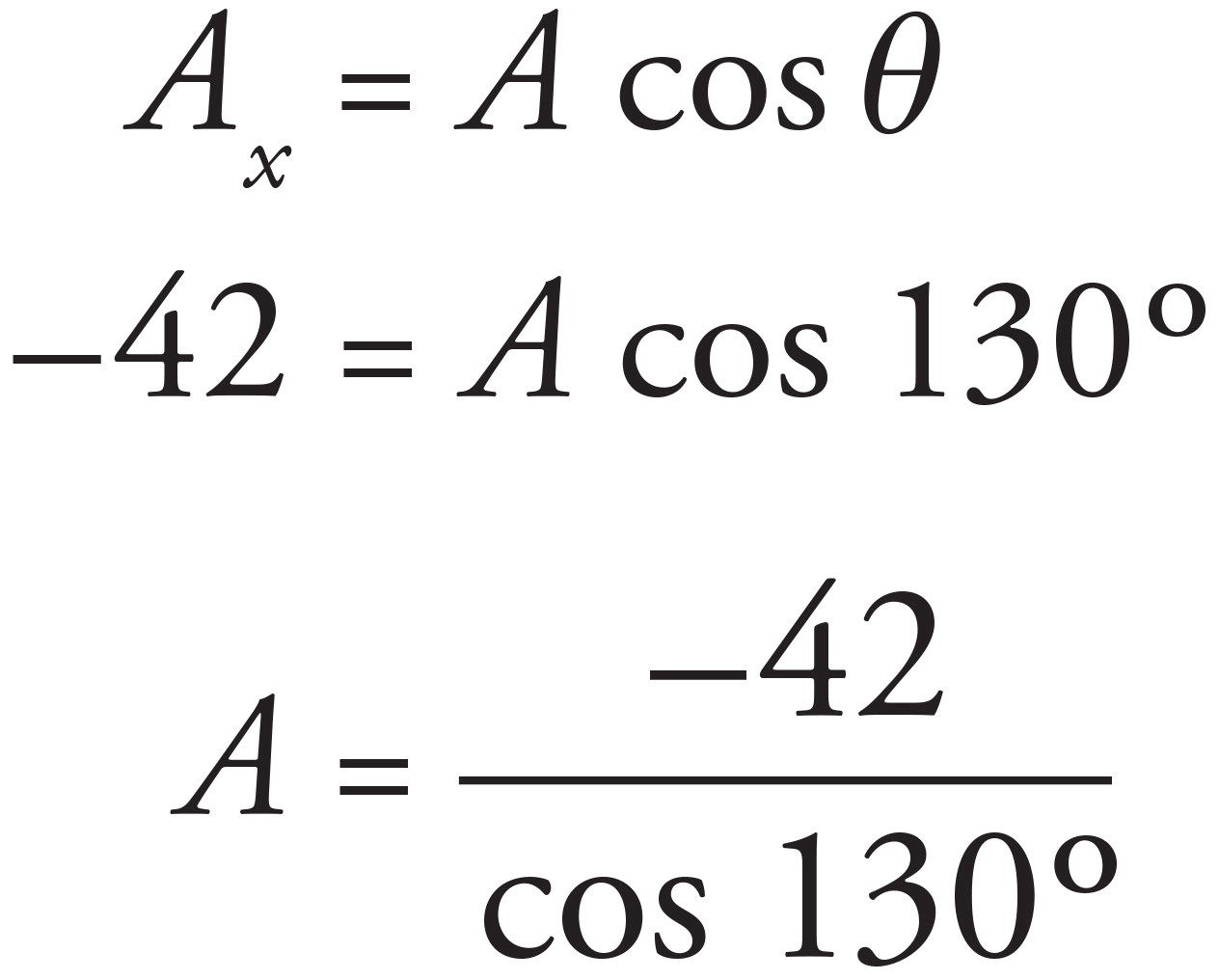
The y-component can then be calculated:
which corresponds to (C).
10. B
If the two vectors were pointed in the same direction, their magnitudes would add, and since magnitudes are positive, the result could not be zero, eliminating (A). If the vectors point in opposite directions, then the magnitude of the resultant vector would be obtained by subtracting the individual magnitudes of the two vectors. The only way for the difference to equal zero is if these two vectors have the same magnitude, eliminating (C) and (D). Choice (B) is therefore correct.
1. (a)
The magnitude of A is
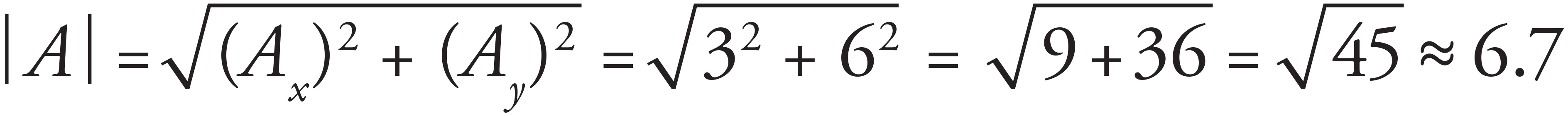
(b)
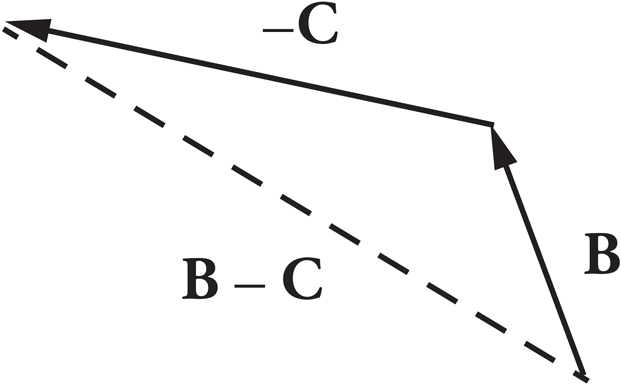
Vector C is subtracted from B by adding −C to B:
The components of B − C are found by subtracting the individual components:
B − C = (−1 − 5)î + (4 − (−2))ĵ = − 6î + 6ĵ
(c)
The components of 2B are found by multiplying each component of B by 2:
2B = (2 × −1)î + (2 × 4)ĵ = −2î + 8ĵ
The components of A + 2B are found by adding the individual components:
A + 2B = (3 + (−2))î + (6 + 8)ĵ = î + 14ĵ
(d)
The components of A − B − C are found by working with the individual components:
A − B − C = (3 − (−1) − 5)î + (6 − 4 − (−2))ĵ = −1î + 4ĵ
Let D = A − B − C The magnitude of D is found using
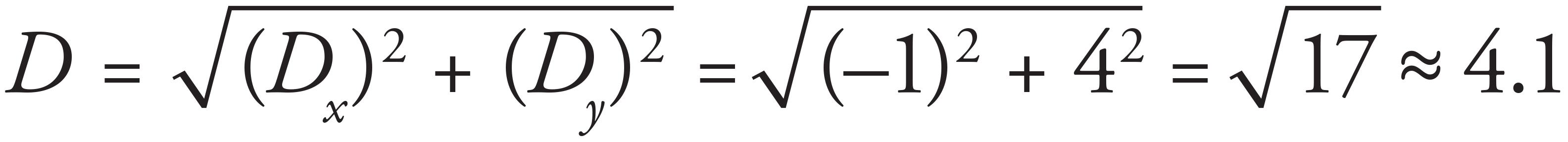
and the direction of D relative to the horizontal is found using
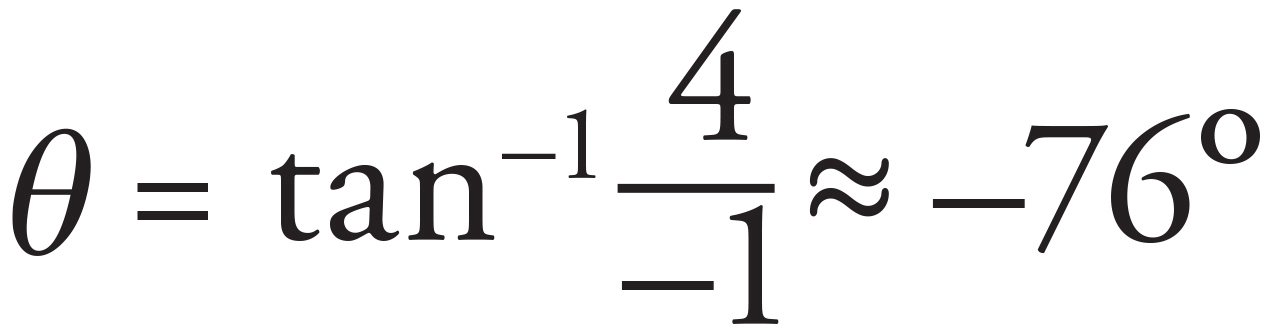
As the resultant vector has components −1î + 4ĵ, it is located in Quadrant II. To obtain an angle in Quadrant II, add 180° to get the correct answer of θ ≈ 104° or 76° north of west.
2. (a)
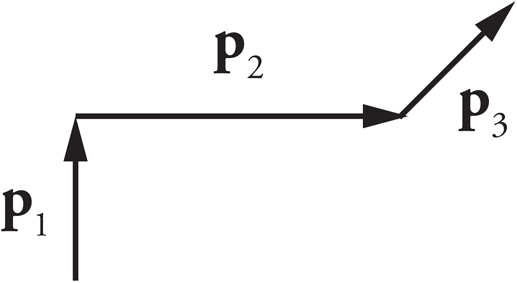
(b)
The distance the ant has travelled, d, is the magnitude of the sum of the individual vectors in the ant’s path: d = p1 + p2 + p3. To do this addition, the components of p3 must be calculated. If due east is the x-direction and due north is the y-direction, then northeast is 45° about the horizontal. Thus,
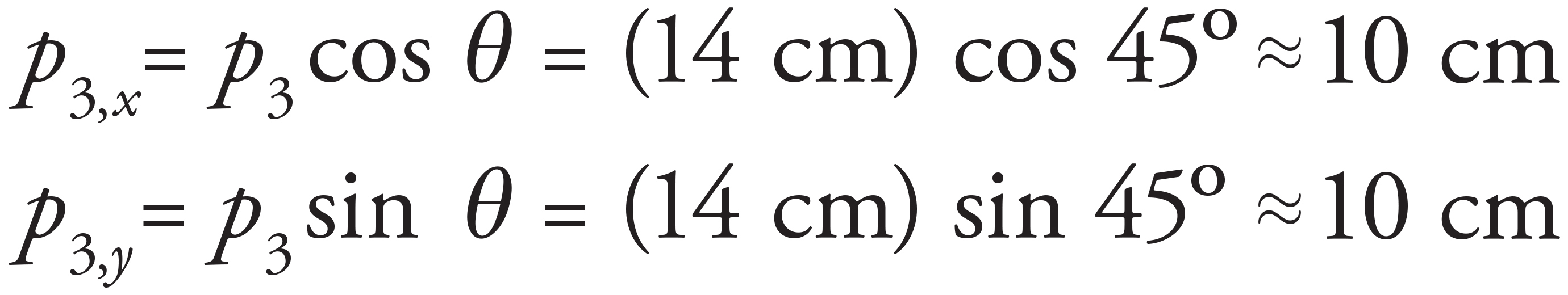
Adding the individual components,
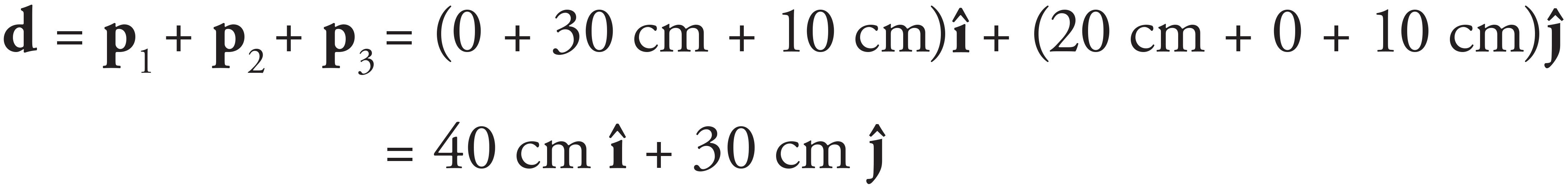
The magnitude of this vector is
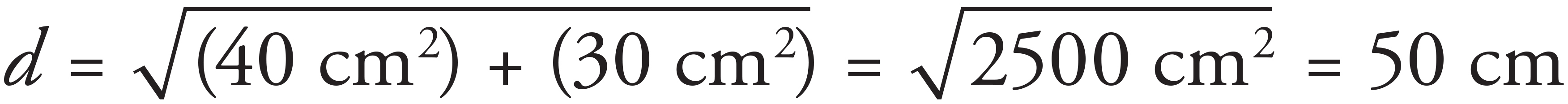
(c)
The ant’s position is d = 40 cm î + 30 cm ĵ. If the ant walks due north, the x-component of its position will not change, but the y-component will increase. Since its final position vector will have a magnitude of 80 cm, the y-component of the final position vector, f, can be calculated:
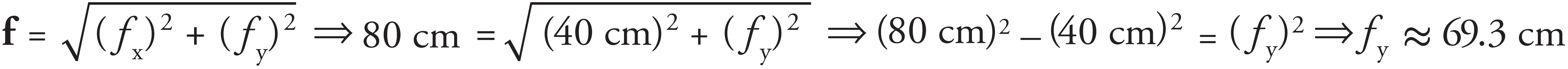
Since the ant was already 30 cm north of his original position, he can walk another 69.3 cm − 30 cm = 39.3 cm due north.
3. (a)
The components of p = 140 m directed 10° above the horizontal are given by
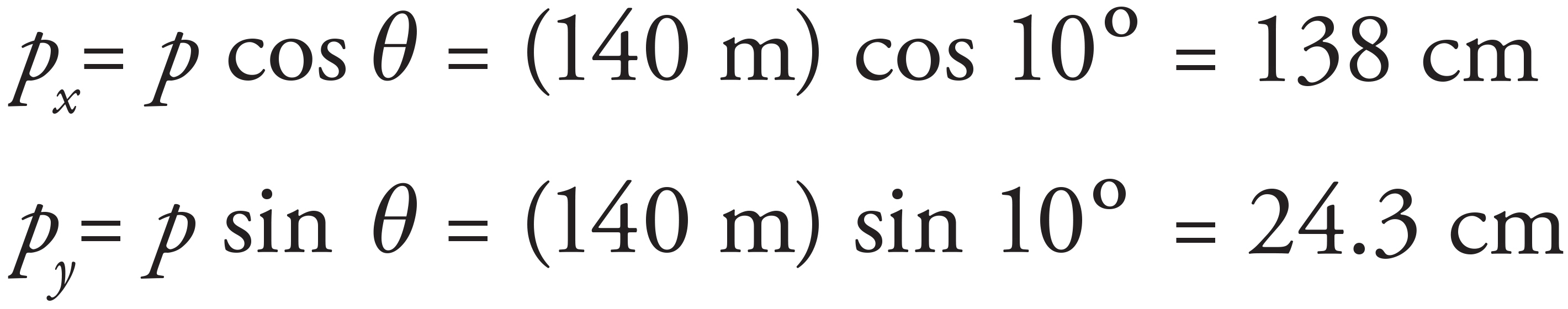
thus, p = 138î + 24.3ĵ.
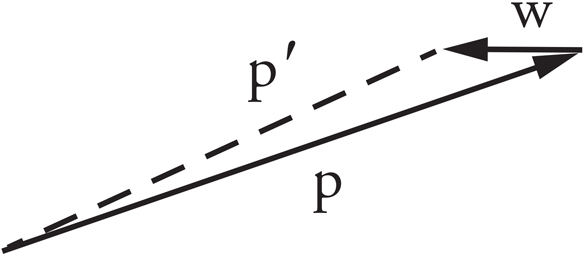
(b)
The vector addition p′ = p + w is accomplished by starting to draw the tail of the second vector at the end of the first:
(c)
Adding the components of p + w yields p′ = (138 m − 30 m)î + 24.3 m ĵ = 108 m î + 24.3 m ĵ. The new angle with the horizontal is therefore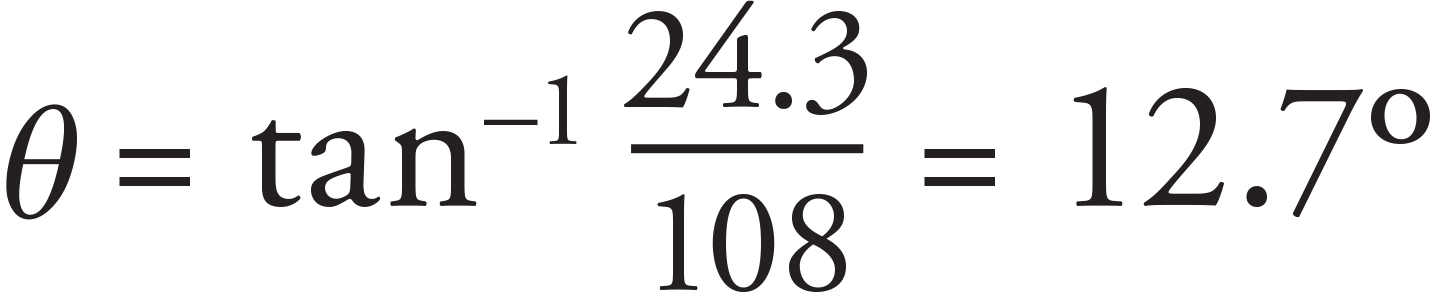 
.
4. (a)
Since v depends on c and r, it makes sense to use v as the resultant vector. The diagram shows that r and c are connected tip-to-tail, indicating that these vectors are being added together, and thus, v = r + c.
(b)
If the angle between v and c is 90°, a right triangle is formed, so that the Pythagorean Theorem can be used to solve for the magnitude of v as a function of the other two vectors:
(c)
Let due east be the î direction and due north be the ĵ direction. Then the vectors c and v are defined as: c = 5m/sî and v = −10 m/sĵ. Solving the vector equation from part (a) for r yields
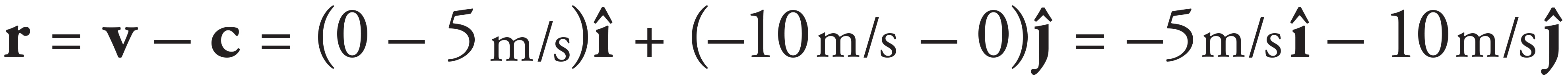
Using these components, the magnitude and direction of r are given by:
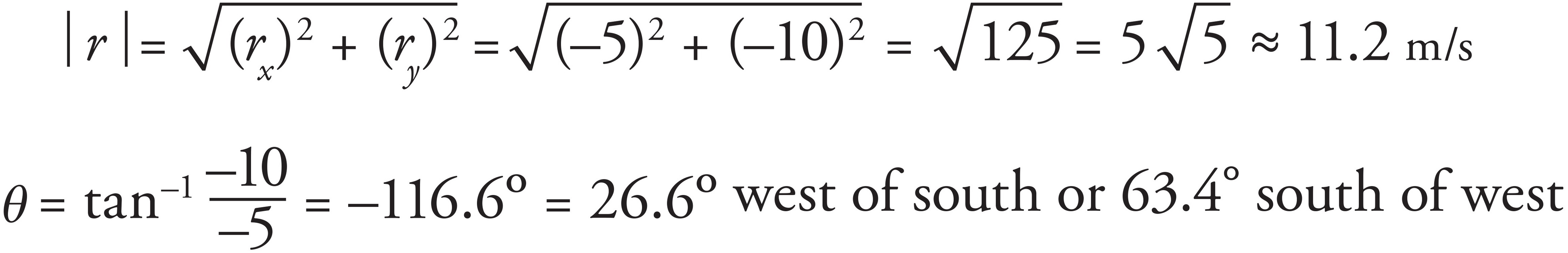
1. A, D
Traveling once around a circular path means that the final position is the same as the initial position. Therefore, the displacement is zero. The average speed, which is total distance traveled divided by elapsed time, cannot be zero. Remember that velocity has direction and magnitude. When the object travels in a circular path the direction is always changing so the velocity is always changing. Because the velocity is changing, this means there is an acceleration that is delivered on the object.
2. D
Section 1 represents a constant positive speed. Section 2 shows an object slowing down, moving in the positive direction. Section 3 represents an object speeding up in the negative direction. Section 4 demonstrates a constant negative speed, and section 5 represents the correct answer: slowing down moving in the negative direction. Though the slope is positive, this corresponds to acceleration, indicating that the direction of acceleration is opposite to the direction of velocity and thus is slowing down. However, the section remains in the negative quadrant, and the velocity becomes slower but is still negative.
3. B, D
In parabolic motion, a projectile experiences only the constant direction due to gravity, but the velocity does not point in the same direction. Eliminate (A). Zero acceleration means no change in speed (or direction), making (B) and (D) true. An object whose speed remains constant but whose velocity vector is changing direction is accelerating. Eliminate (C).
4. B
The baseball is still under the influence of Earth’s gravity. Its acceleration throughout the entire flight is constant, equal to g downward.
5. A
Use Big Five #3 with v0 = 0:
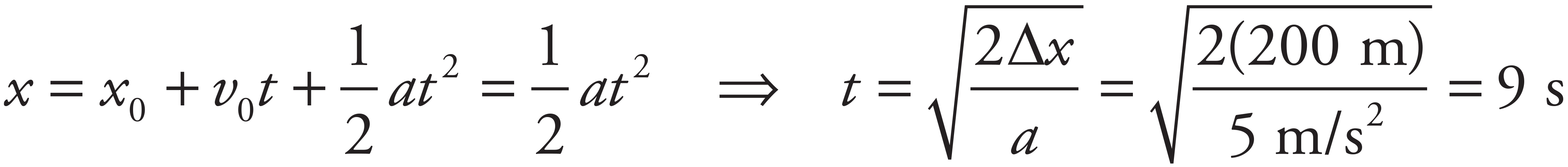
6. C
Use Big Five #5 with v0 = 0 (calling down the positive direction):
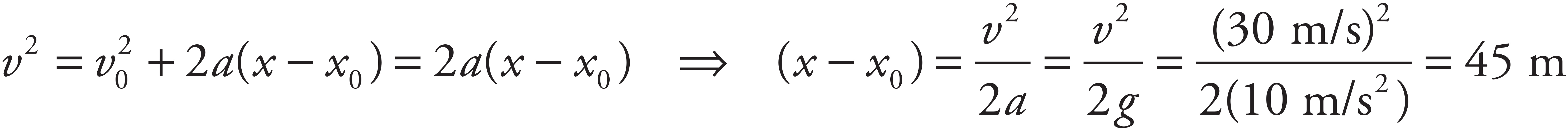
7. C
Apply Big Five #3 to the vertical motion, calling down the positive direction:
Note that the stone’s initial horizontal speed (v0x = 10 m/s) is irrelevant.
8. B
First, determine the time required for the ball to reach the top of its parabolic trajectory (which is the time required for the vertical velocity to drop to zero).
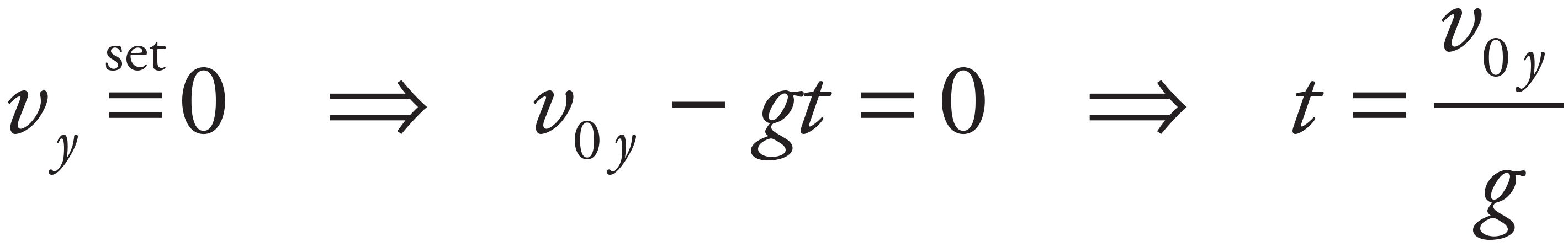
The total flight time is equal to twice this value:
9. C
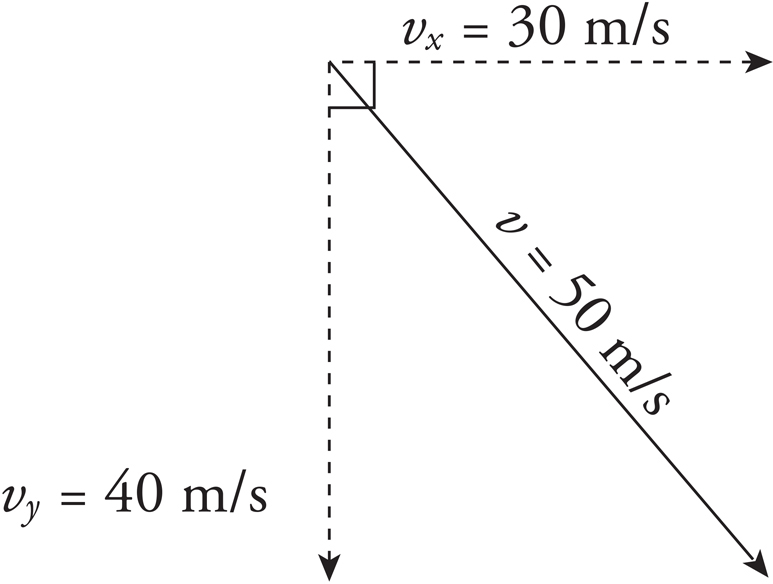
After 4 seconds, the stone’s vertical speed has changed by Δvy = ayt = (10 m/s2)(4 s) = 40 m/s. Since v0y = 0, the value of vy at t = 4 is 40 m/s. The horizontal speed does not change. Therefore, when the rock hits the water, its velocity has a horizontal component of 30 m/s and a vertical component of 40 m/s.
By the Pythagorean Theorem, the magnitude of the total velocity, v, is 50 m/s.
10. D
Since the acceleration of the projectile is always downward (because of its gravitational acceleration), the vertical speed decreases as the projectile rises and increases as the projectile falls. Choices (A), (B), and (C) are all false.
11. B
Use Big Five #2:
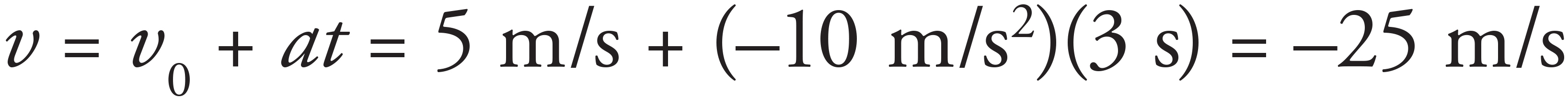
Because you called up the positive direction, the negative sign for the velocity indicates that the stone is traveling downward.
12. C
The variables involved in this question are the initial velocity (given in both cases), the acceleration (constant), final velocity (0 in both cases), and displacement (the skidding distance). As the missing variable is time, use Big Five #5 to solve for the displacement:
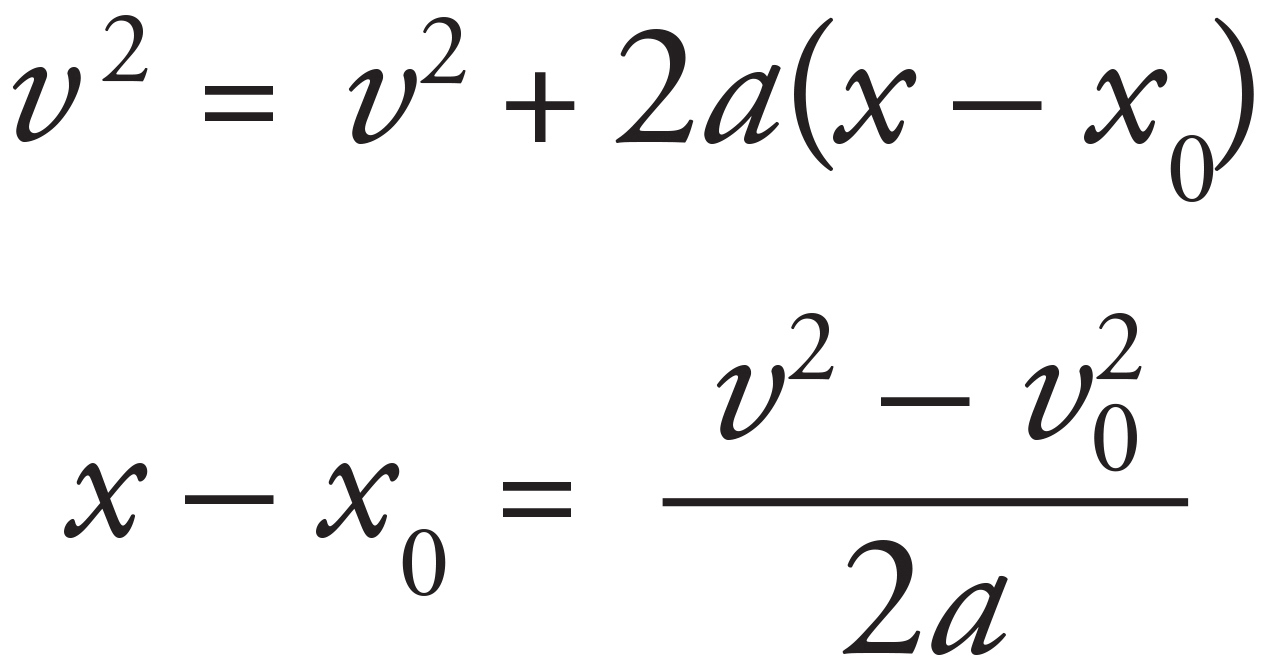
As the initial position, x0, and the final velocity, v2, are equal to 0, this equation simplifies to
When the initial velocity is doubled, the final position quadruples. (Note that the acceleration in this problem is negative, as the brakes cause the car to decelerate).
1. (a)
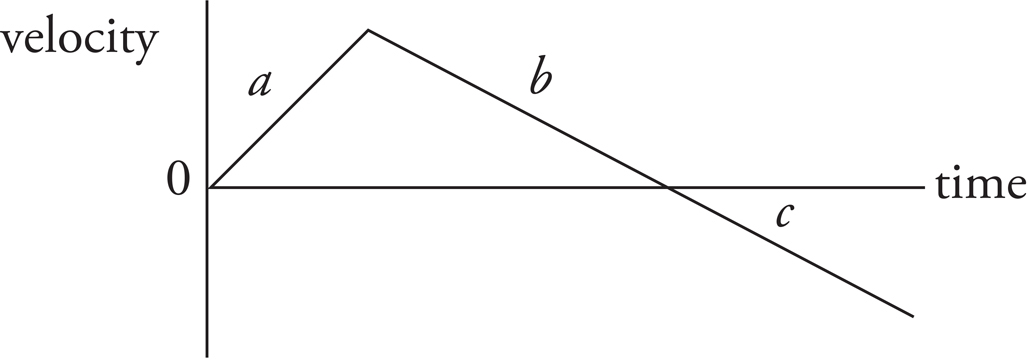
At time t = 1 s, the car’s velocity starts to decrease as the acceleration (which is the slope of the given velocity-versus-time graph) changes from positive to negative.
(b)
The average velocity between t = 0 and t = 1 s is 
(vt=0 + vt=1) = (0 + 20 m/s) = 10 m/s, and the average velocity between t = 1 and t = 5 is (vt=1 + vt=5) = (20 m/s + 0) = 10 m/s. The two average velocities are the same.
(c)
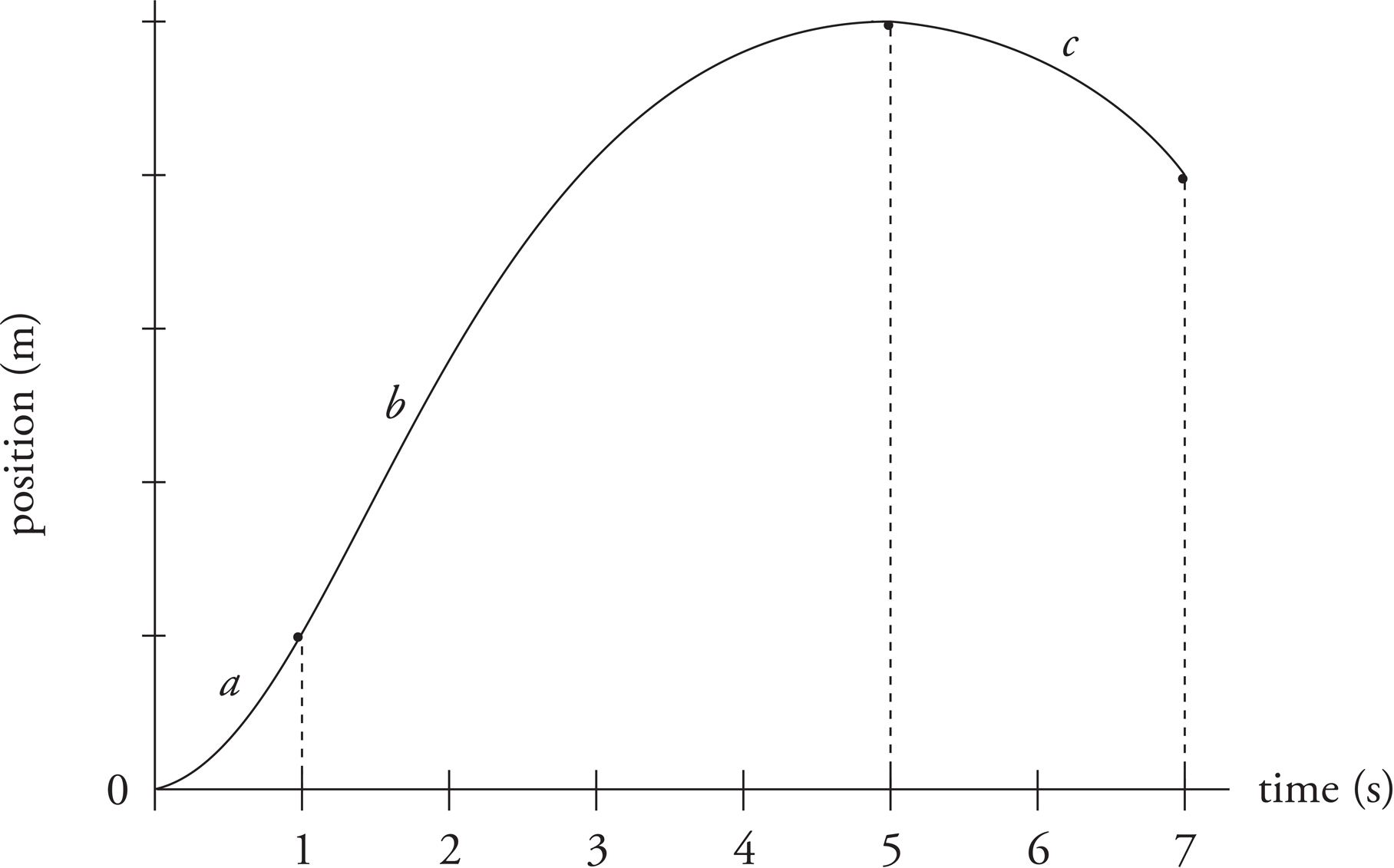
The displacement is equal to the area bounded by the graph and the t-axis, taking areas above the t-axis as positive and those below as negative. In this case, the displacement from t = 0 to t = 5 s is equal to the area of the triangular region whose base is the segment along the t-axis from t = 0 to t = 5 s:
Δx (t = 0 to t = 5 s) = × base × height = (5 s)(20 m/s) = 50 m
The displacement from t = 5 s to t = 7 s is equal to the negative of the area of the triangular region whose base is the segment along the t-axis from t = 5 s to t = 7 s:
Δx (t = 5 s to t = 7 s) = − × base × height = −(2 s)(10 m/s) = −10 m
Therefore, the displacement from t = 0 to t = 7 s is
Δx (t = 0 to t = 5 s) + Δs (t = 5 s to t = 7 s) = 50 m + (−10 m) = 40 m
(d)
The acceleration is the slope of the velocity-versus-time graph. The segment of the graph from t = 0 to t = 1 s has a slope of a = Δv/Δt = (20 m/s − 0)/(1 s − 0) = 20 m/s2, and the segment of the graph from t = 1 s to t = 7 s has a slope of a = Δv/Δt = (−10 m/s − 20 s)/(7 s − 1 s) = −5 m/s2. Therefore, the acceleration-versus-time graph is
(e)
Section a shows that the object is speeding up in the positive direction. Section b shows that the object is slowing down, yet still moving in the positive direction. At five seconds, the object has stopped for an instant. Section c shows that the object is moving in the negative direction and speeding up. The corresponding position-versus-time graph for each section would look like this:
2. (a)
The maximum height of the projectile occurs at the time at which its vertical velocity drops to zero:
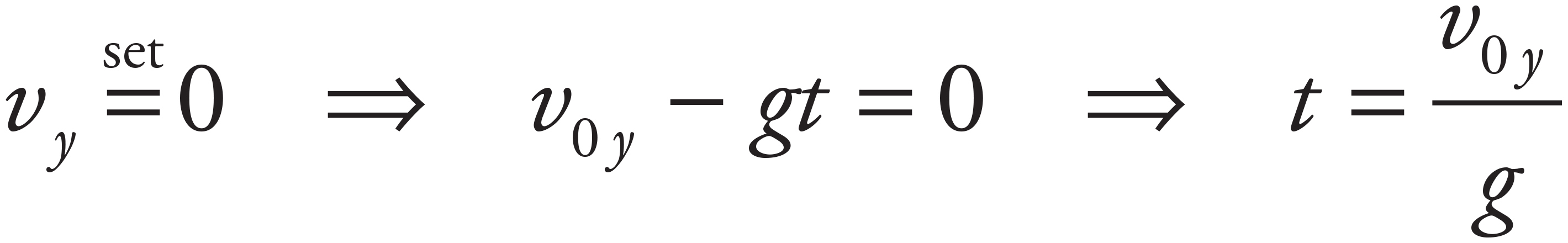
The vertical displacement of the projectile at this time is computed as follows:
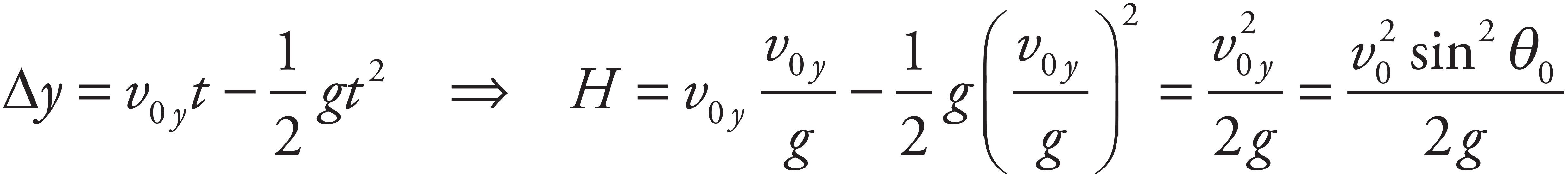
(b)
The total flight time is equal to twice the time computed in part (a):
The horizontal displacement at this time gives the projectile’s range:
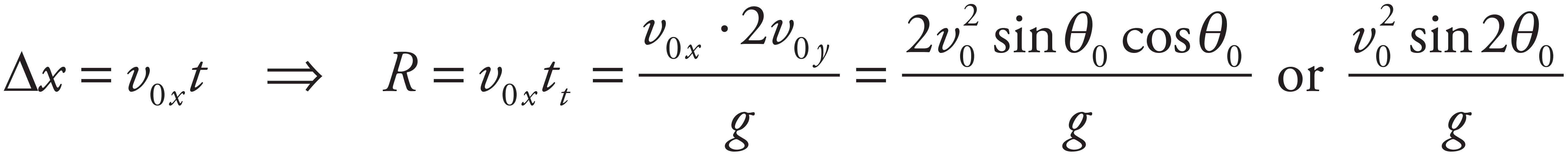
(c)
For any given value of v0, the range,
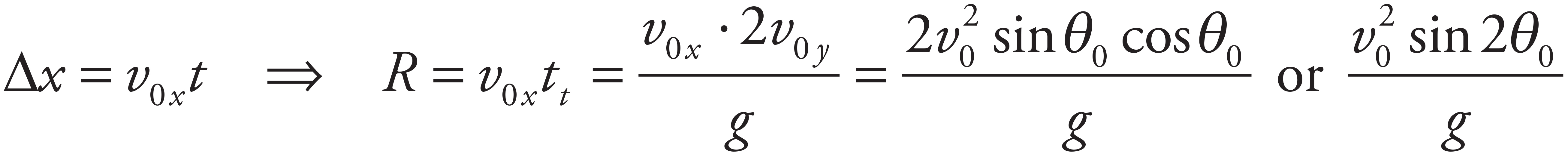
will be maximized when sin 2θ0 is maximized. This occurs when 2θ0 = 90°, that is, when θ0 = 45°.
(d)
Set the general expression for the projectile’s vertical displacement equal to h and solve for the two values of t (assuming that g = +10 m/s2):
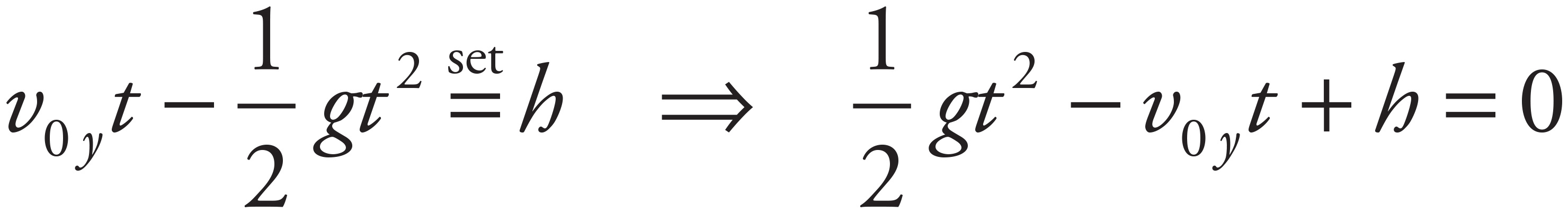
Applying the quadratic formula, find that
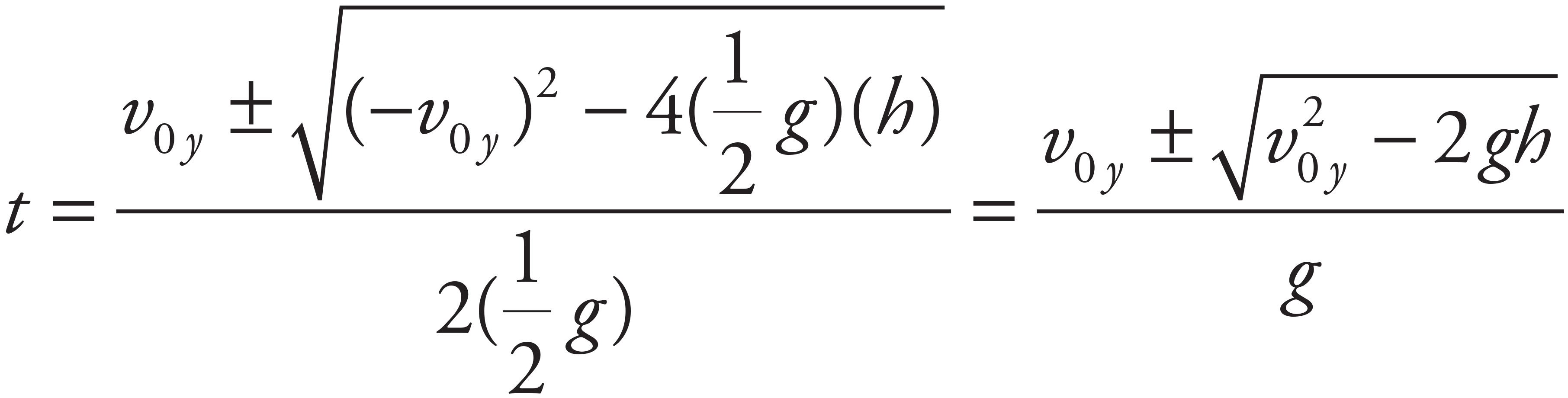
Therefore, the two times at which the projectile crosses the horizontal line at height h are
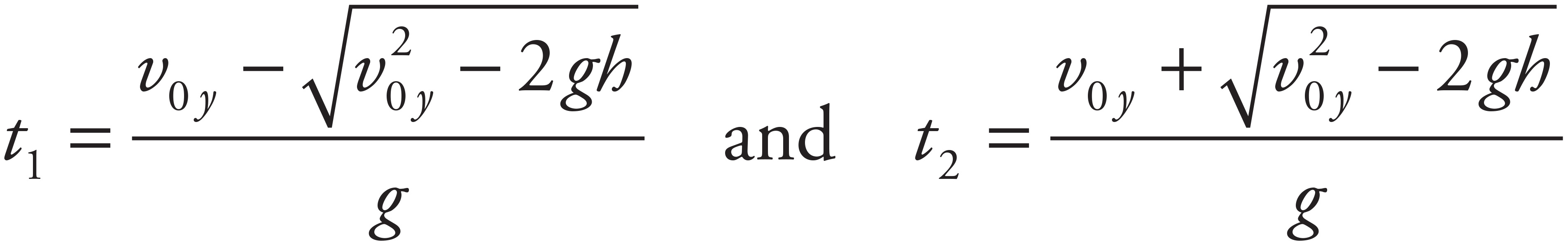
so the amount of time that elapses between these events is
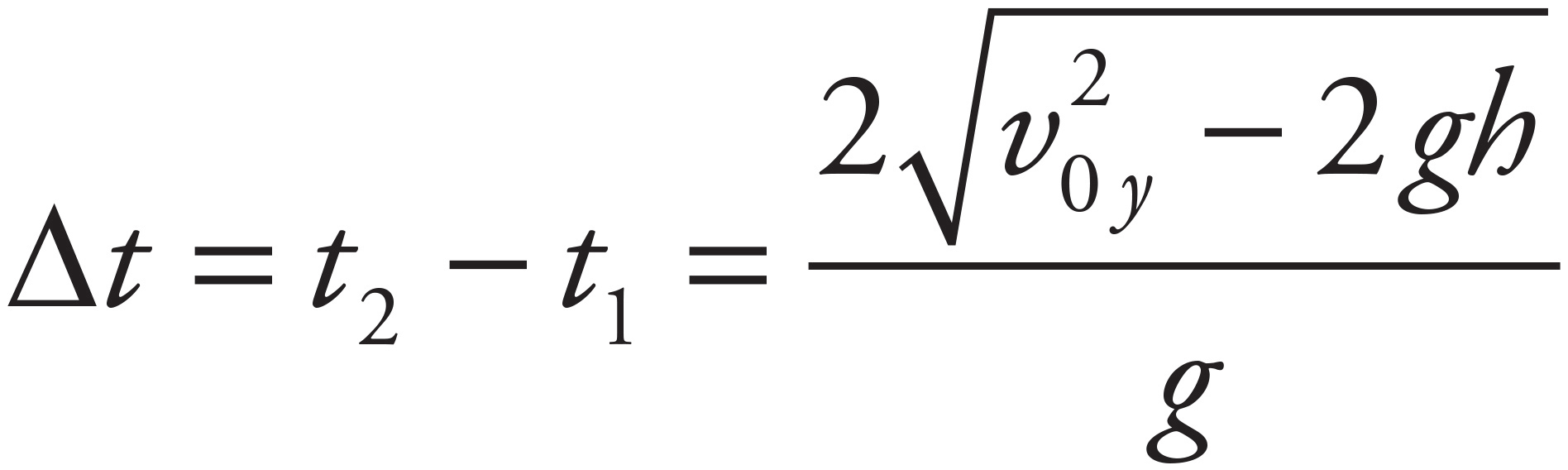
3. (a)
The cannonball will certainly reach the wall (which is only 220 m away) since the ball’s range is
You simply need to make sure that the cannonball’s height is less than 30 m at the point where its horizontal displacement is 220 m (so that the ball actually hits the wall rather than flying over it). To do this, find the time at which x = 220 m by first writing
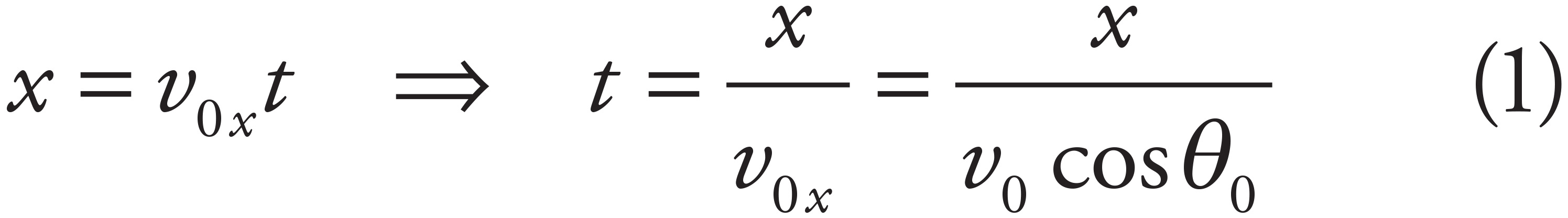
Thus, the cannonball’s vertical position can be written in terms of its horizontal position as follows:
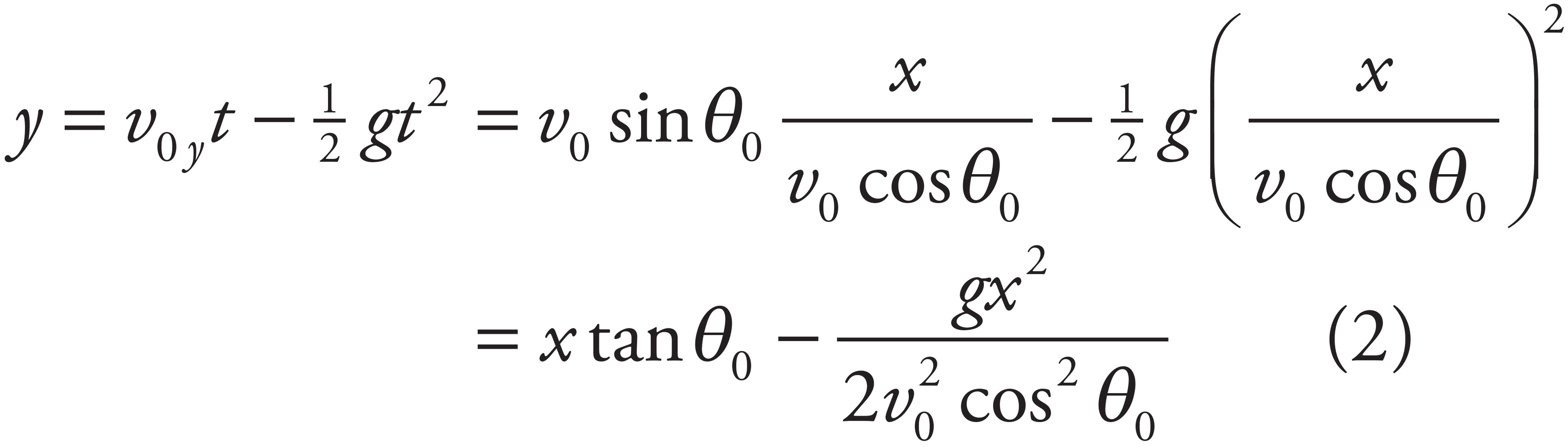
Substituting the known values for x, θ0, g, and v0, you get
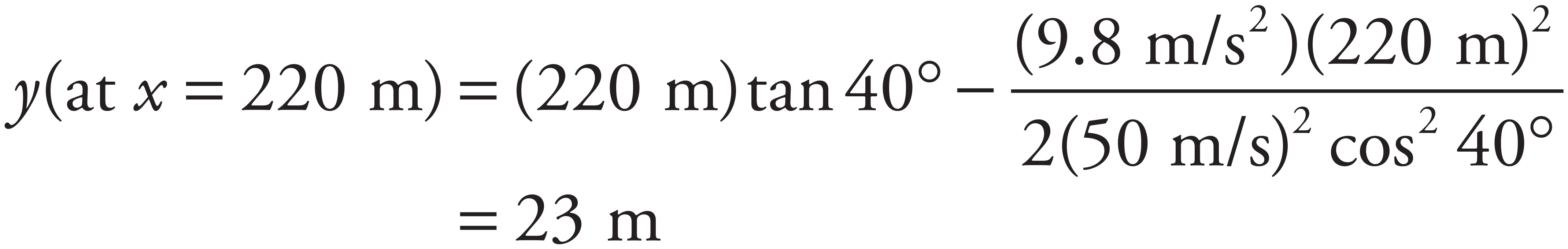
This is indeed less than 30 m, as desired.
(b)
From Equation (1) derived in part (a),
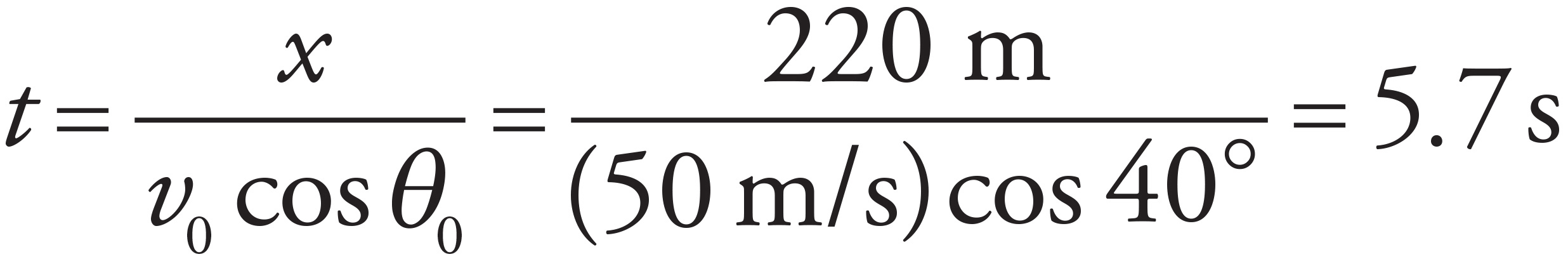
(c)
The height at which the cannonball strikes the wall was determined in part (a) to be 23 m.
4. (a)
For parabolic trajectories, the total flight time can be determined by doubling the amount of time it takes for the projectile to reach its apex. However, this trajectory is NOT parabolic. As the initial position is 25 m, the final position is 0 m, the initial velocity is v0 = v0 sin θ = 40 sin 30° = 40 (
) = 20 m/s, and the acceleration is −10 m/s2; the missing variable is the final velocity, so the flight time of the cannonball can be computed using Big Five #3:
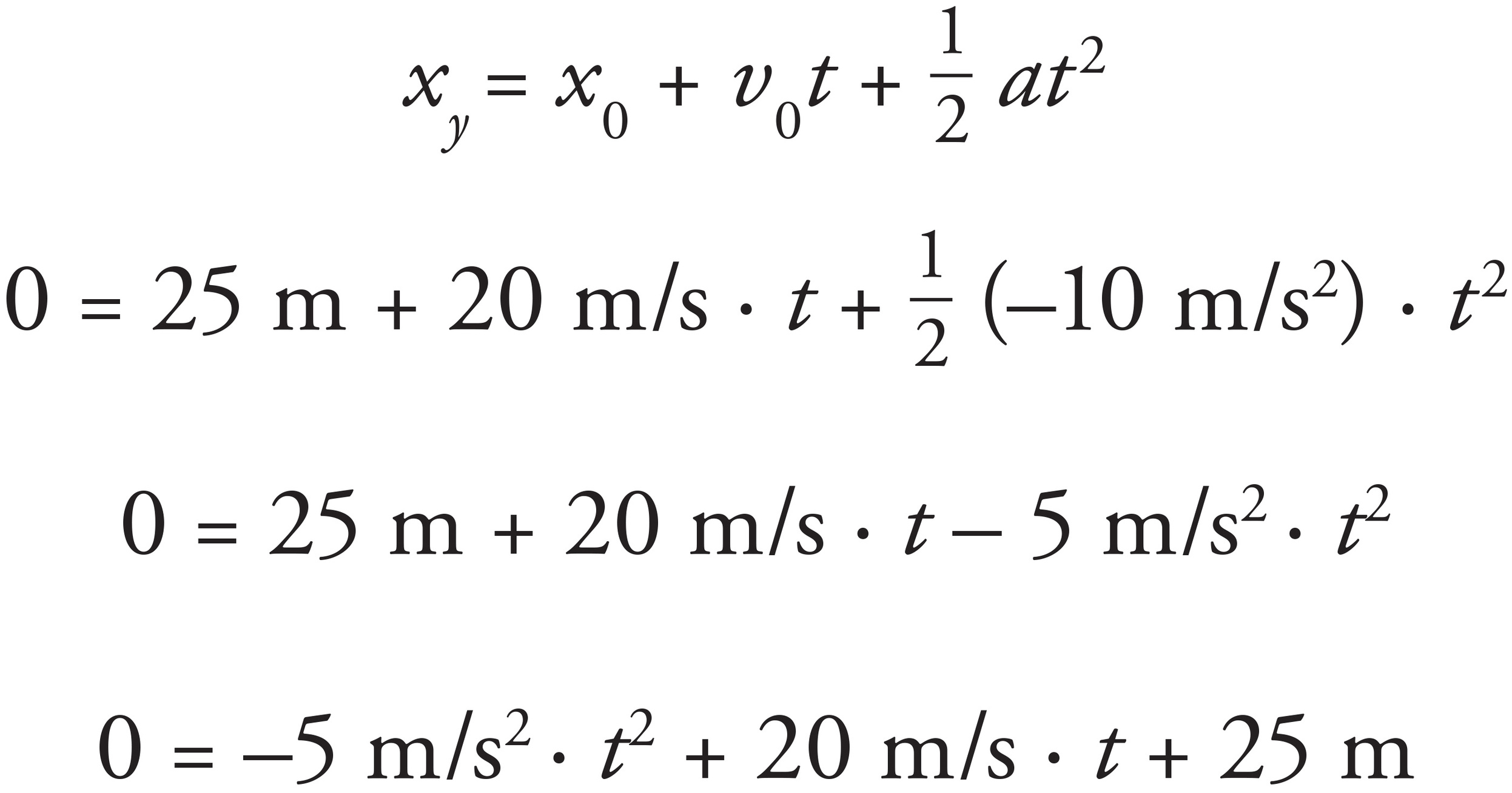
Applying the quadratic formula, find that
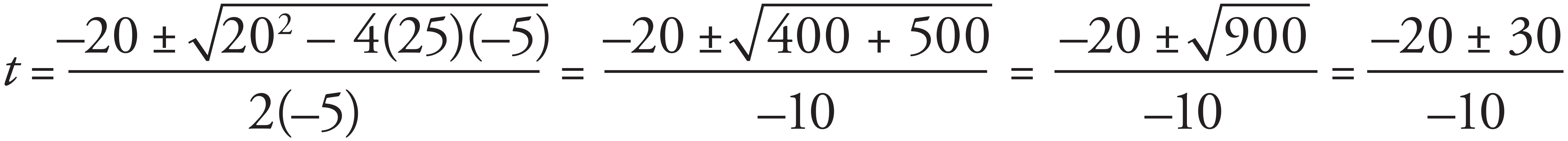
t = −1 s or t = 5 s
As time cannot be a negative value, the flight time of the cannonball is 5 seconds.
(b)
As the horizontal speed of a projectile is constant, the range is given by
Δx = v0xt = 40 m/s · cos 30° · 5 s = 173 m
(c)
The cannonball is fired with an initial horizontal velocity of
v0x = 40 m/s · cos 30° = 34.6 m/s
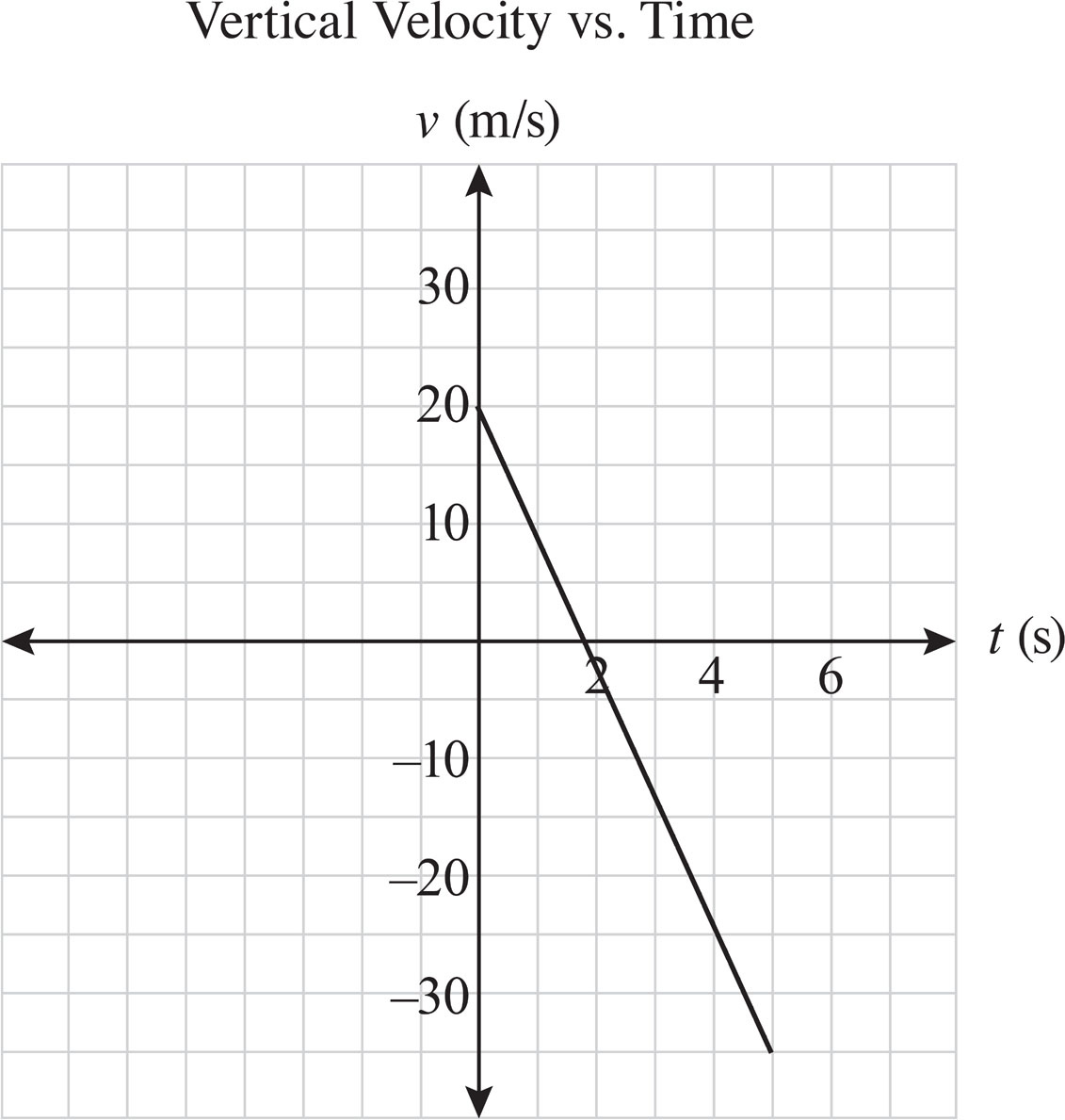
As there is no horizontal acceleration, the horizontal speed of the projectile remains constant throughout the entire flight, leading to a flat line with a y-value of 34.6 m/s over the flight time of 5 s. The horizontal speed-versus-time graph can then be plotted.
The initial vertical velocity of the cannonball is
v0x = 40 m/s · sin 30° = 20 m/s
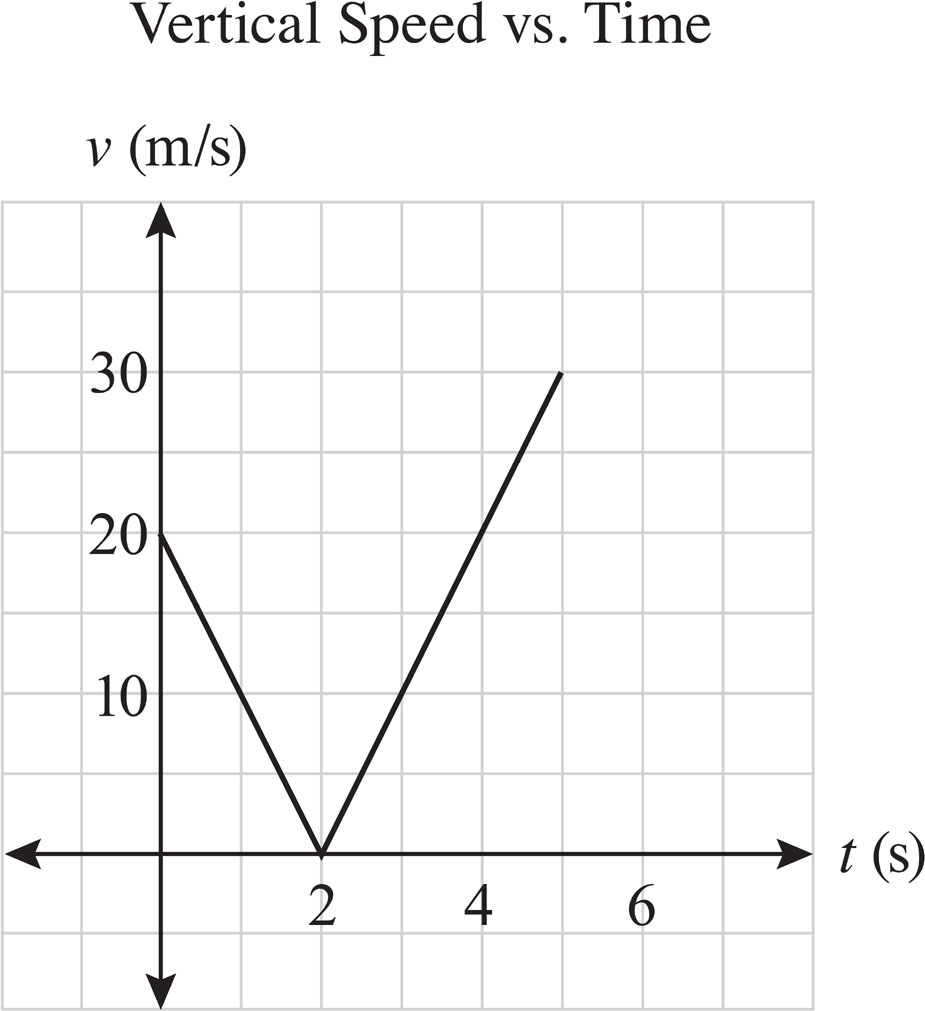
In the vertical direction, there is a constant acceleration due to gravity (a = 10 m/s2). As the slope of the velocity-versus-time graph is equal to the acceleration, the resulting velocity-versus-time graph is a linear line with a negative slope since acceleration due to gravity points downward. As the magnitude of the acceleration of gravity is 10 m/s2, the vertical velocity of the cannonball thus decreases by 10 m/s every second. With an initial velocity of 20 m/s, this means that after 2 s, the vertical velocity of the projectile is 0 m/s. After a total of 5 s, the vertical velocity of the projectile is −30 m/s. This can be visualized in the vertical velocity-versus-time graph below:
As the problem asks for the graph of the vertical speed versus time, the absolute value of the graph must be drawn to get the correct plot.
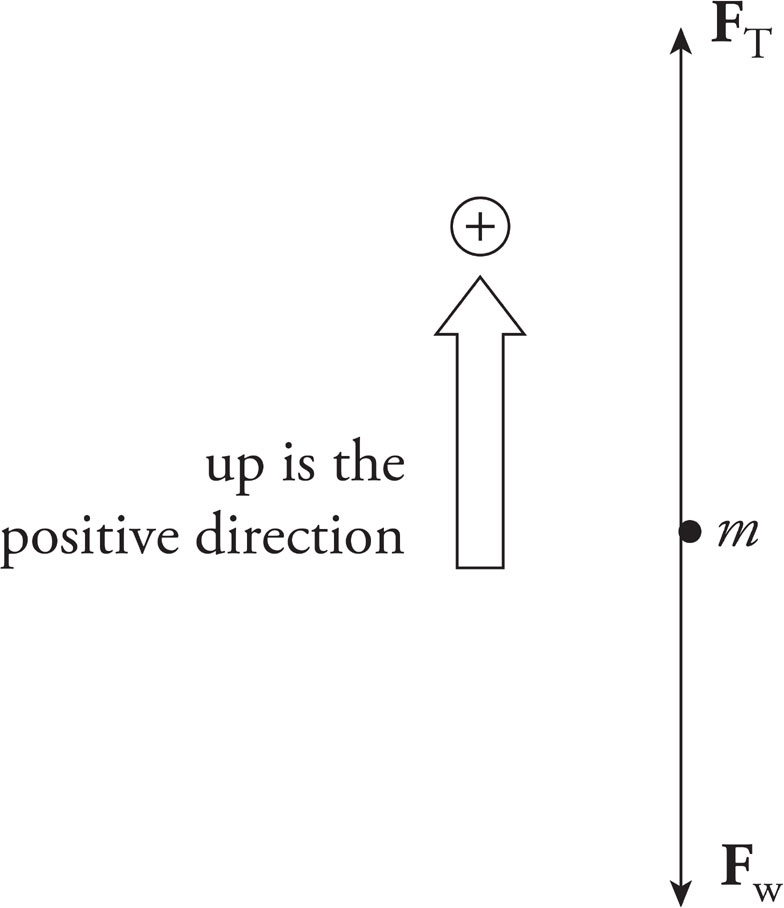
1. B
Because the person is not accelerating, the net force he feels must be zero. Therefore, the magnitude of the upward normal force from the floor must balance that of the downward gravitational force. Although these two forces have equal magnitudes, they do not form an action/reaction pair because they both act on the same object (namely, the person). The forces in an action/reaction pair always act on different objects. The correct action/reaction pair in this situation is the Earth’s pull on the person (the weight) and the person’s pull on the Earth.
2. D
First, draw a free-body diagram:
The person exerts a downward force on the scale, and the scale pushes up on the person with an equal (but opposite) force, FN. Thus, the scale reading is FN, the magnitude of the normal force. Since FN − Fw = ma, you get FN = Fw + ma = (800 N) + [800 N/(10 m/s2)](5 m/s2) = 1,200 N.
3. A
The net force that the object feels on the inclined plane is mg sin θ, the component of the gravitational force that is parallel to the ramp. Since sin θ = (5 m)/(20 m) = 
, you get Fnet = (2 kg)(10 N/kg)() = 5 N.
4. C
The net force on the block is F − Ff = F − µkFN = F − µkFw = (18 N) − (0.4)(20 N) = 10 N. Since Fnet = ma = (Fw/g)a, you get 10 N = [(20 N)/(10 m/s2)]a, which gives a = 5 m/s2.
5. A
The force pulling the block down the ramp is mg sin θ, and the maximum force of static friction is μsFN = μsmg cos θ. If mg sin θ is greater than μsmg cos θ, then there is a net force down the ramp, and the block will accelerate down. So, the question becomes, “Is sin θ greater than μs cos θ?” Since θ = 30° and μs = 0.5, the answer is “yes.”
6. D
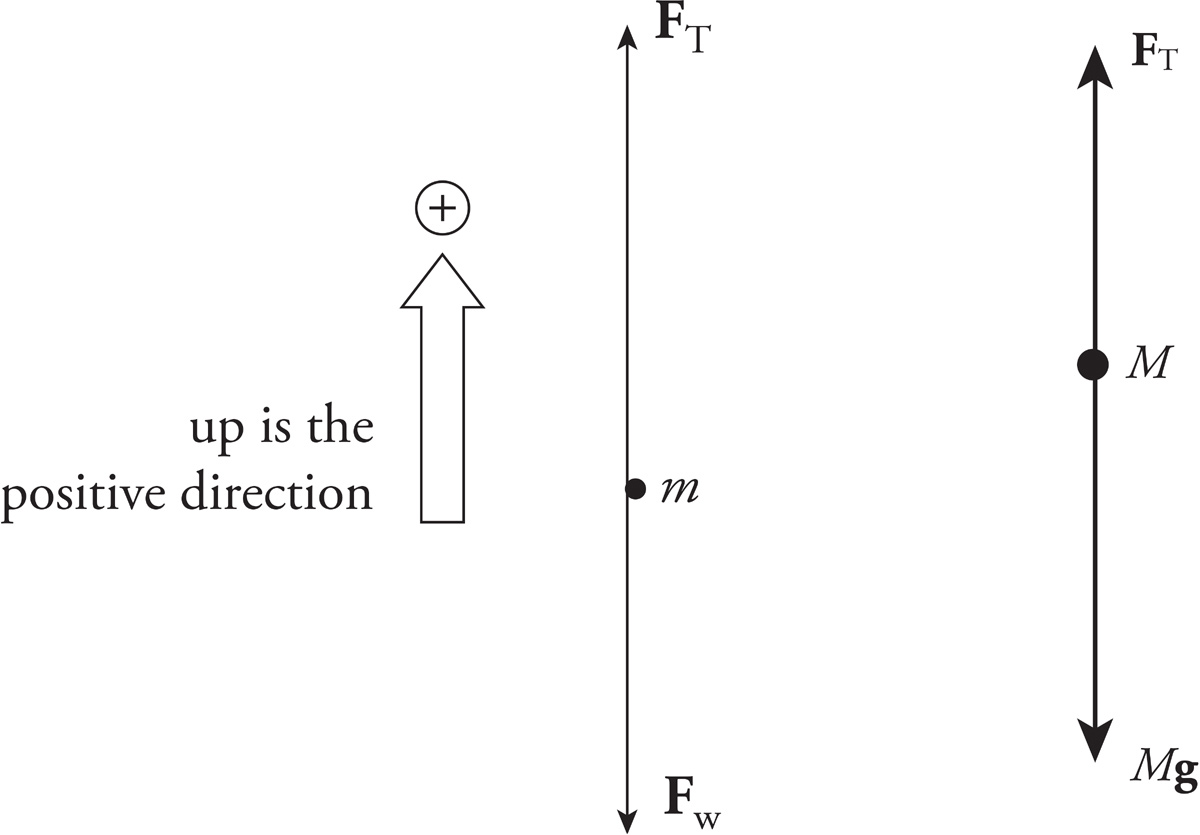
One way to attack this question is to notice that if the two masses happen to be equal, that is, if M = m, then the blocks won’t accelerate (because their weights balance). The only expression given that becomes zero when M = m is the one given in (D). Draw a free-body diagram:
Newton’s Second Law gives the following two equations:
FT − mg = ma (1)
FT − Mg = M(−a) (2)
Subtracting these equations yields Mg − mg = ma + Ma = (M + m)a, so
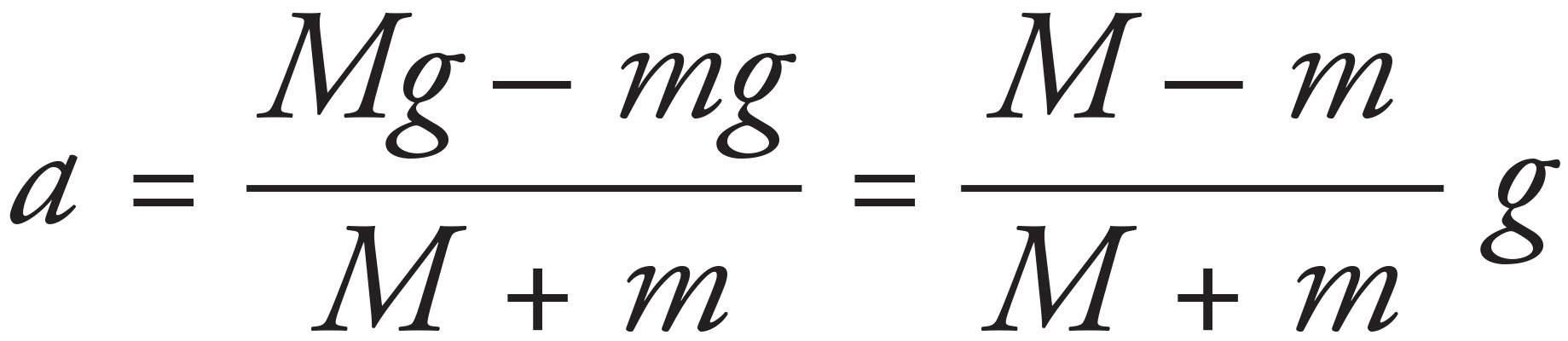
7. D
If Fnet = 0, then a = 0. No acceleration means constant speed (possibly, but not necessarily zero) with no change in direction. Therefore, (B) and (C) are false, and (A) is not necessarily true.
8. C
The horizontal motion across the frictionless tables is unaffected by (vertical) gravitational acceleration. It would take as much force to accelerate the block across the table on Earth as it would on the Moon. (If friction were taken into account, then the smaller weight of the block on the Moon would imply a smaller normal force by the table and hence a smaller frictional force. Less force would be needed on the Moon in this case.)
9. D
The maximum force which static friction can exert on the crate is μsFN = μsFw = μsmg = (0.4)(100 kg)(10 N/kg) = 400 N. Since the force applied to the crate is only 344 N, static friction is able to apply that same magnitude of force on the crate, keeping it stationary. Choice (B) is incorrect because the static friction force is not the reaction force to F; both F and Ff (static) act on the same object (the crate) and therefore cannot form an action/reaction pair.
10. A
With Crate #2 on top of Crate #1, the force pushing downward on the floor is greater, so the normal force exerted by the floor on Crate #1 is greater, which increases the friction force. Choices (B), (C), and (D) are all false.
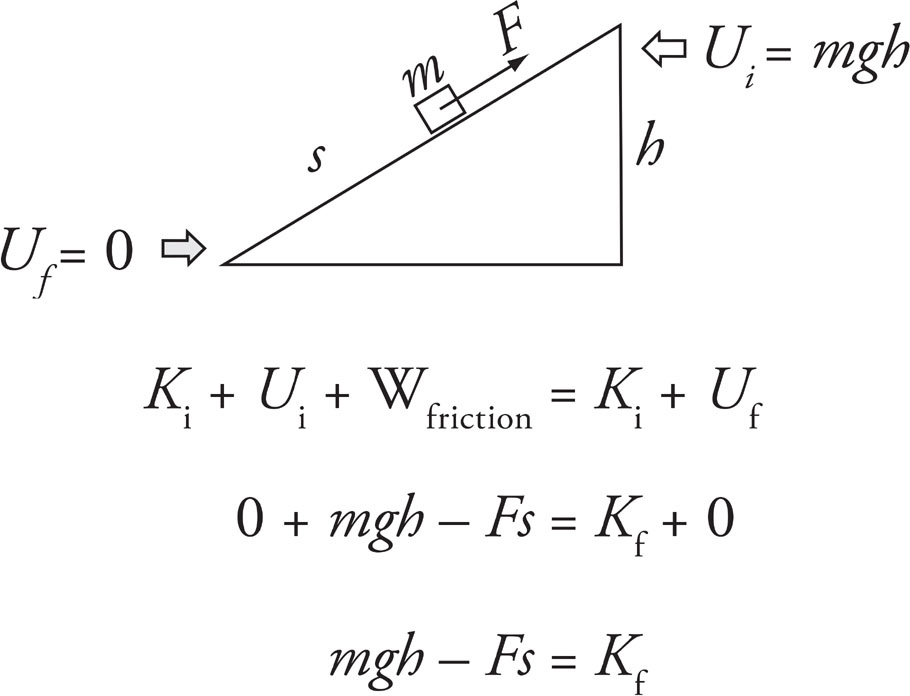
1. (a)
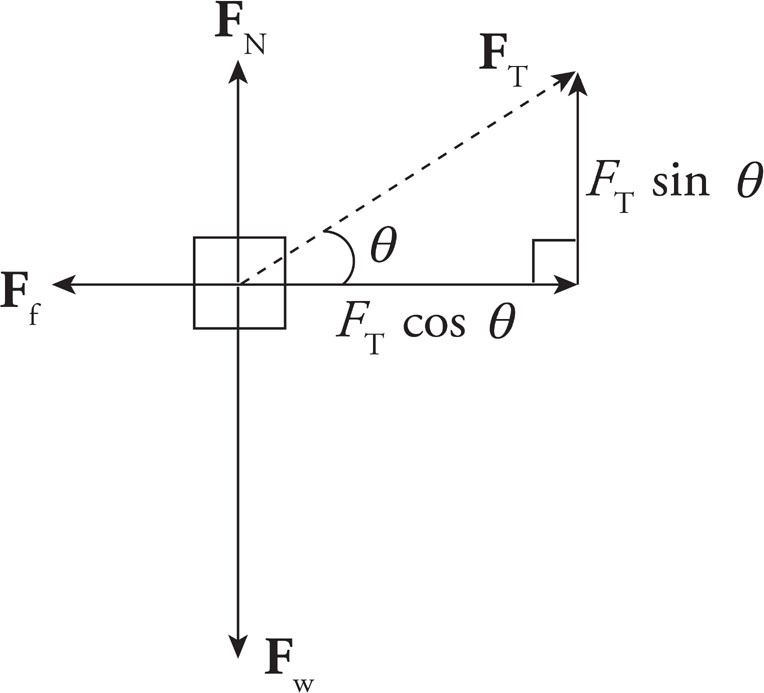
The forces acting on the crate are FT (the tension in the rope), Fw (the weight of the block), FN (the normal force exerted by the floor), and Ff (the force of kinetic friction):
(b)
First, break FT into its horizontal and vertical components:
Since the net vertical force on the crate is zero, you get FN + FT sin θ = Fw, so FN = Fw − FT sin θ = mg − FT sin θ.
(c)
From part (b), notice that the net horizontal force acting on the crate is
so the crate’s horizontal acceleration across the floor is
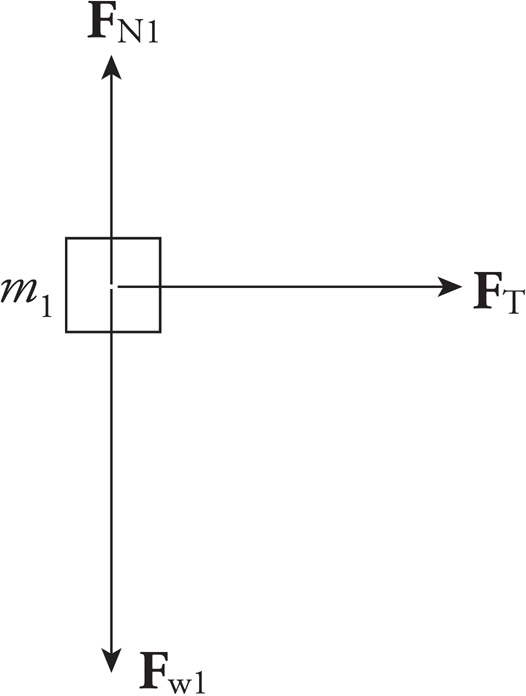
2. (a)
The forces acting on Block #1 are FT (the tension in the string connecting it to Block #2), Fw1 (the weight of the block), and FN1 (the normal force exerted by the tabletop):
(b)
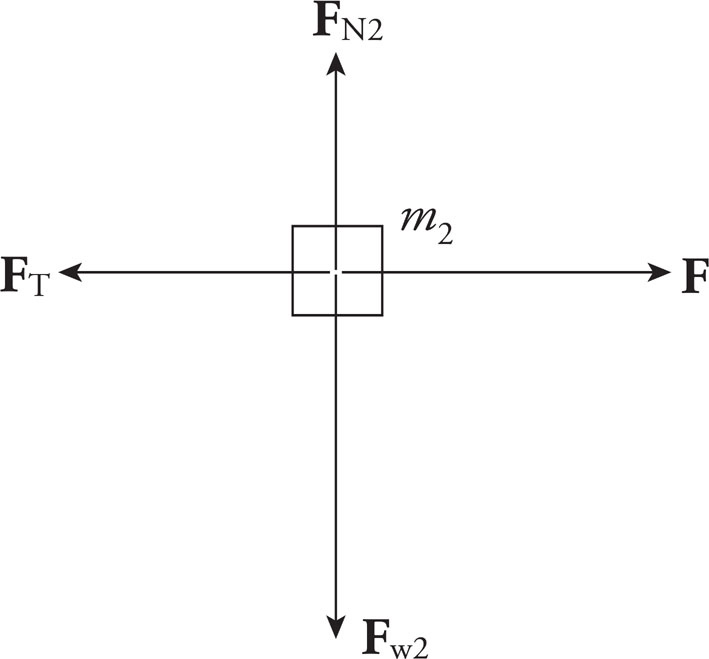
The forces acting on Block #2 are F (the pulling force), FT (the tension in the string connecting it to Block #1), Fw2 (the weight of the block), and FN2 (the normal force exerted by the tabletop):
(c)
Newton’s Second Law applied to Block #2 yields F − FT = m2a, and applied to Block #1 yields FT = m1a. Adding these equations, you get F = (m1 + m2)a, so
(d)
Substituting the result of part (c) into the equation FT = m1a, you get
(e)
(i) Since the force F must accelerate all three masses—m1, m, and m2—the common acceleration of all parts of the system is
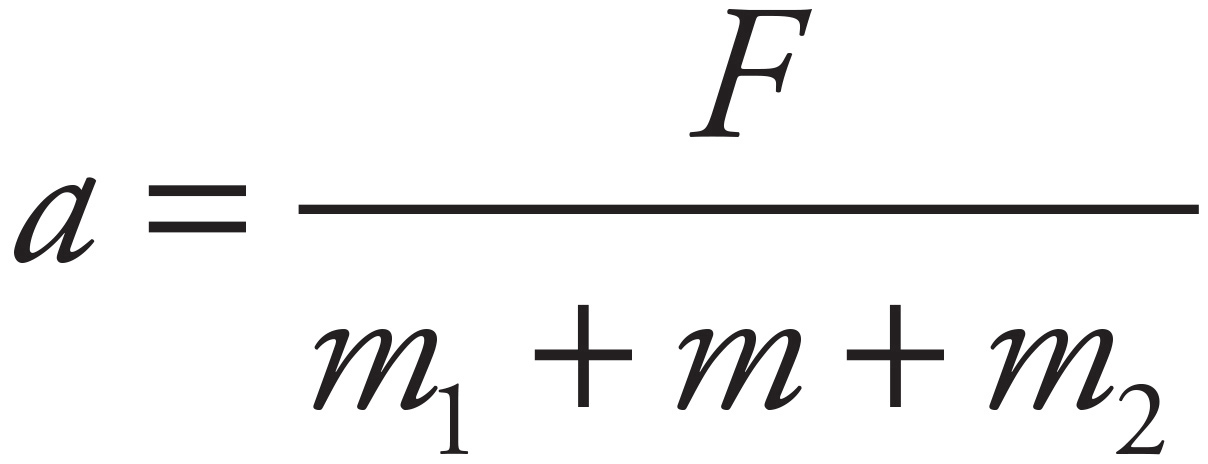
(ii) Let FT1 denote the tension force in the connecting string acting on Block #1, and let FT2 denote the tension force in the connecting string acting on Block #2. Then, Newton’s Second Law applied to Block #1 yields FT1 = m1a and applied to Block #2 yields F − FT2 = m2a. Therefore, using the value for a computed above, you get
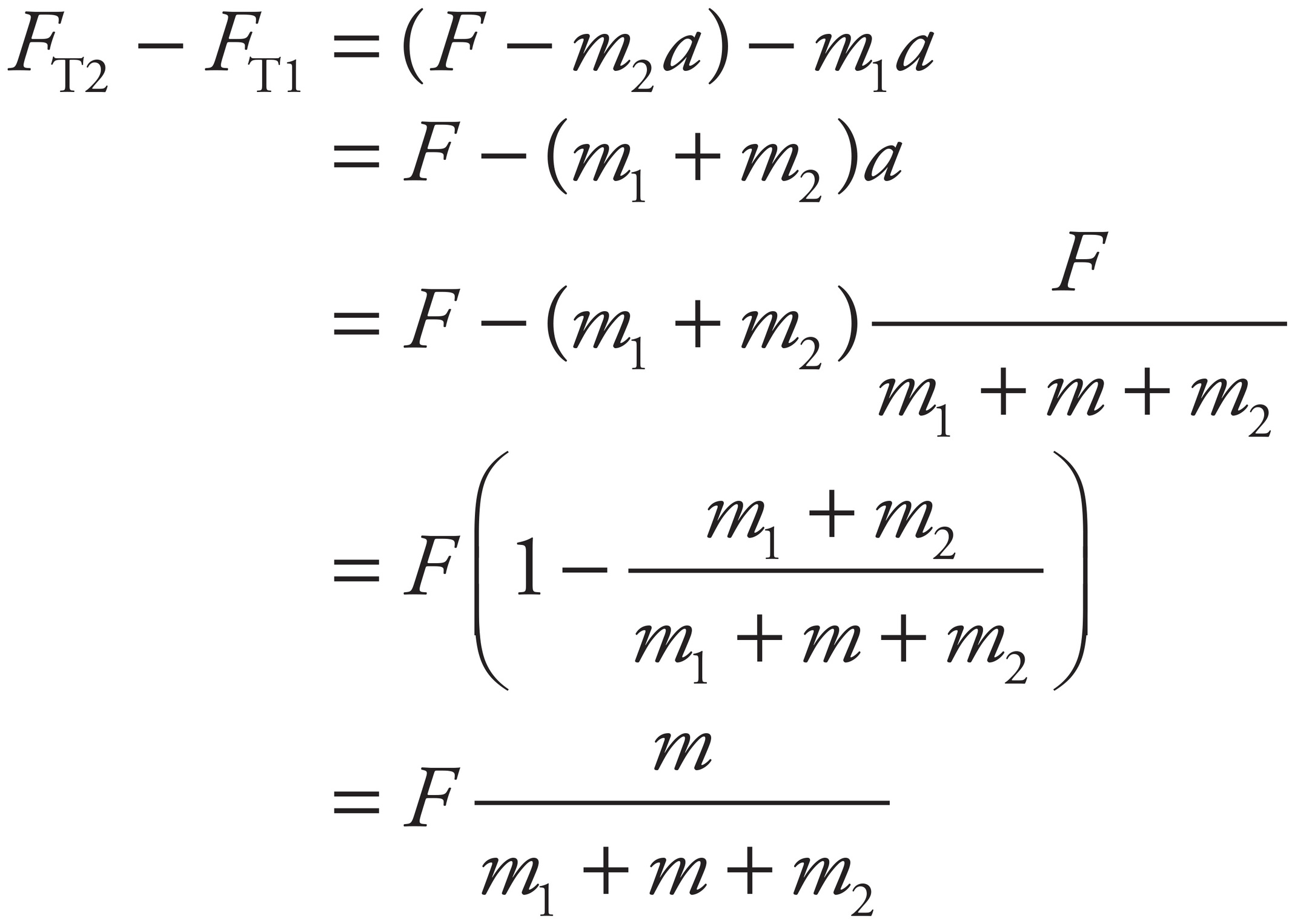
3. (a)
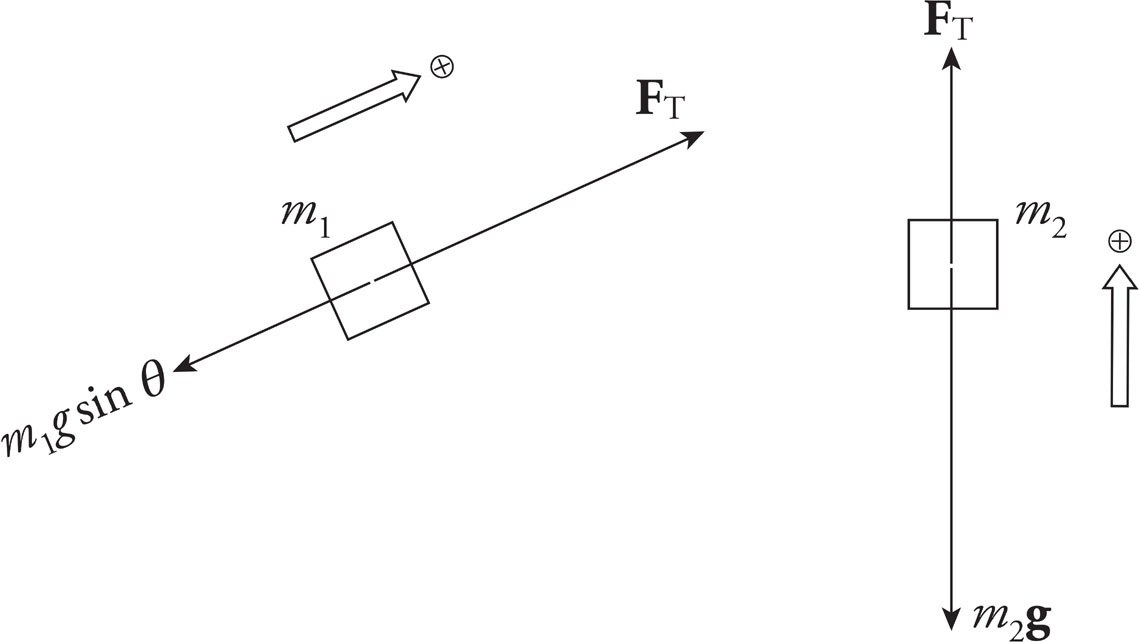
First, draw free-body diagrams for the two boxes:
Applying Newton’s Second Law to the boxes yields the following two equations:
FT − m1g sin θ = m1a (1)
FT − m2g = m2(−a) (2)
Subtract the equations and solve for a:
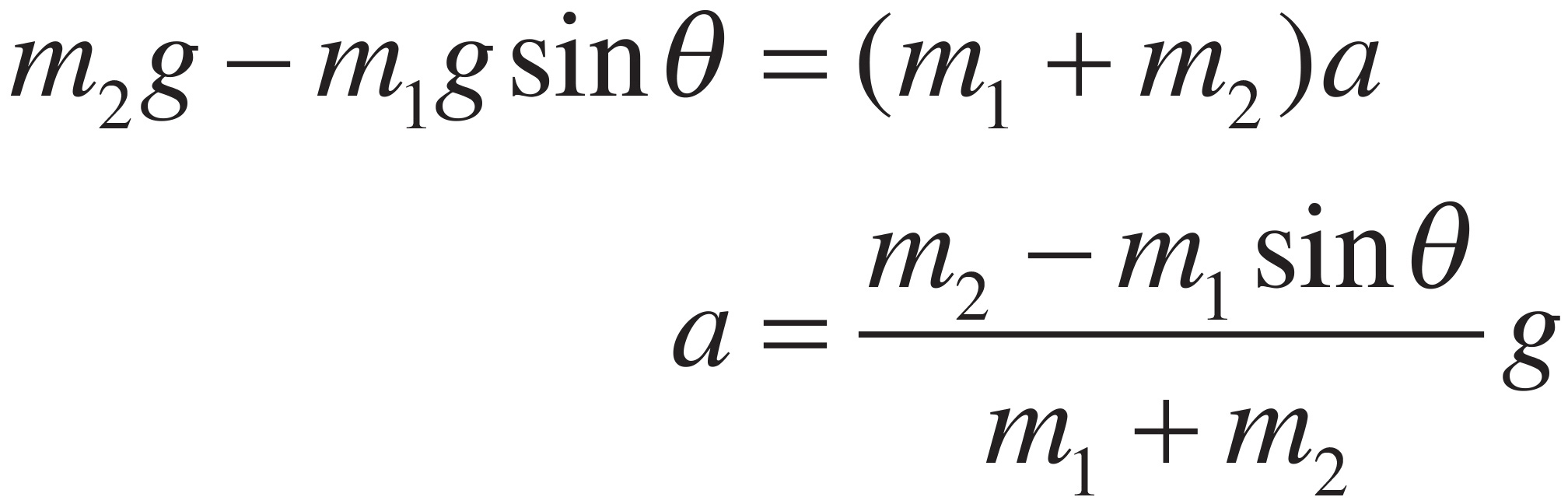
(i) For a to be positive, you must have m2 − m1 sin θ > 0, which implies that sin θ < m2/m1, or, equivalently, θ < sin−1(m2/m1).
(ii) For a to be zero, you must have m2 − m1 sin θ = 0, which implies that sin θ = m2/m1, or, equivalently, θ = sin−1(m2/m1).
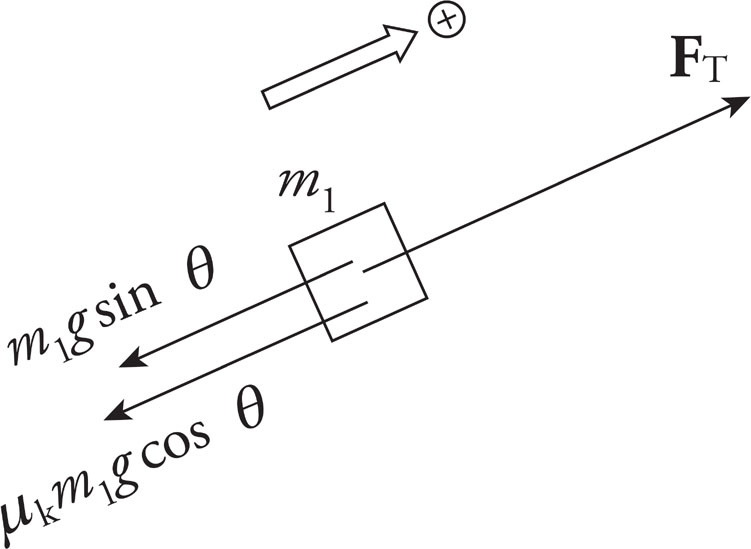
(b)
Including the force of kinetic friction, the force diagram for m1 is
Since Ff = μkFN = μkm1g cos θ, applying Newton’s Second Law to the boxes yields these two equations:
FT − m1g sin θ − μkmg cos θ = m1a (1)
m2g − FT = m2a (2)
Add the equations and solve for a:
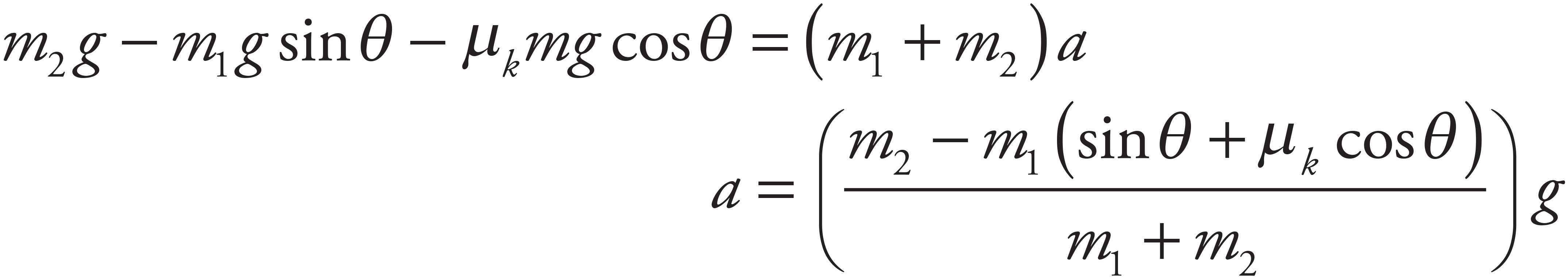
In order for a to be equal to zero (so that the box of mass m1 slides up the ramp with constant velocity),
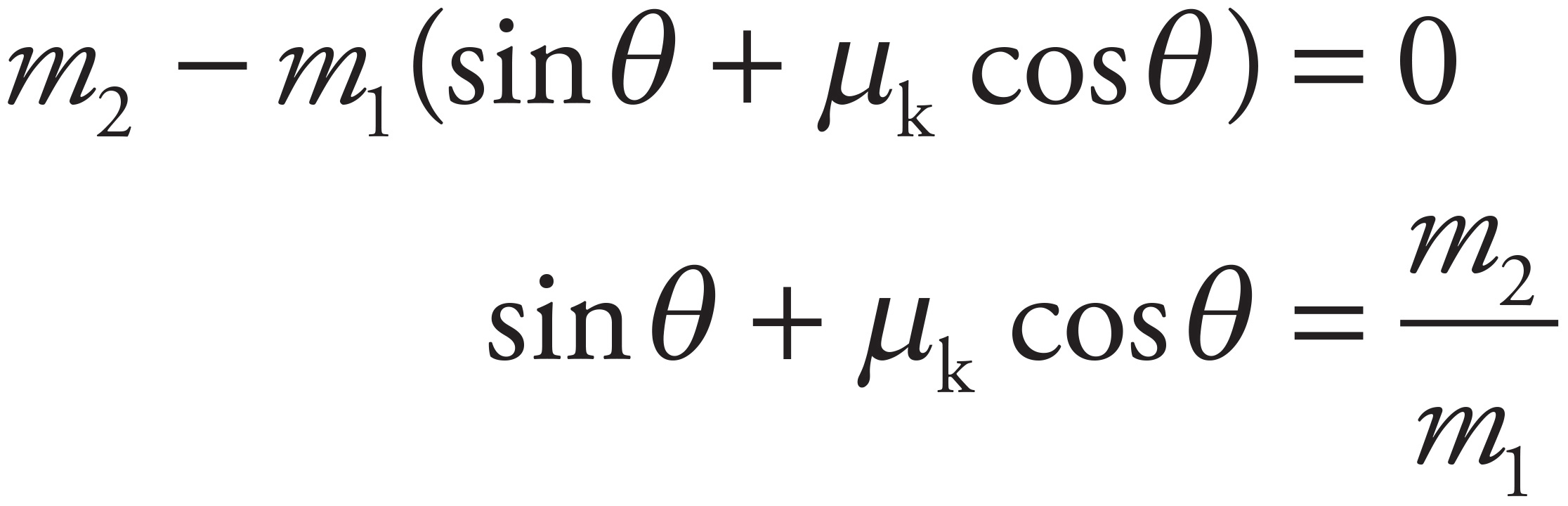
4. (a)
The forces acting on the skydiver are Fr, the force of air resistance (upward), and Fw, the weight of the skydiver (downward):
(b)
Since Fnet = Fw − Fr = mg − kv, the skydiver’s acceleration is
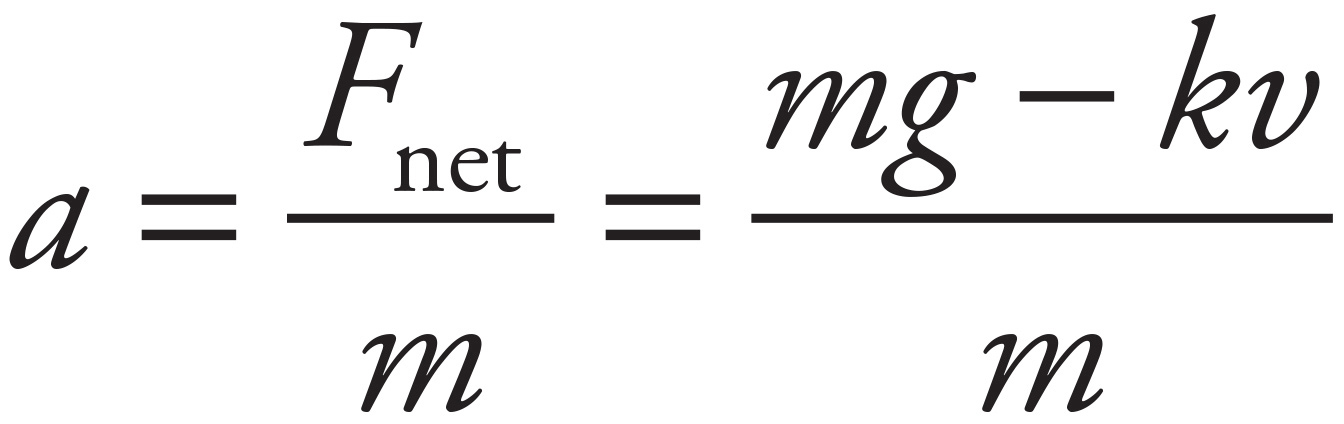
(c)
Terminal speed occurs when the skydiver’s acceleration becomes zero, since then the descent velocity becomes constant. Setting the expression derived in part (b) equal to 0, find the speed v = vt at which this occurs:
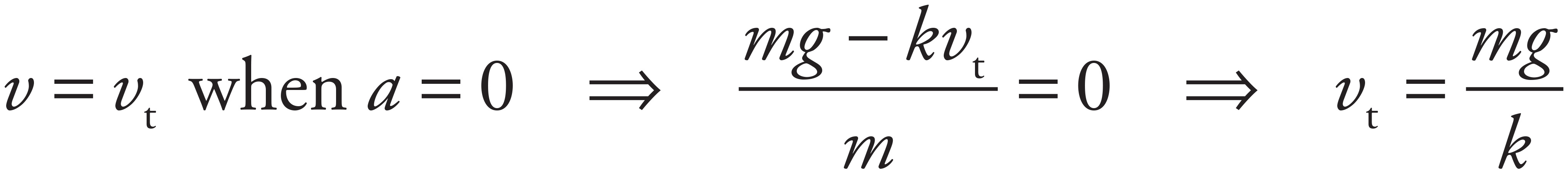
(d)
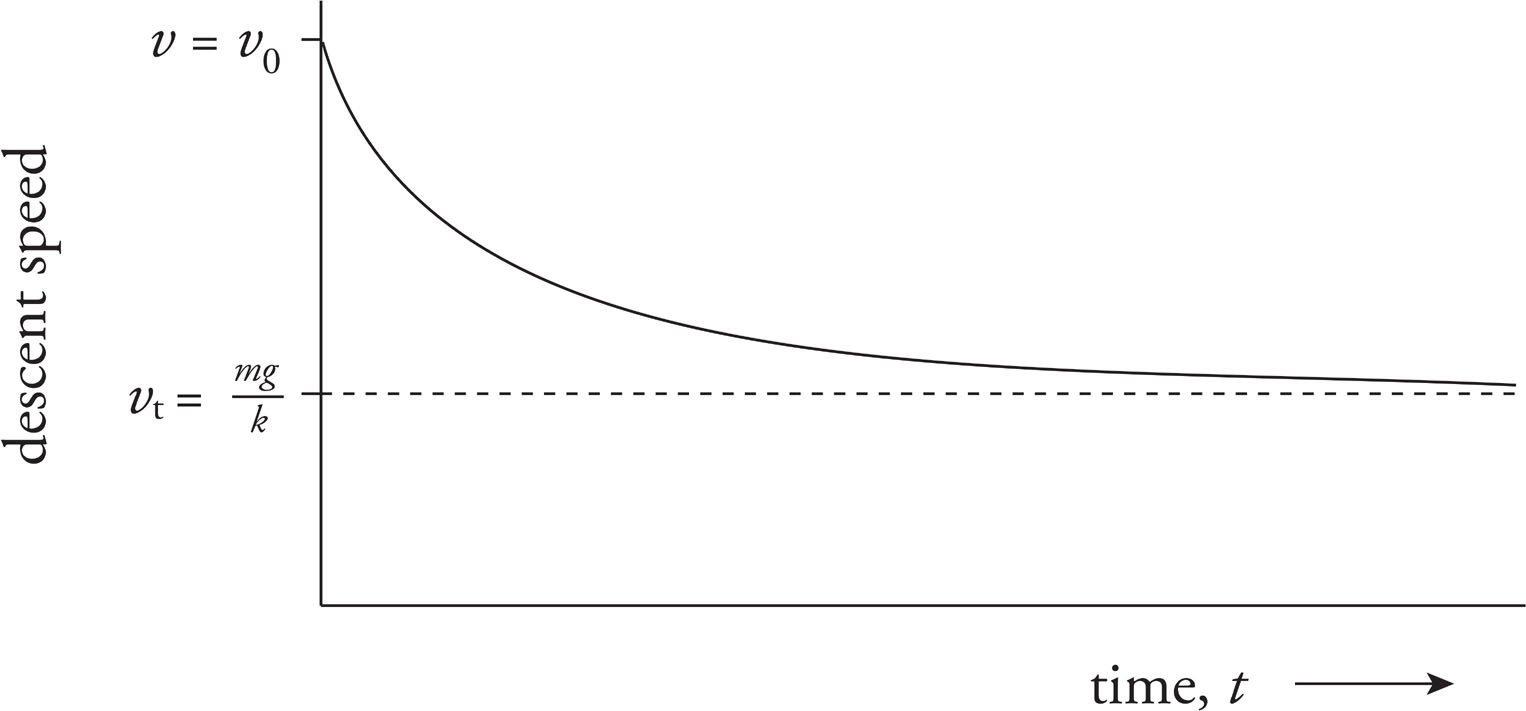
The skydiver’s descent speed is initially v0 and the acceleration is (close to) g. However, once the parachute opens, the force of air resistance provides a large (speed-dependent) upward acceleration, causing her descent velocity to decrease. The slope of the velocity-versus-time graph (the acceleration) is not constant but instead decreases to zero as her descent speed decreases from v0 to vt. Therefore, the graph is not linear.
1. A
Since the force F is perpendicular to the displacement, the work it does is zero.
2. B
By the Work–Energy Theorem,
3. B
Since the box (mass m) falls through a vertical distance of h, its gravitational potential energy decreases by mgh. The length of the ramp is irrelevant here. If friction were involved, then the length of the plane would matter.
4. A
The gravitational force points downward while the book’s displacement is upward. Therefore, the work done by gravity is −mgh = −(2 kg)(10 N/kg)(1.5 m) = −30 J.
5. C
The only force doing work on the block as it slides down the inclined plane is the force of gravity, so the Work–Energy Theorem can be applied with the total work equal to the work done by gravity. The work done by gravity as the block slides down the inclined plane is equal to the negative change in potential energy.
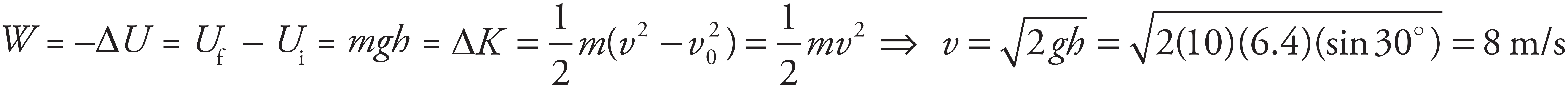
6. C
Since a nonconservative force (namely, friction) is acting during the motion, use the modified Conservation of Mechanical Energy equation.
7. D
Apply Conservation of Mechanical Energy (including the negative work done by Fr, the force of air resistance):
8. D
Because the rock has lost half of its gravitational potential energy, its kinetic energy at the halfway point is half of its kinetic energy at impact. Since K is proportional to v2, if Kat halfway point is equal to Kat impact, then the rock’s speed at the halfway point is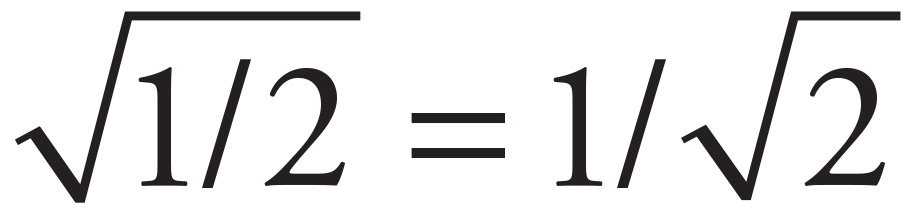 
its speed at impact.
9. D
Using the equation P = Fv, find that P = (200 N)(2 m/s) = 400 W.
1. (a)
Applying Conservation of Energy,
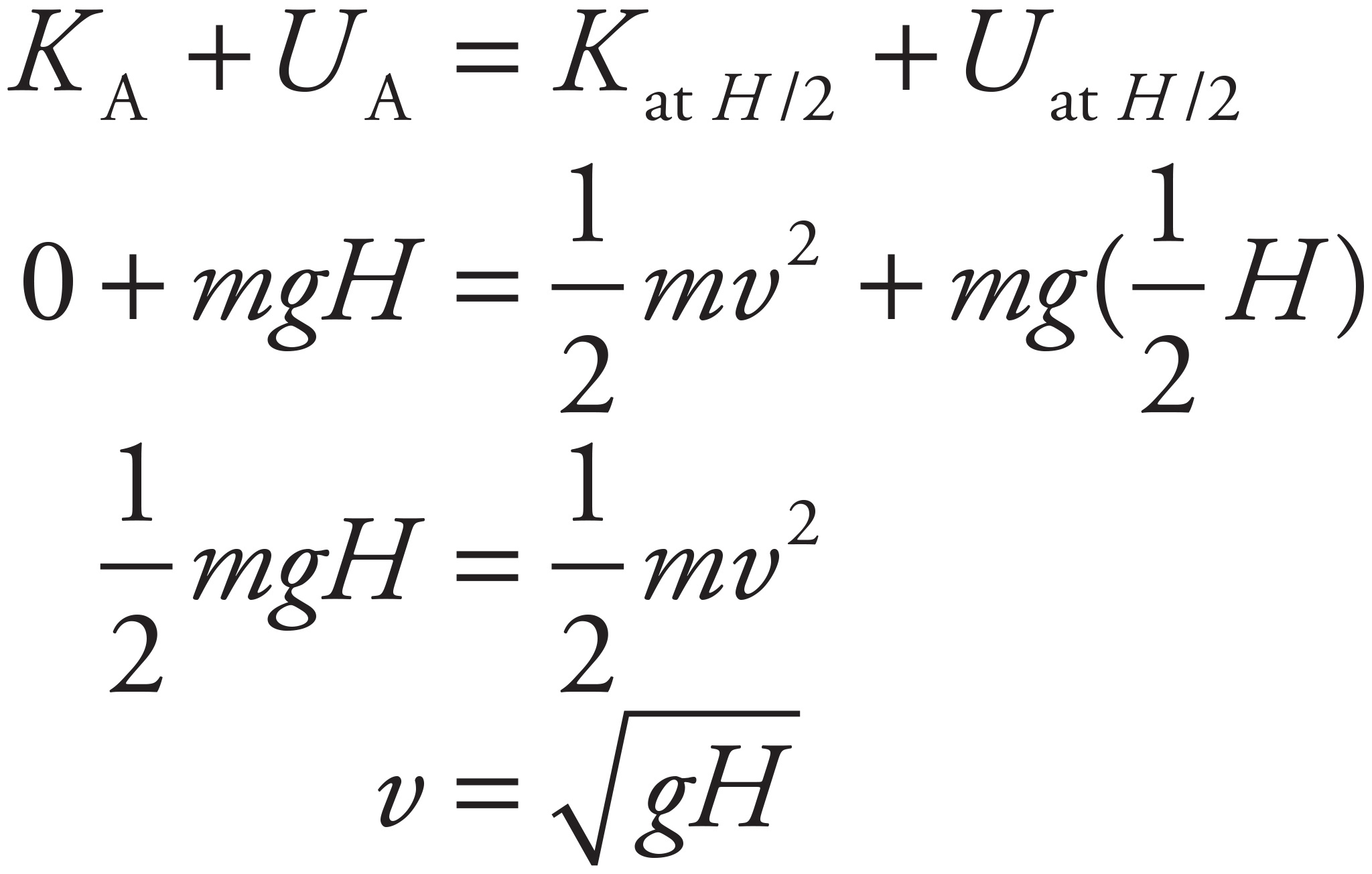
(b)
Applying Conservation of Energy again,
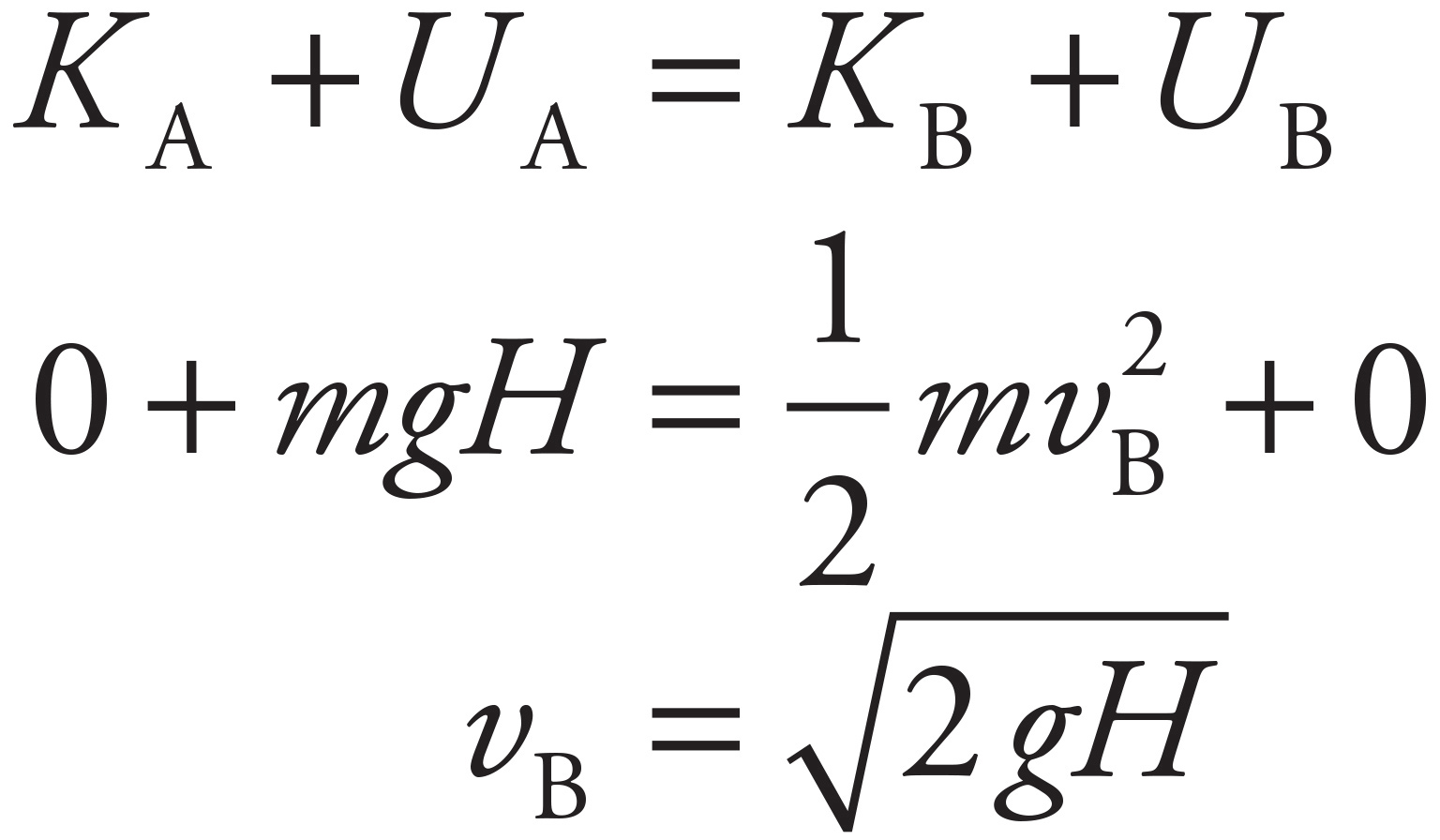
(c)
By the Work–Energy Theorem, you want the work done by friction to be equal (but opposite) to the kinetic energy of the box at Point B:
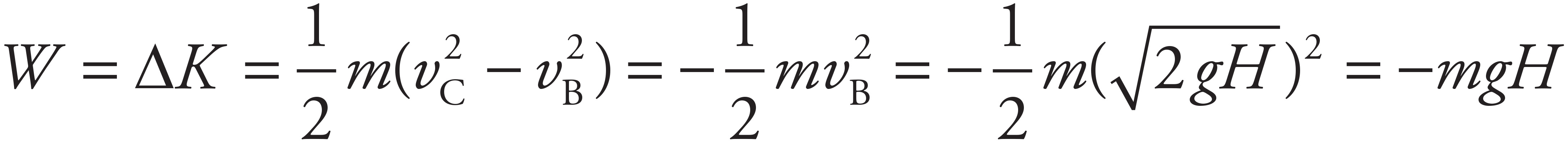
Therefore,
W = −mgH ⇒ −Ffx = −mgH ⇒ −µkmgx = −mgH ⇒ µk = H/x
(d)
Apply Conservation of Energy (including the negative work done by friction as the box slides up the ramp from B to C):
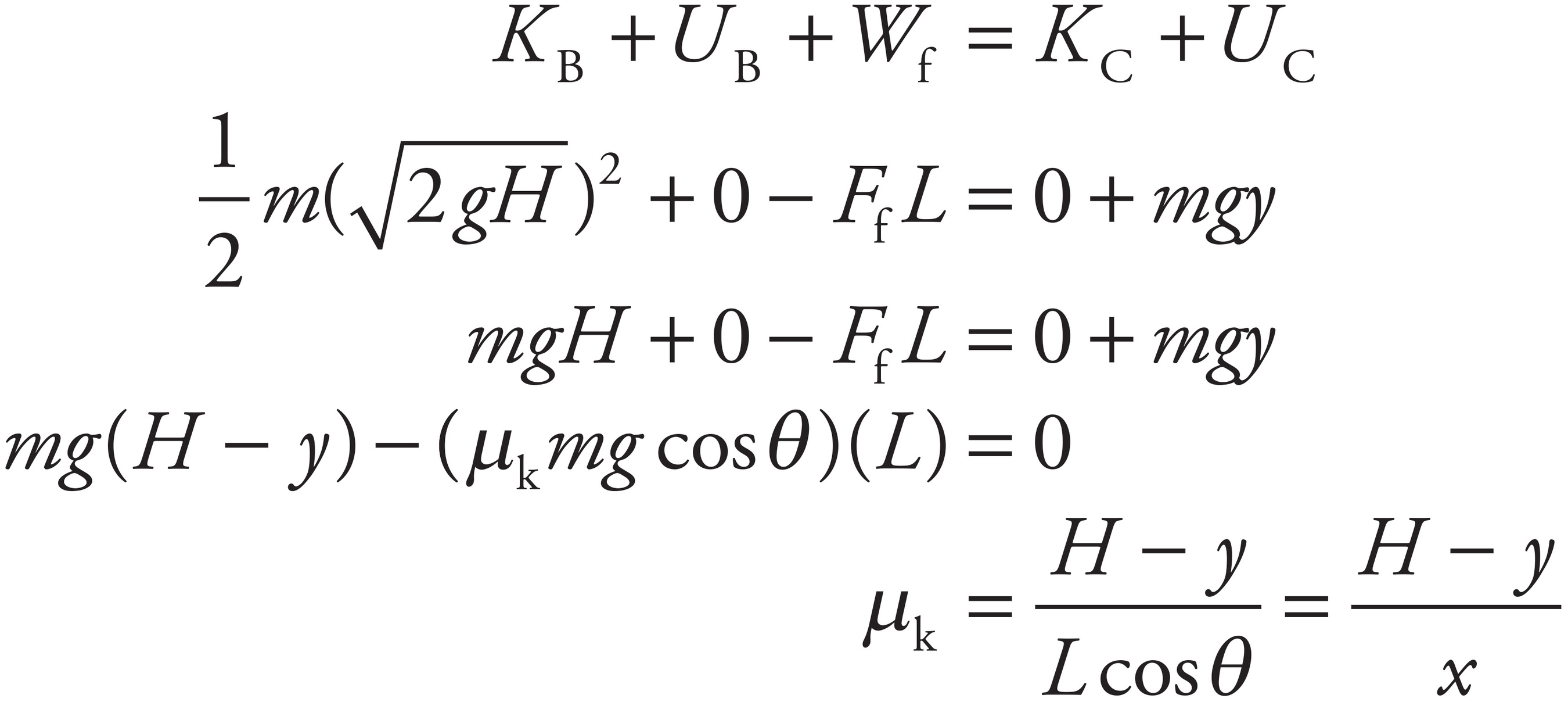
(e)
The result of part (b) reads vB = 
. Therefore, by Conservation of Mechanical Energy (with the work done by the frictional force on the slide included), you get
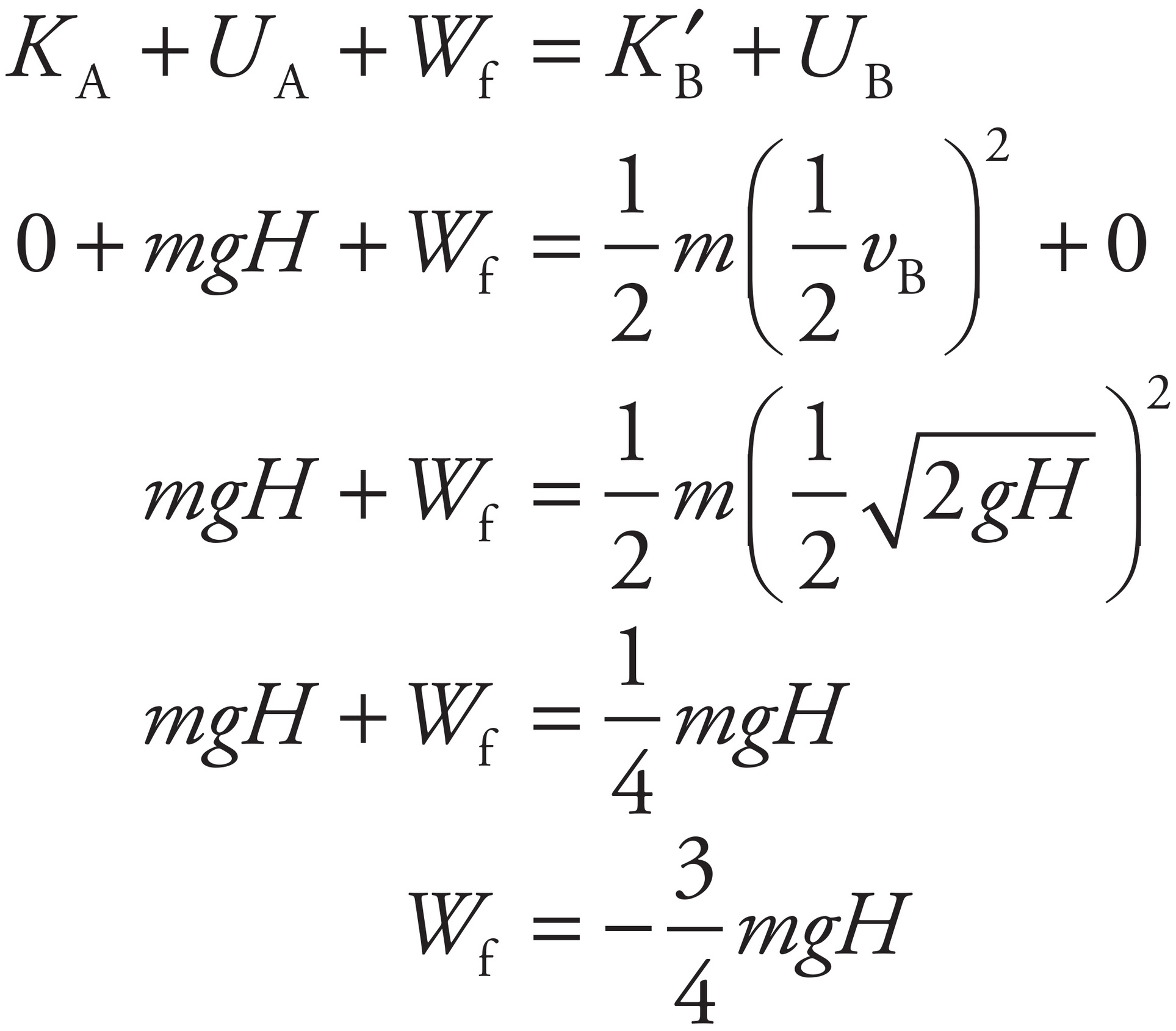
2. (a)
Using Conservation of Energy Ki + Ui = Kf + Uf and vi = 0, this becomes Ui = Kf + Uf or Kf = Ui − Uf. This is equivalent to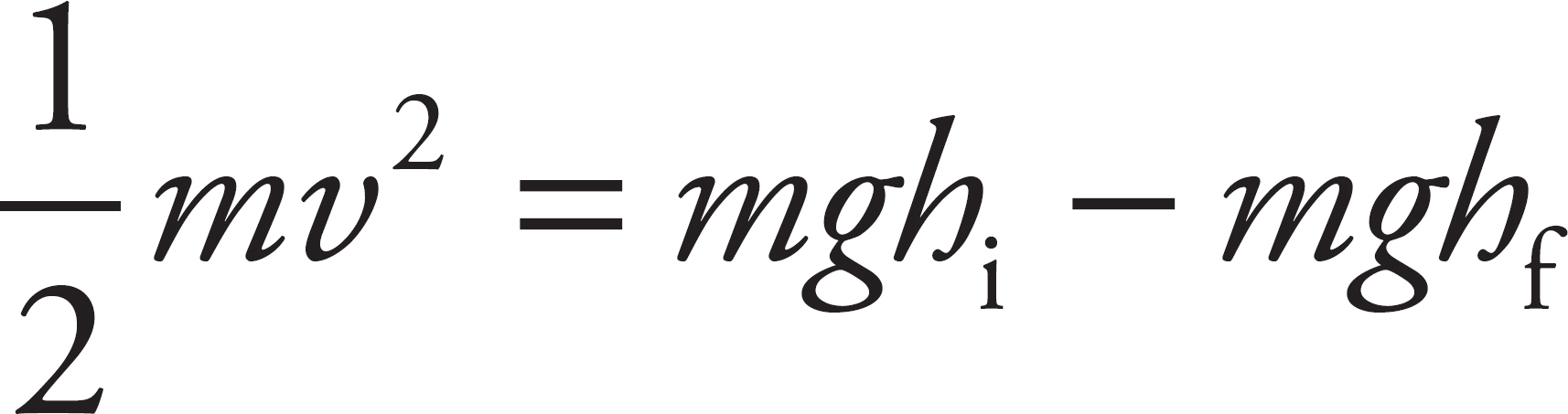 
, which simplifies to 
or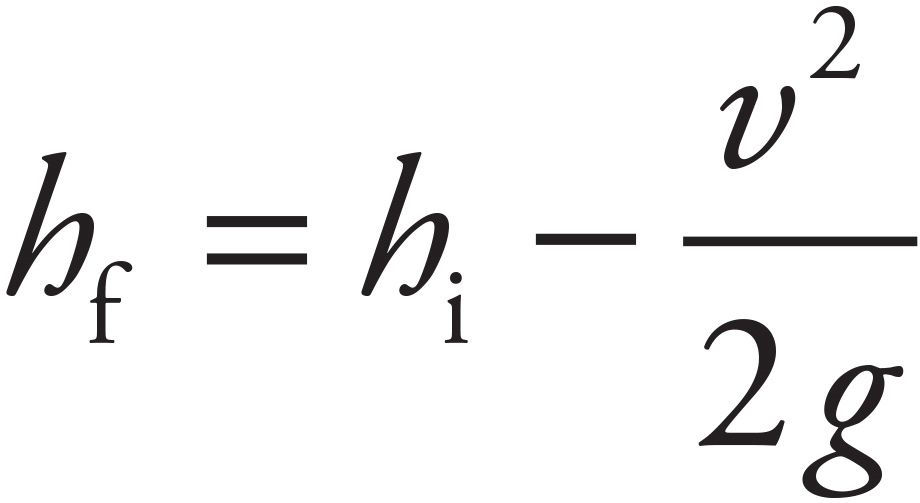 
. Now fill in the table.
|
Time (s)
|
Velocity (m/s)
|
Height (m)
|
|
0.00
|
0.00
|
1.5
|
|
0.05
|
1.41
|
1.4
|
|
0.10
|
2.45
|
1.2
|
|
0.15
|
3.74
|
0.8
|
|
0.20
|
3.74
|
0.8
|
|
0.25
|
3.46
|
0.9
|
|
0.30
|
3.16
|
1.0
|
|
0.35
|
2.83
|
1.1
|
|
0.40
|
3.46
|
0.9
|
|
0.45
|
4.24
|
0.6
|
|
0.50
|
4.47
|
0.5
|
(b)
The greatest acceleration would occur where there is the greatest change in velocity. This occurs between 0.00 and 0.05 seconds. The acceleration during that time interval is given by 
or a = 28 m/s2.
(c)
Changing the mass does not affect the time spent falling or the velocity of the object. Thus, a change in mass will not affect the results.
3. (a)
Use the Work–Energy Theorem:
Wtotal = ΔK
The force doing work during the motion is provided by the force of friction:
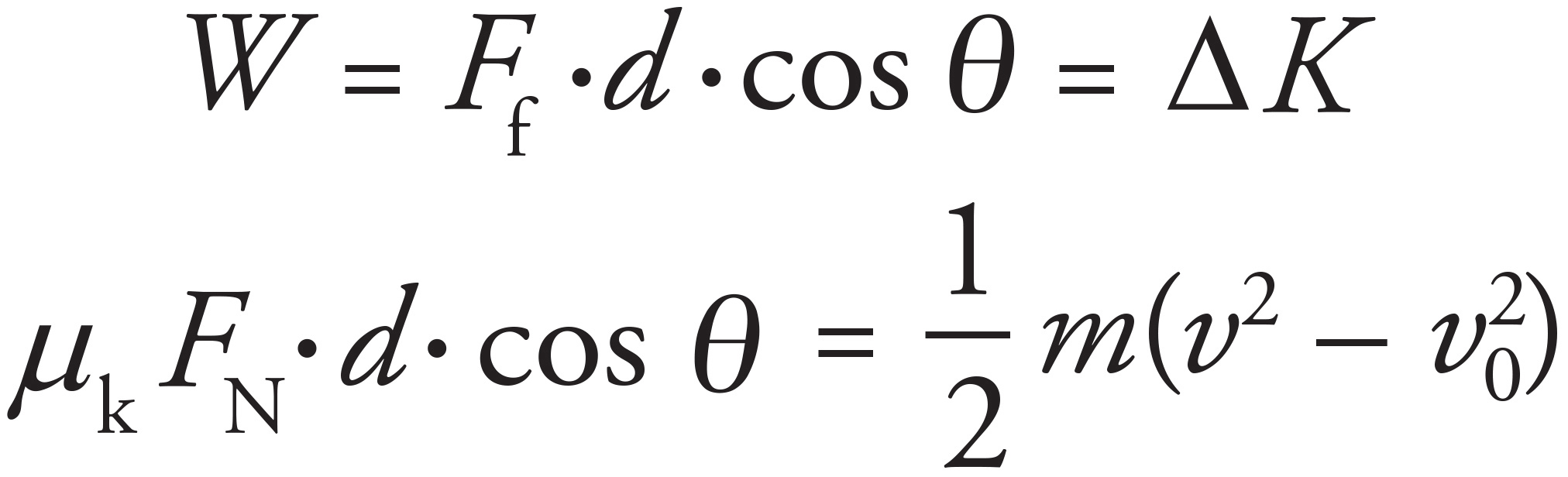
As the force of friction is antiparallel to the direction of the displacement, θ = 180°.
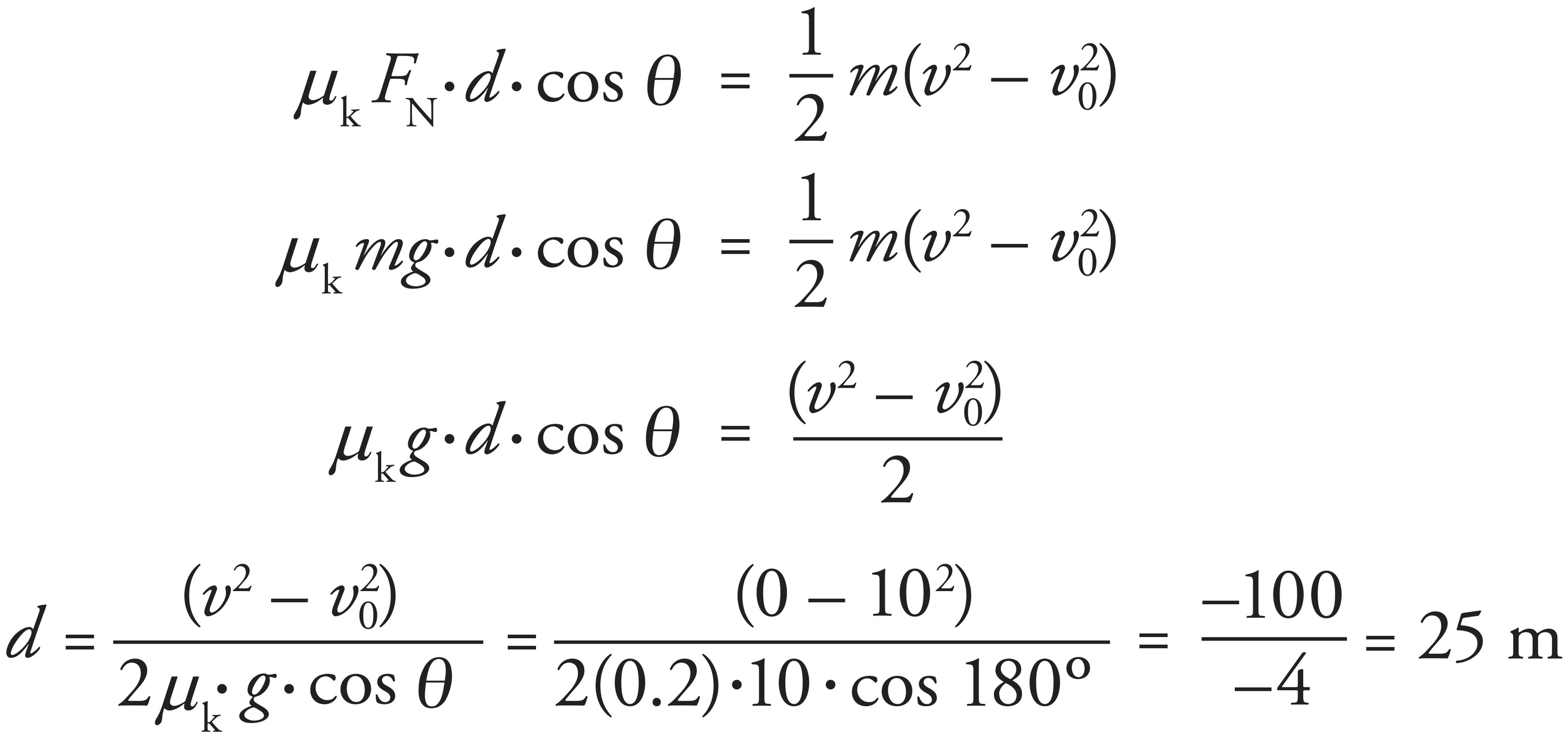
The skidding distance is 25 m.
(b)
The final equation for the skidding distance is
Since the final velocity is 0, the stopping distance is proportional to the initial speed. So if the initial speed is doubled, the skidding distance is quadrupled. This can also be determined by plugging in an initial velocity of 20 m/s:
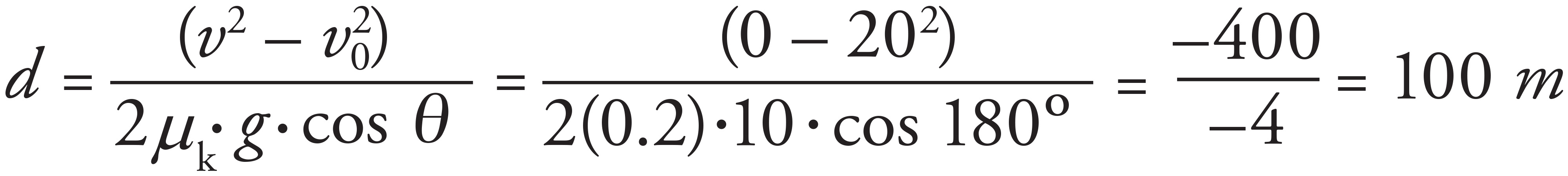
(c)
Look back at the equation for the skidding distance:
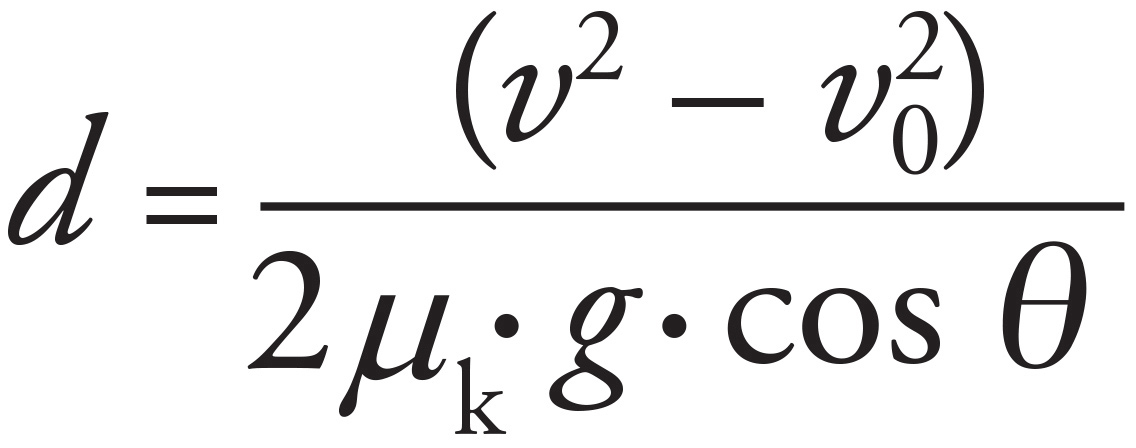
This equation does not include mass, so mass does not affect the skidding distance. (Note: While doubling the mass doubles the initial kinetic energy of the car, it also doubles the normal force and thus the frictional force acting on the car.)
1. C
The magnitude of the object’s linear momentum is p = mv. If p = 6 kg · m/s and m = 2 kg, then v = 3 m/s. Therefore, the object’s kinetic energy is K = mv2 = (2 kg)(3 m/s)2 = 9 J.
2. B
The impulse delivered to the ball, J = FΔt, equals its change in momentum. Since the ball started from rest, you get
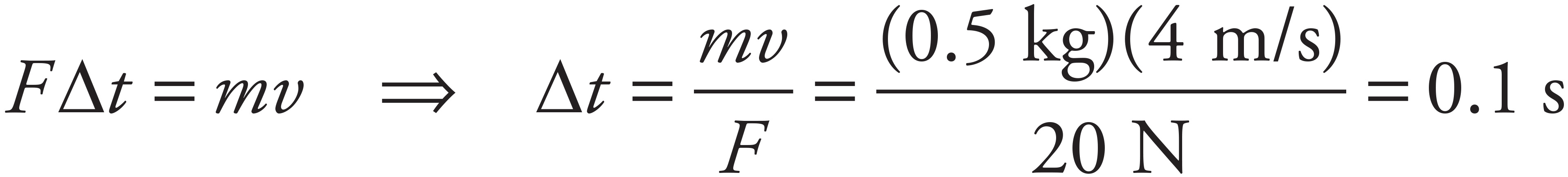
3. D
The impulse delivered to the ball, J = FΔt, equals its change in momentum. Thus,
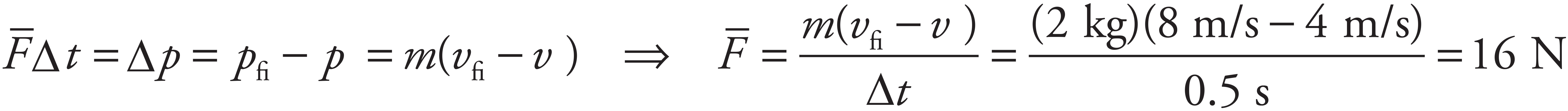
4. C
The impulse delivered to the ball is equal to its change in momentum. The momentum of the ball was mv before hitting the wall and m(−v) after. Therefore, the change in momentum is m(−v) − mv = −2mv, so the magnitude of the momentum change (and the impulse) is 2mv.
5. B
By definition of perfectly inelastic, the objects move off together with one common velocity, v′, after the collision. By Conservation of Linear Momentum,
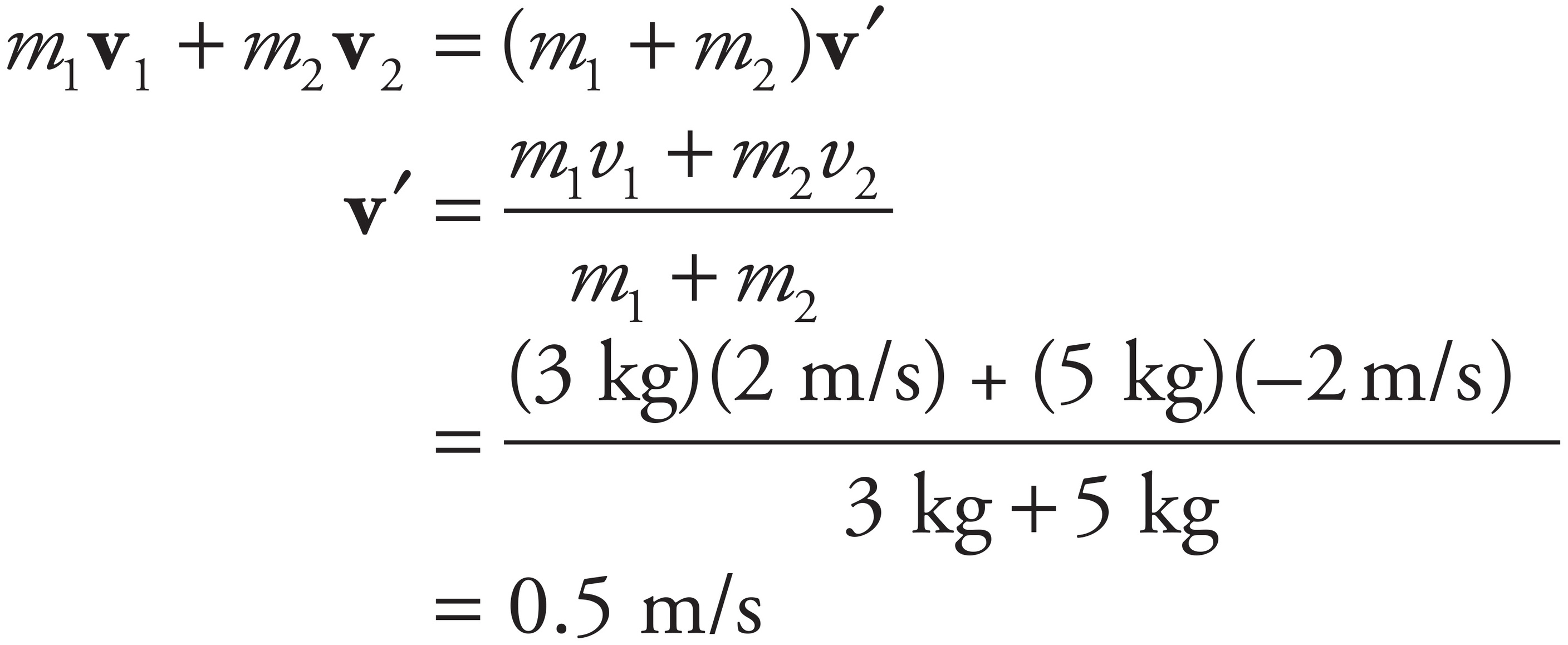
6. D
First, apply Conservation of Linear Momentum to calculate the speed of the combined object after the (perfectly inelastic) collision:
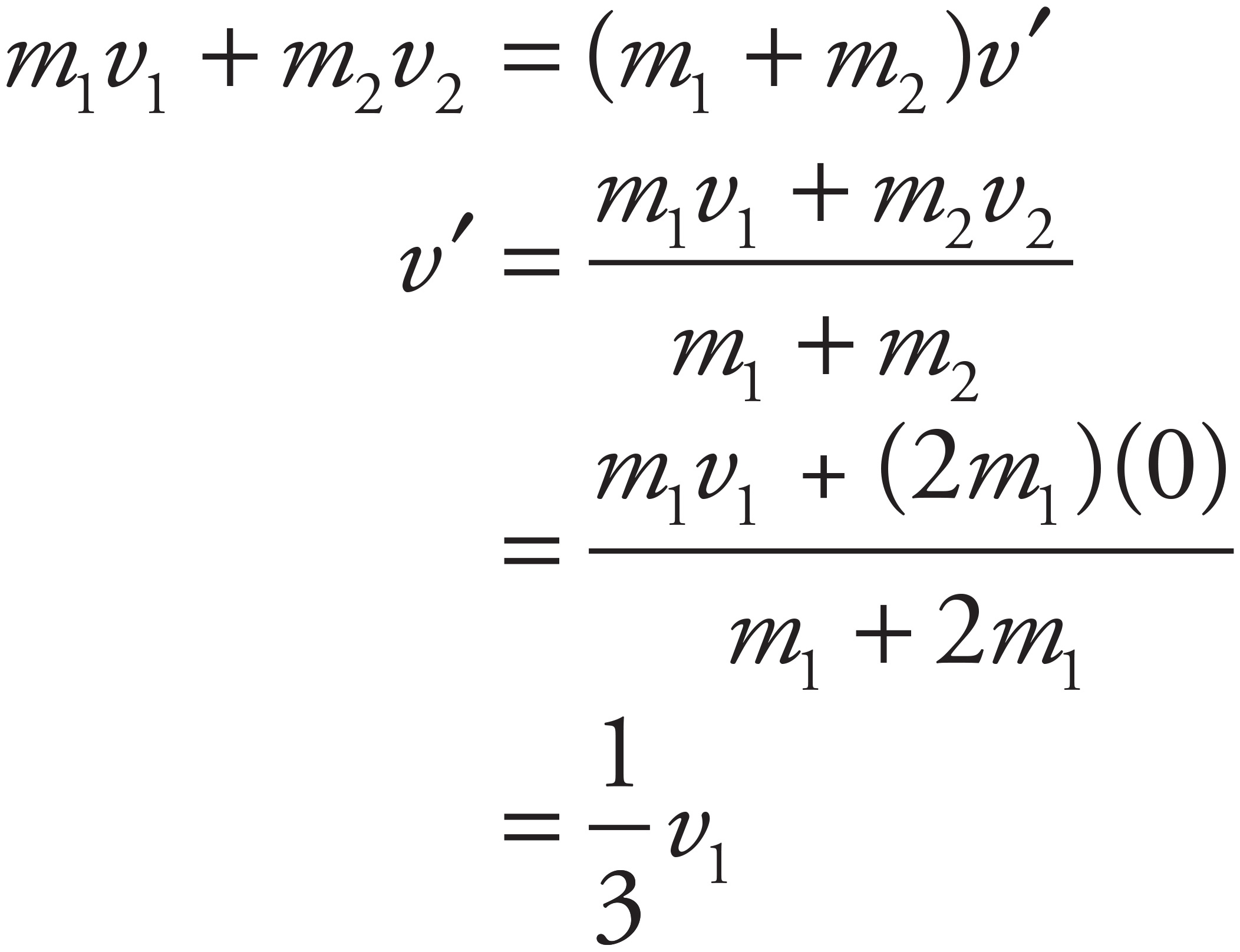
Therefore, the ratio of the kinetic energy after the collision to the kinetic energy before the collision is
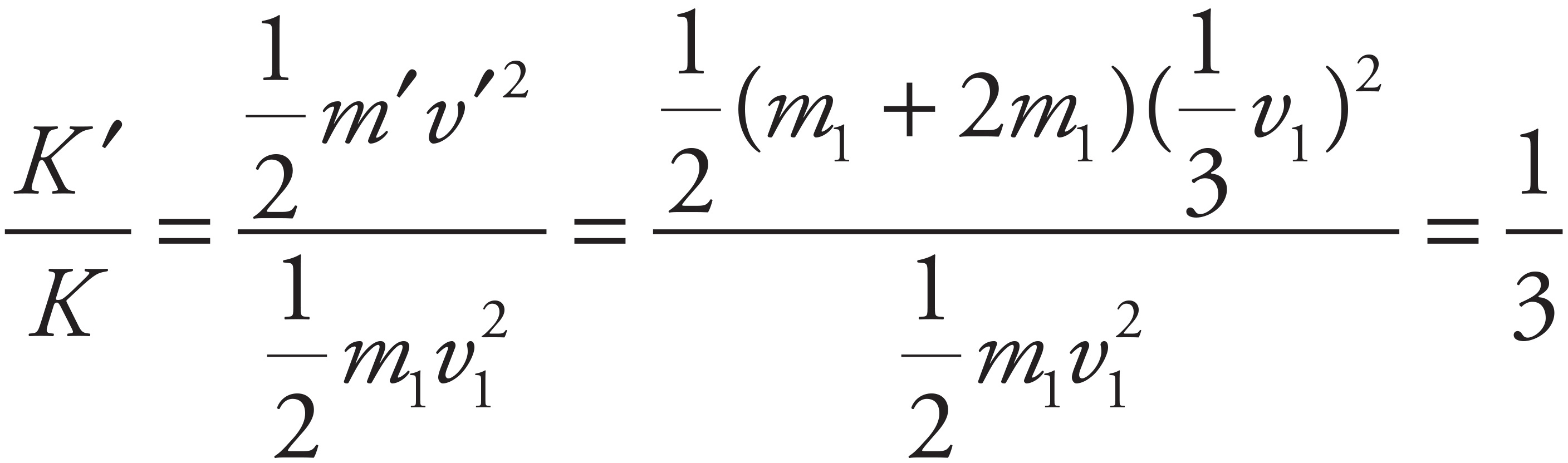
7. C
Total linear momentum is conserved in a collision during which the net external force is zero. If kinetic energy is lost, then by definition, the collision is not elastic.
8. D
Because the two carts are initially at rest, the initial momentum is zero. Therefore, the final total momentum must be zero.
9. C
The linear momentum of the bullet must have the same magnitude as the linear momentum of the block in order for their combined momentum after impact to be zero. The block has momentum MV to the left, so the bullet must have momentum MV to the right. Since the bullet’s mass is m, its speed must be v = MV/m.
10. C
In a perfectly inelastic collision, kinetic energy is never conserved; some of the initial kinetic energy is always lost to heat and some is converted to potential energy in the deformed shapes of the objects as they lock together.
11. B
Total linear momentum is conserved in the absence of external forces. If the final speed of both objects is 0, that means the total linear momentum after the collision is 0, which then implies that the total linear momentum before the collision is also 0. As Object 2 has half the mass of Object 1, Object 2 must have twice the initial speed of Object 1 (and must be travelling in the opposite direction) in order for the total linear momentum to equal 0.
1. (a)
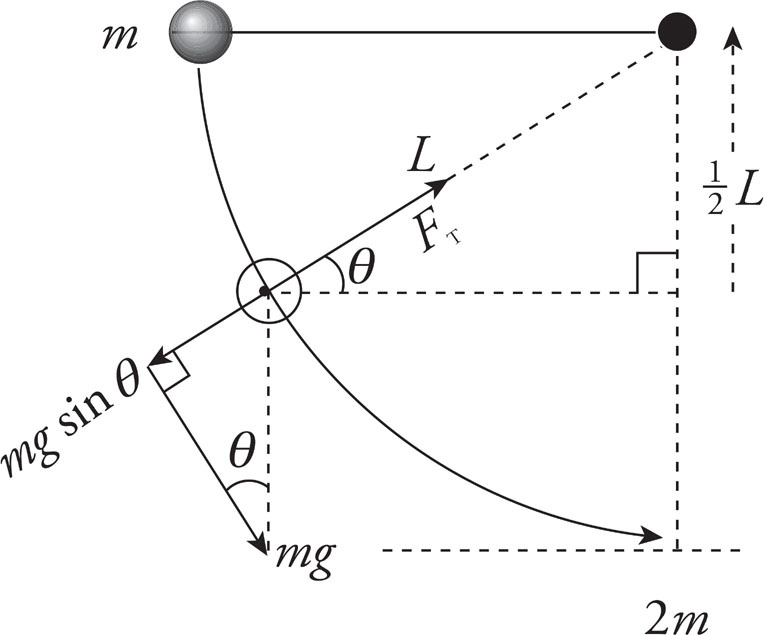
First, draw a free-body diagram:
The net force toward the center of the steel ball’s circular path provides the centripetal force. From the geometry of the diagram, you get
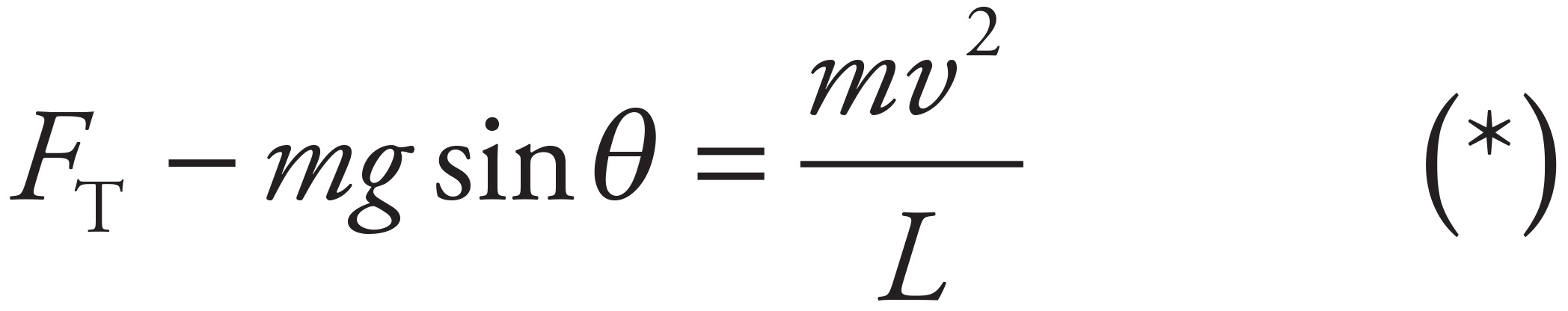
In order to determine the value of mv2, use Conservation of Mechanical Energy:
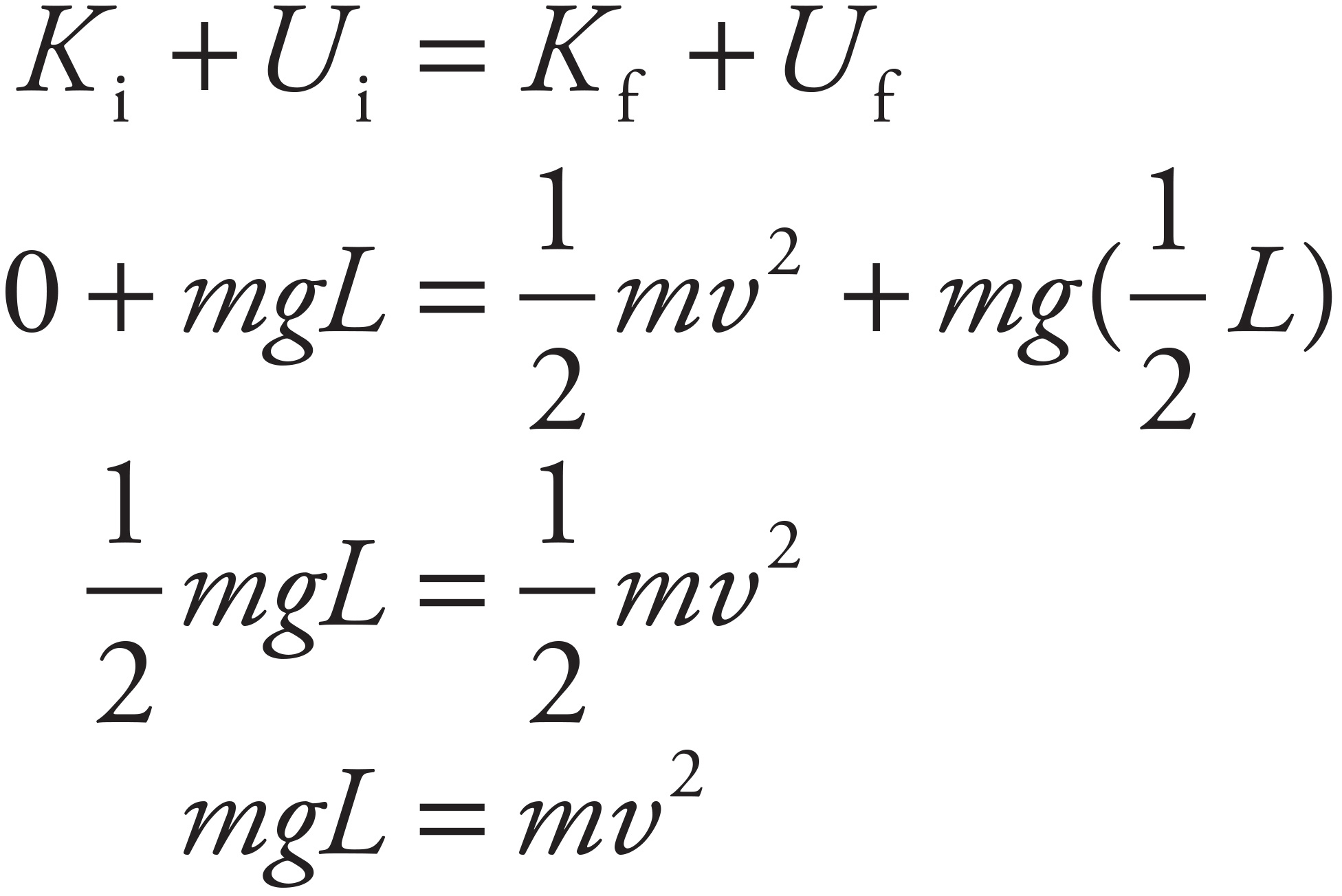
Substituting this result into Equation (*), you get
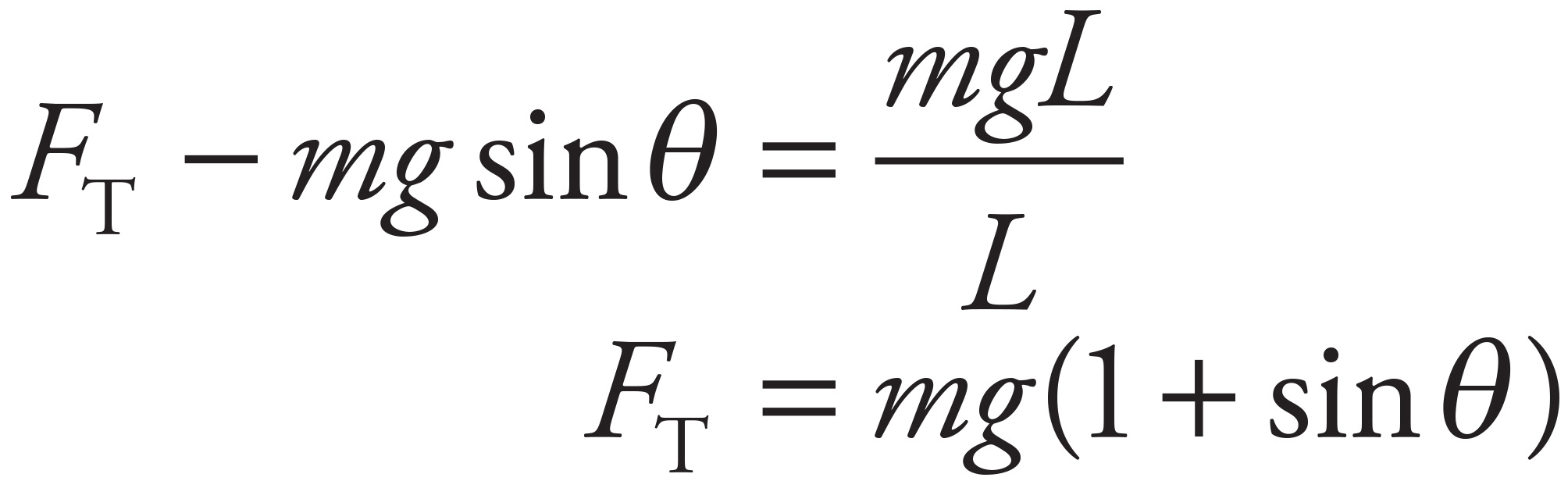
Now, from the free-body diagram, sin θ = L/L = , so
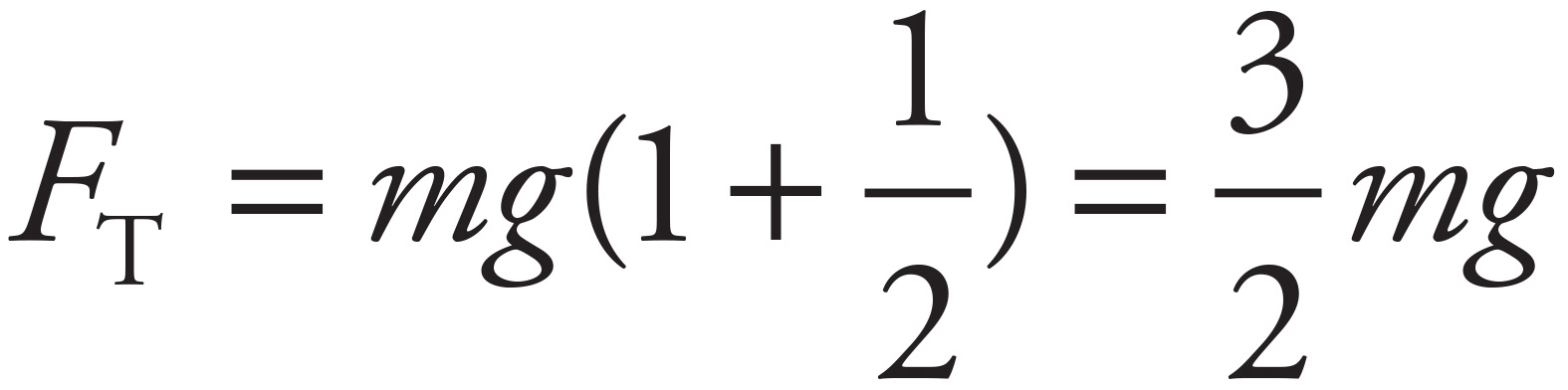
(b)
Apply Conservation of Energy to find the speed of the ball just before impact:
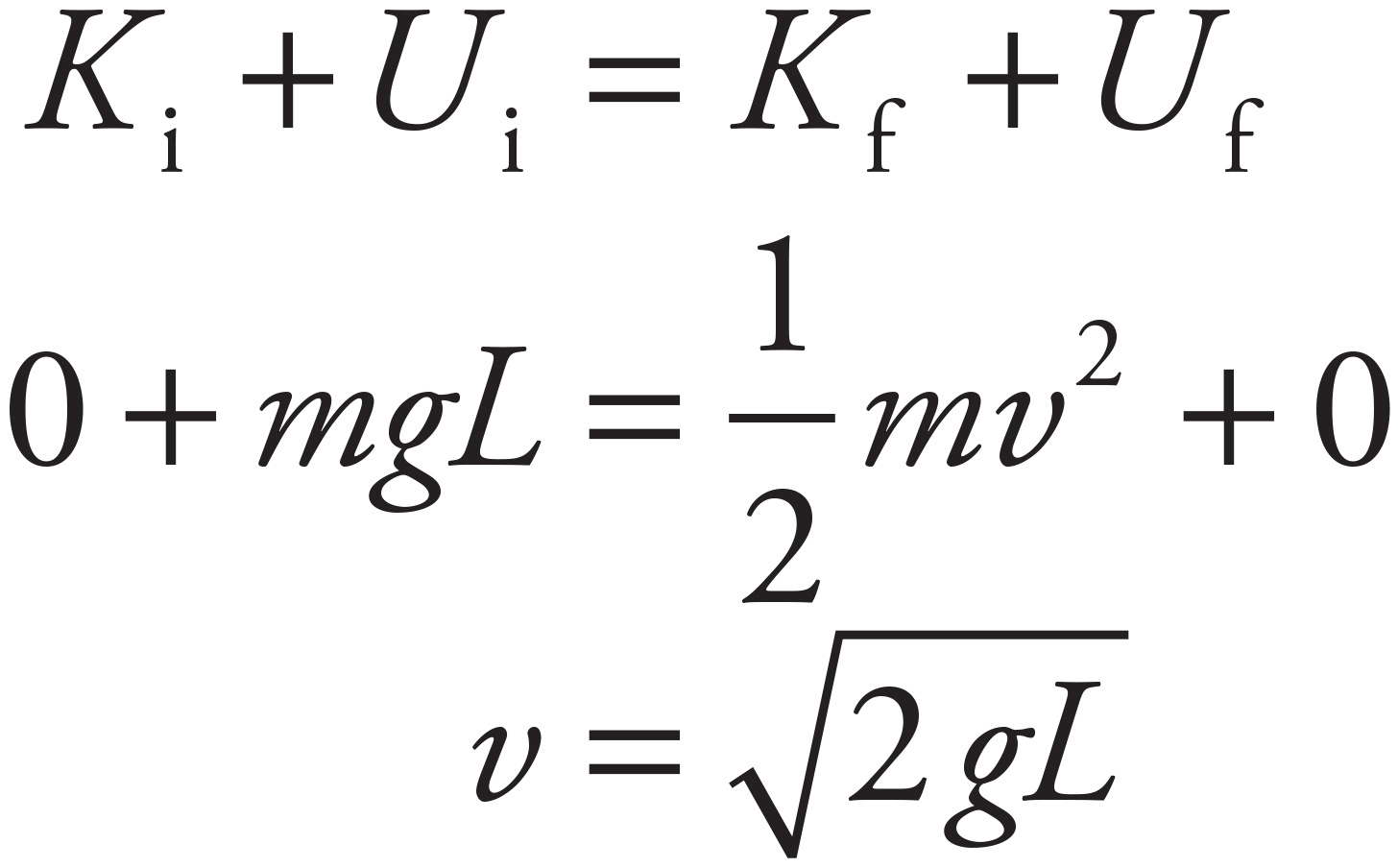
Now use Conservation of Linear Momentum and conservation of kinetic energy for the elastic collision to derive the expressions for the speeds of the ball, v1, and the block, v2, immediately after the collision. Applying Conservation of Linear Momentum yields
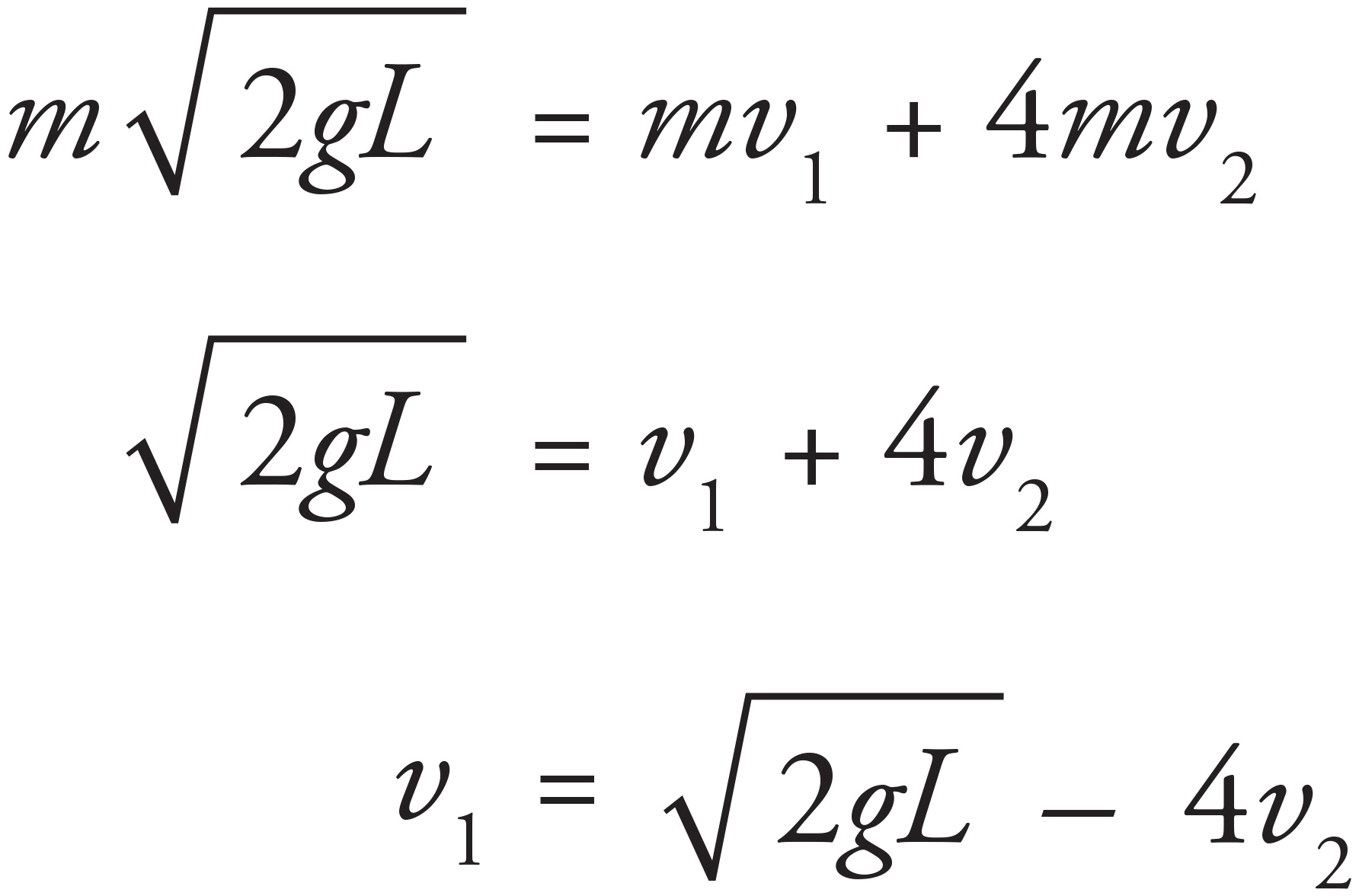
Applying the conservation of kinetic energy for the elastic collision yields
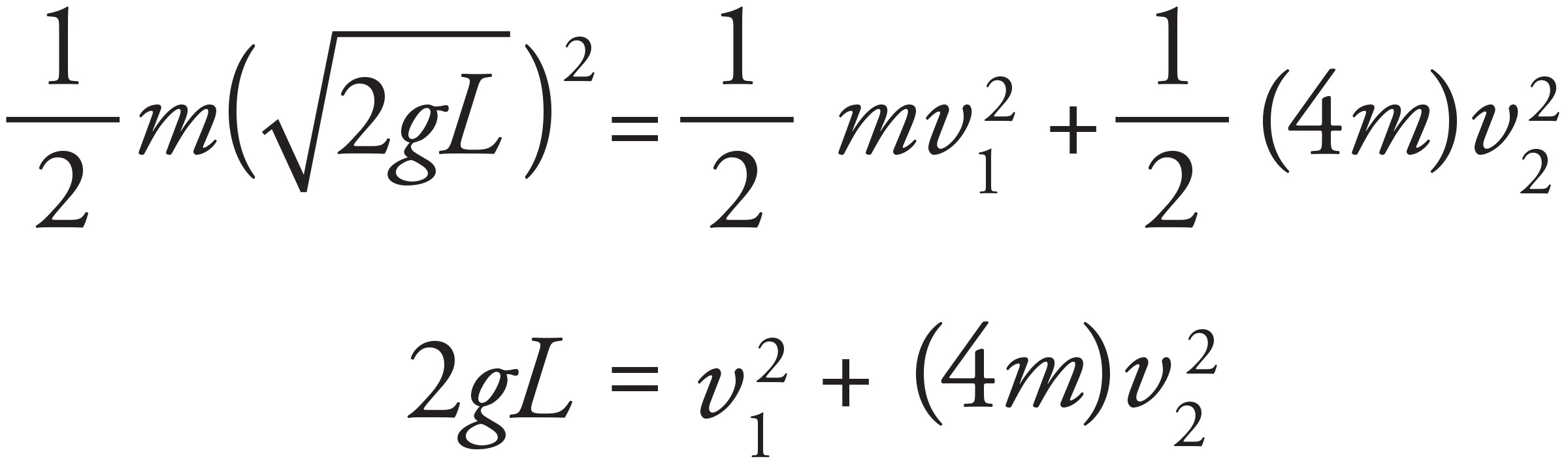
Plugging in the expression for v1 from the Conservation of Linear Momentum yields
(c)
Using the velocity of the block immediately after the collision, v2, solve for the velocity of the ball immediately after the collision:
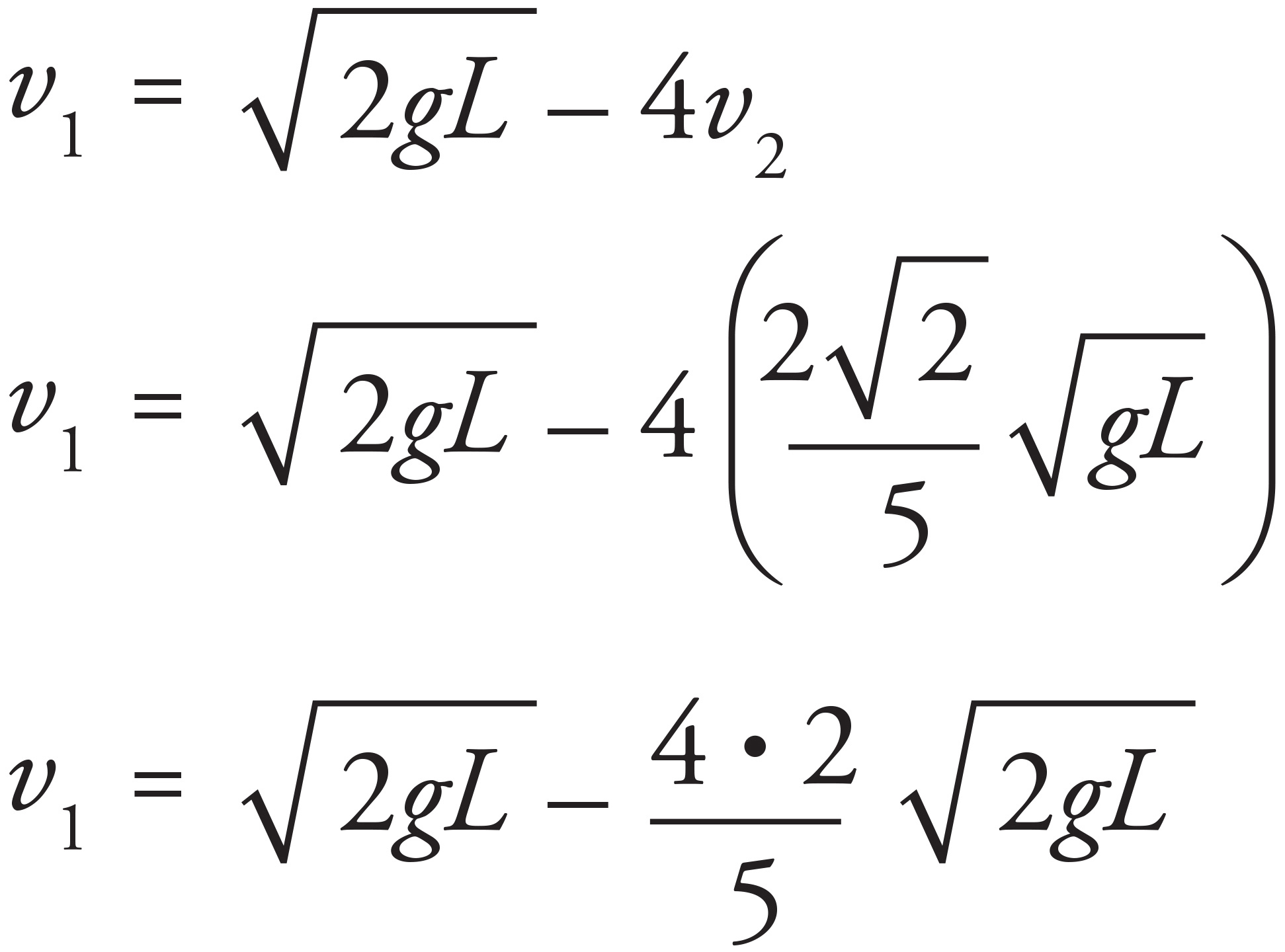
Factor out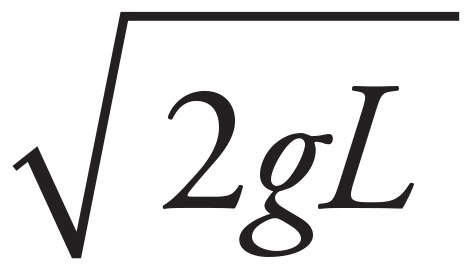 
to get
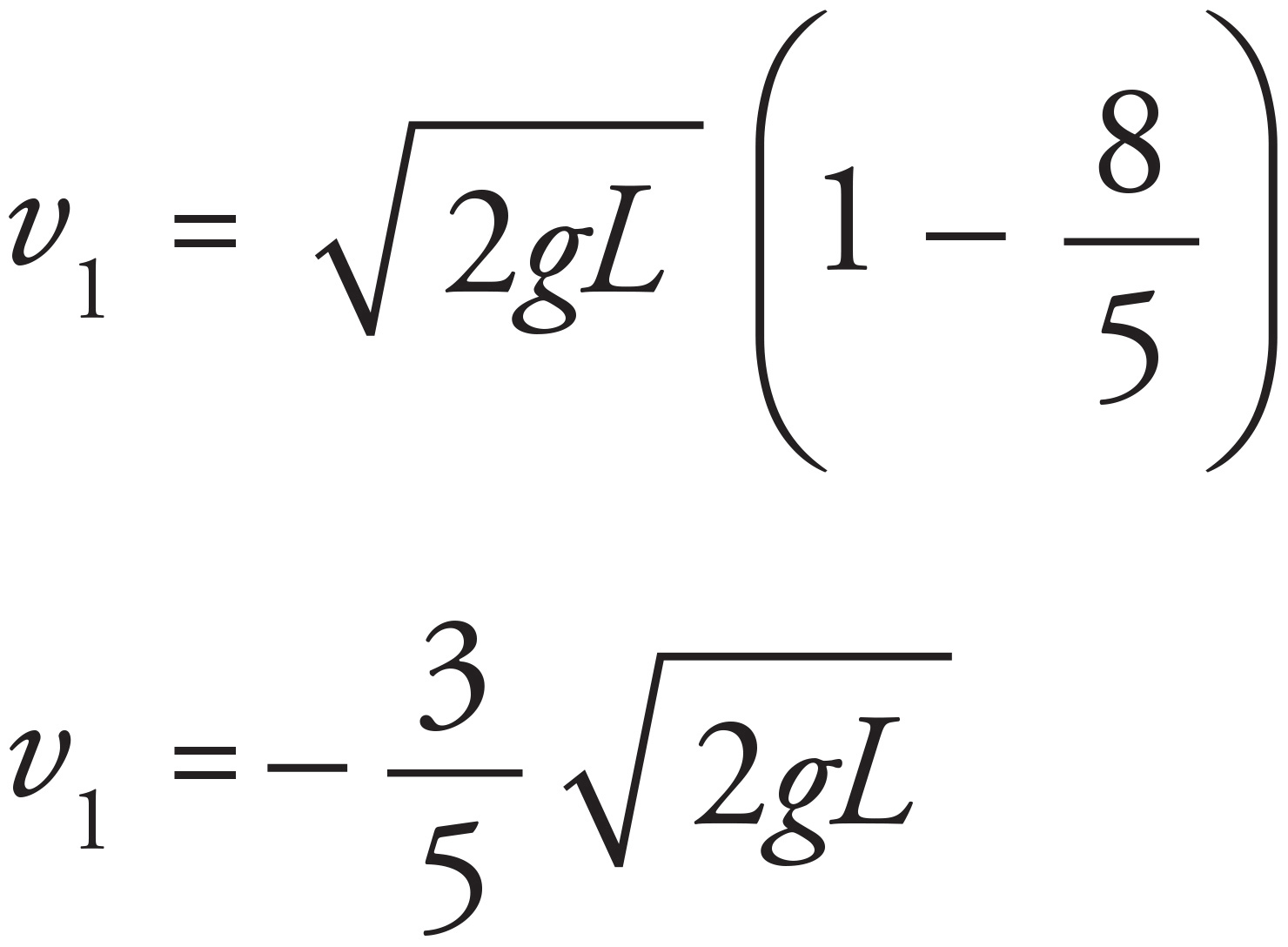
Now, apply Conservation of Mechanical Energy to find
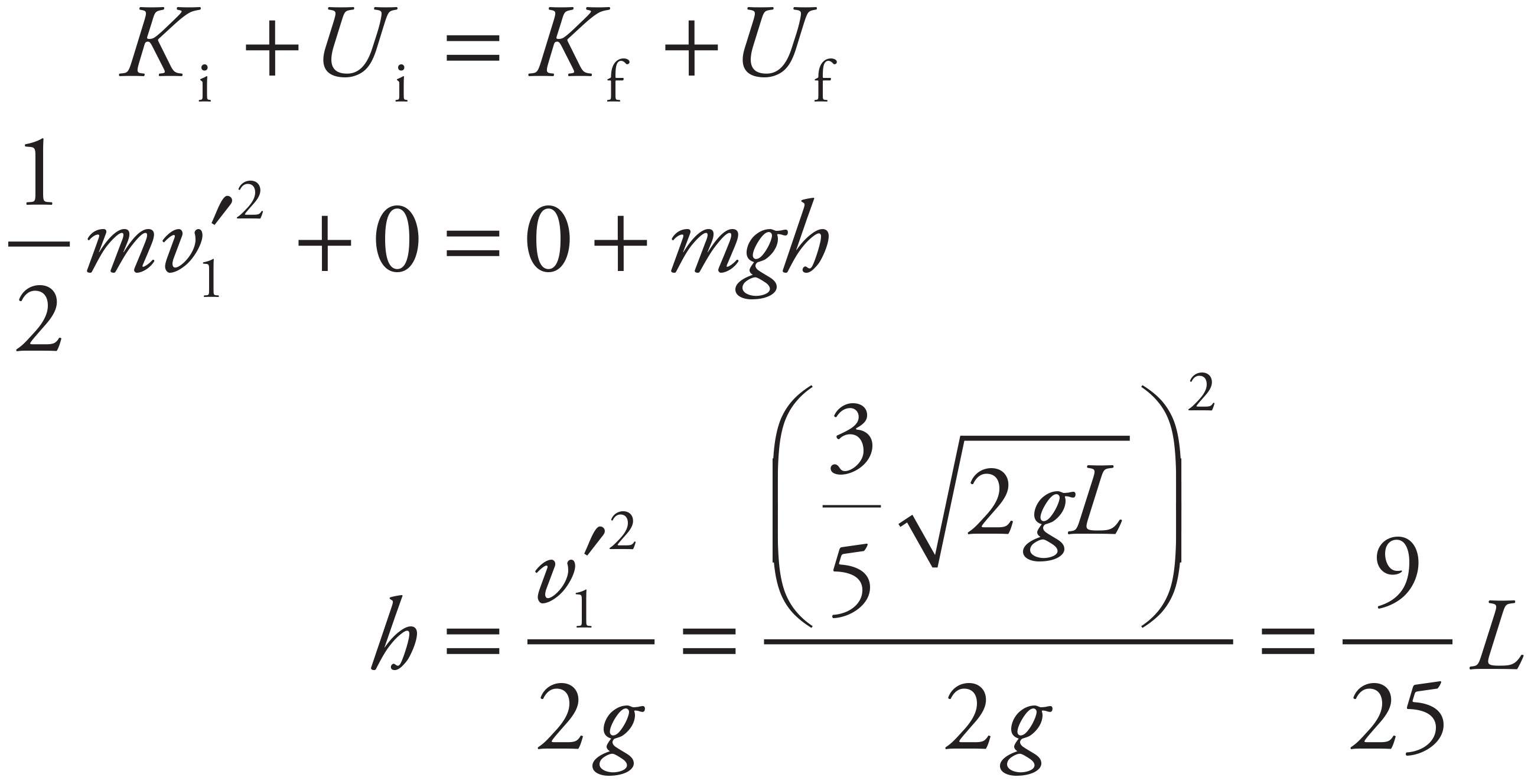
2. (a)
By Conservation of Linear Momentum, mv = (m + M)v′, so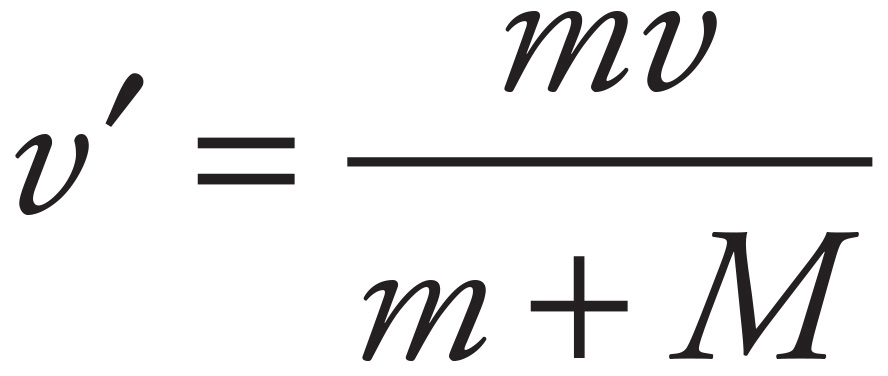 
Now, by Conservation of Mechanical Energy,
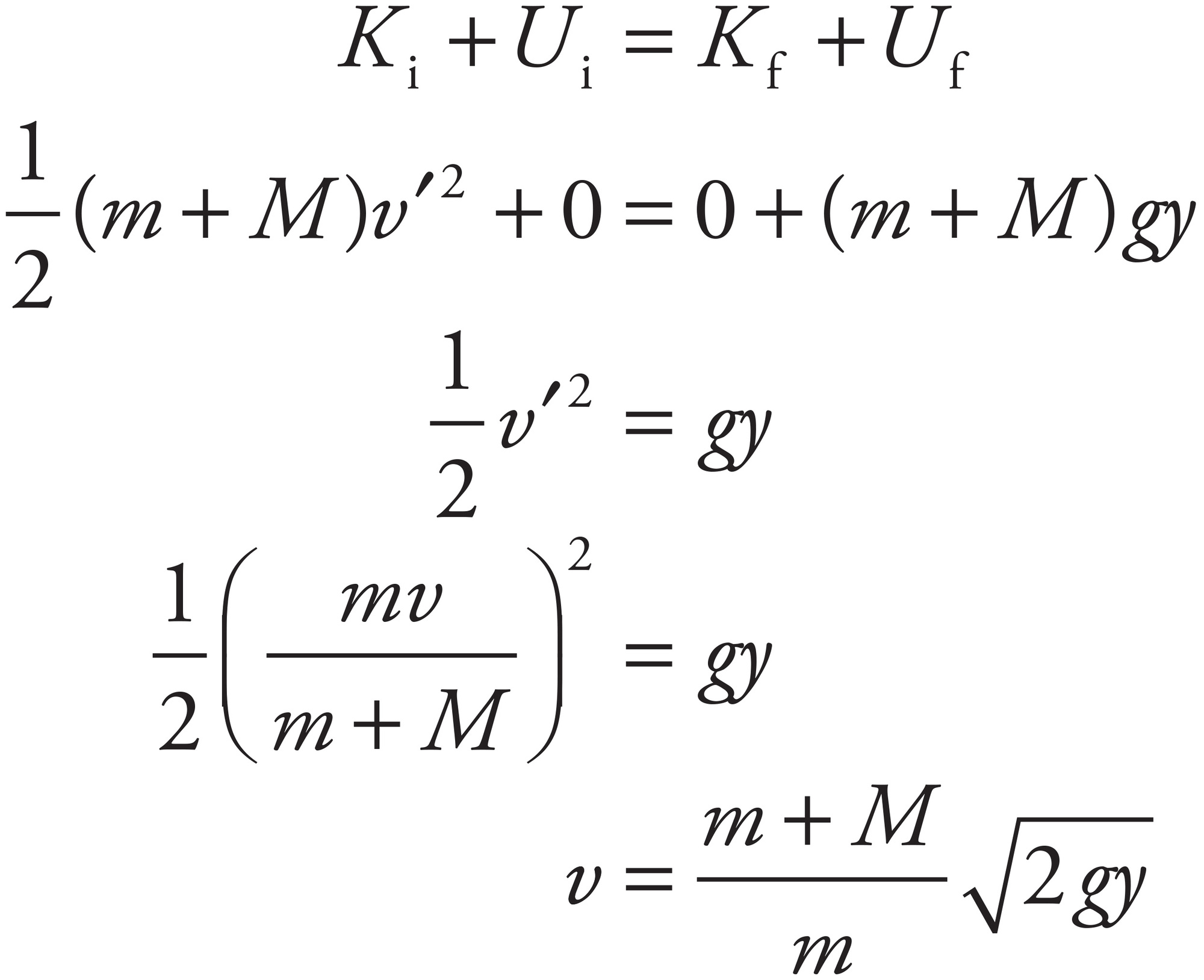
(b)
Use the result derived in part (a) to compute the kinetic energy of the block and bullet immediately after the collision:
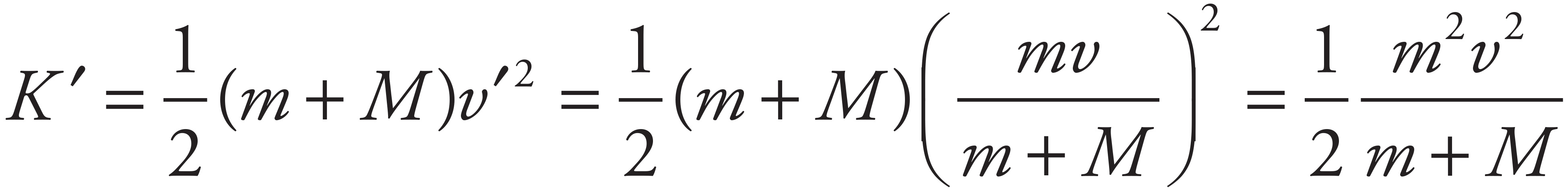
Since K = mv2, the difference is
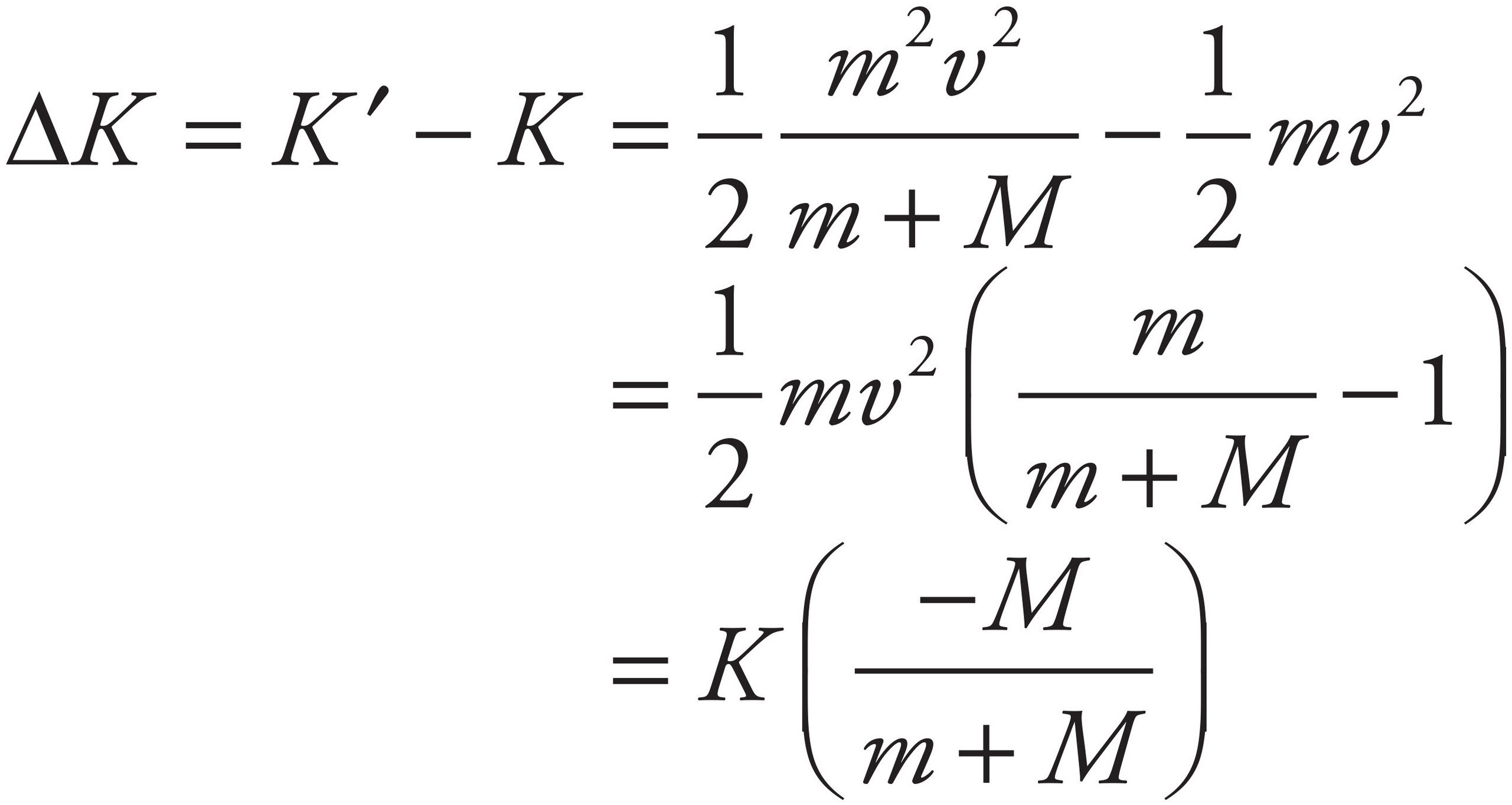
Therefore, the fraction of the bullet’s original kinetic energy that was lost is M/(m + M). This energy is manifested as heat (the bullet and block are warmer after the collision than before), and some was used to break the intermolecular bonds within the wooden block to allow the bullet to penetrate.
(c)
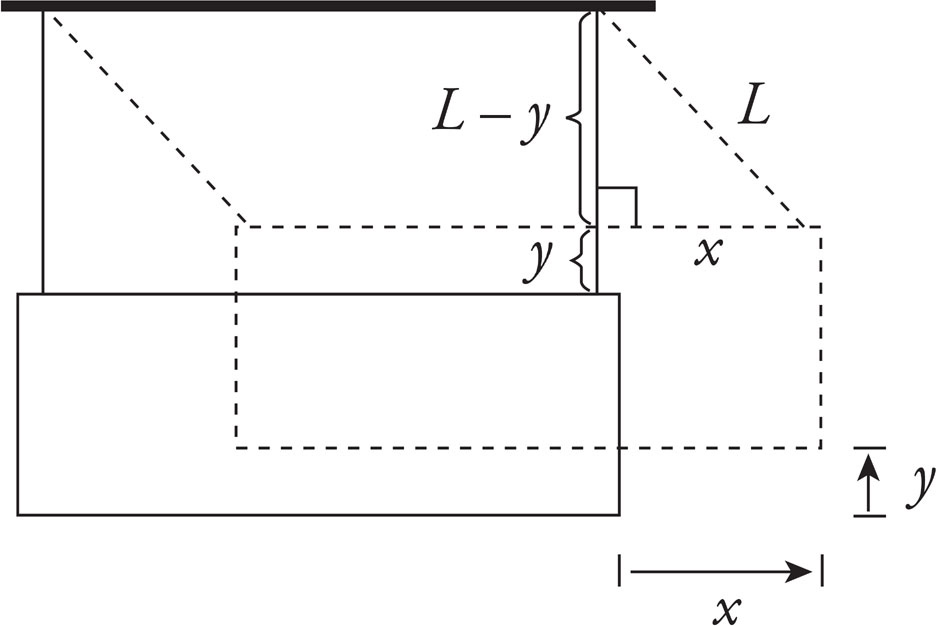
From the geometry of the diagram,
the Pythagorean Theorem implies that (L − y)2 + x2 = L2. Therefore,
(where you have used the fact that y2 is small enough to be neglected). Substituting this into the result of part (a), derive the following equation for the speed of the bullet in terms of x and L instead of y:
(d)
No; momentum is conserved only when the net external force on the system is zero (or at least negligible). In this case, the block and bullet feel a net nonzero force that causes it to slow down as it swings upward. Since its speed is decreasing as it swings upward, its linear momentum cannot remain constant.
1. A, C
In uniform circular motion, the speed is constant but the velocity is constantly changing because the direction is changing. Because the direction is changing, there is an acceleration. The magnitude of acceleration is constant; however, the acceleration is directed toward the center and perpendicular to the velocity. As a result, since the velocity is always changing, so is the direction of acceleration.
2. B
When the bucket is at the lowest point in its vertical circle, it feels a tension force FT upward and the gravitational force Fw downward. The net force toward the center of the circle, which is the centripetal force, is FT − Fw. Thus,
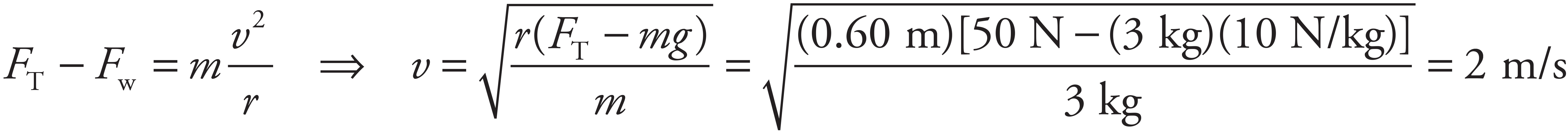
3. C
When the bucket reaches the topmost point in its vertical circle, the forces acting on the bucket are its weight, Fw, and the downward tension force, FT. The net force, Fw + FT, provides the centripetal force. In order for the rope to avoid becoming slack, FT must not vanish. Therefore, the cut-off speed for ensuring that the bucket makes it around the circle is the speed at which FT just becomes zero; any greater speed would imply that the bucket would make it around. Thus,
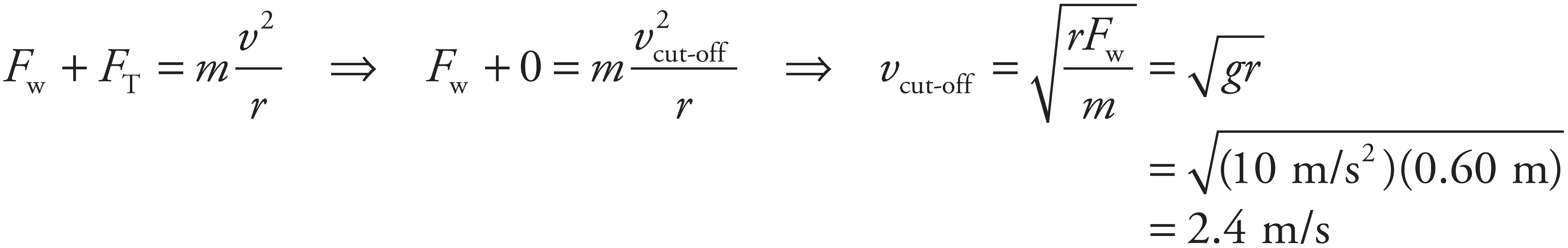
4. D
Centripetal acceleration is given by the equation ac = v2/r. Since the object covers a distance of 2πr in 1 revolution, its speed is 2πr. Therefore,
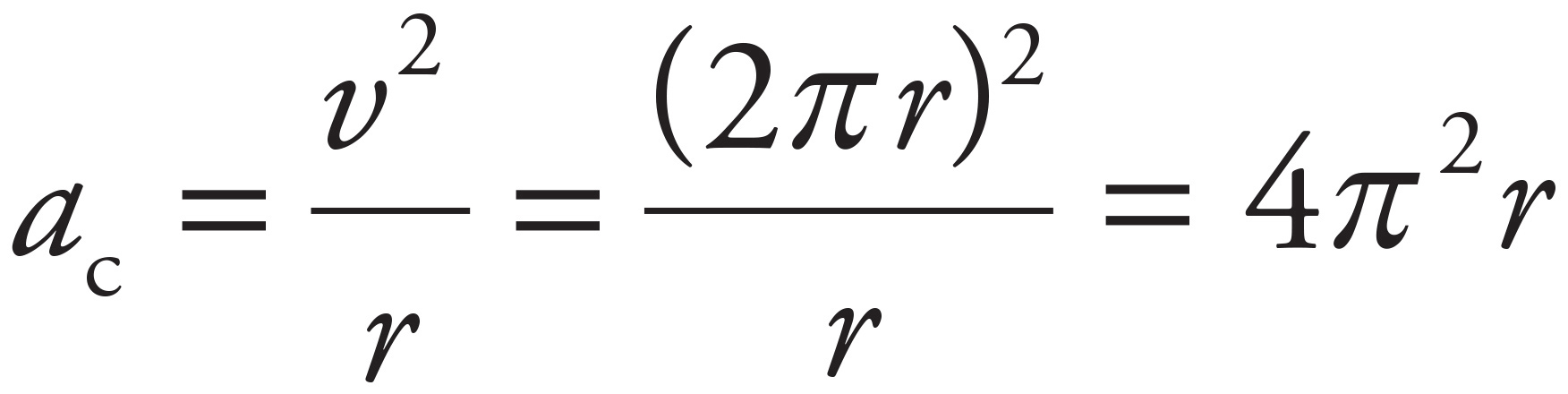
5. C
The torque is τ = rF = (0.20 m)(20 N) = 4 N · m.
6. D
From the diagram,
calculate that
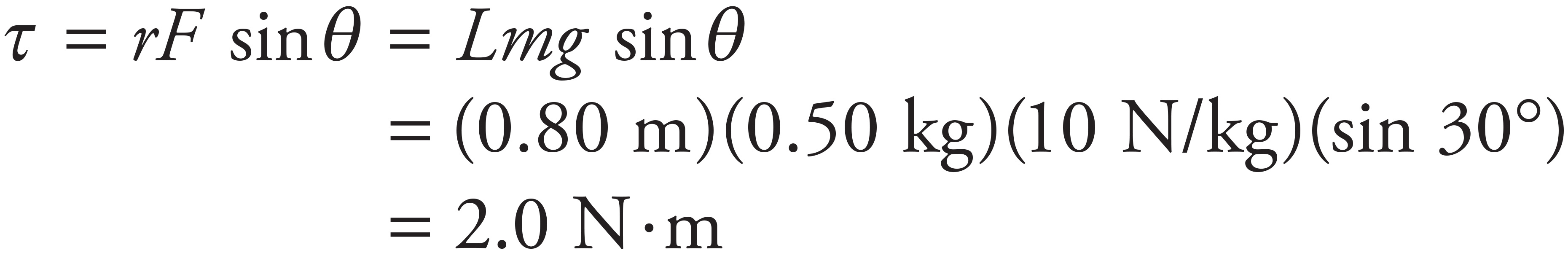
7. B
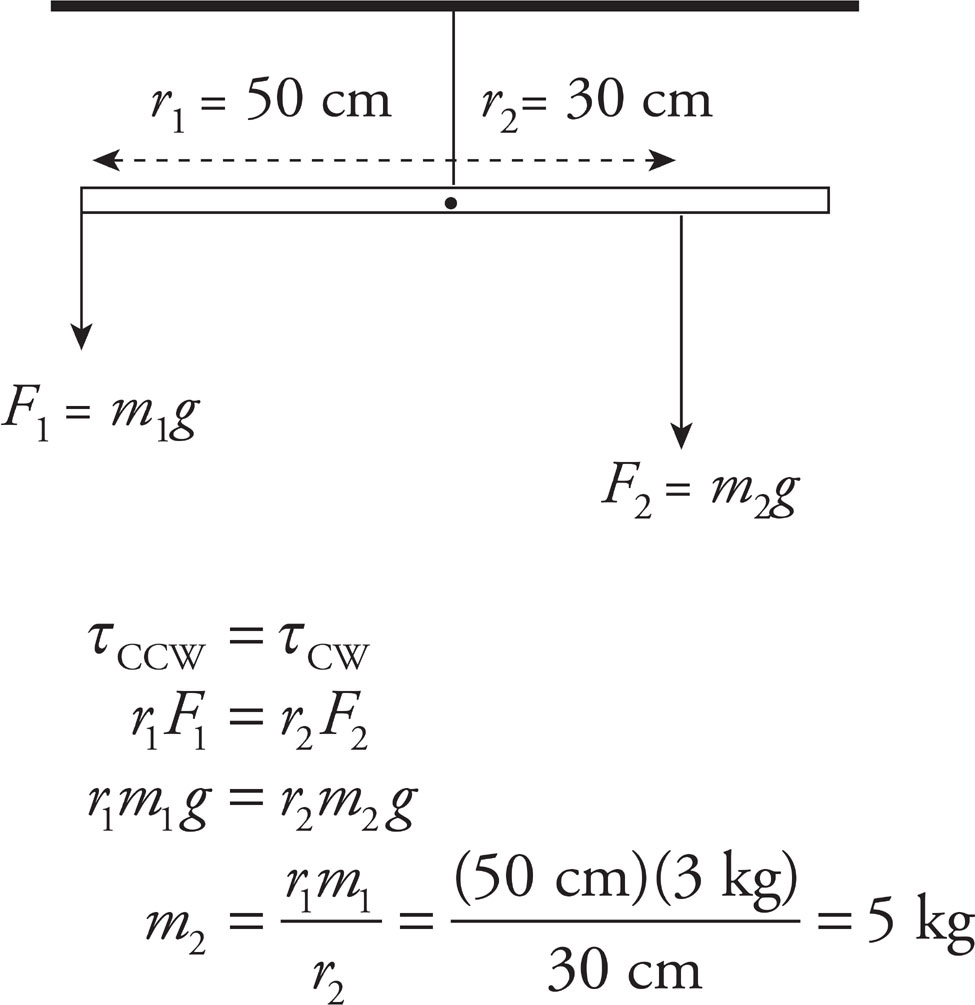
The stick will remain at rest in the horizontal position if the torques about the suspension point are balanced:
8. A
Gravitational force obeys an inverse-square law: Fgrav ∝ 1/r2. Therefore, if r increases by a factor of 2, then Fgrav decreases by a factor of 22 = 4.
9. D
Mass is an intrinsic property of an object and does not change with location. This eliminates (B). If an object’s height above the surface of the Earth is equal to 2RE, then its distance from the center of the Earth is 3RE. Thus, the object’s distance from the Earth’s center increases by a factor of 3, so its weight decreases by a factor of 32 = 9.
10. C
The gravitational force that the Moon exerts on the planet is equal in magnitude to the gravitational force that the planet exerts on the Moon (Newton’s Third Law).
11. D
The gravitational acceleration at the surface of a planet of mass M and radius R is given by the equation g = GM/R2. Therefore, for the dwarf planet Pluto:
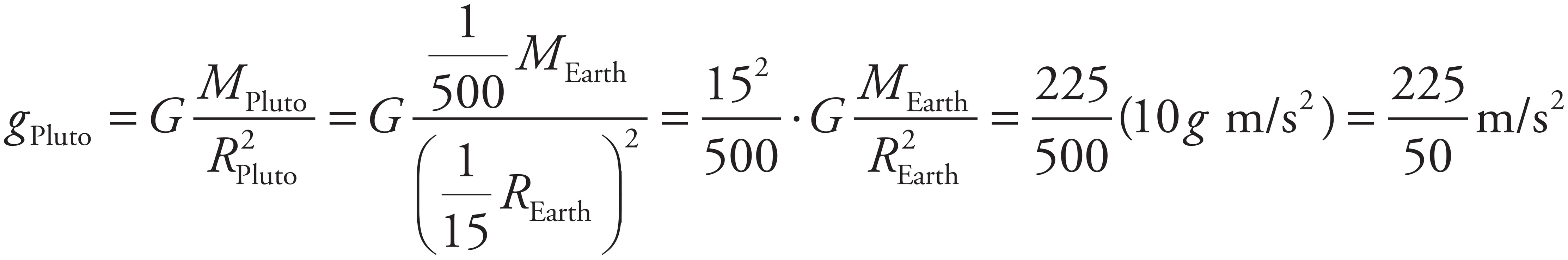
12. B
The gravitational pull by the Earth provides the centripetal force on the satellite, so GMm/R2 = mv2/R. This gives mv2 = GMm/2R, so the kinetic energy K of the satellite is inversely proportional to R. Therefore, if R increases by a factor of 2, then K decreases by a factor of 2.
13. D
The gravitational pull by Jupiter provides the centripetal force on its moon:
14. D
Let the object’s distance from Body A be x; then its distance from Body B is R − x. In order for the object to feel no net gravitational force, the gravitational pull by A must balance the gravitational pull by B. Therefore, if you let M denote the mass of the object, then
15. B
Because the planet is spinning clockwise and the velocity is tangent to the circle, the velocity must point down. The acceleration and force point toward the center of the circle.
16. B, D
If there were no forces or balanced forces, in and out, the satellite would have a net force of zero. If the net force were zero, the satellite would continue in a straight line and not orbit the planet.
The force of gravity produces the centripetal force that keeps the object orbiting (where r is the distance between the center of the planet and the orbiting satellite).
The mass of the satellite does not determine the orbital speed. Only the mass of the planet and its distance from the center of the planet determine orbital speed.
17. B
Since the centripetal force always points along a radius toward the center of the circle, and the velocity of the object is always tangent to the circle (and thus perpendicular to the radius), the work done by the centripetal force is zero. Alternatively, since the object’s speed remains constant, the Work–Energy Theorem tells you that no work is being performed.
1. (a)
Given a mass of 1 kg, weight Fg = 5 N, and diameter = 8 × 106 m (this gives you r = 4 × 106 m), you can fill in this equation:
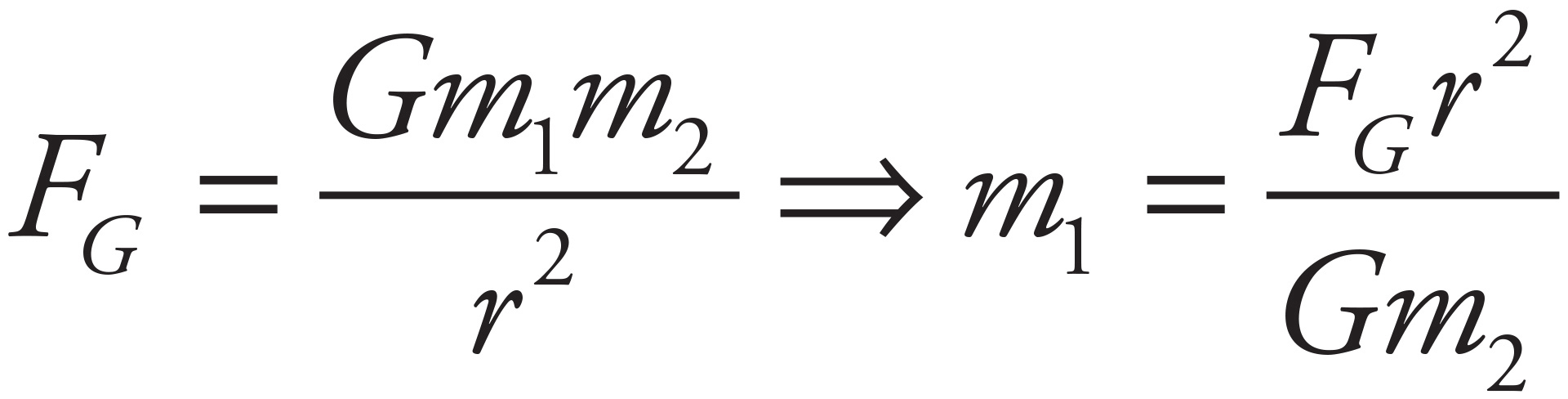
This becomes
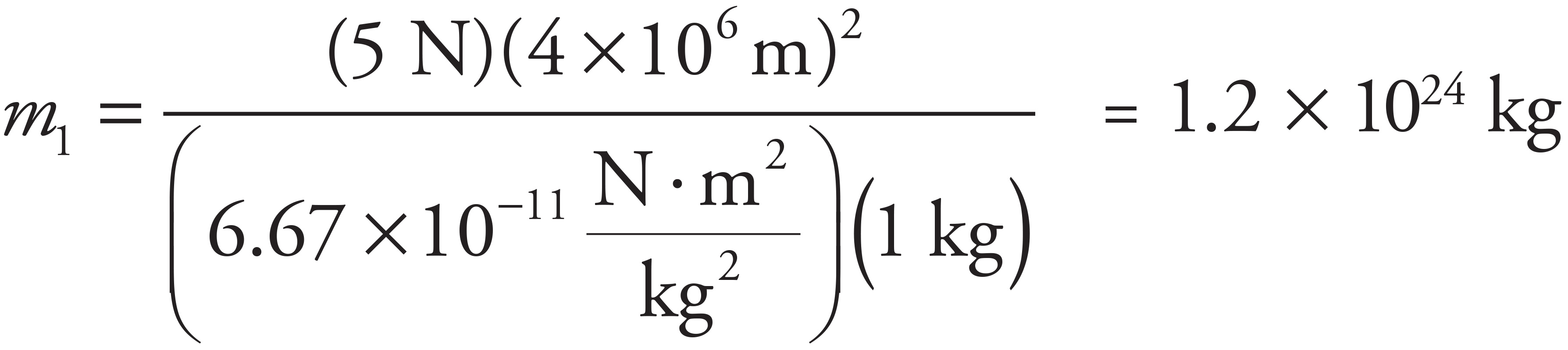
(b)
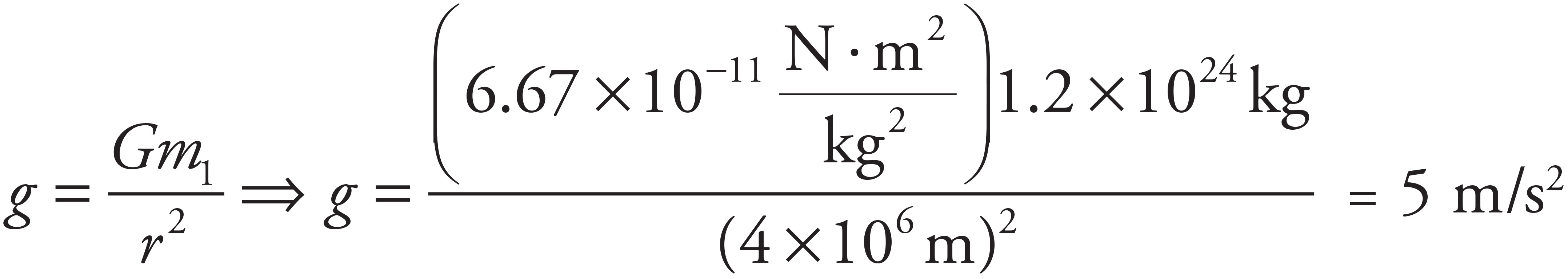
Note that you could have also observed that, because a 1 kg mass (which normally weighs 10 N on the surface of the Earth) only weighed 5 N, gravity on this planet must be half the Earth’s gravity.
If you want to look at it in terms of g, g is 10 m/s2 on Earth, so you can simply convert.
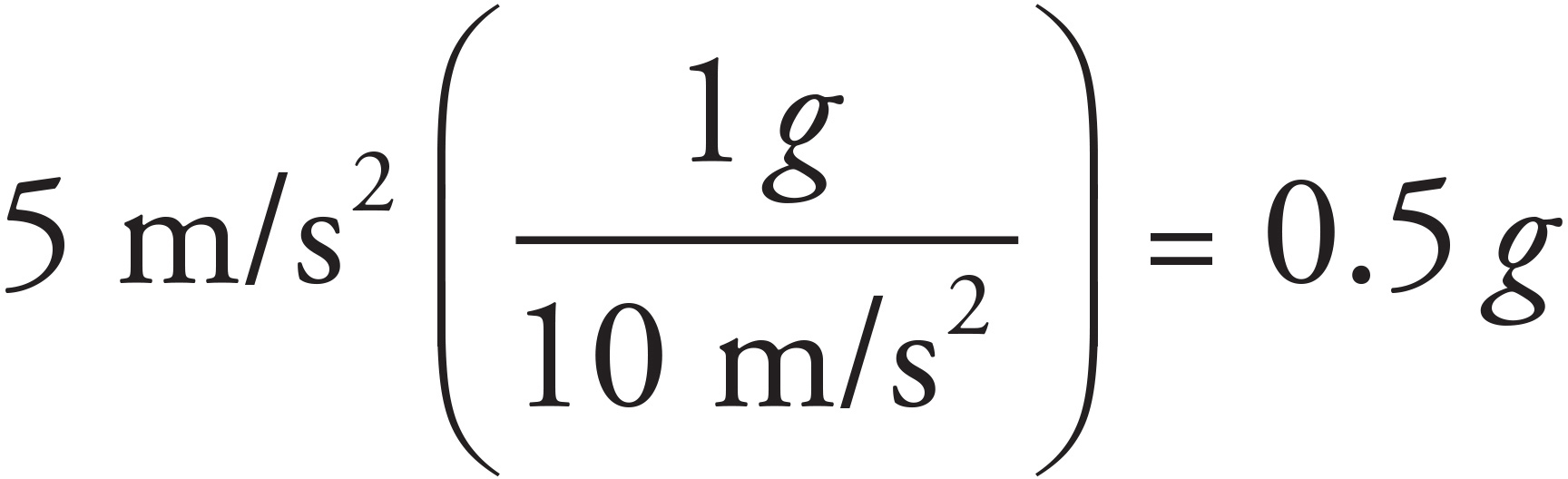
(c)
Density is given by mass per unit volume (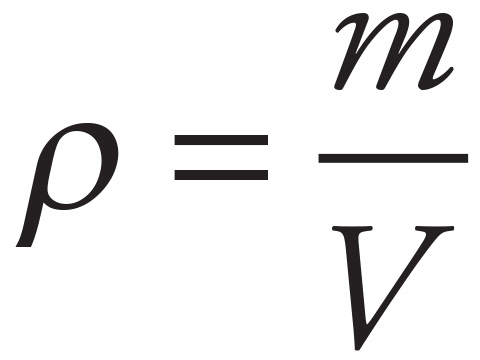
). In addition, use the equation for the volume of a sphere as 
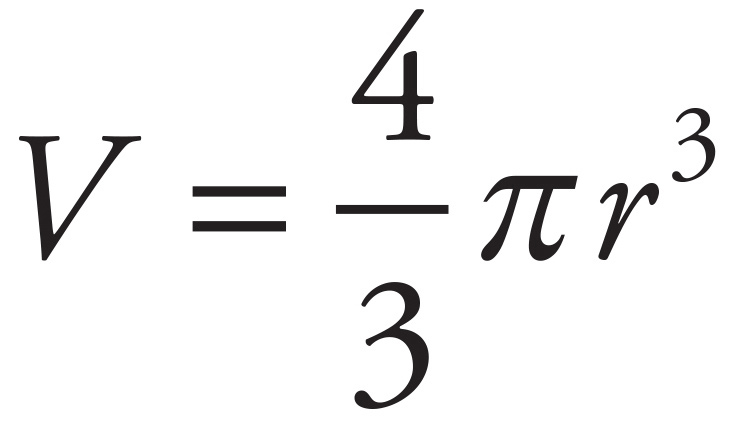to get
2. (a)
The centripetal acceleration is given by the equation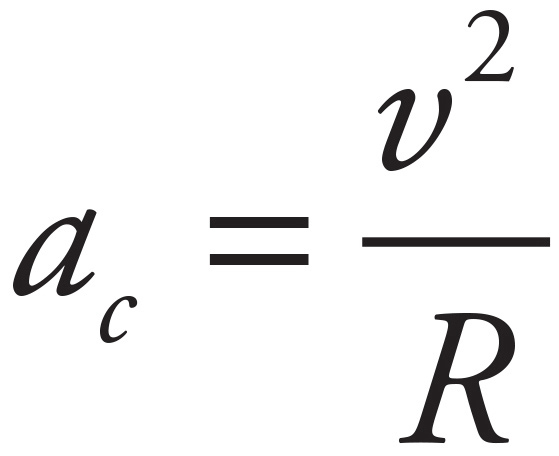 
. You also know that for objects traveling in circles (Earth’s orbit can be considered a circle), 
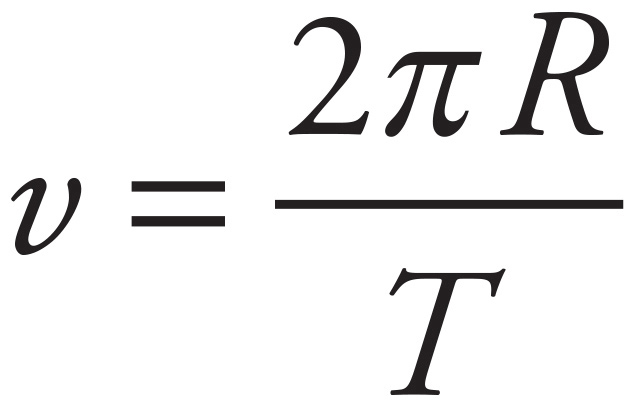. Substituting this v into the previous equation for centripetal acceleration, you get 
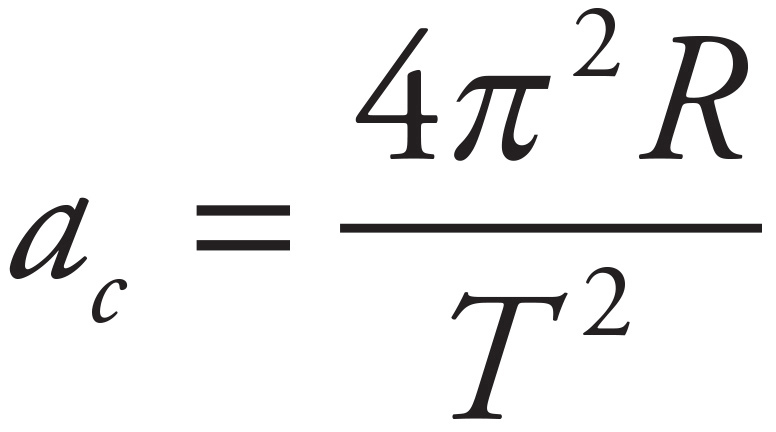. This becomes 
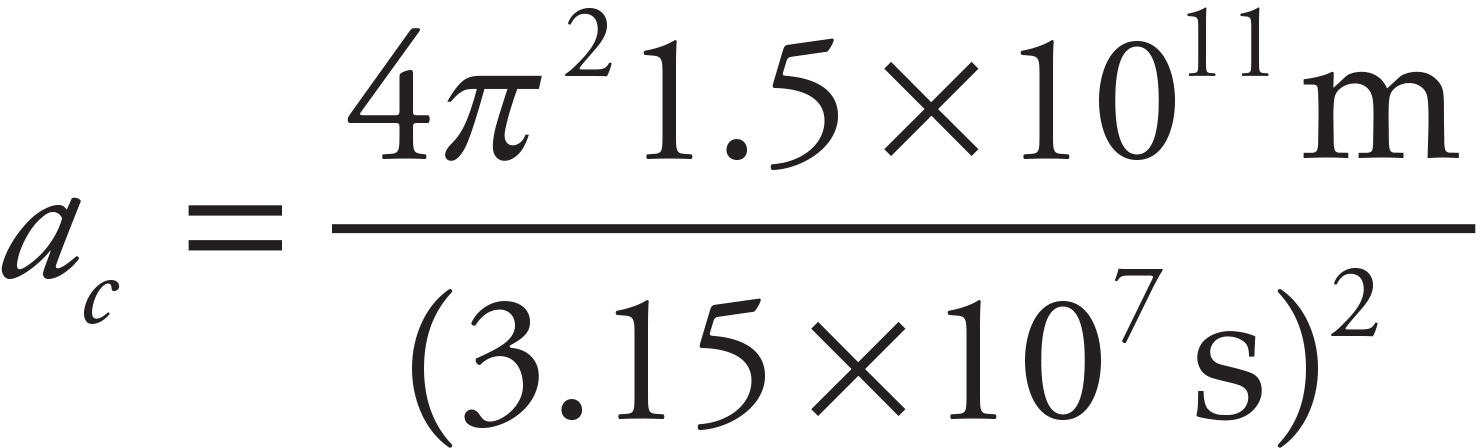= 6.0 × 10−3 m/s2.
(b)
The gravitational force is the force that keeps the Earth traveling in a circle around the Sun. More specifically, mac = (6 × 1024 kg)(6.0 × 10−3 m/s2) = 3.6 × 1022 N.
(c)
Use the Universal Law of Gravitation: F = GmM/r2. You know F from the previous question, G is constant, m is the mass of the Earth (given in question), and r is the radius from Earth to Sun (also given in the question). So you can rearrange this equation to solve for M (mass of the Sun) as M = F·r2/(G·m) and then just plug in the appropriate values.
F = GmM/r2 → M = Fr2/(Gm) = (3.6 × 1022 N)(1.5 × 1011 m)2/{[6.67 × 10−11 Nm2/(kg2)] [6.0 × 1024 kg]} = 2.0 × 1030
3. (a)
The forces acting on a person standing against the cylinder wall are gravity (Fw, downward), the normal force from the wall (FN, directed toward the center of the cylinder), and the force of static friction (Ff, directed upward):
(b)
In order to keep a passenger from sliding down the wall, the maximum force of static friction must be at least as great as the passenger’s weight: Ff (max) ≥ mg. Since Ff (max) = µsFN, this condition becomes µsFN ≥ mg.
Now, consider the circular motion of the passenger. Neither Ff nor Fw has a component toward the center of the path, so the centripetal force is provided entirely by the normal force:
Substituting this expression for FN into the previous equation, you get
Therefore, the coefficient of static friction between the passenger and the wall of the cylinder must satisfy this condition in order to keep the passenger from sliding down.
(c)
Since the mass m canceled out in deriving the expression for μs, the conditions are independent of mass. Thus, the inequality μs ≥ gr/v2 holds for both the adult passenger of mass m and the child of mass m/2.
4. (a)
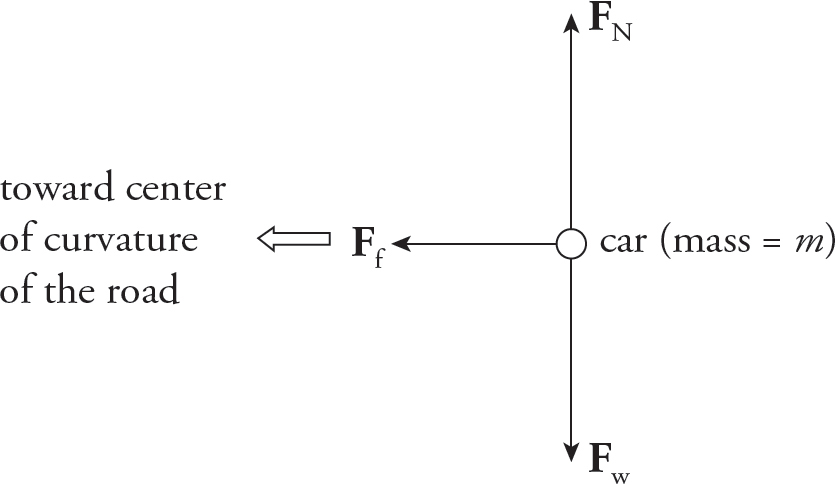
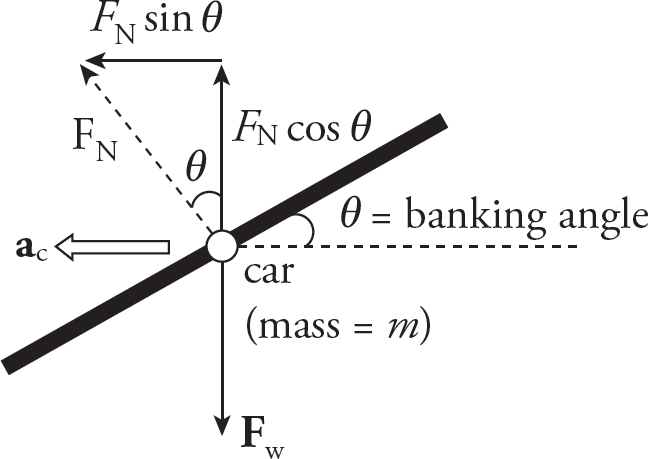
The forces acting on the car are gravity (Fw, downward), the normal force from the road (FN, upward), and the force of static friction (Ff, directed toward the center of curvature of the road):
(b)
The force of static friction (assume static friction because you don’t want the car to slide) provides the necessary centripetal force:
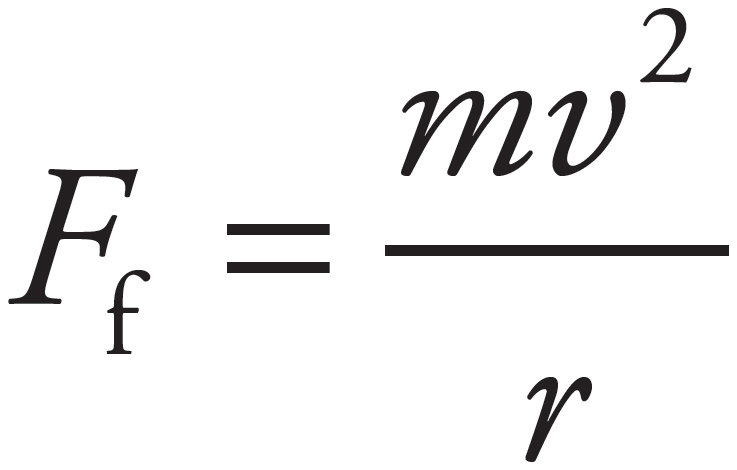
Therefore, to find the maximum speed at which static friction can continue to provide the necessary force, write
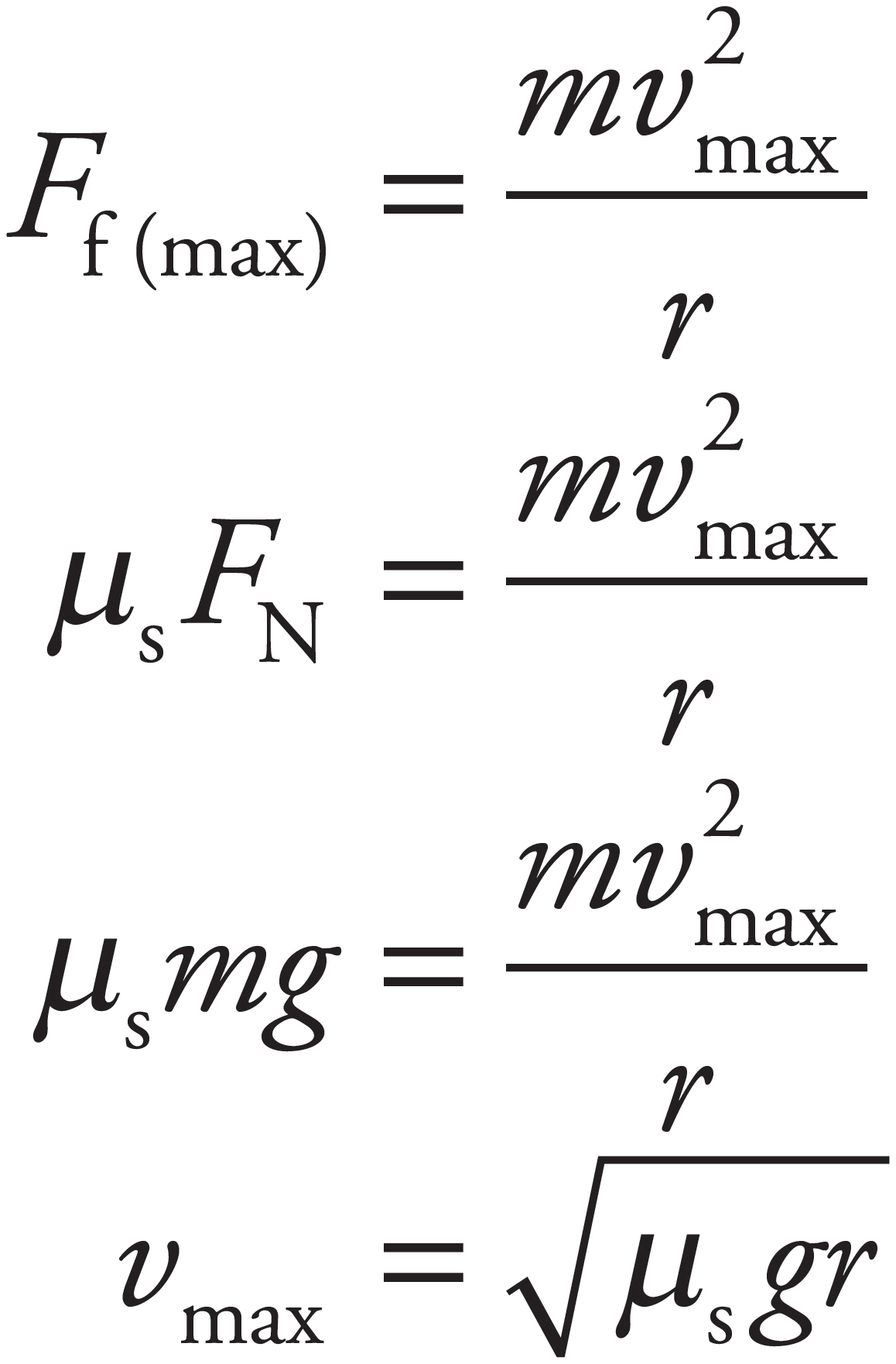
(c)
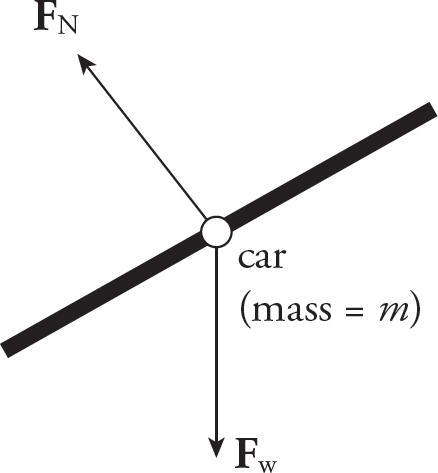
Ignoring friction, the forces acting on the car are gravity (Fw, downward) and the normal force from the road (FN, which is now tilted toward the center of curvature of the road):
(d)
Because of the banking of the turn, the normal force is tilted toward the center of curvature of the road. The component of FN toward the center can provide the centripetal force, making reliance on friction unnecessary.
However, there’s no vertical acceleration, so there is no net vertical force. Therefore, FN cos θ = Fw = mg, so FN = mg/cos θ. The component of FN toward the center of curvature of the turn, FN sin θ, provides the centripetal force:
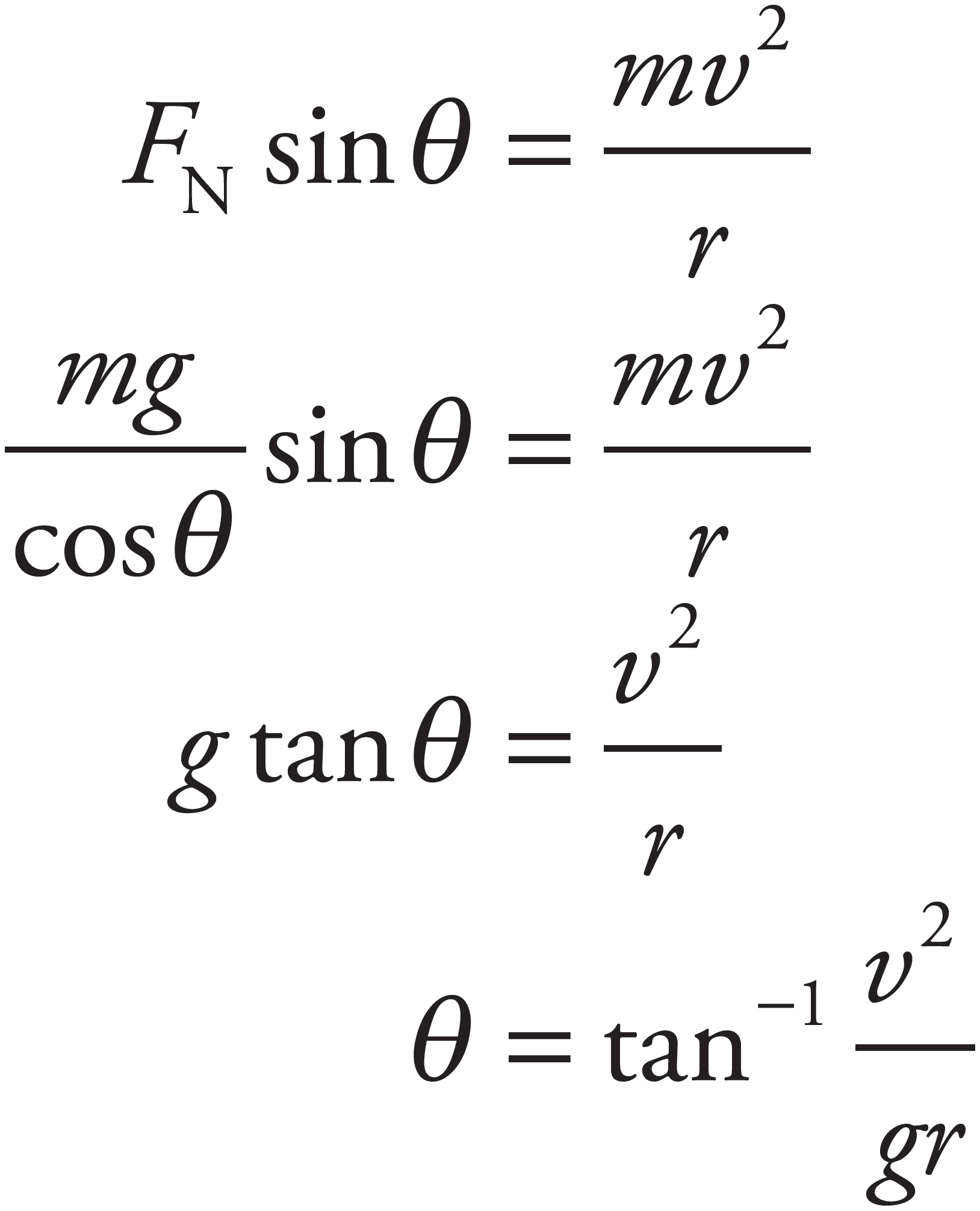
1. B, C
The acceleration of a simple harmonic oscillator is not constant, since the restoring force—and consequently, the acceleration—depends on the position. Eliminate (A). Choices (B) and (C) are defining characteristics of simple harmonic motion; therefore, (D) is also false. Period must also be independent of amplitude, as period and frequency are proportional to one another.
2. B
The acceleration of the block has its maximum magnitude at the points where its displacement from equilibrium has the maximum magnitude (since a = F/m = kx/m). At the endpoints of the oscillation region, the potential energy is maximized and the kinetic energy (and hence the speed) is zero.
3. D
By Conservation of Mechanical Energy, K + US is a constant for the motion of the block. At the endpoints of the oscillation region, the block’s displacement, x, is equal to ±A. Since K = 0 here, all the energy is in the form of potential energy of the spring, kA2. Because kA2 gives the total energy at these positions, it also gives the total energy at any other position.
Using the equation US(x) = kx2, find that, at x = A.
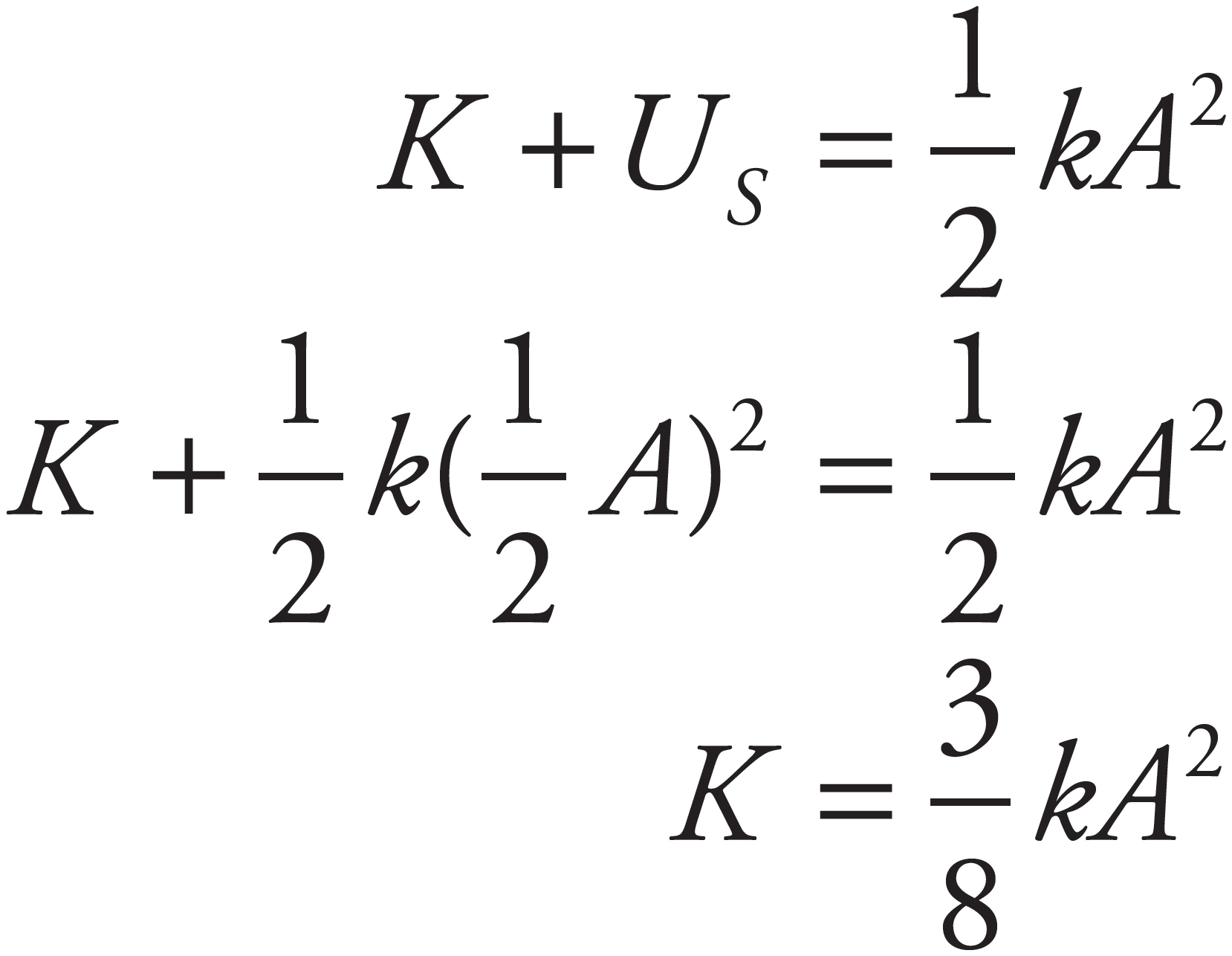
Therefore,
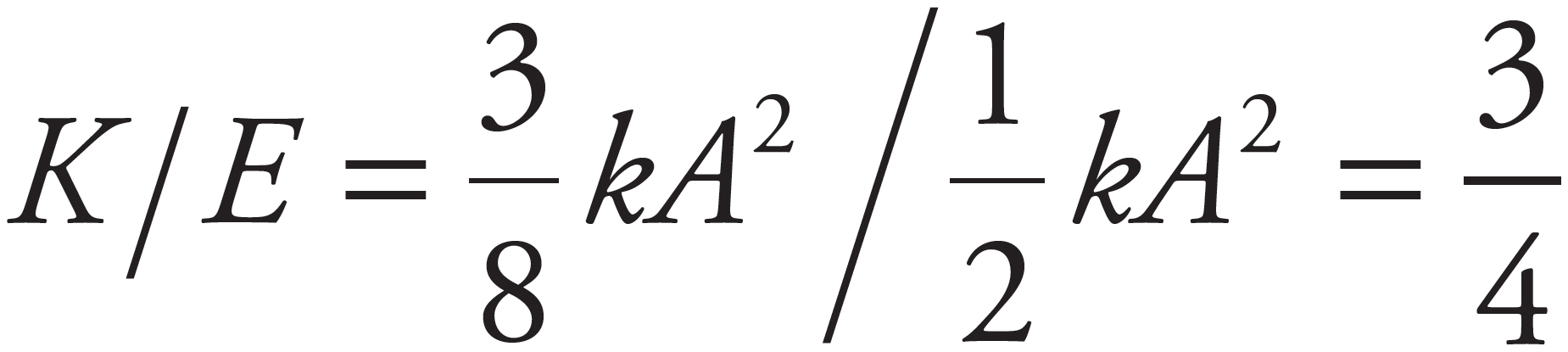
4. C
The maximum speed of the block is given by the equation vmax =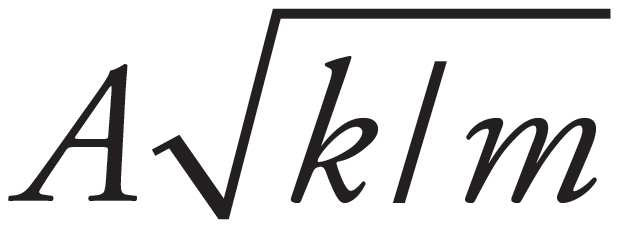 
. Therefore, vmax is inversely proportional to 
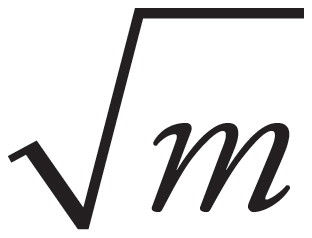. If m is increased by a factor of 2, then vmax will decrease by a factor of 
.
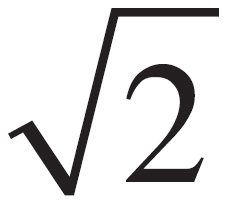5. D
The period of a spring-block simple harmonic oscillator is independent of the value of g. (Recall that T =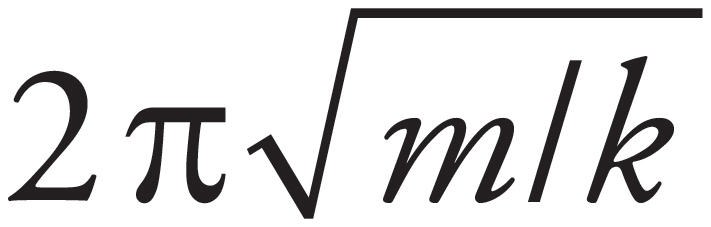 
) Therefore, the period will remain the same.
6. D
The frequency of a spring-block simple harmonic oscillator is given by the equation f = 
. Squaring both sides of this equation, you get f2 =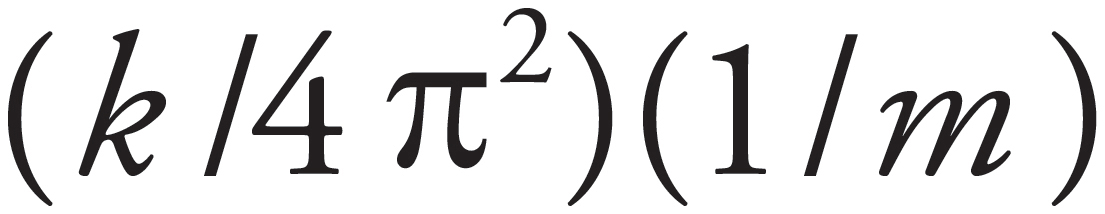 
. Therefore, if f2 is plotted versus (1/m), then the graph will be a straight line with slope k/4π2. (Note: The slope of the line whose equation is y = ax is a.)
7. C
For small angular displacements, the period of a simple pendulum is essentially independent of amplitude.
8. D
Combining Hooke’s Law with Newton’s Second Law, you get
9. B
By Conservation of Mechanical Energy, the energy of the block is the same throughout the motion. At the amplitude, the block has potential energy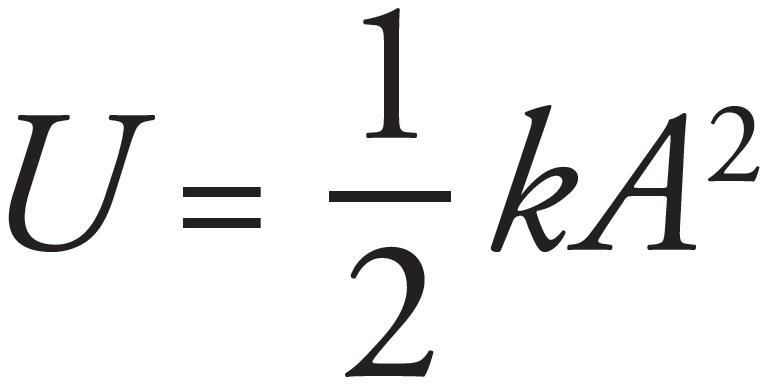 
and zero kinetic energy. At the equilibrium position, the block has kinetic energy 
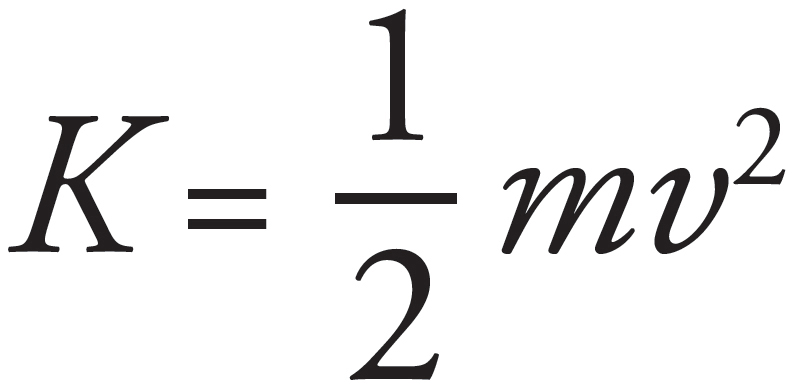and zero potential energy. Applying the Conservation of Mechanical Energy to these two points in the motion yields
The period of the block can then be calculated using the following equation:
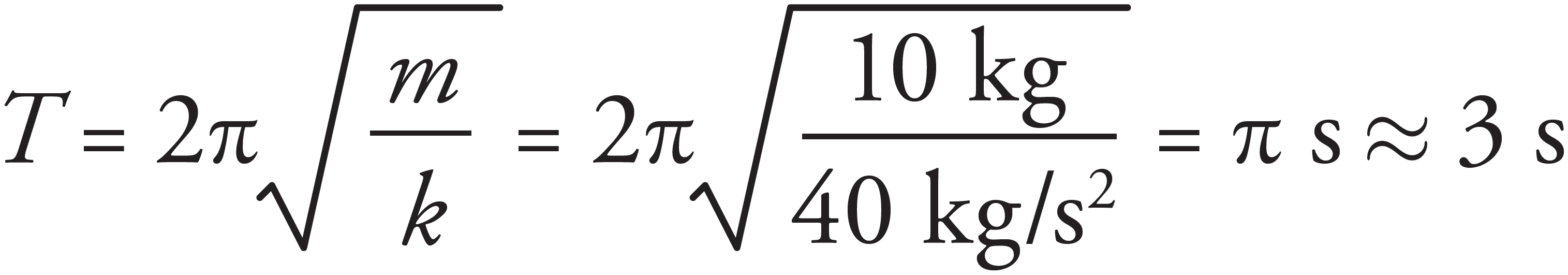
10. B
The frequency of a spring-block simple harmonic oscillator is independent of the amplitude. The equation for the frequency of a spring-block simple harmonic oscillator is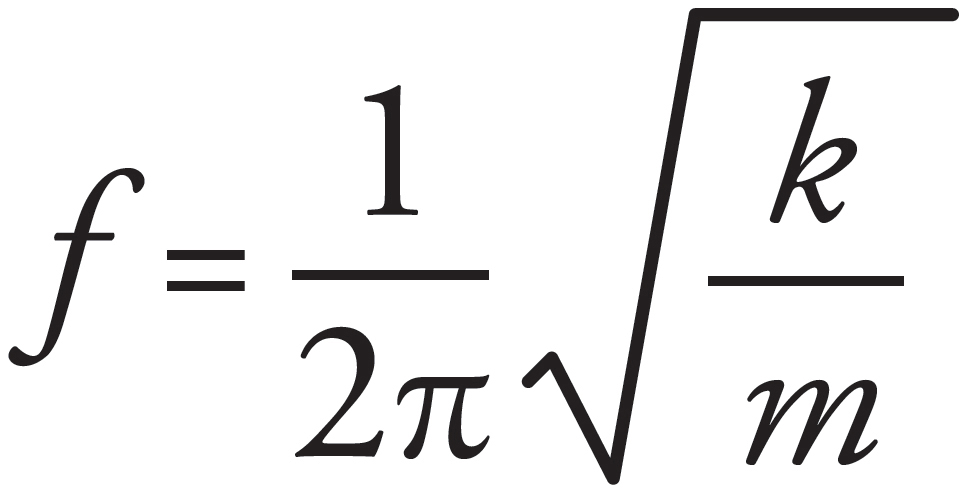 
. The frequency is inversely proportional to the square root of the mass, so decreasing the mass of the block by a factor of 4 would increase the frequency by a factor of 2.
1. (a)
Since the spring is compressed to 3/4 of its natural length, the block’s position relative to equilibrium is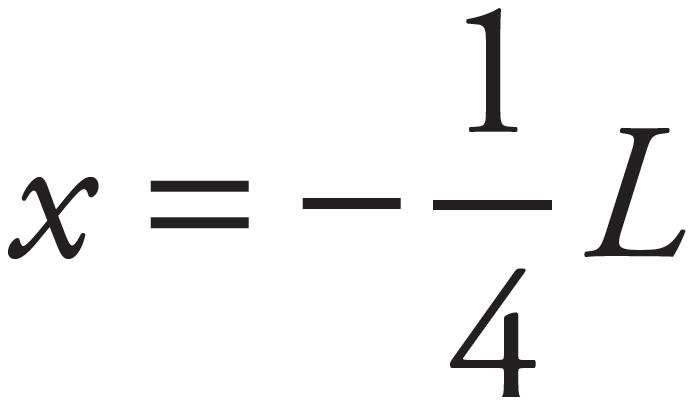 
. Therefore, from FS = −kx, find
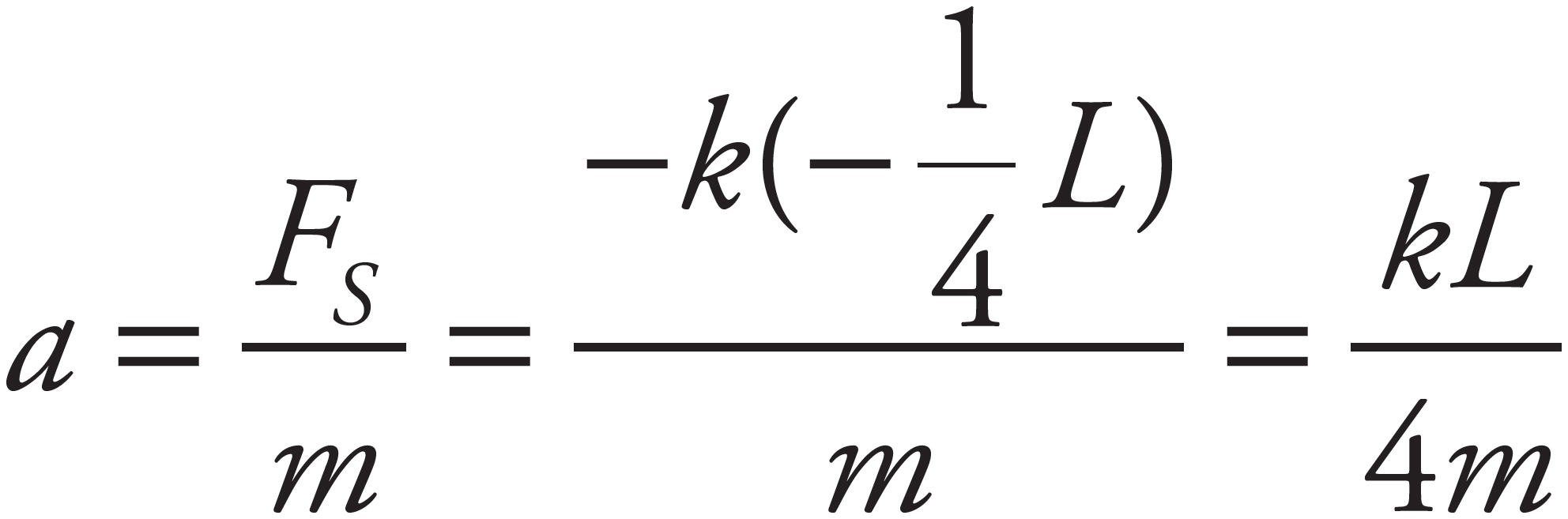
(b)
Let v1 denote the velocity of Block 1 just before impact, and let v′1 and v′2 denote, respectively, the velocities of Block 1 and Block 2 immediately after impact. By Conservation of Linear Momentum, write mv1 = mv′1 + mv′2, or
The initial kinetic energy of Block 1 is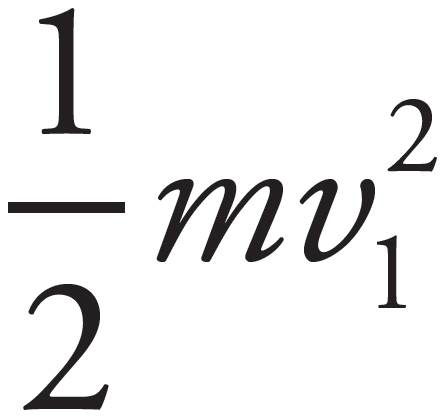 
. If half is lost to heat, then 
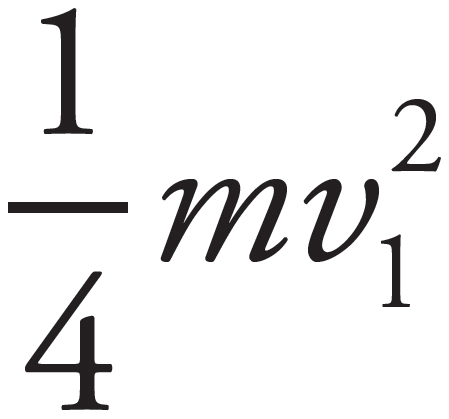is left to be shared by Block 1 and Block 2 after impact: 
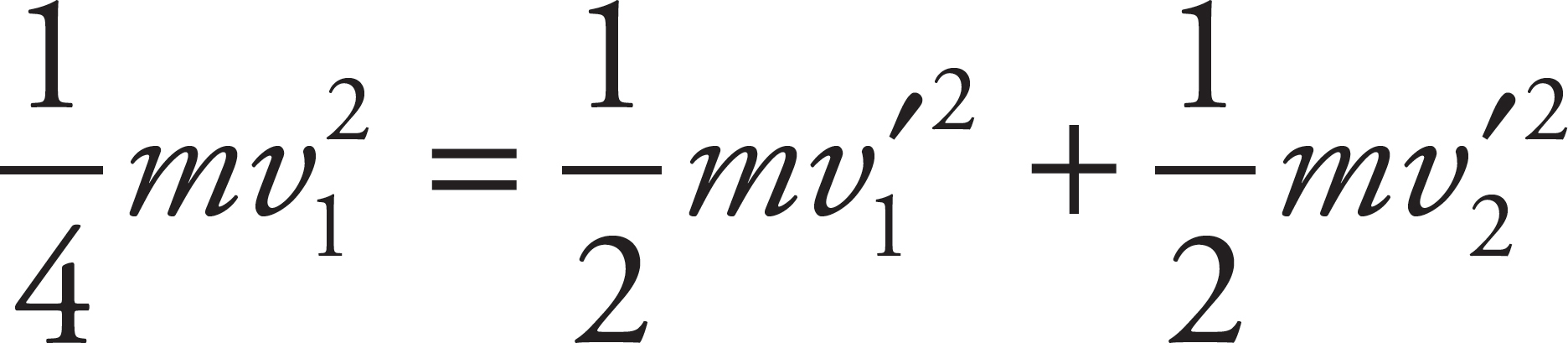, or
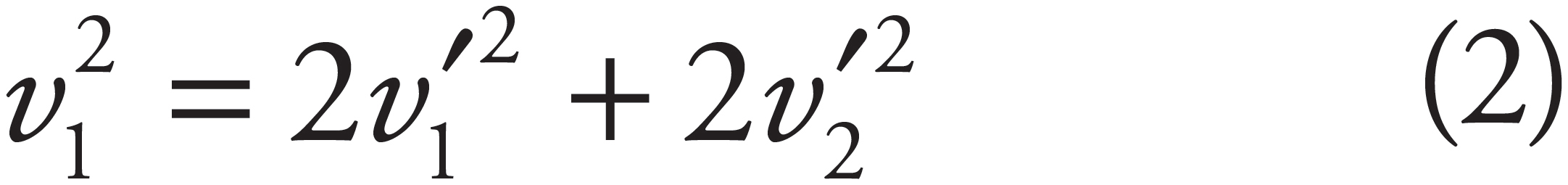
Square Equation (1) and multiply by 2 to give
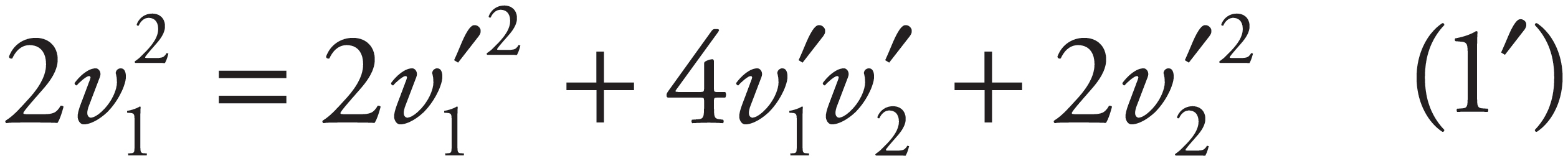
Then subtract Equation (2) from Equation (1′)
Square Equation (1) again,
and substitute into this the result of Equation (3):
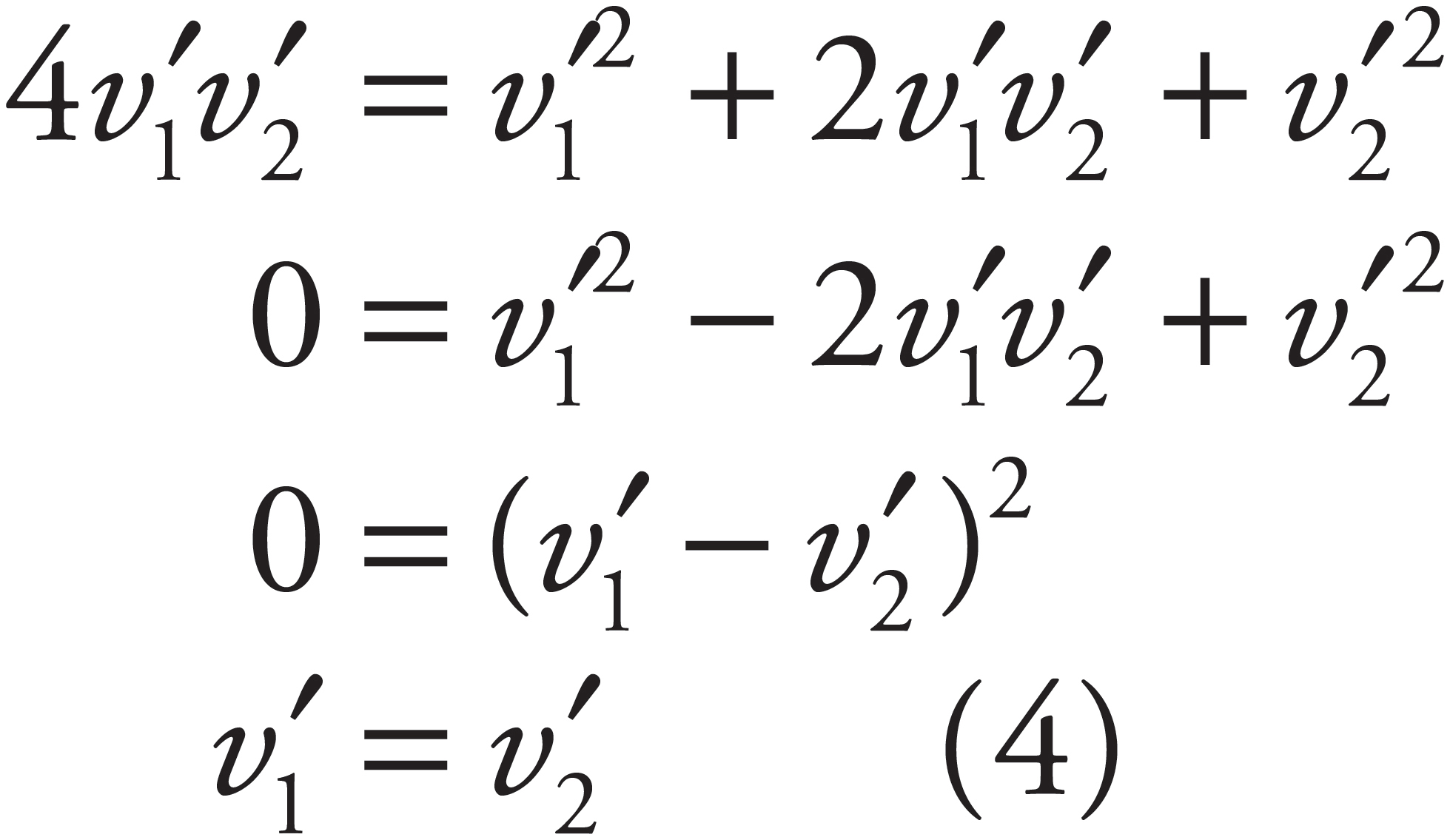
Thus, combining Equations (1) and (4), find that
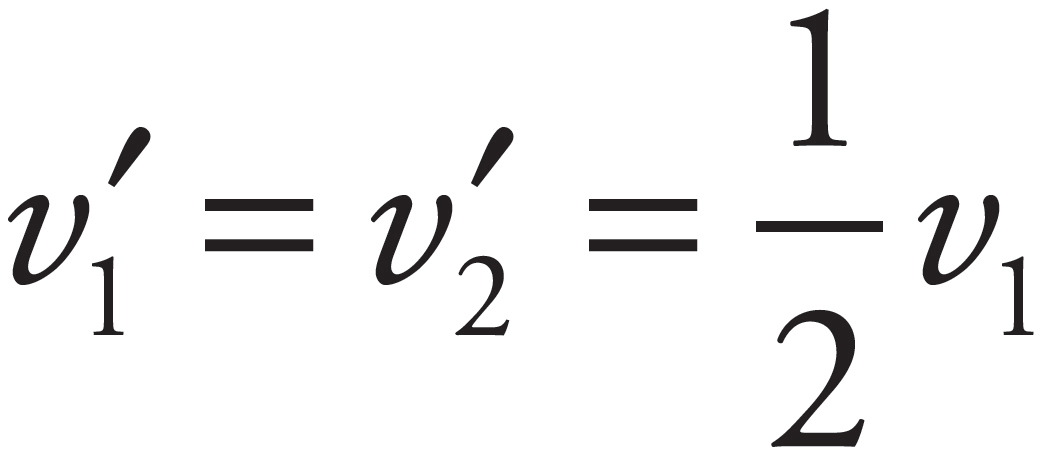
(c)
When Block 1 reaches its new amplitude position, A′, all of its kinetic energy is converted to elastic potential energy of the spring. That is,
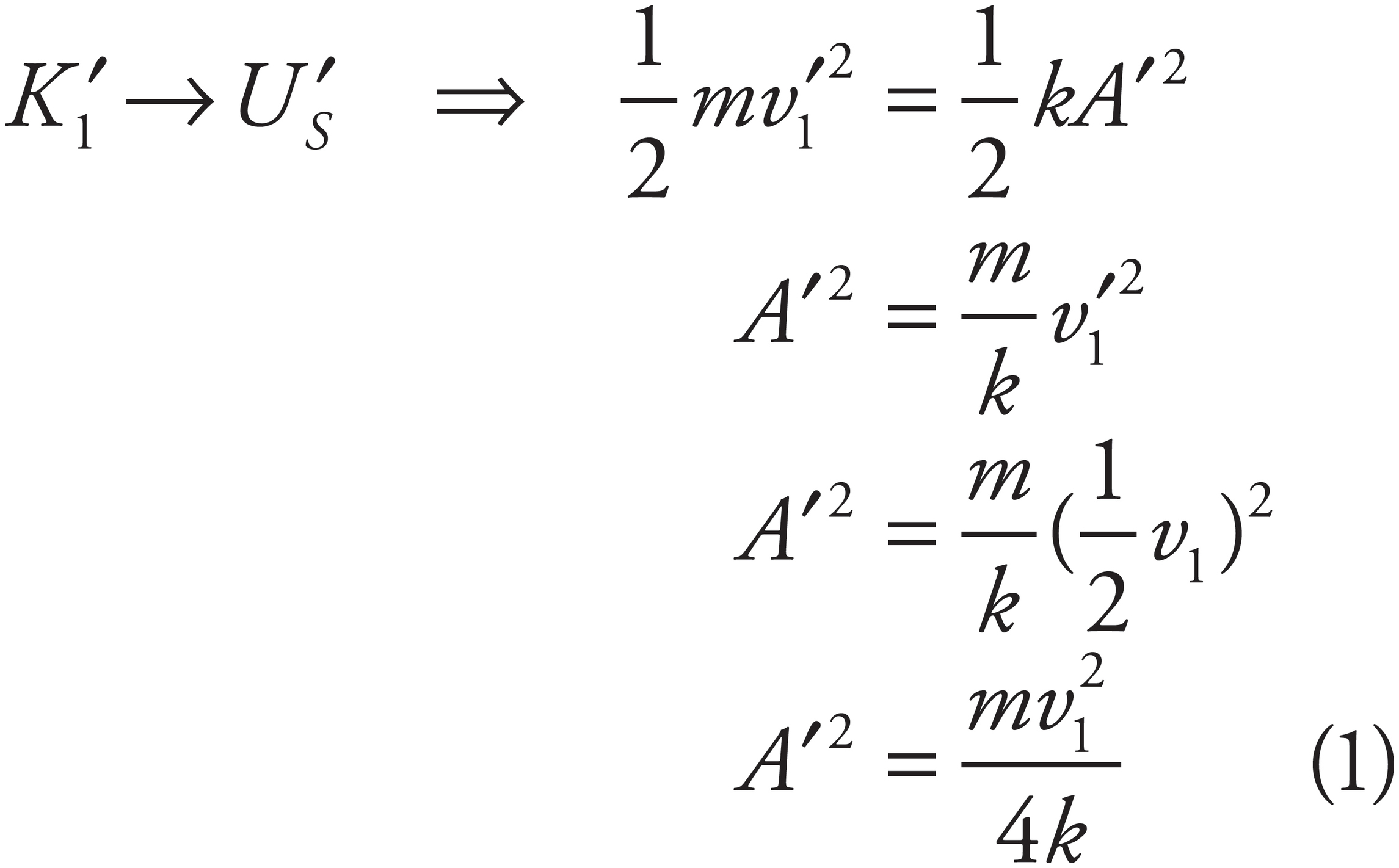
But the original potential energy of the spring,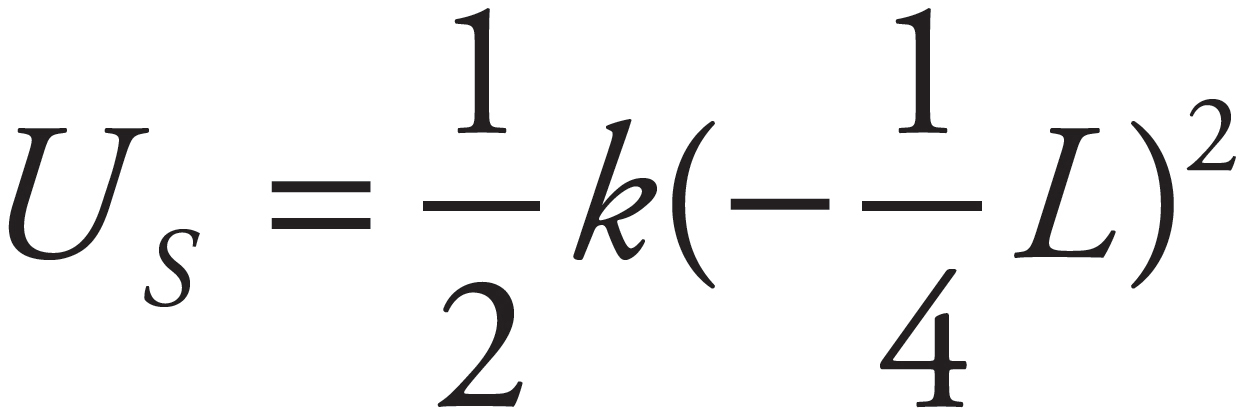 
, gave K1:
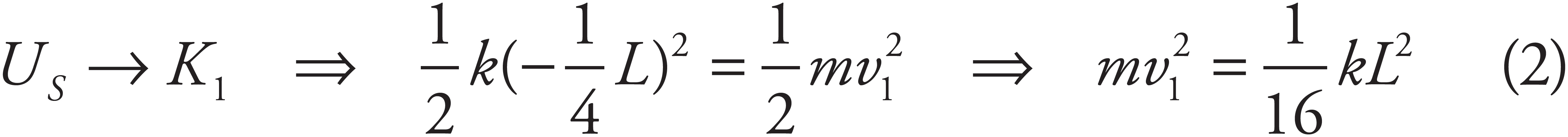
Substituting this result into Equation (1) gives
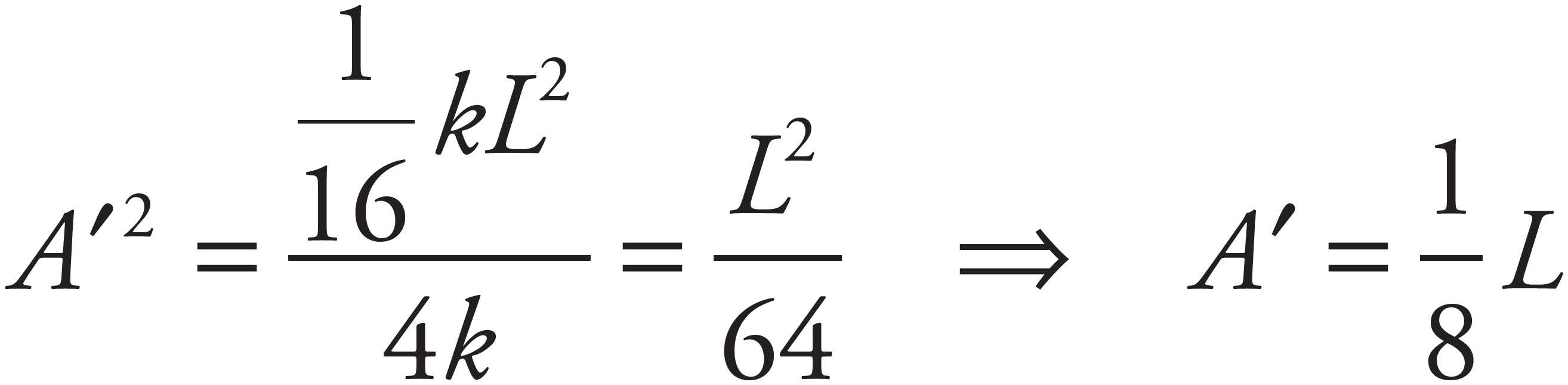
(d)
The period of a spring-block simple harmonic oscillator depends only on the spring constant k and the mass of the block. Since neither of these changes, the period will remain the same; that is, T′ = T0.
(e)
As shown in part (b), Block 2’s velocity as it slides off the table is v1 (horizontally). The time required to drop the vertical distance H is found as follows (calling down the positive direction):
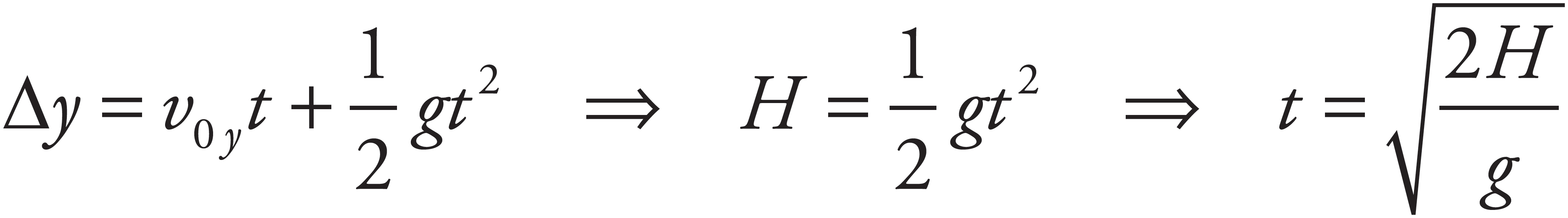
Therefore,
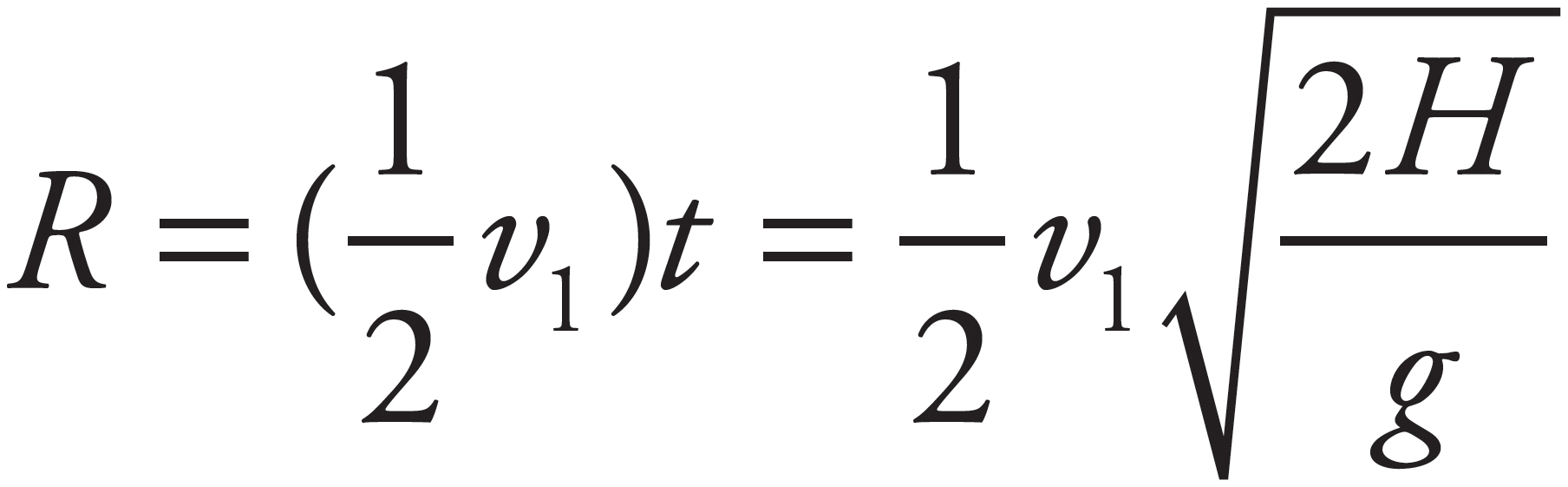
Now, from Equation (2) of part (c), v1 =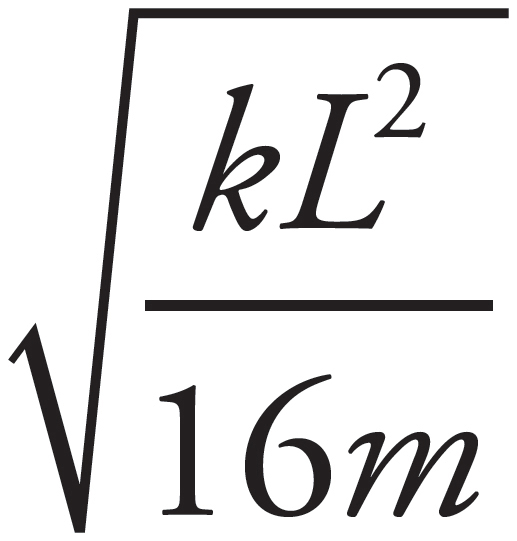 
, so
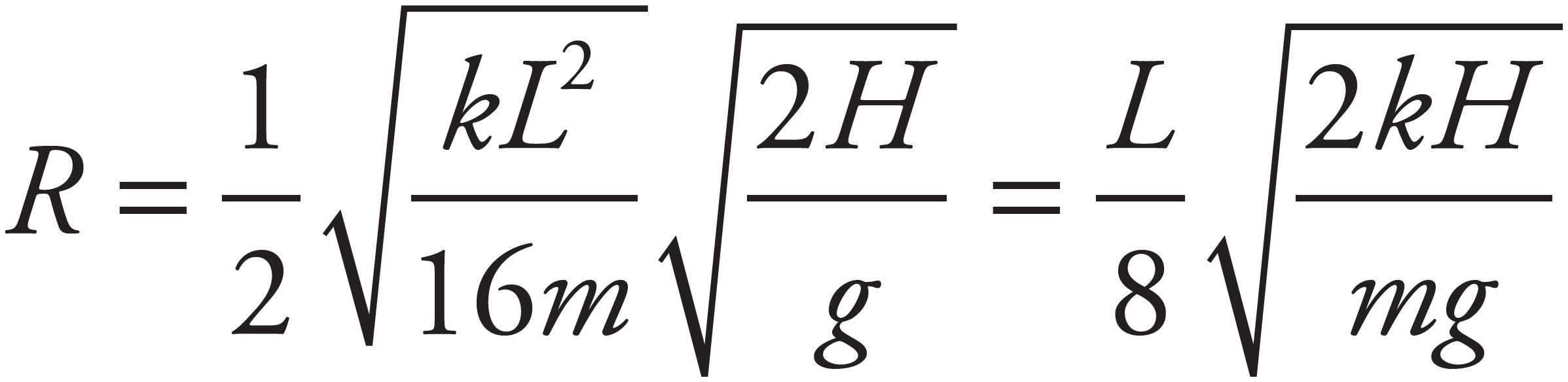
2. (a)
By Conservation of Linear Momentum,
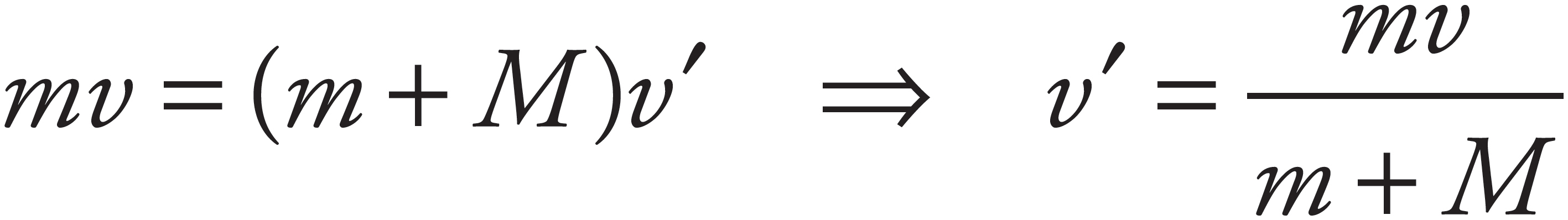
(b)
When the block is at its amplitude position (maximum compression of spring), the kinetic energy it (and the embedded bullet) had just after impact will become the potential energy of the spring:
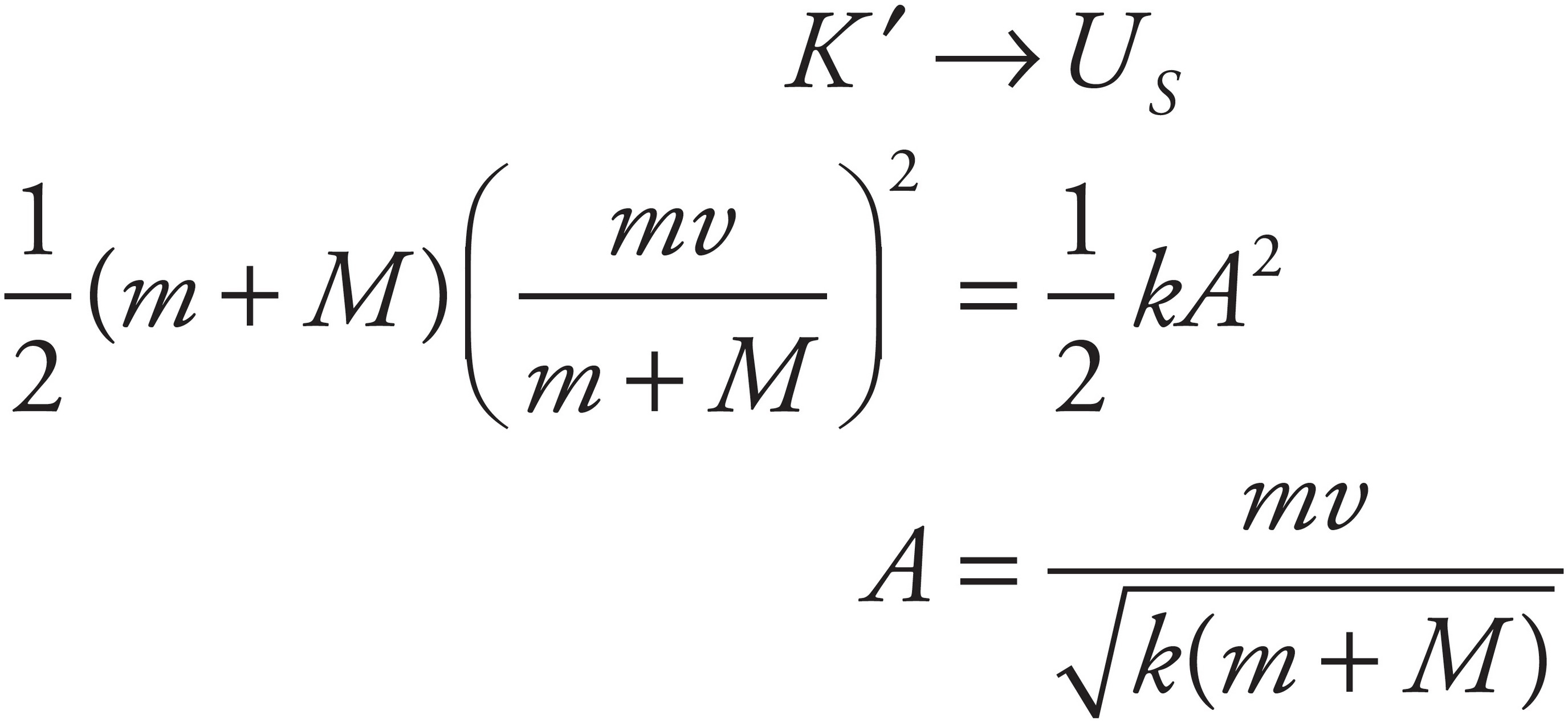
(c)
Since the mass on the spring is m + M,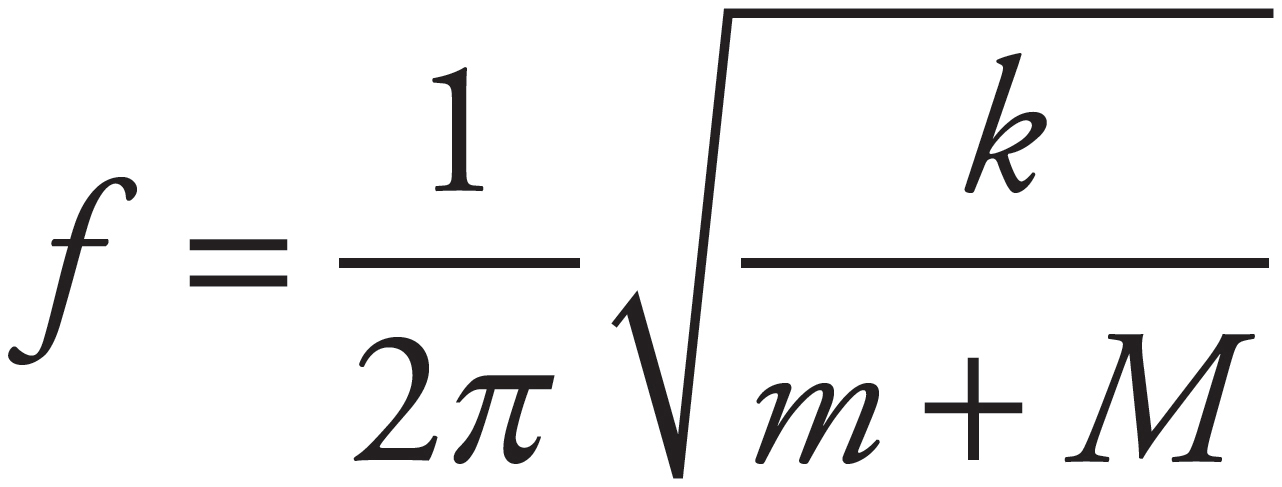 
3. (a)
By Conservation of Mechanical Energy, K + U = E, so
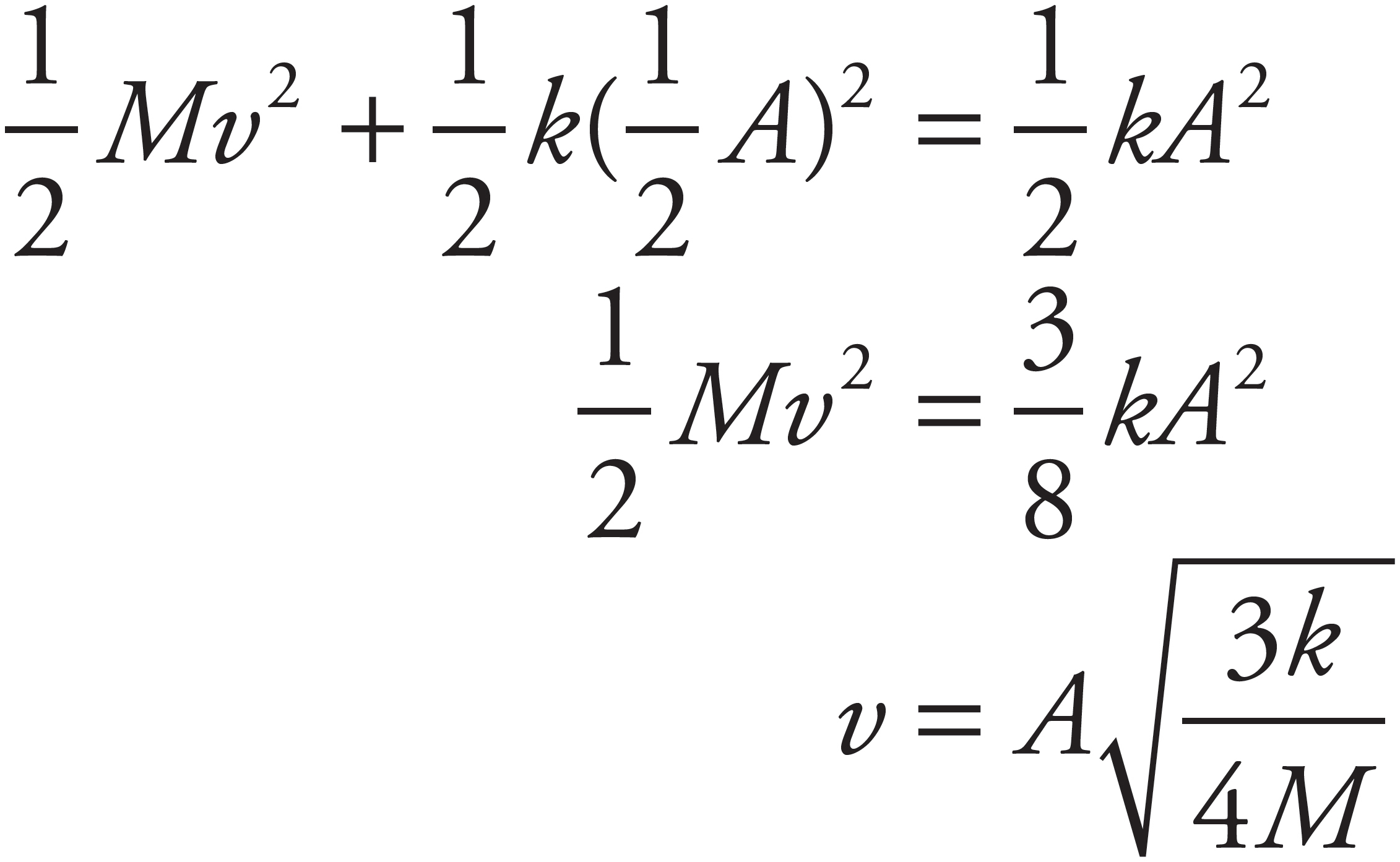
(b)
Since the clay ball delivers no horizontal linear momentum to the block, horizontal linear momentum is conserved. Thus,
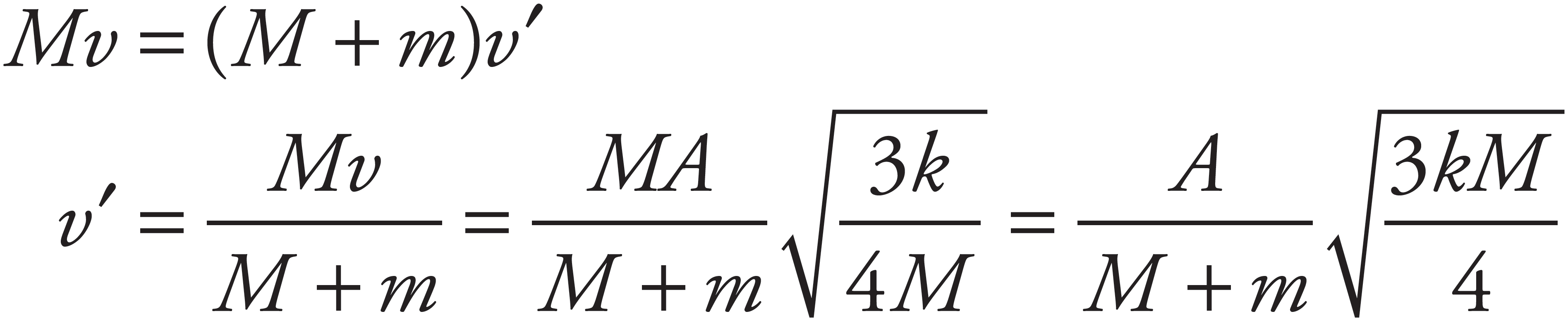
(c)
Applying the general equation for the period of a spring-block simple harmonic oscillator,
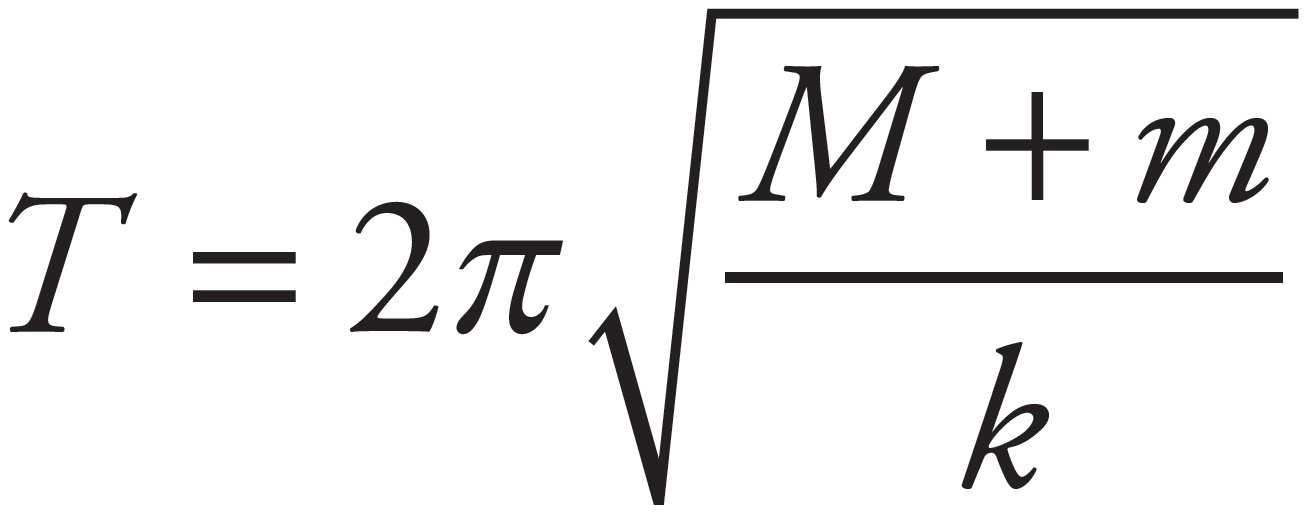
(d)
The total energy of the oscillator after the clay hits is kA′2, where A′ is the new amplitude. Just after the clay hits the block, the total energy is
Substitute for v′ from part (b), set the resulting sum equal to kA′2, and solve for A′.
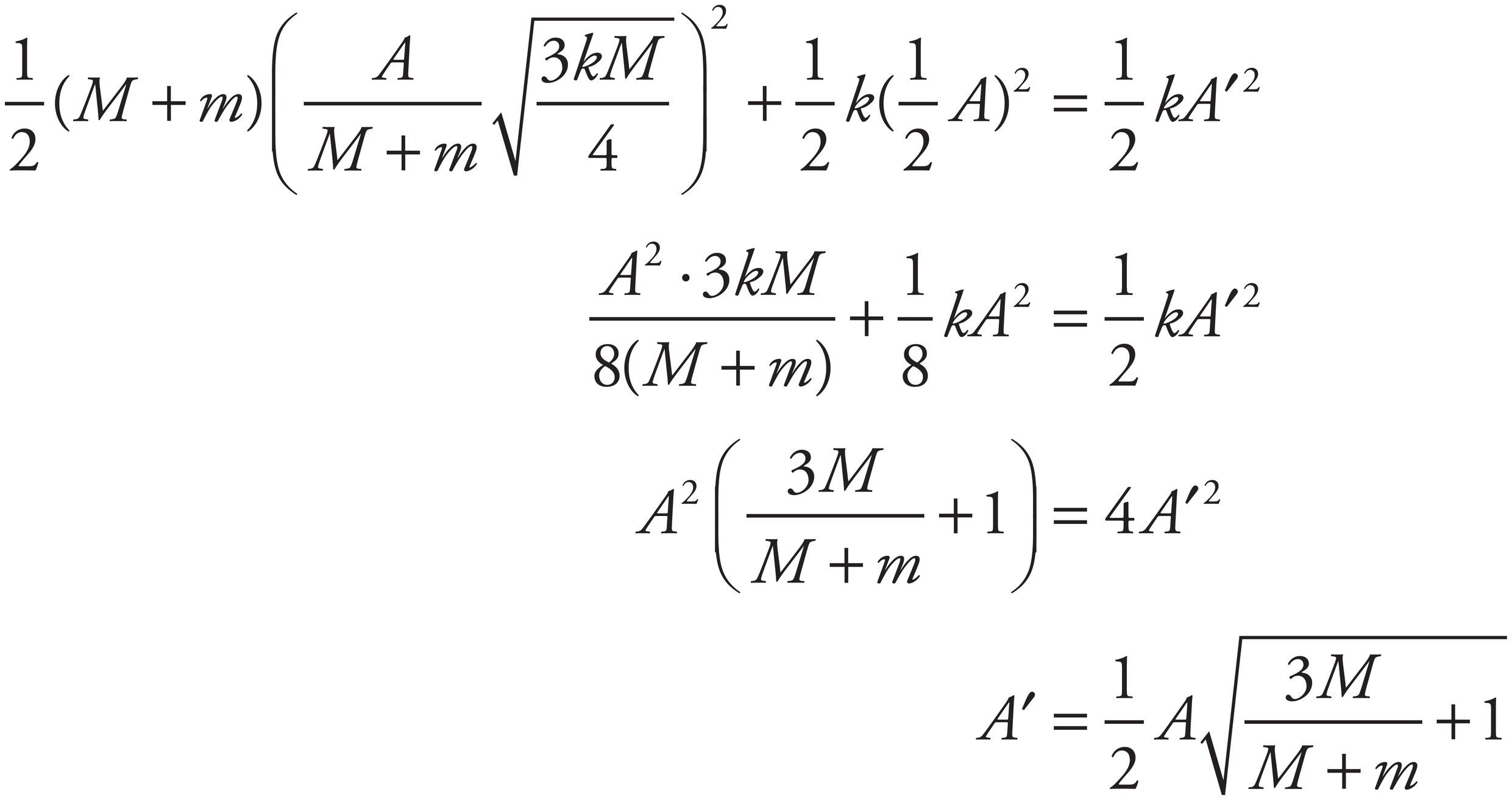
(e)
No, because the period depends only on the mass and the spring constant k.
(f)
Yes. For example, if the clay had landed when the block was at x = A, the speed of the block would have been zero immediately before the collision and immediately after. No change in the block’s speed would have meant no change in K, so no change in E, so no change in A = 
.
1. C
From the equation λf = v, find that
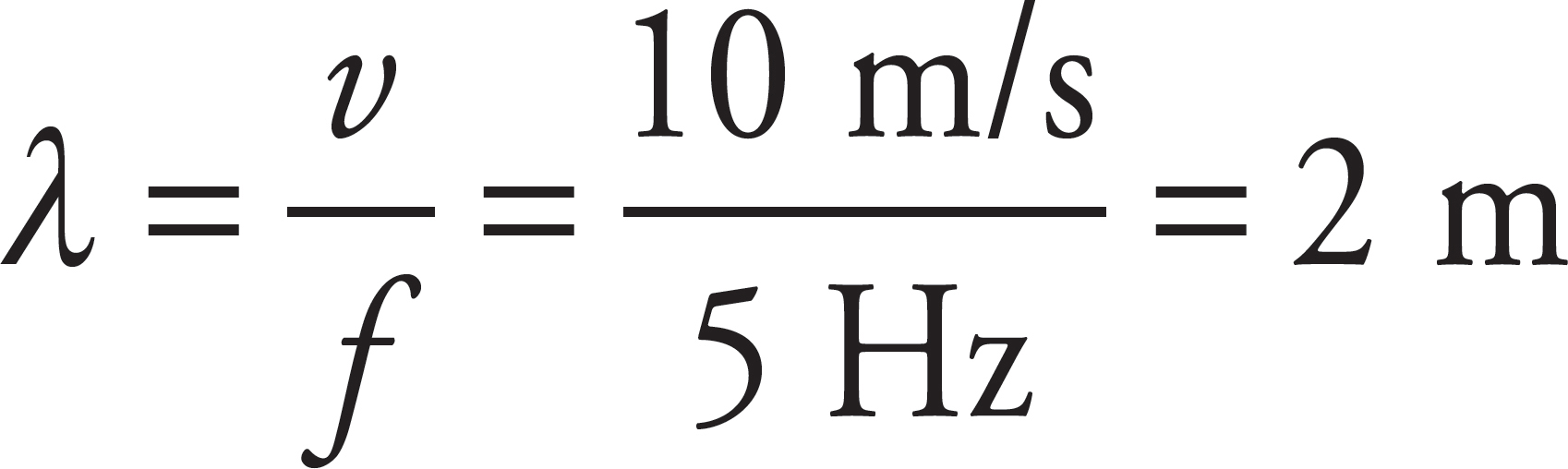
2. C
The speed of a transverse traveling wave on a stretched rope is given by the equation v =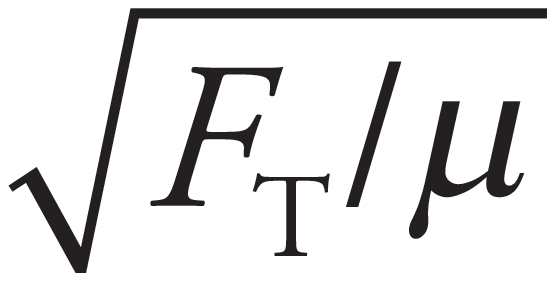 
. Therefore,
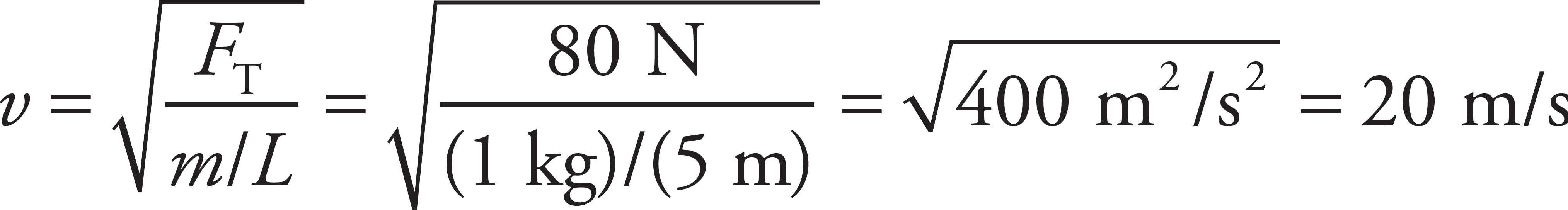
3. C
The time interval from a point moving from its maximum displacement above y = 0 (equilibrium) to its maximum displacement below equilibrium is equal to one-half the period of the wave. In this case,
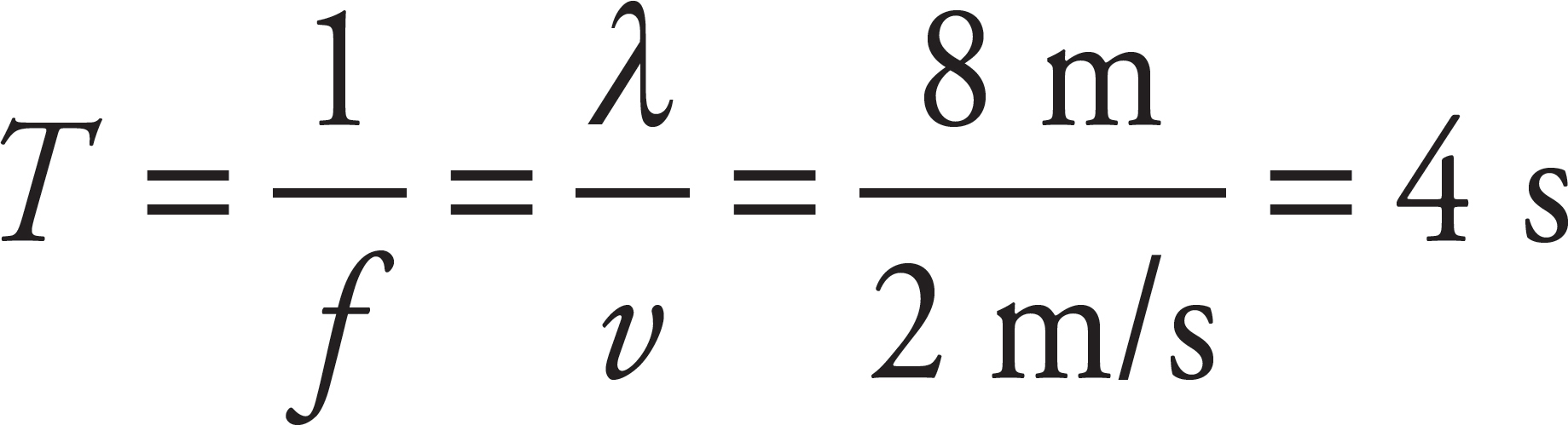
so the desired time is (4 s) = 2 s.
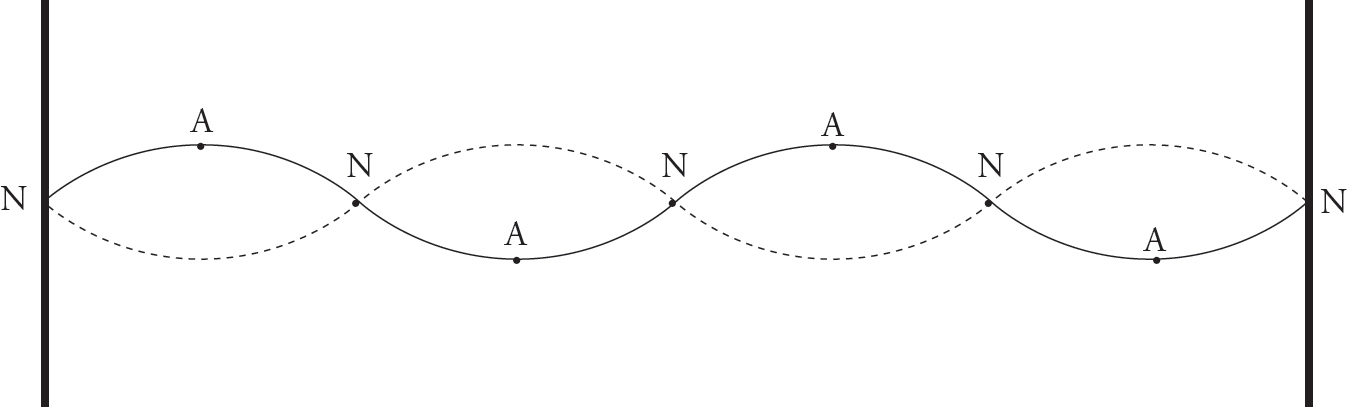
4. D
The distance between successive nodes is always equal to λ. If a standing wave on a string fixed at both ends has a total of 4 nodes, the string must have a length L equal to 3(λ). If L = 6 m, then λ must equal 4 m.
5. B
The previous question showed that λ = 4 m. Since v = 40 m/s, the frequency of this standing wave must be
6. A
In general, sound travels faster through solids than through gases. Therefore, when the wave enters the air from the metal rod, its speed will decrease. The frequency, however, will not change. Since v = λf must always be satisfied, a decrease in v implies a decrease in λ.
7. A
The distance from S2 to P is 5 m (it’s the hypotenuse of 3-4-5 triangle), and the distance from S1 to P is 4 m. The difference between the path lengths to Point P is 1 m, which is half the wavelength. Therefore, the sound waves are always exactly out of phase when they reach Point P from the two speakers, causing destructive interference there. By contrast, since Point Q is equidistant from the two speakers, the sound waves will always arrive in phase at Q, interfering constructively. Since there is destructive interference at P and constructive interference at Q, the amplitude at P will be less than at Q.
8. B
An air column (such as an organ pipe) with one closed end resonates at frequencies given by the equation fn = nv/(4L) for odd integers n. The fundamental frequency corresponds, by definition, to n = 1. Therefore,
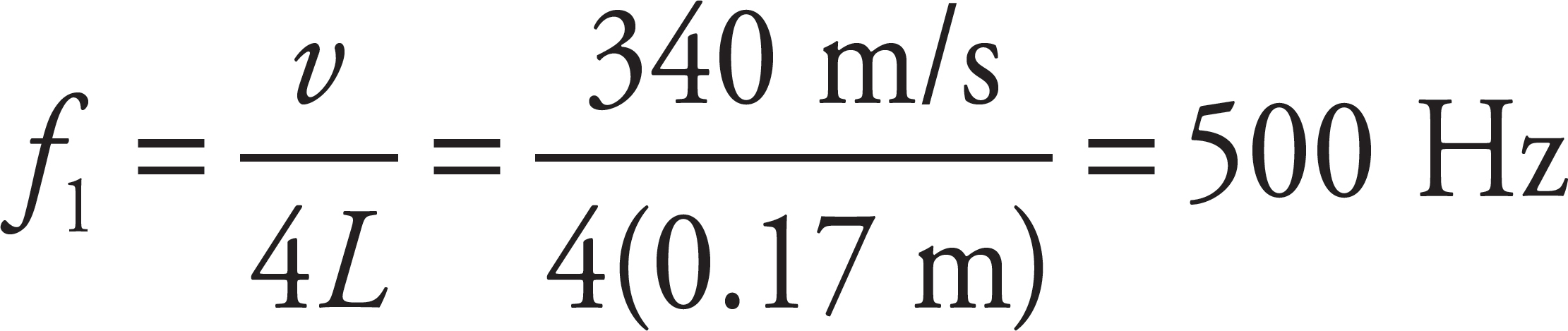
9. B
The speed of the chirp is
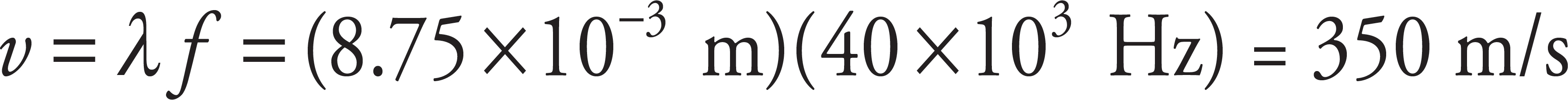
If the distance from the bat to the tree is d, then the wave travels a total distance of d + d = 2d (round-trip distance). If T is the time for this round-trip, then
10. C
The degree to which the Doppler effect alters a wave’s frequency is based on the relative motion between the wave’s source and detector. In this case, the relative motion between the objects in the answer choices is 10 m/s, 15 m/s, 20 m/s, and 0 m/s. Therefore, the scenario in (C) will have the greatest difference between the source and detector.
1. (a)
The speed of a transverse traveling wave on a stretched rope is given by the equation v = 
. Therefore,
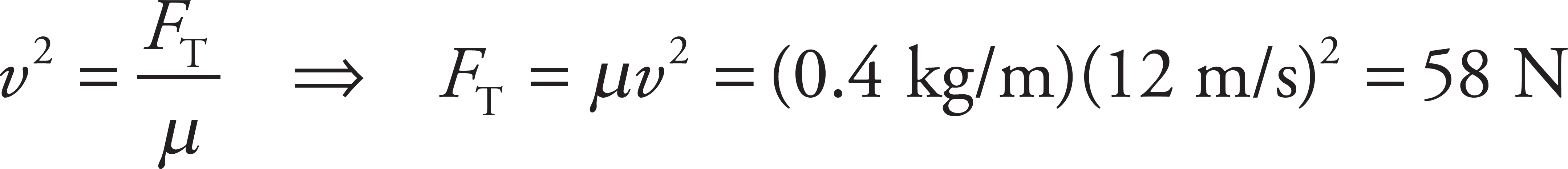
(b)
Use the fundamental equation λf = v:
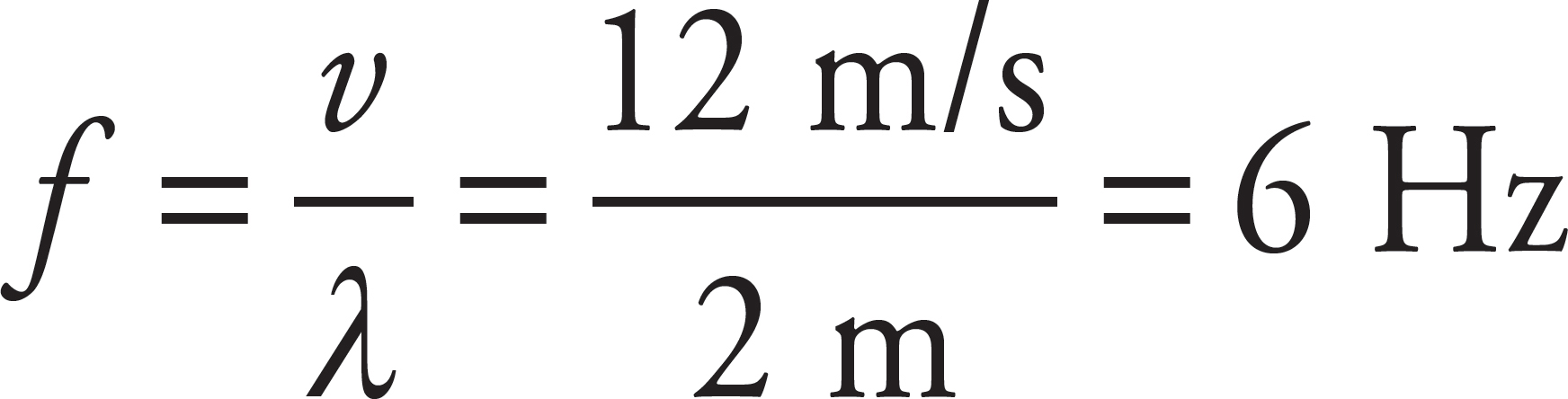
(c)
(i) Because higher harmonic numbers correspond to shorter wavelengths, the harmonic number of the 3.2 m standing wave must be higher than that of the 4 m standing wave. You’re told that these harmonic numbers are consecutive integers, so if n is the harmonic number of the 4 m standing wave, then n + 1 is the harmonic number of the 3.2 m wave. Therefore,
The first equation says that 2L = 4n, and the second one says that 2L = 3.2(n + 1). Therefore, 4n must equal 3.2(n + 1); solving this equation gives n = 4. Substituting this into either one of the displayed equations then gives L = 8 m.
(ii) Because μ = 0.4 kg/m, the mass of the rope must be
m = μL = (0.4 kg/m)(8 m) = 3.2 kg
(d)
You determined this in the solution to part (c) (i). The 4 m standing wave has harmonic number n = 4.
(e)
2. (a)
For a stationary observer and a source moving away, the Doppler effect equation predicts that
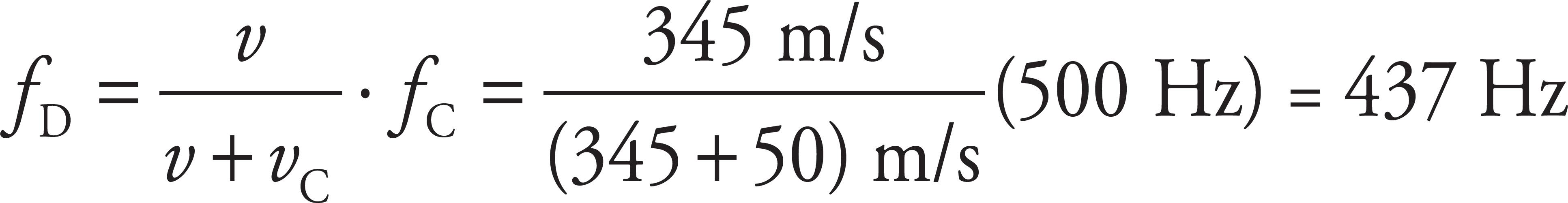
Because the objects are moving farther apart, you know that the detected frequency must be less than the source frequency. That’s how you know to use addition in the denominator.
(b)
Yes. If the source is stationary and the observer moves away, the Doppler effect equation now gives
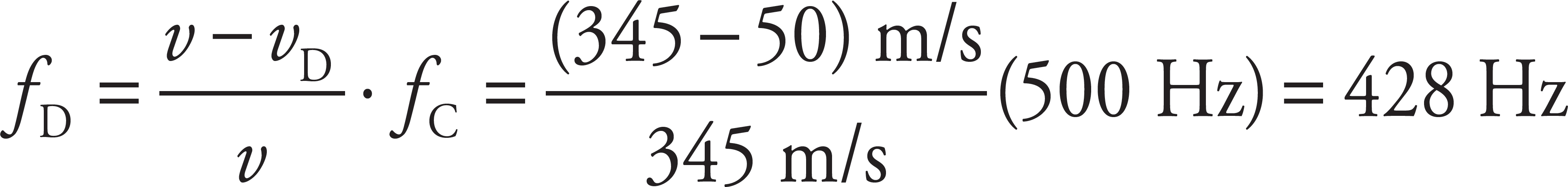
Similar to the reasoning used in part (a), you know to use subtraction in the numerator because the detected frequency must be less than the source frequency, since the objects are once again getting farther apart.
(c)
Since θ = 60°, the given equation becomes
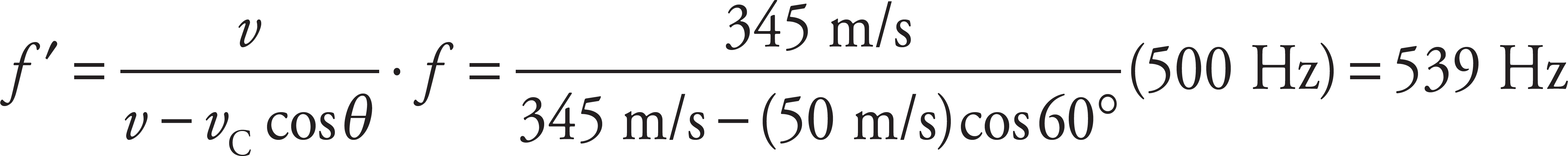
Note that the observed frequency is higher than the source frequency, which you can expect since the car is traveling toward the students.
(d)
With θ = 120°, the given equation becomes
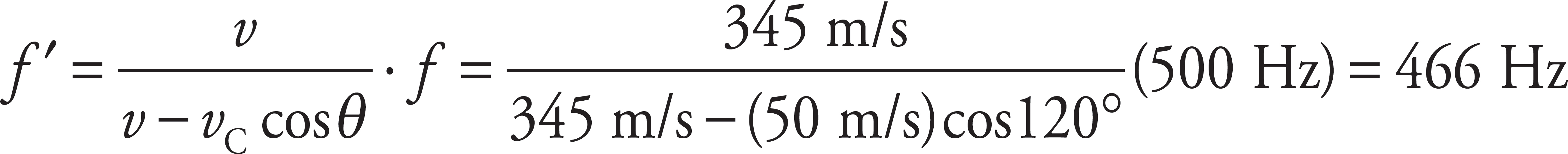
Note that the observed frequency is now lower than the source frequency, which you can expect since the car is traveling away from the students.
(e)
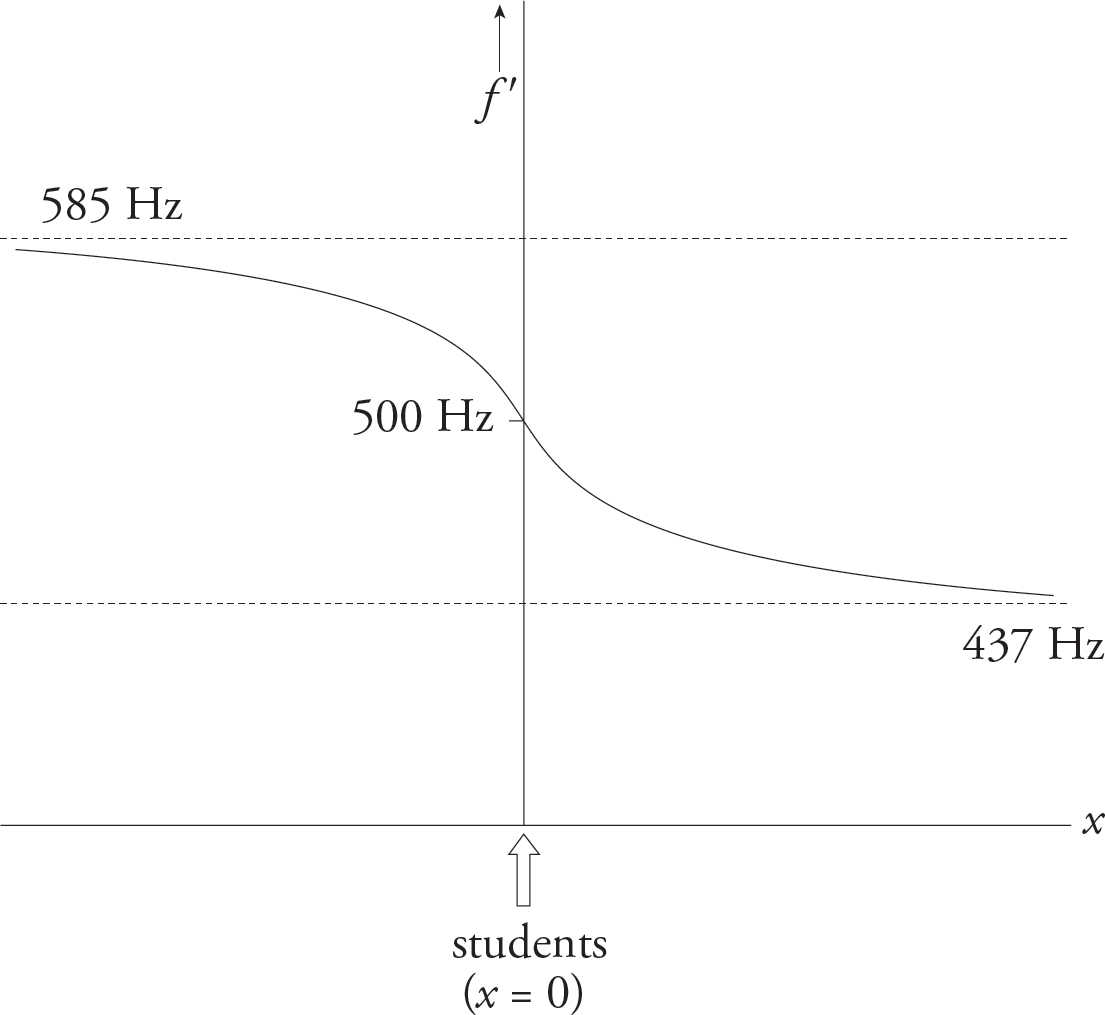
When the car is far to the left of the students’ position, θ is very small (approaches 0°). Therefore, for large negative x, the observed frequency should approach
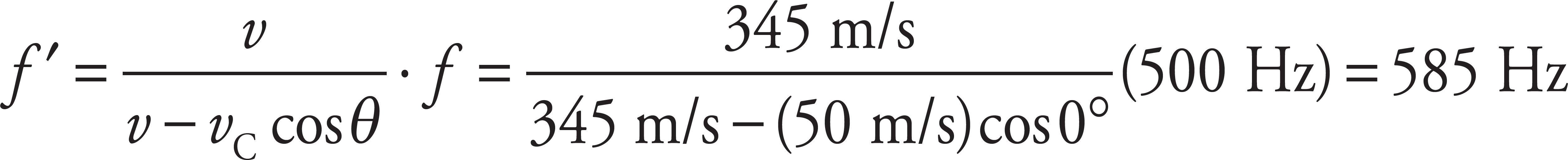
When the car is far to the right of the students’ position, θ approaches 180°. Therefore, for large positive x, the observed frequency should approach
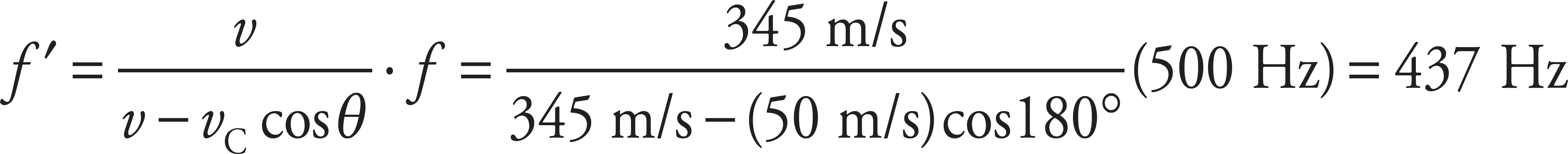
When the car is directly in front of the students—that is, when x = 0 (and θ = 90°)—the equation given predicts that f′ will equal 500 Hz. The graph of f′ versus x should therefore have the following general shape:
3. (a)
Use the equation for the beat frequency:
fbeat = |f1 − f2| = |400 Hz − 440 Hz| = 40 Hz
(b) As sound travels from air into water, the speed of sound will increase as sound travels faster in liquids than in gases (recall the equation v =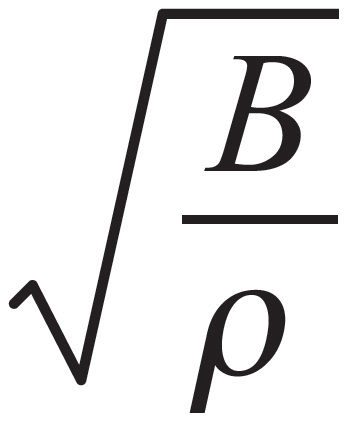 
). By Wave Rule #2, when a wave passes into another medium, its speed changes but its frequency does not. By the equation v = fλ, it can be observed that if speed increases and frequency does not change, then the wavelength must increase.
(c) As the sound source (tuning fork) is traveling toward the stationary detector (the student on the second floor), the observed frequency will be higher than the source frequency. However, the question is asking what happens to the observed frequency as the tuning fork travels upward. Due to acceleration from gravity, the speed of the tuning fork as it moves up will decrease. As the relative speed between the source and detector is decreasing, the impact of the Doppler effect will decrease. This will lead to a decrease in the observed frequency as the tuning fork travels upward (although the observed frequency will still be higher than the source frequency).
1. D
Electrostatic force obeys an inverse-square law: FE ∝ 1/r2. Therefore, if r increases by a factor of 3, then FE decreases by a factor of 32 = 9.
2. C
The strength of the electric force is given by kq2/r2, and the strength of the gravitational force is Gm2/r2. Since both of these quantities have r2 in the denominator, you simply need to compare the numerical values of kq2 and Gm2. There’s no contest. Since
kq2 = (9 × 109 N·m2/C2)(1 C)2 = 9 × 109 N·m2
and
Gm2 = (6.7 × 10−11 N·m2/kg2)(1 kg)2 = 6.7 × 10−11 N·m2
you can see that kq2 > Gm2, so FE is much stronger than FG.
3. C
If the net electric force on the center charge is zero, the electrical repulsion by the +2q charge must balance the electrical repulsion by the +3q charge:
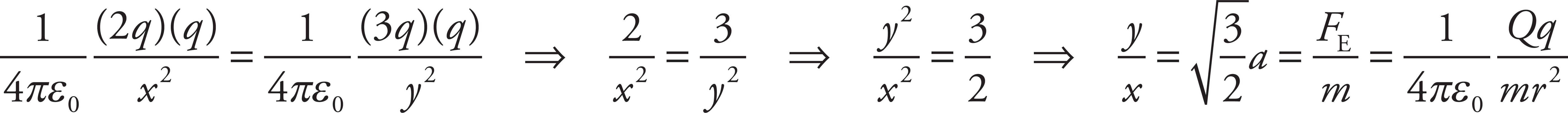
4. D
Since P is equidistant from the two charges, and the magnitudes of the charges are identical, the strength of the electric field at P due to +Q is the same as the strength of the electric field at P due to −Q. The electric field vector at P due to +Q points away from +Q, and the electric field vector at P due to −Q points toward − Q. Since these vectors point in the same direction, the net electric field at P is (E to the right) + (E to the right) = (2E to the right).
5. C
The acceleration of the small sphere is
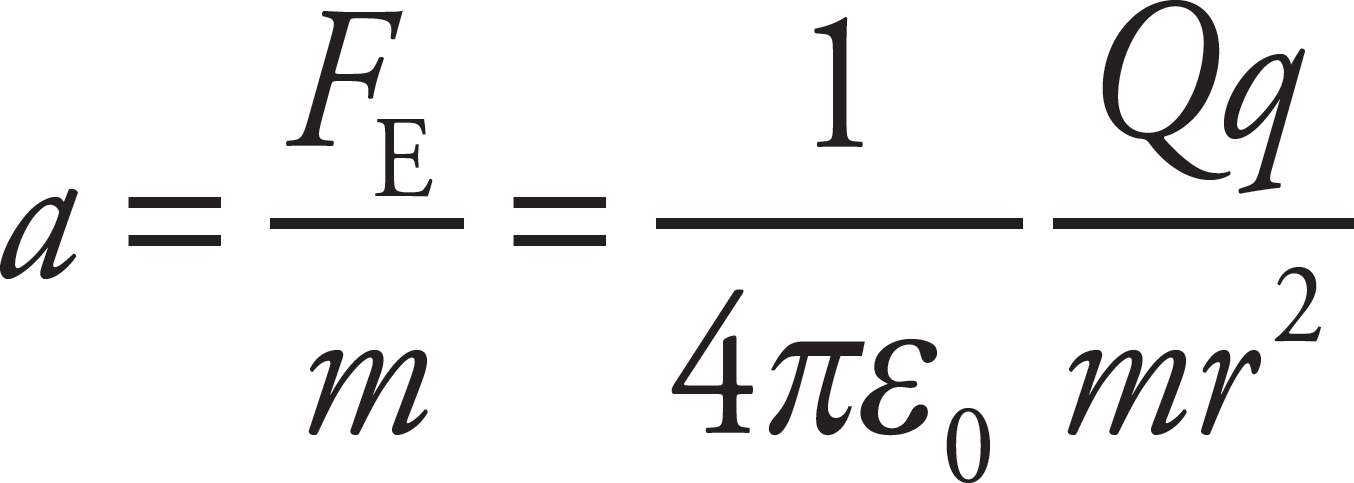
As r increases (that is, as the small sphere is pushed away), a decreases. However, since a is always positive, the small sphere’s speed, v, is always increasing.
6. B
Since FE (on q) = qE, it must be true that FE (on −2q) = −2qE = −2FE.
7. C
All excess electric charge on a conductor resides on the outer surface.
8. D
Use Coulomb’s Law to solve for r,
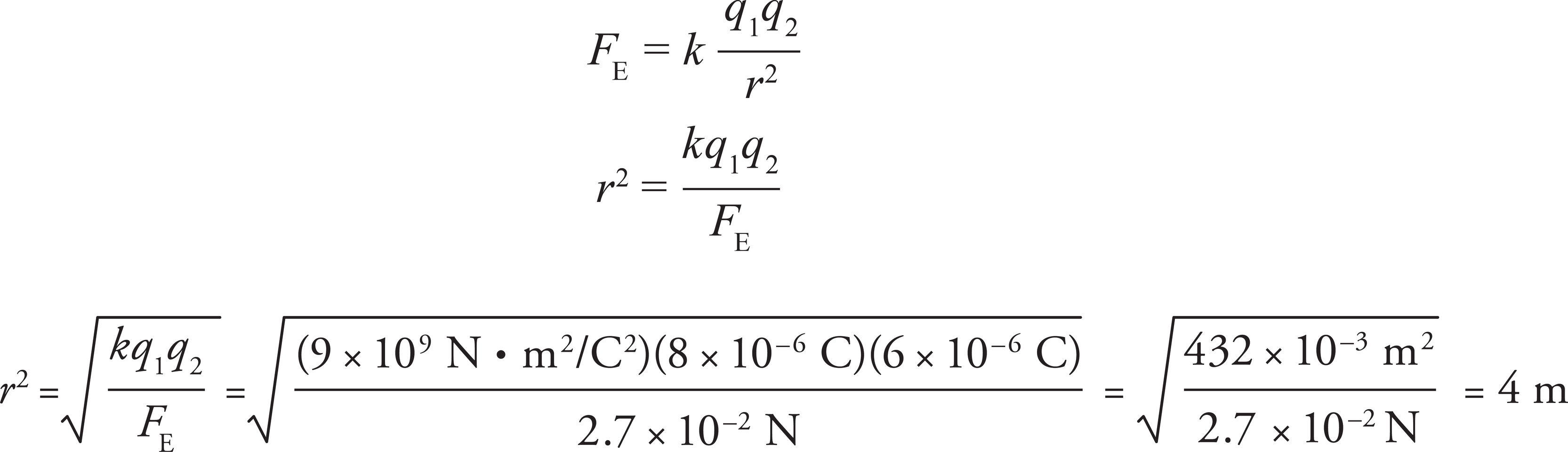
9. C
FG and FE are both proportional to 1/r2. Increasing the distance between the charges by a factor of 3 will reduce the magnitude of both forces by a factor of 9, but the ratio of FG/FE will remain the same.
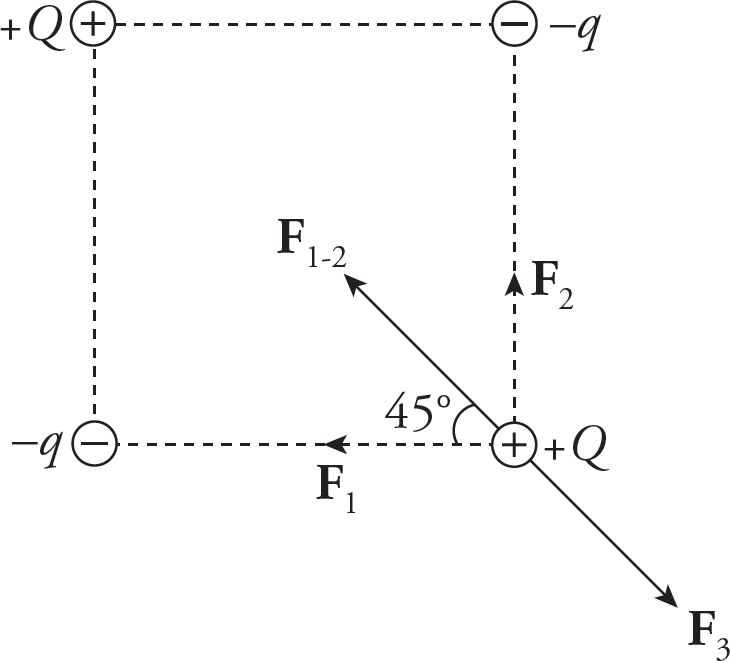
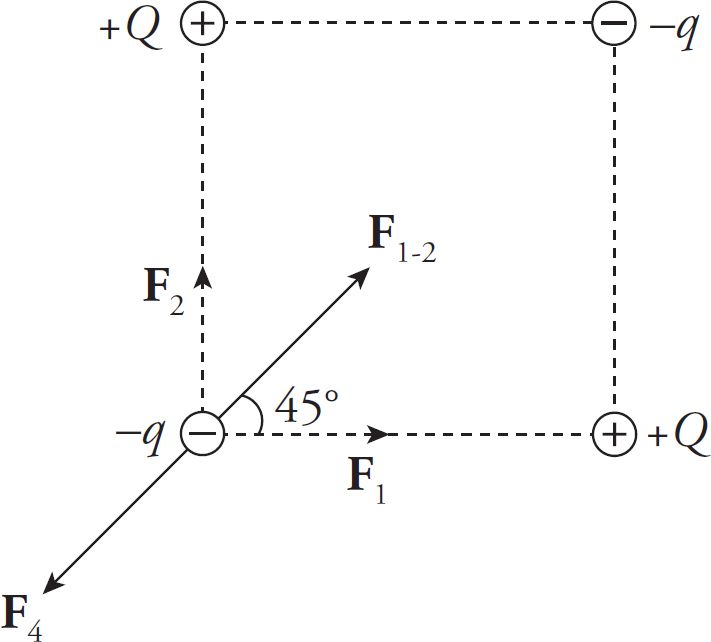
1. (a)
From the figure below, you have F1-2 = F1/cos 45°.
Since the net force on +Q is zero, you want F1-2 = F3. If s is the length of each side of the square, then:
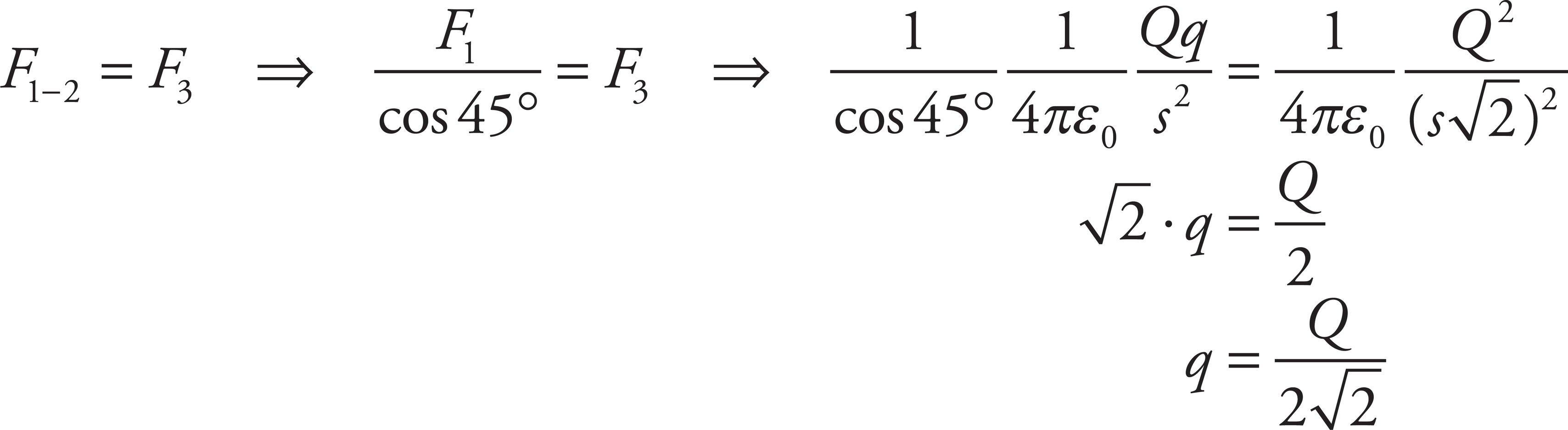
(b)
No. If q = Q/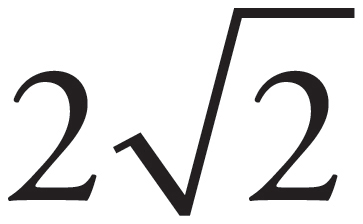
, as found in part (a), then the net force on −q is not zero.
This is because F1-2 ≠ F4, as the following calculations show:
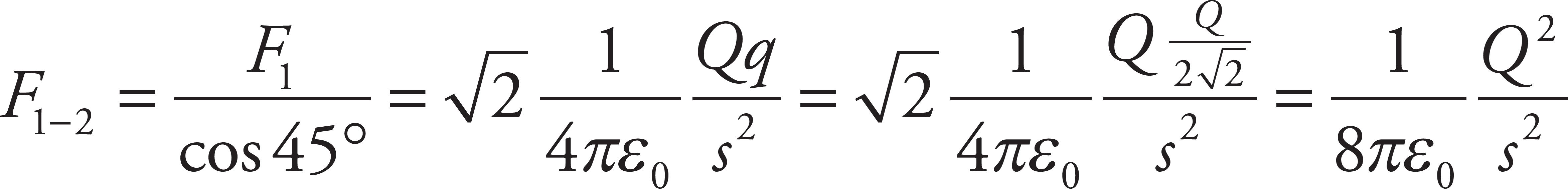
but
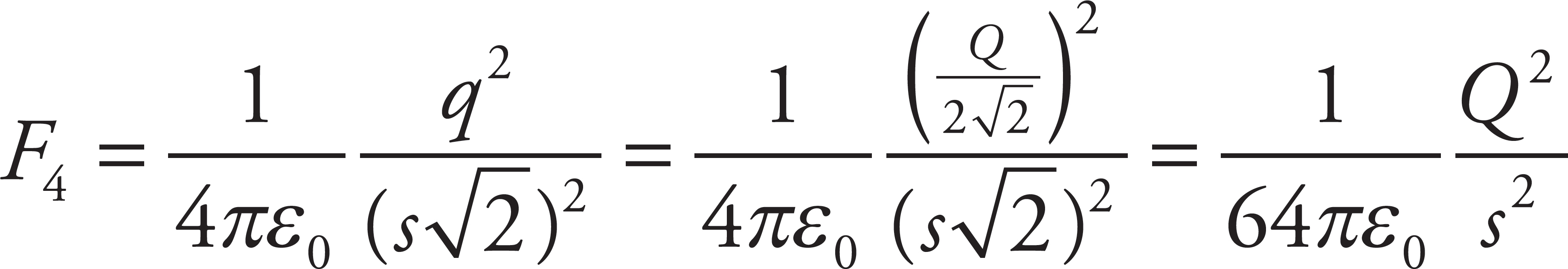
(c)
By symmetry, E1 = E2 and E3 = E4, so the net electric field at the center of the square is zero:
2. (a)
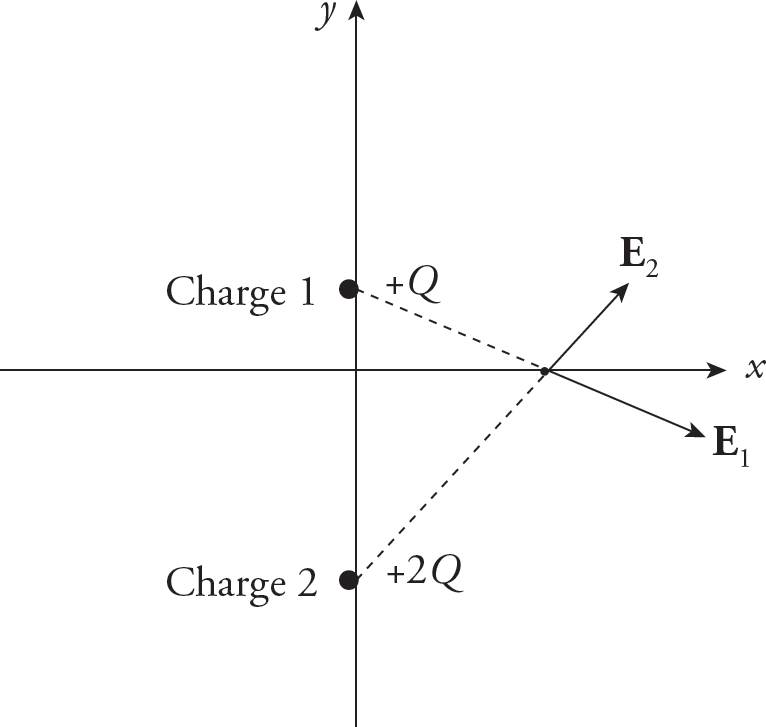
The magnitude of the electric force on Charge 1 is
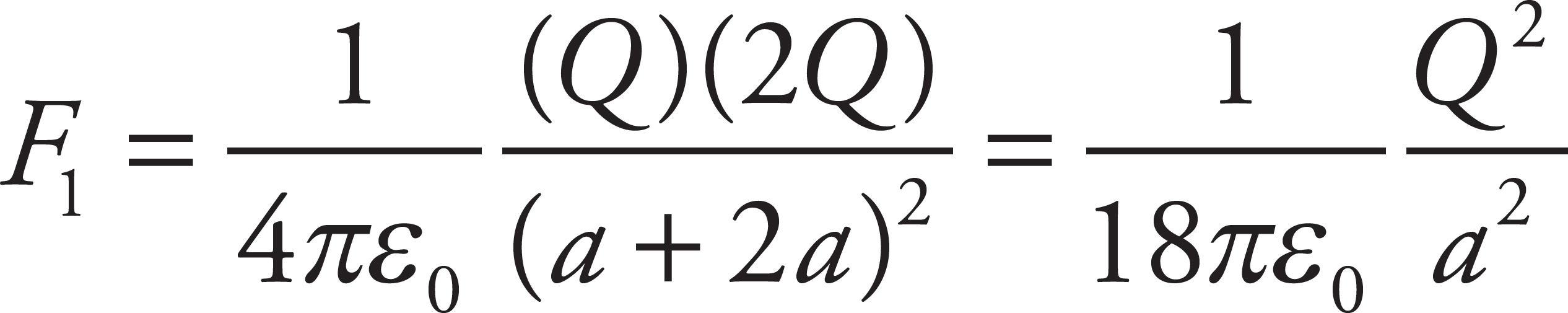
The direction of F1 is directly away from Charge 2; that is, in the +y direction, so
(b)
The electric field vectors at the origin due to Charge 1 and due to Charge 2 are
Therefore, the net electric field at the origin is
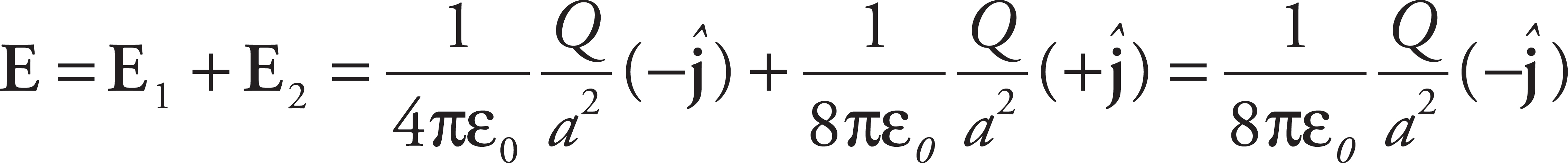
(c)
No. The only point on the x-axis where the individual electric field vectors due to each of the two charges point in exactly opposite directions is the origin (0, 0). But at that point, the two vectors are not equal and thus do not cancel.
Therefore, at no point on the x-axis could the total electric field be zero.
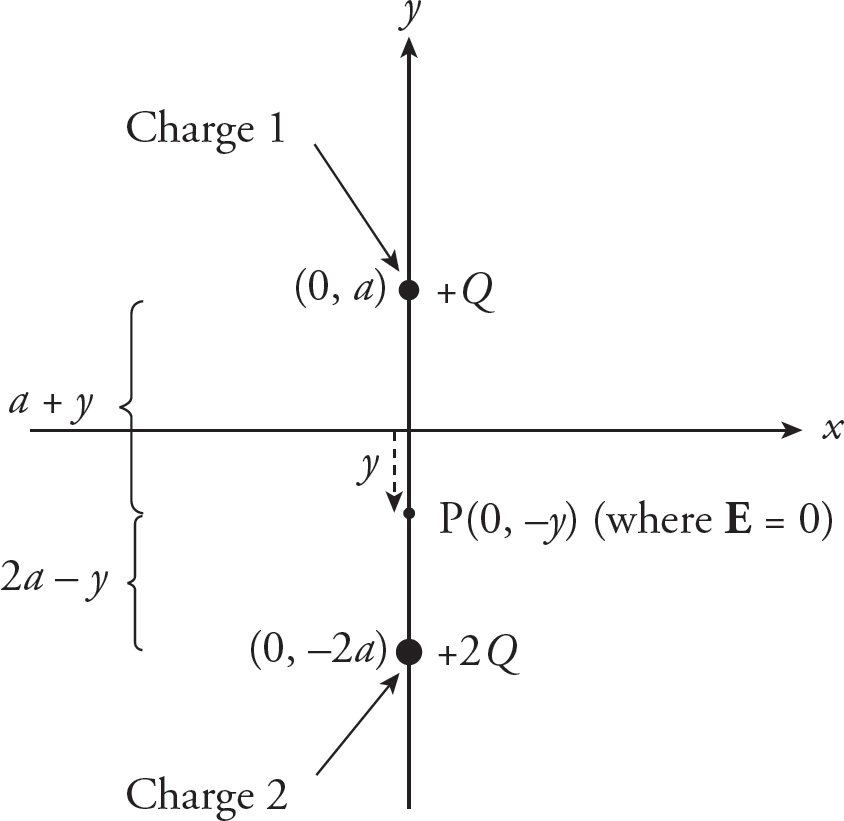
(d)
Yes. There will be a Point P on the y-axis between the two charges,
where the electric fields due to the individual charges will cancel each other out.
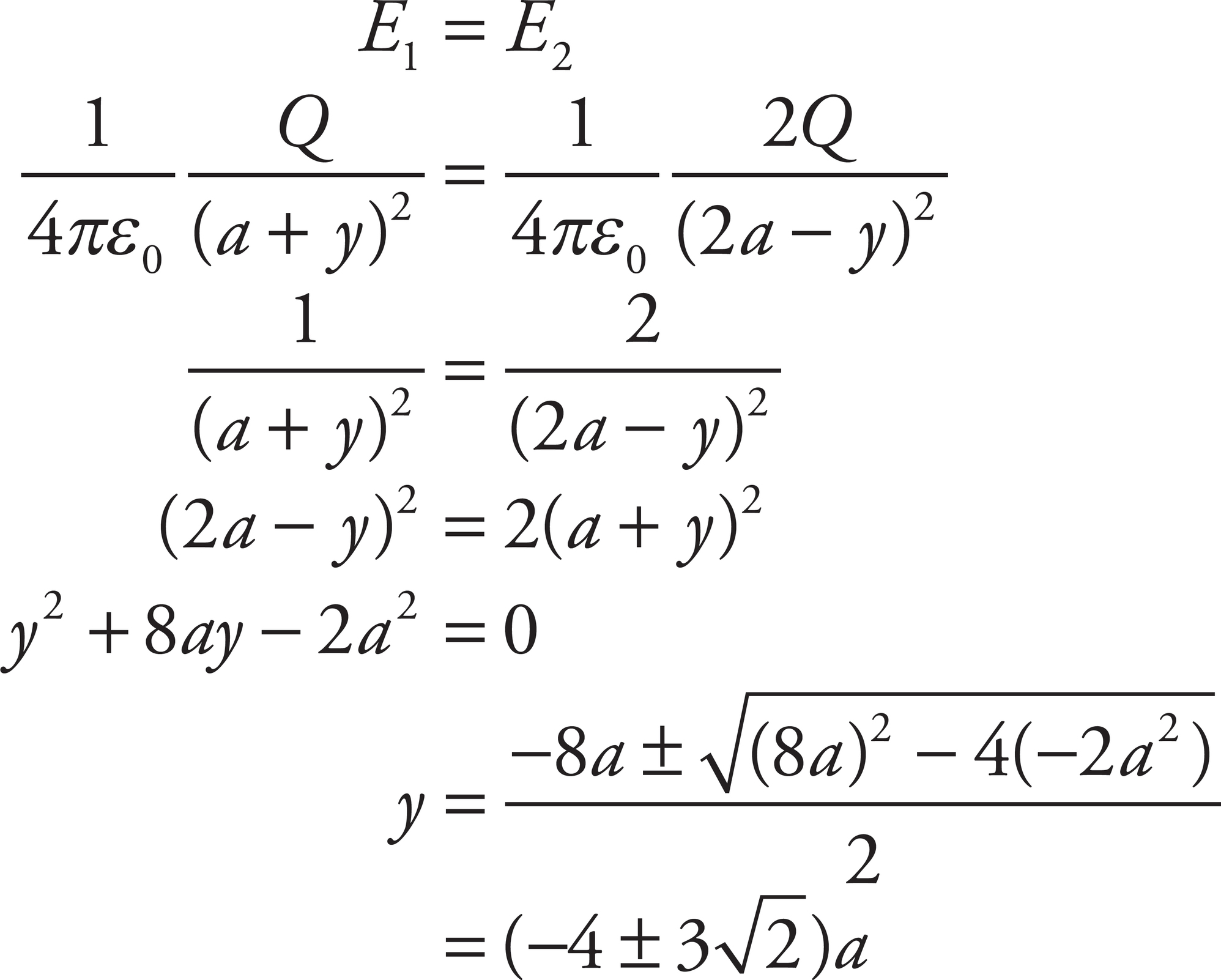
Disregarding the value y =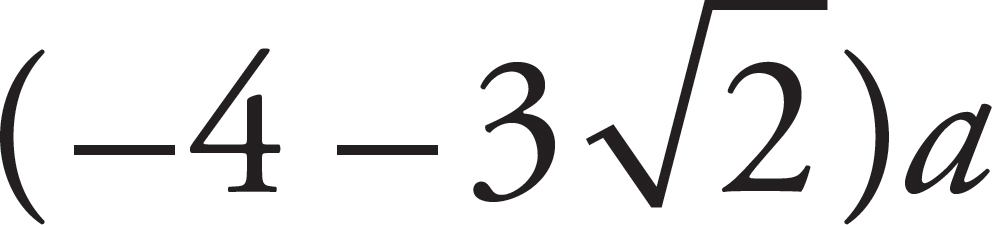 
(because it would place the Point P below Charge 2 on the y-axis, where the electric field vectors do not point in opposite directions), you find that E = 0 at the Point P = (0, −y) = (0, 
).
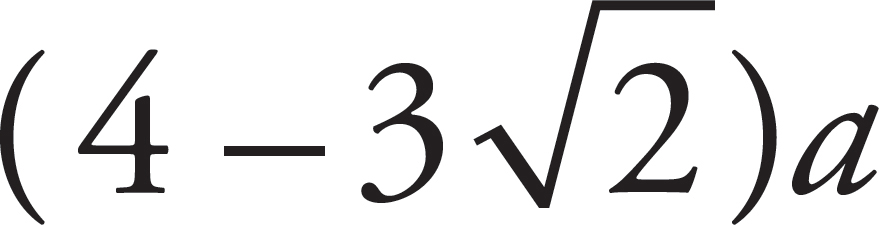(e)
Use the result of part (b) with Newton’s Second Law:
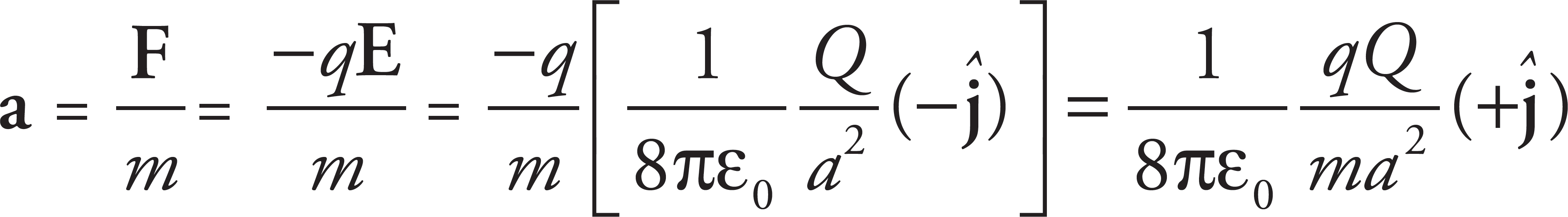
3. (a)
Using the superposition principle, the electric field at the point (0, 4) is equal to the sum of the electric fields from q1 and q2.
E = Eq1 + Eq2
The magnitude of the horizontal and vertical components of the electric field at this point is then the sum of the individual horizontal and vertical components from q1 and q2.
Ex = Eq1, x + Eq2, x
Ey = Eq1, y + Eq2, y
As electric fields point away from the positive charges, the electric field due to q1 points upward in the vertical direction and has no horizontal component. The distance between q1 and the point (0, 4) is r1 = 7 m. The electric field from q2 points northwest, making a 45 degree angle with the horizontal from the point (0, 4), and has both a horizontal and vertical component. Using the Pythagorean Theorem, the distance between q2 and the point (0, 4) is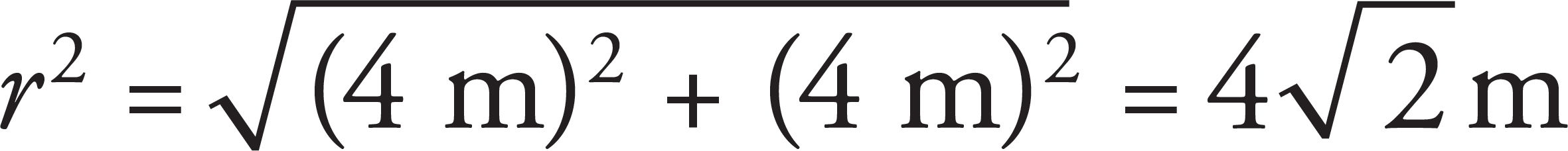 
.
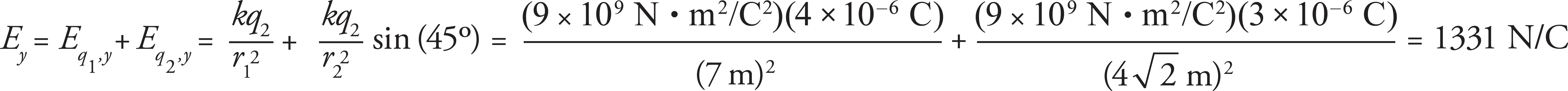
(b)
When a charge is placed at a point with an electric field, the electric force felt by the charge is equal to the product of the charge and the electric field at that point.
FE = qE
To determine the magnitude of the horizontal and vertical components of the electric field, plug in the horizontal and vertical components of the electric field at the point solved in (a).
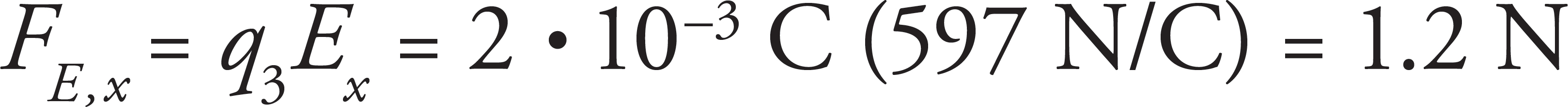
(Note that the sign of q3 is excluded, as it does not affect the magnitude of the electric force.)
(c)
In order for the electric field at the point (0, 4) to equal 0, the electric field produced by q4 must be equal in magnitude but opposite in sign to the electric field produced from q1 and q2. As the electric field produced by q1 points north and the electric field produced by q2 points northwest, the electric field produced by q4 must have a vertical component that points south and a horizontal component that points east. As electric fields point away from positive charges, this is possible only if q4 is to the north and west of the point (0, 4). The only points that fit this criterion are in Quadrant II.
1. C
The equation I = V/R implies that increasing V by a factor of 2 will cause I to increase by a factor of 2.
2. C
Use the equation P = V2/R:
3. B
The formula for calculating resistance is
R = ρL/A
Because resistance is inversely proportional to the cross-sectional area, (B) is correct. Choices (A) and (D) would have the opposite effect, and (C) is incorrect because density and resistance do not have any correlation.
4. D
The 12 Ω and 4 Ω resistors are in parallel and are equivalent to a single 3 Ω resistor, because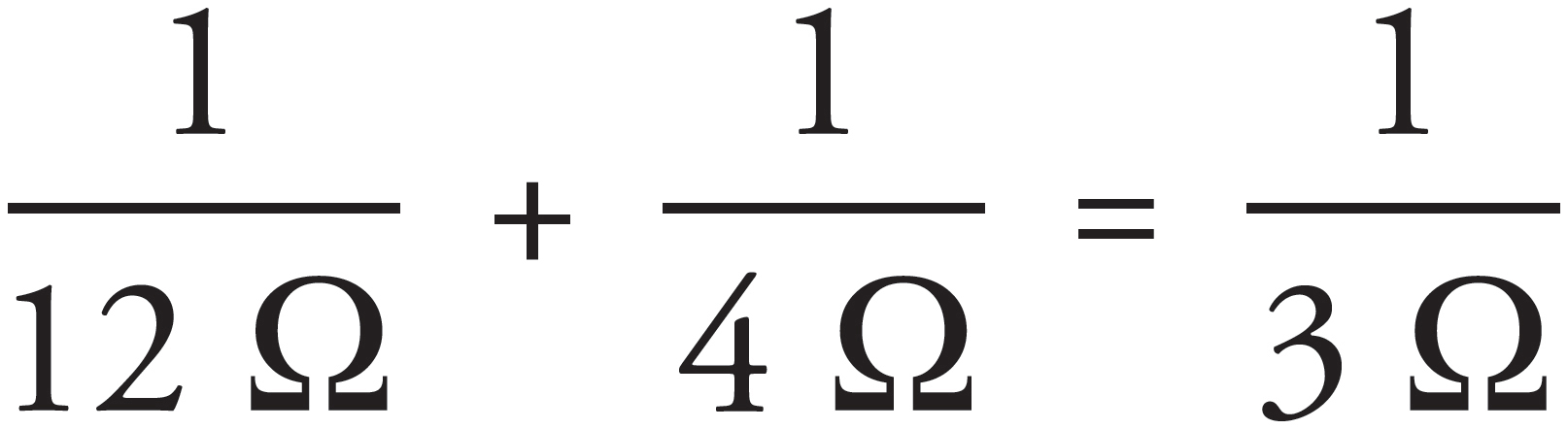 
. This 3 Ω resistor is in series with the top 3 Ω resistor, giving an equivalent resistance in the top branch of 3 + 3 = 6 Ω. Finally, this 6 Ω resistor is in parallel with the bottom 3 Ω resistor, giving an overall equivalent resistance of 2 Ω, because 
.
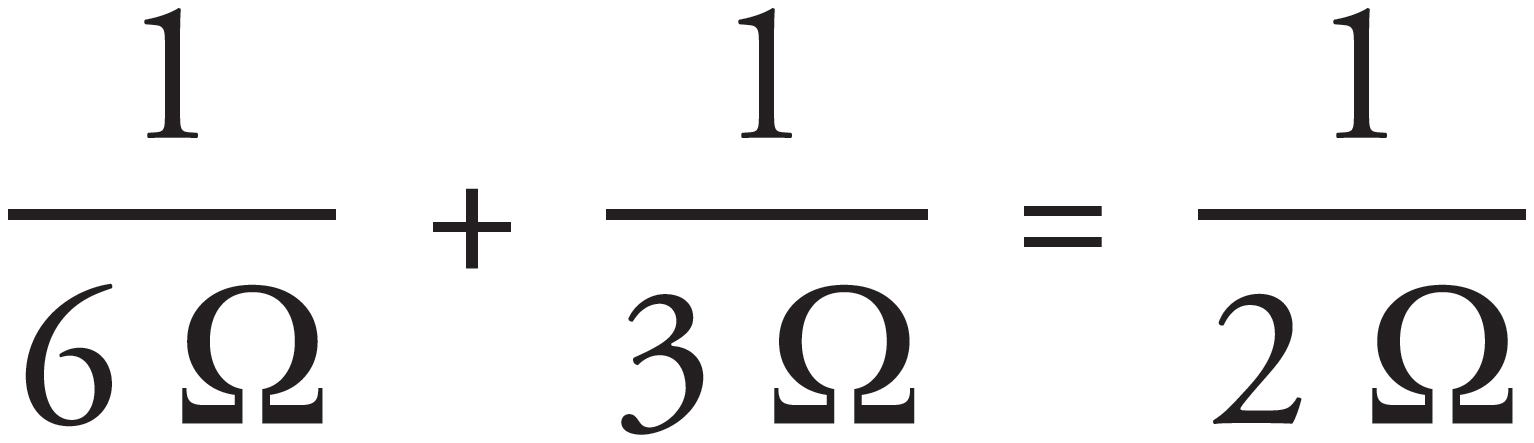5. C
If each of the identical bulbs has resistance R, then the current through each bulb is ε/R. This is unchanged if the middle branch is taken out of the parallel circuit. (What will change is the total amount of current provided by the battery.)
6. B
The three parallel resistors are equivalent to a single 2 Ω resistor, because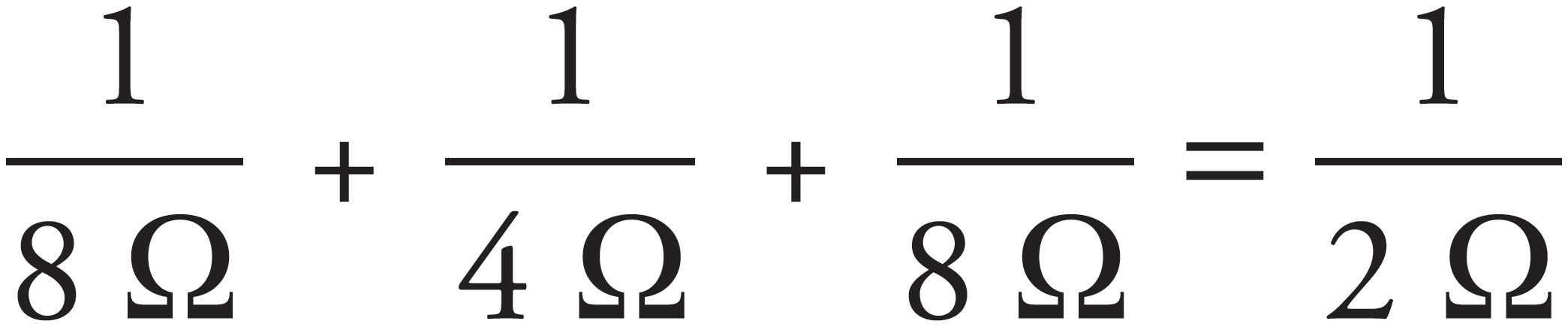 
. This 2 Ω resistance is in series with the given 2 Ω resistor, so their equivalent resistance is 2 + 2 = 4 Ω. Therefore, three times as much current will flow through this equivalent 4 Ω resistance in the top branch as through the parallel 12 Ω resistor in the bottom branch, which implies that the current through the bottom branch is 3 A, and the current through the top branch is 9 A. The voltage drop across the 12 Ω resistor is therefore V = IR = (3 A)(12 Ω) = 36 V.
7. D
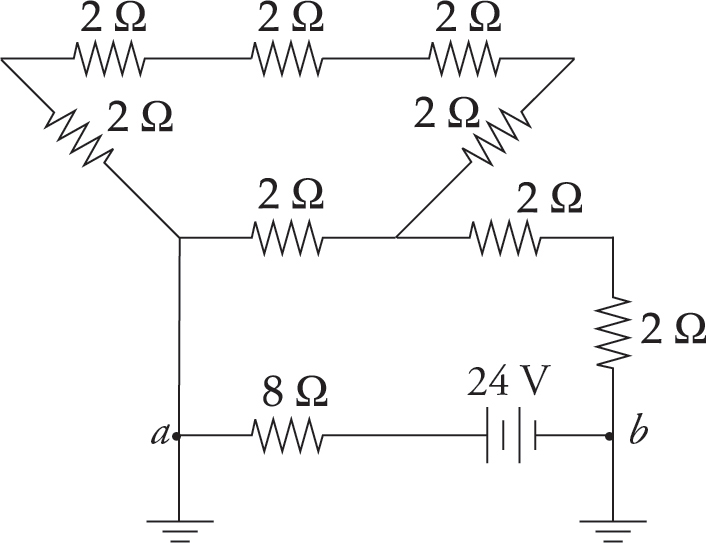
Since points a and b are grounded, they’re at the same potential (call it zero).
Traveling from b to a across the battery, the potential increases by 24 V, so it must decrease by 24 V across the 8 Ω resistor as you reach point a. Thus, I = V/R = (24 V)/(8 Ω) = 3 A.
8. D
The equation P = I2R gives
P = (0.5 A)2(100 Ω) = 25 W = 25 J/s
Therefore, in 20 s, the energy dissipated as heat is
E = Pt = (25 J/s)(20 s) = 500 J
9. C
As the resistance of resistors in series is additive, the addition of a fourth resistor (light bulb) in series will increase the total resistance of the circuit. As the voltage source (battery) is unchanged, this will lead to a decrease in the current supplied by the battery according to the equation V = IR.
1. (a)
The two parallel branches, the one containing the 40 Ω resistor and the other a total of 120 Ω, is equivalent to a single 30 Ω resistance. This 30 Ω resistance is in series with the three 10 Ω resistors, giving an overall equivalent circuit resistance of 10 + 10 + 30 + 10 = 60 Ω. Therefore, the current supplied by the battery is I = V/R = (120 V)/(60 Ω) = 2 A, so it must supply energy at a rate of P = IV = (2 A)(120 V) = 240 W.
(b)
Since three times as much current will flow through the 40 Ω resistor as through the branch containing 120 Ω of resistance, the current through the 40 Ω resistor must be 1.5 A.
(c)
(i) Va − Vb = IR20 + IR100 = (0.5 A)(20 Ω) + (0.5 A)(100 Ω) = 60 V.
(ii) Point a is at the higher potential (current flows from high to low potential).
(b)
Because energy is equal to power multiplied by time, you get
E = Pt = I2Rt = (0.5 A)2(100 Ω)(10 s) = 250 J
2. (a)
There are many ways to solve this problem. If you notice that each of the three branches of the parallel section is 60 Ω, then they must all have the same current flowing through them. The currents through the 20 Ω, 40 Ω, and other 60 Ω resistor are all 0.5 A.
If you had not noticed this, you would have used Ohm’s Law to determine the voltage across the resistors and proceeded from there (see part b below). Because 0.5 A goes through each of the three pathways, Kirchhoff’s Junction Rule tells you that the current that must have come though the 10 Ω resistor is 1.5 A.
(b)
The voltage across the 60 Ω resistor is given by Ohm’s Law. Because V = IR, V = (0.5 A)(60 Ω) = 30 V. All three parallel branches must have the same voltage across them, so the other 60 Ω resistor also has 30 V across it and the combination of the 20 Ω and 40 Ω resistor must also be 30 V. To determine the voltage across the 20 Ω and 40 Ω resistor you can rely on the previously solved currents of 0.5 A and Ohm’s Law to yield V = IR = (0.5 A)(20 Ω) = 10 V and V = (0.5A)(40 Ω) = 20 V.
You also could have used the ratio of the resistors. That is, you know the two voltages must sum to 30 V and the voltage drop across the 40 Ω must be twice the amount across the 20 Ω. The voltage across the 10 Ω resistor can be found using Ohm’s Law: V = (1.5 A)(10 Ω) = 15 V.
(c)
The equivalent resistance of the circuit can be solved either by adding the resistances or by using Ohm’s Law.
If you want to add resistances, start by summing the 20 Ω and 40 Ω resistors to get 60 Ω. Then add the three parallel branches using 
or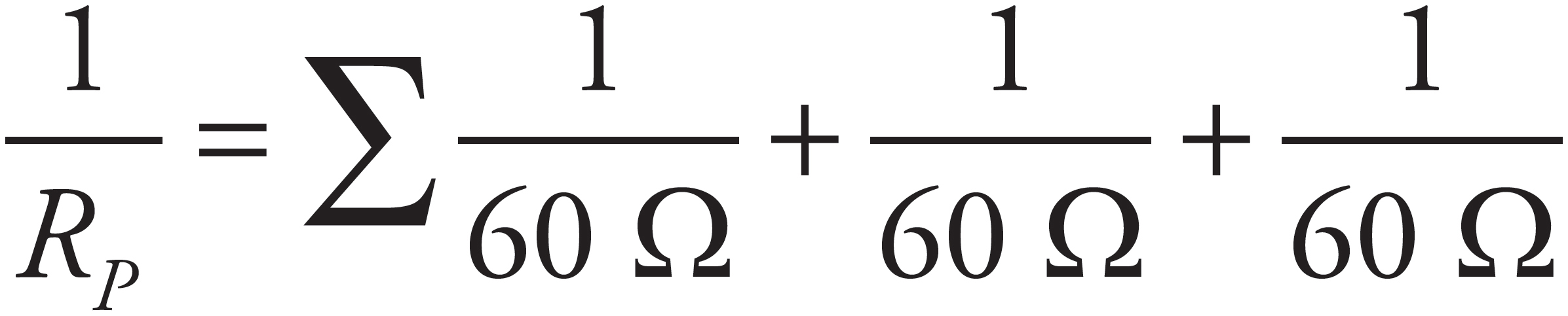 
, which becomes 20 Ω. Then add this section in series to the 10 Ω resistor to get Rp = R1 + R2 = 10 Ω + 20 Ω = 30 Ω.
You could have also realized that the total voltage drop across the battery is 45 V (15 V across the 10 Ω resistor and 30 V across the parallel branch). Use Ohm’s Law again to get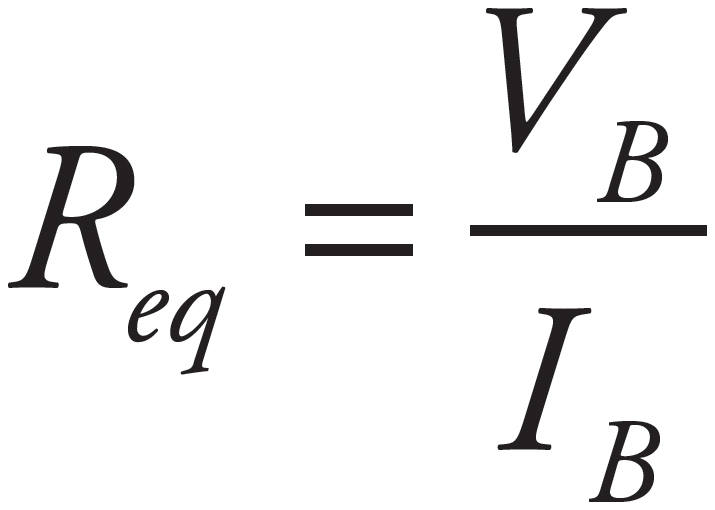 
or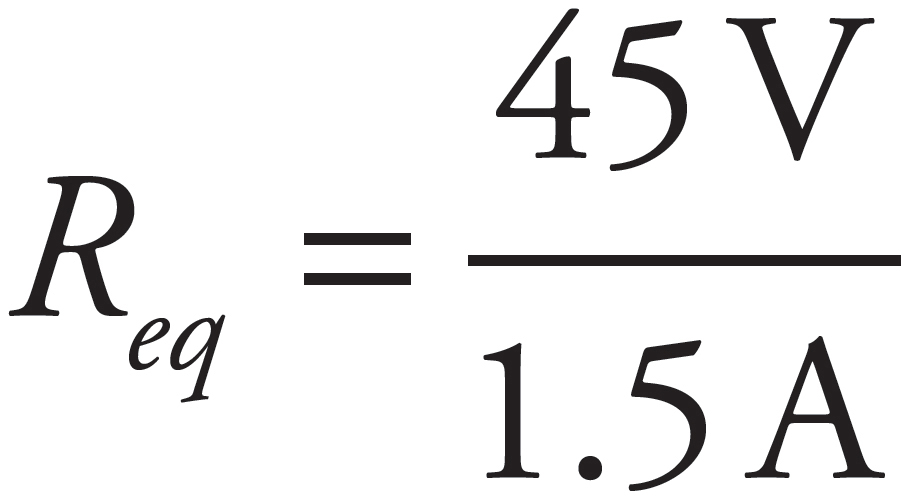 
= 30 Ω.
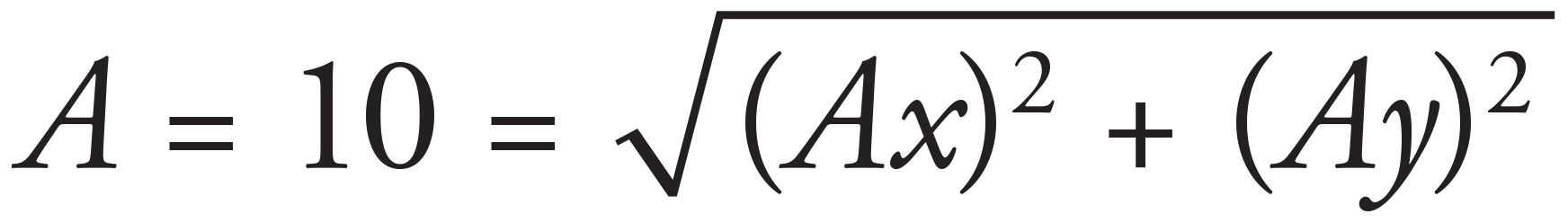
