
“You mean I have to go again tomorrow?” —Aidan Farrell after the first day of school

Most people think of doing arithmetic when they think of math: adding, subtracting, multiplying, and dividing. Although doing arithmetic is pretty easy using calculators and computers, it can still involve a lot of repetitive tasks. For example, to add 20 different numbers using a calculator, you have to enter the + operator 19 times!
In this chapter you learn how to automate some of the tedious parts of arithmetic using Python. First, you learn about math operators and the different data types you can use in Python. Then you learn how to store and calculate values using variables. You also learn to use lists and loops to repeat code. Finally, you combine these programming concepts to write functions that automatically perform complicated calculations for you. You’ll see that Python can be a much more powerful calculator than any calculator you can buy—and best of all, it’s free!
Doing arithmetic in the interactive Python shell is easy: you just enter the expression and press ENTER when you want to do the calculation. Table 2-1 shows some of the most common mathematical operators.
Table 2-1: Common Mathematical Operators in Python
Operator |
Syntax |
Addition |
+ |
Subtraction |
– |
Multiplication |
* |
Division |
/ |
Exponent |
** |
Open your Python shell and try out some basic arithmetic with the example in Listing 2-1.
>>> 23 + 56 #Addition
79
>>> 45 * 89 #Multiplication is with an asterisk
4005
>>> 46 / 13 #Division is with a forward slash
3.5384615384615383
>>> 2 ** 4 #2 to the 4th power
16
Listing 2-1: Trying out some basic math operators
The answer should appear as the output. You can use spaces to make the code more readable (6 + 5) or not (6+5), but it won’t make any difference to Python when you’re doing arithmetic.
Keep in mind that division in Python 2 is a little tricky. For example, Python 2 will take 46/13 and think you’re interested only in integers, thus giving you a whole number (3) for the answer instead of returning a decimal value, like in Listing 2-1. Because you downloaded Python 3, you shouldn’t have that problem. But the graphics package we’ll see later uses Python 2, so we’ll have to make sure we ask for decimals when we divide.
You can also use operators on variables. In Chapter 1 you learned to use variables when defining a function. Like variables in algebra, variables in programming allow long, complicated calculations to be broken into several stages by storing results that can be used again later. Listing 2-2 shows how you can use variables to store numbers and operate on them, no matter what their value is.
>>> x = 5
>>> x = x + 2
>>> length = 12
>>> x + length
19
Listing 2-2: Storing results in variables
Here, we assign the value 5 to the x variable, then increment it by 2, so x becomes 7. We then assign the value 12 to the variable length. When we add x and length, we’re adding 7 + 12, so the result is 19.
Let’s practice using operators to find the mean of a series of numbers. As you may know from math class, to find the mean you add all the numbers together and divide them by how many numbers there are in the series. For example, if your numbers are 10 and 20, you add 10 and 20 and divide the sum by 2, as shown here:
(10 + 20) / 2 = 15
If your numbers are 9, 15, and 23, you add them together and divide the sum by 3:
(9 + 15 + 23) / 3 = 47 / 3 = 15.67
This can be tedious to do by hand but simple to do with code. Let’s start a Python file called arithmetic.py and write a function to find the average of two numbers. You should be able to run the function and give it two numbers as arguments, without any operators, and have it print the average, like this:
>>> average(10,20)
15.0
Let’s give it a try.
Our average() function transforms two numbers, a and b, into half their sum and then returns that value using the return keyword. Here’s the code for our function:
arithmetic.py
def average(a,b):
return a + b / 2
We define a function called average(), which requires two numbers, a and b, as inputs. We write that the function should return the sum of the two numbers divided by 2. However, when we test the function in the shell, we get the wrong output:
>>> average(10,20)
20.0
That’s because we didn’t take the order of operations into account when writing our function. As you probably remember from math class, multiplication and division take precedence over addition and subtraction, so in this case division is performed first. This function is dividing b by 2 and then adding a. So how do we fix this?
We need to use parentheses to tell Python to add the two numbers first, before dividing:
arithmetic.py
def average(a,b):
return (a + b) / 2
Now the function should add a and b before dividing by 2. Here’s what happens when we run the function in the shell:
>>> average(10,20)
15.0
If you perform this same calculation by hand, you can see the output is correct! Try the average() function using different numbers.
Before we continue doing arithmetic on numbers, let’s explore some basic Python data types. Different data types have different capabilities, and you can’t always perform the same operations on all of them, so it’s important to know how each data type works.
Two Python data types you commonly perform operations on are integers and floats. Integers are whole numbers. Floats are numbers containing decimals. You can change integers to floats, and vice versa, by using the float() and int() functions, respectively, like so:
>>> x = 3
>>> x
3
>>> y = float(x)
>>> y
3.0
>>> z = int(y)
>>> z
3
In this example we use x = 3 to assign the value 3 to the variable x. We then convert x into a float using float(x) and assign the result (3.0) to the variable y. Finally, we convert y into an integer and assign the result (3) to the variable z. This shows how you can easily switch between floats and ints.
Strings are ordered alphanumeric characters, which can be a series of letters, like words, or numbers. You define a string by enclosing the characters in single ('') or double quotes (""), like so:
>>> a = "hello"
>>> a + a
'hellohello'
>>> 4*a
'hellohellohellohello'
Here, we store the string "hello" in variable a. When we add variable a to itself, we get a new string, 'hellohello', which is a combination of two hellos. Keep in mind that you can’t add strings and number data types (integers and floats) together, though. If you try adding the integer 2 and the string "hello", you’ll get this error message:
>>> b = 2
>>> b
2
>>> d = "hello"
>>> b + d
Traceback (most recent call last):
File "<pyshell#34>", line 1, in <module>
b + d
TypeError: unsupported operand type(s) for +: 'int' and 'str'
However, if a number is a string (or enclosed in quotes), you can add it to another string, like this:
>>> b = '123'
>>> c = '4'
>>> b + c
'1234'
>>> 'hello' + ' 123'
'hello 123'
In this example both '123' and '4' are strings made up of numbers, not number data types. So when you add the two together you get a longer string ('1234') that is a combination of the two strings. You can do the same with the strings 'hello' and ' 123', even though one is made of letters and the other is made of numbers. Joining strings to create a new string is called concatenation.
You can also multiply a string by an integer to repeat the string, like this:
>>> name = "Marcia"
>>> 3 * name
'MarciaMarciaMarcia'
But you can’t subtract, multiply, or divide a string by another string. Enter the following in the shell to see what happens:
>>> noun = 'dog'
>>> verb = 'bark'
>>> noun * verb
Traceback (most recent call last):
File "<pyshell#6>", line 1, in <module>
noun * verb
TypeError: can't multiply sequence by non-int of type 'str'
As you can see, when you try to multiply 'dog' and 'bark', you get an error telling you that you can’t multiply two string data types.
Booleans are true/false values, which means they can be only one or the other and nothing in between. Boolean values have to be capitalized in Python and are often used to compare the values of two things. To compare values you can use the greater-than (>) and less-than (<) symbols, like so:
>>> 3 > 2
True
Because 3 is greater than 2, this expression returns True. But checking whether two values are equal requires two equal signs (==), because one equal sign simply assigns a value to a variable. Here’s an example of how this works:
>>> b = 5
>>> b == 5
True
>>> b == 6
False
First we assign the value 5 to variable b using one equal sign. Then we use two equal signs to check whether b is equal to 5, which returns True.
You can always check which data type you’re dealing with by using the type() function with a variable. Python conveniently tells you what data type the value in the variable is. For example, let’s assign a Boolean value to a variable, like this:
>>> a = True
>>> type(a)
<class 'bool'>
When you pass variable a into the type() function, Python tells you that the value in a is a Boolean.
Try checking the data type of an integer:
>>> b = 2
>>> type(b)
<class 'int'>
The following checks whether 0.5 is a float:
>>> c = 0.5
>>> type(c)
<class 'float'>
This example confirms that alphanumeric symbols inside quotes are a string:
>>> name = "Steve"
>>> type(name)
<class 'str'>
Now that you know the different data types in Python and how to check the data type of a value you’re working with, let’s start automating simple arithmetic tasks.
So far we’ve used variables to hold a single value. A list is a type of variable that can hold multiple values, which is useful for automating repetitive tasks. To declare a list in Python, you simply create a name for the list, use the = command like you do with variables, and then enclose the items you want to place in the list in square brackets, [], separating each item using a comma, like this:
>>> a = [1,2,3]
>>> a
[1, 2, 3]
Often it’s useful to create an empty list so you can add values, such as numbers, coordinates, and objects, to it later. To do this, just create the list as you would normally but without any values, as shown here:
>>> b = []
>>> b
[]
This creates an empty list called b, which you can fill with different values. Let’s see how to add things to a list.
To add an item to a list, use the append() function, as shown here:
>>> b.append(4)
>>> b
[4]
First, type the name of the list (b) you want to add to, followed by a period, and then use append() to name the item you want to add inside parentheses. You can see the list now contains just the number 4.
You can also add items to lists that aren’t empty, like this:
>>> b.append(5)
>>> b
[4, 5]
>>> b.append(True)
>>> b
[4, 5, True]
Items appended to an existing list appear at the end of the list. As you can see, your list doesn’t have to be just numbers. Here, we append the Boolean value True to a list containing the numbers 4 and 5.
A single list can hold more than one data type, too. For example, you can add text as strings, as shown here:
>>> b.append("hello")
>>> b
[4, 5, True, 'hello']
To add a string, you need to include either double or single quotes around the text. Otherwise, Python looks for a variable named hello, which may or may not exist, thus causing an error or unexpected behavior. Now you have four items in list b: two numbers, a Boolean value, and a string.
Like on strings, you can use addition and multiplication operators on lists, but you can’t simply add a number and a list. Instead, you have to append it using concatenation.
For example, you can add two lists together using the + operator, like this:
>>> c = [7,True]
>>> d = [8,'Python']
>>> c + d #adding two lists
[7, True, 8, 'Python']
We can also multiply a list by a number, like this:
>>> 2 * d #multiplying a list by a number
[8, 'Python', 8, 'Python']
As you can see, multiplying the number 2 by list d doubles the number of items in the original list.
But when we try to add a number and a list using the + operator, we get an error called a TypeError:
>>> d + 2 #you can't add a list and an integer
Traceback (most recent call last):
File "<pyshell#22>", line 1, in <module>
d + 2
TypeError: can only concatenate list (not "int") to list
This is because you can’t add a number and a list using the addition symbol. Although you can add two lists together, append an item to a list, and even multiply a list by a number, you can concatenate a list only to another list.
Removing an item from a list is just as easy: you can use the remove() function with the item you want to remove as the argument, as shown next. Make sure to refer to the item you’re removing exactly as it appears in the code; otherwise, Python won’t understand what to delete.
>>> b = [4,5,True,'hello']
>>> b.remove(5)
>>> b
[4, True, 'hello']
In this example, b.remove(5) removes 5 from the list, but notice that the rest of the items stay in the same order. The fact that the order is maintained like this will become important later.
Often in math you need to apply the same action to multiple numbers. For example, an algebra book might define a function and ask you to plug a bunch of different numbers into the function. You can do this in Python by storing the numbers in a list and then using the for loop you learned about in Chapter 1 to perform the same action on each item in the list. Remember, when you perform an action repeatedly, it’s known as iterating. The iterator is the variable i in for i in range(10), which we’ve used in previous programs, but it doesn’t always have to be called i; it can be called anything you want, as in this example:
>>> a = [12,"apple",True,0.25]
>>> for thing in a:
print(thing)
12
apple
True
0.25
Here, the iterator is called thing and it’s applying the print() function to each item in the list a. Notice that the items are printed in order, with each item on a new line. To print everything on the same line, you need to add an end argument and an empty string to your print() function, like this:
>>> for thing in a:
print(thing, end='')
12appleTrue0.25
This prints all the items on the same line, but all the values run together, making it hard to distinguish between them. The default value for the end argument is the line break, as you saw in the preceding example, but you can insert any character or punctuation you want by putting it in the quotes. Here I’ve added a comma instead:
>>> a = [12,"apple",True,0.25]
>>> for thing in a:
print(thing, end=',')
12,apple,True,0.25,
Now each item is separated by a comma, which is much easier to read.
You can refer to any element in a list by specifying the name of the list and then entering its index in square brackets. The index is an item’s place or position number in the list. The first index of a list is 0. An index enables us to use a meaningful name to store a series of values and access them easily within our program. Try this code out in IDLE to see indices in action:
>>> name_list = ['Abe','Bob','Chloe','Daphne']
>>> score_list = [55,63,72,54]
>>> print(name_list[0], score_list[0])
Abe 55
The index can also be a variable or an iterator, as shown here:
>>> n = 2
>>> print(name_list[n], score_list[n+1])
Chloe 54
>>> for i in range(4):
print(name_list[i], score_list[i])
Abe 55
Bob 63
Chloe 72
Daphne 54
To get both the index and the value of an item in a list, you can use a handy function called enumerate(). Here’s how it works:
>>> name_list = ['Abe','Bob','Chloe','Daphne']
>>> for i, name in enumerate(name_list):
print(name,"has index",i)
Abe has index 0
Bob has index 1
Chloe has index 2
Daphne has index 3
Here, name is the value of the item in the list and i is the index. The important thing to remember with enumerate() is that the index comes first, then the value. You’ll see this later on when we put objects into a list and then access both an object and its exact place in the list.
In Chapter 1 you learned that the range(n) function generates a sequence of numbers starting with 0 and up to, but excluding, n. Similarly, list indices start at 0, not 1, so the index of the first element is 0. Try the following to see how this works:
>>> b = [4,True,'hello']
>>> b[0]
4
>>> b[2]
'hello'
Here, we create a list called b and then ask Python to show us the item at index 0 in list b, which is the first position. We therefore get 4. When we ask for the item in list b at position 2, we get 'hello'.
You can use the range (:) syntax inside the brackets to access a range of elements in a list. For example, to return everything from the second item of a list to the sixth, for example, use the following syntax:
>>> myList = [1,2,3,4,5,6,7]
>>> myList[1:6]
[2, 3, 4, 5, 6]
It’s important to know that the 1:6 range syntax includes the first index in that range, 1, but excludes the last index, 6. That means the range 1:6 actually gives us the items with indexes 1 to 5.
If you don’t specify the ending index of the range, Python defaults to the length of the list. It returns all elements, from the first index to the end of the list, by default. For example, you can access everything from the second element of list b (index 1) to the end of the list using the following syntax:
>>> b[1:]
[True, 'hello']
If you don’t specify the beginning, Python defaults to the first item in the list, and it won’t include the ending index, as shown here:
>>> b[:1]
[4]
In this example, b[:1] includes the first item (index 0) but not the item with index 1. One very useful thing to know is that you can access the last terms in a list even if you don’t know how long it is by using negative numbers. To access the last item, you’d use -1, and to access the second-to-last item, you’d use -2, like this:
>>> b[-1]
'hello'
>>> b[-2]
True
This can be really useful when you are using lists made by other people or using really long lists where it’s hard to keep track of all the index positions.
If you know that a certain value is in the list but don’t know its index, you can find its location by giving the list name, followed by the index function, and placing the value you’re searching for as its argument inside parentheses. In the shell, create list c, as shown here, and try the following:
>>> c = [1,2,3,'hello']
>>> c.index(1)
0
>>> c.index('hello')
3
>>> c.index(4)
Traceback (most recent call last):
File "<pyshell#85>", line 1, in <module>
b.index(4)
ValueError: 4 is not in list
You can see that asking for the value 1 returns the index 0, because it’s the first item in the list. When you ask for the index of 'hello', you’re told it’s 3. That last attempt, however, results in an error message. As you can see from the last line in the error message, the cause of the error is that 4, the value we are looking for, is not in the list, so Python can’t give us its index.
To check whether an item exists in a list, use the in keyword, like this:
>>> c = [1,2,3,'hello']
>>> 4 in c
False
>>> 3 in c
True
Here, Python returns True if an item is in the list and False if the item is not in the list.
Everything you’ve learned about list indices applies to strings, too. A string has a length, and all the characters in the string are indexed. Enter the following in the shell to see how this works:
>>> d = 'Python'
>>> len(d) #How many characters are in 'Python'?
6
>>> d[0]
'P'
>>> d[1]
'y'
>>> d[-1]
'n'
>>> d[2:]
'thon'
>>> d[:5]
'Pytho'
>>> d[1:4]
'yth'
Here, you can see that the string 'Python' is made of six characters. Each character has an index, which you can access using the same syntax you used for lists.
When you’re adding a bunch of numbers inside a loop, it’s useful to keep track of the running total of those numbers. Keeping a running total like this is an important math concept called summation.
In math class you often see summation associated with a capital sigma, which is the Greek letter S (for sum). The notation looks like this:
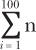
The summation notation means that you replace n with i starting at the minimum value (listed below the sigma) and going up to the maximum value (listed above the sigma). Unlike in Python’s range(n), the summation notation includes the maximum value.
To write a summation program in Python, we can create a variable called running_sum (sum is taken already as a built-in Python function). We set it to a value of zero to begin with and then increment the running_sum variable each time a value is added. For this we use the += notation again. Enter the following in the shell to see an example:
>>> running_sum = 0
>>> running_sum += 3
>>> running_sum
3
>>> running_sum += 5
>>> running_sum
8
You learned how to use the += command as a shortcut: using running_sum += 3 is the same as running_sum = running_sum + 3. Let’s increment the running sum by 3 a bunch of times to test it out. To do this, add the following code to the arithmetic.py program:
arithmetic.py
running_sum = 0
➊ for i in range(10):
➋ running_sum += 3
print(running_sum)
We first create a running_sum variable with the value 0 and then run the for loop 10 times using range(10) ➊. The indented content of the loop adds 3 to the value of running_sum on each run of the loop ➋. After the loop runs 10 times, Python jumps to the final line of code, which in this case is the print statement that displays the value of running_sum at the end of 10 loops.
From this, you might be able to figure out what the final sum is, and here’s the output:
30
In other words, 10 multiplied by 3 is 30, so the output makes sense!
Let’s expand our running sum program into a function called mySum(), which takes an integer as a parameter and returns the sum of all the numbers from 1 up to the number specified, like this:
>>> mySum(10)
55
First, we declare the value of the running sum and then increment it in the loop:
arithmetic.py
def mySum(num):
running_sum = 0
for i in range(1,num+1):
running_sum += i
return running_sum
To define the mySum() function, we start the running sum off at 0. Then we set up a range of values for i, from 1 to num. Keep in mind that range(1,num) won’t include num itself! Then we add i to the running sum after every loop. When the loop is finished, it should return the value of the running sum.
Run the function with a much larger number in the shell. It should be able to return the sum of all the numbers, from 1 to that number, in a flash:
>>> mySum(100)
5050
Pretty convenient! To solve for the sum of our more difficult sigma problem from earlier, simply change your loop to go from 0 to 20 (including 20) and add the square of i plus 1 every loop:
arithmetic.py
def mySum2(num):
running_sum = 0
for i in range(num+1):
running_sum += i**2 + 1
return running_sum
I changed the loop so it would start at 0, as the sigma notation indicates:
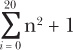
When we run this, we get the following:
>>> mySum2(20)
2891
Now that you have a few new skills under your belt, let’s improve our average function. We can write a function that uses lists to find the average of any list of numbers, without us having to specify how many there are.
In math class you learn that to find the average of a bunch of numbers, you divide the sum of those numbers by how many numbers there are. In Python you can use a function called sum() to add up all the numbers in a list, like this:
>>> sum([8,11,15])
34
Now we just have to find out the number of items in the list. In the average() function we wrote earlier in this chapter, we knew there were only two numbers. But what if there are more? Fortunately, we can use the len() function to count the number of items in a list. Here’s an example:
>>> len([8,11,15])
3
As you can see, you simply enter the function and pass the list as the argument. This means that we can use both the sum() and len() functions to find the average of the items in the list by dividing the sum of the list by the length of the list. Using these built-in keywords, we can create a concise version of the average function, which would look something like this:
arithmetic.py
def average3(numList):
return sum(numList)/len(numList)
When you call the function in the shell, you should get the following output:
>>> average3([8,11,15])
11.333333333333334
The good thing about this version of the average function is that it works for a short list of numbers as well as for a long one!
In this chapter you learned about data types like integers, floats, and Booleans. You learned to create a list, add and remove elements from a list, and find specific items in a list using indices. Then you learned how to use loops, lists, and variables to solve arithmetic problems, such as finding the average of a bunch of numbers and keeping a running sum.
In the next chapter you’ll learn about conditionals, another important programming concept you’ll need to learn to tackle the rest of this book.