One of the fundamental purposes of data analysis is the extrapolation of data. That is, the process of discovering patterns in the data and then projecting those patterns to anticipate unobserved or even future behavior. When a dataset appears to follow a pattern that looks like a mathematical function, then the algorithms used to identify that function or class of functions are characterized as regression analysis. In the simplest cases, when those functions are linear functions, the analysis is called linear regression.
The term "regression" was coined by the English statistician Francis Galton, who also originated the concept of correlation. Galton pioneered the field of data analysis with his studies of heredity. One of those early studies was on the heights of fathers and their sons, in which he observed that the sons of tall fathers tended toward more average heights. The title of that famous research paper was Regression towards Mediocrity in Hereditary Stature.
Figure 6.1: Sir Francis Galton
Linear regression is the simplest form of general regression analysis. The main idea here is to find numbers m and b, so that the line whose equation is y = mx + b will fit closely through the given dataset of (x, y) points. The constants m and b are the slope and the y intercept.
Microsoft Excel is good at doing regression analysis. Figure 6.2 shows an example of linear regression in Excel. The dataset is shown at the upper left corner in columns A-B, lines 1-11. There are two variables, Water and Dextrose, and 10 data points. The data comes from an experiment (source: J. L. Torgesen, V. E. Brown, and E. R. Smith, Boiling Points of Aqueous Solutions of Dextrose within the Pressure Range of 200 to 1500 Millimeters, J. Res. Nat. Bur. Stds. 45, 458-462 (1950).) that measured the boiling points of water and a dextrose solution at various pressures. It suggests a correlation between the two boiling points; that is, that they are affected by pressure in the same way. Although we will let x be the water boiling points and y be the dextrose solution boiling points, we are not suggesting that y depends upon x. In fact, they both depend upon the unmeasured variable, pressure. But, consequently, we do expect to see a linear relationship between these choices for x and y.
Here are the steps we followed to produce the results shown in Figure 6.2:
- Enter the dataset, as shown in the upper left corner of the spreadsheet.
- Select Data Analysis from the Data tab in the Toolbar.
- Select Regression from the pop-up menu.
- Fill in the Input and Output fields as shown in Figure 6.3.
- Click on OK.
The results should look like Figure 6.2, except without the plot.
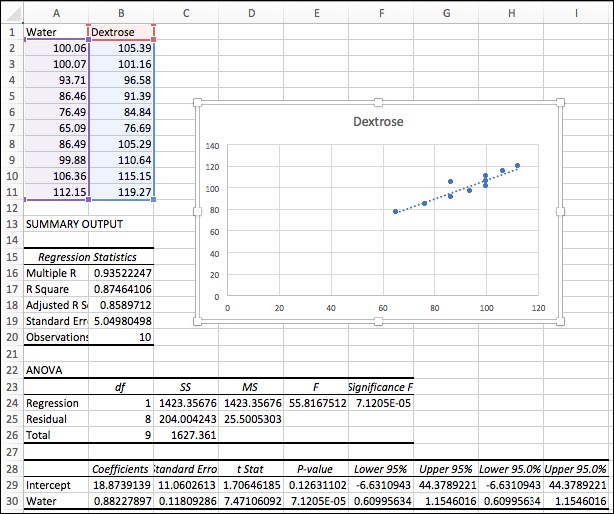
Figure 6.2: Linear Regression in Microsoft Excel
To obtain the plot, follow these additional steps:
- Select the 22 cells, A1-B11.
- Click on the X Y (Scatter) icon on the Insert tab, and then select the Scatter button (the first one) on the pop-up graphic menu.
- In the resulting scatter plot, click on one of the points to select them all. Then right-click on one of the selected points and select Add Trendline… from the pop-up menu.
The dotted line on the scatter plot is the regression line for that data. (Excel calls it a "trendline.") It is the line that best fits the data points. Among all possible lines, it is the one that minimizes the sum of the squares of the vertical distances to the data points.
The two numbers under the Coefficients label (in cells A29 and A30) are the y intercept and the slope for the regression line: b = 18.8739139 and m = 0.88227897. Thus, the equation for that line is:
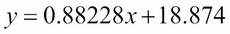
The image in Figure 6.4 is a magnification of the scatter plot in Figure 6.2, where both x and y are around 100. The three points there are (100.07, 101.16), (100.06, 105.39), and (99.88, 110.64).
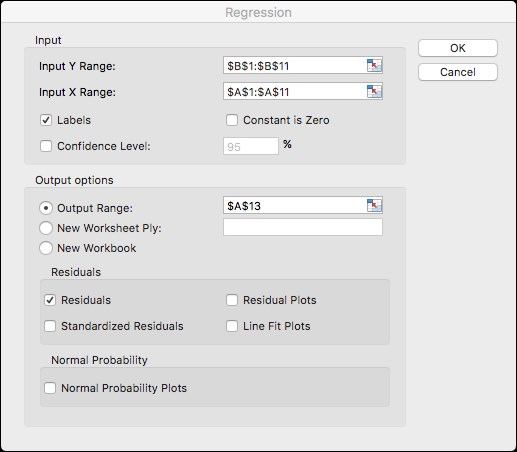
Figure 6.3: Microsoft Excel Linear Regression Dialog
Figure 6.4: Magnification
The second point is the closest to the regression line. The corresponding point on the regression line that has the same x value is (100.06, 107.15). So, the vertical distance from that second point to the line is 107.15 – 105.39 = 1.76. This distance is called the residual for that data point. It is the sum of the squares of these residuals that is minimized by the regression line. (Why squares? Because of the Pythagorean Theorem. Distances in Euclidean space (where we live) are computed by summing the squares of the differences of the points' coordinates.)
In addition to the y intercept, the b slope, and m for the regression line, the Excel generates 29 other statistics. The first one, labelled Multiple R, under regression statistics, is the sample correlation coefficient:
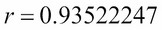
It can be computed from the formula:
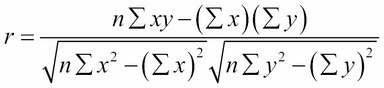
To see how this formula works, let's calculate r for an artificially simple dataset. The dataset in Table 6.1 contains three data points: (1, 4), (2, 5), and (3, 7).
|
x |
y |
x2 |
y2 |
xy |
|---|---|---|---|---|
|
1 |
4 |
1 |
16 |
4 |
|
2 |
5 |
4 |
25 |
10 |
|
3 |
7 |
9 |
49 |
21 |
|
6 |
16 |
14 |
90 |
35 |
Table 6.1: Computing r
The numbers in the 14 shaded cells are all computed from those six given coordinates. Each number in the bottom row is the sum of the three numbers above it. For example:
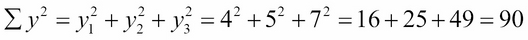
The number of data points is n = 3. Thus:
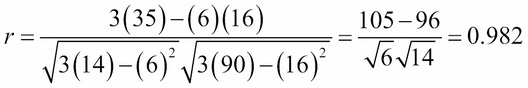
The regression line for these three data points is shown in Figure 6.5:
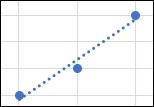
Figure 6.5: Reg. Line for Three Points
Clearly, the points are very close to the line. That is reflected in the value of the correlation coefficient, r = 0.982. That can be interpreted as saying that y is 98.2% linearly correlated with x.
To see what 100% linear correlation would mean, move the third point down, from (3, 7) to (3, 6), and then re-compute r:
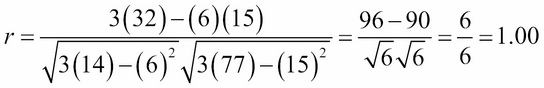
Those three points lie exactly on the line y = x + 3.
At the other extreme, move the third point down to (3, 4) and re-compute r again:
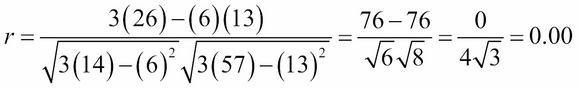
The equation for the regression line is y = mx + b, where the constants m and b are computed from the coordinates of the points in the given dataset. Their formulas are:
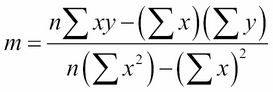
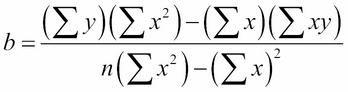
There are four sums here, each one computed directly from the data. We can simplify the formulas a little by renaming these sums A, B, C, and D:
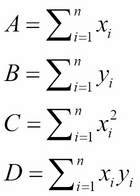
Then we have:
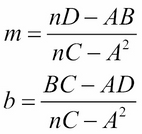
For example, given the preceding three-point dataset in Table 6.1, A = 6, B = 16, C = 14, and D = 35, so:
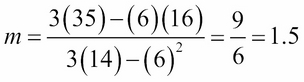
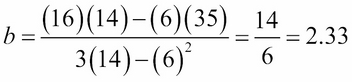
So, the equation for the regression line is y = 1.5x + 2.33.
The derivation of the formulas for m and b is derived here using multivariate calculus. To find the values of m and b that minimize this function:
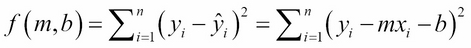
We take its partial derivatives with respect to m and to b, set them both to zero, and then solve the resulting two equations simultaneously for m and b:
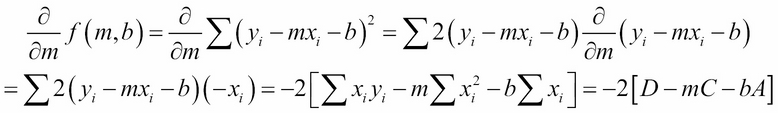
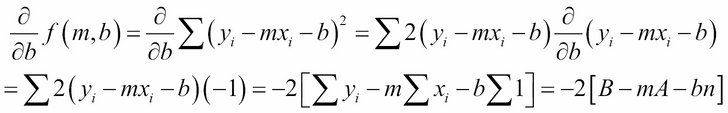
Setting these two expressions to zero gives:
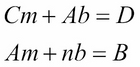
Or, equivalently:
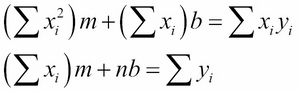
These two equations are called the normal equations for the regression line.
We can now solve the two normal equations simultaneously (for example, using Cramer's Rule) to obtain the formulas for m and b:
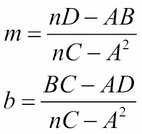
Finally, if we divide both sides of the second normal equation by n, we obtain:
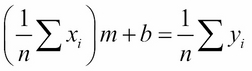
This is, more simply,
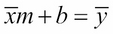
In other words, the point whose coordinates are the means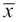 
and 
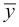lies on the regression line. That fact gives us a simpler formula for computing b in terms of m, assuming that the means have already been computed:
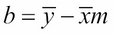
To clarify the meaning of the correlation coefficient r, let's first recall the sample variance that we looked at in Chapter 4, Statistics – Elementary Statistical Methods and Their Implementation in Java. For the y coordinates {y1, y2, … , yn} of a dataset, the formula is:
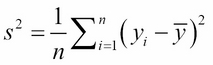
This is simply the average of the squared deviations of the values from their mean. For example, for the set {4, 7, 6, 8, 5}, the mean is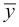
= 6, so:
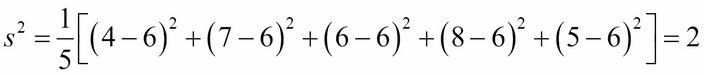
If we compute the sum without then dividing by n, we have what's called the total variation:
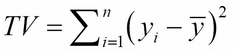
In this little example, TV = 10. That's a simple measure of how much the data varies from its mean.
With linear regression, we can use the equation of the regression line, y = mx + b, to compute the y values of the points on that line that have the same x coordinates that are in the dataset. These y values are denoted by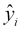 
. So, for each i:
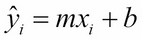
In our Water-Dextrose example in Figure 6.2, the eighth data point (on line 9 in Figure 6.2) is:
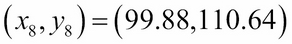
So, x8 = 99.88 and y8 = 110.64. The regression line is:
y = 0.88228x + 18.874
So 
is:
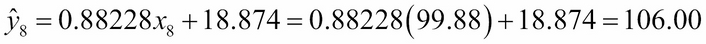
This y value is called an estimate of y on x. This is, of course, different from the mean value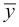
= 100.64.
The actual y value for x8 is y8 = 110.64. So, we can look at three differences:
The deviation of y8 from its mean :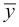
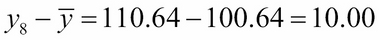
The deviation of y8 from its estimate (also called its residual) :
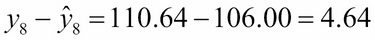
And the deviation the estimate from mean :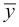
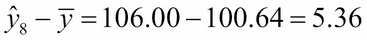
Obviously, the first difference is the sum of the other two:
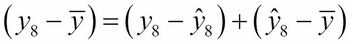
So, in general, we think of the deviation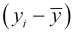 
as the sum of two parts: the residual 
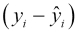and the factor 
.
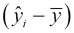As we saw in the previous section, it is a mathematical fact that the mean point (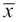, 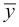) always lies on the regression line. Since the 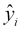-values are computed from the equation of the regression line, we can think of that factor 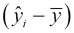as being "explained" by those regression line calculations. So, the deviation 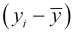is the sum of two parts: the unexplained residual part 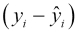, and the explained factor :
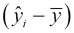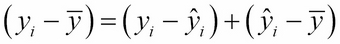
Squaring both sides gives:
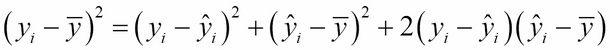
Then summing:
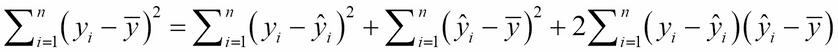
But that last sum is zero:
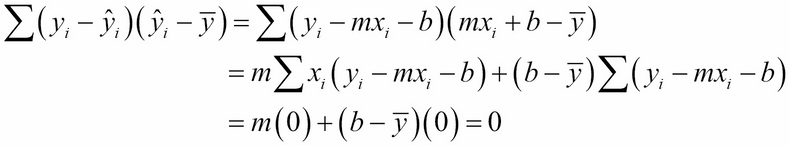
This is because:
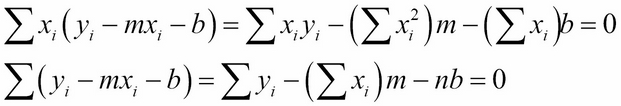
These equation are from the Normal Equations (in the previous section).
Thus:
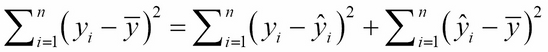
Or:
TV = UV + EV
Here,
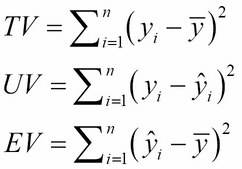
These equations define the total variation TV, the unexplained variation UV, and the explained variation EV.
The variation data in the Water-Dextrose example from Figure 6.2 is reproduced here in Figure 6.6.
Figure 6.6: Variation in W-D Experiment
You can read these values under the SS column (for "sum of squares") of the ANOVA (for "analysis of variance") section:
The Apache Commons Math library includes the package stat.regression. That package has a class named SimpleRegression which includes methods that return many of the statistics discussed in this chapter. (See Appendix, Java Tools on how to install this library in NetBeans.)
The data file Data1.dat, shown in Figure 6.7, contains the data from the Water-Dextrose experiment presented earlier:
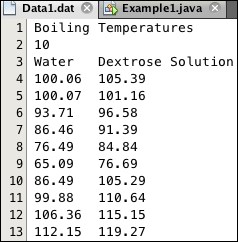
Figure 6.7: Data Source for Example1
The data values on lines 4-13 are separated by tab characters. The program in Listing 6.1 reads that data, uses a SimpleRegression object to extract and then prints the statistics shown in the output panel. These are the same results that we obtained earlier for this data.
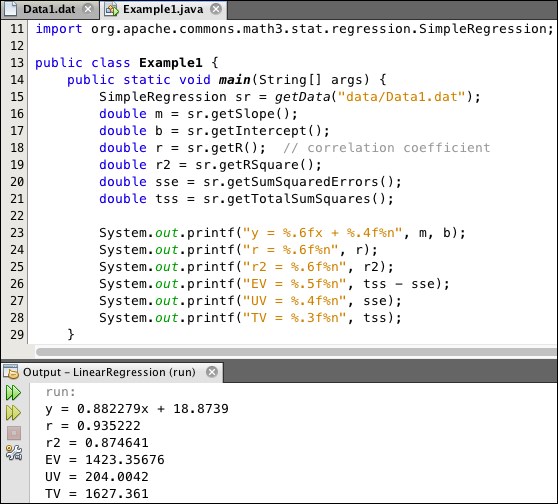
Listing 6.1: Using a SimpleRegression Object
At line 20, the variable sse is assigned the value returned by the method sr.getSumSquaredErrors(). This sum of squared errors is the unexplained variation (UV), which Excel calls the Residual. The output shows its value is 204.0042, which agrees with Figure 6.6.
At line 21, the variable tss is assigned the value returned by the method sr.getTotalSumSquares(). This "total sum of squares" is the total variation (TV). The output shows that its value is 1627.361, also agreeing with Figure 6.6.
The import statement at line 11 shows where the SimpleRegression class is defined. It is instantiated at line 32 in the getData() method shown in Listing 6.2.
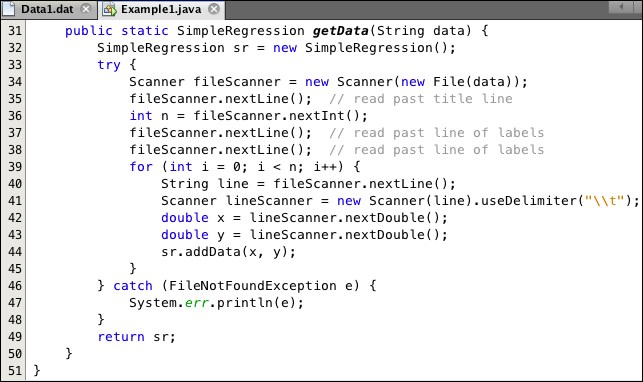
Listing 6.2: The getData() Method from Example1
The fileScanner object instantiated at line 34 reads lines from the data file that is located by the data string passed to it. At lines 35-38, it reads the first three lines of the file, saving the number of data points in the variable n. Then the for loop at lines 39-45 reads each of those n data lines, extracts the x and y values, and then adds them to the sr object at line 44. Note that the lineScanner, instantiated at line 41, is told to use the tab character '\t' as its delimiter. (The backslash symbol \ has to be "escaped" with a preceding backslash for Java to recognize it as such. The expression \\t, then, is a string that contains that single tab character.)
The program Example2, shown in Listing 6.3, is similar to the program Example1. They have the same output:
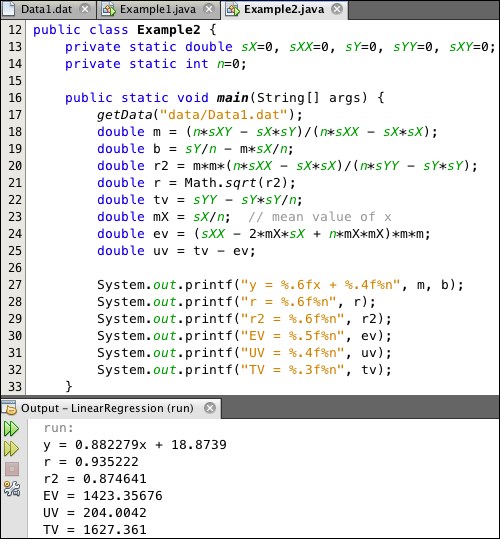
Listing 6.3: Computing Statistics Directly
The difference is that Example2 computes the statistics directly instead of using a SimpleRegression object.
The eight statistics are all computed at lines 18-25 from the formulas developed in the previous sections. They are the slope m and y intercept b for the regression line, the correlation coefficient r and its square r2, the mean 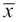, and the three variance statistics, TV, EV, and UV. These are computed from the five sums declared as global variables at line 13: 
, 
, 
, 
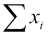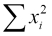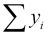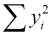, and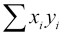 
.
The five sums, denoted as sX, sXX, sY, sYY, and sXY, are accumulated in the for loop at lines 42-52.
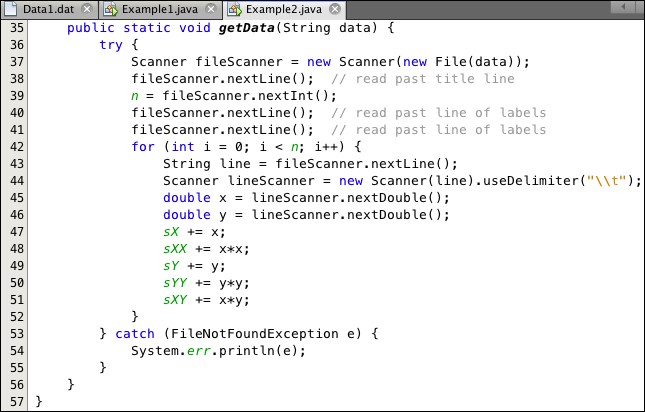
Listing 6.4: The getData() Method from Example2
The program Example3, shown in Listing 6.5, encapsulates the code from Example2 and generates the image in Figure 6.8.
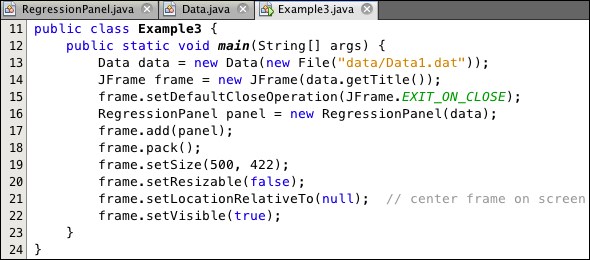
Listing 6.5: Example3 Program
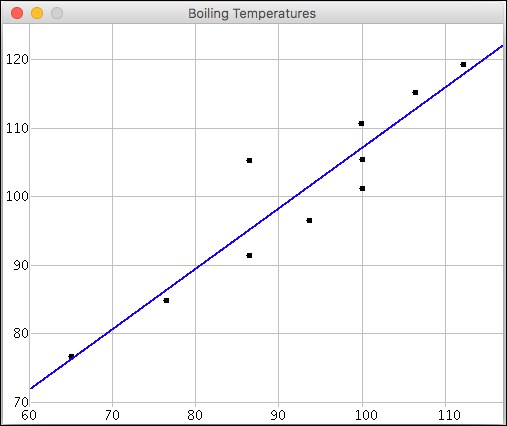
Figure 6-8. Example 3 Output
The program instantiates two auxiliary classes: a Data class at line 13, and a RefressionPanel class at line 16. The rest of the code here is setting up the JFrame.
The Data class constructor is shown in Listing 6.6. That's where the code from Example2 is put.
Listing 6.6: The Data Class for Example 3
The rest of the Data class consists of 16 getter methods. They are listed in Figure 6.9:
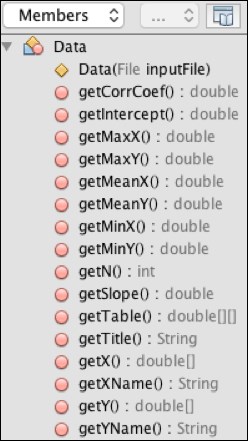
Figure 6.9: Data class members
The RegressionPanel class is shown in Listing 6.7:
Listing 6.7: RegressionPanel Class for Example 3
This contains all the graphics code (not shown here). The image is generated by the three methods called at lines 41-43 in the paintComponent() method:
drawGrid()drawPoints()drawLine()
The resulting image here can be compared to the Excel graph in Figure 6.2.
The linear regression algorithm is appealing, because its implementation is straightforward and it is available from many different sources, such as Microsoft Excel or the Apache Commons Math Java API. However, its popularity sometimes leads the unsuspecting to misuse it.
The underlying assumption upon which the algorithm is based is that the two random variables, X and Y, actually are linearly related. The correlation coefficient r can help the researcher decide whether that assumption is valid for example,: yes if r ≈ ±1, no if r ≈ 0.
For example, the Water-Dextrose data has an r value of 93.5%, suggesting that the relationship is probably linear. But of course, certainty is not possible. The best the researcher can do to raise confidence would be to obtain more data and then "run the numbers" again. After all, a sample size of 10 is not very credible.
The English statistician Frank Anscombe suggested the four examples shown in Figure 6.10:
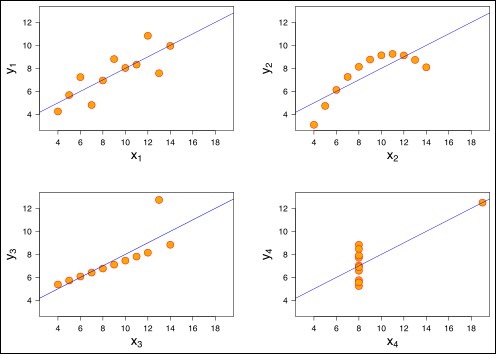
Figure 6.10: Anscombe's Quartet
This shows four 11-point datasets, to each of which the linear regression algorithm has been applied. The data points were chosen so that the same regression line results from each application. The four datasets also have the same mean, variance, and correlation.
Obviously, the data are very different. The scatterplot in the first example looks like the plot of the data points in the Water-Dextrose example. They had a linear correlation coefficient of 93.5%, so the regression line has some validity. In the second example, the data appears quadratic—like time-lapse photos of a projectile fired from the ground, such as a cannonball or a football. We might expect that correlation coefficient to be near 0. The third example has 10 points that are almost perfectly linear, with the 11th point way out of line. A good conclusion here might be that the outlier was an error in measurement or data entry.
The fourth example also has an outlier (the corner point). But this has a more severe problem: all the other points have the same x value. That will cause the algorithm itself to fail, because the denominator of the formula for the slope m will be nearly zero:
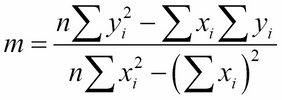
For example, if all the xi = 8 (as they seem to here), then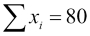 
and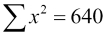 
, so the denominator would be 10(640) – (80)2 = 0.
The points are linear, but the line is vertical, so it cannot have an equation of the form y = mx + b.
To solve the problem revealed in the fourth example in Anscombe's quartet: just reverse the roles of x and y. This will result in an equation of the form x = b0 + b1y, where the constants b0 and b1 are computed from the formulas:
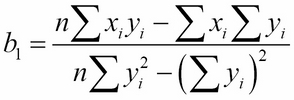
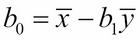
For this particular dataset, it looks like the slope b1 will be nearly zero.