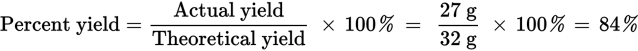Chemical equations express how much and what type of reactants must be used to obtain a given quantity of product. From the law of conservation of mass, the mass of the reactants in a reaction must be equal to the mass of the products. More specifically, chemical equations must be balanced so that there are the same number of atoms of each element in the products as there are in the reactants. Stoichiometric coefficients are used to indicate the number of moles of a given species involved in the reaction. For example, the reaction for the formation of water is:
The coefficients indicate that two moles of H2 gas must be reacted with one mole of O2 gas to produce two moles of water. In general, stoichiometric coefficients are given as whole numbers.
Example:
Balance the following reaction:
Solution:
First, balance the carbon in reactants and products.
Second, balance the hydrogen in reactants and products.
Third, balance the oxygen in reactants and products.
Stoichiometric coefficients are typically written as integers, so double everything to remove the decimal.
Finally, check that all of the elements and the total charge are balanced correctly. If there is a difference in total charge between the reactants and products, then the charge will also have to be balanced. Instructions for balancing charge are found in Chapter 29, Reaction Types, in the context of redox reactions.
Once an equation has been balanced, the ratio of moles of reactant to moles of products is known, and that information can be used to solve many types of stoichiometry problems. It is important to use proper units when solving such problems. When performing these calculations, the units should cancel out such that the units obtained in the answer represent those asked for in the problem.
Example:
How many grams of calcium chloride are needed to prepare 72 g of silver chloride according to the following equation (calcium’s molar mass is 40 g/mol, chlorine’s is 35.5 g/mol, and silver’s is 108 g/mol)?
Solution:
First, note that the equation is balanced. Then, identify that one mole of CaCl2 yields two moles of AgCl when reacted with two moles of AgNO3. The molar mass of CaCl2 is 110 g/mol, and the molar mass of AgCl is approximately 144 g/mol. Starting with the goal mass of AgCl, convert to moles, find the number of moles of CaCl2 required, and then convert into g of CaCl2 (as grams are the units that the question specifies).

Thus, 27.5 g of CaCl2 are needed to produce 72 g of AgCl.
When reactants are mixed, they are seldom added in the exact stoichiometric proportions as shown in the balanced equation. Therefore, in most reactions, one of the reactants will be consumed first. This reactant is known as the limiting reactant or limiting reagent because it limits the amount of product that can be formed in the reaction. The reactant(s) that remains after all of the limiting reactant is used up is called the excess reactant.
Example:
If 28 g of Fe are reacted with 24 g of S to produce FeS, what is the limiting reactant? How many grams of excess reactant are present in the vessel at the end of the reaction?
The balanced equation is:

Solution:
First, the number of moles for each reactant must be determined.

Since one mole of Fe is needed to react with one mole of S, and there are 0.5 moles of Fe for every 0.75 moles of S, the limiting reagent is Fe. Thus, 0.5 moles of Fe will react with 0.5 moles of S, leaving an excess of 0.25 moles of S in the vessel. The mass of the excess reactant will be:
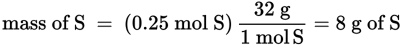
The yield of a reaction, which is the amount of product predicted or obtained when the reaction is carried out, can be predicted from the balanced equation. There are three distinct ways of reporting yields. The theoretical yield is the amount of product that can be predicted from a balanced equation, assuming that all of the limiting reagent has been used, no competing side reactions have occurred, and all of the product has been collected. However, the theoretical yield is seldom obtained in real-world conditions; therefore, chemists speak of the actual yield, which is the amount of product isolated from the reaction experimentally. There are a variety of reasons why the actual yield is less than the theoretical yield. For example, many reactions are reversible (i.e., do not proceed 100 percent from left to right) or use reactants that interact with one another to produce additional end products.
The term percent yield is used to express the relationship between the actual yield and the theoretical yield and is given by the following equation:

Example:
What is the percent yield for a reaction in which 27 g of Cu is produced by reacting 32.5 g of Zn in excess CuSO4 solution (copper’s molar mass is 63.5 g/mol, zinc’s is 65 g/mol, sulfur’s is 32 g/mol, and oxygen’s is 16 g/mol)?
Solution:
The balanced equation is as follows:
Calculate the theoretical yield for Cu.
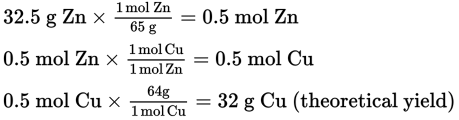
Finally, determine the percent yield.