
The calculation of yield or return can be confusing because there are so many variations on the theme. Return on equity, return on revenue, net return—all of these terms have precise meanings and applications, but they are often erroneously used interchangeably.
Return and yield are really the same thing, but the two terms are sometimes expressed differently. Return is synonymous with rate of return, which can be further distinguished as a return on a specific measurement (percentage of investment, equity, or revenue). Yield is the annual rate of return on real estate (or some other investment), usually expressed as a percentage. The use of yield is often limited to fixed returns, such as the interest income from bonds or certificates of deposit.
While yield and return have the same or a similar meaning, specific calculations use one term or the other. For example, in the bond market, a distinction is made between current yield (actual return on the bond) and nominal yield (the stated yield based on the face value of the bond). Stock market investors use the term current yield to mean the yield of dividends based on the current per share value of stock. So for most investors, yield has a specific meaning, depending on the market. In contrast, return is more frequently used to describe a return based on a fixed investment amount (return on investment) or value (return on equity).
In real estate investing, the terms return and yield have many applications; but the variety of calculations is far more complex, and setting or comparing value has many different formats. These include value calculations used by appraisers, buyers and sellers, accountants, and market analysts.
Cash flow—money available to pay mortgage and investment expenses—is the key to successful real estate investing. It is even more important than profits. In fact, year-to-year success relies on being able to afford to keep up to date on mortgage payments, maintenance, and other nondeductible expenditures, as well as the normal expenses associated with investing. These include utilities, insurance, property taxes, and maintenance. Too many novice investors simplify the equation. They compare the mortgage payment to what they expect to get every month in rent. If the rent income is greater than the mortgage payment, the result is positive cash flow. However, the unknown events surrounding a rental property can destroy the otherwise logical plan. These include:
 Vacancies, perhaps for an extended period
Vacancies, perhaps for an extended period
 Failure by tenants to pay rent
Failure by tenants to pay rent
 Repairs to major systems
Repairs to major systems
 Damage done to property by tenants
Damage done to property by tenants
 Tax consequences or limitations
Tax consequences or limitations
The loss of income due to extended vacancies is disastrous because your mortgage has to be paid every month whether you get income or not. Just as dangerous is having a tenant in your property who does not pay rent. Eviction is not always simple or fast.
The cost to repair broken systems or fix damages is not deductible in the current year. Having to set up these expenditures as assets and depreciating them over many years also affects cash flow. Finally, even with the generous tax benefits of owning rental properties, the annual deductible loss is limited to $25,000. If you earn more than $100,000, even this allowance is phased out. For those earning $150,000 or more per year, no deduction is allowed. So the often-cited tax benefits of real estate are limited and only solve cash flow problems to a degree.
For these reasons, understanding the differences between cash flow and profit is essential. The level of profit is a calculation between rental income and deductible expenses (mortgage principal and the cost of major repairs are examples of capital expenditures, which cannot be deducted in the year the money is spent). Cash flow describes the net of money coming in and money going out, including both deductible expenses and nondeductible items. For most real estate investors, cash flow is everything, and profits do not define success or failure. When properties eventually are sold, the profits in the form of capital gains are a final version of cash flow, and a nice profit on the investment is the defining factor of investment success.
Calculations required to evaluate cash flow are invariably of primary importance. Every real estate investor is concerned with current and future cash flow. If the numbers don’t work out, the entire investment is in jeopardy, even if the long-term profit potential is strong. You need to ensure that you can make it through the next 12 months, and that is more urgent than the outcome over the next 12 years.
A starting point is related to the first question investors are likely to ask: How long will it take to get back my investment from net cash flow? The payback ratio identifies the number of years required for investors to recapture their original investment, which is usually the down payment on property.
•Formula: Payback Ratio
I ÷ C = R
where:
I |
= cash investment |
C |
= net cash flow |
R |
= payback ratio |
•Excel Program: Payback Ratio
A1: |
cash investment |
B1: |
net cash flow |
C1: |
=SUM(A1/B1) |
For example, if the down payment on an investment was $30,000 and the annual net cash flow is $3,450 (rents received minus operating expenses and debt service), the payback ratio is:
$30,000 ÷ $3,450 = 8.7 years
The payback ratio is an excellent comparative tool. If a particular investment produces a faster payback ratio than another, this is a positive indicator. For example, you may consider purchasing two properties, both available for $150,000. One is a single-family house producing annual net cash flow of $3,450; the other may be a duplex with annual net cash flow of $4,100. If both properties would require a $30,000 down payment, the payback ratio will be different. The house’s ratio is 8.7 years, but the duplex’s ratio is 7.3 years:
$30,000 ÷ $4,100 = 7.3 years
A second cash flow-related calculation is cash-on-cash return. This ratio is also called the equity dividend yield. This is a return calculation used in pooled programs such as real estate partnerships. Usually limited to evaluation of programs based on projections of the first-year cash flow, the ratio provides a good means of comparative analysis. Limited partnerships and similar programs are concerned with annual cash flow, just as all investors have to be, and they try to raise investment capital by presenting cash flow projections. One method of analyzing and comparing the cash flow method of different programs is to study the relative health of cash flow. This can be done in two ways: historically and as projected. Historical cash-on-cash return is the actual results reported by a program, and projections are estimates of the future.
•Formula: Cash-on-Cash Return
C ÷ I = R
where:
C |
= annual cash flow |
I |
= cash investment |
R |
= cash-on-cash return |
•Excel Program: Cash-on-Cash Return
A1: |
annual cash flow |
B1: |
cash investment |
C1: |
=SUM(A1/B1) |
You can also use cash-on-cash return to compare properties you are thinking of buying directly. Returning to the previous example of the payback period, compare the cash-on-cash return for the two properties, a house and a duplex. Both required a $30,000 down payment. The house produced estimated first-year cash flow of $3,450, and the cash flow for the duplex was $4,100. The cash-on-cash return in these properties would be 11.5 percent and 13.7 percent. This confirms what the payback ratio indicated: There was stronger cash flow from the duplex for the same down payment. (Additionally, the duplex, with two tenants, provides some protection in the event of vacancies; it is unlikely that both units would be vacant at the same time, whereas the house’s occupancy is either 100 percent or zero.)
Besides providing a comparison of cash-on-cash return between properties, the ratio can also be used to get a sense of how real estate compares to other investments. For example, if you can earn an estimated 7 percent in the stock market compared to 13.7 percent in real estate, it adds to your insight. Owning real estate requires more work, while providing favorable tax advantages; the stock market requires little work once the purchase is made, but there are no tax incentives. So comparisons between dissimilar investments are not easily made; all of the factors have to be considered in the mix, including various forms of risk, levels of capital required, and personal risk tolerance and investing goals.
The discounted cash flow calculates the present value of future cash flow proceeds. All present value calculations are based on assumptions about cash flow, so you are dealing with estimates. However, when considering a particular investment, it is useful to calculate discounted cash flow as one of many analytical steps. Refer to Chapter 3 and check the section about present value formulas. Using the estimated annual cash flow as the “deposit” amount, the discounted cash flow over a period of years can be estimated with this formula.
Calculating return on investment can mean many things. Some may prefer calculating the increase in a property’s market value as the benchmark of success. This is also the most common method of comparison among properties, regions, and other markets. In considering realistically how return really applies, however, the real return to an individual also depends on the cash investment. Consider the differences between the rate of return and current yield.
Rate of return is a calculation used in different markets to describe and compare how investments have performed. It is universally accepted as the ultimate measurement of an investment’s success. For example, if you purchase stock at $20 per share and later sell it for $30, your rate of return is 50 percent (profit of $10 on a $20 original cost). In real estate, the adjusted purchase price and adjusted sales price of property are used in the same way; and even for properties that have not sold, current market value is often used to explain how investments have performed.
•Formula: Rate of Return
(V – C) ÷ C = R
where:
V |
= current value (or sales price) |
C |
= original cost or basis |
R |
= rate of return |
•Excel Program: Rate of Return
A1: |
current value |
B1: |
original cost or basis |
C1: |
=SUM(A1-B1)/B1 |
For example, an investor may point to today’s estimated market value of a property as $300,000 and compare that to an original cost of $235,000. The rate of return in this example is computed by dividing the difference between cost and value by original cost:
($300,000 – $235,000 ) ÷ $235,000 = 0.2766 (27.66%)
To make the calculation reliable (and comparable between different properties), it is also important to annualize the return. Adjust the percentage outcome as it would have been reflected on a one-year holding period. For example, if a property had been purchased for $235,000 and was worth $300,000 today, the annualized rate of return over five years would be:
(( $300,000 – $235,000) ÷ $235,000 )) ÷ 5 = 5.53%
The use of the rate of return formula to calculate the paper profit on real estate is valid. However, in this situation, the details of cash flow and tax benefits over the holding period have not been considered. Thus, rate of return may be viewed as an estimate of how property values have grown in gross market value; as long as the same exclusions are applied to all properties, there is no problem. As in all cases, comparisons are reliable only if performed on the same basis.
If you want to look at returns realistically, especially upon the sale of property, then you need to use an annualized basis that accounts for all types of income or loss. This total return calculation is the dollar amount of net gains from the investment; it includes the net income earned during the period that the property was held on an after-tax basis and capital gains net of income tax liabilities.
This raises an interesting question. Investors can defer their tax liabilities by exchanging income property for new income property. In this case, the tax liability is not eliminated; it is only deferred. So in calculating total return, should you base it on the outcome as completed or on an as-if basis? That would include a calculation of the federal and state tax liabilities that would be incurred if a tax-deferred exchange had not taken place. It is appropriate to compute the tax liability for two reasons. First, you continue to owe the tax, although it won’t be paid until later. Second, to make the calculation comparable to other properties when a tax-deferred gain was not undertaken, you will need to make the two calculations comparable.
•Formula: Total Return
(C + I + T) ÷ Y = R
where:
C |
= capital gains |
I |
= total net income |
= net tax benefit (or cost) |
|
Y |
= years held |
R |
= total return |
•Excel Program: Total Return
A1: |
capital gains |
B1: |
total net income |
C1: |
net tax benefit (or cost) |
D1: |
years held |
E1: |
=SUM(A1+B1+C1)/D1 |
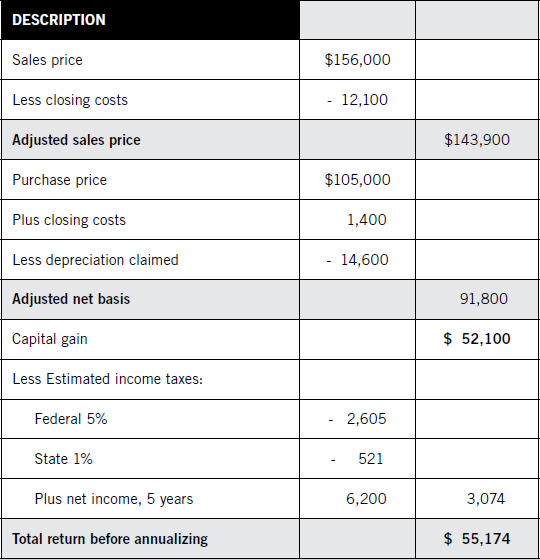
The calculation of total return may involve several steps. For example, if you purchased property for $105,000 plus closing costs of $1,400, the adjusted basis is $106,400. However, under tax rules, depreciation claimed over the holding period has to be deducted from the basis. For example, if you claimed a total of $14,600 over a five-year period, your basis would be reduced by that amount.
The adjusted sale price consists of the price minus the closing costs you paid. For example, if you sold the property for $156,000, but you paid $12,100 in closing costs, the adjusted sales price would be $143,900. You must also calculate federal and state taxes due on the capital gains.
Total return also includes the sum of net income received during the year. This should be the after-tax income including rents minus cash-based expenses and interest. For the purposes of showing the calculation, you are assuming that the five-year net income was $6,200. The overall summary is show in Table 4.1. To arrive at the total return:
($52,100 + $6,200 – $3,126 ) ÷ 5 = $11,034.80
Total return is often called return on investment or return on equity (see Chapter 1).
Total return considers the change in property value as a whole, so under that calculation, “investment” is the same as market value, even though various and different levels of down payment may be involved. The return on equity will vary considerably based on the amount of the down payment, mortgage terms, and interest rate. For example, if you make a minimal down payment and finance property with a 30-year loan and a relatively high interest rate, your equity is going to be minimal. If you make a higher down payment and get a better rate by financing the purchase over 15 or 20 years, your equity will be greater. Equity will also grow at varying rates in different markets depending on local and regional market trends. In a hot market, property values may accelerate in double digits; in very cold markets, values may remain the same or even decline.
Table 4.1: Total Return Worksheet
With these variables in mind, total return (basing the calculation on changed market values as well as cash flow and tax benefits or consequences) is the most consistent and reliable method for calculating the final outcome of a real estate investment.
That final outcome may be many years away. Thus, most real estate investors may be far more concerned with calculating and comparing annual outcomes based on cash flow as a means of determining investment performance. Stock market investors usually measure performance by price per share; real estate investors face a more complex task. However, some of the calculations used by investors in other markets can be useful.
The term current yield is used in the bond market or the stock market to describe interest or dividend yield. However, there is an application for real estate as well.
Current yield in the bond market is the percentage derived from dividing annual income (interest) by the basis in the investment. Because bonds can be purchased at a premium or discount from face value, current yield is not the same as nominal yield, which is the contractual interest percentage paid on the bond. For example, if a bond is at par, current yield and nominal yield will be identical. A $1,000 bond paying a 3 percent nominal yield will also report a 3 percent current yield. However, if a bond with a face value of $1,000 is selling at 97 ($970), current yield will be 3.093 percent (3 ÷ 97). If the bond is sold at 102 ($1,020), current yield will be 2.941 percent (3 ÷ 102).
•Formula: Current Yield (Bond)
N ÷ P = Y
where:
N |
= nominal yield |
P |
= premium or discount |
Y |
= current yield |
•Excel Program: Current Yield (Bond)
A1: |
nominal yield |
B1: |
premium or discount |
C1: |
=SUM(A1/B1) |
Current yield also applies in the stock market. It is the dividend rate as a percentage of the current stock price. As the stock price changes, so does the current yield. For example, if a stock pays a dividend of $1 per share and the current share price is $35, current yield is 2.857 percent ($1 ÷ $35). If the stock’s price rises to $40 per share, current yield changes to 2.5 percent ($1 ÷ $40). If the stock’s price falls to $32 per share, current yield is 3.125 percent ($1 ÷ $32).
•Formula: Current Yield (Stock)
D ÷ P = Y
where:
D |
= dividend per share |
P |
= current price per share |
Y |
= current yield |
•Excel Program: Current Yield (Stock)
A1: |
dividend per share |
B1: |
current price per share |
C1: |
=SUM(A1/B1) |
You can apply the current yield in real estate as well by comparing net operating income to the price paid for the property.
The discount yield is another calculation of return that may be useful to real estate investors. It is more commonly used in the bond market. Because bonds may be purchased at a discount from their par value, bond investors like to calculate their discount yield. This involves dividing the discount by the face value. For example, a bond purchased at 97 (a discount of 3) would produce a discount yield of 3 percent. This is different from current yield, in which the stated interest rate is divided by the actual cost of the bond.
Discount yield may be used in real estate when individual properties are purchased at a price below the property’s appraised value. If you compare appraised value to a bond’s par value, you can make a comparable case for using this formula in real estate. If you want to track the kinds of discounts you are able to get on properties, this could be a useful formula.
•Formula: Discount Yield
(A – P) ÷ A = Y
where:
A |
= appraised value |
P |
= asked price |
Y |
= discount yield |
•Excel Program: Discount Yield
A1: |
appraised value |
B1: |
asked price |
C1: |
=SUM(A1-B1)/B1 |
For example, suppose you are considering buying two properties. In each case, the seller has a recent appraisal in hand. (Alternatively, you may have made an offer contingent on seeing an appraisal.) On one, the asked price is the same as the appraised value; on the other, the asked price is $144,000, $6,000 below the $150,000 appraised value, so an offer could be made at a discount from that value. Applying the formula,
($150,000 – $144,000 ) ÷ $150,000 = 4%
In this example, you earned a 4 percent discount yield by purchasing the property below appraised value. This calculation cannot be applied in every situation because market supply and demand conditions, seller attitudes, and availability of appraisals at the time an offer is made all inhibit your ability to seek out such bargains. However, as a means of judging a series of property investments, this is a worthwhile analysis. It is the equivalent of purchasing shares of stock below current market value. For example, employees may be given stock options at a fixed price, which may be exercised at any time. If and when the market price of the stock rises above that price, shares can be purchased at a discount. There is no good reason why real estate investors should not be able to make similar evaluations of property purchased below appraised value; however, discount yield is only one of many useful calculations you can use to analyze your property portfolio.
Investors in all markets need to devise a series of calculations in order to compare outcomes. The success of an investment has to be measured in a comparative way, either against other similar investments or against a predetermined standard. Because no single calculation works in every situation, investors use a series of formulas to keep track of their investment profits.
The equity dividend yield is a return calculation based on a comparison between cash flow and original investment. It is important to make this calculation on a consistent basis in order to be able to track your progress. For example, cash flow should always be computed in the same way; one recommended basis is the net cash flow after calculating tax benefits. And original investment should be computed the same way as well; original down payment is the recommended basis for this calculation. Equity dividend yield can be used to judge properties against one another. For example, one property might produce only a 2 percent average per year, while another provides an equity dividend yield of 8 percent. This calculation can be used as a means for deciding which properties to keep and which to sell, based on this formula:
•Formula: Equity Dividend Yield
C ÷ D = Y
where:
C |
= net cash flow |
D |
= down payment |
Y |
= equity dividend yield |
•Excel Program: Equity Dividend Yield
A1: |
net cash flow |
B1: |
down payment |
C1: |
=SUM(A1/B1) |
For example, suppose you own two investment properties. One provides an average annual cash flow of $700, and your original down payment was $30,000; the other produces $500 per year in net cash flow, and your original down payment was $10,000. The first property’s equity dividend yield is 2.3 percent ($700 ÷ $30,000), and the second property’s equity dividend yield is 5 percent ($500 ÷ $10,000). Even though the amount of cash from the second property is less, the equity dividend yield is far better.
In comparison, equity return is a calculation of the rate of return on original investment based on net income plus principal reduction, but not the same thing as return on equity. In some situations, this will be identical to the equity dividend yield; however, when you have also spent money for capital improvements, the two formulas will not produce the same result. Net cash flow (as used in equity dividend yield) is the “net net,” the amount of cash after considering all revenue and payments as well as tax benefits. The equity return calculation is a comparison between cash-based net income (plus payments into equity via principal reduction) and original down payment.
Cash-based net income requires a calculation to exclude depreciation. Because depreciation is a major expense but requires no actual cash payment, it is possible and even likely that you will experience positive cash flow while also reporting a net loss for tax purposes. This reported loss is a distortion of the actual outcome caused by depreciation. Thus, the cash income has to add back the expense claimed for depreciation.
•Formula: Cash Income
N ÷ D = C
where:
N |
= net income |
D |
= depreciation expense |
C |
= cash income |
•Excel Program: Cash Income
A1: |
net income |
B1: |
depreciation expense |
C1: |
=SUM(A1/B1) |
To calculate equity return, combine cash income (net income plus depreciation) with the year’s principal reduction on the mortgage debt, and divide the total by the original investment (down payment). To calculate principal reduction, use one of three methods:
1.If your lender reports the annual status of your loan, deduct the current year’s loan balance from the prior year’s loan balance.
2.Refer to a remaining balance table (see Appendix D) for the annual percentage of debt remaining, given an interest rate and amortization schedule; calculate the difference from one year to the next.
3.Track the division of payments between interest and principal and add up each year’s total principal payment.
(C + P) ÷ D = R
where:
C |
= cash income |
P |
= principal reduction |
D |
= down payment |
R |
= equity return |
•Excel Program: Equity Return
A1: |
cash income |
B1: |
principal reduction |
C1: |
down payment |
D1: |
=SUM(A1+B1)/C1 |
For example, suppose that last year your cash income (net income less depreciation) was $815 and your principal reduction was $1,830. Your original down payment was $30,000. Applying the formula:
($815 + $1,830) ÷ $30,000 = 8.8%
Like the equity dividend yield calculation, equity return is a good indicator of how real estate investments are performing. This is especially true when tracking a particular investment from one year to the next or comparing one property to another. For example, consider the case where one property (on which you made a $30,000 down payment) produced cash income of $500 and principal reduction of $830 last year. On a second property on which you made a $10,000 down payment, your cash income last year was only $150, and you reduced the principal by $700. The first property’s equity return was 4.4 percent ($1,330 ÷ $30,000), and the second property’s was 8.5 percent ($850 ÷ $10,000). The numbers cannot always be relied upon without calculating the actual relationship. In this example, the first property produced more cash income and principal reduction but had a relatively dismal equity return. The second property’s equity return was higher, but the dollar amounts were smaller.
Long-term investors struggle with return calculations because they have to deal with several different factors, including market supply and demand and their own cash flow. A higher down payment improves cash flow because mortgage payments and interest expense are lower, but the higher down payment also distorts the return calculations. Different situations are not always comparable. It makes sense to use returns based on down-payment levels solely for comparisons between properties, to track evolving cash flow in one property over time, to evaluate property investments on the basis of the overall market value of the property, or to combine the investment basis (down payment) analysis with the market analysis.
A diligent comparison between different down-payment and cash flow scenarios shows that calculating return is a fiscal art. With this in mind, some investors like to work from investment models. They develop a series of forecast assumptions and use those assumptions to evaluate actual investment outcomes. For example, expected return is a rate you expect to earn from an investment if your capital is left invested. You may expect, for example, that today’s equity return will be marginal but that, as you pay down the principal, the return will improve as well. So in modeling a return expectation, you would factor in ever-increasing principal reductions over the long term.
One form of investment modeling, called internal rate of return (IRR), is a calculation used by most real estate investors because it takes into account the compounding effect of time. So in calculating the internal rate of return, you would estimate an assumed rate of return, an initial down payment, and annual cash flow. This is a complex formula because it requires a series of compound rate calculations. It is also inaccurate because it varies depending on assumed average interest rate, tax benefits, actual cash flow, and compounding method. Most people who like to use IRR employ software because of the complexity of this modeling calculation. Because there are so many variables involved in the calculation, it is of questionable value in a comparative sense. As with many modeling systems, the outcome depends on the assumptions used, so the reliability of IRR is questionable. At the same time, it is widely used and is one of many ways to calculate future return.
Several free IRR calculators are available online. For example:
 http://www.rebuild.org/lawson/irr.asp
http://www.rebuild.org/lawson/irr.asp
Much of the typical investor’s concern involves real estate debt, because in most situations, the majority of a property’s market value is financed. Thus, calculating cash flow and cash income returns is important, but investors also need to track and compare debt-related outcomes.
The debt coverage ratio is a comparison between net operating income and the total of the mortgage payments. The net operating income is defined as rent revenues less operating expenses. These include insurance, taxes, utilities, maintenance and repairs, landscaping, and any other cash expense you incur related to your investment property. It excludes depreciation and interest on the mortgage debt.
•Formula: Debt Coverage Ratio
I ÷ M = R
where:
I |
= net operating income |
M |
= mortgage payment |
R |
= debt coverage ratio |
•Excel Program: Debt Coverage Ratio
A1: |
net operating income |
B1: |
mortgage payment |
C1: |
=SUM(A1/B1) |
The ratio is expressed in factor form. For example, if your mortgage payment is exactly the same as your net operating income, then your debt coverage ratio is 1. If your net operating income is $7,176 and your debt service is $5,450, your ratio is:
$7,176 ÷ $5,450 = 1.32
The debt coverage ratio can be used to compare cash flow between properties. Lenders use various ratios comparing equity to value, estimated cash flow expected from investment properties compared to your monthly income, and other such comparisons for determining qualification for loans. When their ratios are not met, they will reject a loan application or require a higher down payment. For investors, tracking the relationship between cash flow and debt is essential because the larger portion of the property’s market value is financed. So with the high leverage, trends in debt (compared to both current cash flow and to growth in the property’s market value) may ultimately define profitability.
Investors can also use a few math shortcuts to simplify the calculation of interest and rates of return. These rules provide you with methods for fast calculation of how long it takes for values to double or triple, based on assumed rates of return.
For example, you estimate that, in your area, real estate values are growing at the rate of 9 percent per year. The question is, How long will it take for a property’s market value to double, or to triple?
The rule of 72 is an estimate of how long it takes for an investment to double in value based on an assumed interest rate. If you divide 72 by the interest rate, the result is the number of years required to double the value. Using 9 percent, it will take eight years to double your value (72 ÷ 9).
•Formula: Rule of 72
72 ÷ i = Y
where:
i |
= interest rate |
Y |
= years required to double |
A1: |
=SUM(72/interest rate) |
To verify the formula, assume that you purchase real estate valued at $150,000. Using annual interest only (because you’re working with estimates of market value), you can perform a series of calculations:
$150,000 * (1.09)8 = $298,884.40
This is very close to the $300,000 level that would represent a doubling of value. A similar guideline is the rule of 69. This calculation is similar to the rule of 72, but it requires an extra step: Divide 69 by the interest rate and then add 0.35 to the answer. This is slightly more accurate than the rule of 72.
•Formula: Rule of 69
(69 ÷ i) + 0.35 = Y
where:
i |
= interest rate |
Y |
= years required to double |
•Excel Program: Rule of 69
A1: |
=SUM(69/interest rate)+0.35 |
For example, if you apply the formula to the 9 percent example, you find:
(69 ÷ 9%) + 0.35 = 8.02 years
A similar formula reveals how long it will take for real estate to triple in value. The rule of 113 is similar to the rule of 72. Divide 113 by the assumed interest rate and you will know how many years you need to hold your property.
•Formula: Rule of 113
113 ÷ i = Y
where:
i |
= interest rate |
Y |
= years required to triple |
A1: |
=SUM(113/interest rate) |
For example, how long will it take for our $150,000 property investment to triple? Applying the formula,
113 ÷ 9% = 12.56 years
The complexity of calculations involving yield and return rests with the fact that so many different methods and assumptions are involved. A good rule to set for yourself is to critically analyze the accuracy of a particular calculation, make sure you use the same assumptions and values each time you compare properties, and look at all of the possible methods: cash flow, cash-based income, and after-tax net return. By following this suggestion, you will be able to establish like-kind analyses of various properties and trends over time.
These types of analyses become critical in comparative study, not only between different properties but also between different ways to get into an investment. Chapter 5 explores one example of this type, the leveraged approach to acquiring property using the lease option.