IT IS STAMPED ACROSS THE NEWSPAPER. It is mentioned in short sound bites among radio broadcasts. It is discussed at length in the nightly news. We are barraged by updates on how the Dow or NASDAQ or S&P 500 is faring on a given day; the fingers of the media do not slip, even for a moment, from the pulse of the market. As long as there have been financial markets, there have been commentators eager to interpret even their short-term movements—movements that are sometimes muted, sometimes violent, but rarely predictable.
All this leads to a central question: how does one make sense of the movements of the market? How does one sift through all the noise and reach meaning? That is the task of the investor, accomplished by deploying methods of valuation. Valuation is the process of finding logic amid this noise, hoping to uncover areas of the market where the price mechanism has failed—areas that are the exploitable opportunities and the bread and butter of the successful investor.
Investing and the companion enterprise of valuation have always been more of an art than a science. However, in the last century, there has been a burgeoning field of investment science that has profoundly shaped and guided the way practitioners approach their art. This effort has produced a toolbox of sorts for investment professionals. Of course, not all practitioners use all of these ideas. Some professionals use many of the tools in this toolbox with great frequency; others scarcely use them at all. But even those who never use the tools generally know of them—and often have strong opinions about them.
To extend the analogy, one could say that this toolbox of investment science has three drawers; that is, there are three different domains encompassing the output of this intellectual effort. The first drawer of the toolbox is the theory of asset pricing (the core of valuation), the second is the formalization of risk in the context of managing a portfolio of investments (the risks associated with valuation), and the third is measuring and evaluating the performance of investment managers (how well investment professionals perform valuation to exploit investable opportunities). Each domain will be introduced in turn. Along the way, the reader will note that some of these intellectual postulates are just formalizations of long-held understandings: the importance of diversification across many assets and the fact that some financial markets exhibit random processes at work. Other developments radically altered how we think about investing, such as how to allocate funds across an opportunity set of assets with different risk and reward profiles. All of it, though, has left an indelible mark on investment, as its totality relates to the very core of what an investment professional does, which is sorting out valuations and remaining deeply conscious of risk.
DRAWER 1: ASSET PRICING
The first domain, or drawer 1 of the toolbox, is asset pricing. What determines the appropriate price of a financial asset? As with any good, the price is determined by the intersection of supply and demand curves. The supply curve for financial assets tends to be reasonably straightforward in most instances, like shares outstanding for stocks and different segments of the capital stack for debt. However, for financial assets, the story for demand is not so simple. The demand for an asset is dependent on a host of factors such as the healthiness of the balance sheet, perspectives on the sector the asset is associated with, the consensus view of management of the firm, and interest rates (or, more accurately, discount factors applied to future cash flows). Indeed, the demand curve for a financial asset is far more complicated and subject to much greater change than it is, for example, for consumer goods, in which case it emerges out of simple human desires to consume certain quantities of the good at particular prices. What, then, is the appropriate way to think about pricing financial assets?
The Father of Mathematical Finance
It has been said that mathematical finance emerged largely out of Louis Bachelier’s work on the theory of derivatives pricing at the turn of the twentieth century. Bachelier’s father was a vendor of wine who also dabbled in science as a hobby. When Louis’s parents died abruptly after he achieved his bachelor’s degree, he found himself thrust into the position of steward of his family’s business. He became quite fluent in finance as a result of this experience, and soon Bachelier found himself back in academia working under the polymath Henri Poincaré.1
He defended the first portion of his thesis, entitled “Theory of Speculation,” in March 1900. In it, he showed how to value complicated French derivatives using advanced mathematics. In fact, his approach bore some similarity to that of Fischer Black and Myron Scholes many years later. Bachelier’s work was the first use of formal models of randomness to describe and evaluate markets. In his paper, Bachelier used a form of what is called Brownian motion.2 Brownian motion was named after Robert Brown, who studied the random motions of pollen in water. Albert Einstein would describe this same phenomenon in one of his famous 1905 papers. The mathematical underpinnings of this description of randomness could be applied not only to the motions of small particles but also to the movements of markets.
Bachelier’s work did not seem to have an immediate and profound influence on those markets, however. Though it did have some effect, as it showed up in applied probability books and in some prestigious journals, it was really when Paul Samuelson came across Bachelier’s work decades later that this contribution was appropriately appreciated by the financial community.3 Bachelier, though not as lauded as he may have deserved to be among the financial community of his day, was the father of modern mathematical finance.
Irving Fisher: Net Present Value
Whereas Bachelier employed advanced mathematics to think about the price of a derivative, Irving Fisher used mathematics in an approach to a more fundamental question: how does one value the price of the underlying asset (that is, an asset that is not a derivative)?
Born in 1867 in New York, Irving Fisher was a prolific American economist who made contributions to indexing theory as it pertains to measuring quantities like inflation (James Tobin called him the “greatest expert of all time” in this topic), produced work distinguishing between real interest rates and nominal interest rates, and improved the quantity theory of money.4 He also proposed debt deflation as the mechanism that wreaked havoc on the economy in the Great Depression. While John Maynard Keynes’s economic formulations became largely favored over Fisher’s in their own time, interest in debt deflation reemerged in the wake of the global financial crisis of 2007–2009. Given these achievements, it is not entirely surprising that Milton Friedman would call Fisher the “greatest economist the United States has ever produced.”5
Fisher’s primary contribution to investment theory was the development of a metric to assess which income stream represents the optimal investment: “rate of return over cost,” a concept related to what is today referred to as net present value (NPV). Fisher, in The Theory of Interest, presents two principles that can be deployed to choose the best investment. First, he states: “The first (A) of the two investment opportunity principles specifies a given range of choice of optional income streams. Some of the optional income streams, however, would never be chosen, because none of their respective present values could possibly be the maximum.”6 Fisher is essentially calling for the investor to discard any negative NPV projects, as these would never have the maximum NPV because one would clearly choose to not invest rather than invest and receive negative NPV.
The second principle is as follows: “The second (B) investment opportunity principle, that of maximum present value, is of great importance… Let us restate this maximum value principle in an alternative form, thus: one option will be chosen over another if its income possesses comparative advantages outweighing (in present value) its disadvantages.”7 Fisher instructs the investor to discount future cash flow streams and be aware that while some investment opportunities may have higher cash flows in particular years, it is essential to have a broader view and look at all of the discounted cash flows as the basis of comparison. Last, Fisher defines rate of return over cost as the discount rate that equalizes two possible investments in terms of present values.8 New investment can occur when this rate of return over cost is greater than the interest rate.
The formula was simple, but powerful: one could assess the soundness of an investment project by finding the net present value of its future cash flows.
Discounted Cash Flow Models
Fisher helped devise the theory of discounted cash flow for any asset, but it was John Burr Williams who advanced this theory significantly. Williams spent his undergraduate years at Harvard studying mathematics and chemistry, and this mathematical frame of mind would serve him well in the years to come. In the 1920s, he worked as a stock analyst and witnessed firsthand the Crash of 1929. The experience motivated him to study the nature of economics further, and he returned to Harvard for a graduate degree.9
Williams’s dissertation was on the subject of stock valuation and showed that a stock was worth the value of all future dividends discounted to the present. If a firm was not currently paying out dividends, then its value was the expected dividend distribution when the reinvested earnings eventually became dividends. Williams had built what today is referred to as the dividend discount model of stock valuation.10
Williams also believed that much of the market’s fluctuations were due to the role of speculators who were failing to heed the proper valuation method of discounting future dividends and were instead interested only in forecasting the price at which they could later sell the security to another buyer.
It is amusing that given its eventual importance, the 1938 publication of Williams’s The Theory of Investment Value—containing these beliefs and their justifications—came at the displeasure of two different parties, publishers and professors. First, both Macmillan and McGraw-Hill refused to publish the work, convinced that because it employed mathematical symbols in its arguments, it would not be of wide interest to readers. Williams could persuade Harvard University Press to print it only once he said he would bear a portion of the costs of publication. Williams also received the disapprobation of his thesis committee for sending the work to publishers before it was reviewed and accepted by the committee itself as degree worthy.11
Despite being met with this initial displeasure, Williams set the stage for the modern school of financial academics who think in terms of cash flows and a discount factor to value stocks. In some ways, what Williams did was take a known idea of valuing a traditional asset, such as real estate or a bond, as the sum of discounted cash flows and apply it to the stock market, where dividends represented the cash flows. A simple application in retrospect, perhaps, but it was the forward march of intellectual progress.
The Effect of Capital Structure on Asset Pricing
Franco Modigliani and Merton Miller analyzed a rather different question relating to asset pricing: how does the capital structure affect the value of a firm? In other words, how does the breakdown of different forms of capital, like debt and equity, affect valuation? The origins of their collaboration are almost comical. As the story goes, they were both in the Graduate School of Industrial Administration at Carnegie Mellon and were supposed to teach a class in corporate finance. There was only one problem: neither was particularly familiar with the material. So, they worked together to get to the bottom of it, only to find that much of the earlier work was rife with inconsistencies and ambiguity.12 They determined that new work was required, and that was precisely what they produced, publishing their results in the American Economic Review in 1958 with a paper entitled “The Cost of Capital, Corporation Finance and the Theory of Investment.”13
The result was the Modigliani-Miller theorem, which was among the work for which Merton Miller would win the Nobel Prize in Economics in 1990 and would help Modigliani win the 1985 prize (along with his work on the life-cycle hypothesis).14 The Modigliani-Miller theorem first established several conditions under which their results would hold: no taxes or bankruptcy costs, no asymmetric information, a random walk pricing process, and an efficient market. If these conditions hold, the value of a firm should be unaffected by the capital structure it adopts. In other words, the sum of the value of the debt and the value of the equity should remain constant regardless of how that sum is distributed across debt and equity individually. Given that these assumptions do not hold perfectly in the real world, there have been reformulations of the theorem to account for taxes. This was not an obvious result before its publication, and it ultimately generated a flurry of literature in the field of corporate finance on the role of capital structure and its interaction with asset pricing.
Paul Samuelson and Bridging the Gap in Derivatives Theory
We now come full circle within the discussion of the evolution of asset pricing theory and return to the pricing of derivatives. The man who, in a sense, connected the earlier work of Louis Bachelier to that of Black and Scholes, described later, was Paul Samuelson. Samuelson made a stunning breadth of contributions to economics until the end of his life at the age of ninety-four. Hailing from Gary, Indiana, he studied at the University of Chicago in the early 1930s, taking several classes alongside such distinguished classmates as Milton Friedman. After earning his bachelor’s degree at twenty, he went to Harvard for his graduate degree and wrote Foundations of Economic Analysis in 1947, a piece of scholarship that won the David Wells dissertation prize and made Samuelson the very first economist to win the now-prestigious John Bates Clark Medal, earned by economists under the age of forty who have made significant contributions to the field.15 He would soon go to MIT and work on diverse theories of consumer optimization, trade, growth, and equilibrium.
Samuelson was also responsible for bringing much more attention to Bachelier’s work after L. J. Savage wrote postcards to a group of economists asking if any economists were familiar with Bachelier.16 And Samuelson did rethink many of the assumptions Bachelier made, such as noting that the expected return of the speculator should not be zero, as Bachelier suggested, but should rather be positive and commensurate with the risk the speculator is enduring. Otherwise, the investor would simply either not invest or own the risk-free security (short-dated Treasury debt). He also redefined Bachelier’s equations to have the returns in lieu of the actual stock prices move in accordance with a slightly different form of Brownian motion because Bachelier’s form of Brownian motion implied that a stock could potentially have a negative price, which is not sensible, as the concept of limited liability for shareholders implies that the floor of value is zero.17
Samuelson helped motivate the work on derivatives pricing with a 1965 paper on warrants and a 1969 paper with Robert Merton on the same subject—although he did, as he would later note, miss one crucial assumption that Black and Scholes were able to make in their formulation of options prices.18 Samuelson can be considered an intermediary in calling attention to the subfield of derivatives pricing, even if the cornerstone of the most famous final theory was not his own.
Black-Scholes Options Pricing Formula
Myron Scholes spent his graduate years at the University of Chicago, where he studied alongside Merton Miller and Eugene Fama. He went on to teach at the MIT Sloan School of Management, and during his time there he met his future collaborator in the theory of derivatives, Fischer Black. Black was a graduate of Harvard, where he had spent both his undergraduate and graduate years studying applied mathematics, and was working for Arthur D. Little Consultants when he met Scholes.
The revolutionary work of Black and Scholes was published in a 1973 paper, “The Pricing of Options and Corporate Liabilities.”19 There were two main ways the Black-Scholes options pricing scheme revolutionized the way that derivatives were understood. First, and what Samuelson had essentially missed, was that their scheme thought of derivatives with respect to a no-arbitrage condition. The version of the no-arbitrage condition Black and Scholes used was that of dynamic hedging, or the notion that one could construct an instrument with the same payoffs as an option contract by buying or selling different amounts of the underlying stock when there were moves in price (delta hedging), changes in the sensitivity of the contract with respect to price (gamma hedging), and swings in volatility (vega hedging). The hedging is dynamic in the sense that trading must be done any time these factors change.
Black-Scholes does make some unrealistic assumptions about dynamic hedging. First, it assumes that there are no transaction costs that would impede the constant trading required to maintain the hedge. Further, and perhaps even less realistically, there is an implicit assumption that markets follow a continuous pricing regime when they in fact follow a discontinuous one. That is to say, it is possible for a stock price, for instance, to fall from $7.00 per share directly to $6.75, missing all the intermediary values, and thus the dynamic hedging required for a true no-arbitrage condition is difficult to achieve. It turns out, though, that these assumptions are not outrageously unrealistic, as markets are sufficiently liquid to keep transaction costs reasonably low and do not generally experience gaps of such substantial magnitude so as to wreak complete havoc on the idea of dynamic hedging.
The second contribution Black-Scholes made was to one of the models that immediately preceded it: that of James Boness, whose work has since been largely forgotten by practitioners. Boness’s model had a few vital errors that made the difference between his relative obscurity and a chance for enduring acclaim. The first error was the discount rate used.20 The discount rate in the Black-Scholes model is the risk-free rate, again because of the no-arbitrage condition. Boness, though, used the expected return of the stock as the discount rate, but this is not logical in light of the dynamic hedging strategy. Also, Boness tried to incorporate risk preferences into his work, but Black-Scholes imposed the assumption of risk neutrality and did not distinguish between the risk characteristics of various parties.21
As for the equation itself, it is a partial differential equation—with partial derivatives that are now known as the Greeks: delta, gamma, vega, theta, and rho—that bears some semblance to thermodynamic equations. Of course, not all this was completely worked out by the actual 1973 paper. Robert Merton published a subsequent paper explaining the mathematics of the model (in which he also used the term Black-Scholes to refer to this equation for the first time). He described how generalizations of the results were applicable to a variety of other derivatives and markets using the same dynamics present in this model.22 That said, the work of Black and Scholes rounded out that of Samuelson and Bachelier, for they had finally formulated a precise model of options pricing.
Black would not join his collaborators, Scholes and Merton, in winning the Nobel Prize simply because he did not live long enough. Having died of cancer in 1995, two years before the awarding of the prize (not generally awarded posthumously except in a few historical cases when the intended recipient died after being nominated), he was ineligible.23
Where Drawer 1 Has Taken Us
As asset pricing encompasses two fields, the theory of pricing of financial assets in general and the pricing of derivatives, there are two rather different answers to the question of where these achievements have taken us. When it comes to derivatives pricing, particularly the work kicked off by Merton, Samuelson, Black, and Scholes, as well as a flurry of important but less seminal work, the answer is fairly straightforward. The theory of derivatives pricing is largely resolved and can tell us quite successfully what the price of an option on a particular stock should be, given the stock’s price. It is not to say that there is nothing left to do, but rather that we now more or less know what a solution “should look like.” Typically, the modifications for derivatives pricing involve either alterations of some now well-known differential equations or, in the case where there is no explicit mathematical solution, the use of computer simulations.
Of course, upon reflection, it is no real wonder that the theory of derivatives pricing is in a much more advanced state than other theories of pricing of financial assets; it has the benefit of taking the price of the underlying asset as an input, whereas the nonderivative field of asset pricing faces the greater problem of asking what that very stock price should be.
This is also not to say that all market participants have learned to trade derivatives successfully. To say the theory is very successful simply means that inputs map to an output with a high degree of accuracy. This assumes, of course, that the practitioner used the right inputs—which certainly is not assured. Although the theory of derivatives itself is sound, the familiar mantra holds: garbage in, garbage out.
As for asset pricing more generally, there remains a great deal to be done on the academic side, but in truth, determining asset prices is effectively the bread and butter of the entire investment management industry. Some investors try to find value in the equities markets, looking at turnaround stories, improving management, or examining metrics and comparables to find “mispriced” assets. Others like to rummage through the garbage for distressed debt deals and find “diamonds in the rough.” Still others find mispriced assets where there are massive dislocations. Investment management is all about asset pricing, and each manager brings to the task his or her own theories of value. So while there is more to do in the academic arena, we will never resolve a theory of value that is universal and perfect—that, after all, is the very art of investment.
DRAWER 2: RISK
Most of us know where we fall on the spectrum of risk appetites and how close to the edge we care to venture. Some of us are risk lovers, from the gamblers to the entrepreneurs to the adrenaline-loving sports enthusiasts. Others are profoundly risk averse; these are people who are fond of routine, safety, and predictability. Indeed, we know how we interface with risk in our own lives, but rarely do we pause to ponder the simplest questions of all: what is risk, and what is its origin?
Risk is a result of a basic fallibility. That fallibility is our incapacity to see the future. If we knew what tomorrow and every day thereafter would bring, there would be no risk. We could proceed about our lives making decisions whose consequences we knew precisely. We would not feel the trepidation (or, for many, the excitement) that arises from risk, and even more than that, we would not fall victim to the injuries risk delivers. It would be a perfect, though perhaps dull, world. And so risk is yet another burden we bear because of our epistemic limitations.
We are compelled then to walk through life in a certain probabilistic haze, ascribing to all future states of the world certain probabilities of coming to fruition. A collection of future states that is highly dispersed probabilistically with an array of varying consequences is risky, whereas a collection of few states with very similar consequences is not very risky. This is a correct, though slightly imprecise, way of contemplating the essence of risk. The following section traces the frontier of humanity’s formalization of risk in a portfolio management context.
The Beginnings of Diversification
How many generations of parents have told their children some variant of the adage “Do not put all your eggs in one basket”? This pithy precept contains an extraordinary amount of wisdom. Diversification across truly unrelated assets forms the heart of risk management in investment. Virtually all investors would be well served to heed this concept. As it turns out, humanity has been well apprised of the notion of diversification of assets for many centuries. Sagacious advice about diversification appears again and again throughout the Western canon. It appears in the Old Testament of the Bible in the book of Ecclesiastes, which discusses the importance of diversifying: “Ship your grain across the sea; after many days you may receive a return. Invest in seven ventures, yes, in eight; you do not know what disaster may come upon the land.”24 Even William Shakespeare himself addresses the topic in The Merchant of Venice. Antonio declares in the very first scene of the first act, “I thank my Fortune for it, my ventures are not in one bottom trusted, nor to one place; nor is my whole estate upon the Fortune of the present year. Therefore my merchandise makes me not sad.”25
From the Bible to the Bard, humanity has long understood the general notion of spreading risks over a diverse set of projects and ventures. So goes the oft-repeated reference to eggs and baskets. Despite this, there remains disagreement in the investing world as to the importance of diversification—largely because if the goal is extremely large wealth, another option is to embark on a path of nondiversification. In this case, the chances of success are presumably lower, but the payout is significant. As Andrew Carnegie’s famous quip goes, “The way to become rich is to put all your eggs in one basket and then watch that basket.” Bill Gates, too, accumulated substantial wealth early in his career by tying his fate virtually exclusively to that of Microsoft and would diversify only later once his fortune was already earned.
This disagreement regarding diversification hinges upon goals. If the goal is capital preservation and prudent management of funds, the ancient wisdom applies: invest widely. It enhances the probability that a large portion of one’s wealth will remain intact over a variety of different states of the world. However, if one’s goal is not capital preservation but rather extremely large wealth accumulation, diversification is, in many cases, inappropriate.
The source of the disagreement is in how diversification operates on expected returns. Imagine a bell curve sitting over a number line and centered on the expected return of a single asset. The bell curve represents the distribution of possible returns in the future. Adding more and more unrelated assets tightens the tails on the bell curve ever closer to the average expected return. In the process, one reduces the probability of massive loss (the size of the left tail), which is great for capital preservation. Of course, by the same token, one cuts down the size of the right tail, or the likelihood of enormous gain. And thus, both the adage and Carnegie are correct—it is just a question of purpose. Do you accept the left tail risk and swing for the fences, hoping to end up on the right tail with great riches? Or do you abandon the right tail and avoid the left tail, thus maximizing your chances of sitting somewhere in the middle?
Markowitz’s Model and Tobin’s Improvements
Although the concept of diversification has existed for some time, it was not until Harry Markowitz that the mathematical mechanics of diversification were worked out. Harry Markowitz was born in Chicago in 1927, and he stayed in his hometown as a young adult to attend the University of Chicago. Harry was interested in many subjects, including philosophy (having a special interest in David Hume) and physics.26 He eventually gravitated toward economics and stayed at the university to pursue his graduate work under Jacob Marschak, a Russian American economist whose work advanced the field of econometrics. Markowitz happened to have a discussion with a stockbroker while awaiting an opportunity to speak with his thesis adviser, Marschak. The stockbroker seemed to suggest that Markowitz think about the portfolio selection problem in the context of linear optimization, and Marschak later agreed to his doing just that.27 Markowitz was the man for the job; he knew the linear optimization methods, having studied with George Dantzig at the RAND Corporation.28
Philosophically, Markowitz realized that the theory of asset pricing was incomplete without a corresponding theory of risk. Markowitz reasoned that one can indeed perform a calculation of dividends (in truth, proxies for discounted cash flows), but those future dividends themselves are uncertain. And yet, the risks are not captured by the concepts of net present value of Fisher or the dividend discount model of John Burr Williams.29
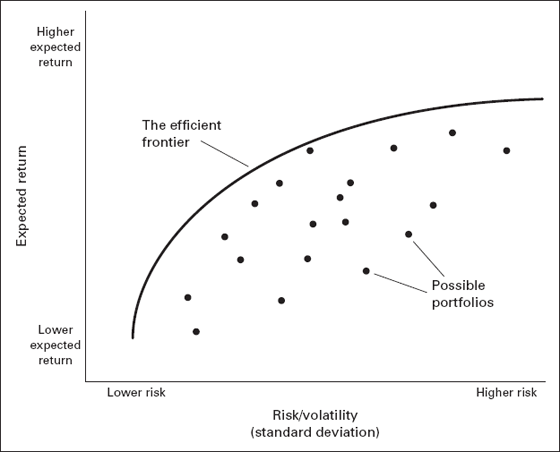
Markowitz offered a technical solution. To give a slightly more modern version of some of his ideas, his approach involves plotting all of the assets available on a graph where the left axis is the expected return and the horizontal axis is the excess volatility, as measured by the standard deviation of returns of the asset (see figure 7.1). The approach is to consider the trade-off between return and volatility: less volatility comes at the cost of lower expected returns for a given portfolio, and achieving higher expected returns requires a portfolio with higher volatility. Then, all possible portfolio risks and rewards are mapped out.30 The portion of the curve representing the highest expected return for a given level of volatility is identified and marked as the “efficient frontier.”
Figure 7.1 Contemporary Understanding of Markowitz’s Efficient Frontier
One would want to invest only in a portfolio that is actually on the efficient frontier with the following simple argument: if one is not on the efficient frontier, one can move to an alternative portfolio that has higher expected return for that same level of risk.
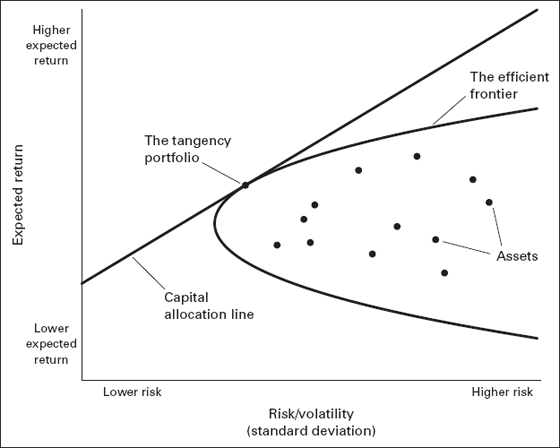
In a 1958 paper, James Tobin enhanced the value of the Markowitz approach by integrating the role of a risk-free asset (thought of more practically as the T-bill), which is plotted on the left axis and identified as having no excess volatility. A line is drawn from this point marking off the risk-free asset and is dropped down upon the efficient frontier to find the most efficient point on the frontier. This line is known as the capital allocation line and represents all possible combinations of the market portfolio and the risk-free asset. It is here that Tobin’s famous separation theorem arises: the agent should hold some linear combination of the risk-free rate and the assets on the point of the efficient frontier that intersects with the capital allocation line (see figure 7.2).31
Figure 7.2 Tobin’s Separation Theorem
There is a remarkable implication of Tobin’s separation theorem: the only difference in the assets every agent in the market should hold is just in the combination of risk-free assets and the tangency portfolio (assuming, of course, that everyone agrees on the risk and return characteristics of all the assets in the opportunity set). Disagreement in these inputs, according to the model, is the only reason to have a portfolio whose components look any different from that of another rational investor doing mean-variance optimization. Which combination of risk-free asset and the tangency portfolio is selected is a function of how much risk one cares to accept. The most risk-averse individuals may hold only the risk-free asset, whereas the most risk-loving investors would theoretically borrow to leverage up exposure to the tangency portfolio.
There have been some criticisms of the Markowitz approach. For instance, some economists have pointed out that volatility may not be sufficiently described by the standard deviation of the returns. The notion of a skewed left tail on return distributions is absent in the Markowitz approach. Even more important, though, is the ability to forecast the expected returns and volatilities. How does one construct a model without knowing ex ante what these returns and volatilities are likely to be? Markowitz suggested using historical data. However, there has been an abundance of subsequent literature showing how notoriously difficult this problem of forecasting returns and volatilities can be (especially returns, as volatilities tend to be more precisely forecasted over short intervals). Nevertheless, despite its drawbacks, Markowitz’s idea was a radical rethinking of portfolio design and allocation and paved the way for the next revolution in the intellectual theory of investing: the capital asset pricing model.
Capital Asset Pricing Model
The capital asset pricing model (CAPM), proposed by William Sharpe in 1964 and John Lintner in 1965, is an extension of the Markowitz model.32 It assumes that investors are in agreement about the expected returns and variances of the assets in the opportunity set and, further, that capital for investment can be borrowed and lent at the risk-free interest rate. This generates the condition that all investors hold the same combination of assets in the same proportions, creating the market portfolio.33
The notion of beta is central in the capital asset pricing model. Beta is a measure of how responsive an asset is to a change in the value of a benchmark. A beta of 1 implies that an asset moves approximately in lockstep with the benchmark over time. A beta of zero, by contrast, means that an asset moves in a manner that is unrelated to the benchmark. More formally, beta is equal to the correlation between an asset’s changes in price and the benchmark’s changes in price multiplied by the ratio of the volatilities (as measured by the standard deviation of returns) of each, with the asset’s volatility as the numerator and the benchmark’s as the denominator.
The capital asset pricing model is of interest for several essential reasons. The first is in considering whether to add an asset to the market portfolio. More specifically, CAPM generates a condition on the minimum expected return, given the beta of the asset to the market portfolio. If the asset’s expected return exceeds the minimum expected return, it is a worthwhile addition to the portfolio; otherwise, it should be avoided.
One radical implication of CAPM that almost universally proves initially uncomfortable is that sometimes it is in the interest of a portfolio manager to add an asset with a negative expected return. One can imagine, for instance, if the risk-free asset has zero return, then an asset that has a negative expected return may be added to the market portfolio if its beta is sufficiently negative. The reason this works is because introducing this asset reduces the total variance of the portfolio. Doing so is attractive because it stabilizes the rest of the blend of assets. It can be likened to vinegar: consuming vinegar on its own is usually undesirable. However, when combined with certain other foodstuffs, such as salad or sushi rice, it can be quite pleasant. CAPM instructs the practitioner that a portfolio analysis involves looking at more than just a collection of individually attractive assets; it involves, rather, a dissection of the blended whole.
The capital asset pricing model is also useful in corporate finance and in determining whether or not firms should invest in particular projects. A firm has a certain cost of capital that can be measured rather simply by beta. If a project has a rate of return on a given investment of capital that is less than the minimum return as prescribed by the CAPM, the firm should steer clear of the project, which would not entail an efficient deployment of funds.
Given this, one of the most difficult aspects of the capital asset pricing model is actually computing the forward beta, not unlike the problems of forecasting forward expected returns and volatilities discussed in the Markowitz model. By far the most common way practitioners calculate beta for the next period is to take the most recent historical beta and use it as the most reasonable proxy. This is known as the constant beta approach and is indeed the most straightforward way to forecast beta, though there are more mathematically sophisticated alternative approaches as well.
Fama-French Three-Factor Model
In 1992, Eugene Fama and Kenneth French wrote a famous paper entitled “The Cross-Section of Expected Stock Returns” that appeared in The Journal of Finance, in which they said that beta alone is insufficient to capture the risk-return trade-off. They introduced two additional factors—size (as measured by the market capitalization) and value (as measured by the book-to-market equity ratio)—as explanatory variables in the performance of stocks. They found that value firms (or firms with low price-to-book value, as compared with growth firms) and small firms (low market capitalization) have higher expected returns in the aggregate but also have higher risk. That is, there is generally a premium earned by holding value and small capitalization stocks. This three-factor model was found to significantly enhance the explanatory capacity of the model when compared to the pure capital asset pricing model.34
This contention was of considerable practical importance. Fama and French were suggesting that there could be other factors driving risk premia and that a single-factor CAPM may be insufficient to adequately describe the risk premium the market offers. It also suggests that for those investors who had previously ignored the effects of these potential sources of risk premia, the returns they experienced in their portfolios may not have been only a function of the market return and their stock selection skills but may also have been a function of exposure to different market factors.35
Where Drawer 2 Has Taken Us
When it comes to risk, we have made great strides, but there is still work to be done. For instance, Markowitz and the later capital asset pricing model suggest that risk can be effectively calculated with metrics like volatility as measured by the standard deviation of asset prices and the betas of assets through time. But how well do these measures really capture risk? To what degree can we rely on price action to tell us the real risk of our investments?
We also need to comprehend the nature of tail risks more effectively; that is, we need to understand how portfolios and markets behave under extreme scenarios. These types of outlier events have monumental consequences on all aspects of money management and lead to corresponding extreme shocks, from liquidity crises to credit crunches to fundamental changes in the economics of the underlying investments. Our failure to really conceptualize the nature of tail risk events has resulted in some investors and institutions becoming far too risky and some others, in truth, acting too conservatively. While the former is clearly worse, as this sort of aggressive behavior can jeopardize the very existence of the institution, being too conservative leaves returns on the table and can result in suboptimal performance.
Our failure to truly apprehend the nuances of tail risk has resulted in an even more pernicious and dominant phenomenon: participants are often too risky or too conservative at precisely the wrong times. When all is going well and it seems as if certain assets cannot possibly fall in value is precisely the moment when the greatest threats are lurking. And by that same token, when the despair seems most unbearable in a postcrisis atmosphere after enormous asset price erosion, many participants feel so pained by the prospect of further loss that they avoid even medium-risk assets. Of course, this is precisely when the market is offering bargains—and some of the best value investors have come to realize this—but much of the market is too shaken to take advantage of the possibilities.
The problem here is not so much one of theory but one of data; the truth is that there have not been an enormous number of these tail scenarios in major markets. In the last 25 years or so, we have seen the crash of 1987, the collapse of Long-Term Capital Management in 1998, the popping of the technology bubble in the late 1990s and into early 2000, and the Great Recession from 2007 to 2009. To build robust theories, or even effective working models, we require a broader set of data from which we can draw, synthesize, and eventually generalize. Of course, one does not want to overemphasize how problematic it is that there have been so few tail events in major markets—one certainly does not want to tempt fate and invite more. And fortunately, the quality of the data associated with the tail event does generally improve through time; for example, the quality of the data in terms of what is available to analyze from the Crash of 1929 is lower than that of the 1987 crash, though the former was arguably a much more monumental event. Because the crises are few in number and so different in content, it is not trivial to know how one should properly hedge a portfolio against extreme downside. All that said, the analysis of tail risk is an area within portfolio management of great practical importance.
DRAWER 3: THE PERFORMANCE OF INVESTMENT PROFESSIONALS
After asset managers estimate prices for individual assets, using the tools in drawer 1, and assemble them into suitable portfolios, with techniques from drawer 2, they can evaluate their performance with a third set of theories. Investment clients can also use these tools to evaluate the outcomes of decisions made by their money managers. As such, the third drawer is the one investment professionals open most fretfully. The theories contained in this third drawer are powerful but perilous. These theories are the yardsticks to measure the performance and value added by an investment manager. This is the set of tools, in short, that can be used to determine which investment professionals are wizards of their craft and which are just Wizards of Oz.
Cowles and the Analysis of Investment Forecasts
Alfred Cowles III was interested in the question of just how well financial forecasters performed. Like his father and uncle before him, Cowles III was educated at Yale, and he graduated in 1913. He found himself disillusioned by a number of financial practitioners who were in the business of forecasting the stock market after all of the projections he had read prior to the Crash of 1929 had missed the collapse. In 1932, Cowles founded the Cowles Commission for Research in Economics, now known as the Cowles Foundation, with the intention of making economics a more rigorous field. Having run his own research group in finance before that, he found himself able to leverage the help of academics, who became affiliated with the organization and took up the banner of studying issues in finance and econometrics.36
Cowles’s most path-breaking research was published in a paper entitled “Can Stock Market Forecasters Forecast?,” which was presented in 1932 and published in 1933. The paper effectively analyzed two groups: those who issued forecasts about particular securities and those who forecast the direction of the stock market as a whole. For the first group, Cowles analyzed four and a half years of data (from the beginning of 1928 until July 1932) from sixteen financial firms and four years of data (from 1928 to 1931) from twenty fire insurance firms that issued forecasts on particular stocks. For the second group, he looked at the projections from twenty-four financial publications on the general direction of the market from January 1, 1928, to June 1, 1932.37
In both cases, Cowles found that not only were their forecasts incorrect most of the time, but their forecasts were, in aggregate, even worse than random chance. With respect to the forecasters of particular securities, he found that the financial services firms tended to underperform the market by 1.43 percent annually and the fire insurance companies by 1.20 percent annually. As for the predictions of general market direction, he found that together, these predictions still underperformed random chance by 4 percent per year.38 Indeed, according to Cowles, one was better off rolling dice than heeding these services. Although his focus on forecasters specifically was too narrow to represent an indictment of the industry of professional money management, it was the first step toward rigorously questioning the value added of some financial services.
The Application of Beta to the Formulation of Alpha
Cowles’s work was a step in the right direction toward meeting the need to measure members of the financial industry, but it was the formulation of Jensen’s alpha that really changed how well this measurement could be done for money managers themselves. In 1968, Michael Jensen created his metric of portfolio performance to determine if mutual fund managers were, in fact, adding value with their touted skills of stock selection.39 The way this is done is to first use the concept of beta in the capital asset pricing model. One starts by calculating the beta of the portfolio compared to a relevant benchmark. A large capitalization US equity money manager might be compared with the S&P 500, for instance. Then, one does a straightforward calculation using the beta and the total return to back out the quantity of alpha, representing excess or abnormal returns. The excess return is Jensen’s alpha. If positive, the alpha means that the manager has beaten the benchmark on a risk-adjusted basis. Positive alpha means the manager has added value. Negative alpha, on the other hand, suggests that an investor would be better off simply investing in the benchmark (fees aside). The manager who earns negative alpha has failed to add value from a performance perspective.
Jensen’s initial study of mutual funds from 1945 to 1964 revealed that very few managers had effectively produced a greater return than one would expect, given the level of risk of the portfolio.40 Investors finally had a mechanism by which they could parse out the risk-adjusted effects of active money management.
Samuelson and Fama: Formalizations of the Efficient Market Hypothesis
The question of whether managers can successfully add alpha remains a consistent and contentious debate in the academic literature. There are many who believe managers cannot consistently add value over the long term because markets are efficient.
One of the theorists behind this “efficient market hypothesis” was Eugene Fama, discussed previously in the context of his three-factor model with French. In his 1970 paper entitled “Efficient Capital Markets: A Review of Theory and Empirical Work,” Fama effectively defined three different types of efficiency. The first is weak-form efficiency, whereby future prices cannot be forecasted based on current information. More practically, a corollary of weak-form efficiency is that technical analysis will not yield excess returns. The second variety of efficiency is semistrong-form efficiency, in which share prices reflect all publicly available information so that excess returns cannot be produced based on public information itself. Last is strong-form efficiency, which implies that all information, both public and private, is reflected in stock prices.41 (Of course, a multitude of legal constraints exist in most regulatory environments to prevent the purest incarnation of strong-form efficiency, particularly laws prohibiting insider trading. Indeed, it is the divergence of the market from strong-form efficiency that makes insider trading profitable.) The critical implication of the efficient market hypothesis is that the market cannot be beaten if it is truly efficient.
To understand the efficient market hypothesis more completely, it is worth discussing perhaps one of its staunchest opponents: the school of value investing, which began with Benjamin Graham and David Dodd’s publication of the famed book Security Analysis in 1934. Graham and Dodd posited that one could, in fact, outperform the market by concentrating on value stocks. These were stocks that had a margin of safety, or were protected by a fundamental valuation that exceeded the market’s valuation. They also championed finding stocks that traded with relatively low price-to-book value or even sold at a discount to net tangible assets. The stock market, they believed, was irrational enough to push stocks out of favor and drive the price away from what it was actually worth based on an analysis of fundamentals.42
Graham would later discuss the short-run irrationality of the market by way of his analogy of “Mr. Market” in his subsequent book, The Intelligent Investor. Graham likened the market to a salesman who came around each day, knocked on the door, and said at what price he was willing to buy or sell, often at ridiculous levels. It was in this analogy that Graham acknowledged the randomness of the market, but he believed it was precisely this randomness that made the market exploitable if one used the right metrics of value. The markets were, in Graham and Dodd’s view, anything but efficient.43
This was not the last word Graham would have on the subject, however. In the twilight of his career, Graham actually gave up most of what he championed in these books, saying that the market was no longer as exploitable as it had been when he wrote the books: “In general, no. I am no longer an advocate of elaborate techniques of security analysis in order to find superior value opportunities. This was a rewarding activity, say, 40 years ago, when our textbook ‘Graham and Dodd’ was first published.” He went on to say that he agreed instead with those who believed the market had almost always priced securities correctly: “To that very limited extent I’m on the side of the ‘efficient market’ school of thought now generally accepted by the professors.”44
While Benjamin Graham may have given up on his work, many adherents of the philosophy of value investing have not. One may consider Warren Buffett’s primary objection to the efficient market hypothesis to illustrate this point: value investors, he claims, seem to have outperformed the market over time. The response of most proponents of the efficient market hypothesis has been that given the number of money managers in the market, statistically some will seem to outperform the market. Buffett’s response in a 1984 speech to the Columbia Business School was to discuss the records of nine investors he had known since fairly early in his career who did value investing and who he said had consistently outperformed the market on a risk-adjusted basis. The essence of Buffett’s retort is that it would be an extreme statistical anomaly not only to have seen this same group of investors beat the market in one year but to do so time and again over their careers, unless their strategies were truly adding value. And yet, supporters of the efficient market hypothesis are able to cast off these arguments as mere aberrations. Their argument is something along the lines of this: if 100 men spend an hour in Las Vegas, at least one of them should come out ahead. Of course, there is a problem with that sort of argument, because one could always claim that random chance is the source of one’s success. Such a claim is not falsifiable in a scientific sense—it cannot be “tested,” as one could always claim that random good fortune is at the root of it all. One is thus left with a decision to believe the claim that the success of the value school is due to just random luck or instead to notice that an array of investors subscribing to the philosophy from the very beginning of their careers (many of whom were eschewing such ideas as the efficient market hypothesis along the way) have produced terrific returns.45
Another Critique: Behavioral Finance
Beyond Buffett’s more anecdotal and biographical approach, there has been a rich debate between efficient market supporters and other schools of thought over the last few decades. In particular, a large body of literature has developed that has come to constitute so-called behavioral finance. Behavioral finance essentially attempts to explain empirical anomalies and deviations from the classical risk models, including the efficient market hypothesis. Instead of considering market participants as hyperrational agents obeying arguably overly elegant utility functions, they are thought of as possessing biases, prejudices, and tendencies that have real and measurable effects on markets and financial transactions. Daniel Kahneman and Amos Tversky wrote a seminal paper in the field outlining what they call prospect theory, a description of individuals’ optimization outside of the classical expected utility framework. Their pioneering paper noted many of the known behaviors that represent aberrations from expected utility theory, including lottery problems (in which individuals tend to elect a lump-sum payment up front even if that is smaller than the expected value of receiving a larger amount or zero when a coin flip is involved) and probabilistic insurance (in which individuals have a more disproportionate dislike for a form of insurance that would cover losses based on a coin flip more than the math suggests they should). Prospect theory contends that individuals’ choices are more centered on changes in utility or wealth rather than end values; it also suggests that most people exhibit loss aversion in which losses cause more harm to one’s welfare than the benefit from happiness one receives from gaining the same amount of reward.46
This theory may seem intellectually interesting, but how does it relate precisely to finance and investing? Since Kahneman and Tversky’s seminal paper, subsequent work has made many connections to markets, one of which is the “equity premium puzzle.” The equity premium puzzle was described first in a 1985 paper by Rajnish Mehra and Edward Prescott.47 The central “puzzle” is that while investors should be compensated more for holding riskier equities than holding the risk-free instrument (Treasury bills), the amount by which they are compensated seems extremely excessive historically. In other words, it seems that equity holders have been “overpaid” to take on this risk. This paper set off a flurry of responses in the years after publication. There were some who suggested that it was merely survivorship bias that explained this phenomenon; that is, there were stocks that went bankrupt or otherwise delisted and so this high premium was not real after all.48 Others suggested that there were frictions unaccounted for, such as transaction costs. The behavioral economists mounted a different set of explanations. One of the most cited and well-regarded explanations, put forth by Shlomo Benartzi and Richard Thaler in 1995, is “myopic loss aversion,” a notion that borrows heavily from the concepts developed in prospect theory, including the fact that individuals tend to exhibit loss aversion and that they care about changes in wealth more keenly than about absolute levels of wealth. Investors who frequently look at the value of their equity portfolio—say, on a daily or weekly basis when the market behaves randomly over these short time frames, moving up and down—will thus experience more disutility on average, given that they derive greater pain from losses than pleasure from the same magnitude of gains. Over long evaluation periods, however, where market movements have a general upward trend, this feeling of loss aversion is reduced because equities tend to appreciate over time, so it is more palatable to hold on to equities. The size of the equity premium, then, is really due to loss aversion experienced by investors whose frequency of evaluations is too great; if investors looked at their equities portfolios over longer time frames, they would demand lower premiums and this puzzle would be resolved.49 Other explanations that have been offered by behavioral economists focus on earnings uncertainty and how that influences investors’ willingness to bear risk, and yet others develop a dynamic loss aversion model where investors react differently to stocks that fall after a run-up compared to those that fall directly after purchase.
Another place where this behavioral lens has been applied to financial markets beyond the equity premium puzzle is momentum. Recent work has looked at momentum in the markets by analyzing serial correlations through time. The idea is that a perfectly efficient market that incorporates all information in prices instantaneously should be a statistical random walk, and a random walk should not exhibit consistent correlations with itself, or “autocorrelations,” through time. Thus, detecting serial autocorrelations may undermine the notion of efficient markets. The behavioral school has proposed two explanations for these results. First, it could be that there are feedback effects whereby market participants see the market rising and decide to buy in; or equivalently, participants could see it falling and then sell their own positions, a reaction also known as the bandwagon effect. An alternative explanation put forward for the momentum seen in markets is that the market could be underreacting to new information such that markets begin to move but do so incompletely when a news shock first occurs, only to continue to drift in that direction for a short time thereafter.50
The thrust of the efficient market theorists’ response to these objections has been that while there may be momentum in some markets, one cannot truly generate outsized returns because of transaction costs. The work used to support these counterarguments by efficient market proponents has thus sought to compare those using momentum strategies to those relying on buy-and-hold approaches as a means of showing that the returns of the latter are greater or equal to the returns of the former. Other work that has sought to shake the foundations of the efficient market hypothesis has centered on predicting returns using various stock characteristics, such as dividend yield and price-to-earnings ratio. The empirical evidence here is also mixed, with some studies advocating such strategies as “Dogs of the Dow” (or dividend-based yield strategies) as generating outsized returns followed by responses showing how this does not hold across all periods, how it may hold for only select aggregations of stocks, or again how one cannot predictably get excess returns by adhering to it.
Where Drawer 3 Has Taken Us
Perhaps the best way to characterize the effects of drawer 3 is to say it has produced monumentally powerful but often underutilized tools. While many sophisticated institutional investors, like some endowment funds, constantly think about how much alpha a manager is producing as a yardstick for the manager’s performance, others simply do not use the concept. Many investors put money with a manager and do not bother to think about how much alpha the manager is generating. This approach is especially disappointing when it comes to mutual funds, for instance, where price data are available each day and a precise alpha calculation can be performed. Alpha allows an investor to determine if a manager is earning his or her fees or not.
Beta, too, is powerful but underutilized. It may be that a manager has produced fantastic returns in an up market. However, upon close inspection with these tools, an investor may determine that the manager’s portfolio is very high beta and that in a down market, the positions may be devastated. Investors should be apprised of how much systematic risk they are enduring, which is not obvious from the absolute return figures alone and requires closer analysis with these tools.
Most of all, though, these tools should inspire a certain sentiment in the investor—an educated sense of skepticism. Markets may not be as efficient as Fama suggests, but that does not mean they are necessarily easy to exploit. Furthermore, some markets are much more efficient than others. It is more believable that a very smart manager might produce more alpha in an unusual corner of the market with understandable dislocations and few participants than in markets that are well trodden and have countless eyes monitoring their frequent moves. Investors should approach managers with this skepticism and compel them to explain their edge, the reasons the pond in which they invest is attractive, their understanding of the associated risks, and the nuances of their investment approach. There are managers who produce alpha, but the bottom line is that many do not, and these tools can aid investors in identifying some shortcomings of manager portfolios as well as the health of their associated performance.
CONCLUSION
We have taken a gentle amble through the history of the theory of asset pricing, risk, and the measurement of manager performance. These stories themselves are remarkably human, often involving very good (or very bad) fortune, random encounters that altered life trajectories, and doubt about the applicability of a scholar’s own work. There were those economists whose work was not understood for decades, like Bachelier, and others whose work induced an almost immediate and remarkable transformation in thought, like Black and Scholes. There were many who either came to these domains or worked on problems within them by chance, like Markowitz and his conversation with the stockbroker outside his adviser’s office, or Miller and Modigliani, who collaborated because neither of them precisely comprehended the original material. There were those who ended up repudiating the value of their own work, like Benjamin Graham, who said his approach no longer applied in a world of so much information availability, only to have some of his ideas validated later (both anecdotally through Warren Buffett and empirically through Fama and French’s recognition of a value factor as a source of excess returns). As much as we like to think science operates on a higher plane than the human world we normally inhabit, the historical episodes of the development of investment science suggest otherwise. Indeed, like the very markets these theorists sought to study, their own paths were fraught with tinges of the world’s inescapable randomness, quirks, and caprices.