5 STEPS TO A 5

ANSWER SHEET

Physics B—Practice Exam—Multiple-Choice Questions

Time: 90 minutes. You may refer to the Constants sheet found in the Appendixes. However, you may not use the Equations sheet, and you may not use a calculator on this portion of the exam.

1. A ball is thrown off of a 25-m-high cliff. Its initial velocity is 25 m/s, directed at an angle of 53° above the horizontal. How much time elapses before the ball hits the ground? (sin 53° = 0.80; cos 53° = 0.60; tan 53° = 1.3)

(A) 3.0 s

(B) 5.0 s

(D) 9.0 s

(E) 11.0 s

2. A ball is dropped off of a cliff of height h. Its velocity upon hitting the ground is v. At what height above the ground is the ball’s velocity equal to v/2?

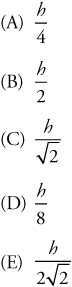
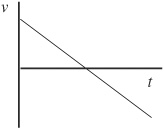
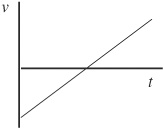
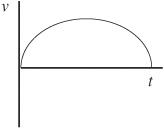
3. A golf cart moves with moderate speed as it reaches the base of a short but steep hill. The cart coasts up the hill (without using its brake or gas pedal). At the top of the hill the cart just about comes to rest; but then the cart starts to coast down the other side of the hill. Consider the forward motion of the cart to be positive. Which of the following velocity–time graphs best represents the motion of the cart?

(A)

(B)

(C)

(D)

(E)

4. The velocity–time graph above represents a car on a freeway. North is defined as the positive direction. Which of the following describes the motion of the car?

(A) The car is traveling north and slowing down.

(B) The car is traveling south and slowing down.

(D) The car is traveling south and speeding up.

(E) The car is traveling northeast and speeding up.

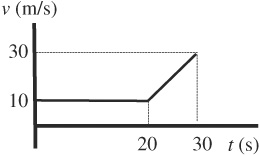
5. A car was caught in heavy traffic. After 20 s of moving at constant speed, traffic cleared a bit, allowing the car to speed up. The car’s motion is represented by the velocity–time graph above. What was the car’s acceleration while it was speeding up?

(A) 0.5 m/s²

(B) 1.0 m/s²

(D) 2.0 m/s²

(E) 3.0 m/s²

6. A block of mass m sits on the ground. A student pulls up on the block with a tension T, but the block remains in contact with the ground. What is the normal force on the block?

(A) T + mg

(B) T – mg

(D) mg – T

(E) T

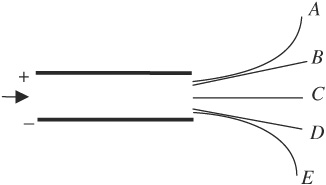
7. A proton moving at constant velocity enters the region between two charged plates, as shown above. Which of the paths shown correctly indicates the proton’s trajectory after leaving the region between the charged plates?

(A) A

(B) B

(D) D

(E) E

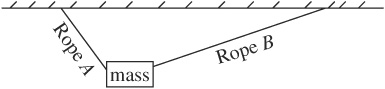
8. A mass hangs from two ropes at unequal angles, as shown above. Which of the following makes correct comparisons of the horizontal and vertical components of the tension in each rope?

9. A free-body diagram includes vectors representing the individual forces acting on an object. Which of these quantities should NOT appear on a free-body diagram?

(A) tension of a rope

(B) mass times acceleration

(D) static friction

(E) weight

10. An object rolls along level ground to the right at constant speed. Must there be any forces pushing this object to the right?

(A) Yes: the only forces that act must be to the right.

(B) Yes: but there could also be a friction force acting to the left.

(D) No: while there can be forces acting, no force MUST act.

(E) The answer depends on the speed of the object.

11. A person stands on a scale in an elevator. He notices that the scale reading is lower than his usual weight. Which of the following could possibly describe the motion of the elevator?

(A) It is moving down at constant speed.

(B) It is moving down and slowing down.

(D) It is moving up and speeding up.

(E) It is moving up with constant speed.

12. A mass m is attached to a mass 3m by a rigid bar of negligible mass and length L. Initially, the smaller mass is located directly above the larger mass, as shown above. How much work is necessary to flip the rod 180° so that the larger mass is directly above the smaller mass?

(A) 4mgL

(B) 2mgL

(D) 4πmgL

(E) 2πpmgL

13. A ball rolls horizontally with speed v off of a table a height h above the ground. Just before the ball hits the ground, what is its speed?

Questions 14 and 15

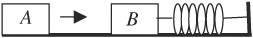
Block B is at rest on a smooth tabletop. It is attached to a long spring, which in turn is anchored to the wall. Block A slides toward and collides with block B. Consider two possible collisions:

Case I: Block A bounces back off of block B.
Case II: Block A sticks to block B.

14. Which of the following is correct about the speed of block B immediately after the collision?

(A) It is faster in case II than in case I ONLY if block B is heavier.

(B) It is faster in case I than in case II ONLY if block B is heavier.

(D) It is faster in case I than in case II regardless of the mass of each block.

(E) It is the same in either case regardless of the mass of each block.

15. Which is correct about the period of the ensuing oscillations after the collision?

(A) The period is greater in case II than in case I if block B is heavier.

(B) The period is greater in case I than in case II if block B is heavier.

(D) The period is greater in case I than in case II regardless of the mass of each block.

(E) The period is the same in either case.

16. A ball collides with a stationary block on a frictionless surface. The ball sticks to the block. Which of the following would NOT increase the force acting on the ball during the collision?

(A) increasing the time it takes the ball to change the block’s speed

(B) arranging for the ball to bounce off of the block rather than stick

(D) increasing the mass of the block

(E) anchoring the block in place so that the ball/block combination cannot move after collision

17. A 0.30-kg bird is flying from right to left at 30 m/s. The bird collides with and sticks to a 0.50-kg ball which is moving straight up with speed 6.0 m/s. What is the magnitude of the momentum of the ball/bird combination immediately after collision?

(A) 12.0 N.s

(B) 9.5 N.s

(D) 6.0 N.s

(E) 3.0 N.s

18. A car slows down on a highway. Its engine is providing a forward force of 1000 N; the force of friction is 3000 N. It takes 20 s for the car to come to rest. What is the car’s change in momentum during these 20 s?

(A) 10,000 kg·m/s

(B) 20,000 kg·m/s

(D) 40,000 kg·m/s

(E) 60,000 kg·m/s

19. Which of the following quantities is NOT a vector?

(A) magnetic field

(B) electric force

(D) electric field

(E) electric potential

20. Which of the following must be true of an object in uniform circular motion?

(A) Its velocity must be constant.

(B) Its acceleration and its velocity must be in opposite directions.

(D) It must experience a force away from the center of the circle.

(E) Its acceleration must be negative.

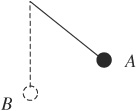
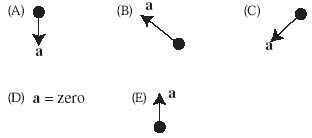
21. A ball of mass m on a string swings back and forth to a maximum angle of 30° to the vertical, as shown above. Which of the following vectors represents the acceleration, a, of the mass at point A, the highest point in the swing?

22. A planet of mass m orbits in a circle around a sun. The speed of the planet in its orbit is v; the distance from the planet to the sun is d. What is the magnitude and direction of the net force experienced by the planet?

23. A mass m on a spring oscillates on a horizontal surface with period T. The total mechanical energy contained in this oscillation is E. Imagine that instead a new mass 4m oscillates on the same spring with the same amplitude. What is the new period and total mechanical energy?

24. A satellite orbits the moon in a circle of radius R. If the satellite must double its speed but maintain a circular orbit, what must the new radius of its orbit be?

(A) 2 R

(B) 4 R

(D) ¼ R

(E) R

25. The Space Shuttle orbits 300 km above the Earth’s surface; the Earth’s radius is 6400 km. What is the gravitational acceleration experienced by the Space Shuttle?

(A) 4.9 m/s²

(B) 8.9 m/s²

(D) 10.8 m/s²

(E) zero

26. A cube of ice (specific gravity 0.90) floats in a cup of water. Several hours later, the ice cube has completely melted into the glass. How does the water level after melting compare to the initial water level?

(A) The water level is 10% higher after melting.

(B) The water level is 90% higher after melting.

(D) The water level is 10% lower after melting.

(E) The water level is 90% lower after melting.

27. A strong hurricane may include 50 m/s winds. Consider a building in such a hurricane. If the air inside the building is kept at standard atmospheric pressure, how will the outside air pressure compare to the inside air pressure?

(A) Outside pressure will be the same.

(B) Outside pressure will be about 2% greater.

(D) Outside pressure will be about twice inside pressure.

(E) Outside pressure will be about half inside pressure.

28. A heavy block sits on the bottom of an aquarium. Which of the following must be correct about the magnitude of the normal force exerted on the block by the aquarium bottom?

(A) The normal force is equal to the block’s weight.

(B) The normal force is less than the block’s weight.

(D) The normal force is equal to the buoyant force on the block.

(E) The normal force is greater than the buoyant force on the block.

29. The density of water near the ocean’s surface is p_o = 1.025 × 10³ kg/m³. At extreme depths, though, ocean water becomes slightly more dense. Let p represent the density of ocean water at the bottom of a trench of depth d. What can be said about the gauge pressure at this depth?

(A) The pressure is greater than ρ_o gd, but less than ρgd.

(B) The pressure is greater than ρgd.

(D) The pressure is greater than ρ_o gd, but could be less than or greater than ρgd.

(E) The pressure is less than ρ gd, but could be less than or greater than ρ_ogd.

30. A 1.0-m-long brass pendulum has a period of 2.0 s on a very cold (–10°C) day. On a very warm day, when the temperature is 30°C, what is the period of this pendulum?

(A) 1.0 s

(B) 1.4 s

(D) 2.0 s

(E) 4.0 s

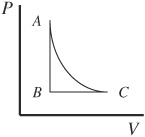
31. The state of a gas in a cylinder is represented by the PV diagram shown above. The gas can be taken through either the cycle ABCA, or the reverse cycle ACBA. Which of the following statements about the work done on or by the gas is correct?

(A) In both cases, the same amount of net work is done by the gas.

(B) In both cases, the same amount of net work is done on the gas.

(D) In cycle ABCA net work is done by the gas; in cycle ACBA the same amount of net work is done on the gas.

(E) In both cycles net work is done by the gas, but more net work is done by the gas in ACBA than in ABCA.

32. At room temperature, the rms speed of nitrogen molecules is about 500 m/s. By what factor must the absolute temperature T of the Earth change for the rms speed of nitrogen to reach escape velocity, 11 km/s?

(A) T must decrease by a factor of 50.

(B) T must increase by a factor of 22.

(D) T must increase by a factor of 200.

(E) T must increase by a factor of 500.

33. One mole of He (atomic mass 4 amu) occupies a volume of 0.022 m³ at room temperature and atmospheric pressure. How much volume is occupied by one mole of O₂ (atomic mass 32 amu) under the same conditions?

(A) 0.022 m³

(B) 0.088 m³

(D) 0.352 m³

(E) 0.003 m³

34. On average, how far apart are N₂ molecules at room temperature?

(A) 10^–21m

(B) 10^–15m

(D) 10^–3 m

(E) 1 m

35. Which of the following is NOT a statement or consequence of the second law of thermodynamics, the law dealing with entropy?

(A) The net work done by a gas cannot be greater than the sum of its loss of internal energy and the heat added to it.

(B) Even an ideal heat engine cannot be 100% efficient.

(D) A system cannot become more ordered unless some net work is done to obtain that order.

(E) Heat does not flow naturally from a low to high temperature.

36. Experimenter A uses a very small test charge q₀, and experimenter B uses a test charge 2q₀ to measure an electric field produced by stationary charges. A finds a field that is

(A) greater than the field found by B

(B) the same as the field found by B

(D) either greater or less than the field found by B, depending on the accelerations of the test charges

(E) either greater or less than the field found by B, depending on the masses of the test charges

37. Two isolated particles, A and B, are 4 m apart. Particle A has a net charge of 2Q, and B has a net charge of Q. The ratio of the magnitude of the electrostatic force on A to that on B is

(A) 4:1

(B) 2:1

(D) 1:2

(E) 1:4

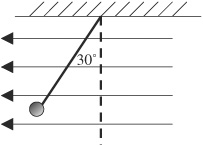
38. A uniform electric field points right to left. A small metal ball charged to +2 mC hangs at a 30° angle from a string of negligible mass, as shown above. The tension in the string is measured to be 0.1 N. What is the magnitude of the electric field? (sin 30° = 0.50; cos 30° = 0.87; tan 30° = 0.58).

(A) 25 N/C

(B) 50 N/C

(D) 5000 N/C

(E) 10,000 N/C

39. 1.0 nC is deposited on a solid metal sphere of diameter 0.30 m. What is the magnitude of the electric field at the center of the sphere?

(A) zero

(B) 25 N/C

(D) 200 N/C

(E) 400 N/C

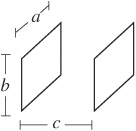
40. The parallel plate capacitor above consists of identical rectangular plates of dimensions a × b, separated by a distance c. To cut the capacitance of this capacitor in half, which of these quantities should be doubled?

(A) a

(B) b

(D) ab

(E) abc

41. Two identical capacitors are connected in parallel to an external circuit. Which of the following quantities must be the same for both capacitors?

I. the charge stored on the capacitor

II. the voltage across the capacitor

III. the capacitance of the capacitor

(A) I only

(B) II only

(D) I and III only

(E) I, II, and III

42. Three resistors are connected to a 1.0 V battery, as shown in the diagram above. What is the current through the 2.0 Ω resistor?

(A) 0.25 A

(B) 0.50 A

(D) 2.0 A

(E) 4.0 A

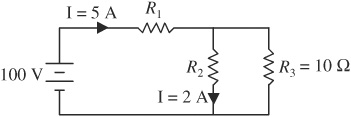
43. What is the voltage drop across R₃ in the circuit diagrammed above?

(A) 10 V

(B) 20 V

(D) 50 V

(E) 100 V

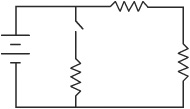
44. Three resistors are connected to an ideal battery as shown in the diagram above. The switch is initially open. When the switch is closed, what happens to the total voltage, current, and resistance in the circuit?

45. On which of the following physics principles does Kirchoff’s loop rule rest?

(A) conservation of charge

(B) conservation of mass

(D) conservation of momentum

(E) conservation of angular momentum

Questions 46 and 47

A uniform magnetic field B is directed into the page. An electron enters this field with initial velocity v to the right.

46. Which of the following best describes the path of the electron while it is still within the magnetic field?

(A) It moves in a straight line.

(B) It bends upward in a parabolic path.

(D) It bends upward in a circular path.

(E) It bends downward in a circular path.

47. The electron travels a distance d, measured along its path, before exiting the magnetic field. How much work is done on the electron by the magnetic field?

(A) evBd

(B) zero

(D) evBd sin (d/2π)

(E) –evBd sin (d/2π)

48. The circular wire shown above carries a current I in the counterclockwise direction. What will be the direction of the magnetic field at the center of the wire?

(A) into the page

(B) out of the page

(D) up

(E) counterclockwise

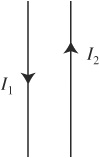
49. Two parallel wires carry currents in opposite directions, as shown above. In what direction will the right-hand wire (the wire carrying current I₂) experience a force?

(A) left

(B) right

(D) out of the page

(E) The right-hand wire will experience no force.

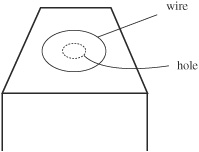
50. A loop of wire surrounds a hole in a table, as shown above. A bar magnet is dropped, north end down, from above the table through the hole. Let the positive direction of current be defined as counterclockwise as viewed from above. Which of the following graphs best represents the induced current I in the loop?

(A)

(B)

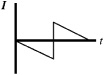
(C)

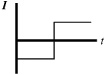
(D)

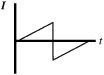
(E)

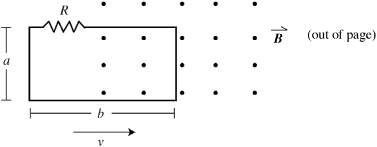
51. A rectangular loop of wire has dimensions a × b and includes a resistor R. This loop is pulled with speed v from a region of no magnetic field into a uniform magnetic field B pointing through the loop, as shown above. What is the magnitude and direction of the current through the resistor?

(A) Bav/R, left-to-right

(B) Bbv/R, left-to-right

(D) Bbv/R, right-to-left

(E) Bba/R, right-to-left

52. A proton moves in a straight line. Which of the following combinations of electric or magnetic fields could NOT allow this motion?

(A) only an electric field pointing in the direction of the proton’s motion

(B) only a magnetic field pointing opposite the direction of the proton’s motion

(D) only a magnetic field pointing perpendicular to the proton’s motion

(E) only a magnetic field pointing in the direction of the proton’s motion

53. A guitar string is plucked, producing a standing wave on the string. A person hears the sound wave generated by the string. Which wave properties are the same for each of these waves, and which are different?

54. A traveling wave passes a point. At this point, the time between successive crests is 0.2 s. Which of the following statements can be justified?

(A) The wavelength is 5 m.

(B) The frequency is 5 Hz.

(D) The wavelength is 0.2 m.

(E) The wavelength is 68 m.

55. What is the frequency of sound waves produced by a string bass whose height is 2 m? The speed of waves on the string is 200 m/s.

(A) 5 Hz

(B) 0.05 Hz

(D) 500 Hz

(E) 5000 Hz

56. What property of a light wave determines the color of the light?

(A) frequency

(B) wavelength

(D) amplitude

(E) the medium through which the light wave travels

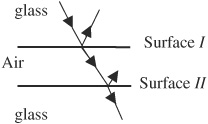
57. Light traveling through glass hits a thin film of air, as shown above. For which of the following beams of light does the light wave change phase by 180°?

(A) the light reflected off of surface I

(B) the light transmitted through surface I

(D) the light transmitted through surface II

(E) both the light reflected off of surface I and the light reflected off of surface II

58. Light from a coherent source passes through a diffraction grating, producing an interference pattern on a screen. Three of the bright spots produced on the screen are 2.2 cm away from one another, as shown above. Now, a new diffraction grating is substituted, whose distance between lines is half of the original grating’s. Which of the following shows the new interference pattern?

(A)

(B)

(C)

(D)

(E)

59. Which colors of visible light have the largest frequency, wavelength, and energy per photon?

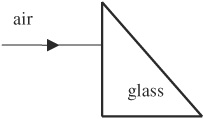
60. White light is incident on the triangular glass prism shown above. Why is it that blue and red light can be seen separately when the light exits the prism?

(A) The blue light speeds up more inside the glass.

(B) Some of the red light reflects at each interface.

(D) The blue light bends farther away from normal at the left-hand interface.

(E) The blue light bends farther away from normal at the right-hand interface.

61. A convex lens projects a clear, focused image of a candle onto a screen. The screen is located 30 cm away from the lens; the candle sits 20 cm from the lens. Later, it is noticed that this same lens can also project a clear, focused image of the lighted windows of a building. If the building is located 60 meters away, what is the distance between the lens and the image of the building?

(A) 12 cm

(B) 24 cm

(D) 80 cm

(E) 90 cm

I. concave mirror

II. convex mirror

III. concave lens

IV. convex lens

62. Which of the optical instruments listed above can produce a virtual image of an object that is smaller than the object itself?

(A) I only

(B) II only

(D) II and III only

(E) I and IV only

63. Which of the following does NOT describe a ray that can be drawn for a concave mirror?

(A) an incident ray through the mirror’s center, reflecting right back through the center

(B) an incident ray through the center point, reflecting through the focal point

(D) an incident ray parallel to the principal axis, reflecting through the focal point

(E) an incident ray to the intersection of the principal axis with the mirror, reflecting at an equal angle.

64. Monochromatic light is incident on a photoelectric surface with work function W. The intensity, I, of the incident light is gradually increased. Which of the following graphs could represent the kinetic energy, KE, of electrons ejected by the photoelectric surface as a function of the intensity?

(A)

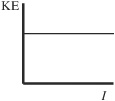
(B)

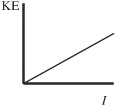
(C)

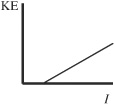
(D)

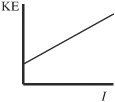
(E)

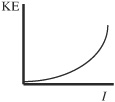
Questions 65 and 66

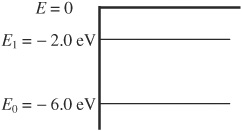
The energy levels of a hypothetical atom are shown above.

65. What wavelength of light must be absorbed to excite electrons from E₀ to E₁?

(A) 1240 nm

(B) 620 nm

(D) 210 nm

(E) 310 nm

66. E₀ and E₁ are the only atomic energy levels available to electrons inside the atom. How many different colored photons can this atom emit when it captures an electron with no kinetic energy?

(A) zero

(B) one

(D) three

(E) four

67. Monochromatic light is incident on a photoelectric surface of work function 3.5 eV. Electrons ejected from the surface create a current in a circuit. It is found that this current can be neutralized using a stopping voltage of 1.0 V. What is the energy contained in one photon of the incident light?

(A) 1.0 eV

(B) 2.5 eV

(D) 4.5 eV

(E) 5.5 eV

68. Which of the following observations provides evidence that massive particles can have a wave nature?

(A) When burning hydrogen is observed through a spectrometer, several discrete lines are seen rather than a continuous spectrum.

(B) When a beam of electrons is passed through slits very close together and then projected on to a phosphorescent screen, several equally spaced bright spots are observed.

(D) When alpha particles are passed through gold foil, most of the alpha particles go through the foil undeflected.

(E) When light is reflected off of a thin film, bright and dark fringes are observed on the film.

69. In which of the following nuclear processes do both the atomic number Z as well as the atomic mass A remain unchanged by the process?

(A) uranium fission

(B) alpha decay

(D) beta^– decay

(E) gamma decay

70. A thorium nucleus emits an alpha particle. Which of the following fundamental physics principles can be used to explain why the direction of the daughter nucleus’s recoil must be in the opposite direcztion of the alpha emission?

I. Newton’s third law

II. conservation of momentum

III. conservation of energy

(A) II only

(B) III only

(D) II and III only

(E) I, II, and III

STOP. End of Physics B—Practice Exam—Multiple-Choice Questions

Physics B—Practice Exam—Free-Response Questions

Time: 90 minutes. You may refer to the Constants sheet and Equations sheet in the Appendixes during this portion of the exam. You may also use a calculator during this portion of the exam.

(Note: In some years, the Physics B free-response section will be reduced to six rather than seven questions, still with a 90-minute time frame. We’ll leave the seventh question in there for you for extra practice.)

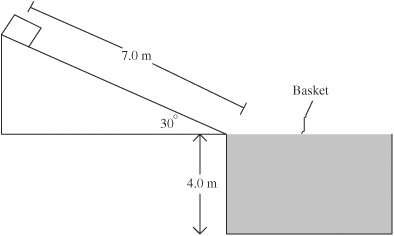
1. (15 points)

A package is at rest on top of a frictionless, 7.0 m long, 30° inclined plane, as shown above. The package slides down the plane, then drops 4.0 vertical meters into a waiting basket.

(a) How long does it take the package to reach the bottom of the plane?

(b) What is the magnitude and direction of the velocity of the package when it reaches the bottom of the plane?

(c) What is the TOTAL time it takes for the package both to slide down the plane and then to hit the bottom of the basket?

(d) How far, horizontally, from the left-hand edge of the basket will the package hit the bottom?

(e) If the basket were 8.0 m deep rather than 4.0 m deep, how would the answer to part (d) change? Check one box, and justify your answer without reference to an explicit numerical calculation.

The horizontal distance would be doubled.

The horizontal distance would be more than doubled.

The horizontal distance would be increased, but less than doubled.

2. (15 points)

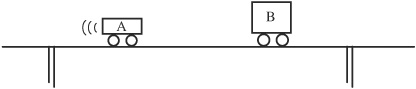
Two carts with different masses collide on a level track on which friction is negligible. Cart B is at rest before the collision. After the collision, the carts bounce off of one another; cart A moves backward, while cart B goes forward.

Consider these definitions of variables:

• m_A, the mass of cart A

• m_B, the mass of cart B

• v_A, the speed of cart A before collision

• v_A, the speed of cart A after collision

• v_B, the speed of cart B after collision

(a) Using only the variables listed above, derive an expression for the fraction of momentum conserved in this collision.

(b) Using only the variables listed above, derive an expression for the fraction of kinetic energy conserved in the collision.

(d) You are given the following equipment:

one sonic motion detector

one stopwatch

one meter stick

Describe a procedure that would allow an experimenter to measure the speeds of the carts before and after collision (keeping in mind that cart B is at rest before collision). Remember to be explicit about the placement of the motion detector; explain clearly how each speed can be determined from your measurements.

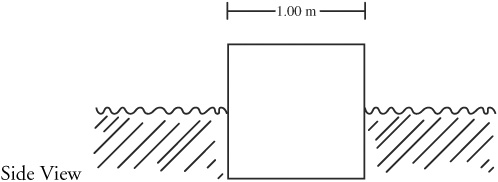
3. (15 points)

A large cube with a side of length 1.00 m is floating on top of a lake. Resting undisturbed, it floats exactly half submerged, as shown above. The density of water is 1000 kg/m³.

(a) Determine the mass of the cube.

A crane pushes the cube down into the water until it is ¾ underwater, as shown; the cube is then released from rest.

(b) Determine the magnitude and direction of the net force on the cube at the moment when it is released.

(c) After release, the cube oscillates up and down in simple harmonic motion, just as if it were attached to an ideal spring of “effective spring constant” k. Determine this effective spring constant.

(d) Determine the frequency of the resulting harmonic motion.

(e) If instead, the block is released after being pushed 4/5 of the way into the water, which of the following is correct about the frequency of the new harmonic motion? Check one of the three boxes below, then justify your answer.

The frequency will be greater than before.

The frequency will be smaller than before.

The frequency will be the same as it was before.

4. (15 points)

An electron starts from rest and is accelerated between two metal plates over a distance of 1.0 cm through a potential difference of 500 V. The electron exits the plates at point B, as shown in the diagram above. Neglect any relativistic effects.

(a) What is the velocity of this electron once it reaches point B?

(b) Once the electron has left point B, it enters directly between a second set of 50-cm-long parallel plates. These are arranged horizontally, separated by 5 cm, and with a 100 V potential difference between them.

i. What are the magnitude and direction of the electric force, F_E, on the electron?

ii. Determine the time it takes for the electron to travel the 50 cm through these plates to point C.

iii. Determine the speed of the electron at point C.

(c) While the electron is traveling, it is simultaneously in the gravitational field of the Earth. Explain why it is legitimate to neglect the influence of the gravitational field; include a calculation in your explanation.

5. (10 points)

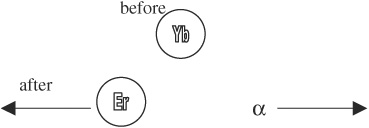
An α-particle is emitted with velocity 1.7 × 10⁷ m/s to the right by an initially motionless Ytterbium nucleus with mass number A = 173, as shown above. Ytterbium has atomic number Z = 70.

(a) Determine the mass number A and atomic number Z of the resulting Erbium nucleus.

(b) Calculate the magnitude of the momentum of the resulting Erbium nucleus.

Radiation beam incident on Erbium nucleus initially moving to the left

After the decay, a beam of radiation of frequency 450 Hz is incident upon the Erbium nucleus opposite the direction of motion. Each photon in the beam is reflected back by the Erbium. Approximately 10²⁵ photons strike the nucleus each second.

6. (10 points)

An accident occurred in a parking lot. Police lieutenants examined the scene of this accident and found that one of the involved cars, which just about came to a stop before the collision, made skid marks 80 m long. The coefficient of kinetic friction between the rubber tires and the dry pavement was about 0.80; a typical car has a mass of 700 kg.

(a) Draw a free-body diagram representing the forces on the car as it skidded. Assume the car was moving to the right.

(b) Assuming a level road, estimate how fast this car was initially traveling.

(d) In court, the driver explains that his car is particularly heavy—it has a mass not of 700 kg, but of 2100 kg. Thus, he suggests that calculations showing he was speeding are invalid. Explain whether the driver’s argument makes sense.

7. (10 points)

A light ray traveling in air is incident upon a glass (n = 1.5) trapezoid as shown above.

(a) Draw and label the normal to the surface at the point at which the light enters the glass.

(b) Determine the angle θ₂ at which the light enters the glass; draw the transmitted ray on the above diagram and label θ₂ on your drawing.

— If the light leaves through the bottom edge, at what angle will it enter the air? Show all calculations and draw the transmitted ray.

— If the light leaves through the right-hand edge, explain why it will not leave through the bottom edge. Show all calculations and draw the path of the ray through the glass.

STOP. End of Physics B—Practice Exam—Free-Response Questions

Physics B—Practice Exam—Multiple-Choice Solutions

1. B—Only the vertical motion affects the time in the air. Set up kinematics, with up positive:

v_o = 25 sin 53° m/s = 20 m/s.

v_f = ?

Δ x = – 25 m.

a= –10 m/s².

t = what we’re looking for.

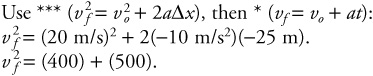
v_f = –30 m/s, negative because ball moves down at the end.

So * says –30 m/s = 20 m/s + (–10)t; t= 5.0 s.

2. A—Set up a kinematics chart with down positive:

v_o = 0 because dropped.

v_f = v, given.

Δ x = h.

a = g.

t = unknown.

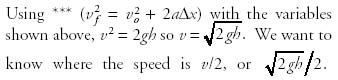
Reset the kinematics chart and solve:

v_o = 0 because ball dropped.

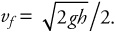
Δx = what we’re looking for.

a = g.

t = unknown.

Using ***, 2gh/2 = 2gΔx; Δx = h/4.

3. D—The cart must slow down as it goes up the hill. Only A, B, and D start with nonzero speed that approaches zero speed after a long time. The speed reaches zero and then the cart speeds up again in the same direction. Only D keeps the motion in the same direction after the pause.

4. B—Because north is positive, and the velocity is always in the negative section of the graph, the car must move to the south. Because the speed is getting closer to zero, the car slows down.

5. D—Acceleration is the slope of the v—t graph. Here, we only want the slope while the car speeds up: (30–10)m/s / (30–20)s = 2.0 m/s².

6. D—The free-body diagram looks like this:

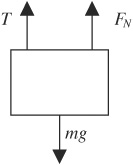
Because the block is in equilibrium, F_N + T = mg. Solving, F_N = mg – T.

7. D—While in the region between the plates, the positively charged proton is attracted to the negative plate, so bends downward. But after leaving the plates, there is no more force acting on the proton. Thus, the proton continues in motion in a straight line by Newton’s first law.

8. B—Consider the horizontal and vertical forces separately. The only horizontal forces are the horizontal components of the tensions. Because the block is in equilibrium, these horizontal tensions must be equal, meaning only choices B and D can be right. But the ropes can’t have equal horizontal AND vertical tensions, otherwise they’d hang at equal angles. So D can’t be the correct choice, and B must be.

9. B—Tension, friction, and weight are specific forces that can pull or drag an object. But “mass times acceleration” is what we set the sum of all forces equal to—ma is not itself a force.

10. D—If the object is rolling straight at constant speed, it is in equilibrium (regardless of its speed), and the net force on it is zero. But zero net force can be obtained either by rightward forces canceling leftward forces, or by no forces acting at all.

11. C—Consider the free-body diagram of the person:

Call up positive, and F_scale – weight= ma. The scale reading is less than his normal weight, so the acceleration is negative; i.e., down. Downward acceleration means either something speeds up while moving downward, or slows down while moving upward.

12. B—Work done by gravity depends only on vertical displacement, not on the total distance moved. The displacement of each mass is L. Work is force (here, weight) times this displacement. It takes 3mgL of work to raise the bottom mass, but while that’s done, the small mass moves down; this means that negative mgL of work was done to lower the small mass. The total work necessary, then, is 3mgL + (–mgL) = 2mgL.

13. C—Speed means the magnitude of the velocity vector, not just the vertical velocity; so you can’t just use vertical kinematics. You find the final velocity in both directions, and add the vectors. It’s easier, though, to use energy. Call point A the top of the table, point B the floor. PE_A + KE_A = PE_B + KE_B; mgh + ¹/₂ mv² = 0 + ¹/₂ mv²_B. Cancel the m and solve for v_B, and you get to

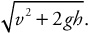
14. D—Momentum must be conserved in the collision. If block A bounces, it changes its momentum by a larger amount than if it sticks. This means that block B picks up more momentum (and thus more speed) when block A bounces. The mass of the blocks is irrelevant because the comparison here is only between bouncing and not bouncing. So B goes faster in case I regardless of mass.

15. C—The period depends only on the mass attached to the spring, not at all on the speed. When block A sticks, more mass is attached, and the period is longer according to

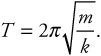
Which mass is bigger is irrelevant; two blocks will always be heavier than one block.

16. A—The relevant equation here is for impulse: Δp = FΔt. The force on the block can be increased either by increasing the momentum change or by decreasing the time of collision. E decreases collision time; B, C, and D all increase the momentum change. But A increases the collision time, thereby decreasing the force.

17. B—The system has momentum 3 N·s up, and 9 N·s left. The magnitude of the momentum vector is the Pythagorean sum of 3 and 9 Nil Error·s Without calculating, we know the answer must be more than 9 and less than 12 N.s.

18. D—Change in momentum is FΔt. What does that force represent? The net force, which here is 2000 N to the left. 2000 N times 20 s is 40,000 N.s, equivalent to 40,000 kg-m/s.

19. E—Fields are vectors because they cause forces, and force is a vector. Current is a vector because charge can flow in either direction in a wire. However, electric potential is related (by PE = qV) to potential energy, and all forms of energy are scalar quantities.

20. C—The velocity of an object in circular motion is NOT constant because the direction of motion changes. The acceleration and net force must be toward the center of the circle. Because the object’s velocity vector is tangent to the circle, acceleration and velocity must be perpendicular to each other.

21. C—At point A the mass is momentarily at rest, just before it retraces its path back to the bottom. Acceleration is a change in velocity. Velocity is zero now, and in a moment will be along the circular path of the pendulum. So acceleration must point in the direction of this velocity change.

22. B—Centripetal acceleration is v²/r, and is always center seeking; here this must be toward the sun. But the problem asks for the net force, which is mass times acceleration.

23. B—The period of a mass on a spring is

so multiplying the mass by 4 multiplies the period by 2. The total mechanical energy is equal to the potential energy at the maximum displacement. Here, because the amplitude (i.e., the maximum displacement) doesn’t change, the total mechanical energy is also unchanged.

24. D—In an orbit, the centripetal force is provided by gravity, mv²/r = GMm/r². Solving for the radius of the orbit, r = GM/v². (Here M is the mass of the moon; the mass of the satellite cancels out.) Doubling the speed, which is squared and in the denominator, divides the radius of the orbit by 4.

25. B—Don’t try to calculate the answer by saying mg = GMm/r²! Not only would you have had to memorize the mass of the Earth, but you have no calculator and you only have a minute or so, anyway. So think: the acceleration must be less than 9.8 m/s² because that value is calculated at the surface of the Earth, and the Shuttle is farther from Earth’s center than that. But the added height of 300 km is a small fraction (~5%) of the Earth’s radius. So the gravitational acceleration will not be THAT much less. The best choice is thus 8.9 m/s². (By the way, acceleration is not zero—if it were, the Shuttle would be moving in a straight line, and not orbiting.)

26. C—Ice is 90% as dense as liquid water. So 90% of its volume is under the water, displacing water. Okay, when the ice melts, the new liquid takes up only 90% of the space it originally occupied. This liquid’s volume is equal to the amount of volume originally displaced by the ice, so the water level does not rise.

27. C—Use Bernoulli’s equation with the flowing fluid. Consider inside and outside the building as the two positions. The y terms are equal, so get rid of them. Call the velocity inside the building zero. We’re left with 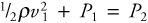, where 2 means inside the building and 1 is outside. So: pressure outside is less than pressure inside. By how much? Well, if you happened to remember that the density of air is about 1 kg/m³, you can make the calculation. But just look at the choices. Ambient pressure doesn’t even drop by half when you go to the top of a mountain! So the answer is that pressure drops by a couple percentage points.

28. B—The free-body diagram of the mass includes the buoyant force AND the normal force up, and mg down. Because the block is in equilibrium, F_N + F_B = mg. So the normal force is less than mg and certainly not equal to the weight.

29. A—For a fluid of uniform density, the pressure at depth d is ρgd because of the weight of the water above depth d. But here, because the density of the water gets bigger, the weight of the water is greater. So the pressure should be greater than ρ_ogd. The pressure is less than ρgd, because ρ is the maximum density.

30. D—Don’t use the length expansion equation here, because we don’t know the expansion coefficient for brass. Rather, just know that the change in an object’s length is always a very small fraction of the original length. By

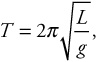
if the length of the pendulum increases, the period increases as well, eliminating choices (A), (B), and (C). In thermal length expansion, length increases by only a small fraction of the original length . . . there’s no possibility of even doubling the pendulum’s original length, let alone quadrupling the original length to produce a 4.0 s period. Choice (D) is correct. Try it on your calculator— if the pendulum’s length increases to, say, 1.01 m, the period is still 2.0 s.

31. C—The net work done on or by a gas is the area inside the cycle on the PV diagram, so the amount of net work is the same in either direction. In ABCA more work is done ON the gas than by the gas because there’s more area under the curve when the volume compresses than when volume expands. By the same logic, in ACBA more work is done BY the gas than on the gas.

32. E—rms velocity is given by

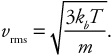
Use round numbers to make calculations easier. v_rms would have to be multiplied by a bit more than 20 to reach escape velocity. So the temperature would have to be multiplied by more than 20², or more than 400 times.

33. A—By the ideal gas law, V = Nk_bT/P. Because none of the terms on the right change when we discuss oxygen rather than helium, the volume should be the same.

34. C—No time or calculator to do the calculation here, but the answer choices allow for an order of magnitude estimate. A molecule is about 1 Angstrom, or 10^–10 m, across. The separation between molecules must be bigger than this. But molecules certainly aren’t a millimeter apart from one another! The only choice that makes sense is C.

35. A—B, D, and E are all alternative statements of the second law. C is a consequence of that law—even though energy would be conserved if the putty cooled off and jumped, this action is never observed. A, the correct choice, is a statement of the FIRST law of thermodynamics, which itself is a statement of conservation of energy.

36. B—An electric field exists regardless of the amount of charge placed in it, and regardless of whether any charge at all is placed in it. So both experimenters must measure the same field (though they will measure different forces on their test charges).

37. C—Ah, the Newton’s third law question. Whether we’re talking about cars or charges, the force on object A due to object B is always the same as the force on object B due to object A. Thus the forces described must be equal.

38. A—The charge is in equilibrium, so the horizontal component of the tension must equal the electric force. This horizontal tension is 0.1 N times sin 30° (not cosine because 30° was measured from the vertical), or 0.05 N. The electric force is qE, where q is 0.002 C. So the electric field is 0.050 N/0.002 C . . . reduce the expression by moving the decimal to get 50/2, or 25 N/C.

39. A—In a metal sphere, charge is free to move, so the charge ends up on the surface evenly distributed. The electric fields due to each of these charges cancel at the center because for every charge causing a field pointing one way, another charge on the other side of the sphere will cause an equal field pointing the other way. (It’s worth knowing that the electric field ANYWHERE inside a conductor is always zero; the justification for this is done in Physics C with Gauss’s law.)

40. C—Capacitance of a parallel plate capacitor is ε_oA/d, where A is the area of the plates and d is the separation between plates. To halve the capacitance, we must halve the area or double the plate separation. The plate separation in the diagram is labeled c, so double distance c.

41. E—Connected in parallel means that the voltage for each capacitor must be the same. The capacitors are identical, so the capacitance of each is the same. Thus, by Q = CV, the charge on each must be the same, too.

42. B—Voltage is always the same across parallel resistors. Because the 2.0 Ω resistor is hooked directly to the battery, the voltage across it is 1.0 V. By Ohm’s law, I = V/R = 0.50 amps.

43. C—The 5 A of current splits into two paths. The path through R₂ takes 2 A, so the path through R₃ takes 3 A. Now use Ohm’s law: V = (3 A) (10 Ω) = 30 V.

44. D—The voltage must stay the same because the battery by definition provides a constant voltage. Closing the switch adds an extra parallel branch to the network of resistors. Adding a parallel resistor REDUCES the total resistance. By Ohm’s law, if voltage stays the same and resistance decreases, total current must increase.

45. C—Kirchoff’s loop rule says that the sum of voltage changes around a closed circuit loop is zero. When a charge gains or loses voltage, it is also gaining or losing energy. The fact that the charge must end up with the same energy it started with is a statement of energy conservation.

46. E—A charge in a uniform magnetic field takes a circular path because the magnetic force changes direction, so it’s always perpendicular to the charge’s velocity. Here the magnetic force by the right-hand rule is initially down. (Did you think the force on the charge was up? An electron has a negative charge, so the right hand rule gives a direction opposite to the direction of the force.)

47. B—Work is force times parallel displacement. Because the magnetic force is always perpendicular to the particle’s direction of motion, no work can be done by the magnetic field.

48. B—The magnetic field caused by a straight wire wraps around the wire by the right-hand rule. Consider just little parts of the curvy wire as if the parts were momentarily straight. The part of the wire at the top of the page produces a B field out of the page in the region inside the loop; the parts of the wire at the bottom of the page or on the side of the page also produce B fields out of the page inside the loop. These fields reinforce each other at the center, so the net B field is out of the page.

49. B—The magnetic field produced by I₁ is out of the page at the location of wire 2. The current I₂ is thus moving in a magnetic field; the force on that current-carrying wire is given by ILB and the right-hand rule, which shows a rightward force.

50. D—Lenz’s law dictates that the direction of induced current is in the direction of decreasing flux by the right-hand rule. The magnetic field from the bar magnet points out of the north end, which is down. When the magnet gets closer to the loop of wire, the field gets stronger, so flux increases in the down direction; therefore, the direction of decreasing flux is the other way, up; and the right-hand rule gives an initial current counterclockwise. As the magnet falls away from the loop, the field still points down (into the south end), but the flux decreases, so now the current flows clockwise. Only choice D shows counterclockwise current changing to clockwise current.

51. A—You remember the equation for the induced EMF in a moving rectangular loop, ε = Blv. Here l represents the length of the wire that doesn’t change within the field; dimension a in the diagram. So the answer is either A or C. To find the direction of induced current, use Lenz’s law: The field points out of the page, but the flux through the loop is increasing as more of the loop enters the field. So, point your right thumb into the page (in the direction of decreasing flux) and curl your fingers; you find the current is clockwise, or left-to-right across the resistor.

52. D—An electric field exerts a force on all charged particles parallel to the field; thus situation (A) would slow the proton down, but not change its direction. Magnetic fields only apply a force if they are perpendicular to a charge’s velocity, so (B) and (E) cannot change the proton’s direction. A magnetic field perpendicular to motion DOES change a proton’s direction, but if a suitable electric field is also included, then the electric force can cancel the magnetic force. So choice D is the only one that must change the direction of the proton.

53. E—The two waves described move through different media (one through the string, one through the air), so must have different speeds. But, because the sound wave was generated by the string wave, the waves have the same frequencies. By v = λf, the wavelength must be different for each as well.

54. B—The time between crests is the period of the wave. Period is 1/frequency. So the frequency is 1/(0.2 s), which is 5 Hz.

55. C—Use v = λf. The wavelength of the string bass is twice the height (because it’s a standing wave fixed at both ends), or 4 m. The frequency is 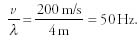When the wave changes materials—from the string to the air—the frequency is unchanged.

56. A—Frequency determines color. Think about seeing underwater. You see the same colors in clear water that you do in air. But underwater, the speed of the light waves is slower, and the wavelength is shorter. So if wavelength or wave speed determined color, you would see different colors underwater. (Amplitude determines brightness, and the medium through which the wave travels just determines wave speed.)

57. C—Light waves change phase by 180° when they are reflected off a material with higher index of refraction; this only happens in the diagram when light reflects off of the bottom surface.

58. C—For simplicity’s sake, let’s assume that the light is not refracted through huge angles, so we can say that x = mλL/d, where x is the distance between spots. d is the distance between lines in the grating. So if d is cut in half, x is doubled; the spots are twice as far apart. The size of the spots themselves should not change.

59. C—E = hf, so the higher frequency light also has higher energy per photon. But wavelength varies inversely with frequency by v = λf, so bigger frequency means smaller wavelength. You should know either that red light has the longest wavelength, or that violet light has the highest frequency.

60. E—(A) is wrong—light slows down in glass. (C) is wrong—waves do not change frequency when changing media. (D) is wrong—light doesn’t change direction at all when hitting an interface directly from the normal. Choice (B) is wrong because, while some red light does reflect at each interface, this doesn’t help explain anything about seeing light upon exiting the prism. However, blue light does experiences a larger index of refraction than red, so it bends farther from normal when it hits an interface at an angle.

61. A—The light from the building that is very far away will be focused at the focal point of the lens. The first part of the problem lets you figure out the focal point using the lensmaker’s equation, 1/f = 1/30 cm + 1/20 cm, so f = 60/5 = 12 cm.

62. D—All can produce virtual images. However, the converging instruments (the concave mirror and convex lens) can only show virtual images if the object is inside the focal point; these images are larger than the object itself. (Think of a magnifying glass and the inside of a spoon.) The convex mirror and concave lens are diverging instruments, which can ONLY produce smaller, upright images. (Think of a Christmas tree ornament.).

63. B—All mirror rays through the center reflect right back through the center.

64. A—The frequency of incident photons affects the energy of ejected electrons; the intensity of the beam (number of photons per second) is irrelevant. Thus, the KE vs. intensity graph is simply a horizontal line.

65. E—To jump from E₀ to E₁ the electron needs to absorb 4.0 eV of energy. So the necessary wavelength is given by 1240 eV·nm/4.0 eV, or 310 nm. (E = hc/λ, and hc = 1240 eV, as stated on the Constant Sheet.)

66. D—The electron can drop from E = 0 to E₀ or to E₁. It can also drop from E₁ to E₀. That makes three different transitions, and three different wavelengths (i.e. colors) of photons.

67. D—The stopping voltage is applied to a beam of electrons. Because 1 eV is the energy of 1 electron moved through 1 V of potential difference, these electrons initially had 1 eV of kinetic energy (that was converted into potential energy in order to stop the electrons). These electrons needed 3.5 eV to escape the atom, plus 1 eV for their kinetic energy; this makes a total of 4.5 eV needed from each photon.

68. B—In choices A and E, it is light exhibiting wave properties; light is not made up of massive particles. C involves surface waves on the ocean, not the wave behavior of water molecules themselves. Choice D describes Rutherford’s experiment, which demonstrated the existence of the atomic nucleus. So choice B is correct: a beam of electrons is a beam of massive particles. The experiment described demonstrates both diffraction (bending) and interference, both of which are wave properties.

69. E—Only gamma decay keeps atomic mass and number the same, because a gamma particle is just a high energy photon; a photon has neither mass nor charge.

70. C—Newton’s third law requires the daughter nucleus to experience a force opposite to the force exerted on the alpha particle; thus, the daughter must move backward. Conservation of momentum requires the net momentum to be zero after the decay as well as before; this only happens if the daughter moves backward to cancel the alpha’s forward momentum. But energy is a scalar, and has no direction. Conservation of energy can be satisfied no matter which way the particles move.

Physics B—Practice Exam—Free-Response Solutions

Notes on grading your free-response section

For answers that are numerical, or in equation form:

* For each part of the problem, look to see if you got the right answer. If you did, and you showed any reasonable (and correct) work, give yourself full credit for that part. It’s okay if you didn’t explicitly show EVERY step, as long as some steps are indicated, and you got the right answer. However:

* If you got the WRONG answer, then look to see if you earned partial credit. Give yourself points for each step toward the answer as indicated in the rubrics below. Without the correct answer, you must show each intermediate step explicitly in order to earn the point for that step. (See why it’s so important to show your work?)

* If you’re off by a decimal place or two, not to worry—you get credit anyway, as long as your approach to the problem was legitimate. This isn’t a math test. You’re not being evaluated on your rounding and calculator-use skills.

* You do not have to simplify expressions in variables all the way. Square roots in the denominator are fine; fractions in nonsimplified form are fine. As long as you’ve solved properly for the requested variable, and as long as your answer is algebraically equivalent to the rubric’s, you earn credit.

* Wrong, but consistent: Often you need to use the answer to part (a) in order to solve part (b). But you might have the answer to part (a) wrong. If you follow the correct procedure for part (b), plugging in your incorrect answer, then you will usually receive full credit for part (b). The major exceptions are when your answer to part (a) is unreasonable (say, a car moving at 10⁵ m/s, or a distance between two cars equal to 10^–100 meters), or when your answer to part (a) makes the rest of the problem trivial or irrelevant.

For answers that require justification:

*Obviously your answer will not match the rubric word-for-word. If the general gist is there, you get credit.

*But the reader is not allowed to interpret for the student. If your response is vague or ambiguous, you will NOT get credit.

*If your response consists of both correct and incorrect parts, you will usually not receive credit. It is not possible to try two answers, hoping that one of them is right. (See why it’s so important to be concise?)

1. (a)

1 pt: It’s a frictionless plane, so the only force parallel to the incline is a component of gravity, mg sin 30°.

1 pt: Set this force equal to ma, so a = g sin 30° = 5m/s² down the plane.

1 pt: Set up kinematics, with v_o = 0, and Δx = 7.0 m. Solve for time using **, (Δ x = v_o t + ½ at²).

1 pt: The result is t = 1.7 s.

(b)

1 pt: Use the kinematics from part (a), but use * (v_f = v_o + at) to get v_f = 8.5 m/s.

1 pt: The direction must be down the plane, or 30° below the horizontal.

(c)

1 pt: Only the vertical motion will affect the time to hit the bottom. (This point awarded for any clear attempt to use vertical kinematics.)

1 pt: In the vertical direction, v_o = (8.5 m/s)sin30°; Δx = 4.0 m and acceleration is g = 10 m/s².

1 pt: You can use ** (Δx = v_o t + ¹/₂at²) and a quadratic to solve for time; it’s probably easier to solve for v_f first using *** (v²_f = v²_o + 2aΔx). v_f works out to 9.9 m/s. Use * (v_f = v_o + at) to get t = 0.6 s.

1 pt: But this time is only the time after the package left the incline. To find the total time, the 1.7 s on the plane must be added to get 2.3 s total.

(d)

1 pt: In the horizontal direction, the package maintains constant speed after leaving the plane.

1 pt: So the horizontal distance is the horizontal velocity (equal to 8.5 m/s[cos 30°]) times the 0.6 seconds the package fell.

1 pt: The package lands 4.4 m from the left-hand edge.

(e)

1 pt: The horizontal distance would be increased, but less than doubled.

1 pt: The package speeds up as it falls; therefore, the package doesn’t take as much time to fall the additional 4 m as it did to fall the original 4 m. The horizontal velocity doesn’t change, so the package can’t go as far in this additional time.

2. (a)

1 pt: The total momentum of both carts before collision is m_A v_A, because cart B has no speed before collision.

1 pt: The total momentum after collision is 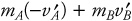, the negative sign arising because cart A moves backward after collision.

1 pt: So the fraction of momentum conserved is the total momentum after collision divided by the total momentum before collision,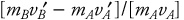

(b)

1 pt: The total kinetic energy of both carts before collision is ½m_A(v_A)².

1 pt: The total kinetic energy after collision is 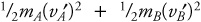(The negative sign on 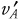disappears when velocity is squared.)

1 pt: So the fraction of KE conserved is the total KE after collision divided by the total KE before collision,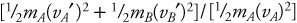

(c)

1 pt: Only the expression in part (a) should always be 100%.

1 pt: Momentum is conserved in all collisions, but kinetic energy can be converted into heat and other forms of energy.

(d)

1 pt: The motion detector can be used to measure the speed of cart A before collision.

1 pt: The detector should be placed at the left edge of the track.

1 pt: The speed can be read directly from the detector’s output.

1 pt: The motion detector can be used in the same manner to measure the speed of cart A after collision.

1 pt: The stopwatch can be used to measure cart B’s speed after collision. Time how long the cart takes to reach the end of the track after the collision.

1 pt: The meter stick can be used to measure the distance cart B traveled in this time

1 pt: Because the track is frictionless, the cart moves at constant speed equal to the distance traveled over the time elapsed.

3. (a)

1 pt: The buoyant force on this cube is equal to the weight of the water displaced.

1 pt: Half of the block displaces water; half of the block’s volume is 0.5 m³.

1 pt: Using the density of water, the mass of 0.5 m³ of water is 500 kg, which has weight 5000 N.

1 pt: Because the cube is in equilibrium, the buoyant force must also equal the weight of the cube. The cube thus has weight 5000 N, and mass 500 kg.

(b)

1 pt: Again, the buoyant force is equal to the weight of the displaced water. This time 0.75 m³ are displaced, making the buoyant force 7500 N.

1 pt: The weight of the mass is 5000 N, so the net force is the up minus down forces, or 2500 N.

(c)

1 pt: When an object is in simple harmonic motion, the net force is equal to kx, where x is the displacement from the equilibrium position.

1 pt: Using the information from part (b), when the displacement from equilibrium is 0.25 m, the net force is 2500 N.

1 pt: So the “spring constant” is 2500 N/0.25 m = 10,000 N/m.

(d)

1 pt: The period of a mass in simple harmonic motion is

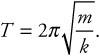
1 pt: Plugging in the mass and spring constant from parts (a) and (c), the period is 1.4 s.

1 pt: Frequency is 1 /T by definition, so the frequency is 0.71 Hz.

(e)

1 pt: The frequency would be the same.

1 pt: The period of a mass in simple harmonic motion is independent of the amplitude.

1 additional point: For correct units on at least three answers in parts (a), (b), (c), or (d), and no incorrect units.

4. (a)

1 pt: Over a potential difference of 500 V, the electron converts qV = 8.0 × 10^–17 J of potential energy into kinetic energy.

1 pt: Set this energy equal to ¹/₂ mv² and solve for v;

1 pt: You get 1.3 × 10⁷ m/s.

(Alternate solution is to approach this part of the problem like part (b); full credit is earned if the solution is correct.)

(b)(i)

1 pt: The electric field due to parallel plates is V/d. This works out to 100 V/0.05 m = 2000 N/C. (d represents the distance between plates.)

1 pt: The force on the electron is qE = 3.2 × 10^–16 N.

1 pt: The force is directed upward, toward the positive plate.

(b)(ii)

1 pt: The electron experiences no forces in the horizontal direction, so it maintains a constant horizontal velocity of 1.3 × 10⁷ m/s.

1 pt: Using distance = velocity × time, it takes 3.8 × 10^–8 s to travel the 0.5 m between the plates.

(b)(iii)

1 pt: The velocity at point C has both a horizontal and vertical component. The horizontal velocity is still 1.3 × 10⁷ m/s.

1 pt: But in the vertical direction, the electron speeds up from rest. (This point is given for ANY recognition that the vertical direction must be treated separately from the horizontal direction.)

1 pt: Its acceleration is given by the force in part (b)i over its mass: a = 3.2 × 10^–16 N/9.1 × 10^–31 kg, = 3.5 × 10¹⁴ m/s².

1 pt: Now use a Kinematics Chart to find the vertical speed at point C, with v_o = 0 and time given in part (b)(ii); this gives 1.3 × 10⁷ m/s.

1 pt: The speed is the magnitude of the velocity vector. The electron’s velocity has components to the right and up; add these using the Pythagorean theorem to get 1.8 × 10⁷m/s.

(c)

1 pt: The electric force, from part (b)(i), was 10^–16 N. The gravitational force is mg= 10^–30N.

1 pt: So the gravitational force is many orders of magnitude smaller than the electric force, and is, thus, negligible.

5. (a)

1 pt: The alpha particle consists of two protons and two neutrons. So the atomic number Z of the Erbium must be two fewer than that of the Ytterbium, Z = 68.

1 pt: The mass number A includes both protons and neutrons, so must be four fewer in the Erbium than in the Ytterbium, A = 169.

(b)

1 pt: Initial momentum of the whole system was zero; so the alpha and the Erbium must have equal and opposite momenta after decay.

1 pt: The alpha’s momentum is (4 amu)(1.7 × 10⁷ m/s) = 1.4 × 10⁸ amu-m/s (or 1.3 × 10^–19 kg-m/s); the Erbium has this same amount of momentum.

(c)

1 pt: The momentum p of each incident photon is given by E = pc, where E is the energy of the photon, equal to hc/λ. Set the two expressions for energy equal to each other.

1 pt: It is found that the momentum of each photon is p = h /λ = (6.6 × 10^–34 J-s)/(450 × 10^–9 m) = 1.5 × 10^–27 Nil Error·s (Note that this answer is in standard units because we plugged in h and λ in standard units.)

1 pt: Each photon is reflected backward, so each photon changes momentum by 1.5 × 10^–27N·s – (–1.5 × 10^–27 N.s) = 3.0 × 10^–27 N·s.

1 pt: The nucleus has 1.3 × 10^–19 N-s of momentum to start with, as found in (b); this point is awarded for both recognizing to use the momentum from part (b) and for putting that momentum in standard units.

1 pt: The nucleus loses 3.0 × 10^–27 N·s with each photon; so divide to find that 4.3 × 10⁷ photons will bring the nucleus to rest.

1 pt: Dividing this by the 10²⁵ photons each second, only 4 × 10^–18 seconds are required to stop the nucleus.

6. (a)

1 pt: The normal force acts up and the weight of the car acts down; friction acts to the left, opposite velocity.

1 pt: There are no forces acting to the right.

(b)

1 pt: Here, the normal force is equal to the car’s weight, mg.

1 pt: The force of friction is μF_N, which is μmg.

1 pt: The net work is done by friction and is equal to the force of friction times the 80 m displacement. Net work done on the car is thus μmg (80 m).

1 pt: Net work is equal to change in kinetic energy . . . because the car comes to rest, the change in KE is equal to the KE when the car was initially moving.

1 pt: So μmg(80 m) = ¹/₂mv², and v = 36 m/s. (Alternate solution: Use F_net = ma, where F_net is the force of friction = μ mg. Solve for acceleration, then use kinematics with final velocity = zero and displacement = 80 m. The answer should still work out to 36 m/s.)

(c)

1 pt: 36 m/s is something like 80 miles per hour . . . in a parking lot?!?!

(d)

1 pt: No, the driver’s argument does not make sense.

1 pt: In the equation to determine the initial speed of the car, as shown in part (b), the mass cancels out (because it shows up both in the friction force and in the kinetic energy term). So this calculation is valid for any mass car.

(a)

1 pt: The normal to the surface is, by definition, perpendicular to the surface, as shown in the diagram above.

(b)

1 pt: Snell’s law is used to determine the angle of transmission: n₁ sin θ₁ = n₂ sin θ₂.

1 pt: Here n₁ = 1.0 (for air) and n₂ = 1.5.

1 pt: The angle of incidence θ₁ must be measured to the normal.

1 pt: From geometry θ₁ is found to be 40°. So the transmission angle is 25°.

1 pt: This angle must be labeled with respect to the normal, as shown in the diagram above.

(c)

1 pt: The light will leave through the right-hand edge.

1 pt: Using geometry, the angle of incidence of the light on the bottom surface can be found. In the above diagram, the angle labeled A is 115° because it is the 90° angle to the normal plus the 25° angle of transmission. So angle B must be 15° because there are 180° total in a triangle. Therefore, the angle of incidence of the light ray to the bottom surface is 75°.

1 pt: Using Snell’s law, the angle of transmission θ₂ is undefined, so total internal reflection must occur. (Or, the critical angle for total internal reflection between glass and air is sin θ_c = 1/1.5, so θ_c = 42°; 75° is thus bigger than the critical angle, so total internal reflection occurs.)

1 pt: For a diagram showing reflection (with an angle of reflection approximately equal to the angle of incidence) at the bottom surface.

AP Physics B
Full Exam Scoring

Multiple Choice:

Number Correct______
Number Wrong ______

Total = right — (¹/₄) wrong ______ 70 max

Free Response: Question 1______15 max

Question 2______15 max

Question 3______15 max

Question 4______15 max

Question 5______10 max

Question 6______10 max

Question 7______10 max

Total Free Response______90 max

1.286 × Multiple Choice + Free Response = Raw Score______180 max

112–1805

84–1114

52–83 3

38–51 2

0–37 1

Physics C—Mechanics Practice Exam—Multiple-Choice Questions

ANSWER SHEET

Physics C—Mechanics Practice Exam—Multiple-Choice Questions

Time: 45 minutes. You may refer to the Constants sheet found in the Appendixes. However, you may not use the Equations sheet, and you may not use a calculator on this portion of the exam.

1. A cannon is mounted on a truck that moves forward at a speed of 5 m/s. The operator wants to launch a ball from a cannon so the ball goes as far as possible before hitting the level surface. The muzzle velocity of the cannon is 50 m/s. What angle from the horizontal should the operator point the cannon?

(A) 5°

(B) 41°

(D) 49°

(E) 85°

2. A car moving with speed v reaches the foot of an incline of angle Θ. The car coasts up the incline without using the engine. Neglecting friction and air resistance, which of the following is correct about the magnitude of the car’s horizontal acceleration a_x and vertical acceleration a_y?

(A) a_x = 0; a_y < g

(B) a_x = 0; a_y = g

(D) a_x < g; a_y = g

(E) a_x < g; a_y > g

3. A bicycle slows down with an acceleration whose magnitude increases linearly with time. Which of the following velocity–time graphs could represent the motion of the bicycle?

(A)

(B)

(C)

(D)

(E)

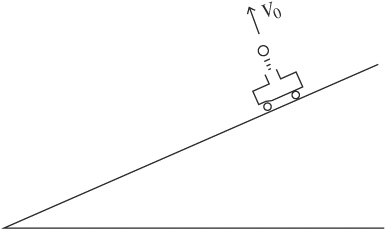
4. A cart is sliding down a low friction incline. A device on the cart launches a ball, forcing the ball perpendicular to the incline, as shown above. Air resistance is negligible. Where will the ball land relative to the cart, and why?

(A) The ball will land in front of the cart, because the ball’s acceleration component parallel to the plane is greater than the cart’s acceleration component parallel to the plane.

(B) The ball will land in front of the cart, because the ball has a greater magnitude of acceleration than the cart.

(C) The ball will land in the cart, because both the ball and the cart have the same component of acceleration parallel to the plane.

(D) The ball will land in the cart, because both the ball and the cart have the same magnitude of acceleration.

(E) The ball will land behind the cart, because the ball slows down in the horizontal direction after it leaves the cart.

5. The quantity “jerk,” j, is defined as the time derivative of an object’s acceleration,

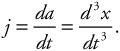
What is the physical meaning of the area under a graph of jerk vs. time?

(A) The area represents the object’s acceleration.

(B) The area represents the object’s change in acceleration.

(D) The area represents the object’s velocity.

(E) The area represents the object’s change in position.

6. A particle moves along the x-axis with a position given by the equation x(t) = 5 + 3t, where x is in meters, and t is in seconds. The positive direction is east. Which of the following statements about the particle is FALSE.

(A) The particle is east of the origin at t = 0.

(B) The particle is at rest at t = 0.

(D) The particle’s acceleration is constant.

(E) The particle will never be west of position x = 0.

7. A mass hangs from two ropes at unequal angles, as shown above. Which of the following makes correct comparisons of the horizontal and vertical components of the tension in each rope?

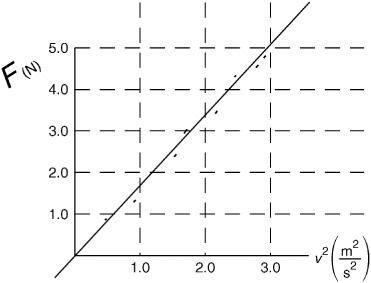
8. The force of air resistance F on a mass is found to obey the equation F = bv², where v is the speed of the mass, for the range of speeds investigated in an experiment. A graph of F_N vs. v² is shown above. What is the value of b?

(A) 0.83 kg/m

(B) 1.7 kg/m

(D) 5.0 kg/m

(E) 1.0 kg/m

(F) zero

9. A box sits on an inclined plane without sliding. As the angle of the plane (measured from the horizontal) increases, the normal force

(A) increases linearly

(B) decreases linearly

(D) decreases nonlinearly

(E) increases nonlinearly

10. Which of the following conditions are necessary for an object to be in static equilibrium?

I. The vector sum of all torques on the object must equal zero.

II. The vector sum of all forces on the object must equal zero.

III. The sum of the object’s potential and kinetic energies must be zero.

(A) I only

(B) II only

(D) I and II only

(E) I, II, and III

11. A student pushes a big 16-kg box across the floor at constant speed. He pushes with a force of 50 N angled 35° from the horizontal, as shown in the diagram above. If the student pulls rather than pushes the box at the same angle, while maintaining a constant speed, what will happen to the force of friction?

(A) It must increase.

(B) It must decrease.

(D) It will increase only if the speed is greater than 3.1 m/s.

(E) It will increase only if the speed is less than 3.1 m/s.

12. Consider a system consisting only of the Earth and a bowling ball, which moves upward in a parabola above Earth’s surface. The downward force of Earth’s gravity on the ball, and the upward force of the ball’s gravity on the Earth, form a Newton’s third law force pair. Which of the following statements about the ball is correct?

(A) The ball must be in equilibrium since the upward forces must cancel downward forces.

(B) The ball accelerates toward the Earth because the force of gravity on the ball is greater than the force of the ball on the Earth.

(D) The ball accelerates away from Earth because the force causing the ball to move upward is greater than the force of gravity on the ball.

(E) The ball accelerates away from Earth because the force causing the ball to move upward plus the force of the ball on the Earth are together greater than the force of gravity on the ball.

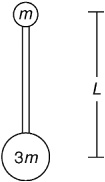
13. A mass m is attached to a mass 3m by a rigid bar of negligible mass and length L. Initially, the smaller mass is located directly above the larger mass, as shown above. How much work is necessary to flip the rod 180° so that the larger mass is directly above the smaller mass?

(A) 4mgL

(B) 2mgL

(D) 4πmgL

(E) 2πmgL

14. A ball rolls horizontally with speed v off of a table a height h above the ground. Just before the ball hits the ground, what is its speed?

(A)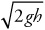

(B)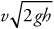

(C)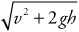

(D) v

(E)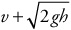

15. A pendulum is launched into simple harmonic motion in two different ways, as shown above, from a point that is a height h above its lowest point. During both launches, the bob is given an initial speed of 3.0 m/s. On the first launch, the initial velocity of the bob is directed upward along the pendulum’s path, and on the second launch it is directed downward along the pendulum’s path. Which launch will cause the pendulum to swing with the larger amplitude?

(A) the first launch

(B) the second launch

(D) The answer depends on the initial height h.

(E) The answer depends on the length of the supporting rope.

16. The mass M is moving to the right with velocity v₀ at position x = x₀. Neglect friction. The spring has force constant k. What is the total mechanical energy of the block at this position?

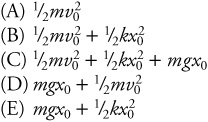
17. A sphere, a cube, and a cylinder, all of equal mass, are released from rest from the top of a short incline. The surface of the incline is extremely slick, so much so that the objects do not rotate when released, but rather slide with negligible friction. Which reaches the base of the incline first?

(A) the sphere

(B) the cube

(D) All reach the base at the same time.

(E) The answer depends on the relative sizes of the objects.

18. Block B is at rest on a smooth tabletop. It is attached to a long spring, which is in turn anchored to the wall. Block A slides toward and collides with block B. Consider two possible collisions:

Collision I: Block A bounces back off of block B.

Collision II: Block A sticks to block B.

Which of the following is correct about the speed of block B immediately after the collision?

(A) It is faster in case II than in case I ONLY if block B is heavier.

(B) It is faster in case I than in case II ONLY if block B is heavier.

(D) It is faster in case I than in case II regardless of the mass of each block.

(E) It is the same in either case regardless of the mass of each block.

19. A 0.30-kg bird is flying from right to left at 30 m/s. The bird collides with and sticks to a 0.50-kg ball which is moving straight up with speed 6.0 m/s. What is the magnitude of the momentum of the ball/bird combination immediately after collision?

(A) 12.0 Nil Error·s

(B) 9.5 N.s

(D) 6.0 N.s

(E) 3.0 N.s

20. The force F on a mass is shown above as a function of time t. Which of the following methods can be used to determine the impulse experienced by the mass?

I. multiplying the average force by t_max I

II. calculating the area under the line on the graph

III. taking the integral

(A) II only

(B) III only

(D) I and II only

(E) I, II, and III

21. A projectile is launched on level ground in a parabolic path so that its range would normally be 500 m. When the projectile is at the peak of its flight, the projectile breaks into two pieces of equal mass. One of these pieces falls straight down, with no further horizontal motion. How far away from the launch point does the other piece land?

(A) 250 m

(B) 375 m

(D) 750 m

(E) 1000 m

Questions 22 and 23

A rigid rod of length L and mass M is floating at rest in space far from a gravitational field. A small blob of putty of mass m < M is moving to the right, as shown above. The putty hits and sticks to the rod a distance 2L/3 from the top end.

22. How will the rod/putty contraption move after the collision?

(A) The contraption will have no translational motion, but will rotate about the rod’s center of mass.

(B) The contraption will have no translational motion, but will rotate about the center of mass of the rod and putty combined.

(D) The contraption will move to the right and rotate about the center of mass of the rod and putty combined.

(E) The contraption will move to the right and rotate about the rod’s center of mass.

23. What quantities are conserved in this collision?

(A) linear and angular momentum, but not kinetic energy

(B) linear momentum only

(D) linear and angular momentum, and linear but not rotational kinetic energy

(E) linear and angular momentum, and linear and rotational kinetic energy

24. A car rounds a banked curve of uniform radius. Three forces act on the car: a friction force between the tires and the road, the normal force from the road, and the weight of the car. Which provides the centripetal force which keeps the car in circular motion?

(A) the friction force alone

(B) the normal force alone

(D) a combination of the normal force and the friction force

(E) a combination of the friction force and the weight

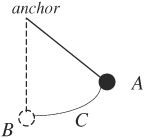
25. A ball of mass m anchored to a string swings back and forth to a maximum position A, as shown above. Point C is partway back to the vertical position. What is the direction of the mass’s acceleration at point C?

(A) along the mass’s path toward point B

(B) toward the anchor

(D) between a line toward the anchor and a line along the mass’s path

(E) along the mass’s path toward point A

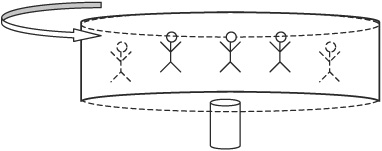
26. In a carnival ride, people of mass m are whirled in a horizontal circle by a floorless cylindrical room of radius r, as shown in the diagram above. If the coefficient of friction between the people and the tube surface is μ, what minimum speed is necessary to keep the people from sliding down the walls?

Questions 27 and 28

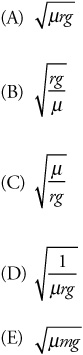
The uniform, rigid rod of mass m, length L, and rotational inertia I shown above is pivoted at its left-hand end. The rod is released from rest from a horizontal position.

27. What is the linear acceleration of the rod’s center of mass the moment after the rod is released?

28. What is the linear speed of the rod’s center of mass when the mass passes through a vertical position?

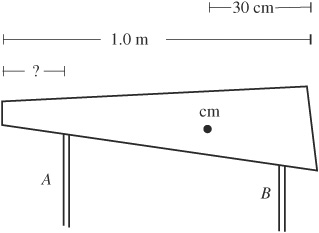
29. The 1.0-m-long nonuniform plank, shown above, has weight 1000 N. It is to be supported by two rods, A and B, as shown above. The center of mass of the plank is 30 cm from the right edge. Each support bears half the weight of the plank. If support B is 10 cm from the right-hand edge, how far from the left-hand edge should support A be?

(A) 0 cm

(B) 10 cm

(D) 50 cm

(E) 70 cm

30. A mass m on a spring oscillates on a horizontal surface with period T. The total mechanical energy contained in this oscillation is E. Imagine that instead a new mass 4m oscillates on the same spring with the same amplitude. What is the new period and total mechanical energy?

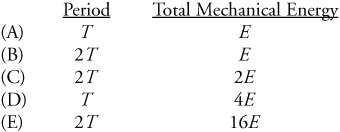
31. A mass m is attached to a horizontal spring of spring constant k. The spring oscillates in simple harmonic motion with amplitude A. What is the maximum speed of this simple harmonic oscillator?

32. An empty bottle goes up and down on the surface of the ocean, obeying the position function x =Acos(ωt). How much time does this bottle take to travel once from its lowest position to its highest position?

33. The Space Shuttle orbits 300 km above the Earth’s surface; the Earth’s radius is 6400 km. What is the acceleration due to Earth’s gravity experienced by the Space Shuttle?

(A) 4.9 m/s²

(B) 8.9 m/s²

(D) 10.8 m/s²

(E) zero

34. An artificial satellite orbits Earth just above the atmosphere in a circle with constant speed. A small meteor collides with the satellite at point P in its orbit, increasing its speed by 1%, but not changing the instantaneous direction of the satellite’s velocity. Which of the following describes the satellite’s new orbit?

(A) The satellite now orbits in an ellipse, with P as the farthest approach to Earth.

(B) The satellite now orbits in an ellipse, with P as the closest approach to Earth.

(D) The satellite now orbits in a circle of smaller radius.

(E) The satellite cannot maintain an orbit, so it flies off into space.

35. Mercury orbits the sun in about one-fifth of an Earth year. If 1 AU is defined as the distance from the Earth to the sun, what is the approximate distance between Mercury and the sun?

(A) (1/25) AU

(B) (1/9) AU

(D) (1/3) AU

(E) (1/2) AU

STOP. End of Physics C—Mechanics Practice Exam—Multiple-Choice Questions

Physics C—Mechanics Practice Exam—Free-Response Questions

Time: 45 minutes. You may refer to the Constants sheet and Equations sheet in the Appendixes. You may also use a calculator on this portion of the exam.

CM 1

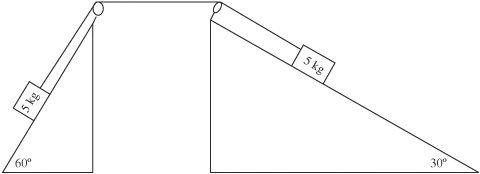
Two 5-kg masses are connected by a light string over two massless, frictionless pulleys. Each block sits on a frictionless inclined plane, as shown above. The blocks are released from rest.

(a) Determine the magnitude of the acceleration of the blocks.

(b) Determine the tension in the string.

Now assume that the 30° incline is rough, so that the coefficient of friction between the block and the plane is 0.10. The 60° incline is still frictionless.

(d) Determine the tension in the string.

CM 2

A hollow glass sphere of radius 8.0 cm rotates about a vertical diameter with frequency 5 revolutions per second. A small wooden ball of mass 2.0 g rotates inside the sphere, as shown in the diagram above.

(a) Draw a free-body diagram indicating the forces acting on the wooden ball when it is at the position shown in the picture above.

(b) Calculate the angle θ, shown in the diagram above, to which the ball rises.

(d) The wooden ball is replaced with a steel ball of mass 20 g. Describe how the angle θ to which the ball rises will be affected. Justify your answer.

CM3

A heavy ball of mass m is attached to a light but rigid rod of length L. The rod is pivoted at the top and is free to rotate in a circle in the plane of the page, as shown above.

(a) The mass oscillates to a maximum angle θ. On the picture of the mass m below, draw a vector representing the direction of the NET force on the mass while it is at angle θ. Justify your choice of direction.

(b) Is the magnitude of the net force at the maximum displacement equal to mg sin θ or mg cos θ? Choose one and justify your choice.

(c) Derive an expression for the ball’s potential energy U as a function of the angle θ. Assume that a negative angle represents displacement from the vertical in the clockwise direction.

(d) On the axes below, sketch a graph of the mass’s potential energy U as a function of the angle θ for angles between -90° and +360°. Label maximum and minimum values on the vertical axis.

(e) The pendulum is considered a classic example of simple harmonic motion when it undergoes small-amplitude oscillation. With specific reference to the graph you made in part (d), explain why the assumption of simple harmonic motion is valid.

STOP. End of Physics C—Mechanics Practice Exam—Free-Response Questions

Physics C—Electricity and Magnetism Practice Exam— Multiple-Choice Questions

ANSWER SHEET

Physics C—Electricity and Magnetism Practice Exam— Multiple-Choice Questions

Time: 45 minutes. You may refer to the Constants sheet found in the Appendixes. However, you may not use the Equations sheet, and you may not use a calculator on this portion of the exam.

36. Experimenter A uses a very small test charge q₀, and experimenter B uses a test charge 2q₀ to measure an electric field produced by two parallel plates. A finds a field that is

(A) greater than the field found by B

(B) the same as the field found by B

(D) either greater or less than the field found by B, depending on the accelerations of the test charges

(E) either greater or less than the field found by B, depending on the masses of the test charges

37. A solid conducting sphere has radius R and carries positive charge Q. Which of the following graphs represents the electric field E as a function of the distance r from the center of the sphere?

(A)

(B)

(C)

(D)

(E)

38. An electron moving at constant velocity enters the region between two charged plates, as shown above. Which of the paths above correctly shows the electron’s trajectory after leaving the region between the charged plates?

(A) A

(B) B

(D) D

(E) E

39. Two isolated particles, A and B, are 4 m apart. Particle A has a net charge of 2Q, and B has a net charge of Q. The ratio of the magnitude of the electric force on A to that on B is

(A) 4:1

(B) 2:1

(D) 1:2

(E) 1:4

40. A uniform electric field points to the left. A small metal ball charged to -2 mC hangs at a 30° angle from a string of negligible mass, as shown above. The tension in the string is measured to be 0.1 N. What is the magnitude of the electric field? (sin 30° = 0.50; cos 30° = 0.87; tan 30° = 0.58).

(A) 25 N/C

(B) 50 N/C

(D) 5000 N/C

(E) 10,000 N/C

41. A thin semicircular conductor of radius R holds charge +Q. What is the magnitude and direction of the electric field at the center of the circle?

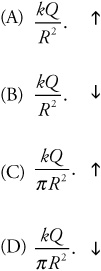
(E) The electric field is zero at the center.

42. Above an infinitely large plane carrying charge density σ, the electric field points up and is equal to σ/2ε_o What is the magnitude and direction of the electric field below the plane?

(A) σ/2ε_o, down

(B) σ/2ε_o, up

(D) σ/ε_o, up

(E) zero

43. Three charges are arranged in an equilateral triangle, as shown above. At which of these points is the electric potential smallest?

(A) A

(B) B

(D) D

(E) E

44. The diagram shows a set of equipotential surfaces. At point P, what is the direction of the electric field?

(A) left

(B) right

(D) down the page

(E) either left or right, which one cannot be determined

45. A metal sphere carries charge Q; a nonconducting sphere of equal size carries the same charge Q, uniformly distributed throughout the sphere. These spheres are isolated from each other. Consider the electric field at the center of the spheres, within the spheres, and outside the spheres. Which of these electric fields will be the same for both spheres, and which will be different?

46. Under what conditions is the net electric flux through a closed surface proportional to the enclosed charge?

(A) under any conditions

(B) only when the enclosed charge is symmetrically distributed

(D) only when there are no charges outside the surface

(E) only when enclosed charges can be considered to be point charges

47. A hollow metal ring of radius r carries charge q. Consider an axis straight through the center of the ring. At what point(s) along this axis is/are the electric field equal to zero?

(A) only at the center of the ring

(B) only at the center of the ring, and a very long distance away

(D) only at the center of the ring, a distance r away from the center, and a very long distance away

(E) everywhere along this axis

48. A parallel plate capacitor consists of identical rectangular plates of dimensions a × b, separated by a distance c. To cut the capacitance of this capacitor in half, which of these quantities should be doubled?

(A) a

(B) b

(D) ab

(E) abc

49. Two identical capacitors are hooked in parallel to an external circuit. Which of the following quantities must be the same for both capacitors?

I. the charge stored on the capacitor

II. the voltage across the capacitor

III. the capacitance of the capacitor

(A) I only

(B) II only

(D) I and III only

(E) I, II, and III

50. A 2-μ.F capacitor is connected directly to a battery. When the capacitor is fully charged, it stores 600 μC of charge. An experimenter replaces the 2-μ. F capacitor with three 18-μ. F capacitors in series connected to the same battery. Once the capacitors are fully charged, what charge is stored on each capacitor?

(A) 100 μC

(B) 200 μC

(D) 1200 μC

(E) 1800 μC

51. A spherical conductor carries a net charge. How is this charge distributed on the sphere?

(A) The charge is evenly distributed on the surface.

(B) The charge resides on the surface only; the distribution of charge on the surface depends on what other charged objects are near the sphere.

(D) The charge is distributed uniformly throughout the sphere.

(E) The charge resides within the sphere; the distribution of charge within the sphere depends on what other charged objects are near the sphere.

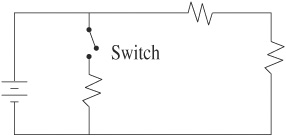
52. Three resistors are connected to a battery as shown in the diagram above. The switch is initially open. When the switch is closed, what happens to the total voltage, current, and resistance in the circuit?

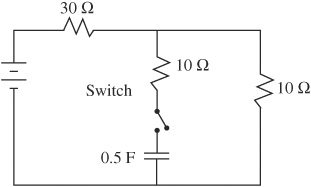
53. In the circuit shown above, the 0.5 F capacitor is initially uncharged. The switch is closed at time t = 0. What is the time constant (the time for the capacitor to charge to 63% of its maximum charge) for the charging of this capacitor?

(A) 5 s

(B) 10 s

(D) 30 s

(E) 40 s

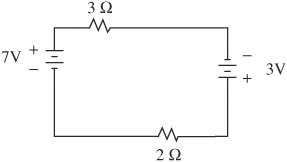
54. In the circuit shown above, what is the current through the 3 Ω resistor?

(A) 0 A

(B) 0.5 A

(D) 1.5 A

(E) 2.0 A

55. A light bulb rated at 100 W is twice as bright as a bulb rated at 50 W when both are connected in parallel directly to a 100-V source. Now imagine that these bulbs are instead connected in series with each other. Which is brighter, and by how much?

(A) The bulbs have the same brightness.

(B) The 100-W bulb is twice as bright.

(D) The 100-W bulb is four times as bright.

(E) The 50-W bulb is four times as bright.

56. A uniform magnetic field B is directed into the page. An electron enters this field with initial velocity v to the right. Which of the following best describes the path of the electron while it is still within the magnetic field?

(A) It moves in a straight line.

(B) It bends upward in a parabolic path.

(D) It bends upward in a circular path.

(E) It bends downward in a circular path.

57. Wire is wound around an insulated circular donut, as shown above. A current I flows in the wire in the direction indicated by the arrows. The inner, average, and outer radii of the donut are indicated by r₁, r₂, and r₃, respectively. What is the magnitude and direction of the magnetic field at point P, the center of the donut?

(A) zero

(B)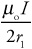

(C)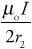

(D)

(E)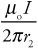

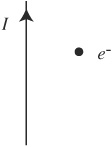
58. A wire carries a current toward the top of the page. An electron is located to the right of the wire, as shown above. In which direction should the electron be moving if it is to experience a magnetic force toward the wire?

(A) into the page

(B) out of the page

(D) toward the top of the page

(E) to the right

59. Which of the following statements about electric and magnetic fields is FALSE:

(A) A charge moving along the direction of an electric field will experience a force, but a charge moving along the direction of a magnetic field will not experience a force.

(B) All charges experience a force in an electric field, but only moving charges can experience a force in a magnetic field.

(C) A positive charge moves in the direction of an electric field; a positive charge moves perpendicular to a magnetic field.

(D) All moving charges experience a force parallel to an electric field and perpendicular to a magnetic field.

(E) A negative charge experiences a force opposite the direction of an electric field; a negative charge experiences a force perpendicular to a magnetic field.

60. Which of these quantities decreases as the inverse square of distance for distances far from the objects producing the fields?

(A) the electric field produced by a finite-length charged rod

(B) the electric field produced by an infinitely long charged cylinder

(D) the magnetic field produced by an infinitely long straight current carrying wire

(E) the magnetic field produced by a wire curled around a torus

61. A proton enters a solenoid. Upon entry, the proton is moving in a straight line along the axis of the solenoid. Which of the following is a correct description of the proton’s motion within the solenoid?

(A) The proton will be bent in a parabolic path.

(B) The proton will be bent in a circular path.

(D) The proton will continue in its straight path and slow down.

(E) The proton will continue in its straight path and speed up.

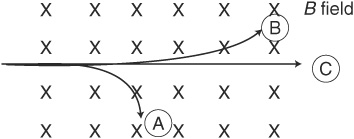
62. A uniform magnetic field points into the page. Three subatomic particles are shot into the field from the left-hand side of the page. All have the same initial speed and direction. These particles take paths A, B, and C, as labeled in the diagram above. Which of the following is a possible identity for each particle?

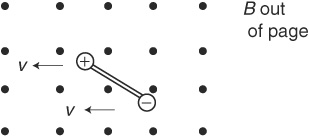
63. The electric dipole shown above consists of equal-magnitude charges and has an initial leftward velocity v in a uniform magnetic field pointing out of the page, as shown above. The dipole experiences

(A) a clockwise net torque, and a net force to the left

(B) a counterclockwise net torque, and a net force to the left

(D) a counterclockwise net torque, and no net force

(E) a clockwise net torque, and no net force

64. A beam of electrons has speed 10⁷ m/s. It is desired to use the magnetic field of the Earth, 5 × 10^¯5 T, to bend the electron beam into a circle. What will be the radius of this circle?

(A) 1 nm

(B) 1 μm

(D) 1 m

(E) 1 km

65. A very small element of wire of length dL carries a current I. What is the direction of the magnetic field produced by this current element at point P, shown above?

(A) to the right

(B) toward the top of the page

(D) out of the page

(E) there is no magnetic field produced at point P by this element.

66. A loop of wire surrounds a hole in a table, as shown above. A bar magnet is dropped, north end down, from far above the table through the hole. Let the positive direction of current be defined as counterclockwise as viewed from above. Which of the following graphs best represents the induced current I in the loop?

(A)

(B)

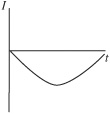
(C)

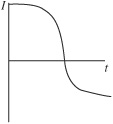
(D)

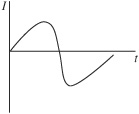
(E)

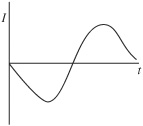
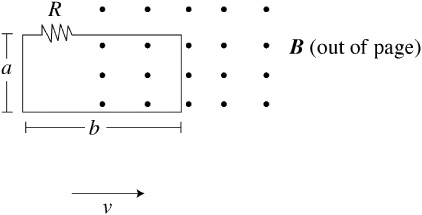
67. A rectangular loop of wire has dimensions a × b and includes a resistor R. This loop is pulled with speed v from a region of no magnetic field into a uniform magnetic field B pointing through the loop, as shown above. What is the magnitude and direction of the current through the resistor?

(A) Bav/R, left-to-right

(B) Bbv/R, left-to-right

(D) Bbv/R, right-to-left

(E) Bba/R, right-to-left

68. A conducting wire sits on smooth metal rails, as shown above. A variable magnetic field points out of the page. The strength of this magnetic field is increased linearly from zero. Immediately after the field starts to increase, what will be the direction of the current in the wire and the direction of the wire’s motion?

69. A uniform magnetic field B points parallel to the ground. A toy car is sliding down a frictionless plane inclined at 30°. A loop of wire of resistance R and cross-sectional area A lies in the flat plane of the car’s body, as shown above. What is the magnetic flux through the wire loop?

(A) zero

(B) BA cos 30°

(D) BA

(E) (BA cos 60°)/R

70. If the two equal resistors R₁ and R₂ are connected in parallel to a 10-V battery with no other circuit components, the current provided by the battery is I. In the circuit shown above, an inductor of inductance L is included in series with R₂. What is the current through R₂ after the circuit has been connected for a long time?

(A) zero

(B) (1/4) I

(D) I

(E)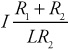

STOP. End of Physics C—Electricity and Magnetism Practice Exam—Multiple-Choice Questions

Physics C—Electricity and Magnetism Practice Exam—Free-Response Questions

Time: 45 minutes. You may refer to the Constants sheet and Equations sheet in the Appendixes. You may also use a calculator on this portion of the exam.

E&M 1

A metal sphere of radius R₁ carries charge +Q. A concentric spherical metal shell, of inner radius R₂ and outer radius R₃, carries charge +2Q.

(a) Let r represent the distance from the center of the spheres. Calculate the electric field as a function of r in each of the following four regions:

1. between r = 0 and r= R₁

2. between r = R₁ and r= R₂

3. between r = R₂ and r = R₃

4. between r = R₃ and r= 0

(b) How much charge is on each surface of the outer spherical shell? Justify your answer.

(d) Determine the electric potential of the inner metal sphere.

E&M 2

A 1 MΩ resistor is connected to the network of capacitors shown above. The circuit is hooked to a 10-V battery. The capacitors are initially uncharged. The battery is connected and the switch is closed at time t = 0.

(a) Determine the equivalent capacitance of C₁, C₂, and C₃.

(b) Determine the charge on and voltage across each capacitor after a long time has elapsed.

(d) After the capacitors have been fully charged, the switch is opened, disconnecting C₁ and C₂ from the circuit. What happens to the voltage across and charge on C₃? Justify your answer.

E&M 3

In the laboratory, far from the influence of other magnetic fields, the Earth’s magnetic field has a value of 5.00 × 10^¯5 T. A compass in this lab reads due north when pointing along the direction of Earth’s magnetic

A long, straight current-carrying wire is brought close to the compass, deflecting the compass to the position shown above, 48° west of north.

(a) Describe one possible orientation of the wire and the current it carries that would produce the deflection shown.

(b) Calculate the magnitude B_wire of the magnetic field produced by the wire that would cause the deflection shown.

(c) The distance d from the wire to the compass is varied, while the current in the wire is kept constant; a graph of B_wire vs. d is produced. On the axes below, sketch the shape of this graph.

(d) It is desired to adjust this plot so that the graph becomes a straight line. The vertical axis is to remain B_wire, the magnetic field produced by the wire. How could the quantity graphed on the horizontal axis be adjusted to produce a straight line graph? Justify your answer.

(e) The current carried by the wire is 500 mA. Determine the slope of the line on the graph suggested in part (d).

STOP. End of Physics C—Electricity and Magnetism Practice Exam—Free-Response Questions

Physics C—Mechanics Practice Exam—Multiple-Choice Solutions

1. D—A projectile has its maximum range when it is shot at an angle of 45° relative to the ground. The cannon’s initial velocity relative to the ground in this problem is given by the vector sum of the man’s 5 m/s forward motion and the cannon’s 50 m/s muzzle velocity. To get a resultant velocity of 45°, the man must shoot the cannon at only a slightly higher angle, as shown in the diagram below.

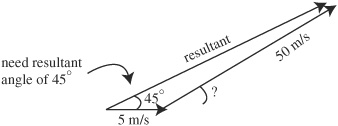
2. C—The car stays on the plane, and slows down as it goes up the plane. Thus, the net acceleration is in the direction down the plane, which has both a nonzero horizontal and vertical component. The car is not in free fall, so its vertical acceleration is less than g.

3. E—Acceleration is the slope of the v—t graph. Because acceleration increases, the slope of the v—t graph must get steeper, eliminating choices A and B. The bike slows down, so the speed must get closer to zero as time goes on, eliminating choices C and D.

4. C—The cart’s acceleration is g sinθ, down the plane, the ball’s acceleration is g, straight down. (So the magnitudes of acceleration are different and choice D is wrong.) The component of the ball’s acceleration along an axis parallel to the plane is also g sinθ, equal to the ball’s acceleration component.

5. B—The area under a jerk—time graph is the quantity jdt. The derivative

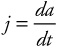
can be interpreted as a change in acceleration over a time interval,

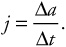
Solving algebraically, jΔt is Δ a, meaning the change in acceleration.

6. B—At t = 0, x = +5 m, so the particle is east of the origin to start with. The velocity is given by the derivative of the position function, v(t) = 3 m/s. This is a constant velocity; the acceleration is thus zero (and constant), but at t = 0 the velocity is also 3 m/s, so choice B is false.

7. B—Consider the horizontal and vertical forces separately. The only horizontal forces are the horizontal components of the tensions. Because the block is in equilibrium, these horizontal tensions must be equal, meaning only choices B and D can be right. But the ropes can’t have equal horizontal AND vertical tensions, otherwise they’d hang at equal angles. So D can’t be the right choice, and B must be right.

8. B—The equation F = bv² is of the form y = mx, the equation of a line. Here F is the vertical axis, v² is the horizontal axis, so b is the slope of the line. Looking at the graph, the slope is 5.0 N/3.0 m²/s² = 1.7 kg/m.

9. D—Because no forces act perpendicular to the incline except for the normal force and the perpendicular component of weight, and there is no acceleration perpendicular to the incline, the normal force is equal to the perpendicular component of weight, which is mg cosθ. As the angle increases, the cosine of the angle decreases. This decrease is nonlinear because a graph of F_N vs. θ would show a curve, not a line.

10. D—In equilibrium, the net force and the net torque must both be zero. Static equilibrium means the object is stationary, so kinetic energy must be zero. However, potential energy can take on any value—a sign suspended above a roadway is in static equilibrium, yet has potential energy relative to Earth’s surface.

11. B—The friction force is equal to the coefficient of friction times the normal force. The coefficient of friction is a property of the surfaces in contact, and thus will not change here. However, the normal force decreases when the cart is pulled rather than pushed—the surface must apply more force to the box when there is a downward component to the applied force than when there is an upward component. Speed is irrelevant because equilibrium in the vertical direction is maintained regardless.

12. C—The ball accelerates toward the Earth because, although it is moving upward, it must be slowing down. The only force acting on the ball is Earth’s gravity. Yes, the ball exerts a force on the Earth, but that force acts on the Earth, not the ball. According to Newton’s 3rd law, force pairs always act on different objects, and thus can never cancel.

13. B—The work done on an object by gravity is independent of the path taken by the object and is equal to the object’s weight times its vertical displacement. Gravity must do 3mgL of work to raise the large mass, but must do mg(-L) of work to lower the small mass. The net work done is thus 2mgL.

14. C—Use conservation of energy. Position 1 will be the top of the table; position 2 will be the ground. PE₁ + KE₁ = PE₂ + KE₂. Take the PE at the ground to be zero. Then 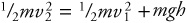. The ms cancel. Solving for v₂, you get choice C. (Choice E is wrong because it’s illegal algebra to take a squared term out of a square root when it is added to another term.)

15. C—Consider the conservation of energy. At the launch point, the potential energy is the same regardless of launch direction. The kinetic energy is also the same because KE depends on speed alone and not direction. So, both balls have the same amount of kinetic energy to convert to potential energy, bringing the ball to the same height in every cycle.

16. B—Total mechanical energy is defined as kinetic energy plus potential energy. The KE here is . The potential energy is provided entirely by the spring—gravitational potential energy requires a vertical displacement, which doesn’t occur here. The PE of the spring is .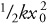

17. D—When an object rotates, some of its potential energy is converted to rotational rather than linear kinetic energy, and thus it moves more slowly than a non-rotating object when it reaches the bottom of the plane. However, here none of the objects rotate! The acceleration does not depend on mass or size.

18. D—Momentum must be conserved in the collision. If block A bounces, it changes its momentum by a larger amount than if it sticks. This means that block B picks up more momentum (and thus more speed) when block A bounces. The mass of the blocks is irrelevant because the comparison here is just between bouncing and not bouncing. So B goes faster in collision I regardless of mass.

19. B—The momentum of the bird before collision is 9 N·s to the left; the momentum of the ball is initially 3 N·s up. The momentum after collision is the vector sum of these two initial momentums. With a calculator you would use the Pythagorean theorem to get 9.5 N.s; without a calculator you should just notice that the resultant vector must have magnitude less than 12 N·s (the algebraic sum) and more than 9 N.s.

20. E—Impulse is defined on the equation sheet as the integral of force with respect to time, so III is right. The meaning of this integral is to take the area under a F vs. t graph, so II is right. Because the force is increasing linearly, the average force will be halfway between zero and the maximum force, and the rectangle formed by this average force will have the same area as the triangle on the graph as shown, so I is right.

21. D—The center of mass of the projectile must maintain the projectile path and land 500 m from the launch point. The first half of the projectile fell straight down from the peak of its flight, which is halfway to the maximum range, or 250 m from the launch point. So the second half of equal mass must be 250 m beyond the center of mass upon hitting the ground, or 750 m from the launch point.

22. D—By conservation of linear momentum, there is momentum to the right before collision, so there must be momentum to the right after collision as well. A free-floating object rotates about its center of mass; because the putty is attached to the rod, the combination will rotate about its combined center of mass.

23. A—Linear and angular momentum are conserved in all collisions (though often angular momentum conservation is irrelevant). Kinetic energy, though, is only conserved in an elastic collision. Because the putty sticks to the rod, this collision cannot be elastic. Some of the kinetic energy must be dissipated as heat.

24. D.

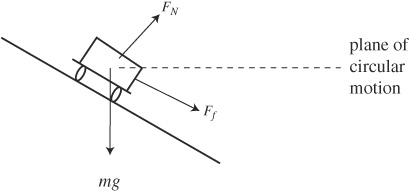
The centripetal force must act toward the center of the car’s circular path. This direction is NOT down the plane, but rather is purely horizontal. The friction force acts down the plane and thus has a horizontal component; the normal force acts perpendicular to the plane and has a horizontal component. So BOTH F_N and F_f contribute to the centripetal force.

25. D—The mass’s acceleration has two components here. Some acceleration must be centripetal (i.e., toward the anchor) because the mass’s path is circular. But the mass is also speeding up, so it must have a tangential component of acceleration toward point B. The vector sum of these two components must be in between the anchor and point B.

26. B—The free-body diagram for a person includes F_N toward the center of the circle, mg down and the force of friction up:

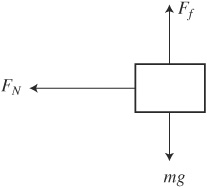
Because the person is not sliding down, mg = F_f. And because the motion of the person is circular, the normal force is a centripetal force, so F_N = mv²/r. The force of friction by definition is μF_N. Combining these equations, we have mg = μmv²/r; solve for v to get answer choice B. Note: Without any calculation, you could recognize that only choices A and B have units of speed, so you would have had a good chance at getting the answer right just by guessing one of these two!

27. B—Use Newton’s second law for rotation, τ_net = Iα. The only torque about the pivot is the rod’s weight, acting at the rod’s center; this torque is thus mgL/2. So the angular acceleration, α, of the rod is mgL/2I. But the question asks for a linear acceleration, a = rα, where r is the distance to the center of rotation. That distance here is L/2. So combining, you get a = (L/2)(mgL/2I) = mgL²/4I.

28. D—We cannot use rotational kinematics here because the net torque, and thus the angular acceleration, is not constant. Use conservation of energy instead. The potential energy at the release point is mg(L/2) (L/2 because the rod’s center of mass is that far vertically above its lowest point). This potential energy is converted entirely into rotational kinetic energy 1/2Iω². The rod’s angular velocity ω is equal to v/(L/2), where v is the linear speed of the center of mass that we’re solving for. Plugging in, you get mgL/2 = 1/2I(v²/[L/2]²). Solving for v, choice D emerges from the mathematics.

29. D—Choose any point at all as the fulcrum; say, the center of mass. Rod B supports 500 N, and is located 20 cm from the fulcrum, producing a total counterclockwise torque of 10,000 Nil Error·cm. Rod A also supports 500 N; call its distance from the fulcrum “x”. So 10,000 = 500x, and x = 20 cm. This means Rod A is located 20 cm left of the center of mass, or 50 cm from the left edge.

30. B—The period of a mass on a spring is

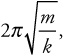
with the mass under the square root. So when the mass is quadrupled, the period is only multiplied by two. The total mechanical energy is the sum of potential plus kinetic energy. At the greatest displacement from equilibrium (i.e., at the amplitude), the mass’s speed is zero and all energy is potential; potential energy of a spring is 1/2kx² and does not depend on mass. So, because the amplitude of oscillation remains the same, the total mechanical energy does not change.

31. D—The maximum potential energy of the mass is at the amplitude, and equal to 1/2kA². This is entirely converted to kinetic energy at the equilibrium position, where the speed is maximum. So set 1/2kA² = 1/2mv²_max. Solving for v_max, you get choice D. (Note: Only choices C and D have units of velocity! So guess between these if you have to!)

32. B—The bottle’s lowest position is x = -A, and its highest position is x = +A. When t = 0, cos (0) = 1 and the bottle is at x = +A. So, find the time when the cosine function goes to -1. This is when ωt = π, so t = π/ω.

33. B—Don’t try to calculate the answer by saying mg = GMm/r²! Not only would you have had to memorize the mass of the Earth, but you have no calculator and you only have a minute or so, anyway. So think: the acceleration must be less than 9.8 m/s², because that value is calculated at the surface of the Earth, and the Shuttle is farther from Earth’s center than that. But the added height of 300 km is a small fraction (~5%) of the Earth’s radius. So the gravitational acceleration will not be THAT much less. The best choice is thus 8.9 m/s². (By the way, acceleration is not zero—if it were, the Shuttle would be moving in a straight line, and not orbiting.)

34. B—The orbit can no longer be circular—circular orbits demand a specific velocity. Because the satellite gains speed while at its original distance from the planet, the orbit is now elliptical. Because the direction of the satellite’s motion is still tangent to the former circular path, in the next instant the satellite will be farther from Earth than at point P, eliminating answer choice A. The satellite will not “fly off into space” unless it reaches escape velocity, which cannot be 1% greater than the speed necessary for a low circular orbit.

35. D—Kepler’s third law states that for all planets in the same system, their period of orbit squared is proportional to the average distance from the sun cubed. Using units of years and AU, for Earth, (1 year)² = (1 AU)³. For Mercury, we have (1/5 year)² = (? AU)³. Solving for the question mark, you find that the distance from Mercury to the sun is the cube root of 1/25 AU, which is closest to 1/3 AU.

Physics C—Electricity and Magnetism Practice Exam—Multiple-Choice Solutions

37. D—You could use Gauss’s law to show that the field outside the sphere has to decrease as 1/r², eliminating choices B and E. But it’s easier just to remember that an important result of Gauss’s law is that the electric field inside a conductor is always zero everywhere, so D is the only possibility.

38. B—While in the region between the plates, the negatively charged electron is attracted to the positive plate, so bends upward. But after leaving the plates, there is no more force acting on the electron. Thus, the electron continues in motion in a straight line by Newton’s first law.

39. C—This is a Newton’s third law problem! The force of A on B is equal (and opposite) to the force of B on A. Or, we can use Coulomb’s law: The field due to A is k (2Q)/(4 m)². The force on B is QE = k2QQ/(4 m)². We can do the same analysis finding the field due to B and the force on A to get the same result.

40. A—The charge is in equilibrium, so the horizontal component of the tension must equal the electric force. This horizontal tension is 0.1 N times sin 30° (not cosine because 30° was measured from the vertical), or 0.05 N. The electric force is qE, where q is 0.002 C. So the electric field is 0.050 N/0.002 C. Reduce the expression by moving the decimal to get 50/2, or 25 N/C.

41. D—The answer could, in principle, be found using the integral form of Coulomb’s law. But you can’t do that on a one-minute multiple-choice problem. The electric field will point down the page—the field due to a positive charge points away from the charge, and there’s an equal amount of charge producing a rightward field as a leftward field, so horizontal fields cancel. So, is the answer B or D? Choice B is not correct because electric fields add as vectors. Only the vertical component of the field due to each little charge element contributes to the net electric field, so the net field must be less than kQ/R².

42. A—Use the symmetry of the situation to see the answer. Because the infinitely large plane looks the same on the up side as the down side, its electric field must look the same, too—the field must point away from the plane and have the same value.

43. C—Another way to look at this question is, “where would a small positive charge end up if released near these charges?” because positive charges seek the smallest potential. The positive charge would be repelled by the +2Q charge and attracted to the -Q charges, so would end up at point C. Or, know that potential due to a point charge is kq/r. Point C is closest to both -Q charges, so the r terms will be smallest, and the negative contribution to the potential will be largest; point C is farthest from the +2Q charge, so the r term will be large, and the positive contribution to the potential will be smallest.

44. A—A positive charge is forced from high to low potential, which is generally to the left; and the force on a positive charge is in the direction of the electric field. At point P itself the electric field is directly to the left because an electric field is always perpendicular to equipotential surfaces.

45. C—The charge on the metal sphere distributes uniformly on its surface. Because the nonconducting sphere also has a uniform charge distribution, by symmetry the electric fields will cancel to zero at the center. Outside the spheres we can use Gauss’s law: E-A =Q_enclosed/ε _o. Because the charge enclosed by a Gaussian surface outside either sphere will be the same, and the spheres are the same size, the electric field will be the same everywhere outside either sphere. But within the sphere? A Gaussian surface drawn inside the conducting sphere encloses no charge, while a Gaussian surface inside the nonconducting sphere does enclose some charge. The fields inside must not be equal.

46. A—That’s what Gauss’s law says: Net flux through a closed surface is equal to the charge enclosed divided by ε_o. Though Gauss’s law is only useful when all charge within or without a Gaussian surface is symmetrically distributed, Gauss’s law is valid always.

47. B—The electric field at the center of the ring is zero because the field caused by any charge element is canceled by the field due to the charge on the other side of the ring. The electric field decreases as 1 /r² by Coulomb’s law, so a long distance away from the ring the field goes to zero. The field is nonzero near the ring, though, because each charge element creates a field pointing away from the ring, resulting in a field always along the axis.

48. C—Capacitance of a parallel plate capacitor is ε_oA/d, where A is the area of the plates, and d is the separation between plates. To halve the capacitance, we must halve the area or double the plate separation. The plate separation in the diagram is labeled c, so double distance c.

49. E—We are told that the capacitors are identical, so their capacitances must be equal. They are hooked in parallel, meaning the voltages across them must be equal as well. By Q = CV, the charge stored by each must also be equal.

50. E—First determine the voltage of the battery by Q = CV. This gives V = 600 C/2 μF = 300 V. This voltage is hooked to the three series capacitors, whose equivalent capacitance is 6 μF (series capacitors add inversely, like parallel resistors). So the total charge stored now is (6 μ F)(300 V) = 1800 μC. This charge is not split evenly among the capacitors, though! Just as the current through series resistors is the same through each and equal to the total current through the circuit, the charge on series capacitors is the same and equal to the total.

51. B—The charge does reside on the surface, and, if the conductor is alone, will distribute evenly. But, if there’s another nearby charge, then this charge can repel or attract the charge on the sphere, causing a redistribution.

52. D—The voltage must stay the same because the battery by definition provides a constant voltage. Closing the switch adds a parallel branch to the network of resistors. Adding a parallel resistor reduces the total resistance. By Ohm’s law, if voltage stays the same and resistance decreases, total current must increase.

53. C—The time constant for an RC circuit is equal to RC. The resistance used is the resistance encountered by charge that’s flowing to the capacitor; in this case, 40 Ω. So RC = 20 s.

54. E—Assume that the current runs clockwise in the circuit, and use Kirchoff’s loop rule. Start with the 7-V battery and trace the circuit with the current: + 7V — I(3Ω) + 3V — I(2Ω) = 0. Solve for I to get 2.0 A.

55. C—The intrinsic property of the light bulb is resistance; the power dissipated by a bulb depends on its voltage and current. When the bulbs are connected to the 100-V source, we can use the expression for power P= V²/R to see that the bulb rated at 50 watts has twice the resistance of the other bulb. Now in series, the bulbs carry the same current. Power is also I²R; thus the 50-watt bulb with twice the resistance dissipates twice the power, and is twice as bright.

56. E—The electron bends downward by the right-hand rule for a charge in a B field—point to the right, curl fingers into the page, and the thumb points up the page. But the electron’s negative charge changes the force to down the page. The path is a circle because the direction of the force continually changes, always pointing perpendicular to the electron’s velocity. Thus, the force on the electron is a centripetal force.

57. A—This is one of the important consequences of Ampere’s law. The magnetic field inside the donut is always along the axis of the donut, so the symmetry demands of Ampére’s law are met. If we draw an “Ampérean Loop” around point P but inside r₁, this loop encloses no current; thus the magnetic field must be zero.

58. C—The magnetic field due to the wire at the position of the electron is into the page. Now use the other right-hand rule, the one for the force on a charged particle in a magnetic field. If the charge moves down the page, then the force on a positive charge would be to the right, but the force on a (negative) electron would be left, toward the wire.

59. C—A positive charge experiences a force in the direction of an electric field, and perpendicular to a magnetic field; but the direction of a force is not necessarily the direction of motion.

60. A—The electric field due to any finite-sized charge distribution drops off as 1 /r² a long distance away because if you go far enough away, the charge looks like a point charge. This is not true for infinite charge distributions, though. The magnetic field due to an infinitely long wire is given by

not proportional to 1 /r²; the magnetic field produced by a wire around a torus is zero outside the torus by Ampére’s law.

61. C—The magnetic field produced by a single loop of wire at the center of the loop is directly out of the loop. A solenoid is a conglomeration of many loops in a row, producing a magnetic field that is uniform and along the axis of the solenoid. So, the proton will be traveling parallel to the magnetic field. By F = qvB sinθ, the angle between the field and the velocity is zero, producing no force on the proton. The proton continues its straightline motion by Newton’s first law.

62. E—By the right-hand rule for the force on a charged particle in a magnetic field, particle C must be neutral, particle B must be positively charged, and particle A must be negatively charged. Charge B must be more massive than charge A because it resists the change in its motion more than A. A proton is positively charged and more massive than the electron; the neutron is not charged.

63. E—The force on the positive charge is upward; the force on the negative charge is downward. These forces will tend to rotate the dipole clockwise, so only A or E could be right. Because the charges and velocities are equal, the magnetic force on each = qvB and is the same. So, there is no net force on the dipole. (Yes, no net force, even though it continues to move to the left.)

64. D—The centripetal force keeping the electrons in a circle is provided by the magnetic force. So set qvB = mv²/r. Solve to get r = (mv)/(qB). Just look at orders of magnitude now: r = (₁₀-31 kg) (₁₀7m/s)/(₁₀-19 C)(₁₀-5 T). This gives r = ₁₀24/₁₀24 = 100 m ∼ 1m.

65. E—An element of current produces a magnetic field that wraps around the current element, pointing out of the page above the current and into the page below. But right in front (or anywhere along the axis of the current), the current element produces no magnetic field at all.

66. D—A long way from the hole, the magnet produces very little flux, and that flux doesn’t change much, so very little current is induced. As the north end approaches the hole, the magnetic field points down. The flux is increasing because the field through the wire gets stronger with the approach of the magnet; so, point your right thumb upward (in the direction of decreasing flux) and curl your fingers. You find the current flows counterclockwise, defined as positive. Only A or D could be correct. Now consider what happens when the magnet leaves the loop. The south end descends away from the loop. The magnetic field still points down, into the south end of the magnet, but now the flux is decreasing. So point your right thumb down (in the direction of decreasing flux) and curl your fingers. Current now flows clockwise, as indicated in choice D. (While the magnet is going through the loop, current goes to zero because the magnetic field of the bar magnet is reasonably constant near the center of the magnet.)

67. A—You remember the equation for the induced EMF in a moving rectangular loop, ε = Blv. Here l represents the length of the wire that doesn’t change within the field; dimension a in the diagram. So the answer is either A or C. To find the direction of induced current, use Lenz’s law: The field points out of the page, but the flux through the loop is increasing as more of the loop enters the field. So, point your right thumb into the page (in the direction of decreasing flux) and curl your fingers; you find the current is clockwise, or left-to-right across the resistor.

68. D—Start by finding the direction of the induced current in the wire using Lenz’s law: the magnetic field is out of the page. The flux increases because the field strength increases. So point your right thumb into the page, and curl your fingers to find the current flowing clockwise, or south in the wire. Now use the right-hand rule for the force on moving charges in a magnetic field (remembering that a current is the flow of positive charge). Point down the page, curl your fingers out of the page, and the force must be to the west.

69. C—There is clearly nonzero flux because the field does pass through the wire loop. The flux is not BA, though, because the field does not go straight through the loop—the field hits the loop at an angle. So is the answer BA cos 30°, using the angle of the plane; or BA cos 60°, using the angle from the vertical? To figure it out, consider the extreme case. If the incline were at zero degrees, there would be zero flux through the loop. Then the flux would be BA cos 90°, because cos 90° is zero, and cos 0° is one. So don’t use the angle of the plane, use the angle from the vertical, BA cos 60°.

70. C—The inductor resists changes in current. But after a long time, the current reaches steady state, meaning the current does not change; thus the inductor, after a long time, might as well be just a straight wire. The battery will still provide current I, of which half goes through each equal resistor.

Physics C—Practice Exam—Free-Response Solutions

Notes on grading your free-response section

For answers that are numerical, or in equation form:

*For each part of the problem, look to see if you got the right answer. If you did, and you showed any reasonable (and correct) work, give yourself full credit for that part. It’s okay if you didn’t explicitly show EVERY step, as long as some steps are indicated and you got the right answer. However:

*If you got the WRONG answer, then look to see if you earned partial credit. Give yourself points for each step toward the answer as indicated in the rubrics below. Without the correct answer, you must show each intermediate step explicitly in order to earn the point for that step. (See why it’s so important to show your work?)

*If you’re off by a decimal place or two, not to worry—you get credit anyway, as long as your approach to the problem was legitimate. This isn’t a math test. You’re not being evaluated on your rounding and calculator-use skills.

*You do not have to simplify expressions in variables all the way. Square roots in the denominator are fine; fractions in nonsimplified form are fine. As long as you’ve solved properly for the requested variable, and as long as your answer is algebraically equivalent to the rubric’s, you earn credit.

*Wrong, but consistent: Often you need to use the answer to part (a) in order to solve part (b). But you might have the answer to part (a) wrong. If you follow the correct procedure for part (b), plugging in your incorrect answer, then you will usually receive full credit for part (b). The major exceptions are when your answer to part (a) is unreasonable (say, a car moving at 10⁵ m/s, or a distance between two cars equal to 10^–100 meters), or when your answer to part (a) makes the rest of the problem trivial or irrelevant.

For answers that require justification:

*Obviously your answer will not match the rubric word-for-word. If the general gist is there, you get credit.

*But the reader is not allowed to interpret for the student. If your response is vague or ambiguous, you will NOT get credit.

CM 1

(a)

1 pt: Write Newton’s second law for the direction along the plane for each block. Call the mass of each identical block m.

1 pt: For the right block, T— mg sin30 = ma.

1 pt: For the left block mg sin60 — T = ma.

1 pt: Here the directions chosen are consistent, so that forces that accelerate the system to the left are positive. (However, you earn this point as long as directions are consistent.)

1 pt: Solve these equations simultaneously (it’s easiest just to add them together).

1 pt: a = 1.8 m/s². (An answer of a= —1.8 m/s²is incorrect because the magnitude of a vector can not be negative.) (Alternatively, you can just recognize that mg sin60 pulls left, while mg cos60 pulls right, and use Newton’s second law directly on the combined system. Be careful, though, because the mass of the ENTIRE system is 10 kg, not 5 kg!)

(b)

1 pt: Just plug the acceleration back into one of the original Newton’s second law equations from part (a).

1 pt: You get T= 34 N.

(c)

For parts (c) and (d), points are awarded principally for showing the difference that friction makes in the solution. You earn credit for properly accounting for this difference, even if your overall solution is wrong, as long as you followed a similar process to parts (a) and (b).

1 pt: Following the solution for part (a), this time the right block’s equation becomes T — mg sin 30 — μ F_N, where μ is the coefficient of friction, given as 0.10.

1 pt: The normal force is equal to mg cos30.

1 pt: The left block’s equation is the same as before, mg sin60 — T= ma.

1 pt: Eliminating T and solving, we get 1.4 m/s². This is reasonable because we get a smaller acceleration when friction is included, as expected. [This answer point is awarded for ANY nonzero acceleration that is less than that calculated in part (a).]

(d)

1 pt: Plugging back into one of the equations in part (c), we find T= 36 N this time, or whatever tension is consistent with part (c).

1 pt: Awarded for ANY nonzero tension greater than that found in part (b).

1 pt: For proper units on at least one acceleration and one tension, and no incorrect units.

CM 2

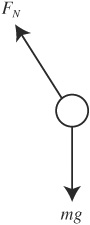
(a)

1 pt: The weight of the ball acts down.

1 pt: The normal force acts up and left, perpendicular to the surface of the glass.

1 pt: No other forces act.

(b)

1 pt: The normal force can be broken into vertical and horizontal components, where the vertical is F_N cos θ and the horizontal is F_N sin θ. (The vertical direction goes with cosine here because θ is measured from the vertical.)

1 pt: The net vertical force is zero because the ball doesn’t rise or fall on the glass. Setting up forces equal to down, F_N cos θ = mg.

1 pt: The horizontal force is a centripetal force, so F_N sin θ = mv ²/r sin θ.

1 pt: For using r sin θ and not just r. (Why? Because you need to use the radius of the actual circular motion, which is not the same as the radius of the sphere.)

1 pt: The tangential speed “v” is the circumference of the circular motion divided by the period. Since period is 1 /f, and because the radius of the circular motion is r sin θ, this speed v = 2p r sin θ f.

1 pt: Now divide the vertical and horizontal force equations to get rid of the F_N term:

sinθ/cosθ = v²/r sinθg.

1 pt: Plug in the speed and the sin θ terms cancel, leaving cos θ = g/4π²rf2.

1 pt: Plugging in the given values (including r = 0.08 m), θ = 83°.

(c)

1 pt: From part (a), the linear speed is 2pr sinθ f.

1 pt: Plugging in values, the speed is 2.5 m/s. (If you didn’t get the point in part (a) for figuring out how to calculate linear speed, but you do it right here, then you can earn the point here.)

(d)

1 pt: The angle will not be affected.

1 pt: Since the mass of the ball does not appear in the equation to calculate the angle in part (b), the mass does not affect the angle.

CM 3

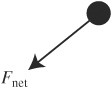
(a)

1 pt: The net force is at an angle down and to the left, perpendicular to the rod.

1 pt: Because the ball is instantaneously at rest, the direction of the velocity in the next instant must also be the direction of the acceleration; this direction is along the arc of the ball’s motion.

(b)

1 pt: The magnitude of the net force is mg sin θ.

1 pt: It’s easiest to use a limiting argument: When θ= 90°, then the net force would be simply the weight of the ball, mg. mg sin 90°=mg, while mg cos 90°=zero; hence the correct answer.

(c)

1 pt: The force on the mass is —mg sinθ, the negative arising because the force is always opposite the displacement.

1 pt: Potential energy is derived from force by U = —∫ Fdx.

1 pt: The distance displaced x = Lθ.

1 pt: The differential dx becomes L dθ.

1 pt: The integral becomes ∫ mgL sin θ dθ, which evaluates to —mgL cos θ (Here the constant of integration can be taken to be any value at all because the zero of potential energy can be chosen arbitrarily.)

[Alternate solution: Using geometry, it can be found that the height of the bob above the lowest point is L — L cos θ. Thus, the potential energy is mgh = mg(L — L cosθ). This gives the same answer, but has defined the arbitrary constant of integration as mgL.]

(d)

1 pt: The graph should look like some sort of sine or cosine function, oscillating smoothly. The graph may be shifted up or down and still receive full credit.

1 pt: The graph should have an amplitude of mgL, though the graph can be shifted arbitrarily up or down on the vertical axis.

1 pt: The graph should have a minimum at θ = 0.

1 pt: The graph should have a maximum at θ = 180°.

(e)

1 pt: For simple harmonic motion, the restoring force must be linearly proportional to the displacement, like F =—kx. This yields an energy function that is quadratic: —(—kx)-dx integrates to give U = ¹/₂ kx². The graph of the energy of a simple harmonic oscillator is, thus, parabolic.

1 pt: Near the θ = 0 position, the graph in part (e) is shaped much like a parabola, only deviating from a parabolic shape at large angles; so the pendulum is a simple harmonic oscillator as long as the energy graph approximates a parabola.

AP Physics C—Mechanics

Full Exam Scoring

Multiple Choice:

Number Correct ———
Number Wrong ———

Total = Right — (1/4) Wrong——35 max

Free Response: Question 1———15 max

Question 2———15 max

Question 3———15 max

Total Free Response———45 max

1.286 X Multiple Choice + Free Response = Raw Score———90 max

56—90 5

40—55 4

29—39 3

15—28 2

0—14 1

CE&M 1

(a)

1 pt: Inside a conductor, the electric field must always be zero. E= 0.

1 pt: Because we have spherical symmetry, use Gauss’s law.

1 pt: The area of a Gaussian surface in this region is 4p r². The charge enclosed by this surface is Q.

1 pt: ^So, ^E Q enclosed/εo^A ^Q/4 πε o^r·

1 pt: Inside a conductor, the electric field must always be zero. E= 0.

2 pts: Just as in part 2, use Gauss’s law, but now the charged enclosed is 3Q.

E = 3Q/4π ε_or².

(b)

1 pt: —Q is on the inner surface.

1 pt: +3 Q is on the outer surface.

1 pt: Because E= 0 inside the outer shell, a Gaussian surface inside this shell must enclose zero charge, so —Q must be on the inside surface to cancel the +Q on the small sphere. Then to keep the total charge of the shell equal to +2 Q,+3 Q must go to the outer surface.

(c)

1 pt: Because we have spherical symmetry, the potential due to both spheres is 3Q/4πε_or, with potential equal to zero an infinite distance away.

1 pt: So at position R₃, the potential is 3Q/4pπε_oR3. (Since E = 0 inside the shell, V is the same value everywhere in the shell.)

(d)

1 pt: Integrate the electric field between R₁ and R₂ to get V = Q/4 πε_or + a constant of integration.

1 pt: To find that constant, we know that V(R₂) was found in part (c), and is 3Q/4π ε_oR ₃. Thus, the constant is

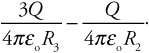
1 pt: Then, potential at R₁ = Q/4pπ ε_oR₁ + the constant of integration.

CE&M 2

(a)

1 pt: The series capacitors add inversely,

so C_eq for the series capacitors is 3 μF.

1 pt: The parallel capacitor just adds in algebraically, so the equivalent capacitance for the whole system is 5 μF.

(b)

1 pt: After a long time, the resistor is irrelevant; no current flows because the fully charged capacitors block direct current.

1 pt: The voltage across C₃ is 10 V (because there’s no voltage drop across the resistor without any current).

1 pt: By Q = CV the charge on C3 is 20 μC.

1 pt: Treating C₁ and C₂ in series; the equivalent capacitance is 3 μF, the voltage is 10 V (in parallel with C₃).

1 pt: The charge on the equivalent capacitance of C₁ and C₂ is 30 μC’ thus the charge on C₁ = 30 μC, and the charge on C₂ is also 30 μC (charge on series capacitors is the same).

1 pt: Using Q= CV, the voltage across C₁ is 7.5 V.

1 pt: Using Q= CV, the voltage across C₂ is 2.5 V.

(c)

1 pt: For a graph that starts at Q= 0.

1 pt: For a graph that asymptotically approaches 20 μC (or whatever charge was calculated for C₃ in part b).

1 pt: For calculating the time constant of the circuit, RC = 5 s.

1 pt: For the graph reaching about 63% of its maximum charge after one time constant.

(d)

1 pt: For recognizing that the voltage does not change.

1 pt: For explaining that if voltage changed, then Kirchoff’s voltage rule would not be valid around a loop including C₃ and the battery (or explaining that voltage is the same across parallel components, so if one is disconnected the other’s voltage is unaffected).

CE&M 3

(a)

1 pt: For placing the wire along a north—south line.

1 pt: The wire could be placed above the compass, with the current traveling due north. (The wire also could be placed underneath the compass, with current traveling due south.) (Points can also be earned for an alternative correct solution: for example, the wire could be placed perpendicular to the face of the compass (just south of it), with the current running up.)

(b)

1 pt: The B field due to Earth plus the B field caused by the wire, when added together as vectors, must give a resultant direction of 48° west of north.

1 pt: Placing these vectors tail-to-tip, as shown below, tan 48° = B_wire/B_Earth.

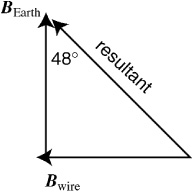
1 pt: So B_wire = B_Earthan 48° = 5.6 × 10 ⁵ T. (c)

(c)

1 pt: The magnetic field due to a long, straight, current-carrying wire is given by

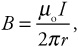
where r is the distance from the wire to the field point, represented in this problem by d.

1 pt: So B is proportional to 1 /d; this results in a hyperbolic graph.

1 pt: This graph should be asymptotic to both the vertical and horizontal axes.

(d)

1 pt: Place 1 /d on the horizontal axis.

2 pts: The equation for the field due the wire can be written

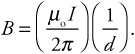
Everything in the first set of parentheses is constant. So, this equation is of the form y= mx, which is the equation of a line, if 1 /d is put on the x-axis of the graph. (1 point can be earned for a partially complete explanation. On this problem, no points can be earned for justification if the answer is incorrect.)

(e)

1 pt: The slope of the graph, from the equation above, is

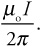
1 pt: For plugging in values correctly, including 0.5 A or 500 mA.

1 pt: For units on the slope equivalent to magnetic field times distance (i.e., T-m, T-cm, mT-m, etc.).

1 pt: For a correct answer, complete with correct units: 1.0 × 10 ⁷ Tm, or 1.0 × 10 ⁴ mT-m.

AP Physics C—Electricity and Magnetism

Full Exam Scoring

Multiple-Choice:

Number Correct———
Number Wrong———

Total = Right — (1/4) Wrong———35 max

Free-Response:

Question 1———15 max
Question 2———15 max
Question 3———15 max

Total Free-Response———45 max

1.286 X Multiple-Choice + Free-Response = Raw Score———90 max

52—90 5

39—51 4

26—38 3

15—25 2

0—14 1