5
A Very Interesting Conclusion
The mass of a body is a measure of its energy content.
Albert Einstein1
As Chapter 4 implies, our understanding of the atomic and molecular nature of matter unfolded at speed in a relatively short time. For more than 2,000 years atoms had been the objects of metaphysical speculation, the preserve of philosophers. Over a period of fifty or sixty years beginning in the early nineteenth century, their status changed rather dramatically. By the early twentieth century, they had become the objects of serious scientific investigation.
The scientists sought to interpret the properties and behaviour of material substance using the structure of classical mechanics, erected on the foundations that had been laid down by Newton more than 200 years before. Small differences between theory and experiment were quite common, but could be reconciled by acknowledging that objects (including atoms and molecules) are more complex than the simplified models needed to make the theory easy to apply.
The simpler theories assume that atoms and molecules behave ‘ideally’, as though they are perfectly elastic point particles, meaning that they don’t deform and don’t occupy any volume in space. They clearly do, and making allowances for this enabled scientists to take account of such ‘non-ideal’ behaviour entirely within the framework of classical mechanics.
But in the last decades of the nineteenth century this structure was beginning to creak under the strain of accumulating evidence to suggest that something was more fundamentally wrong. Many physicists (including Einstein) had by now developed deep reservations about Newton’s conceptualization of an absolute space and time. These were reservations arguably born from a sense of philosophical unease (Mach, the arch-empiricist, rejected them completely), but they were greatly heightened by a growing conflict with James Clerk Maxwell’s wave theory of electromagnetic radiation. Something had to give.
In the Mathematical Principles, Newton had been obliged to contemplate the very nature of space and time. Are these things aspects of an independent physical reality? Do they exist independently of objects and of our perceptions of them? As Kant might have put it, are they absolute things-in-themselves?
We might be tempted to ask: If space and time are not absolute, then what are they? The answer is: relative. Think about it. We measure distances on Earth relative to a co-ordinate system (e.g., of latitude and longitude). We measure time relative to a system based on the orbital motion of the Earth around the Sun and the spin motion of the Earth as it turns around its axis. These systems might seem ‘natural’ choices, but they are natural only for us Earth-bound human beings.
The simple fact is that our experience of space and time is entirely relative. We see objects moving towards or away from each other, changing their relative positions in space and in time. This is relative motion, occurring in a space and time that is in principle defined only by their relationships to the objects that exist within it. Newton was prepared to acknowledge this in what he called our ‘vulgar’ experience, but his system of mechanics demanded absolute motion. He argued that, although we can’t directly perceive them, absolute space and time really must exist, forming a kind of ‘container’ within which actions impress forces on matter and things happen. Take all the matter out of the universe and the empty container would remain: there would still be ‘something’. This was discomfiting to a few philosophically minded scientists perhaps, but it hardly seems something to be losing lots of sleep over.
Then along came Maxwell. We encountered the Scottish physicist James Clerk Maxwell towards the end of Chapter 4. Confronted by compelling experimental evidence for deep connections between the phenomena of electricity and magnetism, over a ten-year period from 1855 to 1865 he published a series of papers which set out a theory of electrodynamics. This theory describes electricity and magnetism in terms of two distinct, but intimately linked, electric and magnetic fields.
Now, there are many different kinds of examples of ‘fields’ in physics. Any physical quantity that has different magnitudes at different points in space and time can be represented in terms of a field. Of all the different possibilities (and we will meet quite a few in this book), the magnetic field is likely to be most familiar.
Think back to that science experiment you did in school. You sprinkle iron filings on a sheet of paper held above a bar magnet. The iron filings become magnetized and, because they are light, they shift position and organize themselves along the ‘lines of force’ of the magnetic field. The resulting pattern reflects the strength of the field and its direction, stretching from north to south poles. The field seems to exist in the ‘empty’ space around the outside of the bar of magnetic material.
The connection between electric and magnetic fields has some very important consequences. Pass electricity along a wire and you generate an electric current. You also create a changing magnetic field. Conversely, change a magnetic field and you generate an electric current. This is the basis for electricity generation in power stations. Maxwell’s equations tie these fields together and explain how one produces the other.
There’s more. When we look hard at Maxwell’s equations we notice that they also happen to be equations that describe the motions of waves. Experimental evidence in support of a wave theory of light (which is one form of electromagnetic radiation) had been steadily accumulating in the years since Newton’s Optiks was first published. When we squeeze light through a narrow aperture or slit in a metal plate, it spreads out (we say it diffracts), in much the same way that ocean waves passing through a narrow gap in a harbour wall will spread out in the sea beyond the wall. All that is required for this to happen is for the slit to be of a size similar to the average wavelength of the waves, the distance for one complete up-and-down, peak-to-trough motion.
Light also exhibits interference. Shine light on two slits side by side and it will diffract through both. The waves diffracted by each slit then run into each other. Where the peak of one wave meets the peak of the other, the result is constructive interference—the waves mutually reinforce to produce a bigger peak. Where trough meets trough the result is a deeper trough. But where peak meets trough the result is destructive interference: the waves cancel each other out. The result is a pattern of alternating brightness and darkness called interference fringes: bright bands are produced by constructive interference and dark bands by destructive interference. This is called two-slit interference (see Figure 2).
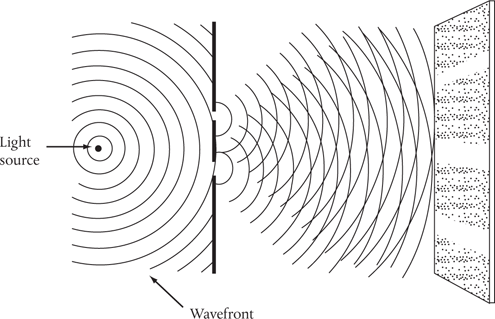
Figure 2. When passed through two narrow, closely spaced apertures or slits, light produces a pattern of alternating light and dark fringes. These can be readily explained in terms of a wave theory of light in which overlapping waves interfere constructively (giving rise to a bright fringe) and destructively (dark fringe).
The waves ‘bend’ and change direction as they squeeze through the slits or around obstacles. This kind of behaviour is really hard to explain if light is presumed to be composed of ‘atoms’ obeying Newton’s laws of motion and moving in straight lines. It is much easier to explain if we suppose light consists of waves.
In fact, Maxwell’s equations can be manipulated to calculate the speed of electromagnetic waves travelling in a vacuum. It turns out that the result is precisely the speed of light, to which we give the special symbol c.* In 1856, the conclusion was inescapable. Light does not consist of atoms. It consists of electromagnetic waves.2
This all seems pretty conclusive, but once again we have to confront the tricky question: if light is indeed a wave disturbance, then what is the medium through which it moves? Maxwell didn’t doubt that light must move through the ether, thought to fill all of space. But if the ether is assumed to be stationary, then in principle it provides a frame of reference—precisely the kind of ‘container’—against which absolute motion can be measured, after all. The ghost of Newton might have been unhappy that his theory of light had been abandoned, but he would surely have liked the ether.
Physicists turned their attentions to practicalities. If all space really is full of ether, then it should be possible to detect it. For sure, the ether was assumed to be quite intangible, and not something we could detect directly (otherwise we would already know about it). Nevertheless, even something pretty tenuous should leave clues that we might be able to detect, indirectly.
The Earth rotates around its axis at 465 metres per second. If a stationary ether really does exist, then the Earth must move through it. Let’s just imagine for a moment that the ether is as thick as the air. Further imagine standing at the Earth’s equator, facing west towards the direction of rotation. What would we experience? We would likely feel an ether wind, much like a strong gale blowing in from the sea which, if we spread our arms and legs, may lift us up and carry us backwards a few metres.* The difference is that the ether is assumed to be stationary: the wind is produced by Earth’s motion through it.
Now, a sound wave carried in a high wind reaches us faster than a sound wave travelling in still air. The faster the medium is moving, the faster the wave it carries must move with it. This means that, although the ether is meant to be a lot more tenuous than the air, we would still expect that light waves carried along with the ether wind should travel faster than light waves moving against this direction. In other words, light travelling in a west-to-east direction, in which the ether wind is greatest, should be carried faster than light travelling east-to-west, in the opposite direction.
In 1887, American physicists Albert Michelson and Edward Morley set out to determine if such differences in the speed of light could be measured. They made use of subtle interference effects in a device called an interferometer, in which a beam of light is split and sent off along two different paths (see Figure 3). The beams along both paths set off ‘in step’, meaning that the position of the peaks along one path matches precisely the position of the peaks travelling along the other path. These beams are then brought back together and recombined. Now, if the total path taken by one beam is slightly longer than the total path taken by the other, then peak may no longer coincide with peak and the result is destructive interference. Alternatively, if the total paths are equal but the speed of light is different along different paths, then the result will again be interference.

Figure 3. The Michelson–Morley experiment involved an apparatus called an interferometer, similar to the one shown here in (a). In this apparatus, a beam of light is passed through a half-silvered mirror or beamsplitter, as shown in (b). Some of the light follows path1, bounces off mirror1 and returns. The rest of the light follows path2, bounces off mirror2 and also returns. Light from both paths is then recombined in the beamsplitter and subsequently detected. If the light waves returning along both paths remain ‘in step’, with peaks and troughs aligned, then the result is a bright fringe (constructive interference). But if the lengths of path1 and path2 differ, or the speed of light is different along different paths, then the waves may no longer be in step, and the result is a dark fringe (destructive interference) as shown in (c).
No differences could be detected. Within the accuracy of the measurements, the speed of light was found to be constant. This is one of the most important ‘negative’ results in the entire history of science.
What’s going on? Electromagnetic waves demand an ether to move in, yet no evidence for the ether could be found. These were rather desperate times, and in an attempt to salvage the ether physicists felt compelled to employ desperate measures. Irish physicist George FitzGerald (in 1889) and Dutch physicist Hendrik Lorentz (in 1892) independently suggested that the negative results of the Michelson–Morley experiments could be explained if the interferometer was assumed to be physically contracting along its length in response to pressure from the ether wind.
Remember, interference should result if the light travelling along the path against the direction of the ether wind is carried a little slower. But if the length of this path is contracted by the ‘pressure’ of the ether wind, this could compensate for the change in the speed of light. The effects of a slower speed would be cancelled by the shortening of the distance, and no interference would be seen.
Fitzgerald and Lorentz figured out that if the ‘proper’ length of the path in the interferometer is l0, it would have to contract to a length l given by l0/γ. Here γ (Greek gamma) is the Lorentz factor, given by 1/√(1 − v2/c2), in which v is the speed of the interferometer relative to the stationary ether and c is the speed of light.
This factor will recur a few times in Chapters 6 and 7, so it’s worthwhile taking a closer look at it here. The value of γ obviously depends on the relationship between v and c, as shown in Figure 4. If v is very much smaller than c, as, for example, in everyday situations such as driving to work, then v2/c2 is very small and the term in brackets is very close to 1. The square root of 1 is 1, so the Lorentz factor γ is also 1. At normal speeds your car doesn’t contract due to the pressure of the ether wind.*
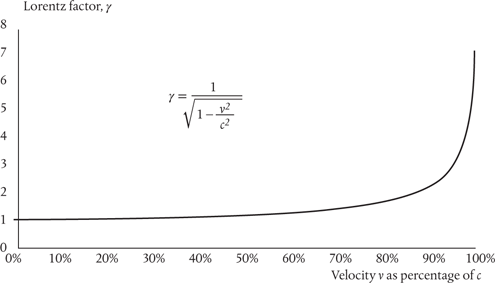
Figure 4. The Lorentz factor γ depends on the relationship between the speed at which an observed object is moving (v) and the speed of light (c).
But now let’s suppose that v is much larger, say 86.6 per cent of the speed of light (i.e., v/c = 0.866). The square of 0.866 (v2/c2) is about 0.75. Subtract this from 1 and we get 0.25. The square root of 0.25 is 0.50. So, in this case γ is equal to 2. A car travelling at this speed would be compressed to half its original length.
Now, the Earth’s rotation speed is just 0.0002 per cent of the speed of light, so γ is only very slightly greater than 1. Any contraction in the path length in the interferometer was therefore expected to be very small.
There was no real explanation for such a contraction, and to some physicists it all looked like a rather grand conspiracy designed simply to preserve the idea of the ether and, by implication, absolute space. Einstein was having none of it. In the third of five papers that he published in 1905, he demolished the idea of the stationary ether and, by inference, absolute space.3
Einstein needed only to invoke two fundamental principles. The first, which became known as the principle of relativity, says that observers who find themselves in relative motion at different (but constant) speeds must make observations that obey precisely the same fundamental laws of physics. If I make a set of physical measurements in a laboratory on Earth and you make the same set of measurements aboard a supersonic aircraft or a spaceship, then we would expect to get the same results. This is, after all, what it means for a relationship between physical properties to be a ‘law’.
The second principle relates to the speed of light. In Newton’s mechanics, velocities are additive. Suppose you’re on an inter-city train moving at 100 miles per hour. You run along the carriage in the same direction as the train at a speed of 10 miles per hour. We deduce that your total speed whilst running measured relative to the track or a stationary observer on a station platform is the sum of these, or 110 miles per hour.
But light doesn’t obey this rule. Setting aside the possibility of a Fitzgerald–Lorentz-style contraction, the Michelson–Morley experiment shows that light always travels at the same speed. If I switch on a flashlight whilst on a stationary train the light moves away at the speed of light, c. If I switch on the same flashlight whilst on a train moving at 100 miles per hour, the speed of the light is still c, not c plus 100 miles per hour. Instead of trying to figure out why the speed of light is constant, irrespective of the motion of the source of the light, Einstein simply accepted this as an established fact and proceeded to work out the consequences.
To be fair, these principles are not really all that obvious. The speed of light is incredibly fast compared with the speeds of objects typical of our everyday observations of the world around us. Normally this means that what we see appears simultaneously with what happens. This happens over here, and we see this ‘instantaneously’. That happens over there shortly afterwards, and we have no difficulty in being able to order these events in time, this first, then that. Einstein was asking a very simple and straightforward question. However, it might appear to us, the speed of light is not infinite. If it actually takes some time for light to reach us from over here and over there, how does this affect our observations of things happening in space and in time?
Let’s try to answer this question by performing a simple experiment in our heads.* Imagine we’re travelling on a train together. It is night, and there is no light in the carriage. We fix a small flashlight to the floor of the carriage and a large mirror on the ceiling. The light flashes once, and the flash is reflected from the mirror and detected by a small light-sensitive cell or photodiode placed on the floor alongside the flashlight. Both flashlight and photodiode are connected to an electronic box of tricks that allows us to measure the time between the flash and its detection.
We make our first set of measurements whilst the train is stationary, and measure the time taken for the light to travel upwards from the flashlight, bounce off the mirror, and back down to the photodiode, as shown in Figure 5(a). Let’s call this time t0.

Figure 5. In this thought experiment, we measure the time taken for light to travel from the flashlight on the floor, bounce off the mirror on the ceiling, and return to the photodiode on the floor. We do this whilst the train is stationary (a), and record the time taken as t0. You then observe the same sequence from the platform, but now as the train moves from left to right with a speed v, which is a substantial fraction of the speed of light (b)—(d). Because the train is moving, it now takes longer for the light to complete the round-trip from floor to ceiling and back, such that t = γt0, where γ is the Lorentz factor. From your perspective on the platform, time on the train appears dilated.
You now step off the train and repeat the measurement as the train moves past from left to right with velocity v, where v is a substantial fraction of the speed of light. Of course, trains can’t move this fast in real life, but that’s okay because this is only a thought experiment.
Now from your vantage point on the platform you see something rather different. The light no longer travels straight up and down. At a certain moment the light flashes, as shown in Figure 5(b). In the small (but finite) amount of time it takes for the light to travel upwards towards the ceiling, the train is moving forward, from left to right, Figure 5(c). It continues to move forward as the light travels back down to the floor to be detected by the photodiode, Figure 5(d).
From your perspective on the platform the light path now looks like a ‘Λ’, a Greek capital lambda or an upside-down ‘V’. Let’s assume that the total time required for the light to travel this longer path is t. A bit of algebraic manipulation and a knowledge of Pythagoras’ theorem allow us to deduce that t = γt0, where γ is the Lorentz factor, as before.4
There is only one possible conclusion. From your perspective as a stationary observer standing on the platform, time is measured to slow down on the moving train. If the train is travelling at about 86.6 per cent of the speed of light, as we now know, the Lorentz factor γ = 2 and what took 1 second when the train was stationary now appears to take 2 seconds when measured from the platform. In different moving frames of reference, time appears to be ‘dilated’.
I’m sure you won’t be surprised to learn that distances measured in the direction of travel also contract, by precisely the amount that FitzGerald and Lorentz had demanded. But now the contraction is not some supposed physical compression due to the ether wind; it is simply a consequence of making measurements in moving frames of reference in which the speed of light is a universal constant.
You might be a little puzzled by this. Perhaps you’re tempted to conclude: okay, I get that distances and times change when the object I’m making my observations on moves past me at different speeds, but isn’t this a measurement problem? Surely there must be a ‘correct’ distance and a ‘correct’ time? Actually, no. There are only different frames of reference, including the so-called ‘rest frame’ of the object when it is stationary. If we’re riding on the object looking out, any observations we make of other objects are subject to this relativity. There is no ‘absolute’ frame of reference, no ‘God’s-eye view’. All observations and measurements are relative.
It turns out that time intervals and distances are like two sides of the same coin. They are linked by the speed of the frame of reference in which measurements are made relative to the speed of light. It’s possible to combine space and time together in such a way that time dilations are compensated by distance contractions, and vice versa. The result is a four-dimensional spacetime, sometimes called a spacetime metric. One such combination was identified by Hermann Minkowski, Einstein’s former maths teacher at the Zurich Polytechnic. Minkowski believed that an independent space and time were now doomed to fade away, to be replaced by a unified spacetime.5
This is Einstein’s special theory of relativity. At the time of its publication in 1905 the theory was breathtaking in its simplicity; the little bit of algebra in it isn’t all that complicated, yet it is profound in its implications. But he wasn’t quite done. He continued to think about the consequences of the theory and just a few months later he published a short addendum.
Before going on to consider what Einstein had to say next, we first need to update the story on Newton’s second law concept of force. Whilst it is certainly true to say that this concept still has some relevance today, the attentions of nineteenth-century physicists switched from force to energy. This is the more fundamental concept. My foot connects with a stone, this action impressing a force upon the stone. But a better way of thinking about this is to see the action as transferring energy to the stone, in this case as an energy of motion (or what we call kinetic energy).
Like force, the concept of energy also has its roots in seventeenth-century philosophy. Leibniz wrote about vis viva, a ‘living force’ expressed as mass times velocity-squared—mv2—which is only a factor of two larger than the expression for kinetic energy we use today (½mv2). Leibniz also speculated that vis viva might be a conserved quantity, meaning that it can only be transferred between objects or transformed from one form to another—it can’t be created or destroyed. The term ‘energy’ was introduced in the early nineteenth century and a law of conservation of energy was subsequently formulated, largely through the efforts of physicists concerned with the principles of thermodynamics.
In 1845, the ghost of ‘caloric’ was finally laid to rest when the English physicist James Joule identified the connection between heat and mechanical work. Heat is not an element, it is simply a measure of thermal (or heat) energy, and the amount of thermal energy in an object is characterized by its temperature. Spend ten minutes in the gym doing some mechanical work, such as lifting weights, and you’ll make the connection between work, thermal energy, and temperature. Today the joule is the standard unit of energy, although the calorie—firmly embedded as a measure of the energy content of foodstuffs and an important dietary consideration—is the more widely known.*
Back to Einstein. He began his addendum with the words: ‘The results of an electrodynamic investigation recently published by me in this journal lead to a very interesting conclusion, which will be derived here.’6 He wasn’t kidding.
He considered the situation in which an object (e.g., an atom) emits two bursts of light in opposite directions, such that the linear momentum of the object is conserved. Each light burst is assumed to carry away an amount of energy equal to ½E, such that the total energy emitted by the object is E. Einstein then examined this process from two different perspectives or frames of reference. The first is the rest frame, the perspective of an observer ‘riding’ on the object and in which the object is judged to be stationary.
But we don’t normally make measurements riding on objects. The second perspective is the more typical frame of reference involving a stationary observer (in a laboratory, say), making measurements as the object moves with velocity v, much as you stood on the platform making observations of the light beam on the moving train. Einstein deduced that the energy carried away by the bursts of light appears slightly larger in the moving frame of reference (it actually increases to γE), just as time appears dilated on the moving train.
But this process is subject to Einstein’s principle of relativity. Irrespective of the frame of reference in which we’re making our measurements, the law of conservation of energy must apply. So, if the energy carried away by the bursts of light is measured to be larger (γE) in the moving frame of reference compared with the rest frame (E), then that extra energy must come from somewhere.
From where? Well, the only difference between the two frames of reference is that one is stationary and the other is moving. We conclude that the extra energy can only come from the object’s kinetic energy, its energy of motion. If we measure the energy carried away by the light bursts to be a little higher in the moving frame of reference, then we expect that the object’s kinetic energy will be measured to be lower, such that the total energy is conserved.
This gives us two options. We know from the expression for kinetic energy—½mv2—that the extra energy must come either from changes in the object’s mass, m, or its velocity, v. Our instinct might be to leave the mass well alone. After all, mass is surely meant to be an intrinsic, ‘primary’ quality of the object. It would perhaps be more logical if the energy carried away by the bursts of light means that the object loses kinetic energy by slowing down instead.
Logical or not, in his paper Einstein showed that the velocity v is unchanged, so the object doesn’t slow down as a result of emitting the bursts of light. Instead, the additional energy carried away by the light bursts in the moving frame of reference comes from the mass of the object, which falls by an amount m = E/c2.7 Einstein concluded:8
If a body emits the energy [E] in the form of radiation, its mass decreases by [E/c2]. Here it is obviously inessential that the energy taken from the body turns into radiant energy, so we are led to a more general conclusion: The mass of a body is a measure of its energy content.
Today we would probably rush to rearrange this equation to give the iconic formula E = mc2.