10
The Wave Equation
When he had finished, [Pieter] Debye casually remarked that this way of talking was rather childish. As a student … he had learned that, to deal properly with waves, one had to have a wave equation.
Felix Bloch1
It was called wave–particle duality. And, as physicists tried desperately to find ways to come to terms with it, they launched into an unprecedented period of imaginative theorizing. Within a few short years our understanding of the atomic nature of matter would be utterly transformed.
Up to this point, experiment had been firmly in the driving seat. Since Bohr’s breakthrough in 1913 ever more detailed studies of atomic spectra had revealed some startling truths. The patterns of absorption and emission lines of the hydrogen atom could be explained through the introduction of the quantum number, n. But, look more closely and what appeared to be one atomic line, with a crisply defined frequency or wavelength, turned out to be two closely spaced lines. Wrap the atoms in a low-intensity electric or magnetic field and some lines would be further split. Quantum numbers proliferated. To n was added k (which, over time, became the azimuthal quantum number l).* To n and l was added m, the magnetic quantum number.
To avoid confusion, the original n was renamed the principal quantum number, closely linked with the total energies of the electron orbits inside the atom, as Bohr had discovered. Physicists realized that the new quantum numbers reflected constraints on the geometries of the different electron orbits and their response to electric and magnetic fields. Relationships between the quantum numbers, such that the value of n constrains the possible values for l, which in turn constrains the possible values for m, told which lines would appear in an atomic spectrum and which were ‘forbidden’, and therefore missing, spawning an elaborate system of ‘selection rules’.2 Nobody understood where these relationships had come from.
Despite its obvious successes, the fledgling quantum theory of the atom creaked under the strain. Whilst the spectrum of the simplest atom—that of hydrogen—could be accounted for using this rather ad hoc system with some degree of confidence, the spectrum of the next simplest atom—helium—could not. The spectra of certain other types of atom, such as sodium and the atoms of rare-earth elements such as lanthanum and cerium, showed ‘anomalous’ splitting when placed in a magnetic field. The puzzles just kept on coming.
It was becoming increasingly clear that a quantum theory created by shoehorning arbitrary quantum rules into an otherwise classical structure was just not going to work. A completely new ‘quantum mechanics’ was needed.
The breakthrough, when it came in June 1925, was made by a young German theorist called Werner Heisenberg. He was studying for a doctorate with esteemed physicist Max Born at Göttingen University when he succumbed to a severe bout of hay fever. He left Göttingen to recuperate on the small island of Helgoland, just off Germany’s north coast.
Heisenberg had chosen to adopt a firmly empiricist approach, electing to focus his attention on what could be seen, rather than what could only be guessed at and speculated on. He reasoned that the secrets of the atom are revealed in atomic spectra, in the precise patterns of frequencies and intensities (or brightness) of individual spectral lines. He now decided that a new quantum mechanics of the atom should deal only in these observable quantities, not unobservable electron ‘orbits’ obliged to obey arbitrary quantum rules.
Free from distractions on Helgoland, he made swift progress. He constructed a rather abstract model consisting of a potentially infinite series of terms, organized into a table with rows and columns, with each term characterized by an amplitude and a frequency, identified with a quantum jump from one orbit to the next in the series. From this table he could work out the intensity of a spectral line resulting from a quantum jump from one orbit to another as the sum of the products of the amplitudes for all possible intermediate jumps.
Whilst this process seemed quite straightforward, Heisenberg became aware of a potential paradox. In conventional arithmetic, if we multiply together two numbers x and y the result (xy) obviously doesn’t depend on the order in which we do the multiplication, because x times y gives precisely the same result as y times x. There’s a word for this. The numbers x and y for which xy = yx are said to commute.*
But Heisenberg’s tables of numbers didn’t obey this simple rule. What you got did depend on the order in which the intermediate terms were multiplied together. Heisenberg was quite unfamiliar with this kind of result and greatly unsettled by it.
He returned to Göttingen and shared his results—and his concerns—with Born. Born realized that this quirk arises in matrix multiplication, a branch of mathematics which deals with the algebra not of single numbers (such as x and y), but of square or rectangular arrays of numbers. Born now worked with his student Pascual Jordan to recast Heisenberg’s theory into the language of matrix multiplication. This version of quantum mechanics therefore came to be known as matrix mechanics.
In January 1926, Austrian physicist Wolfgang Pauli and English physicist Paul Dirac both independently showed how matrix mechanics could be used to explain key features of the hydrogen atomic emission spectrum, such as the Balmer formula. However they had come about and whatever they were supposed to mean, the matrices of matrix mechanics clearly offered a glimpse of the underlying physics.
But matrix mechanics wasn’t to everyone’s taste. Older physicists struggled with its mathematical complexity and lack of anschaulichkeit, or ‘visualizability’. They were therefore quite relieved when, hard on the heels of Heisenberg, Pauli and Dirac (all young upstarts in their early–mid-twenties),† thirty-eight-year-old Austrian physicist Erwin Schrödinger published details of what appeared to be a completely different theory. This became known as wave mechanics.
Intrigued by a throwaway remark in one of Einstein’s papers, Schrödinger had acquired a copy of de Broglie’s Ph.D. thesis in November 1925. He presented a seminar on de Broglie’s work a few days later, attended by physicists at the University of Zurich and the nearby Eidgenossische Technische Hochschule (ETH), the former Zurich Polytechnic where Einstein had completed his graduate studies. In the audience was a young Swiss student named Felix Bloch. Bloch later recalled Schrödinger’s presentation, and remarks by Dutch physicist Pieter Debye, who suggested that to deal properly with waves, it is necessary to write down a wave equation.3
Schrödinger celebrated Christmas 1925 at a villa in the Swiss Alps, taking with him his notes on de Broglie’s thesis. By the time he returned on 8 January 1926, he had discovered wave mechanics.
It’s possible to follow Schrödinger’s reasoning from notebooks he kept at the time. His starting point was the equation of classical wave motion (as Debye had suggested), which describes how an arbitrary wave represented by a wavefunction, typically given the symbol ψ (Greek psi), varies in space and time.
Waves can take many different forms, but we are perhaps most familiar with a simple sine wave.4 Schrödinger introduced some quantum behaviour into the classical wave equation by substituting for the wavelength λ using de Broglie’s relation (λ = h/p) and setting the frequency ν equal to E/h.
The resulting wave equation actually represents yet more shoehorning. It is a rather messy fusion of classical wave and classical particle descriptions. It drags an essentially Newtonian concept of mass into the picture, via the (non-relativistic) assumption that the momentum p can be written as mass times velocity. It is doubtful that anyone would have paid much attention to the result, had it not been for what Schrödinger found he could do with it.
A little like Einstein in pursuit of general relativity, Schrödinger quickly reached the limits of his mathematical competence and sought help from a colleague, German mathematician Hermann Weyl. With Weyl’s help, Schrödinger discovered that by constraining the properties of a three-dimensional electron wavefunction fitted around a central proton, a very specific pattern of possible solutions of the wave equation emerged entirely naturally.
De Broglie had speculated that the quantum number n might result from the electron forming a standing wave pattern around the proton. This was a good intuition. Schrödinger now demonstrated that a full three-dimensional wave description produced solutions which depend on all three quantum numbers n, l, and m, which emerged ‘in the same natural way as the integers specifying the number of nodes in a vibrating string’.5 Schrödinger also showed that the energies of the various solutions depend on n2, thereby reproducing the Balmer formula. Make no mistake. These solutions were (and remain to this day) very beautiful.
The conclusion was startling. The electron in the hydrogen atom can be described by a wavefunction and the shapes of the wavefunctions of different energies are constrained by the electron’s quantum nature. Not all shapes are possible. Those that are possible are governed by the values of the quantum numbers, n, l, and m.
Obviously, it’s no longer appropriate to call these ‘orbits’, but we retain the connection with conventional orbits by using the extension ‘orbital’ instead (see Figure 11). By their very nature such orbitals are distributed through space. The lowest-energy electron orbital has a principal quantum number n equal to 1 and a value of l equal to zero, and forms a sphere around the nucleus.
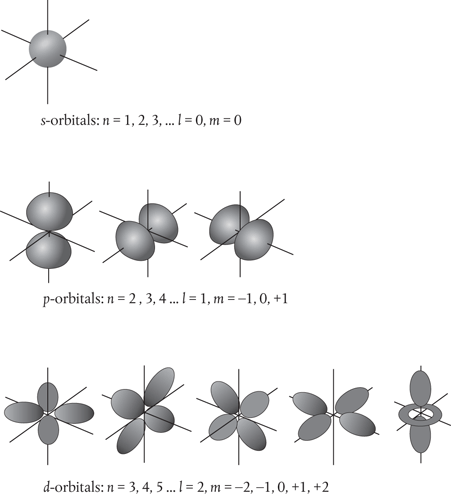
Figure 11. Atomic orbitals, illustrated here for the case of an electron in a hydrogen atom. These represent solutions to the Schrödinger wave equation for different combinations of the quantum numbers n, l, and m. The s-orbitals correspond to solutions with l = 0 and m = 0 and are spherical. The three p-orbitals correspond to solutions with l = 1 and m = –1, 0, and +1 and are shaped like dumbbells. With increasing energy, the orbital shapes become more and more elaborate, as seen here for the five d-orbitals with l = 2 and m = –2, –1, 0, +1 and +2.
So, where could we expect to find the mass of the electron in this orbital? Is it also distributed—in some strange way ‘smeared’—through the space surrounding the nucleus? But how is this possible? Isn’t the electron supposed to be an elementary particle?
Born suggested an interpretation that is still taught to science students today. Perhaps, he said, the wavefunction represents a probability for ‘finding’ the electron at a specific location inside the atom as measured from the nucleus. It’s possible to use the wavefunction to construct a probability ‘distribution’ function, a kind of probability ‘cloud’.* For the lowest-energy orbital of the hydrogen atom, this function peaks at a distance measured from the nucleus of 5.29 × 10−11 metres (or 0.053 nanometres), corresponding to the radius of the electron orbit that Bohr had worked out in 1913 in his original atomic theory. It is called the Bohr radius and can be calculated from a collection of fundamental physical constants. But the probability distribution function tells us only that the electron has the highest probability of being found at this distance. It can in principle be found anywhere within the cloud (see Figure 12). So, where is it exactly?

Figure 12. In the Rutherford-Bohr ‘planetary’ model of the hydrogen atom, a single negatively charged electron occupies a fixed orbit around a nucleus consisting of a single positively charged proton, (a). Quantum mechanics replaces the orbiting electron by an electron ‘orbital’, within which the electron has a varying probability of being ‘found’, and the orbital of lowest energy is spherical, (b). The electron can now be found anywhere within this orbital, but has the highest probability of being found at the distance predicted by the old planetary model.
The conceptual nature of the electron had changed, rather dramatically. It was no longer just a ‘particle’. It had become a ghost. It could be here, or there, within its orbit. And yet, wherever it was, it had somehow to carry all the electron’s mass and electric charge.
And here was something else. The term representing kinetic energy in the Schrödinger wave equation was no longer the familiar ½mv2 of classical mechanics. It had been replaced by a mathematical ‘operator’.6 Now, we can think of a mathematical operator simply as an instruction to do something to a function, such as ‘multiply it’, ‘divide it’, ‘take its square root’, or ‘differentiate it’.
Here’s the thing. Just as the result of multiplying two matrices can depend on the order in which we multiply them together, so the result of two mathematical operations can depend on the order in which we perform them. If we multiply a function and then take the square root of the result, we get a different answer compared with taking the square root first and then multiplying the result.7 Mathematical operations such as these do not commute.
Schrödinger went on to demonstrate that wave mechanics and matrix mechanics are entirely equivalent and give identical results—they express quantum mechanics in two different mathematical ‘languages’. Given the choice between Schrödinger’s rather beautiful three-dimensional orbitals and Heisenberg’s abstract tables of numbers, it’s no surprise that the physics community swiftly adopted wave mechanics.
But Heisenberg wasn’t quite finished. Both matrix and wave mechanics show that multiplying position (x) by momentum (p) and multiplying p by x produce different answers. This really rather strange property has to have a physical basis. In 1927, Heisenberg realized that it belies an inherent uncertainty in the simultaneous measurement of these quantities.
In this context ‘uncertainty’ simply refers to the precision of an observation or measurement. I might measure a distance x to be exactly 1.5 metres, in which case the uncertainty (Δx) is zero. Or I might measure it to be anywhere between 1 and 2 metres, with an average of 1.5 metres and an uncertainty Δx of 0.5 metres either side of the average. Heisenberg determined that if the uncertainty in position is Δx and the uncertainty in momentum is Δp, then the product ΔxΔp must be greater than Planck’s constant h.* This is Heisenberg’s famous uncertainty principle.
There is no such principle in the classical mechanics of Newton. In a classical description there is no limit on the precision with which we can measure the position of an object and its momentum. We are limited only by the precision of our measuring instruments. We assume that a classical object (such as a tennis ball) is precisely in this place, moving at that speed, with that momentum.
Heisenberg’s basic premise was that when making measurements on quantum scales, we run up against a fundamental limit. He reasoned that it is simply impossible to make a measurement without disturbing the object under study in an essential, and wholly unpredictable, way. At the quantum level, no matter how precise our techniques of measurement, we simply can’t get past the fact that they are too ‘clumsy’. In this interpretation, quantum mechanics places limits on what is in principle measureable.
But Bohr fundamentally disagreed. As Heisenberg had worked out the details of his uncertainty principle, Bohr had pondered on how to make sense of wave–particle duality, and he had arrived at what he believed was a profound, and very different, conclusion. The two argued bitterly.8
The contradiction implied by the electron’s wave-like and particle-like behaviours was more apparent than real, Bohr decided. We reach for classical wave and particle concepts to describe the results of experiments because these are the only kinds of concepts with which we are familiar from our experiences as human beings living in a classical world. This is a world consisting of particles and waves.
Whatever the ‘true’ nature of the electron, its behaviour is conditioned by the kinds of experiments we choose to perform. We conclude that in this experiment the electron is a wave. In another kind of experiment, the electron is a particle. These experiments are mutually exclusive. This means that we can ask questions concerning the electron’s wave-like properties and we can ask mutually exclusive questions concerning the electron’s particle-like properties, but we cannot ask what the electron really is.
Bohr suggested that these very different, mutually exclusive behaviours are not contradictory, they are complementary. When he heard about the uncertainty principle from Heisenberg, he realized that this places a fundamental limit not on what is measureable, as Heisenberg had come to believe, but rather on what is knowable.
The clumsiness argument that Heisenberg had employed suggested that quantum wave-particles actually do possess precise properties of position and momentum, and we could in principle measure these if only we had the wit to devise experiments that are subtler, and less clumsy. In contrast, Bohr believed that this has nothing to do with our ingenuity, or lack of it. It has everything to do with the nature of reality at the quantum level. We can’t conceive an experiment of greater subtlety because such an experiment is simply inconceivable.
Imagine we were somehow able to ‘corral’ a wave-particle, bundling it up and fixing it in a specific, well-defined region of space, like herding sheep that had wandered all over the hillside into a pen. This would mean that we could, in principle, measure the position of this wave-particle with any level of precision we liked. In theory, this can be done by adding together a large number of waves with different frequencies in what is known as a superposition. Waves can be piled on top of each other and added together in ways that particles cannot and, if we choose carefully, we can produce a resulting wave which has a large amplitude in one location in space and a small amplitude everywhere else. This allows us to get a fix on the position, x, of the wave-particle with a high degree of precision, so the uncertainty Δx is very small.
But what about the flip side? The wave-particle also has momentum. Well, that’s a bit of a problem. If we express the de Broglie relation in terms of frequency (instead of wavelength), we get ν = pv/h, where v is the speed of the wave.9 Now, we localized the wave-particle in one place by combining together lots of waves with different frequencies. This means that we have a large spread of frequencies in the superposition—Δν is large—and this must mean that Δp is large, too. We can measure the position of the wave-particle with high precision, but only at the cost of considerable uncertainty in its momentum.
The converse is also true. If we have a wave-particle with a single frequency, this implies that we can measure this frequency with high precision. Hence we can determine the momentum with similar precision (Δp is very small). But then we can’t localize the particle; we can’t fix it in one place. We can measure the momentum of a quantum wave-particle with high precision, but only at the cost of considerable uncertainty in the particle’s position.
The anguished debate between Bohr and Heisenberg wore on. Pauli journeyed to Copenhagen in early June 1927 to act as an impartial referee. With Pauli’s support, Bohr and Heisenberg resolved their differences and wounds were healed. But this was no united front, more a rather uneasy alliance. Their perspective became known as the Copenhagen interpretation of quantum mechanics.
Schrödinger’s wave equation was undoubtedly a triumph, but there was more work still to be done. Despite its successes, the equation did not conform to the demands of special relativity. In fact, Schrödinger himself had discovered that a fully relativistic version produced solutions that disagreed with experiment. Until this problem was resolved, the theory would remain only half-baked.
And there was another puzzle. Bohr had shown that the number of energy levels for an electron in an atom scales with n2. There is just one level with n = 1, four with n = 2, nine with n = 3, and so on. The different levels with the same n result from the different possible permutations of the quantum numbers l and m and in principle have exactly the same energy unless the atoms are placed in an electric or magnetic field.
We increase the number of protons in the nucleus as we move from hydrogen to helium to lithium, and so on through the entire periodic table. We must then add a balancing number of electrons in order to make the atoms neutral. We might suppose that we simply add one electron to each energy level, or to each orbital. For hydrogen (one proton) we add one electron, filling the n = 1 orbital. For helium (two protons) we add two electrons, one in the n = 1 orbital and a second in one of the n = 2 orbitals.
But if we do this we simply cannot reproduce the pattern exhibited by the atoms as they are arranged in the periodic table. Helium is a ‘noble gas’—meaning that it is relatively inert and unreactive. Atoms with electrons hovering on the ‘outskirts’ of the atom in higher energy orbitals are much more vulnerable and tend to participate actively in chemical reactions. A helium atom with an electron in an outer n = 2 orbital could be expected to be a lot more reactive than it is.
In fact, the pattern revealed by the periodic table is consistent with the assumption that each level or orbital can accommodate two electrons, not one, such that it scales with 2n2. In helium, the two electrons both go into the n = 1 orbital, ‘closing’ this orbital and rendering the atom unreactive and hence ‘noble’.10 Going back to our planetary analogy, whereas there is only one Earth orbiting the Sun at a fixed orbital distance, it seems that inside the atom there can be up to two ‘Earths’ in each orbit.
Pauli suggested that this must mean that the electron possesses a fourth quantum number. For electrons with the same values of n, l, and m to coexist in the same orbital, they must possess different values of this fourth quantum number. This is Pauli’s exclusion principle.
What could possibly account for this fourth quantum number? There were some clues. A few physicists had earlier suggested that the electron might exhibit a property consistent with a kind of ‘self-rotation’, acting like a top spinning on its axis, just as the Earth spins as it orbits the Sun. It was Dirac who in 1927 suggested that if the electron can be considered to possess two possible ‘spin’ orientations then this, perhaps, explains why each orbital can accommodate up to two electrons (Figure 13). The two electrons must be of opposite spin to ‘fit’ in the same orbital. An orbital can hold a maximum of two electrons provided their spins are paired.
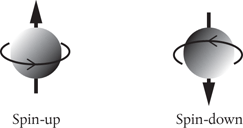
Figure 13. In 1927, Dirac combined quantum mechanics and Einstein’s special theory of relativity to create a fully ‘relativistic’ quantum theory. Out popped the property of electron spin, imagined as through the negatively charged electron was literally spinning on its axis, thereby generating a small, local magnetic field. Today we think of electron spin simply in terms of its possible orientations—spin-up and spin-down.
Although its interpretation is obscure, we do know from experiment that the electron can line itself up in two different spin directions in a magnetic field. We have learned to think of these possibilities as ‘spin-up’ and ‘spin-down’. If we label the electron spin quantum number as s, then this has only one possible value, s = ½. In a magnetic field, the magnetic spin quantum number ms takes values +½ (spin-up) and –½ (spin-down). We re-label the magnetic quantum number m to read ml (to avoid confusion) and the four quantum numbers that now specify the state of an electron inside the atom are n, l, ml, and ms.
Quantum particles with half-integral spins are called fermions, named for Italian physicist Enrico Fermi. We’re free to make what we like of the term ‘spin’, but we need to beware. We know that the Earth needs to make one complete rotation around its axis to get back to where it started (and we also know this takes a day). But fermions would have to spin twice around their axes in order to get back to where they started. Try to imagine it like this. You can make a Möbius band by taking a length of tape, twisting it once and joining the ends together so the band is continuous and seamless (Figure 14). What you have is a ring of tape with only one ‘side’ (it doesn’t have distinct outside and inside surfaces). Now picture yourself walking along this band. You’ll find that, to get back to where you start, you need to walk twice around the ring. This just shows that if you persist in pursuing classical analogies in the quantum world, your likely reward will be a bad headache.

Figure 14. If we start out from any point on a Möbius band, we find that we have to travel twice around it to get back where we started.
Now, electron spin doesn’t feature at all in Schrödinger’s wave equation, so where could it have come from? Dirac provided the answer towards the end of 1927. In wrestling with a version of the wave equation that would conform to the demands of special relativity, Dirac had represented the wavefunction not as a single function (as Schrödinger had done), but as four functions organized in a square four-by-four array, or matrix. Note that in doing this he had not inadvertently wandered into matrix mechanics. These were still the wavefunctions of wave mechanics, but now organized in a square array.
This was the answer. Two of the four solutions correspond to the two different spin orientations of the electron, and emerge naturally from the mathematics. The other two solutions posed something of a conundrum. What did they represent? Dirac hoped for a simple answer. Still in pursuit of the dream of philosophers, he suggested in 1930 that they might represent the proton.