Collecting Reaction Times I
Visual Search and Pop Out
The primary goal of this chapter is to collect and analyze reaction time data using MATLAB®. Reaction time measures to probe the mind have been the backbone of experimental psychology at least since the time of Donders (1868). The basic premise underlying the use of reaction times in cognitive psychology is the assumption that cognitive operations take a certain and measurable amount of time. In addition, it is assumed that additional mental processes add (more or less) linearly. If this is the case, increased reaction times reflect additional mental processes. Let us assume for the time being that this is a reasonable framework. Then, it is highly useful to have a program that allows you to quickly collect reaction time data.
Keywords
visual search; pop out; reaction time; elapsed time
6.1 Goals of this Chapter
The primary goal of this chapter is to collect and analyze reaction time data using MATLAB®. Reaction time measures to probe the mind have been the backbone of experimental psychology at least since the time of Donders (1868). The basic premise underlying the use of reaction times in cognitive psychology is the assumption that cognitive operations take a certain and measurable amount of time. In addition, it is assumed that additional mental processes add (more or less) linearly. If this is the case, increased reaction times reflect additional mental processes. Let us assume for the time being that this is a reasonable framework. Then, it is highly useful to have a program that allows you to quickly collect reaction time data.
6.2 Background
Understanding how the mind/brain decomposes a sensory scene into features is one of the fundamental problems in experimental psychology and systems neuroscience. We take it for granted that the visual system, for example, appears to decompose objects into different edges, colors, textures, shapes, and motion features. However, it is not obvious a priori which features actually represent primitives that are encoded in the visual system. Many neurophysiological experiments have searched for neurons that are tuned to features that were chosen somewhat arbitrarily based on the intuitions of the experimentalists.
Psychologists, however, have developed behavioral experiments by which feature primitives can be revealed. For instance, a study by Treisman and Gelade (1980) has been particularly influential. This is probably due to the fact that it is extremely simple to grasp, yet the pattern of results suggests provocative hypotheses about the nature of perception (e.g., feature primitives, serial search, etc.).
So what is the visual search and pop-out paradigm that was used in the Treisman study?
Research participants were asked to report the presence or absence of a target stimulus (in this case, a colored lowercase letter “o”) among various numbers of distracter stimuli. If the distracter stimuli are just of a different color—that is, if they differ by a single feature—you usually find the “pop-out” effect: the reaction time to detect the target is independent of the number of distracters. Conversely, if more than one stimulus dimension has to be considered to distinguish targets and distracters (conjunction search), you typically find a linear relationship between reaction time and the number of distracters. See Figure 6.1.
As pointed out previously, this pattern of results immediately suggests the existence of “feature primitives”, fundamental dimensions that organize and govern human perception as well as a serial scanner in the case of conjunction search, where one element of the stimulus set after the other is considered as a target (and confirmed or discarded). Often, the ratio of the slopes between conditions where the target is present versus where the target is absent suggests a search process that self-terminates once the target is found.
There are many, many potential confounds in this study (luminance, eye movements, spatial frequency, orientation, etc.). However, the results are extremely robust. Moreover, the study was rather influential. Hence, we will briefly replicate it here.
6.3 Exercises
In this section, we introduce and review some code that will help you to complete the project in Section 6.4. The first thing you need to be able to gather reaction time measures is a way to measure time. There are different ways to measure time in MATLAB. One of the most convenient (and, for our purposes, sufficient ones) comes in the form of the functions tic and toc. They work in conjunction and effectively implement a stopwatch. Try the following on the command line:
What is your elapsed time?
The time reported by MATLAB is the time between pressing Enter after the first statement and pressing Enter after the second statement.
Of course, operating in the real physical world, MATLAB also takes some time to execute the code itself. In most cases, this delay will be negligible. However, you should not take this delay for granted. Try it. In other words, write a program (M-file) that contains only the following lines and execute it:
In my case, toc reported 0.000004 seconds.
You can now create some code to test if MATLAB takes equal amounts of time to increment an index or if it depends on the magnitude of the index. So open a new M-file and enter the following:
format long; %We want to be able to see short differences in time
ii = 1; %Initializing the index, ii
t = [ ]; %Initializing the matrix in which we will store the times
ii = ii + 1; %Incrementing index
t(ii,1) = toc ; %Ending stop-watch and putting respective time into the matrix
Try to run the program. It should execute rather quickly.
Now create a little plot by typing the following on the command line:
The result should be fairly reproducible but the exact shape of the curve as well as the absolute magnitude of the values depends on the computer and its speed.
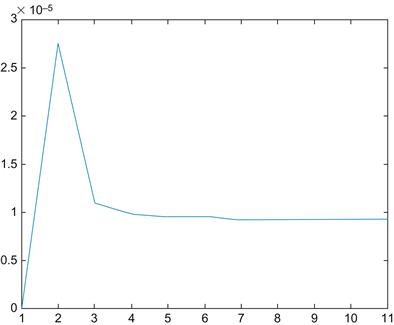
The result should look something like that shown in Figure 6.2.
As you can see, after an initial transient, the time does not depend on the actual value of the index, unlike most human mental processes (e.g., Shepard and Metzler, 1971). This could be taken as evidence for a different kind of information processing in man versus machine.
If you want to know the average time it took for the index to increment, type
If you want to know the maximum and minimum times, you can type max(t) or min(t), respectively.
This example also illustrates several important points. First, when making an inductive claim about all cases all the time, you should sample a substantial range of the problem space (complete would be best). In this case, incrementing an index 10 times is not very impressive. What about incrementing it 100,000 times?
Hence, we discourage premature conclusions on the basis of scant data. Second, it shows that while MATLAB inherently takes care of “plumbing issues” such as memory management or the representation of variables, it cannot avoid the consequences of physical processes. In other words, they might very well impact the execution of your program. Therefore, you should always check that the program is doing what you think it is doing. The structure of the peaks and their robust nature (the subplots show different runs of the program) indicate that they are reliable and not just random fluctuations, probably induced by MATLAB having to change the internal representation of the variable t, which takes longer and longer as it gets larger. This makes sense because MATLAB is shuffling an increasingly large array around in memory, looking for larger and larger chunks thereof. Some of the observed spikes in time taken appear to be distributed largely at random, mostly due to other things going on with the operating system.
Finally, it is a lesson on how to avoid problems like this—namely by preallocating the size and representation of t in memory, if the final size is known in advance.
There are still some issues left, but nowhere near as many as there were before. As you can see, the problem largely goes away (you should also close all programs other than MATLAB when running time-sensitive code). Note also the dramatic difference in the time needed to execute the program. The reason for this is the same—namely memory management. Therefore, if you can, always preallocate memory for your variables, particularly when you know their size in advance and if their size is substantial.
If you’d like to, you can save this data (stored in the t variable) by clicking on the File menu from the MATLAB command window and then clicking on the Save workspace as entry. You can give your file any name you like. Later, you can import the data by clicking on Open in the File menu from the MATLAB command window (not the editor). Try this now. Save your workspace, clear it with clear all, and then open it again.
You can also use the tic-toc stopwatch to check on MATLAB. For example, the following code is supposed to check (use another M-file) whether MATLAB really takes a 0.5 second break:
By running this program several times, you can get a sense of accuracy and variance (precision) within internal timers in MATLAB. So much for time and timing.
What is still missing at this point is a way to handle random events. In the design of experiments, randomness is your friend. Ideally, you want everything that you don’t vary systematically to behave randomly (effectively controlling all other variables, including unknown variables and unknown relations between them).
You encountered the random number generator earlier. Now you can utilize it more systematically. This time, it will be enough to generate random numbers with a uniform distribution. This is achieved by using the function rand( ). Remember that the function randn( ) will generate random numbers drawn from a normal distribution. Conversely, rand( ) draws from a uniform distribution between 0 and 1. This distinction is important to know, since you can use this knowledge to create two events that are equally likely. Now start a new M-file and add the following code:
a = rand(1,1) %Creates a random number and assigns it to the variable a
if a > 0.5 %Check if a is larger than “0.5”
b = 1 %We assign the value “1” to the variable b
Run this code a couple of times and see whether different random values are created every time. Note that this is a rather awkward—but viable—way to create integral random numbers. Recent versions of MATLAB include a new function randi, which draws from a uniform discrete distribution. For example, the command randi(2,30,1) yields a single column vector with 30 elements randomly drawn to be 1 or 2. This new function is a good example of how innovation in MATLAB versions makes previously accepted ways of doing things (such as generating discrete random numbers) obsolete. The old way still works, but the new one is much more elegant.
Next, we will introduce several functions and concepts that will come in handy when you are creating your program for the project in Section 6.4. The first is the concept of handles. A handle typically pertains to an object or a figure, for our purposes. For more detailed treatment of handles, see the Visualization and Documentation tutorial in Chapter 5.
It is simply declared as follows:
This creates a figure with the handle h. Of course, the name can be anything. Just be sure to remember which handle refers to which figure:
This creates the handles as variables in the workspace. You can check this by typing whos or simply by looking in the workspace window.
Handles are extremely useful. They literally give you a handle on things. They are the embodiment of empowerment.
Of course, you probably don’t see that yet because handles are relatively useless without two functions that go hand in hand with the use handles. These functions are get and set.
The get function gives you information about the properties that the handle currently controls as well as the values of these properties. Try it. Type get(h).
You should get a long list of figure properties because you linked the handle h to a particular figure earlier. These are the properties of the figure that you can control. This capability is extremely helpful and implemented via the set function.
Let’s say you don’t like the fact that the pointer in your figure is an arrow. For whatever reasons you have, you would like it to be a cross-hair. Can you guess which figure property [revealed by get(h)] controls this? Try this:
How do you know which property takes which values? This is something you can find in the MATLAB help, under Figure properties. Don’t be discouraged about this. It is always better to check. For example, MathWorks eliminated the former figure property “fullcrosshairs” and renamed it “fullcross.”
Of course, some of the values can be guessed, such as the values taken by the property visible—namely on and off. This also illustrates that the control over a figure with handles is tremendous.
Try set (h,’visible’,’off’) and see what happens. Make sure to put character but not number values between’and’.
Of course, handles don’t just pertain to figures; they also pertain to objects. Make the figure visible again and put some objects into it.
An object that you will need later is text. So try this:
If you did everything correct, text should have appeared in the middle of your figure. Text takes at least three properties: x-position, y-position, and the actual text.
But those are not all the properties of text. Try get(g) to figure out what you can do.
It turns out, you can do a lot. For example, you can change color and size of the text:
Also, note that this object now appears as a “child” of the figure h, which you can check with the usual method.
Now you should have enough control over your figures and objects to complete the project in Section 6.4.
Finally, you need a way for the user (i.e., the participant of the experiment) to interact with the program. You can use the pause function, which waits for the user to press a key before continuing execution of the program. In addition, the program needs to identify the key press.
The variable h725 should contain the character with which you overcame pause. Interestingly enough, it is a figure property that allows you to retrieve the typed character in this case, but that is one of the idiosyncrasies of MATLAB. Be sure to do this within an M-file.
Another function you will need (to be able to analyze the collected data) is corrcoef. It returns the Pearson correlation between two variables, e.g.,
a = rand(100,2); %Creates 2 columns of 100 random values each, puts it in variable a
b = corrcoef(a(:,1),a(:,2)); %Calculates the Pearson correlation between the two columns
In my case, MATLAB returns a value close to 0, which is good because it shows that the random number calculator is doing a reasonable job.
Corrcoef as a function can also take several parameters:
According to MATLAB, there is a probability of 0.95 that the observed values were obtained by chance alone (which is, of course, the case). Hence, you can conclude that the correlation is not significant.
By convention, correlations with p values below 0.05 are called “significant.”
The final function concerns checking of the equality of variables. You can check the equality of numbers simply by typing==(two equal signs in a row):
Since MATLAB 7, this technique is also valid for checking the equality of characters; Try this:
The more conventional way to check the equality of characters is to use the strcmp function:
Together with your knowledge from Chapter 2, “MATLAB Tutorial,” you now have all the necessary tools to create a useful experimental program for data collection.
6.4 Project
Your project is to implement the visual search paradigm described in the preceding sections in MATLAB. Specifically, you should perform the following:
• Show two conditions (pop-out search versus conjunction search) with four levels each (set size=4, 8, 12, 16). These conditions can be blocked (first all pop-out searches, then all conjunction searches or something like that).
• It is imperative to randomly interleave trials with and without target. There should be an equal number of trials with and without targets.
• Make sure that the number of green and red stimuli (if you are red/green blind, use blue and red) is balanced in the conjunction search (it should be 50%/50%). Also, make sure that there is an equal number of x and o elements, if possible.
• Use only correct trials (user indicated no target present when no target was presented or indicated target present when it was present) for the analysis.
• Try to be as quick as possible while making sure to be right. It would be suboptimal if you had a speed/accuracy trade-off in your data.
• The analysis should contain at least 20 correct trials per level and condition for a total of 160 trials. They should go quickly (about 1 second each).
• Pick two keys on the keyboard to indicate responses (one for target present, one for target absent).
• Report and graph the mean reaction times for correct trials as a function of pop-out search versus conjunction search and for trials where the target is present versus where the target is absent. Hence, you need between two and four figures. You can combine graphs for comparison (see below).
• Report the Pearson correlation coefficients between reaction time and set size and indicate whether it is significant or not (for each condition).
• Make a qualitative assessment of the slopes in the different conditions (we will talk about curve fitting in a later chapter).
• Start writing one trial and make sure it works properly.
• Be aware that you effectively have an experimental design with three factors [Set size: 4 levels (4, 8, 12, 16), conjunction versus feature search: 2 levels, target present versus absent: 2 levels]. It might make sense to block the first two factors and randomize the last one.
• Be sure to place the targets and distracters randomly.
• Each trial will essentially consist of newly presented, randomly placed text.
• Be sure to make the figure big enough to see it clearly.
• Make sure to make the text vanish before the beginning of the next trial.
• Your display should look something like Figure 6.5.
• Determine reaction time by measuring time from appearance of target to user reaction.
• Elicit the key press and compare with the expected (correct) press to obtain a value for right and wrong answers.
• Put it into a matrix, depending on condition. It’s probably best to have as many matrices as conditions.
• Write a big loop that goes through trials. Do this at the very end, if individual trials work.
• You might want to have a start screen before the first trial, so as not to bias the times of the first few trials.
• If you can’t do everything at once, focus on subgoals. Implement one function after the other. Start with two conditions.
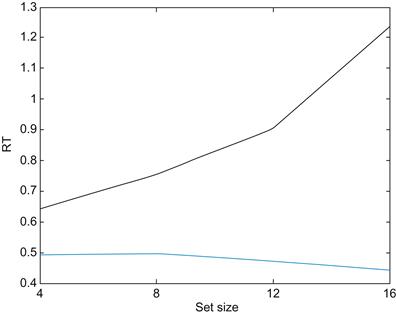
• Figure 6.6 shows one of the exemplary result plots from a participant. Depicted is the relationship between mean reaction time and set size for trials where a target is present (only correct trials). Red: Conjunction search. Blue: Pop-out search. Pearson r for conjunction search in the data above: 0.97.