Decision Theory
In this chapter, you will learn how to implement progressively more comprehensive mathematical models of decision making using MATLAB®. The exploration of decision models will introduce solving partial differential equations as finite differences, focusing on the diffusion equation. A simple model accounting for perceptual decisions and corresponding activity in cortical areas LIP and MT will be discussed.
Keywords
decision models; diffusion drift model; Go/No Go task; Brownian motion; cortical models; error rate; reaction time
31.1 Goals of this Chapter
In this chapter, you will learn how to implement progressively more comprehensive mathematical models of decision making using MATLAB®. The exploration of decision models will introduce solving partial differential equations as finite differences, focusing on the diffusion equation. A simple model accounting for perceptual decisions and corresponding activity in cortical areas LIP and MT will be discussed.
31.2 Background
One of the fundamental behavior characteristics of choice and reaction time (RT) is a trade-off between accuracy (selecting the correct choice) and speed (e.g., Swensson, 1972). Research participants asked to make decisions limited by time make more errors as the time allotment grows shorter. Any serious model for reaction time should account for this phenomenon.
However, accuracy does not improve infinitely. Participants still err, even when given large time windows. Not only must any model handle the inverse relationship between accuracy and speed, but it must also still maintain a small probability of error.
There are many possible ways of addressing this aspect of decision-making behavior. For decades, one of the most successful models has been the diffusion drift model (DDM) (Ratcliff, 1978). In the diffusion drift model, decision processes are described in terms of evidence accumulation over time, with larger durations allowing greater amounts of evidence to accumulate.
Neurobiological investigations of choice in sensory systems have proposed putative mechanisms for the behavior described by the DDM and similar evidence accumulation models of decision. Later in this chapter, we will discuss a biological model for decision behavior in the perception of motion.
31.3 Simple Accumulation of Evidence
To begin, we can write a naïve model of evidence accumulation for a simple task (Go/No Go) in discrete time, in which each time step allows for the accumulation of a small amount of evidence. We will use a basic, discrete version of the diffusion drift model (DDM), a well-established model of decision processes (Ratcliff, 1978).
In this formulation of the accumulation, the evidence will take on continuous values. We can represent this as a differential:
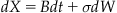
Here, dX represents the change in evidence during the time step dt. B is a constant bias that directs the evidence total over time. The magnitude and sign of B influences the long term behavior of the evidence accumulation process. Larger values cause faster accumulation and smaller magnitude values cause slower accumulation.
The last term, dW, represents a discretized Brownian motion term. Simply put, a Brownian motion is a random walk in which steps follow a Gaussian distribution. (The dW label originates from the Wiener process, another name for Brownian motion.) Formally, the Brownian motion term is characterized by three properties:
3. For any two values of t, t1, and t2, the difference between W(t1) and W(t2) follows an independent normal distribution with mean 0 and variance equal to the difference t2−t1.
Consequently, one important aspect of the Brownian motion term is its scaling with respect to time. Since dW follows an N(0, dt) distribution, increasing or decreasing the time step size increases or decreases the variance of the random portion of the walk. The scalar scaling constant 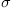 allows for adjustments to uncertainty.
allows for adjustments to uncertainty.
To complete our simple model, we need a start point x0. The start point will represent the evidence accumulated prior to the experiment. Often, we can treat this as completely undecided. An evidence total above the start point implies a positive choice, and an evidence total below the start point will imply a negative choice. In most cases, we will choose a value of 0 for x0, so that a positive accumulation will indicate a positive choice.
We now have enough to write a simple simulation for a Go/No Go task with a fixed time interval. This would correspond to presenting a stimulus and requiring the research participant to select a choice at the end of the time interval.
function choice = simple_model(bias, sigma, dt, time_interval)
dW = randn * (dt^0.5); % randn is always N(0,1)
Under this testing paradigm, in which the participant is interrogated at the end of a fixed time interval, we cannot directly evaluate reaction time. However, we can examine error rate (ER) as a function of the time interval.
As the time interval increases, the influence of the bias parameter affects the evidence accumulation more and more strongly. To explore the probability distribution of the evidence total, X, at some time t, we can integrate the previous difference equation. It is important to note that, being stochastic, the Brownian motion term cannot be integrated using standard integration techniques. Here, the integral is the sum of t/dt independent normally distributed variables with equal mean (0) and variance (dt). Thus, the total should be distributed normally with mean 0 and variance (t/dt)(dt)=t. This corresponds to the distribution of W(t) as defined earlier.
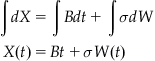
With this expression of X(t), we can calculate an expectation of the first moment (i.e., the mean).
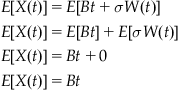
Knowing the distribution of evidence at time t under the fixed time paradigm, we can determine the probability of being above threshold and the expected error rate. X(t) follows a normal distribution with mean Bt and variance 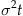 . The proportion of this distribution above the threshold is the probability of exceeding the threshold at time t. The standard function for expressing this is
. The proportion of this distribution above the threshold is the probability of exceeding the threshold at time t. The standard function for expressing this is 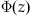 , the cumulative distribution function for the standard normal distribution. The value of
, the cumulative distribution function for the standard normal distribution. The value of 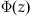 is defined as the integral of the standard normal probability density from negative infinity to z. This is also the probability that a random variable with a standard normal distribution will have a value less than or equal to z.
is defined as the integral of the standard normal probability density from negative infinity to z. This is also the probability that a random variable with a standard normal distribution will have a value less than or equal to z.
Because the value of interest here is the probability of exceeding the threshold, the probability of exceeding the threshold at time t is equivalent to
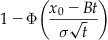
The Statistics Toolbox supplies a function to calculate the value of the cumulative standard normal distribution, but we can easily define it using a function available in the MATLAB core functions, specifically the error function erf. Defined in terms of the error function,
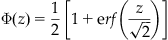
With erf, finding a value of 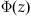 is as simple as
is as simple as
31.4 Free Response Tasks
By adding positive and/or negative thresholds, we can extend our model to simulate a testing paradigm that allows a free response. Under such a paradigm, if the evidence exceeds a threshold, then the trial ends and a choice is made.
A model may have both a positive and a negative threshold or only a single threshold. Which a model has will depend on the task to be simulated. A Go/No Go task in which a participant must respond before an interval when a signal is perceived would be a good match to a simulation paradigm with a single positive threshold. Evidence accumulation would be towards the Go response. Such a simulation would also have a time limit. Trials failing to accumulate enough evidence by the time limit would produce a No Go result.
Two thresholds, positive and negative, could be appropriate for simulating a two alternative forced choice (2 AFC) task. In the simplest case, the two thresholds are equidistant from the evidence start point, x0, but the distances from the start can be asymmetric. Even with two thresholds, there is a single accumulator with only one bias parameter.
Now that our model allows an immediate return once sufficient evidence is accumulated, we can investigate the relationship between error rate (ER) and reaction time (RT) more stringently.
31.5 Multiple Iterators: The Race Model
The discrete version of the diffusion drift model can accommodate a two threshold paradigm, but even with two thresholds, the single iterator allows for only a single set of bias and variance values. Under some two choice scenarios, the race model may be a better match.
Under the race model, each of the two choices has an independent iterator and threshold. The first process whose accumulated evidence exceeds its threshold is the choice of the system. This choice “wins the race.”
The function below simulates a multiple choice task with free response. Parameters are vectors with length equal to the numbers of choices in the task. To specify a set of choices, set the parameters to vectors whose length is equal to the number of choices desired for the task.
It should be noted that while the race model has been demonstrated to account accurately for experimental results in tasks with two choices, the appropriateness of multiple choice models is a subject of active debate.
31.6 Cortical Models
Any neurobiological model should account for the perceived successes of the diffusion model in describing the characteristics of reaction time in decision processes under psychometric testing. One such model has been proposed (Shadlen and Newsome, 2001; Mazurek et al., 2003) to account for interactions between visual areas MT and LIP. Area MT is a cortical area sensitive to visual motion, and area LIP is a cortical area implicated in decision processes. Neurons in area MT have been found to respond strongly to motion, with directional specificity. Many neurons appear to have a characteristic direction, and respond preferentially to stimuli moving in that direction. Mean rates of neurons varying with direction relative to preferred orientation can be found in Figure 31.1.
Under the model proposed by Shadlen and Newsome, the activity of individual neurons in LIP reflects the activity of associated neurons in MT over a long time period. Moreover, area MT neurons directionally tuned to opposite directions inhibit the LIP neuron of the oppositely directed cell. Thus, under this model, LIP neurons integrate the difference in activity between sensory cells with opposing preferred directions.
If we equate evidence with neural activity, we can take spike counts as evidence. This is a subtle difference in from the discrete models we have used thus far, in that evidence will be discrete counts of spikes rather than continuous. Another difference is the absence of a mechanism for retrograde accumulation in the evidence count. Once a spike is counted, it remains counted.
We can represent the spike counts from an MT neuron as N. At any time interval dt, we can simulate activity by drawing from a uniform random distribution and comparing to the mean rate per time interval dt. The mean rate will vary with both time and the current stimulus, if any.
Likewise, we can simulate activity in LIP by adjusting the probability of firing by the current evidence count. The model described above also has a feed-forward inhibitory term to account for strong evidence in the opposite direction. To account for both connections, we will adjust probability of firing by the difference between the two evidence counts. Neural activity above a certain threshold implies sufficient evidence for a choice.
The function lip_activity ahead models the activity of a single LIP neuron with fixed probabilities for its corresponding excitatory and inhibitory MT neurons.
function rt = lip_activity(MT_p_values, ...
% MT_p_values - a vector with 2 elements, firing probabilities for the
% excitatory and inhibitory neurons, resp.
% LIP_weights - a length 2 vector of weighting factors for the evidence
% from the excitatory (positive) and
% inhibitory (negative) neurons
% LIP_threshold - the LIP firing rate that represents the choice threshold
% use fixed time scale of 1 ms
N = [0 0]; % plus is first, minus is second
LIP_event_times = [LIP_event_times t];
% check LIP mean rate for last M spikes
The function expects MT neuron probabilities, weights for the LIP neurons, and a firing threshold for the LIP neuron in impulses per second (ips).
31.7 Project
In this project, you are asked to write a simulation of MT-LIP neurons using the Shadlen-Newsome model discussed in the previous section. Specifically, you are asked to do the following:
• Write code to simulate the effect of presenting a directionally oriented stimulus during intervals of time. This will involve generating a time series where the value at each step is an orientation or a value that indicates the absence of a stimulus.
• You need to allow the probability of firing for the two MT neurons in the model to change with time, based on the orientation of any presented stimulus.
• The model should include two MT neurons and two LIP neurons. Each MT neuron should have feed forward connections to both LIP neurons, one excitatory and one inhibitory.
• Generate activity patterns for both MT neurons and both LIP neurons for various stimulus presentations.
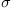 =1, dt=0.1 second. What is the distribution of results? Modify simple_model to return the evidence (x) as well as the resulting choice. Examine the time course of the evidence for B=1, B=10, B=0, B=0.1, and B=−1 over a 10-second trial.
=1, dt=0.1 second. What is the distribution of results? Modify simple_model to return the evidence (x) as well as the resulting choice. Examine the time course of the evidence for B=1, B=10, B=0, B=0.1, and B=−1 over a 10-second trial.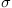 =1, dt=0.1 second. Assume that a positive response is correct. How does ER change with time?
=1, dt=0.1 second. Assume that a positive response is correct. How does ER change with time?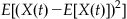 is
is 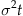 . Generate evidence trajectories for 10 trials over 10 seconds with parameters B=0.1 per second,
. Generate evidence trajectories for 10 trials over 10 seconds with parameters B=0.1 per second, 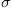 =1, dt=0.1 second. Calculate mean and variance over time. Plot the trajectories, mean trajectory, and one standard deviation above and below the mean. Compare the trajectories to the expected value.
=1, dt=0.1 second. Calculate mean and variance over time. Plot the trajectories, mean trajectory, and one standard deviation above and below the mean. Compare the trajectories to the expected value.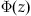 . Write a function simple_model2 that accepts bias, time limit, and start point, and that returns the choice. simple_model2 should use phi and the equations above to calculate the probability of being above or below the start point without iterating through a trajectory. Once a probability of the evidence total being above or below the start point is calculated, a draw from a uniform random distribution can be used to choose an option.
. Write a function simple_model2 that accepts bias, time limit, and start point, and that returns the choice. simple_model2 should use phi and the equations above to calculate the probability of being above or below the start point without iterating through a trajectory. Once a probability of the evidence total being above or below the start point is calculated, a draw from a uniform random distribution can be used to choose an option.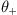 and
and 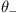 , a variance for accumulation error
, a variance for accumulation error 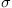 , a start value x0, and a bias B. The function should use the discrete time representation of the decision process by calculating values for the total evidence at successive time intervals until evidence exceeds a threshold. The time at the threshold crossing is the reaction time. The function should return both the reaction time and 1 or −1 for the response.
, a start value x0, and a bias B. The function should use the discrete time representation of the decision process by calculating values for the total evidence at successive time intervals until evidence exceeds a threshold. The time at the threshold crossing is the reaction time. The function should return both the reaction time and 1 or −1 for the response.