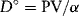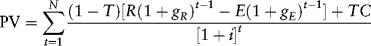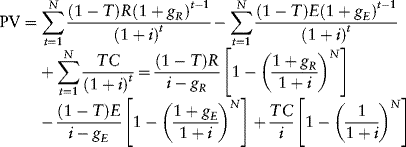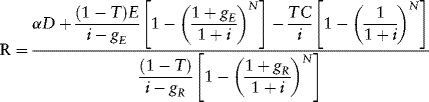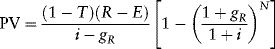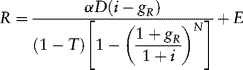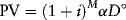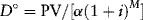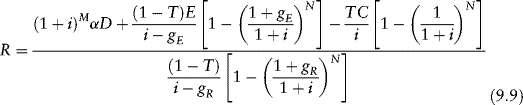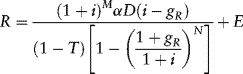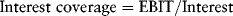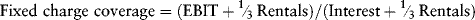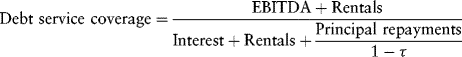Chapter 9
Preparing the Project Financing Plan
Designing the optimal financing plan for a project generally involves meeting six principal objectives: (1) ensuring the availability of sufficient financial resources to complete the project; (2) securing the necessary funds at the lowest realizable cost; (3) minimizing the project sponsors' credit exposure to the project; (4) establishing a dividend policy that maximizes the rate of return on the project sponsors' equity subject to the constraints imposed by lenders and the cash flow generated by the project; (5) maximizing the value of the tax benefits of ownership to which the project will give rise; and (6) achieving the most beneficial regulatory treatment. These objectives may not be perfectly compatible, in which case trade-offs will have to be made. In general, the lowest cost of capital will be achieved in a project financing when (1) debt is maximized as a percentage of total capitalization and (2) the amortization schedule for the project debt is matched, as closely as the capital market will permit, to the cash flows of the project.
General Considerations
A financing plan for a project includes arrangements for both construction financing and permanent financing. The development of a specific financing plan requires a careful analysis of the potential sources of funds in relation to the project's year-to-year funds requirements, available cash flow, and availability of credit support mechanisms to support project debt. The following considerations are important in the design of the financing plan for a project.
Amount of External Funds Required
The formulation of a financing plan begins with an estimate of the total external funds' requirements. The amount of external funds required equals the sum of (1) the total cash cost of facilities required for basic completion plus (2) interest that must be paid on project debt during the construction period and the fees and other out-of-pocket expenses that are incurred in connection with arranging the project financing plus (3) the initial investment in working capital plus (4) the cash to cover salaries and other operating expenses prior to project completion. The amount of funds required is reduced to the extent that any cash revenues are generated by the partial operation of the project during the construction period. Such revenues can be realized when the project will be completed in phases and will commence operations before the final phase has been completed.
Sufficient funds must be arranged to provide a margin of safety beyond this estimated total. The margin of safety is necessary to finance possible cost overruns (or to cover shortfalls in internally generated funds, if any are expected). The magnitude of this required safety margin will depend on the contingency factors included in the project construction cost estimates, and lenders' confidence in the feasibility of the construction plan and the accuracy of the cost estimates.
A related consideration concerns how the funds a particular institution provides to a project might reduce its willingness to lend funds to one or more sponsors for other projects. Where legal lending limits might be reached, the financing plan should provide for alternative sources of funds.
Precommitments of Funds
Commitments from lenders and equity investors to provide funds must be coordinated with the project sponsors' commitments to contractors for initial construction expenditures. The two considerations are interrelated. The amount of funds to be raised will depend on the expected cost of construction. Construction cannot commence until the sponsors have obtained commitments covering the total amount of funds necessary to complete the project. Because various classes of fund providers differ with respect to their willingness to enter into forward commitments, project sponsors must tailor the financing plan accordingly.
Securing financing commitments entails, with respect to equity funds, obtaining contractual undertakings by financially capable investors to provide the required amount of equity. With respect to the debt portion of the planned capitalization, commitments must be obtained from institutional lenders or banks for the full amount required, unless adequate assurances can be obtained from credible financial institutions that the necessary debt funds can be raised in the public or private capital market under all circumstances. Seldom can such assurances be obtained in advance of the commencement of construction. Delays or cost overruns that would adversely affect project economics could jeopardize the project entity's ability to arrange subsequent financings. Thus, any planned public offering during construction must be backstopped by firm commitments from credible financial institutions. Such commitments are usually in the form of standby loan facilities from banks. The commitments obligate the banks to provide funds if the public offerings are not consummated as planned.
Maximum Feasible Debt/Equity Ratio
The appropriate project debt/equity ratio depends on (1) the expected profitability and operating risks of the project, (2) the adequacy of the project's security arrangements, and (3) the creditworthiness of the parties obligated under such arrangements. Of particular importance is whether the purchaser(s) of the project's output or services is willing to lend direct or indirect credit support by entering into sufficiently strong long-term purchase commitments. The weaker these commitments, the less the degree of credit support they provide, and the lower will be the maximum feasible debt/equity ratio. Lenders will make their own assessments of these factors, and they will limit project leverage accordingly. In the past, a broad range of projects has been financed with capitalizations that included 70 percent or more debt.
Depending on the maximum feasible debt/equity ratio and the sponsors' ability to contribute equity to the project, it may be necessary to arrange for outside equity investors. The financing plan must address the requirement for, desirability of, and potential identity of outside equity investors for the project. The requirement for or desirability of outside equity investors will depend on many factors. The potential attractiveness of proposals for outside equity investment in a project by a variety of prospective providers of debt and equity capital—and the extent to which these potential funds sources would wish to participate in operational aspects of the project—will affect the sponsors' willingness to arrange for outside equity investors. It is sometimes advantageous to the project sponsors to make a portion of the equity in the project available to certain lenders or other participants. For example, financial institutions might be induced to lend more—or to lend on superior terms and conditions—to the project if an “equity kicker” is provided, as described later in this chapter. As a second example, purchasers of the project's output might view an equity participation as sufficient inducement to enter into long-term purchase contracts that would provide meaningful credit support to the project.
Timing of Drawdowns
Once construction begins, a number of factors affect the timing of debt and equity drawdowns. In general, the pattern of drawdowns of long-term funds should match the schedule of construction expenditures. Matching will minimize the warehousing of excess funds and/or the need for short-term bridge financing.
Lenders normally require that the sponsors (or outside equity investors) invest a certain amount of equity in the project prior to the initial drawdown of any debt funds. Lenders that do not insist on equity funds being invested first will require, at a minimum, that debt and equity be drawn down in some specified proportion. These requirements assure lenders that the project's equity investors have a substantial financial commitment to the project from its earliest stages.
The maximum forward commitment that long-term lenders are willing to provide imposes another restriction on the pattern of drawdowns. The maximum commitment period varies according to prevailing market conditions and lending practices of the particular institutions that are asked to provide funds to the project. Life insurance companies, for example, are normally willing to enter into longer forward commitments than most other types of financial institutions.
Expected Project Cash Flow Profile
The project's expected pattern of cash generation constrains the amounts and types of securities utilized in the financing plan. In particular, the expected pattern of project cash flow will determine what debt repayment schedules are feasible. The cash flow will, therefore, have an important effect on the mix of bank loans and long-term fixed-rate debt.
As a general rule, a project's financing plan should seek to match the maturities of the funds raised with the project's ability to generate cash to repay those funds. Matching will tend to minimize the project's exposure to refinancing risk. Also, by coordinating the currency and repayment schedule of project debt with projected revenues arising under sales contracts, the project's exposure to foreign exchange risk can be controlled.
Currency Profile of Project Revenues and Costs
When certain revenues will be received, or certain costs paid, in different currencies, project borrowings can be tailored to hedge the project's foreign exchange risk. For example, if a project will have revenues denominated in U.S. dollars but its operating costs will be paid in Australian dollars, a significant proportion of the project's borrowings should be arranged in U.S. dollars. The balance, including a working capital facility for the project, would be arranged in Australian dollars. Typically, in such cases, project sponsors arrange a consolidated multicurrency loan facility that provides for maximum specified funds availability in each of two or more currencies.
Expected Useful Economic Life of the Project
The maturity of project debt cannot exceed the expected useful economic life of the project as of the date project financing is arranged. For natural resource projects, conditional acceleration of project debt—faster repayment—may be triggered if, during project operations, the expected life of natural resource reserves (at normal production levels) associated with the project falls below the remaining term of the debt.
Sources of Supply for the Equipment for the Project
If export financing is available in certain countries at concessionary rates, purchasing equipment for the project from suppliers located in one of those countries can reduce the project's cost of funds. Often, a trade-off must be made involving the quality of the equipment procured and the cost of financing. The concessionary rate must provide a subsidy that is large enough to compensate for any differences in quality if the equipment that is available for export financing is not the most attractive from an engineering standpoint.
Construction Financing
Bank Loan Facility
One alternative for construction financing is to have the project company or a special-purpose finance corporation issue short-term promissory notes or borrow short-term funds for construction directly from commercial banks.1 If a special-purpose finance corporation is used, the project company would borrow the money raised by the special-purpose finance corporation under terms substantially identical to those under which the finance corporation borrowed the money. Under this alternative for construction financing, security for the lending institutions will consist of the same completion undertaking and other contractual arrangements that long-term lenders will rely on for security in connection with the permanent financing. Typically, long-term lending commitments are arranged by the time the construction financing is put in place. The long-term lenders agree to “take out” the construction lenders, provided the project meets all its completion tests.
Syndication Risk
When arranging bank financing, it is desirable to avoid syndication risk—the risk that the lead banks will not be able to enlist a sufficient number of additional banks to provide the needed funds. Project sponsors avoid this risk by asking the prospective lead banks to submit fully underwritten (as opposed to best-effort) financing proposals. An underwritten loan commitment obligates the lead banks to provide the full loan facility whether or not they can enlist any other banks to participate in the credit facility.
A typical loan syndication works in the following manner: The project sponsors contact a small number of banks that possess the necessary in-house project financing expertise and ask them to submit competing proposals. After evaluating the proposals, the sponsors request selected banks to form a group and submit a fully underwritten proposal. This bank group serves as the “lead managers.” The lead managers then syndicate the project loan by inviting co-managers, participants, and others as needed.
Direct Loans by the Sponsors to the Project Company
A second alternative is to have each of the sponsors borrow its share of the required construction financing directly, on a short-term basis, from commercial banks, and then lend such funds to the project company. Following project completion, the project company arranges long-term financing on the basis of the long-term contractual commitments for the sale of project output, use of project processing facilities, and so on. The project company then repays its borrowings from the project sponsors out of the proceeds of the long-term financing. This second alternative makes the project sponsors directly responsible for all the completion risk—unless they can arrange turnkey construction contracts to transfer this risk to the firms responsible for project construction.
Long-Term Financing
Investors are generally reluctant to commit funds more than two years in advance of takedown. Thus, for projects with lengthy construction periods, there will be some uncertainty as to whether permanent financing can be arranged before construction commences. In addition, especially for large projects that involve unproven technology, investors are often unwilling to commit to permanent financing without assurances that all the needed funding commitments have been obtained. In these circumstances, commitments covering all the funds requirements will have to be arranged at the same time, rather than having the project company conduct a series of financings during the construction period. However, when a project has a proven technology and a relatively modest capital cost, it is usually possible to finance a significant portion (or possibly all) of its cost at the beginning of construction, if the project sponsors so desire. Securing such financing commitments would require, at a minimum, that the project sponsors enter into a firm completion agreement. When separate construction financing is not appropriate, permanent financing must be arranged prior to the start of construction. Such loan facilities typically provide for quarterly delayed-delivery takedowns for the amounts to be spent during the construction period. Lenders normally require a commitment fee of approximately .5 percent per annum on the committed but undrawn amounts. The loan agreement should give the project company the flexibility to select alternative borrowing bases, such as prime rate and LIBOR. Bank loans carry floating interest rates. When they are used in long-term financing, the sponsors usually arrange interest rate swaps or interest rate caps to limit the project entity's interest rate risk exposure. These risk-management instruments are described in Chapter 14.
Private Placements
Long-term fixed-rate project debt is normally placed privately with sophisticated financial institutions, such as life insurance companies and pension funds. Direct placement avoids the cumbersome securities registration process that is required to effect a public offering. A private placement memorandum is prepared to describe the project and the security arrangements. It also provides a business description and a set of financial statements for each of the project sponsors.
The maturity of the project debt depends on prevailing market conditions. The debt would have to provide for annual sinking fund payments (to the full extent project economics and cash flow will allow). The sinking fund would probably have to begin the first year after completion of the project. The debt would probably have to be nonrefundable for 10 years, through borrowings at a lower cost of money. The debt would probably also provide for a contingent sinking fund. For example, the amortization schedule could be structured so as to provide for specified repayment amounts subject to a maximum amount and a minimum amount in each period. To the extent project cash flow is stronger than what the parties to the project anticipated at the time the project loans were entered into, the contingent sinking fund ensures that the bulk of the excess cash flow, and perhaps even all of it, will be dedicated to repaying project debt. If available cash flow exceeds the specified maximum, the project sponsors would receive cash flow benefits from the project (in the early years) before retirement of the bank debt.
Equity Kickers
The inclusion of an equity kicker in a privately placed financing can broaden the market for the project's debt, lower the front-end fixed cost components of the financing, and induce lenders to accept less restrictive covenants and less demanding credit support. In effect, lenders receive an equity incentive to assume additional risk. Alternative forms of equity kickers include a direct equity participation, net or gross revenue royalty payments (perhaps only of a limited duration), or one-time or multiyear contingent payments. The equity kicker feature is designed to raise the lenders' expected rate of return commensurate with the incremental risk they are being asked to bear. It is also a useful feature for compensating lenders for their principal-agent risk exposure.
Withholding Tax Considerations
The existence of withholding taxes can influence the design of the financing plan for a project. Countries typically apply a withholding tax to dividend payments, interest payments, management fees, and royalty payments made to foreign entities. Often, the withholding tax rate is governed by a tax treaty; the foreign recipient may not even be subject to withholding tax. Where tax treaties grant favorable withholding tax treatment to recipients in certain specified foreign jurisdictions, the project will have a tax incentive to raise funds in those jurisdictions (if funds need to be raised outside the host country).
To the extent that certain types of cash payments are subject to withholding tax but others are not, the project sponsors have a tax incentive to design the project's capital structure so as to minimize the tax liability. For example, principal repayments generally are not subject to withholding tax (because they represent a return of principal), but dividends typically are subject to withholding tax. Project sponsors therefore often have a tax incentive to advance at least a portion of their investment in the form of a subordinated loan. The project company can repay subordinated advances (before paying dividends) in order to minimize the withholding tax on distributions to the foreign sponsor(s).
Estimating the Borrowing Capacity of a Project
The borrowing capacity of a project is defined as the amount of debt the project can fully service during the loan repayment period. This period is determined by such factors as the bank lenders' general lending policies, the risk characteristics of the project, and the state of the market for bank loans, as well as other considerations.
Bank lenders to a project typically estimate the borrowing capacity of a project in two ways: (1) they employ a discounted cash flow methodology, and (2) they test the ability of the project entity to meet its debt service payment obligations year by year.
This chapter estimates the amount that can be borrowed based on the financial characteristics of the project and the loan parameters established by the lender. In particular, project lenders are generally willing to lend an amount that does not exceed some specified fraction of the present value of the stream of cash flow expected to be available for debt service during the loan repayment period. They also establish certain coverage benchmarks that must be satisfied. Both tests of a project's borrowing capacity will be discussed.
Loan Repayment Parameters
Bank lenders to discrete, stand-alone projects are seldom willing to lend for periods that exceed 10 years from the date the project is completed. Exceptions to this policy do exist; for example, lenders to infrastructure projects, which are typically long-lived, will lend for longer periods. Sponsors of infrastructure projects have been able at times to arrange bank loan facilities that provide for a scheduled final loan repayment 12 years from completion of construction.
As a general rule, project financings are structured so that the project borrowing entity's leverage is consistent with Baa/BBB credit quality. The differential between the interest rate required on Baa/BBB-rated long-term debt and long-term Treasury debt varies, based on the general level of interest rates. The interest rate required on project debt can be estimated by adding an appropriate credit spread (between the yields of Baa/BBB bonds and Treasury bonds) for debt of an appropriate maturity.2 Suppose the estimated credit spread is 100 basis points and the estimated U.S. Treasury rate is 8 percent per annum. Then the estimated interest rate on project debt is 9 percent per annum. To be conservative, and to allow for the possibility that interest rates might increase before financing could be arranged, it might be appropriate to add a safety margin—say, 100 basis points. That would suggest using an interest rate of 10 percent in the borrowing capacity analysis.
Borrowing Capacity, Assuming Full Drawdown Immediately Prior to Project Completion
The borrowing capacity model determines, for a given set of project and loan parameters, the maximum amount of debt the project's cash flow stream will support. The amount the banks will lend equals a fraction of the present value (PV) of the available cash flow stream. Stated equivalently, the present value of the available cash flows must not be less than some specified multiple of the maximum loan amount. Let PV = α D°, where PV denotes the present value of the cash flow stream that is available to service project debt, α is the target cash flow coverage ratio, and D° is the maximum loan amount. Then the maximum loan amount is:
PV is calculated from the cash flow projections for the project. Often, sponsors desire a rough estimate of a project's borrowing capacity before a detailed set of projections is available. So long as the sponsors can estimate (1) the revenues and expenses during the first full year of project operations and (2) the rate(s) at which revenues and expenses are likely to grow during the period when project debt is outstanding, the following model can be used to estimate the project's borrowing capacity.
First, the variables are defined as:
| R | = | cash revenues during the first full year |
| E | = | cash expenses during the first full year |
| C | = | noncash expenses deductible for tax purposes each year |
| T | = | income tax rate |
| gR | = | annual growth rate of cash revenues |
| gE | = | annual growth rate of cash expenses |
| K | = | total capital cost |
| i | = | interest rate on the debt |
| N | = | life of the loan measured from the date of project completion |
The amount of revenue realized in year t is R(1 + gR)t−1. The amount of cash expenses incurred in year t is E(1 + gE)t−1. The amount of annual noncash expenses is assumed to be C each year. Consequently, the amount of cash flow available for debt service in year t is:
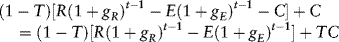
The present value of the cash flow stream that is available during the N-year period between project completion and final loan repayment is:
Equation (9.2) can be rewritten by evaluating the various terms within the summation to obtain:
The maximum loan amount D° is obtained by substituting α and the present value (PV) amount calculated from equation (9.3) into equation (9.1)).
The approach just described calculates the amount of debt D° for given values of revenue R and the other parameters defined above. Some project sponsors have a target, or desired, capital structure and an estimate of the total capital cost of the project. Multiplying the two together gives a target, or desired, debt level. Denote this amount D. Given the desired loan amount D, we can use equation (9.3) to determine how large the first full year's revenue R must be in order for PV = α D to hold. The resulting expression for R is:
Equation (9.4) assumes that either the loan is fully drawn down immediately prior to completion (or upon completion, as, for example, to refinance construction borrowings) or the borrowing capacity formula is applied as of the project completion date without regard to when the loan drawdowns actually take place.
Example 1
Assume the following parameter values:
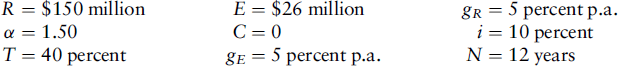
When gE = gR and C = 0, Equation (9.3) simplifies to:
Substituting the parameter values into equation (9.5) implies:
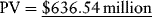
Substituting this value for PV and 1.50 for α in equation (9.1), we find that:
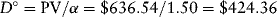
The project is capable of supporting $424.36 million of debt bearing a 10 percent interest rate and amortizing over 12 years.
Example 2
Assume the same parameter values as in Example 1 with one exception. Suppose the sponsors would like to know how much revenue the project would have to generate during the first full year of operations if the debt level is D = $350 million.
When gE = gR and C = 0, equation (9.4) simplifies to:
Substituting the given parameter values into equation (9.6) implies:
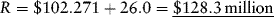
The lower debt level, $350 million versus $424.36 million, requires less revenue than the initial year's revenue assumed in Example 1.
Example 3
Assume the same parameter values as in Example 1 with one exception. Suppose the expected long-run growth rate of revenue is 3 percent rather than 5 percent per annum. Substituting into equation (9.4) gives:
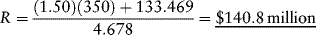
The higher growth rate of operating expenses necessitates a higher initial level of revenue in order to maintain the target debt coverage ratio of 1.50.
Borrowing Capacity, Assuming Periodic Loan Drawdowns
Suppose the revenues and operating expenses do not begin for M years, on average, from the date the loan is initially drawn down. This situation occurs when the loan is drawn down during the construction period, a time when the project is normally not generating any revenue. In that case:
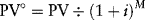
where PV is given by equation (9.3). Also, as before, a target debt coverage ratio of α must be maintained:
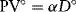
and so
Given any particular present value amount PV, the period of deferral reduces the amount that can be borrowed, given any particular desired target debt coverage ratio α.
The maximum loan amount D° in this case is:
where PV is given by equation (9.3). Equation (9.8) provides the maximum borrowing capacity as of the date of the initial loan drawdown.
Substituting (1 + i)mαD for αD in equation (9.4) gives the following expression for the amount of revenue the project must realize during the first full year of operations in order to meet the cash flow coverage ratio test:
Example 4
Assume the same parameter values as in Example 1. Assume, in addition, that the deferral period is two years. Applying equation (9.8), the maximum loan amount is:
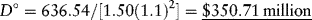
Example 5
Assume the same parameter values as in Example 3. Assume, in addition, that the deferral period is M = 3 years. Applying equation (9.9), the amount of revenue required during the first full year of operations is:
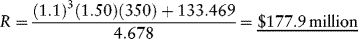
Application to a Hypothetical High-Speed Rail Project
Consider a hypothetical high-speed rail project that will require substantial funding from the U.S. government and from the government of the state in which it will be located. Private sources of funds, including bank loans, will provide the balance of the funds required.
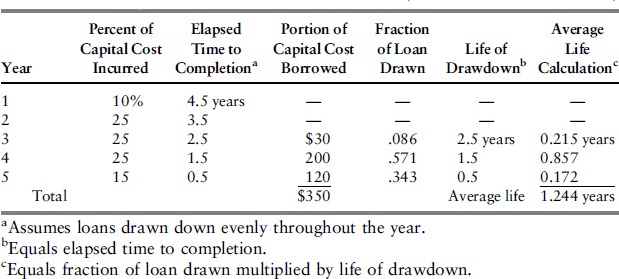
The borrowing capacity of the project will depend on the timing of the loan drawdowns. The equity funds and the governmental funding will probably have to be contributed to the project prior to the drawdown of the private bank loans. Under that assumption, the average life of the bank loans prior to the completion of construction is calculated as shown in Table 9.1.
Table 9.1 Average Life of Loan Drawdown Schedule (Dollar Amounts in Millions).
Example 6
Assume the following parameter values:
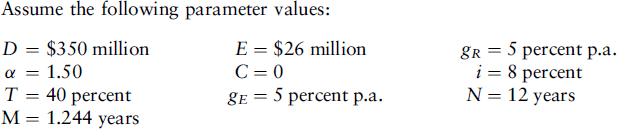
When gE = gR and C = 0, equation (9.9) simplifies to:
Substituting the given parameters into equation (9.10) implies:
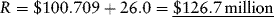
Example 7
Suppose instead that revenues are expected to grow at only a 3 percent annual rate. In that case, applying equation (9.9), the required first full year's revenues increase to R = $137.0 million. The slower growth in revenues increases the amount of revenues that is required during the first full year of operations to meet the target cash flow coverage ratio.
Example 8
Suppose that there is concern about the possibility of sharply rising interest rates. To allow for this concern, let i = 10 percent. If it is assumed that both revenues and operating expenses grow at a 5 percent annual rate, then:
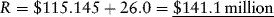
If it is assumed that revenues grow at a 3 percent annual rate while operating expenses grow at a 5 percent annual rate, then:
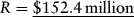
Annual Coverage Tests
Three financial ratios are widely used to measure a project's ability to service its debt: (1) the interest coverage ratio, (2) the fixed charge coverage ratio, and (3) the debt service coverage ratio.
The interest coverage ratio, expressed as:
measures the project's ability to cover interest charges. It equals earnings before interest and taxes (EBIT), or the amount of funds available to pay interest, divided by interest charges. Interest charges represent interest that must be paid in cash, whether or not it is capitalized for accounting purposes.
An interest coverage ratio below 1.00 would indicate that a project cannot cover its interest charges fully out of operating income. An interest coverage ratio below 1.00 for the first few years of project operations would indicate that the project will be incapable of supporting the level of borrowings planned for it. Because of uncertainty regarding future income and cash flow, lenders typically set a threshold greater than 1.00. For example, they might require that projected interest coverage never fall below 1.25.
There may be rental agreements that do not appear on the project company's balance sheet. Rent includes an interest component. The Securities and Exchange Commission (SEC) permits companies to treat one-third of rental payments as the interest component. The fixed charge coverage ratio takes into account these other “interest charges”:
where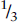 
rentals denotes one-third of annual rental expense.
The fixed charge coverage ratio is interpreted similarly to the interest coverage ratio. A value below 1.00 serves as a warning that the level of debt (including rental arrangements) planned for the project is too high. When the project entity will rent a substantial portion of the equipment it will need to operate the project, it is important to calculate projected fixed charge coverage as well as projected interest coverage in order to assess properly the project's ability to borrow.
Debt service includes principal as well as interest. Unlike interest and rental payments, principal payments are not tax-deductible. Also, if one-third of rental expense consists of an interest charge, the other two-thirds represents a principal component (which is tax-deductible when it is part of a rental payment). To allow properly for the non–tax deductibility of principal repayments on loans, notes, and debentures, those payments are divided by 1.00 minus the income tax rate τ; the payments are made out of after-tax dollars. In addition, depreciation and amortization (DA) expenses represent noncash charges; these amounts are available to repay principal. The debt service coverage ratio accounts for all debt service payment obligations:
where EBITDA denotes earnings before interest, taxes, depreciation, and amortization.
The debt service coverage ratio is interpreted similarly to the other two coverage measures. It is the most comprehensive measure of the three. When debt service coverage falls below 1.00, the project cannot fully service its debt out of project cash flow and will have to borrow funds or seek equity contributions to obtain funds to cover the shortfall. The debt service coverage ratio is particularly useful in designing the amortization schedule for project debt. For example, requiring the debt service coverage ratio never to fall below, say, 1.10 would indicate how much cash flow would be available after making required interest (and rental) payments to pay down principal.
Conclusion
The sponsors of a project will choose to have it financed on a project basis, rather than on their general credit, when project financing represents the lower-cost alternative. Whether project financing turns out to be the lower-cost alternative will depend, to a large extent, on how well the financing plan for the project is designed and how effectively it is executed. In preparing the project's financing plan, project sponsors and their financial advisers need to consider carefully all potential sources of funds in order to determine the financing package that affords the lowest after-tax risk-adjusted cost of capital consistent with regulatory or any other project-specific constraints.
Lenders use the interest coverage ratio, fixed charge coverage ratio, and debt service coverage ratio to gauge the capacity of a project to support debt on a year-by-year basis. These annual measures can be used in conjunction with the discounted cash flow debt capacity model developed in this chapter to determine how much debt a project is capable of supporting and how the repayment schedule for the debt should be designed. Lenders' risk tolerances and loan preferences change over time. The debt capacity model is sufficiently general to accommodate any particular set of lender-imposed constraints by altering the parameters of the model appropriately.