3.1 Free Electron Theory and Density of States

Schematic of the potential within a perfectly periodic crystal lattice of positive cores. The vacuum level V0 is the energy that the electron must acquire in order to leave the crystal
3.1.1 One-Dimensional System
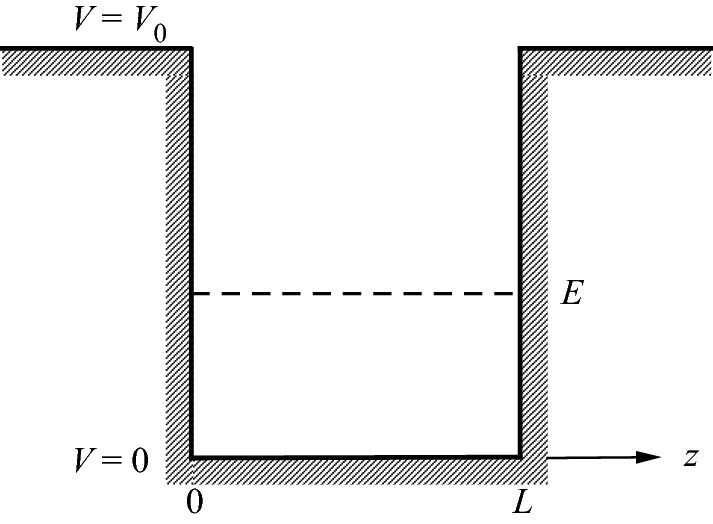
Illustration of a finite square potential well experienced by an electron in the 1D free electron model





![$$ - \frac{{\hbar^{2} }}{2m}\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }}\left[ {A\sin \left( {k_{z} z} \right)} \right] = \frac{{\hbar^{2} }}{2m}k_{z}^{2} \psi = E\psi $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ6.png)
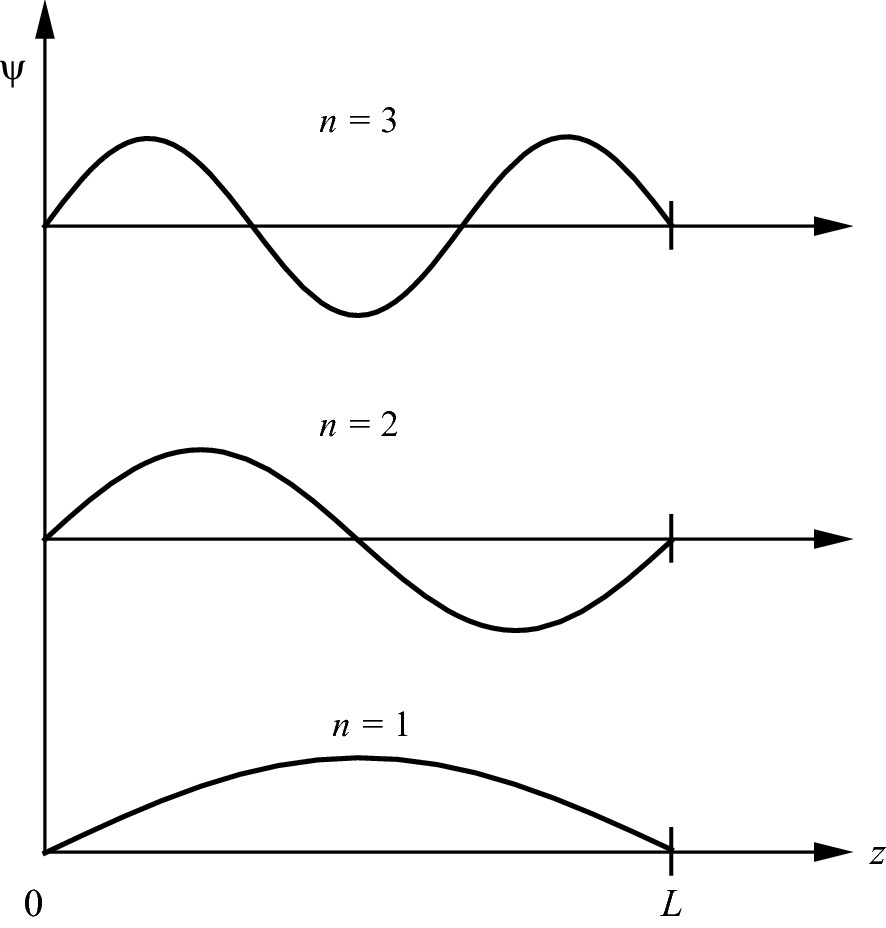
First three wave functions of a free electron in a square potential well of length L


Energy E plotted as a function of k according to (3.6)
3.1.2 Three-Dimensional System
- (a)
Wave function ψ(x, y, z)
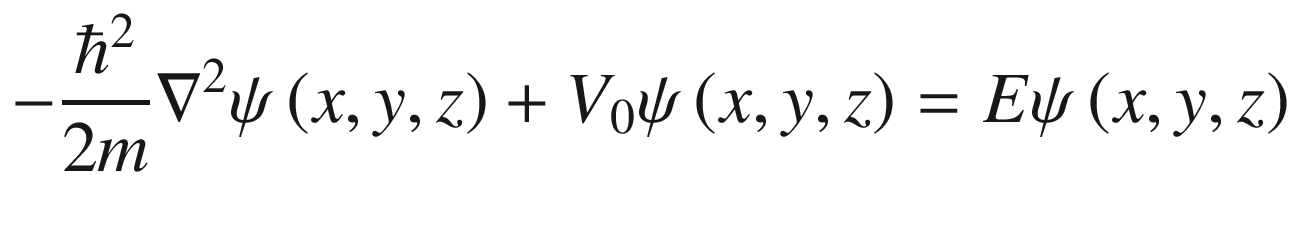
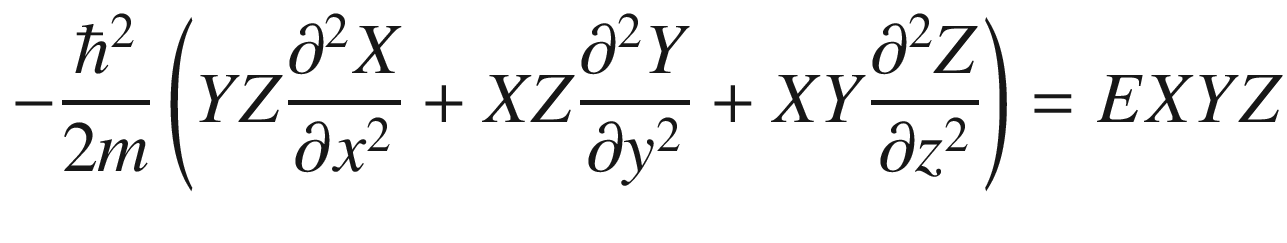



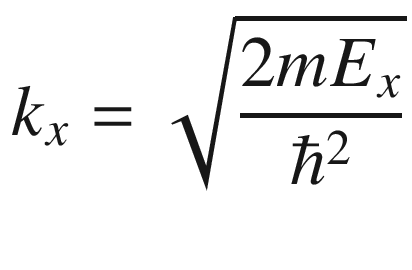
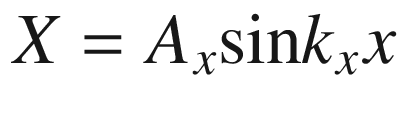
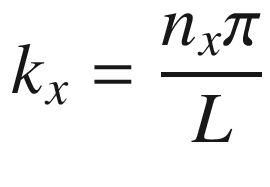
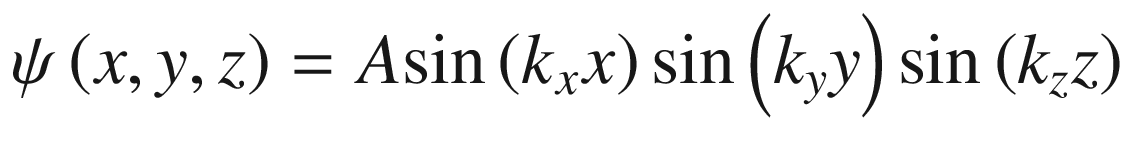

 .
.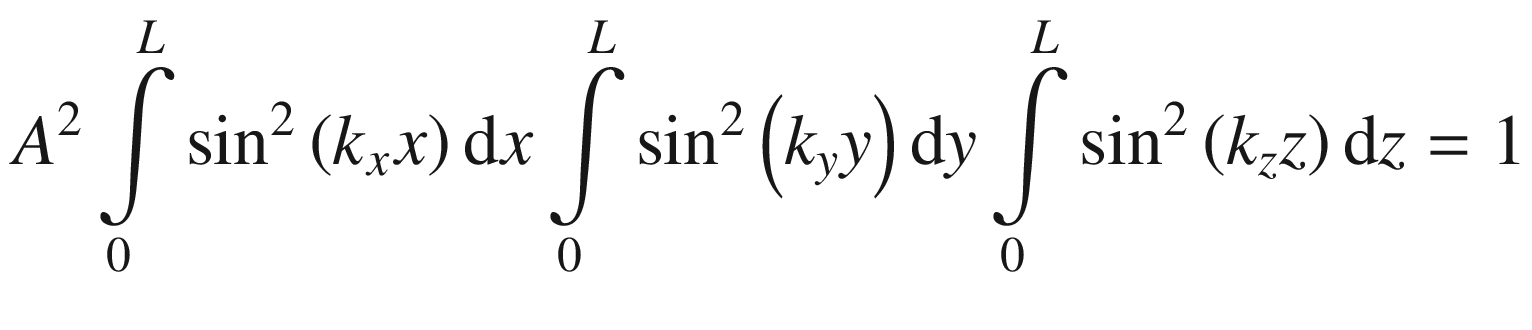
 , for a = ki = niπ/L,
, for a = ki = niπ/L,
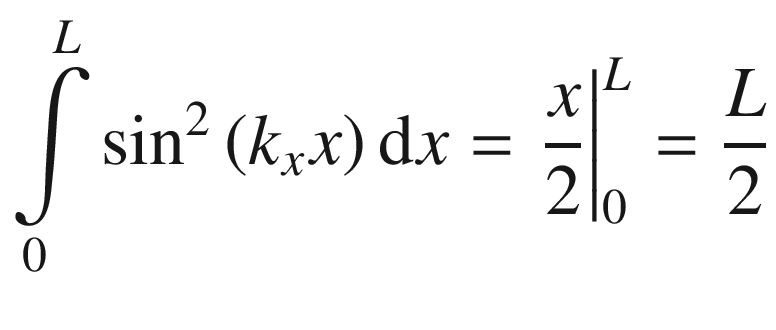

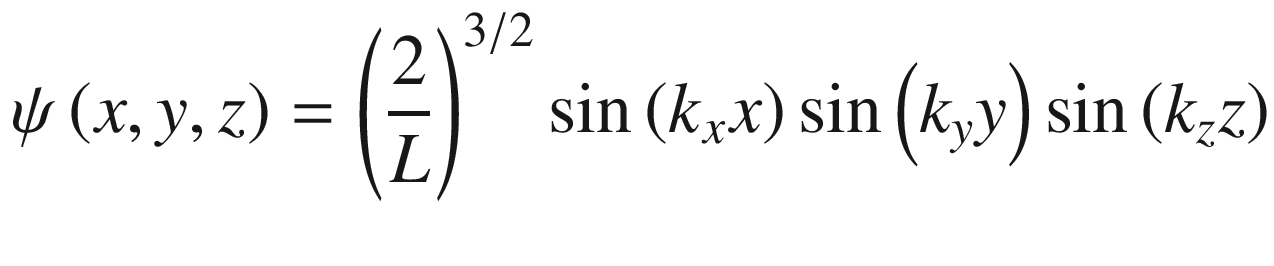
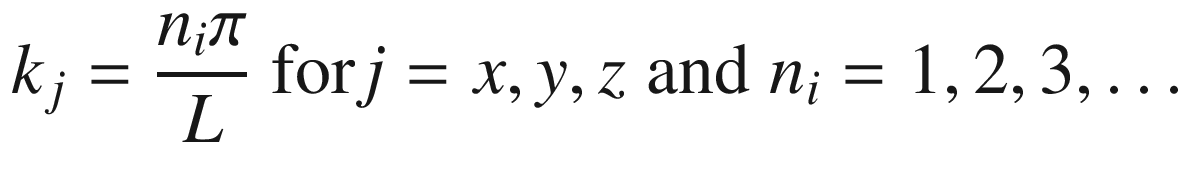
- (b)
Energy eigenvalues (E)
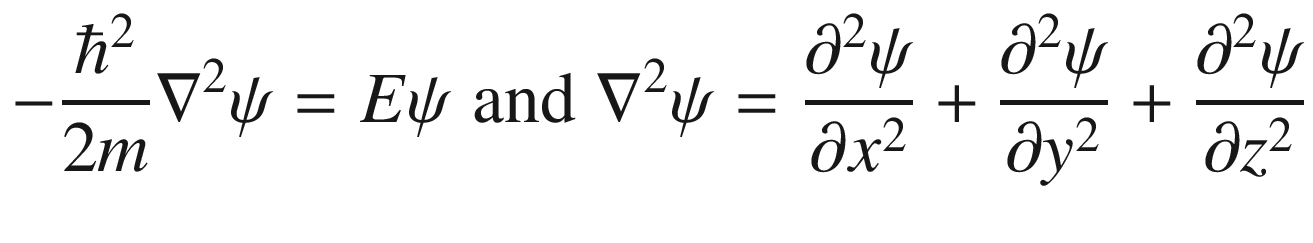

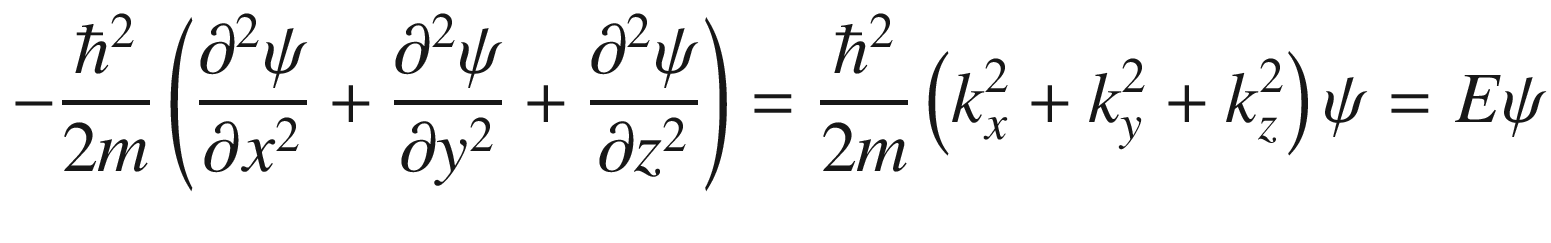

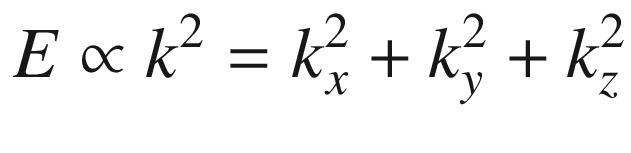
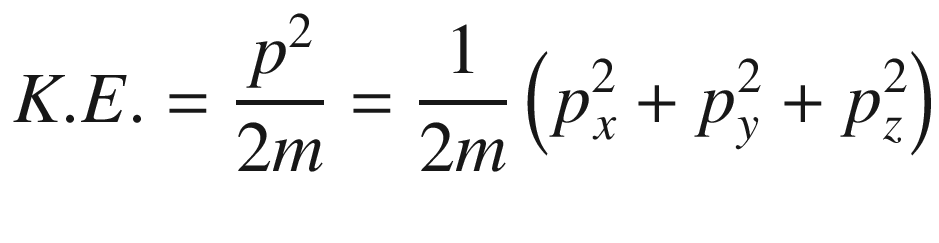

This is the de Broglie relationship, and p is the crystal momentum. However, it should be stressed that the wave vector k for electron wave functions in a periodic potential is not a measure of true physical momentum. As will be discussed later, the physically distinct values of the wave vector (crystal momentum) of an electron in a crystalline lattice—as opposed to those of a free particle, which can take any value—are restricted by the first Brillouin zone.

Therefore, the electron with a momentum p will be diffracted like a wave with a wavelength λ in a crystal!

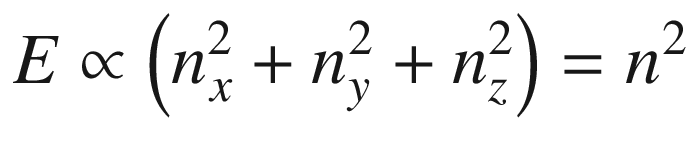
The results of (3.19) and (3.24) indicate that the 3D constant energy surface in n or k-space is a sphere. For each ki determined by ni there is a corresponding λi or mode. Each allowed energy state corresponding to a point ni can be displayed in the n-space with positive integer coordinates nx, ny, and nz. It is obvious that the energy eigenvalues are degenerate for nx ≠ ny ≠ nz. For example, for (nx, ny, nz) equals (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), or (3, 2, 1), there are six degenerate energy states with the same energy. The number of degenerate states increases dramatically with increasing energy.
3.1.3 Density of States (DOS)
In many situations, such as when computing the electron distribution, it is necessary to know how the electrons are distributed in the energy spectrum. This could be done through the use of (3.24) to derive a density of states.
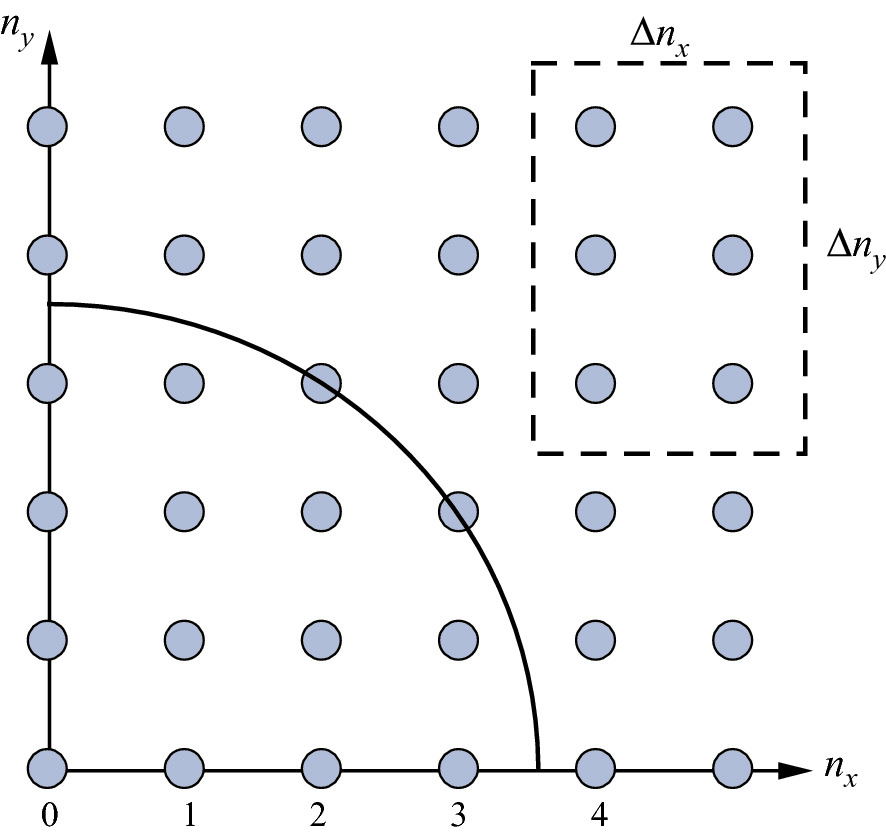
Schematic of the states of an electron in a 2D infinte well. The circle corresponds to a constant energy

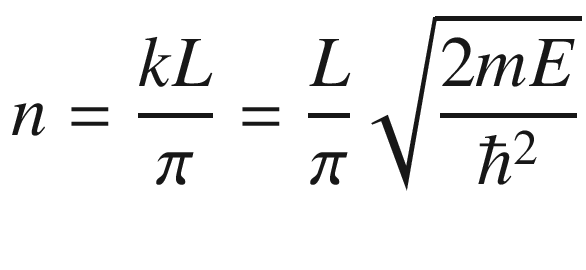

Spherical surface corresponding to constant energies E and E + dE plotted in the momentum (n) space of a particle
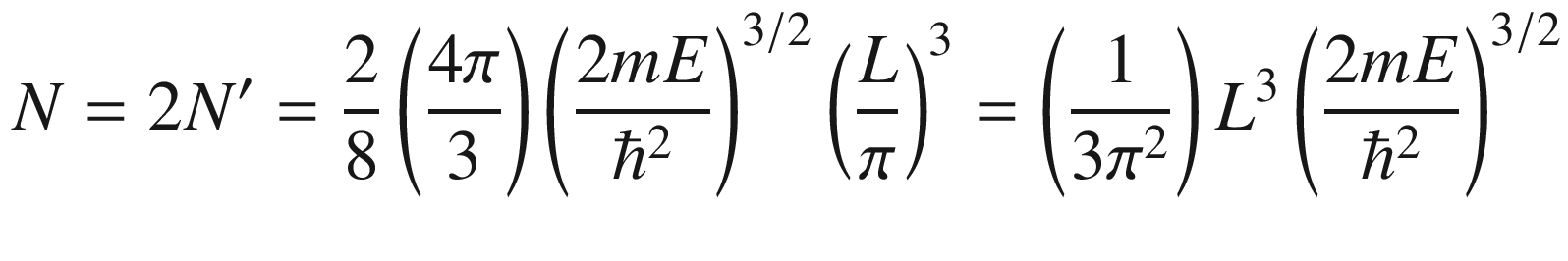

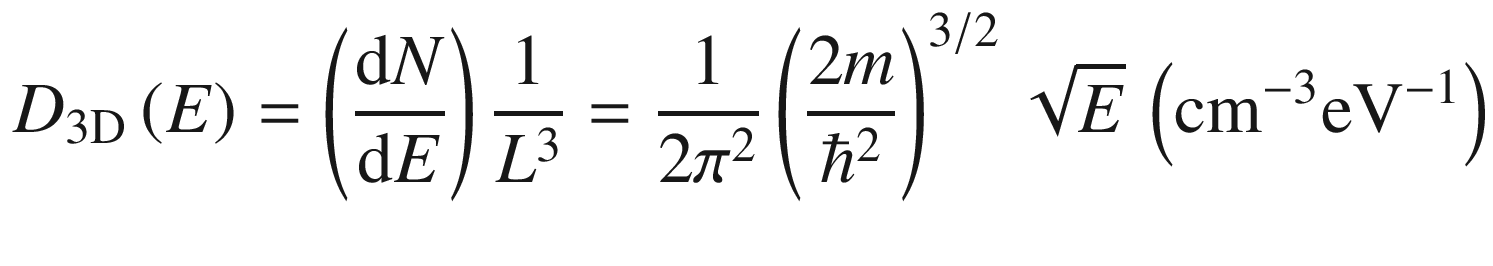
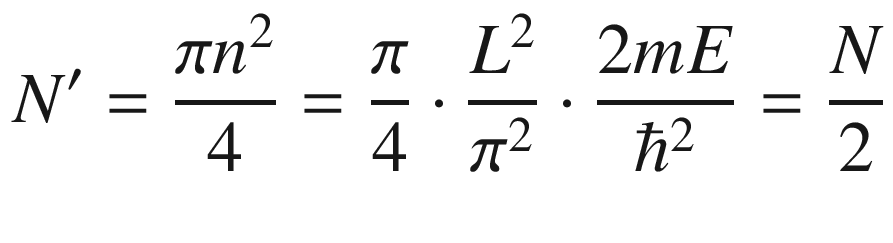
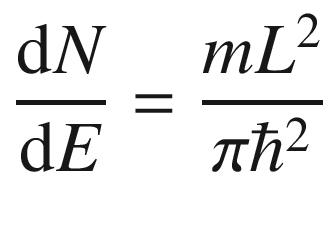



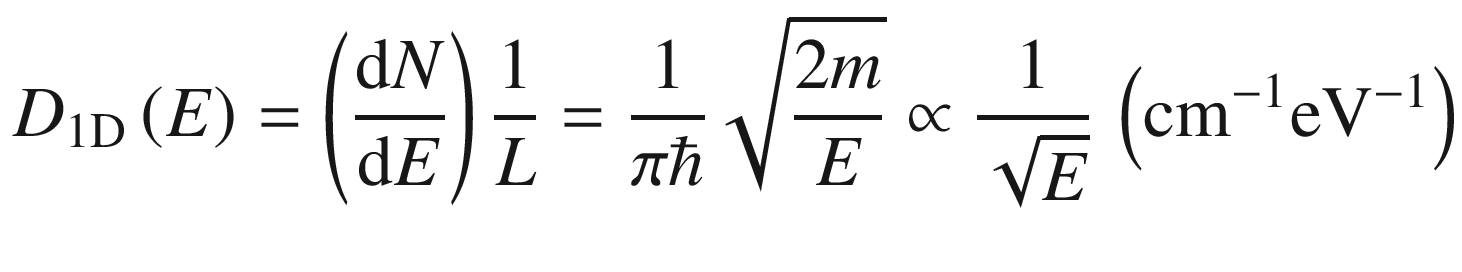
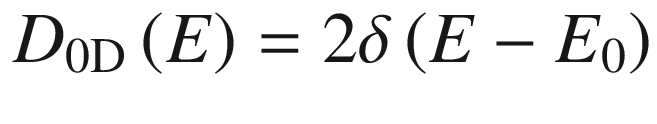

Density of states distributions in bulk (3D), quantum well (2D), quantum wire (1D), and quantum dot (0D) structures
3.2 Periodic Crystal Structure and Bloch’s Theorem
The simple model of the free electron theory using one-electron approximation of a square potential well has been successful in accounting for some physical properties of solids, in particular those of metals. However, in crystals, the ‘free’ electron situation is not very accurate. Therefore, this overly simplified model needs refinements in order to improve its ability to explain the properties of semiconductors. One obvious addition to the model is to add the spatial dependence of the potential experienced by a valence electron in a crystal. The effect of the added potential associated with the ion cores is particularly pronounced in periodic ion-core potentials. However, this also imposes a concomitant constraint on the wave functions that describing the motion of an electron in the periodic potential. Fortunately, this added constraint can be treated easily using the theory that Felix Bloch proposed in 1928.
3.2.1 Bloch’s Theorem
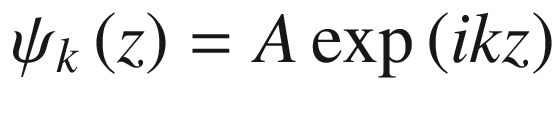
This leads to a uniform distribution function of  = constant. Therefore, the system is translationally invariant.
= constant. Therefore, the system is translationally invariant.
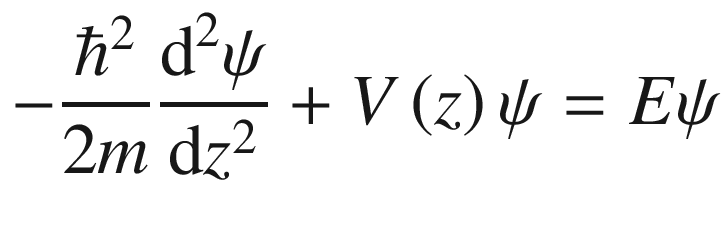
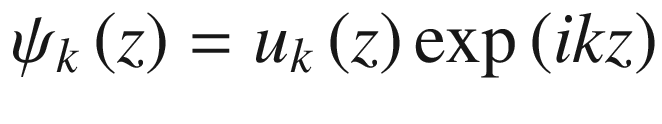
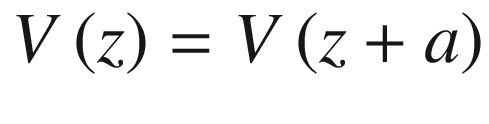

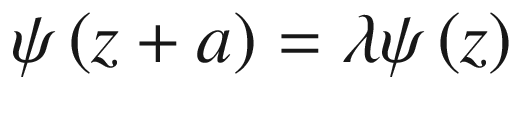


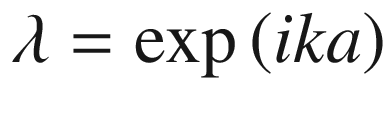
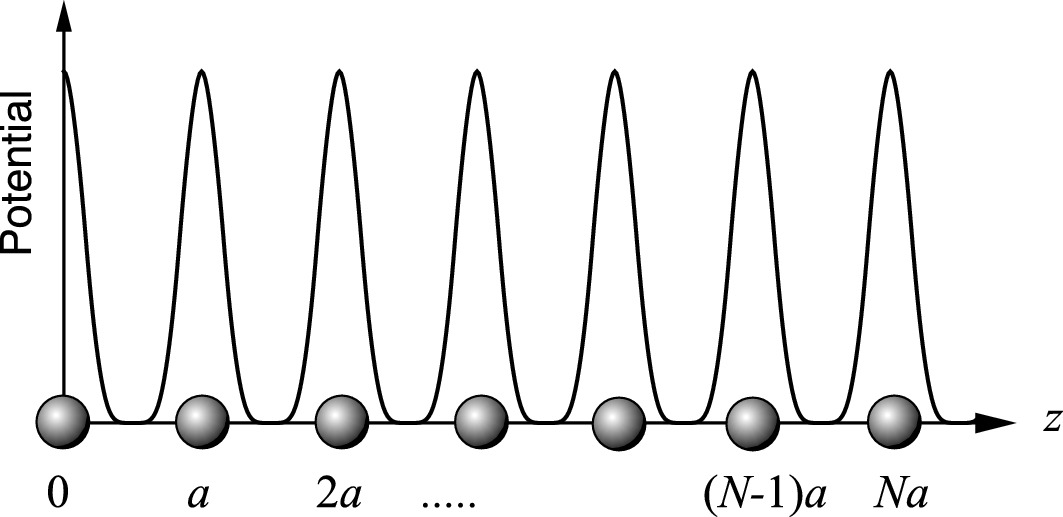
Periodic potential for a linear atomic lattice. We may assume that the wave functions of all eigenstates must repeat after some arbitrary number N of unit cells
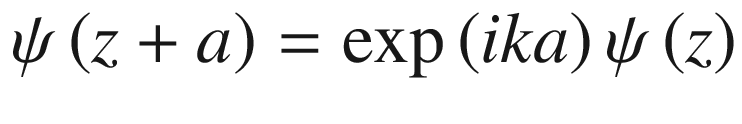

The function uk(z) is thus periodic with a period a.


3.2.2 Reduced Zone Representation
In this equation, as will become clear next, it is not necessary to use the value for P which is larger than ±(N/2), corresponding with k = ±(π/a). Any excess periodicity can be transferred into the uk(z) factor of the Bloch function. We notice that the range of wave vector from k = –(π/a) to k = +(π/a) corresponds to the first Brillouin zone in reciprocal lattice of the 1D lattice with a lattice spacing of a. Thus it is useful to examine the Bloch wave function near the origin of the k-space.

![$$ \begin{aligned} \psi_{{k + {\text{G}}}} \left( \varvec{r} \right) & = u_{{k + {\text{G}}}} \left( \varvec{r} \right)\exp \left[ {i\left( {\varvec{k} + \varvec{G}} \right) \cdot \varvec{r}} \right] \\ & = \left[ {u_{{k + {\text{G}}}} \left( \varvec{r} \right)\exp \left( {i\varvec{G} \cdot \varvec{r}} \right)} \right]\exp \left( {i\varvec{k} \cdot \varvec{r}} \right) \\ & = u_{k} \left( \varvec{r} \right)\exp \left( {i\varvec{k} \cdot \varvec{r}} \right) \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equb.png)

Here, we used  and
and  .
.
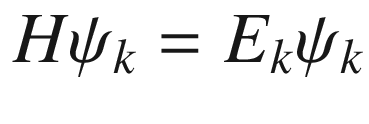
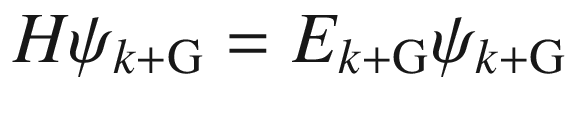
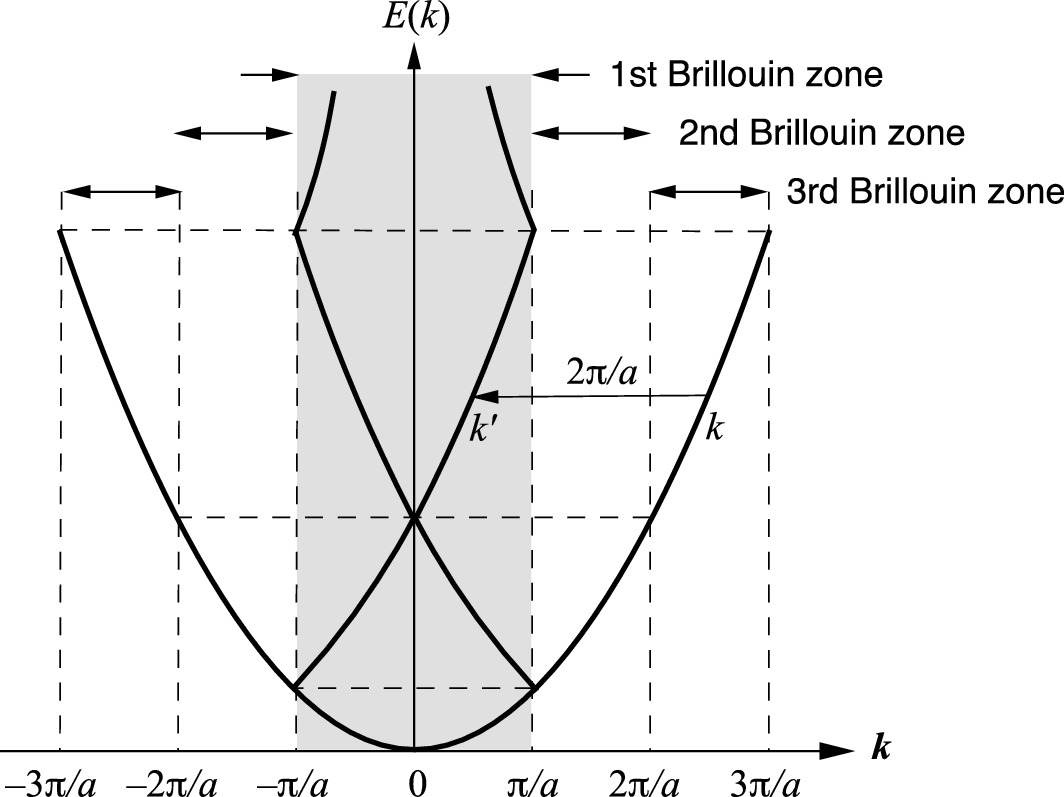
Energy as a function of wave vector for electrons in a one-dimensional crystal of lattice constant a, where the amplitude of the periodic potential is set to zero. The continuous energy function is shown as a multiple-valued function of k in the shaded first Brillouin zone using the reduced zone representation
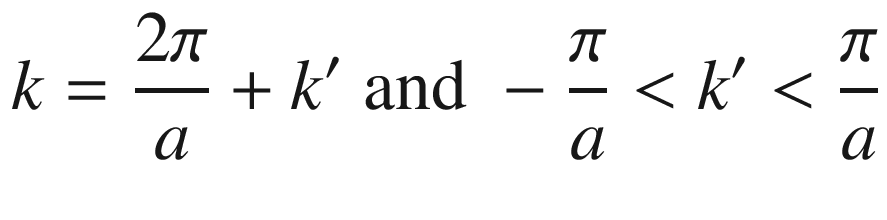
![$$ \begin{aligned} \psi_{k} \left( z \right) & = u_{k} \left( z \right)\exp \left( {ikz} \right) \\ & = \left\{ {u_{k} \left( z \right)\exp \left[ {i\left( {2\pi /a} \right)z} \right]} \right\}\exp \left( {ik^\prime z} \right) \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ67.png)
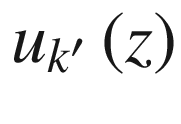 with the same periodicity. Thus,
with the same periodicity. Thus,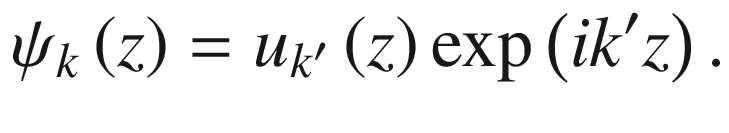
This reduces the Bloch wave number to the range –π/a ≤ k ≤ π/a, which is the first Brillouin zone. Other higher-order wave vectors can also be reduced to the first Brillouin zone using the reduced zone representation.
3.2.3 Empty Lattice Model—Energy Band Calculation for an FCC Crystal
In the free electron model, it is simple to discuss electron energy and wave vector without regard for the crystallography of the solid. As soon as we take the periodic potential into consideration, the Brillouin zone boundaries (surfaces) in k-space become particularly important. Therefore, the following discussion of the relationship between energy and momentum for electrons in crystals will be in k-space.
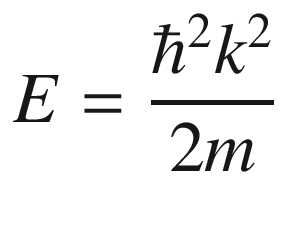

![$$ \begin{aligned} E_{\text{FCC}} & = \frac{{\hbar^{2} }}{2m}\left\{ {\left[ {k_{x} + \frac{2\pi }{a}\left( { - h + k + l} \right)} \right]^{2} } \right. + \left[ {k_{y} + \frac{2\pi }{a}\left( {h - k + l} \right)} \right]^{2} \\ & \quad \quad \quad \quad \left. { + \left[ {k_{z} + \frac{2\pi }{a}\left( {h + k - l} \right)} \right]^{2} } \right\} \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ71.png)

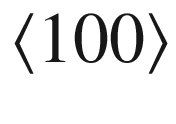 and
and  axes in the reduced zone representation.
axes in the reduced zone representation.- (a)

 . The lowest energy state is located at Gx = Gy = Gz = 0 and
. The lowest energy state is located at Gx = Gy = Gz = 0 and  . The E-k curve follows a parabola and E = 1 at kx = 1. Figure 3.11 shows the lowest three E-k curves along [100].
. The E-k curve follows a parabola and E = 1 at kx = 1. Figure 3.11 shows the lowest three E-k curves along [100].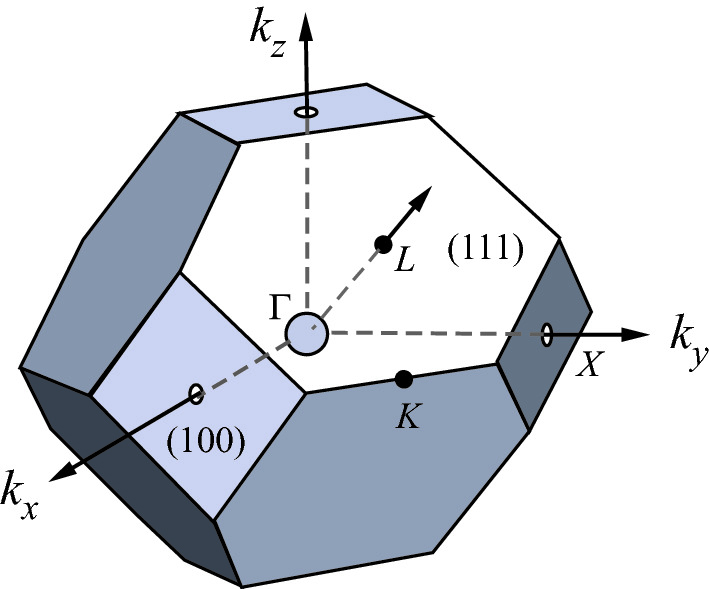
Brillouin zone
of the face-centered cubic lattice. The high symmetry points Γ, L, X, and K correspond to the zone center,  ,
,  , and
, and  directions, respectively
directions, respectively
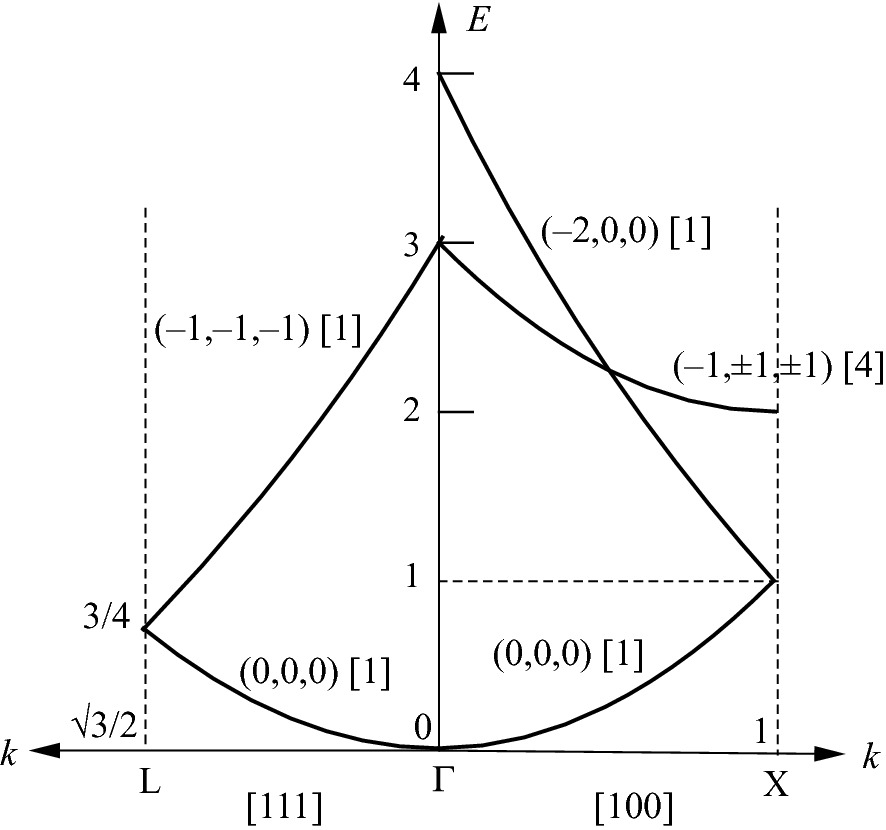
Band structure for a free electron in an FCC lattice along [100] and [111] in the first Brillouin zone. For each curve, the selected G’s and degeneracy (in brackets) are indicated
To continue, using the reduced zone scheme, the next E needs to start at E = 1 (kx = 1) and increase as kx approaches zero. By trial and error, there are two possible G’s that match this condition. However, G(−1, −1, 0) is not selected due to the lack of continuation in the third Brillouin zone and other diffraction directions. The appropriate G’s are (Gx, Gy, Gz) = (–2, 0, 0), and E = (kx – 2)2. Started from kx = 1, E = 1, the E-k curve increases toward kx = 0, E = 4.
The next higher energy level is E = 3 at kx = 0. This energy level matches the second lowest energy state along [111] shown next. This can be calculated by setting (Gx, Gy, Gz) = (–1, ±1, ±1), which has a four-fold degeneracy. The E-k dispersion relationship is E = (kx – 1)2 + 2. At kx = 1, E = 2, and at kx = 0, E = 3.
- (b)

 ) kmax and kx = ky = kz. The lowest energy is at (Gx, Gy, Gz) = (0,0,0).
) kmax and kx = ky = kz. The lowest energy is at (Gx, Gy, Gz) = (0,0,0).  . At k = 0, E = 0, and at
. At k = 0, E = 0, and at  , E = 3/4.
, E = 3/4. . This corresponds to a set of (Gx, Gy, Gz) = (–1, –1, –1). Then
. This corresponds to a set of (Gx, Gy, Gz) = (–1, –1, –1). Then


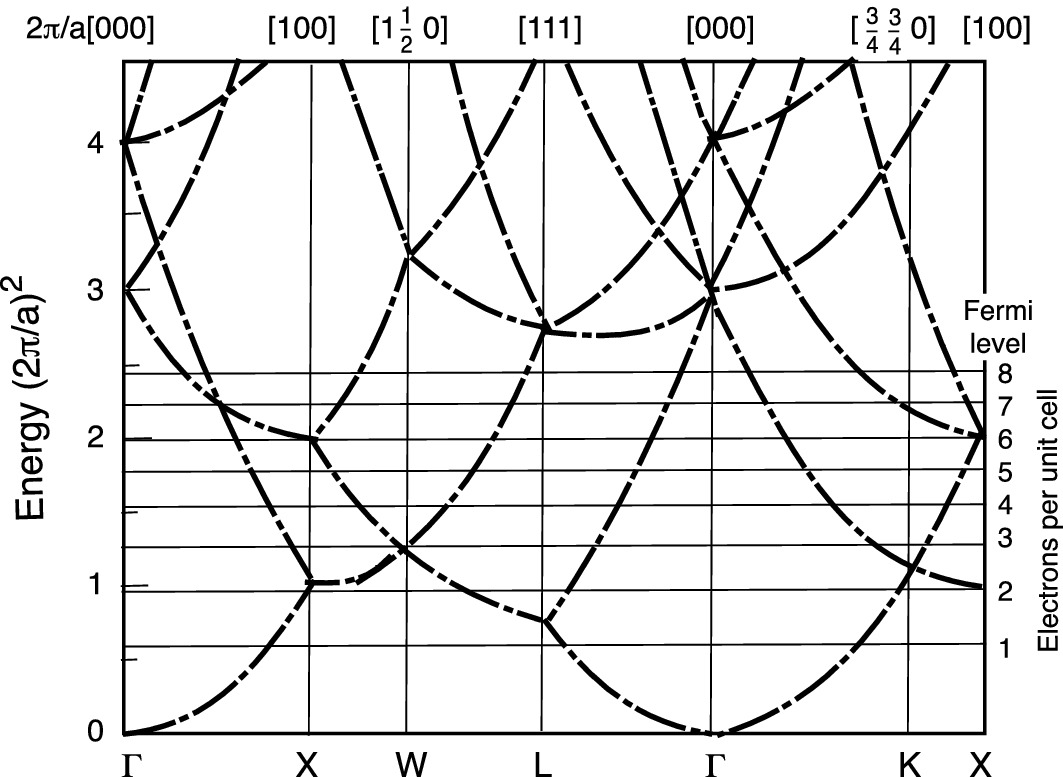
Band structure for a free electron in an FCC lattice in the first Brillouin zone.
Reprinted with permission from [1], copyright Wiley
In the free electron theory, where the potential induced by the core ions is neglected, the energy band is a continuous parabola. However, the above results indicate that the motion of electrons is not free, but is constrained by the spatial arrangement of the periodic potential associated with the lattices. Nevertheless, in this simple ‘one’ electron model, it allows the Bloch function wave of all energies to extend without attenuation through a crystal.
3.3 Nearly Free Electron Approximation and the Energy Gap
3.3.1 Origin of Bandgaps
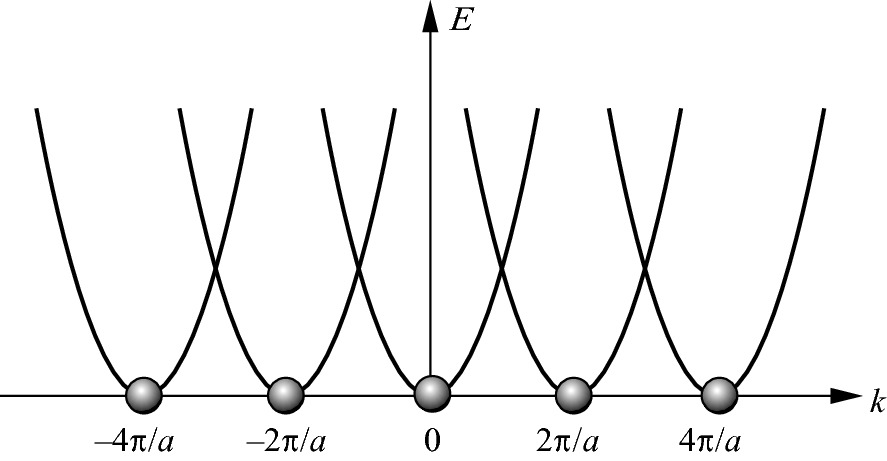
Energy bands for an electron in a 1D periodic array of potential with a periodicity of a plotted in the repeated-zone scheme
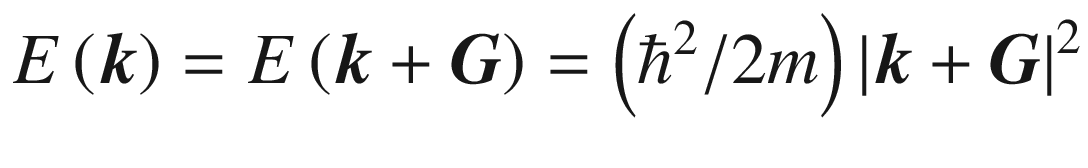
However, when there is only one electron in the system, the electron–electron wave interactions are missing, and the resulting energy band structure shows only the crystal structural property, e.g., as illustrated in Fig. 3.12 for FCC lattices. Of course, in reality, there are extremely large quantities of electrons available in semiconductors. To improve the model, we shall allow more electrons in the crystal lattice such that the electron–electron wave interactions could be included.
When an electron wave propagates through the crystal lattice, it gets scattered in all directions from the lattice atoms. Because of the periodic nature of the lattice, in certain directions, waves scattered by many lattice points interfere constructively and a strong scattered beam results. For example, the Bragg condition for an incident wave normal to the crystal plane with a lattice periodicity of a is nλ = 2a or k = nπ/a. The wave vector that fulfills the Bragg condition simply equals one half of the reciprocal lattice vector G, i.e., k = ± G/2. In general, since the scattering from the lattice involves all wave numbers, a plane wave of wave number k and energy E(k) will mix with other electron waves with wave number k + Gn for all n’s. The mixing becomes strong only when the electron waves propagating through the crystal lattice are of equal energy where E(k) = E(k ± G) or |k| = |k ± G| or k = ± Gn/2. Again, the Bragg condition for strong reflection occurs at k = ± Gn/2. Therefore, the backscattering becomes very strong, and the electron is unable to propagate through. The forward and back reflected waves establish a standing wave in the crystal. Assuming the contributions from the nearest neighboring waves dominate the resulting waves, the contribution from other reciprocal lattice vectors can be neglected.

![$$ \psi \left( { - \pi /a} \right) = A\exp \left[ {i\left( {G/2 - G} \right)z} \right] = A\exp \left( { - iGz/2} \right) $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ77.png)

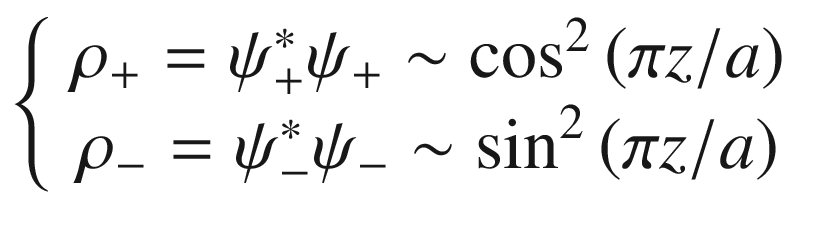
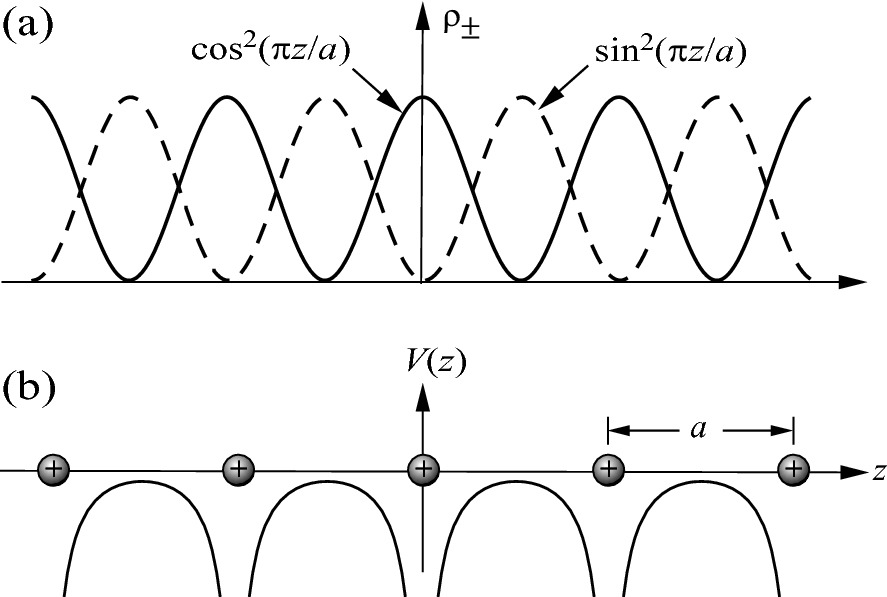
Schematic illustration of the relationship between a electron charge density distribution and b the ion core positions in a 1D lattice

Electronic band structure for a 1D crystal with periodicity a in the nearly free electron approximation. Many electrons are presented. The dashed curve shows the continuous E-k curve of the free electron model
3.3.2 Energy Gap—A Quantitative Approach

![$$ \begin{aligned} V\left( z \right) & \cong V_{0} + \mathop \sum \limits_{n} \left[ {2V_{n} \left( z \right)\cos \left( {2n\pi z/a} \right)} \right] \\ & = V_{0} + V_{1}^{'} \left( z \right) + V_{2}^{'} \left( z \right) + \cdots \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ81.png)

![$$ \begin{aligned} V_{1}^{'} \left( z \right) & = 2V_{1} \cos \left( {2\pi z/a} \right) \\ & = V_{1} \left[ {\exp \left( {i2\pi z/a} \right) + \exp \left( { - i2\pi z/a} \right)} \right] \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ83.png)

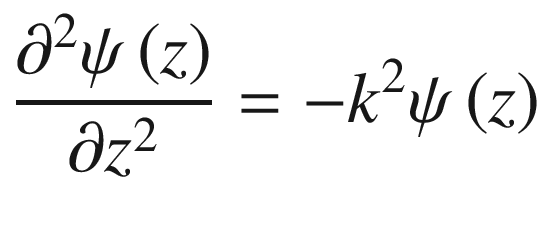
 and using
and using  , the wave equation becomes
, the wave equation becomes![$$ \begin{aligned} & \left( {E - E_{k} } \right)\left[ {A_{1} \exp \left( {ikz} \right) + A_{2} \exp \left( { - ikz} \right)} \right] \\ & = \left[ {V_{0} + V_{1}^{'} \left( z \right)} \right]\left[ {A_{1} \exp \left( {ikz} \right) + A_{2} \exp \left( { - ikz} \right)} \right] \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ88.png)
![$$ \begin{aligned} & \left( {E - E_{k} - V_{0} } \right)\left[ {A_{1} \exp \left( {ikz} \right) + A_{2} \exp \left( { - ikz} \right)} \right] \\ & = \left\{ {V_{1} \left[ {\exp \left( {i2kz} \right) + \exp \left( { - i2kz} \right)} \right]} \right\}\left[ {A_{1} \exp \left( {ikz} \right) + A_{2} \exp \left( { - ikz} \right)} \right] \\ & = V_{1} \left\{ {\left[ {A_{1} \exp \left( { - ikz} \right) + A_{2} \exp \left( {ikz} \right)} \right] + \left[ {A_{1} \exp \left( {i3kz} \right) + A_{2} \exp \left( { - i3kz} \right)} \right]} \right\} \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ89.png)


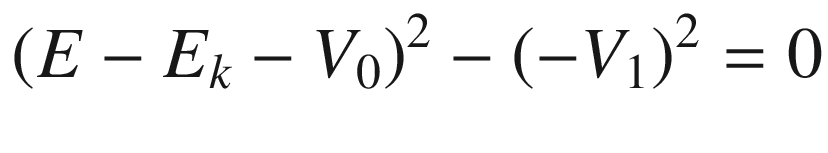


![$$ \left\{ {\begin{array}{*{20}c} {\psi_{ + } \left( z \right) = A\left[ {\exp \left( {ikz} \right) + \exp \left( { - ikz} \right)} \right] = 2A\cos \left( {\pi z/a} \right)} \\ {\psi_{ - } \left( z \right) = A\left[ {\exp \left( {ikz} \right) - \exp \left( { - ikz} \right)} \right] = 2iA\sin \left( {\pi z/a} \right)} \\ \end{array} } \right. $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ95.png)
These are the same qualitative results we obtained in (3.68). The ψ+(z) and ψ–(z) functions near the zone boundary represent two traveling waves of equal amplitude. The interference of these two waves generates two standing waves which represent two different electron distributions with respect to the lattice potential. The difference in potential energy associated with these two standing waves leads to a splitting of the energy bands at the zone boundary as shown in Fig. 3.15. Thus, in the nearly free electron approximation, by considering many electrons propagating through the periodic crystal lattice, bandgaps are formed in the otherwise continuous parabolic energy band.
3.4 The Kronig–Penney Model
In the free electron approximation discussed above, the periodic potential energy of the electron was assumed to be small compared to its total energy, and the wave functions for electrons on neighboring atoms overlap heavily. This model led to the energy band structure where the width of the forbidden energy bands was found to be small compared to that of allowed bands. The other important approach, the tight-binding approximation, proceeds from the opposite point of view, where the atoms of the crystal are so far apart that the wave functions for electrons associated with neighboring atoms overlap only to a small extent. Thus the wave functions and allowed energy levels of the crystal will be closely related to the wave functions and energy levels of isolated atoms. The resulting allowed energy bands are narrow in comparison with the forbidden bands. Depending on the particular solid to be studied, we will use the free electron approximation, the tight-binding approximation, or a mixture of the two. Of course, there are very many advanced methods for full calculations of semiconductor energy bands, but the topic is too complex for an adequate treatment in this book. Fortunately, we still can learn some interesting properties about the appearance of energy gaps when an ‘adjustable’ periodic potential is added by studying a simple 1D model suggested by R. de L. Kronig and W. G. Penney. In the Kronig–Penney model, the depth, width, and periodicity of the potential wells can be varied to simulate the environment that electrons will experience under the condition of the nearly free electron model, the tight-binding approximation, or a mixture of the two.
3.4.1 Theoretical Model

One-dimensional periodic square well potential energy used in Kronig–Penney model

![$$ \frac{{\hbar^{2} }}{2m}\frac{{\partial^{2} \psi }}{{\partial z^{2} }} + \left[ {E - V\left( z \right)} \right]\psi = 0 $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ97.png)




- (1)
In region I, V = 0:
 (3.92)
(3.92) - (2)
In region II, V = V0:
 (3.93)
(3.93)
Note that β becomes an imaginary number for E < V0.
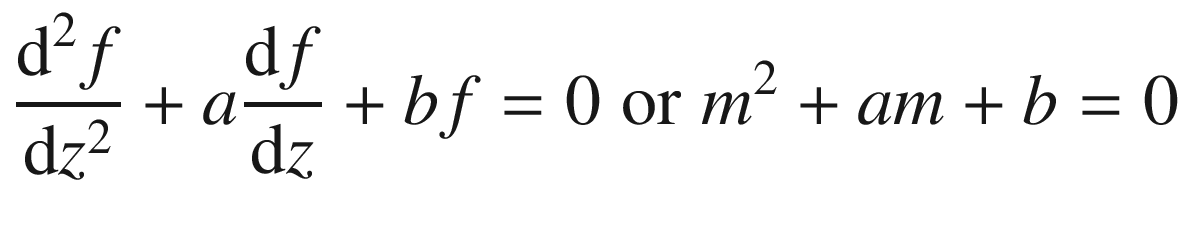
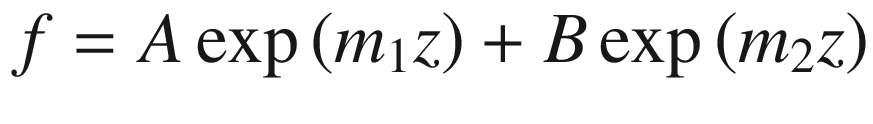
![$$ \left\{ {\begin{array}{*{20}c} {u_{\text{I}} \left( z \right) = A\exp \left[ {i\left( {\alpha - k} \right)z} \right] + B\exp \left[ { - i\left( {\alpha + k} \right)z} \right], 0 < z < a} \\ {u_{\text{II}} \left( z \right) = C\exp \left[ {i\left( {\beta - k} \right)z} \right] + D\exp \left[ { - i\left( {\beta + k} \right)z} \right], - b < z < 0} \\ \end{array} } \right. $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ106.png)
- (i)
At z = 0,
 ,
, (3.97)
(3.97) - (ii)
At z = 0,
 ,
, (3.98)
(3.98) - (iii)
At x = a and –b,
 ,
,![$$ \begin{aligned} & A\exp \left[ {i\left( {\alpha - k} \right)a} \right] + B\exp \left[ { - i\left( {\alpha + k} \right)a} \right] \\ & = C\exp \left[ { - i\left( {\beta - k} \right)b} \right] + D\exp \left[ {i\left( {\beta + k} \right)b} \right] \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ109.png) (3.99)
(3.99) - (iv)
At x = a and –b,
 ,
,![$$ \begin{aligned} & \left( {\alpha - k} \right)A\exp \left[ {i\left( {\alpha - k} \right)a} \right] - \left( {\alpha + k} \right)B\exp \left[ { - i\left( {\alpha + k} \right)a} \right] \\ & = \left( {\beta - k} \right)C\exp \left[ { - i\left( {\beta - k} \right)b} \right] - \left( {\beta + k} \right)D\exp \left[ {i\left( {\beta + k} \right)b} \right] \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ110.png) (3.100)
(3.100)
![$$ \left[ {\begin{array}{*{20}l} 1 & 1 & { - 1} & { - 1} \\ {\alpha - k} & { - \left( {\alpha + k} \right)} & { - \left( {\beta + k} \right)} & {\beta + k} \\ {\exp \left[ {i\left( {\alpha - k} \right)a} \right]} & {\exp \left[ { - i\left( {\alpha + k} \right)a} \right]} & { - \exp \left[ { - i\left( {\beta - k} \right)b} \right]} & { - \exp \left[ {i\left( {\beta + k} \right)b} \right]} \\ {\left( {\alpha - k} \right)e^{{i\left( {\alpha - k} \right)a}} } & { - \left( {\alpha + k} \right)e^{{ - i\left( {\alpha + k} \right)a}} } & { - \left( {\beta + k} \right)e^{{ - i\left( {\beta - k} \right)b}} } & {\left( {\beta + k} \right)e^{{i\left( {\beta + k} \right)b}} } \\ \end{array} } \right] = 0 $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ111.png)
![$$ - \left( {\frac{{\alpha^{2} + \beta^{2} }}{2\alpha \beta }} \right)\sin \left( {\alpha a} \right)\sin \left( {\beta b} \right) + \cos \left( {\alpha a} \right)\cos \left( {\beta b} \right) = \cos \left[ {k\left( {a + b} \right)} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ112.png)
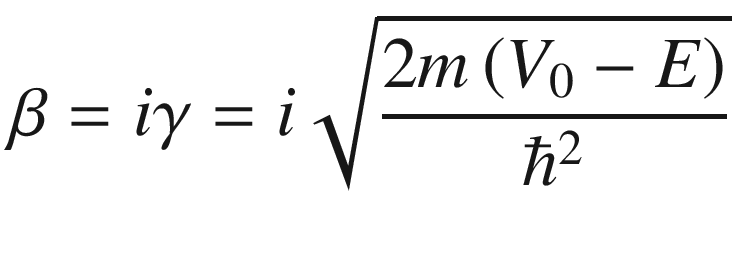
![$$ \left( {\frac{{\gamma^{2} - \alpha^{2} }}{2\alpha \gamma }} \right){ \sin }\left( {\alpha a} \right){ \sinh }\left( {\gamma b} \right) + { \cos }\left( {\alpha a} \right){ \cosh }\left( {\gamma b} \right) = { \cos }\left[ {k\left( {a + b} \right)} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ114.png)
We may use (3.102) or (3.104) to find the energy eigenvalues for various periodic lattice potential settings. Nevertheless, since cos(z) on the right-hand side has a real value in the range of ± 1, any result of |cosk(a + b)| larger than one is not a solution.
3.4.2 Analysis
Both (3.102) and (3.104) represent a rather involved problem unless we consider some set of simplified conditions. In the following, we shall discuss models with the potential function designed to replicate the nearly free electron approximation or the tight-binding approximation.
- (a)
Nearly free electron model
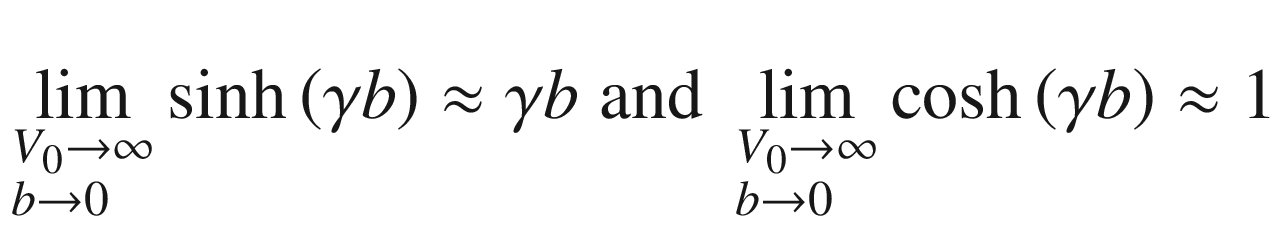

![$$ f\left( E \right) = P\left[ {\frac{{\sin \left( {\alpha a} \right)}}{\alpha a}} \right] + \cos \left( {\alpha a} \right) = \cos \left( {ka} \right) $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ117.png)

 . Therefore, we can plot f(E) in (3.107) as a function of
. Therefore, we can plot f(E) in (3.107) as a function of  and impose a limit of –1 ≤ f(E) ≤ 1 to yield the allowed solutions shown in Fig. 3.17. We note that the ordinate is (1 + P) for α = 0, where sin(αa) ≈ αa, and it is ±1 for α equal to any multiple of (π/a), regardless of the value of P. The left side of (3.107) contains a [sin(αa)]/(αa) term, which is a sinc function, with the same periodicity and phase as cos(αa). Since the amplitude of the sinc function decreases quickly with increasing α, its contribution diminishes after a few periods. Therefore, for a small P, the resultant f(E) has a shape similar to cos(αa) beyond several times of (π/a). Note that, consistent with our earlier discussions of the free electron model, the forbidden bands are narrower than the allowed energy bands.
and impose a limit of –1 ≤ f(E) ≤ 1 to yield the allowed solutions shown in Fig. 3.17. We note that the ordinate is (1 + P) for α = 0, where sin(αa) ≈ αa, and it is ±1 for α equal to any multiple of (π/a), regardless of the value of P. The left side of (3.107) contains a [sin(αa)]/(αa) term, which is a sinc function, with the same periodicity and phase as cos(αa). Since the amplitude of the sinc function decreases quickly with increasing α, its contribution diminishes after a few periods. Therefore, for a small P, the resultant f(E) has a shape similar to cos(αa) beyond several times of (π/a). Note that, consistent with our earlier discussions of the free electron model, the forbidden bands are narrower than the allowed energy bands.
Plot of the left side of (3.107) for P = 2 as a function of α. The allowed states are located within 1 ≥ f(E) ≥ –1, and the shaded areas are the forbidden regions
In the following, we shall discuss two extreme cases of the nearly free electron model.
- (i)
Case I: P → ∞
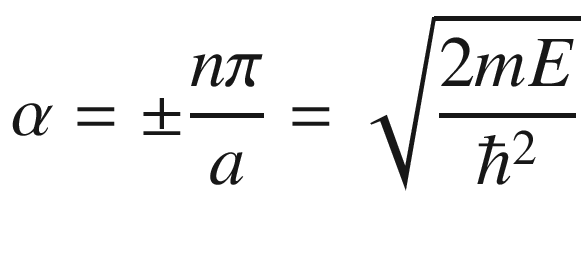

The allowed E’s are discrete levels as seen in an isolated atom.
- (ii)
Case II: P → 0


Therefore,  , and the allowed energy states form a continuous band.
, and the allowed energy states form a continuous band.
- (b)
Tight-binding approximation

![$$ \left[ {\left( {\frac{{\gamma^{2} - \alpha^{2} }}{2\alpha \gamma }} \right)\sin \left( {\alpha a} \right) + \cos \left( {\alpha a} \right)} \right]\frac{{\exp \left( {\gamma b} \right)}}{2} = \cos \left[ {k\left( {a + b} \right)} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ124.png)



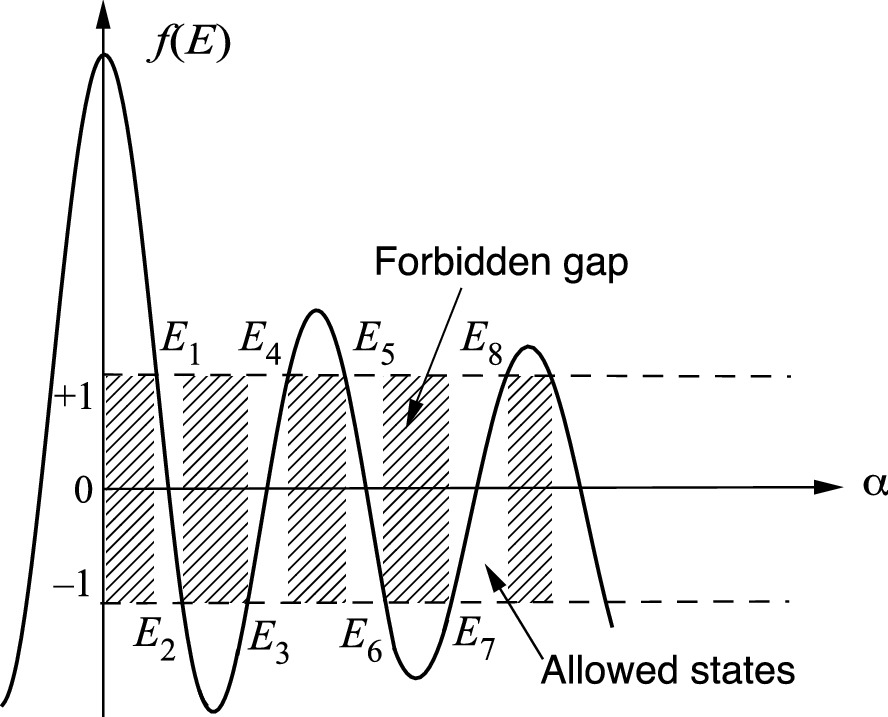
Plot of the left side of (3.115) as a function of α. The allowed states are located within 1 ≥ f(E) ≥ –1, and the shaded areas are the forbidden regions. The allowed energy bands are between E1 and E2, E3 and E4, E5 and E6, etc
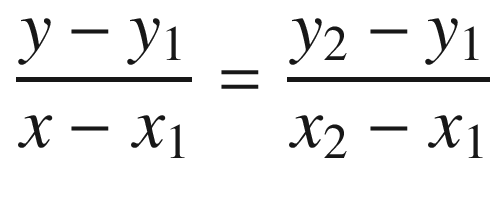

For the allowed energy states, f(E1) = f(E4) = f(E5) = f(E8) =  = +1, f(E2) = f(E3) = f(E6) = f(E7) =
= +1, f(E2) = f(E3) = f(E6) = f(E7) =  = –1, and f(E) = cos[k(a + b)], which lead to the following results.
= –1, and f(E) = cos[k(a + b)], which lead to the following results.
![$$ \cos \left[ {k\left( {a + b} \right)} \right] - 1 = - 2\left( {\frac{{E - E_{1} }}{{E_{2} - E_{1} }}} \right) $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ130.png)

![$$ E = E_{1} + \frac{{\Delta E_{1} }}{2}\left\{ {1 - \cos \left[ {k\left( {a + b} \right)} \right]} \right\} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ132.png)

Plot of the E-k curve of the a first and b second allowed energy bands using tight-binding approximation
![$$ \cos \left[ {k\left( {a + b} \right)} \right] + 1 = 2\left( {\frac{{E - E_{3} }}{{E_{4} - E_{3} }}} \right) $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ133.png)
![$$ E = E_{3} + \frac{{\Delta E_{2} }}{2}\left\{ {1 + { \cos }\left[ {k\left( {a + b} \right)} \right]} \right\} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ134.png)

Plot of the E-k curve according to the tight-binding approximation (solid curves) compared with the free electron mode (long-dashed curves). The reduced zone representation is plotted as short-dashed curves
3.5 Effective Mass




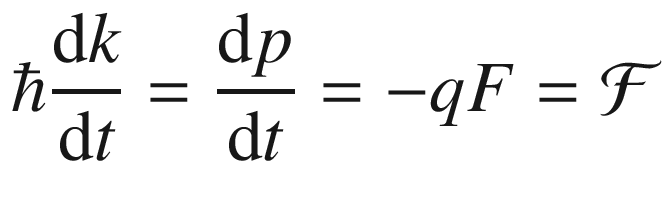
 . Thus it is the analogue of Newton’s law, showing that the crystal momentum of the electron in a periodic lattice changes under the influence of an applied electric field in the same way as does the true momentum of a free electron in free space.
. Thus it is the analogue of Newton’s law, showing that the crystal momentum of the electron in a periodic lattice changes under the influence of an applied electric field in the same way as does the true momentum of a free electron in free space.

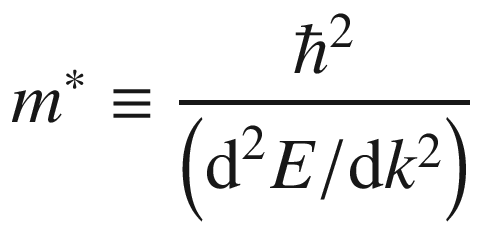




Variation of a, d electron energy, b, e electron velocity, and c, f effective mass with reduced wave vector for states in a band of one-dimensional crystal. The E-k curve is a cosine function for the left panel, and in the form of (1 + coska) for the right panel


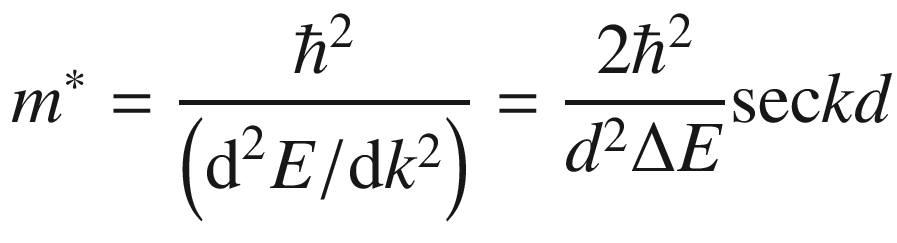
![$$ \begin{aligned} x\left( t \right) = \int \upsilon_{g} \left( t \right){\text{d}}t & = \frac{\Delta E}{2qF}\left[ {1 - \cos \left( {\frac{qFtd}{\hbar }} \right)} \right] \\ & = \frac{\Delta E}{2qF}\left( {1 - \cos kd} \right) \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ149.png)
This velocity oscillation is equivalent to a mass change at critical points in k-space shown in Fig. 3.21c. The electron mass has a constant positive value near the zone center but becomes negative on the zone boundary. One unusual property of the effective mass is that at wave vectors corresponding to the maximum and minimum velocities, the effective mass goes to infinite. This marks the point where a deceleration must begin to slow down the electron. The other peculiar property is that the effective mass has regions in which it is negative. A negative m* means that the acceleration resulting from the externally applied electric field is in a direction opposite to that of the applied field; this is the effect of electron reflection due to the periodic crystal lattice.
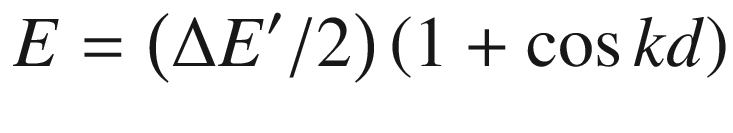
It resembles the E-k curve of the valence band in a semiconductor with an allowed energy bandwidth of ΔE′. By the same procedures, we can derive the group velocity and effective mass as displayed in Fig. 3.21e, f, respectively.
The E-k dispersion curve shown in Fig. 3.21a is very much like the conduction band edge of a direct bandgap semiconductor such as GaAs. We shall use it to discuss some properties related to semiconductor materials. Since the electron effective mass is a function of k within the first Brillouin zone, what value of k should be used for determining m*? Ideally, in a perfect crystal, under the influence of an applied electric field, the electron takes a periodic motion indefinitely within the first Brillouin zone as described by (3.137) and (3.139). This is known as the Bloch oscillation with a frequency ω = qFd/ħ, and there have been many attempts to observe and utilize it as a possible terahertz (THz) radiation source. However, all attempts to observe Bloch oscillation in conventional bulk solids have failed. For all reasonable applied fields, the Bloch oscillation is destroyed by scattering with impurities, defects, and phonons, before a single oscillation cycle is completed. The existence of such periodic oscillations in THz (1 THz = 1012 Hz) range was finally experimentally observed in 1993 in a semiconductor superlattice structure [2]. The multiple periods of GaAs/AlGaAs thin layers form superlattices that have a lattice periodicity much larger than the lattice constant of GaAs. This large lattice periodicity reduces the width of the Brillouin zone in k-space such that the scattering loss is suppressed. Therefore, in real semiconductors, the electron only travels a short range of the periodic E-k curve due to scattering events. The two dominant scattering processes are phonon scattering due to lattice vibration, and impurity and defect scattering. In high quality semiconductor materials, phonon scattering dominates the carrier relaxation process near room temperature and above. Through these processes, an electron can lose its energy quickly and move to the zone center of the E-k curve where the potential energy is the lowest. Near the zone center, the energy can be approximated by a parabolic function of k or E = A(k – k0)2. The effective mass has a constant value of m* = ħ2/2A, and the dynamical behavior of the electron will be the same as that of a free particle with this effective mass. For indirect bandgap semiconductors like Si and Ge, although the minimum conduction band edge is not located at the Γ point, the energy is still a parabolic function of k. The effective mass will also be a constant similar to that of the direct bandgap material.
3.6 Band Structures of Common Semiconductors
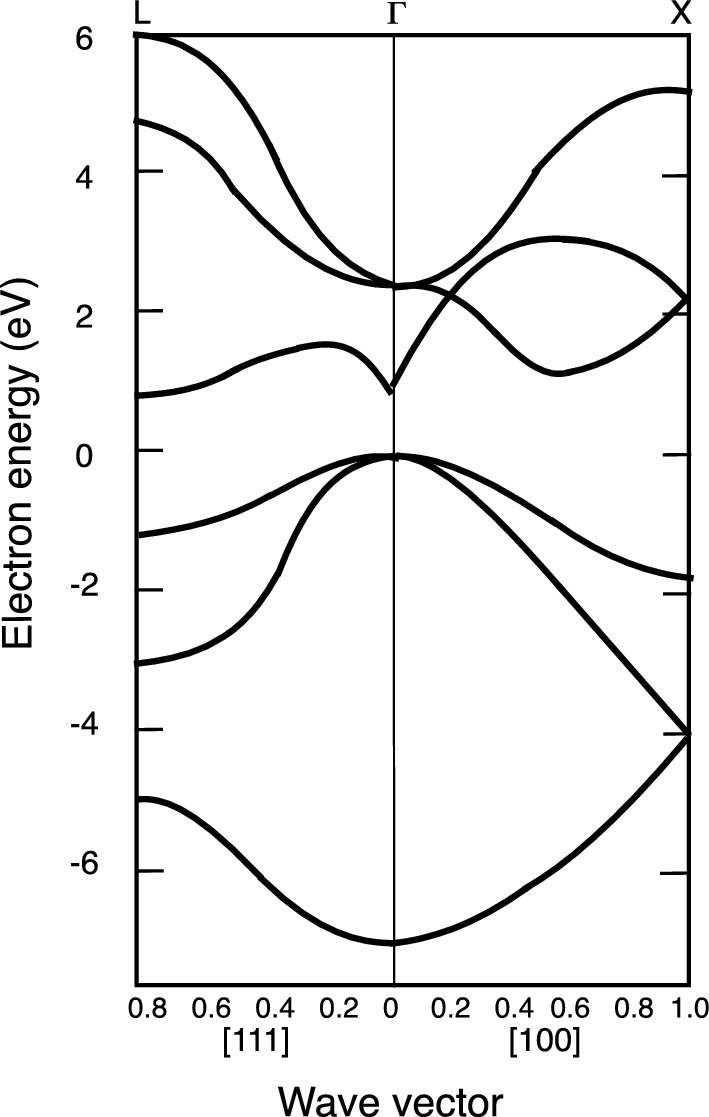
Typical energy bands for a diamond-like crystal structure.
Reprinted with permission from [3], copyright Wiley
3.6.1 General Trend of Energy Band Structure in Semiconductors
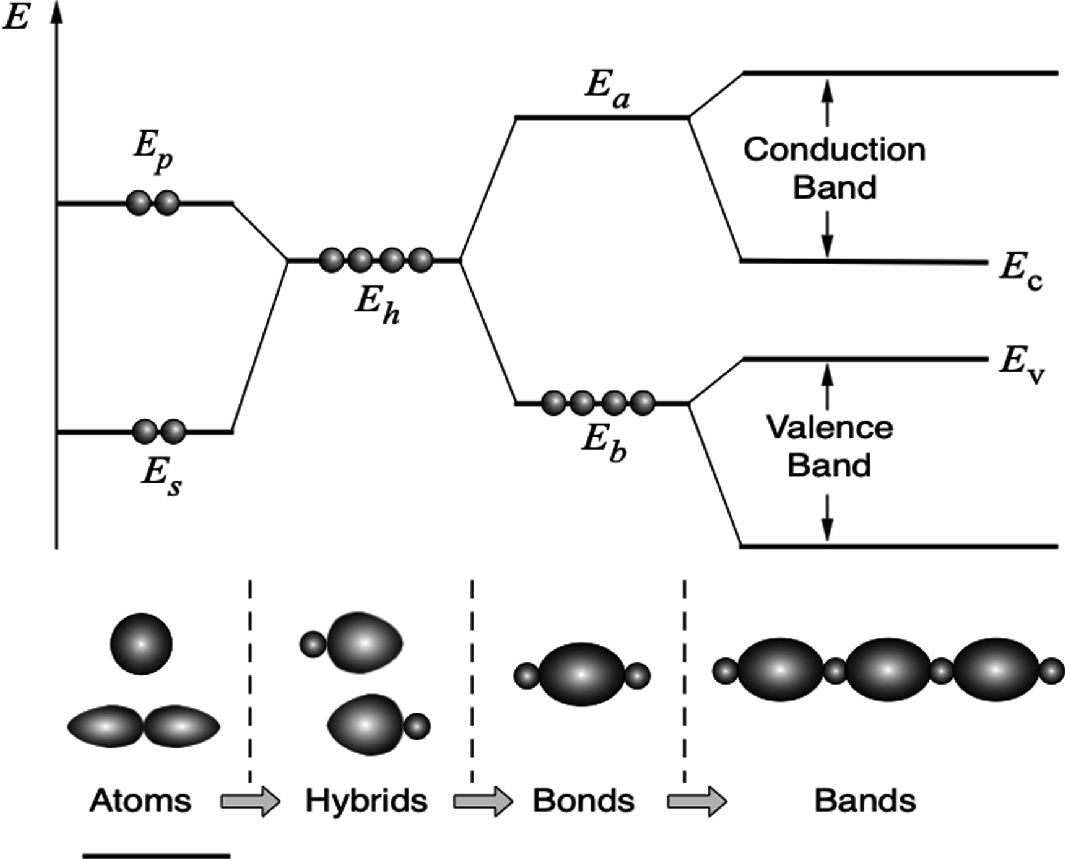
Development of energy band structure of silicon. The single s-states (Es) and p-states (Ep) on each atom are transformed to four hybrid states (Eh), which are combined with neighboring hybrids to form bonds. The bonding (Eb) and anti-bonding (Ea) levels finally broaden into energy bands in the crystal
 directions at the L-point. On the other hand, GaAs is a direct bandgap semiconductor with both the maximum of the valence band and the minimum of the conduction band located at the Γ-point. Therefore, it is instructive to examine the trends in the band structures of tetrahedrally bonded semiconductors, specifically the III–V compounds exhibiting mixed ionic-covalent bonding.
directions at the L-point. On the other hand, GaAs is a direct bandgap semiconductor with both the maximum of the valence band and the minimum of the conduction band located at the Γ-point. Therefore, it is instructive to examine the trends in the band structures of tetrahedrally bonded semiconductors, specifically the III–V compounds exhibiting mixed ionic-covalent bonding.
Energy bands of germanium. a Energy band obtained by pseudopotential calculations. Reprinted with permission from [4], copyright American Physical Society, b energy band calculated using the nearly free electron model
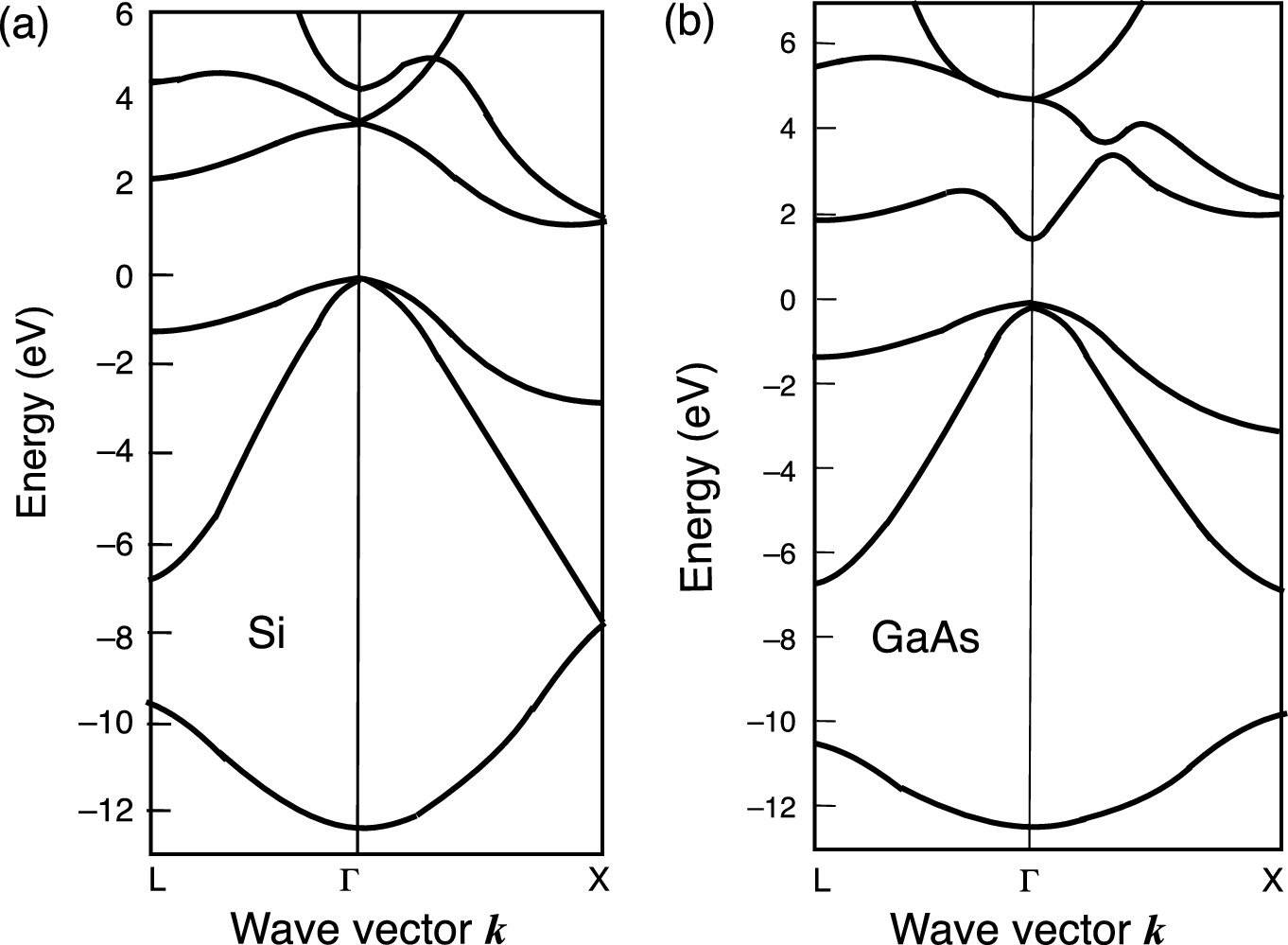
Detailed energy band structures of a Si and b GaAs.
Reprinted with permission from [4], copyright American Physical Society
3.6.2 Valence Band
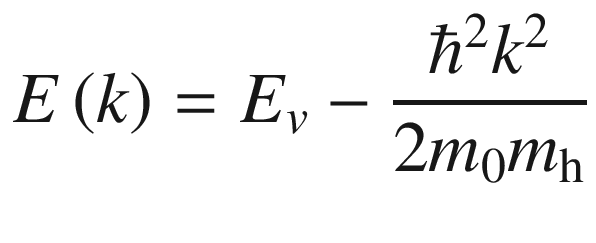

Valence band constructed from pz orbitals. a Regular arrangement of pz orbitals. b E-k curves of pz orbitals only; the band is ‘light’ along kz and ‘heavy’ along kx or ky

Total band structure at the top of the valence band for tetrahedral semiconductors
The decoupling of the spin-orbit split-off band from the top of the valence band is caused by the interaction of the electron spins (s = ±1/2) of the valence electrons with the magnetic moment (l = 1 for p-state) arising from their orbital motion, which yield a total angular momentum j = l + s = 3/2 and 1/2. The separation between the top of the heavy-/light-hole bands and the spin-orbit split-off band, Δso, increases with atomic number, essentially because the greater the nuclear charge, the greater the internal magnetic field experienced by the orbiting electron. Thus, Δso is very small for Si (0.04 eV), fairly large for GaAs (0.34 eV), and quite large for InSb (0.81 eV).
3.6.3 Conduction Band
- (a)
Direct bandgap materials

Thus the constant energy surface of the conduction band has a spherical shape. For direct bandgap semiconductors, the radius of the E-k curve of the lowest conduction band is relatively small, leading to a light electron effective mass. In GaAs,  ≅ 0.063m0 is the electron effective mass.
≅ 0.063m0 is the electron effective mass.
- (b)
Indirect bandgap materials
 about 85% of the way to the X-zone boundary. As illustrated in Fig. 3.28, there are six Δ-directions and, therefore, six equivalent minima in a cubic crystal. Due to their off-center location, these minima (valleys) have anisotropic E-k relationships along kx, ky, and kz.
about 85% of the way to the X-zone boundary. As illustrated in Fig. 3.28, there are six Δ-directions and, therefore, six equivalent minima in a cubic crystal. Due to their off-center location, these minima (valleys) have anisotropic E-k relationships along kx, ky, and kz.![$$ E\left( k \right) = E_{\text{c}} + \frac{{\hbar^{2} }}{{2m_{0} }}\left[ {\frac{{\left( {k_{x} - k_{0} } \right)^{2} }}{{m_{\text{L}} }} + \frac{{k_{y}^{2} }}{{m_{\text{T}} }} + \frac{{k_{z}^{2} }}{{m_{\text{T}} }}} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ153.png)
 in the L-point. In Ge
, as shown in Fig. 3.29, there are eight ellipsoidal equivalent valleys located at the zone boundaries where mL = 1.59 and mT = 0.082. Since only half of the constant energy surface is located inside the first Brillouin zone, the degenerate factor g is 4, not 8.
in the L-point. In Ge
, as shown in Fig. 3.29, there are eight ellipsoidal equivalent valleys located at the zone boundaries where mL = 1.59 and mT = 0.082. Since only half of the constant energy surface is located inside the first Brillouin zone, the degenerate factor g is 4, not 8.
a The Brillouin zone of Si with six equivalent constant energy surfaces along Δ-direction. b Enlarged view of one of the constant energy volumes, showing longitudinal and doubly degenerated transverse masses mL and mT, respectively
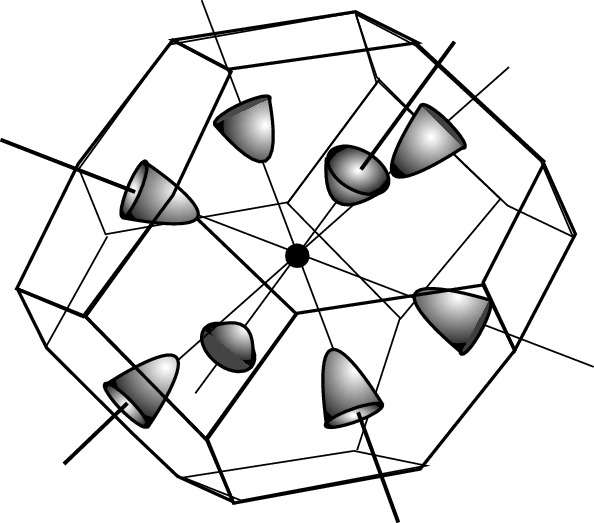
Brillouin zone of Ge with constant energy surfaces for the eight equivalent L-valleys
3.6.4 Band Structures of Wurtzite Crystals





Brillouin zone of zinc-blende and wurtzite-type materials.
Reprinted with permission from [5], copyright American Physical Society

Valence band structure of wurtzite GaN.
Reprinted with permission from [6], copyright AIP Publishing
In general, Δcr and Δso have positive values for III-nitrides except that AlN has a negative Δcr. Thus, the top valence band of AlN is E2 instead, and the valence bands from top to bottom are CH, HH, and LH, respectively. Note that the valence band energy splitting E1 – E2 and E1 – E3 are measurable quantities through inter-band optical transition measurements whereas Δcr and Δso are parameters of theory, obtainable indirectly by fitting experimental energy splitting.

- 1.
Calculate the first two E-k curves along the [110] axis for a BCC crystal using the 3D free electron model.
- 2.For an artificial two-dimensional square lattice structure shown below, calculate the first two energy bands for free electrons along the Γ-X, X-K, and Γ-K directions.
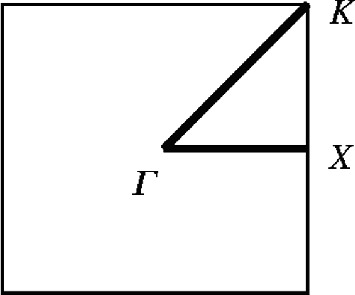
- 3.
Calculate and plot the density of states as a function of energy in the conduction band of a GaAs/AlGaAs quantum well for the first three bound states located at 25, 100, and 225 meV above the conduction band edge. The electron effective mass of GaAs in the conduction band is m* = 0.067m0.
- 4.
Derive the density of states for a quantum dot system. In a quantum dot system, the quantum confinement is three-dimensional.
- 5.
Suppose the E-k relation is given by
 . For very small k. prove that the parabolic approximation holds and determines the effective mass.
. For very small k. prove that the parabolic approximation holds and determines the effective mass. - 6.For the delta function periodic potential (V0 ~ ∞, b ~ 0 and V0b is small but finite or P ≪ 1), use the Kronig–Penney model to calculate
- (a)
The energy of the lowest energy band at k = 0.
- (b)
The bandgap at k = π/a.
- (a)
- 7.
Derive the following solution of the Kronig–Penney model for a crystal:
by setting the determinant of wave functions (3.101) to zero.![$$ - \left( {\frac{{\alpha^{2} + \beta^{2} }}{2\alpha \beta }} \right)\sin \left( {\alpha a} \right)\sin \left( {\beta b} \right) + \cos \left( {\alpha a} \right)\cos \left( {\beta b} \right) = \cos \left[ {k\left( {a + b} \right)} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Eque.png)
- 8.
Consider a simple cosine approximation to the shape of an energy band as

- (a)
For small k, prove that the parabolic approximation holds and
 .
. - (b)
Many semiconductors have a saturation velocity for electrons of around 107 cm/s. How much of the first Brillouin zone do electrons need to explore to reach this velocity? Assume the initial position of electrons is at the zone center. For calculations, use the velocity equation of part (a) and the following material parameters of GaAs: m* = 0.067m0 and lattice constant a0 = 5.653 Å.
- (a)
- 9.Consider a single electron in a perfect crystal. Starting from k = 0 in an empty band, the electron is accelerated by a constant electric field –F toward +k. Assume
 and
and  .
.- (a)
Find the velocity of the electron.
- (b)
Prove that the position of the electron in real space as a function of time is
![$$ x\left( t \right) = \frac{\Delta E}{2qF}\left[ {1 - \cos \left( {\frac{qFa}{\hbar }} \right)t} \right] $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equg.png)
The electron oscillates in real space, rather than accelerating uniformly as in the free electron model. This periodic motion of an electron in a periodic crystal structure is called the Bloch oscillation.
- (c)
The Bloch oscillation frequency is
 . For F = 108 V/m, calculate the Bloch oscillation frequency in GaAs.
. For F = 108 V/m, calculate the Bloch oscillation frequency in GaAs. - (d)
In semiconductors, due to scattering with defects, the Bloch oscillation of electrons in the Brillouin zone cannot be observed. Assuming the average electron can only travel one tenth of the first Brillouin zone, design a GaAs/AlAs superlattice structure such that the Bloch oscillation can be measured. The lattice constants of GaAs and AlAs are 5.653 Å and 5.660 Å, respectively.
- (a)
![$$ \begin{aligned} u_{k} \left( {z + a} \right) & = \exp \left[ { - ik\left( {z + a} \right)} \right]\psi \left( {z + a} \right) \\ & = \exp \left[ { - ik\left( {z + a} \right)} \right]\lambda \psi \left( z \right) \\ & = \exp \left[ { - ik\left( {z + a} \right)} \right]\exp \left( {ika} \right)\psi \left( z \right) \\ & = \exp \left( { - ikz} \right)\psi \left( z \right) = u_{k} \left( z \right) \\ \end{aligned} $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ56.png)



![$$ \frac{{\hbar^{2} }}{2m}\frac{{\partial^{2} \psi }}{{\partial z^{2} }} + \left[ {E - V\left( z \right)} \right]\psi = 0 $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ86.png)
![$$ - \frac{{\hbar^{2} k^{2} }}{2m}\psi \left( z \right) + \left[ {E - V_{0} - V_{1}^{\prime } \left( z \right)} \right]\psi \left( z \right) = 0 $$](../images/325043_1_En_3_Chapter/325043_1_En_3_Chapter_TeX_Equ87.png)
