The HEMT is a voltage-controlled majority carrier device. It shares the same device geometry as the MESFET except for the details of the active region. The control electrode (gate) is coupled to the active region of the device through a capacitor. The conduction carriers, in the form of the two-dimensional electron gas (2DEG), in the active region are generated by modulation doping at the heterostructure interface.
Comparison of BJT and FET
Carriers | Transport | Output control | Input impedance | |
|---|---|---|---|---|
BJT | Minority | Diffusion | Base current | Low |
FET | Majority | Drift | Gate voltage | High |
In late 1990, the inversion-mode GaAs MOSFET with a low interface trap density was finally achieved using in situ electron beam evaporated Ga2O3(Gd2O3) dielectric film on MBE GaAs. Next, using ex situ atomic layer deposited high-κ Al2O3 and HfO2 films as the gate dielectric, similar devices were demonstrated on GaAs and other III–V materials. Further refinement of oxide deposition methods and development of additional high-κ gate dielectrics were exploited in the following two decades. At the moment, III–V MOSFET manufacturing technologies are still under development.
9.1 Metal–Semiconductor Field-Effect Transistors (MESFETs)
9.1.1 Basic Operation Principles
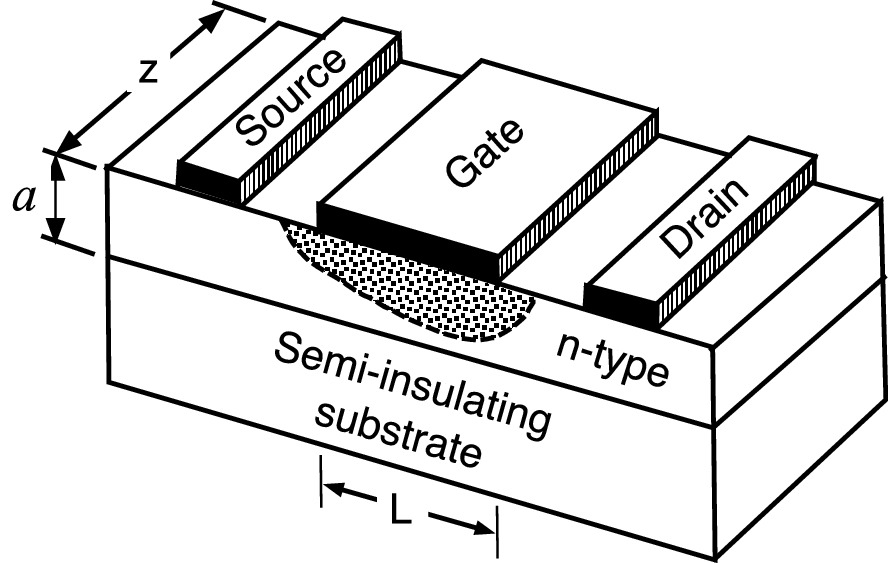
Schematic structure and dimension of a metal–semiconductor FET. The shaded region is the depletion region under the gate electrode
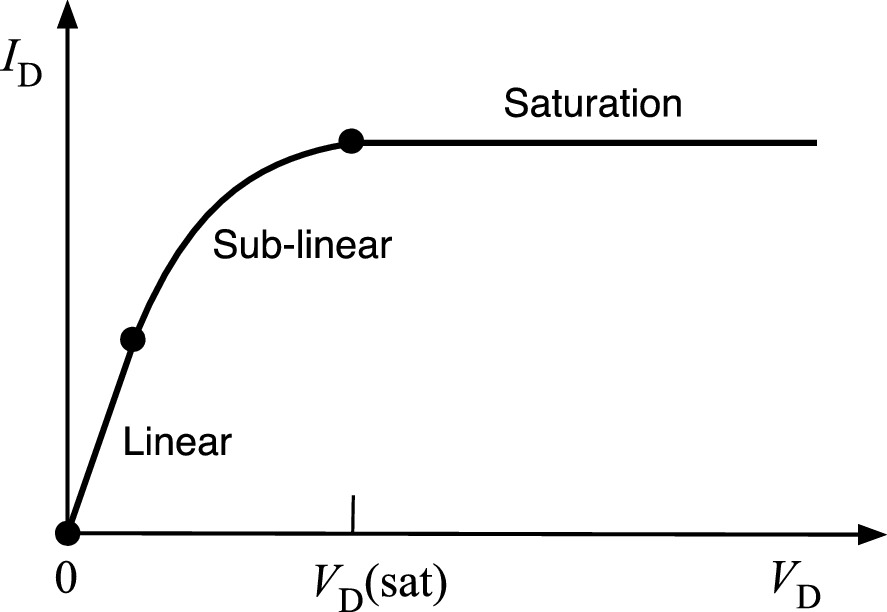
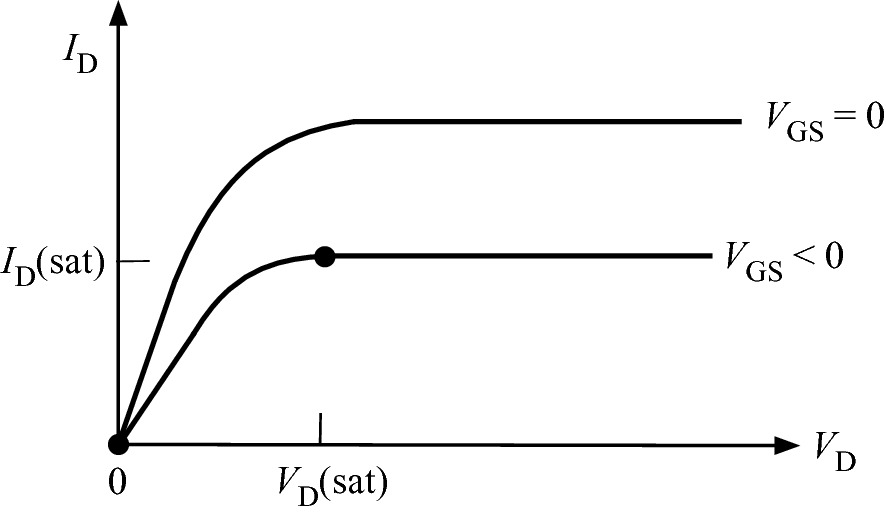
General form of the current–voltage characteristics of a MESFET. The pinch-off point defines the saturation drain voltage, VD(sat)
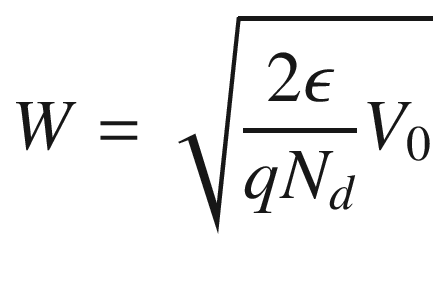
 is the permittivity of the semiconductor.
is the permittivity of the semiconductor.
![$$ W = \sqrt {\frac{2\epsilon }{{qN_{d} }}\left[ {V_{0} + V_{D} \left( {\text{sat}} \right)} \right]} = a $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ3.png)
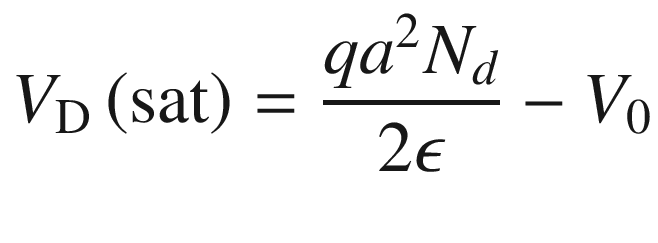
At the saturation voltage and beyond, the drain current becomes saturated, ID(sat) and does not increase with VD.

Modification of current–voltage characteristics for VG < 0

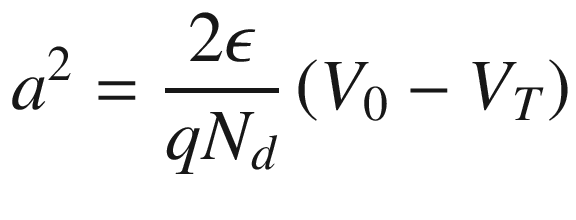


The depletion width in a MESFET with VGS = 0 can be either greater than or less than the channel thickness because of the contact potential. If W < a, a channel exists with zero gate bias. The device is operated in the depletion mode. On the other hand, if W > a, the depletion region extends across the channel in equilibrium, and no significant channel current can flow. A positive gate voltage must be applied to reduce the depletion width to a value smaller than the channel thickness a. The device is operated in the enhancement mode.
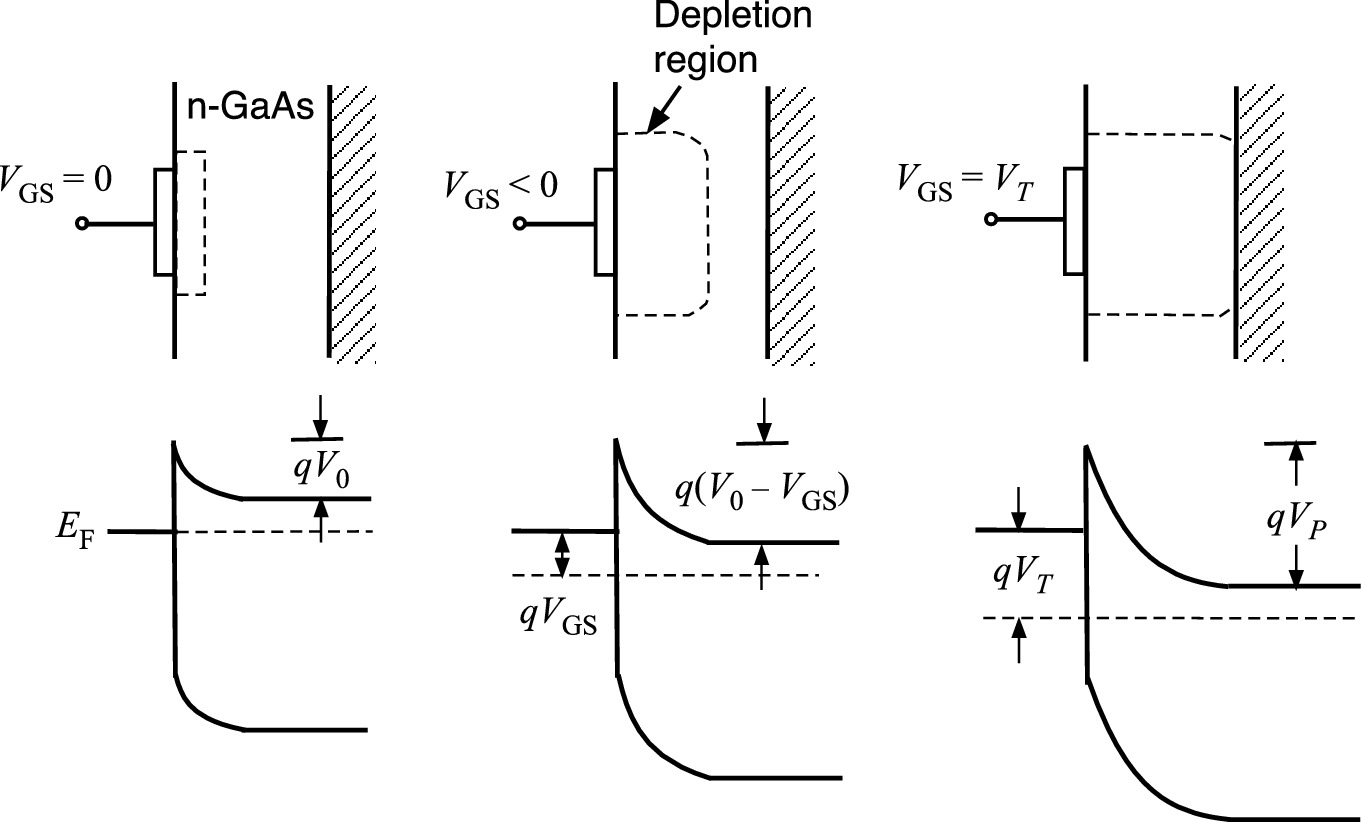
Depletion region profile under the gate and energy band diagrams of depletion-mode MESFET under VD = 0 and various VGS (negative)
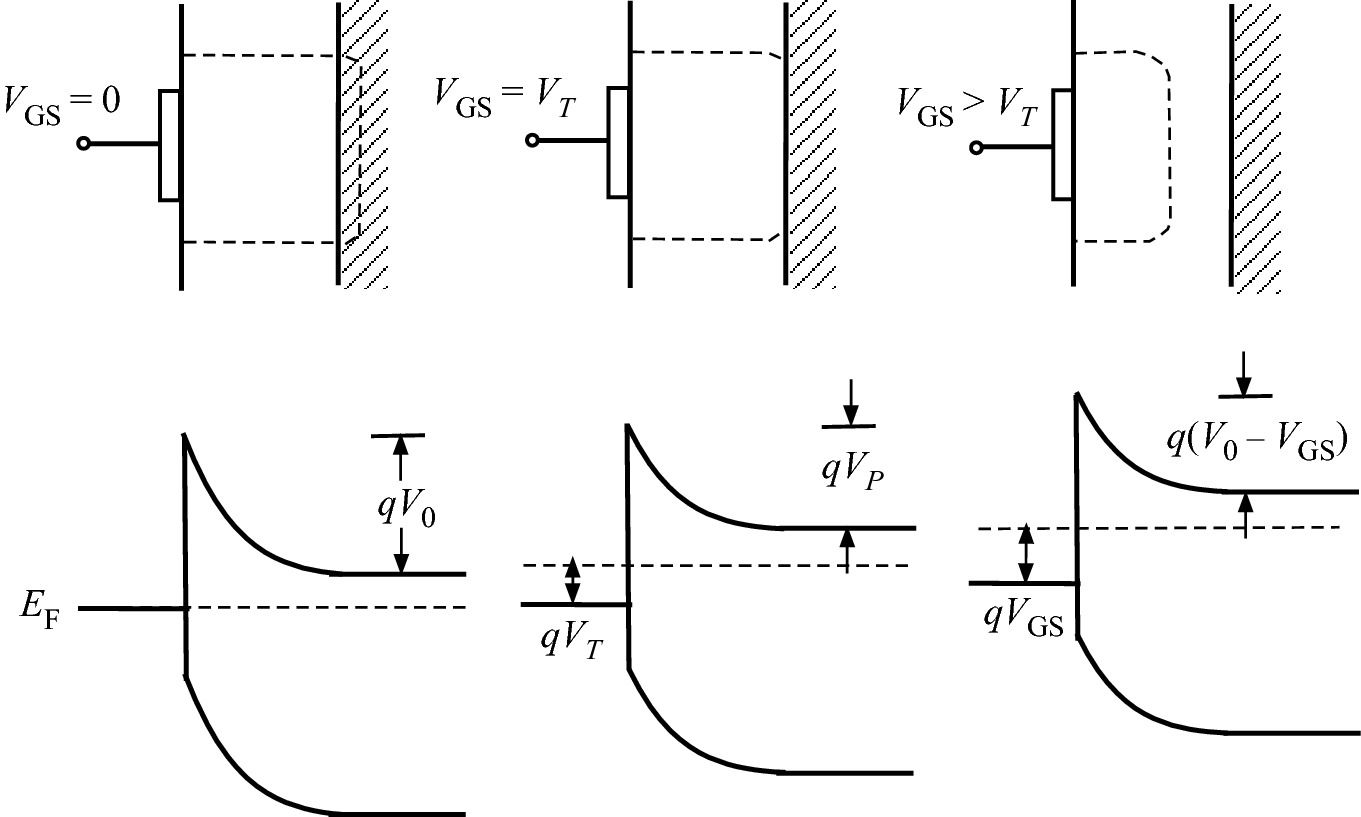
Depletion region profile under the gate and energy band diagrams of enhancement-mode MESFET under VD = 0 and various VGS (positive)
9.1.2 Current–Voltage Characteristics
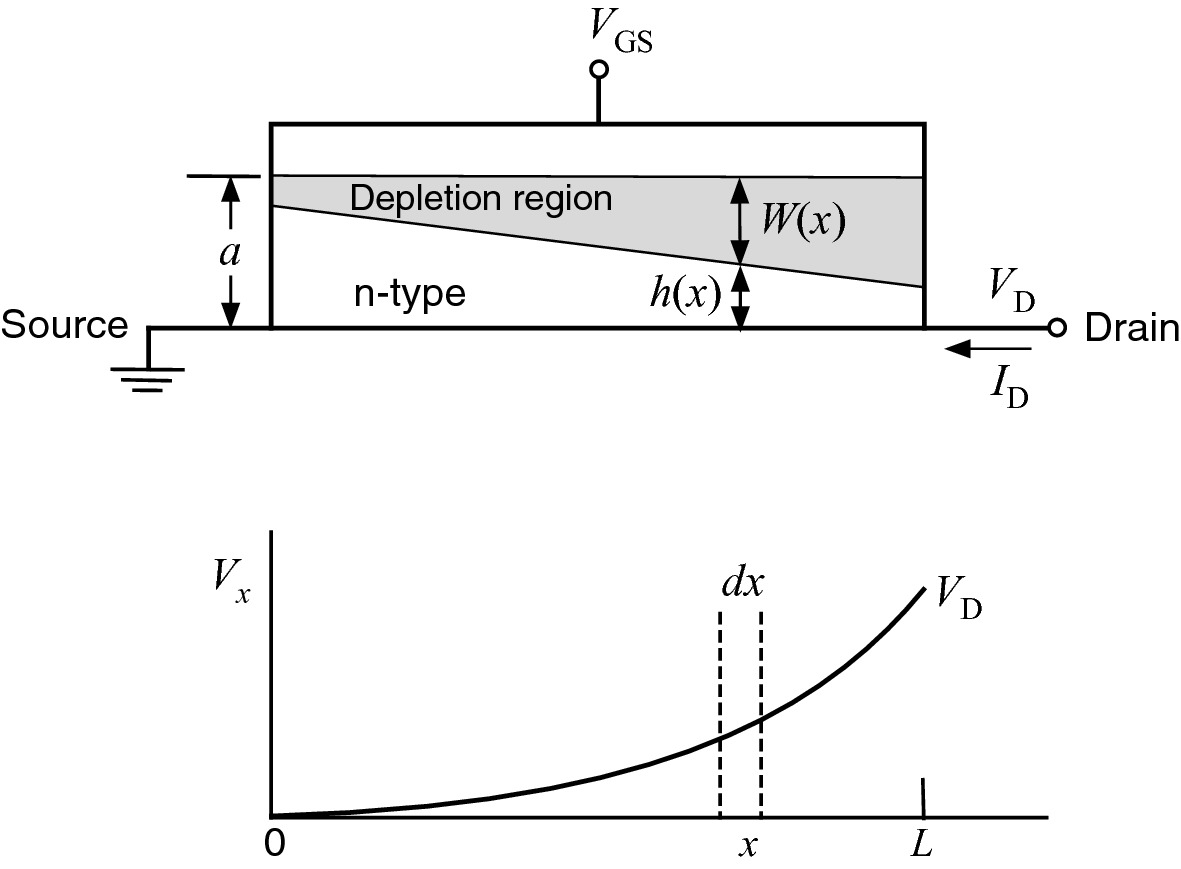
Schematic diagram of the conducting channel, dimensions, and potential drop along the channel
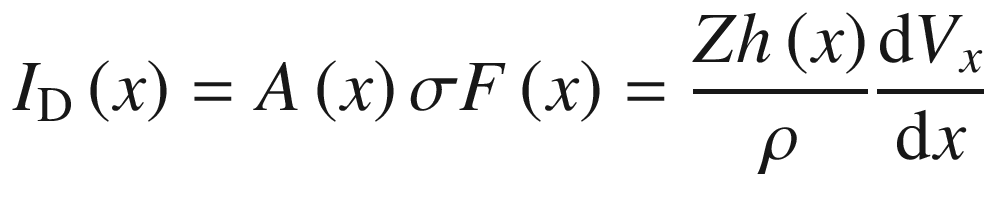
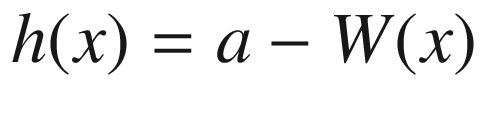 ,
,  and
and  . Since the drain current is a constant and independent of x, we can solve ID by integration.
. Since the drain current is a constant and independent of x, we can solve ID by integration.![$$ \begin{aligned} I_{{\text{D}}} \mathop \int \limits_{0}^{L} {\text{d}}x & = I_{{\text{D}}} L = \frac{{Za}}{\rho }\mathop \int \limits_{0}^{{V_{0} }} \left[ {1 - \sqrt {\frac{{V_{0} + V_{x} - V_{{{\text{GS}}}} }}{{V_{P} }}} } \right]{\text{d}}V_{x} \\ & \quad = \frac{{Za}}{\rho }\left[ {V_{x} - \frac{2}{3}\frac{{\left( {V_{0} + V_{x} - V_{{{\text{GS}}}} } \right)^{{3/2}} }}{{\sqrt {V_{P} } }}} \right]_{0}^{{V_{{\text{D}}} }} \\ \end{aligned} $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equa.png)
![$$ \therefore \quad I_{\text{D}} = G_{0} V_{P} \left[ {\frac{{V_{\text{D}} }}{{V_{P} }} - \frac{2}{3}\left( {\frac{{V_{0} + V_{\text{D}} - V_{\text{GS}} }}{{V_{P} }}} \right)^{3/2} + \frac{2}{3}\left( {\frac{{V_{0} - V_{\text{GS}} }}{{V_{P} }}} \right)^{3/2} } \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ11.png)
![$$ I_{\text{D}} = G_{0} \left\{ {V_{\text{D}} - \frac{2}{{3\sqrt {V_{P} } }}\left( {V_{0} - V_{\text{GS}} } \right)^{3/2} \left[ {\left( {1 + \frac{{V_{\text{D}} }}{{V_{0} - V_{\text{GS}} }}} \right)^{3/2} - 1} \right]} \right\} $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ12.png)
 for x ≪1, we have
for x ≪1, we have![$$ \begin{aligned} I_{{\text{D}}} & \approx G_{0} \left\{ {V_{{\text{D}}} - \frac{2}{{3\sqrt {V_{P} } }}\left( {V_{0} - V_{{{\text{GS}}}} } \right)^{{3/2}} \left[ {\left( {1 + \frac{{3V_{{\text{D}}} /2}}{{V_{0} - V_{{{\text{GS}}}} }}} \right) - 1} \right]} \right\} \\ & \quad = G_{0} V_{{\text{D}}} \left[ {1 - \frac{{\sqrt {V_{0} - V_{{{\text{GS}}}} } }}{\sqrt{{V_{P}} }}} \right] \propto V_{{\text{D}}} \\ \end{aligned} $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ13.png)
The drain current simply increases linearly with drain bias voltage.
 . Using this pinch-off voltage relation in (9.11), the saturation current is obtained as
. Using this pinch-off voltage relation in (9.11), the saturation current is obtained as![$$ I_{\text{D}} \left( {\text{sat}} \right) = G_{0} V_{P} \left[ {\frac{{V_{\text{D}} \left( {\text{sat}} \right)}}{{V_{P} }} - \frac{2}{3} + \frac{2}{3}\left( {\frac{{V_{0} - V_{\text{GS}} }}{{V_{P} }}} \right)^{3/2} } \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ14.png)
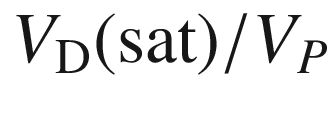 with
with  .
.![$$ I_{\text{D}} \left( {\text{sat}} \right) = G_{0} V_{P} \left[ {\frac{1}{3} - \left( {\frac{{V_{0} - V_{\text{GS}} }}{{V_{P} }}} \right) + \frac{2}{3}\left( {\frac{{V_{0} - V_{\text{GS}} }}{{V_{P} }}} \right)^{3/2} } \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ15.png)
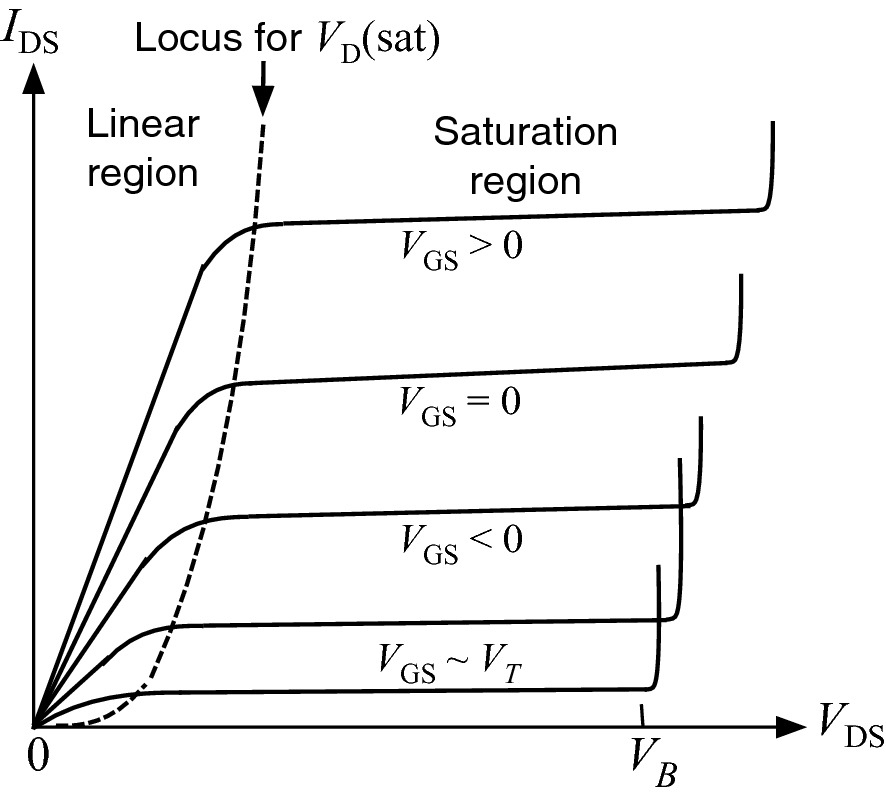
Typical current–voltage characteristics of a depletion-mode MESFET. Breakdowns occur at the breakdown voltages VB
9.1.3 Transconductance and Equivalent Circuit of MESFET


CG is the total gate capacitance and CG = CGS + CDG, where CGS and CDG are the gate-to-source capacitance and drain-to-gate capacitance, respectively. To increase gmi, we have to reduce τ. The minimization of τ can be achieved either by using materials with high drift velocity or by minimizing the channel length through the reduction of gate length. The approach of increasing the total gate capacitance to achieve high gmi is not practical, since it will limit the frequency response of the device.


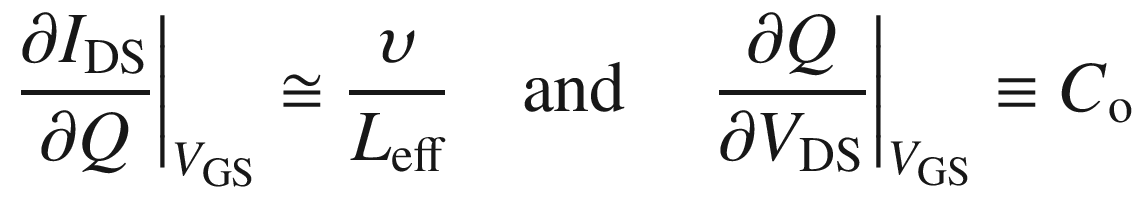

To achieve large Go, high carrier mobility and small gate length are necessary.
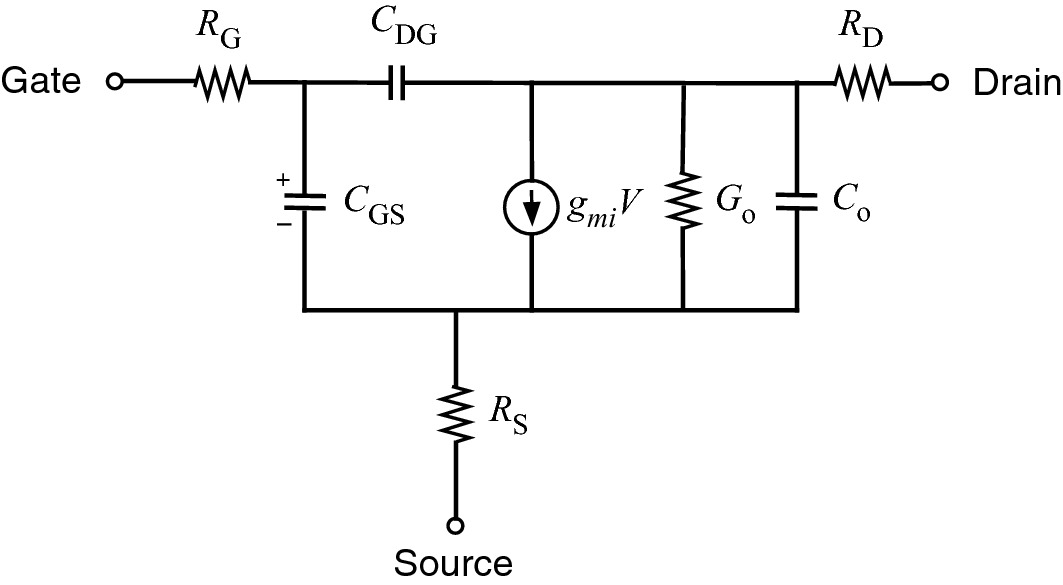
Intrinsic equivalent circuit model of the MESFET including terminal series resistances
9.1.4 High-Speed Figure of Merit
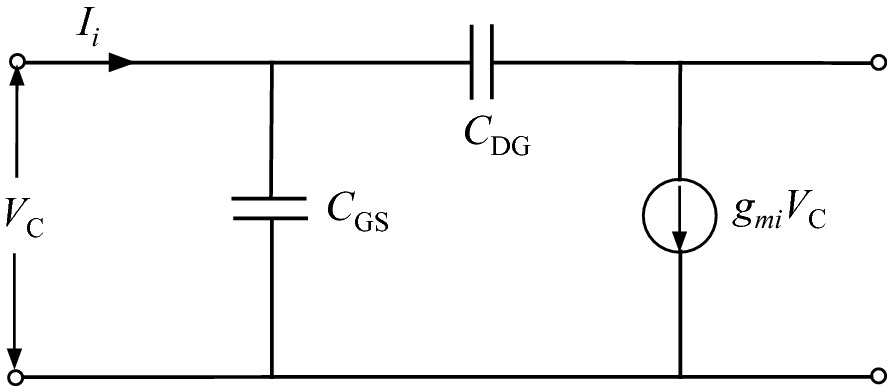
Intrinsic equivalent circuit of a MESFET for frequency response analysis
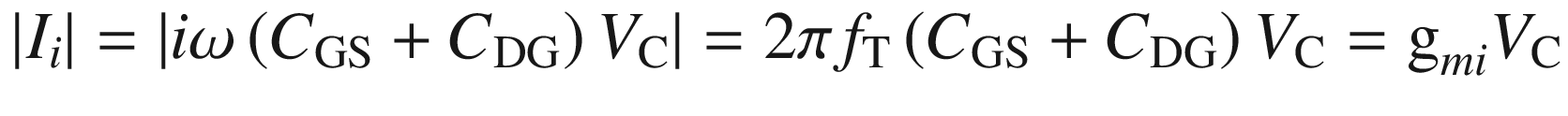

This equation shows that fT is a measure of a quantity that is fundamental to the device—the delay time of the current through the conduction channel.

The fmax of a MESFET may be either above or below its fT, depending on the specific circuit values in the above equation.
9.1.5 MESFET Fabrication and Performance
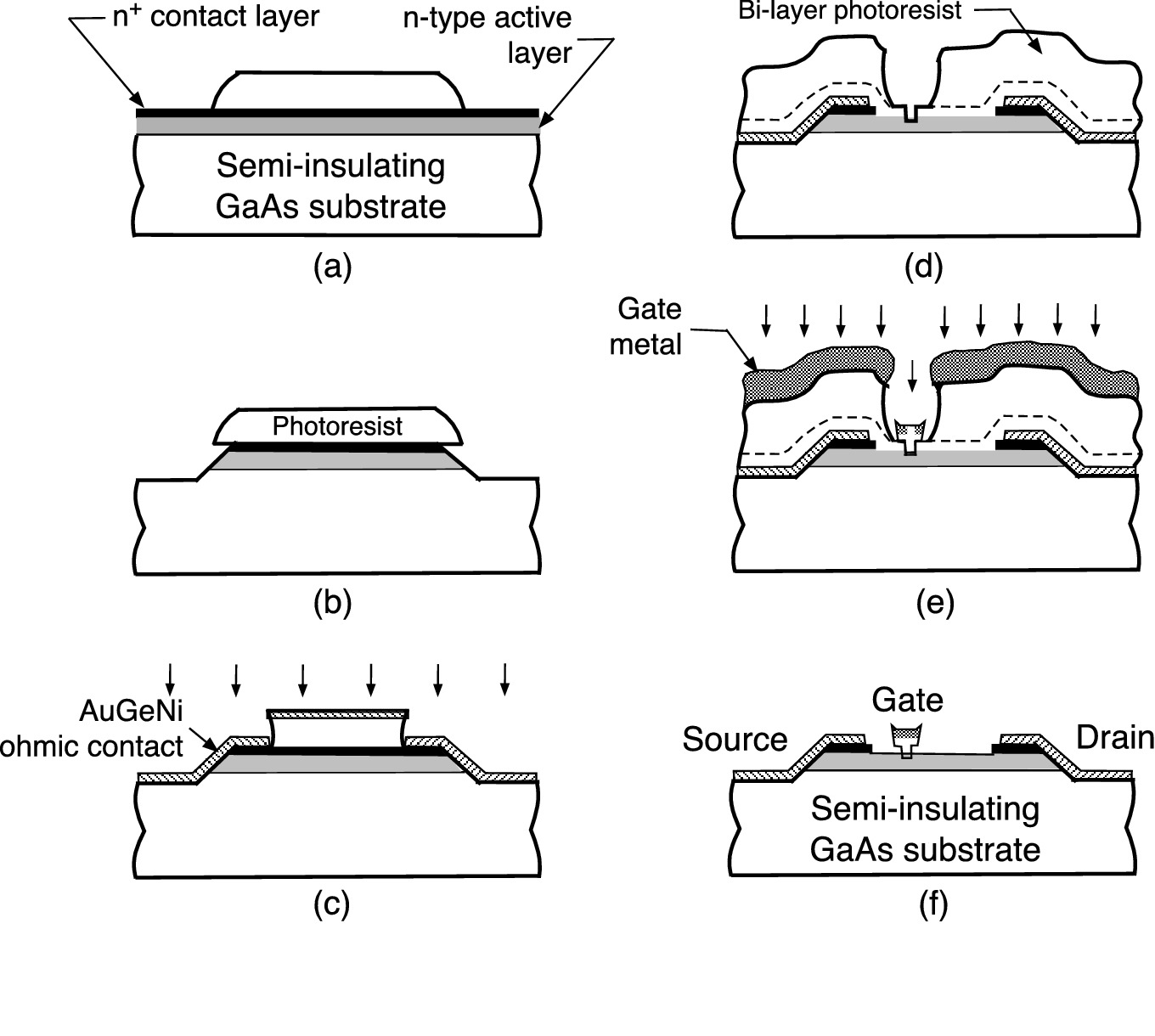
Typical fabrication sequence of submicron GaAs MESFET using the double-recess process. a Epitaxy and using photoresist (PR) to define device active area, b mesa etch for isolation, c source and drain ohmic contacts deposition, d channel recess etch and gate recess etch using bilayer PR process, e T-gate metal deposition, and f PR liftoff to complete MESFET process
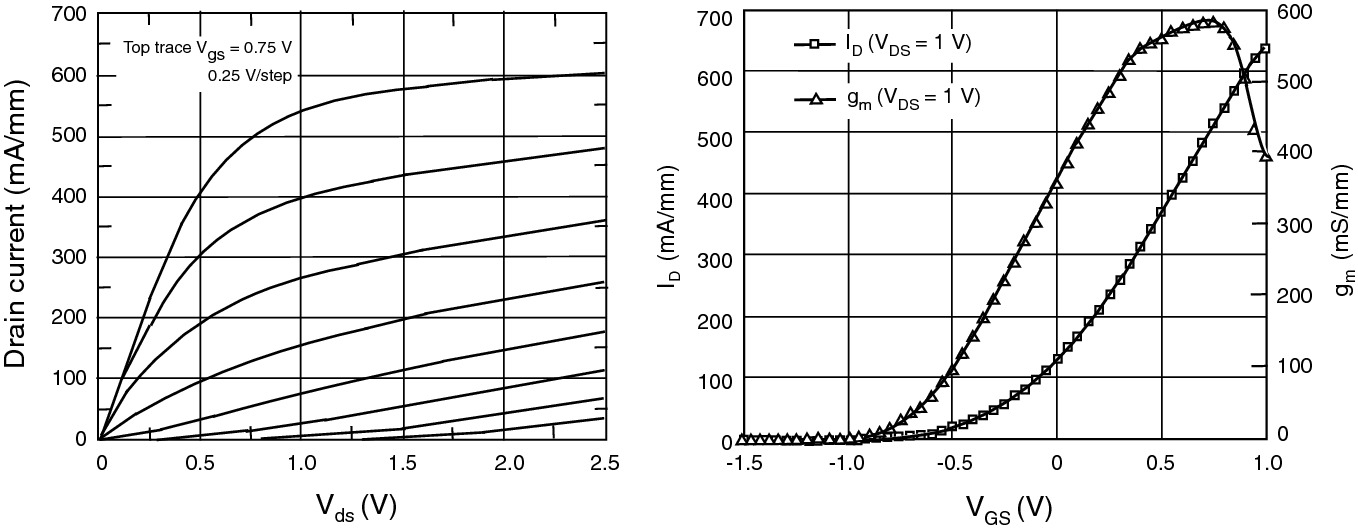
Measured ID-VDS characteristics and channel current and transconductance versus gate bias of a dual-gate (0.12 µm × 50 µm) GaAs MESFET.
Courtesy M. Feng, University of Illinois at Urbana-Champaign

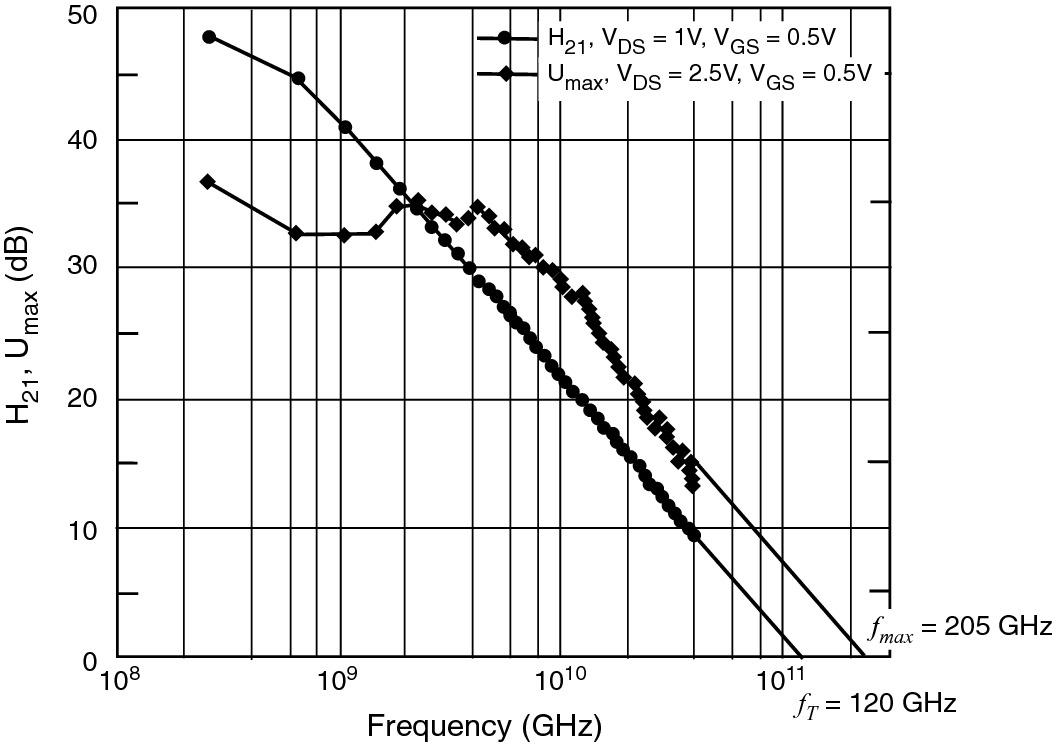
Measured unity current gain frequency fT (H21) and maximum cutoff frequency fmax of the same dual-gate (0.12 µm × 50 µm) GaAs MESFET characterized in Fig. 9.11.
Courtesy M. Feng, University of Illinois at Urbana-Champaign
9.2 Modulation Doping and Two-Dimensional Electron Gas (2DEG)
As shown in Fig. 4.7, the carrier mobility of a semiconductor is determined by the sum of inverse mobility components (µi) due to different scattering mechanisms, i.e., µ−1 = Σ(µi)−1. At a fixed temperature, the lowest mobility component dominates the total carrier mobility. In binary compound semiconductor alloys, the major scattering processes are the optical phonon (polar) scattering at high temperature, the ionized impurity scattering at low temperature, the acoustic phonon scattering due to piezoelectric field, and the acoustic phonon scattering due to deformation potential. With the exception of the impurity scattering, the effect of all scattering mechanisms on electron mobility can be reduced at low temperatures. The total temperature-dependent electron mobility increases with decreasing temperature and reaches a maximum value before decreasing with further reducing temperature. One way to reduce the ionized impurity scattering at low temperature is to use high-purity materials, as evidenced in Fig. 4.7, where there are fewer ionized impurities. However, for most high-speed device applications, certain doping concentrations have to be maintained. Therefore, this option is not practical. In 1978, R. Dingle and colleagues at Bell Laboratories invented a modulation-doping technique to eliminate the influence of ionized impurity scattering in heterojunction superlattices [1]. By separating the physical location of ionized dopants from generated electrons across the heterojunction, with ionized impurities on the large bandgap semiconductor side and generated conduction electrons on the undoped small bandgap semiconductor side, electron mobility much higher than the equivalent bulk material was achieved at low temperature without sacrificing the carrier concentration. Since these conduction electrons occupy a thin layer (≤100 Å) in the triangular quantum well formed at the heterojunction interface, they can only move easily close to and parallel to the heterojunction interface. These electrons form an electron cloud, or a pseudo-two-dimensional electron gas (2DEG), in the modulation-doped heterostructure. Based on this concept, a new type of FET, the high-electron-mobility transistor (HEMT), was derived.
9.2.1 Modulation-Doped (MD) Heterostructures
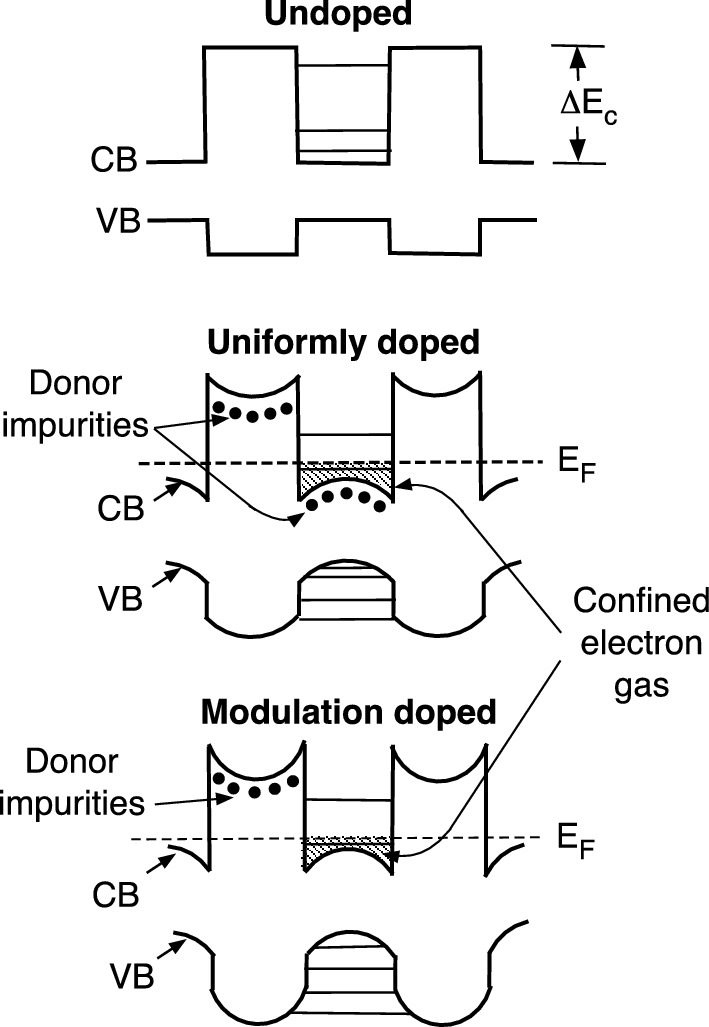
Energy band diagrams for n-doped and undoped GaAs-AlxGa1−xAs superlattices.
Reprinted with permission from [1], copyright AIP Publishing
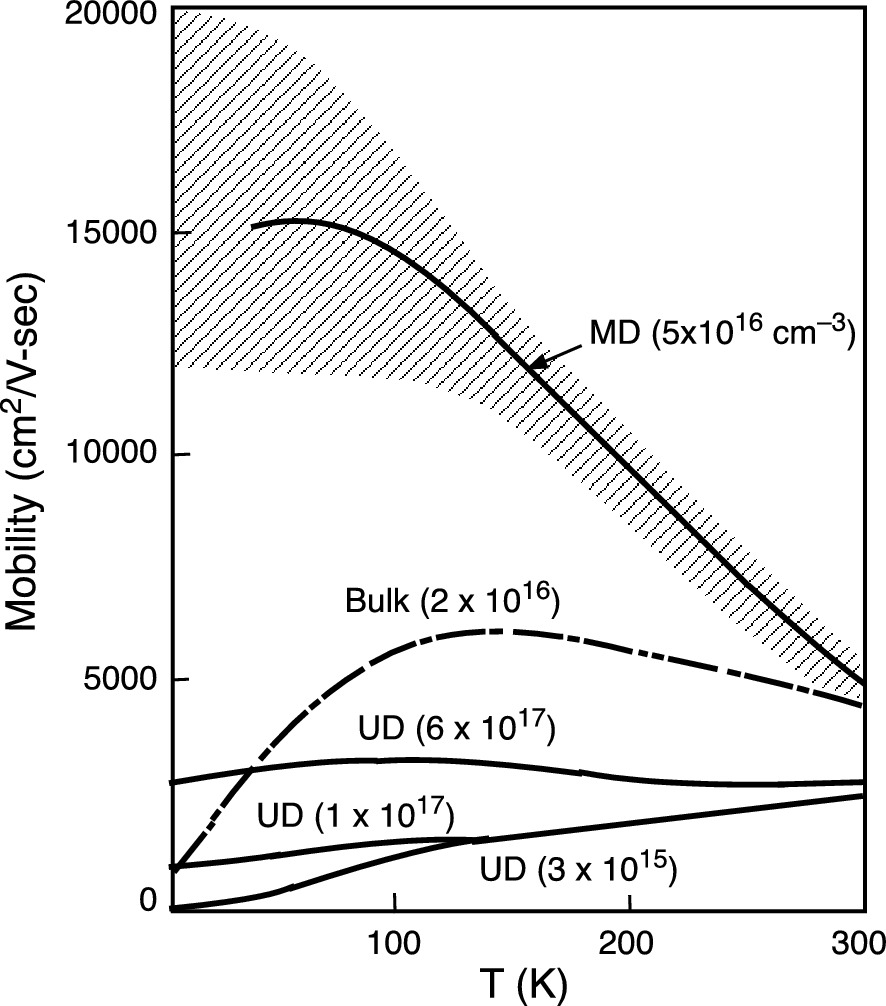
Temperature-dependent electron mobility for bulk GaAs and several undoped UD and MD superlattices. The cross-hatched region includes most of the MD data.
Reprinted with permission from [1], copyright AIP Publishing
9.2.2 Scattering Mechanisms in MD Heterostructures
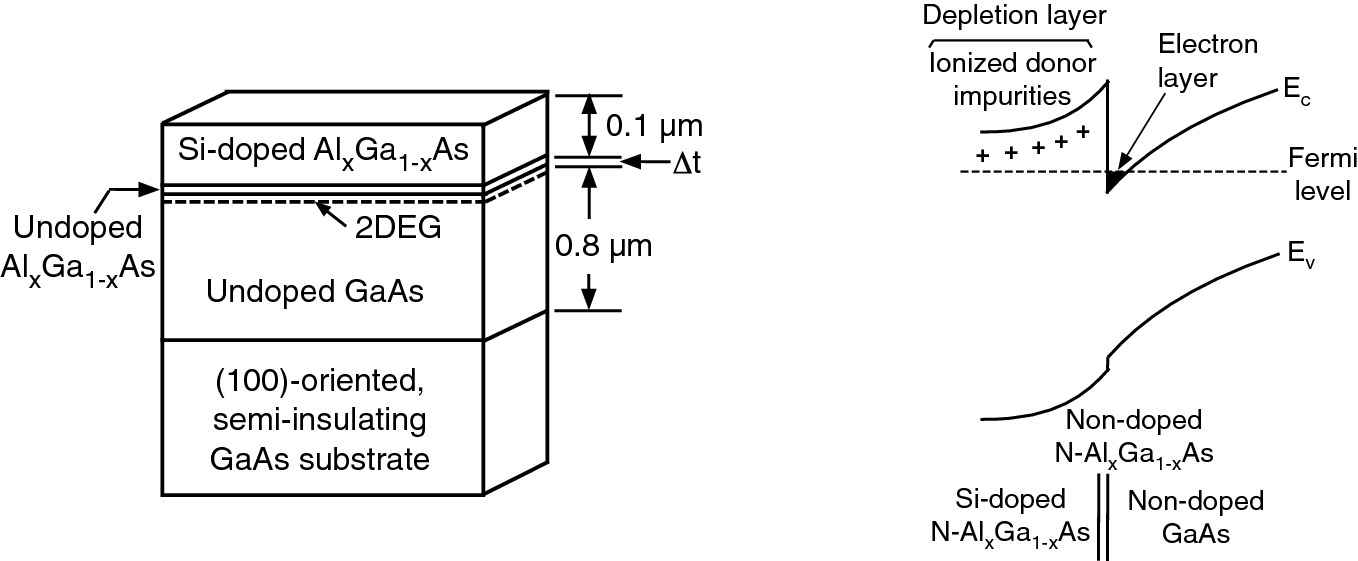
It is important to analyze various scattering mechanisms limiting the mobility in the 2DEG in order to be able to provide interface design rules for yielding high-performance devices. In addition to the bulk scattering mechanisms, some additional scattering mechanisms unique to heterojunctions are introduced here. A GaAs/AlGaAs MD heterostructure similar to the HEMT structure shown in Fig. 9.15 is used to illustrate the properties of added scattering mechanisms. On the semi-insulating GaAs substrate, an undoped GaAs channel layer was first grown, followed by a silicon-doped n-type AlGaAs barrier layer to complete the MD heterostructure. The 2DEG channel will be formed at the GaAs/AlGaAs interface just inside the undoped GaAs layer.
- (a)
Coulomb interaction from ionized impurities located in the barrier
Since the 2DEG is located right next to the hetero-interface, the physical quality of the interface as well as any force exerted that diverts the transport direction toward the interface will affect the nature of carrier scattering. The attraction force due to Coulomb interaction between 2DEG in the conduction channel and its ionized parent donor impurities in the barrier layer will cause electrons to scatter with the hetero-interface. The electron mobility is reduced due to this added scattering mechanism. The carrier mobility is thus a function of the 2DEG sheet charge density. At a low barrier doping density (small 2DEG sheet charge density), the Coulomb interaction is weak and the electron mobility is limited by the background scattering in the undoped GaAs channel. For a heavily doped barrier layer structure, the Coulomb interaction dominates the carrier scattering process.
The Coulomb scattering problem cannot be totally eliminated but can be reduced by setting back the doping region of the barrier layer away from the hetero-interface. This undoped barrier layer inserted between the 2DEG and doped barrier layer is called a spacer layer [4]. Remember, the Coulomb attraction force is inversely proportional to the square of the charge separation distance. For a fixed doping density in the barrier, the Coulomb interaction between the 2DEG and ionized donors weakens with increasing spacer layer thickness, thus increasing electron mobility. However, due to the decreased electron transfer rate from the thicker barrier layer to the conduction channel, for a fixed barrier doping density, the sheet density of the 2DEG will decrease with increasing spacer layer thickness. In practical devices, a compromised spacer layer thickness of 25–30 Å is used to optimize the electron mobility while maintaining a high 2DEG sheet charge density.
- (b)
Interface-roughness-induced scattering
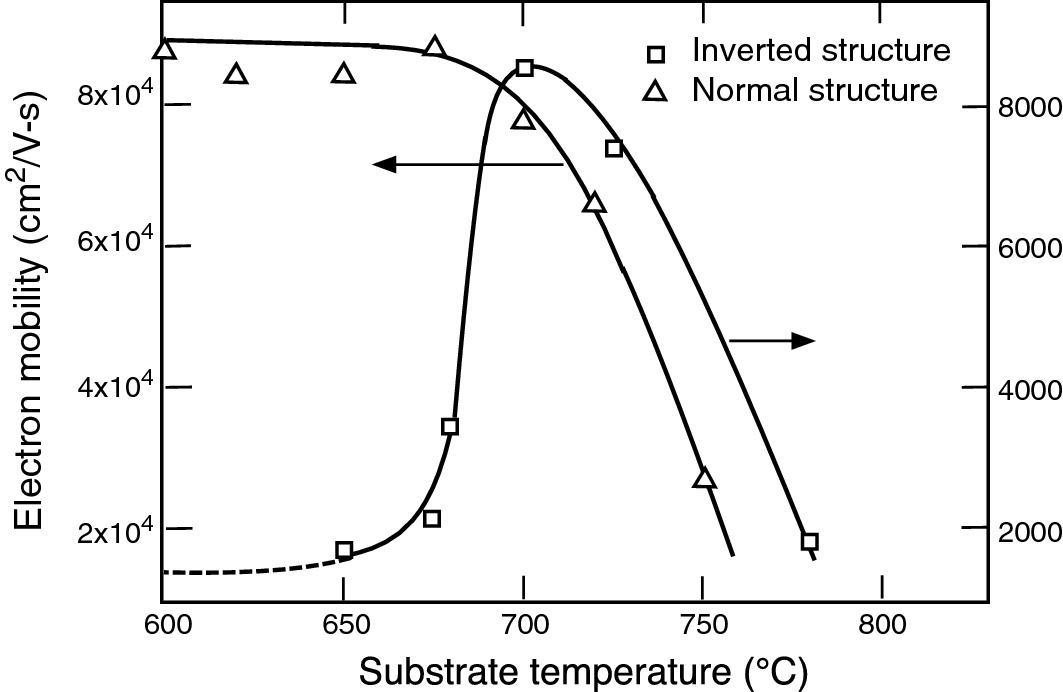
Measured 2DEG mobility of normal and inverted MD GaAs/AlGaAs heterostructures grown at different temperatures.
Reprinted with permission from [4], copyright AIP Publishing
- (c)
Inter-subband scattering at high carrier density
Since the 2DEG is confined in the quasi-triangular QW at the hetero-interface, electrons are occupying the quantized states of the QW. The ground state gets populated first with electrons transferred from the barrier layer. When the ground state is fully populated, any further increase of the transferred electron density will have to occupy the higher energy states. The scattering probability is increased for the multiple-state system, and it reduces the total electron mobility.
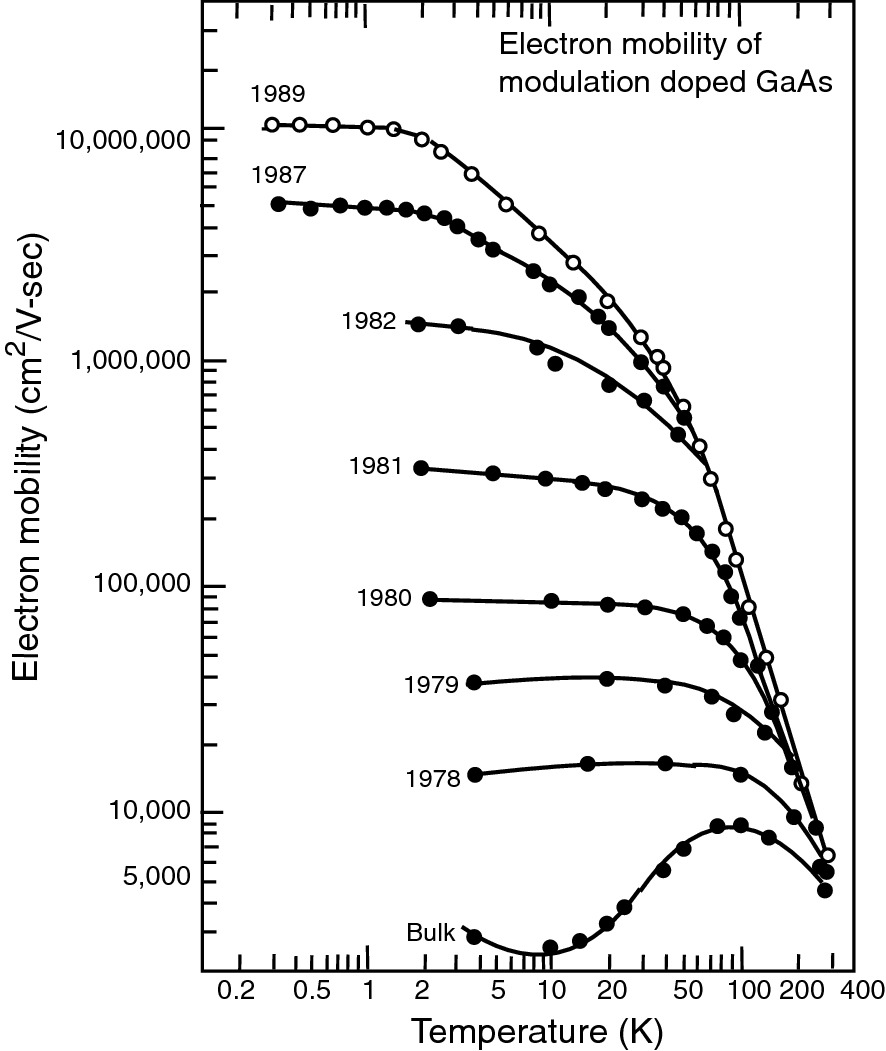
Progress of peak mobility achieved in 2DEG as a function of temperature over a span of 12 years
Reprinted with permission from [5], copyright AIP Publishing
9.3 High-Electron-Mobility Transistor Basics—A Triangular Quantum Well Approach
The FET structure based on a 2DEG in the conduction channel was first demonstrated in 1980 by Fujitsu Laboratory of Japan, less than two years after the inception of the MD concept at Bell Laboratories. Therefore, there were different names used for this newly developed FET. The Fujitsu group called it the HEMT (high-electron-mobility transistor), Bell Laboratories named it SDHT (selectively-doped hetero-field-effect transistor), and the group at Thomson CSF in France called it TEGFET (two-dimensional electron gas field-effect transistor). The name MODFET (modulation-doped field-effect transistor) has also been used. Today, HEMT is the most commonly used name for this kind of FET.

Schematic structure of a GaAs/AlGaAs high-electron-mobility transistor

Heterojunction energy band diagram of the HEMT structure shown in Fig. 9.18. The spacer layer in AlGaAs is removed from the heterojunction interface

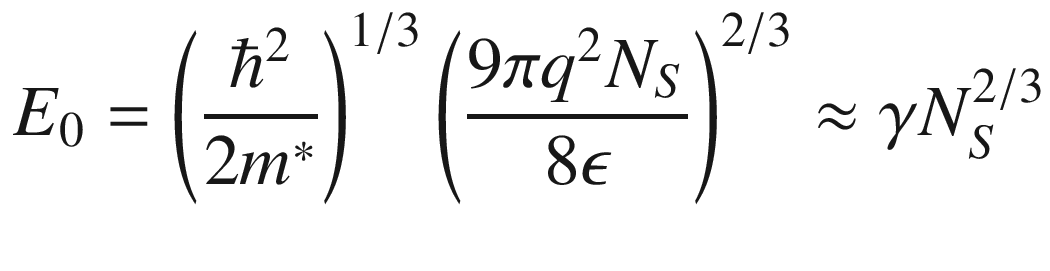

![$$ \begin{aligned} N_{S} & \approx \mathop \int \limits_{{E_{0} }}^{{E_{F} }} D_{{2D}} \left( E \right)\frac{1}{{1 + \exp \left[ {\left( {E_{0} - E_{F} } \right){\it{/kT}}} \right]}}{\text{d}}E \\ & \quad = \frac{{m^{*} }}{{\pi \hbar ^{2} }}{kT}\ln \left\{ {1 + \exp \left[ {\left( {E_{F} - E_{0} } \right){/kT}} \right]} \right\} \\ \end{aligned} $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ29.png)
Heterojunction energy band diagram of the HEMT structure shown in Fig. 9.18. The spacer layer in AlGaAs at the heterojunction interface is included
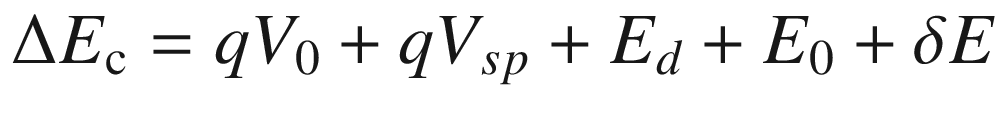

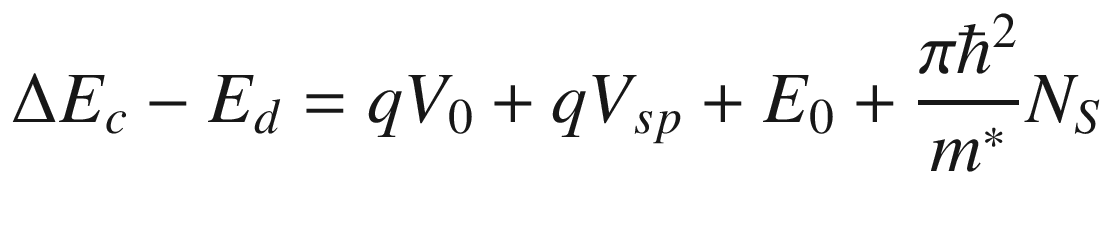

Assuming an Airy function for the ideal triangular QW and using the appropriate material parameters, one can solve NS self-consistently.
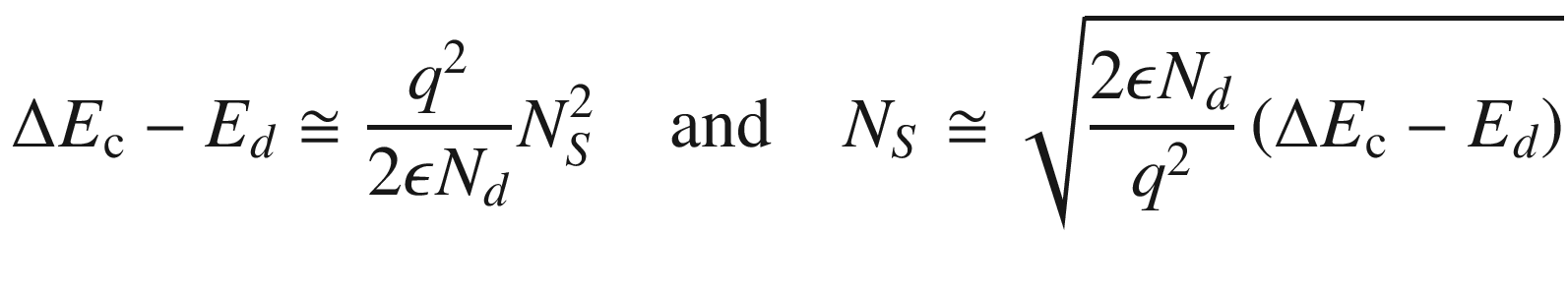
 , the transferred NS is small and we can neglect the term contains
, the transferred NS is small and we can neglect the term contains  .
.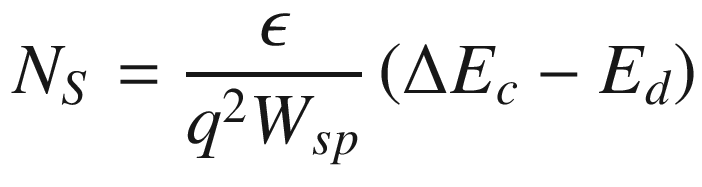
 , the sheet electron concentrations under these two extreme conditions are calculated as
, the sheet electron concentrations under these two extreme conditions are calculated as
These numbers are ~30% overestimated: In the first case, for Wsp = 0, EF ≠ 0 and requires a lot more electrons to fill the subband. In the second case, due to the large extent of the spacer layer, only a portion of the doped barrier is depleted. Even at these overestimated values, they are still much smaller than that of a comparable GaAs MESFET with a 0.2 µm conduction channel doped to 1017 cm−3 (2–3×1012 cm−2). Since a large NS can reduce the channel resistance and increase current drive capability of the FET, a large NS is desirable for device applications. Therefore, it is critical to maximize the carrier density of the HEMT. Empirically, NS is proportional to NdΔEc/Wsp in a HEMT. Based on this relation, we should select material systems with a large ΔEc, a small Wsp, and a maximum Nd.
9.4 Operation Properties of the HEMT
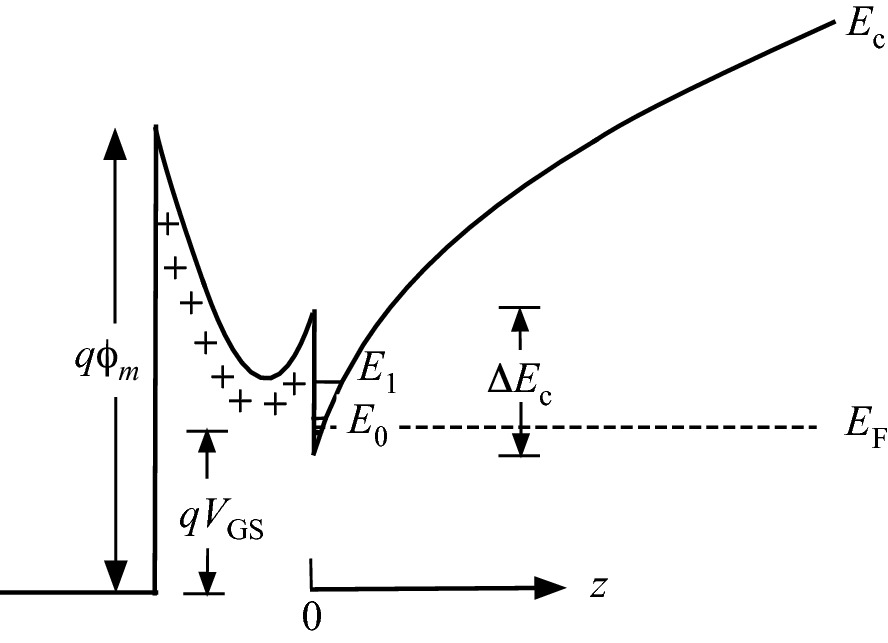
Conduction band diagram of a depletion-mode HEMT under a gate bias of VGS < 0. The work function of the metal contact, qϕm, is also shown
9.4.1 Isolated Heterojunction Under Equilibrium
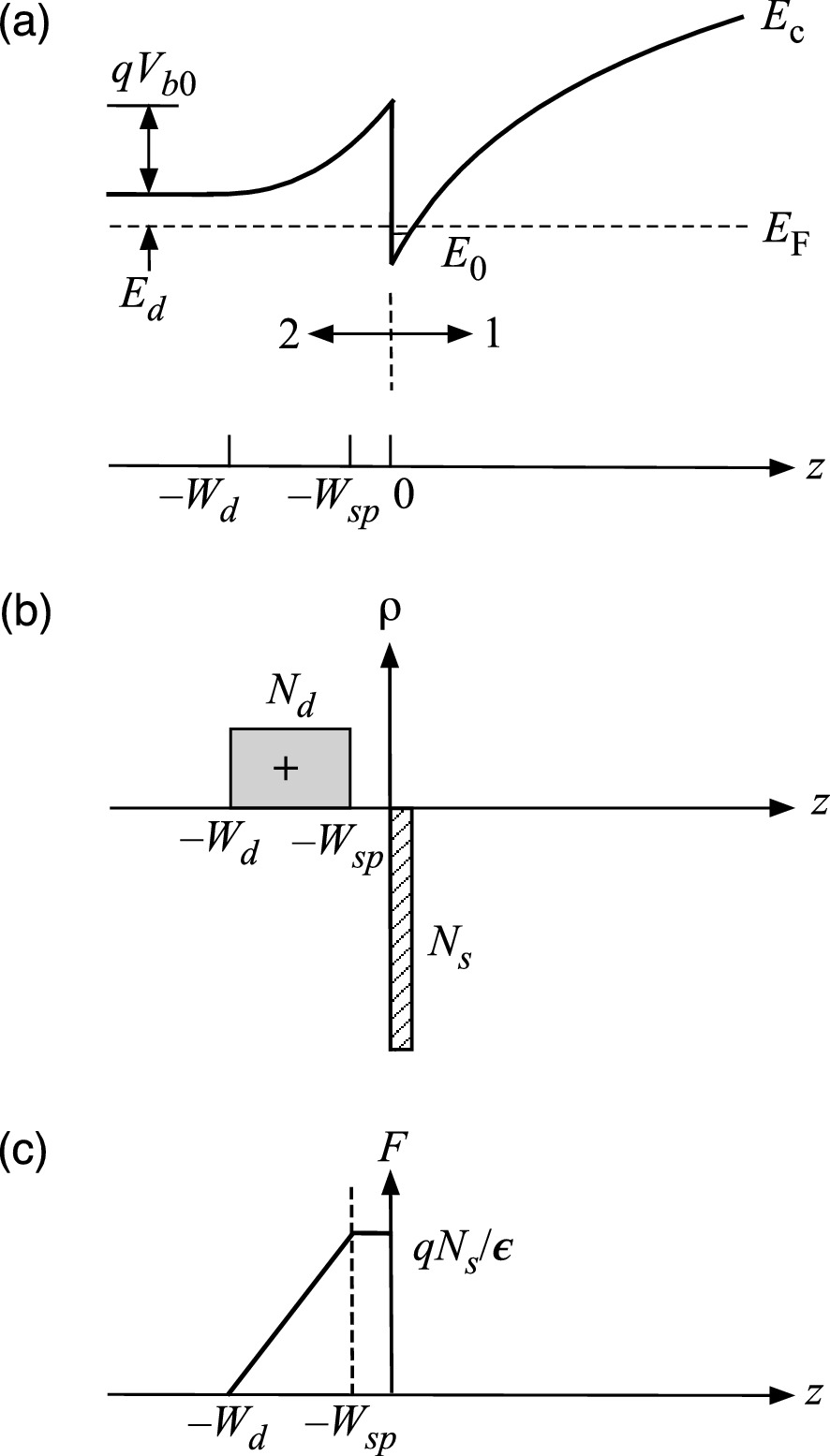
a Energy band diagram in conduction band, b charge distribution, and c electric field distribution at the heterojunction of a HEMT
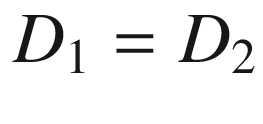


 are the displacement flux density, electric field intensity, and permittivity, respectively. In this section, all discussions concern material 2 only; we will use
are the displacement flux density, electric field intensity, and permittivity, respectively. In this section, all discussions concern material 2 only; we will use  instead of
instead of  for simplicity.
for simplicity.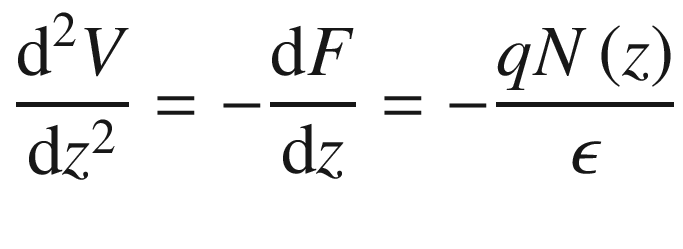

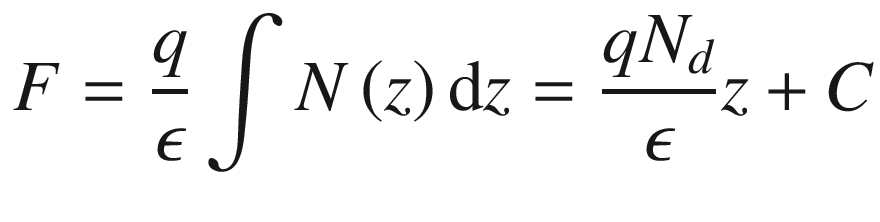


The electric field intensity distribution across the depletion region of the heterojunction is shown in Fig. 9.22c.
 . The potential drop across the doped barrier layer (layer thickness ≫ Wd) can then be calculated as
. The potential drop across the doped barrier layer (layer thickness ≫ Wd) can then be calculated as
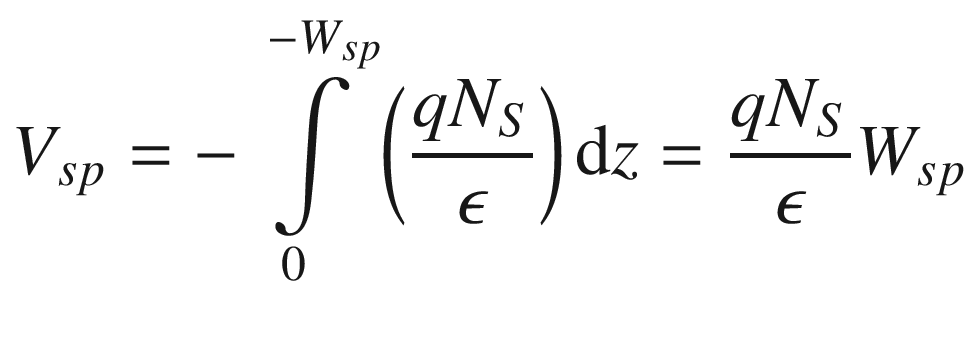

9.4.2 Charge Control by Gate Bias in HEMT
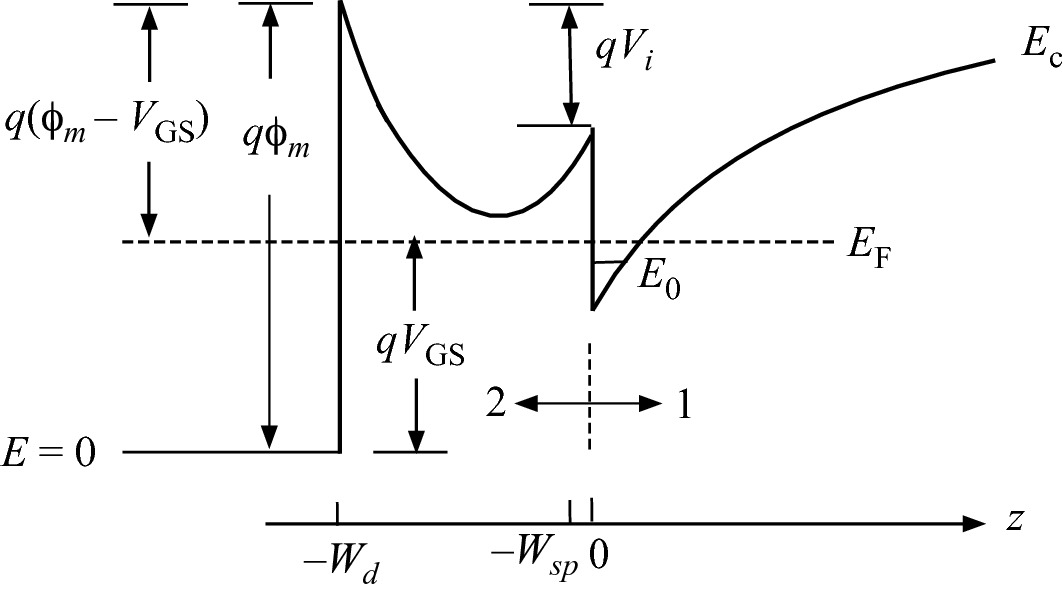
Energy band model of a HEMT under a gate bias VGS < 0. In this model, it is assumed that, under all bias conditions, the barrier layer beneath the gate is completely depleted



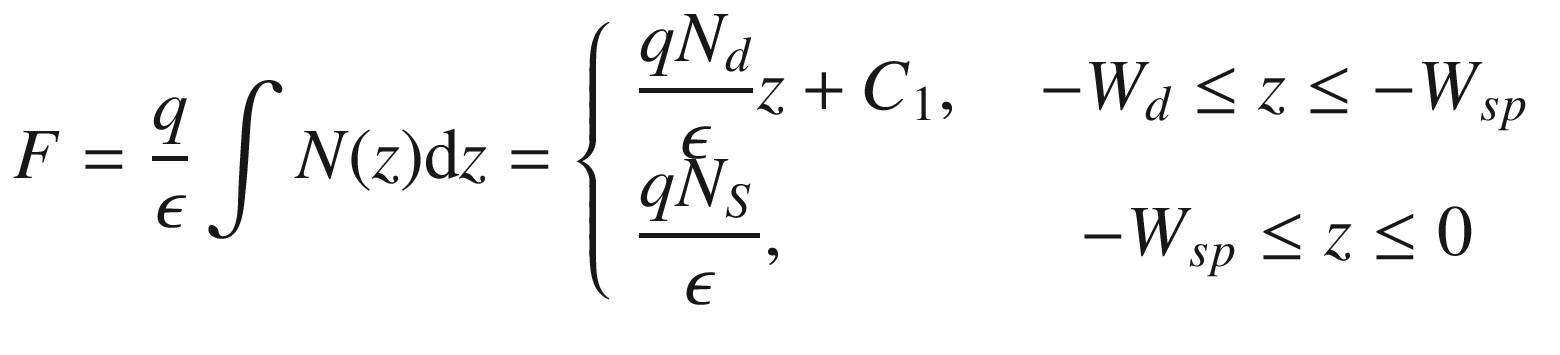
Assuming  .
.



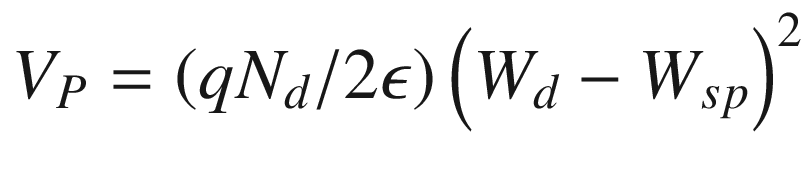 just like a MESFET. Since
just like a MESFET. Since  , we can write the sheet charge density in (9.54) as a function of voltage across the heterostructure.
, we can write the sheet charge density in (9.54) as a function of voltage across the heterostructure.![$$ N_{S} = \frac{\epsilon }{{qW_{d} }}\left[ {V_{\text{GS}} - \left( {\phi_{m} - V_{P} - \frac{{\Delta E_{\text{c}} - E_{\text{F}} }}{q}} \right)} \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ55.png)

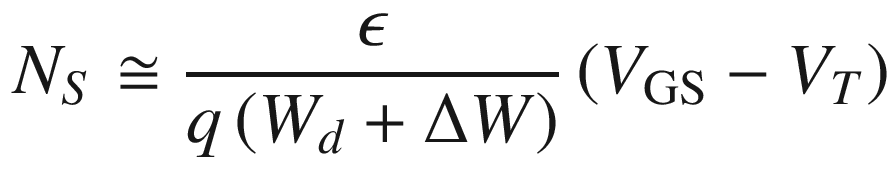
 , as illustrated in Fig. 9.24.
, as illustrated in Fig. 9.24.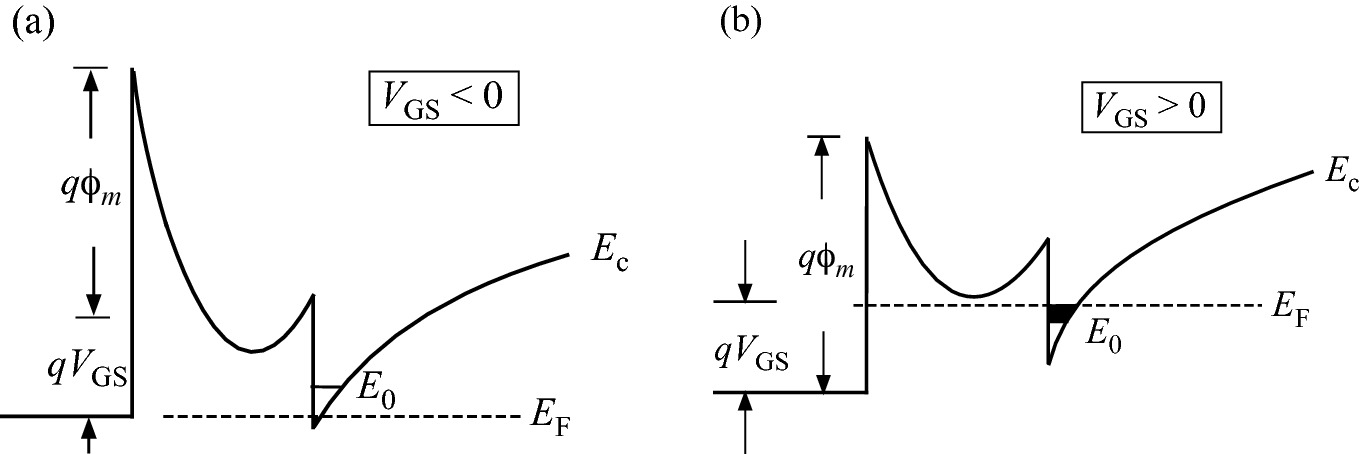
Energy band diagram of a depletion-mode HEMT under different gate biases. a VGS < VT such that the channel is turned off. b Under a high forward gate bias, the 2DEG is saturated
In a HEMT structure with a 2DEG created at zero gate bias, the Fermi level is positioned above the ground state, E0. By applying a reverse gate bias, as shown in Fig. 9.24a, the rise of the total Schottky barrier potential energy at the surface leads to a lowering of EF, which reduces the sheet charge density. When the gate bias is equivalent to the threshold voltage, VT, the conduction channel is turned off. On the other hand, as shown in Fig. 9.24b, under forward gate bias condition, the rising Fermi level allows more electrons to be transferred into the triangular QW, contributing to the current conduction. This process will continue until all donors in the barrier are ionized. The 2DEG sheet carrier density becomes saturated with further increasing of VGS.
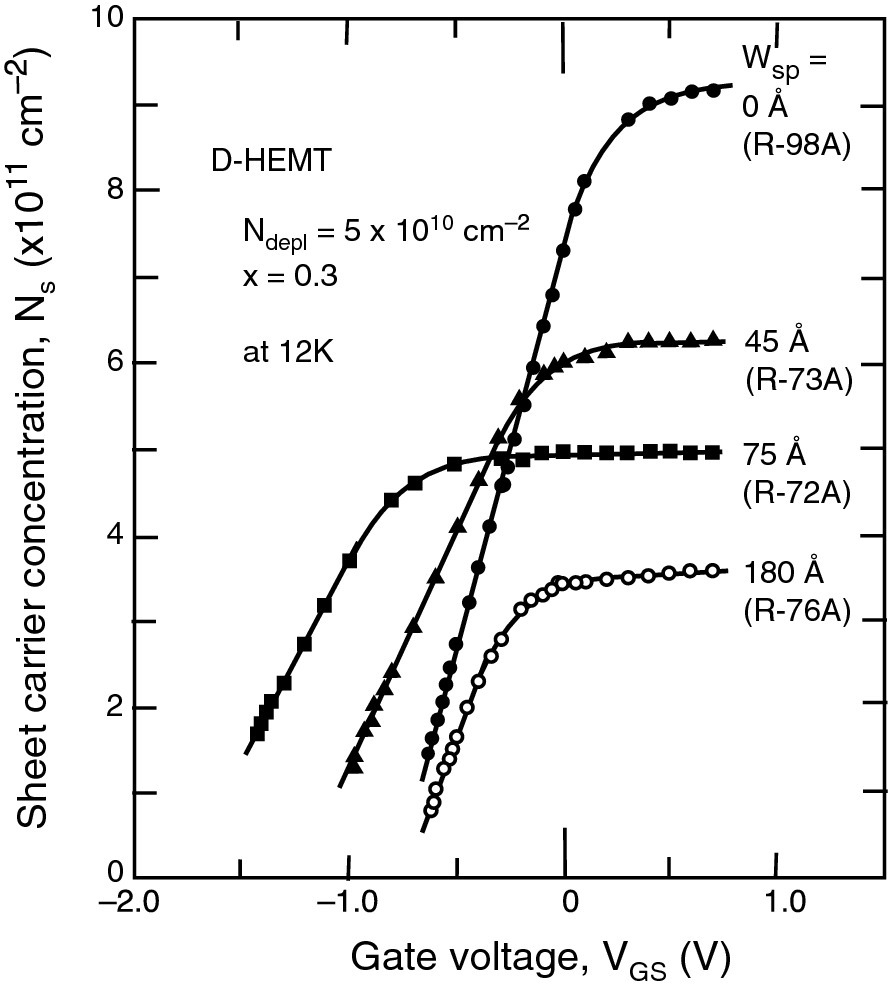
Measured gate-voltage dependence of the sheet carrier density of 2DEG in the GaAs/AlGaAs system. Wsp represents the spacer layer thickness in each sample. All samples have Nd = 4.6 × 1017 cm−3 except sample No. 76, which has Nd = 9.2 × 1017 cm−3.
Reprinted with permission from [6], copyright AIP Publishing
 , which mainly depends on Wd. Therefore, one can design the operation mode of the device by selecting the proper barrier thickness as shown in Fig. 9.26. For example, a thick barrier (large Wd) leads to a larger VP and a more negative VT. A conduction channel is formed in such a HEMT structure even at zero gate bias (Fig. 9.26a). One has to apply a gate bias equal to VT to completely deplete the 2DEG, thus forming a depletion-mode (normally-on) HEMT. When the barrier layer is reduced to a point such that the Fermi level is well below the ground state (E0) of the triangular QW at zero bias, VT becomes positive. A positive gate bias is required to induce the 2DEG for current conduction, and the HEMT is an enhancement-mode (normally-off) FET (Fig. 9.26b).
, which mainly depends on Wd. Therefore, one can design the operation mode of the device by selecting the proper barrier thickness as shown in Fig. 9.26. For example, a thick barrier (large Wd) leads to a larger VP and a more negative VT. A conduction channel is formed in such a HEMT structure even at zero gate bias (Fig. 9.26a). One has to apply a gate bias equal to VT to completely deplete the 2DEG, thus forming a depletion-mode (normally-on) HEMT. When the barrier layer is reduced to a point such that the Fermi level is well below the ground state (E0) of the triangular QW at zero bias, VT becomes positive. A positive gate bias is required to induce the 2DEG for current conduction, and the HEMT is an enhancement-mode (normally-off) FET (Fig. 9.26b).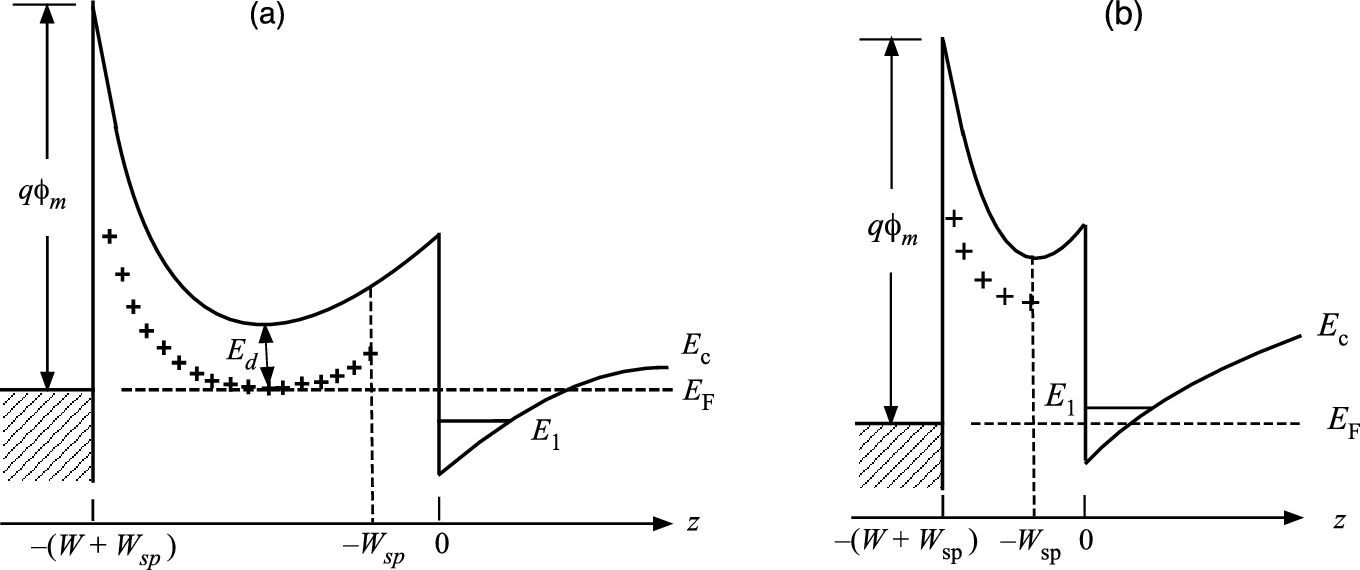
Schematic band diagram at VGS = 0 for a normally-on and b normally-off HEMTs
9.4.3 Current and Voltage Characteristics of HEMT

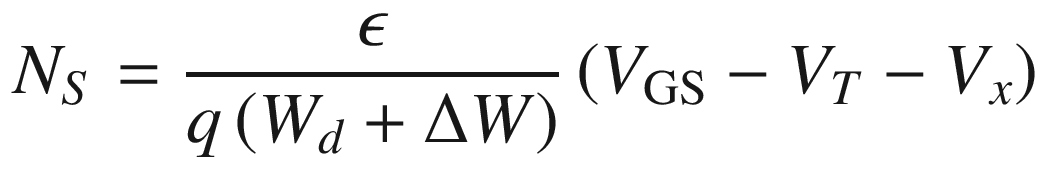

 :
:

![$$ I_{\text{DS}} = \frac{\mu \epsilon Z}{{L\left( {W_{d} +\Delta W} \right)}}\left[ {\left( {V_{\text{GS}} - V_{T} } \right)V_{\text{DS}} - \frac{{V_{\text{DS}}^{2} }}{2}} \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ63.png)
At very low drain bias, the  /2 term is very small and can be neglected. The drain current is linearly proportional to the drain bias. At a sufficiently high drain bias, the
/2 term is very small and can be neglected. The drain current is linearly proportional to the drain bias. At a sufficiently high drain bias, the  /2 term becomes significant and leads to a sublinear IDS-VGS characteristic. Further increasing the drain bias, the drain current becomes saturated.
/2 term becomes significant and leads to a sublinear IDS-VGS characteristic. Further increasing the drain bias, the drain current becomes saturated.
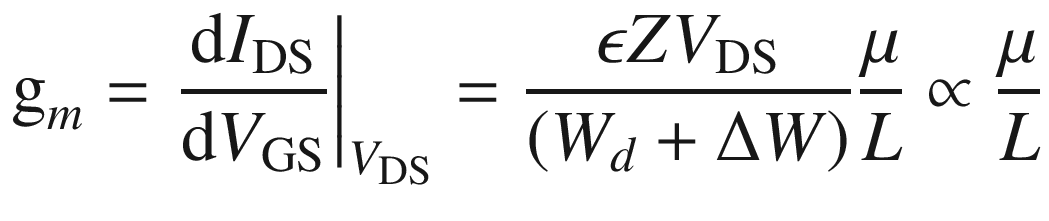
It is clear that large low-field electron mobility and a short channel length are required for a HEMT to achieve a high gm at a fixed VDS. Within the linear region, gm increases with increasing VDS.
![$$ \frac{{{\text{d}}I_{\text{DS}} ({\text{sat}})}}{{{\text{d}}V_{\text{DS}} }} = \frac{\mu \epsilon Z}{{L\left( {W_{d} + W} \right)}}\left[ {\left( {V_{\text{GS}} - V_{T} } \right) - V_{\text{DS}} } \right] = 0 $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ65.png)

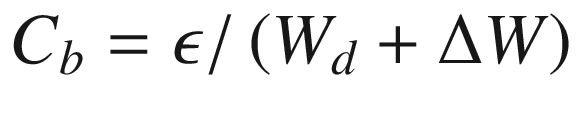 is the capacitance per unit area in the barrier. The transconductance in the saturation region can also be derived as
is the capacitance per unit area in the barrier. The transconductance in the saturation region can also be derived as
Again, large low-field electron mobility and a short channel length are required to achieve a high gm in the saturation region.
9.4.4 Microwave Noise Performance

9.5 Optimal Design of the HEMT
Based on discussions above, to achieve high performance, the optimized HEMT structure should incorporate a large ΔEc (≥0.5 eV) for high sheet carrier density NS and high current carrying capability; furthermore, materials with high electron mobility should be selected for efficient high-speed operation, and small gate length (Lg < 0.1 µm) should be used to increase the cutoff frequency. In addition, to enhance electron transfer from the barrier into the triangular QW, a small spacer layer thickness (Wsp ~ 25 Å) is preferred. However, in practice, it was not straightforward to realize all these requirements in the early development of HEMTs. Specifically, the DX center problem severely limited the use of AlxGa1−xAs with high aluminum content (x ≤ 25%) in the HEMT design. In addition, when increasing the barrier doping level to achieve higher 2DEG density, parallel conduction from free electrons trapped in the barrier and 2DEG could form. To overcome these problems, a pseudomorphic layer and delta-doping designs are incorporated to increase ΔEc and 2DEG density.
9.5.1 DX Center in Si-Doped AlGaAs/GaAs HEMT and Delta Doping
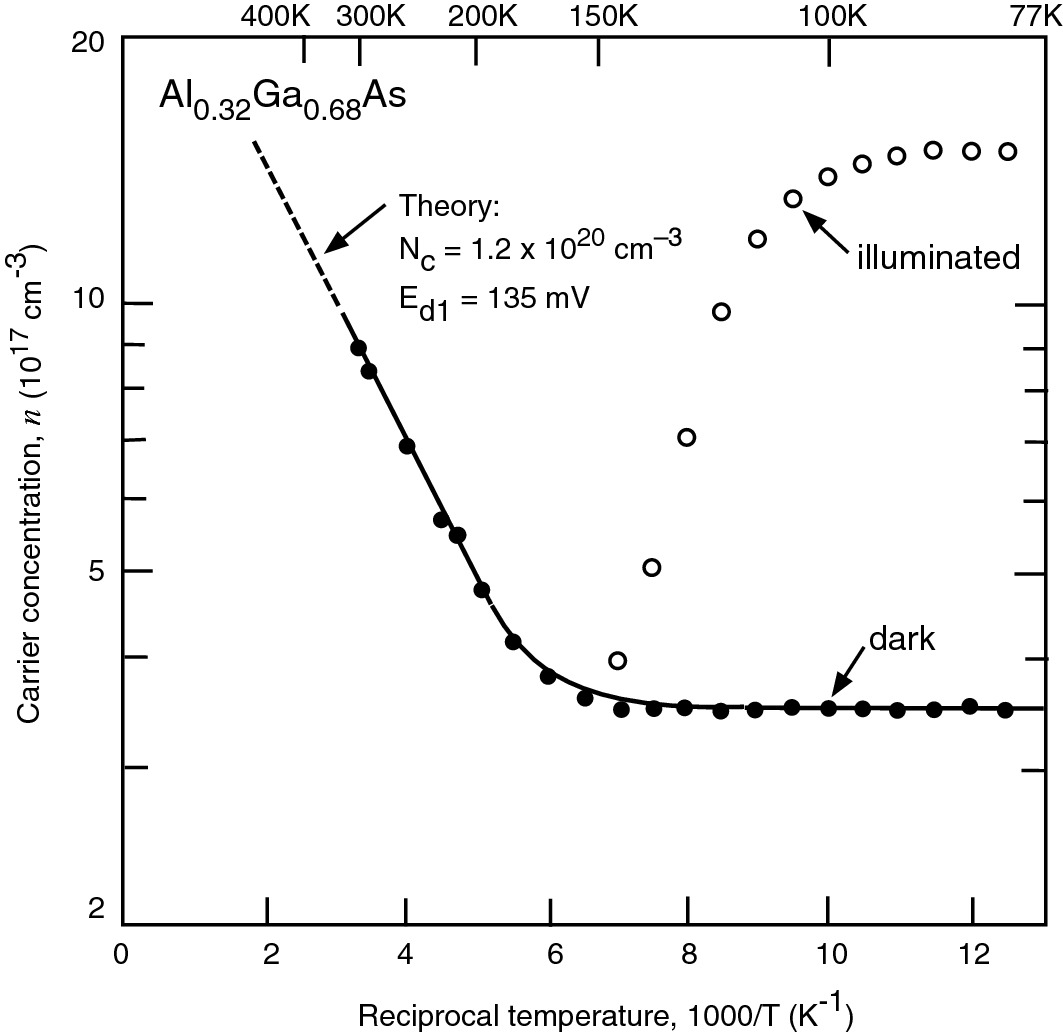
Dependence of the Hall electron concentration in n-type Al0.32Ga0.68As:Si on reciprocal temperature. Solid and open circles indicate experimental data measured in the dark and after illumination at low temperatures, respectively.
Reprinted with permission from [7], copyright AIP Publishing
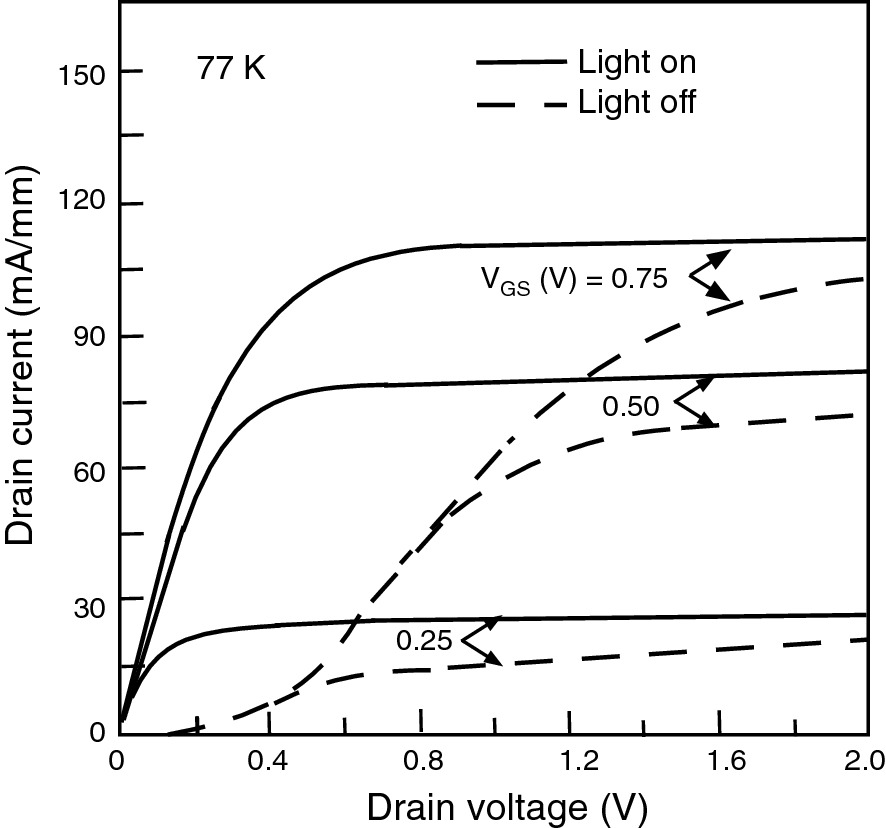
I–V characteristics of a HEMT at 77 K under illumination and in darkness. The degradation of the characteristics upon the elimination of light occurred gradually over a period of 20–30 s.
Reprinted with permission from [8], copyright IEEE
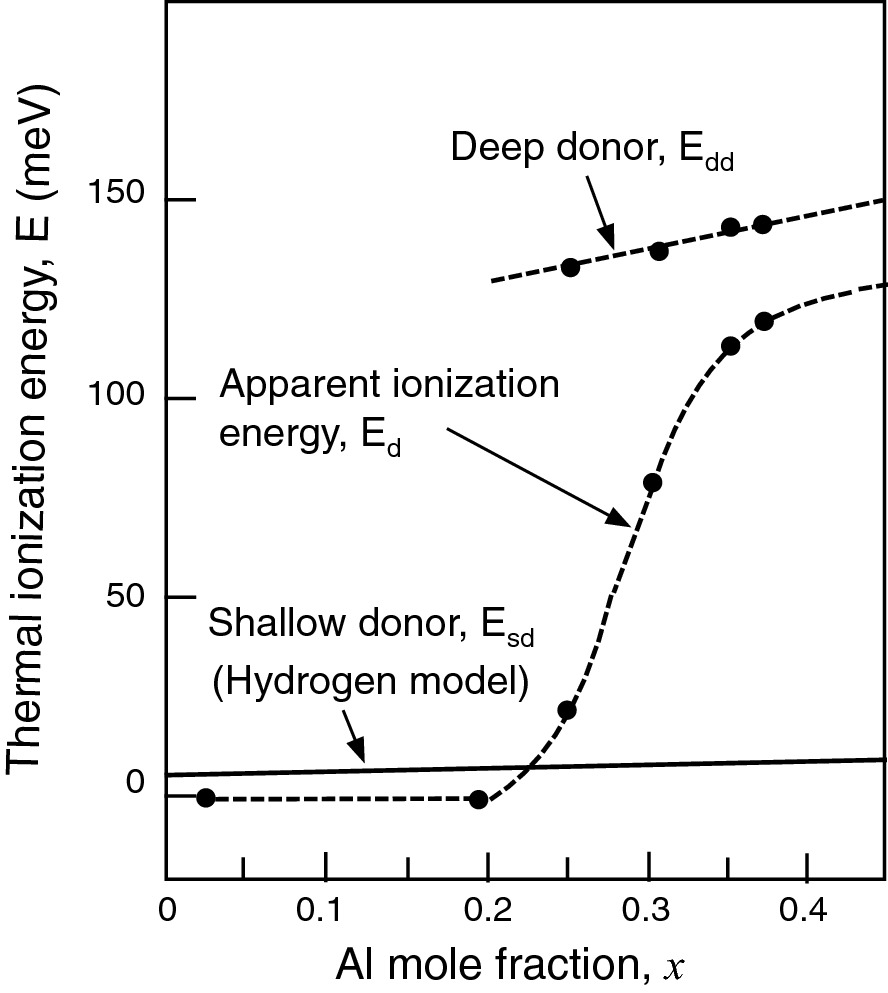
Thermal ionization energy of the Si donor as a function of the Al mole fraction in AlxGa1−xAs.
Reprinted with permission from [7], copyright AIP Publishing
For example, in an AlxGa1−xAs/GaAs HEMT with a composition of x = 30%, the donor level, Ed, is 0.12 eV below the conduction band. Since Ed is very deep, under dark, a portion of the donor level inside the barrier is below the Fermi level and stays neutral (unionized). Only a thin-doped barrier layer adjacent to the spacer layer is contributing electrons to the 2DEG channel and the sheet charge density is very low. The neutral layer in the barrier also decouples the 2DEG and the surface. Therefore, NS in 2DEG is independent of bias! When illuminated with a light source having energy less than the bandgap, electrons are excited out of DX centers. All the donors are ionized and the 2DEG has risen. Due to the finite electron trapping barrier height, there are free electrons remaining in the barrier at low temperatures and these form ‘parallel conduction’ channel in addition to the 2DEG conduction.
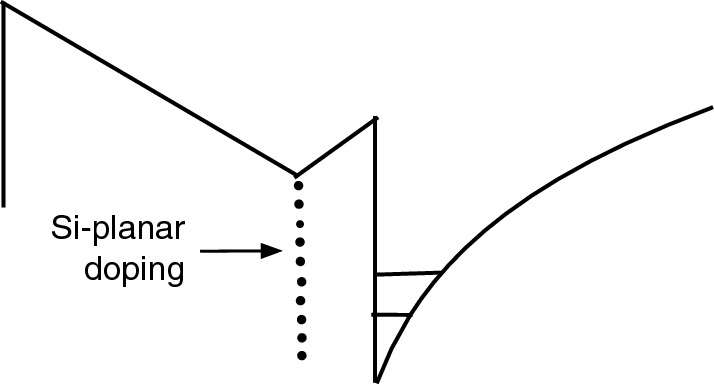
Schematic energy band diagram of Si-planar doping in a MD structure
9.5.2 Pseudomorphic High-Electron-Mobility Transistors (pHEMT)
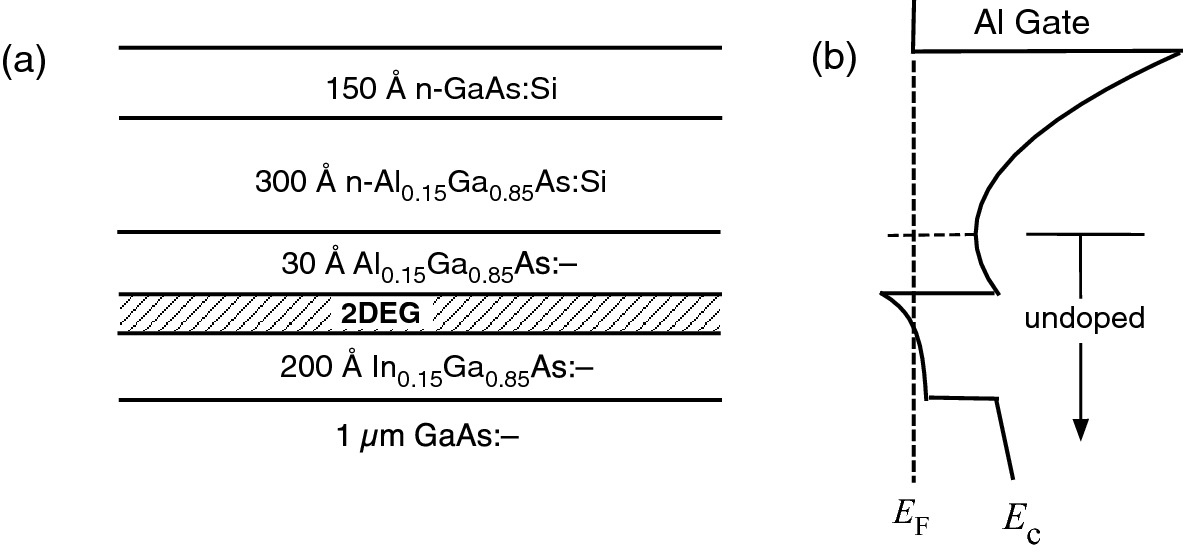
a Schematic of InGaAs/AlGaAs pseudomorphic HEMT. b Conduction band diagram of the pHEMT
9.6 GaN-Based HEMT Structures
Material parameters of GaN and GaAs
Material parameters | GaN | GaAs |
|---|---|---|
Bandgap energy (eV) | 3.438 | 1.424 |
Maximum sheet electron density (cm−2) | 1–5 × 1013 | 2–3 × 1012 |
Breakdown field strength (105 V/cm) | 50 | 4 |
2DEG mobility (cm2/V s) | 2000 | 8500 |
Saturation electron velocity (107 cm/s) | 2.5 | 1.0 |
Thermal conductivity (W/cm K) | ≥2.1 | 0.44 |
9.6.1 Polarization-Induced Sheet Charges at Heterojunctions
 ] capped with a top nitrogen plane (Fig. 9.32). In the MOCVD approach, a low-temperature-grown AlGaN nucleation layer on (0001) sapphire is needed before the growth of GaN. The nitrogen-rich growth condition for the nucleation layer yields a Ga-terminated A-face or Ga-face layer and a growth direction along [0001] capped with a top gallium plane. This growth direction is opposite to the MBE-grown nitrides and causes a sign change in spontaneous polarization.
] capped with a top nitrogen plane (Fig. 9.32). In the MOCVD approach, a low-temperature-grown AlGaN nucleation layer on (0001) sapphire is needed before the growth of GaN. The nitrogen-rich growth condition for the nucleation layer yields a Ga-terminated A-face or Ga-face layer and a growth direction along [0001] capped with a top gallium plane. This growth direction is opposite to the MBE-grown nitrides and causes a sign change in spontaneous polarization.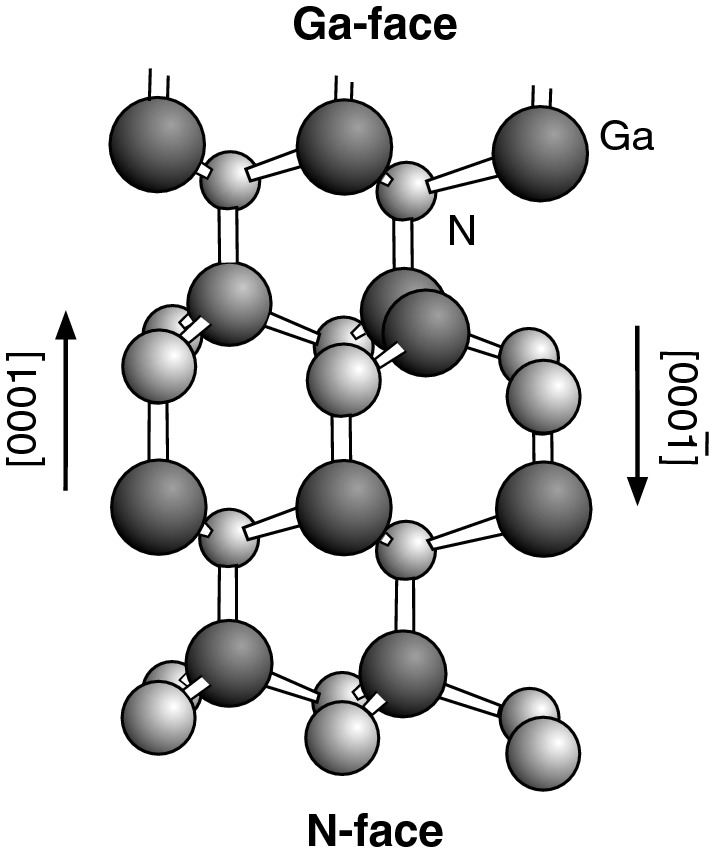
Schematic diagram of the crystal structure of wurtzite Ga-face GaN.
Reprinted with permission from [9], copyright AIP Publishing
 ] direction toward the substrate and has a negative value for all compositions. Here we assumed the polarization along the c-axis or [0001] toward surface is positive. The AlGaN/GaN heterostructures grown by MOCVD and MBE and their polarization components are shown in Fig. 9.33. The magnitude and sign of PPE depend on the strain condition. The thick GaN channel layer is relaxed and has a zero piezoelectric polarization component. Since AlGaN has a smaller lattice constant than GaN, the thin AlGaN barrier layer is under tensile strain and PPE has a negative value. Therefore, the net polarization P is negative at the AlGaN/GaN interface. If the polarity flips over from Ga-face to N-face in structures grown by MBE, both PSP and PPE change their signs.
] direction toward the substrate and has a negative value for all compositions. Here we assumed the polarization along the c-axis or [0001] toward surface is positive. The AlGaN/GaN heterostructures grown by MOCVD and MBE and their polarization components are shown in Fig. 9.33. The magnitude and sign of PPE depend on the strain condition. The thick GaN channel layer is relaxed and has a zero piezoelectric polarization component. Since AlGaN has a smaller lattice constant than GaN, the thin AlGaN barrier layer is under tensile strain and PPE has a negative value. Therefore, the net polarization P is negative at the AlGaN/GaN interface. If the polarity flips over from Ga-face to N-face in structures grown by MBE, both PSP and PPE change their signs.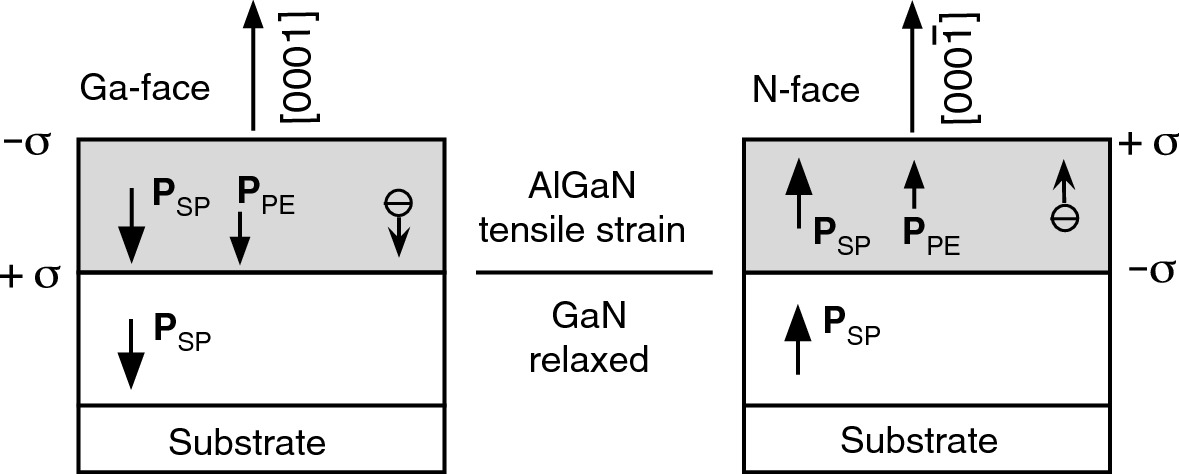
Polarization-induced sheet charge density (σ) and directions of the spontaneous (PSP) and piezoelectric (PPE) polarization in Ga- and N-face tensile strained AlGaN/GaN heterostructures grown by MOCVD (left) and MBE (right).
Reprinted with permission from [9], copyright AIP Publishing
 in a dielectric slab is an induced internal electric field F, which is produced by the fictitious surface charge density
in a dielectric slab is an induced internal electric field F, which is produced by the fictitious surface charge density  , where
, where  is the surface unit vector. By Gauss’ law, the electric field between the plates produced by these charges is
is the surface unit vector. By Gauss’ law, the electric field between the plates produced by these charges is 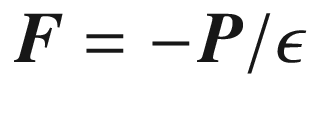 . In analog, the net polarization change within the AlGaN/GaN bilayer heterostructure under discussion induces sheet charge densities at the hetero-interface and on the surface of AlGaN defined as
. In analog, the net polarization change within the AlGaN/GaN bilayer heterostructure under discussion induces sheet charge densities at the hetero-interface and on the surface of AlGaN defined as
![$$ = \left[ {P_{\text{SP}} \left( {\text{bottom}} \right) + P_{\text{PE}} \left( {\text{bottom}} \right)} \right] - \left[ {P_{\text{SP}} \left( {\text{top}} \right) + P_{\text{PE}} \left( {\text{top}} \right)} \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ69.png)
In this heterostructure, the top surface of AlGaN and the underneath AlGaN/GaN hetero-interface carry −σ and +σ, respectively. During the cooling process, after the epitaxial growth, the polarization-induced positive sheet charge, +σ, will attract free electrons to compensate it and form a 2DEG at the hetero-interface. If the heterostructure is grown by MBE, resulting in an N-face material, the piezoelectric polarization, along with the spontaneous polarization, changes its sign. A negative sheet charge, −σ, will form at the AlGaN/GaN hetero-interface and attract holes. To utilize the fictitious positive sheet charge to induce 2DEG on the AlGaN surface, a GaN layer is needed on top of the AlGaN/GaN heterostructure.
9.6.2 Sheet Carrier Concentration of 2DEG
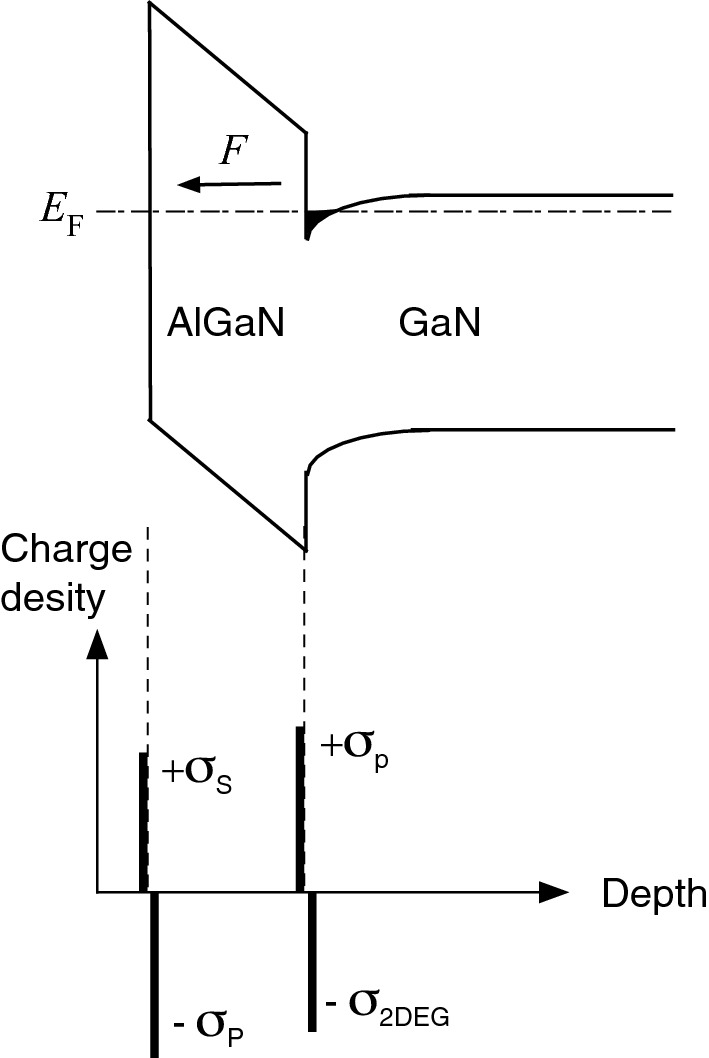
Band diagram of an AlGaN/GaN HEMT structure grown on Ga-face GaN. The sheet charge density distributions in the structure are also shown. σp, σ2DEG, and σs are induced piezoelectrical, 2DEG, and surface charge densities, respectively
![$$ n_{S} \left( x \right) = \frac{{\sigma_{{ 2 {\text{DEG}}}} }}{q} = \frac{{\sigma_{p} \left( x \right)}}{q} - \frac{\epsilon \left( x \right)}{{q^{2} d}}\left[ {q\phi_{m} \left( x \right) -\Delta E_{\text{c}} \left( x \right) + E_{\text{F}} \left( x \right)} \right] $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ70.png)
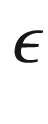 is the dielectric constant of AlGaN barrier, d is the barrier thickness, qϕm is the Schottky barrier height of a gate contact, ΔEc is the conduction band offset at the AlGaN/GaN interface, and EF is the Fermi level with respect to the GaN conduction band-edge energy. To determine the net sheet charge density from the polarization-induced 2DEG, we use the following approximations.
is the dielectric constant of AlGaN barrier, d is the barrier thickness, qϕm is the Schottky barrier height of a gate contact, ΔEc is the conduction band offset at the AlGaN/GaN interface, and EF is the Fermi level with respect to the GaN conduction band-edge energy. To determine the net sheet charge density from the polarization-induced 2DEG, we use the following approximations. (x) = 9.5 − x, and qϕm(x) = 1.3x + 0.84 (eV). The Fermi energy has the form of
(x) = 9.5 − x, and qϕm(x) = 1.3x + 0.84 (eV). The Fermi energy has the form of
![$$ \sigma_{p} \left( x \right) = \left[ {P_{\text{SP}} \left( {\text{GaN}} \right)} \right] - \left[ {P_{\text{SP}} \left( {\text{AlGaN}} \right) + P_{\text{PE}} \left( {\text{AlGaN}} \right)} \right], $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equc.png)


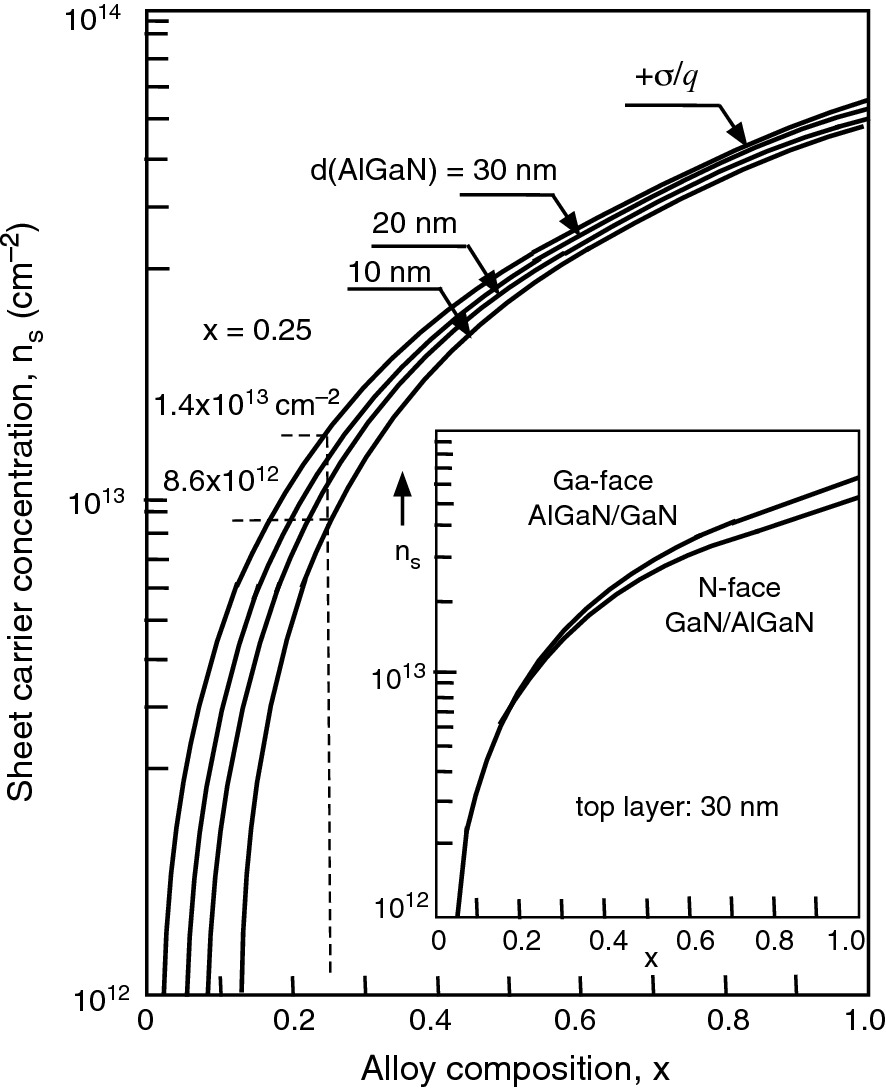
Sheet carrier concentration of the 2DEG confined at a Ga-face GaN/AlGaN/GaN or N-face GaN/AlGaN/GaN interface for different thicknesses of the AlxGa1−xN barrier. The inset shows the maximum sheet carrier concentration of a pseudomorphically grown Ga-face AlGaN/GaN and an N-face GaN/AlGaN heterostructure.
Reprinted with permission from [9], copyright AIP Publishing
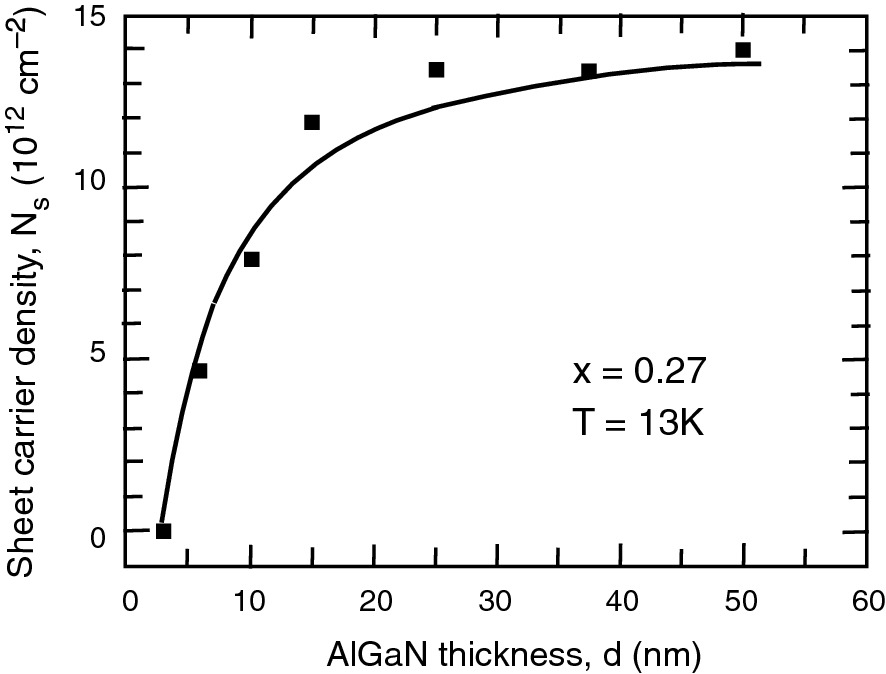
2DEG sheet carrier density in the Al0.27Ga0.73N/GaN structures as a function of AlGaN barrier width.
Reprinted with permission from [10], copyright AIP Publishing
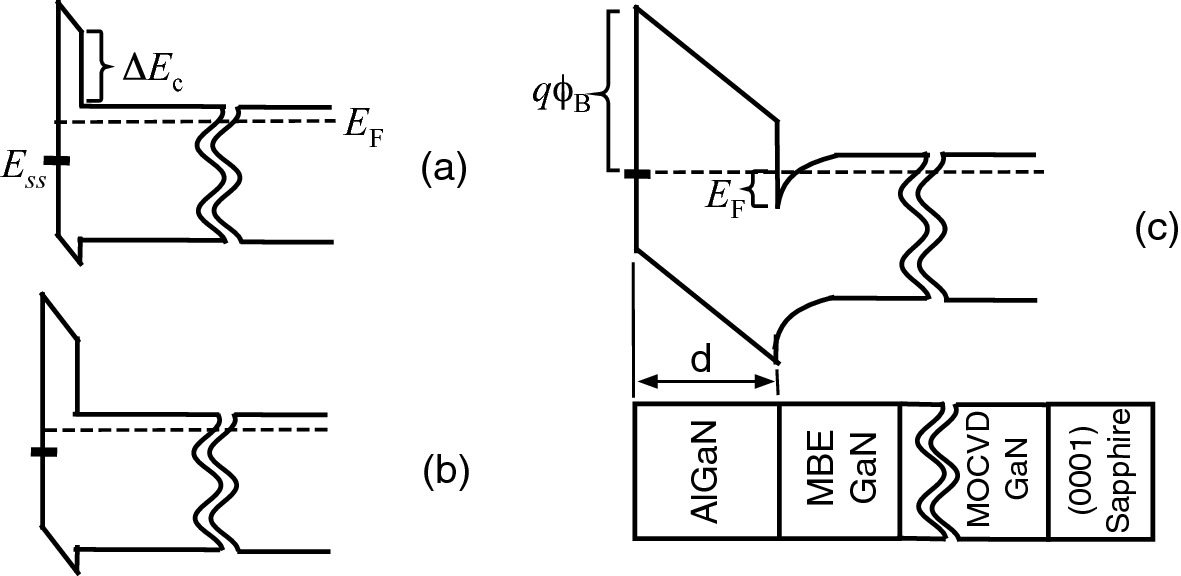
Schematic diagram showing the development of the band structure in AlGaN/GaN samples with increasing AlGaN barrier width.
Reprinted with permission from [10], copyright AIP Publishing
9.7 Heterojunction Bipolar Transistors (HBTs)
9.7.1 Introduction
The idea of using heterostructure at the emitter–base junction in a bipolar junction transistor (BJT) is not new. It was pointed out and patented by William Shockley at the time of the invention of the bipolar transistor at Bell Labs that a large bandgap emitter can be used to increase the efficiency of the device. US Patent 2,569,347 issued to W. Shockley (filed on June 26, 1948; expired on Sept. 24, 1968) claimed.
- Claim 2
“A device as set forth in claim 1 in which one of the separated zones is of a semiconductor material having a wider energy gap than that of the material in the other zones”
Herb Kroemer proposed the first heterojunction bipolar transistor (HBT) structure in 1957 [11]. Like other heterostructure devices, the HBT technology has been progressing rapidly only after the material growth technologies were matured. Currently, the highest operation frequency of fT > 800 GHz has been demonstrated in InP/InGaAs HBTs [12]. New functions, such as high-speed spontaneous and stimulated light emission, have also been demonstrated in HBTs (light-emitting transistors and transistor lasers) [13].
The HBT inherits all the advantages of the BJT including high cutoff frequency due to the short transient time across the thin base region, uniform turn-on voltage which is determined by the built-in potential of the junction, high power capability resulting from the entire emitter area conducting current, and high transconductance which enables low-power applications. By adding a heterojunction to the BJT, additional advantages emerge. The energy band discontinuity at the emitter–base (EB) heterojunction of a HBT suppresses the diffusion of majority carriers from the base into emitter for higher gain. The EB heterojunction also allows the use of a highly doped base region for low base sheet resistance without lowering gain. This means a very thin base layer can be used for a shorter transient time to achieve a higher cutoff frequency. It is expected that HBTs have higher current gain and cutoff frequency than BJT.
At the onset of HBT development, only one heterojunction was used at the EB junction of a single heterojunction bipolar transistor (SHBT). The emitter region of the GaAs-based SHBT is replaced by a larger bandgap AlGaAs, and the base–collector (BC) junction remains a GaAs homojunction. To enhance the breakdown voltage performance of a HBT, a larger bandgap material, such as AlGaAs, is used in the collector region. In this case, both EB and BC junctions are replaced by AlGaAs/GaAs heterojunctions to form a double-heterojunction bipolar transistor (DHBT). Currently, HBTs using different material systems have been developed including InxGa1−xP/GaAs, InP/InxGa1−xAs, Si/SixGe1−x, and InP/GaAs xSb1−x for various applications. Obviously, heterojunctions with either type-I or type-II energy band discontinuity can be used in HBT designs.
9.7.2 Basic Theory of Heterojunction Bipolar Transistors
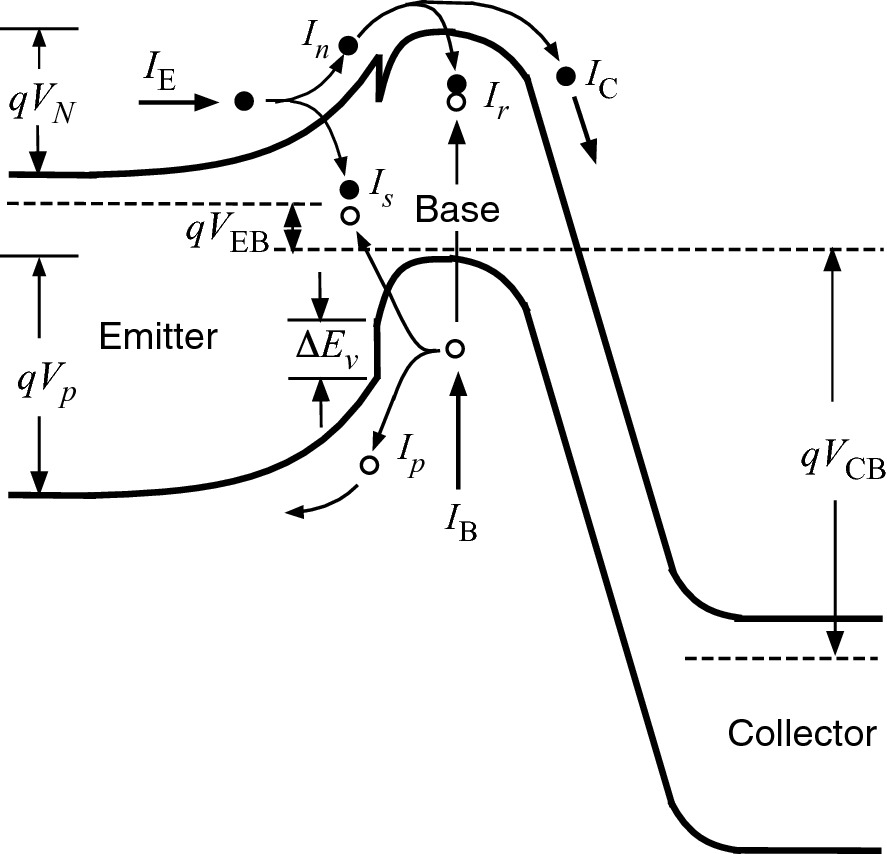
Energy band diagram of an N-p-n HBT, under normal mode operation, showing the various current components and the hole-blocking effect of the valence band discontinuity ΔEv at the EB junction
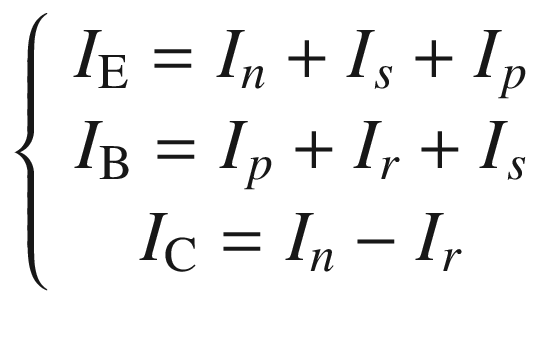




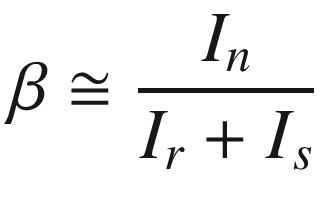


The effect of the base doping on the minority carrier lifetime and the base width in turn directly affects the current gain. Even if for heavy base doping levels the lifetimes may be short, high β’s should be achievable in HBTs with sufficiently thin base region. Furthermore, in a thin base HBT, the electron velocity is likely to approach its saturation velocity of ~107 cm/s, enhancing the current gain. As a result, no serious concerns arise from reduced minority carrier lifetime in HBTs with heavily doped thin (≤ 100 nm) base region.
Now we can examine the current gain property of a BJT. In homojunction bipolar junction transistors, ΔEg = 0. The only way to achieve high current gain is to make NE ≫pB. Since the base doping level is kept low, it requires a thick base layer to minimize the base sheet resistance. A thick base layer will eventually limit the cutoff frequency of the BJT. On the other hand, the doping level in the emitter cannot exceed certain limits. A heavily doped emitter will cause other problems. When the emitter degenerates, the Fermi level can move into the conduction band and cause bandgap shrinkage. This is equivalent to a reduction of conduction band discontinuity at the EB junction or ΔEg < 0. A lowering of βmax is expected. Therefore, the HBT takes advantage of the exponential dependency of ΔEg to achieve high gain with high base doping concentration. Furthermore, the doping profile of the BJT is graded due to diffusion and/or ion implantation processes used in device fabrication. For HBTs, a much sharper doping profile is achieved by controlling doping properties during epitaxy. The abrupt and heavily doped base region is desirable for achieving high current gain and high cutoff frequency in a HBT. Thus, it is critical to use a suitable p-type dopant that possesses a high doping efficiency and a low diffusivity. For GaAs-based HBTs, carbon has proved to be an ideal p-type dopant among other common candidates such as Zn and Be. It can be easily doped to over 1020 cm−3 in many III–V compound semiconductors with negligible out-diffusion. However, carbon atoms are hard to generate from a solid source, such as graphite, due to their extremely low vapor pressure. Currently, the heavily p-type carbon doping is conveniently achieved using gaseous carbon sources such as CCl4 (in MOCVD) and CBr4 (in MBE).
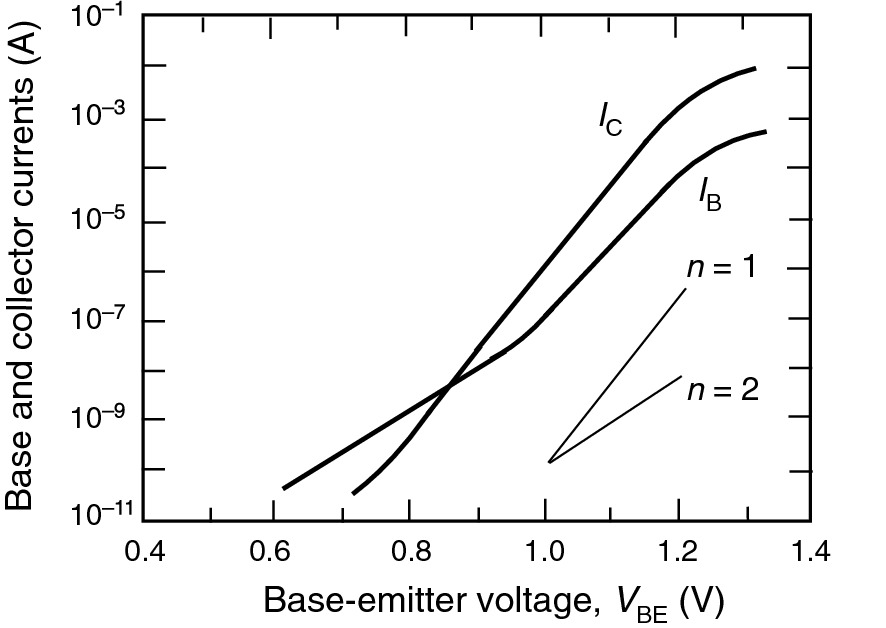
Gummel plot for InGaP/GaAs HBT. The emitter size of the HBT is 60 × 60 µm2.
Reprinted with permission from [15], copyright IEEE
9.7.3 Band Discontinuity of Heterostructures
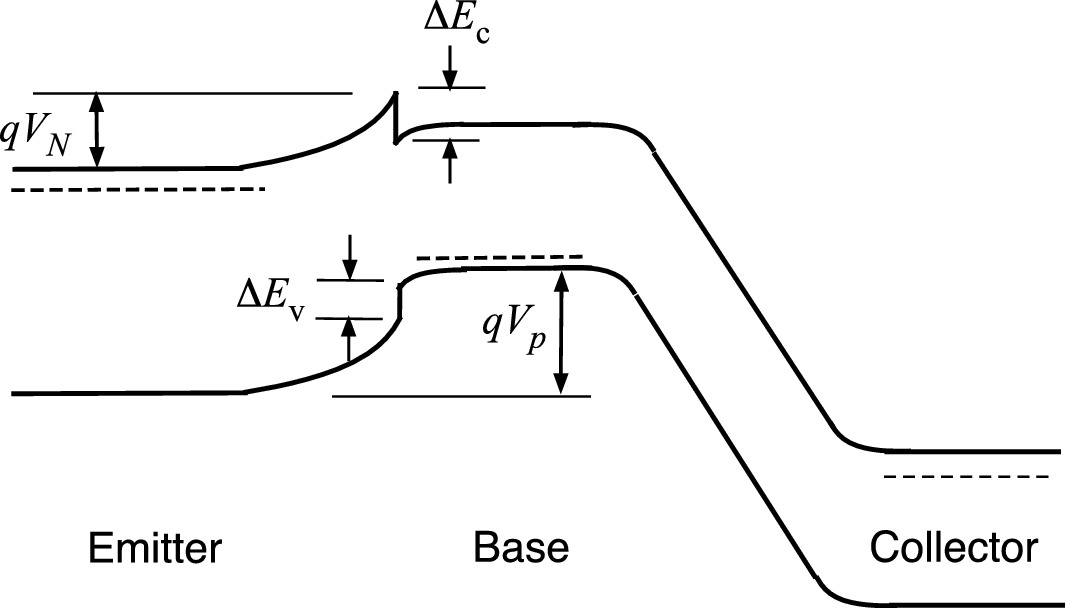
Energy band diagram for HBT with abrupt emitter–base junction
![$$ \frac{{I_{n} \left( {\text{abrupt}} \right)}}{{I_{n} \left( {\text{graded}} \right)}} = \frac{{\exp \left( { - qV_{N} / {kT}} \right)}}{{\exp \left[ { - \left( {qV_{N} -\Delta E_{\text{c}} } \right) / {kT}} \right]}} = \exp \left( { -\Delta E_{\text{c}} /{kT}} \right) $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ80.png)

It is clear that a large ΔEv is preferred in abrupt N-p+-n HBT structures for a high current gain.
The existence of the energy spike in the conduction band at the EB heterojunction has other effects on device performance. A beneficial effect is that electrons injected from emitter into the base have to overcome the EB junction barrier with higher potential energy and become hot electrons with high saturation velocity. The improved travel speed across the base region leads to a reduced base transient time for high frequency operation. A detrimental effect is that the energy spike can block current flow at bias voltages VCE < ΔEc/q = Voff, which is the offset voltage. Also, the triangular QW formed on the base side of the EB junction can trap electrons that lead to an enhanced recombination at the junction. Therefore, the current gain will be reduced due to an increasing Ir.
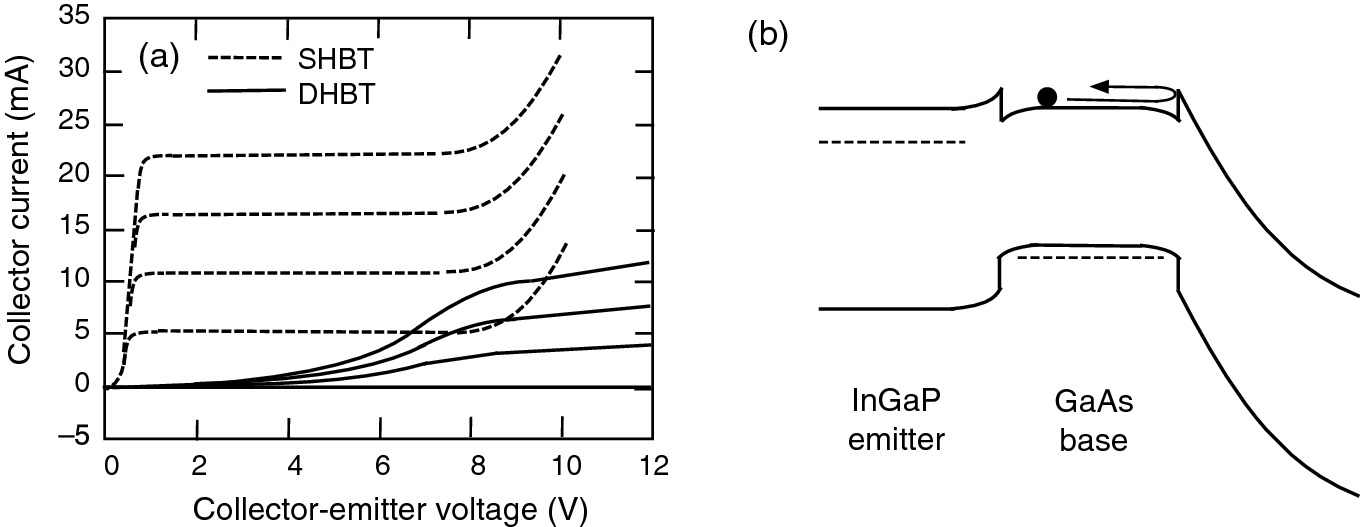
a Comparison of the I–V characteristics of InGaP/GaAs SHBT and DHBT. The base current was stepped from 0 to 400 µm in 100 µA steps. Reprinted with permission from [16], copyright AIP Publishing. b Current blocking at the base–collector junction of an InGaP/GaAs DHBT
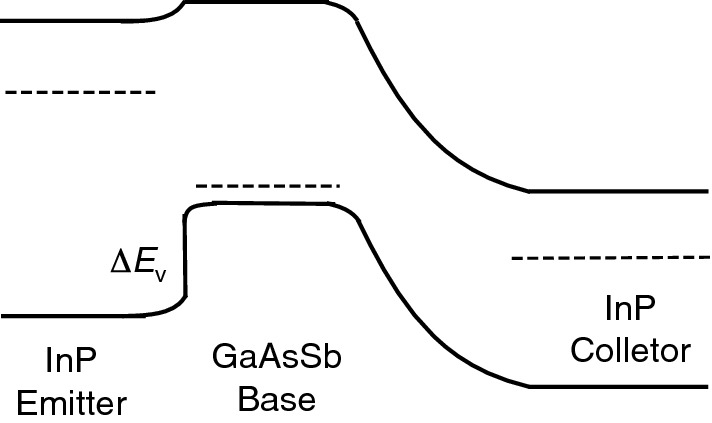
Energy band diagram of an InP/GaAsSb type-II double-heterojunction bipolar transistor
9.7.4 High-Frequency Operation of HBT
The high-frequency performance of HBTs is fundamentally determined by the stored minority carrier charge in the transistor that has to be removed from (added to) the transistor before it can turn off (on). Hence, the maximum frequency at which the transistor is capable of operating depends on the junction capacitance charging time and charge carrier transit time. In forward active operation, the forward transit time τF or the emitter-to-collector transit time τEC represents a fundamental limit for the switching speed and maximum frequency of operation of a HBT. The parameter most commonly used to define this maximum frequency of operation is the cutoff frequency fT. This is the frequency at which the common emitter, small-signal current gain drops to unity under conditions of a short-circuit load.
In practice, parasitic capacitance and resistance of the HBT will slow down the switching of digital circuits and limit the frequency of operation of analog circuits. To include the effect due to parasitic resistances and junction capacitances, the maximum oscillation frequency fmax is a good predictor of transistor performance.
- (a)
Emitter-to-collector transit time







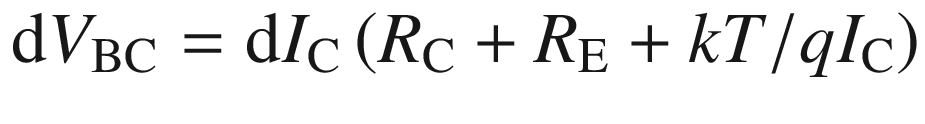

![$$ f_{\text{T}} = \frac{1}{{2\pi \tau_{\text{EC}} }} = \left\{ {2\pi \left[ {\tau_{\text{B}} + \tau_{\text{C}} + \left( {R_{\text{E}} + R_{\text{C}} } \right)C_{\text{BC}} + \frac{kT}{{qI_{\text{C}} }}\left( {C_{\text{E}} + C_{\text{BC}} } \right)} \right]} \right\}^{ - 1} $$](../images/325043_1_En_9_Chapter/325043_1_En_9_Chapter_TeX_Equ90.png)
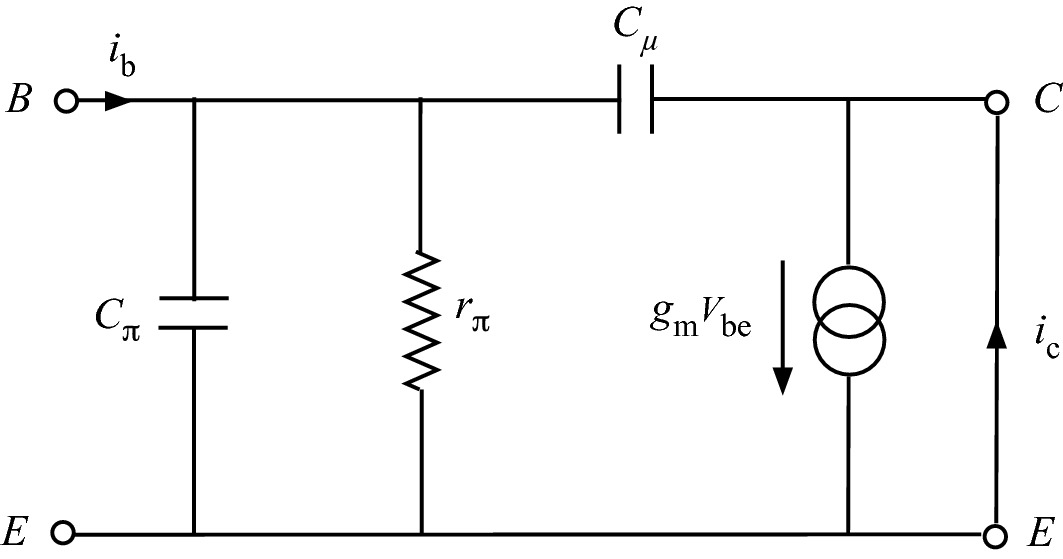
Small-signal hybrid-π circuit model of HBT





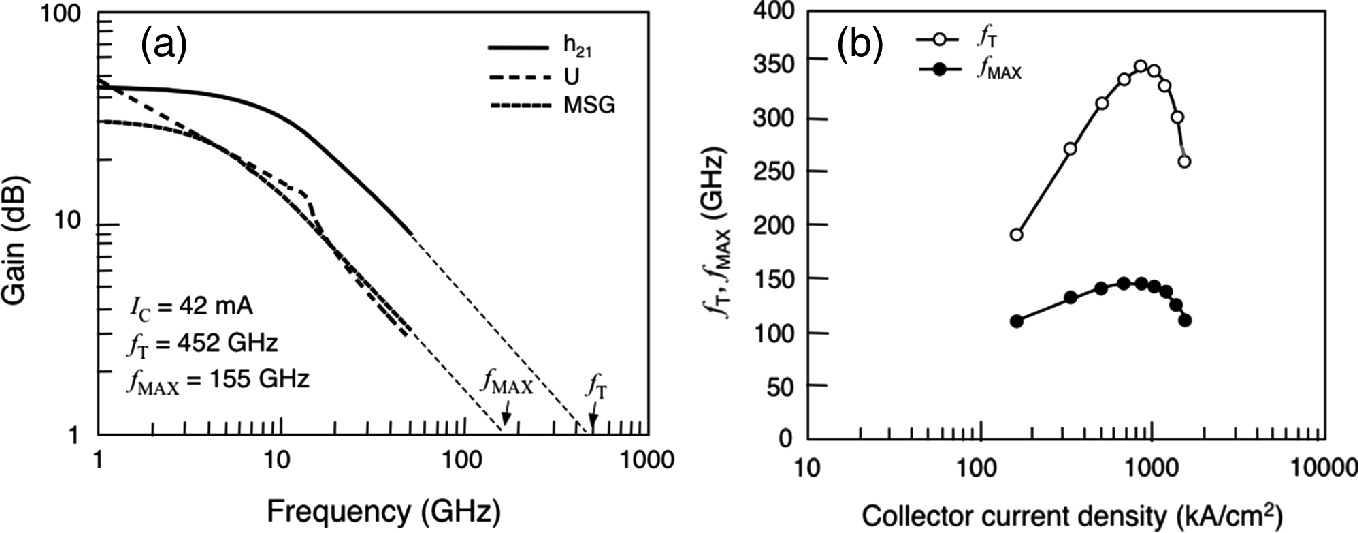
a RF response and performance figure extrapolations for 0.25 × 16 µm2 InP/InGaAs SHBT. Reprinted with permission from [17], copyright IEEE. b fT and fmax as a function of collector current density of a 0.35 × 8 µm2 type-II InP/GaAsSb DHBT. Reprinted with permission from [18], copyright American Vacuum Society
Since τEC is a function of the collector current, the cutoff frequency is also a function of the collector current as illustrated in Fig. 9.44b. At low collector currents, the depletion capacitance term (τBC) in (9.89) dominates and hence fT increases with IC. At medium currents, the transit time terms become larger than the depletion capacitance term, and fT ceases to rise with collector current. At high collector currents, the cutoff frequency decreases markedly due to high current effects, especially the Kirk effect which will be described later.

- (b)
Kirk effect

 and electrons injected from the emitter are transported across the BC junction by drift under high field situations. The electron concentration relates the drift current density Jn by n = Jn/qυsat, where υsat is the electron saturation velocity. Thus,
and electrons injected from the emitter are transported across the BC junction by drift under high field situations. The electron concentration relates the drift current density Jn by n = Jn/qυsat, where υsat is the electron saturation velocity. Thus,
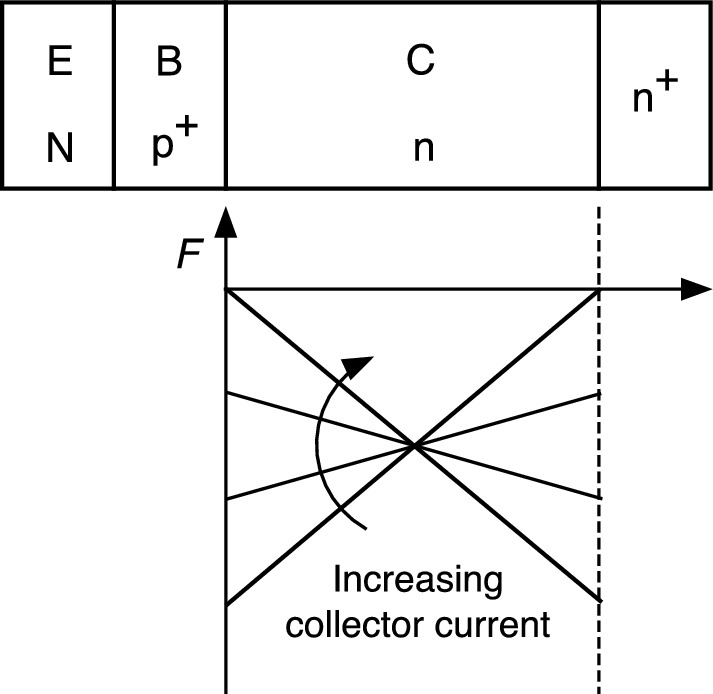
Electric field intensity distribution in the fully depleted collector region under large collector current density. With further increase of collector current density, the slope of the electric field intensity curve changes from positive to negative as indicated by the arrow
- (c)
Device scaling and surface passivation
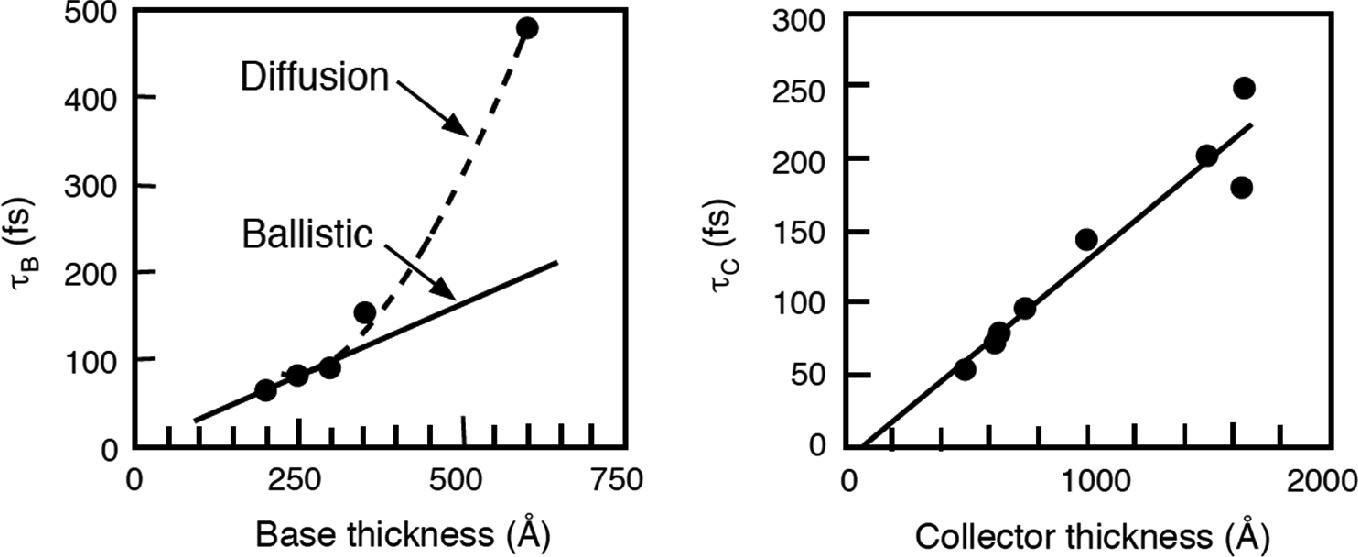
Experimental results on the relationship between vertical scaling of InGaAs/InP SHBT and base/collector transit times
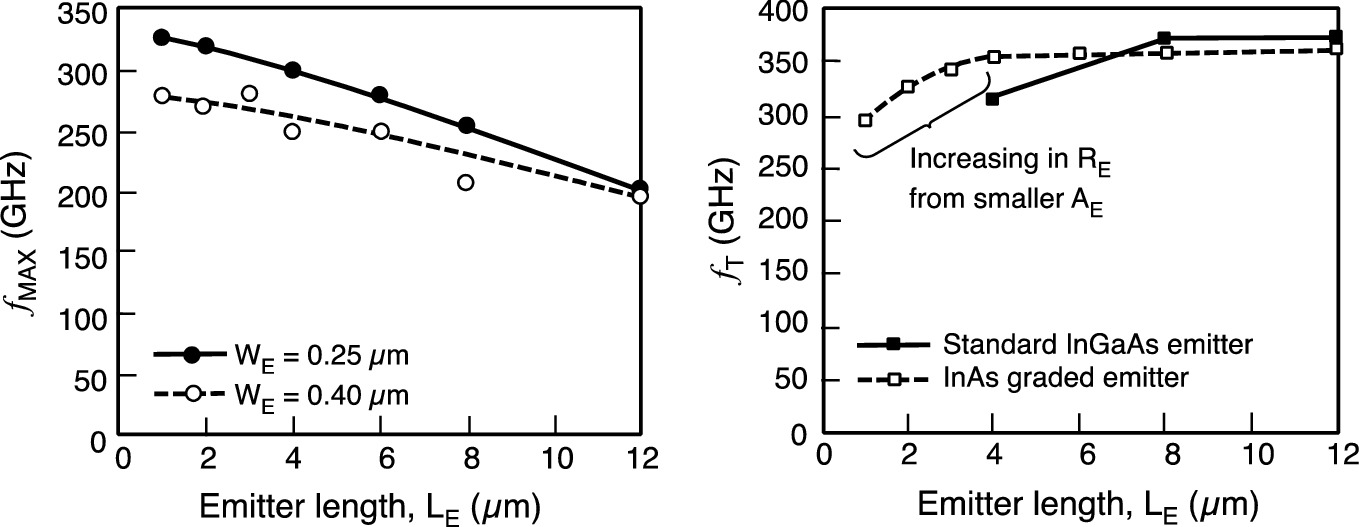
Experimental results on the relationship between emitter lateral scaling of InGaAs/InP SHBT and cutoff frequency
Beyond a certain point, however, scaling has detrimental effects on device performance due to physical limitations imposed by shrinking device dimensions. The significant drop in fT observed in Fig. 9.47 for emitter lengths 8 µm and smaller on a standard InGaAs emitter cap is attributed to an increase in emitter resistance due to smaller contact areas. Ideally, scaling theory predicts that fT should remain constant regardless of emitter length. However, the finite cap doping causes large increases in contact resistance for these emitter areas. The emitter cap cannot be doped higher due to solid solubility limits, but emitter contact resistance can be reduced through emitter cap engineering by using a narrow-bandgap cap material such as InAs. InAs provides a better contact material because of the smaller bandgap, higher doping capability, and higher thermal conductivity when compared to a standard InGaAs cap. The utilization of an InAs emitter cap is shown to reduce the emitter contact resistance by a factor of 2 in submicron HBT devices. The contact resistance reduction enhances the scalability of the emitter by allowing the emitter length to scale to dimensions smaller than 4 µm before the fT degradation occurs. Overall, lateral scaling is often dependent on process maturity, relying on advanced fabrication techniques to counteract the effects of vertical scaling on fmax. Therefore, for HBT development using a new material system, the best indication of the system’s potential is determined by the fT of the transistor. It is assumed that as the process matures, the power gain of the device will be increased through technological advances.
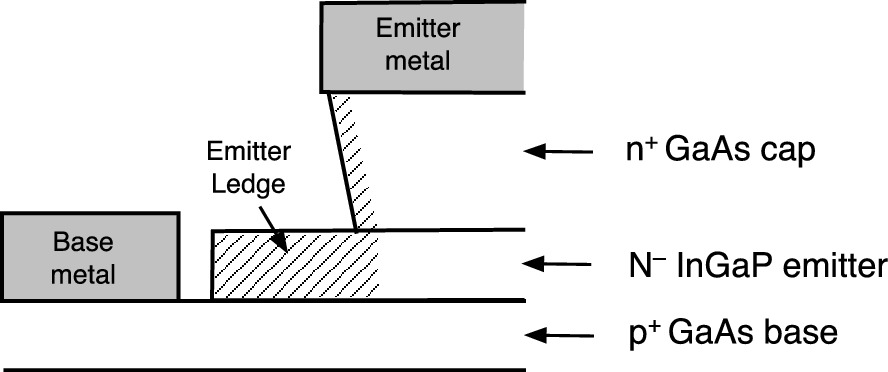
Cross-sectional drawing of a HBT with emitter ledge passivation. The emitter ledge (hatched area) is totally depleted such that the base current underneath is not affected
9.7.5 Basics of HBT Processing
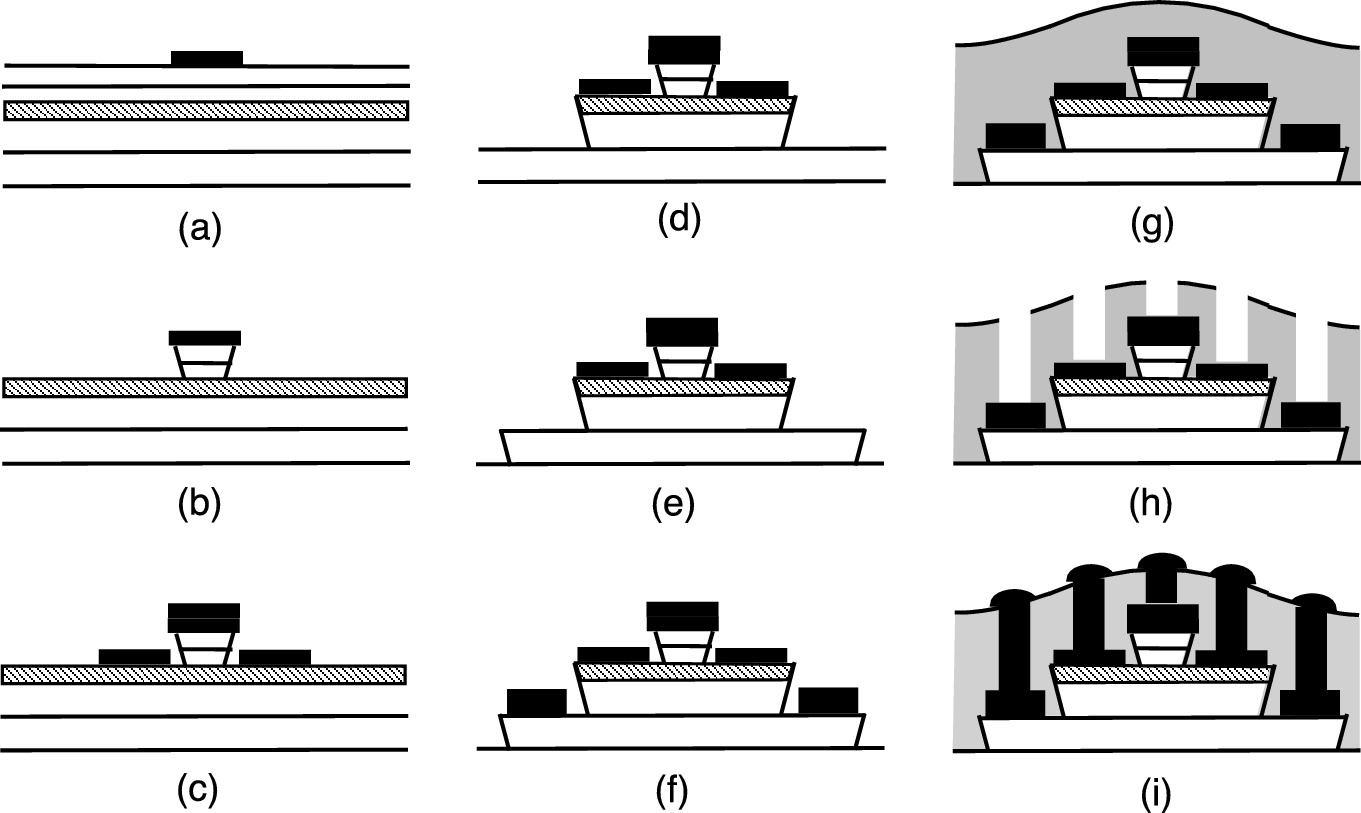
Cross-sectional diagrams of UIUC HBT process: a post-emitter contact liftoff, b post-base etch, c post-base contact liftoff, d post-collector etch, e post-isolation etch, f post-collector contact liftoff, g post-polyimide/SiNx passivation, h post-SiNx via etch, and i post-overlay metal liftoff

Left: Top view SEM micrograph of a fully fabricated GaAsSb/InP DHBT before planarization with an emitter size of 0.25 × 5 µm2. Right: Cross-sectional SEM micrograph of a completed GaAsSb/InP DHBT with an emitter size of 0.35 × 5 µm2.
Courtesy M. Feng, University of Illinois at Urbana-Champaign
At this point, the HBT has a non-planar topology. In order to make the HBT structure more planar to facilitate both via etching and the formation of planar probe pads for high-frequency testing, a planarization process (Fig. 9.49g) is required. The spin-on polyimide followed by a deposited Si3N4 layer completes the planarization process. Contact vias are defined using standard photolithography process (Fig. 9.49h). After the vias have been etched, a 1 µm layer of overlay metallization is deposited to form the probe pads and interconnect metallization. In the last step, an airbridge process is utilized to produce a second level of plated interconnect metallization allowing emitter fingers to connect to common-emitter probe pads. The cross-sectional SEM micrograph of a GaAsSb/InP DHBT with an emitter size of 0.35 × 5 µm2 is shown in Fig. 9.50b.
9.8 III–V Metal-Oxide-Semiconductor Field-Effect Transistors
Silicon metal-oxide-semiconductor field-effect transistor (MOSFET)-based integrated circuit (IC) technology is the dominant semiconductor technology used by all electronics industries with a 2018 worldwide sales of over $470 billion. Miniaturization of the feature size of ICs to increase the density of components has been the foundation of the over 50-year-long steady advance of silicon technology. Following Moore’s law, the exponential increase of transistor count per unit area as a function of time has been faithfully delivered by the industry since 1970. The minimum transistor gate length also decreases with time exponentially by incorporating strained SiGe channel material, high-κ gate dielectrics, and non-planar multigate structures (see Fig. 1.4). Although 5-nm-node CMOS circuits are on the horizon, further reduction of the feature size to below 2 nm will push the device structure into the quantum regime. At that moment, the silicon technology will reach the point at which significant materials and device innovations will be required to further technology developments. One possible solution for the future is the hybrid material system in which silicon, germanium, and III–V compound semiconductors are integrated together on silicon wafers. For example, taking advantage of the very high electron mobility in GaInAs and high hole mobility in germanium, advanced CMOS circuits consisting of n-GaInAs channel and p-Ge channel MOSFETs might be fabricated together on the silicon wafer.
Because of their high bulk electron mobility, III–V MOSFETs have long been pursued in hopes of achieving performance superior to that of their Si counterpart. However, due to the high surface state density, the realization of unpinned surface Fermi level in III–V compound semiconductors had been elusive until two decades ago. In searching for a low defect density, thermodynamically stable gate dielectric, native oxide and deposited oxide using a variety of deposition techniques have been investigated. Unlike the SiO2/Si system, the native surface species in III–V materials are complicated. For example, the stable oxides of GaAs consist of As2O3, As2O5, Ga2O3, Ga2O, and GaAsO4 with different thermodynamic properties. Among all native oxides in this system, the As-oxides are the least stable while Ga2O3 is the most stable oxide. When the low-temperature-grown oxides are annealed at higher temperature, the composition of the oxide layer changes significantly. As temperature increases, the less stable As-oxides either evaporate away or are converted to the most stable oxide in the system (Ga2O3) along with elemental arsenic located at the interface. The pinning of the Fermi level at the GaAs-oxide interface has been unambiguously correlated with significant amounts of As2O3, As2O5, and elemental As present in native oxides. In order to fabricate functional III–V MOSFETs, it is necessary to completely remove the surface native oxide first before a stable and robust dielectric can be deposited. Thus, the successful development of III–V MOSFET technology relies strongly on the surface passivation and interface control technology.
9.8.1 III–V Alloy Surfaces and Semiconductor-Oxide-Metal Interfaces
- (a)
Empirical CNL model of M-S interfaces
In semiconductors, the dangling-bond energy is typically located inside the band gap and the interface trap density (Dit) increases exponentially in the energy ranges close to the band edges. The Dit distribution forms a U-shaped continuum of donor- and acceptor-type states with its minimum, or the pinning energy, located at the charge neutrality level (CNL). The CNL energy level represents a weighted average value over the density of states. CNL is pushed away by the large DOS of the conduction and valence bands from the intrinsic energy level Ei, as shown in Fig. 4.21. Therefore, the semiconductor surface pinning energy CNL is located inside the forbidden gap for most semiconductors. If the Fermi level EF is above CNL, the states are of acceptor type and negatively charged if the states are occupied. If the Fermi level EF is below CNL, the states are of donor type and positively charged if the states are occupied.
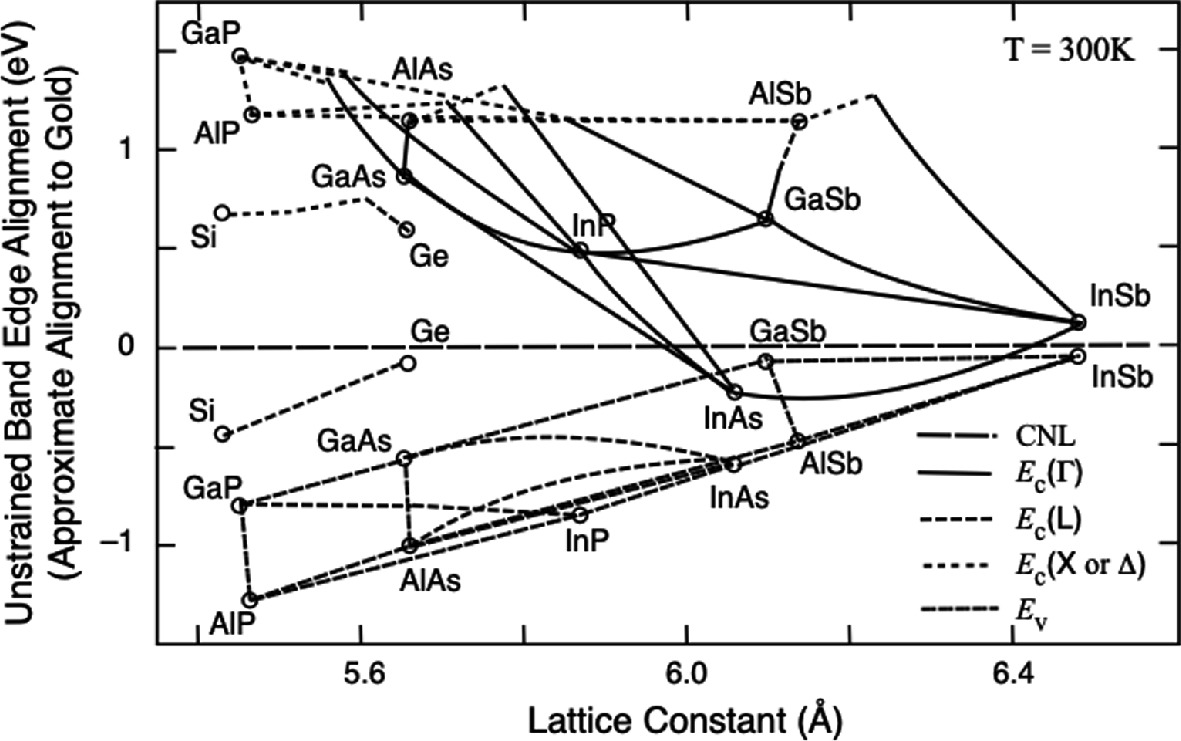
Energy alignment of CNL with the band edges of elemental and III–V semiconductors at MOS interfaces plotted as a function of the lattice constant of semiconductors. For III–V compounds, the circles indicate the band edges of binaries and the lines show the band edges of ternaries
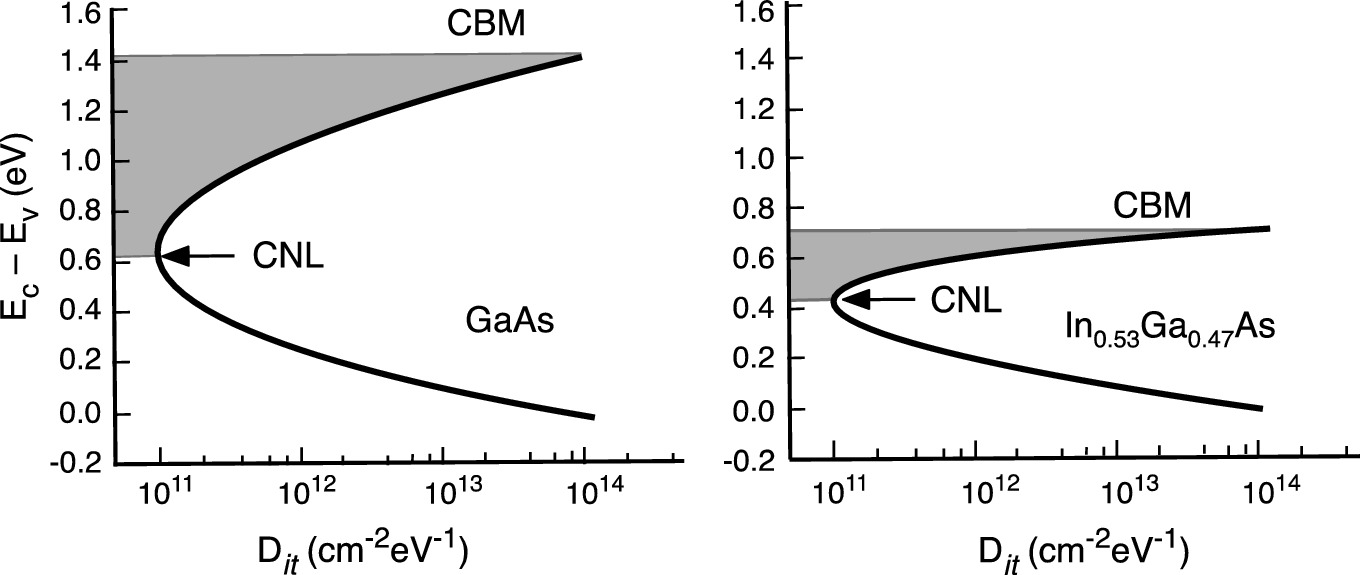
Schematic for the parabolic Dit distribution within energy band of GaAs and In0.53Ga0.47As. The CNL is aligned 0.8 eV and 0.27 eV below CBM for GaAs and In0.53Ga0.47As, respectively. The shaded area shows the built-up negative charges in interface traps after Fermi level moves from CNL to CBM.
Reprinted with permission from [19], copyright AIP Publishing
- (b)
High-κ dielectrics and oxide-semiconductor (O-S) interfaces

 is the permittivity of free space, κ is the relative permittivity (dielectric constant), A is the area, and t is the thickness of the dielectric SiO2. Since the tunneling current decreases exponentially with increasing the dielectric thickness, a new dielectric with a larger dielectric constant than that of SiO2 (κ = 3.9) has to be introduced while maintaining the same capacitance. These non-native new gate oxides are called high-κ dielectrics. In selecting suitable high-κ dielectrics for microelectronics applications, there are several important requirements about their physical properties. First, the κ value must be high enough that it will be used for a reasonable number of years of scaling. A value of κ ≥ 20 is preferred. Second, the oxide must have large bandgap energy and act as an insulator, by having oxide-Si band offsets over 1 eV to minimize leakage current. Third, the oxide must be thermodynamically as well as kinetically stable such that it is compatible with extreme processing conditions. Above all, the selected oxide must form a good electrical interface with the semiconductor, which is dependent on the deposition method. The oxides that satisfy most of these criteria are Al2O3, HfO2, ZrO2, Y2O3, La2O3, and various lanthanides (e.g., Gd2O3).
is the permittivity of free space, κ is the relative permittivity (dielectric constant), A is the area, and t is the thickness of the dielectric SiO2. Since the tunneling current decreases exponentially with increasing the dielectric thickness, a new dielectric with a larger dielectric constant than that of SiO2 (κ = 3.9) has to be introduced while maintaining the same capacitance. These non-native new gate oxides are called high-κ dielectrics. In selecting suitable high-κ dielectrics for microelectronics applications, there are several important requirements about their physical properties. First, the κ value must be high enough that it will be used for a reasonable number of years of scaling. A value of κ ≥ 20 is preferred. Second, the oxide must have large bandgap energy and act as an insulator, by having oxide-Si band offsets over 1 eV to minimize leakage current. Third, the oxide must be thermodynamically as well as kinetically stable such that it is compatible with extreme processing conditions. Above all, the selected oxide must form a good electrical interface with the semiconductor, which is dependent on the deposition method. The oxides that satisfy most of these criteria are Al2O3, HfO2, ZrO2, Y2O3, La2O3, and various lanthanides (e.g., Gd2O3).
 , and follows the trend
, and follows the trend
Eg (eV) | κ | ECNL (eV) | EA (eV) |
| |
|---|---|---|---|---|---|
a-Al2O3 | 6.3 | 7.5 [21] | 3.2 | 3 | 3.2 |
HfO2 | 6 | 25 | 3.7 | 2.2 | 4 |
ZrO2 | 5.8 | 25 | 3.6 | 2.4 | 4.8 |
Y2O3 | 5.7 | 15 | 2.4 | 1.84 | 4.4 |
La2O3 | 6.0 | 30 | 2.4 | 1.9 | 4 |
Gd2O3 | 6 | 10 [22] | 2.4 | 2.5 | 3.8 |
Calculated conduction band offsets (ΔEc, in eV) of various high-κ oxides on III–V semiconductors [20]
Al2O3 | HfO2 | ZrO2 | Y2O3 | La2O3 | Gd2O3 | |
|---|---|---|---|---|---|---|
GaP | 0.67 | 0.77 | 0.73 | 1.65 | 1.65 | 1.2 |
InP | 1.7 | 1.72 | 1.64 | 2.6 | 2.6 | 2.1 |
AlAs | 0.97 | 1.05 | 1.0 | 1.9 | 1.9 | 1.5 |
GaAs | 1.46 | 1.52 | 1.42 | 2.4 | 2.4 | 1.9 |
InAs | 2.38 | 2.54 | 2.44 | 3.4 | 3.4 | 2.9 |
GaSb | 1.50 | 1.58 | 1.53 | 2.46 | 2.46 | 2.0 |
InSb | 2.08 | 2.18 | 2.14 | 3.06 | 3.06 | 2.62 |
GaN | 0.86 | 1.15 | 1.08 | 2.02 | 2.02 | 1.57 |
9.8.2 Atomic Layer Deposition (ALD)
- (a)
Principles of ALD
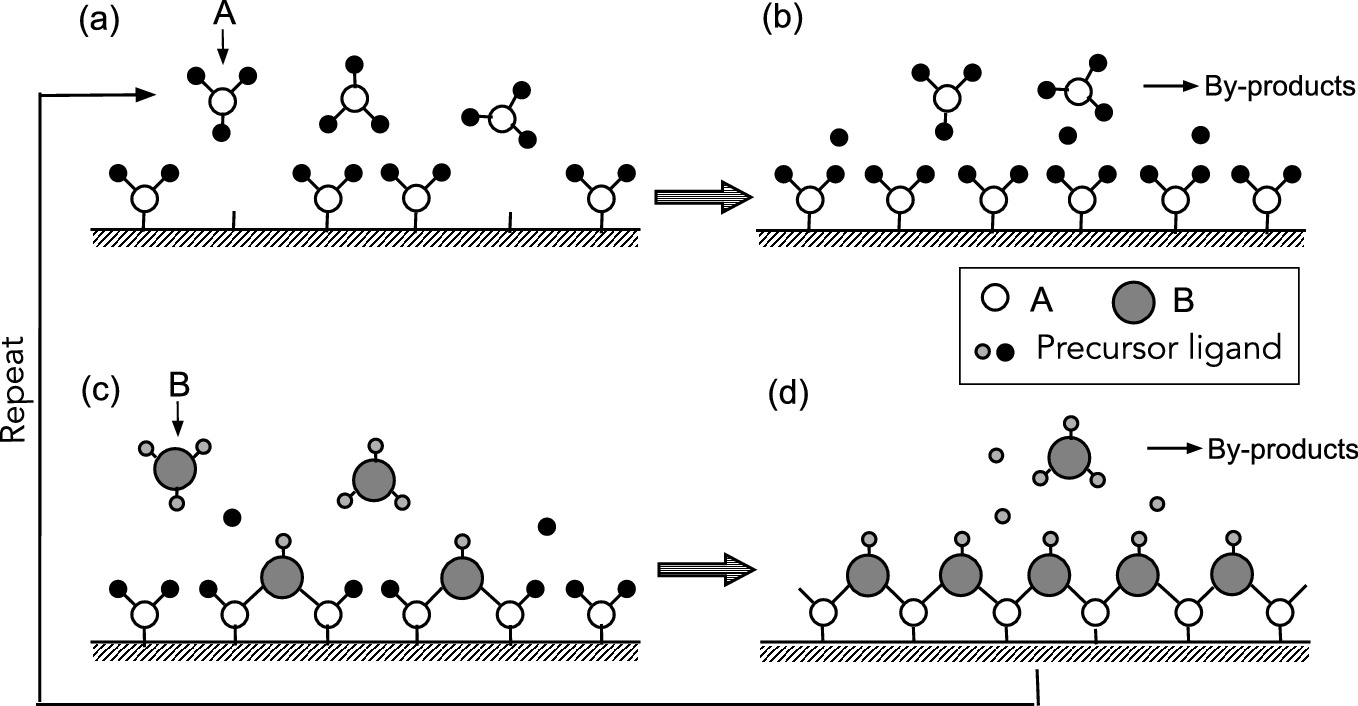
Schematic representation of an ALD growth cycle leading to the formation of a binary dielectric film using self-limiting surface chemistry. a Precursor A is pulsed and reacts with surface, b excess precursor and reaction by-products are purged with inert carrier gas, c precursor B is pulsed and reacts with surface, and d excess precursor and reaction by-products are purged with inert carrier gas. Above procedures are repeated until the desired material thickness is achieved
Typically, the process of ALD is performed at relatively low temperatures (<350 °C). The temperature range, where thin film growth proceeds by the irreversible and saturating surface control in an ALD mode, is referred to as the ‘ALD-window’. Within this ALD-window, the deposition rate per cycle is a constant independent of the growth temperature. The process outside the ALD-window, however, generally results in non-ALD-type deposition due to precursor condensation or insufficient reactivity at low temperatures, and precursor thermal decomposition or rapid precursor desorption at high temperatures. Thus, it is necessary to carry out each deposition process within the designated ALD-window.
- (b)
ALD of high-κ dielectrics on III–V surfaces
Since 2007, the Si semiconductor industry has adopted ALD to integrate non-native oxides, e.g., HfO2-based high-κ dielectric, into its IC mass production lines to advance the technology node beyond 45 nm. Next, at the 22 nm node, a three-dimensional fin field-effect transistor (FinFET) structure is developed. In a FinFET, the fin-shaped gate with a high aspect ratio protruding above the bulk surface needs to be covered with a gate oxide of high compositional and thickness uniformity. This is a task tailored for the conformal ALD process. To further improve the device performance with higher speed and reduced power, it is necessary to look toward alternative semiconductors with higher carrier mobility, such as III–V semiconductors.
For non-native oxide deposited on III–V substrate surface using ALD process, the achieved interface state density is primarily decided by the precursor characteristics and surface preparation of the substrate surface. There are some general requirements for a suitable ALD precursor which include: (a) sufficient volatility but no self-decomposition at the deposition temperature (b) adsorption to the surface sites without etching the substrate, and (c) sufficient reactivity toward the second precursor. The metal precursors used in ALD on III–V surfaces can be divided into two groups, inorganic and organometallic. Halides are the most common inorganic precursors used for both CVD and ALD processes. Chlorides, a kind of halides, are reactive, stable at a broad temperature range, and available for many metals including AlCl3 and HfCl4. However, the deposited film may suffer from high residual chlorine and hydrogen content. On the other hand, alkyls, such as trimethyl aluminum (TMA), are ideal metalorganic precursors containing a direct metal carbon bond. They are highly volatile and very reactive with water through hydrolysis. Other metal precursors including the chelation of C (β-diketronates), O (cyclopendienyls), and N (amidinates) with alkyls to a metal have also been used. The variety in non-metal reactants is rather less than in metal reactants. Water, due to its high stability and reactivity in a broad temperature range, is the most commonly used oxygen source providing a hydroxyl-terminated surface in metal oxide ALD. Ozone is often used for deposition of oxides from metal precursors having bulky ligands that are not reactive with water. However, due to its strong oxidation power, there are potential concerns regarding undesirable surface oxide formation on the substrate by prolonged ozone exposures.
The other important factor that influences the quality of non-native oxide/III–V interfaces is the pre-cleaning or surface passivation of the substrate before ALD. Unlike the SiO2/Si material system, the III–V substrates lack a high-quality, natural insulator. Instead, a number of different native surface species including Ga–O bonds, In-O bonds, As–O bonds, and other III–V–O bonds are readily formed on III–V surfaces when exposed to ambient environment. To achieve a low interface state density on III–V surfaces, these oxides must be removed as much as possible before depositing high-κ dielectrics. Currently, a number of ex situ surface treatments of III–V (100) surfaces have been developed. The use of wet chemical treatment by soaking samples in NH4OH (29%) solution has been found to be effective in removing higher-oxidation states of As and Ga oxides. To prevent re-oxidation of the III–V surface after the etch, the sample can be further protected by monolayers of sulfur using a (NH4)2S treatment before loading into the ALD system. The sulfur is then blown off from the III–V surface during the temperature ramp-up in the ALD system. The key to cleaning up As-oxide and providing high-quality III–V/high-κ interfaces is the self-cleaning effect of the ALD process as described in the following section. However, the removal of Ga oxides by the ALD process is incomplete. Further detailed studies examining Al2O3 and HfO2 deposition on GaAs by ALD indicated that the efficiency of surface oxides removal is affected by the ALD precursors used. An ~1 nm interfacial layer containing significant Ga2O content was observed at the Al2O3/III–V interface deposited using TMA/water precursors, while a thicker interfacial layer (~2.5 nm) was observed from the HfO2 deposition using HfCl4/water precursors. The enhanced reactivity of Al(CH3)3 compared to HfCl4 is responsible for this difference.
Currently, Al2O3, HfO2, and their alloys constitute the major ALD dielectrics studied on III–V substrates. Other metal oxides including Gd2O3, La2O3, and Y2O3 have also been studied. The best achieved interface state densities (Dit) are between 1011 and low-1012/cm2eV, which are orders of magnitude higher than that of (Gd2O3)Ga2O3/GaAs deposited by in situ UHV MBE deposition (~5 × 1010/cm2eV) and far worse than the ideal SiO2/Si system (~109–1010/cm2eV). However, these interface state density values have already been improved significantly to allow the demonstration of inversion-mode MOSFETs on different III–V substrates. To further improve the technology, additional ALD metal oxides need to be developed for gate dielectrics of III–V substrates. Surface passivation methods before ALD require further refinement to achieve the right surface conditions including the formation of particular species of interfacial oxides. Furthermore, to make high-κ dielectric/III–V a manufacturable III–V CMOS technology, it is also necessary to avoid surface and interfacial defect formation in every step of device fabrication.
9.8.3 Oxides Deposition on III–V Substrates
- (a)
Substrate surface preparation
In the process of fabricating III–V-based MOSFETs, the preparation of a suitable surface condition of the semiconductor substrate for oxide deposition is the most critical step. In the ideal case, the surface of III–V semiconductors is a perfect, flat, and homogeneous surface. In reality, the atomic bonds in the terminated plane are sheared off to become unsatisfied dangling bonds. These dangling bonds are fairly susceptible to chemical reactions with atmospheric gases leading to the formation of moderately thick native oxides and carbonaceous adsorbents. These native surface species including, e.g., Ga–O bonds, As–O bonds, elemental As, and As and Ga anti-sites on GaAs, are the culprits of the Fermi level pinning. Thus, it is very important to remove these native oxides and carbonaceous adsorbents on air-exposed III–V substrates such that further surface treatment or ‘passivation’ of the surface can be carried out before the deposition of high-κ dielectrics.
 10] direction, while the Ga-rich (4 × 2) surface has Ga dimers aligned along the [
10] direction, while the Ga-rich (4 × 2) surface has Ga dimers aligned along the [ ] direction. Due to the high diffusivity of surface Ga atoms, prolonged exposure of the GaAs surface under high temperature and low As flux promotes the island formation leading to uneven morphology on Ga-rich GaAs surface. In contrast, the As-rich (2 × 4) surface, obtained under medium (~550 to 600 °C) temperature and As-beam flux conditions, provides a smooth surface. Since the FETs are surface devices, for in situ deposition of oxides under UHV conditions, the As-rich (2 × 4) surface is the one most relevant for MOSFET applications.
] direction. Due to the high diffusivity of surface Ga atoms, prolonged exposure of the GaAs surface under high temperature and low As flux promotes the island formation leading to uneven morphology on Ga-rich GaAs surface. In contrast, the As-rich (2 × 4) surface, obtained under medium (~550 to 600 °C) temperature and As-beam flux conditions, provides a smooth surface. Since the FETs are surface devices, for in situ deposition of oxides under UHV conditions, the As-rich (2 × 4) surface is the one most relevant for MOSFET applications.- (b)
Surface passivation and oxide deposition
Over the past five decades, persistent efforts have been carried out in searching for surface treatment methods to passivate III–V surfaces such that MOSFETs can be demonstrated. However, the conventional practice of thermal, anodic, and plasma oxidation methods failed to achieve this goal. Using an in situ deposition approach, the first successful passivation of GaAs surface was demonstrated in 1995 by Minghwei Hong et al. at Bell Labs [23]. In this method, electron-beam evaporated Ga2O3(Gd2O3) [GGO] dielectric film was deposited on an MBE-grown wafer in a UHV connected multiple chamber system. During the experiment, the freshly grown GaAs with an As-stabilized (2 × 4) surface was transferred under UHV condition from the III–V MBE chamber to another chamber for oxide deposition. Prior to deposition, the GaAs surface stoichiometry and atomic order were preserved, as monitored using RHEED, with extremely low oxygen exposure. Then the GGO film was deposited on the clean, atomically ordered (100) GaAs surface at substrate temperatures below 600 °C to avoid chemical reactions with GaAs substrates. The oxide molecules were supplied by electron-beam evaporation of a single-crystal Gd3Ga5O12 source. MOS structures on GaAs with a low Dit on the order of mid 1010 cm−2 eV−1 were demonstrated for the first time. However, low Dit values were not obtained in other oxide/GaAs systems using Al2O3, SiO2, and MgO prepared by a similar approach. Furthermore, pure Ga2O3 films cannot passivate GaAs surfaces effectively and show very high leakage current with poorly defined breakdown characteristics.
Further studies indicated that the unpinning of the GaAs Fermi level using electron-beam evaporated GGO dielectric film results from the Gd2O3 epilayer restoring the surface As and Ga atoms to near-bulk charge. An understanding of the bonding between Gd2O3 and GaAs is important for the development of new dielectrics used in III–V-based MOSFETs. Based on the consideration of Gibbs free energies of formation of all possible pairs in Ga, As, Gd, and O, the growth initiates from bonding a layer of oxygen atoms to Ga (Ga2O3: −998 kJ/mole) by taking up the As site (GaAs: −70 kJ/mole) in GaAs structure. Then the oxygen atoms would proceed to bind to Gd atoms of the next row due to the very large Gibbs energy for Gd2O3 formation (−1739 kJ/mole). Thus, the initial growth of GGO on GaAs contains only Gd2O3, despite the fact that incoming fluxes consist of various other species including Ga2O3. In addition, this Gd2O3 film is grown in a single-crystal form on GaAs. The Gd2O3 film has a cubic structure isomorphic to Mn2O3 and is (110)-oriented in single domain on the (100) GaAs surface. Once a Gd2O3/GaAs interface is formed, however, the competition for oxygen is significantly reduced and inclusion of Ga2O3 becomes possible, resulting in an oxide mixture of Gd2O3 and Ga2O3. Thus, the high interface quality GGO/GaAs heterostructure consists of a transition from a single-crystal GaAs substrate, to an epitaxial coherent Gd2O3 oxide layer of two to three monolayers in thickness, and then to the amorphous mixed oxides. This result matches well with the model of high-quality SiO2/Si interface, where the crystalline-Si to amorphous-SiO2 transformation takes place via an ordered crystalline oxide layer ~5 Å thick. The in situ UHV deposition of Gd2O3 approach can be extended to other rare earth oxides due to their chemical similarity. For example, using Y2O3 as the high-κ dielectric, low trap densities of (3 − 5) × 1011 eV−1cm−2 have been achieved at the Y2O3/GaAs (001) interface. Similar to Gd2O3, the Y2O3 film is also grown in a single-crystal form on GaAs with Y2O3 (110) planes parallel to GaAs (001) planes.
In contrast to the in situ deposition approach, MOSFETs were also successfully demonstrated in 2003 using ex situ ALD high-κ Al2O3 films as the gate dielectrics on GaAs and other III–V materials. Metalorganic trimethyl aluminum and water were used as the metal precursor and oxygen source for the ALD process, respectively. Since the ALD process was conducted on the GaAs surface exposed to the ambient air after epitaxial growth, a thin native oxide layer consisting of Ga and As oxides as well as spurious organic contamination is formed on the GaAs surface. To achieve a low interface state density on III–V surfaces, these oxides must be removed as much as possible before depositing high-κ dielectrics. Currently, a number of ex situ surface treatments of III–V (100) surfaces using a combination of wet chemical etch in NH4OH (29%) solution and (NH4)2S treatment before loading into the ALD system have been developed as outlined in the previous section. The self-cleaning effect of the ALD process further cleans up the As-oxide and provides high-quality III–V/high-κ interfaces. For selected ALD precursors, the detailed process parameters are mainly decided by the precursor characteristics such as decomposition behavior, sticking coefficient, vapor pressure, etc. So far, a number of suitable metal precursors have been reported for ALD deposition of high-κ dielectrics on various III–V surfaces with Al2O3, HfO2, and their alloys constitute the most studied systems.
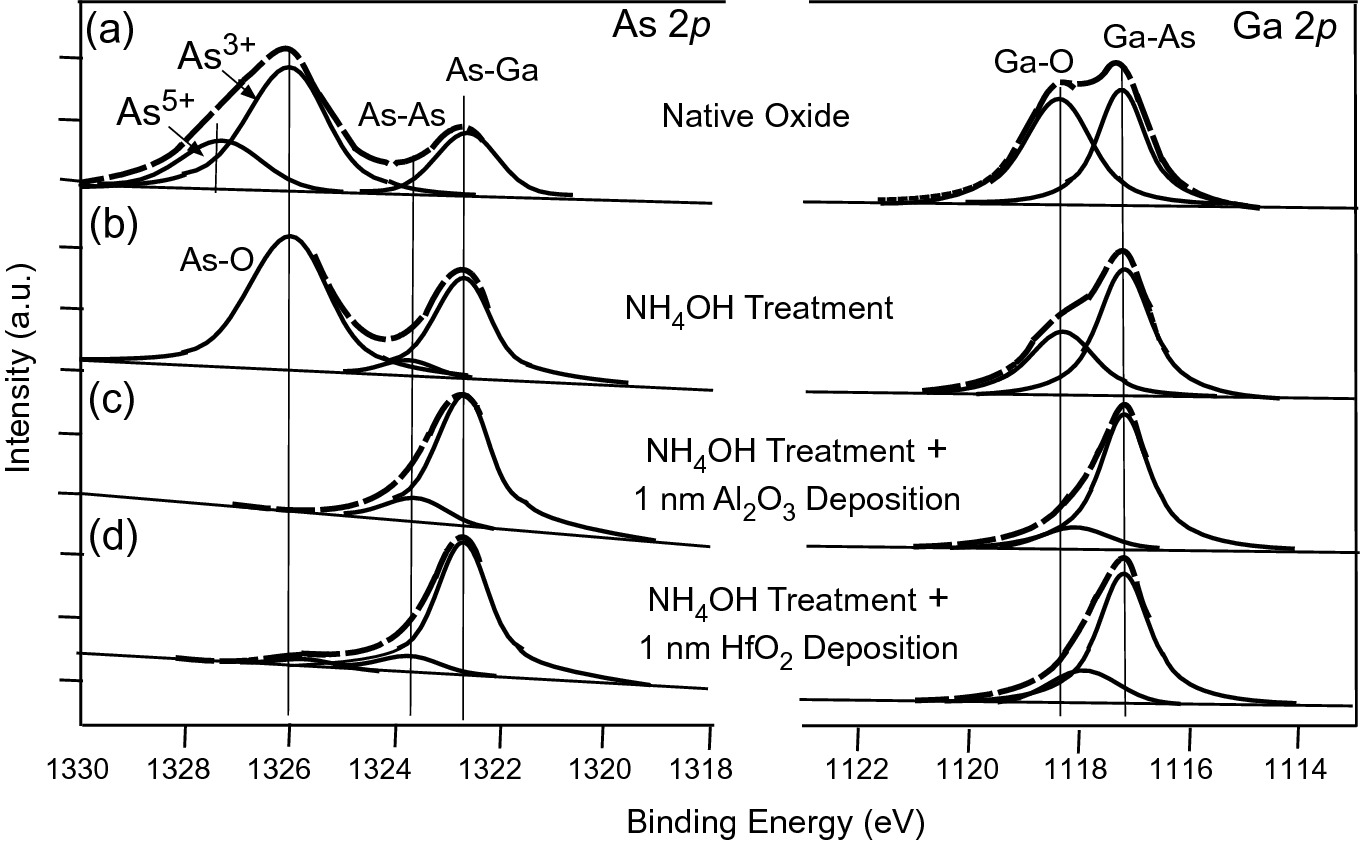
As 2p and Ga 2p X-ray photoelectron spectroscopy (XPS) spectra of a native oxides on GaAs, and interface reactions after b NH4OH-treatment of GaAs, c additional Al2O3 ALD process, and d additional HfO2 ALD process. A substantial reduction of the As- and Ga-oxides is noted. Reprinted with permission from [24], copyright AIP Publishing
As shown in Fig. 9.54, the presence of surface defects such as As-As dimers and AsOx persists in ex situ ALD fabricated high-κ dielectric/III–V semiconductor structures, and has been speculated to be the cause for the high Dit’s, or Dit peaks in the mid-bandgap of III–V materials. These defects mainly originate from the native oxide layer formed during the exposure of semiconductors to the ambient environment in ALD. To improve the high-κ dielectric/III–V semiconductor interface quality, one approach is to combine ALD with in situ UHV deposition, or in situ ALD process, such that the surface exposure to ambient is completely avoided during ALD processes. Direct comparisons between in situ and ex situ deposited ALD-Al2O3 on In0.53Ga0.47As have revealed that the in situ method shows no detectable AsOx component at the dielectric–semiconductor interface, whereas some AsOx residue is detected using the ex situ approach. A reduction of Dit by more than half is observed for the in situ method. Furthermore, as detailed in the following section, the fabricated inversion-channel In0.53Ga0.47As MOSFETs show much improved device performances for the in situ method than the ex situ method. The intrinsic drain current (Id), transconductance (gm), and effective mobility (µeff) are all improved by more than threefold over that of the ex situ method. In0.53Ga0.47As MOSFETs with similar performances have also been achieved using in situ ALD HfO2 and UHV-Y2O3 as gate dielectrics. Similar improvements of Dit using in situ ALD of Al2O3, HfO2, and Y2O3 on GaAs have also been demonstrated. A low interface trap density Dit of ~2 × 1011 cm−2 eV−1 has been achieved in in situ ALD Y2O3 and HfO2 on n-GaAs(001) and p-GaAs(001), respectively. The low interface trap density is key to the high performances of III–V-based MOSFETs.
9.8.4 High-κ Dielectric/III–V MOSFET Development
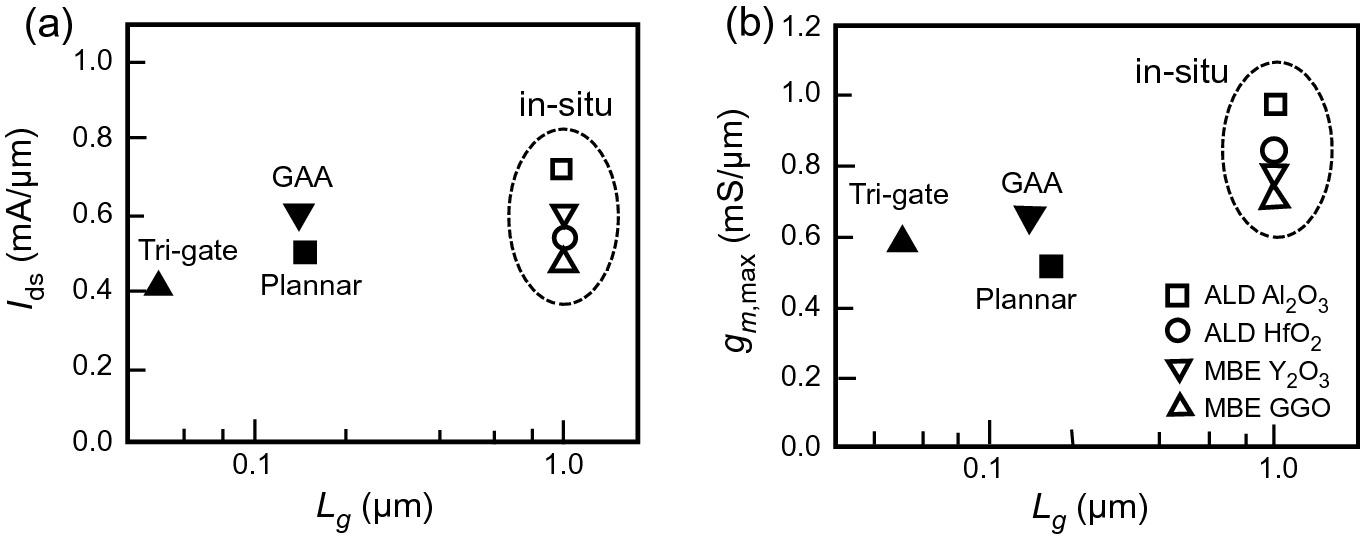
Benchmark of a drain current at VDS = VGS − VT = 1 V and b peak transconductance of in situ high-κ dielectrics/In0.53Ga0.47As MOSFETs and other enhancement-mode planar and non-planar devices using ex situ (solid symbols) high-κ dielectrics.
Reprinted with permission from [25], copyright AIP Publishing
During the past two decades, tremendous progress has been made in realizing both enhancement-mode and depletion-mode high-κ dielectrics/III–V MOSFETs. However, there exist several difficult challenges to overcome before III–V materials become appropriate for future high-speed, low-power logic applications. First, for III–V MOSFETs to be competitive against scaled Si MOSFETs, their physical gate length needs to be scaled to 30 nm and below with acceptable ION/IOFF ratio (>104) at VCC = 0.5 V. Recent demonstration of high-performance devices described above has already laid a solid foundation in achieving this goal. Second, for CMOS logic applications, there is a need for p-channel MOSFETs with very high hole mobility. Although III–V materials show 10–20 times better electron mobility compared to Si, their hole mobility is comparable to that of Si. To improve the hole mobility in III–V materials, one approach is to use compressively strained III–V channels in MOSFETs. Alternatively, other novel materials exhibiting high hole mobility, e.g., strained Ge quantum wells, can be used as the p-channel materials. Finally, to take advantage of the advanced development of Si IC technologies and the high-speed, low-power capabilities of III–V devices, it is desirable to monolithically integrate III–V devices selectively onto the Si platform. To achieve this goal, one has to solve two significant challenges, namely the lattice-mismatch and thermal mismatch between Si and III–V’s.
- 1.
Refer to the experimental results of an Al0.3Ga0.7As/GaAs HEMT reported in [6].
- (a)
Estimate the threshold voltage VT for three samples (R-96A, R-73A, and R-72A).
- (b)
The 2DEG in the triangular quantum well has a sine-wave-like distribution perpendicular to the conduction channel. What is the average concentration peak of the 2DEG located ΔW away from the heterojunction interface? The results can be calculated using the equation

Assume VDS = 0 and comment on your results in terms of whether they are realistic.
- (c)
Estimate ΔW again using Howard–Fang approximation for the triangular QW at the interface. Also discuss your results.
- (a)
- 2.
In an Al0.2Ga0.8As/Ga0.85In0.15As pseudomorphic high-electron-mobility transistor (pHEMT), the Al0.2Ga0.8As barrier is uniformly doped at a level of 2 × 1018 cm−3. At the Al0.2Ga0.8As/Ga0.85In0.15As interface, there is an undoped spacer layer on the Al0.2Ga0.8As side.
- (a)
Calculate the sheet carrier concentration in the triangular Ga0.85In0.15As quantum well for different spacer layer thickness (Wsp) of 25 Å and 100 Å. Assume the donor level in Al0.2Ga0.8As is sufficiently deep (Ed = 50 meV) so that the Fermi level is pinned there. The dielectric constant of Ga0.85In0.15As is 13.41ε0.
- (b)
Plot the equilibrium energy band diagram of the whole pHEMT structure, including metal contact, for the Wsp = 25 Å case using SimWindows. Assume the total Al0.2Ga0.8As barrier has a thickness of 150 Å and the undoped Ga0.85In0.15As 2DEG channel is 100 Å thick. The whole structure is grown on top of an undoped GaAs substrate. The metal-Al0.2Ga0.8As work function qϕm equals ~0.9 eV.
- (c)
Repeat part (a) for a modulation-doped Al0.3Ga0.7As/GaAs heterostructure with a 25 Å spacer layer and ΔEc = 0.2 eV. This HEMT structure has the same doping level in the Al0.3Ga0.7As barrier. The dielectric constant of GaAs is 12.85
 .
. - (d)
Now the 2DEG channel material of the pHEMT is replaced with a GaAs0.8Sb0.2 layer, but keep all other materials unchanged. For Wsp = 25 Å, calculate the sheet carrier concentration in the triangular GaAsSb QW. Will this material system outperform the Al0.2Ga0.8As/Ga0.85In0.15As pHEMT structure? Why?
- (a)
The relevant material parameters are listed below:
For Ga0.85In0.15As:  = 0.025(1 − x) + 0.71x − 0.0163x(1 − x)
= 0.025(1 − x) + 0.71x − 0.0163x(1 − x)
 = 0.00634 − 0.0483x − 0.0252x2.
= 0.00634 − 0.0483x − 0.0252x2.- 3.
The 2DEG with a sheet carrier density of 1013 cm−2 is obtained at the interface of an AlxGa1−xN/GaN HEMT structure grown by MOCVD. The AlxGa1−xN barrier is undoped and has a thickness of 30 nm. Using parameters provided in the reference article [9], verify that the Al-composition (x) of the AlxGa1−xN barrier is about 0.2 as shown in Fig. 11 of the referenced article.
- 4.
Repeat Problem 3 with up-to-date material parameters of AlxGa1−xN shown below:
ΔEc(x) ≈ 2.12x,
Eg(x) = xEg(AlN) + (1–x)Eg(GaN) − 0.7x(1–x).
Dielectric constant  (x) = 9.5 − x,
(x) = 9.5 − x,
m*(x) = 0.22me,
qϕm(x) = 1.3x + 0.84 (eV).


- 5.The active region of a p-channel pseudomorphic high-hole-mobility transistor (pHHMT) has a compressively strained InSb channel material and an Al0.35In0.65Sb barrier. For a 5 nm InSb QW sandwiched between Al0.35In0.65Sb barrier, the type-I band discontinuities, ΔEc and ΔEv, are determined as 0.342 and 0.254 eV, respectively. Assume the 200 Å thick Al0.35In0.65Sb barrier consists of a uniformly Be-doped layer of p = 1018 cm−3 and an undoped spacer layer, Wsp = 70 Å.
- (a)
Calculate the sheet carrier concentration in the triangular InSb quantum well. Assume the acceptor level in Al0.35In0.65Sb is sufficiently deep (Ea = 40 meV) so that the Fermi level is pinned there.
- (b)
Plot the equilibrium energy band diagram of the whole pHHMT structure, including metal contact, using SimWindows. The plot should extend into the AlInSb buffer layer for 200 Å. Assume the metal-Al0.35In0.65Sb work function qϕm equals ~0.16 eV.
- (a)
- 6.
In pursuing high-speed HBTs, InP-based material systems are the most promising. One of the systems being actively studied is based on using GaSb0.5As0.5 lattice-matched to InP as the base material.
- (a)
Find the band discontinuity values between lattice-matched GaSb0.5As0.5 and InP. Is this a type-I or type-II heterojunction?
- (b)
In Ga0.47In0.53As/InP N-p-N DHBTs, the valence band discontinuity between InP emitter and Ga0.47In0.53As base is 0.36 eV. The ΔEc in this type-I heterojunction is 0.252 eV. By replacing the Ga0.47In0.53As with lattice-matched GaSb0.5As0.5, the maximum current gain can be improved. Calculate the maximum current gain improvement.
- (c)
Compare the properties of GaSb0.5As0.5/InP and Ga0.47In0.53As/InP HBTs.
- (a)
- 7.
GaxIn1−xP is a useful material for visible light-emitting and HBT applications.
- (a)
Calculate the composition x and band gap energy of GaxIn1−xP lattice-matched to GaAs.
- (b)
Using model-solid theory, calculate the band discontinuities between lattice-matched GaxIn1−xP and GaAs.
- (c)
In Al0.3Ga0.7As/GaAs HBTs, the valence band discontinuity between Al0.3Ga0.7As emitter and GaAs base is 0.132 eV. By replacing the Al0.3Ga0.7As with lattice-matched GaxIn1−xP the maximum current gain can be improved. Calculate the magnitude of current gain improvement.
- (d)
Does GaxIn1−xP offer any advantages over Al0.3Ga0.7As as the barrier layer in an GaxIn1−xP/GaAs high-electron mobility transistor? Why? Note, the conduction band discontinuity in the Al0.3Ga0.7As/GaAs system is 0.263 eV.
- (a)
- 8.
Mini project: During the last 60 years, the density and feature size of Si ICs have followed Moore’s law faithfully through device scaling. However, the current Si technology will hit a feature size limit in the near future. New channel materials for increased electron and hole mobility, well above those achievable in strained Si, are needed. As gate dielectric scaling becomes increasingly difficult, carrier transport enhancement will become essential for current enhancement in the advanced FETs of future CMOS generations. One of the major problems encountered in developing FETs based on materials other than Si is the large disparity between electron and hole mobility. In order to design complementary FETs (i.e., one n-channel and one p-channel, and not limited to MOSFET), a material system with high hole mobility is required.
In this problem, the goal is to design a p-channel quantum well FET (QWFET) similar to the high-hole-mobility QWFET reported by Intel in 2008. (M. Radosavljevic et al., 2008 IEEE IEDM Tech. Dig., https://doi.org/10.1109/iedm.2008.4796798)
Select a material system among all available III–V materials for high hole mobility. Explain why you select it. However, you cannot copy the structure reported by Intel. Recall that in Chap. 6, we learned that under compressive strain, the heavy-hole band is lifted above the light-hole band in the growth direction (perpendicular to surface). But in the direction parallel to the surface (perpendicular to the growth direction), the effective mass becomes lighter. (See S. L. Chuang, Phys. Rev., B43, 9649, 1991.)
The selected material system should be able to form QWFET structures with high crystal quality. Of course, high-quality heterostructures prepared on metamorphic substrate structures are allowed. (That means you can use materials with any lattice constant as the substrate).
Design the layer structure of a QWFET based on the material system selected. We restrict the selection of FET structure to QWFETs (including pseudomorphic structures). Provide detailed material and device parameters such as ΔEv, NS and layer structures along with full energy band diagram. For heterostructures, the energy band discontinuities should be calculated. The portion of gate contact should also be included.
To simplify the calculation, set the spacer layer thickness as Wsp = 25 Å and the acceptor level in the barrier layer as Ea = 40 meV. The Schottky barrier height of the barrier layer can be determined following the method reported by Tiwari and Frank (Appl. Phys. Lett., 60, 630, 1992).
Your final device layer structure should be a depletion mode FET at zero gate bias.

