This may suffice to make the relation between the inversion problem and the theory of multiplicative functions and differentials clear. Abel himself proved only that part of the theorem above named for him which states that if are the zeros and are the poles of a meromorphic function, then the congruences (18.2) hold. But he proved this part in a sharper form, with congruence modulo G₀ replaced by congruence modulo G.26 Thus with the inversion already proved, one obtains the following.

Abel’s Theorem (second version). The points ; are the sets of zeros and poles, respectively, of a meromorphic function if and only if, for a suitable choice (independent of w) of the paths from to the points and , every Abelian integral w of the first kind satisfies the equation

Let z be any nonconstant meromorphic function on . It assumes, as we know, every value the same number of times, say n times. Then the surface may be regarded as an n-sheeted covering surface over the z-sphere, if one agrees that a point of lies over the point z = a of the z-sphere if the function z has the value a at . This is the conception of a Riemann surface which Riemann himself employed in his works on algebraic functions and their integrals, and one would say today that Abel’s argument is most easily understood from this representation. Over those values a, for which the n points at which z assumes the value a are not all distinct, there are certainly fewer than n points of the covering surface. If the function z assumes the finite value a r times at the point , then is a local parameter at ; the point over a is a branch point of order r − 1. If is any neighborhood of , then there exists a disc on the z-sphere such that over every point of this disc (except the center) there are exactly r points of which lie in the neighborhood . dz has a zero of order r − 1 at . (Therefore there can be only finitely many such values z = a over which there are fewer than n points of .) If z assumes the value ∞ s times at the point , then is a local parameter at and we have a branch point of order s − 1; dz has a pole of order s + 1 at . We denote the sum of the orders of all the branch points of the surface, its “branch order” by V. Then: the number of zeros − the number of poles of where the first sum on the right is over all points of the surface except those over z = ∞, while the second sum is over precisely the points over z = ∞. The right-hand side of this equation is

and the left-hand side = 2p − 2. Hence

The branch order is always even.

Now let dw be an arbitrary differential of the first kind on and let in general be the points of over the point z on the z-sphere. Then

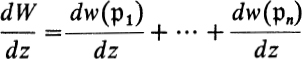
is a differential dW, which is regular everywhere on the z-sphere. But such a differential does not exist, except for dW = 0. If we draw any curve on the z-sphere from the south pole z = 0 to the north pole z = ∞, then the points of over this curve (which sometimes coalesce at branch points) form curves γ₁, …, γ_n and it follows from integrating dW that

Each curve y_v leads from a zero to a pole of z. If one joins to by a curve and denotes the curve then we obtain, as claimed, the equation (18.6).

Conversely, the congruences (18.2) follow from these equations, and hence the fact that the multiplicative function

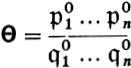
has the multipliers = 1 and is uniform on .

The coincidence of the lattices G and G₀ now comes out as follows. First, by the lemma there exist points such that

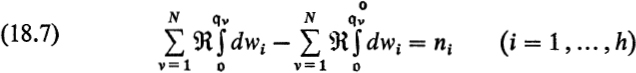
provided that the n_i are given integers. In this process, definite paths and have been chosen. From this it follows that the multiplicative function

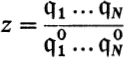
is uniform on . Hence, by the proof just carried out, paths and may be determined so that for these paths the left-hand sides of (18.7) all vanish. Now and are closed paths for which

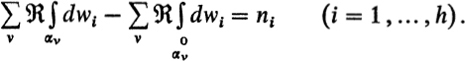
The 2N closed loops and α_v give together a closed path whose intersection numbers with the curves α_i of the integral basis, are the given integers n_i.

Analytically one attacks the Jacobi inversion problem as follows. One uses an arbitrary meromorphic function f() on and attempts to determine, not the points themselves, but the values of the function f at the points from (18.3) in their dependence on F₁, F₂, …, F_p. Since the values are determined only to within a permutation, it makes better sense to replace them by their elementary symmetric functions; that is, by the coefficients of the equation

of degree p whose roots are the numbers

These coefficients A_i, expressed in terms of are called, following Jacobi’s proposal, Abelian functions. Except for the singular systems which form a subspace of dimension only (2p − 4) in the whole 2p-dimensional F-space, the Abelian functions are uniform and regular analytic. Furthermore, they are 2p-fold periodic. For if γ_I (l = 1, 2, …, 2p) is an integral basis for the closed paths on and if

then, for every value of the index l, the numbers are a period system for the Abelian function A((F)):

These 2p period systems are linearly independent in the following sense: the determinant whose lth row is

is nonzero. If one carries through explicitly the proof which has been given here of the solvability of the inversion problem, then one obtains the following result: in every bounded portion

of the F-space, an Abelian function A((F)) may be represented as the quotient of two functions which are regular analytic throughout this bounded portion.27 The indeterminateness for the singular systems (F) arises because for these values both the numerator and the denominator in the representation vanish. The set of the points of indeterminateness possesses no translations onto itself except for those which obviously come from the periodicity of the Abelian functions.

Furthermore, Riemann and Weierstrass showed, by a much more penetrating analysis, that the Abelian functions, without restriction to a bounded set, may be represented as quotients of transcendental entire functions, the θ-functions. They gave an explicit analytic expression in the form of a rapidly convergent infinite series for the θ-functions. These 0-functions also suffice as a basis for the general theory of the 2p-fold periodic functions of p independent complex arguments; the theory of Abelian functions is only a special case.²⁸

The contents of this and the preceding paragraph show convincingly the ruling role played by the genus p, which is in essence a topological quantity, in the theory of functions and integrals on a closed Riemann surface. We were concerned with two trains of thought which we shall state once again with the labels

additive functions, partial fraction decomposition, Riemann-Roch theorem multiplicative functions, product representation, Abel’s theorem.

These two trains of thought permeate the theory of uniform functions on from here on this theory is easily completed with the aid of the reciprocity laws of § 16. But the significance of this structure shows up in the proper light only when we become familiar with the system of meromorphic functions on a closed Riemann surface from a third point of view, as an algebraic function field; this will be done in the next section. And first from this aspect do those functions appear most intimately related to our other interests, the algebraic and the geometric - in so far as these relate to the theory of algebraic curves in the plane and in spaces of higher dimension.

§ 19.    The algebraic function field

The meromorphic functions on a given closed Riemann surface form a field; this means precisely that the sum, difference, product, and quotient of two meromorphic functions (only division by 0 is ruled out) is again such a function. As was already done in the last section, one chooses a definite nonconstant meromorphic function z on for the independent variable. Thereby becomes an n-sheeted covering surface over the z-sphere, and the uniform meromorphic functions f on become n-valued algebraic functions of z. In this fashion there exists an algebraic function field belonging to , which includes the field k(z) = k of rational functions of z. Namely, the meromorphic function f satisfies identically a definite equation

of degree n, in which the r_i(z) are rational functions of z. More precisely, this means the following. Let be any point of , let t be a local parameter at , and let z = z(t) and f = f(t) be the expansions of z and f in integral powers of t in the neighborhood of ; then the left-hand side of (19.1) becomes identically zero when one substitutes the power series z(t) and f(t) for z and f respectively. To derive the equation (19.1), we first exclude the point z = ∞ from the z-sphere as well as those points over which there are branch points, and those points over which f has poles. For every other value of z we form the number

where the sum on the right is over the n points over z. The sum is independent of the ordering of these points. In the neighborhood of a nonexcluded point

become power series in z − z₀, and r₁(z) is a regular analytic function at every nonexcluded point. This function cannot have an essential singularity at any excluded point; hence it has only poles. If one uses a local parameter at a point of _z over an excluded value z₀, this may also be verified by elementary calculation. Hence r₁(z) is a rational function of z. Similarly, one sees that the other elementary symmetric functions of are rational functions of z. The equation (19.1), which is determined uniquely by f is called the field equation of f.

Furthermore, I claim that from the functions g belonging to the function field K associated with _z, an f may he chosen such that every g may be expressed rationally in terms of f and z. This f is called a function determining the function field. If _z, has the n distinct points over z₀, then it suffices to choose f such that it assumes n distinct values at these points. If dτ^k (k = 1, …, n) is a differential that has a pole only at and has the principal part − (z − z₀)⁻²dz, then one can set, for example,

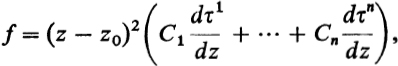
where one chooses any n different constants for C₁, …, C_n. The field equation of f is then irreducible; that is, its left-hand side, the polynomial

of degree n in the variable u, cannot be factored into two polynomials whose coefficients are also rational functions of z. For assume that this were possible; in a neighborhood of , f may be developed in a power series in the local parameter z − z₀ at . Suppose that this power series, replacing u, satisfies the equation . Join to any one of the points by a curve on whose trace on the z-sphere does not pass through any of the excluded points. Then all the function elements (z,f) along this curve must satisfy the equation . Hence f() is also a root of the equation thus it has n distinct roots and must be of degree n. Hence is only of degree 0 in u, and a factorization of the contemplated type does not exist.

To each point of there belongs a function element (z, f) which satisfies the equation F_z(u) = 0. For two distinct points these function elements are always different, and the elements belonging to all points exhaust the totality of those which satisfy that equation. In other words: the totality of those function elements which satisfy the irreducible algebraic equation F_z (u) = 0 constitutes a single analytic form in the sense of Weierstrass. This analytic form, regarded as a Riemann surface, is conformally equivalent to the given Riemann surface. The given surface is- the Riemann surface which belongs to the algebraic form defined by the equation F_z(u) = 0.

In order to express the given element g of the function field K rationally in f, we apply the Lagrange interpolation formula

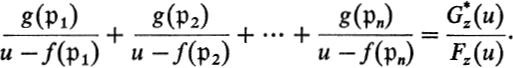
Again denote the n points of over the point z on the z-sphere. By the same argument as above, one finds that the coefficients of the polynomial of degree n − 1, are rational functions of z. For all values of z for which are different, it follows that

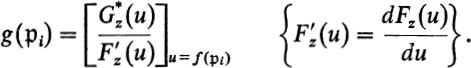
Since the polynomial F_z(u) is irreducible over the coefficient field k(z), F_z(u) and are without common divisor over this field. Therefore the Euclidean division algorithm produces two polynomials, H_z(u) and L_z(u), with coefficients which are rational functions of z, such that

If we introduce the polynomial , then the equation

becomes an identity on the surface. Finally, by means of the equation F_z(u) = 0, the polynomial G_z(u) may be reduced to one of degree n − 1. Hence any element g of our function field has a unique representation of the form

where the R_i(z) are rational functions of z. In this sense the quantities 1, f, …, fⁿ⁻¹ form a basis for the algebraic function field K relative to the ground field k of rational functions of z. Hence one calls n the degree of K over k.

Here one finds a purely algebraic attack on the idea of a function field. One operates with polynomials G(u) with coefficients in the field k. An irreducible polynomial F(u) of degree n is given. By identifying polynomials G(u) which are congruent modulo F(u), the “ring” of polynomials becomes a field K, of degree n over the ground field k,29

If the independent variable z is replaced by any other function, z*, on the surface, then there are infinitely many ways of choosing the function f* on the surface such that all functions may be expressed rationally in terms of z and f*. There is an irreducible algebraic equation F*_z*(f*) = 0 relating z* and f*. Also, z* and f* are rational functions of the variables z and f, which are related by F_z(f) = 0; conversely, z and f are rational functions of the variables z* and f*, which are related by F*_z*(f*) = 0. Through the birational transformation (z,f) (z*, f*) the equations

turn into each other. The degree of this equation is, naturally, not by any means an invariant under birational transformations. But the genus p is invariant under birational transformations.

If there exists a function z on which takes each value just once, then the associated algebraic function field is the field of rational functions of z (and p = 0). If there is no function on which takes each value just once, but if there is a function z which takes each value exactly twice, then we may assume that the algebraic equation (which must be quadratic) determining the function field has the form

where the e_i are all different. These l points and, if l is odd, the point ∞, are branch points of order 1, and hence the genus p is = (l/2) − 1 if l is even, and = (l − 1)/2 if l is odd. We see that l = 1 or 2 leads again to the rational field p = 0; l = 3 or l = 4 gives p = 1, which is the elliptic case; if l > 4, we get the so-called hyperelliptic function fields.

In an arbitrary algebraic function field of genus p = 1 there always exists a function with two prescribed poles, therefore a function which assumes each value only twice. In every function field of genus 2 we obtain a function of the same sort by dividing two linearly independent Abelian differentials of the first kind. But, starting with p = 3, the hyperelliptic case is no longer the general one.

In the theory of algebraic function fields, two paths are clearly indicated along which one can reach a deeper understanding of the laws governing them. One is that of abstract algebra; here the algebraic concepts of field, field extensions, the degree of a field over the ground field, the degree of transcendence, prime place, etc., are paramount; one admits coefficient fields of characteristic other than zero. Here algebraic construction must furnish that which was accomplished in our development by the Dirichlet principle and the method of integration. The other path, that trod by Riemann, is the “topological,” which we have followed. One may describe Weierstrass’ point of view as an algebraic-function-theoretic one lying between these two extremes: explicit construction reigns, but one always operates in the continuum of complex numbers. Similar remarks apply to the “Kurventheoretiker” of the German and Italian schools. The concept of an analytic form as a two-dimensional manifold lies close enough here, even if the further step, of regarding the topological properties of this manifold as more primitive than all others, is not completed. Furthermore, it is characteristic of the Riemannian type of development that it is always the Riemann surface, not the analytic form, which is regarded as the given object; the construction of an associated analytic form is a principal component of the problem to be solved. To be sure, in Riemann’s treatment itself this point of view does not appear with the complete clarity with which we can now distill it from the works of Prym, Dedekind,30 C. Neumann, and particularly Klein.³¹

Every closed Riemann surface of genus p may, as we saw, be represented as a multiple-sheeted covering surface over the sphere (with finitely many branch points, and without boundary). There is a great multitude of these “normal forms,” even when one normalizes the number of sheets by the condition n = p + 1 (which is always possible). A much more fundamental significance attaches to the essentially unique normal form of the Riemann surface of arbitrary genus, which is furnished by the theory of uniformization (theory of automorphic functions).

§ 20.    Uniformization

In the theory of uniformization the ideas of Weierstrass and of Riemann grow into a complete unity. With Weierstrass the analytic form (z, u) is described at each individual point by a particular representation with the aid of a parameter t (the “local parameters”): z = z(t), u = u(t). Certainly Riemann obtains a global representation z = z(), u = u() of the whole form, but he is forced to regard the parameter as a point on a Riemann surface (not as a complex variable in the usual sense). Uniformization theory is concerned with obtaining a global representation z = z(t), u = u(t) with the aid of a parameter t, the uniformizing variable, which varies in a domain of the smooth complex plane. F. Klein and H. Poincaré³² must be named as the true founders of the theory of automorphic functions, to which our problem leads. Their way to the general concepts and results was prepared in the literature by important, but more specialized, investigations of Riemann, Schwarz, Fuchs, Dedekind, Klein, and Schottky. The proof of the possibility of uniformization, based on the concept of a covering surface, was furnished simultaneously in 1907 by P. Koebe and H. Poincaré.³³ From then on, Koebe spent his whole scientific life in studying the problem of uniformization thoroughly from all sides, and with the most varied methods.³⁴ To him above all we owe it that today the theory of uniformization, which certainly may claim a central role in complex function theory, stands before us as a mathematical structure of particular harmony and grandeur.

The basic idea of the following proof, to derive the existence of the uniformizing variable from the Dirichlet principle, comes from Hilbert.³⁵

The uniformizing variable t that we seek should be such that it is suitable as a local parameter at each point of the given surface . Therefore it must be a uniform function, regular analytic except for poles of order one, on the universal covering surface . If we seek that function t which possesses the strongest uniformizing power, then we will attempt to determine t such that it assumes distinct values at any two distinct points of the surface ; then it will map one-to-one and conformally onto a domain of the t-sphere. Then not only the functions on the base surface can be represented as uniform functions of t; but also the much larger class of functions (which are in general infinitely many-valued on ) which arise from any function element on which can be continued, without branching, along all paths in . And since (in contrast to ) is simply connected, the possibility of such a map does not contradict the analysis-situs properties of . We may well drop now the basic assumption of the preceding sections, that be closed; this assumption would not simplify anything in uniformization theory.

We obtain the desired uniformizing variable simply by applying the Dirichlet principle, not to , but to the universal covering surface . We choose a point on with the local parameter ζ; then we construct on , with the aid of the Dirichlet principle, the potential function U which is regular everywhere on except at , which behaves like (1/ζ) at , and with the following properties.

(1) The Dirichlet integral of U over all of , except for an arbitrarily small ζ-disc about , is finite,

(2) For every continuously differentiable function w on , with finite Dirichlet integral, which vanishes in a neighborhood of , the variation D(U, w) satisfies

U generates a differential dτ on ; since is simply connected, this must be the differential of a certain function

whose real part coincides with U, which is regular analytic everywhere except at , and which has a pole of order one at . Then τ is a uniformizing variable of the type we seek. The proof of this fact follows in a very elegant fashion with the aid of the following deduction, due to Koebe.³⁶

We prove first the following fact.

If V₀ is any real constant, then the points of at which V > V₀ form a single domain; similarly for the points where V < V₀.

Now 1/τ is a local parameter at ; let K₀ : | 1/τ | ≤ a₀, be a (l/τ)-disc about . Let (V₀) be the closed set on consistingofthepoints where V = V₀; then certainly only two of the domains determined by (V₀) have points in K₀. If our claim were false, then among the domains determined by (V₀) there would be one, say , that did not penetrate the neighborhood K₀ of . Now let ϕ(u) and ψ(u) be any two real functions, defined and continuously differentiable for all real values u. We form the following function w on the surface :

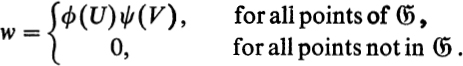
This function is everywhere continuously differentiable, provided that

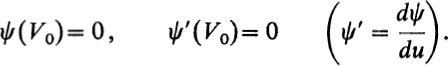
In the neighborhood K₀ of , w vanishes identically. If is any point in and if z = x + iy is a local parameter at , then

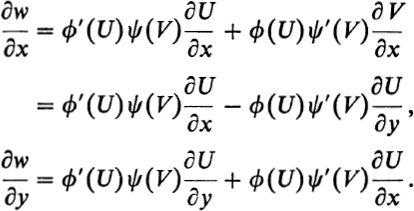
If ϕ, ϕ′, ψ, and ψ′ are bounded functions, then the Dirichlet integral of w over all of will be finite. Then, under the given conditions, D(U, w) = 0. Now

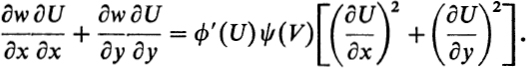
If we choose ϕ and ψ such that and ϕ′ and ψ are positive for all values of their argument (except for u = V₀ in the case of ψ), then we have a contradiction.³⁷

From the fact proved, and the simple connectivity of , one can draw conclusions on the behavior of τ.

(1) dτ has no zeros. If at a point on , where τ = τ₀, dτ = 0, then not τ − τ₀, but (τ − τ₀)^1/r (r an integer ≥ 2) would be a local parameter at ; let us assume r = 2; the proof for larger r is analogous. I set τ − τ₀ = σ² and draw in the complex σ-plane a disc K, with center σ = 0, so small that it is, via the function σ, the conformal image of a certain neighborhood of the point on . I take four points , , , in K, as indicated in Fig. 9, which are the vertices of a cross formed by two linear segments, α and β, crossing at the origin. At and , V > V₀; at and , V < V₀. I think of this figure transferred to the surface ; then I can join and by a curve α′, at every point of which V > V₀; likewise, I can join and by a curve β′ on which V < V₀. The intersection number of the two closed curves, α + α′ and β + β′, is thus = 1. But this contradicts the fact that α + α′, as a curve on the simply connected surface , must be homologous to zero.

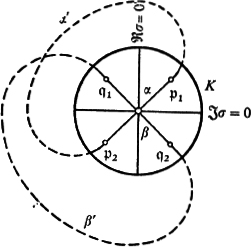
FIGURE 9

(2) If I say that a point of the surface , at which τ has the value τ₀, lies over the point τ₀ of the τ-sphere, then becomes a covering surface of the τ-sphere or the τ-plane. By what we have proved under (1), this covering is unbranched. There is just one point, , over τ = ∞. I follow the line V = V₀, starting at τ = ∞, in the τ-plane in the direction from smaller to larger values of U; on , the point , starting at , traces a curve over this line in the τ-plane. If I do not run into any boundary before returning to ∞, then describes a closed curve , for there is only the single point over ∞ then covers the line V = V₀ in the τ-plane simply. But if I meet an obstruction, then I obtain a curve on which covers a certain piece U < U₁ of the line V = V₀ simply. Then I follow the line V = V₀, now from larger to smaller values of U, and obtain a curve on which covers a piece U > U₂ of the line simply. The sum + forms a curve through , nonclosed, and without end on . In either case, the curve separates the surface , since it is simply connected, into two domains, and . If, outside of , there were points of at which V = V₀, say in , then there would be points in at which V < V₀ and points at which V > V₀. The point set (V₀) would then determine at least three domains. Therefore exhausts the points at which V = V₀. Thus, as a covering of the τ-sphere, is everywhere at most two sheeted. A value U₀ + iV₀ will certainly occur once and only once on , if V = V₀ is a closed curve on .

FIGURE 10

We still want to prove carefully that must always separate the surface . For this purpose we construct a two-sheeted, unbranched, and unlimited covering surface over as follows. Cut along , take two copies of this cut surface and identify the edges of the slits criss-cross. Put abstractly, this amounts to the following. To each point of we associate two points “over it,” and . If is a point not on , τ₀ = τ(), and an arbitrary (τ − τ₀)-disc which does not intersect , then the points (with upper index 1) which lie over the interior points of constitute a “neighborhood” of ; those points over the same points constitute a “neighborhood” of . On the other hand, if is on , let denote an arbitrary (τ − τ₀)-disc. Those points whose trace points lie inside and satisfy the condition V ≥ V₀, together with all points lying over inner points of which satisfy the condition V < V₀, shall constitute a “neighborhood” of . The neighborhood of is defined analogously. In the last case all the points in at which V = V₀ certainly belong to ; hence this definition of the concept of neighborhood is in agreement with all the demands to be made of such a definition. If does not separate , then it is clear that the manifold just defined also satisfies the condition that any two of its points can be joined by a continuous curve. But the existence of such a covering surface would contradict the fact that is simply connected.

The last step in the proof is the demonstration of the following theorem.

There exists at most one real number V₀ such that the associated line V = V₀ on is nonclosed.

For if there were two such lines and , say and then one makes use of a closed line U = U₀ completely contained in K₀ (U₀ is chosen large enough). Let be one of the pieces of the curve ; let be the piece of . Over the heavily drawn path (Fig. 10, the three segments) in the τ-plane there is a curve in , which covers the path simply, and has no ends on . This curve separates the simply connected into two domains; let be that one of the two domains which does not contain the point . Again we set

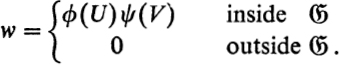
For this function to be continuously differentiable on , we must have

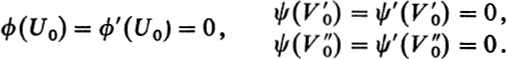
Let ϕ, ϕ′, ψ, ψ′ be bounded and let ϕ′ (except for u = U₀) and ψ (except for u = or ) be positive.³⁸ Then we get a contradiction of the equation D(U, w) = 0. Thus we have proved the following.

    τ maps the surface one-to-one and conformally either onto the complete sphere (case 1)

or

    onto the sphere with one point τ₀ removed (case 2)

or

    onto the sphere with a slit V = V₀, U₁ ≤ U ≤ U₂ removed (case 3).

We replace τ by a somewhat different uniformizing variable t. To be sure, t = τ in case 1. In the second case we arrange it so that the point omitted from the sphere is the point at ∞: set t = 1/(τ − τ₀); t maps the covering surface onto the whole plane (without the point at ∞). In the third case we first apply an entire linear transformation so that the slit is given by

Then, with the aid of the formula

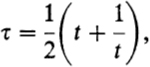
the slit τ-sphere is mapped conformally onto the interior of the unit disc | t | < 1 in the t-plane.

The construction we have described of the uniformizing variable t occurs in two clearly separate steps. First, the surface solves the problem in so far as it belongs to analysis situs. Then the function theoretic theorem, every simply connected Riemann surface may be mapped conformally onto a domain on the sphere, applied to gives the uniformizing variable. By a slight modification of the argument, one can also show that every planar surface may be mapped conformally onto a domain on the sphere. For nonplanar surfaces this is impossible, for reasons of analysis situs: there will not exist even a topological map onto a domain on the sphere. Every uniformizing variable belonging to (unbranched relative to ) will map a certain unbranched, unlimited, planar covering surface over conformally onto a plane domain. One assigns two uniformizing variables which map the same covering surface onto subdomains of the plane to the same class {}. The determination of all uniformizing variables requires then the solution of two problems.

(1) The analysis-situs problem: to determine all unbranched unlimited planar covering surface of a given surface .

(2) The conformal mapping problem: to find all possible conformal maps of a planar surface onto a plane domain.

That the last is always possible in at least one (and hence in infinitely many) way (in other words, that every class of uniformizers {} conceivable under the analysis-situs condition of planarity actually exists in the function theoretic sense) is the content of Koebe’s general uniformization principle.³⁹ As a matter of fact, this principle goes even further; it includes not only the uniformizing variables which are unbranched relative to , but also the great multitude of branched uniformizing variables. But without question, the uniformizing variable which we have set up and denoted by t carries more fundamental significance than any other uniformizing variable.

§ 21.    Riemann surfaces and non-Euclidean groups of motions. Fundamental regions. Poincaré -series

To what extent is the uniformizing variable t determined by the properties stated at the end of the last section? That is, in how many ways can one map the surface conformally onto the sphere, the plane, or the unit disc? This question obviously comes down to the following: in how many ways can one map the sphere, plane, or disc conformally onto one of these three domains? To begin with, it is clear that the sphere, since it is closed, can be mapped onto neither the plane nor the disc. Also, a conformal map of the plane onto the disc is impossible. If the function t^*(t) transformed the t-plane conformally onto the unit disc in the t^*-plane, then it would be an entire function whose absolute value would be bounded by one. By Liouville’s theorem, there is no such function (except for the constants, which make no sense here). Furthermore, the following simple theorems hold.

(CASE 1). The set of conformal maps of the sphere(represented in the usual fashion by a complex variable) onto itself is the set of linear transformations.

(CASE 2). The conformal maps of the complex plane onto itself are given precisely by the entire linear transformations.

(CASE 3). Likewise, the open unit disc can be mapped conformally onto itself only by linear transformations.

Case 1. We have to show that if the t-sphere is mapped conformally onto the t^*-sphere, t^* = t_*(t), so that t = 0 goes into t_* = 0 and t = ∞ goes into t^* = ∞, then the map must be of the form t^* = ct, where c is a constant. Now 1/t^* is regular at the north pole (t = ∞) of the t-sphere and has a zero there; so t/t^* is regular there. Since the relation t → t^* is one-to-one, t^* vanishes only at t = 0, where it has a zero of order one; hence t/t^* is regular on the complete t-sphere, and is thus a constant.

Case 2. Again we may assume that t = 0 is mapped into t^* = 0. Next one has to prove that

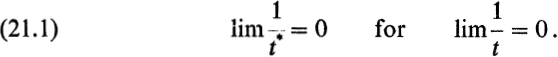
The circle | t^* | = R_* corresponds to a closed curve in the t-plane; let R₀ be the maximum distance of a point on from the origin, and let R be an arbitrary number > R₀. In the disc | t | ≤ R, | t^* | assumes its maximum, which must be > R^* at some boundary point, say t = t₀. The image , of the circle | t | = R, in the t^*-plane cannot meet the circle | t^* | = R^*; for the circle | t | = R and the curve , of which those two curves are the images, do not meet in the t-plane. Since the point t^*(t₀) on has an absolute value > R^*, we must have | t^* | > R^* for all points on . That is, | t | > R₀ implies | t^* | > R^*, and this is the claim (21.1). Hence l/t^*(t) is regular at the north pole of the t-sphere and has a zero there. The rest of the argument is exactly the same as in case 1.

FIGURE 11

We settle case 3 with the aid of the so-called Schwarz lemma.⁴⁰ Again we may assume that t = 0 goes into t^* = 0. If I consider the regular function t^*/t in the disc | t | ≤ q (< 1), it must attain its maximum absolute value on the boundary, and hence this maximum is < 1/q ( | t^* | < 1,| t | = q). Since I can choose q arbitrarily close to 1, | t^*/t | ≤ 1 must hold at all points of the open unit disc. In a similar fashion, | t/t^* | ≤ 1, and hence | t^*/t | = 1. This is possible only if t^*/t is a constant of modulus one.

With this the stated claims are demonstrated: the uniformizing parameter t is always uniquely determined to within a linear transformation. The linear transformations which map the open unit disc onto itself have the form

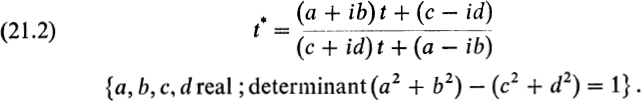
In particular, since the cover transformations of are one-to-one conformal maps of onto itself, these cover transformations must correspond to linear transformations in the t-plane. Thus there corresponds to the group of cover transformations a certain isomorphic group Γ of linear transformations. No transformation of the group Γ (except the identity) can have a fixed point in the image domain (sphere, plane, or disc); a fixed point is a point that goes into itself under the transformation. Since every linear transformation of the sphere has a fixed point, there are no cover transformations in case I, except the identity. Then is the same as , and is identical, as a Riemann surface, with the sphere. Case I can arise only when the given Riemann surface is equivalent to the sphere.

The points of over one point of appear in the map as a system of points t equivalent under Γ. Such a system Σ has the property that any point of the system can be carried into any other by some transformation of Γ; and also, the image of any point of Σ by any transformation of Γ is another point of Σ (see p. 28). The uniform functions on , regular except for poles, appear, when expressed as functions of t, as automorphic functions attached to Γ. That is, functions z(t) which are invariant under the transformations of Γ:

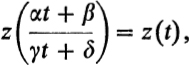
where t^* = (αt + β)/(γt + δ) is any transformation in the group Γ. The group Γ must be discontinuous; that is, a system of equivalent points under Γ can never have a limit point in the image domain. If we define a Riemann surface by taking the “points” of to be the systems of equivalent points under Γ and by carrying the angular measure in the t-plane directly over to , then is equivalent, as a Riemann surface, to the given .

is the most appropriate normal form into which every Riemann surface can be brought.

In case 2, Γ must consist of entire linear transformations which have no finite fixed point. The only transformations satisfying this condition are the translations t′ = t + α. A discontinuous group of translations must be of one of the following types.⁴¹

(1) Γ contains only the identity. Then is identical with , and is equivalent to the plane (the “Simply punched” sphere, that is, the sphere without the north pole).

(2) Γ consists of the iterations of a single translation

then clearly is equivalent to the infinitely long right circular cylinder, and hence, by the Mercator projection, to the doubly punched sphere (the sphere without north and south poles).

(3) Γ will consist of the transformations

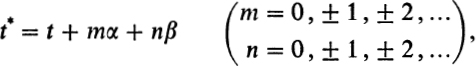
where α and β are translations in different directions. Then is closed; dt is a uniform differential, regular everywhere on , without any zeros, and hence is a closed Riemann surface of genus one. Every such surface - whose type (but not its most general form) is the torus - admits in fact a uniformization by the integral of the first kind, by means of which the universal covering surface is mapped onto the plane.

Aside from the few exceptions listed above ( = sphere, simply or doubly punched sphere, closed surfaces of genus one), case 3, in which the image domain is the open unit disc, always occurs. Since in general the periphery of the unit disc is a natural boundary (cut) for the automorphic functions of t which represent the functions on the base surface , one calls t a cut-circle uniformizing variable [Grenzkreis-Uniformisierende].

The group Γ is not determined uniquely by the given surface. For t may be replaced by any variable t′ obtained from t by a linear transformation T₀ which preserves the open unit disc. This transforms Γ into the group

We introduce the following terminology. Any point t of the open unit disc is a “point of .” For the “straight lines in ” we take the circular arcs in which are orthogonal to the unit circle (the diameters of the unit disc are included in these “straight lines”). Any linear transformation preserving the open unit disc is a “motion in ”; two point sets in are “congruent” if one can be carried onto the other by a “motion.” The usual angular measure is retained. Then the complete Bolyai-Lobatschefsky geometry holds for these “points” and “straight lines.” That is the geometry whose axioms are the same as the axioms of Euclidean geometry, except that the parallel axiom is omitted.⁴² So we may call the non-Euclidean plane. The complex variable t (restricted by the inequality | t | < 1) is to be regarded as a coordinate representing the points in the Lobatschefskian plane, in the same way that the rectangular Cartesian coordinates x, y, or their complex fusion z = x + iy, represent the points of the Euclidean plane. Any linear transformation of t which preserves the unit disc provides another equally valid coordinate system for the Lobatschefskian plane. In this interpretation, Γ now appears as a group of motions of the non-Euclidean plane; or, more precisely, as a representation of such a group by means of a definite coordinate t. If we replace t by t′ obtained from t by a linear transformation preserving the unit disc, then the new group Γ′ thus obtained is to be regarded as a different representation of the same group of motions of the non-Euclidean plane (with the aid of another coordinate t′). There are no rotations in Γ, that is, no motions of which leave some point of fixed.

Thus to every Riemann surface (aside from the four exceptions already listed) there corresponds a single uniquely determined discontinuous group Γ of motions of the Lobatschefskian plane; and Γ contains no rotations. Two Riemann surfaces are conformally equivalent (as Riemann expressed it, belong to the same class or are realizations of one and the same ideal Riemann surface) if and only if the associated groups of non-Euclidean motions are congruent in the sense of Lobatschefskian geometry. Conversely, to every rotation-free discontinuous group of non-Euclidean motions there corresponds a definite class of Riemann surfaces. (The surface constructed on page 169 will serve as a representative of this class.⁴³)

To present a discontinuous group Γ of motions of the n-E plane⁴⁴ in a more visual fashion, one uses, following Klein and Poincaré, a simple gapless covering of the plane by n-E congruent regions (fundamental regions) which are permuted by the motions of Γ. A dissection of this sort, which is as simple as possible, is provided by the following considerations.

Definition of n-E distance. Let t₁ and t₂ be any two distinct points in the open unit disc; join them by a n-E line, that is, a circular arc in the Gaussian t-plane which intersects the unit circle orthogonally at t_∞1 and t_∞2. This circular arc is uniquely determined by t₁ and t₂. The points on it are to come in the sequence t_∞1, t₁, t₂, t_∞2 (Fig. 12). The cross-ratio

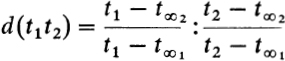
has a positive real value > 1, and its real logarithm

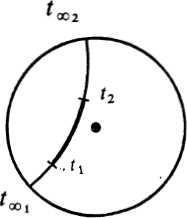
Fig. 12. Non-Euclidean segment.

is positive, r (t_l, t₂) is invariant under all linear transformations preserving the unit disc. The n-E segment t₁t₂ is n-E congruent to another such segment if and only if Furthermore, if the three points t_l, t₂, t₃ lie in that order on an n-E line, then

Because of these two facts, we shall speak of the number r (t_l, t₂) as the non-Euclidean distance between the points t₁ and t₂. Now we are in a position to measure not only angles but also distances in the n-E plane.

If is a system of equivalent points under Γ, if t₀ is a single point of , and t an arbitrary point of the n-E plane, then because of the discontinuity of Γ there are only a finite number of points of whose distance⁴⁵ from t does not exceed an arbitrary given number R. Thus among the points of there is one or several (but certainly only a finite number) of points t_h such that the distance r(t, t_h) is the smallest distance of t from any point of . Then, as I shall express it briefly, t lies closest to t_h. If the distance r (t, t_h) is strictly less than the distance to all other points of , then I can find a neighborhood of t such that every point of this neighborhood lies closest to t_h. Let t_h be any point of ; I collect all those t which lie closest to t_h into a point set with “center” t_h. The resulting sets with all centers in , have disjoint interiors and cover the whole n-E plane. The transformation of Γ which carries t₀ into t_h carries into ; hence is n-E congruent to . To every point t there corresponds a point of which is equivalent to t under Γ; two distinct interior points of are never equivalent. Thus has the properties of a fundamental region. Also, is convex; that is, if t′ and t″ are any two points of . then all points of the n-E segment t′t″ joining t′ and t″ belong to . The perpendicular bisector of the segment t₀t_h is the locus of points equidistant from t₀ and t_h; to every t_h distinct from t₀ we obtain such a line . The boundary of the closed set is composed of segments of these lines; the interior of consists of those points which, for every , lie on the same side of as t₀. All points of the line have a distance from t₀, and there are only a finite number of the centers t_h whose distance from t₀ does not exceed an arbitrarily given 2R. Hence it follows that only a finite number of segments on the boundary of has a distance ≤ R from the principal center t₀. Thus is a convex polygon, with a finite or infinite number of sides, whose vertices (that is, those points which are equidistant from three or more points of the system ) have no limit point in the finite.

Following Fricke, is called a normal polygon belonging to the group Γ. The sides of the normal polygon are associated in pairs; either side of a pair can be carried onto the other by some motion in Γ. Two sides with a common vertex are never associated; for such a common vertex would have to be a fixed point of the motion carrying one side onto the other. These motions carrying one side of onto another (that is, the motions carrying onto a fundamental region which abuts along some side of ) generate the group Γ. That is, every motion of Γ may be obtained by iterating and composing those particular motions. One proves this as follows. Join an arbitrary point t_h of to t₀ by a polygonal path which avoids the vertices of the polygonal decomposition {}. Now observe the succession of polygons in this decomposition through which the polygonal path passes. Suppose there are in all e polygons equivalent to (including itself) which meet at the vertex 1 of . Then there are exactly e centers to which 1 lies closest, and there are e points of which are equivalent to 1 under Γ; or, in the terminology of Poincaré, which constitute a cycle of vertices of the polygon . The sum of the angles in at the vertices of such a cycle is the full angle 1 (= 360°).

The Riemann surface (p. 169) belonging to the group Γ is obviously closed if and only if there exists a positive number R such that for every point in the n-E plane there is at least one equivalent point under Γ whose n-E distance from the center t₀ is ≤ R. Then every point has a distance ≤ R from the closest point in the system ; in particular, is completely contained in the n-E disc of radius R about t₀. Since the vertices of cannot have a limit point in the finite, there are, in this case, only a finite number of such vertices : has finitely many sides. Let the number of sides of , which must be even because of the pairing of the sides, be 2s; let c denote the number of distinct vertex cycles of , so that c is also the sum of the angles in . We wish to show that the genus p of this closed Riemann surface may be computed from s and c by the simple formula

Since every cycle contains at least three vertices, we have

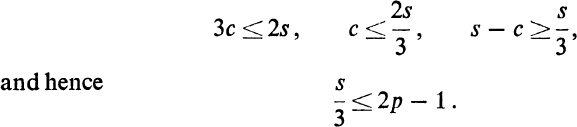
Therefore 12p − 6 is an upper bound for 2s, the number of sides or vertices of a normal polygon.

We choose t₀ = 0. The (n-E as well as Euclidean) linear segments joining 0 to the vertices of separate into 2s triangles. This provides a triangulation of into 2s triangles with 3s edges and c + 1 vertices. Then, from the most basic formula of combinatorial topology, the genus p is in fact determined by the equation

In this book we have adopted the methodological attitude of avoiding boundaries as much as possible, and we have operated with coverings by overlapping neighborhoods rather than with dissections into simple pieces of surface. The appeal here to combinatorial topology would introduce a foreign element. Therefore, instead of this topological proof of the equation (21.3), I prefer a function theoretic proof. It runs as follows.

We take a meromorphic differential dz on the closed surface . As we know, its order is 2p − 2. We shall assume for the moment that none of the zeros or poles of dz lie on the sides of . Consider the analytic function dz/dt of t in the region . Being a convex polygon, is simply connected, and one of the simplest consequences of the Cauchy integral theorem in function theory says that the increase in the azimuth of dz/dt, in tracing the boundary of , is equal to the number of zeros less the number of poles of dz/dt in the interior of ; hence it is = 2p − 2. To determine the increase of the azimuth of dz/dt in tracing the boundary, consider a side σ = t₁ t₂ = AB of and its equivalent side where the second comes from

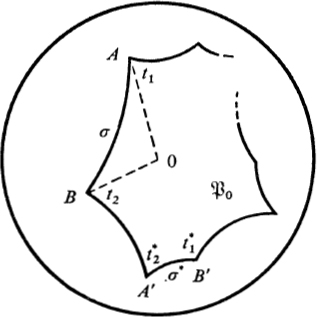
Fig. 13. Determination of the genus from the normal polygon.

the first by the substitution t^* = tS of the group Γ. This substitution S carries the polygon into an equivalent one which abuts on along the side . If, in tracing in the positive sense, the segment σ is traced from t₁ to t₂, then the segment σ* will be traced in the sense Since dz is invariant under the substitution S, the sum of the contributions of these two segments to the increase of the azimuth is equal to the difference

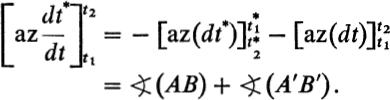
Here denotes the negative of the angle (measured in Euclidean fashion) through which the tangent to σ = AB turns when this side is traced in the positive sense from A to B. This angle is positive and = minus the sum of the angles of the n-E triangle 0AB. In this way we get, for the desired increase in the azimuth of dz/dt when the boundary of is traced in the positive sense, the value

and the equation claimed, 2p − 2 = s − c + 1, follows.

It is inherent in the situation that one cannot completely avoid bordered regions in a dissection into equivalent fundamental regions, but the boundaries here are simple enough to be grasped easily.

If dz has zeros or poles on the boundary of , then one can proceed in one of two ways. Either one cuts out disc neighborhoods of these zeros and poles and later lets the radii tend to zero, or one avoids this unpleasant eventuality by a suitable choice of the center t₀. If t = a is a zero or pole of dz which lies on the mid-line of , that is, if t₀ and have the same distance from a, then t₀ has the same distance from a as from aS^{− 1}. So one need only choose t₀ such that it does not lie on any of the mid-lines associated with a pair of distinct but equivalent zeros or poles of dz; then it is certain that no point a lies on the boundary of the normal polygon with center t₀. Since only a finite number of these mid-lines come within an n-E distance of the origin ≤ a given R, this is certainly possible. Finally, one can bring the point t = t₀ into the point t = 0 by a suitable n-E motion and thus make t = 0 the center of .

The dissection of the n-E plane into normal polygons furnishes not only a visualization of the n-E group of motions, but also a means of constructing such groups directly.⁴⁶

In the group Γ of motions of the non-Euclidean plane (or in the associated manifold ) we meet the purest embodiment of the concept of a Riemann surface, freed of all accidental properties. To crown the whole development of this part of Riemannian function theory, the solution of the following problem would be desired. Given a Riemann surface in its normal form (that is, the associated group of motions of the non-Euclidean plane), to express each of the uniform or many-valued unbranched functions on the surface by means of a closed analytic formula in terms of the coordinate t of the points in the Lobatschefskian plane. The -series introduced by Poincaré⁴⁷ constitute an important attack on the solution of this problem. If the given group Γ which preserves the open unit disc consists of the substitutions

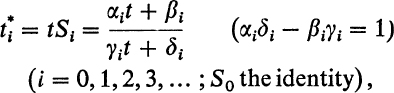
then, for example,

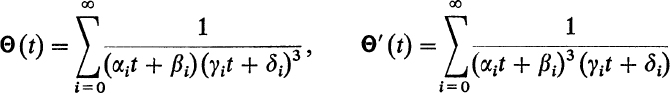
are Poincaré -series. To establish the uniform absolute convergence of these series, take an ordinary disc κ of radius a: |t − t₀ | ≤ a about an arbitrary point t₀ ( | t₀ | < 1) so small that the equivalent discs κS_i are mutually disjoint. The surface integral, J_i, of

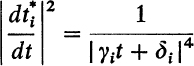
over κ is the (Euclidean) area of κS_i; consequently, is convergent. If the Euclidean distance from t to t₀ satisfies | t − t₀ | ≤ a/2, then by (12.16)

Therefore

is uniformly convergent in the neighborhood of t = t₀. Also,

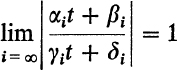
holds uniformly for | t | ≤ q < 1, for the equivalent points condense only on the boundary of the unit disc; the uniform absolute convergence of the two series, , and ′ follows. At t = 0, and at all equivalent points under Γ, has a pole of order 1; otherwise is regular. At the same points ′ has poles of order 3 and is regular everywhere else. From the equation

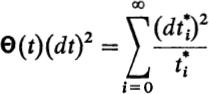
it follows that (t)(dt)² goes into itself under an arbitrary transformation S_i of the group

Similarly,

Hence (t)/′(t) is an automorphic function relative to the group Γ; it is not identically zero, but is has a zero of order 2 at t = 0 (and at every equivalent point). In short, it is a uniform nonconstant function, without essential singularities, on the ground surface .

The examples of -series given here are of dimension − 4. Poincaré succeeded (by using n-E instead of Euclidean area) in proving⁴⁸ the absolute convergence of -series of dimension − r, for r > 2. Once a Riemann surface is given in its normal form, one might hope, on the basis of Poincaré’s attack, that one could succeed in deriving all the theorems on the existence of functions and integrals on the surface with the aid of analytic formulae. This would be the analog of what has long been possible in the case p = 1 with the theory of elliptic functions. Perhaps one would prefer then to construct Riemannian function theory as follows : with the aid of the Dirichlet principle or a competing method derive, not the existence of functions and integrals, but only the existence of the cut-circle uniformizing variable; then construct the functions and differentials by explicit formulae with this uniformizing variable as argument. The recent extensive investigations of H. Petersson are aimed in this direction. The difficulty lies in the limit passage from r > 2 to r = 2. The structural form of the Poincaré series does not appear to furnish an adequate foundation for this process; Petersson reaches his goal only through a new device of regarding the -series as eigenfunctions of certain functionals.⁴⁹ In spite of the tremendous advance attained by Petersson, it seemed advisable to me to retain, in this book, the independent construction of all functions and differentials by means of the Dirichlet principle.

§ 22.    The conformal mapping of a Riemann surface onto itself

We say that a group of motions of the n-E plane contains infinitesimal transformations if there exist motions in the group which differ arbitrarily little from the identity. A discontinuous group of motions, say Γ, certainly contains no infinitesimal transformations. Also the converse of this theorem is true.

An n-E group of motions is discontinuous if and only if it contains no infinitesimal motions.

To prove this we use, as before, the complex coordinate t. In general, a linear transformation T : t → t^* has two fixed points on the t-sphere, τ′ and τ″; then the transformation may be written⁵⁰

the constant μ is called the multiplier of T. If T preserves the open unit disc, then there are two possibilities: (1) either τ′ and τ″ both lie on the circumference of the unit disc, and μ is positive (hyperbolic transformation); or (2) τ′ and τ″ are inverse points relative to the unit circle, and τ′ is interior to the same; then | μ | = 1 (elliptic transformation). In the n-E plane, T is a rotation about τ′, and the real number ϕ, determined to within an additive integer by the equation μ = ex(ϕ), is the angle of rotation of T.

The parabolic transformations insert themselves as the trasnitional case between the hyperbolic and elliptic transformations. A parabolic transformation has only one fixed point, τ′. If it preserves the open unit disc, then it has the form

We base our proof on the following lemma.

Lemma. Let

be two sequences of points, in the n-E plane, which converge to the same point t₀ (| t₀ | < 1). Let T_n be an n-E motion which carries t_n into . If there exists a neighborhood of t₀ which contains no fixed point of any of the motions T_n(n = 1,2,3,…), then T_n converges to the identity.

Let (| | ≤ 1) and be the two fixed points of T_n (they may coincide); then there is a positive number l such that

holds for all n. If I set

then I can assume that

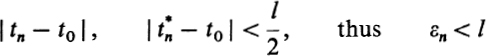
for all n. Then every one of the four differences

is > l. If T_n is not parabolic, then it has the form

If I set t = t_n, and thus t^* = , in here, I get

This yields the estimate

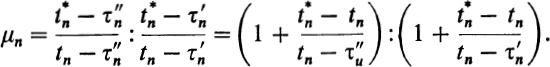
In place of (22.3) I can write

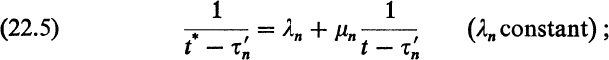
for every linear substitution with the fixed point must be of this form. Also if the transformation T_n is parabolic, I can put it in the form (22.5); in this case μ_n = 1 and (22.4) certainly holds. We get the limit equation

If again we set t = t_n and t^* = now in (22.5), we find

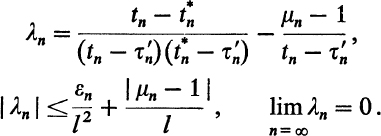
Finally, if we bring (22.5) into its natural form

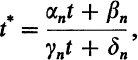
we get the values

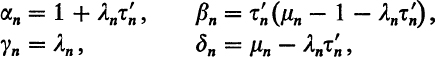
which differ from the corresponding coefficients in the identity substitution

by less than

This completes the proof of the lemma.

Now let Γ^* be an n-E group of motions, without infinitesimal transformations, and let τ be a fixed point in the n-E plane of some rotation belonging to Γ^*. By S_τ I denote all rotations in Γ^* which have the fixed point τ; they form a group in themselves. If I normalize the angles of rotation ϕ of the S_τ by the condition 0 ϕ < 1, then, because of the lack of infinitesimal transformations, there exists one of the S_τ, say , with the smallest angle of rotation ϕ₀ > 0. The angle of rotation of every S_τ is an integral multiple of ϕ₀; for otherwise, by appropriate choice of the integer k, one could generate a transformation S_τ ()^−k with a smaller angle of rotation than . Thus is a “primitive” transformation in the group of the S_τ; all the others are obtained as powers of . If one determines the integer h by the condition

then clearly ()^h+1 has a smaller angle of rotation, (h + 1)ϕ₀ − 1, than , unless hϕ₀ = 1. Therefore ϕ₀ = 1/h must hold, and h is the order of the finite cyclic group (S_τ) which consists of the rotations

The fixed points of the rotations in Γ^* can have no limit point in the finite. If τ (| τ | < 1) were such a limit point and if

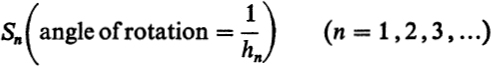
were a sequence of primitive rotations in Γ^*, with distinct fixed points τ_n which converged to τ, then there would be two a priori possibilities.

(1) The orders h_n are bounded for all n. Then there would be infinitely many of the S_n which have the same order h; let them be the transformations . Then is infinitesimal for infinitely large n. Therefore this case is ruled out.

(2) The orders h_n are not bounded. Then one can choose a subsequence of the S_n such that the associated orders tend to ∞ and the angles of rotation tend to zero. But that also would contradict the absence of infinitesimal operations in Γ^*.

Having settled this, we can now show that a system of equivalent points, under Γ^*, can have no limit point in the finite. Suppose that t₀ (| t₀ | < 1) were the limit of a sequence of equivalent points t_n (n = 1, 2, 3, …):

Let S_n be the motion of Γ^* which carries t_n into t_n+1. I pick a neighborhood of t₀ which, with the possible exception of t₀ itself, contains no fixed point of a rotation in Γ^*. By the lemma, the fixed point (| | ≤ 1) of S_n can lie outside of for only finitely many n. Therefore we must have = t₀ for n ≥ n₀; it is no restriction to assume that n₀ = 1. Then all t_n result from t₁ by rotations about t₀, which are contained in Γ^*; but by such rotations I can carry t₁ into only finitely many different positions. Thus the possibility of a limit point is contradicted, and the proof of the theorem stated at the beginning of § 22 is complete.

With this preparation out of the way, we arrive at the real object of this final section of our exposition. We are concerned with the one-to-one conformal maps of a Riemann surface onto itself. These maps form a group; the significance of this group for the theory of the Riemann surface is obviously analogous to that, for example, of the group of motions for metric geometry. Therefore when we formulate the following theorem, due in essence to Klein, we are stating a fact of fundamental importance.

The group of conformal maps of a Riemann surface onto itself is always discontinuous, except for the following seven exceptional cases: = complete sphere, simply or doubly punched sphere, a disc on the sphere [literally, “skull cap on the sphere”], a punched disc (i.e., a disc without its center), a zone on the sphere (between two circles of latitude⁵¹), a closed Riemann surface of genus one.

Proof.⁵² Let denote the universal covering surface over , let t be the cut-circle uniformizing variable which maps conformally onto the open unit disc, and let Γ be the group of n-E motions belonging to the Riemann surface . The cases in which the t-sphere or the infinite t-plane, instead of the unit disc, arises may be ignored; our theorem is obviously invalid in those cases (exceptional cases 1, 2, 3, 7). Let C be a conformal map of onto itself which carries the point into . Let be a point of over , a point of over . Because of the simple connectivity of , there exists a single topological map of onto itself such that:

(1) goes into , and

(2) every point on goes into a point , whose trace point is the image under C of the trace of .

is also conformal, and therefore appears in the t-plane as a linear transformation T, which preserves the open unit disc; also T carries any system of equivalent points under Γ into a system of the same sort. This last fact is expressed by the equation

which states that T and Γ commute; or, for every substitution S in Γ, the “transform” TST⁻¹ also belongs to Γ. Conversely, it is also clear that every linear substitution T that commutes with Γ, and which carries |t| < 1 onto itself, furnishes a conformal map of onto itself. Obviously, the set of motions of the n-E plane which commute with Γ form a group, Γ_c, which contains Γ as a subgroup. The discontinuity of this group Γ_c is to be proved; by the theorem at the beginning of this section, it suffices to demonstrate the absence of infinitesimal operations in Γ_c.

If S and T are any two linear transformations preserving the open unit disc, then the two points which T throws into the fixed points of S are the fixed points of the transformation

If S′ has the same fixed points as S, then either T must carry each of the fixed points of S into itself (that is, if S is not parabolic, T must have the same fixed points as S; if S is parabolic, at least one of the fixed points of T must coincide with the fixed point of S); or T must interchange the two fixed points σ′ and σ″ of the (nonparabolic) transformation S, that is, T must carry σ′ into σ″ and σ″ into σ′. As is clear from (22.2), a parabolic transformation cannot accomplish this last; a nonparabolic T(22.1) can accomplish it only if μ² = 1, μ = − 1, and T is an elliptic transformation with rotation angle . Thus it is possible for S and T to commute

only if

I. both transformations S and T are nonparabolic and have the same fixed points, or

II. both transformations S and T are parabolic and have the same fixed point, or

III. S and T are elliptic transformations with angles of rotation = , or

IV. one of the two transformations, S and T, is the identity.

If Γ consists of only the identity, then is conformally equivalent to the open unit disc, or a disc on the sphere (exceptional case 4).

Now let S be an arbitrary substitution in Γ, distinct from the identity. Assume that, contrary to our claim, there is a sequence of operations T_n ≠ 1 in in Γ_c, such that T_n converges to the identity. Then both and would be elements of Γ. Along with T_n, the last of these operations converges to the identity as n tends to infinity. But since Γ contains no infinitesimal transformations, it must be that

holds for n ≥ n₀; that is, S and T_n commute. We have listed four cases in which this is possible, but since S is not elliptic, only cases I and II remain in question. If we apply this result to all possible operations S ≠ 1 of the group Γ, we find that only two possibilities remain open:

I. All operations in Γ are hyperbolic and have the same two fixed points, which one may assume are + i and − i.

II. All operations in Γ are parabolic and have the same fixed point, which we may take to be + i.

(CASE I). The map

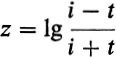
carries the open unit disc in the t-plane onto the parallel strip − π/2 < y < + π/2 in the z = (x + iy)-plane; Γ goes into a group of translations parallel to the x-axis ; that is, Γ takes the form

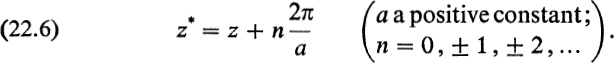
Then

maps one-to-one onto the annulus

and by stereographic projection this may be turned into a zone on the sphere with the equator for its mid-line (exceptional case 6).

(CASE II.) The map

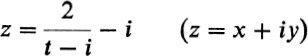
carries the open unit disc in the t-plane into the upper half-plane y > 0, and Γ into a group of translations parallel to the x-axis. So again Γ has the form (22.6) and w = e^iaz carries onto the punched unit disc in the w-plane:

With this our principal theorem is completely proved; at the same time we have had the opportunity to observe the applicability of the normal form of the Riemann surface through an important example. It is trivial that in each of the seven excluded cases there is a continuous group of conformal maps of the surface onto itself. It is also easy to describe these groups completely.

A closed Riemann surface of genus p > 1 admits only a finite number of conformal maps onto itself.⁵³ For a system of equivalent points under this group can have no limit point on the closed surface, and therefore contains only a finite number of points.

---

¹)See Weierstrass, Werke, 2, 49–54, ϋber das sog. Dirichletsche Prinzip (1870).

²) H. A. Schwarz: ϋber einen Grenzübergang durch alternierendes Verfahren, Gesammelte Abh., Vol. II, 133–143; ϋber die Integration der partiellen Differential-gleichung Δu = 0 unter vorgeschriebenen Grenz-und Unstetigkeits-Bedingungen, ibid., 144–171; Zur Integration der partiellen Differentialgleichung Δu = 0, ibid., 175–210. C. Neumann: Ber. Sächs. Akad. d. Wiss. Leipzig, 1870; Vorlesungen über Riemann’s Theorie der Abelschen Integrate, 2nd edition, Leipzig 1884, 388–471. Among the more recent literature I mention in particular the following two works of C. Carathéodory: Elementarer Beweis für den Fundamentalsatz der konformen Abbildung, in the Festschrift zum 50jährigen Doktorjubiläum von H. A. Schwarz, Berlin 1914, 19–41; Conformal Representation, Cambridge Tracts in Math., 28, 1932.

³)See the two papers, ϋber das Dirichletsche Prinzip, in Hilbert’s Gesammelte Abh., 3, Berlin 1935,10–14 and 15–37; and also his paper, Zur Theorie der konformen Abbildung, ibid., 73–80. The second was originally published in the Festschrift zur Feier des 150jährigen Bestehens der Gesellschaft der Wissenschaftenzu Göttingen, 1901, and was reprinted in Math. Ann., 59 (1904). The other two originated in 1905 and 1909.

⁴)I cite here particularly the following early works which appeared before the first edition of this book: B. Levi, Sulprincipio di Dirichlet, Rend. Circ. Mat. Palermo,22 (1906) 293–360; G. Fubini, II principio di minimo e i teoremi di esistenza per i problemi al contorno relativi alle equazione alle derivate parziali di ordini pari, ibid.,23 (1907) 58–84; H. Lebesgue, Sur le probleme de Dirichlet, ibid., 24 (1907) 371–402; S. Zaremba, Sur le principe du minimum, Bull, de l’Ac. des sciences de Cracovie, July 1909, 206fF; R. Courant, ϋber die Methode des Dirichletschen Prinzips, Math. Ann., 72 (1912) 517–550. What I give here, essentially unchanged, is the proof that I developed in 1913 on the basis of the work of Hilbert, B. Levi, and Zaremba; the attack is simpler than that of Riemann and Hilbert. The proof incorporates the modifications which are the natural consequence of Dieudonne’s improved method of surface integration. Since that time a rich literature on the subject has accumulated. Through Courant, among others, the “direct methods of the calculus of variations” has come to be a familiar term in analysis. For a comprehensive presentation we refer to Courant’s book on the Dirichlet principle, already mentioned in the preface.

⁵)Gesammelte Abhandlungen, 2, 186–198.

⁶)J. Hadamard, Sur le principe de Dirichlet, Bull. Soc. math. France, 34 (1906) 135–139. S. Zaremba, loc. cit., 206ff.

⁷) The Schwarz inequality gives

    where . The rest follows from the Bessel inequality corresponding to the annulus (q, 1):

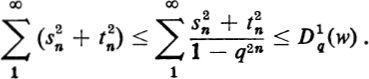
⁸)The presentation in Klein’s monograph of 1882, already cited, is based on these and similar physical considerations. The diagrams of streams in that monograph are very instructive.

⁹)Sul principio di Dirichlet, Rend. Circ. Mat. Palermo, 22 (1908) 293–360, §7. For the method under discussion see H. Weyl, The method of orthogonal projection in potential theory, Duke Math. Jour., 7 (1940) 411–444.

¹⁰)Let it be permitted here that we use the bar to mean something other than the passage from a complex number to its conjugate.

¹¹)Our proof is closely related to that given by Zaremba in his paper cited above.

¹²) The “shrunken block” terminology was introduced in §10: B^θ(): |x | ≤ θb, | y | ≤ θb.

¹³) It would have been quite possible, and might have even meant a simplification, to consider only Riemann surfaces and harmonic and Abelian differentials. Then h would have been introduced as the number of linearly independent everywhere regular harmonic differentials. Instead, we subsumed Riemann surfaces under smooth oriented surfaces. I make this remark with regard to the tendency in the literature, sometimes explicit, to construct the theory of Riemann surfaces “without topology.” For example, see L. Bieberbach, Über die Einordnung des Hauptsatzes der Uniformisierung in die Weierstrasssche Funktionentheorie, Math. Ann., 78 (1918) 312–331. I can see neither difficulties nor any particular profit in this.

¹⁴) Earlier it was customary to derive these symmetry laws (following Riemann and C. Neumann) by integrating around the boundary of the canonically cut surface. Our normalization of the elementary integrals renders this dissection superfluous. I regard this as an essential improvement of the method.

¹⁵) See Riemann, Theorie der Abelschen Funktionen, Werke (2nd edition), p. 140, and especially Appell, Journal de mathematiques, 3. ser., 9 (1883), and Acta Mathematica, 13 (1890).

¹⁶) This terminology comes from the arithmetic theory of algebraic functions of Hensel and Landsberg; see Hensel and Landsberg, Theorie der algebraischen Funktionen einer Variablen, Leipzig, 1902.

¹⁷) Riemann considered only the so-called “general” case (R = p in our notation). The complete result for integral divisors is due to G. Roch, Jour. f. Math., 64 (1865) 372–376. Fractional divisors were considered by Klein (Riemannsche Flächen I, autograph lectures, Göttingen 1892, pp. 110–111), E. Ritter, Math. Ann., 44 (1894) 314, and Hensel and Landsberg loc. cit., pp. 362–364.

¹⁸) Compare the references to Klein and Hensel-Landsberg in the preceding footnote. E. Ritter, loc. cit., argues as follows. If f₀ = ′/ is one function which is a multiple of 1/ (′ integral), then I obtain all such functions f as follows: f = f₀f′, f′ a multiple of 1/′, and thus I come back to the case of an integral divisor ′. But here the proof that [if B + (m + 1 − p) > 0] an f₀ exists is lacking.

¹⁹) The last method is also available on open Riemann surfaces and yields here immediately the proof that there exist functions on the surface which are not constant.

²⁰) A. Brill and M. Noether, Math. Ann., 7 (1874) 283.

²¹) K. Weierstrass, Mathematische Werke, Vol. 4, Vorlesungen über die Theorie der Abelschen Transzendenten, Berlin, 1902, pp. 224–225.

²²) Riemann, Theorie der Abelschen Funktionen, Jour. f. Math., 54 (1857) = Werke, 2nd ed., pp. 88–142; Über das Verschwinden der Theta-Funktionen, Jour. f. Math., 65 (1865) = Werke, pp. 212–224. Weierstrass, Vorlesungen über die Theorie der Abelschen Transzendenten, Werke Vol. 4. Stahl, Theorie der Abelschen Funktionen Leipzig 1896. H. F. Baker, Abel's theorem and the allied theory, including the theory of theta functions, Cambridge 1897. Prym and Rost, Theorie der Prymschen Funktionen erster Ordnung, Leipzig 1911, 2. Teil, 7. Abschnitt. Krazer, Lehrbuch der Thetafunktionen, Leipzig 1903.

    The significance principal of the inversion problem to us today lies primarily, not in its intrinsic value, but in the splendid developments created by Riemann and Weierstrass in their efforts to solve the problem.

²³) Jour. f. Math., 70 (1869) 354–362; 71 (1870) 223–236, and 305–315. See the work of Appell cited on page 133, and also the following. Prym and Rost, Theorie der Prymschen Funktionen erster Ordnung, Leipzig 1911; R. König, Zur arithmethischen Theorie der auf einem algebraischen Gebilde existierenden Funktionen, Ber. d. Verh. Sächs. Ges. Wiss. Leipzig, math.-phys. Kl., 63 (1911) 348–368; O. Haupt, Zur Theorie der Prymschen Funktionen, Math. Ann., 77 (1915) 24–64.

²⁴) First formulated by E. Ritter, Math. Ann., 44, p. 314. (See also the footnote on page. 137). Instead of the symbolism of divisors, Ritter uses the theory of forms on Riemann surfaces, founded by Klein, which makes possible a real representation of divisors with the aid of multiplicative forms. In Math. Ann., 47 (1896) 157–221, aided by the basic theorems introduced into the theory of linear differential equations by Riemann, he generalizes his investigations to systems of n forms which transform in a homogeneous linear way under the influence of a cover transformation S.

²⁵) In case p = 1, X is not present (p. 143); in case p = 2, X consists of a single character system _s⁰.

²⁶) Abel’s theorem [developed in splendid simplicity in the short note, Démonstration d’une propriété générate d’une certaine classe de fonctions transcendentes, Jour. f. Math., 4 (1829) 200–201 = Œuvres complètes, nouvelle édition (1881), 1, pp. 515–517] is more general, in that it concerns not only integrals of the first kind. A paper of Abel, Mémoire sur une propriété générate d’une classe très-étendue de fonctions transcendentes, on this subject, which he submitted to the Paris Academy in 1826, was lost for a long time because of Cauchy’s carelessness; it was first published after Abel’s death: Mémoires présentés par divers savants, 7 (1841) = Abel, Œuvres completes, nouvelle édition (1881), 1. pp. 145–241. Furthermore, the theorem is contained in the manuscript left by Abel, Sur la comparaison des fonctions transcendentes, Œuvres complètes, 2, pp. 55–66. The converse of Abel’s theorem for integrals of the first kind may be read between the lines in Riemann; it was first stated explicitly (without completely adequate proof) by Clebsch, Jour. f. Math., 63 (1864) 198; Clebsch used it for all it was worth in the theory of algebraic curves.

²⁷) See Weierstrass, Werke, 4, pp. 451–456.

²⁸) See the fourth chapter in Krazer, Lehrbuch der Thetafunktionen, Leipzig 1903, where references to the other literature may be found.

²⁹) The z-plane with finitely many points deleted becomes a simply connected surface if one draws linear cuts from these points to infinity. Riemann’s monodromy problem is concerned with a far-reaching generalization of algebraic functions (the meromorphic functions on an n-sheeted Riemann surface over the z-sphere). It asks for a system of n functions analytic in the slit plane, and the functions are to be related across the slits by given linear substitutions. (A side condition ruling out essential singularities must be added.) Hilbert, Grundzüge einer allgemeinen Theorie der Integralgleichungen, Leipzig 1912, 81–108 and S. J. Plemelj, Riemannsche Funktionenscharen mit gegebener Monodromiegruppe, Monatsh. f. Math. u. Physik, Jahrg., 19, 211–245, demonstrated the solvability of the monodromy problem. Then Robert König developed a complete theory of these “Riemann transcendentals,” including the exact analog of the reciprocity laws of § 16. See in particular the following works of König: Die Reduktions- und Reziprozitäts-Theoreme bei den Riemannschen Transzendenten, Math. Ann., 79 (1918) 76–135 (where one also finds his earlier work developed); Die Integrate der Riemannschen Transzendenten, Math. Ann., 80 (1919) 1–28; Die Elementartheoreme bei den Riemannschen Transzendenten, Math. Zeit., 15 (1922) 26–65. See also, R. König and M. Kraft, Über Reihenentwicklung analytischer Funktionen, Jour. f. Math., 154 (1935) 154–173; ibid., Über Primfunktionen, Jour. f. Math., 165 (1931) 96–107. On this foundation is based the work of H. Schmidt, Über multiplikative Funktionen und die daraus entspringenden Differentialsysteme, Math. Ann., 105 (1931) 325–380, and, in most recent times, H. Röhrl, Differentialsysteme, welche aus multiplikativen Klassen mit exponentiellen Singularitaten entspringen, I, Math. Ann., 123 (1951) 53–75; II, ibid., 124 (1952) 187–218; III, ibid., 125 (1953) 448–466. Further: Funktionenklassen auf geschlossenen Riemannschen Flächen, Math. Nachr., 6 (1952) 355–384; Die Elementartheoreme der Funktionenklassen auf geschlossenen Riemannschen Flächen, ibid., 7 (1952) 65–84; Über gewisse Verallgemeinerungen der Abelschen Integrate, ibid., 9 (1953) 23–44.

³⁰) Prym espoused this point of view in his work from 1869 on; here the work of Dedekind, cited on page 33, on elliptic modular functions, from the year 1877, is pertinent.

³¹) See the author’s article, Topologie und abstrakte Algebra als zwei Wege mathematischen Verständnisses, in Unterrichtsblätter f. Math. u. Naturwiss., 38 (1932) 177–188.

    The sketch of the theory of algebraic functions, which we could give here, is very incomplete. From the older literature, which preceded the development of modem abstract algebra, I mention here, besides the works of Riemann, Weierstrass, F. Klein, C. Neumann, H. F. Baker, and Hensel-Landsberg already cited, the following presentations: Clebsch and Gordan, Theorie der Abelschen Funktionen, Leipzig 1866; A Brill and M. Noether, Über die algebraischen Funktionen und ihre Anwendung in der Geometrie, Math. Ann., 7 (1874) 269–310; Brill and Noether, Die Entwicklung der Theorie der algebraischen Funktionen, Bericht der DMV, 3, Berlin 1894; F. Severi, Lezione di Geometria algebrica, Padova 1908 (as representative of the very fruitful Italian school of algebraic geometers). In all of these works the curve-theoretic point of view predominates. A trail-blazing and classical work for the algebraic-arithmetic foundations of the theory is: R. Dedekind and H. Weber, Theorie der algebraischen Funktionen einer Veränderlichen, Jour. f. Math., 92 (1882) 181–290, (also contained in H. Weber, Algebra, v. Ill, 2nd edition, Braunschweig 1908, p. 623ff.). Also, F. Klein, Riemannsche Flächen I, II, autograph lectures, Göttingen 1892/93. Appell et Goursat, Theorie des fonctions algébriques, Paris 1895. H. F. Baker, Analytic principles of the theory of curves, Cambridge 1933. The first steps in the domain of algebraic functions with arbitrary fields of constants (including those with prime characteristic) were due to H. Hasse, Theorie der Differentiate in algebraischen Funktionenkörpern mit vollkommenem Konstantenkörper, Jour. f. Math., 172 (1943) 55–64, F. K. Schmidt, Zur arith-metischen Theorie der algebraischen Funktionen, I, Math. Zeit., 41 (1936) 415, and André Weil, Zur algebraischen Theorie der algebraischen Funktionen, Jour. f. Math., 179 (1938) 129–133. A modern overall presentation is that of Claude Chevalley, Introduction to the theory of algebraic functions of one variable, Math. Surveys No. 6, Am. Math. Soc., New York 1951.

³²) For Poincaré, see, besides the numerous notes in the Comptes Rendus for the years 1881/82, the papers in the Acta Mathematica, Vols. 1, 3, 4, 5 (1882/84). For Klein, see the papers in Math. Ann., Vols. 19, 20, 21 (1882/83), and also the inclusive presentation: Fricke and Klein, Vorlesungen über die Theorie der automorphen Funktionen, Leipzig 1897 to 1912.

³³) H. Poincaré, Sur l’uniformisation des fonctions analytiques, Acta Math., 31 (1907) 1-63. P. Koebe, ϋber die Uniformisierung beliebiger analytischer Kurven. Nachr. d. Ges. Wiss. Göttingen, from 1907 on.

³⁴) I give here the titles and places of publication of the larger series of his works; these were frequently announced in shorter notes in the Nachrichten der Gesellschaft der Wissenschaften zu Göttingen and the Sitzungsberichte der Sächsischen Akademie der Wissenschaften zu Leipzig.

    (a) ϋber die Uniformisierung der algebraischen Kurven, I, II, III (first proof of the general fundamental theorem of Klein, the iteration procedure), IV (second existence proof for the general canonical uniformizing variable: method of continuity), Math. Ann., 67 (1909) 145–224 ; 69 (1910) 1–81; 72 (1912) 437–516; 75 (1914) 42-129.

    (b) ϋber die Uniformisierung beliebiger analytischer Kurven, I. Teil: Das allgemeine Uniformisierungsprinzip; II Teil: Die zentralen Uniformisierungsprobleme, Jour. f. Math., 138 (1910) 192–253, and 139 (1911) 251–292.

    (c) Abhandlungen zur Theorie der konformen Abbildung. I. Die Kreisabbildung des allgemeinsten einfach und zweifach zusammenhängenden schlichten Bereichs und die Ränder Zuordnung bei konformer Abbildung, Jour. f. Math., 145 (1915) 177–223. II. Die Fundamentalabbildung beliebiger mehrfach zusammenhängender schlichter Bereiche nebst einer Anwendung auf die Bestimmung algebraischer Funktionen zu gegebener Riemannscher Fläche, Acta Math., 40 (1916) 251-290. III. Der allgemeine Fundamentalsatz der konformen Abbildung nebst einer Anwendung auf die konforme Abbildung der Oberfläche einer körperlichen Ecke, Jour. f. Math., 147 (1917) 67-104. IV. Abbildung mehrfach zusammenhängender schlichter Bereiche auf Schlitzbereiche, Acta Math., 41 (1918) 305-344. V. Fortsetzung, Math. Zeit., 2 (1918) 198-236. VI. Abbildung mehrfach zusammenhängender Bereiche auf Kreisbereiche. Uniformisierung hyperelliptischer Kurven, Math. Zeit., 7 (1920) 235-301.

    (d) Riemannsche Mannigfaltigkeiten und nichteuklidische Raumformen, acht Mitteilungen; Sitzber. Akad. Berlin, 1927, 164–196; 1928, 345–384 and 385–442; 1929, 414–457; 1930, 304–364 and 505–541; 1931, 506–534; 1932, 249–284. Also the prize winning monograph of 1920, first published in Acta Math., 50 (1927) 27–157, Allgemeine Theorie der Riemannschen Mannigfaltigkeiten.

    See also Koebe’s survey lectures: ϋber ein allgemeines Uniformisierungsprinzip, Int. Math. Cong. Rome, Atti (1909) 25–30; Referat über automorphe Funktionen und Uniformisierung, Jahresber. DMV 21 (1912) 157-163; Methodender konformen Abbildung und Uniformisierung, Math. Congr. Bologna, Atti, 3 (1928) 195–203.

    Of the more recent literature, the following should be noted especially: B. L. van der Waerden, Topologie und Uniformisierung der Riemannschen Flächen, Ber. Sächs. Ak. Wiss. Leipzig, math.-phys. Kl., 93 (1941) 147–160; and R. Nevanlinna’s book, Uniformisierung, Berlin 1953.

³⁵) Zur Theorie der konformen Abbildung, Nachr. Ges. Wiss. Göttingen, 1909, 314–323.

³⁶) ϋber die Hilbertsche Uniformisierungsmethode, Nachr. Ges. Wiss. Göttingen, 1910, 61–65.

³⁷) All the required conditions are satisfied if we use the function

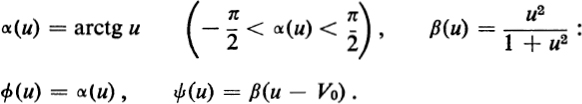
³⁸) All the demands are satisfied by [see footnote 37] :

³⁹) See particularly P. Koebe, ϋber die Uniformisierung beliebiger analytischer Kurven, erster Teil; Das Allgemeine Uniformisierungsprinzip, Jour. f. Math., 138 (1910) 192–253.

⁴⁰) H. A. Schwarz, Gesammelte Abhandlungen, Vol. II, pp. 109-111. The application of this lemma to our problem goes back to Poincare, Acta Math., 4 (1884) 23–232.

⁴¹)That the three cases listed exhaust the possibilities follows from the process of the adaptation of a (two-dimensional) number lattice relative to a sublattice. See page 89 of this book or G. Kowalewski, Die komplexen Veränderlichen und ihre Funktionen, Leipzig 1911, pp. 57 f.

⁴²)The model of the plane non-Euclidean geometry which presents itself here is intimately related to the model, discovered by Klein in the year 1871, which is based on Cayley’s metric. Klein, Über die sogenannte Nicht-Euklidische Geometrie, Math. Ann., 4 (1871) 573-625. See also Fricke and Klein, Vorlesungen über die Theorie der automorphen Funktionen, Vol. I, Leipzig 1897, pp. 3-59. The book of Bonola gives a good orientation on non-Euclidean geometry: Non-Euclidean geometry: a critical and historical study of its developments, English translation by H. S. Carslaw, Dover Pubs., 1955 (originally published 1911)

⁴³)See the final remarks in Koebe’s first communication Über die Uniformisierung beliebiger analytischer Kurven, Göttinger Nachrichten, 1907, 209–210.

⁴⁴) n-E = non-Euclidean

⁴⁵) The word “distance,” and all other geometric expressions, are to be understood, until further notice, in the n-E sense.

⁴⁶) Besides the normal polygons, also the “canonical polygons,” whose theory was developed by Fricke (Fricke-Klein, Vorlesungen über die Theorie der automorphen Funktionen, Leipzig, 1897–1912) are of great importance. With their aid, Fricke succeeded in formulating and proving rigorously the theorem which had already been stated by Riemann: the Riemann surfaces of genus p ( >1) form a (6p ‒ 6)-dimensional manifold. These matters are intimately connected with the “method of continuity,” by means of which Klein and Poincaré attempted to prove, simultaneously at the beginning of the 1880’s, the uniformizibility of algebraic forms. See in particular P. Koebe, Math. Ann., 75 (1914) 42–129.

⁴⁷) Poincaré, Mémoire sur les fonctions fuchsiennes, Acta Math., 1 (1882) 207.

⁴⁸) For a brief formulation of this proof see H. Petersson: Abh. Math. Sem. Univ. Hamburg, 16 (1948) 127–130; and, in more detail, Über den Bereich absoluter Konvergenz der Poincaréschen Reihen, Acta Math., 80 (1948) 23–63. See also: Über die Transformationsfaktoren der relativen Invarianten linearer Substitutionsgruppen, Monatsh. f. Math., 53 (1949) 17’41.

⁴⁹) Automorphe Formen als metrische Invarianten, Vols. I and II, Math. Nachr., 1 (1948) 158–212 and 218–257; Über Weierstrass-Punkte und die expliziten Darstellungen der automorphen Formen von reeller Dimension, Math. Zeit., 52 (1949) 32–59.

⁵⁰) If τ″ = ∞, this becomes

⁵¹) These constitute according to the breadth of the zone, infinitely many essentially differenr Riemann surfaces.

⁵²) This is Poincaré’s proof: Acta Math. 7 (1885) 16–19. To be sure, Poincaré considers only closed Riemann surfaces; but his proof, word for word, remains valid for open surfaces.

⁵³) For this more special theorem, first stated by H. A. Schwarz, there exist other more algebraic proofs. One of Weierstrass (1875), which was first published in 1895 (Werke, Vol. II, pp. 235–244) ; one of M. Noether (Math. Ann., 20, pp. 59–62 and 21, pp. 138–140; 1882); and one of A. Hurwitz, Math. Ann., 41 (1893) 403–411.